摘要:为提高单一混沌系统图像加密的安全性, 本文提出了基于深度学习的图像加密算法. 首先, 利用超混沌Lorenz系统产生混沌序列. 其次, 利用长短期记忆人工神经网络(long-short term memory, LSTM)复杂的网络结构模拟混沌特征构造新的混沌信号. 然后, 利用最大Lyapunov指数, 0-1测试, 功率谱分析、相图以及NIST测试对新信号的动力学特征进行分析. 最后, 将新信号应用到图像加密中. 由于该方法生成的新信号不同于原有混沌信号, 而且加密系统具有很高的复杂结构和非线性特征, 故很难被攻击者攻击. 仿真实验结果表明, 本文提出的图像加密算法相比其他一些传统方法具有更高的安全性, 能够抵抗常见的攻击方式.
关键词: 混沌系统/
图像加密/
深度学习

English Abstract

全文HTML

--> --> -->

近年来, 随着互联网快速的发展, 通过网络进行信息传输越来越频繁, 由于攻击者可以截取信息或者改变信息的数据, 从而达到破坏数据传输的目的, 对信息的传输带来了巨大的威胁. 图像作为信息传递的主要载体, 找到一种实用的图像加密算法是很重要的^[1-4]. 为了提高图像传输过程中的安全性, 研究人员提出了很多传输方案^[5,6]. 随着混沌理论的发展, 研究表明混沌系统具有复杂的动力学行为和初值敏感性等特征^[7-10], 使得其在图像加密中有很好的效果^[11-13]. 因此研究人员结合混沌理论提出了越来越多的混沌图像加密算法^[14-35].
混沌信号是混沌图像加密的核心, 一个具有复杂动力学行为的混沌信号对图像加密有很好的效果, 混沌信号主要由以下主要由以下2种混沌系统产生. 第1种是低维混沌系统, 如Logistic映射和Tent映射^[36,37]. 该系统结构简单, 运行快, 易于硬件实现, 但是该系统容易退化且密钥空间较小. 第2种是高维混沌系统, 该系统具有较复杂的行为和更多的参数, 并且具有很强的抗退化能力^[38], 例如Wang系统, Lorenz系统和Chen系统等. 此外, 在时间和空间方向上均具有混沌行为的时空混沌也是高维混沌系统, 如耦合映像格子系统(coupled map lattice, CML)^[39], 随机连接耦合格子时空混沌系统^[40], 线性与非线性混合耦合时空混沌系统(mixed linear-nonlinear coupled map lattice, MLNCML)^[41].
为了更好地把混沌信号应用到图像加密中, 近年来, 很多****对此进行了研究, 产生了很多基于混沌系统的图像加密算法. 一类是基于非AI技术的混沌图像加密算法, 如Yasser等^[13]提出了一种基于混合混沌系统的图像加密算法; 石航和王丽丹^[42]提出了一种基于压缩感知和多维混沌系统的多过程图像加密方案; 庄志本等^[43]提出了基于新的五维多环多翼超混沌系统的图像加密算法; Zhang和Wei^[44]结合Lorenz系统和DNA计算提出的彩色图像加密算法; Zhang和Wang^[45]结合线性与非线性混合耦合时空混沌系统(MLNCML)提出的对称图像加密算法等. 另一类是基于AI技术的混沌图像加密算法, 如陈炜等^[46]利用BCNN模型对图像进行压缩, 再利用混沌系统对图像进行加密; He等^[47]使用了LSTM的网络结构对图像进行置乱和扩散也取得了不错的效果; 葛钊成和胡汉平^[48]的研究成果表明神经网络在图像加密中已有一定的积累, 并展现出比传统技术更好的应用效果. 虽然这方面的研究成果并不是很多, 但是为混沌密码学开辟了新的思路.
近年来, 随着深度学习技术和硬件条件的提高, 已经有研究人员将深度学习算法运用到混沌时间序列的预测中, 如熊有成和赵鸿^[49]用LSTM搭配合适的组合策略, 验证了低维情况下LSTM预测混沌时间序列能取得较好效果; Sangiorgio等^[50]进一步验证了使用LSTM预测混沌时间序列不仅能取得较好效果, 还可以获得不错的鲁棒性; 黄伟建等^[51]结合混沌系统相空间重构理论, 提出了一种基于深度学习算法的混沌时间序列混合预测模型(Att-CNN-LSTM). 因为深度学习具有较复杂的结构, 它预测生成的新混沌信号与原有混沌信号相比有一定差异, 且具有良好的混沌特性, 所以能够应用在图像加密中. 为了提高单一混沌系统的安全性, 本文提出了一种基于深度学习的混沌图像加密算法. 首先通过深度学习产生新的混沌信号, 然后将其用在图像加密中. 由于深度学习的参数具有敏感性, 故其可以作为加密算法的密钥, 整个加密算法的密钥空间相对传统的混沌系统图像加密算法更大, 增大了穷举攻击的难度, 通过统计分析及与文献的对比可知, 本文具有较高的安全性. 本文首先介绍所提方法使用的混沌系统及神经网络, 接着提出加密算法, 最后进行仿真实验及安全性能分析.

利用深度学习生成新混沌信号用来进行图像加密, 由于新的混沌信号可以基于任意混沌系统(如Logistic映射, Lorenz系统, Chen系统等), 因此选择其中一种混沌系统来说明本文的方法. 接下来, 介绍所提出的加密算法中用到的混沌系统及LSTM神经网络.
2

-->

2.1.混沌系统

由于超混沌系统有多个正的Lyapunov指数, 相对于一般混沌系统具有较强的抗退化的能力, 系统的动态行为更加难以预测, 因此在保密通信方面比一般的混沌系统具有更高的使用价值^[52]. 由于篇幅原因, 本文选择超混沌Lorenz系统来实现本文的方法, 超混沌Lorenz系统可表示为如下方程:

$ \left\{ \begin{aligned}&\dot x = a(y - x) + w, \hfill \\&\dot y = cx - y - xz, \hfill \\&\dot z = xy - bz, \hfill \\&\dot w = - yz + rw, \hfill \\ \end{aligned} \right. $

其中, a, b, c和r为超混沌Lorenz系统的参数. 当a = 10, b = 8/3, c = 28, –1.52＜r＜–0.06时, 该系统呈现超混沌态, 如图1所示, 当r = –1时, (1)式具有4个Lyapunov指数, $ {\lambda _1} = 0.3381 $, ${\lambda _2} = $$ 0.1586$, $ {\lambda _3} = 0 $, ${\lambda _4}{\rm{\; = - 15}}{\rm{.1752}}$.
图 1 超混沌Lorenz相图三维投影
Figure1. Three dimensional projection of hyperchaotic Lorenz phase diagram.

2 -->

2.2.LSTM神经网络

长短期记忆人工神经网络(long-short term memory, LSTM)是一种时间递归的神经网络(RNN)^[53]. 在实际的应用中, RNN容易受梯度消失或梯度爆炸的影响, 难以捕获到序列之间的长期依赖, 使得训练异常困难. 所以为了解决RNN梯度消失的问题, LSTM被提出并广泛被使用. 本文选择LSTM神经网络来实现本文的方法.
LSTM的结构有很多种形式, 但是都有类似的结构(如图2所示), 主要都包含输入门、输出门、遗忘门. LSTM单元的计算公式如下:
图 2 LSTM训练模型示意
Figure2. LSTM training model diagram.

$ {I_t} = \sigma \left( {{X_t}{W_{xi}} + {H_{t - 1}}{W_{hi}} + {b_i}} \right) , $

$ {F_t} = \sigma \left( {{X_t}{W_{xf}} + {H_{t - 1}}{W_{hf}} + {b_f}} \right) {\rm{, }} $

$ {O_t} = \sigma \left( {{X_t}{W_{xo}} + {H_{t - 1}}{W_{ho}} + {b_o}} \right) {\rm{, }} $

$ {\tilde C_t} = \tanh \left( {{X_t}{W_{xc}} + {H_{t - 1}}{W_{hc}} + {b_c}} \right) {\rm{, }} $

$ {C_t} = {F_t}{C_{t - 1}} + {I_t}{\tilde C_t} {\rm{, }} $

$ {H_t} = {O_t}\tanh \left( {{C_t}} \right) {\rm{, }} $

其中, $ {I_t} $是输入门, $ {F_t} $是遗忘门, $ {O_t} $是输出门. $ {X_t} $是时间步t的输入, $ {H_t} $是隐藏状态, $ {C_t} $是记忆细胞, FC代表全连接层. 训练模型示意如图2所示.

本文提出的加密算法是一个扩散到置乱再到扩散的过程. 该加密算法主要步骤如图3和图4所示, 设明文图像记为P, 其大小为$ M \times N $, 灰度等级为$ 256 $.
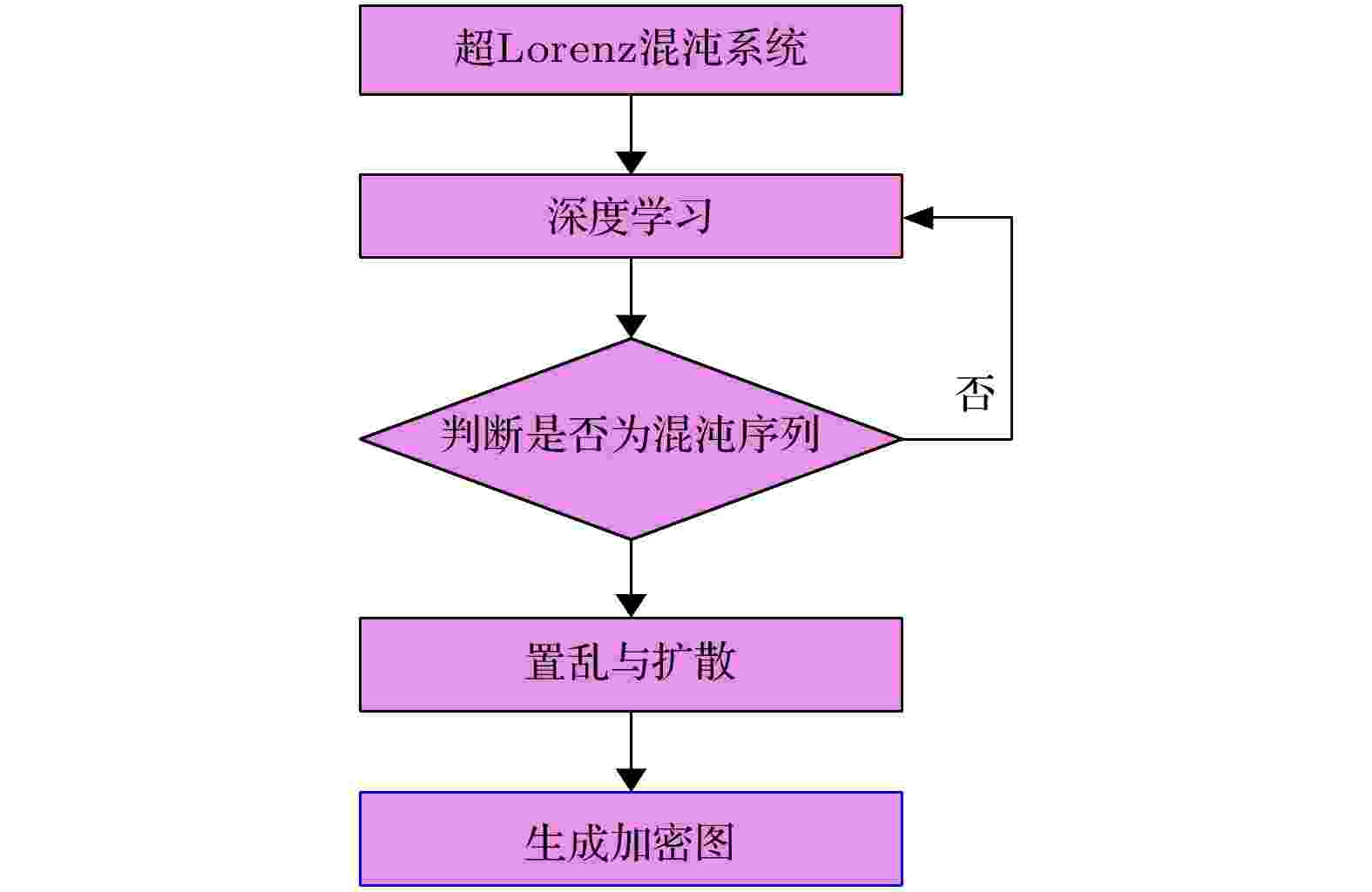图 3 混沌图像加密算法流程图(I)
Figure3. Chaotic image encryption flow chart algorithm (I).

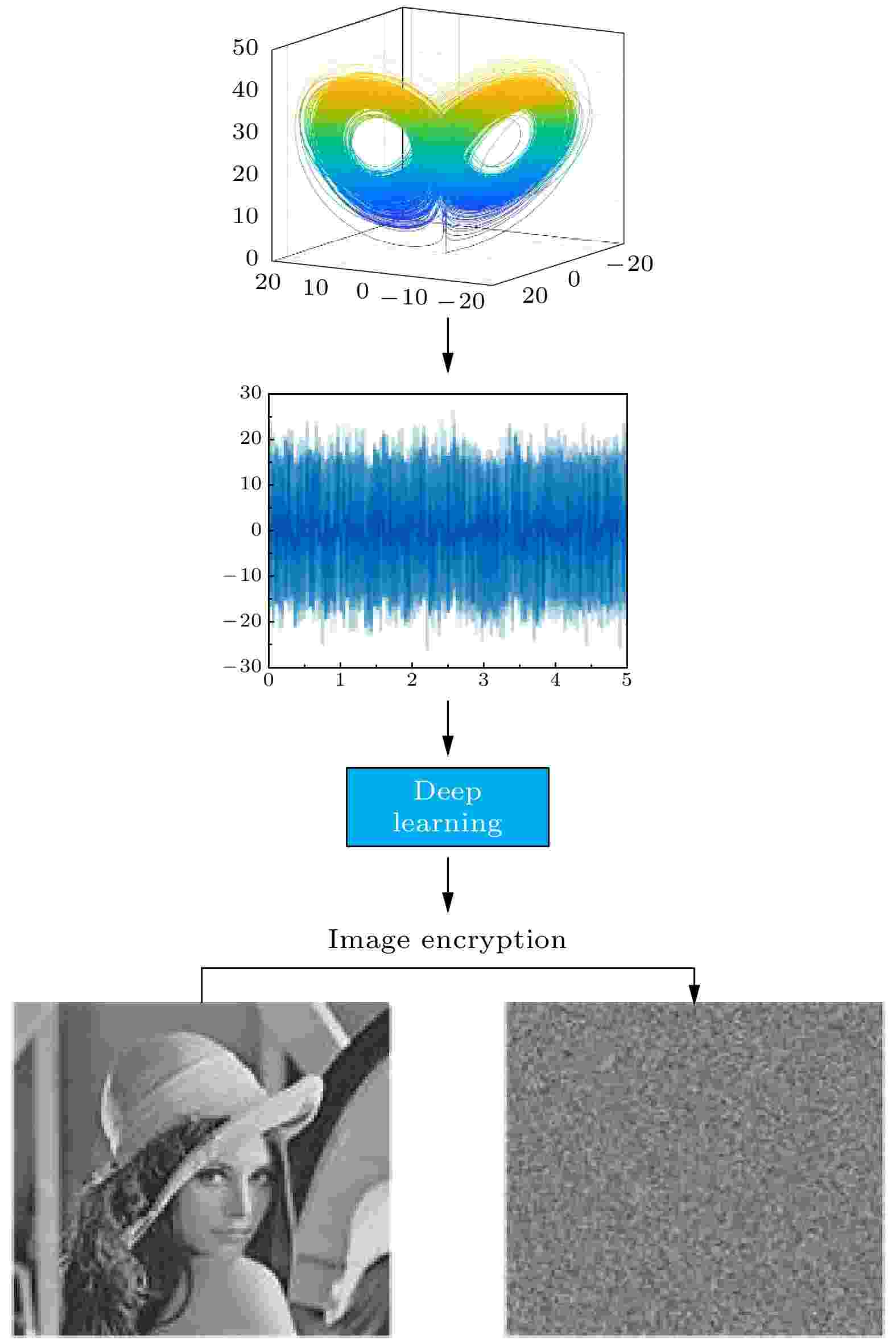图 4 混沌图像加密算法流程图(Ⅱ)
Figure4. Chaotic image encryption flow chart algorithm (Ⅱ).

1) 设置混沌系统的参数以及初值并产生混沌信号. 密钥$ K = \left\{ {{x_0}, {y_0}, {z_0}, {w_0}, {r_1}, {r_2}} \right\} $, 其中$\left\{ {x_0}, {y_0}, $$ {z_0}, {w_0} \right\}$为状态初值, $ {r_1}, {r_2} $是取值范围为$ \left[0, 255\right] $的整数随机数.
2) 设置深度学习的参数并产生新的混沌信号. 借助超混沌Lorenz系统产生4个伪随机信号, 依次记为$ X, Y, Z, W $, 其大小均为$ M \times N $, 具体步骤如下.
Step 1　使用密钥K中的$ \left\{ {{x_0}, {y_0}, {z_0}, {w_0}} \right\} $作为超混沌Lorenz系统的迭代初始值, 使用ode45函数迭代超混沌Lorenz系统, 得到4个伪随机序列, 依次记为$ \left\{ {{x_i}} \right\} $, $ \left\{ {{y_i}} \right\} $, $ \left\{ {{z_i}} \right\} $, $ \left\{ {{w_i}} \right\} $, $i = 1, 2, \cdots , $$ MN$;
Step 2　将伪随机序列$ \left\{ {{y_i}} \right\} $截取长度为s的部分序列用LSTM网络深度学习, 训练数据的比例是p, 初始学习率为q, 学习率下降因子为u, 隐藏节点数为o, 截取训练的序列长度为s. 得到预测后新的序列$ \left\{ {y'_i},i = 1, 2, \cdots , MN \right\} $;
Step 3　对$\left\{ {y'_i} \right\}$进行混沌特性判断, 如果$\left\{ {y'_i} \right\}$为混沌序列, 则进入Step 4; 否则重新设置参数, 返回Step2;
Step 4　借助于下列公式将序列$ \left\{ {{x_i}} \right\} $, $\left\{ {y'_i} \right\}$, $ \left\{ {{z_i}} \right\} $和$ \left\{ {{w_i}} \right\} $, $ i = 1, 2, \cdots , MN $依次生成矩阵X, Y, Z, W:

$ \begin{split} X\left( {k,l} \right) =\;& \big\{ {\rm{floor}}\big[ \big( | {{x_{\left( {k - 1} \right) \times N{\rm{ + }}l}}{\rm{ + }}y_{_{\left( {k - 1} \right) \times N{\rm{ + }}l}}'} |\boldsymbolod 1 \big) \\ &\times {{10}^{13}} \big] \boldsymbolod MN \big\}{\rm{ + }}1, \end{split} $

$ \begin{split} Y\left(k,l\right)=\;&\big\{{\rm floor}\big[\big(|{y}' _{(k-1)\times N\rm+l} |\rm{mod}1\big)\times {10}^{13}\big]\big\}\\ \rm{mod}\;256, \end{split} $

$ \begin{split} Z\left( {k,l} \right) =\;& \big\{ {\rm{floor}}\big[ ( {| {{z_{({k - 1}) \times N + l}}} |\boldsymbolod 1} ) \times {{10}^{13}} \big] \\ \boldsymbolod M\big\} + 1, \end{split} $

$ \begin{split} W\left( {k,l} \right) = \;&\big\{ {\rm{floor}}\big[ ( {| {{w_{({k - 1}) \times N + l}}} |\boldsymbolod 1} )\times {{10}^{13}} \big] \\ \boldsymbolod N \big\}+ 1, \end{split} $

这里, $ k = 1, 2, \cdots , M; l = 1, 2, \cdots , N $, $ {\rm{floor}}\left( t \right) $返回小于或等于t的最大整数, $ \boldsymbolod 1 $用于取序列的小数部分, 绝对值用于将负的状态值$ x + {y'} $, $ {y'} $, z和w转化为正数.
3)置乱与扩散对图像进行加密
① 进行扩散算法Ⅰ, 借助伪随机矩阵Y将明文图像P变换为矩阵A, 具体步骤如下.
Step 1　令$i = 1,\; j = 1$;
Step 2　将$ P\left( {i, j} \right) $变换为$ A\left( {i, j} \right) $, 即

$ A\left( {i,j} \right) = \left[ {P\left( {i,j} \right) \oplus Y\left( {i,j} \right) \oplus {r_1}} \right]\boldsymbolod 256 \rm{; } $

Step 3　令$ j = j + 1 $;
Step 4　将$ P\left( {i, j} \right) $变换为$ A\left( {i, j} \right) $, 即

$ A\left( {i,j} \right) = \left[ {P\left( {i,j} \right) \oplus A\left( {i,j - 1} \right) \oplus Y\left( {i,j} \right)} \right]\boldsymbolod 256 \rm{; } $

Step 5　如果$ j < N $, 跳转到Step 3; 否则, 令$ j = 1, i = i + 1 $, 如果$ i \leqslant M $, 跳转到Step 6; 否则, 跳转到Step 8;
Step 6　将$ P\left( {i, j} \right) $变换为$ A\left( {i, j} \right) $, 即

$ \begin{split} A\left( {i,j} \right) =\;& \left[ {P\left( {i,j} \right) \oplus \sum\limits_{i = 1}^N {A\left( {i - 1,j} \right)} \oplus Y\left( {i,j} \right)} \right]\\ &\boldsymbolod 256 \rm{; } \end{split} $

Step 7　 跳转到Step 3;
Step 8　结束.
② 进行置乱算法. 置乱算法将图像A置乱为图像B, 具体步骤如下.
Step 1　对于图像A中给定的一个像素点坐标$ \left( {i, j} \right) $, 根据(2)式和(3)式计算得到$ \left( {m, n} \right) $的值:

$ m = \left[ {\sum\limits_{l = 1}^N {A\left( {Z\left( {i,j} \right),l} \right)} \times {{10}^{13}}\boldsymbolod M} \right] + 1, $

$ n = \left[ {\sum\limits_{k = 1}^M {A\left( {k,W\left( {i,j} \right)} \right)} \times {{10}^{13}}\boldsymbolod N} \right] + 1. $

如果$ m = i $或$ Z\left( {i, j} \right) $, 或者$ n = j $或$ W\left( {i, j} \right) $, 或者$ Z\left( {i, j} \right) = i $, 或者$ W\left( {i, j} \right) = j $, 则$ A\left( {i, j} \right) $位置保持不变; 否则, $ A\left( {i, j} \right) $与$ A\left( {m, n} \right) $互换位置.
Step 2　当坐标$ \left( {i, j} \right) $按从左到右、从上到下的扫描顺序遍历图像A中的所有像素点时, 重复Step 1, 将图像A转化为图像$A' $.
Step 3　将图像$A' $做如下处理:

$ {A'} = {\rm{reshape}}(A,1,MN), $

$ {\rm{reshape}}({A'}, 1, MN) $把图像A转换成MN维行向量.
Step 4　将伪随机矩阵X做如下处理:

$ {\boldsymbol{X}} = {\rm{reshape}}(X,1,MN) , $

$ {\rm{reshape}}(X, 1, MN) $把伪随机矩阵X转换成MN维行向量.
Step 5　将X中重复的元素只保留一个.
Step 6　将集合$ \left\{1, 2, \cdots , MN\right\} $中未出现在X中的元素按从小到大的顺序排列在X的末尾.
Step 7　对$ {A'} $做如下处理:

$ A'\left( {{X_i}} \right) = A'\left( {{X_{MN - i + 1}}} \right) $

i = $1, 2, \cdots ,$ floor(MN/2), floor(t)表示返回小于或等于t的最大整数.
Step 8　对B做如下处理, 将图像$ {A'} $转化为图像B:

$ B = {\rm{reshape}}({A'},M,N) . $

③ 最后进行扩散算法Ⅱ, 扩散算法Ⅱ是从图像的最后一个像素点向前扩散, 借助于伪随机矩阵Y将图像B变成矩阵C, 具体步骤如下.
Step 1　令$ i = M, j = N $;
Step 2　将$ B\left( {i, j} \right) $变换为$ C\left( {i, j} \right) $, 即

$ C\left( {i,j} \right) = \left[ {B\left( {i,j} \right) \oplus Y\left( {i,j} \right) \oplus {r_2}} \right]\boldsymbolod 256 \rm{; } $

Step 3　令$ j = j - 1 $;
Step 4　将$ B\left( {i, j} \right) $变换为$ C\left( {i, j} \right) $, 即

$ C\left( {i,j} \right) = \left[ {B\left( {i,j} \right) \oplus C\left( {i,j + 1} \right) \oplus Y\left( {i,j} \right)} \right]\boldsymbolod 256 \rm{; } $

Step 5　如果$ j > 1 $, 跳转到Step 3. 否则$ j = N, i = i - 1 $, 如果$ i \geqslant 1 $, 跳转到Step 6; 否则, 跳转到Step 8;
Step 6　将$ B\left( {i, j} \right) $变换为$ C\left( {i, j} \right) $, 即

$ \begin{split} C\left( {i,j} \right) =\;& \left[ {B\left( {i,j} \right) \oplus \sum\limits_{j = 1}^N {\left( {C\left( {i{\rm{ + }}1,j} \right)} \right)} \oplus Y\left( {i,j} \right)} \right]\\ &\boldsymbolod 256 \rm{; } \end{split} $

Step 7　跳转到Step 3;
Step 8　结束.
矩阵C即为所得密文图像.

解密过程为加密过程的逆过程.
Step 1　输入密文图像C, 4个伪随机矩阵${{\boldsymbol{ X}}, {\boldsymbol{Y}}, {\boldsymbol{Z}}, {\boldsymbol{W}}} $以及2个伪随机数$ {r_1}, {r_2} $;
Step 2　进行扩散算法Ⅱ的逆算法, 得到矩阵B₁;
Step 3　进行置乱算法的逆算法, 得到矩阵A₁;
Step 4　进行扩散算法Ⅰ的逆算法, 得到明文图像P.

2

-->

5.1.深度学习产生新混沌信号

为了得到新的序列$ \left\{ {y'_i} \right\} $, 利用LSTM网络对超混沌Lorenz系统生成的序列$ \left\{ {{y_i}} \right\} $进行深度学习. 模型训练过程如图5所示, 可以看出, 在250次迭代后, 得到的LSTM模型的均方根误差(RMSE)和损失函数(Loss)均接近于0, 表示模型的拟合程度较好, 可以进行预测. 从图6和图7可以看出, 深度学习得到的新混沌信号$\left\{ {y'_i} \right\}$与超混沌Lorenz系统生成的混沌信号$ \left\{ {{y_i}} \right\} $是不一样的.
图 5 $ \left\{ {y_i'} \right\} $LSTM模型训练过程
Figure5. LSTM model training process of $ \left\{ {y_i'} \right\} $.

图 6 LSTM模型预测
Figure6. Forecast of LSTM model.

图 7 截取的$ \left\{ {{y_i}} \right\} $
Figure7. Part of $ \left\{ {{y_i}} \right\} $.

2 -->

5.2.动力系统分析

为了说明新混沌信号特点, 在最大Lyapunov指数、0-1测试、功率谱、随机性等方面对新混沌信号$ \left\{ {y_i'} \right\} $进行分析, 并与超混沌Lorenz系统产生的混沌信号$ \left\{ {{y_i}} \right\} $进行对比.
3 -->

5.2.1.最大Lyapunov指数分析

最大Lyapunov指数 (largest Lyapunov exponent, LLE) 是一个较为典型的判断一个系统是否具有混沌特性的工具. 从时间序列提取最大Lyapunov指数是Wolf等^[54]在1985年提出的一种数值方法, 此方法现已广泛应用, 具体如下.
1)设给定时间序列{y(k)}, 重构的m维的相空间为

$ Y(k)=\{y(k),y(k+\tau),\cdots,y(k+(m-1)\tau)\}, $

其中τ为延迟时间.
2)任意选取初始点$ Y\left( {{k_0}} \right) $, 设其与最近的邻近点$ {Y_0}\left( {{k_0}} \right) $的距离为$ {d(k_0)} $, 从$ {k_0} $时刻到$ {k_1} $时刻两点的距离超过设定值 μ:

$ d'(k_1) = \left| {Y\left( {{k_1}} \right) - {Y_0}\left( {{k_1}} \right)} \right| > \mu ,\;\mu > 0. $

3)保留$ Y\left( {{k_1}} \right) $, 并找其最近邻点$ {Y_1}\left( {{k_1}} \right) $, 使得

$ {d(k_1)} = \left| {Y\left( {{k_1}} \right) - {Y_1}\left( {{k_1}} \right)} \right| < \mu {\rm{, }} $

并使得$d'(k_1)$与$ d(k_1)$的夹角达到最小, 然后重复2)—3)过程, 直到穷尽所有的数据点, 此时追踪演化过程中总迭代次数为N, 则最大Lyapunov指数为

$ {\lambda _1} = \frac{1}{{k_N} - {k_0}}\sum\limits_{i = 1}^N {\log_{2}}\frac{d'(k_i)}{d(k_{i-1})}. $

为了检验LSTM预测的序列$ \left\{ {y_i'} \right\} $是否具有混沌特性, 我们使用Wolf方法计算该序列的最大Lyapunov指数. 从图8可以看出, LLE指数曲线一直在y = 0的上方, 因此, 该信号的LLE大于0, 由于$ \left\{ {y_i'} \right\} $是有界的, 因此该序列是混沌的.
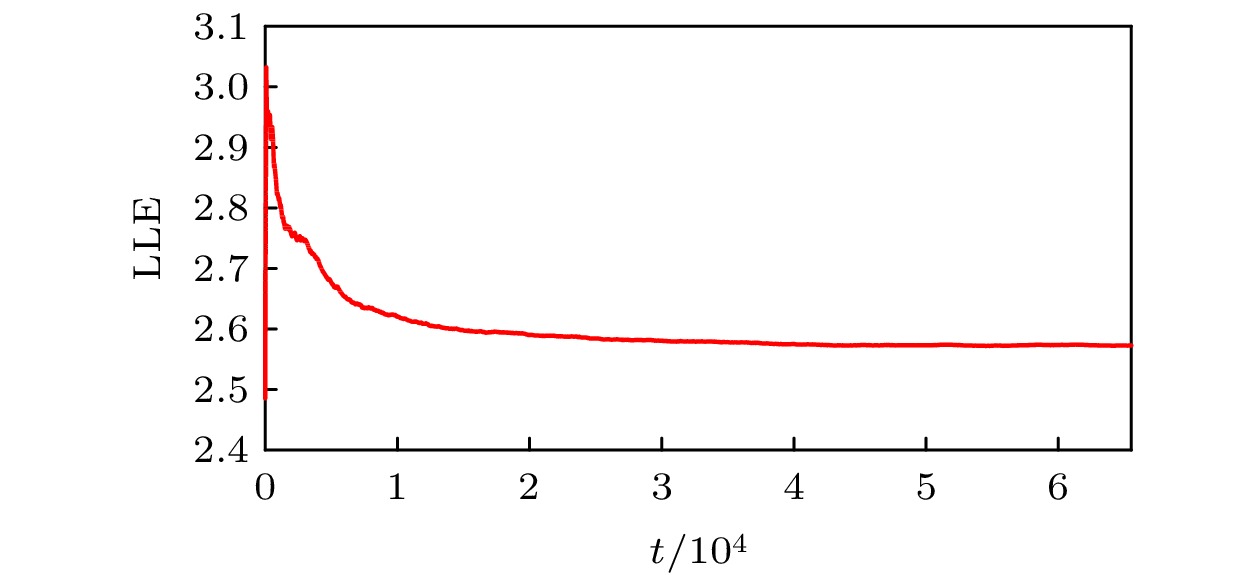图 8 Wolf方法求$ \left\{ {y_i'} \right\} $最大Lyapunov指数过程图
Figure8. Using wolf method to find the largest Lyapunov exponent process of $ \left\{ {y_i'} \right\} $.

3 -->

5.2.2.0-1测试

0-1测试是一个能够衡量时间序列是否有混沌的一种测试算法, 与李雅普诺夫指数不同的是, 它不需要进行相空间重构, 通过输出结果是否接近于1, 来判别混沌现象的产生^[55,56].
对于给定的时间序列$ \{ x(i), i = 1, 2, \cdots, N\} $, 选取任意的$ c \in \left[ {0, {\rm{π }}} \right] $, 定义函数$ p\left( n \right) $与$ q\left( n \right) $如下:

$\begin{split}p\left( n \right) =\;& \sum\limits_{i = 1}^n {x\left( i \right)\cos \left( {\mu \left( i \right)} \right)} ,~~ n = 1,2, \cdots ,N {\rm{, }} \end{split}$

$\begin{split} q\left( n \right) =\;& \sum\limits_{i = 1}^n {x\left( i \right)\sin \left( {\mu \left( i \right)} \right)},~~ n = 1,2, \cdots ,N {\rm{, }} \end{split}$

$ \mu \left( i \right) = ic,~~i = 1,2, \cdots ,n {\rm{, }} $

基于函数$ p\left( n \right) $与$ q\left( n \right) $, 均方位移$ M\left( n \right) $为

$ M(n) = M_c(n) - (E(\eta))^2 \dfrac{1 - \cos nc}{1-\cos c}, $

其中

$ \begin{split} {M_c}\left( n \right) =\;& \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^N \big[ {{\left( {p\left( {i + n} \right) - p\left( i \right)} \right)}^2} \\ &+ {{\left( {q\left( {i + n} \right) - q\left( i \right)} \right)}^2} \big] {\rm{, }} \end{split} $

$ E\left( \eta \right) = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{i = 1}^N {x\left( i \right)} . $

如果函数$ p\left( n \right) $与$ q\left( n \right) $的轨迹表现为布朗运动, 则函数$ M\left( n \right) $随时间线性增长; 如果函数$ p\left( n \right) $与$ q\left( n \right) $的轨迹是有界的, 则函数$ M\left( n \right) $是有界的. 定义均方位移$ M\left( n \right) $的渐进线性增长率$ {K_c} $如下:

$ {K_c} = \lim\limits_{n \to \infty } {\lg M(n)}/ {\lg n} , $

如果$ {K_c} \approx 1 $, 表示该时间序列具有混沌的特性; 如果$ {K_c} \approx 0 $, 则表示该时间序列不具有混沌特性.
为了验证序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $是否具有混沌特性, 对序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $进行0-1测试. 测试结果如图9和图10所示, 均方位移$ M\left( n \right) $的渐进线性增长率$ {K_c} $接近于1, 所以序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $均具有混沌特性.
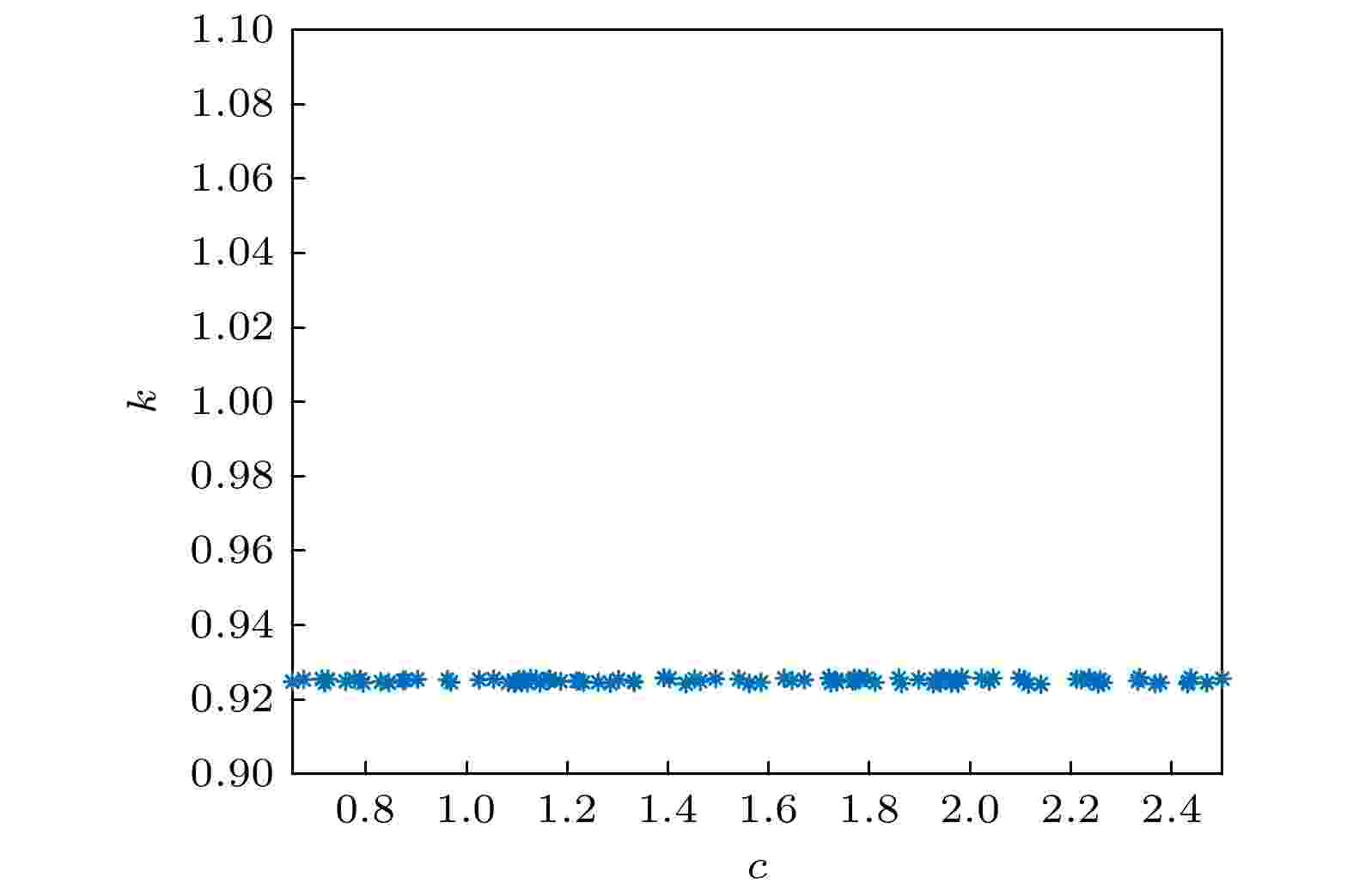图 9 新混沌信号0-1测试图
Figure9. 0-1 test image of the new chaotic signal.

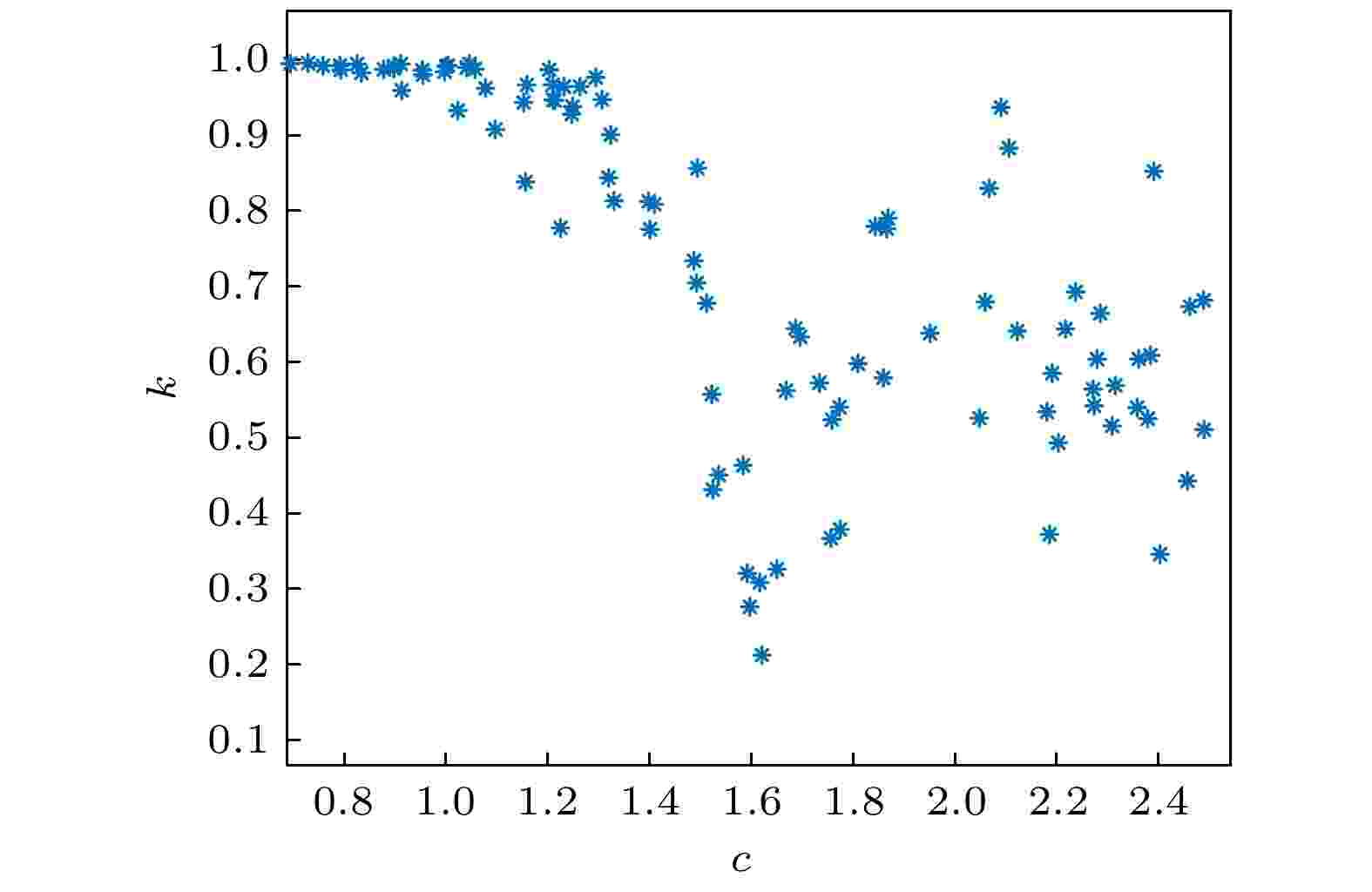图 10 超混沌Lorenz系统混沌信号0-1测试图
Figure10. 0-1 test image of the hyperchaotic Lorenz signal.

3 -->

5.2.3.功率谱分析

为了验证序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $是否具有周期性, 进行功率谱分析, 如图11和图12所示, 实验结果表明, 序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $不具有周期性, 且具有连续性和噪声背景, 因此可以用来进行图像加密.
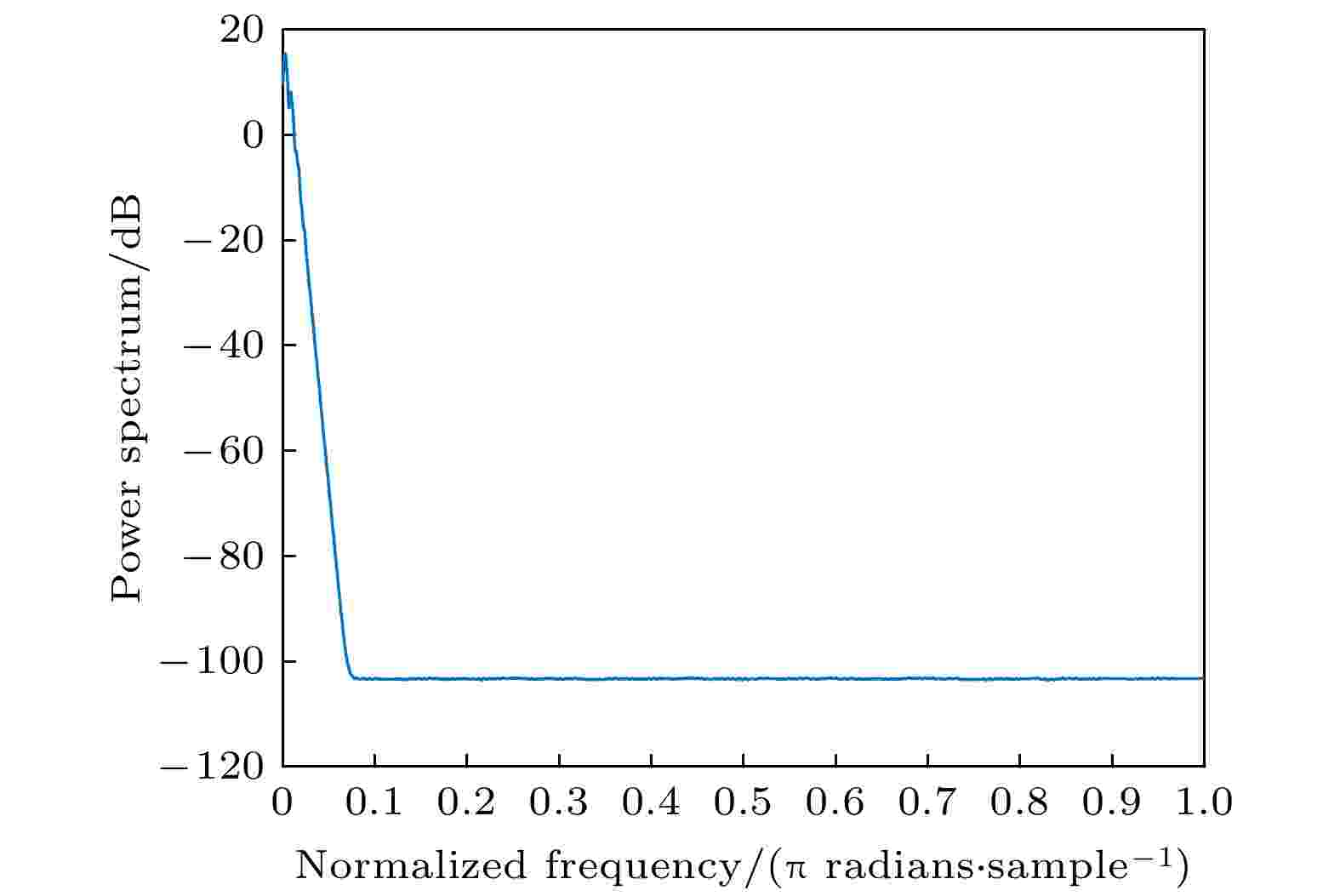图 11 新混沌信号功率谱图
Figure11. The spectrum image of the new chaotic signal

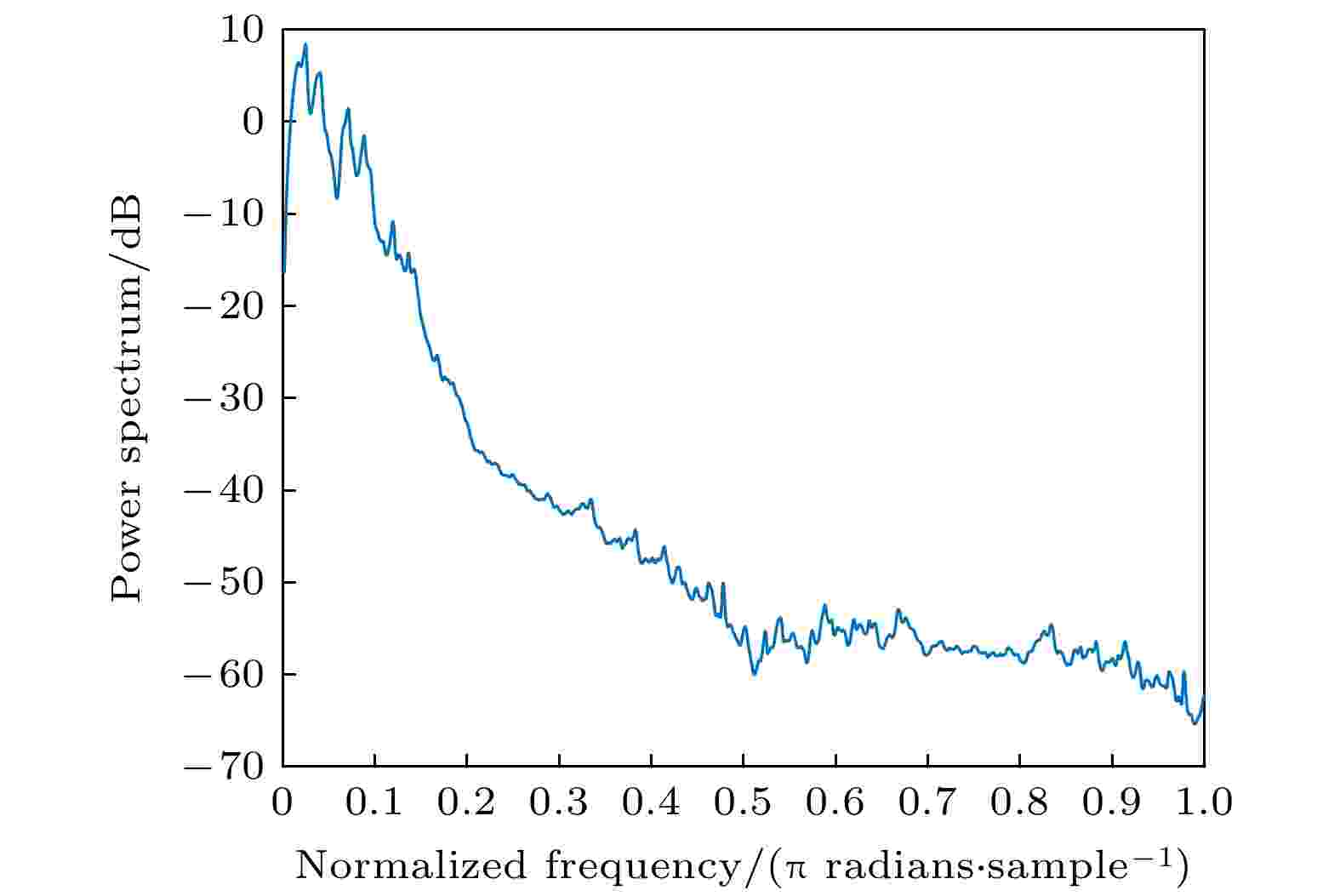图 12 超混沌Lorenz信号功率谱图
Figure12. Spectrum image of hyperchaotic Lorenz signal.

3 -->

5.2.4.三维相图

观察序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $的三维相图, 如图13和图14所示, 从图中可以看出存在一个吸引域, 各个相点不断绕圈、折叠, 不断地靠近和远离这个吸引域, 但又不同于随机运动, 像这样的绕圈运动表示序列是混沌的, 因此序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $是混沌的.
图 13 序列$ \left\{ {y_i'} \right\} $的相图
Figure13. Phase diagram of $ \left\{ {y_i'} \right\} $.

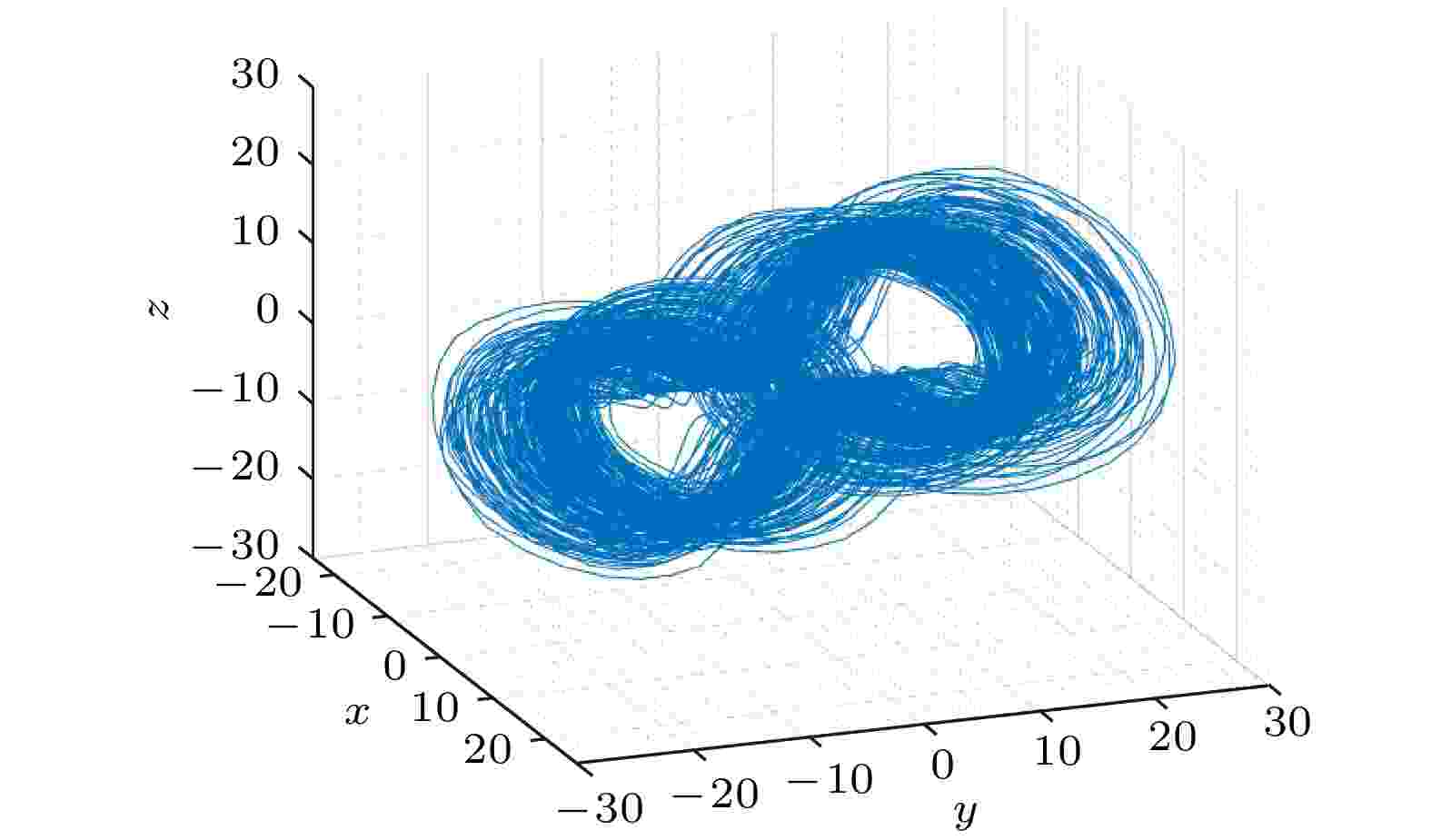图 14 序列$ \left\{ {{y_i}} \right\} $的相图
Figure14. Phase diagram of $ \left\{ {{y_i}} \right\} $.

3 -->

5.2.5.随机性分析

为了验证序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $的随机性, 选择了包括了15个测试的NIST, 统计结果后得到概率(p值), 表1与表2中列出了序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $的NIST测试结果. 从表1和表2可以看出, 所有p值明显大于0.01, 所以序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $与通过了NIST测试, 这意味着序列$ \left\{ {y_i'} \right\} $与$ \left\{ {{y_i}} \right\} $具有很好的随机性.

统计测试	p 值	结果
单比特频率测试	0.8752	通过
块内频率测试	0.8523	通过
游程测试	0.6121	通过
块内最长1游程测试	0.0828	通过
二进制矩阵秩测试	0.1445	通过
离散傅里叶(谱)测试	0.8152	通过
非重叠模板匹配测试	0.3527	通过
重叠模板匹配测试	0.4305	通过
Maurer通用统计测试	0.4214	通过
线性复杂度测试	0.2341	通过
序列测试	0.3053	通过
近似熵测试	0.1568	通过
累加和测试	0.3257	通过
随机旅行测试	0.1523	通过
随机旅行变种测试	0.1057	通过

表1新混沌时间序列NIST测试
Table1.NIST test of the new chotic time series

统计测试	p 值	结果
单比特频率测试	0.8815	通过
块内频率测试	0.7253	通过
游程测试	0.5986	通过
块内最长1游程测试	0.0823	通过
二进制矩阵秩测试	0.1263	通过
离散傅里叶(谱)测试	0.8164	通过
非重叠模板匹配测试	0.3580	通过
重叠模板匹配测试	0.5216	通过
Maurer通用统计测试	0.4418	通过
线性复杂度测试	0.5052	通过
序列测试	0.6015	通过
近似熵测试	0.1435	通过
累加和测试	0.4863	通过
随机旅行测试	0.3997	通过
随机旅行变种测试	0.2265	通过

表2超混沌Lorenz混沌序列NIST测试
Table2.NIST test of the hyperchaotic Lorenz time series.

3 -->

5.2.6.混沌信号的特征对比

通过以上实验, 将对比结果列在表3中. 从此表可知, 新混沌信号与原混沌信号通过功率谱分析、相图及NIST测试结果可以说明均具有混沌特征与随机性. 然而新信号的最大Lyapunov指数与0-1测试结果均高于原信号, 说明其具有更明显的混沌特征. 所以基于深度学习生成的新混沌信号更适合用于图像加密.

信号来源	最大Lyapunov 指数	0-1 测试	功率谱 分析	相图	NIST 测试
超混沌Lorenz	0.3381[52]	0.7937	混沌	混沌	随机
深度学习	2.6002	0.9250	混沌	混沌	随机

表3混沌信号统计参数对比
Table3.Comparison of statistical parameters of chaotic signals.

2 -->

5.3.新混沌信号的应用

本节展示了一些常见的灰度图像仿真结果, 其中Lena图来自网址(https://www.ece.rice.edu/~ wakin/images/ [2021-01-01]), 其余图像来自网址(http://sipi.usc.edu/database/database.php?volume=misc [2021-01-01]). 图像大小分别为$ 256 \times 256 $, $ 512 \times 512 $, $ 1024 \times 1024 $, 灰度图像的加密与解密实验结果如图15所示. 从图15可以看出, 本文方法可以进行有效的加密和解密.
图 15 数字图像加密解密实验图　(a)鸟(256 × 256)原图; (b)鸟(256 × 256)加密图; (c)鸟(256 × 256)解密图; (d)辣椒(256 × 256)原图; (e)辣椒(256 × 256)加密图; (f)辣椒(256 × 256)解密图; (g)Lena(512 × 512)原图; (h) Lena(512 × 512)加密图; (i) Lena(512 × 512)解密图; (j) 液体泼洒(512 × 512)原图; (k) 液体泼洒(512 × 512)加密图; (l) 液体泼洒(512 × 512)解密图; (m)机场(1024 × 1024)原图; (n) 机场(1024 × 1024)加密图; (o) 机场(1024 × 1024)解密图; (p)飞机(1024 × 1024)原图; (q)飞机(1024 × 1024)加密图; (r)飞机(1024 × 1024)解密图
Figure15. Experimental picture of digital image encryption and decryption: (a) Original bird image; (b) encrypted bird image; (c) decrypted bird image; (d) original pepper (256 × 256) image; (e) encrypted pepper (256 × 256) image; (f) decrypted pepper (256 × 256) image; (g) original Lena (512 × 512) image; (h) encrypted Lena (512 × 512) image; (i) decrypted Lena (512 × 512) image; (j) original splash (512 × 512) image; (k) encrypted splash (512 × 512) image; (l) decrypted splash (512 × 512) image; (m) original airport (1024 × 1024) image; (n) encrypted airport (1024 × 1024) image; (o) decrypted airport (1024 × 1024) image; (p) original airplane (1024 × 1024) image; (q) encrypted airplane (1024 × 1024) image; (r) decrypted airplane (1024 × 1024) image.

2 -->

5.4.安全性分析

3 -->

5.4.1.差分攻击

差分攻击是攻击者针对明文图像, 改变一个像素值然后加密图像, 观察两个加密后的密文图像之间的差距, 从而找到规律, 破解算法.
NPCR (number of pixels change rate)与UACI (unified average changing intensity)是差分攻击的两个重要指标, 它们通过 (4)式和(5)式计算出来^[57]:

$ {\rm{NPCR}} = \frac{{\displaystyle\sum\nolimits_{i,j} {D(i,j)} }}{{W \times H}} \times 100, $

$ {\rm{UACI}} = \frac{1}{{W \times H}}\left[\displaystyle\sum\limits_{i,j}{\frac{{\left| {{c_1}(i,j) - {c_2}(i,j)} \right|}}{{255}}} \right] \times 100, $

$ {c_1} $和$ {c_2} $是两幅图像, 图像的尺寸是 $ W \times H $. 如果$ {c_1}\left( {i, j} \right) \ne {c_2}\left( {i, j} \right) $, 则$ D\left( {i, j} \right) = 1 $, 否则, D(i, j) = 0.
理论上NPCR与 UACI的值越接近99.6094%和33.4635%越好. 本文选取P(256, 256)的像素值做出改变, 并计算出它们的NPCR与 UACI结果, 如表4所示. 对比代表性的文献[10, 13, 58, 59]中的NPCR与 UACI, 对比结果如表5所示. 实验结果及对比结果表明, 该算法的NPCR与 UACI已经很接近理论值了, 因此本文提出的加密算法具有很好的抵抗差分攻击的能力.

图片	改变$ P(256, 256) $
	NPCR/%	UACI/%
Bird ($ 256 \times 256 $)	99.56	33.35
Cameraman ($ 256 \times 256 $)	99.63	33.30
Pepper ($ 256 \times 256 $)	99.62	33.39
House ($ 256 \times 256 $)	99.63	33.37
Lena ($ 512 \times 512 $)	99.58	33.38
Airplane ($ 512 \times 512 $)	99.59	33.42
Tank ($ 512 \times 512 $)	99.61	33.49
Splash ($ 512 \times 512 $)	99.64	33.54
Truck ($ 512 \times 512 $)	99.60	33.47
Airport ($ 1024 \times 1024 $)	99.62	33.48
Airplane ($ 1024 \times 1024 $)	99.60	33.47

表4NPCR和UACI
Table4.NPCR and UACI.

	本文平均值	文献[10]	文献[13]	文献[58]	文献[59]
NPCR/%	99.604	99.61	99.6641	99.61	99.6114
UACI/%	33.46	33.48	33.6124	33.46	33.4523

表5NPCR和UACI的平均值与其他加密算法的比较
Table5.The average of NPCR and UACI and comparison with other algorithms.

3 -->

5.4.2.密钥空间分析

在此图像加密系统中, $ {x_0} $, $ {y_0} $, $ {z_0} $和$ {w_0} $的精度为$ {10^{ - 14}} $, $ {r}_{1}和{r}_{2} $为0至255的整数随机数. 训练数据的比例p的精度为$ {10^{ - 14}} $, 初始学习率q的精度为$ {10^{ - 14}} $, 学习率下降因子u的精度为$ {10^{ - 14}} $, 隐藏节点数o的取值范围为$ \left[ {1, M \times N - 2} \right] $, 截取进行深度学习的序列长度s的取值范围为

$\begin{split}& {256 \times 256 \times M \times N \times ( M \times N - 2 ) \times {10^{98}}} \\\approx \; & { 6.5536 \times M \times N \times (M \times N - 2 ) \times {2^{339}} > 2^{100}}. \end{split}$

而代表性的文献[10, 13, 58-61]中的密钥空间分别为10⁹⁸, >255$ \times $1014⁵, 2²⁸³, 2³⁹⁹, 24$ \times $10⁴⁵和2²⁵⁶, 实验结果及对比结果表明, 本算法是足够安全的.
3 -->

5.4.3.密钥敏感性分析

一个好的算法是对密钥敏感的, 即对密钥做出微小的改变, 然后还原, 会得到完全不同的结果. 本文选取的密钥$ {x_0} $:

$ {x_0} = 1.0 , $

对$ {x_0} $改变生成新密钥:

$ x_0' = {x_0} + {10^{ - 14}} . $

由于用错误的密钥进行还原, 所以不能有效解密, 如图16(a)—(c)所示. 此外, 由于本文中对$ \left\{ {{y_i}} \right\} $进行深度学习后生成了新的序列$ \left\{ {y_i'} \right\} $进行加密, 因此对加密图用$ \left\{ {{y_i}} \right\} $不能进行有效解密, 如图16(c)所示. 综上, 本文加密方法具有较高的密钥敏感性.
图 16 密钥敏感性　(a)明文图像; (b)密文用$ x_0' $解密结果; (c)密文用$ \left\{ {{y_i}} \right\} $解密结果
Figure16. Sensitivity of secret key: (a) Original image; (b) error key $ x_0' $ restoring diagram; (c) error key $ \left\{ {{y_i}} \right\} $ restoring diagram.

3 -->

5.4.4.直方图分析

直方图分析是检测密文像素值分布是否均匀, 一个好的加密算法, 密文直方图应该是均匀的. 否则该加密算法是不安全的, 攻击者就能从密文中找到规律, 从而破解该算法.
图17展示了不同分辨率的灰度图像明文直方图与密文直方图. 通过观察, 明文直方图分布是不均匀的, 当经过本文的加密算法, 密文直方图分布是均匀的. 因此攻击者很难从密文中找到规律从而破解算法. 因此本文具有很好的抵抗统计攻击的能力.
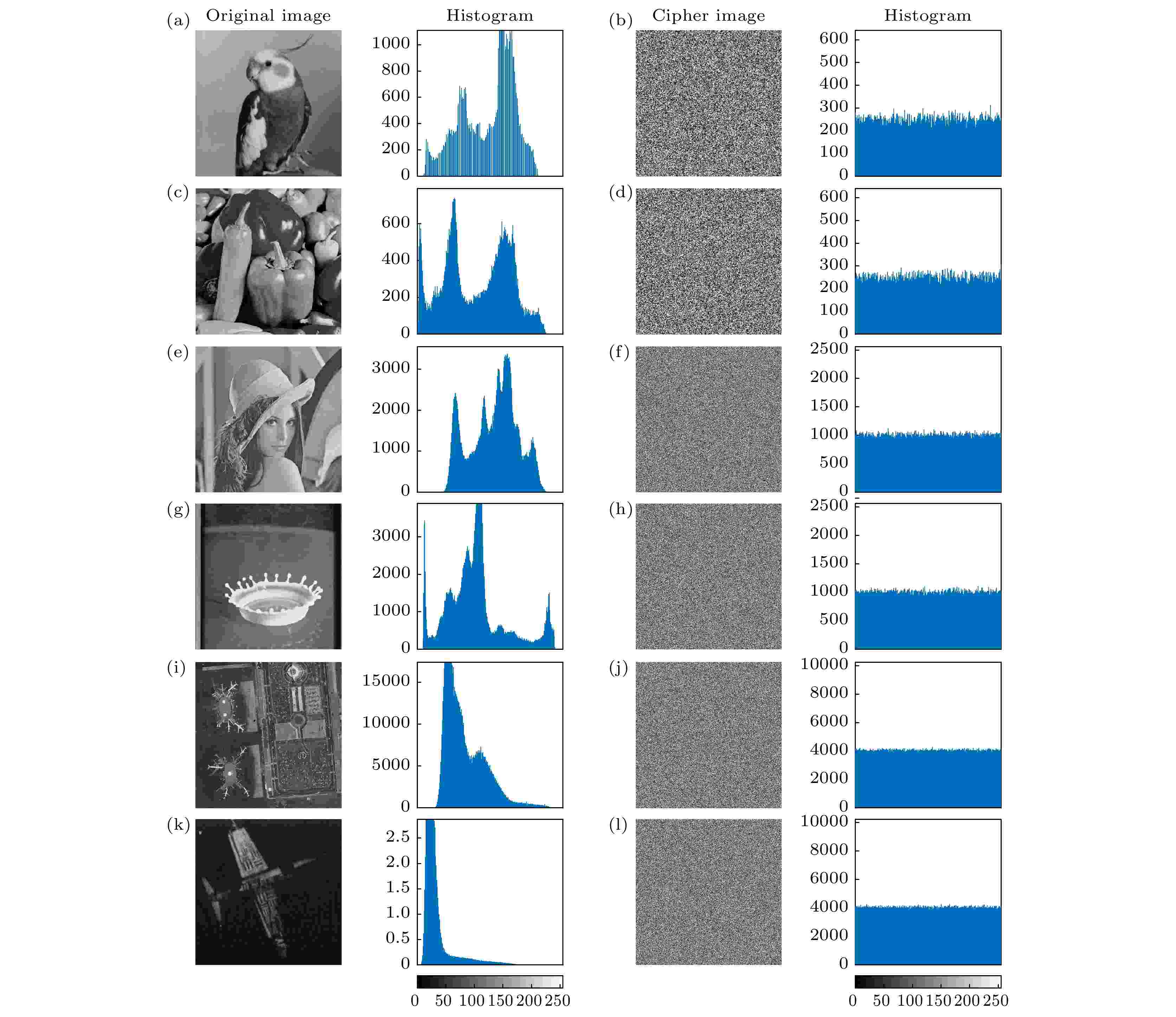图 17 加密解密图像直方图　(a)鸟(256 × 256)原图与明文直方图; (b)鸟(256 × 256)加密图和密图直方图; (c)辣椒(256 × 256)原图与明文直方图; (d)辣椒(256 × 256)加密图和密图直方图; (e) Lena(512 × 512)原图与明文直方图; (f) Lena(512 × 512)加密图和密图直方图; (g)水滴泼洒(512 × 512)原图与明文直方图; (h)水滴泼洒(512 × 512)加密图和密图直方图; (i)机场(1024 × 1024)原图与明文直方图; (j)机场(1024 × 1024)加密图和密图直方图; (k)飞机(1024 × 1024)原图与明文直方图; (l)飞机(1024 × 1024)加密图和密图直方图
Figure17. Histograms of plain images and ciphered images: (a) Original image and histogram of bird (256 × 256); (b)cipher image and histogram of bird (256 × 256); (c) original image and histogram of pepper (256 × 256); (d) cipher image and histogram of pepper(256 × 256); (e) original image and histogram of Lena (512 × 512); (f) cipher image and histogram of Lena (512 × 512); (g) original image and histogram of splash (512 × 512); (h) cipher image and histogram of splash (512 × 512); (i) original image and histogram of airport (1024 × 1024); (j) cipher image and histogram of airport (1024 × 1024); (k) original image and histogram of airplane (1024 × 1024); (l) cipher image and histogram of airplane (1024 × 1024).

3 -->

5.4.5.相关性分析

除上述直方图分析外, 统计分析中还有一种检测指标, 相邻像素值的相关性, 其包括水平相邻像素相关性, 垂直相邻像素相关性, 对角相邻像素相关性. 一个好的加密系统, 加密后得到的密文各个相邻像素值的相关性越接近于0代表加密效果越好, 这样攻击者就不能从密文中得到有效地信息, 很好的保护了加密算法. 接下来, 我们使用下面的公式来计算相邻像素值的相关性^[62]: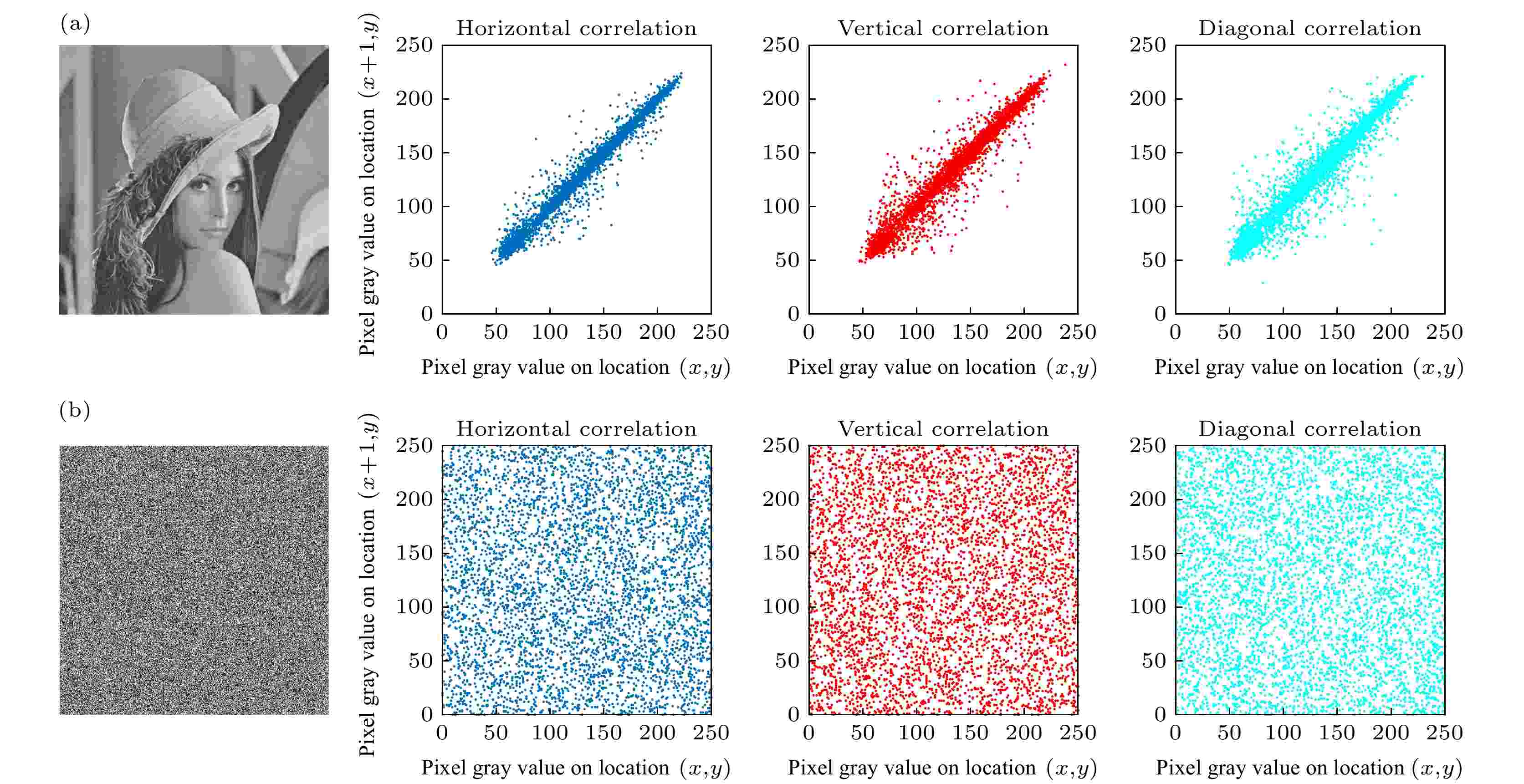

$ {r_{xy}} = \frac{{{\rm{cov}} (x,y)}}{{\sqrt {D(x)} \sqrt {D(y)} }} {\rm{, }} $

其中

$ {{\rm{cov}}} (x, y) = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i} - E(x))({y_i} - E(y))}.$

$ D(x) = \frac{1}{N} \sum\limits_{i + 1}^N {{{({x_i} - E(x))}^2}},E(x) = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}}. $

首先, 本文在Lena明文和密文中随机选取5000对像素点进行测试, 如图18所示. 从图18可以看出, 明文各个方向具有很强的相关性, 而从密文的相关性具有很小的相关性.
图 18 Lena图相关性分析　(a)明文; (b)密图
Figure18. Correlation coefficients of Lena: (a) Original image; (b) encrypted image

接下来, 对其他图片进行仿真, 计算结果陈列在表6中, 并与一些代表性的文献[10, 13, 58, 59]的密文相关性作对比, 其结果展示在表7中. 实验结果表明, 本文的算法与一些代表性的文献作对比, 可以发现, 明文的3个方向上相关性很高, 经过本文算法的加密, 密文的3个方向上相关性变得很低, 与其他方法一样都接近于0. 因此本文具有更好的安全性, 能够抵抗统计攻击.

图片	明文					密文
	水平	垂直	对角	反对角		水平	垂直	对角	反对角
Lena	0.9844	0.9668	0.9620	0.9790		–0.0016	0.0014	–0.0014	–0.0010
Bird	0.9889	0.9826	0.9713	0.9519		0.0114	0.0103	0.0104	–0.0031
Cameraman	0.9591	0.9335	0.9101	0.9377		–0.0099	0.0141	–0.0165	–0.0028
Pepper	0.9638	0.9585	0.9368	0.9339		–0.0127	–0.0014	–0.0079	0.0134
Airport	0.9066	0.9072	0.8446	0.8752		–0.0091	0.0088	–0.0014	–0.0054
Splash	0.9925	0.9850	0.9797	0.9507		0.0082	0.0016	0.0039	–0.0060
Airplane	0.9476	0.9664	0.9418	0.9299		–0.0278	–0.0105	0.0013	–0.0083
House	0.9549	0.9780	0.9399	0.9027		0.0141	–0.0115	–0.0176	0.0005
Tank	0.8678	0.8815	0.8414	0.7949		–0.0036	0.0003	–0.0098	–0.0065
Truck	0.9258	0.9561	0.9114	0.8194		0.0028	–0.0041	0.0018	0.0074

表6图像相关系数
Table6.Correlation coefficients of images.

	Lena	文献[10]	文献[13]	文献[58]	文献[59]
水平	–0.0016	–0.00007	0.00047	–0.00251	–0.038118
垂直	0.0014	–0.0024	–0.03911	–0.00292	–0.029142
对角	–0.0014	0.0019	0.00305	–0.00156	0.002736

表7密文图像相关系数比较
Table7.Comparison of the correlation coefficients of images.

3 -->

5.4.6.信息熵分析

信息熵代表信息混乱的程度, 像素值越混乱信息熵越接近8, 信息泄露的可能性越小, 信息熵通过(6)式计算^[63]:

$ H(s) = \sum\limits_{i = 0}^{{2^L} - 1} {p({s_i})} {\log _2}\frac{1}{{p({s_i})}} , $

在(6)式中, $ p(s{}_i) $代表$ {s_i} $发生概率. 理论上信息熵的值越接近8, 代表像素值分布越混乱, 信息泄露的可能性就越小. 采用灰度图像房屋(house), 摄影师 (cameraman), 鸟(bird), 辣椒 (pepper), Lena, 水滴泼洒 (splash), 飞机(airplane)($ 512 \times 512 $), 坦克(tank), 卡车 (truck), 机场 (airport), 飞机 (airplane)($ 1024 \times 1024 $)进行检测. 选取不同的差分攻击位置, 在表8中分别给出了明文的信息熵以及密文的信息熵, 代表性文献^{[10,13,58,59]}中Lena (512×512)的信息熵分别为7.9993, 7.9993, 7.9993, 7.999239. 实验结果表明我们得到的密文信息熵7.9993和其他方法一样都非常接近于8, 表示信息泄露的可能性很小, 攻击者几乎不能从密文中找到有效信息, 因此本文提出的算法具有很好的安全性.

图片	图片大小	信息熵
House	$ 256 \times 256 $	7.9969
Cameraman	$ 256 \times 256 $	7.9971
Bird	$ 256 \times 256 $	7.9968
Pepper	$ 256 \times 256 $	7.9971
Lena	$ 512 \times 512 $	7.9993
Splash	$ 512 \times 512 $	7.9993
Airplane	$ 512 \times 512 $	7.9993
Tank	$ 512 \times 512 $	7.9994
Truck	$ 512 \times 512 $	7.9993
Airport	$ 1024 \times 1024 $	7.9998
Airplane	$ 1024 \times 1024 $	7.9998

表8信息熵
Table8.Information entropy of images.

3 -->

5.4.7.鲁棒性分析

鲁棒性是检验加密算法抗干扰能力的重要指标. 在传输过程中信息有可能部分丢失或受到噪声污染, 因此需要设计一个加密算法, 即使丢失一部分信息, 也可以通过解密程序得到明文的一些主要信息. 我们通过剪切攻击和噪声攻击两种方式来检测本文加密算法的鲁棒性.
图19(a)—(c)展示了不同程度的剪切攻击, 图19(d)—(f)展示了不同程度的高斯白噪声攻击, 从图中可以看出, 尽管密文丢失一些信息或者一些信息被污染, 还可以通过解密得到明文的一些主要信息, 因此本文的加密算法具有较好的鲁棒性.
图 19 抗攻击性检验　(a) 10%剪切; (b) 30%剪切; (c) 80%剪切; (d) 0.001高斯白噪声攻击; (e) 0.01高斯白噪声攻击; (f) 0.1高斯白噪声攻击
Figure19. Anti attack test: (a) 10% data missed; (b) 30% date missed; (c) 80% data missed; (d) attack of 0.001 Gaussian white noise; (e) attack of 0.01 Gaussian white noise; (f) attack of 0.1 Gaussian white noise.

3 -->

5.4.8.已知明文和选择明文攻击的分析

全黑或全白图像经常被用来评估所提出的密码系统对已知明文和选择明文攻击的抵抗力. 对全黑图像与全白图像进行加密解密, 结果如图20所示, 可见我们的方法可以对这两个图进行有效的加密和解密. 接着对全黑图像与全白图像进行统计分析, 如表9所列. 通过此表可以得出, 各种指标均接近理论值, 因此本图像加密算法对已知明文和选择明文攻击具有较好的抗攻击性.
图 20 全黑全白图加密解密图像
Figure20. Encryption and decryption image of all black and all white image.

	NPCR	UACI	信息熵	相关系数
				水平	垂直		对角
全黑图	0.9958	0.3332	7.9970	0.0016		0.0003	0.0036
全白图	0.9961	0.3351	7.9971	0.0070		0.0004	0.0070

表9全黑全白图的统计分析
Table9.The statistical analysis of all-black image and all-white image.

本文提出了一种基于深度学习的图像加密算法, 利用LSTM神经网络对混沌序列进行深度学习, 生成了新的混沌信号, 将其用来进行图像加密. 相对于其他神经网络模型, 深度学习模型具有复杂的结构和较多的参数, 这给破解带来了很大的难度. 通过对比实验结果表明, 该算法具有更好的安全性, 能抵抗常见的攻击. 但是由于设备条件限制, 对于较大数据集, 加密算法的效率有待提高.