摘要: 指挥控制组织中的任务规划问题可以映射为变量较多、求解难度较大的组合优化问题. 采用传统具有启发性列表规划方法解决这一问题面临求解时间复杂度高、实时响应性较差等问题. 本文针对指挥控制组织中任务规划问题提出一种基于量子近似优化算法的量子线路求解方案. 首先将任务规划问题转化为组合优化中的精确覆盖问题, 通过构建相应的数学模型推导出精确覆盖问题的量子近似优化算法对应的末态哈密顿量表达式; 设计了基于量子近似优化算法的量子线路, 采用动量梯度下降法算法对量子逻辑门中的参数进行优化, 并利用本源量子开发的量子软件开发环境进行仿真实验. 仿真结果表明: 该量子线路方案可以用于求解任务规划问题, 同时降低了算法的时间复杂度, 一定程度上提升了资源利用率, 为进一步应用量子算法求解指挥控制组织中的任务规划问题打下基础.
关键词: 量子近似优化算法 /
量子线路 /
任务规划 English Abstract Application of quantum approximate optimization algorithm to mission planning of command and control organization Zhang Yi-Jun 1,3 ,Mu Xiao-Dong 2 ,Liu Xiao-Wen 3 ,Wang Xing-Yu 4 ,Dong Chen 3 ,Wu Tian-Yi 3 ,Li Kai 3 1.Graduate Institute, Rocket Force University of Engineering, Xi’an 710025, China Received Date: 31 May 2021Accepted Date: 12 July 2021Available Online: 17 August 2021Published Online: 05 December 2021Abstract: The mission planning problem in command and control organization can be mapped into a combinatorial optimization problem with many variables and is difficult to solve. The traditional heuristic list planning method faces the problems of high time complexity and poor real-time response. For the mission planning problem in command and control organization, a quantum circuit solution scheme is proposed based on quantum approximate optimization algorithm in this work. Firstly, the mission planning problem is transformed into a typical combinatorial optimization problem, the exact coverage problem. Then, by constructing the corresponding mathematical model, the final state Hamiltonian expression of the quantum approximate optimization algorithm for the exact coverage problem is derived. The quantum circuit based on the quantum approximate optimization algorithm is designed. Finally the parameters in the quantum logic gate are optimized by the momentum gradient descent algorithm, and the simulation experiment is carried out by using the quantum software development environment of the Origin Quantum Computing Company. The simulation results show that the quantum circuit scheme can be used to solve the mission planning problem, reduce the time complexity of the algorithm, and improve the resource utilization to a certain extent. This work lays the foundation for further application of quantum algorithm to solving the mission planning problem in command and control organization.Keywords: quantum approximate optimization algorithm /quantum circuit /mission planning 全文HTML --> --> --> 1.引 言 指挥控制(command and control, C2)组织是军事领域面向特定的使命任务, 为实现作战资源有序利用, 通过多种关联关系有机结合战场上各单元而形成的作战组织实体[1 ] . C2组织通过构建平台与任务之间的执行关系、决策实体与平台之间的指挥控制关系、各个决策实体之间的协作关系等实现面向任务的组织结构设计[2 ] . 其中, 平台与任务之间执行关系(即任务规划问题)是C2组织设计中的首要环节, 属于涉及变量最多、求解难度最大的组合优化问题.[3 ] 、多维动态列表规划算法 (multidimensional dynamic list scheduling, MDLS)[4 ] 、多优先级列表动态规划算法 (multiPRI list dynamic scheduling, MPLDS)[5 ] . 这些方法通常都是以整个任务完成时间最短或者以资源的充分利用为目标求解问题. 以MDLS和MPLDS方法为例, 两种方法的时间复杂度为$ O\left(m\cdot {n}^{2}\right) $ [4 -6 ] , 其中$ m $ 为平台数量, $ n $ 为任务数量. 而C2组织中的任务规划问题往往对时间要求较高, 特别是在战时, 需要复杂度更低的算法来解决. 随着量子计算机硬件的发展, 一些在经典超级计算机上都很难模拟的量子算法现在可以在量子计算机上运行[7 ] . 如文献[8 -13 ]显示, 目前, 量子近似优化算法(quantum approximate optimization algorithm, QAOA)[14 ] 有望在量子计算机上实现, 其理论基础已被谷歌、IBM、本源量子等研究机构在量子计算机上进行了实验验证. 它是一种用于解决组合优化问题的启发式混合量子经典算法, 由爱德华·法希等首次提出, 可以看作是绝热量子计算的时间离散化[15 ] . QAOA最初主要应用于最大切割问题的求解, 被证明对求解速度相对于现有经典算法而言具有指数级加速[16 -18 ] . 近年来研究成果表明[19 -24 ] , QAOA可以用来求解精确覆盖问题. 精确覆盖问题本质属于NP问题[25 ] , 在经典计算机上需要指数级时间开销; 而对于量子计算机来说, 只需要多项式级时间开销就可以求解. 这为C2组织任务规划问题求解提供了一定的理论借鉴. 为了缩短任务规划问题的求解时间, 采用QAOA求解C2组织中的任务规划问题是一种有意义的且可行的方法.2.C2组织中的任务规划问题的转化 本文以最小化整个任务流程完成时间为优化目标构建模型, 用$ P $ 表示平台集合, 用$ A $ 表示任务集合. 用$ {F}_{ap} $ = 1表示$ p $ 平台执行$ a $ 任务, 用$ {F}_{ap} $ = 0表示$ p $ 平台没有执行$ a $ 任务. 用$ {C}_{p} $ = 1表示$ p $ 平台被选中执行任务, 用$ {C}_{p} $ = 0表示$ p $ 平台没有被选中执行任务. $ {T}_{ap} $ 表示$ p $ 平台执行$ a $ 任务所用的时间. $ {T}_{p} $ 表示$ p $ 平台执行完分配的任务所用时间. $ T $ 表示指挥控制组织系统完成所有任务所用时间. 需要说明的是, 为更好构建模型, 对平台资源进行了约束, 假设所选平台都可以独立完成任务. C2组织任务规划通用模型如下所示:2 )式确保每一个任务都有且仅有一个平台执行, 约束条件(3 )式限制$ {F}_{ap} $ 和$ {C}_{p} $ 的取值范围.2 )式和(3 )式约束条件的解决方案. 而这些已有的平台执行方案都是从经过优化的平台执行方案数据库中随机选取的, 将问题转化成一个精确覆盖问题不仅可以确保所有任务被执行, 还可以减少平台需求数量, 提升平台利用率.3.基于QAOA的C2任务规划问题求解 根据文献[26 , 27 ]论述的研究内容, 大部分的NP完全问题和NP问题(包括精确覆盖问题)都可以生成对应的经典伊辛模型. 而根据文献[25 , 28 ]论述的研究内容, 经典伊辛模型可以通过定义旋转算子的方式转化为量子伊辛模型, 而通过量子伊辛模型可以描述量子系统的哈密顿量. 这样就可以将求解NP问题与求解量子伊辛模型对应的哈密顿量的本征态或最小能量状态联系起来, 使采用QAOA进行求解问题成为可能. 本文将精确覆盖问题的量子伊辛模型对应的哈密顿量表示如下:$ {H}_{\mathrm{c}} $ 为目标哈密顿量(也是QAOA对应的末态哈密顿量), $ n $ 和$ j $ 分别表示第$ n $ 个和第$ j $ 个量子比特位, 它们的取值范围为$1\leqslant n, j\leqslant N$ ; $ {\mathrm{\sigma }}_{n}^{Z} $ 和$ {\mathrm{\sigma }}_{j}^{Z} $ 表示作用在第$ n $ 个量子比特位和第$ j $ 个量子比特位上的泡利$ Z $ 算符; $ {G}_{nj} $ 和$ {q}_{n} $ 为相关系数, 属于常量.3.1.任务规划问题对应的伊辛模型 3.1.任务规划问题对应的伊辛模型 如前所述, 求出问题的解, 必须满足(2 )式和(3 )式的约束, 所以以(2 )式和(3 )式为基础推导该问题对应的伊辛模型. 首先在(2 )式两边同时减1; 然后在(2 )式两边同时进行平方; 最后在所有任务上进行累加运算, 可以得出如下表达式:$ \left|P\right| $ 表示平台集合$ P $ 的数量, $ \left|A\right| $ 表示任务集合$ A $ 的数量. 如果(5 )式等于0, 那么所有约束条件都能得到满足. 下面用旋转变量$ {S}_{p}\in \left\{-1, \right.\left.1\right\} $ 代替 $ {C}_{p}\in \left\{0, \right.\left.1\right\} $ , 公式如下:6 )式代入(5 )式, 并将(5 )式展开, 可以得出如下表达式:${G}_{pp{'}}$ 和$ {q}_{p} $ 分别为$\dfrac{1}{4}\displaystyle\sum \limits _{a=1}^{\left|A\right|}{\left(\displaystyle\sum \limits _{p=1}^{\left|P\right|}{F}_{ap}-2\right)}^{2}$ 为常数, 所以(7 )式可变换为${G}_{pp{'}}$ 具有对称性, (10 )式可以进一步变化为11 )式中的旋转变量, 就可以得到形如 (4 )式的精确覆盖问题的量子伊辛模型对应的哈密顿量表达式. 此表达式中的常量只改变哈密顿量的整体相位, 而对哈密顿量对应的本征态或最小能量状态没有影响.3.2.基于QAOA算法的求解思路 -->3.2.基于QAOA算法的求解思路 首先我们需要制备一个初态, 即一个均匀分布的量子叠加态${|+ \rangle}^{ \otimes N}$ ; 然后需要以$ {H}_{\mathrm{C}} $ 和$ {H}_{\mathrm{B}} $ 两个哈密顿量为生成元制备两个酉变换, 它们分别为$ {H}_{\mathrm{C}} $ 为(4 )式表示的哈密顿量, $ {\gamma }_{i} $ 为参数; $ {H}_{B} $ 为初态量子叠加态${| + \rangle}^{ \otimes N}$ 对应的哈密顿量, 等于$\displaystyle\sum \nolimits _{n=1}^{N}{\mathrm{\sigma }}_{n}^{X}$ , 即所谓的混合哈密顿量, $ {\beta }_{i} $ 为参数. 交替使用含有参数的$ U\left({H}_{\mathrm{C}}, {\gamma }_{i}\right) $ 和$ U\left({H}_{\mathrm{B}}, {\beta }_{i}\right) $ 两个酉变换作用于量子叠加态${| +\rangle }^{ \otimes N}$ . 当交替次数为$ k $ 时, 得到的量子态如下:$ \gamma =\left({\gamma }_{1}, \cdots, {\gamma }_{k}\right) $ , $ \beta =\left({\beta }_{1}, \cdots, {\beta }_{k}\right) $ . 通过计算基对量子态$\left|{\psi }_{k}\left(\gamma, \beta \right) \right\rangle$ 进行测量, 得到$ {H}_{\mathrm{C}} $ 在$\left|{\psi }_{k}\left(\gamma, \beta \right) \right\rangle$ 上的期望值:14 )式可以得出, 当$ {H}_{\mathrm{C}} $ 对应的能量本征值越低的那个本征态出现的概率越高时, 则期望值就越小, 从而$ \mathrm{\mu }\left({C}_{1}, \cdots, {C}_{\left|P\right|}\right) $ 越接近0. 所以, 我们通过经典优化算法对参数$ \gamma $ 和$ \beta $ 进行优化, 使得$ {H}_{\mathrm{C}} $ 的期望值最小化.15 )式中$ \left({\gamma }^{*}, {\beta }^{*}\right) $ 为参数$ \gamma $ 和$ \beta $ 经过优化后所取得数值.图1 所示, 主要由量子处理器和经典处理器两部分组成. 经典处理器部分为辅助模块, 主要采用经典优化方法对参数$ \gamma $ 和$ \beta $ 进行优化, 辅助量子处理器部分完成对酉变化中参数$ \gamma $ 和$ \beta $ 取值的调整; 量子处理器部分为主体模块, 主要采用QAOA算法进行量子态演化和问题求解.图 1 QAOA实现框架示意图Figure1. Schematic diagram of the QAOA implementation.3.3.基于QAOA的量子线路设计方案 -->3.3.基于QAOA的量子线路设计方案 与经典计算相对应, 量子计算机通过量子线路来执行程序. 为了使QAOA在量子软件开发环境中运行, 需要设计相应的量子线路.图2 所示. 首先是制备量子初态${| + \rangle}^{ \otimes N}$ , 主要通过给每个量子比特作用一个$ H $ 门来实现. 然后实现以$ {H}_{\mathrm{C}} $ 和$ {H}_{\mathrm{B}} $ 两个哈密顿量为生成元, 得到两个酉变换乘积的累积$ U\left(\gamma, \beta \right) $ ,图 2 基于QAOA的4个量子比特量子线路图Figure2. Four-qubit quantum circuit based on QAOA.16 )式中$ k $ 代表演化的步数, 两个酉变换之间的乘积代表每一步对应的量子线路; $ {\beta }_{i} $ 和$ {\gamma }_{i} $ 为每一步对应的参数. 一般演化的步数越大, 量子线路得到的效果就越好. 最后采用计算基进行测量. 其中第一部分和第三部分都比较容易实现, 下面重点推导第二部分的量子线路.$ {H}_{\mathrm{B}} $ 为生成元、参数为$ {\beta }_{i} $ 的酉变换, 将哈密顿量$ {H}_{\mathrm{B}} $ 的值代入, 可以推导出一组$ \mathrm{R}\mathrm{X} $ 门操作. 推导如下:$ {H}_{\mathrm{C}} $ 为生成元, 参数为$ {\gamma }_{i} $ 的酉变换, 将哈密顿量$ {H}_{\mathrm{C}} $ 的值代入, 可以推导出$ \mathrm{C}\mathrm{N}\mathrm{O}\mathrm{T} $ 门和$ \mathrm{R}\mathrm{Z} $ 门的组合操作以及一组$ \mathrm{R}\mathrm{Z} $ 门单独操作. 推导如下:图2 所示, 环节2为演化步数为1时对应的量子线路图. 如果演化步数为$ k $ 时, 对应的第二部分量子线路重复$ k $ 次.4.仿真结果与分析 24.1.迭代次数的优化与分析 4.1.迭代次数的优化与分析 本文对6种平台12种任务的C2组织任务规划问题进行实验研究, 问题相关信息在表1 中详细列出. 在整个实验过程中, 为了使QAOA得到理想的结果, 在经典计算部分必须能够取得较优的$ \left({\gamma }^{*}, {\beta }^{*}\right) $ 数值. 这部分通常采用的经典优化算法有梯度下降算法、Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法[29 ] 、Nelder-Mead算法[30 ] 和贝叶斯优化算法[31 ] , 采用动量梯度下降法, 在Python3运行环境下实现. 为了得到较优的$ \left({\gamma }^{*}, {\beta }^{*}\right) $ , 我们在经典优化过程中分别将迭代次数设置为10, 20, 30, 40, 50, 60, 70, 80, 90和100进行计算, 并对结果进行对比分析.平 台 1 2 3 4 5 6 平台可执 1,2,3 1,2,3,4 3,4,5,6 5,6,7,8 7,8,9,10 9,10,11,12
表1 平台对应可执行任务分配方案Table1. Platforms corresponding executable mission allocation.图3 所示为迭代次数为10, 20, 30, 40, 50, 60, 70, 80, 90和100情况下, 演化步数$ k $ 从2至12, 目标函数对应的损失值(因为目标函数对应的损失值趋近于负的const, 所以目标函数绝对值越大表示得到的$ \left({\gamma }^{*}, {\beta }^{*}\right) $ 数值越优, 取得正确解的概率越大). 水平坐标分别表示迭代次数和演化步数, 纵坐标表示目标函数对应的损失值. 图3 中结果显示在演化步数相同的情况下, 迭代次数为50对应的损失值的绝对值普遍高于其他迭代次数对应的损失值的绝对值. 这是因为随着迭代次数增大, 算法在计算的过程中出现了过拟合现象. 如图4 所示为在演化步数为12时, 迭代次数分别为50, 60, 70, 80, 90和100对应损失值的曲线图. 而在迭代次数相同的情况下, 随着演化步数增加, 对应损失值的绝对值也随之增加, 这与相关理论完全吻合. 所以, 在接下来的实验中, 将迭代次数设置为50进行实验研究.图 3 不同迭代次数和演化步数对应的损失值Figure3. Loss values corresponding to different iterations and evolution steps.图 4 演化步数为12, 迭代次数分别为50?100对应的损失值Figure4. The corresponding loss values with 12 evolution steps and 50?100 iterations, respectively.4.2.仿真结果分析 -->4.2.仿真结果分析 本文主要利用本源量子开发的pyQPanda量子软件开发环境在Python3中对上述设计的量子线路进行仿真实现. 图5 表示的是在迭代次数为50情况下, 2至12指定演化步数对应的问题正确解概率. 图5 显示随着演化步数的增加, 问题正确解概率随着增大, 在演化步数为12时取得了最大值(89%). 图6 显示了迭代次数为50, 演化步数为12对应的测量结果. 从结果可以得出, 本文中提出的基于QAOA的求解方案可以用于求解C2组织中任务规划问题.图 5 迭代次数为50, 演化步数为2至12对应的问题正确解概率Figure5. The accuracy of the QAOA with 50 iterations and 2?12 evolution steps.图 6 迭代次数为50, 演化步数为12对应的测量结果Figure6. Results with 50 iterations and 12 evolution steps.4.3.基于QAOA的求解方案复杂度分析 -->4.3.基于QAOA的求解方案复杂度分析 采用了动量梯度下降法对量子线路中的参数进行优化, 属于启发式策略优化方法. 结合文献[32 ]的研究内容和本文仿真实验设计, 提出的基于QAOA的量子线路求解方案的时间复杂度为$ O\left[\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(k\right)\right] $ , 其中$ k $ 为上述中的演化步数. 而传统的求解算法时间复杂度为$ O\left(m\cdot {n}^{2}\right) $ , 其中$ m $ 为平台数量, $ n $ 为任务数量. 所以, 随着平台和任务数量的增加, 基于QAOA的量子线路求解方案的时间复杂度要优于传统求解算法时间复杂度.5.结 论 本文根据C2组织中的任务规划问题特点, 将其转化成组合优化中的精确覆盖问题. 通过理论推导提出了一种基于QAOA算法的量子线路求解方案, 并利用经典优化算法对量子逻辑门中的参数进行优化, 在本源量子开发的pyQPanda量子软件开发环境中进行仿真编译. 仿真结果表明, 本文提出的基于QAOA的量子线路设计及方法可以有效求解C2组织中的任务规划问题, 为提高任务规划问题的求解速度提供了理论支撑. 经过分析, 本文所采用的QAOA算法是一种普适的方法. 实际中能转化为组合优化中的精确覆盖问题的实际问题都可以尝试采用本文的求解方案进行求解. 下一步将通过采用一些群智能算法[33 ] 进一步优化适用于求解任务规划问题的QAOA算法设计与实现, 在降低经典计算部分复杂度的同时提高参数的优化效果; 另一方面对量子线路中的量子逻辑门进行优化, 在降低演化步数的同时提高计算的正确率. 







































































































































 图 1 QAOA实现框架示意图
图 1 QAOA实现框架示意图




 图 2 基于QAOA的4个量子比特量子线路图
图 2 基于QAOA的4个量子比特量子线路图




























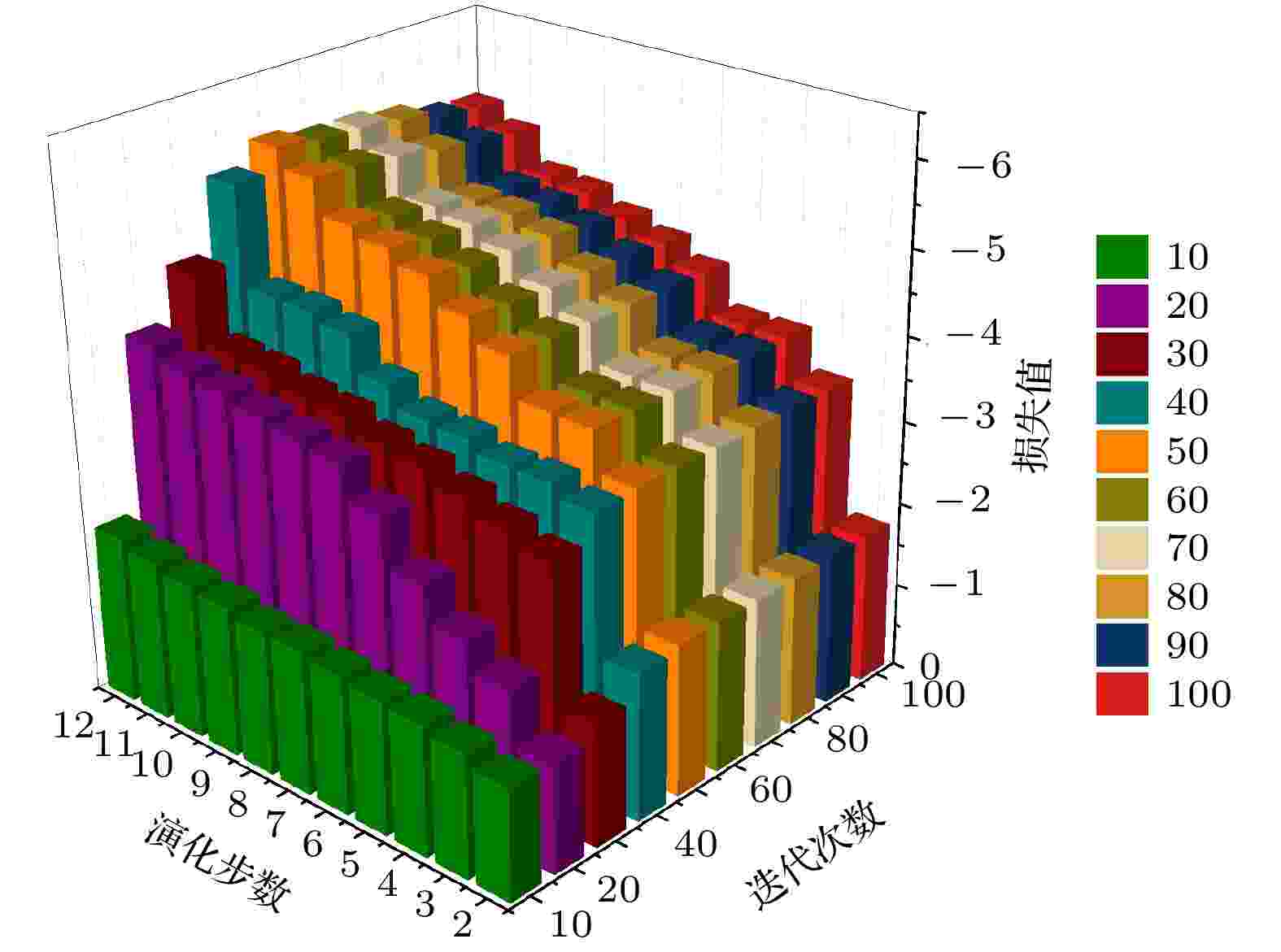 图 3 不同迭代次数和演化步数对应的损失值
图 3 不同迭代次数和演化步数对应的损失值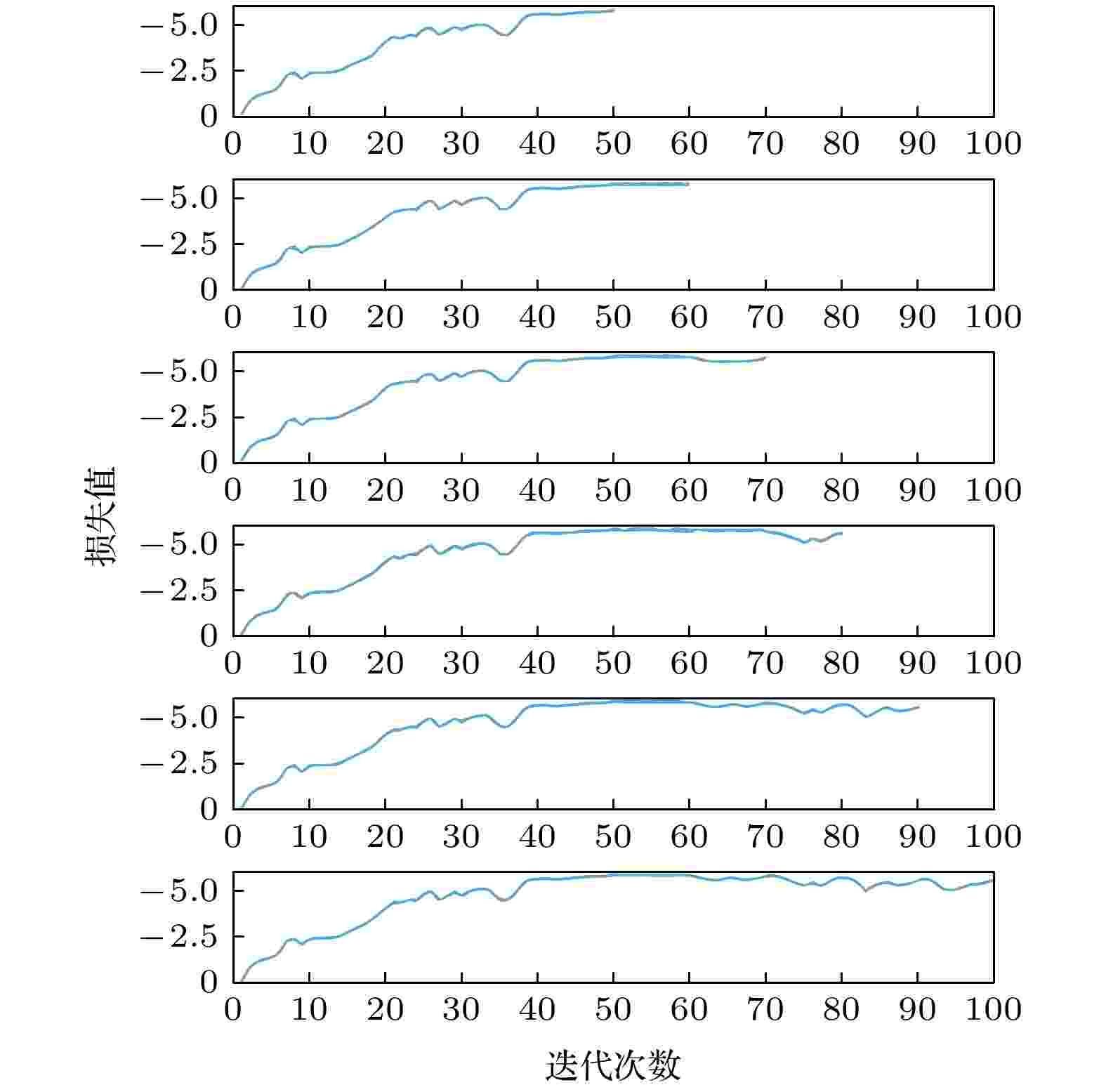 图 4 演化步数为12, 迭代次数分别为50?100对应的损失值
图 4 演化步数为12, 迭代次数分别为50?100对应的损失值 图 5 迭代次数为50, 演化步数为2至12对应的问题正确解概率
图 5 迭代次数为50, 演化步数为2至12对应的问题正确解概率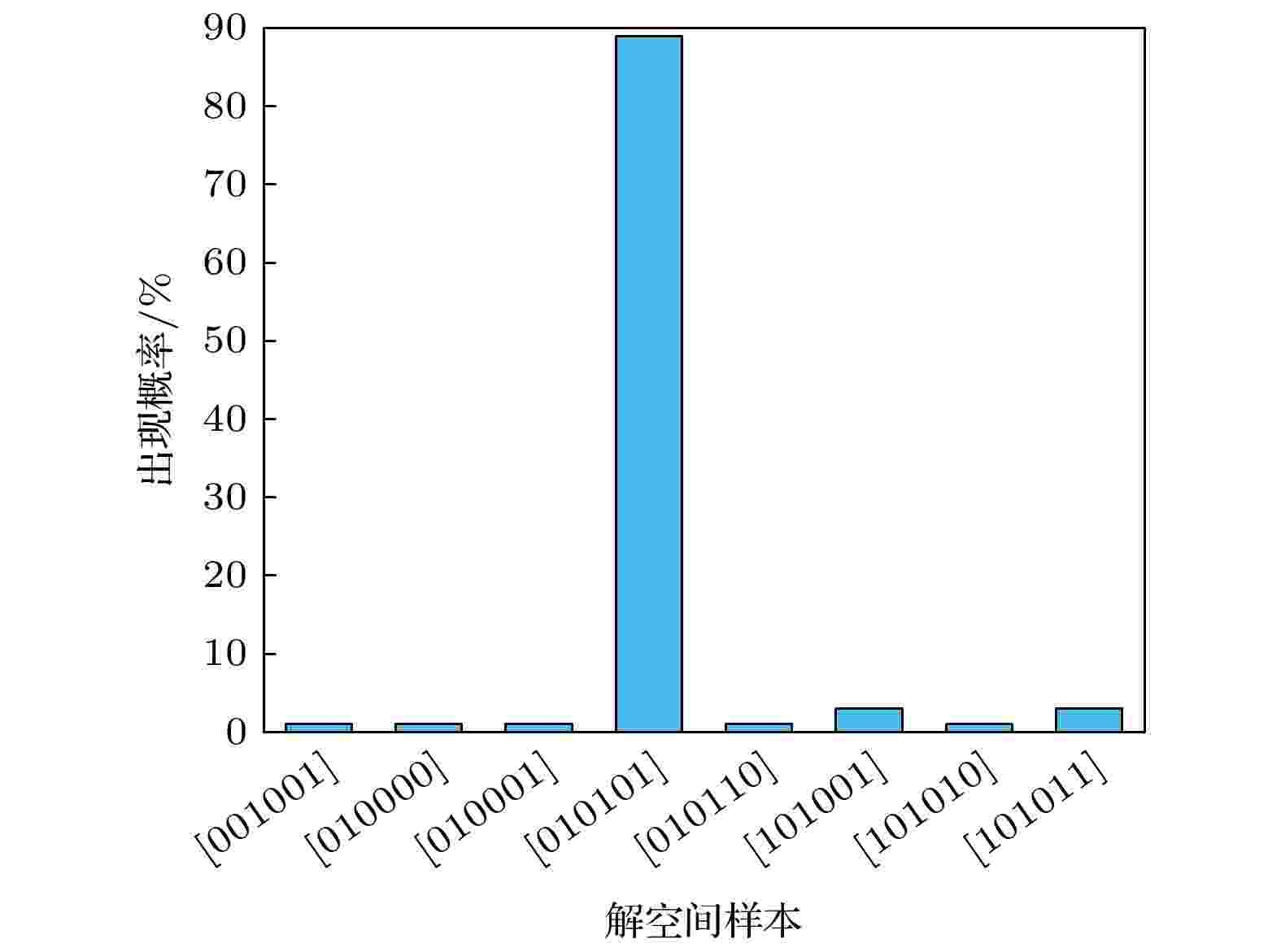 图 6 迭代次数为50, 演化步数为12对应的测量结果
图 6 迭代次数为50, 演化步数为12对应的测量结果




