全文HTML
--> --> -->为了获得高效率CIGS电池, 有效的技术方法包括: 1)“V”型Ga梯度, 可以在不损失光电流的情况下提升开路电压; 2)碱金属后处理(PDT)钝化缺陷; 3)无镉缓冲层减少界面能级失配及CdS电子传输层的光吸收等. 其中, Solar Frontier公司利用Ga梯度调控和无镉双缓冲层的方法获得了23.35%的记录效率. Ga梯度调控可以有效调控CIGS带隙在层中的纵向分布; 调节Ga/(Ga+In)(GGI)占比可以调节CIGS的带隙范围(1.01—1.68 eV)[2]. 因而, 调节GGI及Ga梯度可以平衡电池的光吸收及开路电压输出, 是获得高效率器件性能的关键方法. 目前, 国内外的众多研究中重点研究了Ga含量对电池性能的影响, 给出了GGI最优占比为0.30—0.33[3,4]. 研究者对GGI梯度的影响也进行了一些研究, 在GGI平梯度、单梯度、以及“V”型双梯度三种分布种类中, “V”型Ga梯度分布被证明是一个有效提升器件性能的的方法[5-7]. 采用“V”型梯度分布, 高能量光子可以在薄膜表面宽带隙处被吸收, 而红外区域的光子在穿过薄膜表面以后在薄膜内部被吸收, 这种带隙的梯度分布最大程度地提高了光子的吸收效率.
虽然“V”型Ga梯度分布是一种获得高器件性能的有效方法, 然而, 受限于实验制备的复杂性及时间、材料和人力成本, 对其系统优化以筛选最佳GGI梯度分布比较困难. 器件模拟方法是快速筛选器件结构和材料的一种有效方法, 是太阳能电池研究中的一种有效手段, 但器件模拟存在一些困难, 例如, 如何合理设置材料物理参数以反映器件内的真实情况. 机器学习是近年来迅速发展的一种人工智能方法, 它基于神经网络、随机森林等算法对训练数据集进行学习、建立输入指征与输出性能之间的映射模型; 通过采用合适的训练数据集、优化算法参数, 可以对输入指征与输出之间的关联进行量化分析, 并对输出性能进行较为准确的预测. 近期机器学习在太阳能电池领域(如有机太阳能电池、钙钛矿太阳能电池等)被用来优化和筛选材料及器件结构[8,9]. 我们前期利用机器学习方法, 基于报道的实验数据, 模拟CIGS组分(包含GGI分布)及器件制备参数和结构对器件光电转换性能的影响, 并对器件性能实现了较为准确的预测[10]. 因而, 以实验数据作为训练集建立机器学习模型, 可以从实验经验中进行学习, 从而弥补器件模拟偏向于理想化模型的不足, 并且可以辅助筛选器件模拟中所采用的参数及评估模拟结果的合理性. 另一方面, 器件模拟可以从物理机理上辅助解释机器学习结果, 弥补机器学习可解释性差的问题. 因而, 结合机器学习和器件模拟的方法, 可以结合实验和理论经验, 并对结果进行交叉验证, 有望实现对GGI梯度的系统优化, 为实验提供指导.
因此, 本文采用机器学习与太阳能电池模拟软件wxAMPS模拟分析相结合, 建立了不同的“V”型Ga梯度的CIGS电池模型, 详细分析了Ga梯度对器件性能的影响及规律, 给出了不同位置Ga含量的最优数值, 优化分析了“V”型双梯度的分布, 探究了其内部载流子作用机理.
2.1.CIGS电池效率极限分析
为了明确器件模拟和机器学习优化的目标, 首先对比分析了单结太阳能电池的效率极限(Shockley-Queisser(S-Q)效率极限). 对比了晶硅(c-Si)、CIGS、钙钛矿三种电池最新的实验值记录, 如表1所列. 为了分析这些参数与SQ效率极限值的差异, 计算了每种材料的两个特征参数, 包括: 1)实验与理论极限短路电流比
| Cell type | Eth/eV | PCE/% | VOC/mV | JSC/(mA·cm–2) | FF/% | JSQ/(mA·cm–2) | WOC/mV | JSC/JSQ/% | 机构 | 参考文献 |
| CIGS | 1.088 | 23.35 | 734.0 | 39.58 | 80.4 | 44.0 | 354.0 | 89.95 | SF | [1] |
| CIGS | 1.130 | 22.92 | 746.0 | 38.50 | 79.7 | 43.0 | 384.0 | 89.53 | SF | [11] |
| CIGS | 1.143 | 22.60 | 741.0 | 37.80 | 80.6 | 42.3 | 402.0 | 89.36 | ZSW | [12] |
| CIGS | 1.110 | 22.30 | 722.0 | 39.40 | 78.2 | 43.7 | 388.0 | 90.16 | SF | [13] |
| c-Si | 1.120 | 26.70 | 738.0 | 42.65 | 84.9 | 43.3 | 382.0 | 98.50 | Kaneka | [14] |
| c-Si | 1.120 | 26.60 | 740.3 | 42.50 | 84.7 | 43.3 | 379.7 | 98.15 | Kaneka | [14] |
| c-Si | 1.120 | 26.30 | 744.0 | 42.30 | 83.8 | 43.3 | 376.0 | 97.69 | Kaneka | [15] |
| c-Si | 1.120 | 26.10 | 726.6 | 42.62 | 84.3 | 43.3 | 393.4 | 98.43 | ISFH | [16] |
| 钙钛矿 | 1.550 | 25.20 | 1180.5 | 25.14 | 84.8 | 27.1 | 369.5 | 92.77 | KRICT | [17] |
| 钙钛矿 | 1.480 | 24.64 | 1181.4 | 26.18 | 79.6 | 29.5 | 298.6 | 83.53 | UNIST | [18] |
| 钙钛矿 | 1.574 | 24.20 | 1194.8 | 24.16 | 84.0 | 26.2 | 379.2 | 92.21 | KRICT | [19] |
| 钙钛矿 | 1.536 | 23.70 | 1169.7 | 25.40 | 79.8 | 27.6 | 366.3 | 92.03 | ISCAS | [20] |
表1CIGS, c-Si, 钙钛矿三种电池的光伏特性参数、S-Q极限值及差值分析. Eg, PCE/VOC/JSC/FF, JSQ, WOC分别代表材料的带隙、电池的转换效率/开路电压/短路电流密度/填充因子、SQ极限计算的短路电流密度、VOC损失
Table1.Photovoltaic parameters, S-Q limit value and difference analysis of CIGS, c-Si, and perovskite solar cells. Here, Eg, PCE/VOC/JSC/FF, JSQ, WOC respectively represent the band gap of the absorption material, the photoelectric conversion efficiency/open circuit voltage/short-circuit current density/fill factor of the solar cells, the short-circuit current density calculated by the SQ limit, and the VOC loss.
2
2.2.器件模拟模型设计及模拟参数
为了使器件模拟中采用的物理参数设置值更能反映真实器件情况, 首先模拟了当前最高效率23.35%的器件情况, 所使用的器件结构由衬底/Mo/CIGS/Zn(O, S, OH)x/Zn0.8Mg0.2O/BZO构成. 提取文献中的带隙梯度数据, 将文献中采用的厚度为1 μm的CIGS吸收层分为了20层(等厚度), 通过设置20个分层中每层所对应的不同电子亲和势及禁带宽度, 模拟Ga梯度引起的带隙的变化, 结果如图1所示. 带隙与Ga梯度的关系为Eg =
图 1 CIGS吸收层带隙梯度变化Figure1. Band gap gradient change of CIGS absorber layer.
| B:ZnO | Zn(Mg, O) | Zn(O, S, OH)x | CIGS | |
| Thickness/nm | 500 | 50 | 8 | 1000 |
| Permittivity/1 | 9 | 10 | 9 | 13.6 |
| Eg/eV | 3.3 | 3.6 | 3.6 | 1.06—1.66 |
| Affinity/eV | 4.4 | 4.2 | 4.2 | 3.89—4.49 |
| Nc/(1018 cm–3) | 2.2 | 2.2 | 2.2 | 2.2 |
| Nv/(1019 cm–3) | 1.8 | 1.8 | 1.8 | 1.8 |
| μn/(cm2·V–1·s–1) | 100 | 100 | 100 | 100 |
| μp/(cm2·V–1·s–1) | 25 | 25 | 25 | 25 |
| Nd/(1017 cm–3) | 10 | 10 | 1 | 0 |
| Na/(1016 cm–3) | 0 | 0 | 0 | 2 |
表2器件模拟中使用的参数设置
Table2.Parameter settings used in device simulation.
图2给出了实验获得的和模拟得到的器件电流密度-电压(J-V)曲线, 可以发现二者符合度非常好, 说明模拟参数和模型设置较为合理. 因此, 本文采用这些参数对不同GGI梯度器件性能的影响进行模拟.
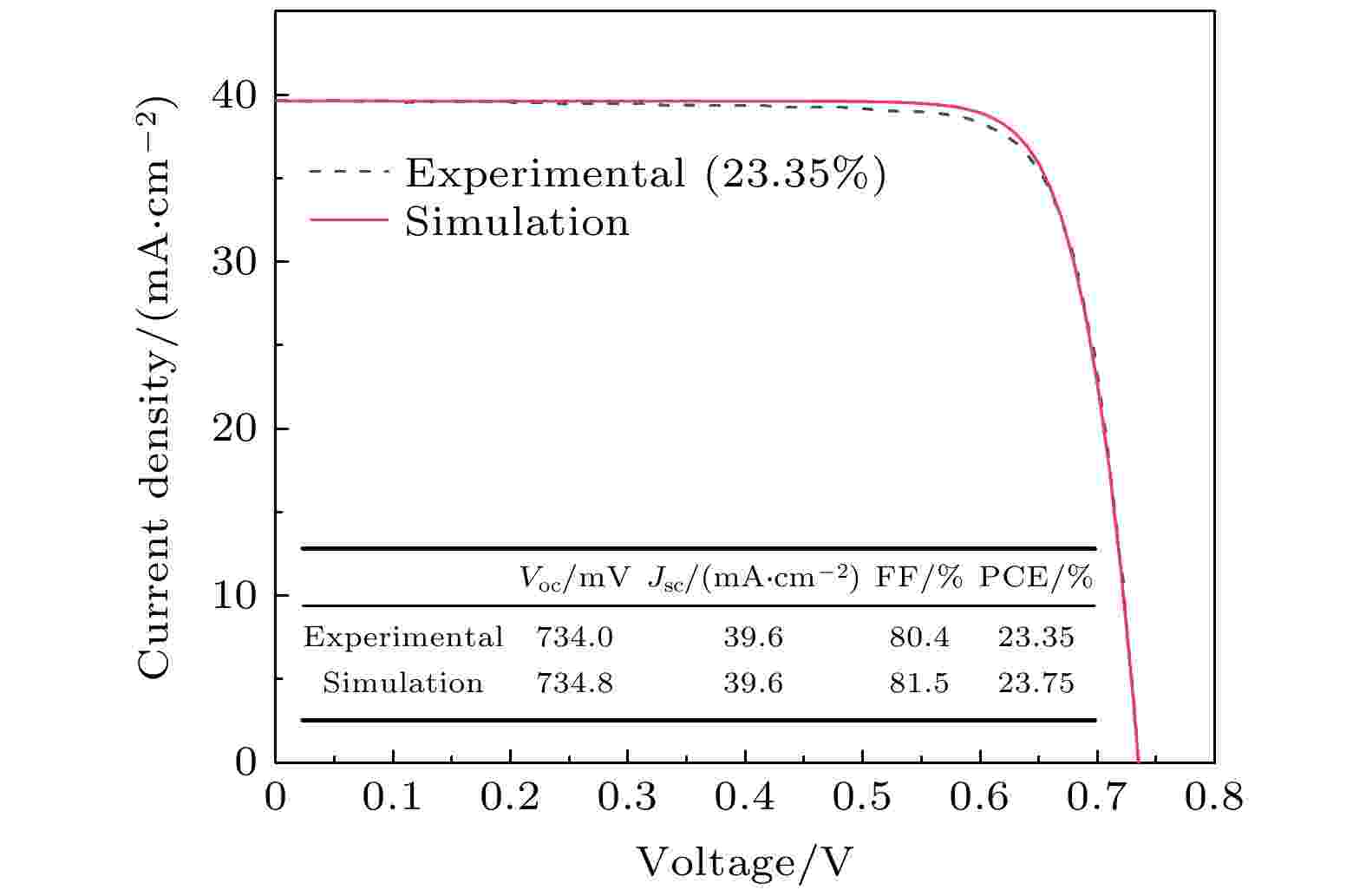图 2 实验与模拟得到的CIGS太阳能电池J-V特性Figure2. J-V characteristic of experimental data and simulation result for the CIGS solar cell.
2
2.3.机器学习算法和参数设置
从文献中收集实验数据作为机器学习的数据集, 包括120多篇最近发表的论文中的300多个数据点, 从中筛选信息记录全、PCE ≥ 10%的数据点作为本文的数据集, 详细的数据集信息记录及数据清洗方法参看我们前期的论文[10]. 使用R工具(版本3.6.2), 基于前期利用随机森林(random forest)算法建立的优化模型进行预测, 随机森林对器件PCE的预测均方根误差小于1.5%. 为了反映CIGS层内的GGI浓度梯度, 对GGI使用了三个特征, 包括背面Ga含量(靠近Mo接触, GGIB)、位于CIGS层内的Ga含量(最小的带隙位置, GGIM)和表面Ga含量(靠近 n型缓冲层接触, GGIF), 如图3(b)所示. 机器学习模型中采用的其他指征包括[Cu]/([Ga]+[In])比率、CIGS吸收层厚度、缓冲层材料及厚度、CIGS制备方法(共蒸发或其他)、基板温度、基板或预沉积层是否含碱金属、是否碱金属后处理.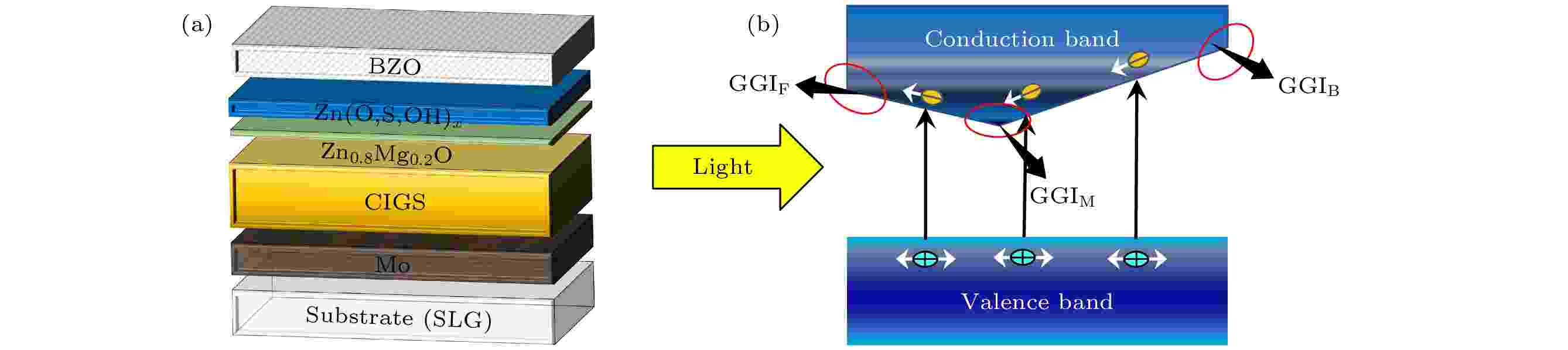
图 3 (a) CIGS电池器件结构; (b) CIGS层中GGI梯度示意图Figure3. (a) Device structure of the CIGS solar cells; (b) schematic illustration of GGI gradient in CIGS.
3.1.机器学习预测结果分析
为了了解不同位置的GGI对光伏参数的特定贡献, 本文基于机器学习数据集计算了GGI与光伏特性参数之间的Pearson相关系数, 如表3所列. 可以看出, GGIF, GGIM, GGIB与VOC整体呈正相关, 与JSC整体呈负相关性, 亦即高的GGI可提升VOC、但不利于获得高JSC. 另外还可以看出, GGIM与JSC相关性更强, 因为在V型梯度中, 越低的GGIM越利于获得高的JSC.| GGIF | GGIM | GGIB | |
| VOC | 0.38 | 0.35 | 0.34 |
| JSC | –0.26 | –0.41 | –0.12 |
表3不同位置GGI与光伏参数之间的相关性
Table3.Correlation between GGI value at different location and photovoltaic parameters.
图4给出了针对不同的GGIB, GGIM和GGIF数据随机森林算法预测的器件效率. 随着GGIB含量的增大, 电池转换效率PCE值也随之增大. 这是因为, 高GGI区会加大背表面的禁带宽度、增强背电场强度, 而背表面电场的存在会促使光电子远离CIGS/Mo界面、减少界面复合. 但是, 过宽的背面带隙也会降低光吸收, 因此在GGIB达到0.8(对应带隙值为1.53 eV)之后, PCE, VOC, FF, JSC不再增加. 文献报道背表面CIGS带隙宽度不超过1.5 eV为宜[27], 这与我们采用机器学习的预测值比较一致.
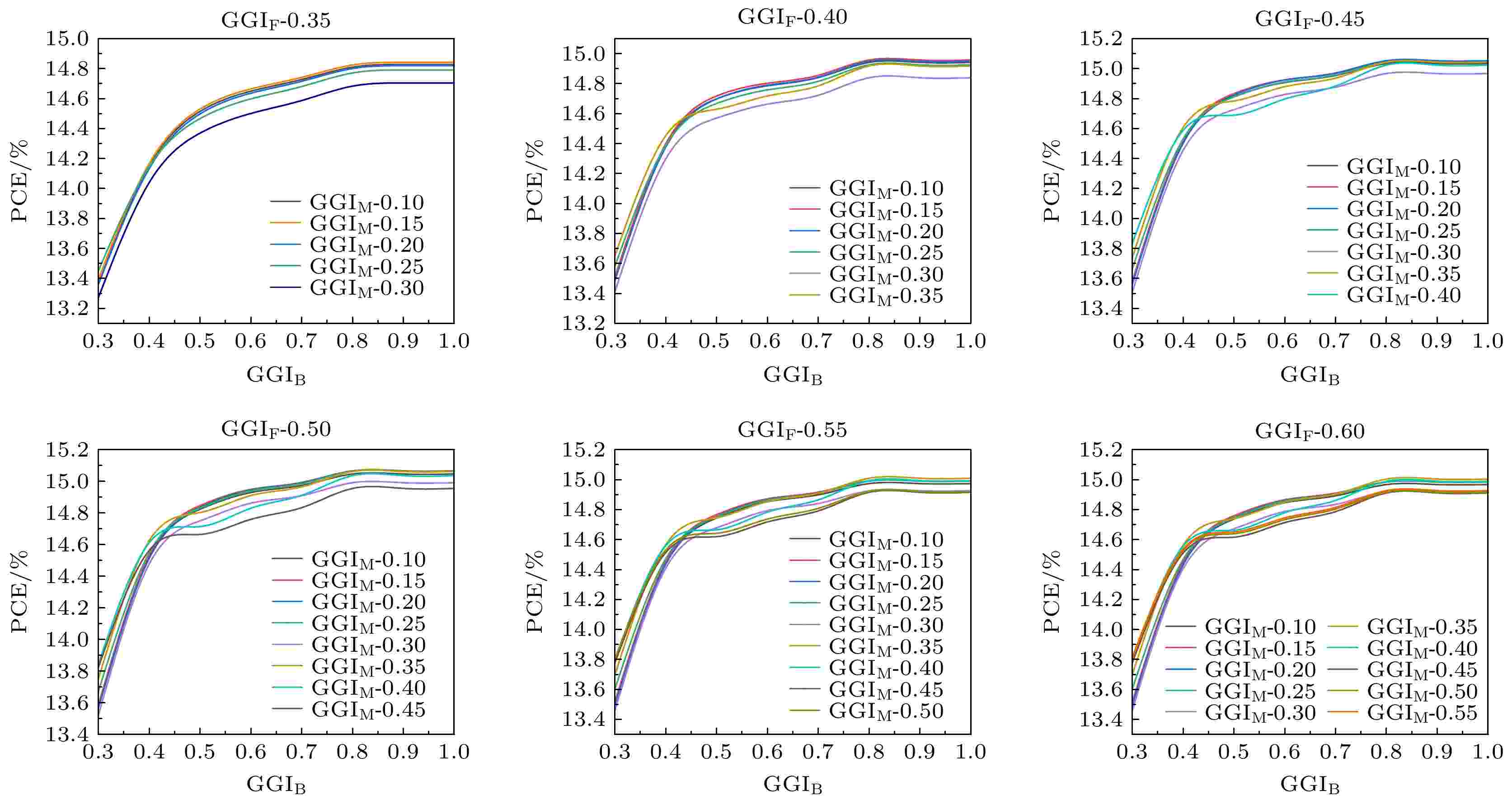图 4 RF算法预测的电池效率随GGIF/GGIM/GGIB变化的曲线Figure4. Changes of predicted efficiency by RF algorithm with GGIF/GGIM/GGIB.
图5是GGI对CIGS电池转换效率影响的三维映射图, 可以看出, 电池转换效率的峰值范围集中在前表面Ga含量GGIF = 0.45—0.50. 有文献研究表明, CIGS吸收层与缓冲层的导带失调值(ΔEC)在合适的范围内, 可以抑制电池吸收区的复合, 有效提高电池的VOC[27]. 因此, 对于特定带隙的缓冲层材料, 必然会有一个最优的GGIF范围构成最优的导带失调值. 相比于CdS缓冲层, Zn(Mg, O)/Zn(O, S, OH)x缓冲层拥有更高的带隙, 前表面Ga含量GGIF能够接受的数值比CdS材料更大, 因而有可能获得更高的效率.
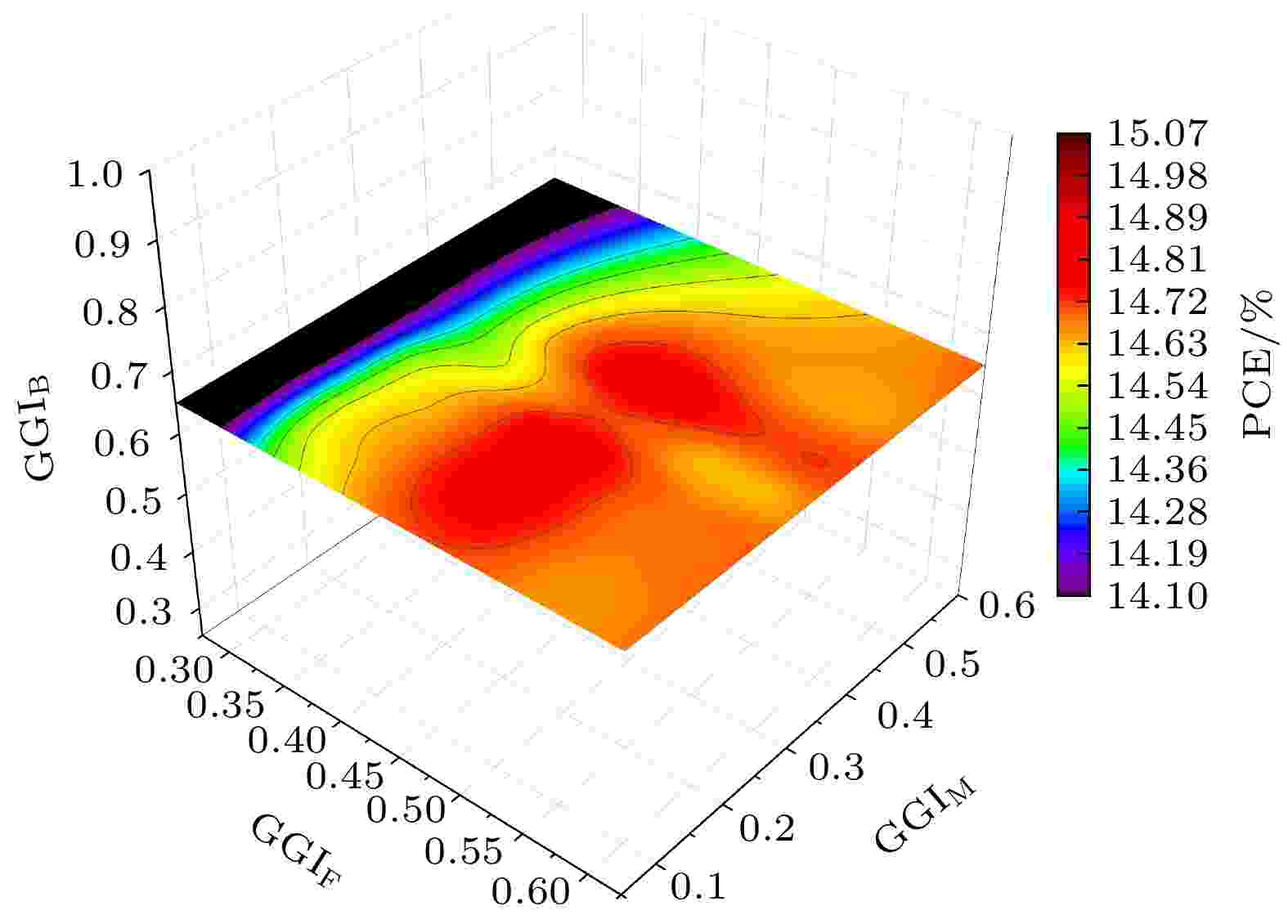图 5 RF算法预测的不同GGI值情况下的器件效率Figure5. Device efficiency predicted by RF algorithm under different GGI values.
从图5可以发现, 在最优的GGIF范围内对应了两个高效率峰值等高线, 一个在GGIF与GGIM梯度差ΔGGIFM为0.25—0.35时; 一个在GGIF与GGIM梯度差ΔGGIFM为0—0.1时. 这是因为当GGIF与GGIM相差大的时候, 较小的GGIM提升了长波长光子的吸收, 此时, 较大的GGIB带来的背电场使得器件性能的增益较明显, 即“深V”型梯度更好. 而当GGIF与GGIM相差小的时候, 大的背梯度GGIB带来的背电场对器件性能的增益不明显, 而过高的背梯度反而减少了长波段光的吸收, 因而采用小的GGIB更利于获得更高的效率, 即“浅V”型梯度更好.
图6给出了机器学习筛选的6个优化GGI梯度(模型1—模型6)及预测的器件性能.模型0为转换效率为23.35%, 文献中采用的GGI梯度(0.55—0.98)及机器学习对该梯度预测的性能. 可以发现, 模型0的VOC, JSC, FF, PCE都不是所有模型中最高的数值, GGI梯度模型3—模型6所获得的效率也都比其高, 这说明文献[1](效率23.35%)中所形成的GGI梯度并不是最优的梯度, 可以通过优化GGI的梯度分布进一步提高其转换效率. 另外需要说明的是, 机器学习预测效率整体偏低. 例如, 对于模型0, 预测效率约为14.97%, 低于实验获得的23.35%的效率, 这是由于机器学习训练数据集中有很多较低效率的报道, 因而对高效率电池的预测值相对偏低. 为了模拟高效率电池性能, 进一步采用器件模拟方法, 因为器件模拟中的器件模型是较为理想情况下的器件, 更接近高效率器件的情况.
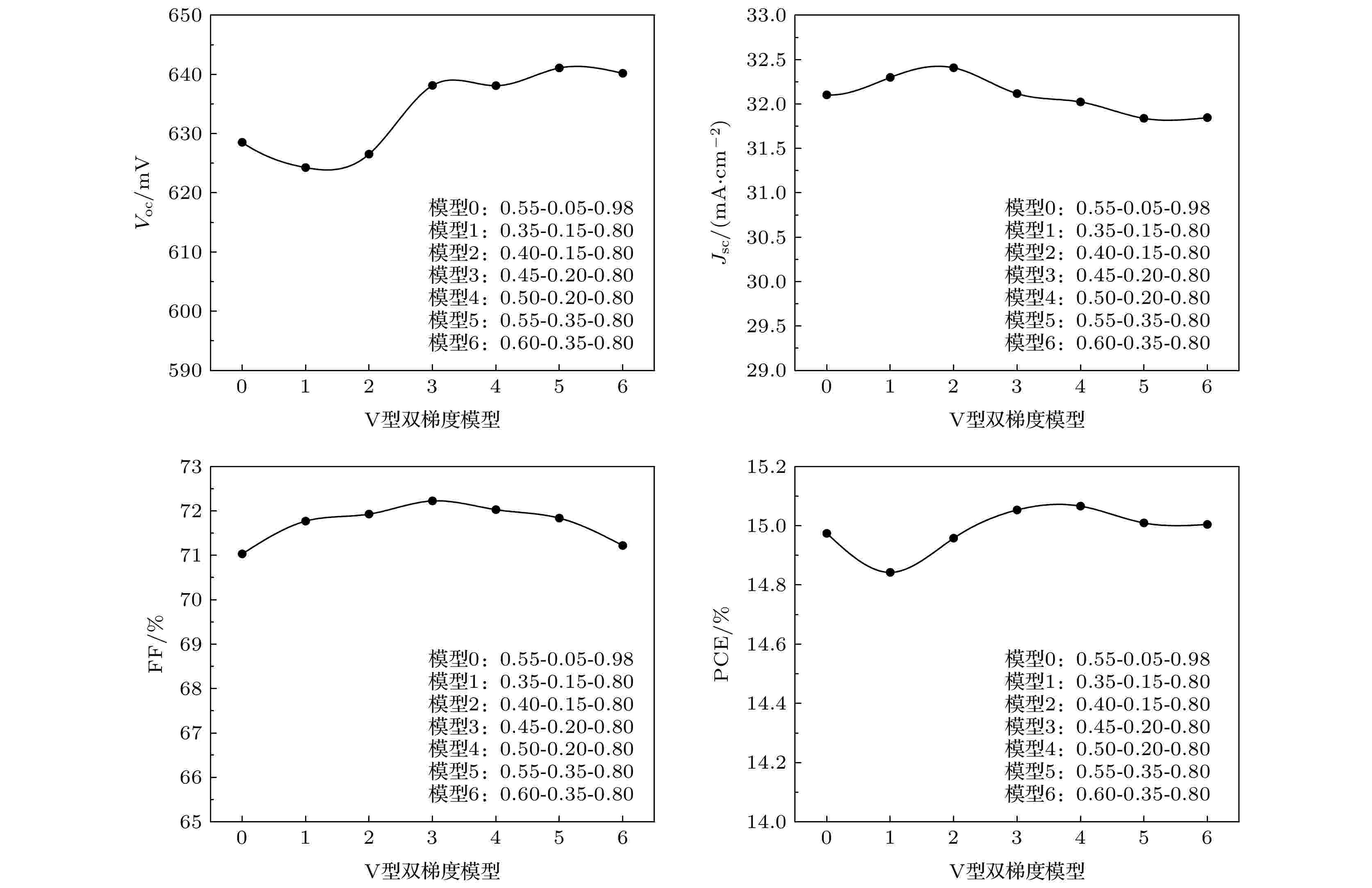图 6 RF算法预测的不同GGI梯度的器件性能. 其中, 0代表实验效率为23.35%的电池所采用的GGI梯度, 模型1—模型6为预测效率最高的6组器件的GGI梯度Figure6. Predicted device performance of the CIGS solar cells based on different GGI gradients by RF algorithm. 0 represents for the GGI gradient used in the device with 23.35% experimental efficiency, while 1–6 are the GGI gradients of the devices with the highest predicted efficiency.
2
3.2.器件模拟结果与分析
考虑CIGS薄膜不同位置上的Ga含量变化, 设计了不同的Ga梯度变化的CIGS电池模型, 参考机器学习的预测结果, 器件模拟中GGIF值的设置范围为0.4—0.6, GGIM值的设置范围为0.1—0.4. 为了避免其他非Ga梯度因素带来的影响, 需要保证总的Ga平均含量与基础器件一致, 这有利于对薄膜表面、内部和背面的Ga含量的差别带来的影响进行比较分析. 在此基础上考虑薄膜不同位置上的GGIB变化并设计了14个不同的Ga梯度变化模型, 然后使用wxAMPS进行模拟仿真. 梯度范围如表4所列, 梯度曲线如图7所示. 模型1—模型6是GGIF = 0.4情况下, GGIM依次增大, GGIB依次减小; 模型7—模型10是GGIF = 0.5情况下, GGIM依次增大, GGIB依次减小; 模型11—模型14是GGIF = 0.6情况下, GGIM依次增大, GGIB依次减小.| 模型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| GGIF | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.50 |
| GGIM | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.10 |
| GGIB | 0.84 | 0.77 | 0.71 | 0.65 | 0.58 | 0.52 | 0.80 |
| 模型 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| GGIF | 0.50 | 0.50 | 0.50 | 0.60 | 0.60 | 0.60 | 0.60 |
| GGIM | 0.20 | 0.30 | 0.40 | 0.10 | 0.20 | 0.30 | 0.40 |
| GGIB | 0.67 | 0.54 | 0.42 | 0.76 | 0.63 | 0.50 | 0.44 |
表4wxAMPS器件模拟所用的GGI梯度模型
Table4.Schemes of GGI gradient used for wxAMPS device simulation.
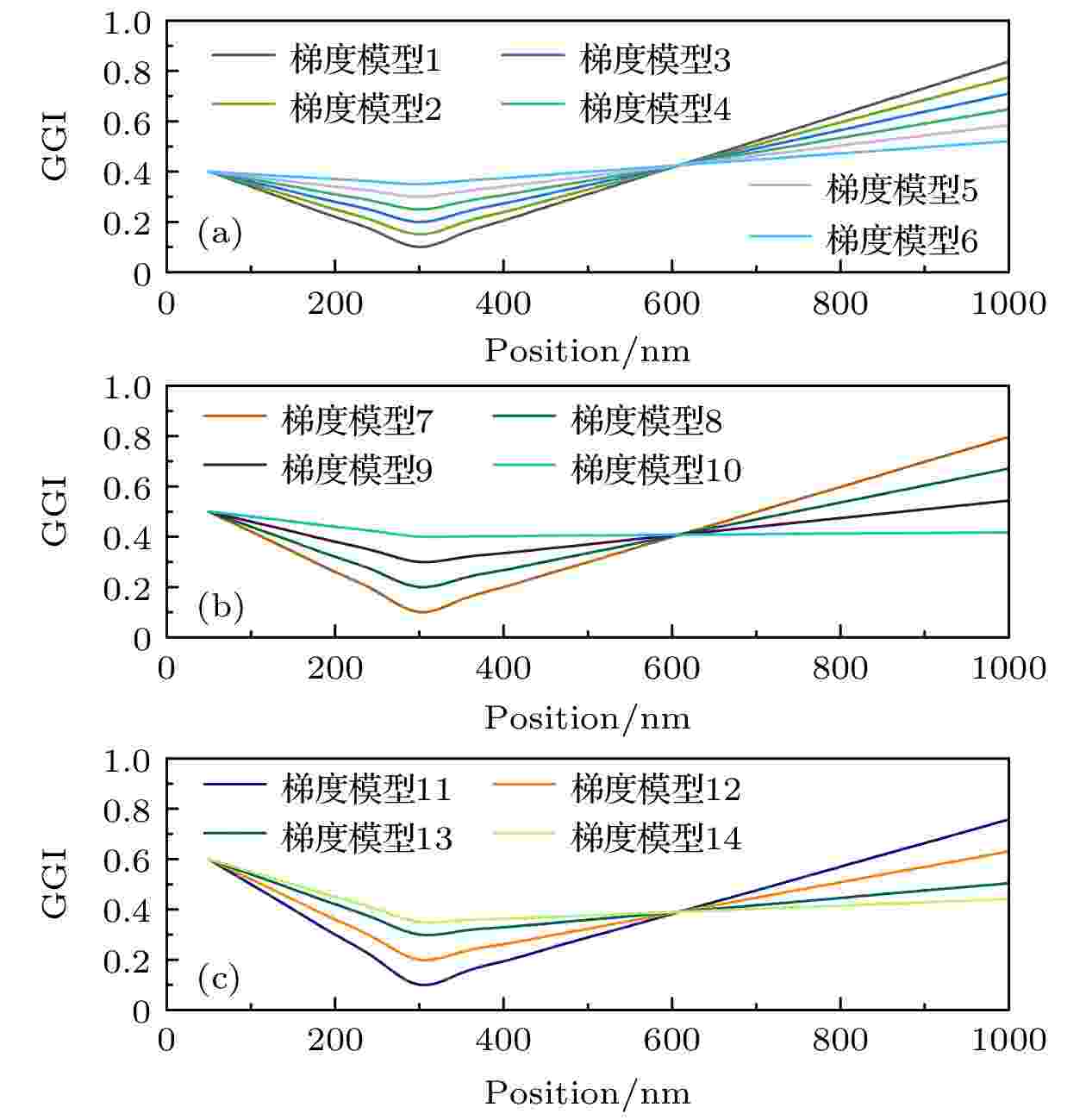图 7 器件模拟采用的14种“V”型双梯度模型 (a) GGIF = 0.4; (b) GGIF = 0.5; (c) GGIF = 0.6Figure7. 14 types of “V”-shaped double GGI gradient schemes used in the device simulation: (a) GGIF = 0.4; (b) GGIF = 0.5; (c) GGIF = 0.6.
图8给出了14个不同梯度变化的“V”型梯度器件性能参数. 图8(a)为CIGS电池的VOC参数图, 可以看出, 电池内部的Ga含量极小值GGIM的大小在很大程度上影响着开路电压. 在不同的前表面Ga含量中(GGIF = 0.4, 0.5, 0.6), 随着GGIM的增大(模型1—模型6、模型7—模型10、模型10—模型14), 电池开路电压随之增加, 这归因于吸收层内部最小禁带宽度的增加. 但是随着Ga含量极小值GGIM的进一步增大, 开路电压VOC和填充因子FF(图8(c))出现下降. 图8(b)为CIGS电池的短路电流参数图, 当前表面Ga含量GGIF确定后, 随着GGIM的增大(模型1—模型6、模型7—模型10、模型10—模型14), 电池的短路电流JSC随之减小, 这是因为大的GGIM增大了吸收层的最小禁带宽度, 使得吸收层在长波段的光谱响应下降. 因此, 对于每一个前表面Ga含量GGIF, 都将存在一个最优的转换效率(如图8(d)所示), 它是平衡了VOC带来的增益和JSC的损失的结果.
图 8 器件模拟得到的不同GGI梯度模型的器件性能Figure8. Device performance of the CIGS solar cells based on different GGI gradient schemes obtained by device simulation.
为了深入探究器件内部载流子机理, 选取每个模型在前表面、内部、后表面的载流子复合速率值进行了对比分析, 如图9所示. 在前表面Ga含量GGIF一定的情况下, 器件内部的载流子复合率随着Ga含量极小值GGIM的增大而增加, 如图9(b)所示; 同时, 后表面Ga含量减小(如表4和图7所示)导致背电场强度减小(如图10所示). 内部的载流子复合率的增加导致了载流子收集效率的降低, 同时CIGS背面电场的减小不利于抑制少数载流子在后表面的复合, 这使得短路电流JSC下降.
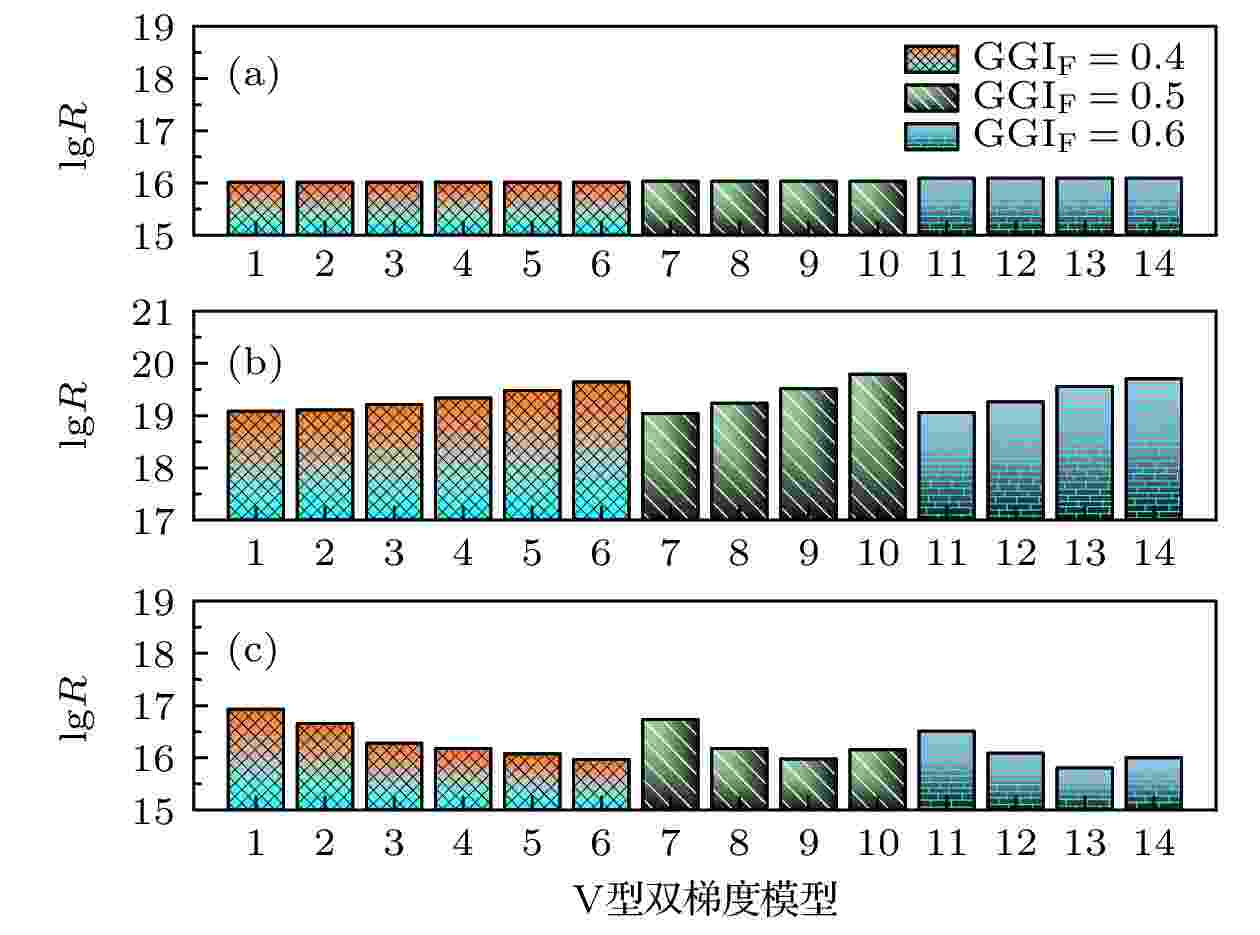图 9 器件模拟得到的CIGS电池不同位置载流子复合速率 (a) 前表面; (b) 电池内部; (c) 后表面. R为复合速率, 单位cm–3·s–1Figure9. Carrier recombination rate at different positions of CIGS solar cells obtained by device simulation: (a) Front surface; (b) interior; (c) rear surface. Here, R is the recombination rate, which unit is cm–3·s–1.
图 10 器件模拟得到的CIGS薄膜背电场强度Figure10. Back electric field intensity of CIGS film obtained by device simulation.
图8(d)为CIGS电池的转换效率参数图, 相比于效率为23.35%的器件所采用的梯度, 本文所设立的14种模型梯度实现了更高PCE, 最大值高于26%. 这也说明“V”型GGI梯度的进一步优化有望实现CIGS效率的进一步突破. 从实验技术的实现来说, 本文设计的多个模型的GGI值的变化范围相对效率为23.35%的器件所采用的更小, 因而实验技术上相对更容易实现. 因此, 这些研究结果可以为实验优化提供指导.
1) GGIF, GGIM, GGIB与VOC整体呈正相关, 与JSC整体呈负相关性, 高的GGI可提升VOC、但不利于获得高JSC. GGIM与JSC的相关性更强, 在V型梯度中, 越低的GGIM越利于获得高的JSC; 2)背面Ga含量GGIB的增大会增强背电场强度, 减少界面复合; 但过宽的背面带隙会提高背表面复合速度, 增加吸收损失. 机器学习筛选的最佳Ga含量背梯度GGIB = 0.8; 3) Ga梯度的优化是实现效率突破的有效方法, 基于优化的Ga梯度, 器件模拟效率最大值高于26%.
