摘要:流体动画模拟的真实感与实时性一直是流体模拟研究中的热点. 针对在复杂地形场景中不稳定的流体表面运动现象, 本文提出一种基于地形差异的自适应流体速度控制力, 建立了稳定性光滑粒子流体动力学方法以求解浅水方程数值模型. 首先, 将模拟域从三维降至二维表面来降低计算量, 通过粒子的密度大小表示其水深高度值; 其次, 采用变长光滑搜索半径, 确保搜索邻域内的粒子数目稳定在固定范围内, 提高模拟精度; 最后引入一种基于地形差异的自适应流体速度控制力, 根据粒子密度大小的实时变化来确定计算速度控制力的地形研究范围, 通过插值计算粒子运动前后时间步所处地形位置的差异来修正粒子的速度和位置. 本文使用屏幕空间流体渲染方法对流体表面进行绘制, 避免了表面网格的提取与重建, 流体的运动数值计算和渲染均被加载到GPU上并行化执行, 实验结果表明在达到实时交互级别的同时, 本文方法有效地改善了在复杂地形场景中流体表面的不稳定运动现象, 同时流体模拟过程中密度与压强的分布均匀.
关键词: 光滑粒子动力学/
浅水方程/
并行计算/
复杂地形

English Abstract

全文HTML

--> --> -->

随着流体仿真技术的发展, 真实感实时流体动画模拟已被广泛应用到商业电影、大型游戏和城市灾害预测系统当中, 其中, 稳定精确的数值求解模型与高计算效率一直是研究中的重要内容^[1].
基于物理的流体模拟方法主要分为欧拉网格法与拉格朗日粒子法, 前者将流体模拟域离散为固定网格, 通过跟踪空间固定点上的质点运动参数来模拟流体表面运动行为; 后者通过将流体离散为自由移动的质点粒子, 通过跟踪单个流体质点的运动参数来还原流体的整体运动情况, 与早期基于过程的流体模拟方法相比, 基于物理的特性使得二者在中小规模的真实感流体动画模拟中有着相当的优势^[2]. 然而, 高分辨率的实时流体动画模拟通常需要上百万个网格质点或粒子^[3], 对计算资源的需求量过于庞大, 因此, 更多的研究工作倾向于将模拟域从三维简化至二维表面, 并在此基础上确保流体运动的真实感^[4]. 一种较为常用的方法是通过欧拉法求解浅水方程(shallow water equations, SWE)来模拟流体表面运动, 将流体所在区域离散为2D固定网格, 在网格点上存储流体表面高度信息值. 离散网格虽然保证了的流体场景模拟的高效率, 但是处理与网格无法精确对齐的不规则域和边界是一大难题, 并且网格的结构难以模拟流体中的稀疏区域和流体流入空区域的情况, 与不规则刚体的交互处理较为困难, 在复杂地形中的通用性较差^[5]. 与欧拉网格方法相比, 基于拉格朗日法的流体粒子可以自由移动到任意位置, 很好地解决了欧拉方法下存在的问题, 典型代表是光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法^[6]. 相比欧拉网格法, 使用SPH方法求解SWE不仅能够将模拟域从3D体积减少到2D表面, 还能够更好地处理与网格无法精确对齐的不规则域和复杂边界问题, 与不规则刚体交互的处理方法也较为完善, 同时粒子的形式也便于在模拟中还原浪花、泡沫等细节效果, 在不同场景中的通用性较强^[7]. 因此, SPH-SWE数值模型在真实感实时流体动画模拟中的研究尤为重要.
在流体动画模拟研究中, SPH-SWE数值模型的应用已较为普遍, 然而, 典型的数值模型存在一些关键问题, 首先是不完善的数值求解模型会直接导致不稳定的流体表面运动现象; 其次是SPH粒子与固体之间的稳定交互问题; 最后是数值的加速计算和渲染等问题. 针对数值求解模型存在的低精度与稳定性问题, 2005年, Ata等^[8]将光滑质点流体动力学方法应用于SWE的求解, 提出了一种基于黎曼解算器的新方法来提高算法的稳定性, 论述并使用了SPH插值的变分公式, 推导得出的新人工黏度项稳定性更好. 同时, 为提高模拟精度, 同年Rodriguez-Paz等^[9]提出了一种使用变平滑长度SPH法解SWE的公式, 这个新公式将流体连续体视为粒子的哈密顿系统, 提出了一种适用于一般地形上浅水类流体数值模拟的新方法, 在处理溃坝、崩塌、泥石流、雪崩和海啸等问题上显示出很大的潜力, 同时具有较强的鲁棒性和稳定性. 为提高数值求解模型的通用性, 2011年, Chang等^[10]使用SPH方法求解SWE, 建立了一维明渠浅水溃坝的无网格数值模型, 采用了切片水颗粒(shallow water particle, SWP)的概念, 研究得出了一维干湿河床溃坝流中合适的SWP值和变平滑长度. 模拟结果表明, 在激波间断、激波前缘运动、水力跃变、干/湿床流、超临界/亚临界/跨临界流、反向流、收缩流、超顶流、部分反射和多波相互作用等条件下, 无需特殊的数值处理便能获得稳定的数值求解结果. 2013年Xia等^[11]讨论了使用坡度源项对SWE进行标准SPH离散化时所引起的良好平衡问题, 推导出一种校正后的SPH算法, 新的数值模型可应对不同类型的实际浅层流动问题.
对于包含复杂边界的流体模拟场景, 2010年Chentanez等^[12]提出了一种基于网格和粒子的混合水体模拟方法, 其中提出的新求解器可处理任意的地下地形斜坡, 为了处理开放水域场景, 引入了一种处理非反射边界条件的方法, 模拟了海滩、陡峭的悬崖和山谷中瀑布水流的场景, 并基于CUDA实现了在GPU上运行的实时交互性能. 同年, De Leffe等^[13]提出了一种改进的SPH-SWE模型, 该模型的目的是进行涉及海底和陆地复杂水深的洪水模拟, 提出使用具有可变平滑长度的各向异性核及粒子的周期性再分配法, 得到的公式是鲁棒的, 适用于包含复杂地形边界的模拟场景, 如水流侵入一个复杂的二维形状的海岸, 或水流经过一座岛屿. 2015年, Chládek等^[14]对模拟中使用的核函数进行修正来提高光滑质点流体动力学近似的精度, 介绍了一种新的边界处理算法, 可以处理任意边界域, 同时提出了一种曲面生成方法, 即使在接近边界的区域也能生成平坦和无凹凸曲面. 对于模拟过程中刚体与流体粒子的稳定双向交互问题, 2011年, Solenthaler等^[15]提出一种用使用SPH粒子求解二维SWE的方法, 根据每个粒子位置的密度计算高度, 粒子的引入大大简化了稀疏区域和任意边界的问题. 同时, 文章提出的求解模型可以处理地形斜坡, 支持基于粒子的高度场与刚体对象的双向交互, 通过提出一种改进后的表面定义法, 在渲染时平滑了粒子稀疏区域的坑洼现象, 通过GPU处理计算与渲染使得模拟达到了可交互级别的效率.
为提高数值模型在复杂场景中的计算效率, 基于GPU将数值计算并行化能够有效地使模拟达到实时交互级别, 2010年, Lee等^[16]将基于粒子的拉格朗日框架应用到二维浅水模拟中, 使水粒子不受网格约束自由移动, 通过在GPU上进行数值计算, 展示了在可交互速率下水面的真实运动. 2015年, Chentanez等^[3]提出了一种结合粒子、三维网格和高度场模拟大尺度水体运动的新方法, 能够以可交互的速率模拟具有中、小细节的大尺度场景. 2016年, 张海超等^[17]提出一种改进的模型, 使用了一种基于动态网格的邻近粒子搜索方法, 并使用虚粒子和惩罚力相结合的方法处理边界条件以高效率应对复杂边界, 在渲染重建流体表面时, 将粒子映射并插值到规则网格内得到流体表面, 避免三维流体表面重构复杂度高的问题, 使得模拟达到可交互的效果. 同时, 为拓展SPH-SWE数值模型的应用范围, 2018年, Capecelatro^[18]提出了一种用于模拟旋转球体表面浅水流的SPH-SWE数值模型, 该方法扩展了经典SPH计算最先进的方法, 通过流体的形式约束一个球面上的表面, 为全球尺度大气、海洋流动现象的模拟提供了新的思路. 针对数值求解模型的稳定性问题, 本文将基于粒子的拉格朗日框架应用到SWE求解中, 根据粒子的密度变化实时修改光滑搜索半径, 并提出基于地形差异的自适应流体粒子速度修正方案, 提高模拟精度的同时有效地改善了流体在复杂地形影响下杂乱分散运动的趋势, 建立了稳定性SPH-SWE数值模型. 对于流体粒子的渲染, 本文使用屏幕空间流体渲染(screen space fluid rendering, SSFR)方法^[19], 避免了表面网格提取重建, 高效地对流体进行绘制. 本文的SPH-SWE数值求解、流体速度修正计算、渲染均在GPU上并行化加速执行, 实验结果表明, 本文方法保证了流体模拟真实性和计算效率, 并达到实时交互级别, 实现了在复杂地形情况下稳定的真实感流体动画实时模拟.

2

-->

2.1.基于SWE的SPH求解公式

基于粒子的拉格朗日方法将流体离散成一系列粒子质点, 各个质点上承载着流体粒子的物理量如密度、速度、加速度、黏滞力等^[20]. 典型的SPH方法通过追踪各个粒子的运动情况来获得整体的流体运动效果, SPH-SWE数值模型则在流体粒子存储的物理量中增加了粒子高度值这一属性.
首先, 根据SWE写出其拉格朗日形式下的动量守恒方程(1)和连续性方程(2):

$ \frac{{{\rm{D}}{\boldsymbol{u}}}}{{{\rm{D}}t}} = - g\nabla h \text{, } $

$ \frac{{{\rm{D}}h}}{{{\rm{D}}t}} = - h\nabla \cdot {\boldsymbol{u}} \text{, } $

式中, $\dfrac{{\rm{D}}}{{{\rm{D}}t}} = \dfrac{\partial }{{\partial t}} + u\dfrac{\partial }{{\partial x}} + v\dfrac{\partial }{{\partial y}}$为物质导数, h为水体的整体高度, $ {\boldsymbol{u}} $为水平方向上的速度矢量.
其次, 引入流体粒子的高度近似计算方程$h = \dfrac{{{\rho ^{2{\text{D}}}}}}{{{\rho ^{3{\text{D}}}}}}$, 考虑地形与外力得出新动量守恒公式:

$ \frac{{{\rm{D}}{\boldsymbol{u}}}}{{{\rm{D}}t}} = - \frac{g}{{{\rho ^{{\text{3D}}}}}}\nabla {\rho ^{2{\text{D}}}} - g\nabla H + {a_{{\text{ext}}}} \text{, } $

式中, $\rho ^{2{\rm{D}}}$为2D情况下SPH粒子的密度, $\rho ^{3{\rm{D}}}$为3D情况下的水密度, 为恒定值, $ H $为地形高度值, $ {a_{{\text{ext}}}} $为外力加速度, $ {\rho ^{2{\text{D}}}} $的计算公式与2D情况下SPH粒子密度计算公式同理:

$ {\rho ^{{\text{2D}}}}\left( {{{\boldsymbol{r}}_i}} \right) = {\sum\limits_j m_j ^{{\text{2D}}}}{W_{{\text{poly6}}}}\left( {{{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_j},h} \right) \text{, } $

式中, $m_j^{2{\text{D}}}$为SPH粒子的质量, ${W_{{\text{poly6}}}}\left( {{{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_j}, h} \right)$为poly6光滑核函数, $ h $为光滑搜索半径.
在结合复杂地形的实时模拟中, 粒子i运动时的最终高度值应为$y_i^{2{\text{D}}} = {h_i} + {H_i}$ ^[21], 其中${h_i} = $$ {{\rho _i^{2{\text{D}}}}}/{{{\rho ^{3{\text{D}}}}}}$, $ {H_i} $为水底对应的地形高度值. 综上, (3)式和$y_i ^{2{\text{D}}} = {h_i} + {H_i}$则为SPH方法求解SWE的基础数值模型, 且本文采用适用于2D SPH流体模拟的光滑核函数^[22]:

$ {W}_{\text{poly6}}({\boldsymbol{r}},h)=\frac{4}{\text{π}{h}^{8}}\left\{\begin{aligned}&{\left({h}^{2}-{{{r}}}^{2}\right)}^{3},\hfill & 0\leqslant {{r}}\leqslant h,\hfill \\ &0,\hfill & 其他,\;\,\qquad\end{aligned}\right. $

$ \nabla {W_{{\text{spiky}}}}({\boldsymbol{r}},h) = \frac{{ - 30}}{{{\text{π}}r{h^5}}}{(h - r)^2}({{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_j}) \text{, } $

$ {\nabla ^2}{W_{{\text{viscosity}}}}({\boldsymbol{r}},h) = \frac{{40}}{{{\text{π}}{h^5}}}(h - r) \text{, } $

其中, (5)式为计算密度所使用的poly6核函数, h代表光滑核半径, r为当前粒子与邻居粒子之间的距离长度; (6)式为计算压力所使用的梯度函数, ${{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_j}$代表当前粒子与邻居粒子之间位置的向量差; (7)式为计算黏性力所使用的拉普拉斯算子.
2 -->

2.2.变长光滑核半径

在SPH流体模拟中, 光滑半径长度的选取将直接影响模拟精度. 当流体粒子在均匀分布的情况下, 若光滑半径选取较小, 有限的范围内没有足够的邻居粒子对该粒子施加作用力, 将直接导致模拟精度低; 若光滑半径选取较大, 粒子的运动细节等可能被过度平滑同样导致低精度. 同时, 在流体运动大变形的情况下, 由于粒子的分布不均匀, 选取固定的光滑半径造成的运动效果失真现象将更加明显, 因此有必要针对研究对象附近的粒子分布情况来调整光滑核半径大小, 使得在求解范围内所包含的粒子数目始终稳定在固定的区间内.
在本文研究的情形中, 当流体运动的大变形导致粒子堆积时, 若选取固定的光滑半径, 粒子的聚集导致邻居粒子数目剧增, 计算效率、精度将受影响, 同时压力等物理量过大, 使得运动行为更加不可控, 发生地形穿透、剧烈飞溅等现象; 当流体流入新的空区域时粒子数目较少, 粒子分布稀疏, 固定的光滑半径同样会造成计算误差较大的结果. 因此, 本文在计算粒子物理量时使用变长光滑核半径. 传统变长光滑核半径初始大小计算方法为^[23]

$ h_i^0 = {c_d}{\left( {\frac1{{\rho _i^0}}\;{{\displaystyle\sum\limits_{j = 1}^{N_i^0} {{m_j}} }} } \right)^{\tfrac{1}{d}}} , $

式中$ {c_d} $由当前模拟的维度决定, 一维情况下取$\dfrac{1}{4}$, 二维取${\Big(\dfrac{1}{{4{\text{π }}}}\Big)^{\tfrac{1}{2}}}$, 三维取${\Big(\dfrac{3}{{32{\text{π }}}}\Big)^{\tfrac{1}{3}}}$, d的取值分别为1, 2, 3; $ N_i^0 $代表初始情况下粒子i附近的粒子数, 针对三种维度下不同的情况, 为统计$ N_i^0 $的数目而选取的空间大小基于初始粒子间距的一定倍数, 通常选取1.2倍; $ \rho _i^0 $为静密度; $ {m_j} $为粒子质量.
根据得到的初始光滑核半径, 各个粒子的光滑核半径的更新方法为

$ \frac{{Dh_i^n}}{{Dt}} = - \frac{{h_i^n}}{{\rho _i^nd}}\sum\limits_{j = 1}^N {{m_j}} \left( {v_i^n - v_j^n} \right) \cdot \nabla _i^n{W_{ij}} \text{, } $

式中, n代表当前为第n时间步, $ v_i^n $代表第n时间步时粒子i的速度大小, $ \nabla _i^n{W_{ij}} $为梯度核函数, d的取值与(8)式相同. 于是可根据(9)式更新粒子的光滑核半径长度$h_i^{n + 1} = h_i^n + \dfrac{{{\text{d}}h_i^n}}{{{\text{d}}t}}$.
综上, 本文根据2D情况下粒子的密度变化对光滑核半径长度进行动态调整, 使用简化后的光滑核半径计算更新方法

$ h = {h_0}{\left(\dfrac{{{\rho _0}}}{{{\rho _i}}}\right)^{\tfrac{1}{2}}} \text{, } $

式中, $ {h_0} $为初始光滑核半径长度, $ {\rho _0} $为静密度, $ {\rho _i} $为粒子i的密度, $\dfrac{1}{2}$代表该式适用于二维情况的SPH流体计算.
2 -->

2.3.基于地形差异的自适应流体速度控制力

当流体流经不规则地形表面时, 根据粒子高度表示公式$y_i ^{\rm 2D} = {h_i} + {H_i}$和实验结果, 我们发现在时间步长较小时, 频繁的地形高度值剧烈变化易导致流体粒子杂乱分散地运动, 造成不稳定的流体表面运动现象. 如图1, 当流体粒子流经崎岖不平的区域时, 由于地形的影响造成了粒子的短暂堆积, 该区域密度剧增造成的压力骤变会引起粒子无序飞溅的运动趋势, 因此本文提出一种基于地形差异的自适应流体粒子速度控制方法来改善这种现象. 如图2所示, 点N为粒子i当前所处位置的地形坐标点, P为粒子i上一时间步所处的地形坐标点, 本文提出速度控制力计算公式为
图 1 地形引起粒子堆积、无序飞溅趋势
Figure1. The tendency of particle accumulation and disordered splashing caused by terrain.

$ {f_{{\text{restrain}}}} = \frac{{ \rho _i^{2{\text{D}}}}}{{{\rho ^{3{\text{D}}}}}}{\boldsymbol{NP}} \text{, } $

式中, $\dfrac{{ \rho _i^{2{\text{D}}}}}{{{\rho ^{3{\text{D}}}}}}$=$ {h_i} $, 为粒子i当前的水体高度值.
图 2 速度控制力计算模型
Figure2. The calculation model of velocity control force.

由于$ {h_i} $是由粒子i当前密度大小决定的, 当粒子由于地形情况多变而产生堆积现象时, $ {h_i} $和压力大小会因粒子密度增大而骤增, 造成该区域粒子运动行为趋向于散乱, 出现粒子穿透地形或不合理的粒子飞溅现象. 由(11)式可知, 本文根据粒子的高度值和前后时间步所处地形的差异来提前反向抑制这种趋势, 粒子堆积越密集, 前后流经地形位置差异越大时, 流体粒子运动抑制力$ {f_{{\text{restrain}}}} $也越大, 可有效防止过多粒子过快进入易堆积区域.
其次, 为提高该方法在多种地形情况下的通用性, 本文基于双线性插值的思想对上述公式进行改良, 提出一种基于地形差异的自适应流体速度控制力计算模型. 首先参考图3的情况, 平坦的斜坡地形中, 有一处凹陷严重, 流经凹陷区域的粒子易产生堆积, 从而导致穿透或杂乱飞溅现象, 引入流体控制力可以改善这种现象, 但流体粒子在这种情况下运动时前后地形落差较大, 部分粒子根据地形落差产生的流体控制力会导致流体粒子无法保持原本的运动趋势离开该区域, 造成谷底更严重的堆积现象. 针对上述情况, 实验发现若取该谷底粒子在周围较平坦位置运动前后产生的控制力可以保证在控制流体速度的前提下有效避免上述现象. 因此本文提出, 根据当前流体粒子的速度控制力计算模型, 计算其周围4个地形点位处该粒子的流体速度控制力计算结果, 通过插值来得到该点的$ {f_{{\text{restrain}}}} $.
图 3 地形整体平坦但局部凹陷严重
Figure3. A terrain which is flat on the whole but severely depressed locally.

如图4所示, 在三维地形的xOz平面上, P点为当前求速度控制力的粒子所处地形坐标点, 取周围A, B, C, D 4个地形点位, P处于正方形ABCD的中心, 4个点位的位置选取根据当前粒子密度大小动态改变, 改良后的计算公式为
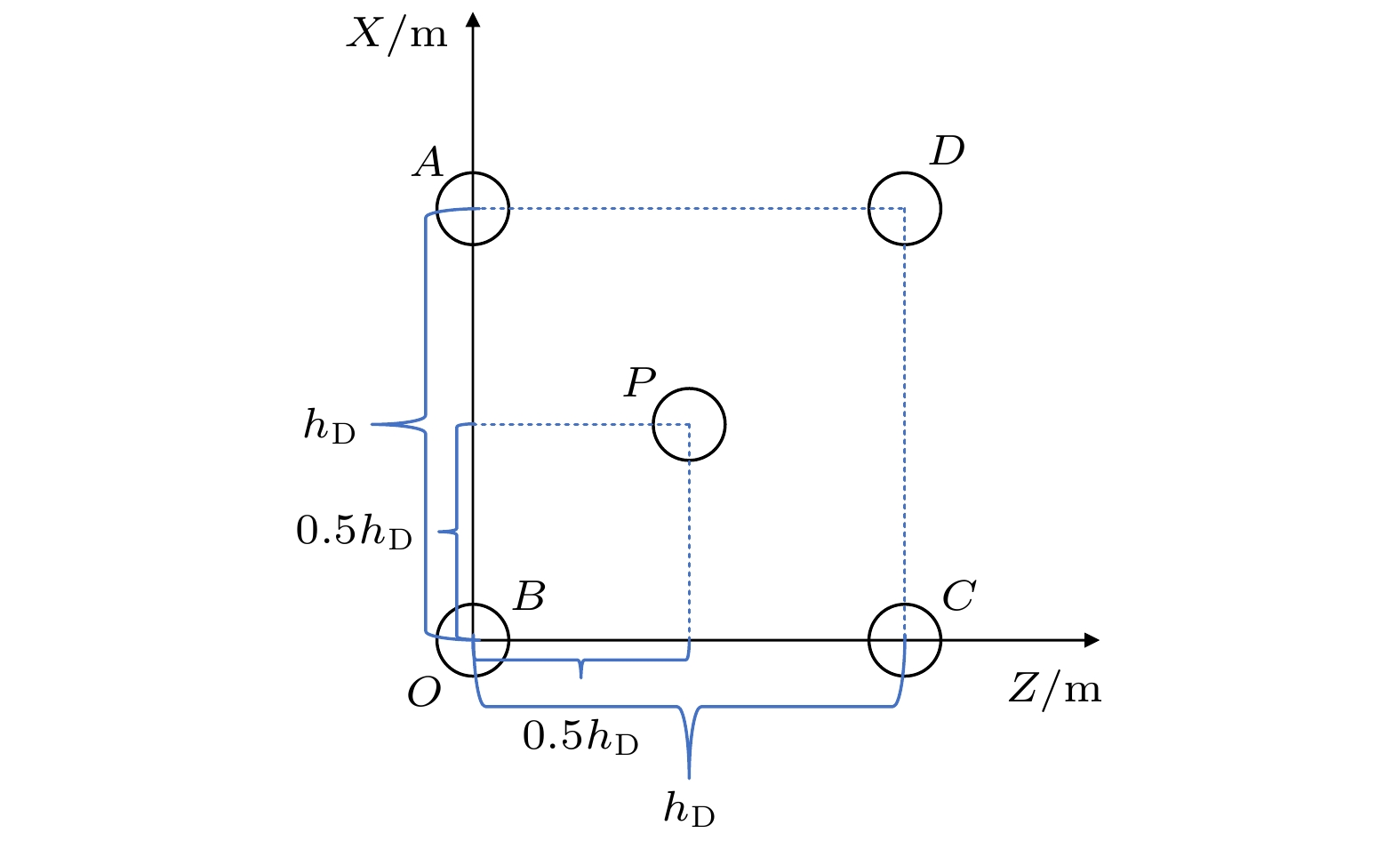图 4 基于地形差异的自适应流体速度控制力计算模型
Figure4. An adaptive fluid velocity control force calculation model based on terrain difference.

$ \begin{split} {f_{{\text{restrain}}}} =\;& {f_A}\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right)\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right)\\ &+ {f_B}\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right)\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right) \\ & +{f_C}\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right)\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right) \\ & + {f_D}\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right)\left({h_{\text{D}}} - \frac{1}{2}{h_{\text{D}}}\right) \\ =\;& \frac{1}{{\text{4}}}{f_A}h_{\text{D}}^{\text{2}} + \frac{1}{{\text{4}}}{f_B}h_{\text{D}}^{\text{2}} + \frac{1}{{\text{4}}}{f_C}h_{\text{D}}^{\text{2}} + \frac{1}{{\text{4}}}{f_D}h_{\text{D}}^{\text{2}}, \end{split} $

式中: $ {f_A} $, $ {f_B} $, ${f_C}$, ${f_D}$分别为根据粒子P的速度控制力计算模型在点A, B, C, D处计算所得控制力, 4个点位的位置由${h_{\text{D}}} = \alpha {h_0}{\big( {{{\rho _0}}}/{{{\rho _i}}}\big)^{\tfrac{1}{2}}}$决定, 其中$ \alpha $为人工控制系数, 本文取0.5, $ {h_0} $为初始光滑核长度, $ {\rho _i} $为当前粒子密度大小, $ {\rho _0} $为静密度大小. $ {h_{\text{D}}} $的计算首先是以当前粒子的动态光滑搜索半径大小为依据, 其次, 根据场景地形的具体复杂程度选取不同的$ \alpha $值大小, 若在较小的地形范围内, 地形高度值频繁变化且落差明显时, 系数$ \alpha $应设置偏小, 从而调整使得最终选取的地形研究点位距离粒子位置较近, 避免产生较大的计算误差. 同时, 由于光滑搜索半径随粒子密度变化而变化, 粒子的密度大小会因地形变化而受影响, 因此$ {h_{\text{D}}} $的大小也会自适应地随地形情况而变化, 系数$ \alpha $的取值实则起辅助作用, 便于人工干预$ {h_D} $的最终计算结果, 从而观察判断最佳流体运动效果下$ \alpha $与$ {h_{\text{D}}} $应为何值. 在本文的实验场景中, 通过取不同值进行对比, 当$ \alpha $选取0.5时流体表面运动行为较其他取值更为稳定, 计算得到的控制力对流体整体运动改善效果较好.
在地形复杂且时间步长较小的情况下, 粒子密度会受地形的影响而频变, 因此可动态根据复杂地形造成的流体粒子密度变化来更好地计算流体速度控制力. 从(12)式可知, 当粒子密度开始增大时, 极有可能即将发生堆积情况且导致粒子无法离开该局部区域, 因此在计算速度控制力时研究其邻近区域, 提前根据附近地形情况来施加速度控制力, 能够有效避免流体过快流入易堆积区域, 如图3的情形, 可有效地及时避免后来的粒子过快进入谷底而造成粒子更严重的堆积和无序飞溅等现象; 当粒子密度减小, 流体可能流入了新的地形区域, 此时研究更远范围处地形情况, 提前为可能发生的地形骤变作应对, 同样有效地提前避免了粒子的堆积与流体表面运动现象不稳定的后果.
2 -->

2.4.固流交互

本文的数值模型考虑位置固定的刚体与流体粒子之间的相互影响作用, 使用边界粒子对刚体进行采样表示, 它们可以被视为与SPH流体粒子相同的粒子, 但在模拟过程中只考虑它们对流体粒子密度、压力计算时的贡献, 不更新其速度、位置等信息^[24]. 当刚体表面的边界粒子进入SPH流体粒子i的邻居搜索范围时, 粒子i的密度会逐渐增加, 使得$ {\rho _i} $>$ {\rho _0} $, 从而产生压强, 导致一个使得流体粒子远离边界粒子的压力, 在这种情况下, 粒子i的密度计算应考虑邻域内的流体粒子与边界粒子的贡献:

$\begin{split}{\rho ^{{\text{2D}}}}\left( {{r_i}} \right) =\;& {\sum\limits_j m_j ^{{\text{2D}}}}{W_{{\text{poly6}}}}\left( {{r_i} - {r_j},h} \right) \\&+ {\sum\limits_k m_k^{{\text{2D}}}}{W_{{\text{poly6}}}}\left( {{r_i} - {r_k},h} \right) \text{, }\end{split} $

式中, k为邻域内的边界粒子数. 由于在SPH粒子的物理量近似计算中, 邻居粒子对该粒子的贡献应当基于其体积大小:

$ \begin{split}\rho \left( {{r_i}} \right) =\;& \sum\limits_j {{V_j}} {\rho _j}{W_{{\text{poly6}}}}\left( {{r_i} - {r_j},h} \right) \\=\;& \sum\limits_j {{m_j}} {W_{{\text{poly6}}}}\left( {{r_i} - {r_j},h} \right) \text{, } \end{split}$

式中, $ {V_j} $为粒子j的体积, 基于此, 如图5所示, 本文使用小于流体粒子体积大小的边界粒子对刚体表面进行表示, 边界粒子的分布更加密集, 能够更有效防止粒子穿透. 同时, 在计算边界粒子对流体粒子运动的贡献时考虑其体积, 可以保证近似结果的稳定性. 因此, 边界粒子对流体粒子的贡献计算中, 粒子k的质量计算表示为
图 5 用于表示刚体的SPH粒子
Figure5. The SPH particles used to represent a rigid body.

$ {\varPsi _k} = {\rho _0}{V_k} . $

使用(15)式的质量计算方法替换(13)式中的$ {m_k} $可得最终粒子i的密度计算公式:

$\begin{split}{\rho ^{{\text{2D}}}}\left( {{{\boldsymbol{r}}_i}} \right) =\;& {\sum\limits_j {{m_j}} ^{{\text{2D}}}}{W_{{\text{poly6}}}}\left( {{{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_j},h} \right)\\&+ \sum\limits_k {{\rho _0}} {V_k}{W_{{\text{poly6}}}}\left( {{{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_k},h} \right) . \end{split}$

根据(16)式的计算方法得出粒子密度后, 再根据粒子i的压强, 并将边界粒子质量用(15)式替换后, 粒子k对流体粒子i的压力计算方式为

$ f_{i \leftarrow k}^{\text{p}} = - {m_i}{\rho _0}{V_k}\left( {\frac{{{p_i}}}{{\rho _i^2}}} \right)\nabla {W_{ik}} \text{, } $

式中, $ {p_i} $为粒子i的压强.
在本文方法中, 刚体表面的边界粒子排列密集, 较为有效地避免了粒子的穿透现象, 在计算边界粒子对流体粒子运动的贡献时使用其体积, 使得密度、压力等物理量的近似结果更加精确, 同时基于地形差异的自适应流体速度控制力计算模型有效控制了流体粒子速度的激增, 从而更进一步改善了穿透现象.

2

-->

3.1.屏幕空间流体渲染方法

对于SPH流体粒子的渲染常用的方法是流体表面网格重建, 典型的方法是通过行进立方体(marching cube, MC)算法提取流体表面的三角面片集, 然后使用光照模型对三角形面片进行渲染从而重建流体表面^[22], 对于实时流体模拟的性能影响较大. SSFR方法则避免了表面网格提取与重建的工作, 从屏幕空间^[25]直接对SPH流体粒子进行绘制获得表面深度纹理图, 然后对深度图进行平滑处理, 最后基于深度图对流体表面进行绘制^[26]. SSFR方法与需要进行表面网格重建的方法相比性能较高, 使得计算能够达到实时交互级别, 本文则基于SSFR方法对流体粒子进行渲染绘制.
SSFR算法完全在屏幕空间内进行操作, 如图6所示, 从相机的视角出发, 只对距离相机最近的流体表面进行生成渲染. 本文SSFR算法的执行流程如图7所示, 首先对场景进行处理得到背景信息, 其次以点精灵形式对粒子渲染得到深度图, 然后表面着色器对平滑后的深度图、流体的厚度信息图和背景信息进行处理得到最终的着色信息图.
图 6 相机与流体表面关系示意图
Figure6. Schematic diagram of the relationship between camera and fluid surface.

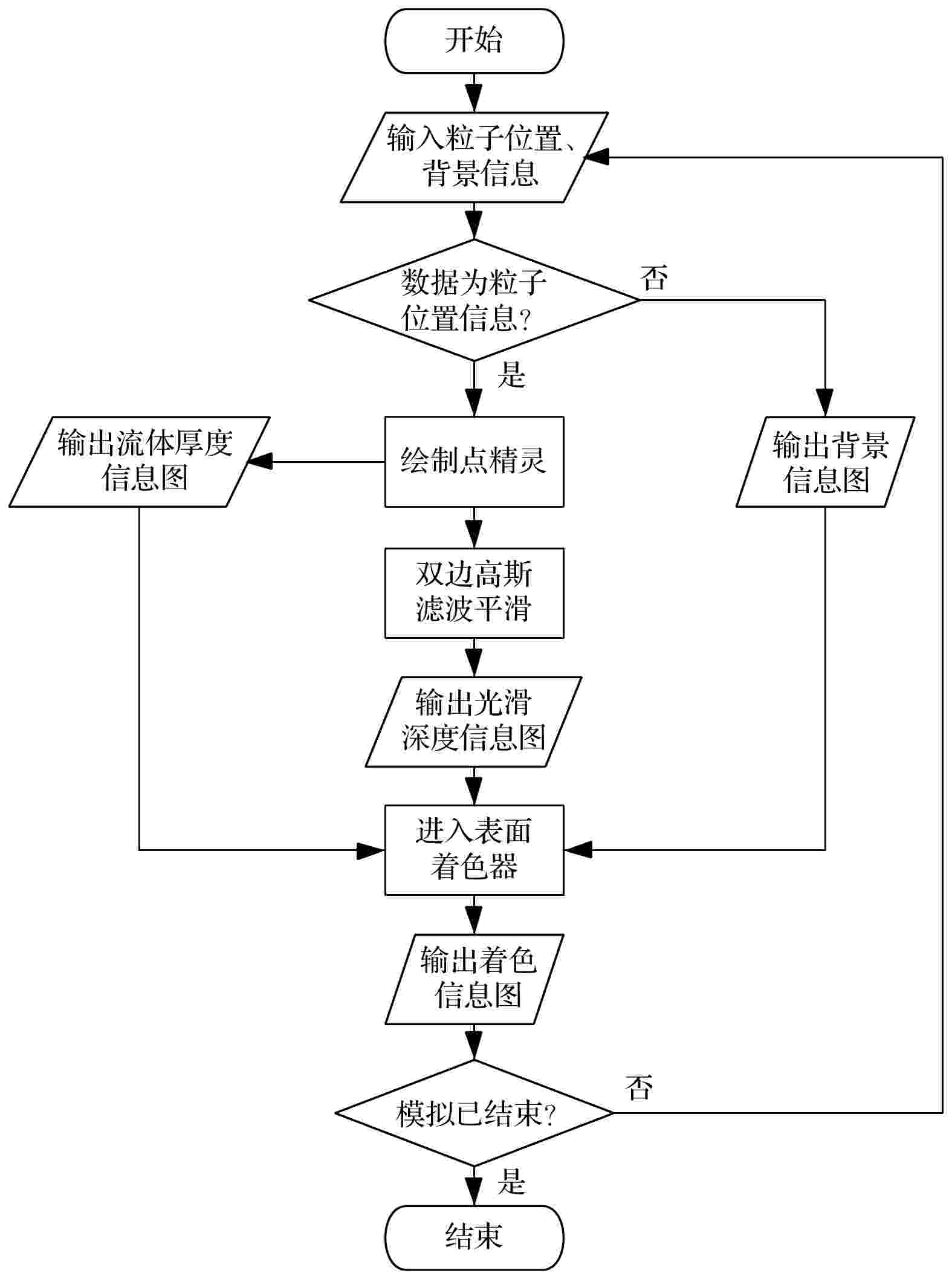图 7 SSFR算法执行流程图
Figure7. The flow diagram of our SSFR algorithm.

平滑处理是SSFR方法中较为重要的一个步骤, 不经过平滑处理的流体表面会有明显的颗粒感, 常用的平滑方法有高斯滤波及其改进后的双边高斯滤波法. 本文使用双边高斯滤波法进行平滑处理, 可保存深度图中的轮廓边缘, 因此粒子不会与背景表面掺杂在一起. 其次, 在计算流体厚度时, 由于无法观测到流体表面背后的信息, 因此视流体为半透明, 根据体积的厚度变化来衰减颜色效果, 通过累加混合方式来计算流体的厚度信息. 通过计算得到平滑后的粒子的深度纹理图、厚度信息图及背景环境信息图后, 本文采用基于菲涅耳方程的光照模型, 其中考虑了折射、反射因素及Phong镜面高光, 某像素点处最终输出的颜色计算方式为

$ {C_{{\text{out}}}} = a(1 - F({\boldsymbol{n}} \cdot {\boldsymbol{v}})) + bF({\boldsymbol{n}} \cdot {\boldsymbol{v}}) + {k_{\text{s}}}{({\boldsymbol{n }}\cdot {\boldsymbol{h}})^\alpha } \text{, } $

式中, F为菲涅耳函数, ${\boldsymbol{n}}$为表面法线, ${\boldsymbol{v}}$为相机方向的单位矢量, ${\boldsymbol{ h}}$为相机方向与光照方向之间半夹角方向的单位矢量, a为流体折射颜色, b为场景反射颜色, $ {k_{\text{s}}} $与$ \alpha $为镜面高光常数. 为进一步模糊粒子之间的界限与改善流体表面凹凸不平的现象, 本文在渲染过程中使用双边高斯滤波法进行多次迭代, 提升了对粒子深度纹理图的平滑效果, 在保证模拟实时性的前提下获得了更好的流体渲染效果.
2 -->

3.2.基于Compute Shader的数值加速计算方案

本文的流体模拟场景基于Unity平台实现, 其中使用了C#脚本与Unity的Compute Shader. 在Unity中, C#脚本的运算是基于CPU串行执行的, 而Compute Shader是在GPU运行却又独立在普通渲染管线之外的程序, Compute Shader允许用户将大量可以并行的计算放到GPU中, 从而节省CPU资源, 提高计算效率, 因此, 本文的粒子初始化创建在C#中执行, 而各个粒子之间的物理量计算更新则在Compute Shader中独立并行执行. 首先, 所有粒子在C#脚本中一次性被初始化创建并存储在一个游戏物体数组GameObject[ ]中, 然后, 为粒子的全部物理属性分别创建各自的结构体, 结构体内包含该属性的具体定义, 例如粒子位置由三维向量表示, 粒子的密度大小则由浮点数表示. 其次, 为C#脚本与Compute Shader中的物理量数据交换创建各自对应的Compute Buffer, 创建完成后, 在C#脚本中使用InitBuffer$\langle $结构体类型$\rangle $(粒子数目, ref 对应物理量的Buffer), 为所有粒子初始化用于存储自身物理量计算结果的独立Buffer. 完成Buffer初始化后, 将计算划分为N个线程组, 每个线程组内有1024个线程, 单个线程负责单个粒子的物理量计算, 然后, 在Compute Shader中依次定义4个kernel函数, 负责密度、压强、粒子受力、粒子最终位置的计算. 程序初始化运行时, 通过SetBuffer方法, 将粒子的初始物理属性传到Compute Shader中, 按照密度、压强、受力、粒子最终位置的计算流程, 各个粒子之间线程独立并行进行运算, 计算得到新的粒子位置后, 通过SwapBuffer操作, 将计算得到的粒子位置信息传到C#脚本, 更新粒子的最新位置, 并根据粒子位置信息绘制点精灵, 进行屏幕空间渲染.
在Unity中, 粒子当前位置的对应地形高度只能由C#脚本中的Terrain.activeTerrain.SampleHeight( )函数进行获取, 对于流体速度控制力的计算, 实验在C#脚本中定义了一个辅助三维向量数组, 用于存储上一时间步的粒子位置信息. 在第一个时间步内, 并未考虑速度控制力的计算, 而是在第一次计算完成得到新的粒子位置后, 在C#脚本中通过地形高度获取函数得到粒子运动前后位置的地形高度值, 根据本文设计的计算模型得出速度控制力后, 使用一个辅助Buffer将各个粒子的控制力计算结果传到Compute Shader中, 在第二个时间步的粒子受力计算中, 才开始对粒子根据地形情况施加流体速度控制力, 控制粒子下一个时间步的运动趋势.

本文流体场景数值模拟所基于的实验硬件平台为Intel i7-8700 CPU和NVIDIA Geforce GTX 1060 GPU, 编程环境为C#, Unity三维引擎, ShaderLab着色语言, 实验中的参数取值在表1中给出. 为证明提出的基于地形差异的自适应流体速度控制力计算模型的有效性, 本文在实验模拟过程中首先对比施加速度控制力前后的效果, 然后将本文方法应用到两个真实地形场景中, 从而进一步验证本文方法的通用性和稳定性.

物理量	值	单位
粒子半径 $ r $	0.5	m
时间步长 $ \Delta t $	0.02	s
初始粒子间距 $ {r_0} $	1	m
初始搜索半径 $ {h_0} $	2.66	m
静密度 $ {\rho _0} $	1000	kg/${{\rm{m}}^3}$
粒子质量 $ m $	1000	kg
气体常数 $ k $	10	—
黏度系数 $ \mu $	0.1	—

表1实验参数取值
Table1.The values of parameters in experiment.

本文首先基于Unity地形系统随机生成复杂地形, 然后在模拟过程中引入基于地形差异的自适应流体速度控制力以验证该方法的有效性. 如图8(a), 在Unity随机生成的地形场景中, 通过噪音调整得到的地形情况是复杂频变的, 在这种情况下流体行进过程中受地形影响极易发生粒子堆积和无序飞溅的现象, 特别是经过高度落差剧烈变化以及坑洼的区域时, 整体流体运动行为趋于散乱, 密度压强分布不均匀. 针对这种复杂地形造成的流体运动不稳定现象, 本文动态地根据粒子密度变化实时修改光滑搜索半径, 同时依据搜索半径的大小和地形落差变化对流体粒子施加速度控制力, 从图8(b)中可以对比看出, 谷底处的粒子堆积现象明显改善, 同时也有效地避免了地形骤变造成的粒子无序飞溅情况, 流体整体压强密度分布均匀, 运动行为趋于稳定.
图 8 施加控制力前后效果对比　(a) 未施加控制力; (b) 施加控制力
Figure8. The comparison before and after applying control force: (a) Without adding control force; (b) with control force.

为说明静态边界粒子法在本文数值模型下的有效性, 流体粒子分别与固定圆柱体、长方体交互. 本文使用与流体粒子相同的粒子表示这两种几何体, 但在模拟环节中使其完全透明, 其在模拟环节中参与流体计算但不修改自身速度等物理量, 可通过调整采样粒子的半径大小, 使其分布更加密集从而更有效地防止穿透. 从图9可看出, 流体粒子在流经长方体和圆柱体时有效避免了穿透现象, 流体粒子能够绕过障碍继续行进, 实验说明静态边界粒子法在本文的情况下有效可行.
图 9 流体与几何体交互　(a) 流体与长方体交互; (b) 流体与圆柱体交互
Figure9. Fluid interacts with geometry: (a) Fluid interacts with the cuboid; (b) fluid interacts with the cylinder.

为了进一步说明本文方法在复杂地形中模拟的稳定和有效性, 首先, 实验将本文方法应用到爱荷华河真实地形中, 其中, 使用的粒子数为12000, 时间步长0.02, 取0 s, 30 s, 90 s, 120 s时刻模拟结果. 如图10所示, 首先在河道上方30 m处初始化流体粒子, 见图10(a); 流体粒子在重力作用下落到山谷顶部与河道中, 在不规则地形的影响下并未发生粒子飞溅等散乱运动现象, 见图10(b); 随后山体顶部的部分流体粒子流入河道中, 与河道中的流体粒子结合并沿河道的走势逐渐蔓延, 部分流体粒子则滞留在山体顶部的凹陷地形处形成水坑, 见图10(c); 最后流体运动逐渐平缓, 将爱荷华河的河道区域整体覆盖, 见图10(d). 在爱荷华河实验场景中, 流体运动行为整体较为稳定, 流体的压强、密度分布均匀, 模拟帧率保持在30帧/s左右, 达到实时级别.
图 10 爱荷华河场景的四个时刻模拟渲染图　(a) 0 s时刻; (b) 30 s时刻; (c) 90 s时刻; (d) 120 s时刻
Figure10. Fluid surface rendering of the Iowa river scene at four moments: (a) 0 s; (b) 30 s; (c) 90 s; (d) 120 s.

其次, 实验采用赤水河谷真实地形来验证本文方法, 同样地, 使用的粒子数为12000, 时间步长取0.02, 取15 s, 30 s, 45 s, 60 s时刻模拟结果. 如图11, 流体在河谷源头被初始化, 随后根据河谷中沟壑的走势开始运动. 在重力与地形走势的影响下, 水体逐渐从地势高的位置向地势低的区域蔓延, 在流经复杂颠簸的地形区域后并未出现粒子严重堆积与散乱运动现象, 行进到平缓地形后流体整体仍能稳定地根据沟壑走向继续流动, 流体整体压强与密度分布均匀.
图 11 赤水河谷场景的四个时刻模拟渲染图　(a) 15 s时刻; (b) 30 s时刻; (c) 45 s时刻; (d) 60 s时刻
Figure11. Fluid surface rendering of the Chishui river valley scene at four moments: (a) 15 s; (b) 30 s; (c) 45 s; (d) 60 s.

最后, 实验将图10爱荷华河场景中使用的粒子数增加到60000, 地形分辨率提升至1024×1024, 将最终淹没模拟结果与爱荷华洪水信息系统官方提供的真实淹没情况进行对比, 对比结果如图12所示, 其中, 图12(a)为根据爱荷华市历年洪水事件绘制的淹没范围图, 其中, 蓝色区域表示在100 a内, 每年会有1%的概率在该区域产生洪水灾害现象, 橙色区域则代表在500 a内, 每年会有2%的概率在该区域产生洪水灾害现象; 图12(b)为2008年6月, 爱荷华州由于雷暴大雨造成的雨洪淹没情况示意图, 颜色由浅蓝到深紫色代表淹没水深逐渐由低增高; 图12(c)为爱荷华河中总水量水深为25 ft (1 ft = 3.048 × 10^–1 m), 河流流量为31200 cfs (1 cfs = 1 ft³/s = 0.028316847 m³/s)情况下的城市淹没真实场景图, 该场景提供每个淹没点位的具体水深数值; 图12(d)为本文模拟情况下爱荷华河场景的最终淹没结果图, 通过与图12(a)、图12(b)、图12(c)对比, 本文模拟的淹没范围基本在真实淹没情况的区域范围内. 同时, 对比图12(c)的水深数据, 实验选取4个模拟场景中的水深点位数据与其对比, 如表2所示. 本文模拟结果较图12(c)的真实情况相比, 误差在2.60%到9.79%之间, 模拟的水淹分布及水深与真实结果较为吻合, 误差的产生原因包括模拟过程中未考虑建筑分布情况或土质因素等.
图 12 爱荷华场景水淹情况示意图　(a) 依据历年水淹范围统计的淹没概率图; (b) 2008年6月爱荷华雨洪淹没范围图; (c) 水深25 ft, 流量31200 cfs情况下淹没范围图; (d) 本文淹没模拟结果示意图
Figure12. The flood inundation maps of iowa scene: (a) The inundation probability map based on the statistics of the flooding range over the years; (b) the flood inundation map of iowa in June, 2008; (c) map of inundation range under the condition of 25 ft water depth and 31200 cfs water flow; (d) the simulated inundation map of our method.

点位	模拟水深/m	实测水深/m	相对误差/%
A	1.29	1.43	9.79
B	1.51	1.65	8.48
C	1.97	1.92	2.60
D	1.50	1.40	7.14

表2实际水深与模拟水深数据对比
Table2.Comparison between actual and simulated water depth

爱荷华河、赤水河谷实验有效验证了本文提出的基于地形差异的自适应流体速度控制力计算模型的有效性和稳定通用性, 模拟过程中流体运动的数值计算与渲染均基于GPU并行执行, 能够达到实时交互级别. 如表3所示, 本文给出上述实验场景使用的粒子数、地形分辨率与渲染前后平均模拟帧率, 其中, 图8至图11的实验中, 为了更好地观察粒子实体的具体运动行为, 在保证达到实时交互级别的前提下, 实验模拟过程中同时创建了粒子球实体与点精灵, 另外包括C#与Compute Shader之间的数据交换, 给模拟效率带来了一定限制; 在图12的淹没水深对比实验中, 本文着重分析流体最终淹没所覆盖的范围与淹没深度, 因此, 在将粒子数提升至60000、地形分辨率提升至1024 × 1024的条件下, 当Compute Shader中计算得到的粒子位置结果返回C#脚本中时, 粒子实体的创建使用仅包含位置信息的空物体替代, 不再进行粒子的GameObject实体Sphere的创建, 同时将位置信息直接送入表面着色器, 在对应位置直接绘制点精灵, 进行屏幕空间渲染从而可视化, 模拟效率得到了提升. 另外, 在图12的实验中, 实时模拟的粒子总数上限约为100000, 当粒子数目增加到100000并加上实时屏幕空间渲染时, 模拟帧数将低于20 ft/s, 达不到实时交互级别.

场景	粒子总数/103	地形 分辨率	渲染前帧率/(ft·s–1)	渲染后帧率/(ft·s–1)
图8	12	1024×1024	70	34
图9(a)	12.2	1024×1024	64	28
图9(b)	12.1	1024×1024	65	30
图10	12	512×512	68	32
图11	12	256×256	68	33
图12(d)	60	1024×1024	75	35

表3各实验场景的平均模拟帧率
Table3.The average simulation frame rate of each scene.

本文在传统的SPH-SWE数值模型基础上提出一种基于地形差异的自适应流体速度控制力计算模型, 根据流体粒子运动前后时间步所处的地形位置来确定粒子的当前运动趋势, 通过粒子的实时密度大小来修改光滑搜索核半径并动态确定计算速度控制力时选取的坐标点位置, 建立了稳定性SPH-SWE数值模型, 有效改善了流体在复杂地形影响下粒子堆积、散乱运动的问题, 计算得到的密度和压强分布是均匀的. 同时基于SSFR算法对流体粒子进行绘制, 避免了表面网格提取重建, 通过将计算并行化加载到GPU使模拟达到实时交互级别, 实验表明在保证了计算效率的同时对流体的运动整体效果进行了改善. 然而, 本文的SPH-SWE数值求解、流体速度、位置修正计算等虽然是在GPU上并行执行, 但是整体的模拟过程中, C#脚本与Compute Shader之间, 即CPU与GPU之间存在数据交换, 模拟结果虽能达到实时性, 但是计算效率受到了一定的限制, 提高本文方法在大规模场景中应用时的计算效率、还原流体模拟过程中浪花与泡沫等细节是今后研究的重要内容.