摘要: 研究了偏压控制下的粒子在破缺媒介中的扩散动力学. 基于平均首次通过时间理论导出了粒子在偏压破缺势场中的有效扩散系数的近似表达式. 结果显示粒子的有效扩散系数被显著地增大, 用粒子概率密度分布函数的波包展宽对此机制给出了解释. 进一步, 本文提出有效动力学温度和有效阻尼相结合的概念, 对爱因斯坦扩散关系进行了推广.
关键词: 破缺 /
随机关联势 /
扩散增强 English Abstract Diffusion enhancement of the particle in disorder medium by biased force Fan Li-Ming Bao Jing-Dong Department of Physics, Beijing Normal University, Beijing 100875, China Fund Project: Project supported by the Key Program of the National Natural Science Foundation of China (Grant No. 11735005)Received Date: 06 December 2020Accepted Date: 19 May 2021Available Online: 16 September 2021Published Online: 05 October 2021Abstract: The diffusion dynamics of a particle in the biased disorder medium is investigated in this paper. Based on the mean first passage time (MFPT) theory, the analytical approximate expression of effective diffusion coefficient of a particle in the biased disorder potential is obtained. The results show that the effective diffusion of a particle in the biased disorder potential is significantly enhanced. We explain the enhancement mechanism by using the wave packet broadening of probability density distribution function. In addition, we propose the concepts of effective kinetic temperature and effective friction, and further find that the effective diffusion behavior of a particle strongly depends on the biased force.Keywords: disorder /random correlation potential /diffusion enhancement 全文HTML --> --> --> 1.引 言 靶粒子在固体表面的扩散是一个普遍存在的物理现象, 并且媒介具有周期结构, 即存在周期势[1 ,2 ] . 由于各向同性等原因, 为研究方便起见, 理论上仅需在一维上来探讨粒子的扩散行为[3 ] . 众所周知, 扩散系数能够衡量粒子扩散的快慢, 而自由扩散系数$ D_0 $ 由著名的爱因斯坦关系确定: $D_0 = $ $ k_{\rm B}T/(m\gamma)$ (这里, m 是靶粒子质量, $ \gamma $ 为黏滞常量). Lifson和Jackson[4 ] 考虑了无偏周期势下粒子的扩散, 推导给出了粒子的有效扩散系数为$ D_{\rm eff} = D_0/G $ , 其中G 的形式为双重积分且积分值恒大于1, 故无偏周期势下的扩散变慢, 即$ D_{\rm eff} < $ $ D_0 $ . 然而, 在约瑟夫森结[5 ] 、超离子导体[6 ] 、神经活动[7 ] 、细胞内输运[8 ] 等大量实际系统中, 通过外加一个常数力(例如对于带电粒子而言, 就是一个恒定电场)控制扩散, 这引起了理论及实验工作者的极大兴趣[9 —11 ] . Reimann和H?nggi等[8 ] 在周期势场上叠加常量力, 计算了偏压周期势下粒子的有效扩散系数, 发现当偏压力达到一个临界值, 使得总的势的局部极小刚好消失, $ D_{\rm eff} $ 比$ D_0 $ 放大$1 —2$ 个量级. Bao等[12 ,13 ] 从物理机理上给出了一种解释: 由于粒子以一定概率翻越势垒形成的“跑态”与无法逃出势阱的“锁态”共存, 故粒子在偏压周期势中的概率密度分布函数的分布波包展宽, 从而导致粒子位移方差被显著地放大.[14 ] , 导致周期结构的对称性被破坏, 那么固体表面会发生破缺, 甚至使表面粗糙无序失去周期结构[1 ] . 应该说, 破缺广泛存在于现实的物理、生物和化学系统[9 ,15 -18 ] , 且在实验上不可避免[19 ] , 例如在研究锂离子扩散通过锂离子电池的电极[20 ] 、分子通过多孔介质的输运[21 ] 、旋转玻璃和大分子中的异常弛豫[1 ] 、沿异质基质移动的分子马达的动力学[22 ] 、细胞内蛋白质的运动[23 ] 、蛋白质折叠[24 ] 及表面颗粒筛选分类[14 ] 时均发现破缺对系统动力学的显著影响. 从扩散输运的角度分析, 粒子在破缺势中运动需要不断翻越势垒消耗动能, 所以通过势场中相同空间距离的时间较自由场所需的时间更长, 那么它的有效扩散系数远小于自由扩散系数. Zwanzig在文献[3 ]中推导了无偏势场叠加周期形式的破缺后, 粒子的有效扩散系数对破缺强度$ \varepsilon $ 及温度T 的依赖满足阿伦尼乌斯关系$D_{\rm eff}\propto\exp[-2\varepsilon/(k_{\rm B}T)]$ . 有趣的是, 若破缺强度随机变化(假设强度满足高斯分布且方差为$ \varepsilon^2 $ ), 则有效扩散系数对强度和温度的依赖更加敏感, 具体为$D_{\rm eff} = D_0\exp\big\{-\left[\varepsilon/(k_{\rm B}T)\right]^2\big\}$ . 人们甚至认为在其他势场下, 破缺对输运和扩散动力学过程也有害, 此前就有观点认为, 若在光滑的偏压周期势上叠加破缺会破坏粒子扩散被增强的结论[25 -27 ] .[18 ] , 推导出偏压破缺势下粒子的有效扩散系数的表达式. 将久保关系[28 ] 和爱因斯坦关系进行比较, 提出有效动力学温度$ k_{\rm B}T^* $ (即正比于粒子速度方差的稳定值)和有效阻尼$ \gamma^* $ (即速度关联函数积分的倒数)的概念. 探讨这两个等效物理量对粒子扩散输运的影响. 本文考虑相邻位置的破缺并非独立的实际情形, 借助时间域Ornstein-Uhlenbeck (OU)色噪声, 将其转化到空间域, 递推产生具有指数关联的空间OU和OU涨落的导数随机关联势(RCP), 分析粒子在偏压随机势及偏压周期随机势中的扩散规律.2.有效扩散系数 不失实际性, 考虑过阻尼粒子在一维势场中的扩散. 基于平均首次通过时间(MFPT)理论[18 ] , 有效扩散系数的解析表达式为[25 ] $ x_0 $ 为势场中任意参考点, L 为势场的周期长度, $\left \langle t^{n}(x_0 \rightarrow x_0+L) \right \rangle$ 表示粒子由$ x_0 \rightarrow x_0+L $ 的平均首次通过时间的n 阶矩, 其为$n = 1,\;2,\;\cdots$ , $ U(x) $ 为粒子所处势场. 将(2 )式代入(1 )式, 可得一维势场下的有效扩散系数解析表达式$D_0 = k_{\rm B}T/(m\gamma)$ , 且a 和b 表示为$ V(x) = V_{\rm p}(x)-Fx $ , $ V_{\rm p}(x) $ 为周期势, F 为偏压力, $C(x) = [g(0)-g(x)]/(k_{\rm B}T)$ , $ g(x) $ 为随机势的关联函数, 见下面的(9 )式. 随机关联势对粒子扩散的影响仅体现在$ C(x) $ 项.$ \gamma $ 为摩擦系数; $ \xi(t) $ 是高斯白噪声, 其均值$ \left \langle \xi(t) \right \rangle = 0 $ , 关联函数 $ \left \langle \xi(t) \xi(t') \right \rangle = 2 \gamma k_{\rm B}T \delta(t-t') $ . 粒子所在势场$ U_0(x) = V_{\rm p}(x) + V_{\rm r}(x) $ , 周期势$V_{{\rm p}}(x) = $ $ V_0\cos(2\pi x/\lambda_0)$ , $ V_0 $ 和$ \lambda_0 $ 分别为振幅和周期, $ V_{\rm r}(x) $ 表示随机势(RCP), 当$ V_0 = 0 $ 时, 方程(8 )描述粒子在偏压随机势(简记为$ V_{\rm br} $ ) 中的运动.D 为关联强度, $ \lambda $ 为关联长度. 对应的空间随机力$ F_{\rm r}{(x)} $ 的统计性质[29 ,30 ] 满足:10 )式也作为OU空间噪声的导数RCP的关联函数. 本文提出如下精确递推关系在坐标空间产生OU-RCP[31 ] :$ \Delta x $ 是将RCP离散化的空间格点间隔, $ \omega_0 $ 是高斯随机数, 满足 $ \left \langle \omega_0 \right \rangle = 0 $ , $\left \langle \omega_0 ^ 2 \right \rangle = (\lambda / 2)\; [1 - $ $ \exp(-2 \Delta x / \lambda)]$ . 进一步给出$ F_{\rm r}(x) $ 的递推关系:12 )式也用来产生OU的导数RCP, 其中$ \xi_1 $ 和$ \xi_2 $ 是产生随机势时相邻格点的两个独立高斯随机数.$ \lambda_0 $ , 能量尺度$ V_0 $ 及时间尺度$ t_0 $ , 且$ t_0 = \gamma \lambda_0^2 / V_0 $ , 得到无量纲变量: $ \tilde{x} = x / \lambda_0 $ , $ \tilde{t} = t / t_0 $ , $ \tilde{U}_0(\tilde{x}) = U_0(x) / V_0 $ , $ \tilde{F} = (\lambda_0 / V_0) F $ , $ \tilde{T} = k_{\rm B} T / V_0 $ . 方程(8 )被重写为如下无量纲形式:$ \big \langle \tilde{\xi}(\tilde{t}) \tilde{\xi}(\tilde{t'})\big \rangle = $ $ 2 \tilde{T} \delta (\tilde{t} - \tilde{t}') $ . 应用蒙特卡罗方法模拟方程(13 ), 用粒子的位移方差的长时结果来计算有效扩散系数[26 ] :15 ]发现, 多条随机势下得到粒子的有效扩散系数存在涨落, 本文为解决这一问题应用双统计平均方法[32 ] , 即分别取粒子数和随机势轨道数的双平均值, 模拟计算有效扩散系数均采用此方法. 计算中采用的参数分别为: 随机势轨道数$ K = 50 $ , 每条轨道模拟的粒子数$ N = 1000 $ , 每个粒子的演化时间$ \tilde{\tau} = 500 $ , 时间步长$ \Delta \tilde{\tau} = 0.01 $ , 离散势场的格点间隔$ \Delta \tilde{x} = 0.1 $ , 温度$ \tilde{T} = 0.2 $ . 图1 —5 给出了本文的计算结果.图 1 偏压OU-RCP及OU的空间导数RCP示意图. 参数选取为$ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ , $ \tilde{F} = 0.8 $ Figure1. The schematic diagram of the biased OU-RCP and the derivative of OU-RCP. The parameters used are $ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ , $ \tilde{F} = 0.8 $ .3.结果与分析 23.1.关联对扩散增强的影响 3.1.关联对扩散增强的影响 首先研究不同关联下, 粒子在偏压随机势中的有效扩散系数的变化. 图1 给出了在相同的关联强度$ \tilde{D} $ 和关联长度$ \tilde{\lambda} $ 下的偏压OU及OU的导数RCP. 与OU-RCP比较可以发现, OU的导数RCP呈现更密集且更高的势垒, 这些势垒对粒子的扩散有两个相互竞争的作用: 粒子的空间分布可被劈裂成很多子波包, 使得空间概率包络线展宽, 进而粒子的无规扩散被有效地增加了[33 ] ; 若粒子的动能远小于势垒高度, 则粒子以较大概率在某一势阱底部振荡, 此时势垒减弱粒子的扩散.图2 给出了粒子在偏压RCP中的有效扩散系数$ D_{\rm eff} $ 随偏压力$ \tilde{F} $ 的变化. 结果显示: 1) 两关联形式下的$ \tilde{V}_{\rm br} $ 中的粒子扩散均出现增强现象, 且$ D_{\rm eff}/D_0 $ 不是$ \tilde{F} $ 的单调函数; 2)在强偏压下的OU的导数RCP中, 粒子扩散增强的峰值更大. 当粒子在随机势中扩散时, 可通过粒子分布波包的包络线宽度的展宽来理解粒子的有效扩散增强, 空间分布的宽度越宽, 则表明粒子扩散增强越明显.图 2 偏压随机势中粒子的有效扩散系数$ D_{\rm eff} $ 随$ \tilde{F} $ 的变化. 这里比较了OU-RCP和OU的导数RCP中的结果. 内图: 继续增大$ \tilde{F} $ , OU的导数RCP对应的绿色方块曲线的变化趋势. 参数选取为$ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ Figure2. Dependence of the effective diffusion coefficient $ D_{\rm eff} $ on the biased force $ \tilde{F} $ in $ \tilde{V}_{\rm br} $ . Here, the results of OU-RCP and OU’s derivative RCP are compared. Illustration: The trend of the green square curve when continuing to increase $ \tilde{F} $ . The parameters used are $ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ .图2 中红色圆圈曲线峰值对应的$ \tilde{F} = 0.8 $ , 此时粒子分布波包的包络线展宽最宽, $ D_{\rm eff}/D_0 $ 达到峰值; 若粒子获得的动能过大(例如在$ \tilde{F} = 10.0 $ 的情况下), 则抵消势垒效应(图3 内图的上方红线), 粒子的空间概率密度函数如图3 右边红线所示, 呈高斯分布. 粒子的自由扩散得以被恢复($ D_{\rm eff}/D_0 \rightarrow 1 $ ), 这意味着更快的迁移并不带来更强的扩散. 然而, 强偏压下的OU的导数RCP的势垒效应依然明显(图3 内图的下方绿线), 该势对粒子的空间分布波包仍具有劈裂作用, 如图3 左边绿线显示的粒子空间概率分布的包络线宽度较右边红线的宽度更宽, 导致OU的导数RCP中粒子的有效扩散明显强于OU-RCP中的情形. 本文重点讨论OU-RCP和OU的导数RCP, 但计算发现不同势结构叠加相同关联形式的RCP同样会影响粒子的扩散增强.图 3 分别叠加OU-RCP, OU的导数RCP的偏压随机势中粒子的概率密度分布函数. 内图: 叠加OU-RCP, OU的导数RCP的偏压随机势$ V_{\rm br} $ 的示意图. 参数选取为$ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ , $ \tilde{F} = 10.0 $ Figure3. The PDF of a particle in $ V_{\rm br} $ , the OU-RCP and OU’s derivative RCP are considered. Illustration: the schematic diagram of $ V_{\rm br} $ . The parameters used are $\tilde{\lambda} = $ $ 0.5$ , $ \tilde{D} = 0.1 $ , $ \tilde{F} = 10.0 $ 3.2.势结构对扩散增强的影响 -->3.2.势结构对扩散增强的影响 为揭示不同势结构叠加破缺后, 粒子的扩散被增强的现象, 图4 给出3种势下粒子的有效扩散系数随偏压力的变化. 本文讨论的势分别为偏压周期势$ \tilde{V}_{\rm bp} $ , 偏压周期随机势$ \tilde{V}_{\rm bpr} $ 和偏压随机势$ \tilde{V}_{\rm br} $ . 从图4 可见, 模拟结果与解析近似结果的规律性一致. 需要说明的是, 在推导破缺势场中的有效扩散系数的解析表达式时, 我们对OU-RCP引入周期近似[34 ] , 这会导致解析结果与模拟结果存在一定的偏差. 其中, $ \tilde{V}_{\rm bp} $ 下的$ D_{\rm eff}/D_0 $ 在$ \tilde{F} \rightarrow \tilde{F}_{\rm c} = 1.0 $ 附近达到最大值, 这是因为随着偏压的变大, 周期势的有效势垒高度降低, 粒子“锁态”和“跑态”的速度双模会达到最佳的混合状态, 导致位移方差$ \left \langle \Delta {x} ^2 {(t)}\right \rangle $ 迅速增大, 根据(14 )式, $ D_{\rm eff} $ 随之增大. 在$ \tilde{F} = \tilde{F}_{\rm c} $ 时, 势的局域极小值消失, 粒子运动模式仅为“跑态”, 这不利于$ \left \langle \Delta {x} ^2 {(t)}\right \rangle $ 的变大, 导致$ D_{\rm eff} $ 由峰值开始降低. 但将OU-RCP叠加在光滑的$ \tilde{V}_{\rm bp} $ 后, 发现有效扩散系数最大值显著增加, 甚至高于$ \tilde{V}_{\rm br} $ 中的峰值.图 4 3种势$ \tilde{V}_{\rm br} $ , $ \tilde{V}_{\rm bpr} $ 和$ \tilde{V}_{\rm bp} $ 中粒子的有效扩散系数$ D_{\rm eff} $ 作为偏压力$ \tilde{F} $ 的函数. 比较了解析和模拟结果. 参数选取为$ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ Figure4. The effective diffusion coefficient $ D_{\rm eff} $ of a particle as a function of the biased force $ \tilde{F} $ in $ \tilde{V}_{\rm br} $ , $ \tilde{V}_{\rm bpr} $ and $ \tilde{V}_{\rm bp} $ . The analytical result and simulation result are compared. The parameters used are $ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ .$ \tilde{V}_{\rm bp} $ 的临界偏压力$ \tilde{F}_{\rm c} = 1.0 $ 来对3种势情况的结果进行比较. 图5 内图所示的$ \Delta \tilde{L} $ ($ \Delta \tilde{L} $ 为$ \tilde{V}_{\rm bp} $ 的每个周期中基态至鞍点位置的空间间隔)中, 仅有$ \tilde{V}_{\rm br} $ 是明显倾斜的, 而另外两势几乎是平的, 此偏压力下光滑的$ \tilde{V}_{\rm bp} $ 中的粒子以单一“跑态”存在, 如图5(a) 所示的空间分布波包的包络线近似高斯分布; 而图5(c) 中的初始位置附近的分布波包表明了$ \tilde{V}_{\rm bpr} $ 中粒子在长时间演化后, 仍以大概率被束缚在距其初始位置最近的空间间隔$ \Delta \tilde{L} $ 中; 但$ \tilde{V}_{\rm br} $ 中$ \Delta \tilde{L} $ 部分势场倾斜, 由于粒子获得动能易于越过$ \Delta \tilde{L} $ 中的势垒, 所以图5(b) 所示的分布波包相比图5(a) 和图5(c) 的展宽更宽, 导致$ \tilde{F} = 1.0 $ 时$ \tilde{V}_{\rm br} $ 中粒子的有效扩散系数最大. 继续增大偏压力, $ \tilde{V}_{\rm br} $ 逐渐失去势垒效应, 而$ \tilde{V}_{\rm bpr} $ 中的$ \Delta \tilde{L} $ 部分被倾斜, 粒子获得动能越过间隔$ \Delta \tilde{L} $ , 与图5(c) 相比较, 图5(d) 所示的粒子分布波包明显展宽, 扩散增强.图 5 $ \tilde{F} = 1.0 $ 时, $ \tilde{V}_{\rm bp} $ , $ \tilde{V}_{\rm br} $ 及$ \tilde{V}_{\rm bpr} $ 中粒子的概率密度分布函数($(\rm a)—(\rm c)$ ); (d) $ \tilde{F} = 1.7 $ (图4 的红线加三角形曲线的最大值对应的偏压力)时, $ \tilde{V}_{\rm bpr} $ 中粒子的概率密度分布函数. 内图: $ \tilde{F} = 1.0 $ 时的$ \tilde{V}_{\rm br} $ , $ \tilde{V}_{\rm bpr} $ 示意图. 参数选取为$ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ Figure5. The PDF corresponding to $ \tilde{V}_{\rm bp} $ , $ \tilde{V}_{\rm br} $ and $ \tilde{V}_{\rm bpr} $ for $ \tilde{F} = 1.0 $ ((a)–(c)); (d) the PDF of particle in $ \tilde{V}_{\rm bpr} $ for $ \tilde{F} = 1.7 $ (the optimal biased force for $ \tilde{V}_{\rm bpr} $ in Fig. 4 ). Illustration: the schematic diagram of $ \tilde{V}_{\rm br} $ , $ \tilde{V}_{\rm bpr} $ for $ \tilde{F} = 1.0 $ . The parameters used are $ \tilde{\lambda} = 0.5 $ , $ \tilde{D} = 0.1 $ .$ k_{\rm B}T^* $ 和有效阻尼$ \gamma^* $ 的概念, 从新的视角研究$ k_{\rm B}T^* $ 和$ \gamma^* $ 对粒子扩散变化的效应, 因为在倾斜的周期场中, 两者皆不是常量. 其具体表达式为表1 所列, 虽然粒子在无偏势($ \tilde F $ = 0)中扩散时的有效动力学温度不变, 但是粒子的有效阻尼明显增大, 如果$D_{\rm eff} = k_{\rm B} T^*/(m \gamma^*)$ 中的分子不变, 分母增大, 那么易得3种无偏势中的粒子$D_{\rm eff} < $ $ D_0$ , 文献[3 ]由首通时间理论出发得到的结果证实了本文的结论. 随偏压力的增加, $ k_{\rm B}T^* $ 和$ \gamma^* $ 均呈现非单调的变化规律, 更有趣的是, 在相同的偏压下$ k_{\rm B}T^* $ 达到最大值, 而$ \gamma^* $ 降至最小值, 这导致了有效扩散增强峰值的出现. 总结上述规律可得结论: 在无偏势中, 粒子有效阻尼的增加抑制了扩散; 而在偏压势中, 粒子的有效动力学温度和有效阻尼的共同调制导致了扩散增强. $\tilde F=0$ 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 偏压周期势 $k_{\rm B}T^*$ 0.20 0.21 0.45 0.42 0.32 0.28 0.25 0.24 0.23 偏压周期随机势 $k_{\rm B}T^*$ 0.20 0.21 0.22 0.36 1.09 0.62 0.32 0.31 0.23 偏压随机势 $k_{\rm B}T^*$ 0.20 0.22 0.28 0.62 1.09 0.34 0.25 0.26 0.27
表1 3种势结构下粒子的有效动力学温度$k_{\rm B}T^*$ 及有效阻尼$\gamma^*$ 随偏压力的变化Table1. The effective kinetic temperature $k_{\rm B}T^*$ and effective friction $\gamma^*$ of a particle under the three potential structures change with the biased force.4.总 结 本文研究了不同破缺势结构中粒子的有效扩散. 基于平均首次通过时间理论推导出粒子在破缺势中的有效扩散系数的近似解析表达式, 并结合蒙特卡罗模拟结果, 得出如下结论: 通过施加偏压, 随机势中粒子的扩散可被增强, 且在较大的偏压力下, 比OU随机关联势的势垒更高且更密集的OU的导数随机关联势对粒子有效扩散的增强效果更加明显, 这表明空间随机势的关联形式影响粒子的有效扩散; 随着力的不断变大, 偏压随机势中粒子的有效扩散系数能够达到的最大值大于偏压周期势的最大值, 但小于偏压周期随机势的峰值, 这表明不同的势结构对粒子扩散的增强能力存在差异, 用粒子的空间概率密度分布函数的波包展宽对扩散增强机制做出了解释. 此外, 通过比较久保关系和爱因斯坦关系, 提出有效动力学温度和有效阻尼的概念, 进一步发现: 在无偏势场中, 由于粒子有效阻尼的变大导致了有效扩散减弱; 而在偏压势场中, 粒子有效动力学温度和有效阻尼的共同调制导致了有效扩散的增强. 以上结论在物理学和生物学等领域均可被应用, 例如, 在物理学方面的应用包括: 电泳分离颗粒[35 ] 、原子在金属表面扩散的控制[36 ] 、纳米机器的设计[37 ] ; 在生物学方面的应用包括通过单分子拉伸实验来研究蛋白质[38 ] 、DNA[39 ] 及RNA[40 ] 等生物分子的折叠和展开能态等. 



































































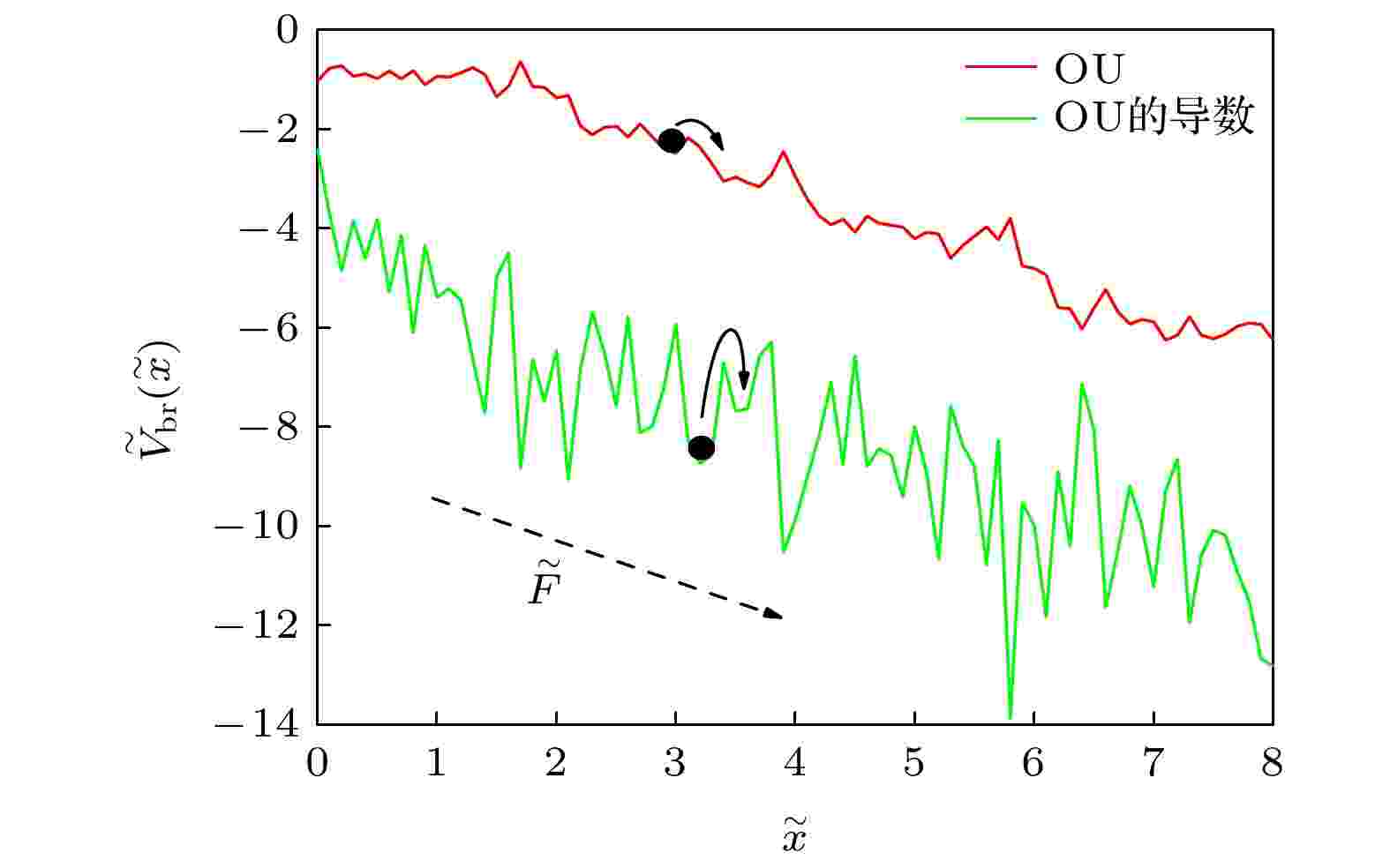 图 1 偏压OU-RCP及OU的空间导数RCP示意图. 参数选取为
图 1 偏压OU-RCP及OU的空间导数RCP示意图. 参数选取为














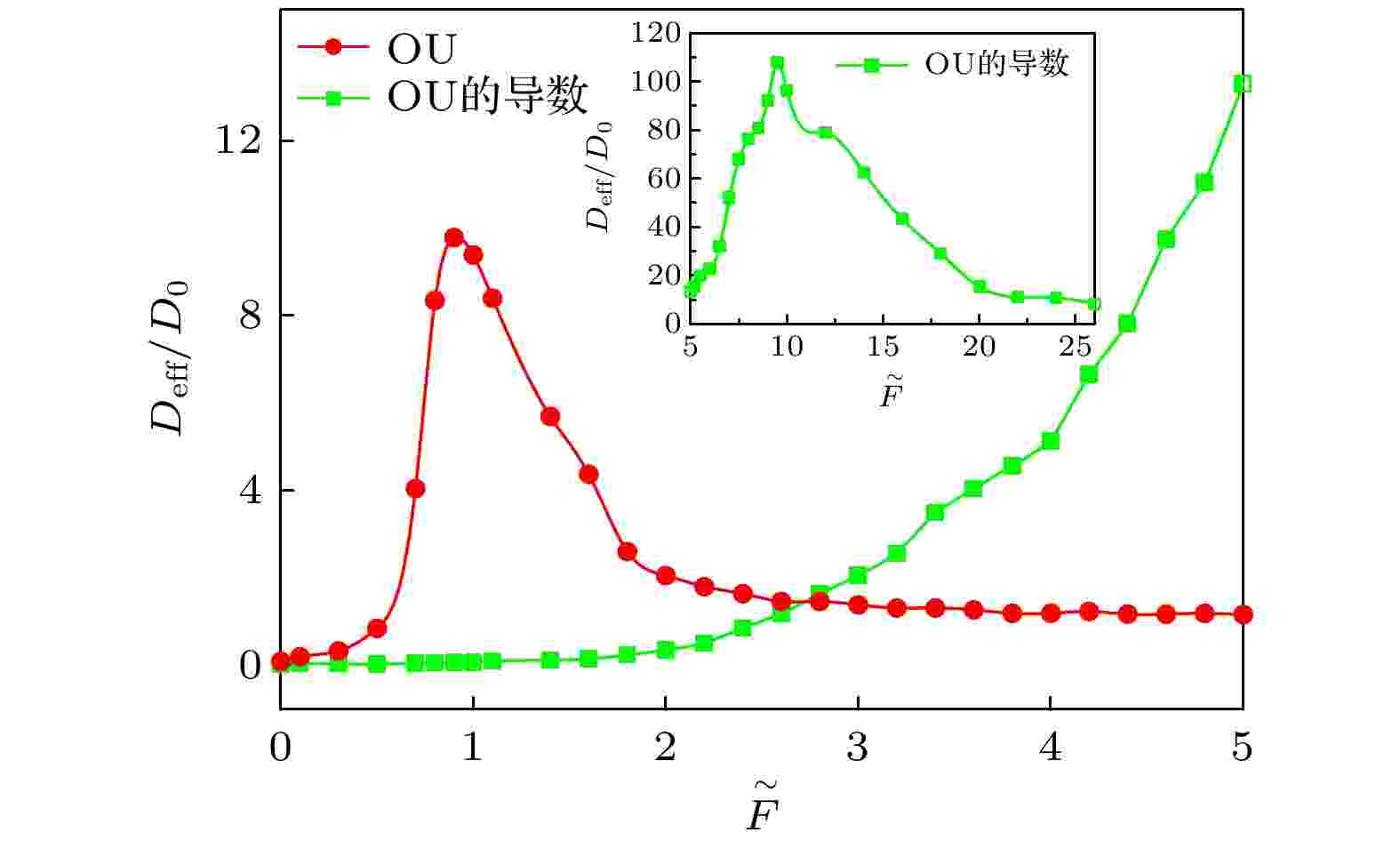 图 2 偏压随机势中粒子的有效扩散系数
图 2 偏压随机势中粒子的有效扩散系数


















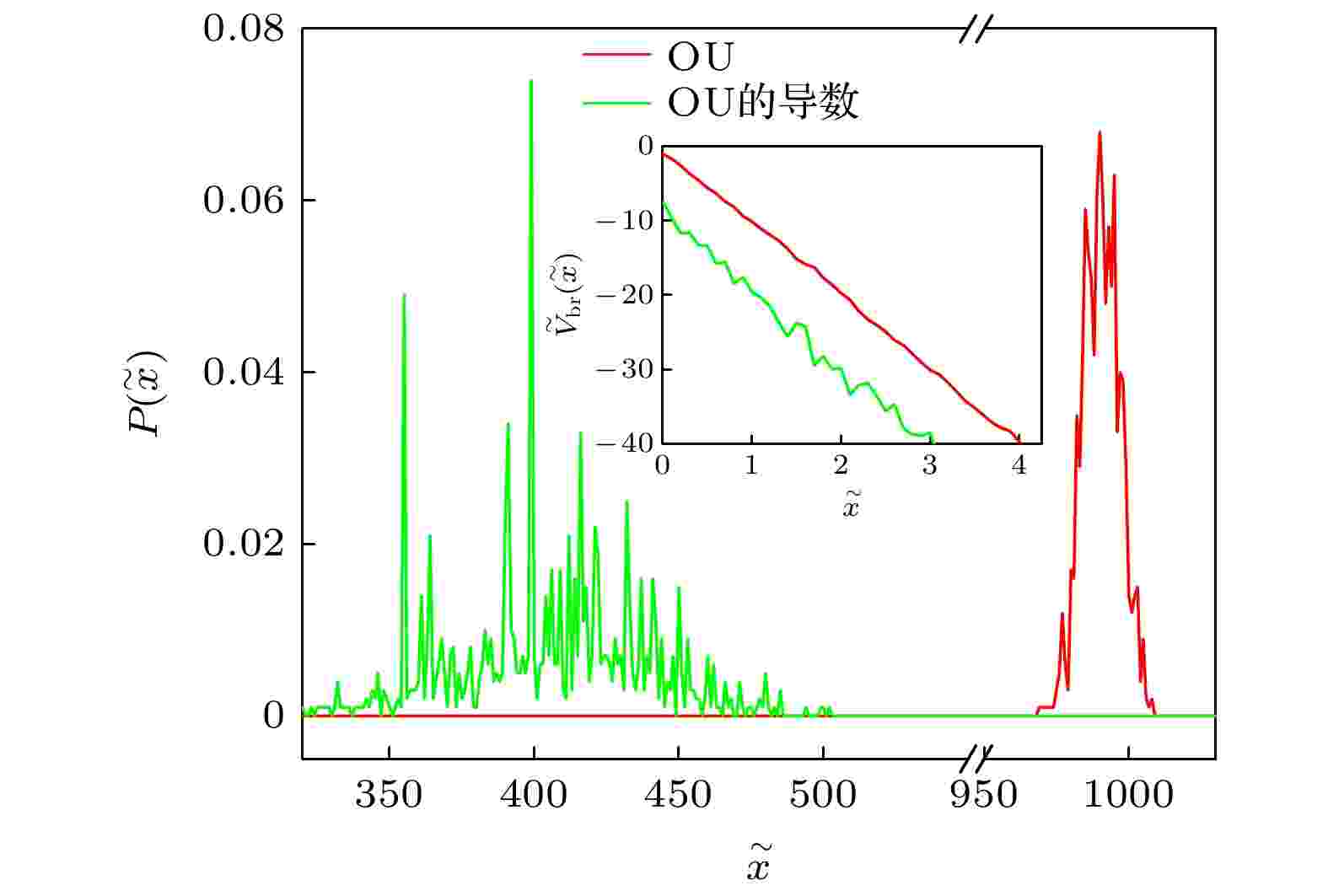 图 3 分别叠加OU-RCP, OU的导数RCP的偏压随机势中粒子的概率密度分布函数. 内图: 叠加OU-RCP, OU的导数RCP的偏压随机势
图 3 分别叠加OU-RCP, OU的导数RCP的偏压随机势中粒子的概率密度分布函数. 内图: 叠加OU-RCP, OU的导数RCP的偏压随机势




































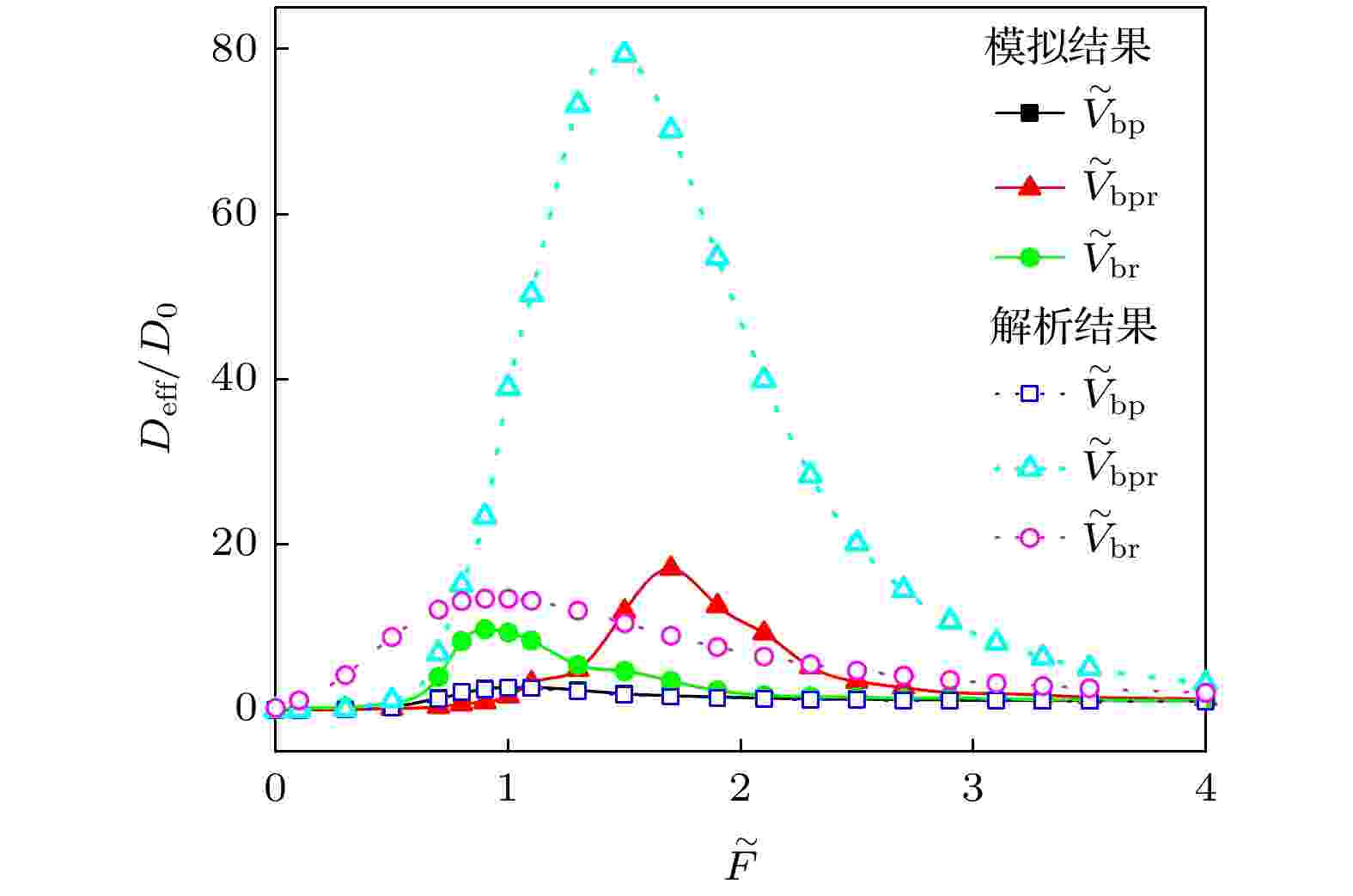 图 4 3种势
图 4 3种势





























































































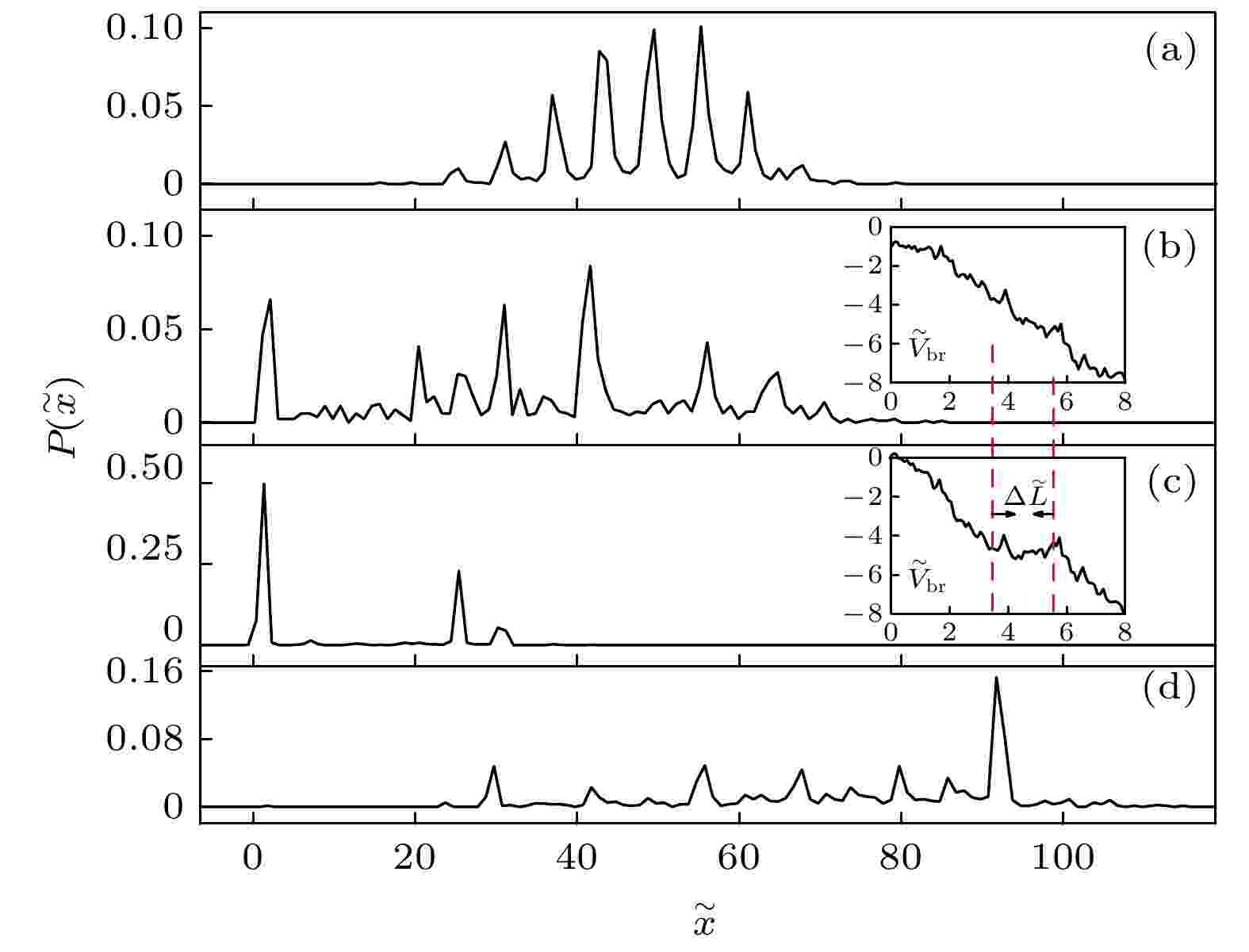 图 5
图 5 









































































