摘要:硅石墨烯 (siligraphene) 作为石墨烯和硅烯的复合物, 由于其具有石墨烯和硅烯不具备的许多优异性能而受到了广泛关注. Siligraphene的性质与Si原子的分布以及它的结构密切相关, 但是目前对siligraphene的研究主要限于Si的规则分布和具有高对称性的平面结构. 为了超越这些限制, 本文基于密度泛函理论研究了siligraphene g-SiC₇所有可能的Si分布及其平面和非平面结构. 首先从g-SiC₇的35960种Si分布中筛选出了365种不等价的Si分布, 然后针对每个不等价的Si分布, 比较了平面结构和非平面结构的稳定性. 就Si分布而言, Si原子倾向于聚集在一起以降低能量, 而更分散的Si分布通常具有更高的能量; 就结构的平面性而言, 研究发现存在很多的非平面结构, 其能量明显低于平面结构. 在所有可能的Si分布中, 仅有8个平面结构对面外扰动是稳定的. 本文进一步研究了能量最低三种结构的动力学、热力学和机械稳定性, 发现它们都是稳定的. 能带计算发现, 尽管能量最低的几种结构存在明显的翘曲, 它们在第一布里渊区中两个狄拉克能谷仍得以保留, 并且在狄拉克点处打开了相当大的带隙. 本文计算了其贝里曲率, 发现在不等价狄拉克能谷处的贝里曲率是相反的, 这表明系统具有能谷自由度. 研究表明, siligraphene倾向于具有更集中的Si分布和翘曲结构, 并且最稳定的结构具有良好的电子性质.
关键词: 硅石墨烯/
Si原子分布/
平面和非平面结构/
第一性原理计算

English Abstract

全文HTML

--> --> -->

石墨烯自发现以来, 因其优异的性能和巨大的应用价值而受到广泛关注和深入研究. 受石墨烯研究的启发, 人们发现第IV主族元素的Si和Ge也能形成类石墨烯的硅烯和锗烯. 石墨烯是完全平的^[1-3], 而硅烯和锗烯具有翘曲结构^[4-6], 不是完全平整的. 由第IV主族单质元素构成的六角单原子层结构, 都有很高的电子迁移率和热导率, 但是它们都没有带隙, 因而不易应用于逻辑开关元件中. 石墨烯和硅烯在K和–K处有两个不等价的狄拉克锥可以作为能谷, 但是能谷处没有带隙, 限制了其在能谷电子学方面的应用. 研究者们致力于打开石墨烯和硅烯的带隙, 但是要在室温下得到0.5 eV以上的能隙并且保留狄拉克锥, 仍是一个挑战.
第IV主族元素Si和Ge具有和C原子相同的外层电子结构, 因此用Si或Ge掺杂石墨烯, 有希望保留狄拉克锥, 从而保存石墨烯原有的优异性质. 掺杂打破其对称性可能产生带隙, 从而克服石墨烯零带隙的缺点. 最近Si掺杂的石墨烯-硅石墨烯 (siligraphene)—作为一种新的二维材料被广泛地研究^[7-10]. g-SiC_n表示C和Si原子数比例为n∶1的siligraphene. 不同于一般的Si掺杂, siligraphene中的Si的含量很高, 因而又被看作是石墨烯和硅烯的复合体. 研究表明siligraphene性质比石墨烯和硅烯更丰富. 改变siligraphene的化学计量比, 带隙可在很宽的范围内变化 (0—2.87 eV)^[11]. 研究发现, g-SiC₂具有1.09 eV的带隙, 有望成为太阳能电池材料^[12,13]. g-SiC₃被发现是一种拓扑绝缘体, 其边缘态具有受拓扑保护的带隙^[14]. 而g-SiC₅是半金属, 具有出色的气体传感性能^[15]. g-SiC₇的能隙 (1.13 eV) 在红外和可见光范围内^[16], 研究发现其具有出色的吸光率和太阳能转化率, 在光伏电池中具有很大的应用价值. g-SiC₇还被发现具有很高的电导率、良好的热学和光学性质^[17,18].
到目前为止, 关于siligraphene的研究都基于两个假设. 第一, 假设Si原子在siligraphene中的分布是具有较高对称性. 这样假设的目的可能是为了尽量不打破石墨烯的原有对称性, 从而使石墨烯的优良性质得以保留. 第二, 假设siligraphene具有平面结构. 其原因可能是在g-SiC_n (n > 1) 中, 大多数化学键与石墨烯中的键类似, 是具有sp²杂化的C—C键, 因此认为不会发生翘曲. 但是由于Si—C键 (1.785 ?) 要比C—C (1.420 ?) 键明显长^[19-21], 为了容纳更长的Si-C键, 石墨烯中原有的C原子正六边形环会发生形变. 该形变是否导致翘曲与Si原子浓度及其分布有关, 因此需要对比平面与非平面结构的稳定性. 图1所示的是文献中重点研究的g-SiC₇, 它具有高对称的Si分布和全平的结构^[17,18,22]. 但是哪一种分布是更可能的, 应该根据稳定性来判断, 而不是根据高对称性和平面性的要求或假设. 此前还没有研究表明在siligraphene中Si原子高对称分布比低对称的能量更低, 或者全平结构比非平面结构的能量低. 所以有必要研究各种可能的Si分布及其平面和非平面结构, 从中找出能量最低的情形.
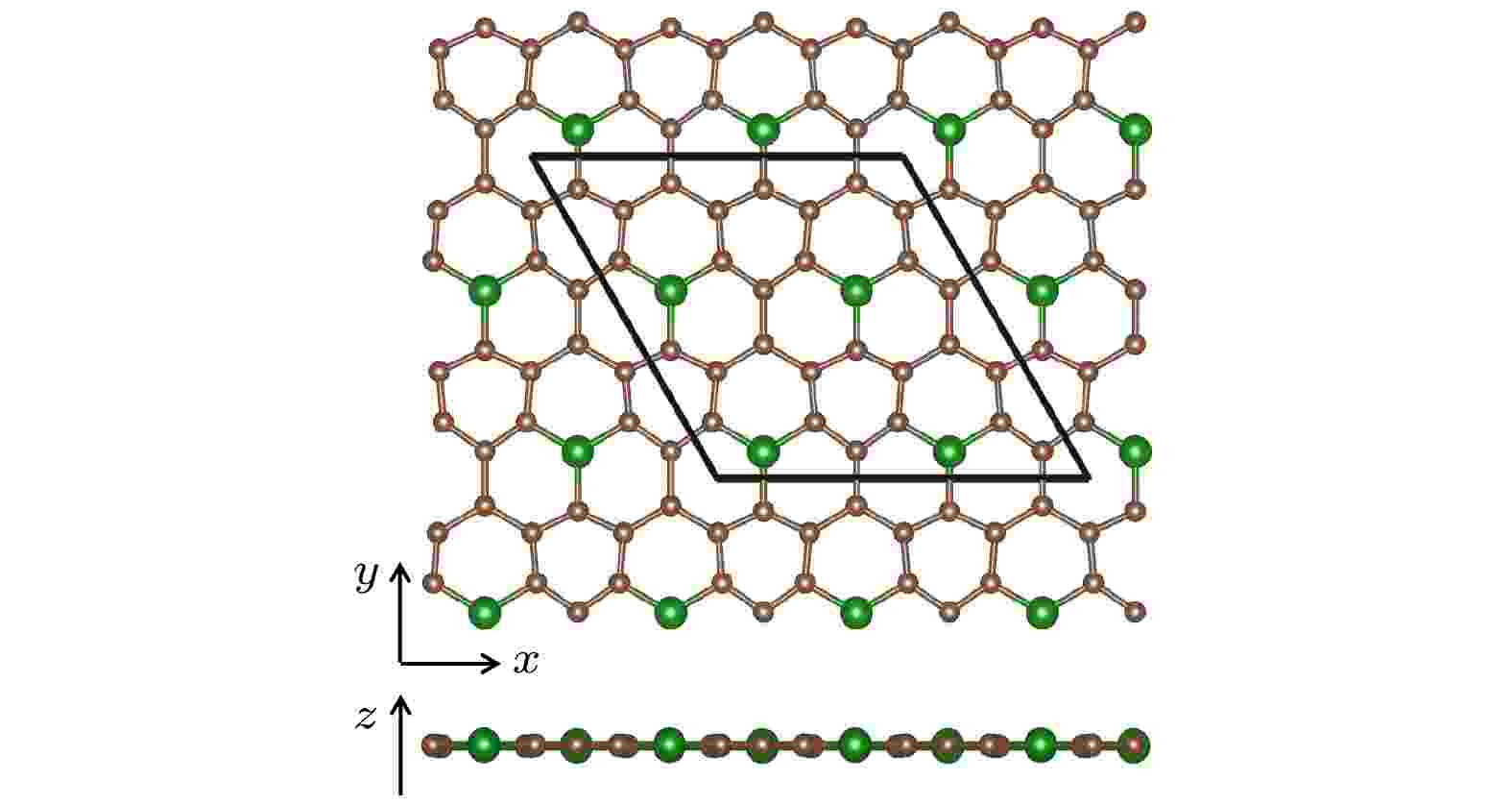图 1 文献[16]中研究g₀-SiC₇的原子结构. 其中棕色和绿色球分别代表C原子和平面内的Si原子, 棱形代表原胞
Figure1. The atomic structure of g₀-SiC₇ are studied in the literature [16]. The brown and green spheres represent C atoms and Si atoms in the plane, respectively. The rhombus denotes the unit cell.

为了研究siligraphene的Si原子分布和其结构, 将不局限于上述两个假设, 充分考虑各种可能的分布和结构, 从中找出能量更低的siligraphene, 并研究其性质. 在本文中, 选取g-SiC₇为研究对象, 因为在众多的siligraphene中, g-SiC₇在光伏、储氢、电学、热学和光学方面有优异潜质而受到广泛研究, 而且还因为相较于g-SiC₂, g-SiC₃和g-SiC₅, g-SiC₇中的Si原子有足够多的分布方式, 有利于探索Si原子分布的规律. 通过排列组合, 考虑所有Si原子可能的占位, 从中筛选出不等价的分布, 然后对每种分布考虑平面和各种非平面结构, 通过第一性原理计算总能来比较其稳定性, 找到了几种能量相近最稳定的结构, 并通过计算声子谱、电子能带和贝里曲率, 研究了它们的稳定性、电子性质和能谷自由度, 发现它们仍然保留狄拉克锥, 并且打开了带隙. 这些研究将有助于未来研究IV族原子掺杂的石墨烯、硅烯和锗烯的物理性质.

第一性原理计算基于密度泛函理论 (density functional theory, DFT), 使用Vienna ab initio simulation package (VASP) ^[23,24]程序包, 离子实对价电子的作用采用投影缀加波 (projector augmented wave, PAW) 赝势来描述, 交换关联函数选取广义梯度近似下的Perdew- Burke-Ernzerhof (PBE) 泛函^[25,26]. 平面波截断能设定为500 eV, K点用以Γ点为中心的3 × 3 × 1网格进行采样. 对每个原子的位置都进行优化, 原子弛豫收敛标准是所有原子受力都小于1 meV/?. 用超胞中的薄片模型来描述二维siligraphene, 为避免相邻超胞中不同原子层之间的相互作用, 加约15 ?的真空层. 利用PHONOPY程序包^[27]计算得到声子谱验证其动力学稳定性, 利用第一性原理分子动力学验证其热力学稳定性, 计算弹性模量证明其机械稳定性^[28]. 贝里曲率的计算, 使用了WANNIER90程序包^[29,30]. 先利用排列组合方式构建所有硅掺杂的siligraphene构型, 并利用RG²软件^[31-33]筛选出其中非等价的硅元素分布构型, 这里所用的RG²是一款基于群论和图论的晶体结构预测软件, 它能对具有可描述结构特征的晶体结构进行快速高效的预测^[34-36]. RG²中判断结构是否等价的算法有两个步骤: 考虑周期性和超胞, 首先判断化学计量比、对称性是否相同, 不相同的则可以确定是不等价构型, 化学计量比、对称性都相同的继续判断两个结构的非等价原子坐标, 如果一致则认为是相同构型. 对化学计量比、对称性相同, 但非等价坐标不同的结构, 则进一步利用迭代最近点算法对原子坐标进行点云匹配, 以尝试寻找使得两个结构的所有原子能够完全重合的刚性变换 (旋转或平移), 如果可以找到则说明两个结构相同, 否则认为是不等价构型.

文献中研究的 g-SiC₇ 具有高对称的 Si 分布^[16-18,22], 可通过在4 × 4的石墨烯超胞中 (32个C原子) 用四个Si原子替代C原子得到, 如图1所示. 后面的讨论都以此高对称分布为参照, 记其为g₀-SiC₇. 在实际中, 不能排除有其它Si分布的可能性, 而且也没有研究证实g₀-SiC₇在能量上是更低的. 为了考虑g-SiC₇中各种可能的Si原子分布, 在4 × 4的石墨烯超胞中用四个Si原子任意替换四个C原子, 共有$C_{32}^4 = 35960$种分布. 在这些分布中, 有很多是等价的, 因此需要筛除重复的分布. 借助RG²的去重复功能, 最终确认了365种不等价Si分布构型, 进而避免了大量的重复计算.
以往对g-SiC₇的研究一般只考虑了如图1所示的平面结构^[16,17]. 在本文中, 对每种Si分布分别考虑两种不同的初始翘曲. 一种初始翘曲类似于硅烯的翘曲结构, 其中所有相邻原子(包括Si和C原子) 在z方向相对位移0.3 ?; 另一种是C原子固定在平面内不动, 仅掺杂Si原子在z方向有相对位移0.3 ?. 首先优化图1中所示平面结构获得其总能量E₀, 并以此能量为参照进行比较. 为了探索非平面siligraphene, 对每种Si分布的两种初始非平面结构进行弛豫, 并选择能量较低的情况进行研究, 以查看它们最终是非平面还是平面结构. 如果弛豫得到的结构是平面的, 则非平面结构是不稳定的. 如果得到的是非平面结构, 则将其能量和总能量E₀比较, 以确定哪个更稳定.
按照以上思路, 对这365种分布的结构进行优化, 计算其总能. 在以下讨论某种Si分布的能量时, 如无特别指出, 都是指该分布经弛豫后所得到结构的最低能量. 用Si原子间绝对距离 (考虑z方向的移动) 的平均值作为指标来描述Si原子的聚集度, 以文献[17, 18]中的高对称和全平g₀-SiC₇ (图1)的总能E₀为参照, 分析总能与Si原子聚集度的关系, 从中找出具有较低能量的分布和结构所具有的特征. 从图2可见, 在文献[17]中具有高对称Si分布和平面结构的g₀-SiC₇ (图1)的能量几乎处于最高位置, 绝大多数Si分布的能量比g₀-SiC₇的低很多, g₀-SiC₇的Si原子平均距离也是最大的. 计算发现的趋势是: 比较聚集的Si原子分布一般有较低的能量; 在相同的Si原子分布情况下, 具有翘曲的非平面结构大多数情况下具有较低能量.
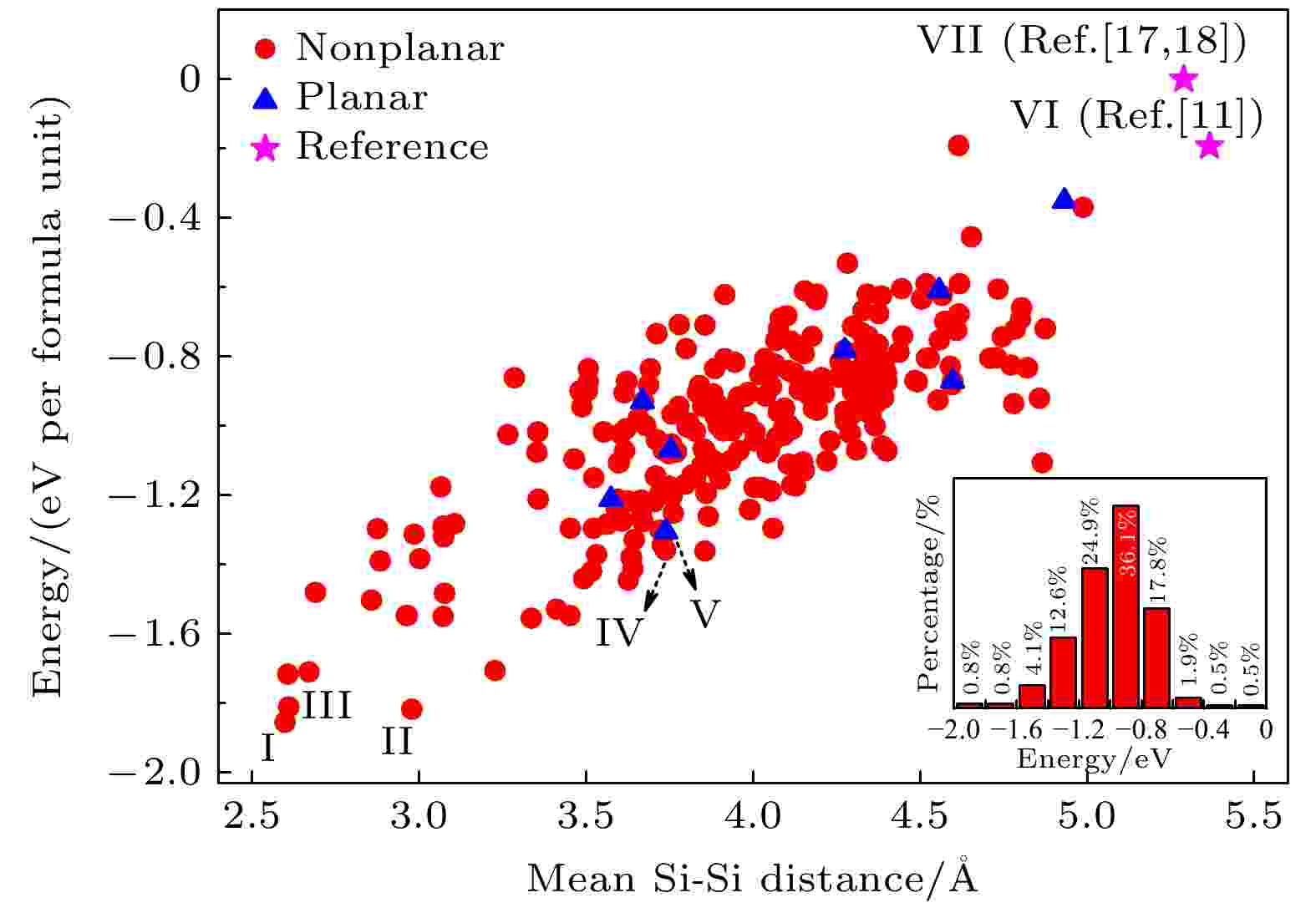图 2 g-SiC₇的总能与Si原子间平均距离的关系, 选取文献[17, 18]中g₀-SiC₇的总能为参考零点. 图中的罗马数字标记的是能量最低的非平面结构、平面结构和本文中与它们作为比较的一些结构. 插图柱状图代表在在不同能量区间中不等价Si分布在总分布数中的百分比
Figure2. For the relationship between the total energy of g-SiC₇ and the average distance between Si atoms, the total energy of g₀-SiC₇ in the literature [17, 18] is selected as the reference zero point. The Roman numerals in the figure mark the non-planar structures with the lowest energy, planar structures, and some structures compared with them in this article. The inset histogram represents the percentage of unequal Si distribution in the total distribution in different energy intervals.

尽管图2表明对绝大多数Si分布是非平面结构更稳定, 仍有8种分布的平面结构是稳定的, 即从初始具有翘曲的结构出发, 弛豫后体系会回到全平状态. 在这些全平结构中也有Si平均距越小能量越低的趋势(图2). 图2中的结构Ⅴ是能量最低的平面结构, 其原子结构和Si原子分布如图3(a)所示, 其中Si原子分布在一条带上, 占据了原来石墨烯C原子六环中长对角线端点的位置. 在图2中可见, 几乎在结构V的正下方有个非平面结构Ⅳ, 其Si平均距离几乎与结构Ⅴ的相等, 但其能量比平面结构Ⅴ的小. 图3(b)所示为非平面结构Ⅳ, Si原子也分布在一条带上, 占据了C环的短对角线的端点, 两个一组, 高低交错排列. 其他平面结构也都有类似情况, 总存在与其Si分布相近的能量更低的非平面结构. 计算了图2中Ⅴ和Ⅳ结构的声子谱, 发现没有虚频, 所以它们是动力学稳定的. 同时计算了它们的能带, 如图3所示, 可见它们在K和–K处的狄拉克锥仍然保留, 结构Ⅴ和Ⅳ在狄拉克点处分别有0.007 eV和0.009 eV的带隙. 这八种稳定的全平分布不包括文献[16-18]中研究的g₀-SiC₇ (图2中的结构VII), 因为以往计算g₀-SiC₇时只考虑了其全平初始结构, 如果让其初始结构中原子具有垂直于平面的位移, 弛豫后会得到能量低得多的非平面结构^[11] (图2中的结构VI).
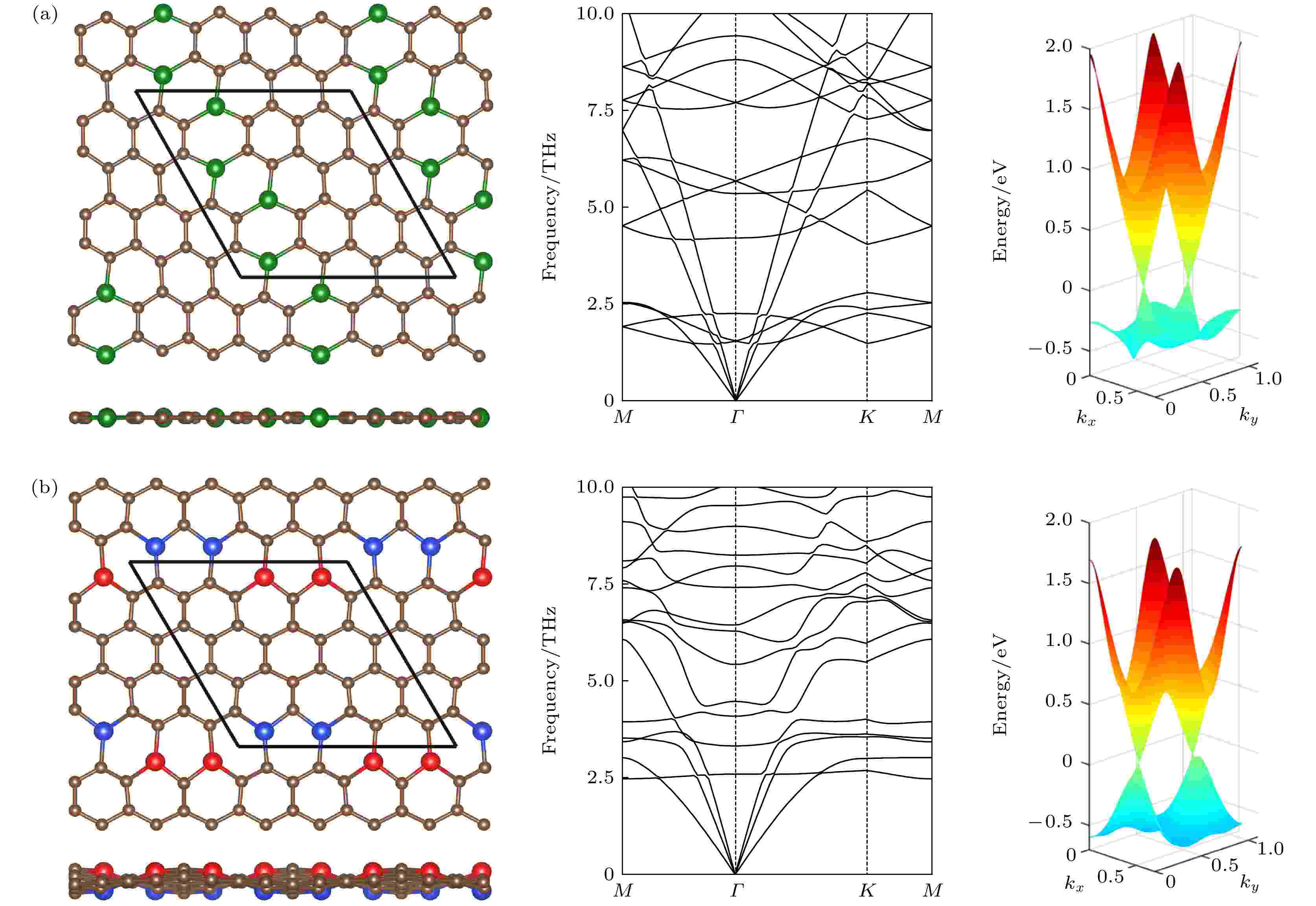图 3 (a)和(b)中的左图分别对应图2中结构Ⅴ和Ⅳ的俯视图和侧视图, 其中棕色球表示C原子, 红色、绿色和蓝色球分别表示在平面上、平面内和平面下的Si原子, 棱形代表原胞. 中图和右图分别是它们的声子谱和能带
Figure3. The left panels of (a) and (b) are the top and side views of the structures V and IV in Fig. 2, respectively. The brown spheres stand for C atoms. The red, green and blue spheres denote the Si atoms above, inside and below the plane, respectively. The rhombus denotes the unit cell. The middle and right panels are their phonon spectra and energy bands, respectively.

除了这八种分布的平面结构, 其余分布的稳定结构都是有翘曲的, 它们从有初始面外偏移的结构出发, 弛豫后原子不回到平面, 而是得到有翘曲的结构, 且能量比全平结构的能量低. 从图2可见, 随着Si原子平均距离减小, 能量也减小, 说明在siligraphene中, Si原子倾向于聚集. 我们对图2中左下角能量最低的三种结构Ⅰ, Ⅱ和Ⅲ进行了更详细的研究, 其优化后的结构如图4所示, 结构Ⅰ(Ⅱ, Ⅲ)的晶格常数a和b分别为9.88 (9.93, 10.05) ?和10.18 (10.30, 9.90) ?, 计算的能量、带隙和翘曲高度如表1所列. 结构Ⅰ的能量最低, 一个g-SiC₇原胞里的四个Si原子聚在一起构成一个Si原子环, 这个环中两个相邻Si原子在平面上面, 另两个相邻Si原子在平面下面, Si的最大翘曲高度有2.84 ?, 比硅烯中的翘曲高度0.44 ?大了很多. 能量比g₀-SiC₇的能量低了每单位化学式1.85 eV. 为验证其动力学稳定性, 计算了其声子谱, 如图4(a)所示. 声子谱中没有虚频, 说明结构Ⅰ是动力学稳定的. 对其进行第一性原理分子动力学计算, 如图5(a)所示, 在500 K温度下能量在平衡位置附近震荡, 基本维持了原来的形貌, 说明其具有热力学稳定性. 对其弹性模量计算, 如表1所列, 其C₁₁, C₁₂, C₂₂以及C₄₄满足二维材料的玻恩准则(C₁₁C₂₂ – C₁₂ > 0, C₄₄ > 0)^[28], 说明它们都是机械稳定的. 计算的能带表明, 虽然翘曲较大, 但是狄拉克能谷得以保存, 在狄拉克点处打开了0.02 eV的带隙.
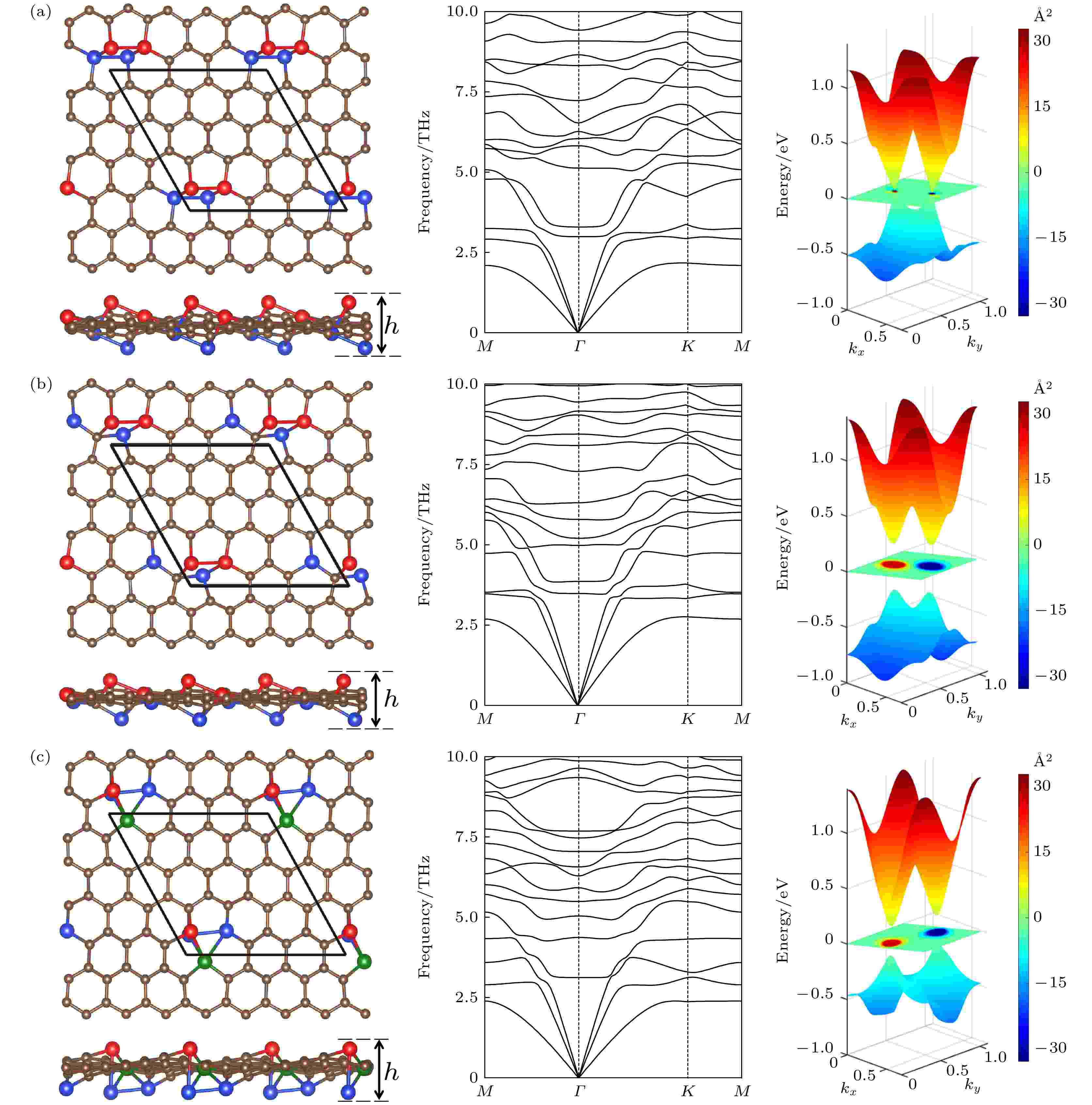图 4 (a), (b)和(c)中的左图分别是图2中能量最低结构Ⅰ, Ⅱ和Ⅲ的俯视图和侧视图, 其中棕色球表示C原子, 红色、绿色和蓝色球分别表示在平面上、平面内和平面下的Si原子, 棱形代表原胞, h代表翘曲高度. 中图和右图分别是它们的声子谱和能带. 在能带图中间的颜色梯度图为价带总贝里曲率
Figure4. The left panels in Fig. (a), (b) and (c) are the top and side views of the structures I, II and III in Fig. 2 with the lowest energies, respectively. The brown spheres stand for C atoms. The red, green and blue spheres denote the Si atoms above, inside and below the plane, respectively. The rhombus denotes the unit cell, h denote buckling height. The middle and right panels are their phonon spectra and energy bands, respectively. The central color gradient plane between the bands shows the calculated total Berry curvature of the valence bands.

Structure	Ⅰ-SiC7	Ⅱ-SiC7	Ⅲ-SiC7
Energy/(eV per formula unit)	–1.85	–1.81	–1.80
h/?	2.84	2.45	2.63
Band gap/eV	0.02	0.42	0.26
C11/(N·m–1)	237.30	270.45	219.15
C22/(N·m–1)	178.20	209.40	218.55
C12/(N·m–1)	12.30	31.50	21.90
C44/(N·m–1)	93.60	97.65	95.70

表1最稳定的三种g-SiC₇的总能(以g₀-SiC₇的总能为参照)、翘曲高度h、带隙和弹性模量, 罗马数字与图2中的对应
Table1.The total energy (with respect to the total energy of g₀-SiC₇), buckling height h, band gap and elastic moduli of the three most stable g-SiC₇, the Roman numbers correspond to those in Fig. 2.

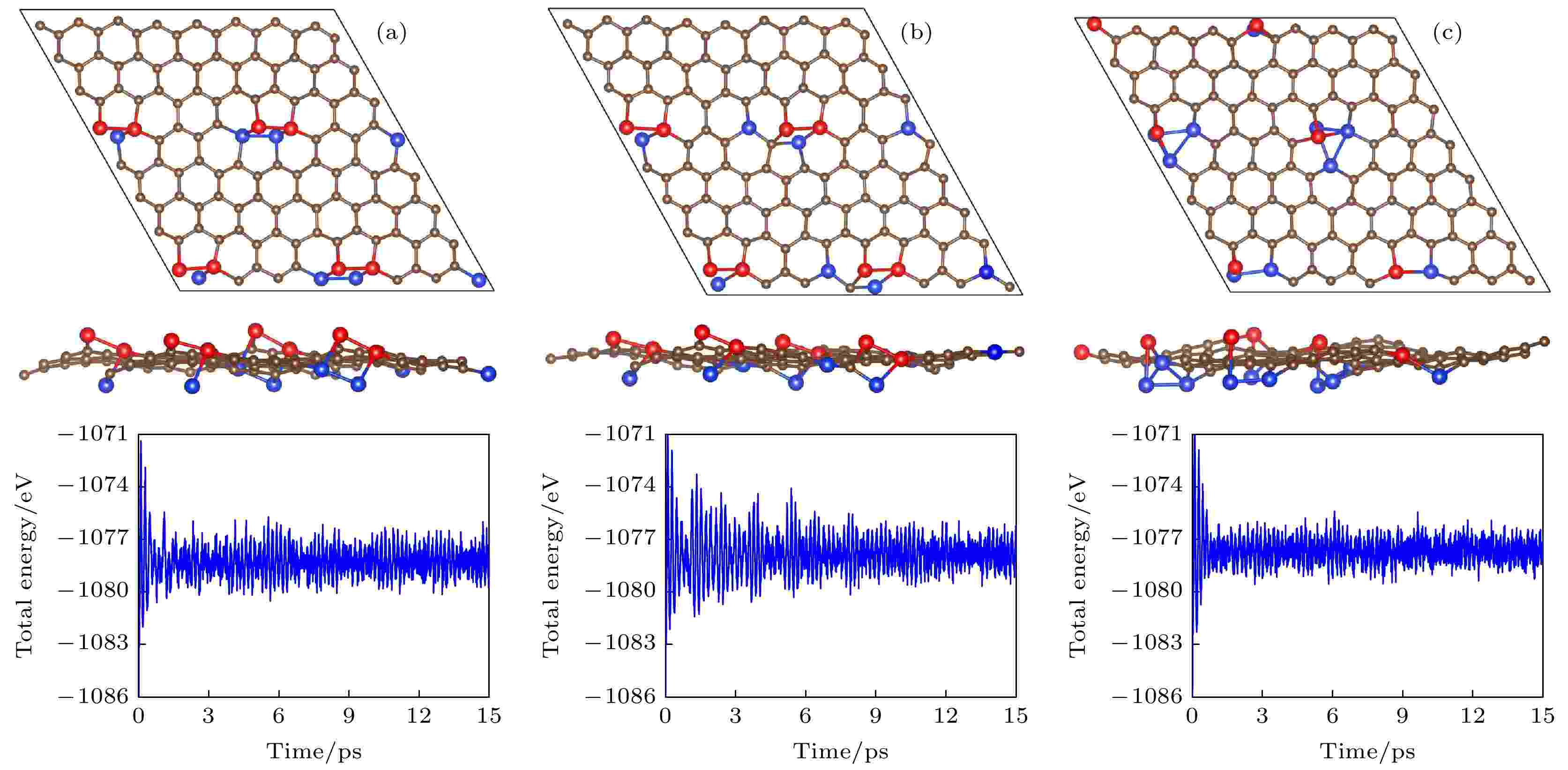图 5 (a), (b)和(c)分别为图2中g-SiC₇的能量最低结构Ⅰ, Ⅱ和Ⅲ在500 K温度下的分子动力学模拟结果. 左图为15 ps后的几何结构, 右图为模拟过程中的能量随时间变化
Figure5. (a), (b) and (c) are the molecular dynamics simulations (at 500 K) of the three most stable structures I, II and III of g-SiC₇ in Fig. 2. The left and right panels show the structures after 15 ps and the total energies vs time, respectively.

结构Ⅱ和Ⅲ的能量更相近, 比结构Ⅰ的能量高, 如表1所列. 结构Ⅱ中, 由4个Si原子和1个C原子构成一个5-原子环. 结构Ⅲ中, 有两个Si原子上下正对着分布在平面的两侧, 另两个Si原子分别于平面两侧的这两个Si原子成键. 结构Ⅱ和Ⅲ的最大翘曲高度分别为2.45 ?和2.63 ?. 如图4(b)和图4(c)所示, 它们的声子谱也没有虚频, 所以也是动力学稳定的. 对它们进行第一性原理分子动力学计算, 如图5(b)和图5(c)所示, 在500 K温度下它们的能量在平衡位置附近震荡, 结构基本维持了原来的形貌, 说明它们都具有热力学稳定性. 它们的弹性模量如表1所列, 也满足二维材料的玻恩准则, 是机械稳定的. 结构Ⅱ和Ⅲ的能带中仍然保持了狄拉克能谷, 在狄拉克点处的带隙分别为0.42 eV和0.26 eV, 远大于结构Ⅰ的带隙.
由于结构Ⅰ, Ⅱ和Ⅲ都具有狄拉克能谷而且打开了带隙, 所以有可能具有能谷自由度. 为验证这一点, 用WANNIER90计算了他们的价带总贝里曲率, 如图4能带图中间的颜色梯度图所示, 发现在K和-K处不等价的狄拉克能谷处有较大的贝里曲率, 而且符号是相反的, 因此结构Ⅰ, Ⅱ和Ⅲ都可作为能谷电子学材料, 具有能谷霍尔效应 (valley Hall effect) 和圆偏振光的二色性 (circular dichroism) 等量子效应.
我们统计了在每个能量区间内Si分布所占的百分比. 从图2中可见, 在能量区间–1.0—–0.8 eV内Si的分布数最多, 占总分布数的36.1%, 能量在–0.8—–0.6 eV和–1.0—–1.2 eV之间Si的分布数分别为17.8%和24.9%, 这三个能量区间的分布数占总数的78.8%.

基于第一性原理计算, 探索了g-SiC₇的稳定性与其Si原子分布和其结构的关系. 考虑了g-SiC₇中所有可能的35960种Si原子分布, 从中找出了365种不等价的分布, 并分别研究了每种不等价Si分布的平面和非平面结构. 通过比较它们的总能, 发现以往文献所研究的具有高对称分布和全平的g₀-SiC₇的能量是最高的, 整体的趋势是Si原子分布比较集中的能量较低, 在Si原子分布相近的情况下, g-SiC₇的非平面结构能量更低. 在365种不等价的分布中, 只有八种分布的稳定结构是平面的, 但同时总存在与其相近的分布具有能量更低的非平面结构. 我们着重研究了能量最低的三种结构, 发现它们的Si原子分布很集中, 而且是动力学、热力学和机械稳定的. 虽然局部形变较大, 但狄拉克锥仍然得以保存, 而且打开了可观的带隙. 它们在K和–K处狄拉克的能谷有显著的贝里曲率且符号相反, 说明SiC₇有可能成为能谷电子学的候选材料.