删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

磁场中HD分子振转跃迁的超精细结构

本站小编 Free考研考试/2021-12-29
摘要:HD分子红外跃迁的精密测量被用以检验量子电动力学、确定质子-电子质量比等. 但HD分子的超精细结构分裂对于测量精度是一个很重要的限制因素, 并可能是实验中测得ν = 2—0谱带跃迁呈特殊线型的原因之一. 本文分别在耦合表象和非耦合表象下计算了HD分子振转跃迁的超精细结构, 并计算了不同外加磁场下HD分子(2–0)带中R(0), P(1), R(1)线的超精细结构, 模拟了10 K低温下对应的光谱结构. 结果表明, HD分子跃迁结构可随磁场发生明显变化. 这可能有助于分析HD分子跃迁特异线型产生的机制, 进一步获得其准确的跃迁中心频率, 用于基础物理学检验.
关键词: HD/
超精细结构/
塞曼效应/
振转跃迁

English Abstract


全文HTML

--> --> -->
1.引　言
分子的精密光谱对于大气探测[1]、检验量子电动力学(QED)[2-4]、测定基本物理常数[5]和探测物理常数的变化[6]等都有重要的意义. 饱和吸收光谱是最常用的克服分子光谱多普勒展宽的实验方法[7-11]. 此时, 谱线的加宽主要来源于压力加宽、渡越时间加宽、功率加宽等. 我们发展了基于腔增强和光频梳锁定的分子光谱测量技术, 对于分子近红外振转跃迁的饱和吸收可实现很高的测量精度[12]. HD分子精密光谱的探测对于QED的检验、质子-电子质量比的确定有着重要的作用. 我们之前用光梳锁定的腔衰荡光谱(CRDS)方法测量了HD第一泛频带R(1) (2–0)线的饱和吸收光谱, 拟合得到的谱线中心位置[8]和Ubachs研究组[13]用噪声免疫腔增强光外差光谱(NICE-OHMS)方法测得的结果之间存在明显偏差. 进一步的实验表明, HD分子跃迁饱和吸收谱呈明显的非对称线型[14,15]. Ubachs研究组[14]认为, 这是HD分子饱和吸收中多个超精细分裂结构子能级间干涉叠加的结果. 但该模型强烈依赖于分子间碰撞导致的布居转移, 这方面还缺乏有力的实验和理论支持.
60多年前, Quinn等[16]利用磁共振方法研究过HD分子基态的超精细结构, 近期, Dupre[17]和Komasa等[18]分别计算了HD分子红外跃迁的超精细结构, 在未考虑测量中泵浦探测效应的情况下, 得到了基本一致的跃迁结构, 但仍然难以预测实验条件下的光谱线型, 不能和实验结果进行直接对比. Pachalski等[19]认为, HD超精细结构的精密测量对于精确认识氘原子电四极矩, 理解自旋依赖的核子相互作用有着重要意义. 本文提出, 通过在不同磁场下观测HD红外谱线结构的变化以检验其线型的模型. 本文将计算不同磁场下HD分子ν = 2—0带中各塞曼子能级间电偶极跃迁的结构. 由于分子间碰撞和能级布居转移的动力学效应对能级结构十分敏感, 通过实验和理论的比对, 有望判定HD分子红外跃迁呈现特别的非对称线型的真正机制.
2.计算方法
由于HD分子ν = 2—0谱带振转跃迁极其微弱(爱因斯坦系数A ≈ 10–5/s), 目前只有在腔增强光谱实验中才能得到其无多普勒的吸收光谱. 这样的实验中, 比较方便的实验条件是加上一个和探测光同轴的外磁场. 实验构想图如图1所示, 从ECDL激光器出来的探测光耦合进入一个光学共振腔, 腔外线圈产生一个与探测光同轴的磁场. 利用光腔衰荡光谱[7]等腔增强光谱方法来测量HD分子在不同磁场下的饱和吸收光谱.
图 1 在磁场中测定HD分子振转跃迁
Figure1. Determination of the ro-vibrational transition of HD molecule in magnetic field.

以下将分析HD振转跃迁在外磁场下的结构. 为减小谱线的渡越加宽、增加下态布居, 比较理想的实验方式将是在低温下测量R(0)谱线. 低温下HD分子主要布居在J = 0的转动能级, 相对来说, 超精细结构较为简单, 也有利于分辨其光谱结构. 因此, 本文将主要以ν = 2—0带中R(0)跃迁为例进行讨论. 当然, 相关的计算方法很容易推广到其他跃迁.
可以用两种表象分别来计算HD分子振转跃迁的超精细结构. 一种是选用N, iD, F1, iH, F, mF这6个量子数构成的耦合表象, 另一种是用N, mN, iH, mH, iD, mD这6个量子数构成的非耦合表象. 其中N是转动角动量量子数, iD, iH分别是氘、氢原子核自旋角动量量子数, F1, F为耦合得到的量子数, mF, mN, mH, mD为对应的磁量子数.
2
2.1.耦合表象
-->

2.1.耦合表象

耦合表象下, 选用N, iD, F1, iH, F, mF这6个量子数构成的基函数. 此时, 可以认为HD分子的转动角动量N与氘原子核自旋角动量iD耦合为F1, F1再与氢原子核自旋角动量iH耦合为总角动量F, F在Z轴方向的投影记为mF, 如图2所示. 即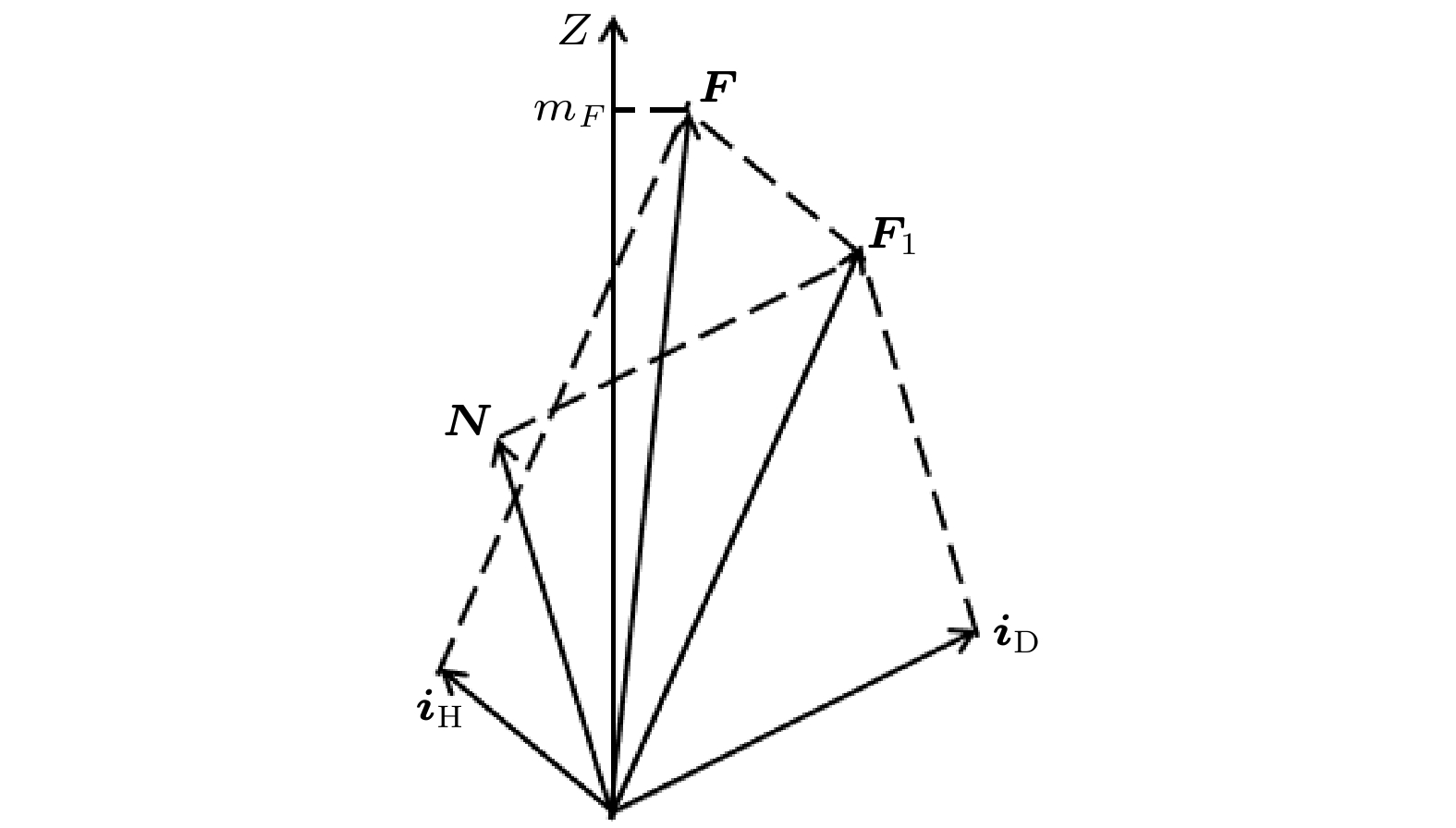
图 2 耦合表象下HD分子的角动量耦合示意图
Figure2. Angular momentums of the HD molecule in the coupled representation.

$ {\boldsymbol{F}}_{1} = \boldsymbol{N} + {\boldsymbol{i}}_{\rm{D}}, $
$ \boldsymbol{F} = {\boldsymbol{F}}_{1} + {\boldsymbol{i}}_{\rm{H}}. $
在无外加磁场的情况下, 能级对于mF量子数是简并的. 此时, 可以选择N, iD, F1, iH, F这5个量子数构成的表象来计算哈密顿矩阵. 对于HD ν = 2—0带的R(0)跃迁, 上能级ν = 2, N = 1的态共有5组基. 5组基│N iD F1 iH F$\rangle $分别记为
1: │1 1 0 1/2 1/2$\rangle $,
2: │1 1 1 1/2 1/2$\rangle $,
3: │1 1 1 1/2 3/2$\rangle $,
4: │1 1 2 1/2 3/2$\rangle $,
5: │1 1 2 1/2 5/2$\rangle $.
系统的相互作用哈密顿量分为下面四个部分. 第一部分为分子转动与氢原子核自旋的相互作用, 其中cH为氢原子核的自旋-转动常数:
$ {H}_{1} = -{c}_{\rm{H}}{\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}}; $
第二部分为分子转动与氘原子核自旋的相互作用, 其中cD为氘原子核的自旋-转动常数:
$ {H}_{2} = -{c}_{\rm{D}}{\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}; $
第三部分为由Breit方程[20]得到的两个原子核自旋磁矩之间的偶极-偶极相互作用, 其中cs为两个原子核自旋之间的相互作用常数, rHD为核间距, gH, gD分别为氢原子核和氘原子核的朗德因子, μN为核磁子, μ0为真空磁导率:
$ \begin{split} {H}_{3} =\;& {c}_{\rm{s}}{\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{i}}_{\rm{D}} + {g}_{\rm{H}}{g}_{\rm{D}}\frac{{\mu }_{0}{\mu }_{ {N}}^{2}}{4{\rm{\pi }}}\\&\times\left[\frac{{\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{i}}_{\rm{D}}}{{\boldsymbol{r}}_{\rm{HD}}^{3}}-\frac{3\left({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{r}}_{\rm{HD}}\right)\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{r}}_{\rm{HD}}\right)}{{\boldsymbol{r}}_{\rm{HD}}^{5}}\right];\end{split} $
第四部分为电四极相互作用, Q为核电四极张量, $ \nabla $E为静电场梯度:
$ {H}_{4} = -\frac{1}{6}{\boldsymbol{Q}}:\nabla E. $
在N, iD, F1, iH, F这5个量子数构成的耦合表象下, 由于上能级ν = 2, N = 1只有5组基, 其哈密顿矩阵为一个5 × 5的矩阵. 由于分子转动与核自旋之间的相互作用, 以及两个原子核自旋之间的相互作用, 哈密顿矩阵为一个非对角的矩阵.为了计算其矩阵元, 需要将系统的相互作用哈密顿量写成张量形式[21]:
$ {H}_{1} = - {c}_{\rm{H}}{\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{H}}\right)\cdot {\boldsymbol{T}}^{\left(1\right)}\left(N\right), $
$ {H}_{2} = - {c}_{\rm{D}}{\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{D}}\right)\cdot {\boldsymbol{T}}^{\left(1\right)}\left(N\right), $
$\begin{split}{H}_{3} =\;& {c}_{\rm{s}}{\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{H}}\right)\cdot {\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{D}}\right)-{g}_{\rm{H}}{g}_{\rm{D}}\frac{{\mu }_{0}{\mu }_{\rm{N}}^{2}}{4{\rm{\pi }}}\\& \times\sqrt{10}{\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{H}}\right)\cdot {\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{D}},{C}^{2}\right),\end{split}$
$ {H}_{4} = -e{\boldsymbol{T}}^{\left(2\right)}\left(Q\right)\cdot {\boldsymbol{T}}^{\left(2\right)}\left(\nabla E\right), $
其中
$ {\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{D}},{C}^{2}\right) = {\left[{\boldsymbol{T}}^{\left(1\right)}\left({{{i}}}_{\rm{D}}\right)\otimes {\boldsymbol{T}}^{\left(2\right)}\left(C\right)\right]}^{\left(1\right)}. $
按照Dupre[17]的方法, 可以计算得到上能级的5 × 5的哈密顿矩阵中所有的矩阵元, 计算中用到的cH, cD等常数已经有了比较精确的计算结果[17,18,22]. 本文使用Komasa等[18]通过Born-Oppenheimer近似得到的结果, 上能级ν = 2, N = 1对应的cH = 82.183 kHz, cD = 12.524 kHz, d1 = 16.654 kHz, d2 = –22.043 kHz. 得到的哈密顿矩阵的本征值即为各超精细分裂能级的能量移动, 本征向量即为对应的本征波函数. 记5个本征态分别为:
$\begin{split}&{\rm{A}}\!:\; │F = 1/2 \;N = 1 +\rangle =-0.9493│1\rangle + 0.3142│2\rangle ,\;\\&\qquad 能量移动为-114.15\;{\rm{kHz}},\\&{\rm{B}}\!:\; │F = 1/2\; N = 1 -\rangle = 0.3142│1\rangle + 0.9493│2\rangle ,\;\\&\qquad 能量移动为179.34\;{\rm{kHz}},\\&{\rm{C}}\!:\; │F = 3/2\; N = 1 +\rangle = -0.7114│3\rangle - 0.7028│4\rangle ,\;\\&\qquad 能量移动为53.26\;{\rm{kHz}},\\&{\rm{D}}\!:\; │F = 3/2\; N = 1 -\rangle = 0.7028│3\rangle-0.7114│4\rangle ,\;\\&\qquad 能量移动为-1.39\;{\rm{kHz}},\\&{\rm{E}}\!:\; │F \!=\! 5/2\; N \!=\! 1\rangle \!=\!│5\rangle ,~~ 能量移动为-56.31\;{\rm{kHz}}, \end{split}$
对于下能级ν = 0, N = 0的态, 只有F = 1/2和F = 3/2两个能级, 且能量是简并的, 分别记为a态和b态.
各超精细跃迁谱线相对线强度主要由各跃迁电偶极矩的平方|μul|2决定, 计算下能级a, b两个态分别到上能级A, B, C, D, E五个态的跃迁电偶极矩的平方即可得到所有超精细跃迁谱线的相对线强度.
根据文献[17], 上下能级间的跃迁电偶极矩 ,$\mu_{ul} \,=\, \langle X || \boldsymbol T^{(1)} (\mu)|| Y\rangle \,=\, c_1 \langle n|| \boldsymbol T^{(1)}(\mu) || Y \rangle + c_2 \langle n'| $$ | \boldsymbol T^{(1)}(\mu) | | Y\rangle$ 其中, X代表A, B, C, D, E中的一个态, Y代表a, b中的一个态, n和n' 代表1, 2, 3, 4, 5中的一个态, c为归一化的叠加系数, 数值为对应的本征波函数的系数. $\langle n | | \boldsymbol T ^{(1)}(\mu) | | Y \rangle $的值可以按照文献[17]中的公式计算得到:
$ \begin{split}& \langle n||{\boldsymbol{T}}^{\left(1\right)}\left(\mu \right)||Y\rangle \\ =\;&\langle {N}_{n}{i}_{\rm{D}}{F}_{{1}_{n}}{i}_{\rm{H}}{F}_{n}||{\boldsymbol{T}}^{\left(1\right)}\left(\mu \right)||{N}_{Y}{i}_{\rm{D}}{F}_{{1}_{Y}}{i}_{\rm{H}}{F}_{Y}\rangle \\=\;&{\left(-1\right)}^{{F}_{Y} + {i}_{\rm{H}} + {F}_{{1}_{n}} + 1}\times \sqrt{\left(2{F}_{Y} + 1\right)\left(2{F}_{n} + 1\right)} \\& \times \left\{\begin{array}{ccc}{i}_{\rm{H}}&{F}_{Y}&{F}_{{1}_{Y}}\\ 1&{F}_{{1}_{n}}&{F}_{n}\end{array}\right\}\times {\left(-1\right)}^{{F}_{{1}_{Y}} + {i}_{\rm{D}} + {N}_{n} + 1}\\&\times \sqrt{\left(2{F}_{{1}_{Y}} + 1\right)\left(2{F}_{{1}_{n}} + 1\right)}\times \left\{\!\!\begin{array}{ccc}{i}_{\rm{D}}&{F}_{{1}_{Y}}&{N}_{Y}\\ 1&{N}_{n}&{F}_{{1}_{n}}\end{array} \!\!\right\}\\& \times \langle {N}_{n}||{\boldsymbol{T}}^{\left(1\right)}\left(\mu \right)||{N}_{Y} \rangle.\\[-12pt] \end{split} $
由于上能级Nn = 1, 下能级NY = 0, 最后一项$\langle N_n ||\boldsymbol T^{(1)}(\mu)||N_Y\rangle$的值对于所有超精细跃迁都是相等的, 只需计算前面的系数即可. 例如, 要计算$ b\to A $的跃迁强度, 记其相对线强度为Sul, 由(12)式可以计算出, $\langle 1| |\boldsymbol T^{(1)}(\mu)||b \rangle$和$\langle 2| |\boldsymbol T^{(1)}(\mu)||b \rangle$分别为$\sqrt{\dfrac{4}{9}}$ 和$\sqrt{\dfrac{2}{9}}$, 由于$|A\rangle \!=\! -0.9493|1\rangle\!+\! 0.3142|2\rangle$, 则
$ \begin{split}\;& {\mu }_{ul} = \langle A||{\boldsymbol{T}}^{(1)}(\mu)||b \rangle\\=\;&-0.9493\langle1||{\boldsymbol{T}}^{(1)}(\mu)| |b\rangle + 0.3142 \langle 2||{\boldsymbol{T}}^{(1)}(\mu)||b\rangle \\=\;& -0.4848,\\[-12pt]\end{split}$
$ {S}_{ul} = {\left|{\mu }_{ul}\right|}^{2} =0.235. $
按照这种方法, 可以计算出HD分子ν = 2—0带R(0)线的所有超精细跃迁谱线的频率和相对线强度, 得到的结果如图3最下面一栏所示. 如果进一步考虑Zeeman子能级间的跃迁, 其相对线强度为
$ {{S}}_{u{m}_{u};l{m}_{l}} = {\left(\begin{array}{ccc}{F}_{X} & 1 & {F}_{Y}\\ -{m}_{{F}_{X}} & ?{m}_{F} & {m}_{{F}_{Y}}\end{array}\right)}^{2}{S}_{ul}\text{.} $
图 3 计算得到的HD分子ν = 2—0带R(0)线的所有超精细跃迁谱线的频率偏移及其对应的相对线强度(有部分弱线在显示范围之外)
Figure3. Calculated frequency shifts of all hyperfine transition lines in the R(0) line in the ν = 2–0 band and their corresponding line intensities (some weak lines are outside the display range).

2
2.2.非耦合表象
-->

2.2.非耦合表象

也可以选择N, mN, iH, mH, iD, mD这6个量子数构成的非耦合基来进行计算. 此时, 可以认为HD分子的转动角动量N、氘原子核自旋角动量iD以及氢原子核自旋角动量iH分别与磁场耦合. 对于HD ν = 2—0带的R(0)线, 上能级ν = 2; N = 1; mN = 0, ± 1; mH = ± 1/2; mD = 0, ± 1, 共有3 × 2 × 3=18组基. 下能级ν = 0; N = 0; mN = 0; mH = ± 1/2; mD = 0, ± 1, 共有2 × 3 = 6组基. 在无外加磁场的情况下, 按照Ramsey和Lewis[22]的表示方法, 系统的有效哈密顿量为
$ \begin{split} {H}_{\rm{hfs}} =\;& -{c}_{\rm{H}}{\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}}-{c}_{\rm{D}}{\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\! +\! \frac{5{d}_{1}}{2\left(2N-1\right)\left(2N + 3\right)}\\&\times[3\left({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}}\right)\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right) + 3\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)({\boldsymbol{i}}_{\rm{H}}\cdot {\boldsymbol{N}})\\&-{2{\boldsymbol{i}}}_{\rm{H}}\cdot{\boldsymbol{i}}_{\rm{D}}{\boldsymbol{N}}^{2}] + \frac{5{d}_{2}}{\left(2N-1\right)\left(2N + 3\right)}\\&\times\left[3{\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)}^{2} + \frac{3}{2}\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)-{\boldsymbol{i}}_{\rm{D}}^{2}{\boldsymbol{N}}^{2}\right], \\[-12pt]\end{split} $
其中, 前两项对应于自旋-转动磁相互作用, 第三项对应于两个核自旋磁矩之间的偶极-偶极相互作用, 第四项代表氘核电四极矩的相互作用. 跃迁矩阵元可以按照角动量算符的性质来进行计算:
$ 〈m|{L}_{z}|m〉=m, $
$ 〈m|{L}_{x} + {{\rm{i}}L}_{y}|m-1〉={\left[\left(L + m\right)\left(L-m + 1\right)\right]}^{\tfrac{1}{2}}, $
$ 〈m|{L}_{x}-{{\rm{i}}L}_{y}|m + 1〉={\left[\left(L-m\right)\left(L + m + 1\right)\right]}^{\tfrac{1}{2}}. $
(16)式中角动量算符矢量积可以分别化为如下形式:

$ {\boldsymbol{i}}\cdot {\boldsymbol{N}} = {i}_{z}{N}_{z} + \frac{1}{2}\left({i}_{x} + {\rm{i}}{i}_{y}\right)\left({N}_{x}-{\rm{i}}{N}_{y}\right) + \frac{1}{2}\left({i}_{x}-{\rm{i}}{i}_{y}\right)\left({N}_{x} + {\rm{i}}{N}_{y}\right), $
$ \begin{split} &3({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}})({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}) \!+\! 3({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}})({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}})-{2{\boldsymbol{i}}}_{\rm{H}}\cdot{\boldsymbol{i}}_{\rm{D}}{\boldsymbol{N}}^{2} \!=\! 3({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}})({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}) \!+\! 3\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)\left({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}}\right)-{2{\boldsymbol{i}}}_{\rm{H}}\cdot{\boldsymbol{i}}_{\rm{D}}N(N \!+\! 1)\\=& 2{i}_{{\rm{H}}_{z}}{i}_{{\rm{D}}_{z}}\left[3{N}_{z}^{2}-N (N \!+\! 1)\right]-\frac{1}{2}[({{i}_{\rm{H}}}_{x} \!+\! {\rm{i}}{{i}_{\rm{H}}}_{y})\left({{i}_{\rm{D}}}_{x}-{\rm{i}}{{i}_{\rm{D}}}_{y}\right) \!+\! \left({{i}_{\rm{H}}}_{x}-{\rm{i}}{{i}_{\rm{H}}}_{y}\right)\left({{i}_{\rm{D}}}_{x} + {\rm{i}}{{i}_{\rm{D}}}_{y}\right)]\left[3{N}_{z}^{2}-N(N \!+\! 1)\right] \\& + \frac{3}{2}[{i}_{{\rm{H}}_{z}}({{i}_{\rm{D}}}_{x} -{\rm{i}}{{i}_{\rm{D}}}_{y}) + {i}_{{\rm{D}}_{z}}\left({{i}_{\rm{H}}}_{x}-{\rm{i}}{{i}_{\rm{H}}}_{y}\right)]\left[{N}_{z}\left({N}_{x} + {\rm{i}}{N}_{y}\right) + \left({N}_{x} + {\rm{i}}{N}_{y}\right){N}_{z}\right]\\& + \frac{3}{2}[{i}_{{\rm{H}}_{z}}\left({{i}_{\rm{D}}}_{x} + {\rm{i}}{{i}_{\rm{D}}}_{y}\right) +{i}_{{\rm{D}}_{z}}\left({{i}_{\rm{H}}}_{x} + {\rm{i}}{{i}_{\rm{H}}}_{y}\right)]\left[{N}_{z}\left({N}_{x}-{\rm{i}}{N}_{y}\right) + \left({N}_{x}-{\rm{i}}{N}_{y}\right){N}_{z}\right] \\& + \frac{3}{2}\left({{i}_{\rm{H}}}_{x} + {\rm{i}}{{i}_{\rm{H}}}_{y}\right)({{i}_{\rm{D}}}_{x} +{\rm{i}}{{i}_{\rm{D}}}_{y}){\left({N}_{x}-{\rm{i}}{N}_{y}\right)}^{2} + \frac{3}{2}\left({{i}_{\rm{H}}}_{x}-{\rm{i}}{{i}_{\rm{H}}}_{y}\right)\left({{i}_{\rm{D}}}_{x}-{\rm{i}}{{i}_{\rm{D}}}_{y}\right){\left({N}_{x} + {\rm{i}}{N}_{y}\right)}^{2},\\[-12pt] \end{split} $
$ \begin{split} &3{\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)}^{2} + \frac{3}{2}\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)-{\boldsymbol{i}}_{\rm{D}}^{2}{\boldsymbol{N}}^{2} = \frac{1}{2}\left[3{N}_{z}^{2}-N\left(N + 1\right)\right]\left[3{{i}_{\rm{D}}}_{z}^{2}-{i}_{\rm{D}}\left({i}_{\rm{D}} + 1\right)\right] \\&+\frac{3}{4}\left[{N}_{z}\left({N}_{x} + {\rm{i}}{N}_{y}\right) + \left({N}_{x} + {\rm{i}}{N}_{y}\right){N}_{z}\right]\left[{{i}_{\rm{D}}}_{z}\left({{i}_{\rm{D}}}_{x}-{\rm{i}}{{i}_{\rm{D}}}_{y}\right) + \left({{i}_{\rm{D}}}_{x}-{\rm{i}}{{i}_{\rm{D}}}_{y}\right){{i}_{\rm{D}}}_{z}\right] \\&+\frac{3}{4}\left[{N}_{z}\left({N}_{x}-{\rm{i}}{N}_{y}\right) + \left({N}_{x}-{\rm{i}}{N}_{y}\right){N}_{z}\right]\left[{{i}_{\rm{D}}}_{z}\left({{i}_{\rm{D}}}_{x} + {\rm{i}}{{i}_{\rm{D}}}_{y}\right) + \left({{i}_{\rm{D}}}_{x} + {\rm{i}}{{i}_{\rm{D}}}_{y}\right){{i}_{\rm{D}}}_{z}\right] \\ &+\frac{3}{4}[{\left({{i}_{\rm{D}}}_{x} + {\rm{i}}{{i}_{\rm{D}}}_{y}\right)}^{2}{\left({N}_{x}-{\rm{i}}{N}_{y}\right)}^{2} + {\left({{i}_{\rm{D}}}_{x}-{\rm{i}}{{i}_{\rm{D}}}_{y}\right)}^{2}{\left({N}_{x} + {\rm{i}}{N}_{y}\right)}^{2}]\text{.} \end{split} $
按照(17)式—(19)式给出的角动量算符的性质来计算有效哈密顿量Hhfs的矩阵元, 可以得到上能级18 × 18的哈密顿矩阵(注意是块对角化的). 将得到的哈密顿矩阵求本征值和本征向量, 即可得到对应的各超精细分裂能级的能量移动和本征波函数, 非耦合表象基之间的跃迁矩可以由耦合表象基之间的跃迁矩得到. 而对于下能级ν = 0, N = 0态的6个能级, 由于N = 0, 所以Hhfs = 0, 能量是简并的, 且能量移动为0.
3.外磁场下的电偶极跃迁
在无磁场情形下, 可以分别用耦合表象和非耦合表象得到各超精细能级的位移和能级间的跃迁矩. 我们计算得到的结果和文献[18]的结果一致. 受限于光谱实验的分辨, 目前还没有HD振转跃迁的测量可以分辨超精细结构. 例如, Hua等[15]测量了HD在ν = 2—0带R(1)线的光谱, 分辨率仅为800 kHz, 无磁场下完全无法分辨超精细结构. 而有外加磁场时, HD超精细结构可以分辨开来, 这为分辨超精细结构提供了契机.
在有磁场情况下, 采用非耦合表象更为方便. 从N, mN, iH, mH, iD, mD这6个量子数构成的非耦合表象出发, 按照Ramsey和Lewis[22]的表示方法, 系统的有效哈密顿量为

$\begin{split}{H}_{\rm{hfs}} =\;& -\left[1-{\sigma }_{\rm{H}}\left({\boldsymbol{N}}\right)\right]{a}_{\rm{H}}{\boldsymbol{i}}_{\rm{H}}\cdot\frac{\boldsymbol{H}}{H}-\left[1-{\sigma }_{\rm{D}}\left({\boldsymbol{N}}\right)\right]{a}_{\rm{D}}{\boldsymbol{i}}_{\rm{D}}\cdot\frac{\boldsymbol{H}}{H}-\left[1-{\sigma }_{\rm{N}}\left({\boldsymbol{N}}\right)\right]b{\boldsymbol{N}}\cdot\frac{\boldsymbol{H}}{H}- {c}_{\rm{H}}{\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}} \\& -{c}_{\rm{D}}{\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}} + \frac{5{d}_{1}}{\left(2N-1\right)\left(2N + 3\right)}\bigg[\frac{3}{2}\left({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}}\right)\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right) + \frac{3}{2}\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)\left({\boldsymbol{i}}_{\rm{H}}\cdot{\boldsymbol{N}}\right)-{\boldsymbol{i}}_{\rm{H}}\cdot {\boldsymbol{i}}_{\rm{D}}{\boldsymbol{N}}^{2}\bigg] \\&+ \frac{5{d}_{2}}{\left(2N-1\right)\left(2N + 3\right)}\left[3{\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)}^{2} + \frac{3}{2}\left({\boldsymbol{i}}_{\rm{D}}\cdot{\boldsymbol{N}}\right)-{\boldsymbol{i}}_{\rm{D}}^{2}{\boldsymbol{N}}^{2}\right], \end{split}$

其中, 前两项对应于核磁矩与外加磁场的相互作用, 第三项为分子转动磁矩与外加磁场的相互作用, 第四项和第五项对应于自旋转动磁相互作用, 第六项对应于两个核自旋磁矩之间的偶极-偶极相互作用, 第七项代表氘核电四极矩的相互作用. 式中H为磁场强度, 单位为G ($1~{\rm{G}} = \dfrac{{10}^{3}}{4{\rm{{\pi A}}}}/{\rm{m}}$), 其他各系数的定义与文献[22]中的相同, 各系数的数值该文献中也有给出.
取磁场方向为Z方向, 由于光的方向与磁场方向相同, 这时只能探测Δm = + 1和Δm = –1的跃迁. 因此以下只考虑这两种跃迁, 而不考虑Δm = 0的跃迁. Hhfs中前三项角动量算符只有Z方向的分量, 因此其对应的哈密顿矩阵元只有对角项不为零, 根据(17)式可以很容易算出. 而后四项哈密顿矩阵元的计算与2.2节中的计算方法相同. 得到哈密顿矩阵后, 求本征值和本征向量, 即可得到上、下能级分别在对应磁场下的各超精细分裂能级的能量移动和本征波函数, 由每条跃迁谱线上下能级的能量移动即可得到该跃迁谱线的频率移动. 按照(13)式的叠加方法, 从非耦合表象基之间的跃迁矩按照叠加系数叠加即可得到对应超精细跃迁的跃迁矩, 进而得到每条超精细跃迁谱线的相对跃迁强度. 在100, 300 和1000 G的外加磁场下计算得到的结果分别如图3上面三部分所示. 结果的具体数值如表1所列. 图3中频率偏移的零点对应于不考虑超精细分裂结构时的跃迁频率. 相对跃迁强度的值取对应的跃迁电偶极矩的平方. 在加上外加磁场后, 跃迁分为Δm = + 1和Δm = –1两支, 分别用红、绿两种颜色标注. 为了显示某一条跃迁在考虑塞曼分裂后随磁场强度的变化, 选出了3条线分别用深紫、墨绿、蓝三种颜色的粗线标出, 这3条线都由无外加磁场中的紫色线分裂而出.
跃迁线0 G 100 G 300 G 1000 G
频率偏移/kHz相对强度频率偏移/kHz相对强度频率偏移/kHz相对强度频率偏移/kHz相对强度
Δm = + 1a→A–56.30.3333 –106.90.3333 –208.00.3333 –561.90.3333
b1→B1–56.30.0000–100.60.1800–216.40.1157–656.90.0197
b1→B2–1.40.2922–33.30.1533–146.50.2176–516.30.3136
b1→B353.30.0411323.40.0000940.30.00003108.30.0000
b2→B1–56.30.2000–461.00.0019–1297.60.0003–4261.10.0000
b2→B2–1.40.0164–393.70.0018–1227.70.0001–4120.50.0000
b2→B353.30.1169–37.00.3297–141.00.3329–495.90.3333
c1→C1–114.10.1439–165.40.1619–286.00.1273–776.70.0315
c1→C2–56.30.0000–93.40.0640–222.50.0372–699.20.0029
c1→C3–1.40.0974–2.20.1070–129.50.1688–528.60.2990
c1→C453.30.0137298.60.0000893.30.00002972.70.0000
c1→C5179.30.0783432.10.00041032.20.00003181.20.0000
c2→C1–114.10.0196–525.80.0018–1367.30.0004–4380.90.0000
c2→C2–56.30.1000–453.80.0025–1303.80.0002–4303.50.0000
c2→C3–1.40.0219–362.60.0015–1210.80.0003–4132.80.0000
c2→C453.30.1559–61.90.1248–188.00.0859–631.60.0292
c2→C5179.30.036071.70.2028–49.10.2465–423.00.3040
d→D1–114.10.0587–445.70.0018–1309.30.0001–4366.40.0000
d→D2–56.30.0333–353.70.0170–1198.00.0018–4198.30.0002
d→D3–1.40.0164–163.30.0232–321.70.0236–867.00.0083
d→D453.30.1169–84.80.0197–223.80.0063–690.00.0002
d→D5179.30.107945.60.2716–73.90.3015–442.10.3247
Δm =–1a→C1–114.10.0587–34.70.0616106.10.0884530.40.2835
a→C2–56.30.033337.30.0446169.60.0865607.90.0249
a→C3–1.40.0164128.50.2139262.60.1567778.50.0248
a→C453.30.1169429.20.00461285.40.00064279.80.0001
a→C5179.30.1079562.80.00861424.30.00114488.30.0001
b1→D1–114.10.143945.50.1473164.20.1950545.00.2888
b1→D2–56.30.0000137.50.1648275.50.1368713.10.0444
b1→D3–1.40.0974327.90.00851151.70.00034044.40.0000
b1→D453.30.0137406.40.00811249.60.00084221.40.0001
b1→D5179.30.0783536.80.00451399.50.00044469.30.0000
b2→D1–114.10.0196–314.90.0001–917.10.0000–3059.20.0000
b2→D2–56.30.1000–222.90.0021–805.80.0000–2891.10.0000
b2→D3–1.40.0219–32.50.249670.40.2653440.20.3123
b2→D453.30.155946.00.0372168.40.0383617.20.0125
b2→D5179.30.0360176.40.0442318.30.0297865.20.0085
c1→E1–56.30.000055.20.3291159.40.3329514.40.3333
c1→E2–1.40.2922375.00.00191201.00.00014084.70.0000
c1→E353.30.0411452.70.00231297.20.00034269.70.0000
c2→E1–56.30.2000–305.30.0003–921.90.0000–3089.90.0000
c2→E2–1.40.016414.60.2593119.70.2884480.50.3223
c2→E353.30.116992.30.0737215.90.0450665.50.0110
d→F–56.30.3333–5.80.333395.30.3333449.30.3333


表1计算得到的R(0)线所有超精细跃迁谱线的频率偏移及其对应的相对线强度
Table1.Calculated frequency shifts of all hyperfine transition lines in the R(0) line and their corresponding line intensities

从图3可以看出, 当外加磁场强度较大时, 超精细跃迁谱线明显分为两支, 分别为Δm = + 1和Δm = –1的跃迁. 随着外加磁场强度的增大, 各超精细跃迁谱线频率偏移的数值也在增大. 可以看出, 当外加磁场强度达到1000 G时, 两支超精细跃迁谱线已经完全分开, 此时分子转动角动量以及原子核自旋角动量之间的相互作用已经远小于外加磁场导致的磁能级的分裂, 此时使用非耦合表象更加直观.
同时, 我们也分别在无外加磁场以及100, 300, 1000 G外加磁场的条件下, 按照上述的计算方法计算了HD分子ν = 2—0带中P(1), R(1)线的超精细分裂结构及各超精细跃迁谱线的相对线强度. 得到的结果分别如图4和图5所示, 频率偏移的零点对应于不考虑超精细分裂结构时的跃迁频率, 相对跃迁强度的值取对应的跃迁电偶极矩的平方, 不同颜色的标注与图3中的意义相同.
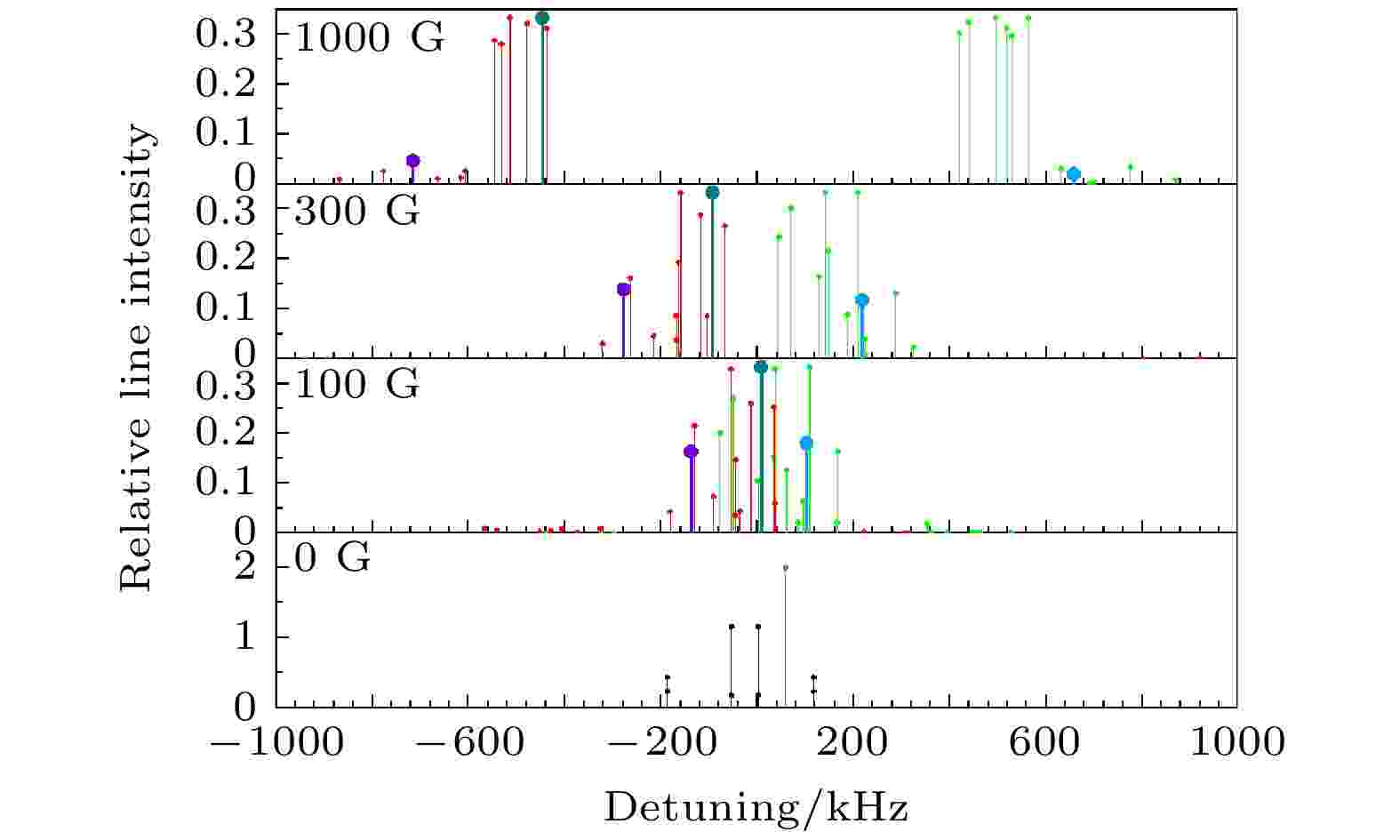图 4 计算得到的HD分子ν = 2—0带P(1)线的所有超精细跃迁谱线的频率偏移及其对应的相对线强度(有部分弱线在显示范围之外)
Figure4. Calculated frequency shifts of all hyperfine transition lines of ν = 2–0 band P (1) lines of HD molecule and their corresponding relative line intensities (some weak lines are outside the display range).

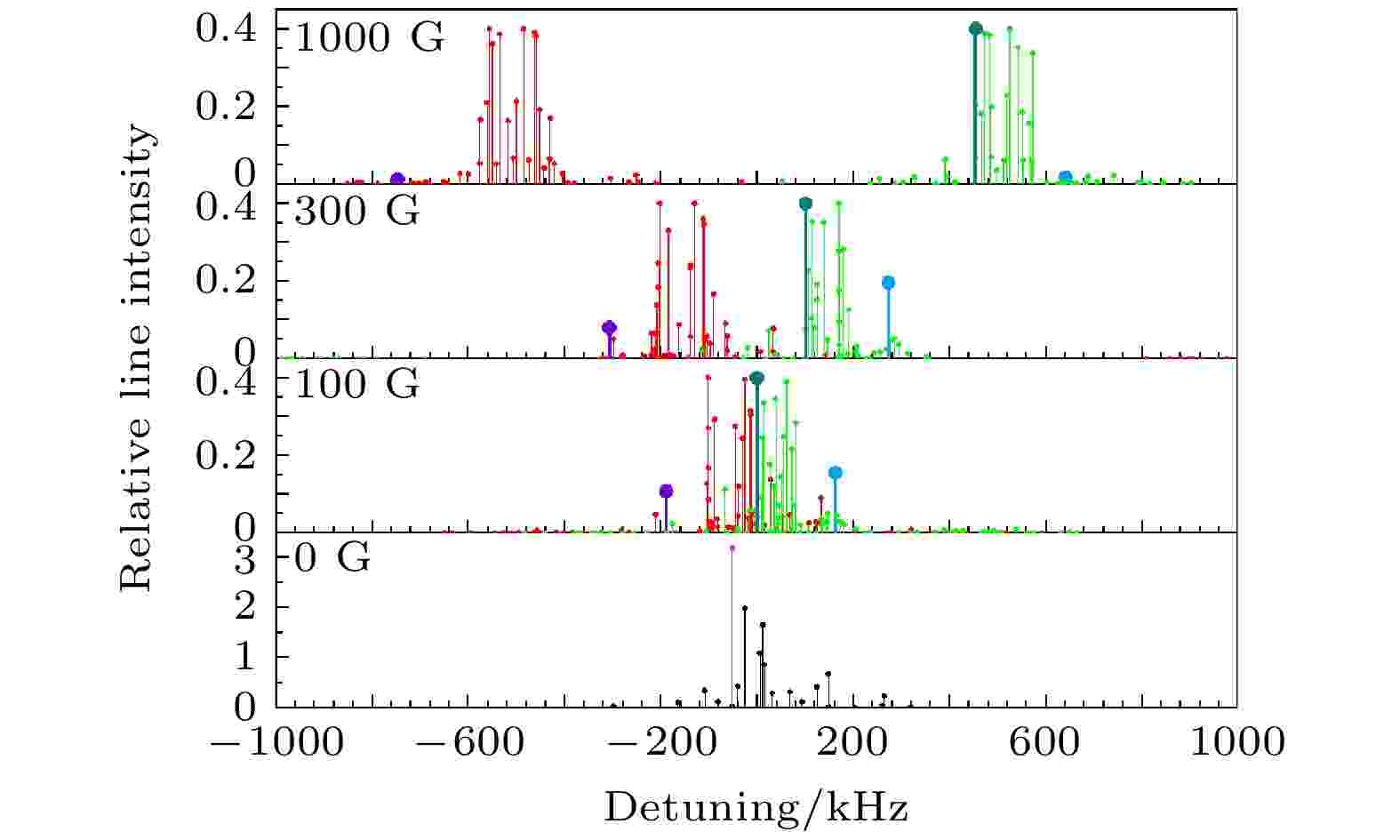图 5 计算得到的HD分子ν = 2—0带R(1)线的所有超精细跃迁谱线的频率偏移及其对应的相对线强度(有部分弱线在显示范围之外)
Figure5. Calculated frequency shifts of all hyperfine transition lines of HD molecule ν = 2–0 band R (1) line and their corresponding relative line intensities (some weak lines are outside the display range).

将计算得到的超精细跃迁谱线以相对强度为权重做加权平均, 可以发现两支超精细跃迁谱线叠加后的光谱中心位置的频率偏移与磁场强度都基本成线性关系, 斜率分别为0.5056和–0.5056 kHz/G, 如图6所示.
图 6 HD分子R(0) (ν = 2—0)跃迁在轴向磁场下, Δm = + 1和Δm = –1两支超精细跃迁谱线光谱中心的频率偏移与磁场强度的关系
Figure6. Relationship between the magnetic field intensity and the frequency shift of the spectral center of the Δm = + 1 and Δm = – 1 hyperfine transitions of the R(0) (ν = 2–0) line of HD.

4.低温下光谱线型
在低压情况下, 每条超精细跃迁谱线的饱和吸收光谱的线宽可以近似认为是渡越时间加宽导致的. 可以用公式[23] Δ$\nu \approx \dfrac{u}{9.5{\omega }_{0}}$来估算渡越时间展宽的大小, 其中$u=\sqrt{\dfrac{2{k}_{\rm{B}}T}{m}}$, 为分子的最概然速度. 通过估算得到, 在10 K的温度下, 每条超精细跃迁谱线的半高全宽(FWHM)约为99 kHz. 根据文献[24], 辐射场和吸收子之间的动量交换产生的recoil效应会导致每条超精细跃迁谱线的饱和吸收光谱分裂为两个峰. 两个峰的中心位置分别位于未考虑recoil效应前该超精细跃迁谱线峰中心的两侧, 且偏移量相同, 记为δ, $\delta =\dfrac{\rm{\pi \hslash }}{M{c}^{2}}{\nu }_{0}^{2}$. 对于HD分子ν = 2—0带的R(0)线, recoil效应产生的偏移量δ约为34 kHz, 即两峰间距约为68 kHz.
本文在理论上模拟了在10 K的低温条件下, 分别在无磁场、100 G外加磁场、300 G外加磁场、1000 G外加磁场下HD分子ν = 2—0带R(0), P(1), R(1)线的光谱. 模拟中只考虑了Δm = + 1和Δm = –1的跃迁. 由于recoil效应产生的分裂, 每条超精细跃迁谱线都分为间距为2δ的两个峰. 每个峰都用FWHM为99 kHz的洛伦兹线型来模拟, 模拟得到的结果如图7所示.
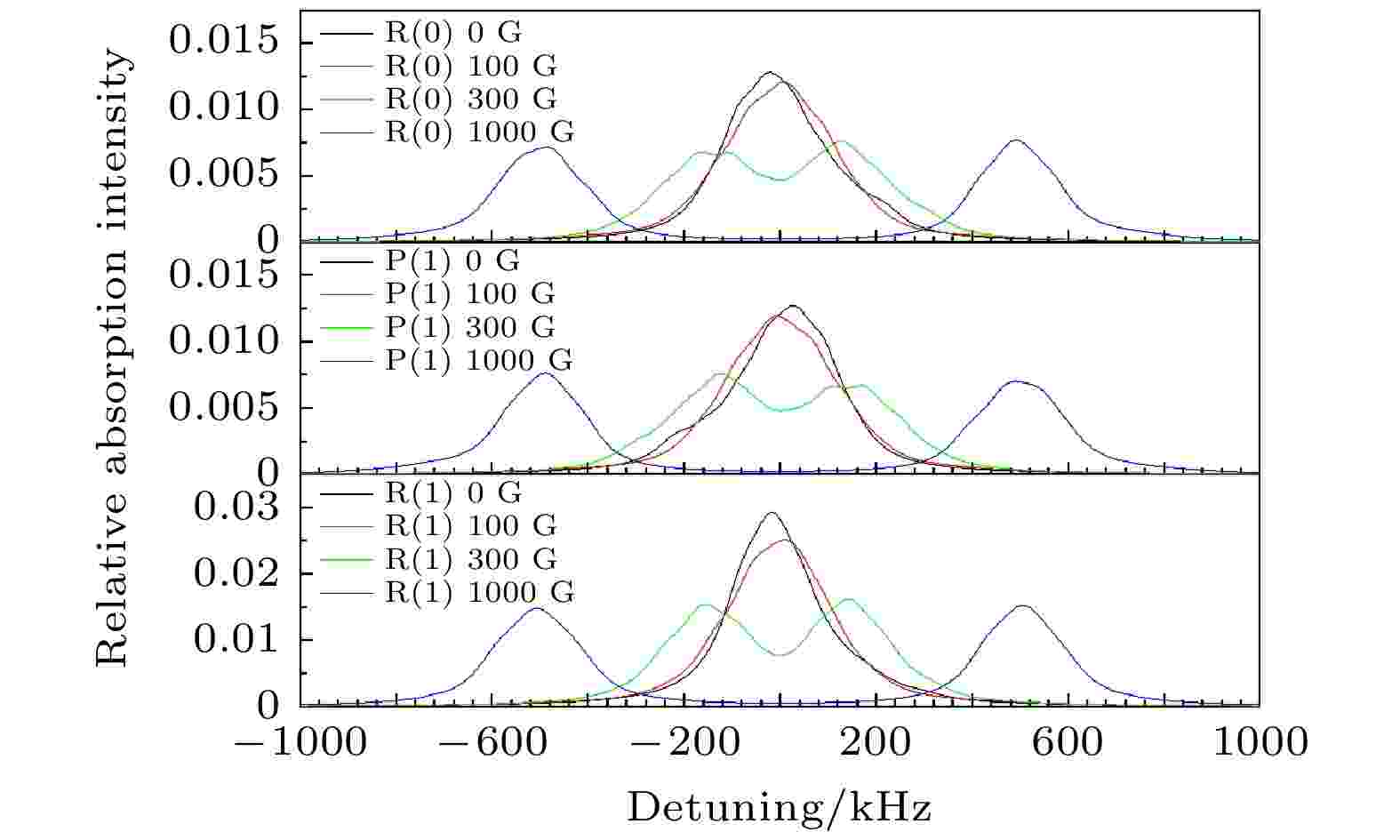图 7 在10 K的低温条件下, 分别在不同外加磁场下模拟的HD分子(2—0)带R(0)线、P(1)线、R(1)线的光谱
Figure7. Simulated spectra of R (0), P (1) and R (1) lines in the (2–0) band of HD under different magnetic fields at the temperature of 10 K.

5.结　论
为了检验超精细分裂结构对HD分子的光谱线型带来的影响, 在无外加磁场的条件下, 分别使用耦合表象和非耦合表象计算了HD分子(2—0)带中R(0), P(1), R(1)线的超精细分裂结构及各超精细跃迁谱线的相对线强度. 利用无外加磁场得到的计算结果, 推导出了非耦合表象下各塞曼子能级之间的跃迁矩, 并分别在100, 300, 1000 G的外加磁场下, 计算出了R(0), P(1), R(1)线的所有超精细跃迁谱线的频率和相对线强度. 模拟了在10 K的低温条件下, 在不同磁场下HD分子ν = 2—0带R(0), P(1), R(1)线的饱和吸收光谱. 通过分析在低温下考虑渡越加宽和反冲分裂后叠加的光谱线型, 发现能级中心位置的频率偏移与磁场强度近似成线性关系, 斜率约为0.5 kHz/G. 我们计划使用光梳锁定的腔衰荡光谱的方法, 在不同外加磁场的条件下, 测量常温下HD分子(2—0)带R(0), P(1), R(1)线的饱和吸收光谱, 与理论上模拟得到的结果进行对比, 来检验相关的光谱线型模型.
相关话题/计算 结构 光谱 实验 测量
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 超导约瑟夫森结物理参数的实验推算
    摘要:超导约瑟夫森结是实现超导量子计算和微波单光子探测的核心器件,其物理参数很难直接测定.与之前常用的测量结微波激励效应估计方法不同,本文通过实验测量低频电流驱动下的约瑟夫森结I-V曲线及其跳变电流统计分布,并与基于标准电阻电容分路结模型数值模拟进行比对,推算出了约瑟夫森结的临界电流$I_{mc ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种铅铋合金薄膜低温相的结构及超导物性表征
    摘要:铅铋(Pb-Bi)合金超导材料被广泛研究,但对其低温物相的结构和超导物性却知之甚少.本文采用低温共沉积和低温退火的方法,在Si(111)-(7×7)衬底生长的Bi(111)超薄薄膜上制备了铅铋合金薄膜,利用扫描隧道显微术对其结构和电子学性质进行表征.通过结构表征,确定了薄膜中存在相分离,同时存 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种同步研究透明材料折射率和动力学特性的实验方法
    摘要:基于电磁加载装置CQ-4,建立了一种同步开展透明材料折射率和高压声速测量的实验方法.完成了聚甲基丙烯酸甲酯(PMMA)窗口材料14GPa斜波压缩实验,利用多点双光源外差位移干涉测速仪(duallaserheterodynevelocimetry,DLHV),获得了PMMA样品后表面的速度历史曲 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • NiCu双金属纳米粒子的表面偏析、结构特征与扩散
    摘要:NiCu双金属核壳纳米粒子不仅由于其优异的稳定性、选择性以及磁学和催化性能而受到广泛关注,而且可以通过改变其纳米粒子的形貌、表面元素分布和粒径大小而具有可调谐性能.采用分子动力学与蒙特罗方法并结合嵌入原子势对NiCu双金属纳米粒子的表面偏析、结构特征以及Cu吸附原子在Ni基底沉积生长与表面扩散 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 金刚石/铝复合材料界面性质第一性原理计算及界面反应
    摘要:采用第一性原理计算和实验相结合的方法,研究了金刚石/铝复合材料的界面性质及界面反应.计算结果表明:金刚石(100)/铝(111)界面粘附功更大,相比金刚石(111)/铝(111)的界面粘附功4.14J/m2提高了41%.同时,金刚石(100)/铝(111)界面处形成Al—C键合的趋势更强.Al ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于电化学-应力耦合模型的锂离子电池硅/碳核壳结构的模拟与优化
    摘要:硅基电极材料在应用中的一个主要问题是巨大的体积膨胀,以及由此带来的电极材料破裂、粉化.本文在有限变形假设前提下,基于电化学-力学耦合理论,研究球形Si/C核壳结构在嵌锂过程中的浓度、应力场的演化,并在此基础上讨论了核壳结构的优化设计.计算结果显示:壳层可以很好地保护硅颗粒的膨胀;然而核内产生的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 双层结构突触仿生忆阻器的时空信息传递及稳定性
    摘要:现有计算机体系架构下的神经网络难以对多任务复杂数据进行高效处理,成为制约人工智能技术发展的瓶颈之一,而人脑的并行运算方式具有高效率、低功耗和存算一体的特点,被视为打破传统冯·诺依曼计算体系最具潜力的运算体系.突触仿生器件是指从硬件层面上实现人脑神经拟态的器件,它可以模拟脑神经对信息的处理方式, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 新型双模式加权机制及其对网络计算的影响
    摘要:高效率的网络分析方法对于分析、预测和优化现实群体行为具有重要的作用,而加权机制作为网络重构化的重要方式,在生物、工程和社会等各个领域都有极高的应用价值.虽然已经得到越来越多的关注,但是现有加权方法数量还很少,而且在不同拓扑类型和结构特性现实网络中的效果和性能有待继续提高.本文提出了一种新型的双 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于石英增强光声光谱的气体传感技术研究进展
    摘要:基于石英增强光声光谱(quartz-enhancedphotoacousticspectroscopy,QEPAS)的气体传感技术具有系统体积小、成本低、环境适应性强等优点,是目前一种重要的光谱式痕量气体检测方法.探测灵敏度是传感器系统的重要指标,关系到能否满足实际应用,因此,本文从提高QEP ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 结构改进的厘米尺寸谐振腔的磁场传感特性
    摘要:基于光力谐振腔的磁力仪在应用时主要受限于灵敏度和检测带宽两个指标.本文设计了一种厘米尺寸的回音壁模式谐振腔结构,可探测6Hz至1MHz频率范围内的交变磁场,在无磁屏蔽、室温环境下、无直流偏置磁场时,其最佳灵敏度在123.8kHz可达530pT·Hz–1/2,探测带宽和最佳灵敏度分别为同尺寸谐振 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.