摘要:铅铋(Pb-Bi)合金超导材料被广泛研究, 但对其低温物相的结构和超导物性却知之甚少. 本文采用低温共沉积和低温退火的方法, 在Si(111)-(7 × 7)衬底生长的Bi(111)超薄薄膜上制备了铅铋合金薄膜, 利用扫描隧道显微术对其结构和电子学性质进行表征. 通过结构表征, 确定了薄膜中存在相分离, 同时存在具有三次对称性的纯Bi(111)相和合金相Pb_1–xBi_x, 可归属于部分铋取代的Pb(111)结构. 通过电子学性质测量, 进一步证实了Bi(111)相中特征的电子学结构及合金相中的超导行为. 变温实验表明, 合金相Pb_1–xBi_x的超导转变温度是7.77 K, 属于强耦合超导体. 测量了由Bi(111)-Pb_1–xBi_x组成的正常金属-超导体异质结和超导体-正常金属-超导体异质结中的邻近效应, 指出了超导穿透深度可能受界面接触面积的影响. 考虑到铋可能具有的拓扑属性, Bi(111)-Pb_1–xBi_x面内异质结界面结构可进一步用于研究其新奇物理效应.
关键词: 铅铋合金/
超导转变温度/
邻近效应/
扫描隧道显微术

English Abstract

全文HTML

--> --> -->

铋(bismuth, Bi)因具有强的自旋轨道耦合, 无论单质铋还是各种铋基化合物, 都受到了研究者们的广泛关注^[1,2]. 铅铋(Pb-Bi)合金作为一种超导材料, 不同元素配比的合金相的超导转变温度和临界磁场性质都被大量研究^[3-5]. 有研究表明, 在铅膜中少量掺铋可以有效改善薄膜的量子稳定性, 提高薄膜的超导转变温度^[6]. 由于铋原子和铅原子半径相差较小, 根据Hume-Rothery定则^[7], 它们混合在一起会形成替代型合金. 在合金相图中, 较高温度制备的铅铋合金的稳定相为ε相, 即Pb₇Bi₃^[8]. Adler和Ng^[3]以及Gandhi等^[9]的电输运结果表明合金相大多数是不同相的混合, 多数针对铅铋合金的研究工作都围绕它的ε稳定相^[10-14]. 人们发现, 低温条件下制备的铅铋合金具有不同于ε相的结构^[15,16], 然而少有研究工作能直接给出低温条件下制备的铅铋合金的结构信息, 对其性质更是知之甚少. 如, Fujime^[15]用电子衍射的方法观察到Pb-12%Bi在8.9 K下发生了结构相变; Borromee等^[16]发现铋含量为52%—65%和87%—91%的合金淬火到–190 ℃时分别出现了两种结构未知的亚稳相. 本文主要目标是表征低温条件下生成的未知合金相物相的结构和超导物性.
本文采用低温共沉积铅和铋的方法在Bi(111)/Si(111)衬底上制备铅铋合金薄膜, 利用扫描隧道显微术(scanning tunneling microscopy, STM)及其谱学技术(scanning tunneling spectroscopy, STS)测量薄膜表面结构和电子学性质. 实验观测到了铅铋薄膜表面存在具有三次对称结构的两种物相, 可分别归属为Bi(111)相和Pb_1–xBi_x合金相, 其中Pb_1–xBi_x合金相的结构与Pb(111)相似, 部分铅原子被Bi取代(x ≈ 0.1). 变温STS测量的能隙得到合金相的超导转变温度为7.77 K, 明显高于纯铅膜的超导转变温度, 可用Mattias rules经验关系予以解释^[17]. 实验测量了不同正常金属-超导体(normal metal-superconductor, N-S)异质结与超导体-正常金属-超导体(superconductor-normal metal-superconductor, S-N-S)异质结中邻近效应的穿透深度, 讨论了N-S界面的接触面积可能对穿透深度的影响^[18-20].

2

-->

2.1.薄膜制备

薄膜制备主要在超高真空(本底真空约为1 × 10^–10 mbar (1 mbar = 100 Pa))制备腔中进行. Si(111)单晶衬底(10 mm × 2 mm × 1 mm, 合肥科晶)用去离子水、无水乙醇(分析纯)、丙酮(分析纯)进行超声清洗. 清洗后的Si(111) 衬底传入真空腔中通过直流加热的方法进行多次高温退火(1200 K, 约60 s), 获得大面积的(7 × 7)重构表面后, 首先沉积约10层(4 nm)左右的Bi(111)单晶膜^[21], 再共沉积名义比例约为Pb∶Bi = 1∶1的合金薄膜. Pb和Bi金属颗粒(Mateck公司, 纯度99.995%)用努森源(Knudsen cell)加热蒸发. 合金薄膜沉积时, 衬底温度保持在100 K, Pb和Bi蒸发速率为1.5 ?/min, 沉积时间约40 min, 得到合金薄膜名义厚度约 6 nm. 合金膜沉积后, 样品温度升至约200 K进行低温退火2 h.
2 -->

2.2.合金薄膜表面结构和电子结构表征

制备的铅铋合金薄膜用扫描隧道显微镜(日本, Unisoku USM-1300, 本底真空优于1 × 10^–10 mbar)进行表面原子和电子结构表征, 样品温度为4.2 K或400 mK, 采用恒流模式扫描, 同时收集拓扑图像和电流图像. 薄膜表面的微分电导谱(dI/dV)用锁相放大技术采集, 正弦调制电压约0.05— 2.00 mV (root mean square, rms), 频率971 Hz. 所用偏压为相对于针尖的样品电压.
根据STM隧穿原理, 微分电导正比于准粒子的局域态密度, 而超导态的态密度N_s为

${N_{\rm{s}}} = {N_{\rm{n}}}\left| {{\rm{Re}} \frac{E}{{\sqrt {{E^2} - {\varDelta ^2}} }}} \right|,$

其中, N_n为正常态的态密度, E为能量, Δ为超导能隙.
因此, 可以根据测量的dI/dV谱计算合金相的超导能隙. 在实际测量结果中, 必须考虑费米分布函数的温度展宽修正, Dynes等^[22]引入展宽因子Γ来描述准粒子寿命, (1)式变为

${N_{\rm{s}}} \propto {\rm{Re}} \frac{{\left| {E - {\rm{i}}\varGamma } \right|}}{{\sqrt {{{(E - {\rm{i}}\varGamma )}^2} - {\varDelta ^2}} }}.$

同时还有一些测量因素也会带来能隙特征展宽, 例如所加小的调制电压和仪器的展宽, 这些外加展宽会带来系统误差, 在计算处理时可以用高斯分布函数来描述这一作用, 因此在能隙拟合时还要卷积一个高斯分布函数.
利用不同温度T下的微分电导谱, 拟合出一系列超导能隙, 再根据超导能隙和温度的关系((3)式)^[22], 计算出合金相超导转变温度T_c.

$\varDelta (T) = \varDelta (0) \times {[1 - {(T/{T_{\rm{c}}})^{\rm{p}}}]^{1/2}},$

其中, $\varDelta (0)$为0 K下的超导能隙.

通过在Bi(111)薄膜衬底表面共沉积铅铋原子得到了薄膜样品(图1(a)), 其大范围STM拓扑图像(图1(b))显示出平整的台阶结构. 样品表面存在具有明显台阶高度差的区域A和区域B. 如图1(c)和图1(d)所示的统计分析表明, A和B两区域的单层台阶高度分别为d_A = 3.9 ?和d_B = 2.8 ?, 其中A区域表面台阶主要以单层高度分布为主, 而B区域表面台阶单层和双层高度分布相当. A和B两个区域的高分辨原子像如图1(e)和图1(g)所示, 对应的快速傅里叶变换(FFT)图谱分别如图1(f)和图1(h)所示. 两相的表面原子结构均表现为三次对称性, 并确定出A和B相的晶格常数a_A = 4.5 ?和a_B = 3.5 ?. 根据晶格参数, A相结构与Bi(111)结构一致^[23], 可将A相归属为由于相分离所形成的近似纯相的Bi(111)单晶薄膜, 符合其在Bi(111)衬底表面同质外延生长模式. 考虑到铋易溶于铅中形成固溶合金^[3,8,9], B相应该是部分铋取代铅的铅铋合金相, 表示为Pb_1–xBi_x, 其晶格参数与Pb(111) 结构参数相似. 根据表面A和B两相的面积统计, 同时考虑制备的薄膜厚度约6 nm(21个单原子层), 估算出铅铋合金中固溶Bi原子浓度x ≈ 0.1. 图1(g)的原子图像中表面原子亮度的不均一性反映了铋替代原子的存在. ?zer等^[6]的研究表明, 铋原子浓度在11%时, 薄膜厚度在24个单原子层之前为双层生长, 之后为单层生长; 而在Bi原子浓度在20%时, 一直保持单层模式生长.
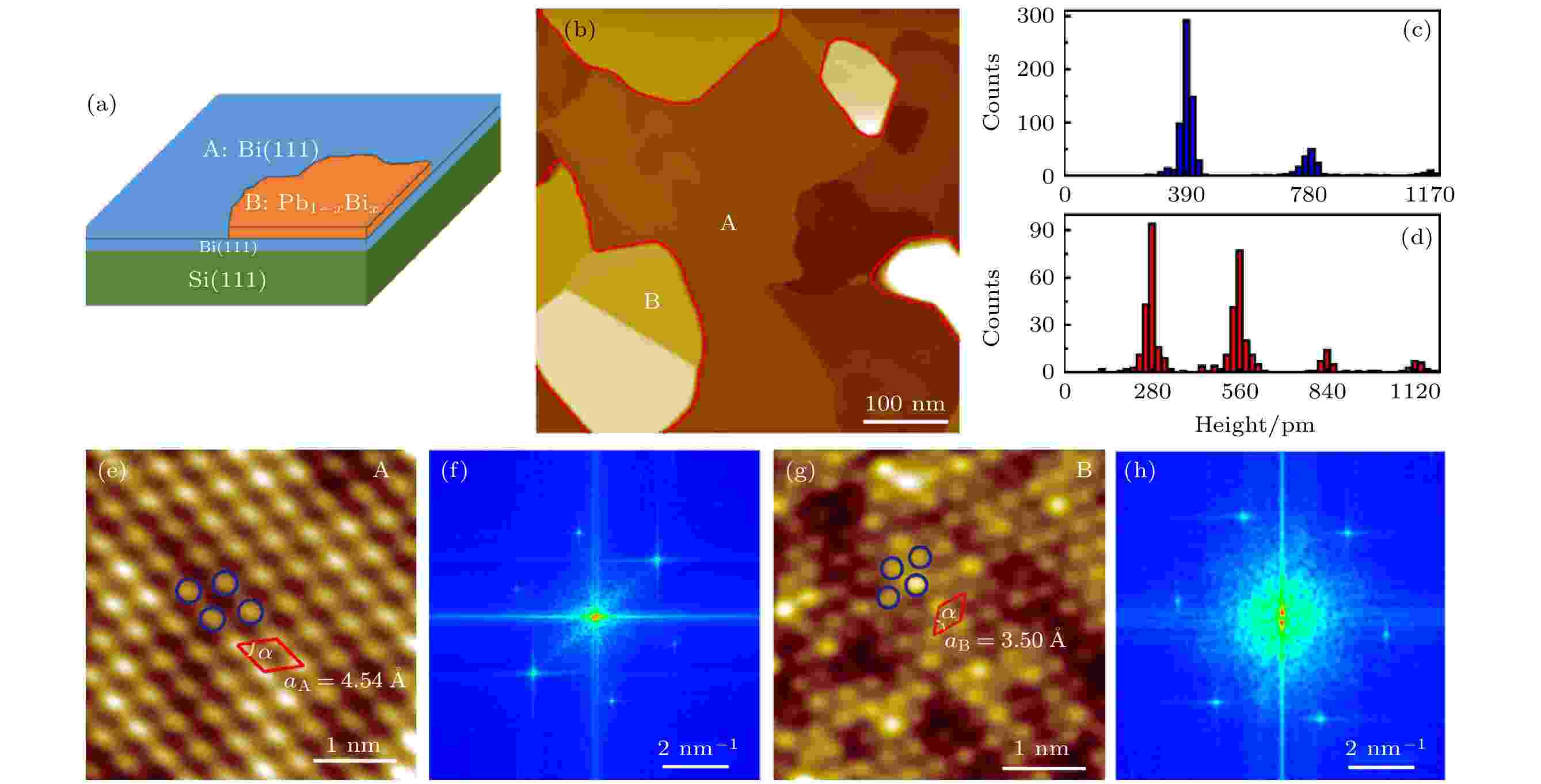图 1 Pb_1–xBi_x合金薄膜的生长与结构表征　(a) 在Bi(111)/Si(111)-(7 × 7)衬底低温共沉积铅铋原子得到的样品结构示意图; (b) 样品表面大范围的STM图像; (c), (d) A和B区域台阶高度分布统计的结果(统计不同区域大范围图像约110幅); (e), (f) A区域的STM原子图像及其快速傅里叶变换(fast Fourier transform, FFT)图谱; (g), (h) B区域的STM原子图像及其FFT图谱. 扫描条件: (b) 样品偏压V_s = –1 V, 隧穿电流I_t = 20 pA, 扫描尺寸为500 nm × 500 nm; (e) V_s = –20 mV, I_t = 2 nA; (g) V_s = 5 mV, I_t = 1 nA, 扫描尺寸为4 nm × 4 nm
Figure1. Growth of the Pb_1–xBi_x alloy film and characterization of surface structures: (a) Schematics of the Pb-Bi alloy film grown on Bi(111)/Si(111)-(7 × 7) substrate; (b) STM topography image of the alloy surface (500 nm × 500 nm, sample bias V_s = –1 V and tunneling current I_t = 20 pA); (c) and (d) step height distribution of A and B phases counted in around 110 images; (e) and (f) atomically-resolved STM image and corresponding fast Fourier transform (FFT) pattern of the A phase (V_s = –20 mV and I_t = 2 nA, 4 nm × 4 nm); (g) and (h) atomically-resolved STM image and corresponding FFT pattern of the B phase (V_s = 5 mV and I_t = 1 nA, 4 nm × 4 nm).

如图2(a)和图2(b)所示, 由于Bi(111)在4.2 K是不超导的, 而铅铋合金是超导的, 通过零偏压电导(zero-bias conductance, ZBC)图可以进一步清晰地分辨出A和B两个不同的区域, 分别对应于不超导的Bi(111)相和Pb_1–xBi_x超导合金相. 利用STS表征两个区域特征的电子学性质, 如图2(c)所示, Bi(111)区域测得的谱(黑线)表现出两个峰, 分别位于0 和+250 mV附近, 这两个峰是Bi(111)的特征峰, 对应其表面态^[24,25], 与我们之前得到的Bi(111)的特征dI/dV谱一致^[21]. 在0.4 K极低温条件下测量的小范围谱上, A相的Bi(111)表面没有出现超导能隙, 如图2(d)黑线所示, 这些谱学特征也证实A区域符合Bi(111)特征. 与A相不同, 在合金相的B区域, 大范围dI/dV谱没有明显的特征峰(图2(c)红线), 但在0.4 K温度下的测量结果出现明显的超导能隙(图2(d)红线), 清楚地显示合金相Pb_1–xBi_x具有超导电性. 图2(b)中的ZBC电导谱图的衬度反映了零偏压时的A和B两相的电导差异.
图 2 Pb_1–xBi_x合金薄膜的超导物性表征　(a), (b) STM拓扑图及其相同区域无磁场时的零偏压电导像, STM扫描条件: V_s = –90 mV, I_t = 20 pA, 扫描尺寸为280 nm × 280 nm. (c), (d) 4.2和0.4 K下在Bi(111)(黑线)和Pb_1–xBi_x(红线)表面区域采集的不同能量范围的典型dI/dV谱, 采谱条件: (c) V_s = –1 V, I_t = 2 nA, 调制偏压V_mod = 2 mV; (d) V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV. (e) 不同温度下dI/dV谱, 叠加在实验谱线上的黑线段(± 3 mV)是基于BCS理论对能隙的拟合. 采谱条件: V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV; (f)超导能隙大小和温度的依赖关系及拟合结果
Figure2. Electronic properties of the Bi(111) and Pb_1–xBi_x phases: (a) STM image (280 nm × 280 nm) of the Pb-Bi alloy surface; (b) zero-bias conductance (ZBC) image acquired within the same area in Fig. (a); (c), (d) representative dI/dV spectra of the Bi(111) region (black line) and Pb_1–xBi_x region (red line) measured with a W tip at 4.2 and 0.4 K in different energy ranges, respectively; (e) temperature-dependent dI/dV spectra, overlaid with the fitting segments (in black) on the basis of BCS theory, and the spectra are shifted vertically for clarity; (f) temperature dependence of the superconducting energy gap extracted from Fig. (e) (black circle) and fitting with temperature-dependent superconducting gap ?(T) (red line) using BCS theory.

如图2(e)所示, 当样品温度从0.45 K逐渐升高时, 测量得到的合金相Pb_1–xBi_x超导能隙逐渐变弱. 在温度高于7.5 K时, 超导能隙几乎消失. 为了获得不同温度下的超导能隙, 对 ± 3 mV范围内的谱做拟合, 如图2(e)中黑线所示. 相应地, Dynes公式中得到的拟合准粒子寿命从0.45 K时的12.86 ps (Γ = 0.051 meV)降低到7.51 K 时的1.82 ps (Γ = 0.359 meV). 图2(f)给出了拟合得到的超导能隙与温度的依赖关系. 采用(3)式进行拟合, 可以得到超导转变温度T_c = 7.77 K. 这明显比文献报道的纯铅膜的超导转变温度(6.0—6.5 K^[26])高, 因此可以进一步说明B相为合金相而非纯铅相. 根据Mattias rules经验关系, 当合金结构保持不变时, 用价电子数为5的铋原子取代价电子数为4的铅原子时, 超导转变温度会因为原子平均价电子数增加而升高, 这与我们观察到的实验结果相符合, 同时也与之前的报道一致^[6]. 另外, 通过外延得到的0 K下的超导能隙$\varDelta (0) = 1.66$ meV, 对应的超导耦合强度$ 2\varDelta (0)/({k}_{\rm{B}}{T}_{\rm{C}})=4.94$, 表明Pb_1–xBi_x合金相是强耦合超导体.
实验中获得的存在Bi(111)相和Pb_1–xBi_x相相分离的薄膜样品, 形成了一般很难实现的具有准二维界面的面内正常金属-超导体(N-S)异质结. 同时, 薄膜样品中正常金属-超导体异质结有着丰富的构型, 为研究超导邻近效应, 如穿透深度与异质结几何构型的关系提供了理想的平台. 对于正常金属-超导体异质结, 该准二维界面相当于一个约瑟夫森势垒^[18,19], 会显著影响Andreev反射^[20], 进而影响库伯对的传输与超导邻近效应. 图3中比较了不同N-S界面对正常金属一侧超导邻近效应穿透深度的影响. 图3(a)给出了一个N-S异质结, 其中Pb_1–xBi_x平台较Bi(111)平台高约960 pm(图3(b)). 沿着图3(a)中白色带箭头直线(Line 1)从台阶上的超导区向台阶下的正常金属区采集dI/dV谱, 经归一化后根据空间位置关系画成图3(c)所示的二维图像. 可以看到超导能隙在越过台阶进入正常金属一侧后明显减小, 远离后逐渐消失. 值得注意的是, 在远离台阶约20 nm以后, 仍然能观测到一个不明显变化的较小类能隙, 其为Bi(111)表面的特征行为(如图2(d)所示), 在我们之前的报导中也观察到过^[21]. 图3(d)—图3(f)研究了另外一个N-S异质结, 如图3(d)中白色带箭头直线(Line 2)所示, 这里Pb_1–xBi_x平台较Bi(111)平台仅高约210 pm (图3(e)). 可以看到, 对比图3(c), 在距离台阶20 nm处仍保持较明显的超导能隙(图3(f)). 进一步, 分别提取图3(c)和图3(f)中各位点的归一化零偏压电导, 如图3(g)所示. 在两个N-S异质结中, 台阶上侧的Pb_1–xBi_x平台内零偏压电导都基本为零, 且相对恒定, 仅在靠近台阶处开始增大. 在进入较低的正常金属Bi(111)一侧后, Line 1上的零偏压电导的增加呈现出明显的不连续性, 而Line 2上零偏压电导增加得更为缓慢. 用指数衰减公式对实验数据进行拟合^[27], 得到邻近效应穿透深度分别为22 nm(Line 1)和55 nm(Line 2), 更准确的计算应该用复杂的Usadel公式进行拟合^[28].
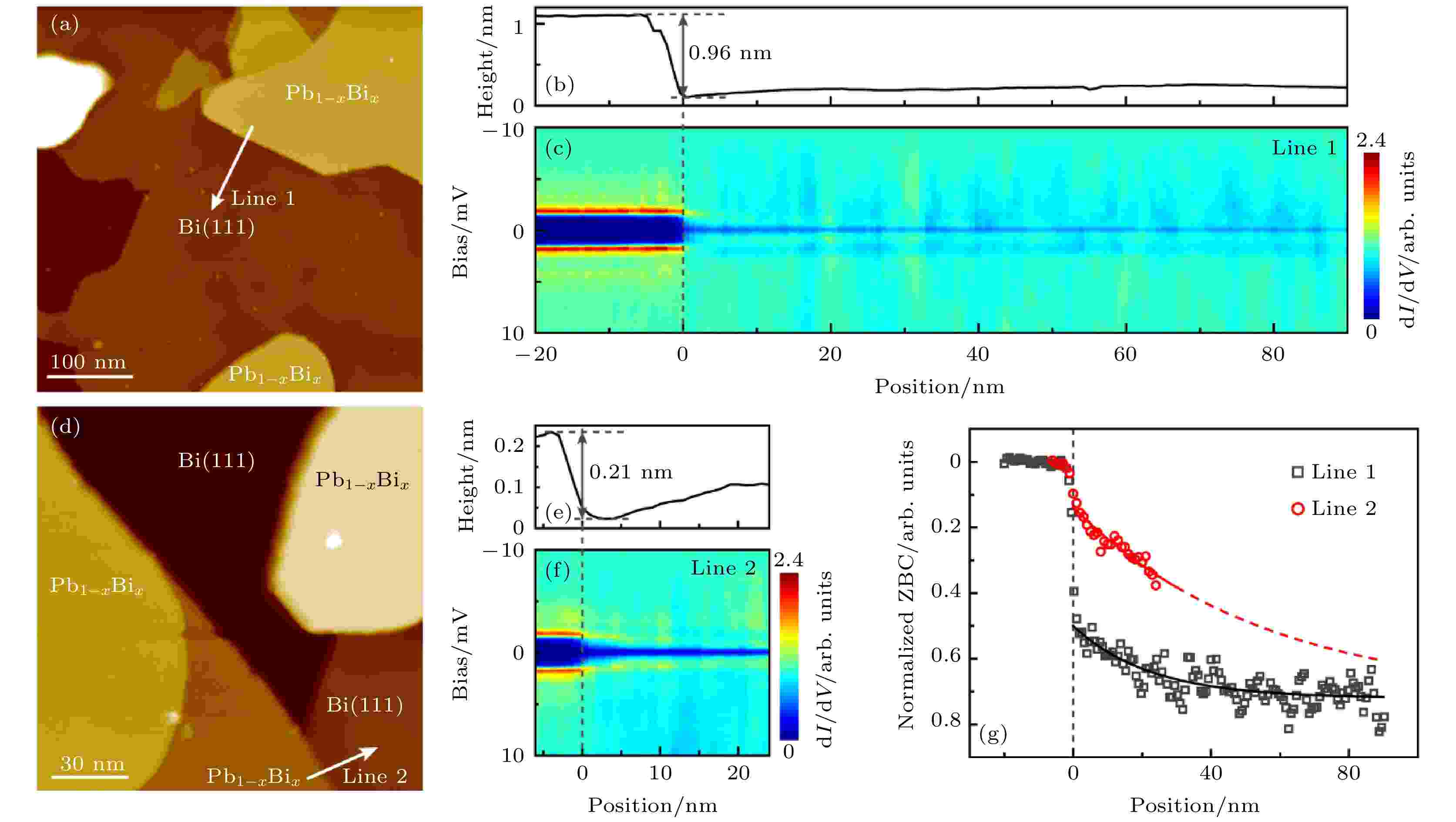图 3 正常金属-超导体(N-S)异质结处的邻近效应　(a) 合金表面大面积STM图像, 扫描条件为V_s = –98 mV, I_t = 20 pA, 450 nm × 450 nm. (b) 沿图(a)中白色带箭头直线(Line 1)得到的N-S异质结表面高度轮廓线, 显示异质结两侧高度差约为960 pm. (c) 沿Line 1所采的dI/dV谱经归一化后画成的二维电导图, 采谱间隔为0.75 nm, 采谱条件为V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV. (d) 合金表面大面积STM图像, 扫描条件为V_s = –1 V, I_t = 20 pA, 150 nm × 150 nm. (e) 沿图(d)中白色带箭头直线(Line 2)得到的N-S异质结表面高度轮廓线, 显示异质结两侧高度差约为210 pm. (f) 由沿Line 2所采的dI/dV谱经归一化后画成的二维电导图, 采谱间隔为1 nm, 采谱条件为V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV. 在图(c)和图(f)中, 所有谱已根据V_s = –10 mV处的电导做了归一化. (g) 沿Line 1和Line 2的归一化零偏压电导随位置的依赖关系. 图中实线为指数衰减公式拟合结果, 红色: –0.58 e^–y/55.23 + 0.72, 黑色: –0.22 e^–y/22.33 + 0.72, y是距离台阶下边缘的位置坐标
Figure3. Proximity effect at normal metal-superconductor (N-S) heterojunctions: (a) Large-area STM image of the alloy surface (V_s = –98 mV, I_t = 20 pA, 450 nm × 450 nm). (b) Height profile along the white-arrowed Line 1 as marked in Fig. (a). (c) Two-dimensional (2D) conductance map plotted with normalized dI/dV spectra acquired across the N-S heterojunction along Line 1 with a spacing of 0.75 nm (V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV). (d) Large-area STM image of the alloy surface (V_s = –1 V, I_t = 20 pA, 150 nm × 150 nm). (e) Height profile along the white-arrowed Line 2 in Fig. (d). (f) 2D conductance map plotted with normalized dI/dV spectra acquired across the N-S heterojunction along Line 2 with a spacing of 1 nm (V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV). In Fig. (c) and Fig. (f), the conductance at the setpoint bias (V_s = –10 mV) in the dI/dV curves is normalized to 1. (g) Plots of the normalized zero-bias conductance (ZBC) along Line 1 (black rectangles) and Line 2 (red circles). The red and black curves are exponential fittings of the data with functions as –0.58 e^–y/55.23 + 0.72 and –0.22 e^–y/22.33 + 0.72, respectively. y is the distance away from the lower step edge.

对比两个异质结的结果, 可以观察到沿箭头线Line 1的超导能隙在界面处有显著的变化(图3(c)), 而沿箭头线Line 2的超导能隙在界面处变化相对较小(图3(f)), 分别表现为零偏压电导的陡降和相对平缓的减小(图3(g)). 这一现象与准一维N-S结界面上的邻近效应类似^[27,29-31]. 在我们的实验中, 产生这一差异的原因可能和Pb-Bi合金与Bi膜的接触面积大小有关. 由于低温相的Pb-Bi合金是在200 K退火条件下生成的, 导致形成的不同的Pb-Bi合金岛与Bi膜的接触面积不同, 从而引起在Bi膜中的超导穿透深度差异. 较大的界面台阶高度主要是由退火过程中Pb-Bi岛的外延生长产生的, 图3(a)和图3(d)中Pb-Bi相的形貌也可以体现出这一特征, 因而导致较高的Pb-Bi岛与Bi膜的N-S接触面积反而较小.
图4(a)给出了超导体-正常金属-超导体(S-N-S)约瑟夫森结, 即面内的Pb_1–xBi_x-Bi(111)-Pb_1–xBi_x的结构, 其中, 正常金属区域宽度为23 nm, 两侧超导体的台阶高度分别为0.61和1.14 nm. 图4(b)和图4(c)分别给出了沿该S-N-S异质结采的归一化后的dI/dV谱和由其转化而成的二维微分电导图. 可以看到, 超导能隙在两侧超导区域始终保持均一大小, 跨过N-S界面时能隙有所减小, 但在整个Bi(111)区域都保持明显的超导能隙. 对比图3(c)和图3(f)中N-S异质结的结果, 可以看到S-N-S异质结中的超导邻近效应被显著增强了. 这是在两侧N-S界面发生多次Andreev反射的结果. 从归一化的隧穿谱中取出零偏压电导, 如图4(d)所示, 零偏压电导在经过Bi(111)区域时只有轻微的增加, 且在不同高度台阶附近的变化是不一样的: 左侧较低的台阶处, 零偏压电导变化缓慢连续; 而在右侧高台阶处, 则突变不连续. 这一结果与图3一致. 考虑到铋可能存在的拓扑属性, 由类似的S-N和S-N-S异质结引起的Bi(111)超导可能蕴含着新颖物理效应, 如拓扑超导^[32-36]与Majorana零能模^[37-39]等.
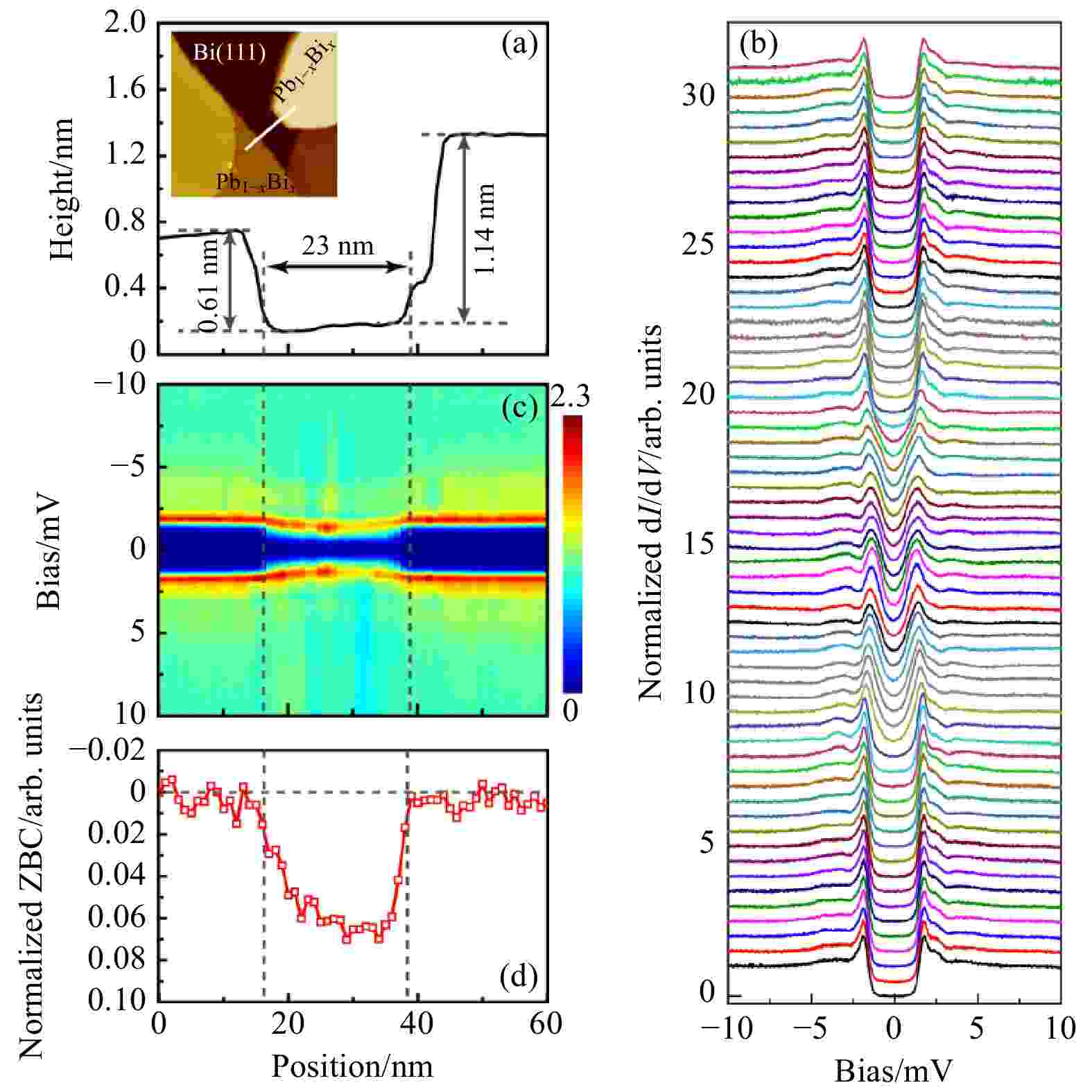图 4 超导体-正常金属-超导体(S-N-S)异质结中的邻近效应　(a) 沿着插图所示白线得到的S-N-S异质结高度轮廓线, 插图是与图3(d)相同的铅铋合金表面STM图像, 扫描条件为V_s = –1 V, I_t = 20 pA, 150 nm × 150 nm; (b) 沿图(a)中白线所采的归一化后的61条dI/dV谱, 采谱间隔1 nm, 采谱条件为V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV; (c) 由图(b)所示的归一化dI/dV谱画成的二维微分电导图; (d) 从图(c)中得到的S-N-S异质结中零偏压电导随位置的变化
Figure4. Proximity effect at the superconductor-normal metal-superconductor (S-N-S) heterojunction: (a) Height profile of the S-N-S heterojunction along the white line shown in the inset STM image, which is the same as Fig. 3(d) (V_s = –1 V, I_t = 20 pA, 150 nm × 150 nm); (b) normalized dI/dV curves acquired across the S-N-S heterojunction along the white line in Fig. (a) with a spacing of 1 nm (V_s = –10 mV, I_t = 1 nA, V_mod = 100 μV); (c) 2D conductance map plotted with the normalized dI/dV spectra in Fig. (b); (d) plot of the site-dependent ZBC in Fig. (c) along the S-N-S heterojunction.

采用低温共沉积的方法制备了铅铋合金薄膜, 利用STM/STS研究了其原子结构和超导物性. 实验发现了合金样品中存在相分离现象, 产生纯铋相Bi(111)和合金相Pb_1–xBi_x. 通过原子结构与超导特性表征, 确定合金相是部分铅被铋取代的Pb(111)结构. 通过测量变温STS谱及BCS理论拟合, 得到合金相的超导转变温度为7.77 K, 较纯铅膜的超导转变温度高, 符合Mattias rules经验关系. 研究了Bi(111)-Pb_1–xBi_x组成的正常金属-超导体及超导体-正常金属-超导体异质结中准二维界面处的邻近效应, 发现超导穿透深度可能受到界面接触面积的影响. 鉴于铋可能具有的拓扑属性, 本文制备的合金薄膜中的Bi(111)-Pb_1–xBi_x异质结处可能存在新奇物理效应, 值得未来进一步研究.