删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

1 μm波段水分子吸收光谱双光程同步测量方法研究

本站小编 Free考研考试/2021-12-29
摘要:基于双光程气体多通吸收池, 提出了一种单吸收池双光程(长光程: 72.46 m; 短光程: 36.23 m)同步测量水分子吸收光谱的测量方法, 并结合窄线宽外腔半导体激光器和高精度Fabry-Perot标准具, 发展了一套1 μm波段的高分辨率水分子吸收光谱双光程同步测量装置. 在测量装置建立后, 精确测量了Fabry-Perot标准具的自由光谱范围, 并详细评估了该系统中Fabry-Perot标准具以及双光程气体多通吸收池内压力和温度的稳定性. 利用该装置测量了9152.53 cm–1处水分子在双光程下的吸收光谱, 分别反演得到了长光程和短光程下的分子吸收线强和自加宽系数. 双光程吸收线强和自加宽系数的平均值与HITRAN2016数据库相应数据的相对偏差分别为0.78 %和3.8 %, 该结果验证了双光程同步测量方法的可行性和测量装置的可靠性.
关键词: 双光程/
近红外光谱/
谱线强度/
自加宽系数

English Abstract


全文HTML

--> --> -->
1.引　言
水分子在红外波段的吸收主要由独立谱线形成的吸收谱带以及分布于这些谱带之间的大气“窗口”区域组成[1]. 处于“窗口”区域的某些红外波段在光线传输时也被认为是“透明”的, 可为大气遥感探测等应用提供地表、海面和云的信息[2,3]. 然而对于激光大气传输而言, 虽然这些“窗口”波段对于光线的透过率较高, 但仍会受到水分子弱吸收的影响, 从而导致激光大气传输过程中的衰减效应和热晕效应[4], 进而使得到达远距离目标处的激光功率密度下降.
近年来, 随着光纤激光和固体激光技术的高速发展, 1 μm波段的高能量激光器在国家重大光电工程应用中受到越来越多的关注[5,6]. 水分子作为1 μm窗口区最主要的吸收和辐射分子, 其吸收光谱参数的准确获取是优化激光器发射谱, 提高大气传输效率的基础科学依据. 对于该波段水分子吸收光谱特性的研究主要有实验测量和理论计算两种方法. 实验测量方面, Mandi等[7]基于分辨率为0.01 cm–1的傅里叶变换光谱仪(FTS), 给出了8000—9500 cm–1范围内不确定度在6%左右的500条水分子吸收谱线强度; Schermaul等[8]则基于分辨率为0.03 cm–1的FTS, 给出了8600—15000 cm–1范围内综合不确定度在6%—26%的水分子线强; Brown等[9]基于分辨率在0.012—0.02 cm–1的FTS, 测量了9650—11400 cm–1范围内超过3300条水分子吸收谱线的线强, 不确定度为3%—25%; Mérienne等[10]基于分辨率为0.06 cm–1的FTS, 测量了9250—13000 cm–1范围内共7061条谱线的线位置和线强度, 给出了与Brown等[9]非常接近的结果. 然而傅里叶变换光谱法的代价非常昂贵, 且分辨率限制了光谱参数的准确度, 同时, 仪器函数的不确定性及由此带来的光谱参数测量误差也不可忽略. 此外, 在理论研究方面, 研究人员基于CRB模型、Ab initio方法以及MARVEL算法等计算了1 μm附近水分子吸收谱线的强度、线位置、能级值以及空气展宽和压力位移系数等参数[11–15], 这些计算结果的准确度仍有待实验测量的进一步验证[16].
直接吸收光谱测量方法(DAS)可以通过增加与吸收气体作用的光学程长达到提高信噪比的目的[17,18]. 目前, 近红外波段的外腔半导体激光器(external cavity diode laser, ECDL)发展迅速, 已实现常温下数百毫瓦功率的输出, 且具有线宽窄(约10–4 cm–1量级)、调谐范围宽(约102 nm量级)等优点, 是测量高分辨气体分子吸收光谱的优质光源; 高稳定度的Fabry-Perot(F-P)标准具可以提供更为准确的相对波数信息; 而双光程气体多通吸收池可以实现不同光程谱线参数的相互验证. 为获得高分辨率水分子吸收光谱, 本文基于上述主要装置, 介绍了一种双光程吸收光谱同步测量方法, 通过搭建双光程光谱同步测量系统, 实现了两个不同吸收光程上水分子高分辨率吸收光谱的同步测量. 利用该系统, 测量了9152.53 cm–1处的水分子吸收谱线, 获得了相应谱线的线强与自加宽系数, 通过与HITRAN2016数据库相应数据的对比验证了测量装置的可靠性, 为宽范围、高精度的水分子吸收光谱参数测量奠定了良好的基础.
2.实验系统
2
2.1.实验系统概述
-->

2.1.实验系统概述

实验系统示意图如图1所示. 光源为Toptica公司生产的ECDL, 最大输出功率为90 mW, 波长扫描范围为1.01—1.10 μm. 如图1所示, 激光器输出的线偏振光首先经过光隔离器(OI); 随后, 光束被第一组1/2波片(HWP 1)和偏振分束器(PBS 1)分为光束1和光束2, 其中光束1经由反射镜M4, M5, M6以及一个焦距为400 mm的模式匹配透镜(L1)导入吸收池, 产生短光程吸收信号; 光束2被第二组1/2波片(HWP 2)和偏振分束器(PBS 2)分成光束3和光束4, 光束3由反射镜M7, M8, M9以及一个焦距为400 mm的模式匹配透镜(L2)导入吸收池, 产生长光程吸收信号; 光束4经由反射镜M2, M3以及一个1/4波片(QWP)导入F-P标准具用于定标信号光的相对频率. 从吸收池出射的短光程和长光程吸收信号分别经由两个离轴抛物面镜(fPM2 = fPM3 = 38.1 mm)聚焦到光电探测器(PDB210C/M, Thorlabs)上; F-P标准具的出射信号同样经由离轴抛物面镜(fPM1 = 101.6 mm)会聚于光电探测器(PDA10CF-EC, Thorlabs)上, 所有光电探测器的信号由采集卡(NI, USB6356)采集并传输到计算机作后续处理. 实验期间气体吸收池的温度通过温控器(SR8809, Sunny)控制, 吸收池内压力由两个薄膜压力计(CTR100N: 量程为0—13332.2 Pa, 精度为0.01%; CTR101 N: 量程为0—2666.44 Pa, 精度为0.01%, Leybold)监测.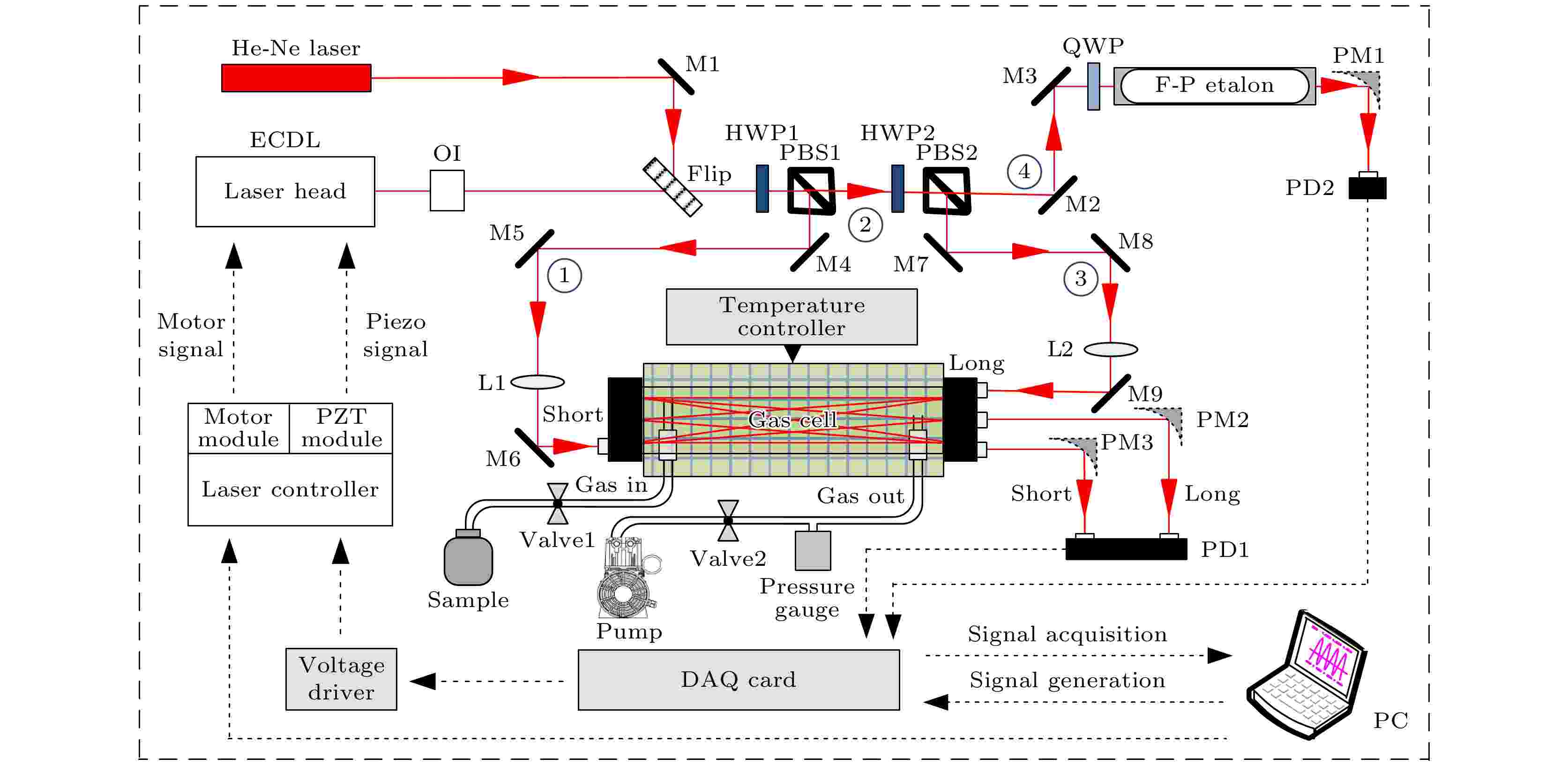
图 1 实验装置示意图
Figure1. Sketch of the experimental setup.

实验中控制激光器内的压电陶瓷(PZT)实现在待测波段的波长扫描, 每次扫描范围约为0.4 cm–1. 实验中所用的气态水分子由蒸馏水产生, 实验前将蒸馏水结冰, 使其中的混杂气体析出, 并利用真空泵将整个气路抽至真空(压力 < 1 Pa), 然后待蒸馏水蒸发产生水分子, 冲刷整个气路约30 min, 使水分子充满整个池体后, 通过Valve 1和Valve 2调节池内水分子压力到设定压力值附近, 最后关闭所有阀门, 待吸收池内压力稳定后开始实验测量.
2
2.2.双光程吸收池
-->

2.2.双光程吸收池

实验中所用双光程气体吸收池示意图如图2所示. 气体吸收池为Herriott型, 该结构简单可靠, 低压情况下形变小. 吸收池内两个镀银膜反射镜的直径为80 mm, 间距为450 mm. 在如图2所示的反射镜上共开有四个直径为4 mm的通光孔, 长、短光程的入射端和出射端各自对应, 长光程的等效光程为72.46 m, 短光程的等效光程为36.23 m. 当光束同时从长、短光程的入射光孔进入吸收池时, 则可实现双光程, 并且两个光程互不干扰(镜内光斑如图3所示). 此时, 在激光频率单次扫描的情况下, 可同时获得两张不同光程的吸收光谱, 在增加数据冗余的同时并未延长测量时间. 此外, 池壁外部包裹控温层, 使用温控器可保持吸收池温度的稳定性, 实验测得的整体温度波动小于 ± 0.05 K.
图 2 吸收池结构示意图　(a)吸收池的正面; (b)吸收池的背面
Figure2. Schematics of absorption cell structure: (a) Front of the absorption cell; (b) back of the absorption cell.

图 3 He-Ne激光器在反射镜上的长光程(外圈与中圈)和短光程(内圈)实际光斑
Figure3. The actual spots of long optical path (outer circle and middle circle) and short optical path (inner circle) of He-Ne laser on the mirror.

实验中通过系统漏率评估吸收池压力系统的稳定性, 首先利用真空泵将气路压力抽至低于1 Pa, 然后在恒温条件下(300 K), 使用CTR-100压力计持续监测吸收池内部压力, 连续记录了70 h的压力值, 结果如图4所示. 结合实际的吸收池容积(2.6 L), 计算得出的系统泄漏率为4.54 × 10–4 Pa·L·s–1. 所以在1 h内的压力变化为0.62 Pa, 影响可以忽略不计.
图 4 70 h内的多通吸收池中压力变化图
Figure4. Pressure change in the multi-pass absorption cell in 70 h.

2
2.3.F-P标准具
-->

2.3.F-P标准具

实验采用具有温度和压力控制的F-P标准具对采集到的光谱数据作相对波数定标. F-P标准具的自由光谱范围(free spectral range, FSR)公式为[19]
${\rm{FSR = }}\frac{c}{{2 \cdot {n_{\rm{i}}} \cdot d}},$
其中, c为真空中的光速, ni为F-P标准具内部介质的折射率, d为F-P标准具的腔长. 实验中测得的总频率变化为760.01338 GHz, 在此期间观测到的FSR周期移动个数为1014个, 因此, 标准具的FSR为749.52 MHz (760.01338 GHz/1014), 此数值与依据(1)式计算的理论值(749.36 MHz)符合较好.
根据(1)式可知, 标准具FSR的稳定性主要受到其长度的影响, 而温度变化是引起长度变化的主要因素. 假设石英玻璃管的热膨胀系数为$\xi $, 则温度变化$\Delta T$与FSR频率变化$\Delta \nu $之间的关系为[20]
$\Delta \nu = - \nu \cdot \xi \cdot \Delta T.$
为评估实验中F-P标准具的稳定性, 在低压(10–5 Pa)恒温(约(303.65 ± 0.005) K)状态下, 利用Pound-Drever-Hall(PDH)锁频技术将激光频率准确锁定到F-P标准具的纵模上, 并使用光梳拍频的方法持续测量1.5 h内激光器频率的相对变化值. 光梳拍频法测量标准具FSR的原理[21,22]为
${f_{\rm{b}}} = m \cdot {f_{\rm{r}}} \pm \delta \pm {f_m},$
式中m为整数, fr和$\delta $分别是光频梳的脉冲重复频率和载波包络相位偏移, fm为激光锁定在标准具上的频率, fb为标准具信号与光梳信号的拍频. 因此, 可以根据拍频信号fb的变化评估F-P标准具FSR的稳定性, 结果如图5所示. 激光器的相对频率漂移约为5.39 MHz·h–1. 即1 h内由于标准具FSR波动造成波数测量的相对偏差约为0.72%, 可以认为标准具的稳定性良好.
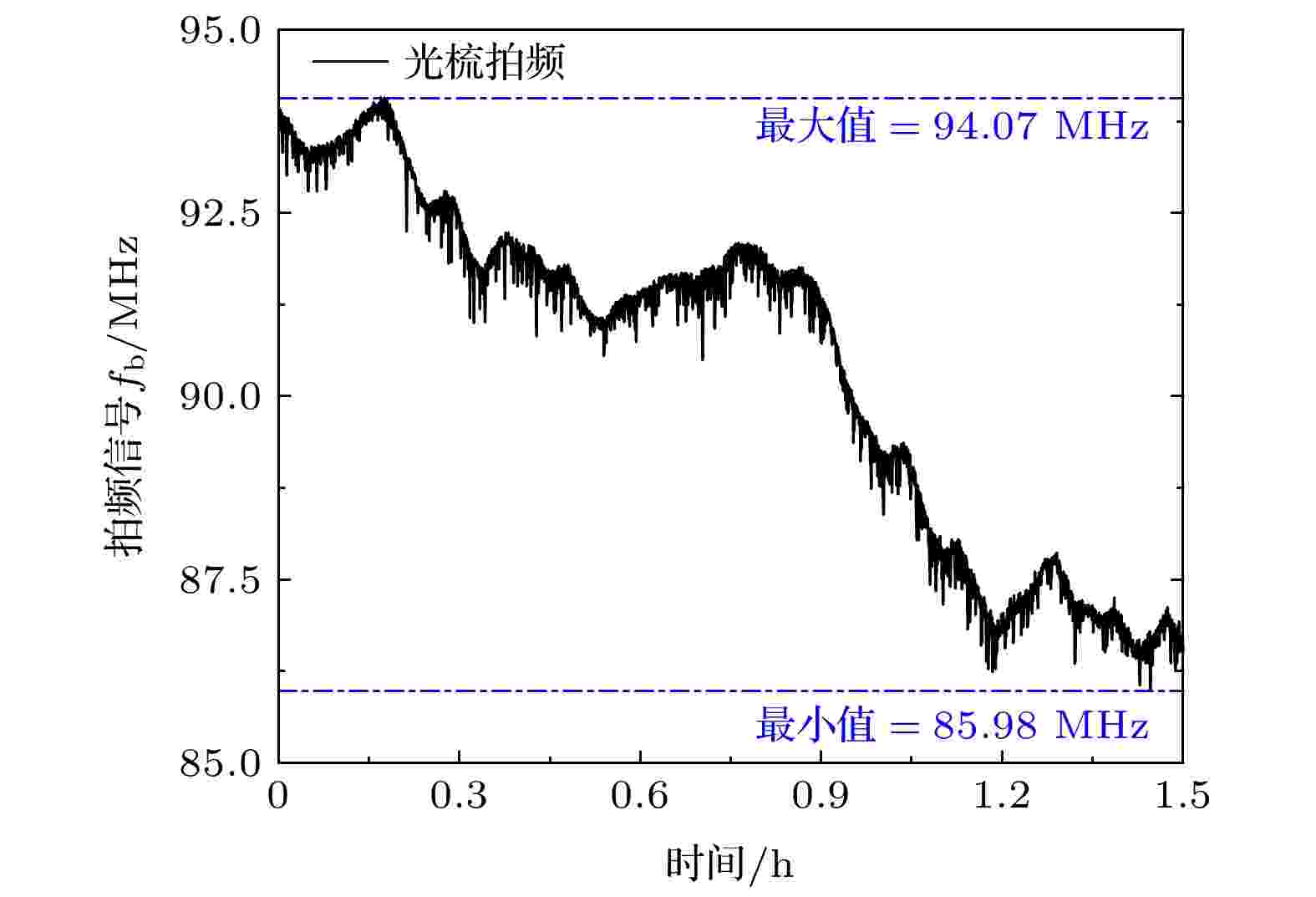图 5 1.5 h内激光器与光梳拍频信号(fb)的频率变化
Figure5. Frequency variation of the beat signal (fb) between the laser and the optical comb within 1.5 h.

3.双光程系统的水分子吸收光谱测量
2
3.1.水分子的双光程吸收光谱特征
-->

3.1.水分子的双光程吸收光谱特征

通常单次扫描只能获得一张光谱, 为保证实验数据的冗余需对相同实验条件下的气体进行重复测量, 获得多张光谱, 然而在重复测量期间样品气体的温度、压力以及激光器的扫描特性等条件的变化容易引起实验误差. 相反, 双光程同步测量单次扫描可以获得除光程外其他实验条件完全相同的两张光谱, 这既保证了数据的冗余, 又可避免重复扫描过程中由于实验条件的变化而引起的误差.
基于双光程吸收光谱测量系统, 实验采集了394.9, 585.3, 804.2, 980.1, 1501.9和1990.7 Pa共6组压力下9152.53 cm–1处水分子跃迁谱线的吸收光谱. 图6(a)和图6(b)分别为单次扫描同步测量获得的水分子的短光程吸收光谱和长光程吸收光谱, 图6(c)为同时测量得到的F-P标准具纵模信号, 图6右侧为左侧图中半个周期内的放大图. 实验中利用图6(c)的信号定标水分子吸收光谱的相对波数, 通过寻找基模信号的横坐标(实验点数), 并构建实验点数和FSR关系(基模信号的间隔即为FSR, 其数值为0.024984 cm–1), 再进行多项式拟合即可得到以波数为横坐标的吸收光谱. 绝对波数采用HITRAN2016数据库的相应数据.
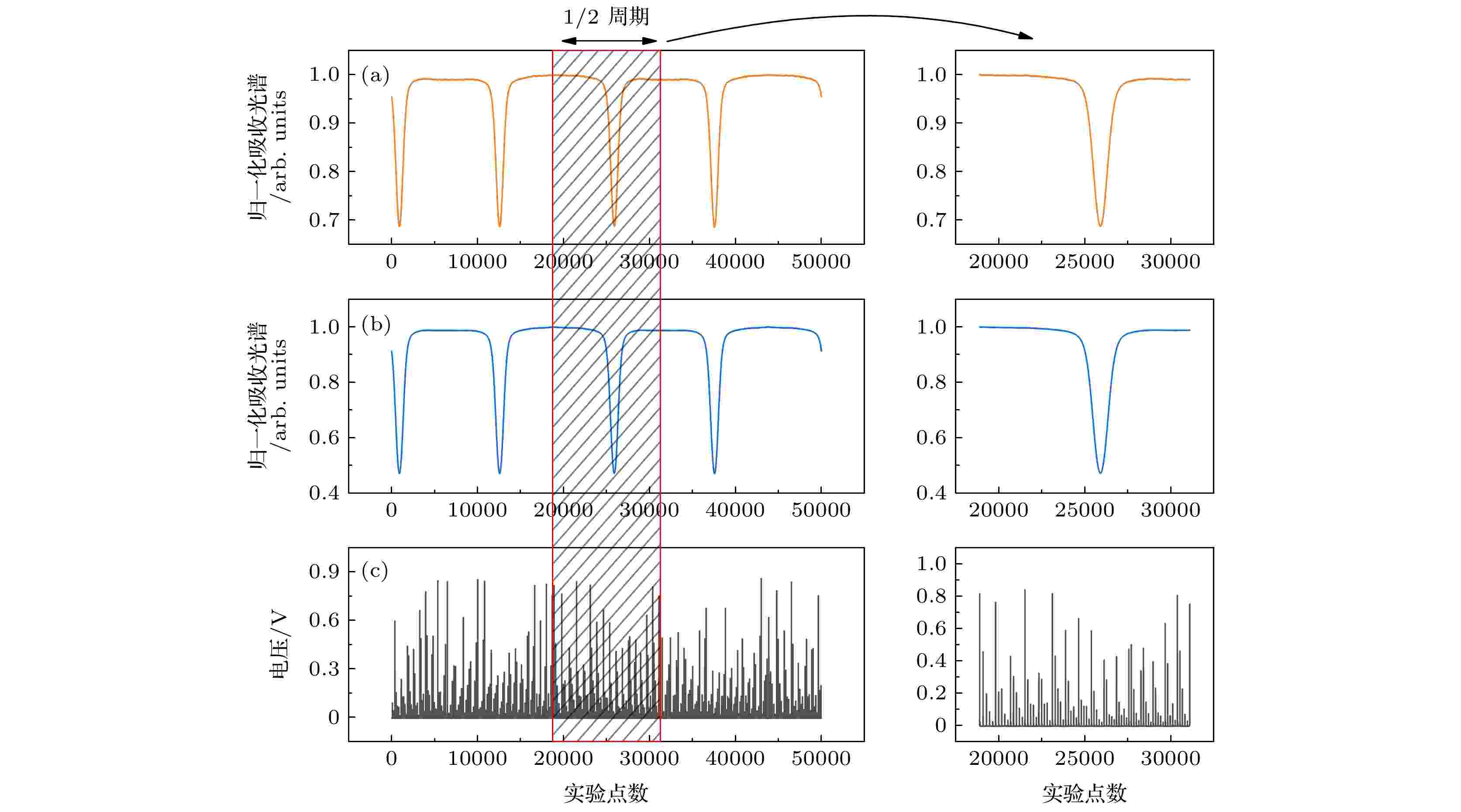图 6 同时记录的光谱示例　(a)短光程水分子吸收信号; (b)长光程水分子吸收信号; (c)F-P标准具纵模信号
Figure6. Examples of spectra recorded simultaneously: (a) Short optical path water vapor absorption signal; (b) long optical path water vapor absorption signal; (c) the longitudinal mode signal of F-P etalon.

为获取水分子吸收谱线的线强和自加宽系数, 首先需要得到不同压力下的吸收系数, 可采用Voigt线型对去基线后的光谱进行拟合获得, 吸收光谱的基线可通过对远离吸收线中心位置的数据点执行三次多项式拟合的方法取得. 图7给出了长光程和短光程下, 温度为300 K时, 6组压力下9152.53 cm–1处水分子的吸收谱线采用Voigt线型的拟合结果及其残差值. 需要注意的是, 采用Voigt线型对高分辨率、高频率精度的吸收光谱进行拟合时, 拟合残差会呈“W”形. 拟合过程中, 吸收谱线的多普勒线宽固定为温度为300 K时的理论值.
图 7 (a), (b)在长光程中9152.53 cm–1处纯水分子的吸收系数和拟合残差; (c), (d)在短光程中纯水分子在相同光谱线位置的吸收系数和拟合残差
Figure7. (a), (b) Absorption coefficient and fitting residual of water vapor at 9152.53 cm–1 in long optical path; (c), (d) absorption coefficients and fitting residuals of pure water vapor at the same spectral line position in a short optical path.

2
3.2.水分子的线强测量
-->

3.2.水分子的线强测量

水分子跃迁吸收线的积分吸光度A(cm–1)与线强S(cm·molecule–1)之间的关系为
$\begin{split}A =\;& - \int_{ - \infty }^{ + \infty } {\ln } \left[ {\frac{{I(\nu )}}{{{I_0}(\nu )}}} \right]{\rm{d}}\nu = L\int_{ - \infty }^\infty N \sigma (\nu ){\rm{d}}\nu \\=\;& NL\int_{ - \infty }^\infty S {\phi _V}(\nu ){\rm{d}}\nu = NLS,\end{split}$
$N = \frac{{{N_A} \cdot P}}{{8.314472 \times {{10}^6} \cdot T}},$
其中, N(molecule·cm–3)为水分子的粒子数浓度, L(cm)为吸收光谱的实际光程, NA为阿伏伽德罗常数, P(Pa)为水分子所占的压力. 根据(4)式和(5)式即可反演得出${\nu _0}$处吸收谱线的线强S. 另外, 由于线强S是温度的函数, 不同温度下线强的转换关系为

$S\left( {{T_0}} \right) = S(T) \cdot {K_T} = S(T)\frac{{Q(T)}}{{Q\left( {{T_0}} \right)}}\frac{{\left[ {1 - \exp \left( { - \dfrac{{hc{\nu _{nm}}}}{{k{T_0}}}} \right)} \right]}}{{\left[ {1 - \exp \left( { - \dfrac{{hc{\nu _{nm}}}}{{kT}}} \right)} \right]}}\exp \left[ {\frac{{hc{E^{\prime \prime }}}}{k}\left( {\frac{1}{{{T_0}}} - \frac{1}{T}} \right)} \right],$

式中KT为不同温度间线强的转换系数, Q为体系的总配分函数, h为普朗克常数, ${\nu _{nm}}$为跃迁频率, $E'' $为下势能面, 具体数值均可在HITRAN2016数据库中查询.
构建粒子数浓度和单位距离上相应的积分吸光度(吸收系数对波数的积分, 单位为cm–2)的线性关系, 结果如图8所示, 拟合得出的斜率即为线强. 图中红色实线对应长光程下线强拟合结果; 蓝色虚线对应短光程下线强拟合结果; 误差棒则代表了单位距离上积分吸光度的不确定度.
图 8 温度300 K时, 水分子在9152.53 cm–1处单位距离上的积分吸光度与粒子数浓度的线性拟合结果及其拟合残差(左上角小图显示了3.626 × 1017 molecule·cm–3下5组单位距离上积分吸光度平均后的标准差. 因标准差过小, 主图上未完全显示)
Figure8. At a temperature of 300 K, the linear fitting results and fitting residual errors of the integrated absorbance per unit distance of water vapor at 9152.53 cm–1 against the particle number concentration. (The minor image in the upper left corner shows the average standard deviation of the integrated absorbance of the 5 groups of unit distances under 3.626 × 1017 molecule·cm–3. However, the standard deviation is so small that it is not fully displayed on the main image)

在9152.53 cm–1处测得长、短光程下的线强(已转换到296 K温度下)分别为SL = 1.666 × 10–23 cm·molecule–1和SS = 1.635 × 10–23 cm·molecule–1, 实验测量的线强与HITRAN2016数据库相应的线强[23] SH对比(不确定度在1 %—2 %), 相对偏差分别为1.35 %和–0.57 %, 即线强平均值SA的相对偏差为0.78 %.
同时考虑到池体漏率和标准具带给线强测量的影响, 结合(6)式可以将(4)式修正为
$ \begin{split} {S_0} = \;&8.314472 \times {10^6} \\ &\times \frac{{{A_{{\rm{fit}}}} \cdot {k_{\rm{w}}} \cdot K_T^\prime }}{{{N_A} \cdot \left( {P + {q_{{\rm{leak }}}}/V \cdot \Delta t} \right) \cdot L \cdot {r_{{\rm{iso}}}}}}, \end{split} $
式中, S0和ST分别为标准温度和实验温度下的线强值, Afit为拟合积分吸光度, kw为标准具频率漂移对拟合吸光度的修正项(以下简称修正项), $K_T^\prime $为温度T和温度转换因子KT的乘积, qleak为漏率, V为吸收池容积, $\Delta t$为测量时长, riso为同位素丰度. 根据(7)式, 线强的不确定度[24]可表示为
$\begin{split}\Delta {S_0} =\;& \left[ {{\left( {\frac{{\partial S}}{{\partial A}}} \right)}^2}\Delta _{\rm{A}}^2 + {{\left( {\frac{{\partial S}}{{\partial P}}} \right)}^2}\Delta _{\rm{P}}^2 + {{\left( {\frac{{\partial S}}{{\partial T}}} \right)}^2}\Delta _T^2 \right.\\&\left.+ {{\left( {\frac{{\partial S}}{{\partial L}}} \right)}^2}\Delta _{\rm{L}}^2 + {{\left( {\frac{{\partial S}}{{\partial {r_{{\rm{iso}}}}}}} \right)}^2}\Delta _{{r_{{\rm{iso}}}}}^2 \right]^{{1 / 2}}.\\[-15pt]\end{split}$
通过(8)式可分析各参数误差对线强不确定度的贡献. 以积分吸光度为例, 其对线强不确定度的贡献为
$\begin{split}&{\left( {\frac{{\partial S}}{{\partial A}}} \right)^2} \cdot \left[ {{\left( {\frac{{\partial S}}{{\partial A}}} \right)}^2} + {{\left( {\frac{{\partial S}}{{\partial P}}} \right)}^2} + {{\left( {\frac{{\partial S}}{{\partial T}}} \right)}^2}\right.\\&\left.+ {{\left( {\frac{{\partial S}}{{\partial L}}} \right)}^2} + {{\left( {\frac{{\partial S}}{{\partial {r_{{\rm{iso}}}}}}} \right)}^2} \right]^{ - 1}.\end{split}$
根据实验测量结果, 在温度为300 K以及压力为397.3 Pa的情况下, 各参数对线强不确定度的贡献如表1所列(KT是关于T的函数, 故未计算其贡献). 可以看到, 池体漏率和修正项的相对不确定度分别为0.003%和0.72%, 对于线强不确定度的贡献均不超过0.013%, 说明漏率和修正项对于线强测量结果的影响十分微弱, 体现了系统良好的稳定性.
参数参数值相对不确
定度/%		对线强不确定度的贡献/%
Afit0.01126542 cm–10.01499.9746
kw10.720.0127
T300 K0.017~0
KT1.011390.028—
V2.6 L00
P397.3 Pa0.025~0
L7246 cm0.13~0
qleak4.54 × 10–4 Pa·L·s–10.003~0
riso0.99730.010.0127
S1.6435 × 10–23 cm·molecule–10.74


表1296 K温度下9153 cm–1处各参数与其对线强不确定度的贡献
Table1.Parameters at 9153 cm–1 and their contribution to the uncertainty of line intensityat 296 K.

2
3.3.水分子的自加宽系数测量
-->

3.3.水分子的自加宽系数测量

洛伦兹半宽${\gamma _{\rm{L}}}$与温度和压力的关系为
${\gamma _{\rm{L}}} = \left( {{\gamma _{{\rm{self }}}} \cdot \frac{{{P_{{\rm{self }}}}}}{{{P_{{\rm{atm }}}}}} + {\gamma _{{\rm{out }}}} \cdot \frac{{{P_{{\rm{out }}}}}}{{{P_{{\rm{atm }}}}}}} \right) \cdot {\left( {\frac{{{T_0}}}{T}} \right)^n},$
其中Pself和Pout分别为吸收气体分压和外部加宽气体分压, ${\gamma _{{\rm{self}}}}$为自加宽系数, ${\gamma _{{\rm{out}}}}$为外加宽系数, Patm为标准大气压, T0为标准温度296 K, n为加宽系数的温度依赖系数, 实验采用HITRAN2016数据库给定的n值.
由于实验采用纯水分子作为吸收气体而无外加宽气体, 认为(10)式中的洛伦兹线宽不受外加宽系数影响. 基于6组压力下的吸收系数, 通过对长、短光程中不同压力下的洛伦兹线宽作线性拟合, 可以分别获得水分子在9152.53 cm–1处各自光程下的自加宽系数, 结果如图9所示.
图 9 300 K时, 9152.53 cm–1处水分子洛伦兹线宽与压力的线性拟合结果
Figure9. At a temperature of 300 K, the linear fitting result of the Lorentzian line width against pressure of water vapor at 9152.53 cm–1.

在9152.53 cm-1处测得长、短光程下的自加宽系数分别为$\gamma _{{\rm{self }}}^{\rm{L}}$= 0.478 cm–1·atm–1和$\gamma _{{\rm{self }}}^{\rm{S}}$= 0.468 cm–1·atm–1, 与HITRAN2016数据库给定值(自加宽系数$\gamma _{{\rm{self }}}^{\rm{H}}$约为0.456 cm–1·atm–1)的相对偏差分别为4.8 %和2.6 %. 值得注意的是, HITRAN2016并未给出此条吸收谱线准确的自加宽系数不确定度.
4.结　论
本文基于ECDL、双光程吸收池和高精度F-P标准具搭建了一套适用于1 μm波段水分子吸收光谱的高分辨率测量系统. 其中, 双光程吸收池可以同步实现72.46和36.23 m两个光程, 由F-P标准具的频率漂移、池内压力和温度波动造成的误差分别为0.72%, 0.025%和0.017%. 基于此系统测量了400—2000 Pa压力下9152.53 cm–1处的水分子吸收谱线, 分别获得了长、短光程下的线强和自加宽系数以及相应的平均值, 与HITRAN2016数据库相应数据作对比, 得出线强和自加宽系数的平均相对偏差分别为0.78%和3.8%. 以上结果表明了该系统的性能良好, 双光程平均基于该系统的双光程测量方法能够胜任1 μm波段水分子吸收光谱的测量研究工作.
感谢中国科学技术大学刘安雯副教授在F-P标准具制作和使用过程中给予的支持
相关话题/测量 实验 系统 信号 光谱
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 二次电子发射对系统电磁脉冲的影响
    摘要:系统电磁脉冲难以有效屏蔽,会显著影响低轨航天器等重要装置和基础设施的性能.为了评估二次电子对系统电磁脉冲的影响,本文基于粒子云网格方法,建立了三维非稳态系统电磁脉冲模型,计算并比较了不同电流密度、金属材料等条件下,两种典型结构的电磁脉冲响应.结果表明,在计算模型中忽略二次电子发射会使部分位置的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 拉曼光谱研究退火氧化镍中二阶磁振子散射增强
    摘要:运用激光拉曼光谱研究了450—1050℃退火处理对氧化镍中二阶磁振子散射的增强效应,同时分析了激光功率对氧化镍中二阶磁振子散射的影响.研究发现,退火处理可显著增强氧化镍中二阶磁振子散射,在450—1050℃范围内,退火温度越高,增强效应越明显,经过1050℃退火处理后二阶磁振子散射增强效应可达 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 掺Tm<sup>3+</sup>和Tb<sup>3+</sup>的LiMgPO<sub>4</sub>磷光体的发光光谱与能量转移
    摘要:稀土掺杂的LiMgPO4(LMP)磷光体是一种很有前景的辐射剂量计材料,热释光谱技术是研究材料中载流子陷阱和发光中心的有效手段.为研究稀土掺杂LMP的发光机制,用高温固相法研制了LMP:Tm,LMP:Tb和LMP:Tm,Tb磷光体,用线性升温法测量了磷光体的热释光发光曲线和热释光谱,并将之与荧 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • SiH<sup>+</sup>(X<sup>1</sup>Σ<sup>+</sup>)的势能曲线、光谱常数、振转能级和自旋-轨道
    摘要:基于Molpro2012程序包,应用包含Davidson修正的多参考组态相互作用方法,使用AVXZ和AVXdZ(X=T,Q,5,6)基组进行单点能从头算,然后采用Aguado-Paniagua函数进行拟合,得到了SiH+(X1Σ+)离子在不同基组、不同方法和是否考虑自旋-轨道耦合(SOC)情况 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于非相干宽带腔增强吸收光谱技术对碘氧自由基的定量研究
    摘要:介绍了435—465nm波段非相干宽带腔增强吸收光谱(IBBCEAS)技术对碘氧自由基(IO)的定量方法.为准确获取IO的浓度信息,对IBBCEAS系统高反镜的镜片反射率、有效腔长及损耗等参数进行了标定.利用氮气和氦气之间瑞利散射的差异性标定了高反镜的反射率曲线,在IO吸收峰436.1nm处镜 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • <sup>87</sup>Rb玻色-爱因斯坦凝聚体中双拉曼相对相位对相干跃迁操控的实验研究
    摘要:发展了利用两对拉曼光之间的相对相位精确调控拉曼耦合强度的新方法,实现了两个量子态相干跃迁的操控.对两对拉曼光的光路进行了特殊设计,从而保证两对拉曼激光在传输过程中的相对相位保持恒定,然后作用到87Rb原子的两个超精细塞曼能级$\left|{1,1}ightangle$和$\left|{ ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 双层耦合非对称反应扩散系统中的振荡图灵斑图
    摘要:采用线性耦合Brusselator模型和Lengyel-Epstein模型,数值研究了双层耦合非对称反应扩散系统中振荡图灵斑图的动力学,并分析了图灵模、高阶模以及霍普夫模之间的相互作用及其对振荡图灵斑图的影响.模拟结果表明,在Lengyel-Epstein模型激发的超临界图灵模${k_1}$的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于自旋体系的量子机器学习实验进展
    摘要:机器学习因其在模式识别等问题上的优势已经被广泛应用到各个研究领域,然而其运算能力在一定程度上受到经典计算机算力的制约.近年来,随着量子技术的高速发展,量子计算加速的机器学习在诸多量子体系中进行了初步实验验证,并在某些特定问题上展示出了超越经典算法的优势.本文主要介绍两类典型的自旋体系—核磁共振 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于波动与扩散物理系统的机器学习
    摘要:物理学在机器学习中的应用以及两者的交叉融合正引起广泛关注,尤其是在波动系统和扩散系统中.本文重点关注波动与扩散物理系统和机器学习之间的内在联系以及对机器学习算法和物理实现的推进作用,综述了波动系统和扩散系统中的机器学习研究,介绍了部分最新研究成果.文中首先讨论了监督学习的波动系统实现,包括神经 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 硼中子俘获治疗中的含硼-10药物分布及浓度在体测量方法研究进展
    摘要:硼中子俘获治疗(boronneutroncapturetherapy,BNCT)是一种结合含硼-10靶向药物和重离子肿瘤治疗的二元精确放射治疗方法,但经过近70年的发展,BNCT仍然未能真正进入临床应用.含硼-10药物在体内的浓度分布测量方法不能满足临床需求,影响治疗的效果和安全性,是目前BN ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.