摘要:系统电磁脉冲难以有效屏蔽, 会显著影响低轨航天器等重要装置和基础设施的性能. 为了评估二次电子对系统电磁脉冲的影响, 本文基于粒子云网格方法, 建立了三维非稳态系统电磁脉冲模型, 计算并比较了不同电流密度、金属材料等条件下, 两种典型结构的电磁脉冲响应. 结果表明, 在计算模型中忽略二次电子发射会使部分位置的峰值电场强度被低估2—3倍, 电场响应持续的时间也会被低估10%以上. 在各类二次电子中, 背散射电子对系统电磁脉冲的影响占主导, 而真二次电子的作用约为背散射电子的1/5. 二次电子发射对系统电磁脉冲的影响随着系统所用材料原子序数的增高而加大. 空间电荷效应较强时, 二次电子才会对腔体外系统电磁脉冲产生影响. 本研究有助于更好地通过数值模拟来获得具体装置在强辐射环境下的系统电磁脉冲响应.
关键词: 二次电子发射/
系统电磁脉冲/
光电子/
全电磁粒子模拟方法

English Abstract

全文HTML

--> --> -->

系统电磁脉冲(system generated electromagnetic pulse, SGEMP)是指在γ射线和X射线(特别是由高空核爆炸释放)的辐照下, 系统(卫星、导弹以及各种电子仪器)表面或内部产生高速运动的电子流, 进而在系统周围激励起的瞬态电磁脉冲^[1]. SGEMP不同于环境电磁脉冲, 后者是高能射线与大气相互作用所激励出来的大范围恶劣电磁环境. 一般情况下, 这两类电磁脉冲不会对人员造成直接伤害, 主要毁伤作用在于干扰、损伤电子或电力系统. 环境电磁脉冲对系统的影响可以通过加装金属屏蔽壳等常规抗电磁干扰方法屏蔽, 但是SGEMP的响应源为自身电子流, 难以有效屏蔽. SGEMP效应的毁伤效应评估以及针对性的加固设计对于保障通讯等关乎国家安全的基础设施具有重要意义. 美国于2001年成立“电磁脉冲袭击对美威胁评估委员会”, 对十大类重要基础设施在电磁脉冲打击下的保护和恢复给出建议^[2].
全面禁止核试验条约的签订使得获取新的SGEMP数据变得不可能, 而已公布的试验数据也极其有限. 使用较大空间范围、高强度的射线源可以部分模拟核爆炸的辐射环境, 但此类替代实验成本高昂、准备周期长, 出于保密等原因, 仅有一些典型简化结构下的公开数据^[3,4], 因此数值模拟成为研究SGEMP, 获得电磁响应的重要手段. SGEMP的数值模拟研究始于20世纪70年代, 代表性成果是美国国防部原子能机构Woods等^[5,6]编制的二维SGEMP数值模拟程序ABORC. 该程序的准确性约在1977年美国陆军哈瑞戴蒙德实验室的一系列标定实验^[7]中得到了验证. 本单位相关理论计算工作与美国基本同时开展^[8], 与核爆模拟装置“闪光”–I的实验结果总体趋势上一致. 这一阶段国内外的数值模拟均以二维轴对称腔体为研究对象, 采用粒子云网格方法(particle in cell, PIC)^[9]或直接差分法求解玻尔兹曼方程^[10]来描述带电粒子的运动.
近5年来, 国内外****在SGEMP的数值模拟方面取得了新的进展. Pointon 等^[11]在报告中展示了使用二维粒子云网格-蒙特卡罗碰撞(PIC-MCC)方法模拟稀薄氮气环境下内电磁脉冲结果. Angus等^[12]考虑多种分子、原子亚稳态, 建立了零维反应动力学模型, 用于筛选高能电子–空气作用中的主要反应路径. 北京应用物理与计算数学研究所孙会芳等^[13]使用三维PIC方法计算真空中圆柱腔体的SGEMP. 西北核技术研究院的Chen等^[14]系统地研究了初级电子能谱等对空间电荷层形成特征时间的影响. 中物院应用电子学研究所的Chen等^[15]提出了一种描述SGEMP空间电荷层的方法, 可以有效降低PIC模拟所需计算资源. 清华大学的Meng等^[16,17]模拟了神光-III装置的SGEMP响应, 并使用时偏时域有限差分法减弱电磁场中的高频噪声. 然而, 此前的研究中大多忽略了高能电子与金属材料作用产生的二次电子, Wenaas等^[18]的二维模型中也没有考虑弹性背散射以及真二次电子发射. 为了更好地评估强辐射环境对具体装置的影响, 本文基于PIC方法, 考虑二次电子发射过程, 建立三维非稳态SGEMP数值模拟模型, 研究各类二次电子发射机制对SGEMP数值模拟结果的影响.

2

-->

2.1.电磁粒子模拟方法

本文关注高能光电子、二次电子的运动以及随之激励出的电磁场响应, 采用PIC方法描述电子的运动^[19], 该方法通常不会跟踪所有实际粒子, 而是用“宏粒子”代表若干相邻的电子, 粒子的位移x和速度v随时间t的变化服从(1)式:

$ \left\{ \begin{aligned}&\frac{{{\rm{d}}{\boldsymbol{x}}}}{{{\rm{d}}t}} = {\boldsymbol{v}}, \\&\frac{{{\rm{d}}(\gamma {m_{\rm{e}}}{\boldsymbol{v}})}}{{{\rm{d}}t}} = q({\boldsymbol{E}} + {\boldsymbol{v}} \times {\boldsymbol{B}}),\end{aligned} \right.$

其中, $\gamma = 1/\sqrt {1 - {{(v/c)}^2}} $为相对论因子, v为粒子速率, c为光速, m_e和q分别为电子的静止质量和电量, E和B分别为电场强度和磁感应强度. 电磁场在空间上基于Yee元胞离散化, 采用时域有限差分法求解如下的Maxwell方程组:

$\left\{ \begin{aligned} &\nabla \times {\boldsymbol{E}} = - \frac{{\partial {\boldsymbol{B}}}}{{\partial t}}, \\ &\nabla \times {\boldsymbol{H}} = \frac{{\partial {\boldsymbol{D}}}}{{\partial t}} + {\boldsymbol{J}} , \end{aligned} \right.$

其中, H, D和J分别为磁场强度、电位移矢量和电流密度. 由初始条件出发, 电磁场的更新和带电粒子的运动交替进行. 通过校正电流连续性方程来满足空间电荷守恒^[19].
2 -->

2.2.二次电子发射

在具有一定能量电子的撞击下, 固体靶表面会通过各种机制发射电子. 本文主要考虑两类二次电子, 分别是真二次电子和背散射电子. 入射电子与固体靶发生非弹性碰撞, 从固体靶中激发出高于其材料功函数的电子, 称这类电子为真二次电子^[20]. 而部分入射电子与靶材经过一次或多次碰撞后会从固体靶表面射出, 这部分电子被称为背散射电子, 背散射电子又可进一步细分为弹性和非弹性背散射电子. 通常, 真二次电子的能量小于50 eV, 背散射电子的能量更高, 其中弹性背散射电子的能量与入射电子相当^[21]. 背散射电子数与入射电子数之比为背散射电子发射系数(反射系数), 真二次电子数与入射电子数之比为真二次电子发射系数. 除了发射系数, 在对二次电子进行建模时, 还需要明确出射二次电子的能谱与角分布.下文将分别对真二次电子和背散射电子的建模进行说明.
3 -->

2.2.1.真二次电子的发射特性

真二次电子发射系数与入射电子能量E_in、角度θ以及固体靶的材料、表面光洁度相关. 对于入射电子能量小于1 keV的情况, 普遍使用Vaughan模型^[22]描述真二次电子发射系数. 在更高的入射电子能量下, 可以利用法向入射真二次电子的发射系数δ₀与入射电子能量的比例关系^[23]((3)式)以及与入射电子角度的关系^[21]((4)式)来近似获得该发射系数. 真二次电子的能谱和角分布设置可以基于Furman与Pivi提出的概率模型^[24]:

$\frac{\delta _0}{E_{\rm in}^{-0.8}} = \frac{\delta _0'}{E_{\rm in}^{\prime-0.8}}, $

$\delta = {\delta _0}\sec \theta .$

3 -->

2.2.2.背散射电子的发射特性

背散射电子发射系数与入射电子能量弱相关^[25], 与入射电子角度、固体靶的材料强相关^[18], 该发射系数可以通过实验测量^[26]或蒙特卡罗模拟^[27]获得. 在数值建模中, 通常使用经验公式来描述背散射电子发射系数, 如Hunger-Küchler公式^[23], 但该公式在入射电子能量小于3.5 keV, 或固体靶材原子序数Z较大时的偏差较高^[28]. 本文结合Staub^[29]的工作, 使用如(5)式所示的法向入射电子的背散射电子发射系数η₀, 该式普遍适用于0.5 keV < E_in < 100 keV, 且Z > 4的情况:

$\left\{ \begin{aligned} & {\eta _0} = {E_{{\rm{in}}}}^{m(Z)}C(Z),\;{E_{{\rm{in}}}} > 30\;{\rm{keV}} ,\\& {\eta _0} = A[1 - \exp ( - 6.6 \times {10^{ - 3}}{A^{ - 2.5}}Z)],\;\\&0.5\;{\rm{keV}} \leqslant {E_{{\rm{in}}}} \leqslant 30\;{\rm{keV}} , \end{aligned} \right. $

其中, 拟合参数 $C(Z) = 0.1904 - 0.2236\ln Z + $$ 0.1292{(\ln Z)^2} - 0.01491{(\ln Z)^3}$, $m(Z) = 0.13182 - $$ 0.9211/{Z^{0.5}}$, $A{\rm{ = }}0.4 + 0.065\ln ({E_{{\rm{in}}}})$, 入射电子能量单位keV. 图1绘出了由(5)式计算出的η₀以及铝、铜、金三种材料背散射电子发射系数的实验数据^[20]. 除E_in = 0.5 keV的电子射入铜制靶面条件下不同实验数据间存在较大差异外, (5)式的计算结果与实验数据均符合得较好.
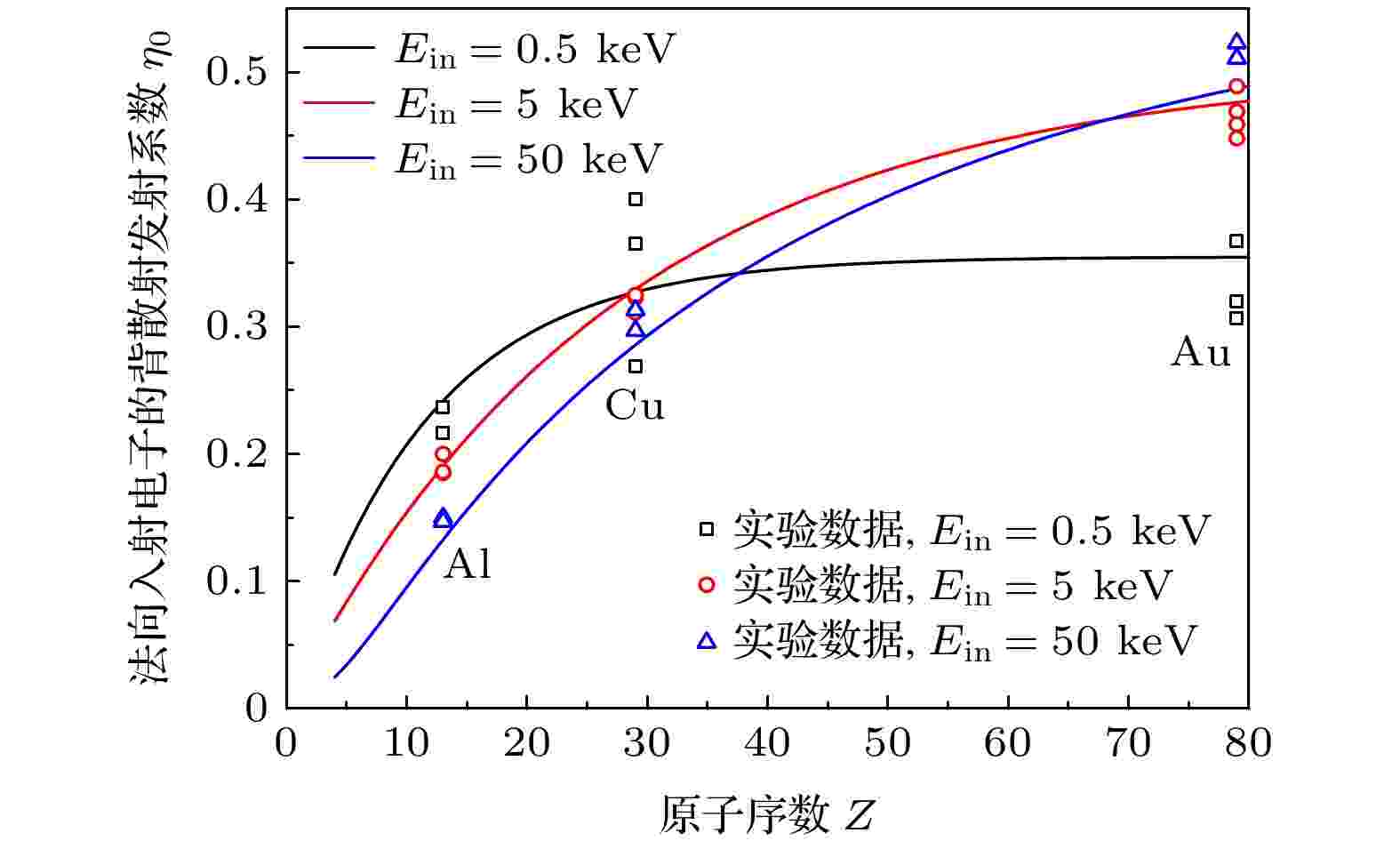图 1 不同原子序数、入射能量条件下, 法向入射电子的背散射电子发射系数(离散点来自Joy^[20]总结的实验数据, 实线由式(5)计算)
Figure1. Backscattering coefficient of normally incident electrons for different E_in and atomic numbers. Symbols, experimental data from Joy^[20]; lines, calculated by Equation (5).

入射电子角度θ [0, π/2]对背散射电子发射系数η的影响可由(6)式描述^[20]:

$\eta {\rm{ = 0}}{\rm{.89(}}{\eta _0}{\rm{/0}}{\rm{.89}}{{\rm{)}}^{\cos \theta }}.$

弹性、非弹性背散射电子的发射系数η_els和η_ine主要与固体的材料相关, Reimer^[20]总结实验数据, 给出非弹性、弹性碰撞截面之比${\sigma _{{\rm{ine}}}}/{\sigma _{{\rm{els}}}} \approx $$ 20/Z$. 可得η_els/η = 1–(η_ine/η) = Z/(Z+20), 即金属材料的原子序数越大, 背散射电子中弹性散射的占比越高.
弹性背散射电子的角分布可按镜面反射处理, 即散射角与入射角关于靶平面的法线对称. 非弹性背散射电子的角分布较为复杂, 是与材料、入射电子能量和入射角均相关的分布函数, 这里进行简化处理^[28], 设置非弹性散射角等于最概然散射角${\theta _{{\rm{inels}}}} = - 27\theta /40$, 式中负号表示散射电子与入射电子分别在法向量两侧. 根据发生散射的类型, 分别设置背散射电子的能量. 弹性背散射电子相较于入射电子基本没有能量损失, 本模型参考刘腊群等^[28]的工作, 统一设置弹性背散射电子的能量比入射电子低20 eV. 而非弹性背散射电子的能量分布函数按照Matsukawa等^[30]实验测量的二次电子能谱分布来赋值, 忽略入射电子能量与入射角度对能量分布函数的影响^[18,23].
2 -->

2.3.计算区域和边界条件

图2为本文涉及的两种典型SGEMP计算模型的示意图. 图2(a)所述模型用于模拟X射线(沿圆柱轴向自右向左均匀射入金属的右侧端面)辐照长度为h, 半径为R的金属圆柱体所激发的腔体外SGEMP. X射线与固体介质相互作用并发射光电子的过程比较复杂^[31]. 本文主要研究二次电子对SGEMP的影响, 因此对端面产生的光电子进行简化处理, 假设其均为单能电子(能量E₀), 运动方向垂直于受辐照面向外^[14,17], 光电子发射面的电流密度J_emi(正比于X射线功率密度与光电产率)在时间上表现为单个脉冲且该脉冲服从正弦平方分布^[13], 如(7)式所示: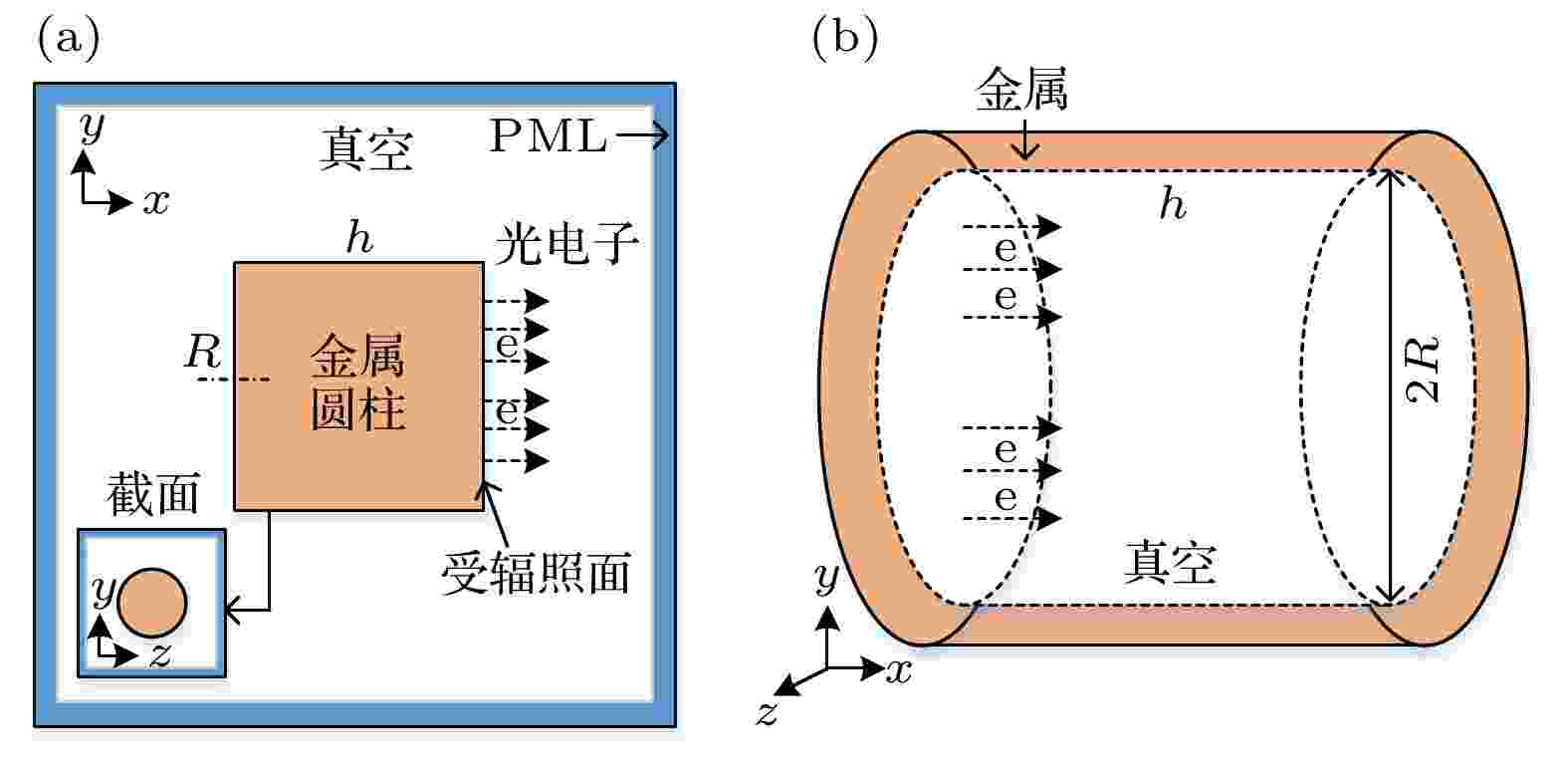
图 2 计算模型示意图　(a)腔体外SGEMP; (b)腔体内SGEMP
Figure2. Schematics of the calculation domain: (a) The external SGEMP; (b) the internal SGEMP.

${J_{{\rm{emi}}}} = {J_0}{\sin ^2}[{\rm{\pi }}t/(2\tau )],$

其中, 峰值电流密度为J₀(A/cm²), τ为时间脉冲的半高宽, 设为1 ns. 图2(b)中的模型用于模拟封闭空心金属腔体的内SGEMP ^[17], 光电子仅由左侧内端面发射, 光电子的发射特性与图2(a)所述模型一致. 本文计算模型的金属圆柱体均为正圆柱, h = 2R = 100 mm.
在每一计算时间步中统计越过金属边界的宏粒子, 认为该宏粒子被金属边界吸收, 计算被吸收宏粒子的能量及入射角, 并按2.2节所述的发射系数释放出若干个二次电子. 电子的产生和在真空区域的运动会激发出电磁场. 假设金属为理想导体, 导体内部电场、边界上的切向电场分量和磁场强度的法向分量为零^[17], 在图2(a)中计算模型的最外侧对电磁场设置理想吸收层边界(perfectly matched layer, PML), 为减小边缘效应, 设置PML边界的空间尺寸为金属圆柱尺寸的3倍^[13]. 计算所用网格的空间尺寸为5 mm, 时间步长10^–12 s, 峰值宏粒子数约为10⁶.

2

-->

3.1.腔体外SGEMP

本节首先研究如图2(a)所示腔体外SGEMP的特性, 受辐照金属圆柱的材料为中等Z值的铜. 图3比较了是否考虑二次电子发射对电子空间分布的影响(图3(a)—图3(c))中包括光电子、背散射电子和真二次电子). 虚线部分表示金属圆柱, 光电子由金属圆柱的右端面向外发射. 光电子发射后会在金属表面留下正电荷, 与光电子共同激发出电场, 当这一电场强度足够高, 光电子会被减速, 导致大量电子聚集在金属表面附近, 形成空间电荷层(space-charge barrier). 一部分光电子无法穿出空间电荷层, 返回金属表面. 不考虑二次电子发射的情况下(如图3(d)), 受空间电荷层作用返回金属表面的光电子被直接吸收. 对比图3(c)与3(d), 可以发现在金属表面, 特别是右侧端面, 产生了相当数量的二次电子.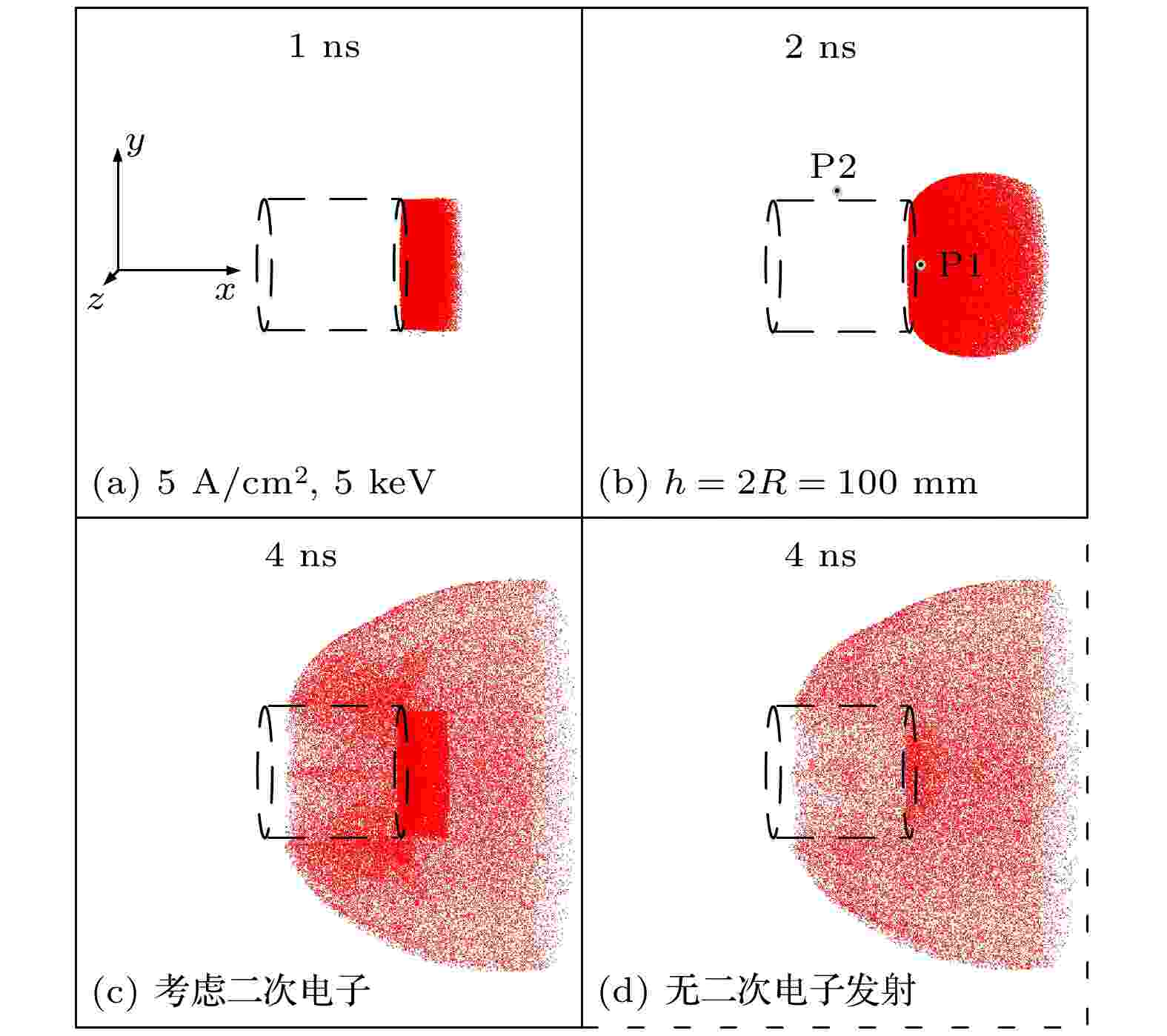
图 3 不同时刻电子的空间分布(J₀ = 5 A/cm², E₀ = 5 keV).　(a)(b)(c)考虑二次电子发射; (d)无二次电子发射的情况
Figure3. Distribution of electrons at different moments on the condition J₀ = 5 A/cm² and E₀ = 5 keV:　(a)(b)(c)Including secondary emission; (d)without secondary electrons.

图4为不同峰值电流密度条件下, 光电子发射面中心P1位置(距右端面5 mm, 如图3(b)所示)的轴向电场强度, 根据在模型中是否考虑了二次电子发射可分别得到图中虚线和实线所示的结果. P1处的轴向电场强度随着时间的延长先快速上升达到峰值, 随后趋于饱和并发生振荡, 最后随着发射光电子数量的降低, 电场强度快速下降至小于$5 \times {10^5}$ V/m. 峰值电流密度升高, 初始阶段轴向电场的上升速率增大, 电场强度的最大值也随之增大. 然而, 电场强度的最大值与峰值电流密度不满足线性关系, 例如, 当峰值电流密度J₀由5 A/cm²上升至100 A/cm², 最大电场强度仅由$9.6 \times {10^5}$ V/m增至$2.2 \times {10^6}$ V/m. 对比是否考虑二次电子条件下的电场强度, 可发现在模型中加入二次电子过程会使饱和阶段计算出来的电场增强约25%—30%, 电场在时间上的半高宽也会增宽约10%—15%. 两模型计算结果出现差异的时刻均在电场强度第一峰值后, 且该时刻随着峰值电流密度的增大而提前, 由5 A/cm²条件下的1.81 ns提前至100 A/cm²时的0.76 ns.
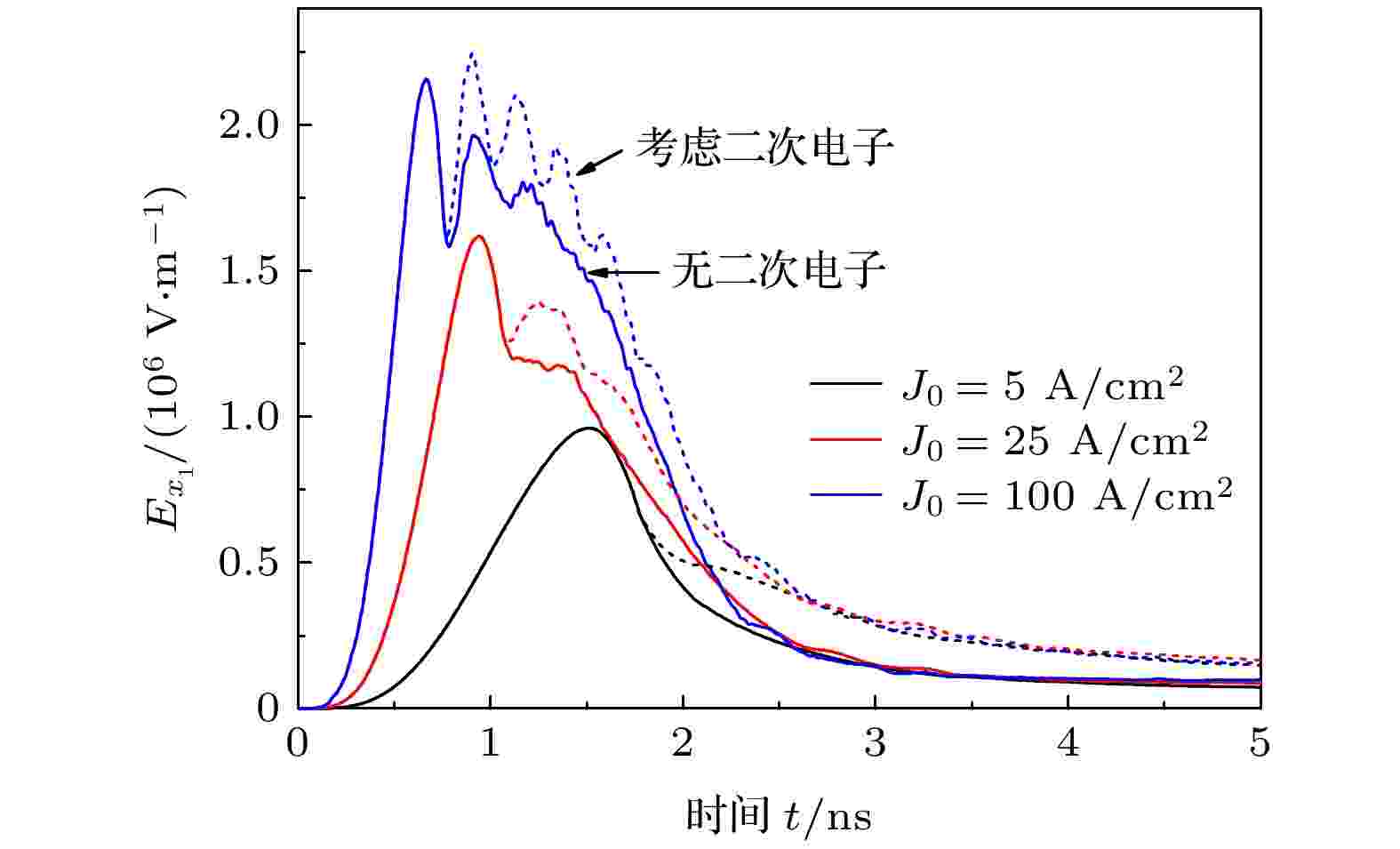图 4 不同峰值电流密度条件下, P1位置的轴向电场强度E_x (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, E₀ = 5 keV)
Figure4. Axial electric field E_x at P1 for different peak current densities (Solid line: not including secondary electrons; dash line: including secondary electrons, E₀ = 5 keV).

如前文所述, 金属在X射线辐照下向外发射光电子并使本身带正电, 发射的光电子数目越多, 电场强度越强, 对应着电场强度在初始阶段的快速上升. 然而, 该电场会阻碍光电子继续向外运动, 当受辐照面附近累计发射的光电子足够多, 空间电荷层内的电场强度升高至使一部分光电子反向运动, 电场强度减弱, 电子返发射面降低了空间电荷层内电子数目, 进一步削弱了电场强度, 随后更多的电子能够进入空间电荷层, 如此反复, 导致了电场的振荡^[32].电荷累积并形成空间电荷层需要一定时间, 对于腔体外SGEMP, 在空间电荷层形成前, 不会有光电子返回金属表面, 也就不会产生二次电子, 所以图4中最初一段时间内考虑二次电子发射不会对电场结果产生影响. 定义电子首次返回发射面的时刻(也即二次电子产生的时刻)为空间电荷层产生的特征时间, 光电子能量越高、电流密度越小, 特征时间越长^[14].
图5给出了不同峰值电流密度下, 圆柱侧面中点P2处的径向电场强度. 相比于P1, P2位置电场强度受二次电子的影响更为显著, 特别是对于峰值电流密度较强的情况. 如J₀ = 100 A/cm², t = 3 ns, 考虑二次电子时的径向电场强度为$1.93 \times $$ {10^5}$ V/m, 约为不考虑二次电子条件下的1.8倍. 由于P1点位于金属受辐照面附近, 其电场强度直接受高能光电子特性以及空间电荷层的影响, 而P2位置几乎没有光电子, 光电子以及二次电子主要通过改变金属的电荷分布来间接影响P2位置的电场. 在持续的时间上, 考虑二次电子也会使算得的电场强度出现明显的拖尾现象. 图中还给出了在计算模型中仅考虑二次电子里的背散射电子, 忽略真二次电子的仿真结果. 对于能量5 keV的电子撞击铜靶面的情况, 真二次电子发射系数略高于背散射电子发射系数, 但真二次电子对计算出的电场强度差异的贡献仅为背散射电子的1/5左右. 这主要是因为真二次电子的能量远低于背散射电子, 受金属表面电场的作用, 大部分真二次电子在产生后又迅速被金属吸收, 所以对电场响应的贡献有限.
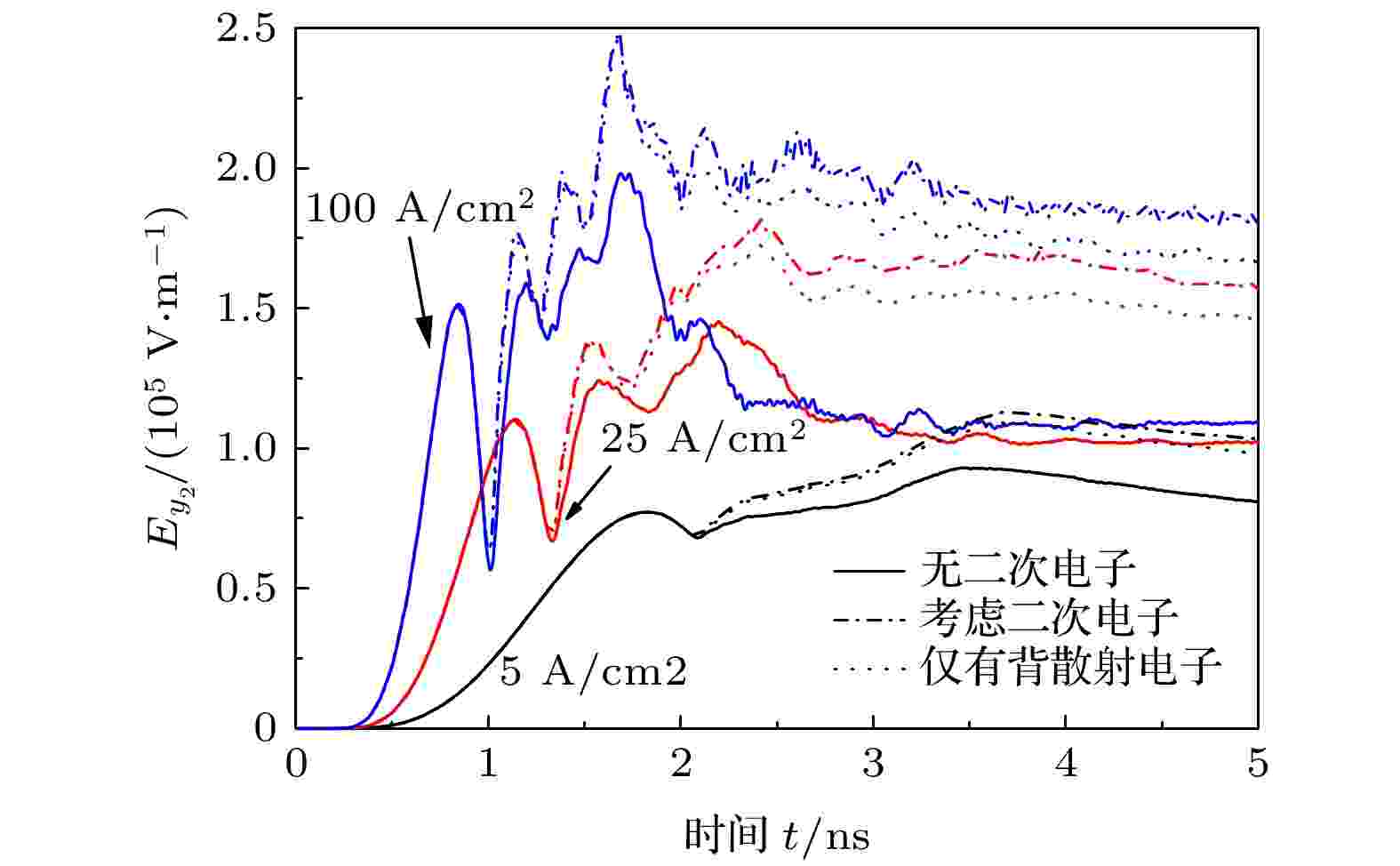图 5 不同峰值电流密度条件下, P2位置的径向电场强度E_y (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, 点线: 仅考虑背散射电子, E₀ = 5 keV)
Figure5. Radial electric field E_y at P2 for different peak current densities (Solid line: not including secondary electrons; dash line: including secondary electrons; dot line: only considering backscattering electrons, E₀ = 5 keV).

图6对比了峰值电流密度5和100 A/cm²条件下, P2位置切向磁感应强度B_z. 空间磁场的分布主要受金属导体上电荷重新分布时产生的置换电流影响, 峰值电流密度越大, 磁感应强度的极值越大, 但受空间电荷层的限制, 磁感应强度的极值与峰值电流密度之间也不满足线性关系. J₀ = 5 A/cm², 空间电荷效应弱, 光电子返回金属表面所产生的二次电子较少, 对置换电流的影响也较低, 是否考虑二次电子发射对计算出的磁场基本没有影响. 提高峰值电流密度至100 A/cm², 空间电荷效应增强, 磁感应强度会表现出明显的振荡, 振荡频率约为3.5 GHz.考虑二次电子使B_z第二负峰的幅值由$1.3 \times {10^{ - 4}}$ T增至$2.0 \times {10^{ - 4}}$ T, 磁场的振荡频率也略微升高.
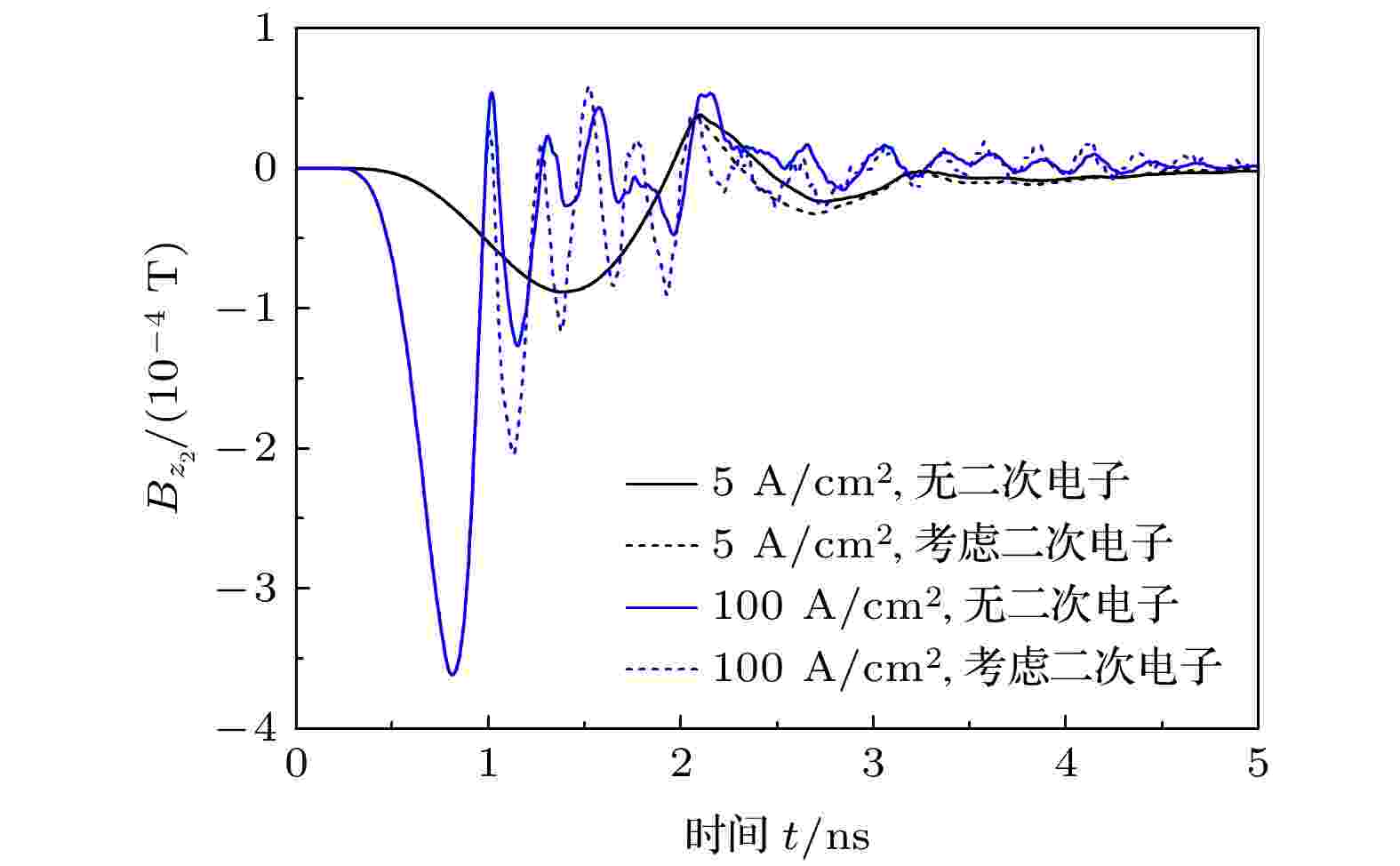图 6 在J₀ = 5, 100 A/cm²条件下, P2位置的磁感应强度B_Z (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, E₀ = 5 keV)
Figure6. Magnetic field B_Z at P2 for J₀ = 5, 100 A/cm² (Solid line: not including secondary electrons; dash line: including secondary electrons, E₀ = 5 keV)

2 -->

3.2.腔体内SGEMP

不同于3.1节的腔体外SGEMP, 本节研究的腔体内SGEMP, 其光电子的发射面在金属腔体内部, 特别是对于封闭金属腔体, 所有光电子都会撞击到腔体表面, 并按一定概率产生二次电子. 图7比较了不同腔体材料对P1位置(圆柱腔体末端中心点)轴向电场强度的影响. 考虑二次电子发射后, E_x1出现谷值的时刻由2.19 ns后移至约3.55 ns, 幅值由$7.56 \times {10^4}$ V/m增大至Al腔体下的$1.52 \times {10^5}$ V/m、Au腔体的$2.75 \times {10^5}$ V/m, 分别为未考虑二次电子条件下的2.01倍、3.64倍. Cu腔体条件下的电场强度变化介于Al和Au之间, 约为无二次电子条件下的2.84倍. 不同材料条件下电场的脉冲宽度都发生了加宽. 图7还给出了Cu制腔体、仅考虑背散射电子条件下的计算结果, 可以发现, 真二次电子导致E_x1差异的占比随着时间延长而逐渐增大, 5 ns时, 约为考虑二次电子导致电场总差异的24%.
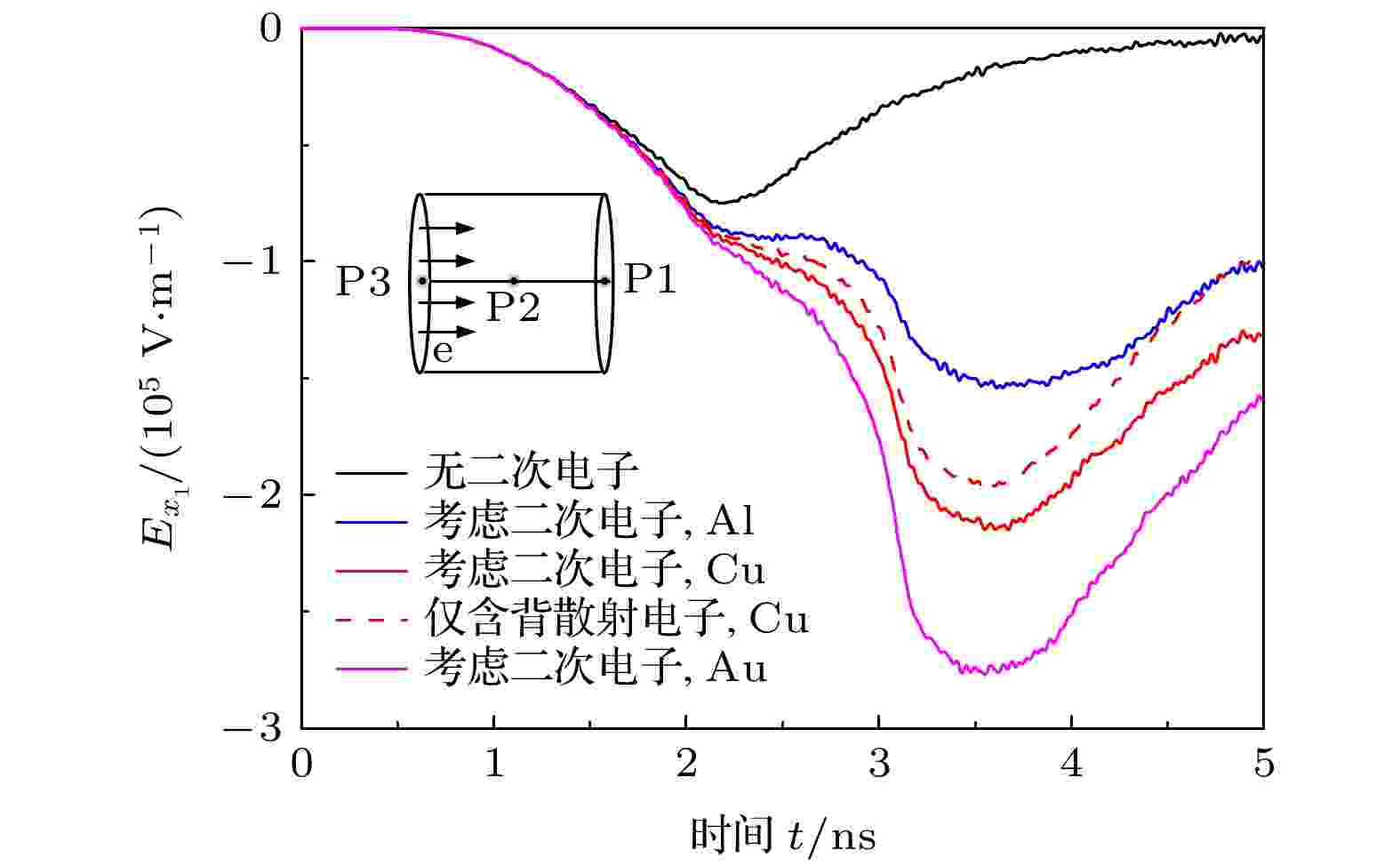图 7 不同腔体材料, P1位置的轴向电场强度E_x(J₀ = 1 A/cm², E₀ = 5 keV)
Figure7. Axial electric field E_x at P1 for different materials (J₀ = 1 A/cm², E₀ = 5 keV).

图7的结果表明, 在各类二次电子中, 背散射电子对内SGEMP的影响最为重要. 在约3.5 ns后, 真二次电子导致的电场差异占比随时间延长逐渐增大, 主要是因为金属表面的电场幅值降低, 受该电场作用返回金属表面的真二次电子数减小. 腔体所用金属材料的原子序数越高, 背散射电子发射系数就越大, 同时, 非弹性背散射电子能谱的峰值也向更高能量区域移动, 共同导致了高Z材料下算得电场强度差异的增大.
图8给出了光电子发射面中心P3 (距左侧端面5 mm)、轴向中点P2以及末端面中点P1 (距右侧端面5 mm)三点的电场强度. 可以发现, 二次电子发射对腔体内不同位置电场都有显著影响, 如P3处电场的半高宽增加了11%(Al)—57%(Au).然而, P3处电场强度的幅值没有发生显著变化, 仅增大了约4%, 远小于P1位置电场强度的变化. 这主要是由于在较低的电流密度下(J₀ = 1 A/cm²), 光电子发射面附近累积的电子数目太少, 空间电荷限制效应较弱, 穿过空间电荷层并撞击到腔体末端面的光电子占主导, 导致末端面二次电子发射数目大于光电子发射面附近的二次电子数, 所以P1处电场幅值的变化更大.
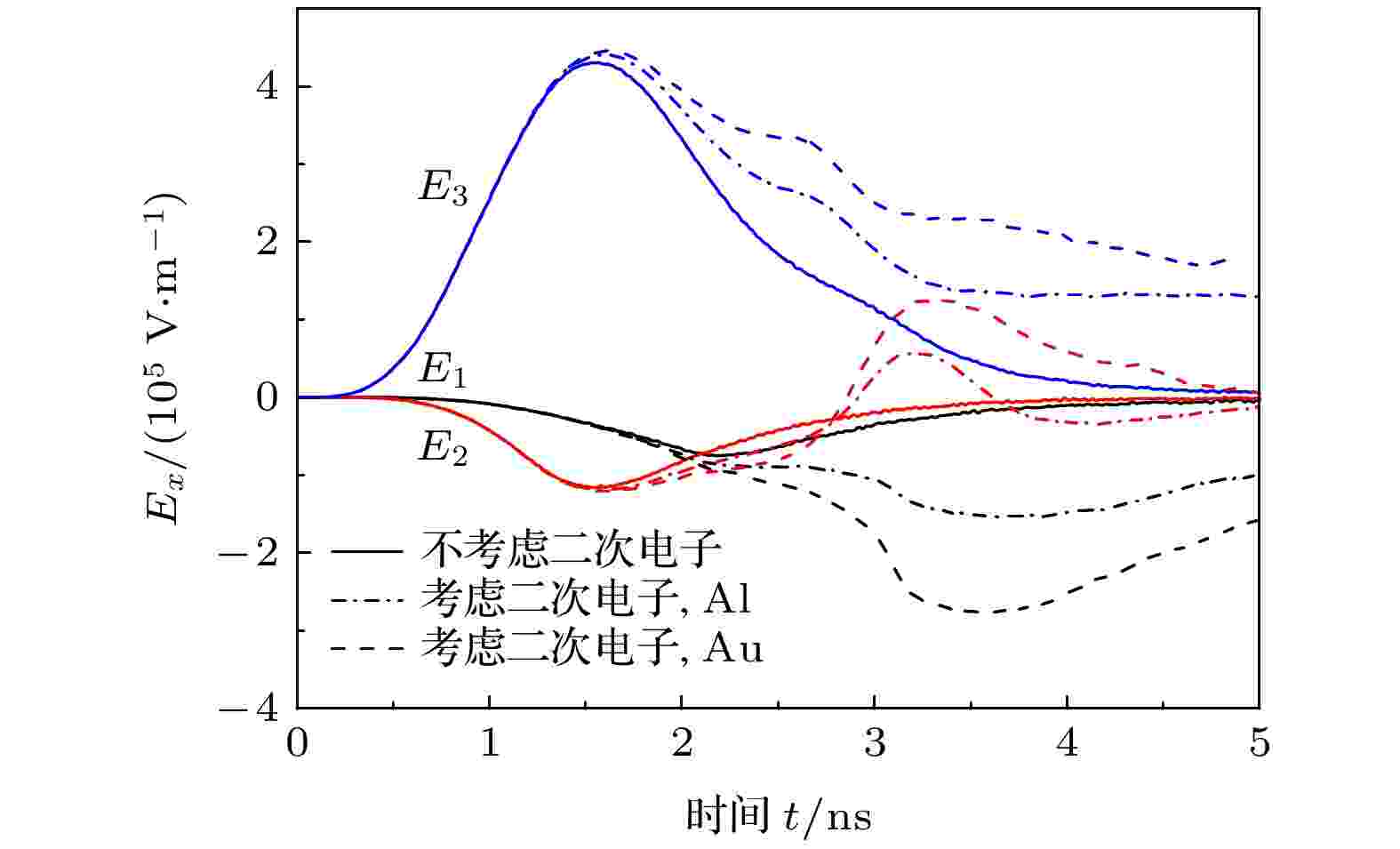图 8 不同位置(P1, P2, P3)的轴向电场强度E_x (J₀ = 1 A/cm², E₀ = 5 keV)
Figure8. Axial electric field E_x at P1, P2 and P3 (J₀ = 1 A/cm², E₀ = 5 keV).

不同峰值电流密度下, 腔体末端P1点的轴向电场强度如图9所示. 在发射面的峰值电流密度(对应X射线注量)很低时, 如J₀ = 0.1 A/cm², 空间电荷效应极弱, 考虑二次电子发射就会使模拟得到的电场强度峰值增大约0.6倍. 增大发射面的峰值电流密度至J₀ = 5 A/cm², 空间电荷效应显著增强, 无二次电子条件下P1处的电场强度发生振荡. 打到腔体末端面的光电子数量在较强的空间电荷限制作用下减少, 但考虑二次电子发射后, J₀ = 5 A/cm²条件下算得的电场强度幅值仍为无二次电子条件下的3倍左右. 在金属腔体中, 为保证导体为等势体, 腔体的电荷需要重新分布从而影响整个腔体内部的电磁场分布, 二次电子在这里主要是通过增大金属导体上的电荷数来影响腔体末端的电场强度. P3处的轴向电场强度随电流密度的变化与图4中所示腔体外SGEMP在发射面附近的变化规律类似, 这里不再给出.
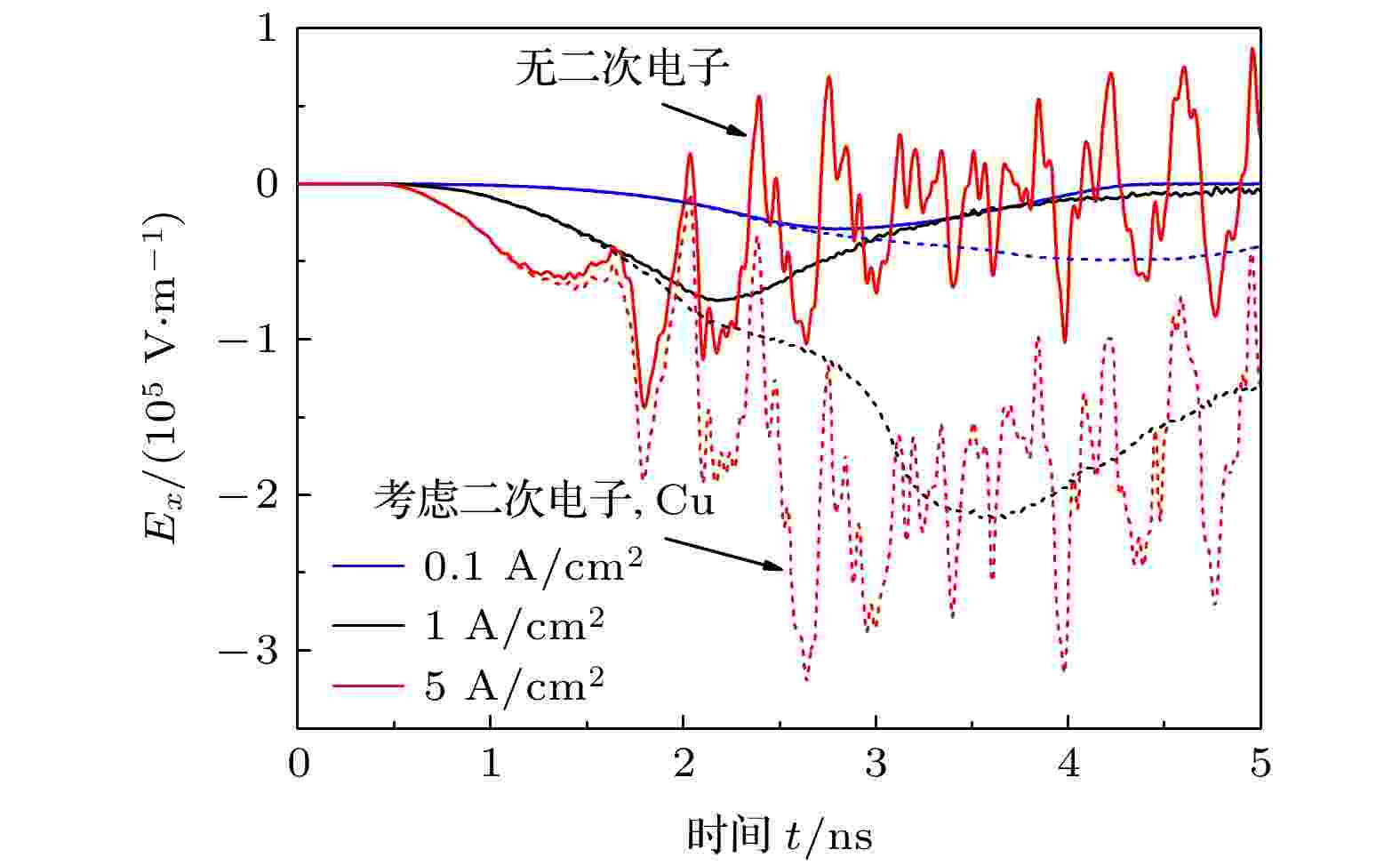图 9 不同峰值电流密度下, P1位置的轴向电场强度E_x (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, E₀ = 5 keV)
Figure9. Axial electric field E_x at P1 for different peak current densities (Solid line: not including secondary electrons; dash line: including secondary electrons, E₀ = 5 keV).

图10给出了不同初始光电子能量E₀下, P1处的电场强度(Cu腔体). 不同电子能量下, 考虑二次电子发射都会使P1位置算得电场的极值增大一倍以上. 这是因为光电子能量越高, 空间电荷效应越弱, 光电子更容易打到末端面, 且其运动速度更快, 所以两计算模型中电场强度表现出差异的时刻越早, 由5 keV时的1.46 ns提前至50 keV的1.06 ns. 而是否考虑二次电子发射条件下, 计算出的E_x1谷值时刻之差也由5 keV的1.41 ns缩短至50 keV的0.46 ns.这是因为测量点P1距金属腔体右端面仍有一定距离(5 mm), 无二次电子条件下, 电场谷值时刻对应大量光电子到达P1的时刻; 考虑二次电子时, 谷值时刻由向右运动的光电子与向左发射的二次电子共同决定. 二次电子的作用又主要由背散射电子体现, 由于高入射电子能量下背散射电子的平均能量更高, 背散射电子由右侧端面运动到P1位置所需时间更短, 谷值出现时刻之差也越小.
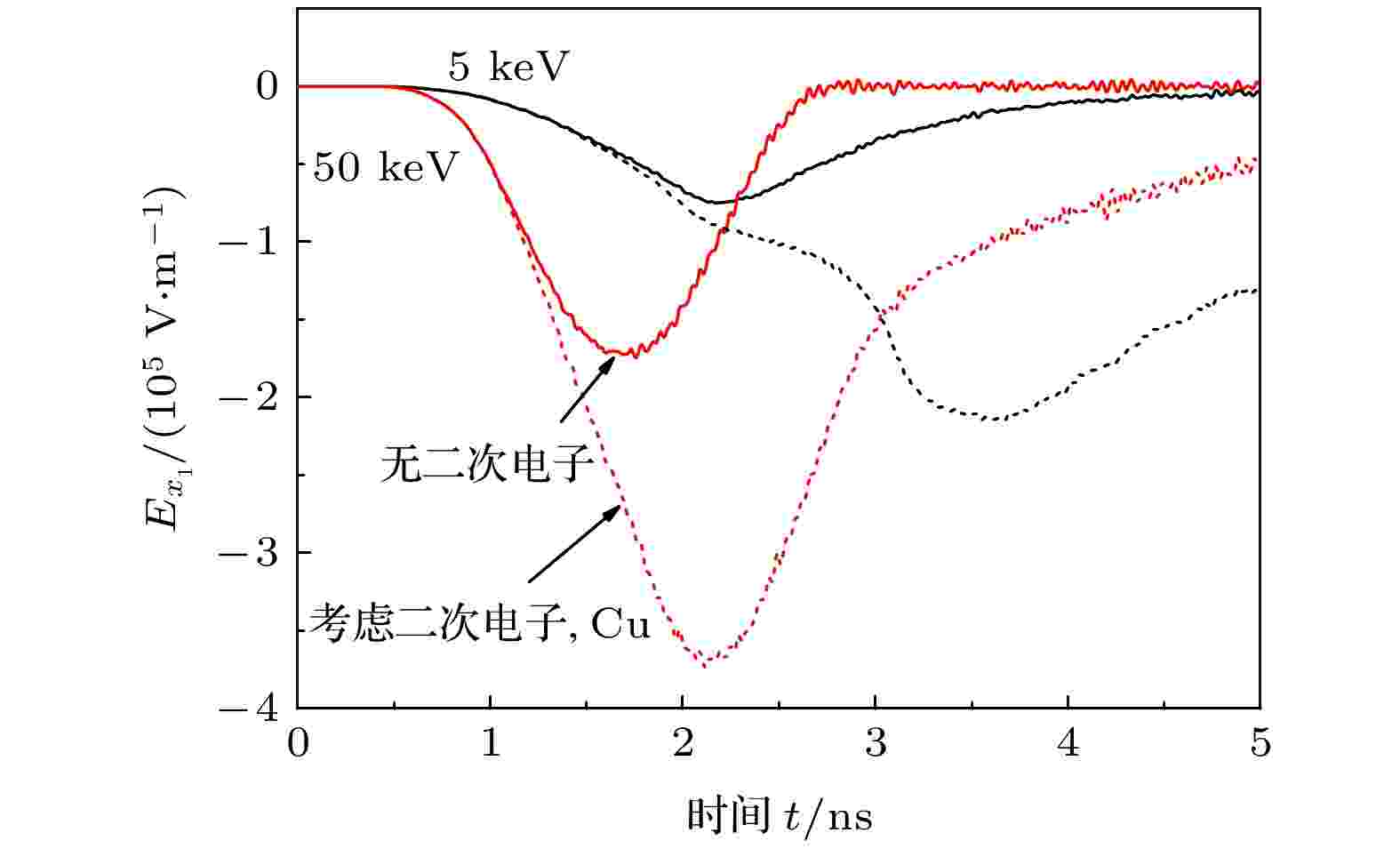图 10 E₀ = 5 keV与E₀ = 50 keV条件下, P1位置的轴向电场强度E_x(J₀ = 1 A/cm²)
Figure10. Axial electric field E_x at P1 for E₀ = 5 keV and E₀ = 50 keV (J₀ = 1 A/cm²).

为了研究二次电子发射对SGEMP数值模拟结果的影响, 本文较为全面地考虑了电子–金属相互作用产生二次电子的物理过程, 实现了基于PIC方法的三维非稳态SGEMP数值模拟.针对圆柱腔体外部、内部两种典型结构下的SGEMP, 计算并比较了不同电流密度、初始光电子能量以及金属材料条件下的电磁场响应, 主要结论如下:
1)在数值模拟中忽略二次电子发射会导致对电场、磁场强度的低估, 对于非受辐照面, 峰值电场强度会被低估2—3倍, 响应的时间宽度也会被低估10%以上.
2)在各类二次电子中, 背散射电子对SGEMP的影响占主导, 真二次电子对电场强度差异的贡献约为背散射电子的1/5. 构成系统的金属材料的原子序数越高, 二次电子发射对电磁场响应的影响越大.
3)受结构影响, 对于腔体外SGEMP, 仅有高X射线注量, 空间电荷效应较强时, 二次电子才会对电磁场响应产生影响, 而在较低的辐照注量下, 腔体内SGEMP受二次电子发射的影响就较为显著.