摘要: 发展了利用两对拉曼光之间的相对相位精确调控拉曼耦合强度的新方法, 实现了两个量子态相干跃迁的操控. 对两对拉曼光的光路进行了特殊设计, 从而保证两对拉曼激光在传输过程中的相对相位保持恒定, 然后作用到
87 Rb原子的两个超精细塞曼能级
$\left| {1,1} \right\rangle $ 和
$\left| {1,0} \right\rangle $ 上, 实验观测了两个量子态的布居数随两对拉曼光之间的相对相位的变化关系. 该方法为超冷原子量子模拟实验提供了一个独特的操控参量——激光相位, 由此拓展了受激拉曼跃迁的应用范围, 为研究光与原子相互作用提供了一种新的方法.
关键词: 受激拉曼跃迁 /
激光相位 /
拉曼耦合强度 /
三能级原子系统 English Abstract Experimental study of coherent manipulation in 87 Rb Bose-Einstein condensate with phase difference of double stimulated Raman adiabatic passage Zhou Fang 1,2 ,Wen Kai 1,2 ,Wang Liang-Wei 1,2 ,Liu Fang-De 1,2 ,Han Wei 1,2 ,Wang Peng-Jun 1,2 ,Huang Liang-Hui 1,2 ,Chen Liang-Chao 1,2 ,Meng Zeng-Ming 1,2 ,Zhang Jing 1,2 1.State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Key Research and Development Program of China (Grant Nos. 2016YFA0301602, 2018YFA0307601) and the National Natural Science Foundation of China (Grant Nos. 11804203, 12004229)Received Date: 25 January 2021Accepted Date: 29 March 2021Available Online: 07 June 2021Published Online: 05 August 2021Abstract: In this paper, we develop a new method to adjust the Raman coupling strength by using the relative phase between two pairs of Raman lasers. The stimulated Raman transition process is highly controllable and has the characteristics of multiple degrees of freedom. In experiments on ultracold atoms, the populations of atomic energy levels can be adjusted by taking an appropriate Raman light intensity and interaction time, and by detuning the two-photon frequency. The intensity of the Raman laser is usually changed to adjust the Raman coupling strength. Based on two-level atoms, a new method of accurately controlling the Raman coupling strength by using the relative phase between two pairs of Raman light beams is developed. This technology can achieve coherent manipulation of atomic quantum states, which greatly broadens the ability of ultracold atoms to perform quantum simulations. First, the 87 Rb Bose-Einstein condensate is realized by using an optical dipole trap. Then, the two pairs of Raman lasers are designed with a special optical path to keep the relative phase of the two pairs of Raman lasers stable in the transmission process, and can be controlled accurately. Then the two pairs of Raman light beams act on the two ground state hyperfine energy levels $ |1, 1\rangle $ and $ |1, 0\rangle $ of the 87 Rb atom. In the experiment, we observe the relation between the percentage of atoms in the two quantum states and the relative phase between the two pairs of Raman light beams. This method provides a unique control parameter for ultracold atom quantum simulation experiments, which is the laser phase. It is hoped that this technology can be used to manipulate the interaction between light and atoms in the future to achieve more abundant physical phenomena.Keywords: stimulated Raman transition /laser phase /Raman coupling strength /three-level atomic system 全文HTML --> --> --> 1.引 言 受激拉曼跃迁过程具有高度人为可控、多自由度的特性, 通过控制激光的功率、频率、相位和原子能级构型等可实现受激拉曼跃迁的精确调控[1 ] . 该技术可实现原子量子态的相干操控, 而不受自发辐射的影响, 因此该方法在物理和化学等许多领域得到了广泛应用[2 ] , 如: 物质波原子干涉仪[3 ,4 ] 、拉曼冷却[5 -8 ] 、量子比特操控[9 ,10 ] 、量子精密测量[11 ,12 ] 、量子存储[13 ] 、手性分子[14 ,15 ] 等.[16 -18 ] 、人造磁场[19 ] 、自旋-轨道耦合[20 -22 ] 以及人造维度[23 ] 等, 这极大地拓宽了超冷原子进行量子模拟的能力. 激光的相位信息在光与原子耦合方面扮演非常重要的角色. 通过控制激光的相位信息可实现对各种新奇的拓扑量子态和拓扑量子相变的操控, 例如: 实现人造垂直塞曼磁场操控狄拉克点处的拓扑能隙[24 ] 、通过调节激光相位实现一维和二维自旋-轨道耦合之间的转变[25 ] 、利用拉曼激光的拉盖尔-高斯轨道角动量实现原子的自旋与轨道角动量耦合[26 ] 等.87 Rb原子玻色-爱因斯坦凝聚体, 对两对拉曼激光进行了特殊的光路设计, 使两对拉曼激光在传输过程中相对相位保持稳定, 并可以精确调控, 然后作用到87 Rb原子的两个超精细塞曼能级$\left| {F = 1, {m_{\rm{F}}} = 1} \right\rangle $ 和$ \left| {F = 1, {m_{\rm{F}}} = 0} \right\rangle $ 上. 测量了两个量子态的布居数随两对拉曼光之间的相对相位的变化关系. 该技术拓展了受激拉曼跃迁的应用范围, 为研究光与原子相互作用提供了一种新的方法.2.理论模型 情况1 单受激拉曼过程图1(a) 为一个简单的三能级原子系统, 其中$\left| {{g_1}} \right\rangle $ 和$\left| {{g_2}} \right\rangle $ 为原子的两个基态, $ \left|e\right\rangle $ 为原子的激发态, 原子初始全部处于基态$\left| {{g_1}} \right\rangle $ , 利用一对同向传播、频率分别为$ {\omega }_{1}, {\omega }_{2} $ 的红失谐拉曼光(Raman 1, 2)作用于该三能级原子系统, 由此实现原子在基态之间的拉曼跃迁. $ {\omega }_{01} $ 和$ {\omega }_{02} $ 为原子共振跃迁频率, 两束激光的单光子失谐为: ${\varDelta _{\rm{1}}} = {\omega _{{\rm{01}}}} - {\omega _{\rm{1}}}$ , ${\varDelta _{\rm{2}}} = $ $ {\omega _{{\rm{02}}}} - {\omega _{\rm{2}}}$ . 两束激光的相位为: ${\varphi _1} = {{\boldsymbol{k}}_1} \cdot {\boldsymbol{r}} + {\varphi _{{\rm{ext}}}}$ , ${\varphi _2} = {{\boldsymbol{k}}_2} \cdot {\boldsymbol{r}}$ , 其中$ {\boldsymbol{k}}_{\mathrm{1, 2}} $ 为激光的波矢; $ {\boldsymbol{r}} $ 为空间坐标; $ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ 为外加的相位.图 1 (a)单受激拉曼跃迁过程; (b)双受激拉曼跃迁过程Figure1. (a) Energy levels and stimulated Raman transitions by using two Raman lasers; (b) energy levels and double stimulated Raman transitions by using four Raman lasers.$ {A}_{1} $ , $ {A}_{2} $ 和$ {A}_{3} $ 是各个量子态的分量; 有效哈密顿量写为${\varOmega _\alpha } = - {{\left\langle {{g_\alpha }} \right|{{\hat \varepsilon }_\alpha } * {\boldsymbol{d}}\left| e \right\rangle {E_{0\alpha }}}}/{\hbar }$ , 为拉比频率, 其中$ \alpha =\mathrm{1, 2} $ , 代表两个基态能级. $ {\varOmega }_{\alpha } $ 描述了原子从基态$\left| {{g_\alpha }} \right\rangle $ 通过拉曼激光$ {E}_{0\alpha } $ 跃迁到激发态$ \left|e\right\rangle $ 的耦合强度. p 为原子的动量, m 为原子质量.$ {A}_{3} $ ), 由此将三能级系统简化为二能级系统, 体系的有效哈密顿量可以写为${\delta _\alpha } = \hbar \left( {{\varDelta _\alpha }{\rm{ + }}{\omega _{{\rm{AC}}\alpha }}} \right)$ , AC Stark频移为${\omega _{{\rm{AC}}\alpha }} = $ $ {{{\varOmega _\alpha ^2}}}/({{{\rm{4}}\varDelta }})$ , 频率失谐为$\varDelta = ({\varDelta _1} + {\varDelta _2})/2$ ; 拉比频率为${\varOmega _{\rm{R}}} = {{{\varOmega _{\rm{1}}}{\varOmega _{\rm{2}}}}}/({{{\rm{2}}\varDelta }})$ .$\Delta \varphi = {\varphi _1} - {\varphi _2} = ({{\boldsymbol{k}}_1} - {{\boldsymbol{k}}_2}) \cdot {\boldsymbol{r}} + $ $ {\varphi _{{\rm{ext}}}} \approx {\varphi _{{\rm{ext}}}}$ . 利用幺正变换可消除拉曼光相位差$ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ , 有效的哈密顿量为[27 ] 5 )式中幺正矩阵为 ${\boldsymbol{U}} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{{{\rm{e}}^{{\rm{i}}{\varphi _{{\rm{ext}}}}}}} \end{array}} \right)$ .图2(a) 为原子在基态$ \left|{g}_{2}\right\rangle $ 的布居数与相位差$ \varDelta \varphi $ 的关系图, 可以清晰地看出, 原子的跃迁不受拉曼激光相位差的影响.图 2 原子在$\left| {{g_2}} \right\rangle $ 态的布居数分布与拉曼光相位差的关系 (a)单受激拉曼过程; (b)双受激拉曼过程Figure2. Relationship between the population in $\left| {{g_2}} \right\rangle $ and the phase difference of Raman laser: (a) Single stimulated Raman transitions; (b) double stimulated Raman transitions.情况2 双受激拉曼过程$ {\omega }_{3},\; {\omega }_{4} $ , 相位为${\varphi _3} = {{\boldsymbol{k}}_3}{{\boldsymbol{r}}_{}}$ , ${\varphi _4} = {{\boldsymbol{k}}_4}{{\boldsymbol{r}}_{}}$ , 失谐为${\varDelta _{\rm{3}}} = {\omega _{{\rm{01}}}} - {\omega _{\rm{3}}}$ , ${\varDelta _{\rm{4}}} = {\omega _{{\rm{02}}}} - {\omega _{\rm{4}}}$ , 见图1(b) , 此时系统的有效哈密顿方程可以写为${\delta _\alpha } = \hbar \left( {{\varDelta _\alpha }{\rm{ + }}{\omega _{{\rm{AC}}\alpha }}} \right)$ , $ \alpha =1, 2, 3, 4 $ , 其余参数与情况1类似.$\Delta \varphi = $ $ ( {\varphi _1} - {\varphi _2} ) - \left( {{\varphi _3} - {\varphi _4}} \right) = ({{\boldsymbol{k}}_1} - {{\boldsymbol{k}}_2}) \cdot {\boldsymbol{r}} + {\varphi _{{\rm{ext}}}} - ({{\boldsymbol{k}}_3} - {{\boldsymbol{k}}_4}) \cdot {\boldsymbol{r}} \approx $ ${\varphi _{{\rm{ext}}}} $ . 在这种情况下, 利用幺正变换可得有效的哈密顿量为7 )式中幺正矩阵为${\varOmega _{\rm{R}}} = {\varOmega '_{\rm{R}}}$ , (7 )式可简化为图2(b) , 可以清晰地看出, 当两对拉曼激光同时作用原子时, 它们之间的相对相位差$ \Delta \varphi $ 可以调控原子在基态$\left| {{g_2}} \right\rangle $ 的布居数. 由此说明在双受激拉曼过程中, 两对拉曼光之间的相对相位差发挥着非常重要的角色, 在实验中需要设计恒定的光路, 从而避免额外的相对相位抖动影响拉曼耦合过程.3.实验过程 图3 为产生拉曼激光的实验光路图, 为了获得两对拉曼激光, 利用两台可调谐钛宝石激光器1和2、两个声光调制器(acoustic optical modulator, AOM)、两个功率分配器(power splitter, PS)和一台四通道信号源. 信号源的1, 2端口分别输出频率为f 1 = 76 MHz和f 2 = 98.305 MHz的射频信号, 将两路信号接到PS的两个输入端口, 然后将PS的输出接到AOM的射频输入端. 钛宝石激光器1产生一束红失谐的激光, 频率为f C = 384.0000 THz, 然后将其注入到AOM中, 由此产生一对空间分离的+1级的拉曼激光: Raman 1, 2. 通过类似的办法, 钛宝石激光器2产生一束蓝失谐的激光, 频率为f S = 384.2484 THz, 通过AOM后就可以得到+1级的另一对拉曼激光: Raman 3, 4. 两对拉曼激光的频率与87 Rb原子超精细能级分裂的对应关系见图4 .图 3 实验光路图Figure3. Experimental optical diagram.图 4 三能级87 Rb原子系统中的拉曼跃迁示意图Figure4. Schematic diagram of Raman transitions in three level 87 Rb atomic system.$ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ 加载到激光Raman 1上($ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}}\in \left[-2\mathrm{\pi }, 2\mathrm{\pi }\right] $ ), 在情况1和2中, 通过调节射频相位$ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ 即可实现调控一对或两对拉曼光之间的相对相位, 进而研究相对相位与原子拉曼耦合强度的对应关系.z 轴, 详细的光路设计见图3 .87 Rb原子进行预冷却, 当87 Rb原子温度到达5 μK时, 将预冷却的原子样品绝热装载到光学偶极阱中, 光学偶极阱是由两束波长为1064 nm的红外激光在x -y 平面90°交叉构成, 两束激光频率相差10 MHz, 在原子云处的腰斑直径大约为200 μm, 最终通过光阱蒸发冷却实现87 Rb原子的玻色-爱因斯坦凝聚体, 原子总数约为$ {10}^{5} $ 个, 全部处于$ \left| {{\rm{2, 2}}} \right\rangle $ 态. 然后微波将所有原子绝热转移至$ \left|\mathrm{1, 1}\right\rangle $ 态, 此时原子处于z 方向的磁场中, 对应$ \left| {{\rm{1}}, {\rm{1}}} \right\rangle $ 和$ \left| {{\rm{1, 0}}} \right\rangle $ 的塞曼能级分裂为22.305 MHz, 见图4 , 自此完成了原子的初始制备过程. 为了研究单双受激拉曼过程中拉曼光之间的相对相位是如何操控原子的拉曼耦合强度, 需要将实验过程分为三步: 第一步, 沿着$ x $ 方向输出12 μs的$ \mathrm{\pi }/2 $ 脉冲(红失谐的Raman 1, 2), 其偏振相互垂直, 两束光频差与塞曼能级分裂相同, 最后利用自由飞行展开(time of flight, TOF)测量原子数, 通过调节光强, 让原子经历12 μs的$ \mathrm{\pi }/2 $ 拉曼跃迁后, $ \left| {{\rm{1}}, {\rm{1}}} \right\rangle $ 和$ \left| {{\rm{1, 0}}} \right\rangle $ 布居数各占50%; 第二步, 方法类似于第一步, 沿着$ x $ 方向输出12 μs的$ \mathrm{\pi }/2 $ 脉冲(蓝失谐的Raman 3, 4), 其偏振相互垂直, 通过调节光强, 使其作用后原子在$ \left| {{\rm{1}}, {\rm{1}}} \right\rangle $ 和$ \left| {{\rm{1, 0}}} \right\rangle $ 布居数也各占50%; 第三步, 同时输出12 μs的$ \mathrm{\pi }/2 $ 脉冲(Raman 1, 2和3, 4), 通过调节Raman 1的相位, 利用TOF测量原子在$ \left| {{\rm{1}}, {\rm{1}}} \right\rangle $ 和$ \left| {{\rm{1, 0}}} \right\rangle $ 的布居数比值, 观察拉曼光之间的相对相位与拉曼耦合强度的对应关系.4.实验结果和分析 情况1 单受激拉曼过程$ \mathrm{\pi }/2 $ 脉冲的拉曼光Raman 1, 2实现单受激拉曼过程, 见图3 , 通过改变Raman 1的射频场的相位$ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ 测量原子在$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 态的布居数分布, 见图5 , 可以看到一对拉曼光之间的相位差对拉曼跃迁没有影响, 处于量子态$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 的原子布居数始终为50%.图 5 量子态$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 的布居数随一对拉曼光之间的相位差的关系图Figure5. Measure the population in $ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ as a function of phase difference of two Raman lasers.情况2 双受激拉曼过程图3 , 其中钛宝石激光器1输出激光频率为: $ {f}_{\mathrm{C}}=384.0000\;\mathrm{T}\mathrm{H}\mathrm{z} $ , 钛宝石激光器2输出激光频率为: $ {f}_{\mathrm{S}}=384.2484\mathrm{T}\mathrm{H}\mathrm{z} $ , 通过相应的AOM移频后, 便可以实现双受激拉曼跃迁过程. 在这种频率状态下, Raman 1, 2和3, 4之间的相对相位为$\Delta \varphi = {\varphi '_{{\rm{initial}}}} + {\varphi _{{\rm{ext}}}}$ , $\varphi '_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}$ 为相对相位的初始相位差. 通过改变相对相位$ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ 测得图6 的红色实线(红色虚线为理论拟合的结果, 得: $\varphi '_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}=-0.157\mathrm{\pi }$ ), 图中横坐标为两对拉曼光的相对相位(即: 射频1的相位), 纵坐标为原子处于$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 量子态占总量子态布居数的比例, 可以看出, 通过改变两对拉曼光的相对相位可以控制原子的受激拉曼耦合强度.图 6 实验测量量子态$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 的布居数随两对拉曼光间的相对相位的变化关系. 红色实线使用的钛宝石激光器1, 2输出频率分别为: $ {f}_{\mathrm{C}}=384.0000\;\mathrm{T}\mathrm{H}\mathrm{z} $ , $ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ , 红色虚线为理论计算图. 蓝色实线使用的钛宝石激光器1, 2输出频率分别为: $ {f}_{\mathrm{C}}=383.7652\;\mathrm{T}\mathrm{H}\mathrm{z} $ , $ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ , 蓝色虚线为理论计算图Figure6. Measure the population in $ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ as a function of phase of four Raman lasers. The red solid line: $ {f}_{\mathrm{C}}=384.0000\;\mathrm{T}\mathrm{H}\mathrm{z} $ , $ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ . The blue solid line: $ {f}_{\mathrm{C}}=383.7652\;\mathrm{T}\mathrm{H}\mathrm{z} $ , $ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ . The red and blue dotted line is the theoretical diagram.$ {f}_{\mathrm{S}} $ 固定的情况下, 调节钛宝石激光器1输出激光频率为: $ {f}_{\mathrm{C}}=383.7652\;\mathrm{T}\mathrm{H}\mathrm{z} $ , 在这种频率状态下, Raman 1, 2和3, 4之间的相对相位为$\Delta \varphi = $ $ {\varphi ''_{{\rm{initial}}}} + {\varphi _{{\rm{ext}}}}$ , $\varphi ''_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}$ 为相对相位的初始相位差. 通过改变相对相位$ {\varphi }_{\mathrm{e}\mathrm{x}\mathrm{t}} $ 测量得到图6 蓝色实线(蓝色虚线为改变初始相位后, 理论拟合的结果, 得: $\varphi ''_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}=-0.755\mathrm{\pi }$ ). 该结果证明了通过改变两对拉曼光的相对相位就可以实现对拉曼耦合强度的控制. 进一步改变钛宝石激光器1输出激光频率后, 布居数曲线发生了平移, 该现象是由于改变钛宝石激光器1输出激光频率导致引入额外的固定相移, 主要来源为钛宝石激光器1频率的改变导致波矢$ {\boldsymbol{k}}_{\mathrm{1, 2}} $ 发生改变, 从而改变一对拉曼激光的光程差. 综上可知: 当改变频率$ {\omega }_{\mathrm{C}} $ 时, 同时改变了激光的波矢和光程, 间接地改变了两对拉曼光之间的相对相位, 因此布居数曲线发生了平移.5.总 结 本文发展了一种利用两对拉曼光间的相对相位精确控制拉曼耦合强度的新方法, 设计了稳定的拉曼激光的光路, 从而保证两对拉曼光在传输过程中光程稳定. 在此基础上, 测量了两个量子态的布居数随两对拉曼光之间的相对相位的变化关系. 该方法为超冷原子量子模拟实验提供了一个独特的操控参量—激光相位, 希望未来能够利用该技术对光与原子相互作用进行操控从而实现更为丰富的物理现象. 


















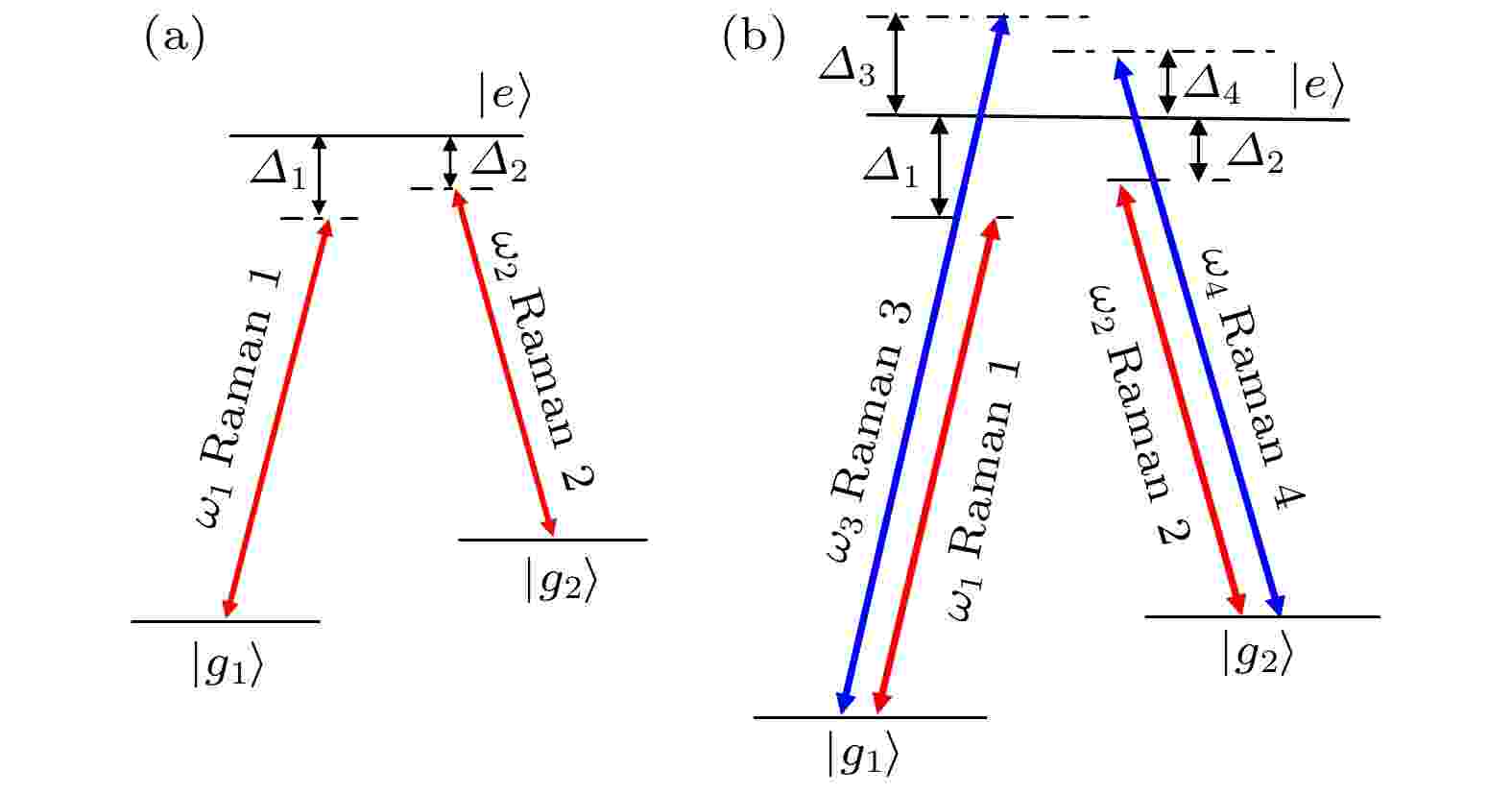 图 1 (a)单受激拉曼跃迁过程; (b)双受激拉曼跃迁过程
图 1 (a)单受激拉曼跃迁过程; (b)双受激拉曼跃迁过程




















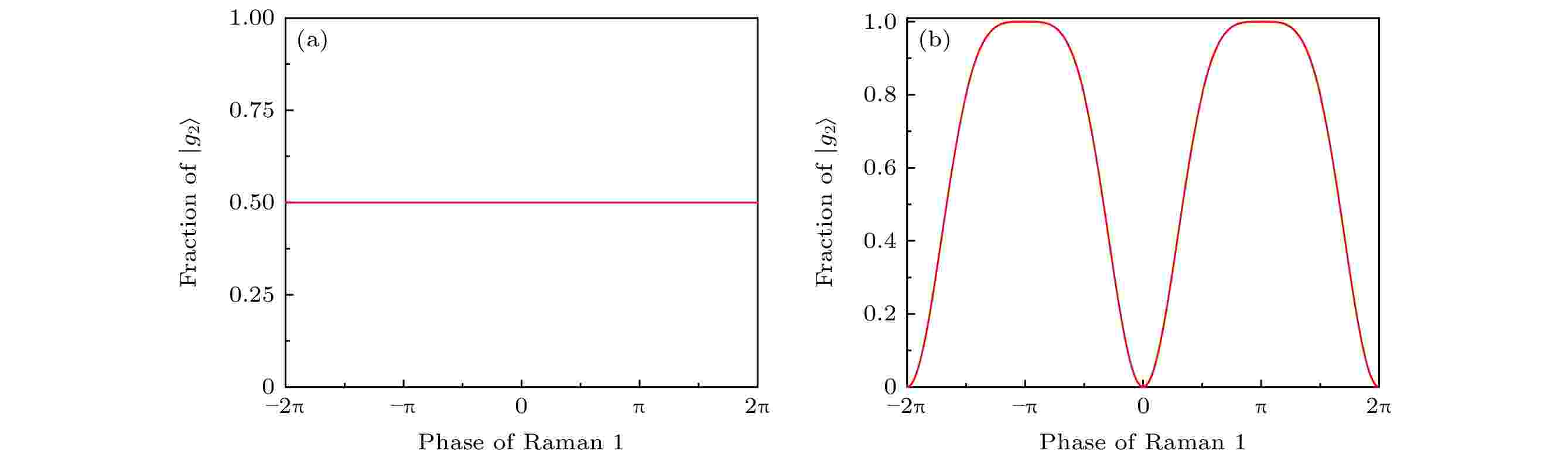 图 2 原子在
图 2 原子在














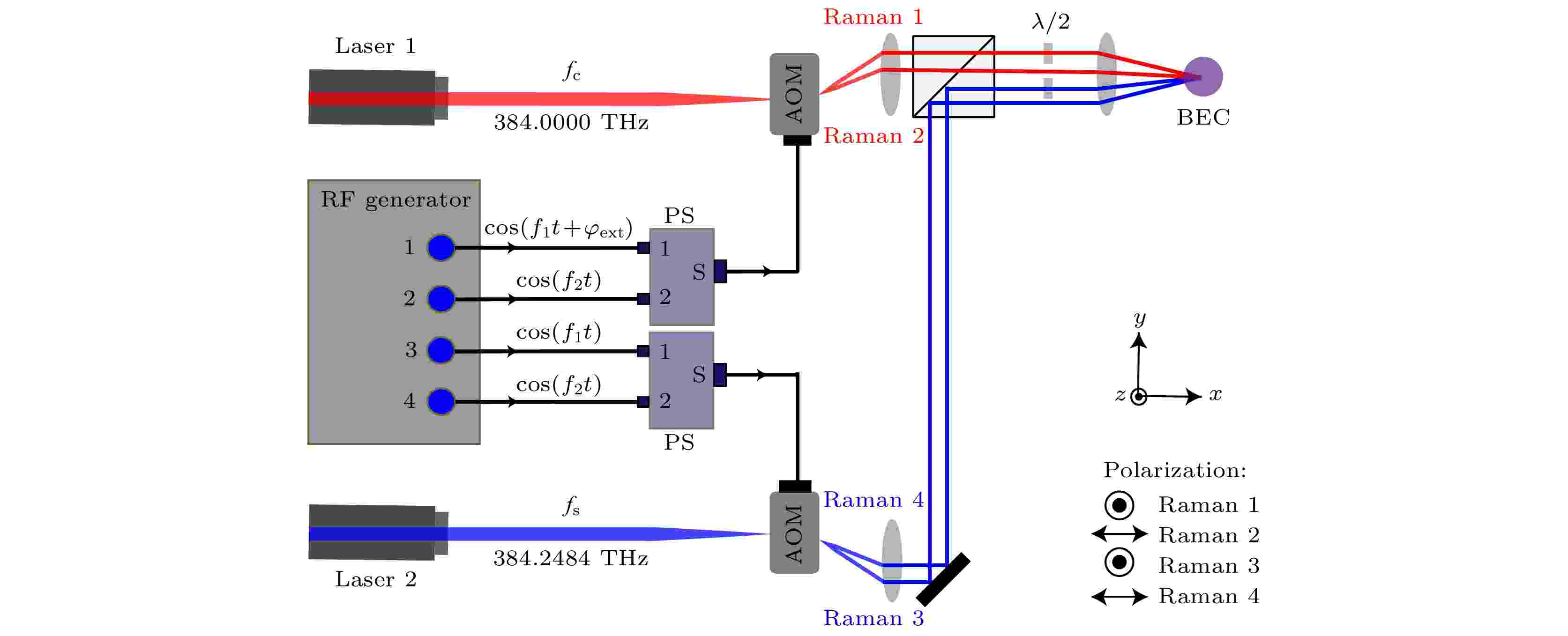 图 3 实验光路图
图 3 实验光路图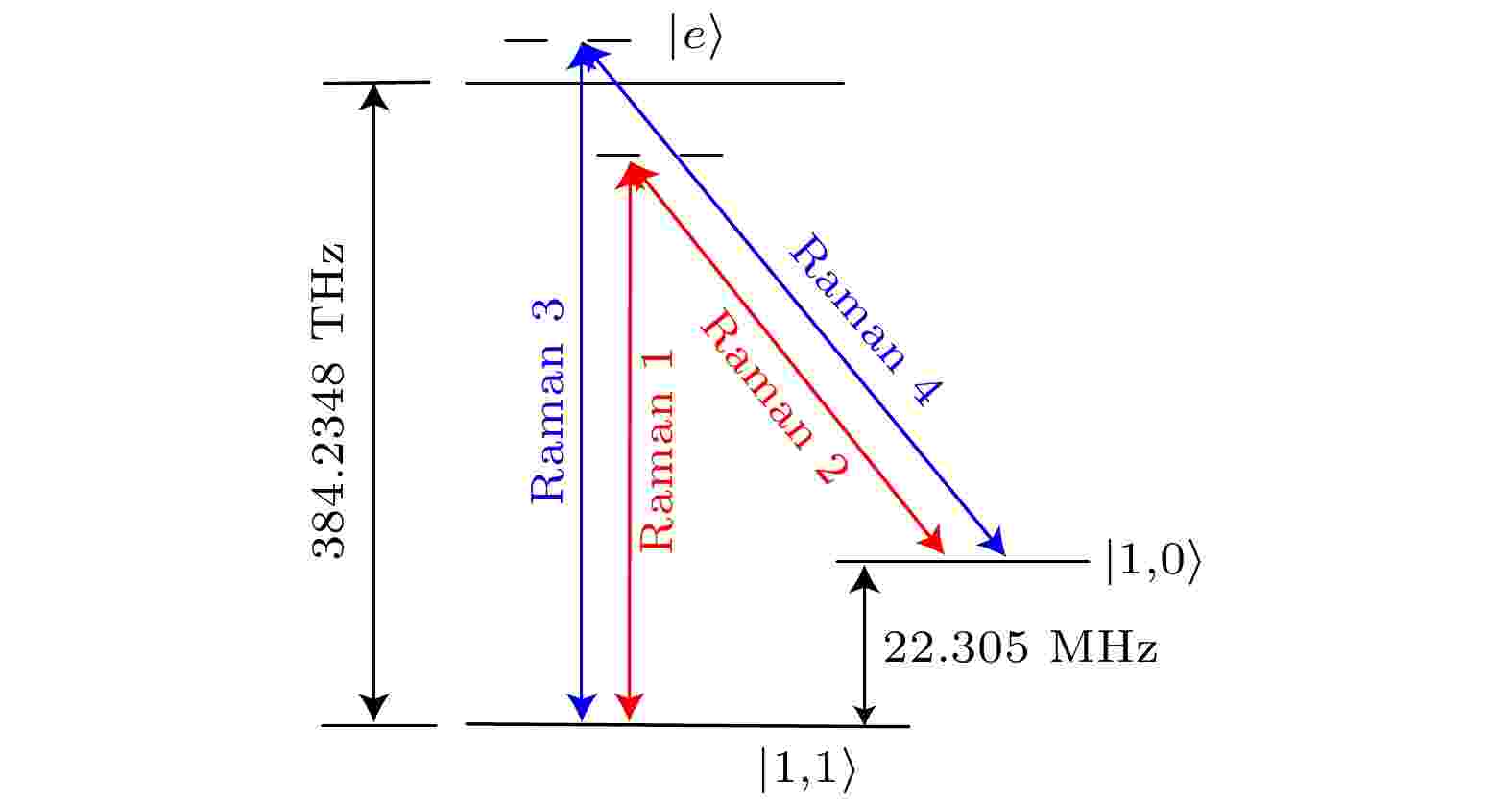 图 4 三能级87Rb原子系统中的拉曼跃迁示意图
图 4 三能级87Rb原子系统中的拉曼跃迁示意图

































































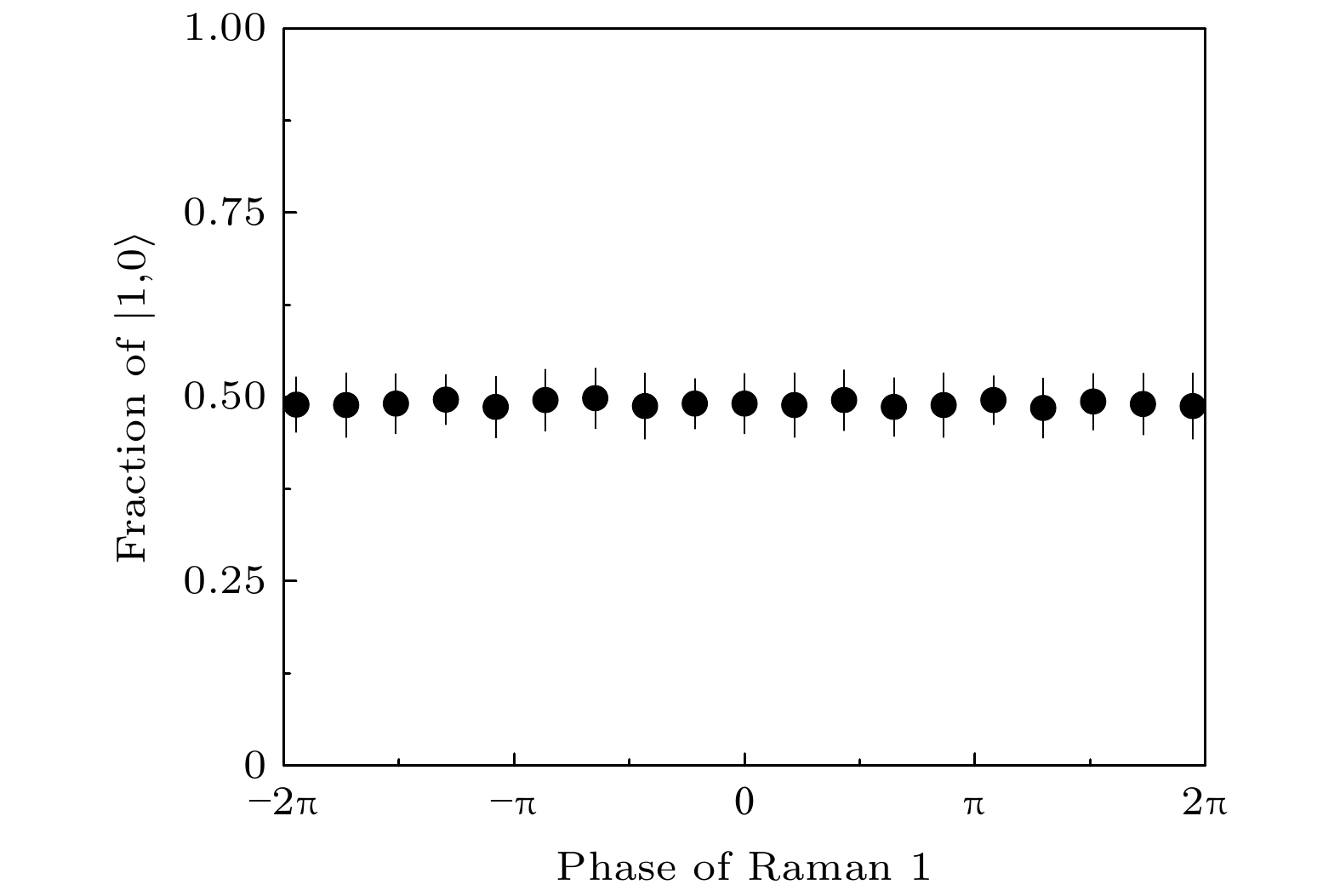 图 5 量子态
图 5 量子态








 图 6 实验测量量子态
图 6 实验测量量子态


























