删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于阶梯相位调制的窄谱激光主动照明均匀性

本站小编 Free考研考试/2021-12-29
摘要:提出一种基于阶梯相位调制的窄谱激光主动照明方法, 利用阶梯型相位调制器对窄谱激光进行相位调制, 提高照明激光到达目标处的光斑均匀性和稳定性. 建立了窄谱激光阶梯相位调制和照明激光远场光斑均匀性的理论模型, 搭建了光束经过1.8 km水平传输的窄谱激光主动照明实验平台, 通过5阶梯相位调制器对0.05 nm线宽的照明激光进行相位调制, 实现了照明激光远场光斑匀化实验. 实验结果表明, 通过5阶梯相位调制器进行相位调制后, 远场光斑包含57%能量区域的空间闪烁率从0.73改善到0.33, 中心光强时间闪烁指数从0.38改善到0.14, 照明激光远场光斑均匀性和稳定性都得到明显提升.
关键词: 主动激光照明/
闪烁指数/
大气湍流/
相位调制

English Abstract


全文HTML

--> --> -->
1.引　言
主动激光照明是主动跟踪、主动成像、目标识别、激光瞄准等领域的关键技术[1-4]. 由于大气湍流的随机扰动及单波长照明激光高相干性, 主动照明激光到达目标处的光斑呈散斑分布且随时间快速变化[5,6], 使照射到目标上的光能量随时间快速变化, 目标回光光子数强烈起伏, 严重影响系统对目标的成像清晰度、探测识别率、跟踪瞄准精度[7-9]. 如何抑制大气湍流引起的随机散斑效应, 提高远场光斑均匀性和稳定性成为主动激光照明技术迫切需要解决的问题.
1998年, Billman[10]提出多光束发射技术, 采用多束互不相干的激光束组成的发射光源, 在目标平面非相干叠加, 抑制大气湍流引起的光场不均匀性. 该方法中互不相干的激光光源可以由多个激光器组成, 也可以由单个激光器分光后增加每个光束之间的光程差实现, 其本质是多个光束非相干叠加, 以改善照明光斑在目标平面处的均匀性. 1998年至1999年, 林肯实验室Higgs等[1,11,12]利用Firepond望远镜开展了一系列单光束、4光束和9光束的主动激光照明试验, 对比分析多光束照明相对于单光束照明对改善光斑均匀性、提高成像清晰度的作用. 试验结果显示, 9光束照明激光在目标平面的光场强度起伏(闪烁指数)相对于单光束照明减少了近2/3, 均匀性得到明显改善. 2002年至2003年, 万敏等[13,14]提出了利用空间相干性较差的激光器作为照明光源的方法, 实现了激光空间相干性对照明光斑均匀性的影响实验, 结果显示, 降低激光空间相干性有利于提高照明均匀性. 2009年, Qian等[15]利用激光大气传输数值模拟技术分析了部分相干光及随机相位屏旋转速度对远场光斑的光束扩展、光轴抖动和光强闪烁的影响, 进一步证明了部分相干光能有效提高激光照明远场光斑均匀性. 2014年, Poyet等[16]通过模拟与实验研究了光管照明技术, 照明光斑空间闪烁指数改善了2.5倍. 2016年, 罗文等[17]提出将光束整形技术应用到主动激光照明中, 以提高照明光斑均匀性. 结果表明在无湍流情况下, 光束整形能有效提高照明光斑均匀性, 但是该方法不能弥补湍流引起的散斑效应. 2019年, 康凯[18]研究了基于相位调制的高斯光束空域匀化技术, 通过对光束相位进行调制, 将高斯光束匀化为平顶光束. 研究表明, 目前的主动激光照明主要通过增加照明激光数量、降低照明激光相干性、采用多波长激光、加入相位扰动来匀化远场光斑分布, 从而提高主动激光照明远场光斑均匀性和稳定性. 多光束照明需要将多束激光聚焦到同一目标上, 光学系统复杂, 伺服控制和共轴更加困难. 部分相干光源照明对均匀性提升效果有限, 且光斑扩展需要更高功率照明光源. 因此, 研究匀化效果好、结构简单、易集成的均匀照明方法十分重要.
本文提出一种基于阶梯相位调制的窄谱激光主动照明方法, 针对高功率照明激光的窄谱特性, 结合纯相位结构扰动调制, 通过特制的阶梯型光学相位调制器(ladderlike phase modulator, LPM)引入激光相位扰动, 打乱原有窄谱激光近场分布, 实现远场匀化的目的, 且能够抑制大气湍流引起的散斑效应的影响. 该方法结构简单、具有共孔径发射和便于集成等特点, 且光斑匀化效果与多光束照明相同. 本文建立了窄谱激光相位调制和大气传输的物理模型, 推导了远场光斑分布表达式, 开展了照明激光传输数值模拟, 实现了1.8 km主动激光照明传输实验, 并对实验结果进行了分析和总结.
2.窄谱激光相位调制均匀照明方法
基于阶梯相位调制的窄谱激光主动照明远场光斑匀化原理如图1所示. 激光光源发出照明激光束, 激光束通过阶梯型相位调制器被分为多个部分进行相位调制, 每个部分光束的相位调制都不相同, 光束经过望远镜扩束后聚焦发射, 经过大气传输后到达目标处, 形成均匀光斑照明目标.
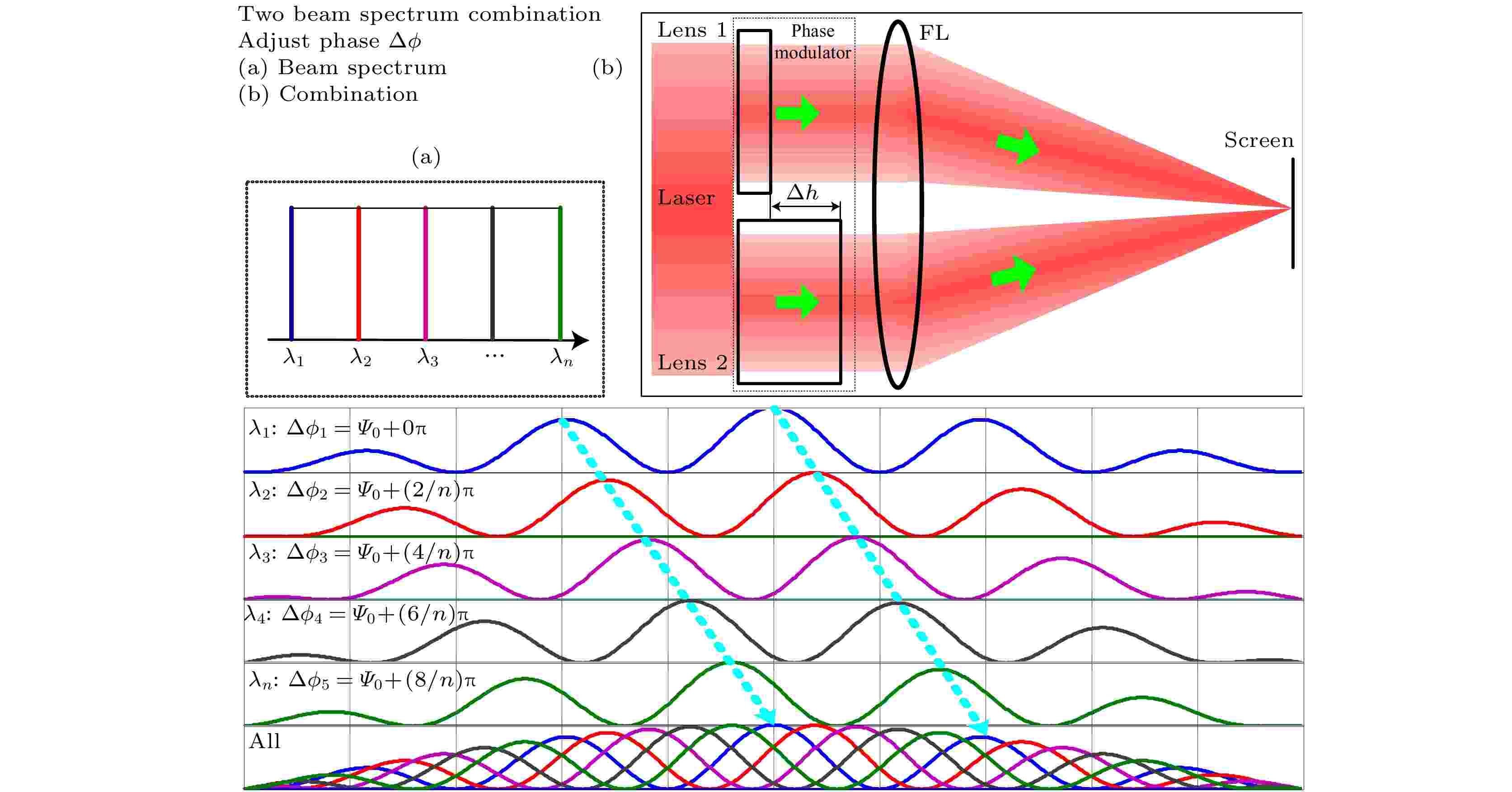图 1 阶梯相位调制的窄谱激光远场光斑匀化原理
Figure1. Uniformity principle of narrow spectrum laser illumination with ladderlike phase modulating

照明激光束线宽为$\Delta \lambda $, 对激光谱线进行离散化, 等间隔分为多个波长激光. 阶梯型相位调制器由厚度阶梯变化的多个光学镜组成, 第$j$个光学镜厚度为${h_j}$, 相邻光学镜厚度(厚度梯度)为$\Delta h = $$ {h_j} - {h_{j - 1}}$. 光束经过阶梯型相位调制器后被分为多个部分, 每个单一波长的激光通过大气传输后在远场相干叠加形成干涉光斑. 由于光学元件色散效应, 阶梯型相位调制器对不同波长激光的相位调制量不同, 通过精密设计阶梯型相位调制器的光学镜厚度, 使不同波长激光束的远场干涉光斑强弱互补. 根据不同波长光束的非相干原理, 不同波长远场干涉光斑非相干叠加后产生均匀分布的照明光斑.
3.理论与模拟研究
2
3.1.窄谱激光相位调制
-->

3.1.窄谱激光相位调制

照明激光中心波长为${\lambda _0}$, 激光线宽为$\Delta \lambda $, 即中心波束为${k_0}{\rm{ = }}2{\text{π}}/{\lambda _0}$, 波数宽度为$\Delta k$. 在发射平面($z = 0$)的激光光场为
$\begin{split} E({\boldsymbol{r}},0,t) =\;& \int_{{k_0} - \Delta k/2}^{{k_0} + \Delta k/2} {{E_k}({\boldsymbol{r}},0,t)} {\rm{d}}k \\ =\;& \int_{{k_0} - \Delta k/2}^{{k_0} + \Delta k/2} {{U_k}({\boldsymbol{r}},0)} \exp \left( { - {\rm{i}}{w_k}t} \right){\rm{d}}k, \end{split} $
其中, ${E_k}({\boldsymbol{r}}, 0, t)$是波束为$k$的单频激光光场, ${\boldsymbol{r}}$是发射平面的半径向量, $t$是时间, ${U_k}({\boldsymbol{r}}, 0) = 1$, ${w_k} = $$ kc$是角频率, $c$是光束.
阶梯型相位调制器由$N$个光学镜组成, 激光束经过阶梯型相位调制器后被分为$N$个部分:
${U_k}({\boldsymbol{r}},0) = \sum\limits_{j = 1}^N {{U_{kj}}({{\boldsymbol{r}}_j},0)}, $
式中, ${{\boldsymbol{r}}_j} = {\boldsymbol{r}} - {{\boldsymbol{d}}_j}$是第$j$部分激光相对于中心的位置, 其中${{\boldsymbol{d}}_j}$是第$j$部分激光的中心位置.
阶梯型相位调制器第$j$个光学镜厚度为${h_j}$, 厚度梯度为$\Delta h = {h_j} - {h_{j - 1}}$, 第$j$部分波数为$k$的光束被调制的相位为
${\phi _{kj}} = (n - 1)k{h_j}, $
其中, $n$是光学元件的折射率.
窄谱激光经相位调制后的光场分布为
$\begin{split}E'({\boldsymbol{r}},0,t) = \;&\int_{{k_0} - \Delta k/2}^{{k_0} + \Delta k/2} {\sum\limits_{j = 1}^N {{U_{kj}}({{\boldsymbol{r}}_j},0)} } \\&\times\exp \left( { - {\rm{i}}{w_k}t} \right)\exp \left( { - {\rm{i}}{\phi _{kj}}} \right){\rm{d}}k.\end{split}$

2
3.2.窄谱激光大气传输
-->

3.2.窄谱激光大气传输

激光大气传输满足线性波束方程[6,19]
${\nabla ^2}{U_{kj}} + k_{}^2{\left[ {1 + {n_1}({\boldsymbol{r}},z)} \right]^2}{U_{kj}} = 0,$
其中, ${n_1}({\boldsymbol{r}}, z)$是大气湍流引起的折射率系数, $z$是传输距离.
窄谱激光经大气传输到达目标处($z = L$)的光场分布为
$\begin{split}E({\boldsymbol{r}},L,t) =\;& \int_{{k_0} - \Delta k/2}^{{k_0} + \Delta k/2} {\sum\limits_{j = 1}^N {{U_{kj}}({{\boldsymbol{r}}_j},L)} }\\&\times\exp \left( { - {\rm{i}}{w_k}t} \right)\exp \left( { - {\rm{i}}{\phi _{kj}}} \right){\rm{d}}k,\end{split}$
其中, ${U_{kj}}({{\boldsymbol{r}}_j}, L)$是第$j$部分波数为$k$的激光经过大气传输后在目标处的场分布.
对于波数为$k$的单频激光, $N$部分激光束的总光强分布为
$\begin{split}{I_k}({\boldsymbol{r}},L) = \;&\sum\limits_{j = 1}^N {{I_{kj}}({{\boldsymbol{r}}_j},L)}+ \sum\limits_{j = 1}^N \sum\limits_{p \ne j}^N | {U_{kj}}({{\boldsymbol{r}}_j},L)\\&\times U_{kp}^*({{\boldsymbol{r}}_p},L)\exp \left( { - {\rm{i}}\Delta {\phi _{kjp}}} \right) | ,\end{split}$
其中, ${I_{kj}}({{\boldsymbol{r}}_j}, L) = {\left| {{U_{kj}}({{\boldsymbol{r}}_j}, L)} \right|^2}$是第$j$部分波数为$k$的激光光强分布, $\Delta {\phi _{kjp}} \!=\! ({\phi _{kj}} \!-\! {\phi _{kp}}) \!=\! (n \!-\! 1)k\Delta {h_{jp}}$是第$j$部分和第$p$部分光学镜对波束为$k$的激光的调制相位差, $\Delta {h_{jp}} = {h_j} - {h_p}$是第$j$部分和第$p$部分光学镜厚度差.
假设激光谱线为均匀分布, 不同谱线激光远场光斑为非相干叠加, 则同一部分不同波数激光的光强分布满足
$ {I_{kj}} \approx {I_{{k_0}j}},\tag{8a} $
$ {U_{kj}}({{\boldsymbol{r}}_j},L)U_{kp}^*({{\boldsymbol{r}}_p},L) \approx {U_{{k_0}j}}({{\boldsymbol{r}}_j},L)U_{{k_0}p}^*({{\boldsymbol{r}}_p},L),\tag{8b} $
其中, ${k_0}$是中心波束.
因此, 窄谱激光在目标处的总光强分布可表示为
$ \begin{split} I({\boldsymbol{r}},L) \approx\;& \sum\limits_{j = 1}^N {\Delta k{I_{{k_0}j}}({{\boldsymbol{r}}_j},L)} \\ &+ \sum\limits_{j = 1}^N \sum\limits_{p \ne j}^N \Bigg| {U_{{k_0}j}}({{\boldsymbol{r}}_j},L)U_{{k_0}p}^*({{\boldsymbol{r}}_p},L)\\ &\times \int_{{k_0} - \Delta k/2}^{{k_0} + \Delta k/2} {\exp \left( { - {\rm{i}}\Delta {\phi _{kjp}}} \right){\rm{d}}k} \Bigg| ,\end{split} $
其中,
$\begin{split}&\int_{{k_0} - \Delta k/2}^{{k_0} + \Delta k/2} {\exp \left( { - {\rm{i}}\Delta {\phi _{kjp}}} \right)} {\rm{d}}k \\=\;& f(\Delta {h_{jp}})\sin \left[ {(n - 1)\Delta k\Delta {h_{jp}}/2} \right],\end{split} \tag{10a}$
$\begin{split}f(\Delta {h_{jp}}) = \;&- \frac{{\rm{i}}}{{(n - 1)\Delta {h_{jp}}}}2[ \sin \left( {\Delta {\phi _{{k_0}jp}}} \right) \\&+ {\rm{i}}\cos \left( {\Delta {\phi _{{k_0}jp}}} \right) ],\end{split} \tag{10b}$
$\Delta {\phi _{{k_0}jp}}=(n - 1){k_0}\Delta {h_{jp}}. \tag{10c}$
由(9)式可以看出, 经阶梯型相位调制器调制后窄谱激光在目标处的总光强分布由两部分组成, 第一部分是各部分光束光强之和, 第二部分是各部分光束间的相关项. (10)式表明, 各部分光束间的相关项与阶梯型相位调制器第$j$部分和第$p$部分光学镜厚度差密切相关, 通过精密设计光学镜的厚度梯度$\Delta h$可以消除相关项.
当阶梯型相位调制器光学镜厚度梯度为
$\Delta h = q \times \frac{{2{\rm{\pi }}}}{{\left( {n - 1} \right)\Delta k}},$
则阶梯型相位调制器第$j$部分和第$p$部分光学镜厚度差为
$\begin{split} \Delta {h_{jp}} =\;& {h_j} - {h_p} \\ =\;& (j - p) \times \frac{{q \times 2{\rm{\pi }}}}{{\left( {n - 1} \right)\Delta k}}, \end{split}$
其中, $q$是大于0的整数.
因此
$\sin \left[ {(n - 1)\Delta k\Delta {h_{jp}}/2} \right] = \sin \left[ {(j - p) \times q \times {\rm{\pi }}} \right] = 0.$
将(13)式代入(10a)式和(9)式, 得到窄谱激光在目标处的光强分布为
$ I({\boldsymbol{r}},L) \approx\sum\limits_{j = 1}^N {\Delta k{I_{{k_0}j}}({{\boldsymbol{r}}_j},L)} = \sum\limits_{j = 1}^N {{I_j}({{\boldsymbol{r}}_j},L)}, $
其中, ${I_j}({{\boldsymbol{r}}_j}, L) = \Delta k{I_{{k_0}j}}({{\boldsymbol{r}}_j}, L)$为各部分光束在目标处的光强分布.
(14)式表明, 基于阶梯相位调制的窄谱激光照明远场光斑等价于阶梯相位调制器各部分光束的非相干叠加, 照明结果等效于多光束照明, 采用阶梯型相位调制器可实现多光束照明效果.
2
3.3.远场光斑闪烁指数
-->

3.3.远场光斑闪烁指数

激光照明远场光斑的空间闪烁率为[20]
$\begin{split} \sigma _{{\rm{Is}}}^{\rm{2}} =\;& \left\langle {{I^2}({\boldsymbol{r}},L)} \right\rangle /{\left\langle {I({\boldsymbol{r}},L)} \right\rangle ^2} - 1 \\ =\;& {\left( {\sum\limits_{j = 1}^N {\left\langle {{I_j}({{\boldsymbol{r}}_j},L)} \right\rangle } } \right)^{ - 2}} \times \left[ \sum\limits_{j = 1}^N {\left\langle {I_j^2({{\boldsymbol{r}}_j},L)} \right\rangle } \right.\\ &\left.+ 2\sum\limits_{j = 1}^N {\sum\limits_{m > j}^N {\left\langle {{I_j}({{\boldsymbol{r}}_j},L){I_m}({{\boldsymbol{r}}_m},L)} \right\rangle } } \right] - 1, \end{split} $
其中, $\left\langle \cdots \right\rangle $是一帧光斑在面积为$s$圆形孔径中的平均.
激光照明远场光斑的时间闪烁率为
$\sigma _{{\rm{It}}}^{\rm{2}} = \dfrac{ \left\langle {\widetilde I_{\rm{t}}^2(s,L)} \right\rangle}{{\left\langle {{{\widetilde I}_{\rm{t}}}(s,L)} \right\rangle ^2}} - 1, $
其中, ${\widetilde I_{\rm{t}}}(r, L)$是一帧光斑在面积为$s$圆形孔径中的总光强, $\left\langle \cdots \right\rangle $是圆形孔径中总光强随时间的平均.
2
3.4.数值模拟
-->

3.4.数值模拟

利用激光系统仿真软件EasyLaser[21]开展主动激光照明数值模拟, 研究基于阶梯相位调制的窄谱激光主动照明技术对远场光斑均匀性的改善效果. EasyLaser仿真软件中的激光大气传输过程采用多层相位屏方法[22], 大气湍流采用Zernike多项式构造相位屏方法[23], 大气湍流服从Kolmogorov谱.
照明光源产生激光的中心波长${\lambda _0}$为1064 nm, 谱线宽度$\Delta \lambda $为0.05 nm (13 GHz), 光束形状为圆形, 光束发射口径为800 mm, 阶梯型相位调制器由5个环形排布的光学镜组成, 光学镜材料折射率$n$为1.45, 系数$q$取1, 根据(11)式设计光学镜厚度梯度$\Delta h$为50.3 mm. 大气条件取激光传输L为1.8 km, 大气相干长度$C_{\rm{n}}^{\rm{2}}$为$1 \times {10^{ - 15}}$ m–2/3至$5 \;\times $$ {10^{ - 14}} $ m–2/3, 得到空间闪烁指数和时间闪烁指数分别如图2和图3. 结果表明, 在弱湍流和强湍流条件下, 基于阶梯相位调制的窄谱激光照明远场光斑空间闪烁率和时间闪烁率都得到明显改善, 在$C_{ {n}}^2$为$1 \times {10^{ - 14}}$ m–2/3时, 照明光斑出现闪烁饱和效应.
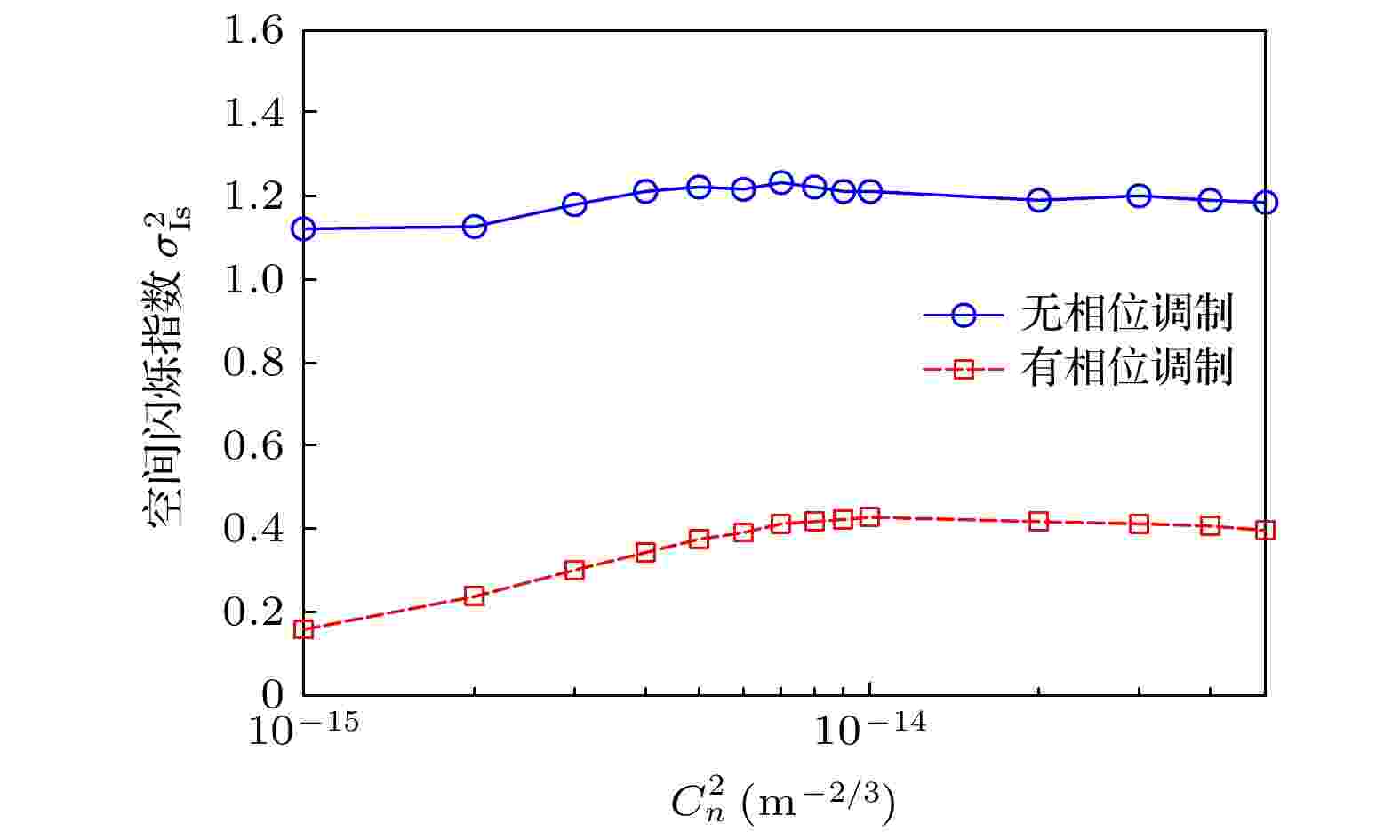图 2 不同湍流条件下照明光斑空间闪烁率
Figure2. Spatial scintillation index of illumination facular in atmosphere turbulence.

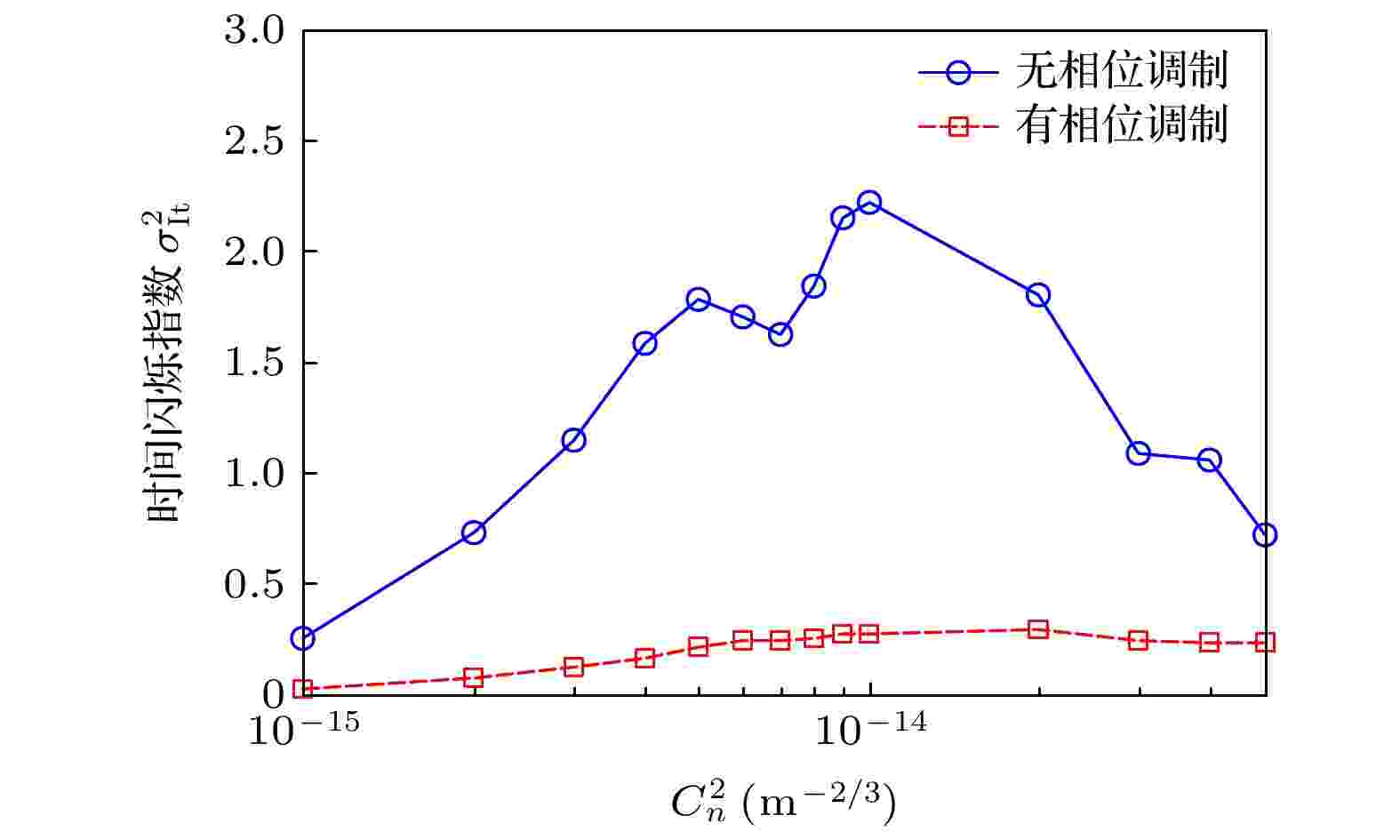图 3 不同湍流条件下照明光斑时间闪烁率
Figure3. Time scintillation index of illumination facular in atmosphere turbulence.

4.实验研究
2
4.1.实验方案
-->

4.1.实验方案

搭建了1.8 km水平传输的窄谱激光主动照明实验平台, 开展无阶梯型相位调制器和有阶梯型相位调制器的窄谱激光照明实验, 实验装置原理如图4所示.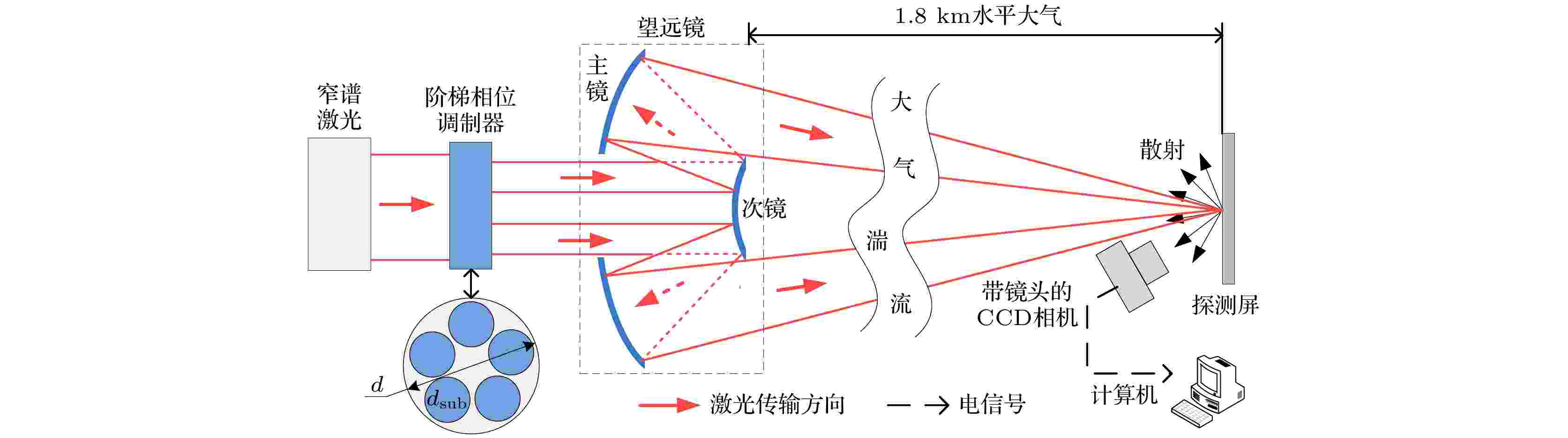
图 4 实验装置示意图
Figure4. Scheme of active illumination experiment.

照明光源产生激光的中心波长${\lambda _0}$为1064 nm, 谱线宽度$\Delta \lambda $为0.05 nm (13 GHz), 光束形状为圆形, 口径$d$为120 mm. 阶梯型相位调制器由5个环形排布的光学镜组成, 光学镜口径${d_{{\rm{sub}}}}$为40 mm, 光学镜材料折射率$n$为1.45, 系数$q$取1, 根据(11)式设计光学镜厚度梯度$\Delta h$为50.3 mm. 阶梯型相位调制器的5个光学镜中心位置及厚度见表1.
光学镜
序号		中心位置厚度
X/mmY/mmh/mm
1037.80
235.911.750.3
322.2–30.6100.6
4–22.2–30.6150.9
5–35.911.7201.3


表1阶梯型相位调制器光学镜中心位置及厚度
Table1.Central position and thickness of optic lens.

望远镜扩束倍数为7, 激光束经过望远镜后外径${D_1}$为850 mm. 调节望远镜主次镜距离使焦距为1.8 km, 望远镜将发射光束聚焦到1.8 km靶点处的探测屏上, 通过电荷耦合器件(CCD)相机对探测屏进行成像, 记录照明激光传输到靶点的光斑分布, 分析光斑均匀性等特征. CCD相机像素数为256 × 300, 单像素对应光斑尺寸约0.794 mm. 实验期间近地面大气折射率结构常数$C_{ {n}}^{\rm{2}}$约$1.14 \times $$ {10^{ - 15}}$ m–2/3.
采用无阶梯相位调制和有阶梯相位调制的激光照明方案, 分别开展3次照明实验, 每次实验采集200帧光斑. 通过分析照明光斑光强分布的空间闪烁率和时间闪烁率, 定量分析激光照明光斑均匀性和稳定性.
2
4.2.照明光斑分布
-->

4.2.照明光斑分布

图5是无相位调制和有相位调制时, 照明激光在1.8 km探测屏上的典型光强分布. 图5(a)和图5(b)是无相位调制时的两帧远场光斑, 远场光斑散斑多且分布不均匀, 不同帧的光强分布不同且随时间快速变化; 图5(c)和图5(d)是有相位调制时的两帧远场光斑, 远场光斑散斑消失且分布更均匀, 不同帧之间光强分布有变化, 但中心区域的光强分布始终较均匀.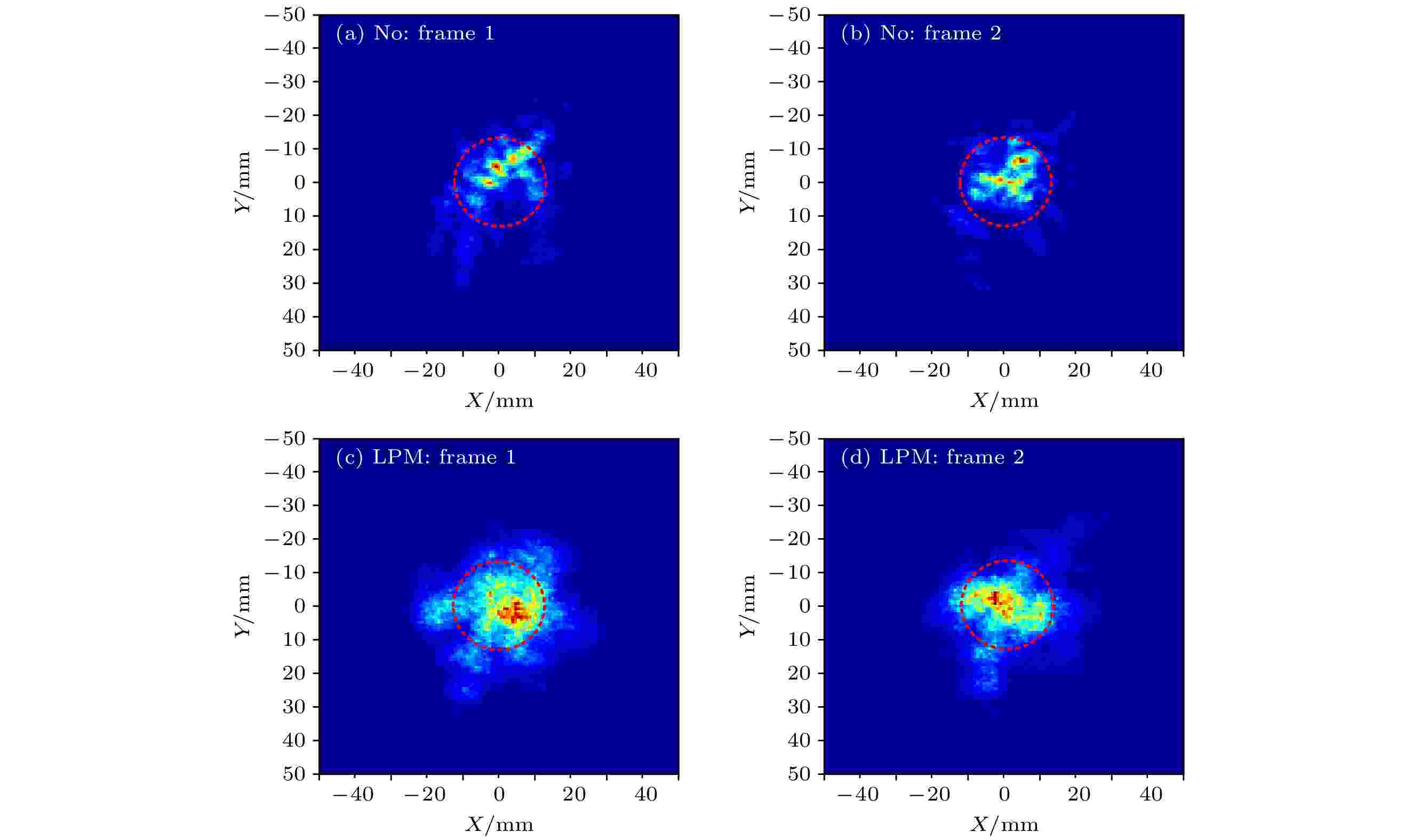
图 5 1.8 km处远场光斑分布　(a), (b)无阶梯型相位调制器; (c), (d)有阶梯型相位调制器
Figure5. Focal patterns at 1.8 km: (a), (b) No phase modulation; (c), (d) ladderlike phase modulation (LPM).

2
4.3.光斑闪烁指数
-->

4.3.光斑闪烁指数

以光斑质心为中心, 计算包含57%能量的光斑半径R57%, 无相位调制照明远场光斑平均半径为11.5 mm, 有相位调制照明远场光斑平均半径为13.5 mm, 如图5中红色虚线圆圈所示. 图6是R57%光斑半径区域内空间闪烁率随采集帧的变化曲线, 加入阶梯相位调制器对窄谱激光进行相位调制后, 空间闪烁率均值由0.73改善到0.33, 降低到原来的45%.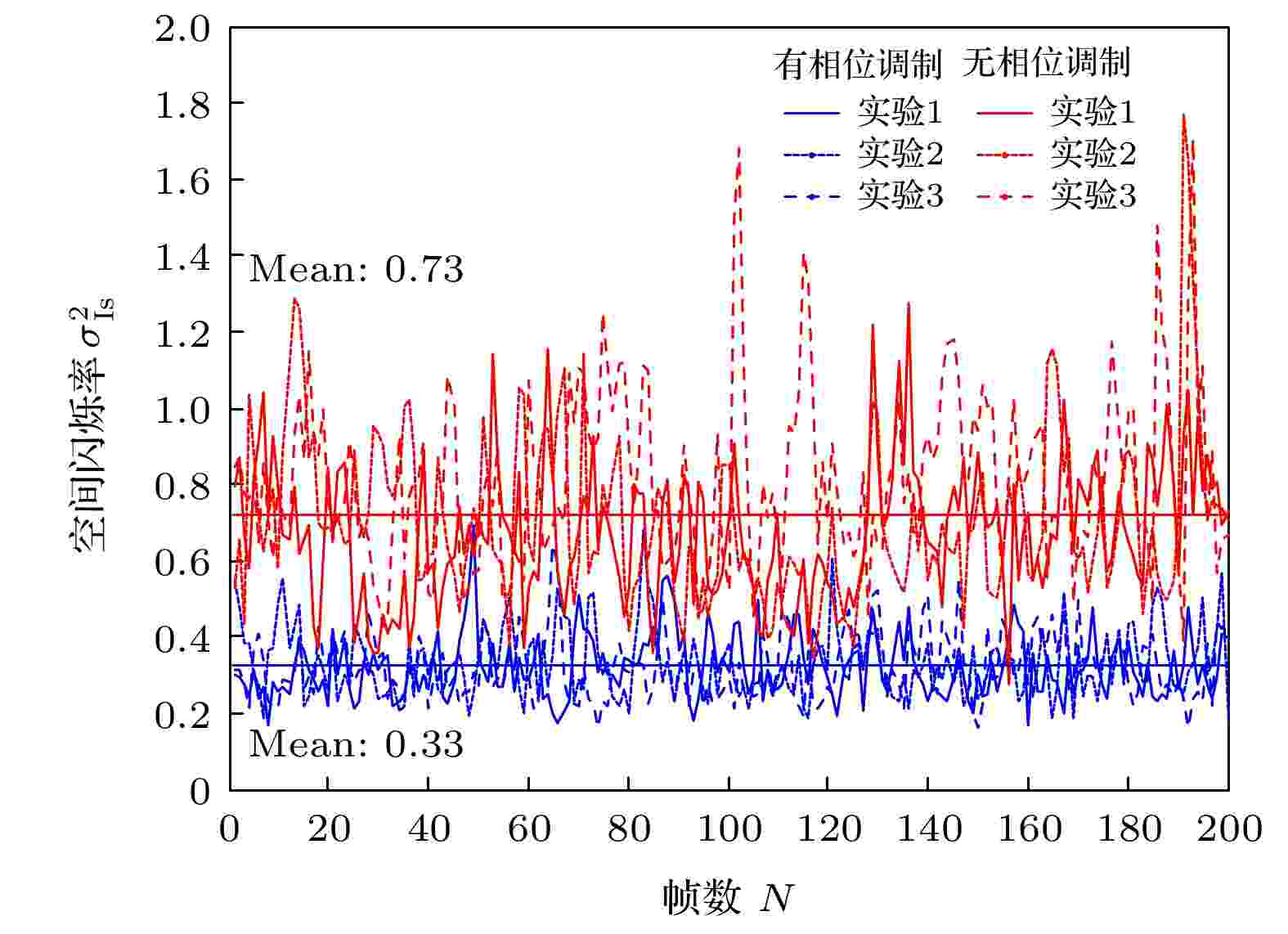
图 6 包含57%能量的光斑半径内空间闪烁率
Figure6. Spatial scintillation index in the area of ${R_{57\% }}$.

图7是实验测量得到的以光斑中心像素(0.794 mm × 0.794 mm)光强占总能量比例随帧数的变化. 无相位调制时, 中心像素光强随时间变化较大, 中心光强在0—0.5%之间变化, 时间闪烁率约0.38; 有相位调制时, 中心像素光强随时间变化起伏减弱, 中心光强在0—0.2%之间变化, 时间闪烁率改善到0.14, 降低到原来的37%. 在$C_{ {n}}^{\rm{2}}$为$1.14 \times {10^{ - 15}}$ m–2/3时, 数值模拟照明光斑时间闪烁率由0.32 (无相位调制)改善到0.078 (有相位调制), 降低到原来的1/4, 实验与模拟结果基本相符.
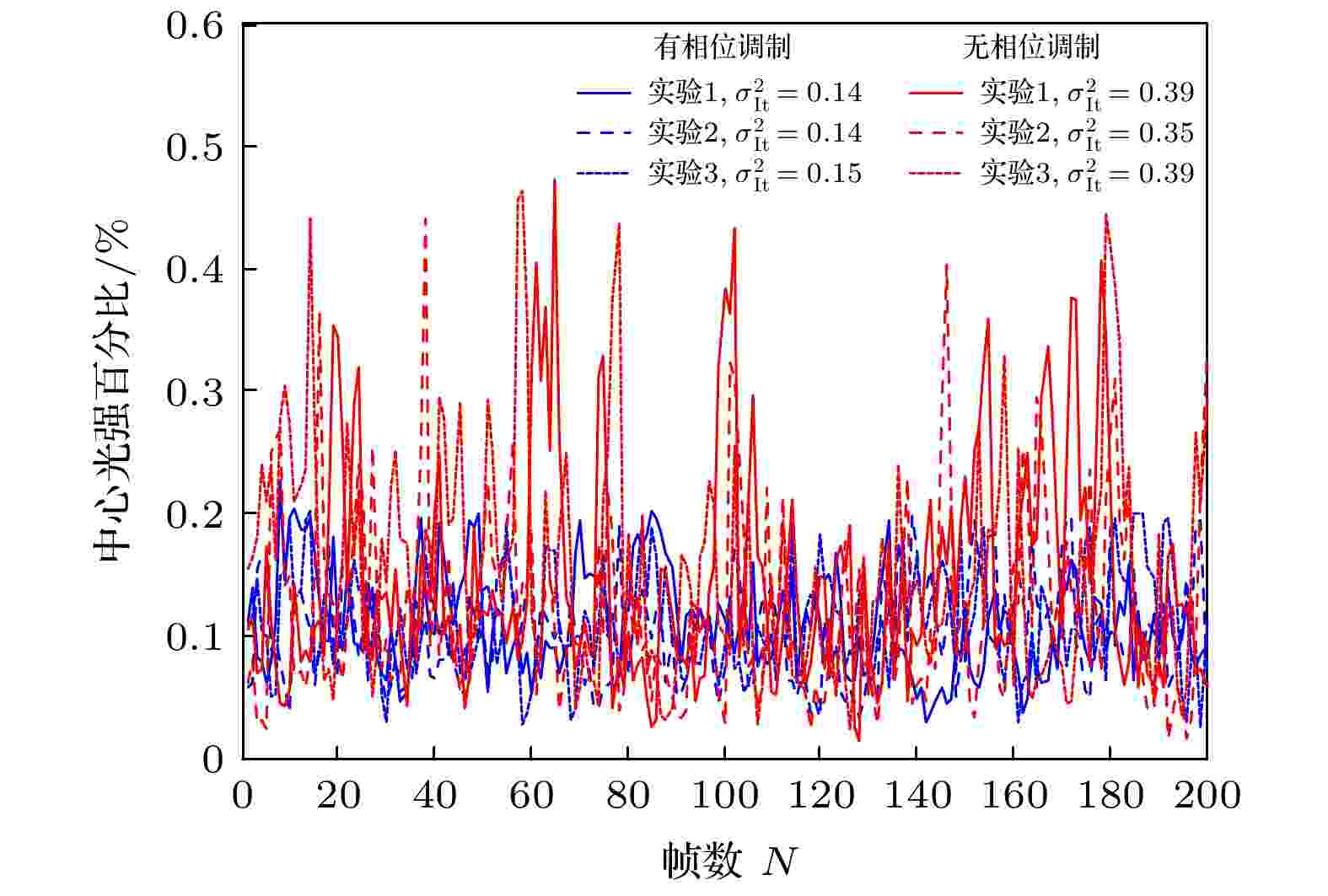图 7 光斑中心像素光强百分比变化曲线
Figure7. Time scintillation index of central intensity.

2
4.4.孔径效应
-->

4.4.孔径效应

由于激光照明目标尺寸不同, 因此定量分析照明激光远场光斑不同大小区域的空间闪烁率和时间闪烁率. 无相位调制时照明激光在1.8 km处的散斑半径等价于大口径光束在远场的艾里斑半径, 约2.7 mm; 加入阶梯型相位调制器后, 照明激光到达远处的散斑半径等价于相位调制器光学镜口径光束在远场的艾里斑半径, 约8.3 mm.
图8是200帧远场光斑不同大小区域的空间闪烁率均值随区域半径的变化, 图9是远场光斑不同大小区域的空间闪烁率均值改善比, 即无相位调制远场光斑空间闪烁率除以有相位调制远场光斑空间闪烁率, 反映有相位调制远场光斑空间闪烁率相对于无相位调制远场光斑空间闪烁率的减小程度. 结果表明, 采用阶梯型相位调制器对窄谱激光进行相位调制后, 远场光斑不同大小区域的空间闪烁率明显改善; 空间闪烁率改善比随计算区域增大而先增大后减小, 在计算区域半径接近2.7 mm时, 空间闪烁率改善比最高, 为3.67. 计算区域半径小于2.7 mm时, 空间闪烁率改善比随计算区域增大而增大, 这是因为无相位调制时计算区域在一个散斑内, 半径越大光斑强度分布变化越大, 空间闪烁率越大; 有相位调制时, 光学镜散斑约8.3 mm, 计算区域在散斑的中心区域, 强度分布变化不明显, 空间闪烁率变化小; 因此, 空间闪烁率改善比随计算区域增大而增大. 计算区域半径大于2.7 mm时, 空间闪烁率改善比随计算区域增大而减小, 这是因为无相位调制时远场光斑计算区域至少包含一个散斑, 空间闪烁率增长速度变缓; 有相位调制时远场光斑计算区域仍在一个大散斑内, 空间闪烁率增长速度并未减缓; 因此, 空间闪烁率改善比随计算区域增大而逐渐减小.
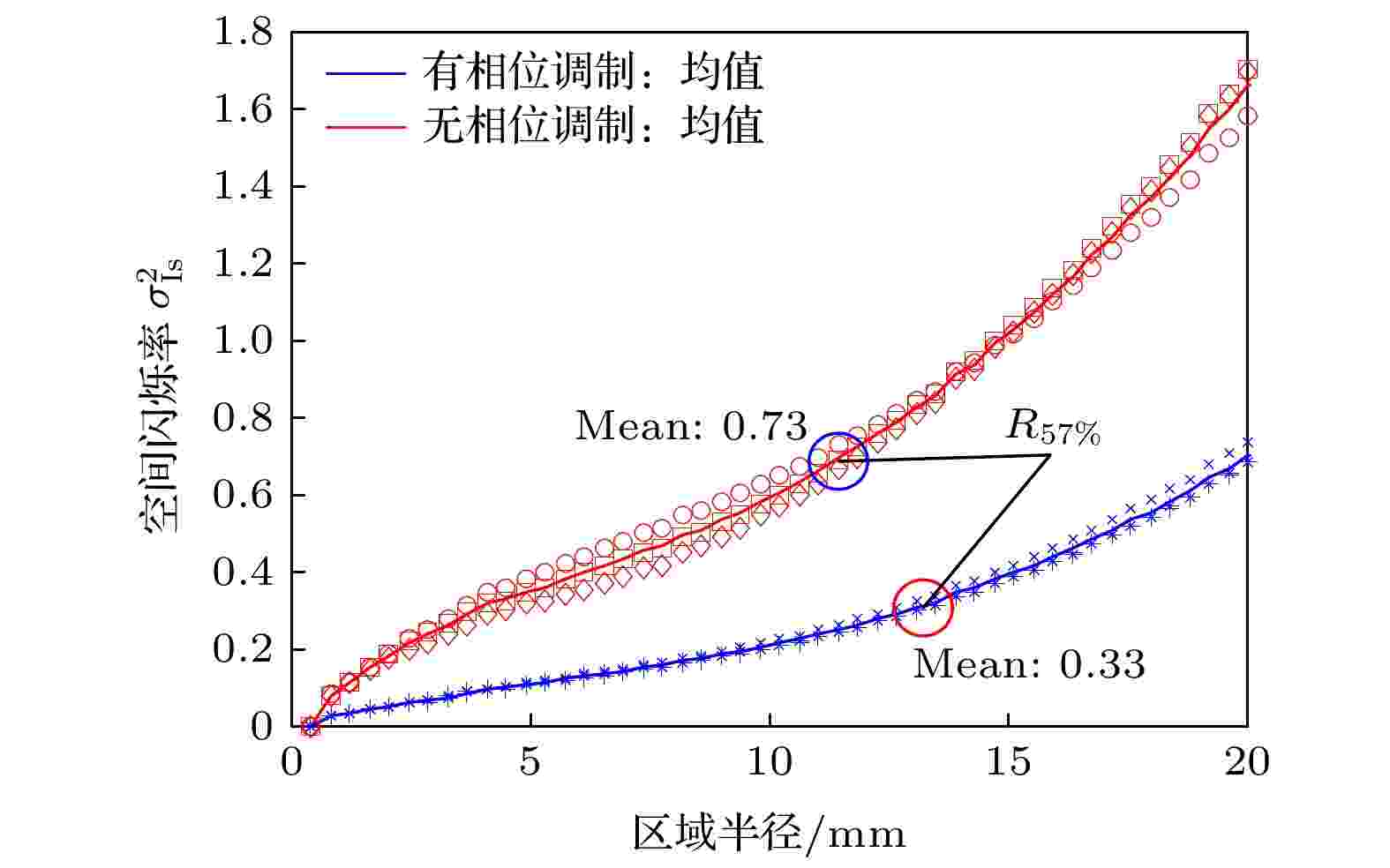图 8 远场光斑不同大小区域的空间闪烁率
Figure8. Spatial scintillation index in different area.

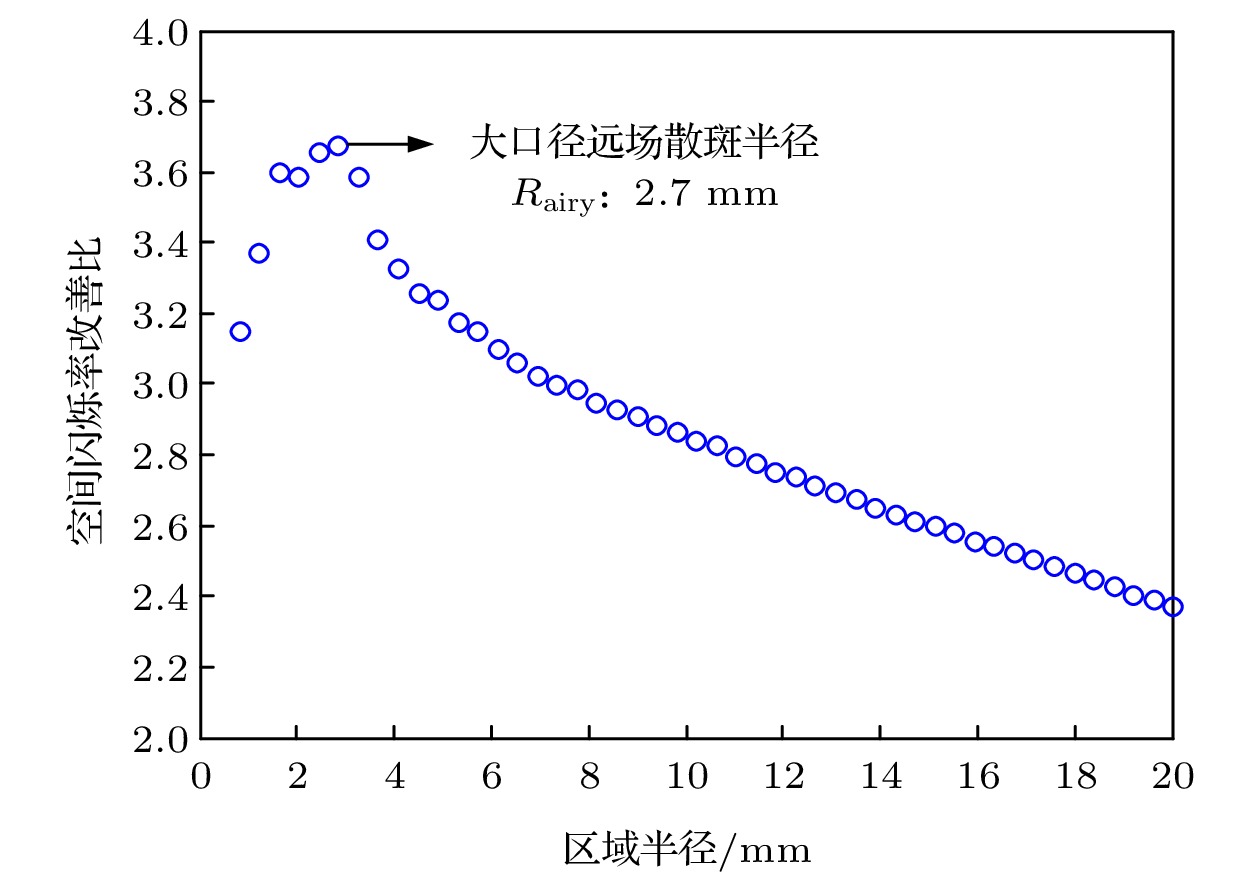图 9 远场光斑不同大小区域的空间闪烁率改善比
Figure9. Improving ratio of spatial scintillation index in different area.

图10是远场光斑不同大小区域光强占比的时间闪烁率, 图11是远场光斑不同大小区域光强占比的时间闪烁率改善比, 即有相位调制远场光斑时间闪烁率相对于无相位调制远场光斑时间闪烁率的减小比值. 结果表明, 计算区域越大时间闪烁率越小, 这是因为计算区域越大包含能量越多、且随时间的变化越小, 时间闪烁率越小. 计算区域半径大于8.3 mm时, 时间闪烁率小于0.03, 此时光强随时间变化非常小, 因此, 主要分析区域半径小于8.3 mm时的时间闪烁率及改善比. 采用阶梯型相位调制器对窄谱激光进行相位调制后, 远场光斑不同大小区域的光强时间闪烁率明显改善; 时间闪烁率改善比随计算区域增大而逐渐减小, 中心光强时间闪烁率改善比最大, 为2.6. 计算区域半径小于2.7 mm时, 时间闪烁率改善比随计算区域增大而快速降低, 这是因为无相位调制时计算区域在一个散斑内, 由于散斑随时间快速变化, 不同帧的光强为散斑的不同部分, 计算区域越小光强随时间变化越大, 时间闪烁率越大; 有相位调制时光斑的散斑被均匀化, 计算区域始终在散斑的中心区域, 光强随时间变化较小, 时间闪烁率变化小. 因此, 时间闪烁率改善比随计算区域增大而快速减小. 计算区域半径大于2.7 mm时, 时间闪烁率改善比随计算区域增大的减小速度变缓, 这是因为无相位调制时远场光斑计算区域至少包含一个散斑, 时间闪烁率随计算区域增大的变化速度减小; 有相位调制时计算区域仍在散斑内, 时间闪烁率随计算区域增大的变化速度基本不变. 因此, 时间闪烁率改善比随计算区域增大而减小的速度降低.
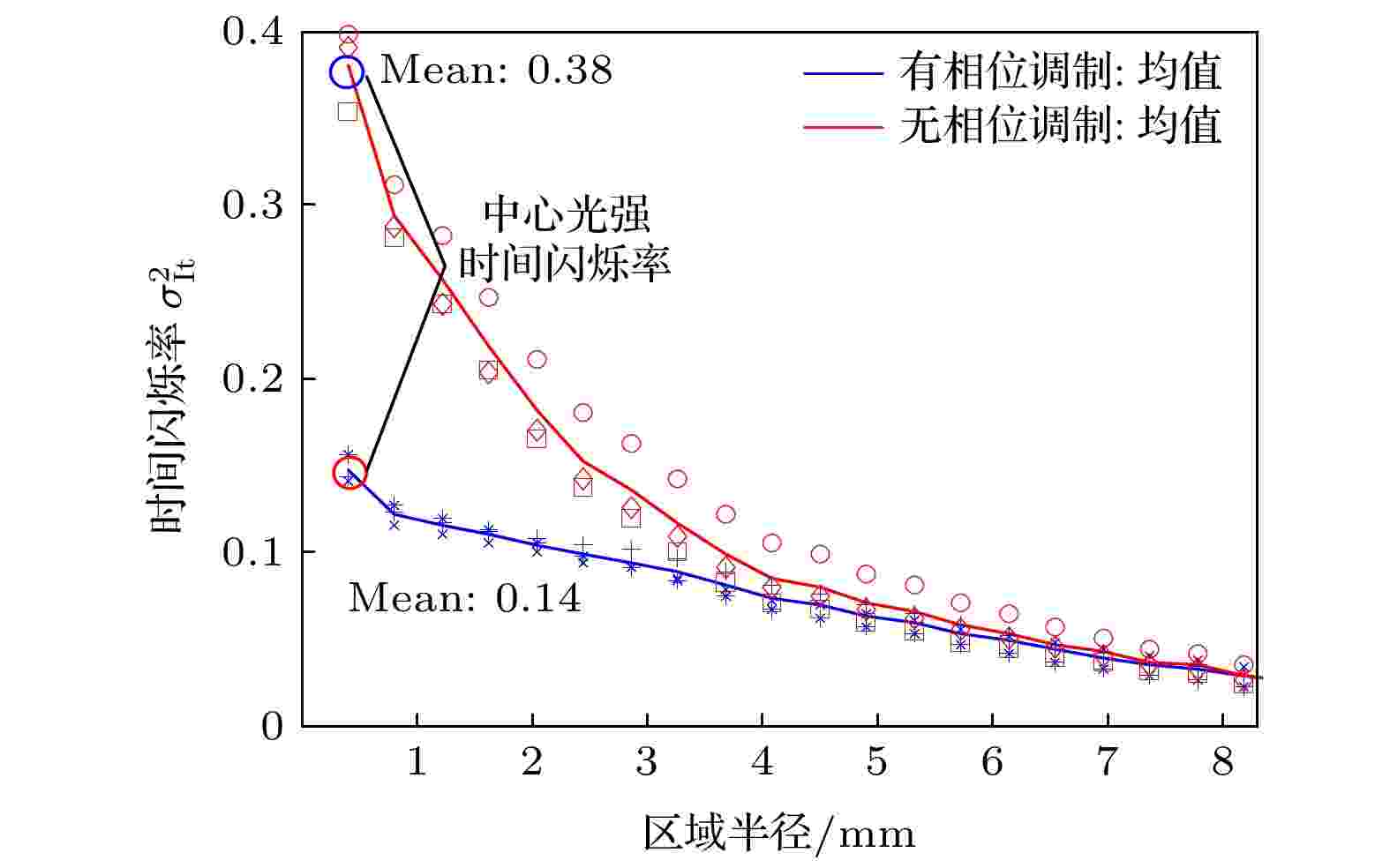图 10 远场光斑不同大小区域能量占比的时间闪烁率
Figure10. Time scintillation index of energy ratio in different area.

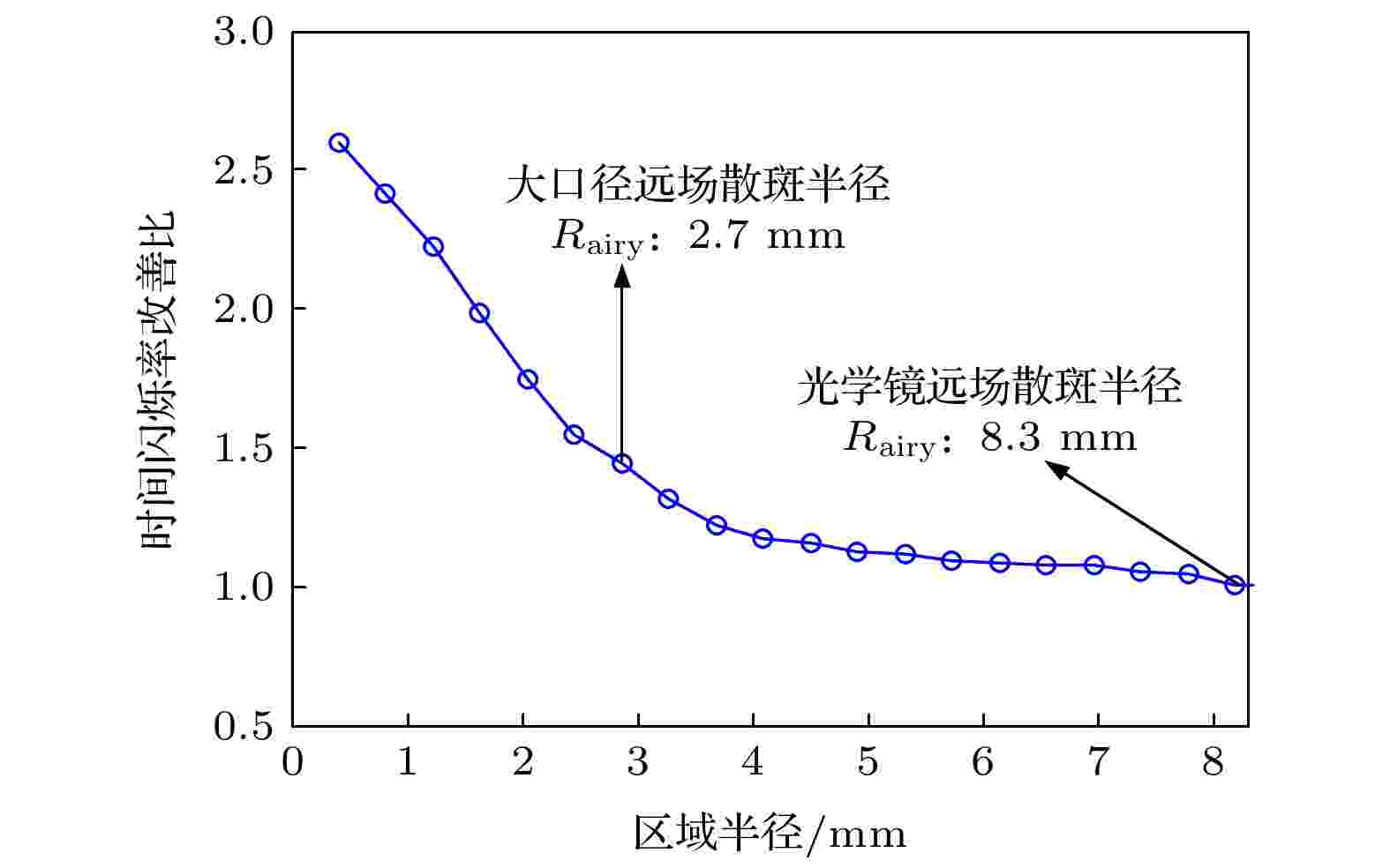图 11 远场光斑不同大小区域能量占比的时间闪烁率改善比
Figure11. Improving ratio of time scintillation index of energy ratio in different area.

5.结　论
提出一种基于阶梯相位调制的窄谱激光主动照明方法, 针对高功率照明激光的窄谱特性, 结合纯相位结构扰动调制, 通过特制的阶梯型光学相位调制器引入激光相位扰动, 打乱原有窄谱激光近场分布, 实现远场匀化的目的, 且能够抑制大气湍流引起的散斑效应的影响. 通过理论、数值模拟和实验研究了该方法对提升照明激光经过大气湍流后的光斑均匀性和稳定性的效果. 实验结果表明, 采用阶梯型相位调制器对窄谱激光进行相位调制后, 照明激光受大气湍流影响后的远场光斑的均匀性和稳定性都得到明显改善. 对于空间闪烁率, 远场光斑包含57%能量区域的空间闪烁率从0.73改善到0.33, 降低到原来的45%, 计算区域半径接近大口径远场散斑尺寸时空间闪烁率改善效果最好, 改善比为3.67; 对于时间闪烁率, 中心光强时间闪烁指数从0.38改善到0.14, 降低到原来的37%, 与数值模拟结果基本相符.
照明光斑不均匀性主要原因是大气湍流, 基于阶梯相位调制的窄谱激光照明方法与激光谱线、阶梯型相位调制光学镜数量和厚度有直接关系. 今后, 将分析光学镜数量、光学镜厚度误差、激光谱线线型对激光照明远场光斑均匀性和稳定性的影响, 同时开展不同大气湍流条件下的照明光斑匀化效果研究.
相关话题/激光 空间 光学 计算 大气
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于时延光子储备池计算的混沌激光短期预测
    摘要:提出并证明了一种利用时延光子储备池计算短期预测混沌激光的时间序列.具体来说,建立基于光反馈和光注入半导体激光器的储备池结构,通过选择合适的系统参数,时延光子储备池计算可以有效地预测混沌激光约2ns的动态轨迹.此外,研究了系统参数对预测结果的影响,包括掩模类型、虚拟节点数、训练数据长度、输入增益 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 大气压氩气刷形等离子体羽的特性研究
    摘要:大气压非平衡低温等离子体在生物医学和表面处理等方面具有广泛的应用前景,引起研究者的关注.等离子体射流是产生大气压非平衡等离子体的重要方式,但通常产生的等离子体羽尺度较小.针对于此,本文采用一个具有三电极的介质阻挡放电装置,在交流电压与负偏置电压的共同作用下,在流动氩气的下游产生了大尺度刷状等离 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种计算非平衡等离子体中粒子能级布居的简化方法
    摘要:获得粒子能级布居是研究非平衡等离子体辐射性质的一个重要方面.对于复杂三维等离子体,采用细致碰撞辐射模型虽然精确,但计算耗费大.本文提出了一种束缚态特征温度法,能够快速计算得到非平衡等离子体中的粒子能级布居.对非平衡氖等离子体算例的研究表明,本文方法是有效的,在等离子体非平衡程度不太高时与碰撞辐 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维冰相I的电子和光学性质
    摘要:二维冰是典型的原子制造技术获得的新型原子级材料,其结构和成核生长在材料科学、摩擦学、生物学、大气科学和行星科学等众多领域具有至关重要的作用.虽然二维冰的结构性质已被广泛研究,但对其电学和光学性质知之甚少.本文通过密度泛函理论和线性响应理论计算了二维冰相I在零温时的主要电学、光学、介电性质和红外 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于光学频率梳的超低噪声微波频率产生
    摘要:低噪声的微波频率在雷达,长基线干涉仪等领域有重要应用.基于光学频率梳产生的微波信号的相位噪声在1Hz频偏处低于–100dBc/Hz,在高频(>100kHz)处低于–170dBc/Hz,是目前所有的微波频率产生技术中噪声最低的.文章介绍了光学频率梳产生微波频率的基本原理,对基于光梳产生的微波频率 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光源光谱特性对空间相机调制传递函数检测的影响
    摘要:调制传递函数(modulationtransferfunction,MTF)检测是评价空间相机像质的重要手段.空间相机光学系统透过率和色差、探测器量子效率均与波长相关,采用不同光谱特征的光源所得到的MTF会出现偏差,光源光谱特性的影响不可忽略.针对这一问题,提出了一种分析光源光谱特性对空间相机 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 飞秒激光在空气中成丝诱导氮荧光发射的空间分布
    摘要:测量了线偏振飞秒激光脉冲在空气中成丝产生的氮荧光发射的空间分布.通过改变激光的偏振方向研究成丝过程中氮荧光发射的径向角分布,发现${m{N}}_{{2}}^{{+}}$荧光发射在垂直于激光偏振方向上更强,而在平行于激光偏振方向上较弱;${{m{N}}_{{2}}}$荧光发射在所有方向上 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 亚米级光学卫星影像邻近效应校正
    摘要:邻近效应是指卫星成像过程中目标物周围自然环境反射的太阳辐射对卫星入瞳处目标像元辐亮度的贡献.它会导致卫星图像清晰度、对比度和信息熵值降低,并且导致表观反射率卫星影像中目标像元反射率介于其真实反射率和背景像元平均反射率之间,严重影响定量遥感精度.背景各像元对邻近效应的贡献权重值主要取决于大气分子 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 柿单宁特征功能基团与金属离子作用的计算分析
    摘要:柿单宁具有优良的吸附重金属离子的效能,表没食子儿茶素没食子酸酯(EGCG)是柿单宁发挥其活性作用的关键结构单体.为分析柿单宁与金属离子相互作用的本质,本文利用密度泛函理论(densityfunctionalthoery,DFT)的B3LYP方法,从EGCG-金属复合物的构型、Mayer键级、自 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 空间电荷层效应对固体氧化物燃料电池三相界面附近氧空位传输的影响
    摘要:纳米复合电极是提高中低温固体氧化物燃料电池(solidoxidefuelcell,SOFC)性能的新型前沿技术,其内部三相界面(threephaseboundary,TPB)处空间电荷层(spacechargelayer,SCL)效应凸显,显著影响氧空位传输能力,是其性能优异的重要原因之一.现 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.