摘要:基于Molpro 2012程序包, 应用包含Davidson修正的多参考组态相互作用方法, 使用AVX Z和AVX dZ (X = T, Q, 5, 6)基组进行单点能从头算, 然后采用Aguado-Paniagua函数进行拟合, 得到了SiH⁺(X¹Σ⁺)离子在不同基组、不同方法和是否考虑自旋-轨道耦合(SOC)情况下的解析势能函数(APEFs). 以APEFs为基础, 计算了SiH⁺(X¹Σ⁺)离子的解离能D_e, 平衡键长R_e, 振动频率ω_e, 光谱常数B_e, α_e和ω_eχ_e, 同时讨论了SOC对该体系的影响. 本文的计算结果与其他理论计算符合得较好, 与实验数值也基本吻合. 基于SOC-AV6dZ方法下的APEF, 通过求解径向薛定谔方程, 给出了SiH⁺(X¹Σ⁺)离子的前23个振动能级(j = 0), 并详细列出了每1个振动能级及其相应的经典拐点, 每个振动态的转动常数和6个离心畸变常数, 且提供了振动能级图. 该工作对于实验和后续的理论工作有参考和指导作用.
关键词: SiH⁺(X¹Σ⁺)离子/
势能曲线/
光谱常数/
自旋-轨道耦合

English Abstract

全文HTML

--> --> -->

分子离子是自然界中普遍存在的物质形态. 在星际化学研究中, 分子离子的电子结构和光谱特性对了解在恒星大气和星际空间中发生的物理和化学过程有重要意义^[1-6]. 例如, CH⁺离子, 作为星云扩散过程中形成的较大碳氢化合物, 研究者们在理论和实验上对其进行了大量的研究^[7-9]. 由于在星际空间中含有丰富的Si和H元素^[10], 从理论上来讲, SiH⁺离子应广泛存在于星际介质和恒星大气中, 实际上, 在太阳光球层的光谱中已观测到了SiH⁺离子的存在^[1]. 考虑到SiH⁺离子在星际化学和等离子体物理中重要性^[1-4], 不论是在实验还是在理论上对其都予以了足够的关注.
实验上, Douglas和Lutz^[2]首先在含硅烷的氦的空心阴极放电发射谱中观察到了SiH⁺离子的不同电子态${{\rm{A}}^1}\Pi —{{\rm{X}}^1}{\Sigma ^ + }$跃迁光谱带, 并测量了(1, 0), (2, 1)和(2, 0)的谱线位置. 1970年, Grevesse和Sauval^[1,3]在太阳光谱中观测到SiH⁺离子${{\rm{A}}^1}\Pi —$${{\rm{X}}^1}{\Sigma ^ + } $的吸收光谱, 确认了太阳光球层SiH⁺的存在, 同时计算出了SiH⁺离子${{\rm{A}}^1}\Pi —{{\rm{X}}^1}{\Sigma ^ + }$光谱带中(0, 0)和(0, 1)跃迁以及SiH⁺离子${{\rm{A}}^2}\Delta —{{\rm{X}}^2}\Pi$光谱带中(0, 0)跃迁的振子强度. 1977年, Singh和Vanlandingham^[11]在实验室中测量了SiH⁺基态振动跃迁(1, 0), (2, 1)和(2, 0)的谱线位置, 并计算了其振动能级. Carlson等^[12]确认并分析了SiH⁺离子${{\rm{A}}^1}\Pi —{{\rm{X}}^1}{\Sigma ^ + }$的(2, 0)和(3, 0)振动跃迁光谱带, 测定了${{\rm{A}}^1}\Pi$态的ν = 0, 1, 2和3时的寿命, 并把他们转换成A—X跃迁的振子强度的表达形式. Hishikawa和Karawajczyk^[13]测定了SiH⁺离子的(0, 3)和(0, 4)的A—X跃迁光谱带, 并结合(0, 0), (0, 1), (0, 2), (1, 0), (1, 1)^[2], (2, 0), (3, 0)^[12]光谱带的跃迁数据计算出了SiH⁺(${{\rm{X}}^1}{\Sigma ^ + }$)的光谱常数. Davies和Martineau^[14]使用激光光谱学的方法在硅烷的等离子体中测量了SiH⁺基态${{\rm{X}}^1}{\Sigma ^ + }$态的基本振转光谱带. 2016年, Mosnier等^[15]测量了SiH⁺离子L-内壳层光谱中主要共振的能量和光解离截面, 并通过组态相互作用的方法对光谱特征进行了理论分析.
理论上, 人们也对SiH⁺离子开展了一系列高水平的从头算研究. 1986年, Hirst等^[16]用多参考组态相互作用(MRCI)的方法^[17]计算了SiH⁺离子${{\rm{X}}^1}{\Sigma ^ + }$, ${{\rm{A}}^1}\Pi $, ${{\rm{a}}^3}\Pi $和${{\rm{1}}^3}{\Sigma ^ + }$态的势能曲线, 并给出了${{\rm{X}}^1}{\Sigma ^ + }$和${{\rm{a}}^3}\Pi $的光谱常数. 1998年, Matos等^[18]采用完全活性空间的自洽场(CASSCF)和多体微扰理论的方法计算了SiH⁺离子的${{\rm{X}}^1}{\Sigma ^ + }$态的势能曲线和光谱常数, 同时使用完全活性空间的耦合簇方法和MRCI的方法研究了SiH⁺离子的${{\rm{A}}^1}\Pi$态. Sannigrahi等^[19]使用大高斯基组, 应用组态相互作用的方法计算了SiH⁺离子${{\rm{X}}^1}{\Sigma ^ + }$和${{\rm{A}}^1}\Pi$态的光谱常数, 同时计算了激发态${{\rm{A}}^1}\Pi$的寿命和${{\rm{A}}^1}\Pi — {{\rm{X}}^1}{\Sigma ^ + }$的跃迁振子强度${f_{00}}$, 并且与实验进了对比. 2018年, 应用Molpro 2015程序包^[20], Zhang等^[21]采用包含Davidson修正的多参考组态相互作用方法(MRCI(Q))计算了SiH⁺离子最低的7个$\Lambda — {\rm{S}}$态的势能曲线和光谱常数, 计算中使用了AWCV5Z-DK基组. 同年, 应用ORCA2.9.0程序^[22], Biglari等^[23]采用包含标量相对论效应的MRCI方法计算了SiH⁺离子的基态和低激发态的势能函数, 同时计算了自旋允许的Einstein跃迁系数A和激发态的束缚振动能级的寿命.
尽管已经对SiH⁺离子的各个电子态进行了大量的理论和实验研究, 但是精确的SiH⁺离子${{\rm{X}}^1}{\Sigma^ + }$态的解析势能函数(APEF)、光谱常数、振转能级和自旋-轨道耦合(SOC)等方面仍然缺乏系统的研究. 本文基于Molpro 2012程序包^[24], 应用MRCI(Q)的方法, 使用aug-cc-pVXZ(AVXZ)和aug-cc-pV(X+d)Z(AVXdZ)基组进行能量点的从头计算, 其中X = Q, 5, 6. 然后应用Aguado-Paniagua函数^[25,26]拟合势能曲线函数, 并对AVX Z和AVX dZ(X = Q, 5)基组的能量点应用外插到完全基组集极限(CBS)方法^[27,28]进行修正. 基于该势能函数, 计算了SiH⁺离子基态X¹Σ⁺态的光谱常数和振动能级, 并研究了SOC效应对该体系的影响. 该工作对于实验和后续的理论工作有参考价值和指导作用.

2

-->

2.1.单点能计算

SiH⁺$({{\rm{X}}^1}{\Sigma ^ + })$离子所有的单点能都采用MRCI(Q)方法进行从头算, 计算采用AVX Z和AVX dZ (X = Q, 5, 6)基组. SiH⁺离子是双原子离子, 对称点群是$ {C_{\infty v}}$, 在Molpro 2012程序包中使用其阿贝尔点群C_2v子群. 在本文的计算中将5个分子轨道确定为活化空间, 分别是3个a1, 1个b1和1个b2分子轨道. Si⁺原子在3S3P轨道上的3个电子, H原子1S轨道上的1个电子被放在活化空间, 即这4个电子分布在上述5个分子轨道上, 剩下的10个电子放在5个闭壳层轨道, 包括3个a1, 1个b1, 1个b2. 除此之外, 还有310个外部轨道, 分别是108个a1, 76个b1, 76个b2和50个a2分子轨道. SiH⁺离子的核间距都选择在0.8a₀—29a₀之间.
2 -->

2.2.CBS方法

计算电子结构时通常采用1个高斯型轨道展开基组, 基组的不完备性产生基组重叠误差(BSSE)^[29,30], 影响计算的准确性. Varandas^[27,28]提出, BSSE误差可以通过有限基组单点能计算外推到完备基组(CBS)极限来纠正, 其基于Dunning的相关一致基组外推电子能量的方案如下.
MRCI计算水平下的能量可写成

$ {E}_{X}({\boldsymbol{R}})={E}^{\rm{CAS}}({\boldsymbol{R}})+{E}^{\rm{dc}}({\boldsymbol{R}}), $

其中下标X表示计算中使用的AVXZ基组的类型, R是空间坐标的向量, 上标CAS和dc分别表示完备活性空间能量及动态相关能量.
应用Karton和Martin^[31]提出的KM方案可得CAS能量

$ {E}_{X}^{\rm{CAS}}({\boldsymbol{R}})={E}_{\infty }^{\rm{CAS}}({\boldsymbol{R}})+B/{X}^{{\rm{\alpha}} }, $

其中α = 5.34是衰变指数, $E_{\infty} ^{{\rm{CAS}}}({\boldsymbol{R}})$为$X \to \infty $的能量, 参数B和$E_{\infty} ^{{\rm{CAS}}}({\boldsymbol{R}})$可通过原始CAS能量点拟合得到.
根据Varandas^[27,28]提出的统一的单重态和三重态外推方案, 动态相关(dc)能量为

$ {E}_{X}^{\rm{dc}}({\boldsymbol{R}})={E}_{\infty }^{\rm{dc}}({\boldsymbol{R}})+\frac{{A}_{3}}{{(X+\alpha )}^{3}}+\frac{{A}_{5}}{{(X+\alpha )}^{5}}, $

其中系数A₅满足下式关系

${A_5} = {A_5}(0) + cA_3^{5/4};$

$E_{\infty} ^{{\rm{dc}}}$和A₃由能量点拟合得到; α =–3/8; $c = $$ –1.17847713 E_{\rm h}^{-5/4}$; A₅(0) = 0.0037685459E_h.
2 -->

2.3.势能曲线函数

本文中的势能函数曲线采用的是Aguado-Paniagua函数, 即双原子势能函数${V_{{\rm{AB}}}}$可以表示为短程势和长程势之和^[25,26]:

$ \begin{split}{V_{{\rm{AB}}}} =\;& {V_{{\rm{short}}}} + {V_{{\rm{long}}}} = \frac{{{a_0}}}{{{R_{{\rm{AB}}}}}}{{\rm{e}}^{ - {\beta _1}{R_{{\rm{AB}}}}}}\\&+ \sum\limits_{i = 1}^n {{a_i}{{\left({{R_{{\rm{AB}}}}{{\rm{e}}^{ - {\beta _2}{R_{{\rm{AB}}}}}}} \right)}^i}} , \end{split}$

这种函数形式可以保证双原子势能${V_{{\rm{AB}}}}$在${R_{{\rm{AB}}}} \to 0$时为无限大, 同时保证原子势能在解离极限时(${R_{{\rm{AB}}}} \to \infty $)趋于0. (5)式中的线性参量${a_i}~(i = 0, $$ 1, 2, \cdots, n)$和非线性参量${\beta _i}~{{(}}i = 1, 2{{)}}$可以从拟合过程中得到, 本文中取n = 12, 这是综合考虑后拟合的最优结果.

2

-->

3.1.势能函数

分别使用几种不同的基组和方法(AVQZ, AV5Z, AV6Z, CBS(Q, 5), AVQdZ, AV5dZ, AV6dZ, CBS(Qd, 5d)), 获得了SiH⁺(X¹Σ⁺)离子的0.8a₀—29a₀范围内的112个从头算能量点. 基于这些能量点, 应用Aguado-Paniagua函数拟合得到APEF. 为了提高精确度, 使用了12个参数, 得到了几种不同基组和不同方法下的APEFs, 函数的具体参数列于表1 (表中只列出了主要讨论的AV6Z, CBS(Q, 5), AV6dZ和CBS(Qd, 5d)).

	AV6Z	CBS(Q, 5)	AV6dZ	CBS(Qd, 5d)	SA-AV6dZ	SOC-AV6dZ
a0	0.50876826×101	0.50552062×101	0.50858283×101	0.50691706×101	0.50773275×101	0.50772768×101
a1	–0.13804619×100	–0.14563907×100	–0.13801387×100	–0.14215220×100	–0.13720269×100	–0.15322183×100
a2	–0.13563746×101	–0.14531223×101	–0.13570613×101	–0.14215828×101	–0.16375066×101	0.30937784×100
a3	–0.51802913×102	–0.49687570×102	–0.51738027×102	–0.50317640×102	–0.42586263×102	–0.92938545×102
a4	0.62749955×103	0.59645776×103	0.62624067×103	0.60422890×103	0.45856480×103	0.11152320×104
a5	–0.48068238×104	–0.45486708×104	–0.47942732×104	–0.45972031×104	–0.30344319×104	–0.81653091×104
a6	0.26148147×105	0.24858810×105	0.26073093×105	0.24994077×105	0.14706913×105	0.40426343×105
a7	–0.98935973×105	–0.94946694×105	–0.98651660×105	–0.94886015×105	–0.51962969×105	–0.13681997×106
a8	0.24960293×106	0.24200403×106	0.24891691×106	0.24047472×106	0.12676883×106	0.31028426×106
a9	–0.39722347×106	–0.38879401×106	–0.39620641×106	–0.38442238×106	–0.19927330×106	–0.44979467×106
a10	0.35937312×106	0.35468541×106	0.35853489×106	0.34921672×106	0.18029764×106	0.37617755×106
a11	–0.14069370×106	–0.13986829×106	–0.14040272×106	–0.13721966×106	–0.71149416×106	–0.13802294×106
β1	0.6890	0.6800	0.6890	0.6840	0.6870	0.6870
β2	0.7470	0.7470	0.7470	0.7470	0.7470	0.7470
?Ermsd/ (kcal·mol–1)	1.60176420×10–2	1.61755859×10–2	1.60042370×10–2	1.627559848×10–2	9.45767662×10–3	1.11170443×10–2

表1SiH⁺(X¹Σ⁺) APEFs的拟合参数
Table1.Parameters of APEFs for SiH⁺(X¹Σ⁺).

图1是使用AV6Z基组和CBS(Q, 5)方法得到的SiH⁺(X¹Σ⁺)离子的从头算能量点(蓝色圆点)和拟合给出的势能曲线(红色实线). 两幅图中的上部区域是短程作用范围, 由于在该范围内能量变化范围较大, 因此纵坐标采用对数标度, 横坐标的取值范围是1a₀—2a₀, 纵坐标的取值范围为10^–2E_h—10¹E_h. 中间区域横坐标取值范围是2a₀—10a₀, 纵坐标的取值范围为0至–0.14E_h, 其内插图为长程作用范围, 相应的横坐标取值范围是6a₀—26a₀和纵坐标的取值范围为0至–0.005E_h. 通过将曲线纵坐标标度的减小和横坐标标度的增大, 清晰地展示出渐近区域内势能曲线和从头算能量点相吻合的特征. 底部是拟合的势能曲线与从头算能量点之间的误差, 单位为cm^–1. 从整体来看, 两种方案拟合得到的APEFs不论是在短程区域还是长程区域都表现出平滑的行为特征, 从头算能量点和拟合曲线之间符合得非常好, 误差均小于10 cm^–1. 从表1可以看出, 使用CBS(Q, 5)和AV6Z基组的方均根误差(RMSD)为1.61755859 × 10^–2和1.60176420 × 10^–2 kcal/mol.
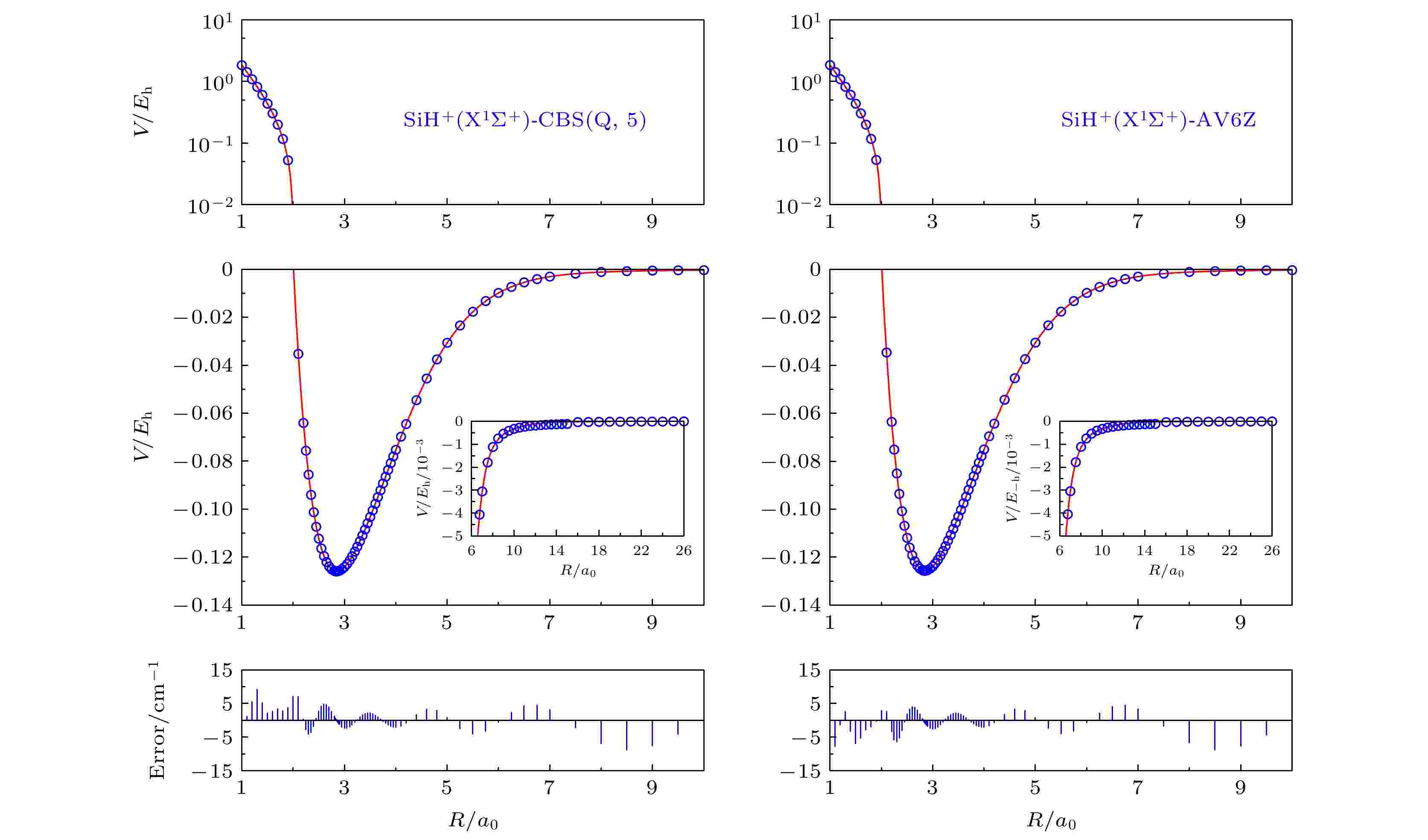图 1 SiH⁺(X¹Σ⁺)在CBS(Q, 5)和AV6Z基组下的势能曲线和从头算能量点
Figure1. Potential energy curves and ab initio points at CBS(Q, 5) and AV6Z results.

为了提高计算精度, 本文还使用了AVQdZ, AV5dZ, AV6dZ基组及CBS(Qd, 5d)方法计算和拟合了SiH⁺(X¹Σ⁺)离子的势能曲线. AVX Z和AVX dZ基组二者都属于Dunning的关联一致基组, 而后者在AVX Z基础上加入了扩散函数, 得到了紧凑的扩充集. 需要说明的是, 在使用AVQdZ和AV5dZ基组计算时, 对于Si和H元素都是使用AVQdZ和AV5dZ基组; 当使用AV6dZ基组计算时, 由于Molpro程序基组使用的限定, 对于Si和H元素分别使用AV6dZ基组和AV6Z基组计算.
图2给出了分别使用CBS(Qd, 5d)方法和AV6dZ基组所得势能曲线和从头算能量点, 蓝色圆点是从头计算得到的能量点, 红色实线是拟合得到的势能曲线函数. 从图2可以看出, 不论是在长程区还是在短程区, 使用CBS(Qd, 5d)方法和AV6dZ基组所得势能曲线光滑且与从头算能量点都符合较好, RMSD较小, 分别为1.60042370 × 10^–2 kcal/mol和1.627559848 × 10^–2 kcal/mol. 在短程区域, 应用AV6dZ基组的拟合曲线和从头算能量点的误差上限为15 cm^–1, CBS(Qd, 5d)方法的误差上限为10 cm^–1, CBS(Qd, 5d)方法相对于应用较耗费机时的AV6dZ基组计算更有优势.
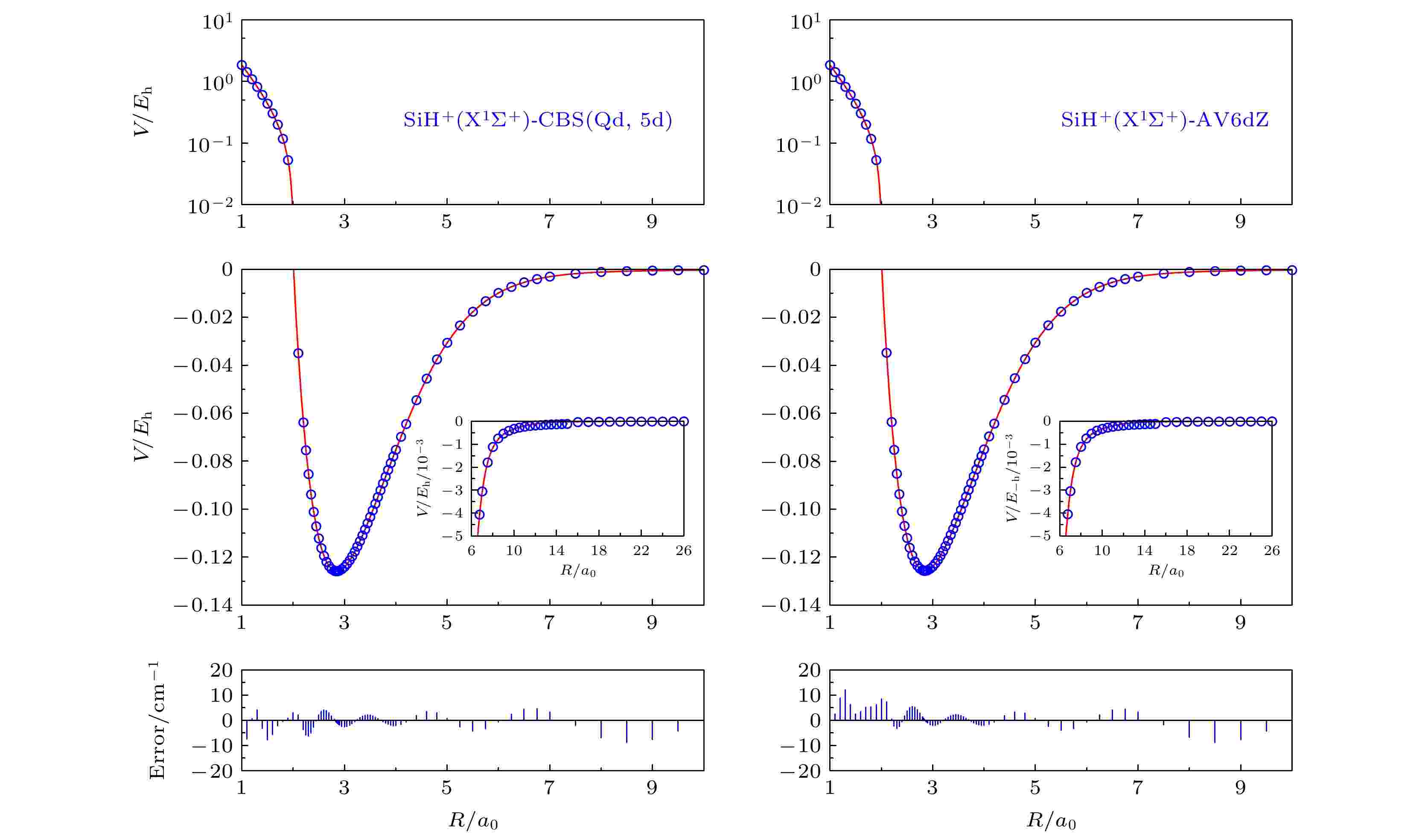图 2 SiH⁺(X¹Σ⁺)应用CBS(Qd, 5d)和AV6dZ基组的势能曲线和从头算能量点
Figure2. Potential energy curves and ab initio points at CBS(Qd, 5d) and AV6dZ results.

2 -->

3.2.自旋-轨道耦合计算

关于SiH⁺(X¹Σ⁺)离子的SOC效应的讨论涉及到对应同一解离极限${\rm{S}}{{\rm{i}}^ + }({}^2{{\rm{P}}_{\rm{u}}}) + {\rm{H}}({}^2{{\rm{S}}_{\rm{g}}})$的${{\rm{X}}^1}{\Sigma ^ + }$, ${{\rm{A}}^1}\Pi $, ${{\rm{b}}^3}{\Sigma ^ + }$和${{\rm{a}}^3}\Pi $分子态^[19,21]. 应用AV6dZ基组, 在限定这4个分子态的态平均多组态自洽场(SA-CASSCF)和包含Davidson修正的多参考组态相互作用(SA-AV6dZ)的计算基础上, 再考虑SOC的影响, 所得从头算能量点(SOC-AV6dZ)如图3所示.
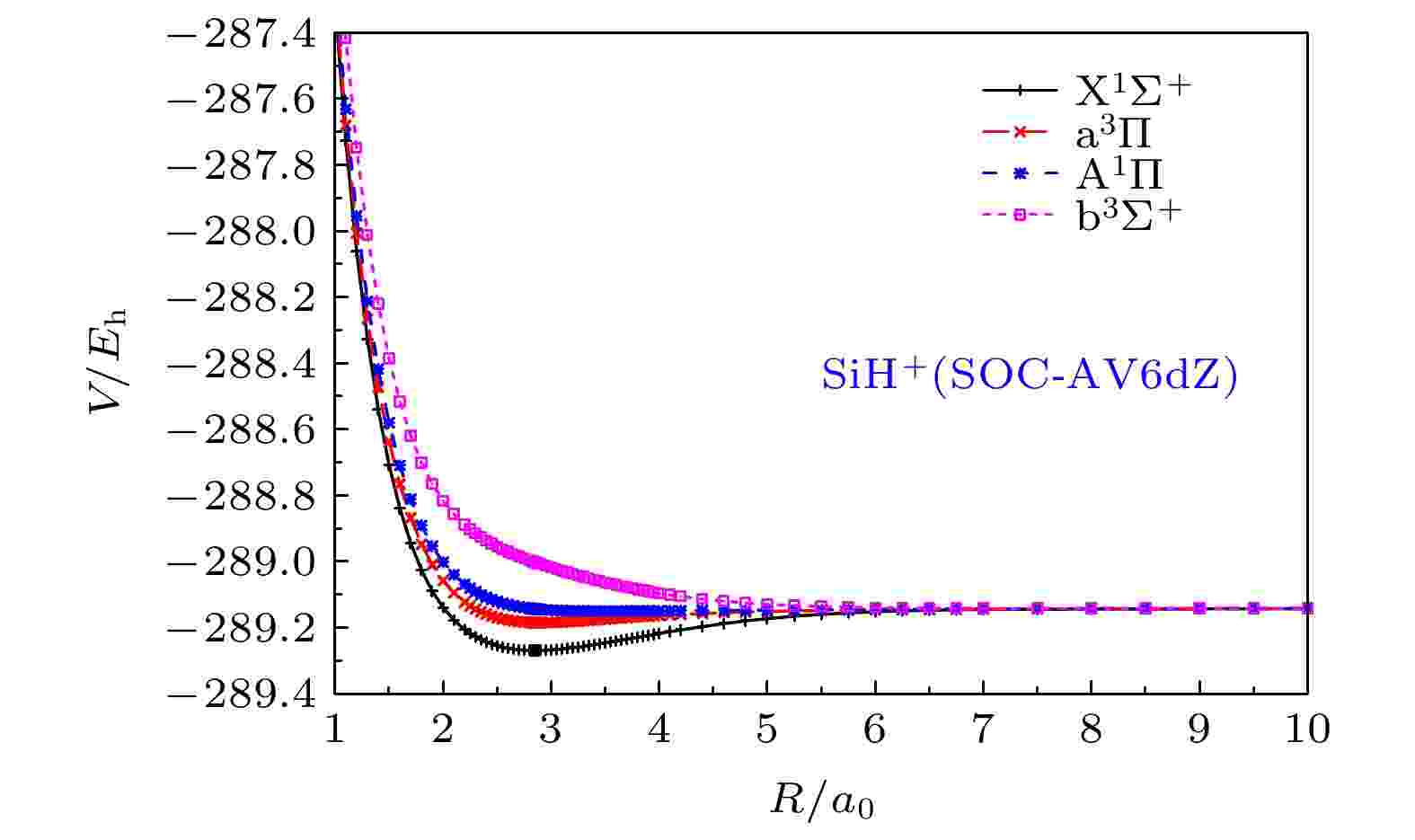图 3 SiH⁺离子的${{\rm{X}}^1}{\Sigma ^ + }$, ${{\rm{A}}^1}\Pi$, ${\rm{b}}{}^3{\Sigma ^ + }$和${{\rm{a}}^3}\Pi$态在SOC-AV6dZ基组下的从头算能量点
Figure3. The ab initio points of ${{\rm{X}}^1}{\Sigma ^ + }$, ${{\rm{A}}^1}\Pi$, ${\rm{b}}{}^3{\Sigma ^ + }$ and ${{\rm{a}}^3}\Pi$ states for SiH⁺ cation at SOC-AV6dZ results.

基于SA-AV6dZ和SOC-AV6dZ两种方法得到的单点能, 应用Aguado-Paniagua函数进行拟合, 拟合的参数如表1所列. 从表1可以看出, SA-AV6dZ和SOC-AV6dZ两种方法的RMSD分别为9.45767662 × 10^–3和1.11170443 × 10^–2 kcal/mol, 是略小于使用基组AV6Z, AV6dZ以及应用CBS (Q, 5), CBS(Qd, 5d)方法的结果. 图4为相应的从头算单点能和拟合势能曲线, 可以看出, 在长程区和短程区域, 使用SA-AV6dZ和SOC-AV6dZ方法所得的势能曲线光滑且与单点能量点符合都比较好, 误差上限分别为10 cm^–1和20 cm^–1, 其中单纯的态平均计算结果(SA-AV6dZ)更优.
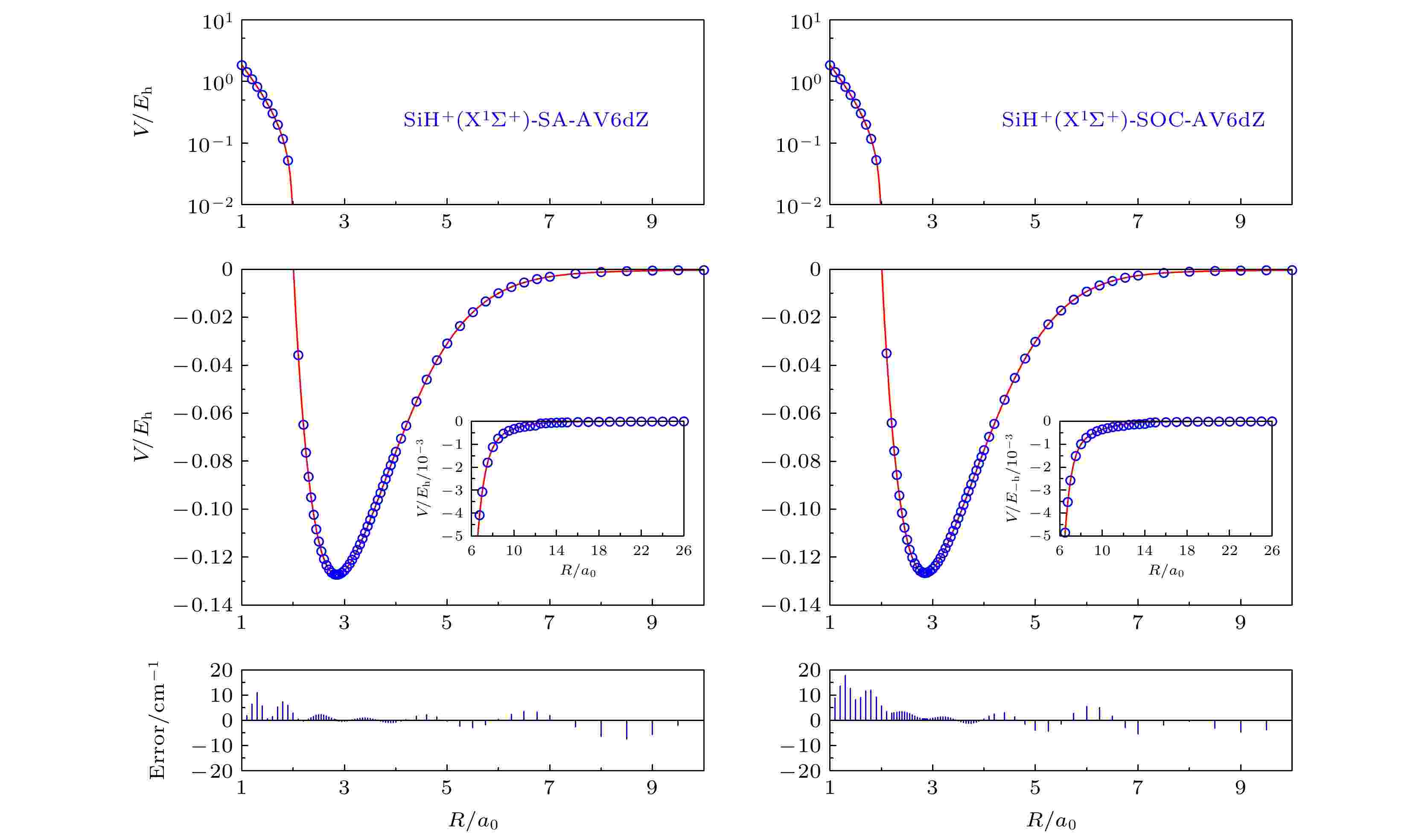图 4 SiH⁺(X¹Σ⁺)在SA-AV6dZ和SOC-AV6dZ基组下的从头算能量点与拟合势能曲线
Figure4. Potential energy curves and ab initio points at SA-AV6dZ and SOC-AV6dZ results.

2 -->

3.3.光谱常数

基于不同的基组和拟合方法(AVQZ, AV5Z, AV6Z, CBS(Q, 5), AVQdZ, AV5dZ, AV6dZ, CBS(Qd, 5d), SA-AV6dZ和SOC-AV6dZ)得到的APEFs, 本文计算了SiH⁺(X¹Σ⁺)离子的平衡键长R_e, 解离能D_e, 振动频率ω_e, 光谱常数ω_eχ_e, α_e, β_e. 各个光谱常数的公式如下:

${B_{\rm{e}}} = \frac{h}{{8{\rm{\pi }}c\mu R_{\rm{e}}^2}},$

$ {\omega _{\rm{e}}} = \sqrt {\frac{{{f_2}}}{{4{{\rm{\pi }}^2}m{c^2}}}} , $

$ {\alpha }_{\rm{e}}=-\frac{6{B}_{\rm{e}}^{\rm{2}}}{{\omega }_{\rm{e}}}\left(\frac{{f}_{3}{R}_{\rm{e}}}{3{f}_{2}}+1\right), $

${\omega }_{\rm{e}}{\chi }_{\rm{e}}=\frac{{B}_{\rm{e}}}{8}\left[-\frac{{f}_{4}{R}_{\rm{e}}^{\rm{2}}}{{f}_{2}}+15{\left(1+\frac{{\omega }_{\rm{e}}{\alpha }_{\rm{e}}}{6{B}_{\rm{e}}^{\rm{2}}}\right)}^{2}\right], $

其中, f₂, f₃和f₄分别是二阶、三阶和四阶力常数^[32,33].
SiH⁺ (X¹Σ⁺)离子的光谱常数列于表2, 表中同时列出了实验^[12,34]和其他一些理论研究结果^{[16,18,21,23]}. 通过对比发现, 本文的计算结果与其他理论计算^{[16,18,21,23]}符合得较好, 与实验数值^[12,34]也基本吻合. 需要说明的是, 就解离能D_e而言, 与实验最接近的是使用AVQZ基组得到的结果, 实验值^[12,34]D_e为0.123203E_h, 用AVQZ基组得到的D_e为0.124640E_h, 与实验值的误差为1.166367%, 理论计算值和实验值差别较大. Zhang等^[21]计算结果是0.125317E_h, 与实验值的误差是1.715867%; Biglari等^[23]的数值是0.124980E_h, 与实验值的误差为1.442335%, 与实验同样偏差较大, 而与本工作的计算结果符合较好. 另外, 应用更巨大的基组、更高级的方法和考虑SOC效应(AV5Z, AV6Z, CBS(Q, 5), AVQdZ, AV5dZ, AV6dZ, CBS(Qd, 5d), SA-AV6dZ和SOC-AV6dZ), 本应得到更精确的结果, 却发现其理论计算值与实验值的偏差反而增大. 基于此, 有理由对实验结果提出疑问, 建议实验工作者重新测定SiH⁺离子的包含解离能在内的各项光谱常数.

基组	De(Eh)	Re(a0)	ωe/cm–1	βe/cm–1	αe/cm–1	ωeχe/cm–1
AVQZ	0.124640	2.851925	2153.245	7.607440	0.219327	42.373
AV5Z	0.125388	2.848589	2155.792	7.625272	0.218960	42.220
AV6Z	0.125584	2.848001	2156.686	7.628410	0.218833	42.189
CBS(Q, 5)	0.125856	2.847053	2157.189	7.633502	0.218622	42.117
AVQdZ	0.125067	2.848877	2156.187	7.623729	0.219427	42.343
AV5dZ	0.125461	2.848067	2156.737	7.628067	0.219011	42.232
AV6dZ	0.125622	2.847728	2157.046	7.629881	0.218849	42.190
CBS(Qd, 5d)	0.125801	2.847782	2156.602	7.629593	0.218534	42.112
SA-AV6dZ	0.127264	2.848531	2163.448	7.625581	0.216725	41.893
SOC-AV6dZ	0.126533	2.848382	2164.033	7.626378	0.217885	42.158
Expe[12,34]	0.123203	2.842338	2157.17	7.6603	0.2096	34.24
Theory[16]	0.118665	2.834590	2155.4	7.6786	0.2082	38.8
Theory[18]	0.123982	2.844039	2172.0	—	—	—
Theory[21]	0.125317	2.834590	2177.9	7.6984	—	36.7
Theory[23]	0.124980	2.842149	2154.3	7.6609	0.2032	35.0

表2SiH⁺(X¹Σ⁺)的平衡键长R_e, 解离能D_e, 振动频率ω_e, 光谱常数ω_eχ_e, α_e和β_e
Table2.Spectroscopic constants compared with the experimental values and other theoretical results for SiH⁺(X¹Σ⁺).

从表2还可知, 基于态平均技术的SA-AV6dZ方法的平衡键长R_e、解离能D_e分别是2.848531a₀和0.127264E_h, 考虑SOC效应后的(SOC-AV6dZ)的R_e和D_e分别是2.848382a₀和0.126533E_h, 平衡位置基本吻合, 误差为0.005231%, 解离能误差为0.577715%, 偏差较小. 基于SA-AV6dZ方法的振动频率ω_e, 光谱常数ω_eχ_e, α_e, β_e分别为2163.448 cm^–1, 7.625581 cm^–1, 0.216725 cm^–1和41.893 cm^–1, 考虑SOC效应后的数值分别为2164.033 cm^–1, 7.626378 cm^–1, 0.217885 cm^–1和42.158 cm^–1, 误差分别为0.027033%, 0.010451%, 0.532391%和0.628588%, 偏差均较小. 根据以上数值对比, 发现SOC效应对SiH⁺离子光谱常数各项的影响较小.
2 -->

3.4.振动能级

基于SiH⁺(X¹Σ⁺)离子的APEF, 核运动的径向薛定谔方程^[35]为

$\begin{split}&\left[ { - \frac{{{\hbar ^2}}}{{2\mu }}\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{r^2}}} + \frac{{{\hbar ^2}}}{{2\mu {r^2}}}j{{(}}j + 1{{)}} + V{{(}}r{{)}}} \right]{\psi _{v,j}}{{(}}r{{)}} \\=\;& {E_{v,j}}{\psi _{v,j}}{{(}}r{{),}}\end{split}$

其中, μ是约化质量, j是转动量子数, v是振动量子数, r是核间距, V(r)是该体系的APEF. 在给定振动能级的基础上, 转动能级表达形式如下:

$\begin{split} {E_{v,j}} =\;& G(v) + {B_v}\left[ {j(j + 1)} \right] + {D_v}{\left[ {j(j + 1)} \right]^2} \\ &+ {H_v}{\left[ {j(j + 1)} \right]^3} + {L_v}{\left[ {j(j + 1)} \right]^4} \\& + {M_v}{\left[ {j(j + 1)} \right]^5} + {N_v}{\left[ {j(j + 1)} \right]^6} \\&+ {O_v}{\left[ {j(j + 1)} \right]^7} ,\end{split} $

式中, G(v)为体系的振动能级; B_v为体系惯性转动常数; D_v, H_v, L_v, M_v, N_v和O_v分别是为6个离心畸变常数.
表3和表4列出了SiH⁺(X¹Σ⁺)离子在SOC-AV6dZ方法下, 转动量子数j = 0时的前23个振动能级G(v), 经典拐点, 转动常数B_v和6个离心畸变常数D_v, H_v, L_v, M_v, N_v和O_v. 理论上说, SOC-AV6dZ方法的计算结果由于采用更巨大的基组(AV6dZ)、更高级的方法(SA-MRCI(Q))和考虑SOC效应可以得到最高精度的APEF、光谱常数和振动能级. 图5给出了SiH⁺(X¹Σ⁺)离子在SOC-AV6dZ方法下, j = 0时的前23个振动能级图.

v	G(v)/ cm–1	Rmin(a0)	Rmax(a0)	Bv/ cm–1
0	1074.467	2.62981	3.11141	7.530487
1	3171.224	2.49347	3.33862	7.336827
2	5200.543	2.40984	3.51594	7.142529
3	7162.231	2.34756	3.67498	6.947281
4	9055.742	2.29761	3.82512	6.750433
5	10880.124	2.25595	3.97091	6.551101
6	12634.005	2.22031	3.91505	6.348250
7	14315.600	2.18934	4.26009	6.140735
8	15922.726	2.16213	4.40742	5.927312
9	17452.802	2.13803	4.55893	5.706603
10	18902.835	2.11661	4.71650	5.477032
11	20269.364	2.09752	4.88227	5.236702
12	21548.363	2.08051	5.05888	4.983201
13	22735.066	2.06540	5.24986	4.713296
14	23823.694	2.05206	5.46016	4.422419
15	24807.010	2.04041	5.69731	4.103776
16	25675.599	2.03041	5.97379	3.746622
17	26416.625	2.02208	6.31278	3.332604
18	27011.579	2.01553	6.76545	2.826988
19	27432.546	2.01096	7.48310	2.158867
20	27650.956	2.00861	9.05975	1.323582
21	27734.462	2.00771	11.47553	0.838944
22	27769.256	2.00734	16.60576	0.360244

表3SiH⁺(X¹Σ⁺)离子在SOC-AV6dZ方法下, j = 0时的前23个振动能级G(v)、经典拐点和惯性转动常数B_v
Table3.Vibrational levels G(v), classical turn point androtational constant B_v for SiH⁺(X¹Σ⁺) when j = 0 at SOC-AV6dZ result.

v	Dv (× 10–4)	Hv (× 10–8)	Lv	Mv	Nv	Ov
0	–3.7712102	1.4824556	–9.1045 × 10–13	4.1069 × 10–17	–2.4011 × 10–21	6.9631 × 10–26
1	–3.7362090	1.4243863	–8.8032 × 10–13	3.5297 × 10–17	–4.1863 × 10–21	1.8363 × 10–25
2	–3.7039865	1.3618539	–8.9866 × 10–13	2.9262 × 10–17	–5.1444 × 10–21	1.9171 × 10–25
3	–3.6778687	1.2884893	–9.4914 × 10–13	2.3397 × 10–17	–5.8593 × 10–21	9.6796 × 10–26
4	–3.6608093	1.2011917	–1.0216 × 10–12	1.6648 × 10–17	–6.8904 × 10–21	–1.1678 × 10–25
5	–3.6553038	1.0982022	–1.1140 × 10–12	6.8522 × 10–18	–8.7371 × 10–21	–4.8697 × 10–25
6	–3.6635199	0.9774540	–1.2320 × 10–12	–9.1302 × 10–18	–1.2003 × 10–20	–1.1229 × 10–24
7	–3.6875661	0.8351772	–1.3901 × 10–12	–3.5900 × 10–17	–1.7702 × 10–20	–2.2781 × 10–24
8	–3.7298613	0.6645057	–1.6143 × 10–12	–8.0925 × 10–17	–2.7799 × 10–20	–4.5064 × 10–24
9	–3.7936180	0.4536483	–1.9481 × 10–12	–1.5748 × 10–16	–4.6321 × 10–20	–9.0505 × 10–24
10	–3.8835055	1.8293995	–2.4663 × 10–12	–2.9088 × 10–16	–8.1928 × 10–20	–1.8869 × 10–23
11	–4.0066389	–0.1804552	–3.3026 × 10–12	–5.3251 × 10–16	–1.5445 × 10–19	–4.1577 × 10–23
12	–4.1741837	–0.6927552	–4.7113 × 10–12	–9.9426 × 10–16	–3.1311 × 10–19	–9.8710 × 10–23
13	–4.4041727	–1.4546951	–7.2135 × 10–12	–1.9417 × 10–15	–6.9300 × 10–19	–2.5871 × 10–22
14	–4.7268845	–2.6591579	–1.1978 × 10–11	–4.0783 × 10–15	–1.7160 × 10–18	–7.7417 × 10–22
15	–5.1961278	–4.7106022	–2.1959 × 10–11	–9.5527 × 10–15	–4.9431 × 10–18	–2.7809 × 10–21
16	–5.9157772	–8.5688303	–4.5904 × 10–11	–2.6336 × 10–14	–1.7665 × 10–17	–1.2991 × 10–20
17	–7.1117968	–16.938203	–1.1615 × 10–10	–9.3420 × 10–14	–8.7454 × 10–17	–9.0301 × 10–20
18	–9.3643712	–39.467832	–3.9578 × 10–10	–4.9264 × 10–13	–7.1396 × 10–16	–1.1444 × 10–18
19	–14.323856	–114.68916	–1.7949 × 10–9	–3.4005 × 10–12	–7.1696 × 10–15	–1.6154 × 10–17
20	–18.399913	–47.324191	1.5501 × 10–9	–7.5768 × 10–13	–3.7548 × 10–14	–1.9274 × 10–17
21	–14.637253	–291.40012	–2.0665 × 10–8	–1.4452 × 10–10	–1.3084 × 10–12	–1.3806 × 10–14
22	–57.213156	–20756.133	–1.6655 × 10–5	–1.7512 × 10–6	–2.1241 × 10–7	–2.8187 × 10–8

表4SiH⁺(X¹Σ⁺)离子在SOC-AV6dZ方法下, j = 0时的前23个振动能级的6个离心畸变常数D_v, H_v, L_v, M_v, N_v和O_v
Table4.Six centrifugal distortion constants D_v, H_v, L_v, M_v, N_v和O_v for the top 23 vibrational states of SiH⁺(X¹Σ⁺) when j = 0 at SOC-AV6dZ result.

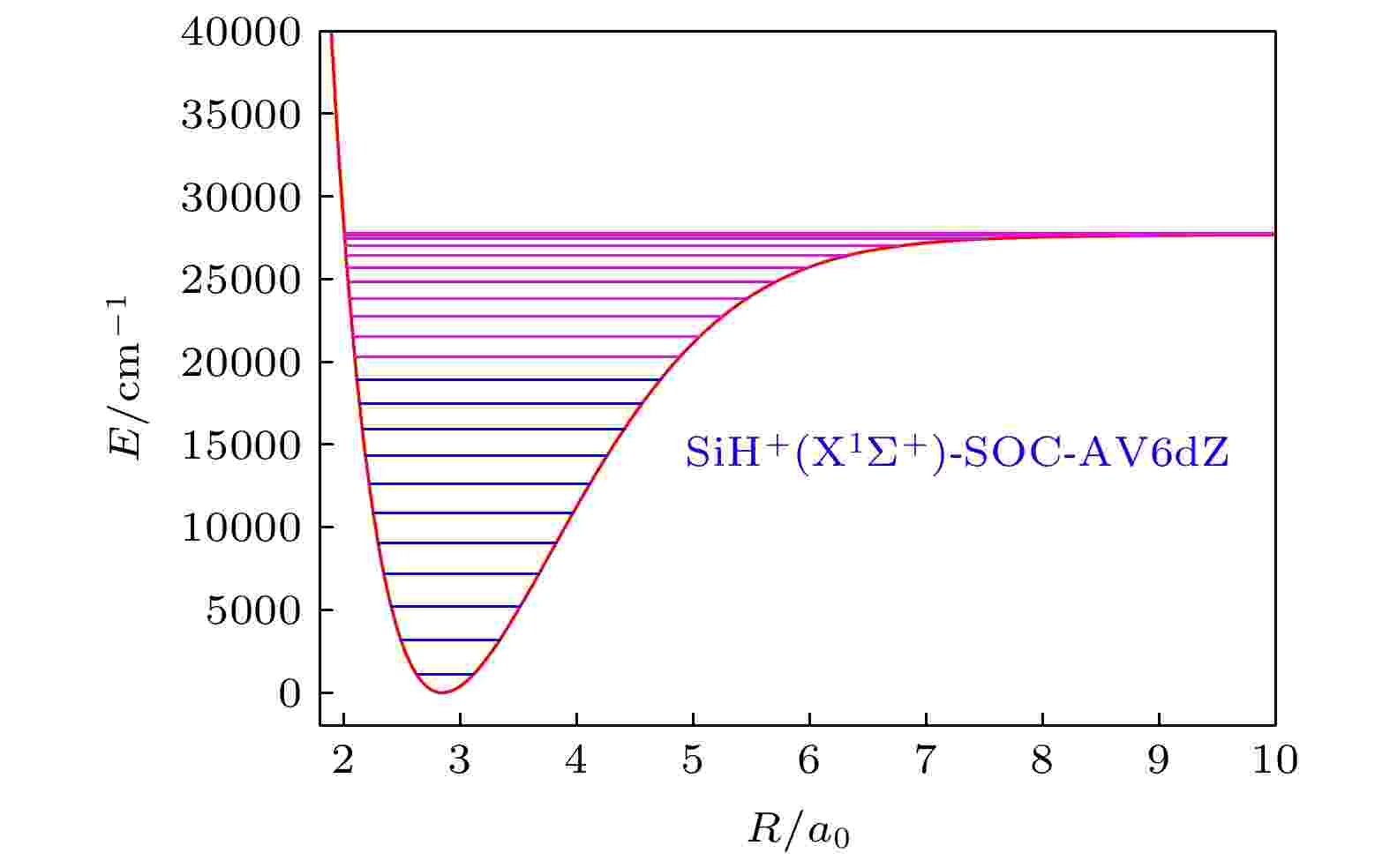图 5 SiH⁺(X¹Σ⁺)离子在SOC-AV6 dZ方法下, j = 0时的前23个振动能级
Figure5. Top 23 vibrational energy levels of SiH⁺(X¹Σ⁺) when j = 0 at SOC-AV6 dZ result.

从表3可以看出, 对于j = 0的前23个能级, 其经典拐点的取值范围较大, 从v = 0的R_min = 2.62981a₀, R_max = 3.11141a₀到v = 22的R_min = 2.00734a₀, R_max = 16.60576a₀, 这与能级较多相关. v = 22的振动能级(27769.256 cm^–1)与解离极限(27770.8 cm^–1)非常接近, 二者差值仅为1.544 cm^–1. 并且v = 22和v = 21的振动能级差值非常小, 为34.794 cm^–1, 仅为v = 22的振动能级的0.125%, 以至于在图5的能级图中几乎区别不出这两个振动能级.
由表4可以看出, 在这6个离心畸变常数中, 除D_v范围变化较小外(–3.7712102 × 10^–4— –5.721315 × 10^–3), 其余的5个数值变化范围非常大, 例如, O_v的范围为6.9631 × 10^–26— –2.8187 × 10^–8, 横跨了18个数量级. 所以在表4中只有D_v和H_v把数量级标注在第1行, 其余各常数的数量级都附在数值后.

本文基于Molpro 2012程序包, 应用MRCI(Q)的方法进行单点能从头算, 然后采用Aguado-Paniagua函数进行拟合, 得到了SiH⁺(X¹Σ⁺)离子的不同基组、不同方法和是否考虑SOC情况(AVQZ, AV5Z, AV6Z, CBS(Q, 5), AVQdZ, AV5dZ, AV6dZ, CBS(Qd, 5d), SA-AV6dZ和SOC-AV6dZ)下的APEFs. 基于APEFs计算了光谱常数D_e, R_e, ω_e, B_e, α_e和ω_eχ_e, 本文的计算结果与其他理论计算^{[16,18,21,23]}符合得较好, 与实验数值^[12,34]也基本吻合, 同时讨论了SOC效应对光谱常数的影响. 基于SOC-AV6dZ方法下的APEF, 通过求解径向薛定谔方程, 首次计算了SiH⁺ (X¹Σ⁺)离子前23个振动态(j = 0), 并详细列出了每一个振动能级及其相应的经典拐点, 每个振动态的转动常数和6个离心畸变常数并提供了振动能级图. 该工作对于实验和后续的理论工作有参考和指导作用.