摘要: 针对大口径干涉型红外光谱辐射计, 分析了不平行于主光轴的入射光, 对理想仪器线型函数的影响. 本文系统介绍了对仪器线型函数产生影响的截断效应、有限视场效应、离轴效应和离焦效应, 并通过HITRAN数据库对理想的水汽吸收光谱进行仿真, 建立了仪器线型函数误差与光谱畸变的定量关系. 根据仿真结果, 提出了因子权重校正算法. 利用水汽吸收的仿真数据对因子权重校正算法进行验证, 光谱漂移从0.51 cm
–1 降低到0.01 cm
–1 以下. 通过自研干涉型红外光谱辐射计对标准黑体的观测实验, 验证因子权重校正算法的准确性, 实测数据的光谱漂移从0.226 cm
–1 降低到0.012 cm
–1 , 校正后的光谱数据更为准确.
关键词: 遥感 /
干涉型红外光谱辐射计 /
仪器线型函数 /
因子权重法 English Abstract Calibration method of instrument line shape for infrared radiometer Sun Yong-Feng 1,2 ,Xu Liang 1 ,Shen Xian-Chun 1 ,Wang Yu-Hao 1,2 ,Xu Han-Yang 1 ,Liu Wen-Qing 1 1.Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China Fund Project: Project supported by the Key Research Program of Frontier Sciences of Chinese Academy of Sciences (Grant No. QYZDY-SSW-DQC016), the Key Research and Development Plan of Anhui Province, China (Grant No. 1804d08020300), the National Natural Science Foundation of China (Grant No. 41941011), and the National Key Research and Development Project, China (Grant Nos. 2016YFC0201002, 2016YFC0803001-08)Received Date: 09 February 2021Accepted Date: 15 March 2021Available Online: 07 June 2021Published Online: 20 July 2021Abstract: Interferometric infrared spectral radiometer has high luminous flux and large passing aperture, so the spectral data collected by the instrument are the convolution of the target spectral data and the instrument line shape (ILS). The main factors affecting the ILS include truncation effect, finite field of view effect, off-axis effect, defocus effect and relative position of detector and so on. In this paper the truncation effect, finite field of view effect, off-axis effect and defocus effect on ILS are expounded. These ILS errors all cause the ideal spectrum to drift towards the low wave number and widen. In this paper, the ideal absorption spectrum of water vapor is simulated by the line-by-line integration, through using MATLAB software and combining with the data of water vapor spectrum in HITRAN database, and the quantitative relationship between the error of instrument linear function and spectral distortion is established. According to the simulation results, a factor weight correction algorithm is proposed. It is believed that with this method, the error spectrum caused by ILS has the same optical properties as the ideal spectrum, but the optical path difference is different. Therefore, the coefficient matrix H can be constructed to establish the quantitative relationship between the error spectrum and the ideal spectrum, and the error spectrum can be corrected by using Landweber iterative algorithm. In this paper, the simulation data of water vapor absorption are used to verify the factor weight correction algorithm, and the spectral drift decreases from 0.51 cm–1 to less than 0.01 cm–1 . The accuracy of the factor weight correction algorithm is verified by the experimental observation of the standard black body with self-developed interferometric infrared spectral radiometer. The spectral drift of the measured data decreases from 0.226 cm–1 to 0.012 cm–1 , and the corrected spectral data are more accurate.Keywords: remote sensing /infrared spectrometer /instrument line shape /weight factor method 全文HTML --> --> --> 1.引 言 干涉型红外光谱辐射计采用干涉分光技术, 通过反演目标的红外辐射光谱, 可以定量获取被观测物体的温度、湿度和化学组分等物理特征, 在遥感和大气监测等领域有着广泛的应用[1 ] . 干涉型红外光谱辐射计具有大视场、宽谱段和高通量的技术优点[2 ,3 ] , 其单次观测即可反演多种气体组分, 是重点发展的大气探测仪器. 但是由于辐射计的干涉原理, 其采集到的原始数据为干涉数据, 需要经过傅里叶变换、辐射定标和仪器响应函数校正等过程, 才可以得到准确的大气辐亮度光谱[4 -6 ] .[4 ] , 但是由于傅里叶变换原理和红外光谱辐射计的光学系统设计, 采集到的光谱数据是目标理想光谱数据和自身仪器线型函数(ILS, instrument line shape)的卷积. 影响仪器线型函数的因素有很多种, 主要有: 截断效应、有限视场效应、离轴效应、离焦效应和探测器相对位置等等[7 ,8 ] . 通过理论模型分析校正仪器线型函数误差的方法主要两种, 美国极轨气象卫星Suomi-NPP上搭载的干涉型大气垂直探测仪(CRIS)[9 ] , 通过退卷积的方法校正仪器线型函数畸变带来的测量光谱误差; 我国风云四号气象卫星搭载的大气垂直探测仪[10 ] , 通过准确仪器各项参数, 对仪器线型函数理论模型进行仿真, 校正光谱误差.[11 ] , 对HFY-300A型标准黑体进行观测, 测量不同孔径光阑情况下的黑体辐射光谱. 通过因子权重法对黑体辐射光谱进行校正, 考察仪器线型函数引起的光谱误差是否减小, 复原光谱的波数精度是否提高.2.干涉型红外光谱辐射计仪器线型函数原理及校正分析 仪器线型函数定义为干涉仪系统对接近于狄拉克函数的单色光(线宽可以忽略)所得到的谱线分布函数[12 ] . 仪器线型函数主要由干涉仪动镜的运动范围(窗口截断)决定, 但还受到有限视场、离轴效应、离焦效应和动镜失准直等因素的影响.2.1.仪器线型函数原理分析 2.1.仪器线型函数原理分析 对于波数为$ {v}_{0} $ 的单色光, 其理想的光谱数据$ B\left({v}_{0}\right) $ 可以表示为$ x $ 为光程差, $ I\left(x\right) $ 为干涉数据强度. 事实上, 红外光谱辐射计所测量的干涉图, 永远只能采集到某一有限的极大光程差L , 而不能是无限大. 因此, 在计算复原光谱时, 计算的是区间(–L , L )内的干涉数据:$ {B}_{\mathrm{e}}\left({v}_{0}\right) $ 等于输入光谱$ B\left({v}_{0}\right) $ 与仪器线型函数的卷积, $ \mathrm{*} $ 为卷积符号.图1 仿真波数为1555 $ {\mathrm{c}\mathrm{m}}^{-1} $ 和1580 $ {\mathrm{c}\mathrm{m}}^{-1} $ 的两束单频激光, 在动镜运动距离不同情况下, 截断效应对复原光谱的影响. 图1(a) , (b) 为动镜运动距离为2500个采样点时, 两束单频激光的干涉数据及其复原光谱. 此时复原光谱受到截断效应影响较小. 图1(c) 中的干涉数据, 动镜运动距离为图1(a) 中的一半, 其复原光谱如图1(d) 所示. 可以看到, 相较于图1(c) , 动镜运动距离变短时, 复原光谱会产生旁瓣并展宽. 因此需要对干涉数据进行切趾, 减小光谱旁瓣.图 1 波数1555 cm–1 和1580 cm–1 入射光不同动镜运动距离干涉数据和复原光谱Figure1. Wavenumber 1555 cm–1 and 1580 cm–1 interferometric data and reconstructed spectra of different moving distance of incident light.图2 所示, 假定仪器的孔径光阑宽度为d , 轴外光线跟主光轴的夹角为$ \theta $ . 通过几何关系可知, 动镜运动相同的距离, 轴外光线相较于轴上光线有更小的光程差, 此时离轴角度为$ \theta $ 的反射光和透射光, 两束光线之间的光程差$ \mathrm{O}\mathrm{P}\mathrm{D} $ 为图 2 有限视场效应光路示意图Figure2. Schematic diagram of finite field-of-view effect light path.$ \Delta {X}_{\mathrm{m}} $ 为动镜的运动距离, $ {\Delta X}_{0} $ 为轴上光最大光程差, $ \theta $ 为离轴角度. 此时, 波数为$ {v}_{0} $ 的单色光, 其在焦平面的干涉图为$ L $ 为入射光强. 离轴光束存在着一定的立体角$ \varOmega $ , 在整个立体角上进行积分, 可得到干涉图表达式为8 )式可以看到, 在干涉光路中, 有限视场效应使轴外光线波数向低频方向漂移并展宽, 漂移波数由(9 )式给出:[13 ] . 探测器位置的微小偏差将会对仪器线型函数产生明显影响, 所以需要对离轴效应和离焦效应进行分析. 离轴效应和离焦效应的光路图如图3 所示.图 3 离焦效应与离轴效应光路示意图Figure3. Diagram of light path of defocus effect and off-axis effect图3 显示了探测器离焦时孔径上的点与有限视场效应入瞳上光源之间的关系. 离焦探元上的点可以投影到入瞳处, 相当于将入射角为$ \theta $ 的轴外光线改变为$ {\theta }_{\mathrm{e}\mathrm{f}\mathrm{f}} $ . 入射角$ {\theta }_{\mathrm{e}\mathrm{f}\mathrm{f}} $ 由离焦距离$ \Delta {L}_{\mathrm{f}\mathrm{o}\mathrm{c}\mathrm{u}\mathrm{s}} $ 和入瞳到焦平面的距离L 决定:$ \cos\theta =\theta $ . 因此离焦探元$ \Delta {L}_{\mathrm{f}\mathrm{o}\mathrm{c}\mathrm{u}\mathrm{s}} $ 和离轴探元$ \Delta {L}_{\mathrm{a}\mathrm{i}\mathrm{x}} $ 之间的关系为$ {\beta }_{\mathrm{e}\mathrm{f}\mathrm{f}} $ 可以表示为[14 ] 的研究指出, 对于一个中等分辨率的干涉仪系统, 光学衍射所带来波数漂移小于$ {10}^{-5} $ 数量级, 这个数量级的波数漂移影响可以忽略. 动镜失准直对红外光谱辐射计的光谱影响与有限视场效应类似, 也会导致反演后的光谱向低波数偏移, 并造成频谱的展宽. 中国科学院安徽光学精密机械研究所自主研发的干涉型红外光谱辐射计, 搭载动镜自准直系统[15 ] , 保证动镜倾斜角度小于$ \lambda /25 $ , 此时动镜倾斜对光谱复原的影响也可忽略[16 ] .2.2.仪器线型函数仿真及校正 -->2.2.仪器线型函数仿真及校正 美国极轨气象卫星Suomi-NPP[9 ] 上搭载的干涉型大气垂直探测仪(CRIS), 其采用CO2 激光器对探测仪的仪器线型函数进行标定, 通过退卷积的方法校正测量光谱的仪器线型函数误差. 根据(4 )式可以看出, 仪器实际测量光谱, 可以等效为理想光谱卷积仪器线型函数. 因此, 可以将有限视场、离轴效应和离焦效应对仪器线型函数的影响统一为算子SA, 通过中心波数为950 $ {\mathrm{c}\mathrm{m}}^{-1} $ 的CO2 激光器对探测器的仪器线型函数进行标定. 然后通过(4 )式对光谱进行校正, 即可得到校正后的光谱数据.[10 ] , 其采用面阵型傅里叶变换干涉仪, 长波和中波波段各对应32行4列128个相元. 由于采用面阵探测器, 探测器的中心相元和边缘相元的仪器线型函数必然不同, 但是可以根据边缘相元和中心相元的相对位置, 计算不同位置仪器线型函数的几何关系, 从而校正光谱. 实际上该探测仪的仪器线型函数校正, 是获得准确仪器各项参数后, 根据探测器中心相元和光轴的相对位置, 计算中心相元的仪器线型函数. 然后通过激光器和积分球对光谱仪进行波数标定, 修正探测器和光轴的位置参数, 获得准确的测量光谱的仪器线型函数, 再根据每个相元的相对位置, 计算每个相元的仪器线型函数, 构建数据库校正仪器线型函数.8 )式可以看出, 仪器线型函数的偏差, 改变了轴外光线的光程差, 导致测量光谱向低波数漂移. 具有发散角的光线和平行于主光轴的光线, 具有相同的光谱性质, 只是由于光程差变小的原因, 导致复原光谱展宽并向低波数漂移. 所以我们可以认为, 具有相同光谱性质的轴外光线, 相较于轴上光线, 其光谱能量向低波数进行了溢出, 如图4 所示.图 4 理想光谱与误差光谱权重关系示意图Figure4. Diagram of weight relation between ideal spectrum and error spectrum.图4 理想光谱与误差光谱权重关系示意图. 其中图4(a) 为理想光谱示意图, 从左到右分别为: 平行于主光轴的单色入射光, 经探测器采集到的干涉数据, 复原光谱后波数$ {v}_{0} $ 处光谱强度为$ {p}_{0} $ . 图4(b) 为包含仪器线型函数误差的光谱示意图, 从左到右分别为: 考虑轴外光线和探测器相对位置误差后的入射光, 经探测器采集到的误差干涉数据, 复原光谱后波数为$ {v}_{0} $ 的单色光向低波数展宽, 并且能量向低波数溢出. 假定我们测量到的真实光谱为$ {p}_{\mathrm{r}} $ , 根据图4 $ {p}_{\mathrm{r}} $ 其实由不同发散角产生的光谱叠加而成. 理论上所有具有发散角的光谱与理想光谱$ {p}_{0} $ 具有相同的光谱性质, 所以可以通过下式, 将实测光谱分解为包含不同权重的理想光谱, 则波数为为$ v $ 的误差光谱$ {p}_{\mathrm{r}} $ 为$ {a}_{i} $ 为不同波数的理想光谱对误差光谱的因子权重, $ \Delta v $ 为光谱的采样间隔, n 是理想光谱向低波数漂移的范围, e 是仪器的噪声. 理想光谱向低波数漂移的范围受最大视场角和探元与主光轴偏移的距离影响.12 )式我们可以构建系数矩阵H H 14 )式给出:14 )式, 应用Landweber迭代算法[17 ] , 寻找$ {p}_{0} $ 的最大似然值, 直至迭代收敛. Landweber迭代算法公式为$ \beta $ 为Landweber迭代参数, 范围为(0.01, 1.00).$ 1\;{\mathrm{c}\mathrm{m}}^{-1} $ , 光谱范围为300—2300 cm–1 , 参考激光波长为632.8 nm, 环境温度21 ℃, 大气压力101.325 kPa, 水汽浓度为9 × 10–4 (相对湿度41%), 最大离轴角度4'' , 离焦距离$ \lambda /25 $ . 通过HITRAN数据库获取水汽的吸收谱线, 结合吸收谱线的Lorentz展宽和Doppler展宽[18 -20 ] , 根据逐线积分方法[21 ] 和(8 )式、(10 )式、(11 )式通过MATLAB软件可以仿真仪器在光源为100 ℃黑体时, 所测量到的理想光谱和误差光谱, 仿真流程如图5 所示. 图6(a) 为HITRAN数据库的水汽吸收谱线, 经过Lorentz展宽、Doppler展宽和逐线积分后的透过率谱, 图6(b) 为100 ℃黑体辐射, 加载水汽透过率后的辐亮度谱.图 5 水汽吸收光谱仿真及校正流程图Figure5. Flow chart of water vapor absorption spectrum simulation and correction.图 6 (a)水汽透过率谱; (b)包含水汽吸收峰的辐亮度谱Figure6. (a) Water vapor transmittance spectrum; (b) radiance spectra containing water vapor absorption peaks.图7 所示. 可以看到, 相较于理想光谱光谱, 误差光谱存在明显的展宽和向低波数漂移, 选取波数为1653.14 $ {\mathrm{c}\mathrm{m}}^{-1} $ 的特征吸收峰, 可以看到误差光谱的吸收峰偏移了0.52 $ { \mathrm{c}\mathrm{m}}^{-1} $ .图 7 100 ℃时水汽的理想吸收光谱、仪器线型函数误差光谱与校正光谱Figure7. Ideal absorption spectra of water vapor at 100 ℃, error spectra of instrument linear function and correction spectra.14 )式, 选取波数为1653.14 $ {\mathrm{c}\mathrm{m}}^{-1} $ 的水汽特征吸收峰, 获取n =5的校正系数矩阵H 图5 所示. 可以看到校正后光谱其吸收峰的漂移和展宽明显减小. 选择中心波数在1464.95 $ {\mathrm{c}\mathrm{m}}^{-1} $ (波段$ 1460.01—1470.22\;{\mathrm{c}\mathrm{m}}^{-1} $ )的水汽吸收峰进行对比, 校正前误差光谱的吸收峰漂移为0.49 $ {\mathrm{ }\mathrm{c}\mathrm{m}}^{-1} $ , 校正后水汽吸收峰漂移小于0.01$ {\mathrm{c}\mathrm{m}}^{-1} $ . 该算法可以减小由于宽视场和探测器偏移所导致的光谱向低波数漂移和展宽.3.仪器线型函数校正实验 本文采用干涉型红外光谱辐射计对标准黑体光源进行观测, 验证仪器线型函数校正方法的可行性. 实验采用的干涉型红外光谱辐射计是中国科学院安徽光学精密机械研究所自主研发的被动式遥感外光谱辐射计, 光谱范围1.6—20.0 μm, 光谱分辨率1 $ {\mathrm{c}\mathrm{m}}^{-1} $ , 光谱稳定度0.004 $ {\mathrm{c}\mathrm{m}}^{-1} $ . 辐射计配有大口径窄视场镜头, 其通光口径为, 辐射计在探测器前设有孔径光阑, 光阑大小为$ 1—14\;\mathrm{ }\mathrm{m}\mathrm{m} $ 可调. 黑体光源选择中国科学院上海技术物理研究所研制的HFY-300A型标准黑体, 其温度范围为+5—400 ℃, 温度精度为0.01 ℃, 温度稳定度为0.01 ℃/8 h. 实验方式采用辐射计实验室条件下观测黑体辐射源, 在保证黑体辐射充满整个视场的情况下, 调整孔径光阑大小. 实验共采集4组不同孔径大小的黑体辐射数据, 黑体温度为100 ℃, 每组数据采集64条光谱进行叠加平均, 可以有效降低随机噪声对光谱数据的干扰. 图8 显示了实测数据复原光谱. 实际上随着孔径光阑变大, 仪器线型函数对光谱产生的影响更加明显, 水汽的吸收峰向低波数漂移并展宽. 图9 显示了不同孔径光阑的光谱图, 归一化后的对比. 归一化后可以看到, 水汽在中心波数为1464.95$ { \mathrm{c}\mathrm{m}}^{-1} $ 的和1653.14 $ { \mathrm{c}\mathrm{m}}^{-1} $ 特征吸收峰, 随着孔径光阑的变大, 其吸收强度逐渐变小, 并向低波数漂移和展宽.图 8 100 ℃黑体光源不同视场光阑复原光谱图Figure8. Resurrected spectrum of 100 ℃ blackbody source with different field of view by diaphragm.图 9 100 ℃黑体光源不同视场光阑复原光谱归一化光谱图Figure9. Normalized spectral images of 100 ℃ black-body light source with different field of view apertures.[21 ] 对水汽温度压力展宽的研究, 温度压力的变化仅影响水汽吸收峰面积的大小, 并不影响水汽吸收峰波数的准确度, 因此可以通过水汽吸收峰的波数位置, 来判断测量光谱的准确性. 红外光谱辐射计采用大口径的窄视场镜头, 实际测试中孔径光阑为2 mm的光谱数据, 其水汽在$ 1460.01—1470.22\;{\mathrm{c}\mathrm{m}}^{-1} $ 和$ 1650.08—1660.21\;{\mathrm{c}\mathrm{m}}^{-1} $ 波段吸收峰波数分别为1464.95 $ {\mathrm{c}\mathrm{m}}^{-1} $ 和1653.14 $ {\mathrm{c}\mathrm{m}}^{-1} $ , 与第2 节仿真的理想光谱特征吸收峰波数一致, 可以近似认为是理想光谱数据. 实验采用的HFY-300 A型标准黑体, 其辐射面是直径为230 mm的圆形面源. 红外辐射计配有大口径窄视场的准直镜头, 黑体实验时红外辐射计镜头贴近黑体辐射面源, 入射光可以认为全部来自黑体辐射和仪器自发辐射, 因此可以忽略实验室环境背景的入射光.2 节提出的仪器线型函数校正算法, 可以将归一化后孔径光阑为2 mm的光谱数据作为理想光谱数据, 归一化后11 mm的光谱数据作为误差数据, 对数据进行仪器线型函数校正, 校正结果如图10 所示. 对比图9 可以看出, 中心波数为1464.95 $ { \mathrm{c}\mathrm{m}}^{-1} $ 的水汽吸收峰, 校正前波数误差为0.215 $ {\mathrm{c}\mathrm{m}}^{-1} $ , 校正后波数误差为0.008 $ {\mathrm{c}\mathrm{m}}^{-1} $ , 波数误差减小了0.207 $ {\mathrm{c}\mathrm{m}}^{-1} $ . 因子权重校正算法显著降低了仪器线型函数带来的光谱误差. 表1 选取了4组水汽的特征吸收峰, 对比了校正前和校正后的光谱波数误差, 可以看到, 校正前光谱平均波数误差为0.226 $ { \mathrm{c}\mathrm{m}}^{-1} $ , 校正后为0.012 $ {\mathrm{c}\mathrm{m}}^{-1} $ , 波数误差减小了0.214 $ { \mathrm{c}\mathrm{m}}^{-1} $ .图 10 波数为1465. 2 $ {\mathrm{c}\mathrm{m}}^{-1} $ 的水汽吸收峰校正前后对比Figure10. Comparison of water vapor absorption peak with wave number of 1465. 2 $ {\mathrm{c}\mathrm{m}}^{-1} $ before and after correction.Wavenumbers /$ {\mathrm{c}\mathrm{m}}^{-1} $ Wavenumber Error-reduction value/$ {\mathrm{c}\mathrm{m}}^{-1} $ Measured spectrum Correction spectrum 1430—1440 0.242 0.018 0.224 1460—1470 0.215 0.008 0.207 1572—1582 0.217 0.010 0.207 1650—1660 0.231 0.012 0.219 Average 0.226 0.012 0.214
表1 100 ℃黑体光源孔径光阑为11 mm光谱校正前后波数误差对比Table1. Comparison of wave number errors before and after spectral correction of 11 mm aperture diaphragm of 100 ℃ blackbody light source.4.结 论 本文主要研究了大口径干涉型红外光谱辐射计, 其不平行于主光轴的入射光, 对理想仪器线型函数的影响. 首先研究了对仪器线型函数产生影响的截断效应、有限视场效应、离轴效应和离焦效应, 并通过HITRAN数据库结合吸收谱线的Lorentz展宽和Doppler展宽, 对理想的水汽吸收光谱进行仿真, 建立了仪器线型函数误差与光谱畸变的定量关系. 根据仿真结果, 提出了因子权重校正算法校正仪器线型函数引起的光谱误差. 并利用因子权重算法, 对波段为$ 1460.01—1470.22\;{\mathrm{c}\mathrm{m}}^{-1} $ 的仿真水汽误差数据进行校正, 校正后光谱漂移从0.51 $ {\mathrm{c}\mathrm{m}}^{-1} $ 降低到0.01 $ \;{\mathrm{c}\mathrm{m}}^{-1} $ 以下. 在自研红外光谱辐射计对标准黑体的观测实验中, 验证因子权重校正算法的准确性, 实测数据的光谱漂移从0.226 $ {\mathrm{c}\mathrm{m}}^{-1} $ 降低到0.012 $ \;{\mathrm{c}\mathrm{m}}^{-1} $ , 结果表明校正后的光谱数据更为准确. 










 图 1 波数1555 cm–1和1580 cm–1入射光不同动镜运动距离干涉数据和复原光谱
图 1 波数1555 cm–1和1580 cm–1入射光不同动镜运动距离干涉数据和复原光谱




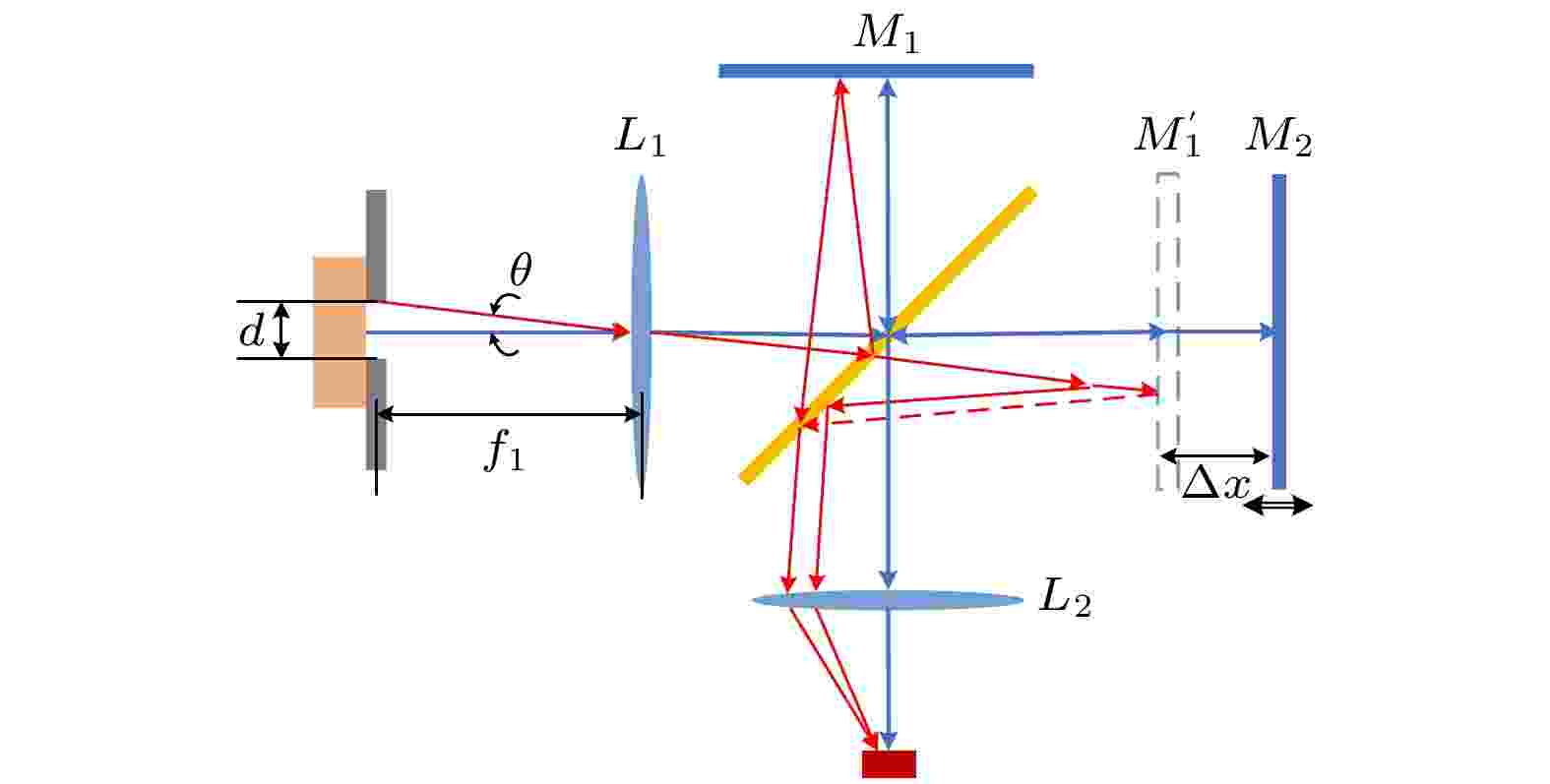 图 2 有限视场效应光路示意图
图 2 有限视场效应光路示意图





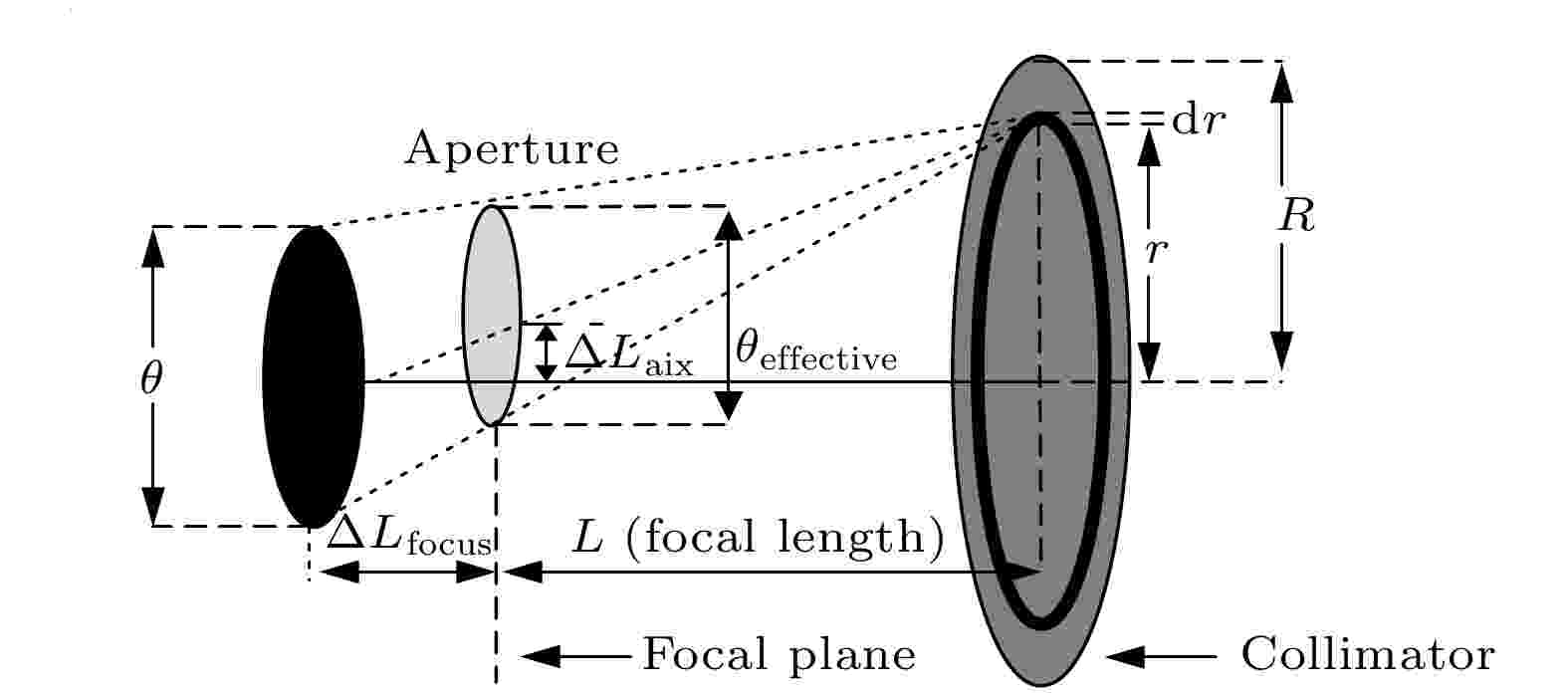 图 3 离焦效应与离轴效应光路示意图
图 3 离焦效应与离轴效应光路示意图












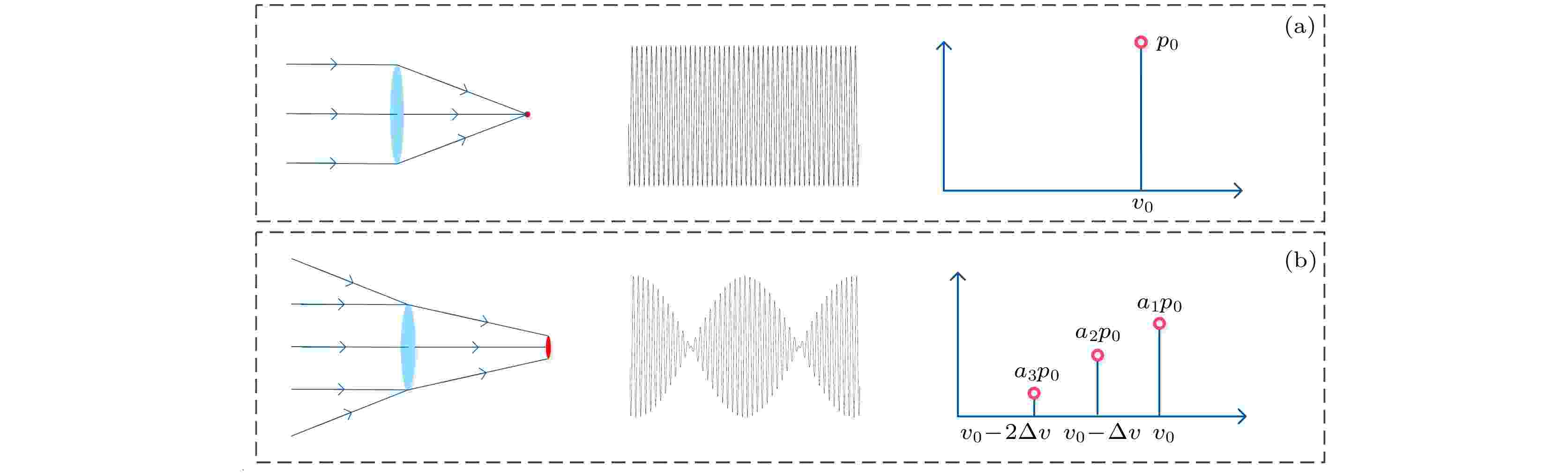 图 4 理想光谱与误差光谱权重关系示意图
图 4 理想光谱与误差光谱权重关系示意图























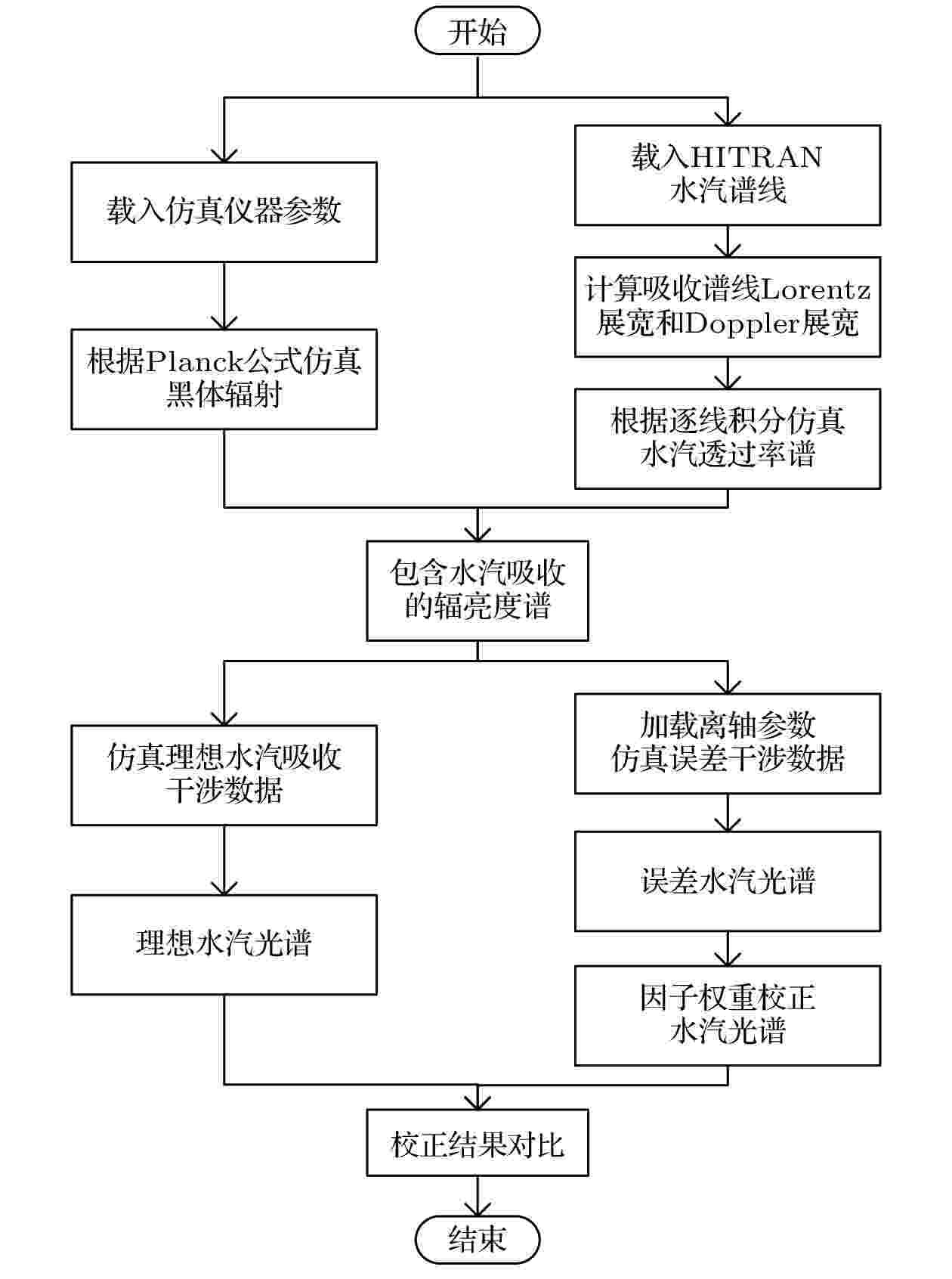 图 5 水汽吸收光谱仿真及校正流程图
图 5 水汽吸收光谱仿真及校正流程图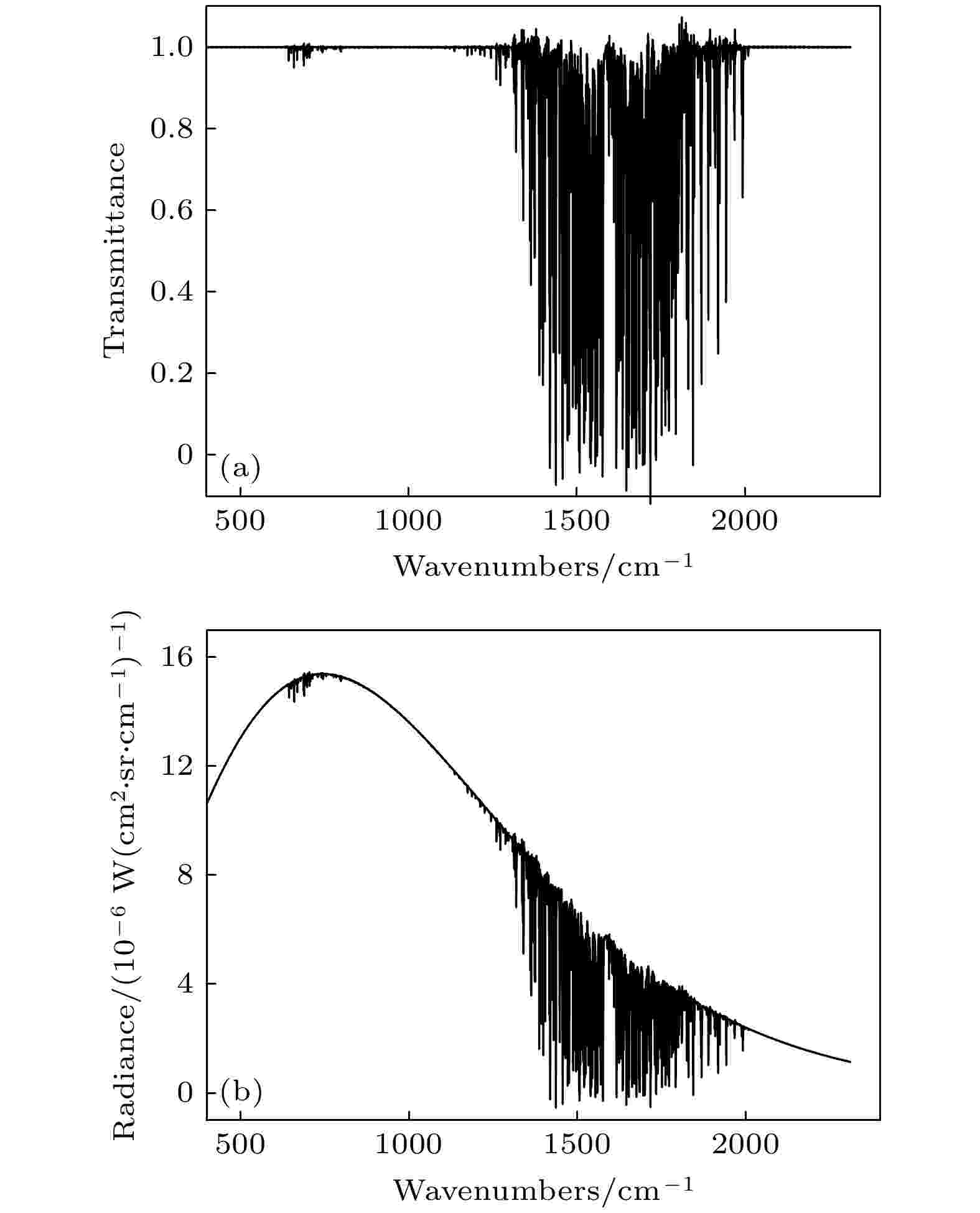 图 6 (a)水汽透过率谱; (b)包含水汽吸收峰的辐亮度谱
图 6 (a)水汽透过率谱; (b)包含水汽吸收峰的辐亮度谱

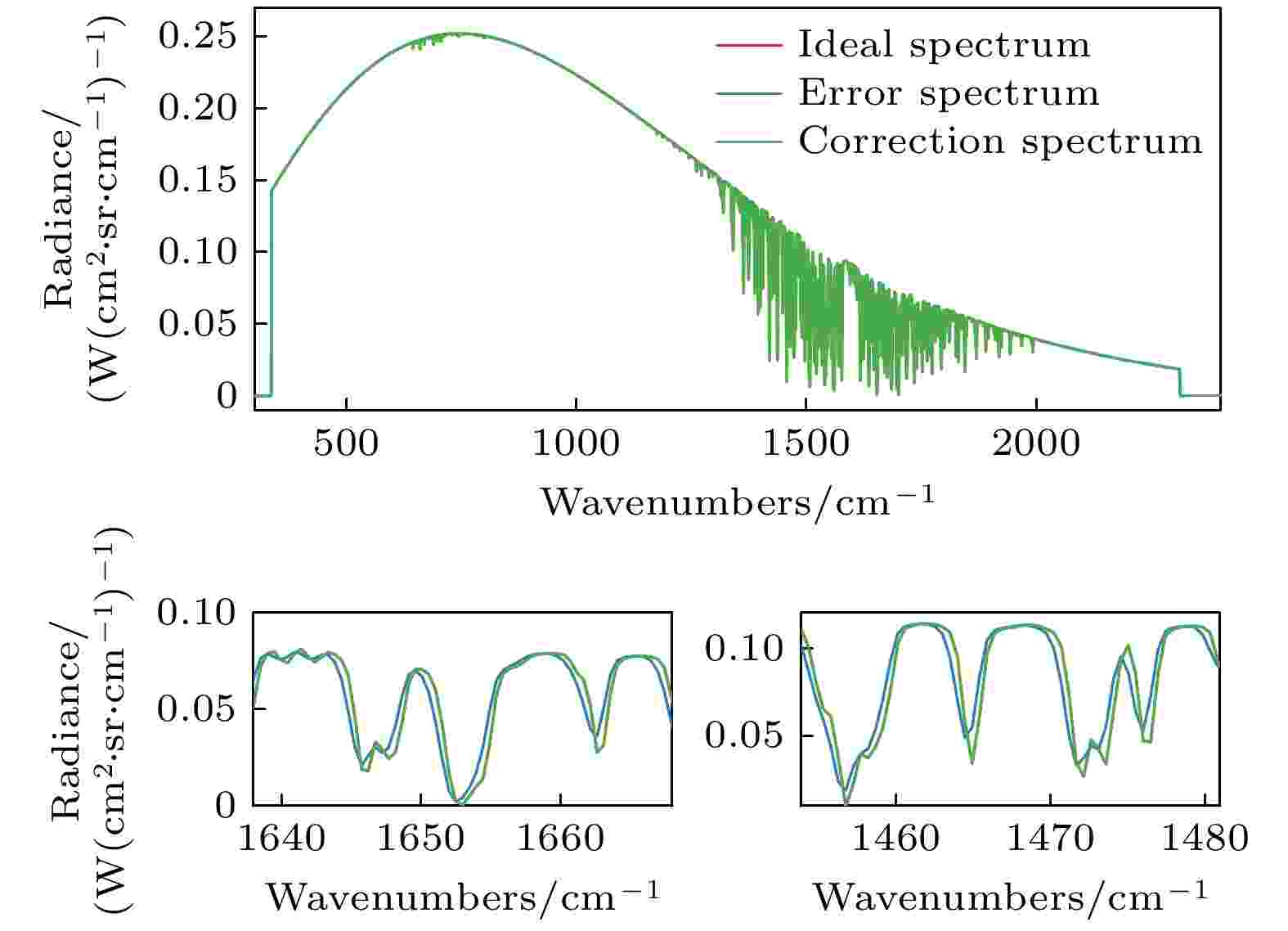 图 7 100 ℃时水汽的理想吸收光谱、仪器线型函数误差光谱与校正光谱
图 7 100 ℃时水汽的理想吸收光谱、仪器线型函数误差光谱与校正光谱



















 图 8 100 ℃黑体光源不同视场光阑复原光谱图
图 8 100 ℃黑体光源不同视场光阑复原光谱图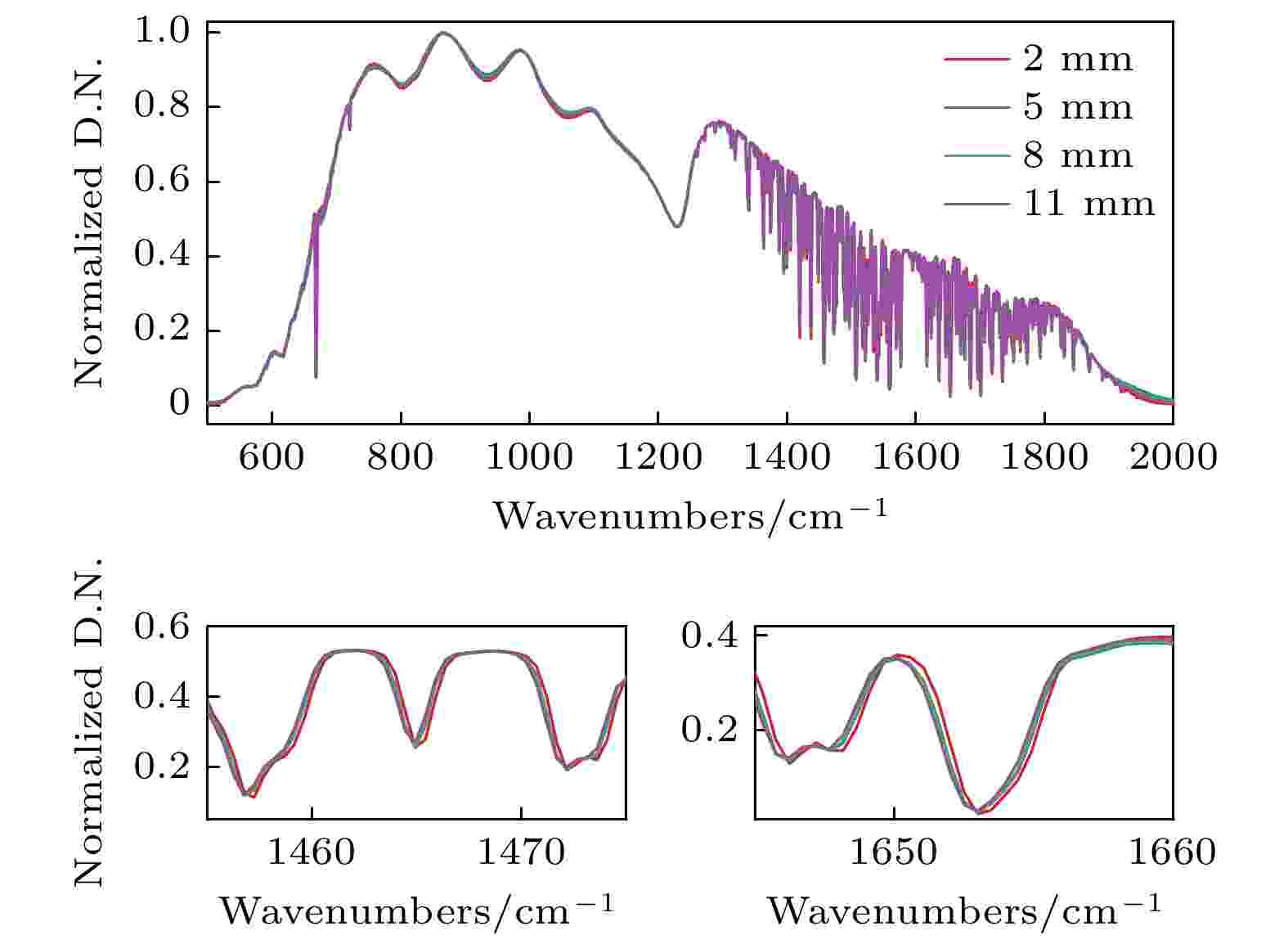 图 9 100 ℃黑体光源不同视场光阑复原光谱归一化光谱图
图 9 100 ℃黑体光源不同视场光阑复原光谱归一化光谱图






























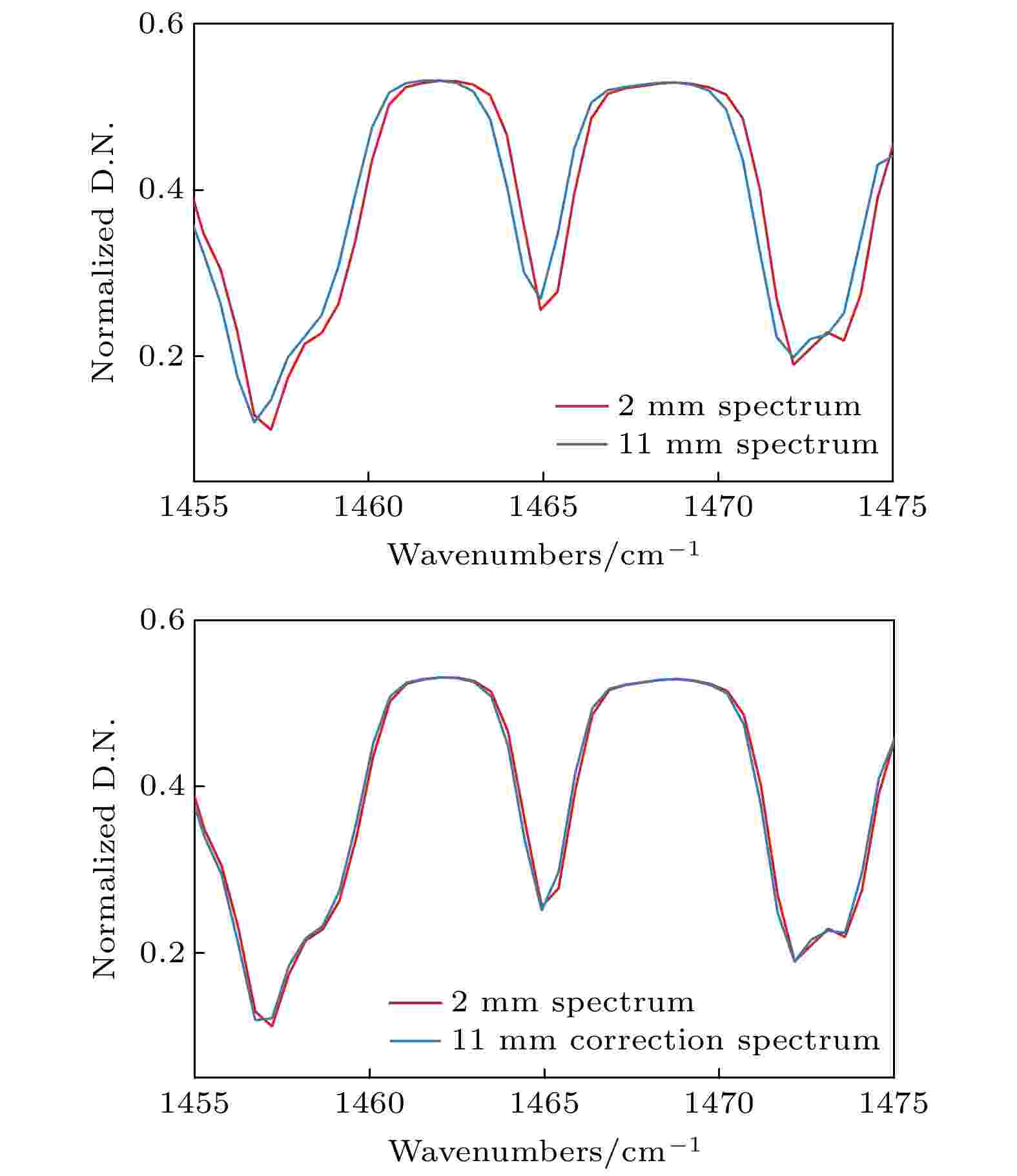 图 10 波数为1465. 2
图 10 波数为1465. 2 










