删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

混合气体测量中重叠吸收谱线交叉干扰的分离解析方法

本站小编 Free考研考试/2021-12-29
摘要:在基于可调谐二极管激光吸收光谱技术(tunable diode laser absorption spectroscopy, TDLAS)进行多种组分混合气体测量时, 经常会遇到吸收谱线之间存在相互干扰的现象, 这也是使用该技术测量过程中的主要“瓶颈”. 比如在前期的应用中: 微量一氧化碳(CO)和甲烷气体(CH4)在同时检测时两者的吸收谱线存在严重的重叠干扰现象, 特别是在高浓度CH4存在的环境下, 微量CO气体吸收信号会被干扰甚至湮没, 无法实现有效解调, 这是通过谱线选取所不能解决的问题. 因此, 针对此问题本文提出了基于支持向量回归模型, 以CO和CH4吸收谱线的严重重叠干扰问题为例, 通过选择线性核函数建立CO支持向量回归模型和CH4支持向量回归模型, 可对CO和CH4的混合气体吸收谱线进行解调, 最终获得两种气体浓度的准确测量结果. 通过实验分别实现了四种不同浓度CH4环境下微量CO气体的检测, 得到的CO和CH4浓度(气体的体积分数)测量的绝对误差分别小于2 × 10–6和0.2 × 10–2; 通过不同浓度的固定配比实验分析, CO和CH4气体的测量值与实际值之间的相关系数分别达到了0.998和0.9995, 且CO和CH4气体测量结果的绝对误差分别不超过2 × 10–6和0.1 × 10–2, 完全满足了混合气体的精确测量, 为实现多场合混合气体目标的实时监测提出了解决方案.
关键词: 可调谐二极管激光吸收光谱/
混合气体/
谱线重叠/
支持向量回归

English Abstract


全文HTML

--> --> -->
1.引　言
可调谐二极管激光吸收光谱(tunable diode laser absorption spectroscopy, TDLAS)具有非接触实时测量、分辨率高、灵敏度高、响应速度快等优点[1-6], 能够实现对特定气体分子的高选择性精确测量. 结合波长调制技术和长光程技术的TDLAS系统能够得到更高的检测灵敏度和更低的检测下限[7-9], 已被广泛应用于环境监测、汽车尾气监测、工业气体检测、燃烧诊断、医学诊断等众多领域[10-14].
通常情况下, 采用TDLAS技术同时测量混合气体浓度时, 需要根据每一种气体分子吸收谱线的“指纹识别区”设计一套特定波段的监测系统, 也就是气体和激光光源是一一对应的关系, 这也就导致了整套系统的复杂程度和成本的增加. 虽然当两种气体的吸收谱线比较接近并且不会互相重叠时(如CO和CO2在1579 nm附近的吸收谱线), 可以采用温度控制和驱动电流控制的方法使得一台分布反馈式激光器(distributed feedback laser, DFB laser)能够同时扫描过这两种气体的吸收波长, 进而实现两种气体同时在线检测[15]. 这样不仅能够降低检测系统的复杂程度以节省成本, 也提高了系统的响应率和检测速度. 然而像CO和CO2气体的这类相近而又独立的吸收谱线是特殊的, 大多数情况下两种气体之间的吸收谱线足够接近且存在交叉干扰现象. 为了对混合气体中多种成分进行测量, 科研人员进行了多种相关研究[16,17], 如: Zhang等[18]利用中心波长为1578和1747 nm的两个激光器对比了分时锯齿法、光开关法和多频正弦调制法同时检测H2S和HCl两种气体的优缺点; Shao等[19]利用中心波长为2.3 μm的DFB激光器在低压条件下完成了CO和CH4气体的同时检测. 以上方法虽然提高了混合气体实时检测的可靠性, 但是同时也会增加系统电路、光路或者气路的复杂性. 此外, 在某些应用场合, 上述处理方式仍不可避免地遇到谱线间的交叉干扰问题. 例如常温常压下, CO和CH4的吸收谱线存在严重的交叉干扰现象, 特别是在含有高浓度CH4的特殊场合(例如矿井、天然气泄漏检测等), CO的吸收信号会被湮没在不规则的多峰CH4吸收谱线之下, 此时难以对这两种气体, 特别是微量CO气体进行准确地解析.
为了解决上述谱线干扰的共性问题, 进一步实现简化系统复杂程度、降低系统成本、增加系统可靠性的目的, 本文提出了一种基于支持向量回归(support vector regression, SVR)模型的方法, 来解决TDLAS系统遇到的多组分混合气体检测中的谱线干扰问题. 支持向量机在气体检测方面已经得到了广泛应用. Qu等[20]利用改进的网格搜索算法对支持向量机进行参数优化, 建立了气体的红外光谱定量分析方法, 并且在1%—25%浓度范围内对CO2气体进行定量分析, 得到的绝对误差小于4%; Laref等[21]对比了支持向量回归和偏最小二乘回归在定量分析松树精油蒸气应用中的性能, 得出了支持向量回归具有更高测量精度的结论. 本文以微量CO和较高浓度CH4为例, 经过小样本数据集训练得到CO和CH4气体浓度回归模型, 分别为CO-SVRmodel和CH4-SVRmodel. 经不同浓度的气体测量实验验证, 该模型能够显著解决微量CO气体吸收信号在高浓度CH4吸收信号下被湮没的谱线重叠干扰问题, 实现了微量CO和较高浓度CH4的同时检测, 为实现多组分气体的TDLAS同时测量技术奠定了基础和可行性论证.
2.实验原理
2
2.1.TDLAS原理
-->

2.1.TDLAS原理

根据Lambert-Beer定律, 特定波长的激光光束穿过待测气体会被吸收, 透射光强变化可以表示为
${I_{\rm{t}}} \!=\! {I_0}{\rm{exp}}[ { - S(T)XPL\phi (\upsilon)}] \!=\! {I_0}{\rm{exp}}[ { - \alpha (\upsilon)L}],$
其中I0是激光出射强度; It是透射激光强度; S(T)(cm–2·atm–1)为气体温度为T时的吸收谱线强度; X为待测气体浓度; P(atm)为气体压强; L(cm)为光在待测气体中传播的距离即光程; $ \phi \left(\upsilon \right) $是吸收线型函数, 与气体温度和压力有关, 描述了气体吸收谱线的形状; $ \alpha \left(\upsilon \right) $(cm–1)为待测气体对特定波数$ \upsilon $的吸收率.
为了提高系统的抗干扰能力和检测灵敏度, 引入波长调制技术. 在激光器的扫描信号上叠加一个高频的正弦调制信号, 则激光器在某一时刻t的瞬时频率和出光强度可以表示为
$\upsilon \left( t \right) = \bar \upsilon + a{\rm{cos}}\left( {\omega t + \varphi } \right){\rm{,}}$
${I_0}\left( t \right) = {{\bar I}_0} + {i_0}{\rm{cos}}\left( {\omega t + \varphi } \right){\rm{,}}$
其中$ \bar{\upsilon } $和${\bar I}_{0}$分别为激光器的中心波长和平均光强; $ a $和$ {i}_{0} $分别为频率调制幅度和光强调制幅度; $ \omega $和$ \varphi $分别为正弦调制的频率和初始相位. 调制之后的激光, 被待测气体吸收, 经锁相放大器检测可以获得各个分量的谐波信号, 并且一般情况下$ -\alpha \left(\upsilon \right)L\ll 1 $, 结合Reid和Labrie[22]给出的二次谐波表达式, 得到二次谐波信号峰值与气体浓度成正比, 即
${P_{2{\rm{f}}}} \!\propto\! \frac{{{I_0}S(T)PXL}}{{\pi \Delta \upsilon }}\left\{ {\frac{2}{{{m^2}}}\left[ {\frac{{2 + {m^2}}}{{{{({1 \!+\! {m^2}} )}^{1/2}}}} - 2} \right]} \right\}{\rm{,}}$
其中$ {P}_{2\mathrm{f}} $为二次谐波的峰值; $ \Delta \upsilon $为气体吸收谱线的半高宽; m为无量纲变量, $ m=a/\Delta \upsilon $. 二次谐波信号的峰值和初始光强$ {I}_{0} $也成正比关系. 因此实际测量中, 常使用一次谐波进行光强修正, 消除光强波动引起的峰值变化.
2
2.2.支持向量回归(SVR)原理
-->

2.2.支持向量回归(SVR)原理

SVR原理可以分为线性回归和非线性回归[23], 首先给定一组样本集: (x1, y1), (x2, y2), ···, (xn, yn). 其中, xi (xi∈$ \mathbb{R}$)是第i个样本的光谱数据; yi (yi∈$ \mathbb{R} $)为实际测量得到的第i个样本的气体浓度值.
当所测气体为单一气体时, 气体浓度与光谱数据之间符合线性关系, 构造线性回归模型如下:
$f\left(x\right)={{w}}^{\mathrm{T}}x+b\text{,}$
其中$ {{w}} $为权重向量; b为偏置.
采用ε-不敏感损失函数作为误差函数, 表达式如下:
${l_\epsilon } = \left\{ {\begin{aligned}&0,\;\;\;\;\;\qquad\left| z \right| \leqslant \epsilon ,\\&\left| z \right| - \epsilon ,\;\;\;\;{\rm{otherwise}}.\end{aligned}} \right.$
回归函数的求解问题可以描述为一个二次凸优化问题, 即:
$\begin{split}&{\min _{{{w}},b}}\frac{1}{2}{\left| {\left| {{w}} \right|} \right|^2},\\&{\rm{s.t.}}\left\{ {\begin{aligned}&{{y_i} - \left( {{{w}}\cdot {x_i} + b} \right) \leqslant \epsilon },\\&{\left( {{{w}}\cdot {x_i} + b} \right) - {y_i} \leqslant \epsilon },\end{aligned}} \right.~~ ({i \!=\! 1,2, \cdots ,n}).\end{split}$
根据(6)式和(7)式, 将SVR问题形式化定义为
${\min _{{{w}},b}}\frac{1}{2}{| {| {{w}}|}|^2} + C\mathop \sum \limits_{i = 1}^n {l_\epsilon }( {f( {{x_i}} ) - {y_i}})~~(i = 1,2, \cdots ,n), $
其中C为正则化常数, C越大表示对训练误差大于ε的样本惩罚越大; $ {l}_{\epsilon} $是(6)式对应的ε-不敏感损失函数. 当我们允许SVR在某些样本上出错时, 即引入松弛变量$ {\xi }_{i} $, $ {\xi }_{i}^{*} $后, 目标函数变为
$\begin{split}&~~~~{\min _{{{w}},b}}\frac{1}{2}{\left| {\left| {{w}} \right|} \right|^2} + C\mathop \sum \limits_{i = 1}^n \left( {{\xi _i} + \xi _i^*} \right),\\&{\rm{s.t.}}\left\{ {\begin{aligned}&{{y_i} - \left( {{{w}}\cdot {x_i} + b} \right) \leqslant \epsilon + \xi _i^*,}\\&{\left( {{{w}}\cdot {x_i} + b} \right) - {y_i} \leqslant \epsilon + {\xi _i}}, \\&{{\xi _i},~\xi _i^* \geqslant 0.}\end{aligned}} \right.~\left( {i = 1,2, \cdots ,n} \right),\end{split}$
为了更加高效地求解目标函数, 可以对(9)式使用拉格朗日乘子法. 引入拉格朗日乘子${\mu }_{i}\geqslant 0, $$ \widehat {\mu }_{i}\geqslant 0, {\alpha }_{i}\geqslant 0,~ \widehat{\alpha}_{i}\geqslant 0$, 最终得到目标优化函数的“对偶问题”如下:
$\begin{split}& ~~~ \mathop {\max }\limits_{\alpha ,\hat \alpha } \mathop \sum \limits_{i = 1}^n {y_i}\left( {{{\widehat \alpha _i}} - {\alpha _i}} \right) - \varepsilon \left( {{{\widehat \alpha _i}} + {\alpha _i}} \right) \\& ~~~ - \frac{1}{2}\mathop \sum \limits_{i = 1}^n \mathop \sum \limits_{j = 1}^n \left( {{{\widehat \alpha _i}} - {\alpha _i}} \right)\left( {{{\widehat \alpha _j}} - {\alpha _j}} \right)x_i^{\rm{T}}{x_j}\\&{\rm{s.t.}}~\mathop \sum \nolimits_{i = 1}^m \left( {{{\widehat \alpha _i}} - {\alpha _i}} \right) = 0,\\& \qquad 0 \leqslant {\alpha _i},~~ {{\widehat \alpha _i}} \leqslant C.\end{split}$
通过对偶问题的最优值求解, 可以得到线性SVR的解如下:
$f\left(x\right)=\sum\limits_{i=1}^{n}\left(\widehat{{\alpha }_{i}}-{\alpha }_{i}\right){x}_{i}^{\mathrm{T}}x+b\text{.}$
但是对于混合气体而言, 在原始样本空间是线性不可分的, 此时可以通过引入非线性映射, 将样本空间映射到一个高维的特征空间中, 然后在该特征空间应用SVR线性回归方法求解回归函数.
令$ {{\varphi }}\left(x\right) $表示将样本x映射后的特征向量, 于是, 在特征空间中划分超平面所对应的模型可表示为
$f\left(x\right)={{w}}^{\mathrm{T}}{{\varphi}}\left(x\right)+b\text{.}$
对于(12)式, 经过与线性回归中相同的一系列求解后, 可以得到特征空间中回归模型的解如下:
$f\left(x\right)=\sum\limits_{i=1}^{n}\left(\widehat{{\alpha }_{i}}-{\alpha }_{i}\right){{{\varphi}}\left({x}_{i}\right)}^{\mathrm{T}}{{\varphi}}\left(x\right)+b\text{,}$
其中$ {{{\varphi}}\left({x}_{i}\right)}^{\mathrm{T}}{{\varphi}}\left(x\right) $是样本映射到特征空间之后的内积, 而特征空间维数很高, 甚至可能是无穷维, 因此直接计算$ {{{\varphi}}\left({x}_{i}\right)}^{\mathrm{T}}{{\varphi}}\left(x\right) $是困难的, 为了避开这个障碍, 引入了核函数:
$\kappa \left( {{x_i},{x_j}} \right) = \left\langle {{{\varphi}} \left( {{x_i}} \right),{{\varphi}} \left( {{x_j}} \right)} \right\rangle = {{\varphi}} {\left( {{x_i}} \right)^{\rm{T}}}{{\varphi}} \left( {{x_j}} \right).$
最终, 特征空间下SVM回归模型的解如下:
$f\left(x\right)=\sum\limits_{i=1}^{n}\left(\widehat{{\alpha }_{i}}-{\alpha }_{i}\right)\kappa \left(x,{x}_{i}\right)+b\text{.}$
常用的核函数有线性核函数、多项式核函数和高斯核函数等, 经过实验得出结论, 对于混合气体数据, 使用线性核函数得到的SVR模型效果最优.
3.实验装置
为了实现CO的低浓度测量, 该实验系统选择中心波长为2.3 μm的DFB激光器作为光源. 其波长随着温度和电流变化的调谐性能如图1所示. 共测试了6组不同温度下的电流调谐性能, 均能够获得较好的线性特征, 因此在调谐过程中不会出现激光输出的不稳定性因素. 在本实验中将激光驱动器的扫描电流调节到合适的范围, 使得DFB激光器从2326.6 nm扫描到2327.7 nm的波数范围, 此时中心发射波长为2327.2 nm, 完全覆盖CO的中心吸收谱线.
图 1 DFB激光器电流-波长调谐性能曲线
Figure1. Current-wavelength tuning curve of DFB laser.

实验装置原理图如图2所示, 分别由电路部分(Part A)、光学部分(Part B)、数据采集与分析部分(Part C)、配气系统(Part D)四个功能模块组成. 首先, 电路部分包括函数发生器、激光驱动器和双通道锁相放大器, 该部分完成DFB激光器驱动以及信号调制和解调的功能. 函数发生器产生低频扫描信号和高频正弦信号, 频率分别为10 Hz和10 kHz. 低频扫描信号使得激光器扫描输出2 cm–1的波长范围, 而高频正弦信号使激光器波长得到调制输出. 通过锁相放大器对接收到的信号进行解调而获得一次谐波信号(1f)和二次谐波信号(2f). 其次, 光学部分包括蝶形封装的DFB激光器、带有光纤准直和光电探测器的光学吸收池, 其光程为20 m. 最后, 在数据采集和分析部分中, 从锁相放大器获得的1f和2f分别包含2000个采样点, 采集触发信号为10 Hz. 最后将1f和2f数据通过串口通信发送给计算机进行分析和计算. 配气系统主要用于不同浓度CO和CH4混合气体的配比, 标准浓度的CO和CH4气体分别通过质量流量计1和质量流量计2混合后通入吸收池, 通过已知的CO和CH4气体浓度和对应质量流量计的读数, 可计算得到混合气体中CO和CH4的浓度.
图 2 实验系统原理图
Figure2. Schematic diagram of the experimental system.

图3为HITRAN数据库[24]仿真得到的在上述DFB激光器的扫描波数范围内浓度分别为20 × 10–6和400 × 10–6的CO气体、浓度为1 × 10–2的CH4气体吸收谱线, 该处及下文(包括表1)中气体浓度均为气体对应的体积分数. 可以发现浓度为400 × 10–6的CO气体, 其吸收谱线的峰值信号强度仍然小于浓度为1 × 10–2的CH4气体在该波长位置的吸收信号强度. 所以利用传统的浓度反演方法, 在高浓度CH4气体的大信号背景下, 要实现精确地定量检测微量CO气体是非常困难的, 因此本文采用基于支持向量回归模型解决激光吸收光谱遇到的类似谱线重叠的共性问题.
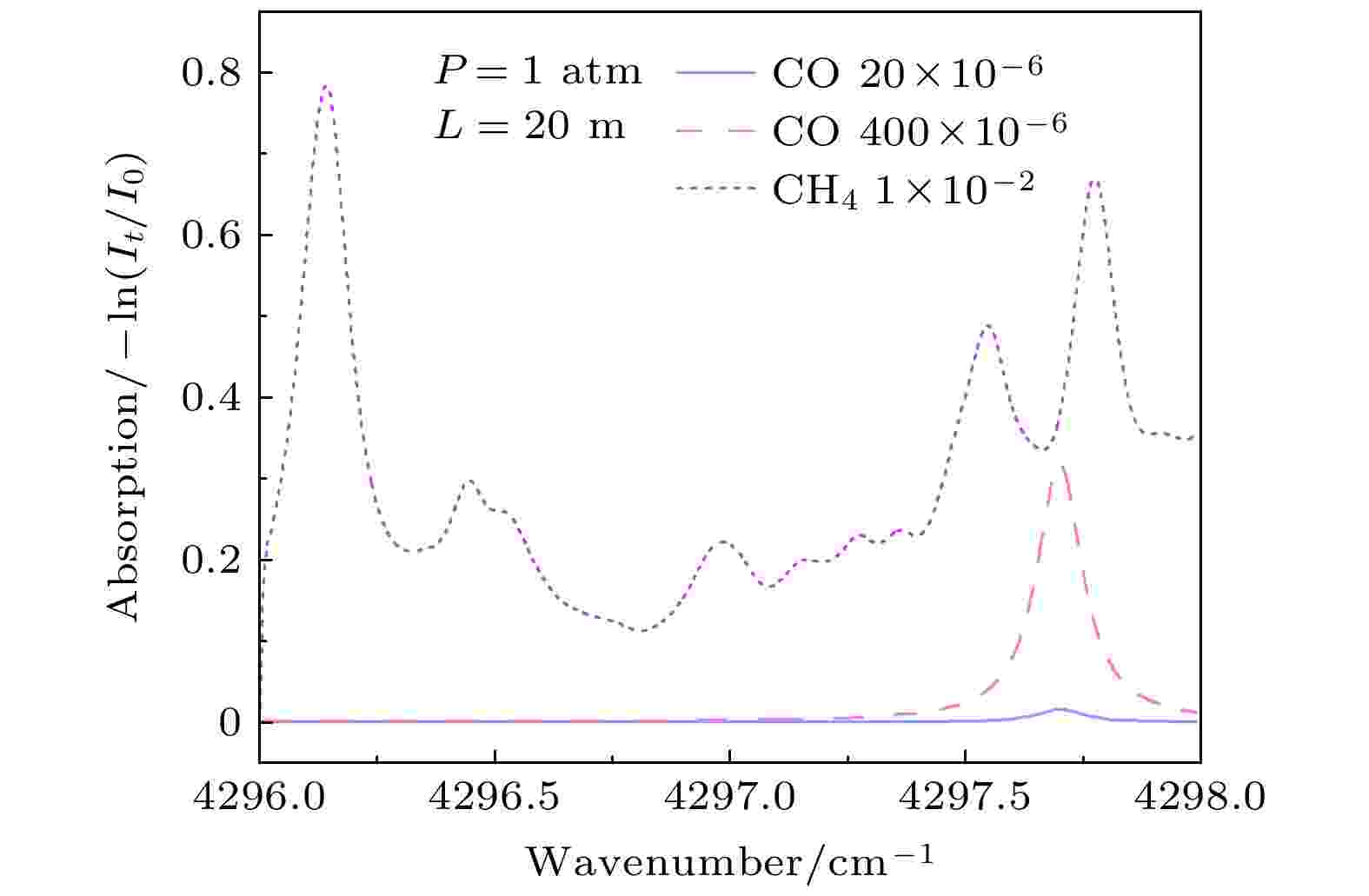图 3 CO (20 × 10–6, 400 × 10–6)和CH4 (1 × 10–2)的模拟吸收光谱图
Figure3. Simulated absorption spectra of CO (20 × 10–6, 400 × 10–6) and CH4 (1 × 10–2).

Group
Standard gas
category and
concentration		Ratio
Gas category and
concentration in
multi-pass cell
CO/10–6CH4/10–2CO/10–6CH4/10–2
119.30—19.30
254.00—54.00
3102.00—102.00
400.50—00.50
501.04—01.04
602.02—02.02
705.02—05.02
854.01.041∶127.00.52
9102.01.041∶151.00.52
1019.31.041∶19.60.52
1119.30.501∶19.60.25
1219.35.021∶19.62.51
1319.32.021∶19.61.01
1419.38.501∶19.64.25


表1训练数据集
Table1.Training data set.

4.实验结果与分析
2
4.1.模型训练
-->

4.1.模型训练

基于支持向量回归原理和CO, CH4两种气体在2327 nm附近的重叠吸收光谱特征, 选择了14组经过1f归一化处理之后的2f数据(2f/1f)[19]作为训练集构建SVR模型. 训练数据集的气体种类及其对应浓度如表1所列. 其中包含3组CO标气、4组CH4标气、7组CO和CH4混合气体(标气按照1∶1比例配比而成). 经过计算, 光学多通池中气体种类及实际浓度如表1中最后两列所示.
选择表1中三组气体, 分别为Group 1 (CO标气), Group 4 (CH4标气)和Group 10 (混合气体), 它们的信号如图4所示, 其对应浓度如图4中图例所示. 对比图4中曲线和划线的差别可知, CH4气体的吸收信号(Group 4)和包含微量CO的混合气体信号(Group 10)在图4黑框中(对应采样点范围为100到500之间)基本一致, 采用传统的计算方法无法将微弱的CO吸收信号解调出来.
图 4 三组气体(Group 1、Group 4、Group 10)的2f/1f信号
Figure4. 2f/1f signals of three groups of gases (Group 1, Group 4, Group 10).

而本文基于Matlab R2018a平台, 采用5折交叉验证经过15次迭代构建SVR模型, 并且采用序列最小最优化(sequential minimal optimization, SMO)算法进行参数优化, 得到两个SVR模型, 分别命名为CO-SVRmodel和CH4-SVRmodel, 这两个模型的主要参数如表2中所列. 其中, BoxConstraint(C)为惩罚系数, 主要影响模型的泛化能力; KernelScale是归一化常数; ε是不敏感损失函数设置的损失阈值.
CO-SVRmodelCH4-SVRmodel
BoxConstraint(C )0.34430.0180
KernelScale0.06170.9205
ε0.171065.1810
Total function evaluations1515
Total elapsed time in seconds26.254512.5730


表2SVR模型主要参数
Table2.Optimal parameters of SVR model.

鉴于混合气体中CO和CH4气体的浓度差距在103—104量级, 且两种气体的吸收峰会产生明显的交叠, 所以为了使两种气体的回归模型都能够得到精准的结果, 两个模型采用的训练数据集不完全相同. CH4-SVRmodel的训练采用整个2f/1f光谱数据进行训练, 能够充分反映CH4气体的吸收谱线特征; CO-SVRmodel则放弃了光谱冗余数据, 选择只包含CO吸收信息的光谱数据(光谱中的第100—500个点之间的范围)进行训练, 如图4中黑色方框所示.
为了初步验证两种气体SVR模型的可用性, 首先对表1中的14组气体分别进行60组测试, 然后根据回归模型(CO-SVRmodel, CH4-SVRmodel)分别对CO和CH4气体进行浓度计算, 得到CO和CH4气体浓度的计算结果分别如图5(a) 和图5(b)所示. 从图5中可以看出, 不管是CO气体还是CH4气体, 基于SVR模型计算得到的结果和真实值相差都不大, 其中CO气体的误差最大值为2 × 10–6, CH4气体的误差最大值为0.16 × 10–2, 该处及下文中误差均是指气体浓度的绝对误差. 并且可以发现CO和CH4气体发生最大误差具有统一性, 即都发生在CO气体浓度为0, CH4气体浓度为5.02 × 10–2时的测量结果. 出现这种结果的原因是CO和CH4气体的浓度相差越大, 就会导致CO信号被湮没地越彻底, 并且在实验中也发现了浓度为5.02 × 10–2的CH4气体在信号稳定(观察信号稳定)后仍然会存在相对大的波动, 也导致了CO和CH4气体的测量结果在此处产生了最大的误差. 经过验证, 采用线性核函数, 并且基于以上两个数据集分别训练得到的两个浓度回归模型比采用整个光谱数据集得到的回归模型更加精确.
图 5 CO和CH4浓度设置值和测试值对比　(a) CO浓度值; (b) CH4浓度值
Figure5. Comparisons between set and test values: (a) CO concentration; (b) CH4 concentration.

2
4.2.CO和CH4配比实验
-->

4.2.CO和CH4配比实验

4.1节训练集数据的验证从一定程度上反映了SVR模型对CO和CH4两种气体浓度计算有效. 但是其中训练集和测试集的浓度设置完全一致, 所以不能很好地说明系统具有良好的泛化能力(泛化能力是指对于训练数据集之外的数据仍然能够得到准确的计算结果, 标志着模型是否具有通用性和普适性). 为了更进一步探讨该模型的泛化能力, 进行了气体配比实验.
将浓度为102 × 10–6的CO气体与浓度分别为2.02 × 10–2, 4.5 × 10–2的CH4气体进行1∶4, 2∶3, 3∶2, 4∶1比例的混合, 并利用该实验系统对以上配比的混合气体进行检测, 待信号稳定后记录每组混合气体30组的数据, 并对其求平均值, 然后根据两个气体浓度回归模型(CO-SVRmodel和CH4-SVRmodel)对得到的数据进行回归计算. CO和CH4气体浓度的真实值和测量值之间的相关性, 及其测量误差如图6所示.
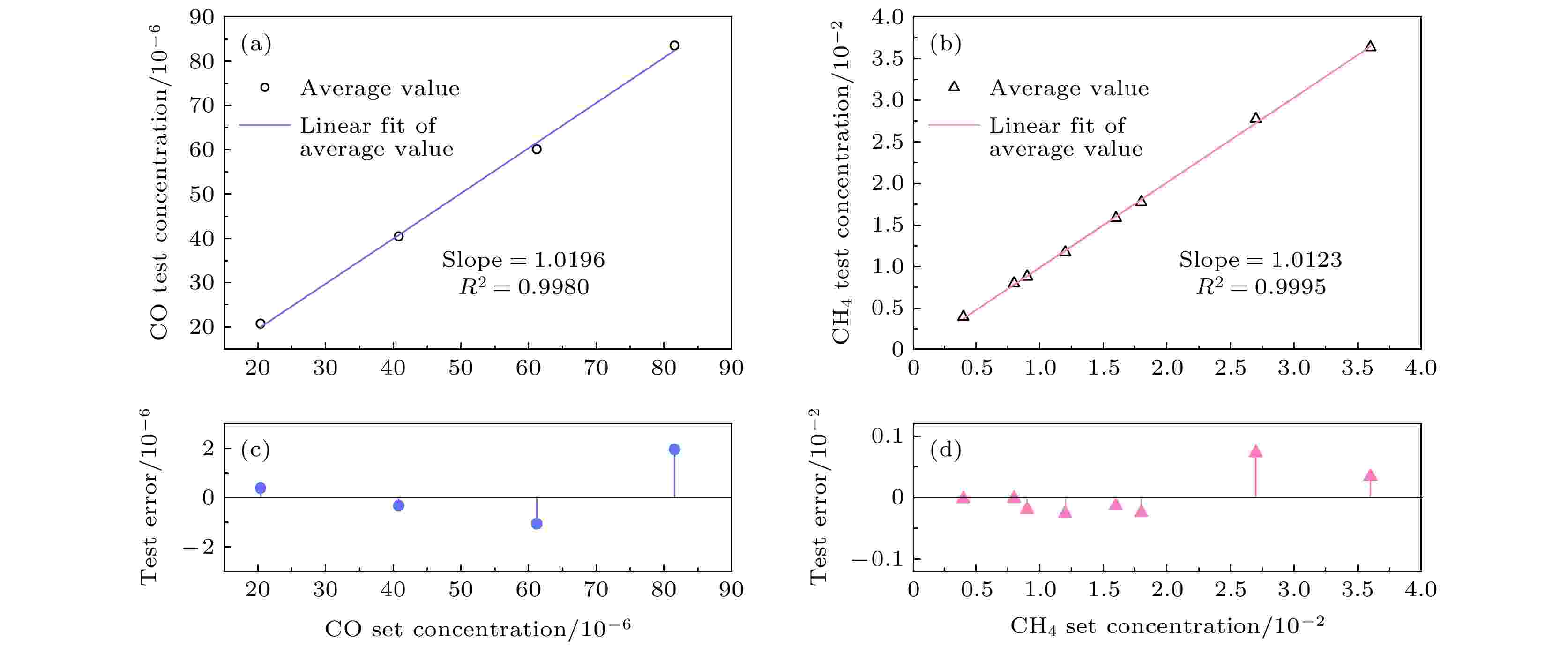图 6 设置值和测量值之间相关性及测量误差　(a) CO相关性; (b) CH4相关性; (c) CO测量误差; (d) CH4测量误差
Figure6. Correlation and test errors between set and average values: (a) CO correlation; (b) CH4 correlation; (c) CO errors; (d) CH4 errors.

图6(c), (d)可以说明: 基于上文的浓度回归模型分别对CO和CH4气体浓度进行浓度测量, CO和CH4气体浓度误差分别不超过2 × 10–6和0.1 × 10–2; 且由图6(a),(b)可知, CO和CH4的真实值与预测值之间的相关系数分别为0.998和0.9995. 由此可得CO-SVRmodel和CH4-SVRmodel回归模型在固定配比数据集上能够取得良好的浓度回归测量效果, 证明上述两个模型良好的泛化能力.
2
4.3.混合气体浓度定量解析
-->

4.3.混合气体浓度定量解析

为了验证该算法在不同浓度的CH4环境下仍能够对微量CO进行准确测量. 将18 × 10–6的CO气体和四种浓度的CH4气体(浓度分别为0.5 × 10–2, 1.04 × 10–2, 2.02 × 10–2, 5.02 × 10–2)进行1∶3的配比, 待信号稳定后进行浓度结果回归计算, 每组配比的气体进行120组数据测量, 其中CO和CH4的浓度真实值如图7中黑色数字标注. CO浓度回归结果和CH4回归结果如图7所示. 从图7中可以看出, 该TDLAS系统结合SVR模型计算得到的CO和CH4气体浓度在较小的范围之内波动. 微量CO气体在受高浓度CH4气体干扰的条件下, 其最大误差小于2 × 10–6; 而CH4气体得到的测量结果最大误差小于0.2 × 10–2, 证明了系统的抗干扰能力, 说明CO-SVRmodel和CH4-SVRmodel能够克服吸收谱线数据中的特征干扰问题并得到精确的浓度回归结果.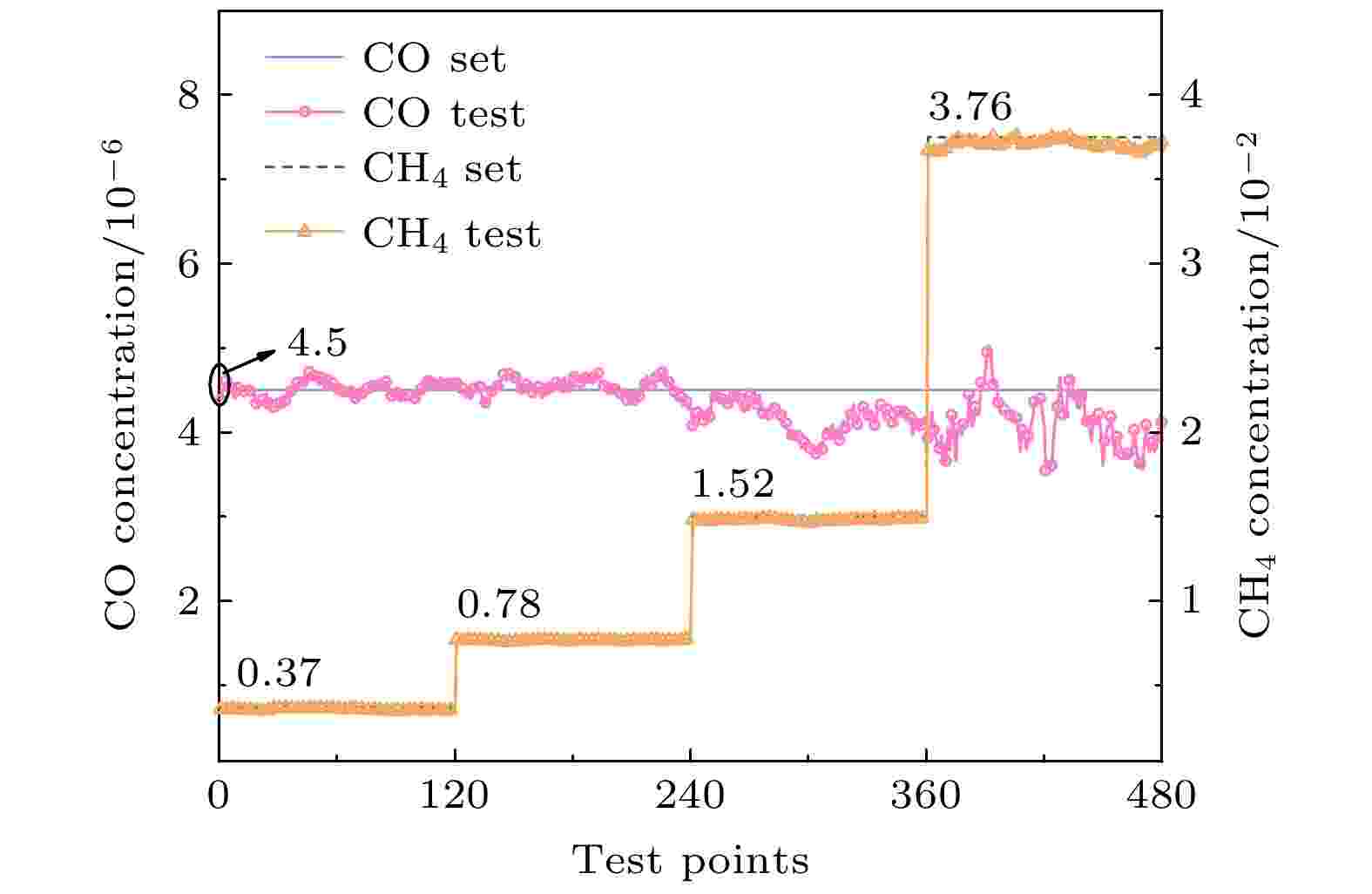
图 7 不同浓度CH4对CO测量结果的干扰
Figure7. Interference on CO measurement results by different concentrations of CH4.

为了更进一步验证CO-SVRmodel和CH4-SVRmodel两个浓度回归模型的动态可靠性, 利用上述实验系统进行了两组充气过程实验, 分别如下: 在两组过程中均利用CO-SVRmodel和CH4-SVRmodel得到CO和CH4的浓度结果.
第一组充气过程中CO和CH4气体的浓度变化趋势如图8所示. 初始状态气体池中底气为1.04 × 10–2的CH4气体, 在某一时刻, 将浓度为20 × 10–6的CO气体和浓度为1.04 × 10–2的CH4气体按照1:1的配比同时打开, 可以观察到CO气体浓度逐渐上升, CH4气体浓度逐渐下降, 且两者浓度变化过程具有时间上的统一性, 也会随着时间的推移接近按照1:1比例配比的浓度(CO浓度接近10 × 10–6, CH4浓度接近0.52 × 10–2); 当CO和CH4混合气体吸收信号无明显变化, 待信号稳定一段时间后, 关闭CH4气体气阀, 保持CO气体气阀打开, 可以观察到CO气体浓度逐渐上升并趋近20 × 10–6, CH4气体浓度继续逐渐下降并趋近0, 且两者浓度变化过程具有时间上的统一性.
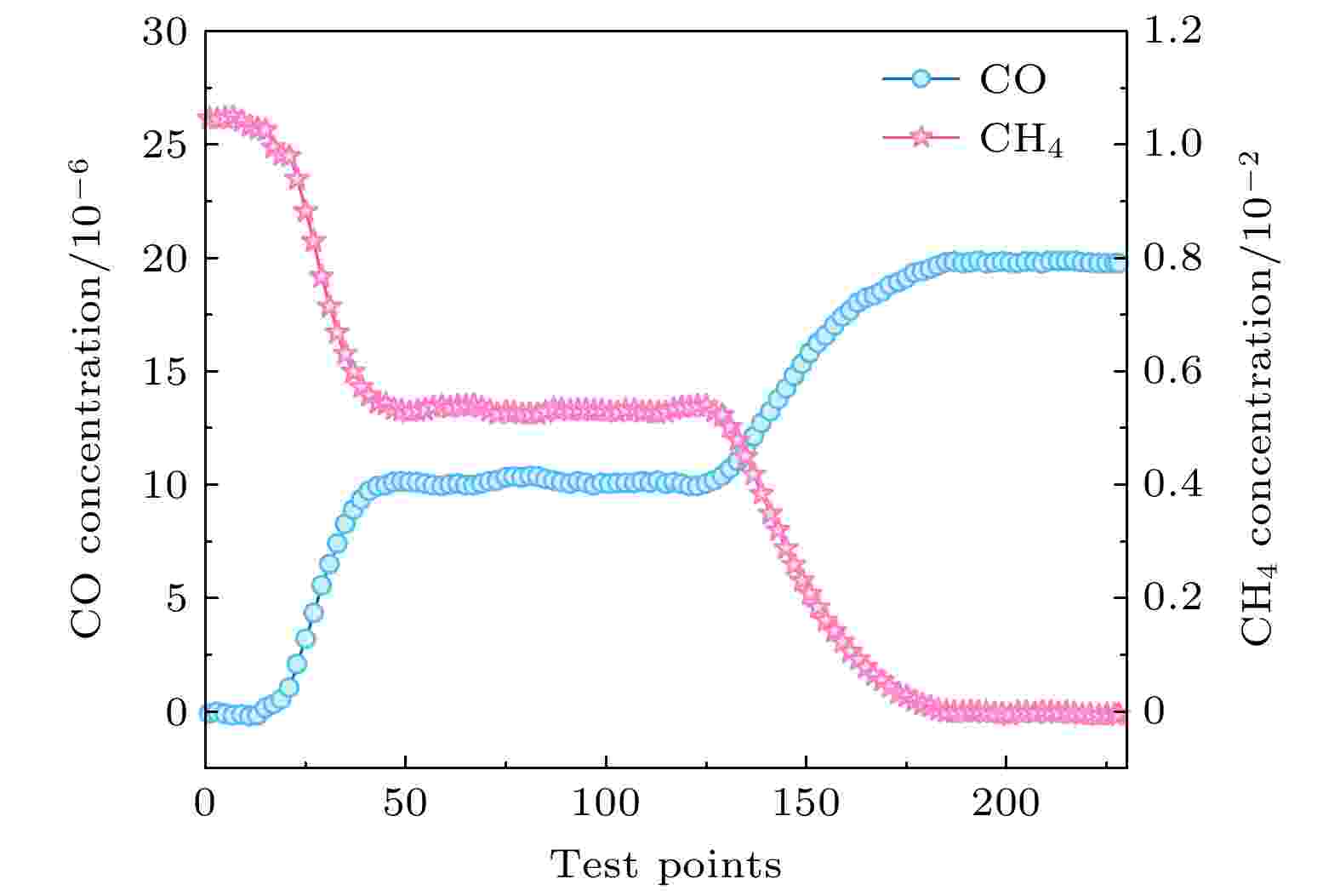图 8 第一组充气过程中CO和CH4浓度变化
Figure8. Concentration measured of CO and CH4 during the first set of inflation.

第二组充气过程中CO和CH4气体的浓度变化趋势如图9所示. 气体池中底气为浓度8.5 × 10–2的CH4气体和浓度20 × 10–6的CO气体按照1:1比例混合的气体, 从图9中可以看出CO和CH4气体均能够获得比较准确且稳定的结果, 在某一时刻, 关闭CH4气体气阀, 保持CO气体气阀打开, 此时会发现CH4气体浓度会微微增大, 再缓慢减小, 直至信号稳定, 此时CH4气体浓度已经减小到0附近并保持; 在关闭CH4气阀的同时, 观察到CO气体浓度会下降约3 × 10–6, 然后再逐渐上升至20 × 10–6左右并保持. 出现上述现象的原因是由于此时混合气体中CH4含量较高(为4.25 × 10–2), 关闭CH4气阀瞬间, 信号会产生波动, 而该波动对多峰的CH4浓度回归计算影响较小, 但是对特征量较少的CO气体浓度回归计算会产生较大的影响.
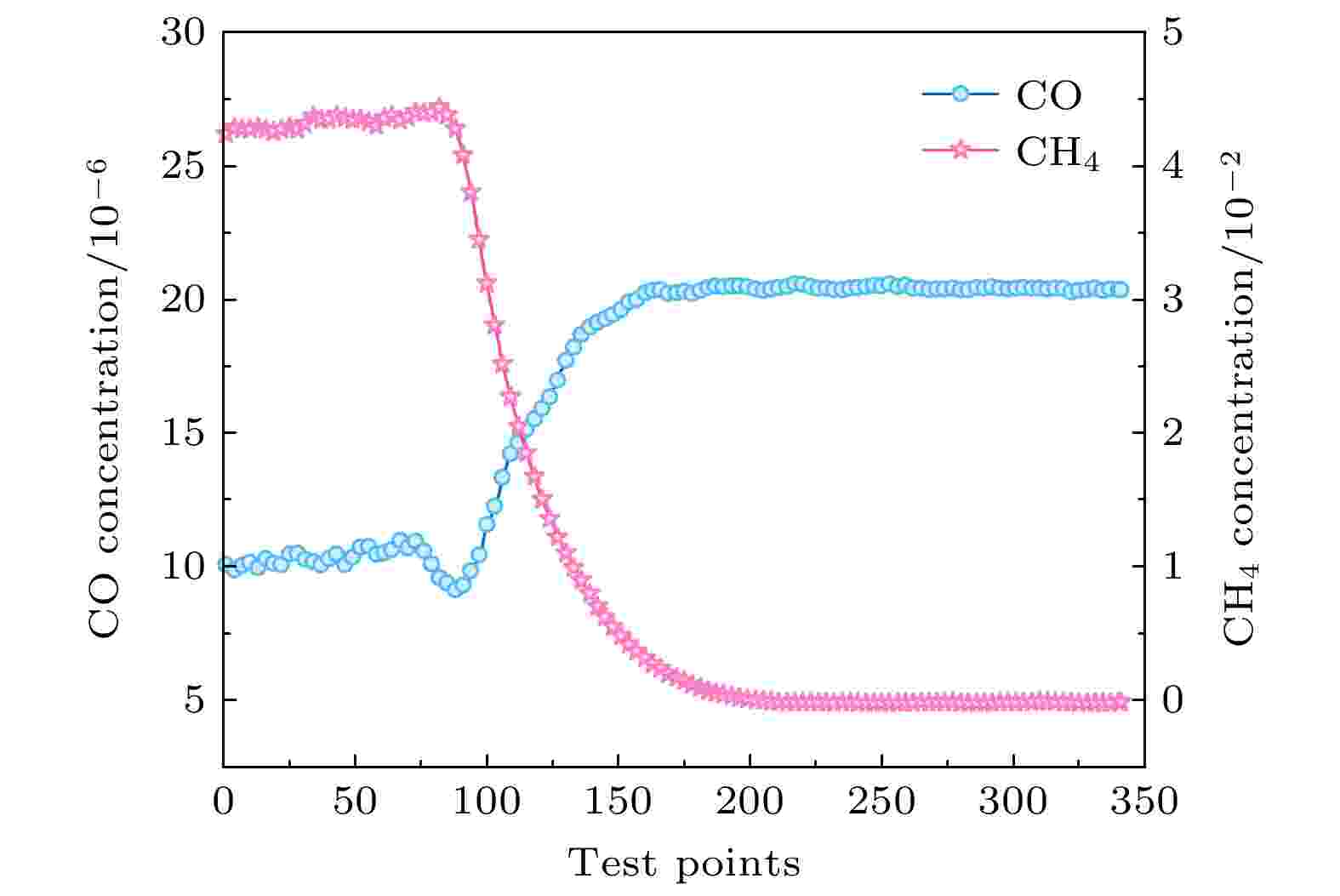图 9 第二组充气过程中CO和CH4浓度变化
Figure9. Concentration measured of CO and CH4 during the second set of inflation.

通过上述两组充气过程的验证, TDLAS系统结合SVR模型能够对包含微量CO和浓度不超过4.25 × 10–2的CH4的混合气体进行动态实时监测, 且在整个动态过程中能够将CO和CH4的误差分别控制在3 × 10–6和0.5 × 10–2; 待信号稳定后, 利用该回归模型得到的CO和CH4浓度误差仍然不超过2 × 10–6和0.2 × 10–2. 充气动态过程实验充分验证了基于SVR模型解调CO和CH4混合气体重叠干扰吸收谱线的可靠性和完备性.
5.结　论
本文基于2.3 μm的DFB激光器以CO、CH4和氮气混合气体浓度测量时的谱线交叉干扰共性问题为例, 提出了基于支持向量回归模型的混合气体浓度解析方法, 实现了CH4和微量CO的混合气体浓度的同时测量. 为了确保浓度回归模型的准确性和高效性, 根据吸收谱线的特征对2f/1f数据进行了合理切割和利用, 分别得到了两种气体的回归预测模型. 基于这两个模型, 进行了固定配比的验证实验、混合气体浓度定量解析及组分变化过程实验. 在固定配比实验中, 可以得到CO和CH4气体的测量值与真实值的相关性分别为0.998, 0.9995, 证明了该系统具有良好的泛化能力. 混合气体浓度同时测量实验说明在高浓度CH4与微量CO气体同时共存的气体环境下, CO气体回归计算结果绝对误差不超过2 × 10–6, CH4回归结果的绝对误差不超过0.2 × 10–2. 上述结果证明, 基于SVR原理构建的回归预测模型具有自动提取吸收谱线特征、抗干扰性强、回归预测结果准确等优点, 可有效地解决激光光谱技术在混合气体测量过程中遇到的吸收谱线重叠干扰问题, 为该技术面临的共性技术难题及其应用提供了新的解决方法.
相关话题/信号 测量 实验 数据 系统
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于剪切模量和热分析数据研究Zr<sub>50–</sub><i><sub>x</sub></i>Cu<sub>34
    摘要:非晶合金具有独特物理和力学性能,如何建立非晶合金微观结构非均匀性与物理/力学性能之间的关联是非晶固体的重要研究课题之一.微合金化是调控非晶合金微观结构有效手段之一.本研究以玻璃形成能力优异的Zr50–xCu34Ag8Al8Pdx(x=0,2)非晶合金为模型合金,借助差示扫描量热仪和电磁声转换设 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • L型步行通道内行人转弯行为的实验分析与仿真
    摘要:以L型步行通道内的单向行人流为研究对象,基于可控实验与微观仿真研究行人转弯行为.首先,构建转弯区无障碍物、障碍物沿转弯区对角线布局、以及障碍物垂直转弯区对角线布局三种实验场景,通过行人可控实验分析行人移动轨迹、速度分布等行为特征;然后,基于L型通道内的行人微观行为,改进基于Voronoi图的速 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 甚低频台站信号对地球内辐射带和槽区能量电子的散射效应分析
    摘要:人工地面甚低频台站发射的10—30kHz信号主要在地球—低电离层波导传播,部分能量会泄露进入内磁层,进而会影响近地空间中高能电子的动态变化过程.本文详细研究了NWC,NAA和DHO38三个人工甚低频台站信号对内辐射带和槽区高能电子的散射作用.基于准线性理论,分别计算了三个甚低频台站信号单独和共 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于微波-电子康普顿背散射的环形正负电子对撞机束流能量测量方案
    摘要:环形正负电子对撞机(CEPC)束流能量的精确标定是希格斯粒子质量宽度、W/Z玻色子质量的精确测量,从而精确检验标准模型的基本实验依据.基于此,束流能量的误差控制要求在10–5水平.康普顿背散射方法是适用于百GeV高能电子对撞机束流能量高精度标定的测量方法.本文拟采用微波电子康普顿背散射后对散射 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高超声速三角翼上横流不稳定性的实验研究
    摘要:本文研究了三角翼迎风面边界层中的非定常横流不稳定性.实验在马赫6低噪声风洞中进行,模型为平板构型,攻角为5°和10°.通过温敏漆技术,观察到在远离头部的区域,边界层转捩阵面光滑且平行于前缘,通过Kulite高频脉动压力传感器得到的功率谱密度曲线中有明显的f≈10kHz的扰动波信号峰值.利用基于 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 液态金属软表面池沸腾传热的实验研究
    摘要:池沸腾是一种高效的传热方式,目前主要通过刚性固体表面改性强化沸腾传热.本文以乙醇为工质,实验研究了光滑铜表面和液态金属软表面池沸腾传热.发现液态金属软表面可有效降低沸腾起始点(ONB)壁面过热度,饱和沸腾时,ONB壁面过热度从光滑铜表面的约18℃降低到软表面的约6℃,沸腾传热系数最大提高了14 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 面向综合定位导航授时系统的天地基脉冲星时间研究
    摘要:中国综合定位导航授时(positioningnavigationtiming,PNT)体系是以北斗卫星导航系统(BeiDounavigationsatellitesystem,BDS)为核心的多源信息融合系统,高精度的毫秒脉冲星计时能够增强BDS时间基准的长期稳定性,并能维持未来深空用户的时间 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 层状磁性拓扑材料中的物理问题与实验进展
    摘要:层状磁性材料与拓扑材料的交汇点同时结合了二者的优势,形成了在最小二维单元下同时具有磁序和拓扑性的材料体系,即层状磁性拓扑材料.这类材料的电子结构中可能存在狄拉克点、外尔点、节线等具有螺旋性或手性的拓扑电子态,同时涵盖了绝缘体、半金属和金属等的材料分类,导致新物性、新现象成为可能,因此引起了广泛 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维CrI<sub>3</sub>晶体的磁性测量与调控
    摘要:长久以来,人们普遍相信低维(三维以下)长程序无法在任何有限的温度下稳定存在.这是因为温度带来的热涨落会破坏由各向同性的短程相互作用支撑的低维体系中对称性破缺的有序态.然而,这个定理同时要求相互作用是短程且各向同性的.事实上很多低维体系是不满足这两个限定条件的.比如二维CrI3晶体中由于强各向异 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 纠缠光子对的级联Hong-Ou-Mandel干涉研究及其在多时延参数测量中的应用
    摘要:基于纠缠光子对的Hong-Ou-Mandel(HOM)干涉仪在量子精密测量等领域有着重要应用.本文提出了利用一个级联HOM干涉仪实现多个独立时延参数的同时测量方案.通过理论分析得出纠缠光子对经过多个50∶50分束器级联传输后,其HOM二阶量子干涉图谱中凹陷位置与各级传输路径间独立时延参数的对应 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.