摘要: 忆阻器、忆容器和忆感器是具有记忆特性的非线性元件, 隶属于记忆元件系统. 目前, 由于现有可购忆阻器芯片尚存在许多不足, 且忆容器和忆感器的硬件实物研究仍处于实验室验证阶段, 因此, 研究者们获取此类记忆元件硬件仍有难度. 为了解决这个问题, 建立有效的记忆元件等效电路模型, 以促进对记忆元件及其系统的特性和应用研究. 本文根据忆阻器、忆容器和忆感器的本构关系, 提出一种新型浮地记忆元件建模方法, 即采用搭建通用模拟器的方式, 在保证电路拓扑结构不变的情况下, 通过改变接入通用模拟器的无源电路元件分别实现浮地忆阻器、忆容器和忆感器模型. 相比于其他能实现3种浮地记忆元件模型的研究, 本文所搭建的记忆元件模型结构简单, 工作频率更高, 易于电路实现. 结合理论分析、PSPICE仿真及硬件电路实验结果的一致性, 验证基于该通用模拟器搭建记忆元件模型的可行性和有效性.
关键词: 记忆元件 /
硬件实验 /
磁滞回线特性 /
浮地模拟器 English Abstract A novel modeling method and implementation of floating memory elements Zheng Ci-Yan 1 ,Zhuang Chu-Yuan 2 ,Li Ya 2 ,Lian Ming-Jian 2 ,Liang Yan 3 ,Yu Dong-Sheng 4 1.School of Automation, Guangdong Polytechnic Normal University, Guangzhou 510665, China Fund Project: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant Nos. 61801154, 62101142), the Science and Technology Program of Guangzhou, China (Grant Nos. 201904010302, 202102020874), the Featured Innovation Foundation of the Education Department of Guangdong Province, China (Grant Nos. 2021ZDZX1079, 2021KTSCX062), and the Doctoral Scientific Research Startup Fund of Guangdong Polytechnic Normal University, China (Grant No. 2021SDKYA009).Received Date: 30 May 2021Accepted Date: 13 July 2021Available Online: 17 August 2021Published Online: 05 December 2021Abstract: Memristors, memcapacitors and meminductors are nonlinear circuit components with memory effects and belong to memory element (mem-element) system. Since there are many shortcomings in the existing available commercial memristor chips, and the physical realizations of memcapacitor and meminductor hardware are still in early stages, it is still difficult for researchers to obtain hardware mem-elements for research. In order to solve this problem, it is still necessary to build effective equivalent models of mem-elements to facilitate the research on their characteristics and applications. In this paper, a novel floating mem-element modeling method is proposed by connecting different passive circuit component to a universal interface while keeping the circuit topology unchanged. Compared with other floating universal mem-element models, the model built in this paper has simple structure, high working frequencies, thus making proposed models easier to implement. The feasibility and effectiveness of the mem-elements models based on the universal interface are successfully verified through theoretical analysis, PSPICE simulation results and hardware experimental results.Keywords: memory element /hardware experiment /hysteresis loop /floating emulator 全文HTML --> --> --> 1.引 言 忆阻器是一种新型记忆元件, 其概念由蔡少棠[1 ] 于1971年提出, 并在2008年由惠普(HP)实验室成功制备为纳米级固态元件[2 ] . 此后蔡少棠团队[3 ] 将记忆系统的概念拓展到容性和感性元件中, 形成了一种基于忆阻器、忆容器和忆感器的记忆元件系统. 现有研究表明忆阻器、忆容器和忆感器凭借其独特的记忆特性以及非线性特性, 在混沌电路[4 ,5 ] 、信号处理[6 ,7 ] 、非易失性存储器[8 ] 、存算一体芯片[9 ,10 ] 和人工神经网络[11 ,12 ] 等多个领域具有广阔的应用前景. 最近研究表明存在基于磁电耦合效应实现的第4种记忆元件—忆耦器[13 ,14 ] , 其概念的提出拓宽了记忆元件的定义和概念, 极大地提升了记忆元件的应用潜力.[15 ] 、忆感器[16 ] 和忆耦器[13 ,14 ] 的物理实现仍停留于实验室验证阶段, 尚未市场化. 然而, Knowm忆阻器芯片作为全球目前唯一一款可购记忆元件, 在使用过程中存在以下问题: 该器件两端存在较大的寄生电容, 可能导致出现忆阻器极性翻转及记忆衰退等现象; 其阻变存储技术所具有的随机性导致忆阻器可编程忆阻值参数可控性和稳定性不足; 其直流和交流响应不稳定等[17 ,18 ] . 为此, 根据记忆元件本构关系和电学特性, 搭建记忆元件等效电路模型以用于其特性研究和应用开发[19 ,20 ] 成为近年来的研究热点. 目前, 已有对记忆元件中的忆阻器、忆容器和忆感器的等效电路模型搭建研究, 但尚未出现关于忆耦器的等效电路模型搭建相关研究. 例如, 研究者根据记忆元件的本构关系搭建单个忆阻器[21 ,22 ] 、忆容器[23 ] 或忆感器模型[24 ] . 此外, 有****根据记忆元件本构关系之间的联系, 利用现有的忆阻器模型和外围转化电路来构造忆容器和忆感器模型[25 ,26 ] , 然而, 由于上述忆容器和忆感器模型是基于忆阻器转化得到, 使所转化的忆容器和忆感器模型依赖于原有忆阻器特性, 且结构复杂、难以简化. 因此, 为了搭建模型更简单的记忆元件, Fouda等[27 ] 提出了不含忆阻器的忆容器模型. 梁燕等[28 ] 采用相似设计思路, 提出了不含忆阻器的忆感器模型. 近年来, 研究者在以往单个记忆元件模型设计的基础上, 提出通用的记忆元件模型. 李志军等[29 ] 提出了一个由基本电路元件和可购芯片构成的通用记忆元件模拟器, 在保证电路拓扑结构不变的情况下, 通过接入不同性质元件, 分别模拟忆阻器、忆容器和忆感器的电路行为. 然而, 其搭建的记忆元件需确保模型中的场效应管工作于线性区域方能呈现出记忆特性, 限制了模型的工作电压范围, 且其工作频率较低(0.8 kHz左右). Wang等[30 ] 基于通用模拟器实现3种浮地型记忆元件模型, 然而, 其呈现磁滞特性曲线的最高工作频率约为5 kHz. Zheng等[31 ] 和Yu等[32 ] 利用变容二极管设计通用模拟器, 并基于通用模拟器搭建了记忆元件模型, 但所搭建记忆元件输入输出特性通过近似模型获得. Sharma等[33 ] 利用硬件实验实现了基于通用模拟器的记忆元件, 然而其设计的模型的输入和输出电流不相等, 无法等效模拟浮地型二端口记忆元器件, 存在“伪浮地”的不足.2.基于通用模拟器的记忆元件模型设计 记忆元件具有存储过往电路信息的特性, 由其本构关系数学模型中的状态变量反映. 以忆阻器为例, 其本构关系为$q\text-\phi$ 间的非线性关系, 可以由分段线性、二次非线性、三次非线性等非线性数学模型描述[34 -36 ] . 忆容器和忆感器模型的本构关系分别为$\sigma \text-\phi$ 和$q{{ \text- }}\rho$ 之间的非线性关系, 也可由二次非线性数学模型描述[37 ,38 ] . 上述本构关系中, $ q $ 代表电荷量, $ \phi $ 代表磁通量, 即电压对时间的积分, $ \sigma $ 代表$ q $ 对时间的积分, $ \rho $ 代表$ \phi $ 对时间的积分. 因此, 本文采用二次非线性数学模型分别描述忆阻器、忆容器和忆感器本构关系.$q\text-\phi$ 本构关系以及忆导值W m (忆阻值倒数)可定义为$ {\alpha _{\text{1}}} $ 代表忆导值$ {W_{\text{m}}} $ 的变化率, $ {\beta _{\text{1}}} $ 代表$ {W_{\text{m}}} $ 的初始值.$\sigma \text{-}\phi$ 本构关系以及忆容值$ {C_{\text{m}}} $ 可定义为$ {\alpha _{\text{2}}} $ 代表忆容值$ {C_{\text{m}}} $ 的变化率, $ {\beta _{\text{2}}} $ 代表$ {C_{\text{m}}} $ 的初始值.$q\text{-}\rho$ 本构关系以及忆感值倒数值$ L_{\text{m}}^{ - 1} $ 可定义为$ {\alpha _{\text{3}}} $ 代表忆感值倒数值$ L_{\text{m}}^{ - 1} $ 的变化率, $ {\beta _{\text{3}}} $ 代表$ L_{\text{m}}^{ - 1} $ 的初始值.2.1.通用模拟器及基于通用模拟器的记忆元件电路实现 2.1.通用模拟器及基于通用模拟器的记忆元件电路实现 本文根据忆阻器、忆容器和忆感器本构关系, 提出一种可用于构造记忆元件模型的通用模拟器等效电路, 如图1 所示, 其电路结构包含4个电流反馈放大器AD844 (标为U1, U2, U3和U4)、1个乘法器AD633(U5)、2个阻抗元件(标为$ {Z_1} $ , $ {Z_{\text{2}}} $ )、电阻$ {R_1} $ 、电容$ {C_1} $ 以及直流电压源$ {V_{\text{s}}} $ , 其中端口A和B作为通用模拟器的外接二端口, 用于与外围电路进行连接.图 1 通用模拟器设计Figure1. Design of a universal emulator for building models of mem-elements.$ {i_{{\text{AB}}}} $ 与流经阻抗元件$ {Z_2} $ 电流$ {i_{\text{4}}} $ 在复频域上的表达式:${ {\dot V} _{\text{w}}}$ 为AD633的w端输出电压$ {v_{\text{w}}} $ 在复频域的表达式.7 )式, 得流经阻抗元件$ {Z_1} $ 电流${ {\dot I} _{\text{1}}}$ 、流经C 1 的电流${ {{\dot I} } _{\text{2}}}$ 与流经R 1 的电流${ {\dot I} _{\text{3}}}$ 可以表示为8 )式可得可计算AD633的${{\text{y}}_1}$ 端输入电压${v_{\text{y}}}_1$ 在复频域上的表达式:$ {C_1} $ 在电路中起电流积分器作用, 设积分电容$ {C_1} $ 的初始电压为0, 根据(10 )式可求得$ {C_1} $ 两端电压表达式, 且由(8 )式, 可得U5的${{\text{x}}_1}$ 端输入电压${v_{\text{x}_1}}$ 在复频域上的表达式:$ {v_{\text{w}}} $ 在复频域上的表达式:$ {V_{\text{s}}} $ 为常量直流电压.11 )式和(12 )式代入(13 )式, 并将(13 )式代入(9 )式可得通用模拟器二端口输出方程:$ {Z_1} $ 和$ {Z_{\text{2}}} $ 分别为电阻$ {R_{\text{2}}} $ 和$ {R_{\text{3}}} $ 时, 此时模拟器模拟为磁通控制忆阻器模型, 其忆导值在时域上可描述为2 )式, (16 )式可等效表示为$ {\alpha _{\text{1}}} $ 和$ {\beta _{\text{1}}} $ 可表示为$ {Z_1} $ 和$ {Z_{\text{2}}} $ 分别为电阻$ {R_{\text{2}}} $ 、电容$ {C_{\text{2}}} $ 时, 有:4 )式, 可得磁通控制忆容器的忆容值$C_{\text{m}}$ 在数学上的定义:$ {\alpha _{\text{2}}} $ 和$ {\beta _{\text{2}}} $ 可表示为$ {Z_1} $ 和$ {Z_{\text{2}}} $ 分别为电感$ {L_{\text{1}}} $ 、电阻$ {R_{\text{2}}} $ 时, 有:6 )式, 可得磁通忆感器的忆感值倒数值$ L_{\text{m}}^{ - 1} $ 在数学上的定义:$ {\alpha _{\text{3}}} $ 和$ {\beta _{\text{3}}} $ 可表示为2.2.记忆元件模型特征对比 -->2.2.记忆元件模型特征对比 本文基于通用模拟器电路分别搭建了忆阻器、忆容器和忆感器模型, 其各特征量对比如表1 所示.记忆元件类型 忆阻器 忆容器 忆感器 电路拓扑结构 通用模拟器 阻抗元件$ {Z_1} $ 电阻$ {R_{\text{2}}} $ 电阻$ {R_{\text{2}}} $ 电感$ {L_{\text{1}}} $ 阻抗元件$ {Z_{\text{2}}} $ 电阻$ {R_{\text{3}}} $ 电容$ {C_{\text{2}}} $ 电阻$ {R_{\text{2}}} $ 内部状态变量 $q {\text{-}} \phi$ $\sigma {\text{-}} \phi$ $q {\text{-}} \rho$ 本构方程 $ W\left( {{\phi _{{\text{AB}}}}} \right) = {\alpha _1}{\phi _{{\text{AB}}}} + {\beta _1} $ $C_{\text{m} }\left( { {\phi _{ {\text{AB} } } }} \right) = {\alpha _2}{\phi _{ {\text{AB} } } } + {\beta _2}$ $L{_ {\text{m} }^{ - 1} }\left( { {\rho _{ {\text{AB} } } }} \right) = {\alpha _3}{\rho _{ {\text{AB} } } } + {\beta _3}$ $ {\alpha _x} $值 ${\alpha _{\text{1} } } = \dfrac{ { {R_{\text{1} } } }}{ {10 R_{\text{2} }^{\text{2} }{R_{\text{3} } }{C_{\text{1} } } }}$ ${\alpha _{\text{2} } } = \dfrac{ { {R_{\text{1} } }{C_{\text{2} } } }}{ {10 R_{\text{2} }^{\text{2} }{C_{\text{1} } } }}$ ${\alpha _{\text{3} } } = \dfrac{ { {R_{\text{1} } } }}{ {10 L_{\text{1} }^{\text{2} }{R_{\text{2} } }{C_{\text{1} } } }}$ $ {\beta _x} $值 $ {\beta _{\text{1} } } = - \dfrac{ { {R_{\text{1} } } } }{ { {\text{10} }{R_{\text{2} } }{R_{\text{3} } } } }V_{\text{s} } $ $ {\beta _{\text{2} } } = - \dfrac{ { {R_{\text{1} } }{C_{\text{2} } } } }{ { {\text{10} }{R_{\text{2} } } } }V_{\text{s} } $ ${\beta _{\text{3} } } = - \dfrac{ { {R_{\text{1} } } }}{ { {\text{10} }{L_{\text{1} } }{R_{\text{2} } } }}{V_{\text{s} } }$
表1 基于通用模拟器的记忆元件模型对应特征比较Table1. Comparison of characteristics of different kinds of mem-element models based on the proposed universal emulator.3.基于通用模拟器的记忆元件模型仿真分析 在本节中, 为了初步验证本文所提基于通用模拟器的记忆元件模型的正确性, 采用PSPICE软件进行仿真分析, 并提供相对应的仿真分析结果. 其中, 采用正弦信号 ${v_{{\text{AB}}}} = {U_{\text{o}}}{\text{sin}}\left( {2{\text{π }}ft} \right) = $ $ {U_{\text{o}}}{\text{sin}}\left( {\omega t} \right)$ (V)作为电路模型的二端口激励电压, 芯片直流供电电压为±15 V.3.1.忆阻器模型仿真分析 3.1.忆阻器模型仿真分析 基于图1 所示通用模拟器设计PSPICE电路仿真模型, 分别选取阻抗元件$ {Z_1} $ , $ {Z_{\text{2}}} $ 为电阻$ {R_2} $ , $ {R_3} $ . 根据正弦激励电压表达式${v_{{\text{AB}}}} = {U_{\text{o}}}{\text{sin}}\left( {2{\text{π }}ft} \right) = $ $ {U_{\text{o}}}{\text{sin}}\left( {\omega t} \right)$ (V), 由于磁通$ {\phi _{{\text{AB}}}} $ 是电压$ {v_{{\text{AB}}}} $ 对时间的积分, 结合(16 )式, 可以得到在正弦波电压激励下, 浮地忆阻器的磁通$ {\phi _{{\text{AB}}}} $ 和等效忆导值$ {W_{\text{m}}}\left( {{\phi _{{\text{AB}}}}} \right) $ 为${i_{{\text{AB}}}}$ 可表示为$i_{{\rm{AB}}}'$ 和${i}_{\rm{AB}}''$ 分别为27 )式与(29 )式可知, 忆阻器磁通$ {\phi _{{\text{AB}}}} $ 的幅值正比于${{{U_{\text{o}}}}}/{\omega }$ , 流经忆阻器的电流${i_{{\text{AB}}}}$ 由二次谐波$i_{{\text{AB}}}'$ 和基波$ {i}_{\text{AB}}'' $ 组成, $ {i}_{\text{AB}}' $ 与${v_{{\text{AB}}}}$ 相位相同, 且幅值呈正比例关系. $i_{{\text{AB}}}'$ 的幅值与${{U_{\text{o}}^2}}/({{{\text{2}}\omega }})$ 成正比, 二次谐波的存在使得忆阻器两端电压与流经忆阻器电流的相轨迹呈现磁滞环形. 通过对(29 )式分析可知: 在相同的激励电压幅值下, 随着激励频率的增大, 电压${v_{{\text{AB}}}}$ 幅值保持不变, 电流$ {i_{{\text{AB}}}} $ 幅值变小, 因此忆阻器两端电压与流经忆阻器电流的相轨迹${v_{{\text{AB}}}}$ -$ {i_{{\text{AB}}}} $ 会随着激励频率增大呈现内缩现象.$ {C_1} = {\text{0}}{\text{.1 nF}} $ , $ {R_1} = {\text{45 k}}\Omega $ , $ {R_2} = {\text{16 k}}\Omega $ , $ {R_{\text{3}}} = $ $ {\text{55 k}}\Omega $ , 直流电压${V_{\text{s}}} =-$ 2.5 V. 根据(18 )式, 可计算得到${\alpha _1} = {\text{3}}{\text{.20 S/Wb}}$ , $ {\beta _1} = 1.28 \times {10^{ - 5}}{\text{ S}} $ . 采用U 0 = 1 V, 激励频率f 分别为$ f = $ 80 kHz, 100 kHz以及130 kHz的正弦波电压${v_{{\text{AB}}}}$ 驱动忆阻器模型, 得到如图2 所示忆阻器PSPICE仿真结果图. 根据忆阻器模型中Z 1 是元件R 2 和公式(12 ), 得到忆阻器两端的磁通${\phi _{{\text{AB}}}}$ 正比于电容${C_1}$ 两端电压, 因此可以用${v_{C1}}$ 等效表示$ {\phi _{{\text{AB}}}} $ .图 2 忆阻器模型的PSPICE仿真结果 (a) 不同频率激励下的忆阻器${v_{{\text{AB}}}}\text-{i_{{\text{AB}}}}$ 特性曲线; (b) 不同频率激励下的忆阻器忆导值$W_{\text{m}}$ 与${v_{{\text{AB}}}}$ 的关系图; (c) 在U o = 1 V, f = 100 kHz下, ${v_{{\text{AB}}}}$ , ${i_{{\text{AB}}}}$ , $ {\phi _{{\text{AB}}}}_{} $ (用$v_{C_1}$ 表示)和$W_{\text{m}}$ 的时域波形图Figure2. Measured simulation results of the proposed memristor emulator: (a) Pinched hysteresis loops under different working frequencies; (b) variation curves of the memductance $W_{\text{m}}$ plotted against the terminal voltage ${v_{{\text{AB}}}}$ ; (c) time-domain wave-forms of ${v_{{\text{AB}}}}$ , ${i_{{\text{AB}}}}$ , $ {\phi _{{\text{AB}}}} $ (represented by $v_{C_1}$ ) and the memductance $W_{\text{m}}$ when U o = 1 V, f = 100 kHz.图2(a) 中频率为80 kHz, 100 kHz以及130 kHz时的电压${v_{{\text{AB}}}}$ 和电流${i_{{\text{AB}}}}$ 轨迹图, 可以得到忆阻器的重要特征: 在${v_{{\text{AB}}}} \text- {i_{{\text{AB}}}}$ 平面内, 其斜率等效为忆导值$W_{\text{m}}$ 且等效忆导值$W_{\text{m}}$ 保持形如斜“8”字形的磁滞环, 在正弦激励电压幅值保持不变时, 随着激励频率的增大, 磁滞环向内收缩. 图2(b) 表明, 在电压取值不为极值的情况下, 等效忆导值$W_{\text{m}}$ 不唯一. 以$ f = 80{\text{ kHz}} $ 条件下的${v_{{\text{AB}}}}\text{-}{W_{\text{m}}}$ 特性曲线图为例, 沿着箭头方向, 忆导值$ W_{\text{m}} $ 幅值在${v_{{\text{AB}}}}$ 正区间增大, 在$ {v_{{\text{AB}}}} $ 负区间减小. 图2(c) 表明在频率为100 kHz情况下, 与(29 )式分析一致, 电流$ {i_{{\text{AB}}}} $ 在输出电压$ {v_{{\text{AB}}}} $ 为正弦激励电压下, 呈现出非标准的正弦波形, 并且比较电流$ {i_{{\text{AB}}}} $ 与电压$ {v_{{\text{AB}}}} $ 波形图相位可知该记忆元件模型具有非线性特性且呈阻性, 即说明该器件为忆阻器. 图2 表明仿真结果与理论分析一致, 证明了本文基于通用模拟器的忆阻器等效电路模型的正确性.3.2.忆容器模型仿真分析 -->3.2.忆容器模型仿真分析 当阻抗元件$ {Z_1} $ 和$ {Z_{\text{2}}} $ 分别为电阻$ {R_{\text{2}}} $ 和电容$ {C_{\text{2}}} $ 时, 此时模拟器模拟为磁通控制忆容器模型, 同理于忆阻器, 忆容器的重要特点是其容值的受控性, 当对其施加正弦电压激励时, 忆容器端电压与流经忆容器电荷的相图呈现磁滞环形. 对于正弦激励电压${v_{{\text{AB}}}} = {U_{\text{o}}}\sin (2{\text{π}}ft) = {U_{\text{o}}} \sin(\omega t)$ (V), 同理于(27 )与(28 )式, 由(20 )式可得忆容器等效忆容值$ {C_{\text{m}}}\left( {{\phi _{{\text{AB}}}}} \right) $ 的表达式:30 )式可得: 忆容器磁通$ {\phi _{{\text{AB}}}} $ 的幅值正比于${{{U_{\text{o}}}}}/{\omega }$ , 在相同的正弦波激励电压幅值下, 随着激励电压频率的增大, 磁通$ {\phi _{{\text{AB}}}} $ 的幅值逐渐减小并趋近于0, 使得其等效忆容值趋近于固定值$ {\beta _2} $ , 从而导致端电压和流经忆容器的电荷的李萨如相轨迹${v_{{\text{AB}}}}\text{-}{q_{{\text{AB}}}}$ 呈现向内收缩现象.$ {C_1} = 0.25{\text{ nF}} $ , ${C_{\text{2}}} = $ $ 0.1{\text{ nF}}$ 、电阻${R_1} = 3{\text{ k}}\Omega$ , $ {R_{\text{2}}} = {\text{11 k}}\Omega $ 、直流电压$V_{\text{s}} = $ $ -0.5\;{\rm{V}}$ , 计算(22 )式可得$\alpha _2 = 9.92 \times 10^{-7}{\text{ F/Wb}}$ , ${\beta _{\text{2}}} = {\text{1}}{\text{.36}} \times {\text{1}}{{\text{0}}^{{{ - 12}}}}{\text{ F}}$ . 根据忆容器模型中Z 1 是元件R 1 和公式(12 ), 得到忆容器两端的磁通${\phi _{{\text{AB}}}}$ 正比于电容${C_1}$ 两端电压, 因此可以用${v_{C_1}}$ 等效表示${\phi _{{\text{AB}}}}$ ; 根据Z 2 是元件C 2 和公式(9 ), 得到流经忆容器的电荷${q_{{\text{AB}}}}$ 正比于电容$ {C_2} $ 两端电压负值, 因此可以用${-}{v_{C_2}}$ 等效表示${q_{{\text{AB}}}}$ . 采用U o = 1 V, 频率f 分别取80 kHz, 85 kHz以及90 kHz的正弦波电压${v_{{\text{AB}}}}$ 驱动忆容器模型, 得到如图3 所示忆容器模型的PSPICE仿真结果.图 3 忆容器模型的PSPICE仿真结果 (a) 不同频率激励下的忆容器${v_{{\text{AB}}}}\text-{q_{{\text{AB}}}}$ (用${v_{{\text{AB}}}} \text- \left( {{{ - }}{v_{C2}}} \right)$ 表示)特性曲线; (b)不同频率激励下的忆容器忆容值$ {C_{\text{m}}} $ 与${v_{{\text{AB}}}}$ 的关系图; (c) 在U o = 1 V, $ f $ = 80 kHz下, ${v_{{\text{AB}}}}$ 和${q_{{\text{AB}}}}$ (用${{ - }}{v_{C2}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用${v_{C_1}}$ 表示)和$ {C_{\text{m}}} $ 的时域波形图Figure3. Measured simulation results of the proposed memcapacitor emulator: (a) Pinched hysteresis loops under different working frequencies; (b) variation curves of the memcapacitance$ {C_{\text{m}}} $ plotted against the terminal voltage $ {v_{{\text{AB}}}} $ ; (c) time-domain wave-forms of $ {v_{{\text{AB}}}} $ , $ {q_{{\text{AB}}}} $ (represented by${{ - }}{v_{C_2}}$ ), $ {\phi _{{\text{AB}}}} $ (represented by${v_{C_1}}$ ) and the memcapacitance $ {C_{\text{m}}} $ when U o = 1 V, $ f $ = 80 kHz.图3(a) 表明, ${v_{{\text{AB}}}}\text{-}{q_{{\text{AB}}}}$ 相图由${v_{{\text{AB}}}}$ -(${-}{v_{C_2}}$ )等效表示, 在频率为80 kHz, 85 kHz和90 kHz的同幅值正弦激励电压下, 其端电压$ {v_{{\text{AB}}}} $ 和瞬时电荷${q_{{\text{AB}}}}$ 的相图呈现斜“8”字形磁滞环, 并且随着频率增大, 磁滞环围成的瓣面积变小. 图3(a) 表明PSPICE仿真结果同理论分析一致, 证明了本文设计的忆容器等效电路模型的正确性.图3(b) 表明相同电压下的等效忆容值$ {C_{\text{m}}} $ 的取值不唯一, 并且随着激励电压频率的升高, $ {C_{\text{m}}} $ 的最大值和最小值区间上下限减小. 图3(c) 所示为在激励频率为80 kHz下, 忆容器各变量端电压$ {v_{{\text{AB}}}} $ 、等效于${q_{{\text{AB}}}}$ 的$- {v_{C_2}}$ 、等效于磁通$ {\phi _{{\text{AB}}}} $ 的${v_{C_1}}$ 以及忆容值$ {C_{\text{m}}} $ 的时域图, 明显看出, $ {v_{{\text{AB}}}} $ 和${v_{C_1}}$ 的波形存在相位差, 这也是${v_{{\text{AB}}}}\text{-}{q_{{\text{AB}}}}$ 相图呈现磁滞特性的原因, 而$ {v_{{\text{AB}}}} $ 和$- {v_{C_2}}$ 的同相位表明该模拟器实现的是容性忆容器元件模型.3.3.忆感器仿真分析 -->3.3.忆感器仿真分析 当阻抗元件$ {Z_1} $ 和$ {Z_{\text{2}}} $ 分别为电感$ {L_1} $ 、电阻$ {R_2} $ 时, 此时模拟器模拟为磁通控制忆感器模型, 采用以下电路参数: 电容$ {C_1} = 0.{\text{02 nF}} $ 、电阻$ {R_1} = 3{\text{ k}}\Omega $ 、$ {R_{\text{2}}} = {\text{8 k}}\Omega $ 、电感$ {L_1} = {\text{0}}{\text{.05 H}} $ 、直流电压${V_{\text{s}}} = - 2.5$ V. 根据(26 )式可计算得α 3 =7.50 ×1011 (H·Wb)–1 , ${\beta _{\text{3}}} = $ $ {\text{1}}{\text{.875 }}{{\text{H}}^{{{ - 1}}}}$ . 根据忆感器模型中Z 1 是元件L 1 和公式(10 ), 得到忆感器两端的磁通${\phi _{{\text{AB}}}}$ 正比于流过忆感器的电流${i_1}$ , 因此可以用${i_1}$ 等效表示${\phi _{{\text{AB}}}}$ ; 根据模型中Z 1 是元件L 1 和公式(12 ), 得到忆感器两端磁通的积分${\rho _{{\text{AB}}}}$ 正比于流过C 1 两端的电压, 因此可以用${v_{C_1}}$ 等效表示${\rho _{{\text{AB}}}}$ .${v_{{\text{AB}}}} = {U_{\text{o}}}\sin \left( {\omega t} \right)$ (V), 可以得到正弦波电压激励情况下, 忆感器的磁通积分${\rho _{{\text{AB}}}}$ (假设积分初始值为0)和等效忆感值倒数$L_{\text{m}}^{{{ - 1}}}\left( {{\rho _{{\text{AB}}}}} \right)$ 为31 )式, (33 )式分析可知: 在相同幅值的激励电压下, 随着频率的增大, 磁通与电流幅值均减少, 在同一时刻$ t $ , 电流减小的幅度大于磁通减小的幅度.图4(a) 所示为不同频率下忆感器磁通和流经忆感器的电流的李萨如相轨迹${\phi _{{\text{AB}}}} \text- {i_{{\text{AB}}}}$ , 比较频率为95, 100以及105 kHz的相轨迹图, 可以明显看出, 忆感器磁通和流经忆感器的电流的相图${\phi _{{\text{AB}}}} \text- {i_{{\text{AB}}}}$ 保持斜“8”字形的磁滞环, 且随着激励频率增大, 电流和磁通幅值均减小, 磁滞环向内收缩.图 4 忆感器模型的PSPICE仿真结果 (a) 不同频率激励下的忆感器${\phi _{{\text{AB}}}} \text- {i_{{\text{AB}}}}$ (用${i_1} \text- {i_{{\text{AB}}}}$ 表示)特性曲线; (b)不同频率激励下忆感器的忆感值倒数$ L_{\text{m}}^{ - 1} $ 与$ {\phi _{{\text{AB}}}} $ (用${i_1}$ 表示)的关系图; (c) 当U o = 1 V, $ f $ = 100 kHz时, ${i_{{\text{AB}}}}$ , ${\rho _{{\text{AB}}}}$ (用${v_{C_1}}$ 表示)、$ {\phi _{{\text{AB}}}} $ 和$ L_{\text{m}}^{ - 1} $ 的时域波形图Figure4. Measured simulation results of the proposed meminductor emulator: (a) Pinched hysteresis loops under different working frequencies; (b) variation curves of the inverse meminductance $ L_{\text{m}}^{ - 1} $ plotted against the flux$ {\phi _{{\text{AB}}}} $ (represented by $ i_1 $ ); (c) time-domain wave-forms of $ {i_{{\text{AB}}}} $ , ${\rho _{{\text{AB}}}}$ (represented by${v_{C_1}}$ ), $ {\phi _{{\text{AB}}}} $ and the inverse meminductance $ L_{\text{m}}^{ - 1} $ when U o = 1 V, $ f $ = 100 kHz.图4(b) 为U o = 1 V, 激励频率为95, 100和105 kHz下忆感值的倒数$L_{\text{m}}^{{{ - 1}}}$ 与磁通$ {\phi _{{\text{AB}}}} $ 的相图变化曲线. 等同于忆阻器的忆导值和忆容器的忆容值, 忆感器的忆感值倒数$L_{\text{m}}^{{{ - 1}}}$ 在交变激励电压的取值为非最值情况下存在两个可能值, 并且沿着频率为95 kHz的$ {\phi _{{\text{AB}}}} $ $\text- L_{\text{m}}^{{{ - 1}}}$ 相图曲线的箭头方向, 可以发现$L_{\text{m}}^{{{ - 1}}}$ 在正磁通范围内增大, 在负磁通范围内减少.图4(c) 绘制了在激励频率为100 kHz下各变量${i_{{\text{AB}}}}$ , ${\rho _{{\text{AB}}}}$ (用${v_{C_1}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用$ {i_{\text{1}}} $ 表示)和$L_{\text{m}}^{{{ - 1}}}$ 的时域波形图, 由(33 )式可知${i_{{\text{AB}}}}$ 的波形呈现非标准式正弦波, 说明该忆感器模型具有非线性特性, 并且$ {i_{{\text{AB}}}} $ 的波形与$ {\phi _{{\text{AB}}}} $ 的波形相位相同, 表明该模拟器实现的是感性忆感器元件模型.图4 表明仿真结果和实验结果同理论分析一致, 证明了所搭建的浮地忆感器等效电路模型的正确性.4.硬件实验验证 搭建基于图1 所示通用模拟器的硬件实验电路, 如图5 所示: 绿色电路板上所焊接为图1 中的通用模拟器电路, 以黄框标出阻抗元件Z 1 与Z 2 , 以红框标出AD844芯片, 以白框标出AD633芯片, 并在右下角标出±15 V直流电源线与接地线. 根据表1 所示, 在通用模拟器的Z 1 与Z 2 处接入不同的电阻、电容和电感元件组合, 能够分别在硬件电路实验中实现忆阻器、忆容器和忆感器模型, 如图6 所示, 黄框与黄色字母R , L , C 表示在通用模拟器中接入的不同阻抗元件的组合.图 5 通用模拟器硬件实验电路实现Figure5. Implementation of the universal emulator in hardware experiment.图 6 在通用模拟器的Z 1 和Z 2 接入不同的电阻、电容和电感元件组合, 分别实现忆阻器、忆容器和忆感器模型的硬件实验电路 (a) 忆阻器; (b) 忆容器; (c) 忆感器Figure6. The experimental breadboard implementation of (a) memristor, (b) memcapacitor, (c) meminductor models based on the universal emulator by connecting different combinations of resistor, capacitor or inductor to Z 1 and Z 2 .${v_{{\text{AB}}}} = {U_{\text{o}}}{\text{sin}}\left( {2{\text{π}}ft} \right) = {U_{\text{o}}}{\text{sin}}\left( {\omega t} \right)$ (V), 作为电路模型的二端口激励电压, 芯片直流供电电压为±15 V. 为了与仿真结果进行比较, 采用示波器GW Instek-2102A对实验结果进行记录, 并通过Origin 9软件绘制实验结果.4.1.忆阻器电路响应 4.1.忆阻器电路响应 忆阻器硬件实验电路所采用的参数为: 电容$C_1 = 1.22{\text{ nF}}$ 、电阻$ {R_1} = 3{\text{ k}}\Omega $ , $ {R_{\text{2}}} = 1.5{\text{ k}}\Omega $ , ${R_{\text{3}}} = $ $ 1{\text{00 k}}\Omega$ , 直流电压$V_{\text{s}} = - 4$ V, 根据(18 )式, 可计算得到${\alpha _1} = {\text{1}}{\text{.09 S/Wb}}$ , ${\beta _1} = 8 \times {10^{ - 6}}{\text{ S}}$ . 加在忆阻器两端的正弦电压信号, 幅值U o = 3 V, 频率分别取70 kHz, 80 kHz和100 kHz, 得到图7 实验结果. 在实验中, 根据忆阻器模型中Z 2 是元件R 3 和公式(9 ), 得到流经忆阻器电流${i_{{\text{AB}}}}$ 正比于R 3 两端电压的负值, 因此可以用$- {v_{R_3}}$ 等效表示${i_{{\text{AB}}}}$ .图 7 忆阻器模型的硬件电路实验结果 (a) 不同频率激励下的忆阻器${v_{{\text{AB}}}} \text- {i_{{\text{AB}}}}$ (用${v_{{\text{AB}}}} \text- ({{ - }}{v_{R_3}})$ 表示)特性曲线; (b)不同频率激励下的忆阻器忆导值$ {W_{\text{m}}} $ 与${v_{{\text{AB}}}}$ 的关系图; (c)在U o = 3 V, $ f $ = 100 kHz下, $ {v_{{\text{AB}}}} $ , $ {i_{{\text{AB}}}} $ (用${{ - }}{v_{R_3}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用${v_{C_1}}$ 表示)和$ {W_{\text{m}}} $ 的时域波形图Figure7. Experimental results of the proposed memristor emulator: (a) Pinched hysteresis loops under different working frequencies; (b) variation curves of the memductance $ {W_{\text{m}}} $ plotted against the terminal voltage $ {v_{{\text{AB}}}} $ ; (c) time-domain wave-forms of ${v_{{\text{AB}}}}$ , ${i_{{\text{AB}}}}$ (represented by${{ - }}{v_{R_3}}$ ), $ {\phi _{{\text{AB}}}} $ (represented by${v_{C_1}}$ ) and the memductance $ {W_{\text{m}}} $ when U o = 3 V, $ f $ = 100 kHz.图7(a) 可以看出, 随着激励电压频率增大, 忆阻器端电压与流经忆阻器两端的电流的李萨如相轨迹图${v_{{\text{AB}}}}\text{-}{i_{{\text{AB}}}}$ 呈现磁滞环且逐渐向内收缩, 磁滞回线的面积变小, 与图2(a) 一致. 图7(b) 显示的$ {v_{{\text{AB}}}} $ $\text- {W_{\text{m}}}$ 关系图和图2(b) 一致, $ {W_{\text{m}}} $ 的变化区间随激励电压的频率增大而减小. 等同于图2(c) , 图7(c) 各变量在频率为100 kHz下很好地呈现了忆阻器的非线性特性和阻性. 图7 的实验结果同理论分析和仿真结果趋势一致, 证明了本文基于通用记忆元件模拟器搭建的浮地忆阻器等效电路模型的正确性和可行性.4.2.忆容器电路响应 -->4.2.忆容器电路响应 忆容器硬件实验电路参数为: 电容$ {C_1} = 1.22{\text{ nF}} $ , $ {C_{\text{2}}} = {\text{0}}.22{\text{ nF}} $ ; 电阻$ {R_1} = 3{\text{ k}}\Omega $ , $ {R_{\text{2}}} = 1.5{\text{ k}}\Omega $ ; 直流电压$V_{\text{s}} = - 4$ V, 通过计算(22 )式可得${\alpha _{\text{2}}} = {\text{2}}{\text{.40}} \times $ $ {\text{1}}{{\text{0}}^{{{ - 5}}}}{\text{ F/Wb}}$ ${\beta _{\text{2}}} = {\text{1}}{\text{.76}} \times {\text{1}}{{\text{0}}^{{{ - 10}}}}{\text{ F}}$ . 忆容器的激励电压为正弦波, 幅值${U_{\text{o}}}$ = 3 V、频率f 分别取$ f = $ 65 kHz, 80 kHz以及100 kHz, 实验结果如图8 所示, 图8(a) 是忆容值的磁滞环波形${v_{{\text{AB}}}}\text{-}{q_{{\text{AB}}}}$ (用${v_{{\text{AB}}}}\text{-}\left( { - {v_{C_2}}} \right)$ 表示), 图8(b) 是忆容值$ {C_{\text{m}}} $ 和${v_{{\text{AB}}}}$ 的关系图, 图8(c) 所示为$ {v_{{\text{AB}}}} $ , ${q_{{\text{AB}}}}$ (用$- {v_{C_2}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用${v_{C_1}}$ 表示)和$ {C_{\text{m}}} $ 的时域波形图.图 8 忆容器模型的硬件实验结果 (a) 不同频率激励下的忆容器${v_{{\text{AB}}}}\text-{q_{{\text{AB}}}}$ (用${v_{{\text{AB}}}}{{\text-}}\left( { - {v_{C_2}}} \right)$ 表示)特性曲线; (b)不同频率激励下的忆容器忆容值$ {C_{\text{m}}} $ 与${v_{{\text{AB}}}}$ 的关系图; (c) 在U o = 3 V, $ f $ = 80 kHz下${v_{{\text{AB}}}}$ , ${q_{{\text{AB}}}}$ (用${{ - }}{v_{C_2}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用${v_{C_1}}$ 表示)和$ {C_{\text{m}}} $ 的时域波形图Figure8. Experimental results of the proposed memcapacitor emulator: (a) Pinched hysteresis loops under different working frequencies; (b) variation curves of the memcapacitance $ {C_{\text{m}}} $ plotted against the terminal voltage ${v_{{\text{AB}}}}$ ; (c) time-domain wave-forms of ${v_{{\text{AB}}}}$ , ${q_{{\text{AB}}}}$ (represented by ${{ - }}{v_{C_2}}$ ), $ {\phi _{{\text{AB}}}} $ (represented by ${v_{C_1}}$ ) and the memcapacitance $ {C_{\text{m}}} $ when U o = 3 V, $ f $ = 80 kHz.图8 和图3 可以看出, 忆容器模型的硬件实验结果和Pspice仿真结果一致, 忆容器端电压和瞬时电荷的相图呈斜“8”字形的磁滞环, 且磁滞环在相同幅值的正弦电压下, 随着激励频率增大而向内收缩. 并且图8(c) 中$- {v_{C_2}}$ 呈非标准正弦波, 验证了忆容器的非线性特性. 通过其电路仿真和电路实验结果对比, 验证了所搭建的浮地忆容器等效模型的有效性.4.3.忆感器电路响应 -->4.3.忆感器电路响应 忆感器硬件实验电路参数如下所示: 电容${C_1} = $ $ {\text{2}}.2{\text{ nF}}$ 、电阻${R_1} = 3{\text{ k}}\Omega$ 、${R_{\text{2}}} = 1{\text{0 k}}\Omega$ 、电感L 1 = 20 mH, 直流电压$V_{\text{s}} = - {\text{2}}$ V, 根据(26 )式可计算得α 3 = 3.41 × 1010 (H·Wb)–1 , ${\beta _{\text{3}}} = {\text{3 }}{{\text{H}}^{{{ - 1}}}}$ . 忆感器的激励电压幅值U o = 3 V, 频率$ f = $ 75 kHz, 80 kHz以及100 kHz, 得到图9 所示实验结果. 根据忆感器模型中Z 1 是元件L 1 和公式(10 )和(11 ), 得到忆感器两端的磁通${\phi _{{\text{AB}}}}$ 正比于电阻R 1 两端电压的负值, 因此可以用$ - {v_{R1}}$ 等效表示${\phi _{{\text{AB}}}}$ .图 9 忆感器模型的硬件实验结果 (a) 不同频率激励下的忆感器${\phi _{{\text{AB}}}}\text-{i_{{\text{AB}}}}$ (用$( - {v_{R1}}){{\text- (}} - {v_{R2}})$ 表示)特性曲线; (b)不同频率激励下忆感器的忆感值倒数$L_{\text{m}}^{{{ - 1}}}$ 与$ {\phi _{{\text{AB}}}} $ (用$ - {v_{R1}} $ 表示)的关系图; (c) 在U o = 3 V, $ f $ = 80 kHz下$ {i_{{\text{AB}}}} $ (用$- {v_{R_2}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用$- {v_{R_1}}$ 表示)、$ {\rho _{{\text{AB}}}} $ (用${v_{C_1}}$ 表示)和$L_{\text{m}}^{ - 1}$ 的时域波形图Figure9. Experimental results of the proposed meminductor emulator: (a) Pinched hysteresis loops under different working frequencies; (b) variation curves of the inverse meminductance $L_{{{\rm{m}}}}^{{{ - 1}}}$ plotted against the flux $ {\phi _{{\text{AB}}}} $ (represented by${{ - }}{v_{R_1}}$ ) ; (c) time-domain wave-forms of ${i_{{\text{AB}}}}$ (represented by${{ - }}{v_{R_2}}$ ), ${\rho _{{\text{AB}}}}$ (represented by${v_{C_1}}$ ), $ {\phi _{{\text{AB}}}} $ (represented by$- {v_{R_1}}$ ), $ {\rho _{{\text{AB}}}} $ (represented by ${v_{C_1}}$ ) and the inverse meminductance $L_{\text{m}}^{{{ - 1}}}$ when U o = 3 V, $ f $ = 80 kHz.图4 和图9 可知, 忆感器模型实验结果与仿真结果趋势基本一致. 图9(a) 表明忆感器磁通与流经忆感器电流的相图${\phi _{{\text{AB}}}} \text- {i_{{\text{AB}}}}$ 呈斜“8”字形磁滞环, 且随着激励频率增大, 磁滞环向内收缩. 图9(b) 为激励频率为75 kHz, 80 kHz和100 kHz下忆感值的倒数$L_{\text{m}}^{{{ - 1}}}$ 与磁通$ {\phi _{{\text{AB}}}} $ 的变化曲线, 可以明显看出, $L_{\text{m}}^{{{ - 1}}}$ 具有频率依赖性, 随着频率上升, $L_{\text{m}}^{{{ - 1}}}$ 取值以及$ {\phi _{{\text{AB}}}} $ 取值范围减小. 图9(c) 绘制了在激励频率为80 kHz下各变量$ {i_{{\text{AB}}}} $ (用$- {v_{R_2}}$ 表示)、$ {\phi _{{\text{AB}}}} $ (用$- {v_{R_1}}$ 表示)、$ {\rho _{{\text{AB}}}} $ (用${v_{C_1}}$ 表示)和$L_{\text{m}}^{{{ - 1}}}$ 的时域波形图, $- {v_{R_2}}$ 不再为正弦型波形, 但$- {v_{R_2}}$ 与$- {v_{R_1}}$ 两者相位相同, 说明了此时模拟器具有非线性及感性特性, 进而验证了该等效电路模型为忆感器. 图4 和图9 表明仿真结果和实验结果同理论分析一致, 证明了所搭建的忆感器等效电路模型的正确性.5.结 论 本文提出一种新型通用模拟器, 并基于该模拟器实现浮地忆阻器、忆容器和忆感器建模, 通过理论分析、仿真电路和硬件电路实验的一致性表明所搭建的3种记忆元件模型具有记忆特性和非线性特性. 与现有同类能够实现3种浮地记忆元件模型的研究相比, 本文所提基于通用模拟器的新型浮地记忆元件模型结构简单, 易于硬件实现, 工作频率高, 对后续记忆元件研究和应用开发具有一定的参考价值. 为了更好地完善记忆元件等效电路模型的研究理论, 未来的研究工作可以着眼于忆耦器等效电路模型的搭建, 并基于该模型进行忆耦器特性和应用研究. 








































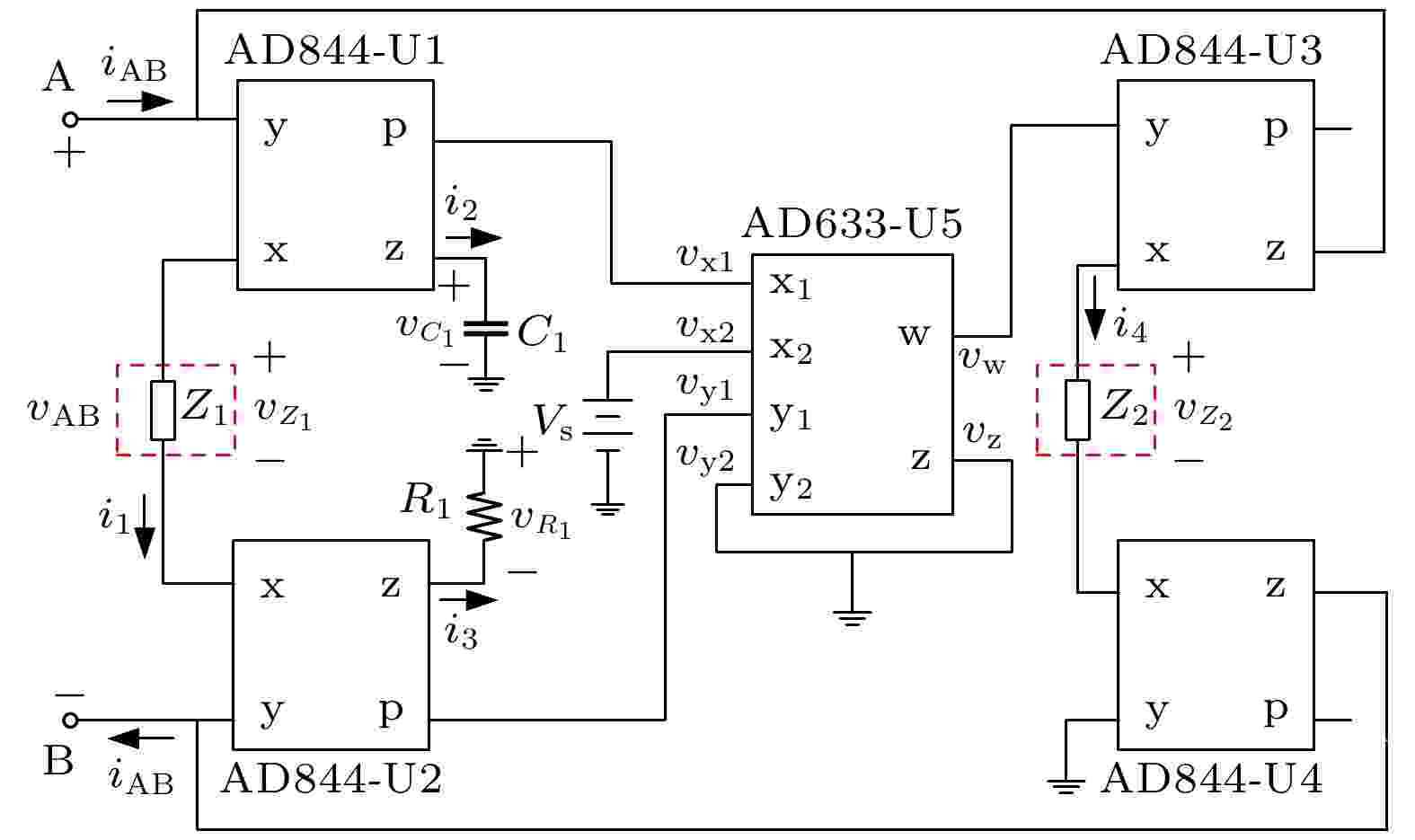 图 1 通用模拟器设计
图 1 通用模拟器设计

































































































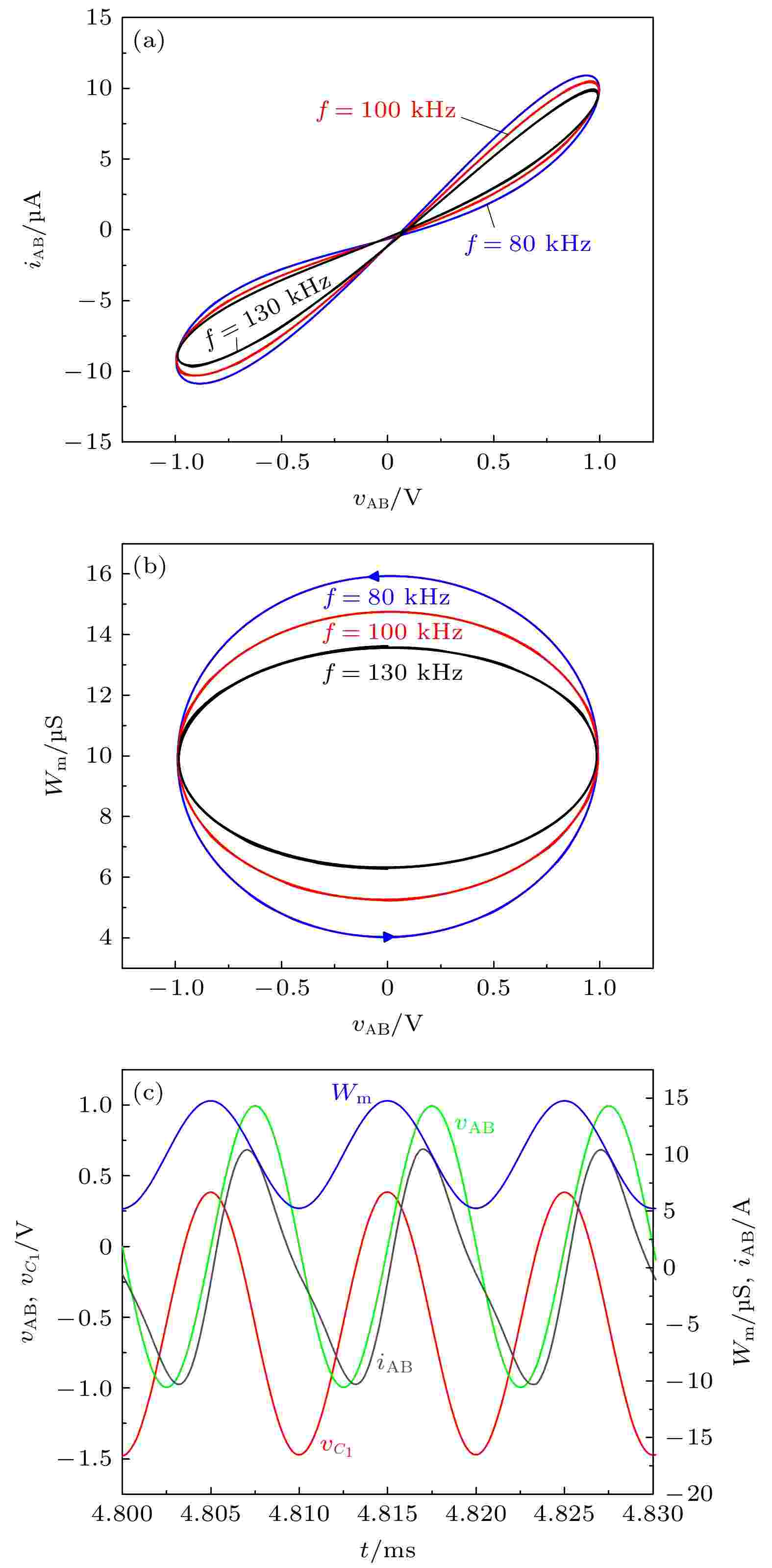 图 2 忆阻器模型的PSPICE仿真结果 (a) 不同频率激励下的忆阻器
图 2 忆阻器模型的PSPICE仿真结果 (a) 不同频率激励下的忆阻器
























































































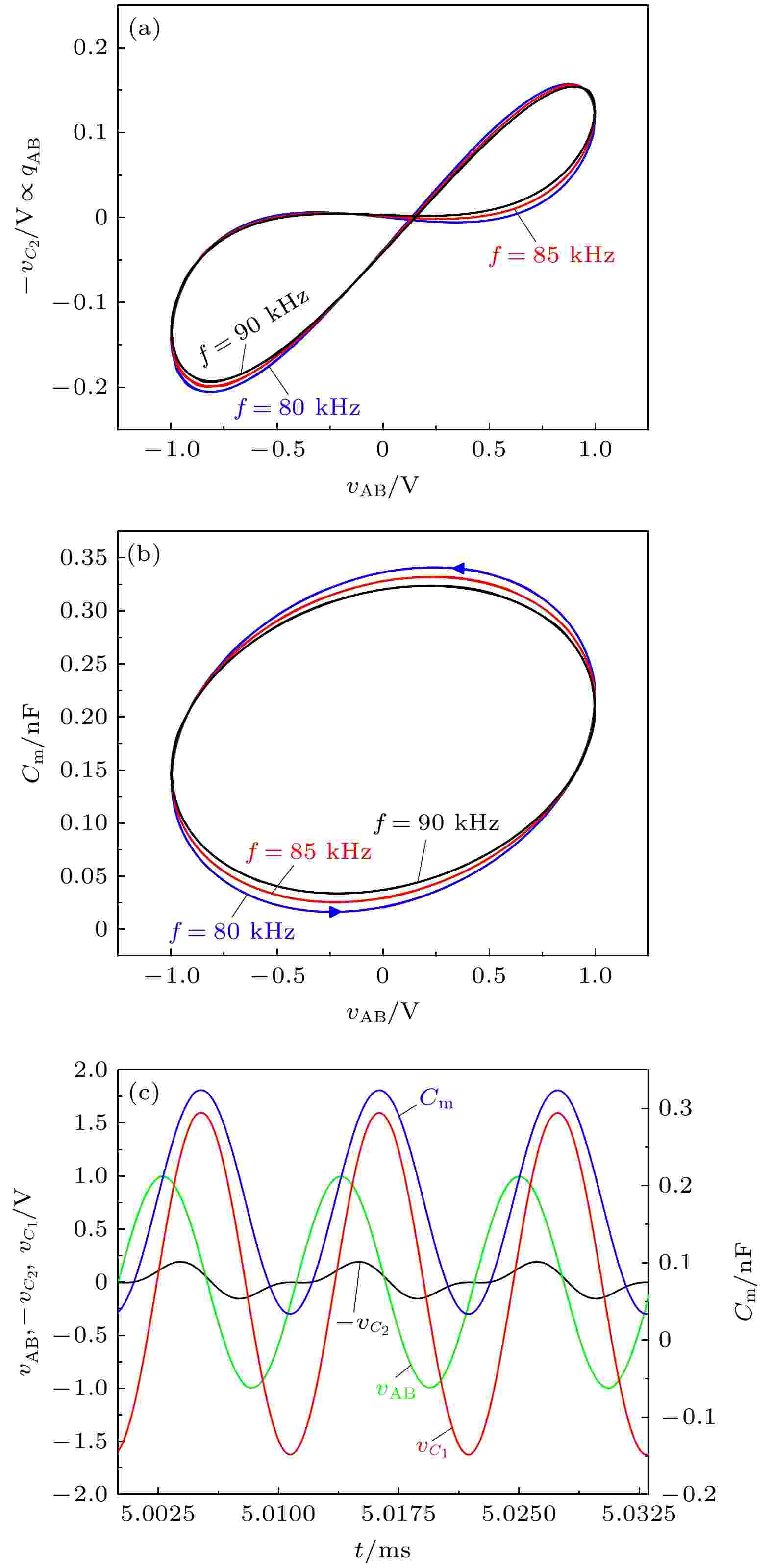 图 3 忆容器模型的PSPICE仿真结果 (a) 不同频率激励下的忆容器
图 3 忆容器模型的PSPICE仿真结果 (a) 不同频率激励下的忆容器





























































































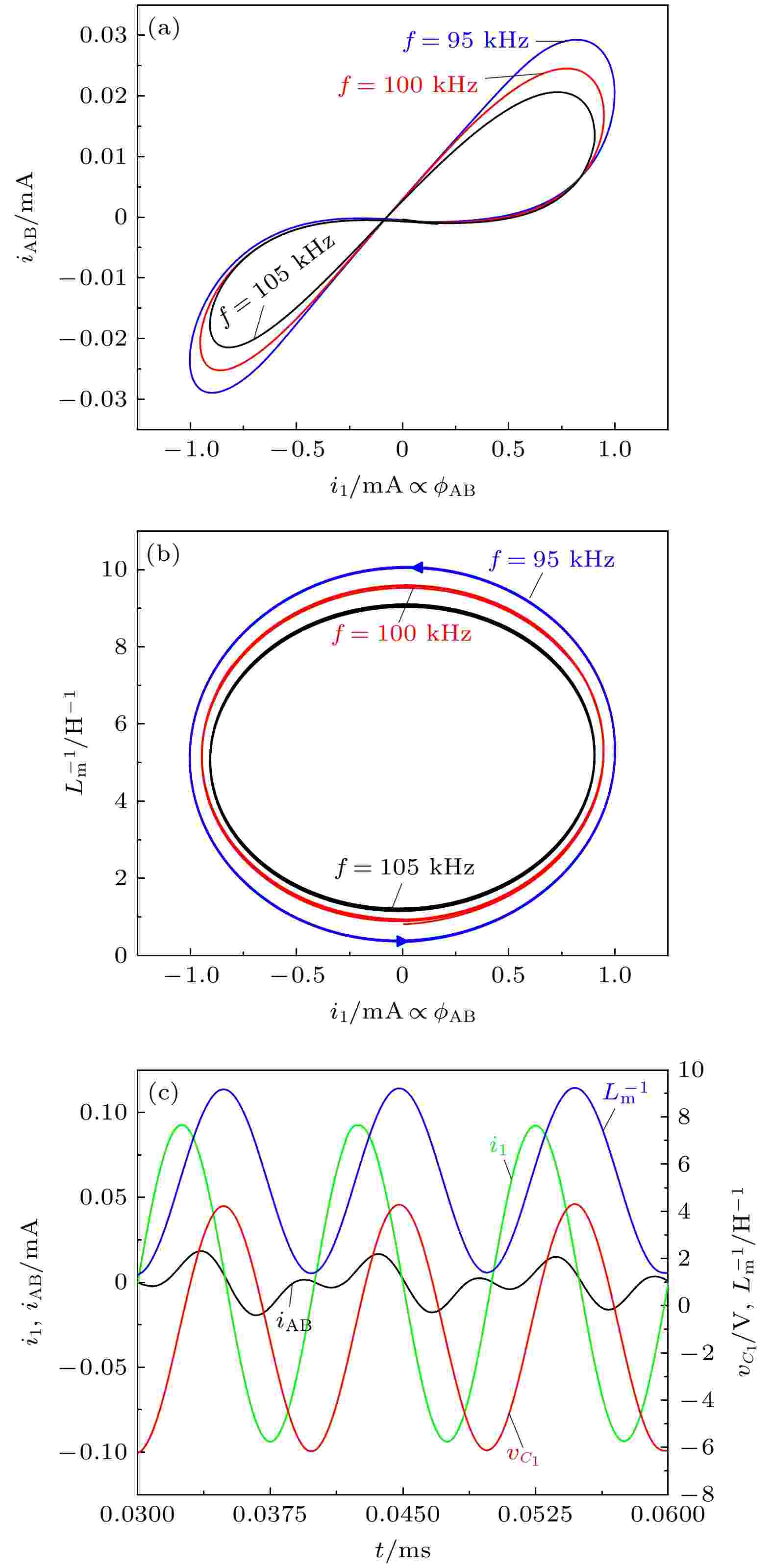 图 4 忆感器模型的PSPICE仿真结果 (a) 不同频率激励下的忆感器
图 4 忆感器模型的PSPICE仿真结果 (a) 不同频率激励下的忆感器






















































 图 5 通用模拟器硬件实验电路实现
图 5 通用模拟器硬件实验电路实现 图 6 在通用模拟器的Z1和Z2接入不同的电阻、电容和电感元件组合, 分别实现忆阻器、忆容器和忆感器模型的硬件实验电路 (a) 忆阻器; (b) 忆容器; (c) 忆感器
图 6 在通用模拟器的Z1和Z2接入不同的电阻、电容和电感元件组合, 分别实现忆阻器、忆容器和忆感器模型的硬件实验电路 (a) 忆阻器; (b) 忆容器; (c) 忆感器













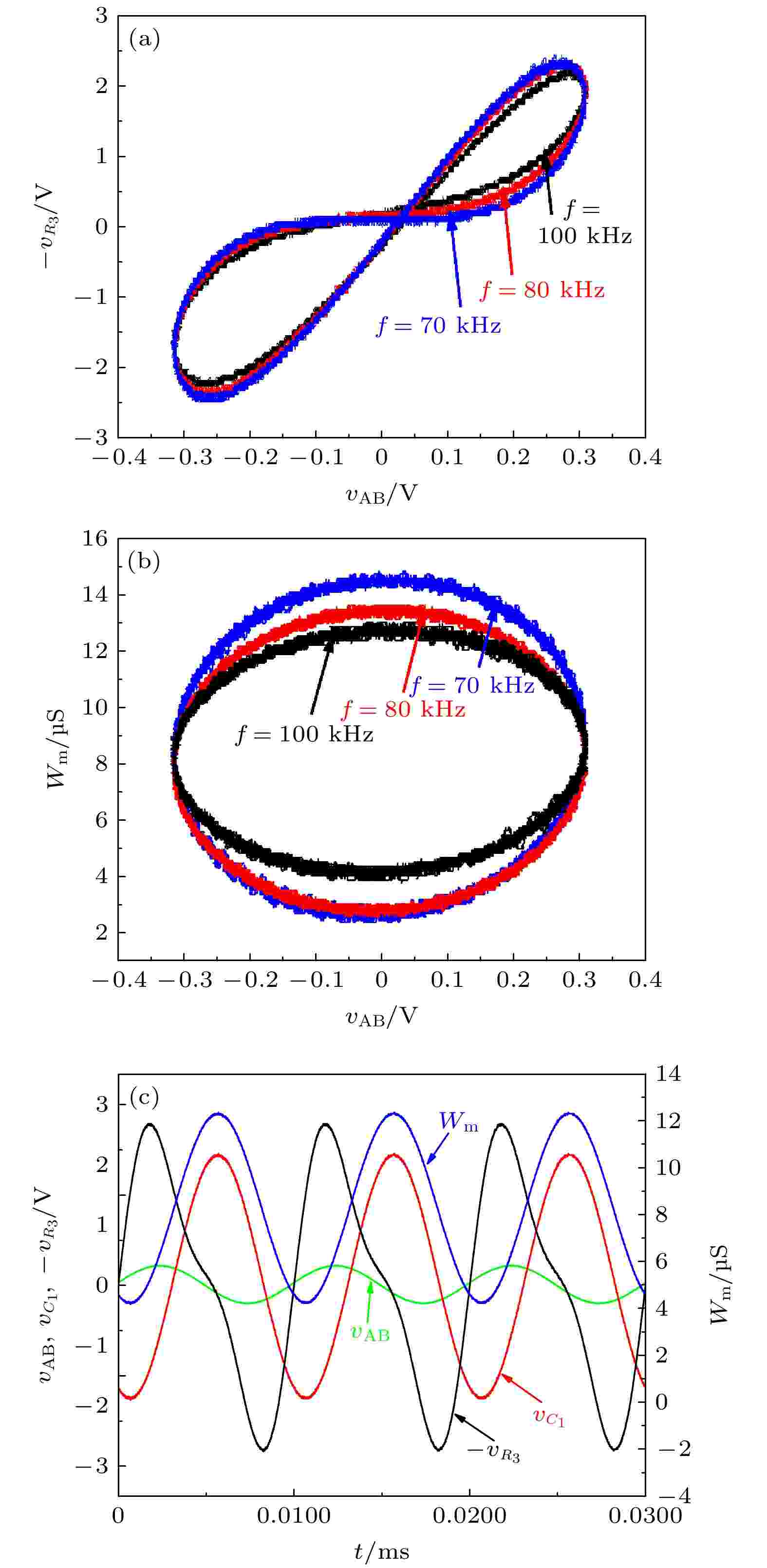 图 7 忆阻器模型的硬件电路实验结果 (a) 不同频率激励下的忆阻器
图 7 忆阻器模型的硬件电路实验结果 (a) 不同频率激励下的忆阻器

















































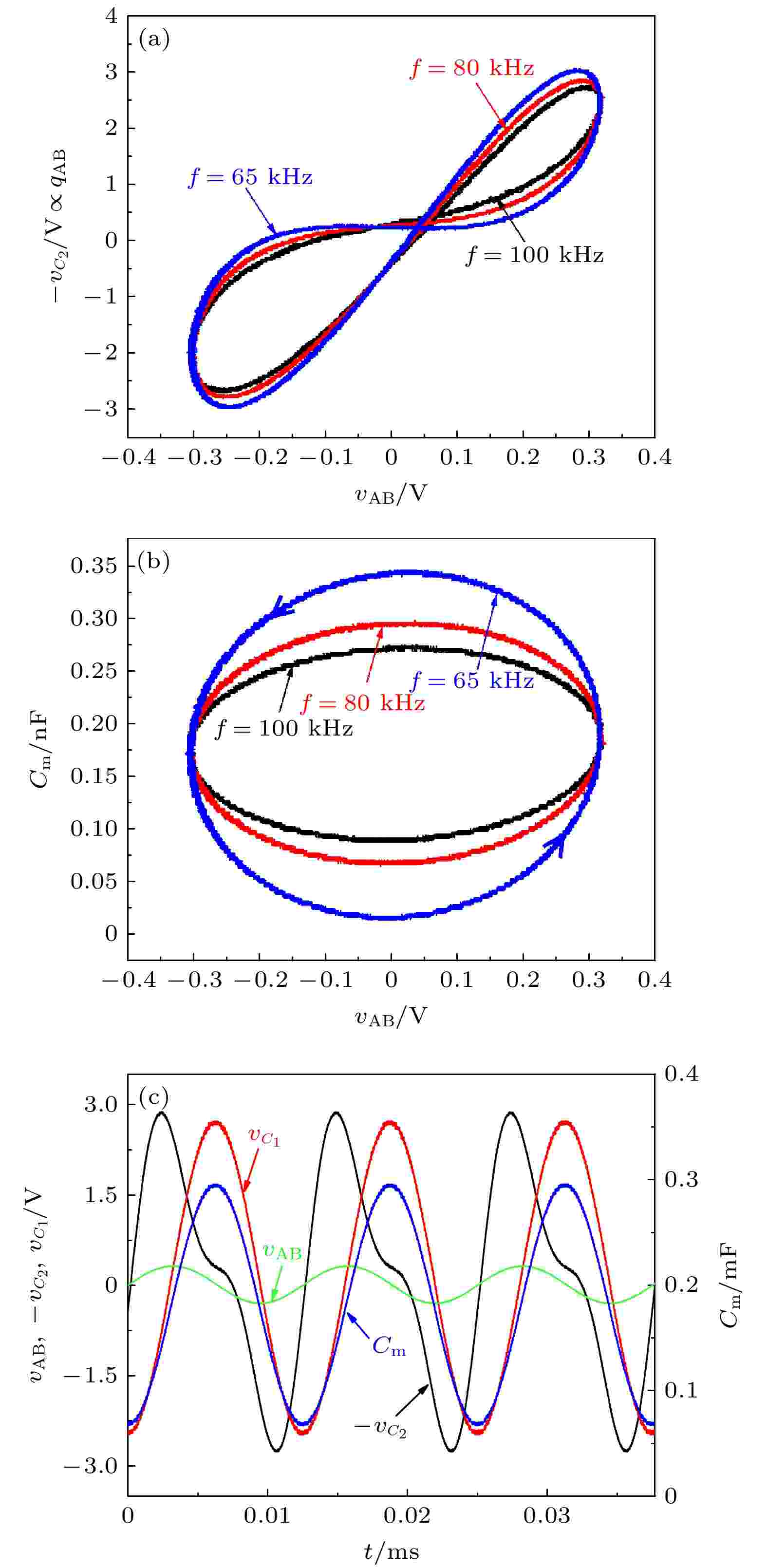 图 8 忆容器模型的硬件实验结果 (a) 不同频率激励下的忆容器
图 8 忆容器模型的硬件实验结果 (a) 不同频率激励下的忆容器








































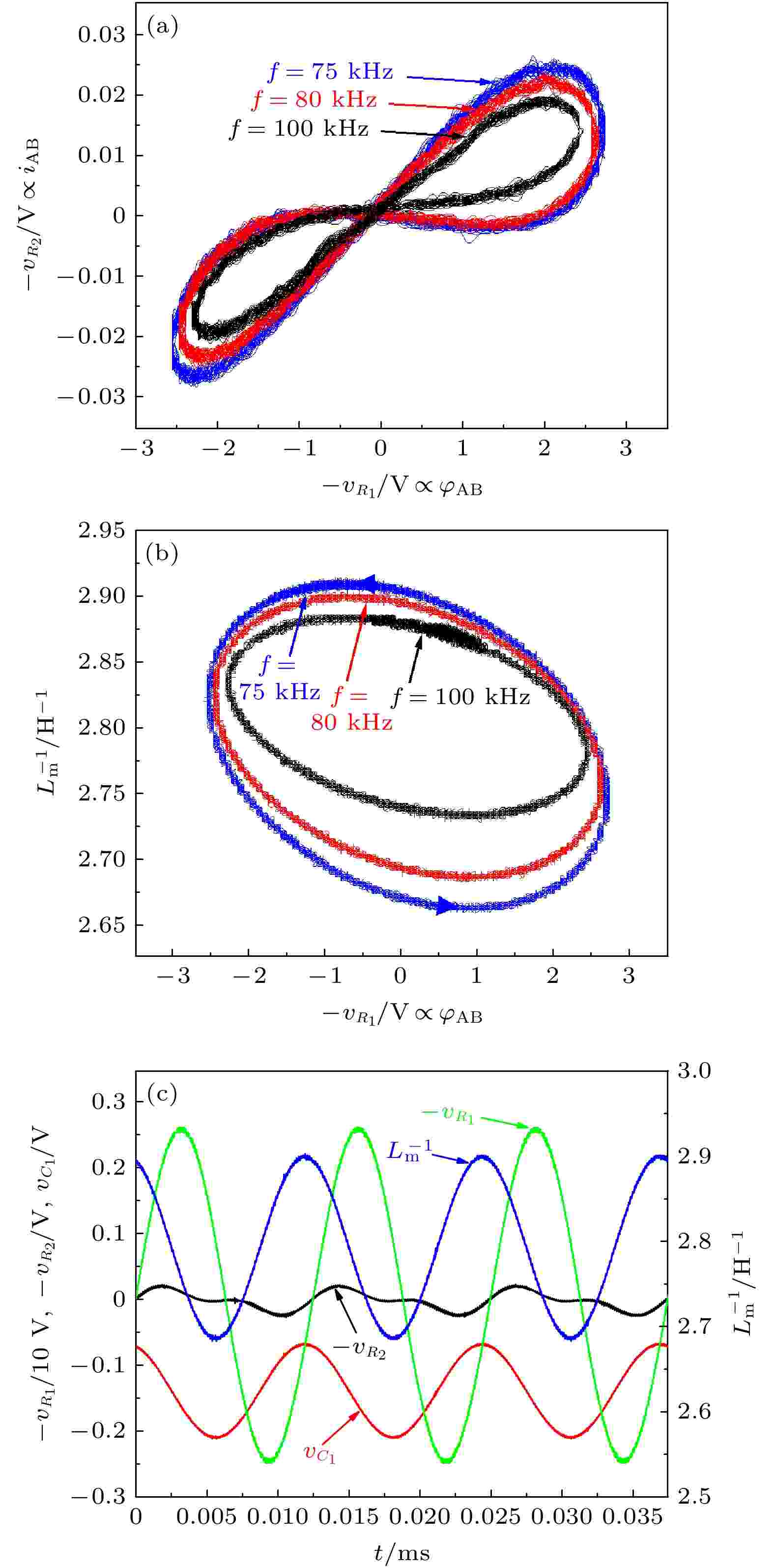 图 9 忆感器模型的硬件实验结果 (a) 不同频率激励下的忆感器
图 9 忆感器模型的硬件实验结果 (a) 不同频率激励下的忆感器









































































