摘要:放电模态是可以识别生物神经元的电活动, 即细胞内和细胞外的离子被泵送并在细胞内交换的过程. 通过适当的物理刺激, 人工神经元电路可以被设计以重现类似生物神经元的放电模式. 光电管中产生的光电流可以作为信号源, 对神经元电路进行刺激. 但由于不同支路上的通道电流对功能神经元动力学的控制程度不同, 所以光电管接入不同的支路, 将会使神经元电路的放电模式产生很大差异. 本文所采用的非线性神经元是由一个电容器、感应线圈、非线性电阻、两个理想电阻和一个周期电压源组成的FHN (FitzHugh-Nagumo neuron)电路. 在此基础上, 将光电管引入不同的支路来改变通道电流, 以研究光电流的生物物理作用. 当光电管连接到电容上, 光电管被激活从而改变通道电流时, 细胞膜电位可以直接改变, 并切换激发模式. 当光电管串联连接到感应线圈时, 通过感应线圈的感应电流被调节以平衡外部刺激. 这些结果表明, 在本文构建的两类光敏神经元模型中, 相比光电流驱动电感支路, 光电流驱动电容器支路可以更有效地调节膜电位, 大大提高感光灵敏度.
关键词: 神经元电路/
光电管/
分岔/
功能神经元

English Abstract

全文HTML

--> --> -->

神经系统是庞大的复杂网络, 由神经元(即神经细胞)和神经胶质细胞组成. 神经系统可以将各类信息进行编码处理^[1], 而主要的信息整合和传递是由神经细胞完成的. 生物神经系统中神经元的放电活动是通过离子在细胞膜间泵送和交换实现的, 通过数学模型, 可以研究其复杂的非线性动力学行为^[2-5]. 当神经元受到一定刺激会产生沿细胞膜表面传导的膜电位^[6,7], 即动作电位, 它是神经元兴奋或活动的标志. 神经元的主要功能是在动作电位的刺激下, 由钙离子触发细胞分泌神经递质, 并将神经冲动传递给其他神经元. 而神经系统中, 神经元之间信息传递的主要方式是突触传递, 包括神经递质释放、扩散等过程. 在一些中间神经元中存在一种特定的突触, 即自突触^[8]. 自突触可以改变神经元的电活动以及神经网络的集体行为^[9-12], 反映神经系统的复杂时空动力学.
神经元或神经网络电活动和受到一系列因素的影响, 如外界刺激(光照、温度等)、外界噪声等外部因素, 以及离子通道噪声、热噪声等内部因素^[13]. 事实上, 常见的神经元模型主要考虑离子通道电流对细胞膜电位的影响. 当考虑不同的物理刺激对通道电流的影响时, 神经元模型可以被构造成为人工智能处理单元, 用来感知和捕获外部刺激来触发适当的电活动, 甚至可以展现出明显的自适应能力^[14]. 但直接对生物神经元放电活动的研究是困难的, 而神经元电路以其简便易搭建等优点为研究神经元的动力学行为提供了有效的途径. 在过去的几十年中, 不同的非线性神经元电路被设计用来模拟和研究神经动力学^[15-17].
神经元电路的兴奋性可以通过其输出电压体现. 通过调整非线性电路中元件的参数, 可以使神经元电路的输出电压呈现出与神经元的膜电位类似的静息态、尖峰放电态、簇放电态, 甚至是混沌放电态. 当非线性电路^[18-25]被激活时, 用电容或电感耦合两个非线性电路, 连续的能量流在感应线圈和电容器中传播和交换^[26]. 能量的释放和储存在很大程度上取决于物理变量和电子元件, 非线性电路的每个分支将共享和贡献能量流, 以便进一步交换. Wang等^[19]基于一种电阻电容电感分流的约瑟夫森结模型, 用来论证了自适应控制器能耗与目标信号之间的关系, 结果表明, 利用追踪控制方案来驱动混沌系统达到预定目标信号是可行的. 文献[25]以电磁感应效应为研究对象, 利用FPGA设计了1个数字神经元电路, 该电路具有自动转换连接的动态响应和生物学功能. 另一方面, 可靠的神经元模型^[27-30]对于估计神经活动中的动力学特性和预测放电模式转换具有重要意义. 文献[31]分别采用电突触和化学突触对基于忆阻器的Hindmarsh-Rose神经元模型进行耦合, 并分析了神经元的同步动力学特性. Wang等^[32]研究了非全同的神经元电路耦合模型动力学, 数值结果表明通过调节耦合强度可以引起丰富的分岔行为.
事实上, 在神经元电路中产生类似生物神经元电活动需要考虑一些现实因素, 如电磁辐射^[33,34]等. 从物理角度来说, 可以用等效的非线性振荡器来描述一些复杂的神经网络系统^[9,35,36], 如感温触觉神经系统、感光视觉神经系统等, 来构造功能神经元. 当神经元处于光照条件时, 需要考虑光照对神经元放电活动的影响. 实验表明, 光学参数振荡器可以产生簇放电行为^[37,38]. Zhang等 ^[39]设计的一种约瑟夫森结耦合的功能性神经元系统, 可以实现对外界磁场变化的感知. Xu等 ^[40]用热敏电阻控制神经回路的分支电流或电流源, 从而使神经元对温度变得敏感, 同时, 该文献还对比了热敏电阻在不同支路对通道电流的影响, 从而为设计感温传感器提供了理论依据. 文献[41]提出了一种新的模型, 使突触通过光纤通信通道耦合神经振荡器, 模拟脑神经元之间脉冲信号的突触传递, 发现接收振荡器受到光电二极管的影响, 光纤通信通道可以保证不同频率比的同步.
在以前的大部分工作中, 基本是把非线性元件固定在某个支路上分析某种非线性混沌电路的动力学特性. Liu等^[42]设计了一种简单的光电管耦合神经电路, 结果表明光电池可以与产生连续电压源的神经电路耦合并捕获外部光信号. 该电路在人工眼设计方面具有潜在的应用前景. Guo等^[43]研究了忆阻器耦合的两个光敏神经电路, 并利用物理变量和参数的标度变换研究了耦合动力系统的同步稳定性, 通过调节耦合通道得到相位同步和完全同步. 基于一类光电神经元^[42]相关研究结果的启发, 本文研究了光电管/信号源在神经元电路的不同位置处对神经元电路放电活动的影响, 分别采用分岔分析^[44-46]、相轨图、李雅普诺夫指数等数值模拟方法分析了电路分岔参数对神经元模态转化动力学行为的影响.

2

-->

2.1.系统(1)—FHN神经元电路

首先考虑以余弦电压源为外界激励源的简单FHN神经元电路模型, 电路如图1所示.
图 1 余弦电压源驱动的简单FHN电路的示意图, 其中NR为非线性电阻, C为电容, L为感应线圈, R和R_S为线性电阻(分压电阻), E为恒压源, V_S为余弦电压源.
Figure1. Schematic diagram for the FHN neural circuit. NR is a nonlinear resistor, C is capacitor, L represents induction coil, R and R_S are linear resistors, E is a constant voltage source, and V_S is the external voltage source.

在此基础上, 在电路中引入光电管, 并研究光电管对神经元电路的物理特性影响(参见2.2节、2.3节). 非线性电阻NR的电压和电流之间的关系式为

$ {i_{NR}} = - \frac{1}{\rho }\left(V - \frac{1}{3}\frac{{{V^3}}}{{V_0^2}}\right),\quad $

其中, ρ, V₀是电阻的归一化参数; V是非线性电阻的电压.
根据基尔霍夫定律及电路各元件的伏安关系得图1所示的电路方程:

$ \left\{ \begin{gathered} C\frac{{{\rm d}{V_C}}}{{{\rm d}t}} = \frac{{{V_S} - {V_C}}}{{{R_S}}} - {i_L} - {i_{NR}}, \hfill \\ L\frac{{{\rm d}{i_L}}}{{{\rm d}t}} = {V_C} + E - R{i_L}. \hfill \\ \end{gathered} \right.\quad $

为了使电路方程具有普适性和一般性, 对 (2) 式采用以下的无量纲变换:

$ \left\{ \begin{gathered} x = \frac{{{V_C}}}{{{V_0}}},\;y = \frac{{\rho {i_L}}}{{{V_0}}},\;\tau = \frac{t}{{\rho C}},\;a = \frac{E}{{{V_0}}},\hfill \\ b = \frac{R}{\rho }, ~~ c = \frac{{{\rho ^2}C}}{L},\;\xi =\frac{\rho }{{{R_S}}},\;{u_S} = \frac{{{V_S}}}{{{V_0}}}. \hfill \\ \end{gathered} \right.\quad$

无量纲变换后的动力学方程(4)可以表达光敏神经元的动力学

$ \left\{ \begin{gathered} \dot x = \frac{{{\rm d}x}}{{{\rm d}\tau }} = x(1 - \xi ) - \frac{1}{3}{x^3} - y + \xi {u_S}, \hfill \\ \dot y = \frac{{{\rm d}y}}{{{\rm d}\tau }} = c(x - by + a), \hfill \\ \end{gathered} \right.\quad $

其中, 变量x表示膜电位, y表示恢复变量对应的慢电流. 将外部激励源选择为

$ {u_S}{\text{ = }}{B_1}\cos \omega \tau .\; $

2 -->

2.2.系统(2)—电容C串联光电管的FHN神经元电路

当将光电管串联在电容C所在支路时, 神经元电路图如图2所示.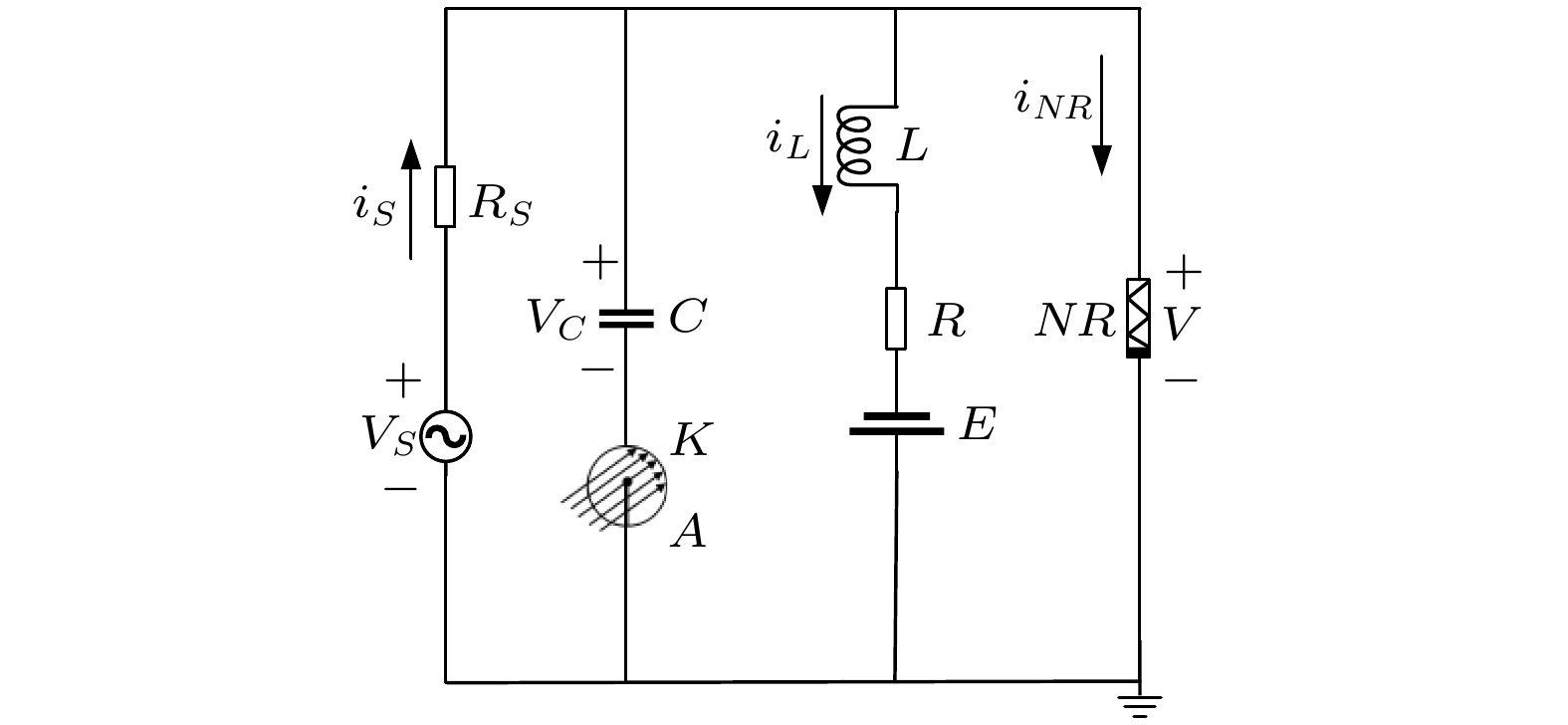
图 2 将光电管和电容串联的FHN电路原理示意图, 其中K表示光电管中的阴极, A表示光电管中的阳极
Figure2. Schematic diagram for the FHN neural circuit while phototube couples with capacitor. K denotes cathode and A represents anode in the phototube.

光管的光电流取决于外部照明和阴极的材料性能, 当外部照明强度达到一定阈值时, 光电流达到饱和值, 如图3所示.
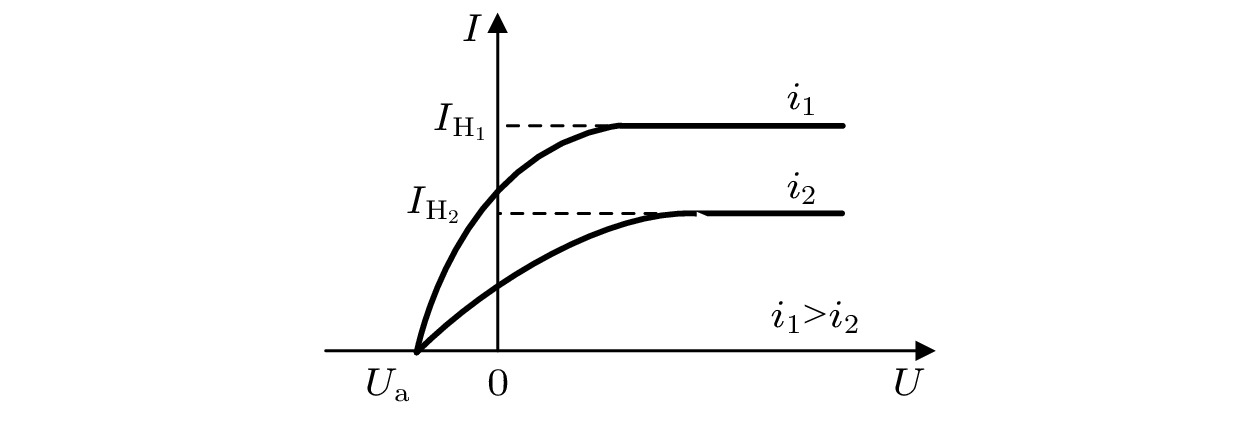图 3 光电管电压与光电流关系图
Figure3. Plot of the relationship between voltage and photocurrent.

光电管的光电流和电压的关系式为^[47]

$ {i_{\text{g}}} = \frac{{2{I_{\text{H}}}}}{\pi }\arctan ({V_{\text{g}}} - {V_{\text{a}}}),\quad $

其中I_H是光电管的最大电流, V_g是光电管的输出电压, V_a是与光电管相关的反向截止电压. 事实上真正驱动电路系统的是光照强度i, 其大小直接体现在饱和电流I_H上. 设饱和电流随时间变化I_H = I_H(t), 为了处理方便, 假设饱和电流的变化导致偏置电压随时间的变化为简单的余弦函数关系, $V_{\rm g} = $$ V_0 B_2\cos\omega' t$. 通过计算微分方程数值解得到电容两端的电压V_C随时间的变化(dV_C/dt)后可以利用(6)式反推饱和电压I_H (与光照强度i_g一一对应)真实的时间序列i_g = i_C = CdV_C/dt.

$ {i_{\text{g}}} = \frac{{2{I_{\text{H}}}}}{{\text{π}}}\arctan ({V_{\text{g}}} - {V_{\text{a}}}){\text{ = }}\frac{{{V_S} - ({V_C} + {V_{\text{g}}})}}{{{R_S}}} - {i_L} - {i_{NR}},\quad $

其中, V = V_C + V_g是非线性电阻NR两端的电压, V_C是电容器的输出电压, R_S是线性分压电阻, 则对应图2的电路方程表达为

$ \left\{ \begin{gathered} C\frac{{{\rm d}{V_C}}}{{{\rm d}t}} = \frac{{{V_S} - ({V_C} + {V_{\text{g}}})}}{{{R_S}}} - {i_L} - {i_{NR}}, \hfill \\ L\frac{{{\rm d}{i_L}}}{{{\rm d}t}} = {V_{C}} + {V_{\rm g}} + E - R{i_L}. \hfill \\ \end{gathered} \right.\quad $

为了使电路方程具有普适性和一般性, 对方程采用以下的无量纲变换:

$ \left\{ \begin{gathered} x = \frac{{{V_C}}}{{{V_0}}},\;y = \frac{{\rho {i_L}}}{{{V_0}}},\;\tau = \frac{t}{{\rho C}},\;a = \frac{E}{{{V_0}}},\;b = \frac{R}{\rho }, \hfill \\ \omega = \frac{{\omega '}}{{\rho C}},\;c = \frac{{{\rho ^2}C}}{L},\;\xi {\text{ = }}\frac{\rho }{{{R_S}}},\;{u_S} = \frac{{{V_S}}}{{{V_0}}},\;{u_{\rm g}} = \frac{{{V_{\rm g}}}}{{{V_0}}}, \hfill \\ \end{gathered} \right.\quad$

无量纲变换后的动力学方程为

$\begin{aligned}\left\{ \begin{aligned}&\dot x = \frac{{{\rm d}x}}{{{\rm d}\tau }} = x(1 - \xi ) - \frac{1}{3}{x^3} - y + \xi {u_S}\\&\quad\quad - {u_{\rm g}}\left( \frac{1}{3}{u_{\rm g}}^2 + {u_{\rm g}}x + {x^2} + \xi - 1 \right), \hfill \\& \dot y = \frac{{{\rm d}y}}{{{\rm d}\tau }} = c(x - by + a + {u_{\rm g}}), \hfill \\ \end{aligned} \right.\quad \end{aligned}$

其中外部激励源u_S选择同(5)式, 且$u_{\rm g} = B_2 \cos \omega t$. 需要说明的是, 在本文中, 之所以选择外部激励源的频率与光电管信号频率相同, 主要基于以下3点考虑: 1)为了简单起见, 神经元电路在相同频率下驱动可以突出输入信号强度的影响. 2)避免出现不必要的准周期输出信号. 多频信号驱动的特征之一是准周期的出现, 即输出信号的频谱中具有多个基频, 这徒然增加了信号的模式识别复杂度. 3)从实验角度可以实现对光电信号的滤波. 这也是以上两点说明的基础. 当采用外部激励频率作为滤波的窗口频率时, 可以将光电管的光电信号调整为具有较窄频谱的单色.
2 -->

2.3.系统(3)—电感L串联光电管的FHN神经元电路

当光电管串联在电感线圈L所在支路时, 其电路图如图4所示.
图 4 将光电管和恒压源串联的FHN电路原理示意图
Figure4. Schematic diagram for the FHN neural circuit while phototube couples with induction coil.

根据基尔霍夫定律及电路各元件的伏安关系得到电路图4的电路方程如下:

$ \left\{ \begin{gathered} C\frac{{{\rm d}{V_C}}}{{{\rm d}t}} = \frac{{{V_S} - {V_C}}}{{{R_S}}} - {i_L} - {i_{NR}}, \hfill \\ L\frac{{{\rm d}{i_L}}}{{{\rm d}t}} = {V_C} + E - R{i_L} - {V_{\text{g}}}. \hfill \\ \end{gathered} \right.\quad $

对方程(11)采用相似的无量纲变换, 得到的光敏神经元模型为

$ \left\{ \begin{gathered} \dot x = \frac{{{\rm d}x}}{{{\rm d}\tau }} = x(1 - \xi ) - \frac{1}{3}{x^3} - y + \xi {u_S}, \hfill \\ \dot y = \frac{{{\rm d}y}}{{{\rm d}\tau }} = c(x - by + a - {u_{\text{g}}}), \hfill \\ \end{gathered} \right.\quad $

其中, 外部激励源和光电管输出为$ u_S = B_1\cos \omega \tau $, 且$ u_{\rm g} = B_2 \cos \omega \tau $.

在数值模拟中, 采用四阶龙格-库塔算法解微分方程, 时间积分步长选取为h = 0.01, 变量初始值为(x, y) = (0.2, 0.1), FNH神经元的归一化参数选取为a = 0.7, b = 0.8, c = 0.1.
2

-->

3.1.系统(1)—FHN神经元电路

首先, 为了讨论神经元电路系统(4)(无光电管驱动)的动力学特性, 确定各种放电模式, 进行相关的数值计算, 并绘制系统的动力学随参数B₁, ω, ξ变化的分岔图和李雅普诺夫指数图, 分别如图5和图6所示.
图 5 不同分岔参数(B₁, ω, ξ)下的分岔图　(a) ω = 0.4, ξ = 0.175; (b) B₁ = 0.8, ξ = 0.175; (c) B₁ = 0.8, ω = 0.4, 其中参数a = 0.7, b = 0.8, c = 0.1, 初始值为(x, y) = (0.2, 0.1).
Figure5. Bifurcation diagram calculated by changing the bifurcation parameters (B, ω, ξ) at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a) ω = 0.4, ξ = 0.175; (b) B₁ = 0.8, ξ = 0.175; (c) B₁ = 0.8, ω = 0.4.

图 6 不同分岔参数(B₁, ω, ξ)下的李雅普诺夫指数图　(a) ω = 0.4, ξ = 0.175; (b) B₁ = 0.8, ξ = 0.175; (c) B₁ = 0.8, ω = 0.4, 其中参数a = 0.7, b = 0.8, c = 0.1, 初始值为(x, y) = (0.2, 0.1).
Figure6. Distribution for the Lyapunov exponent spectrum calculated by changing the bifurcation parameters (B₁, ω, ξ) at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a) ω = 0.4, ξ = 0.175; (b) B₁ = 0.8, ξ = 0.175; (c) B₁ = 0.8, ω = 0.4.

由图5可知, 当FHN神经元电路的参数a, b, c固定时, 改变外界驱动参数B₁, ω, ξ, 系统可以呈现出不同的放电模式, 特别是可以出现混沌放电态. 系统出现混沌态的参数区域分别为B₁∈[0.81, 1.05], ω∈[0.36, 0.42], ξ∈[0.17, 0.2].
图5和图6的结果表明: 分岔图和李雅普诺夫指数谱所表现的动力学行为完全一致, 当选取适当的外部刺激, 最大李雅普诺夫指数为正, 可以诱发混沌行为. 为了更直观地了解不同参数下的放电模式及其动力学性质, 画出各种放电状态下的时间序列图(图7).
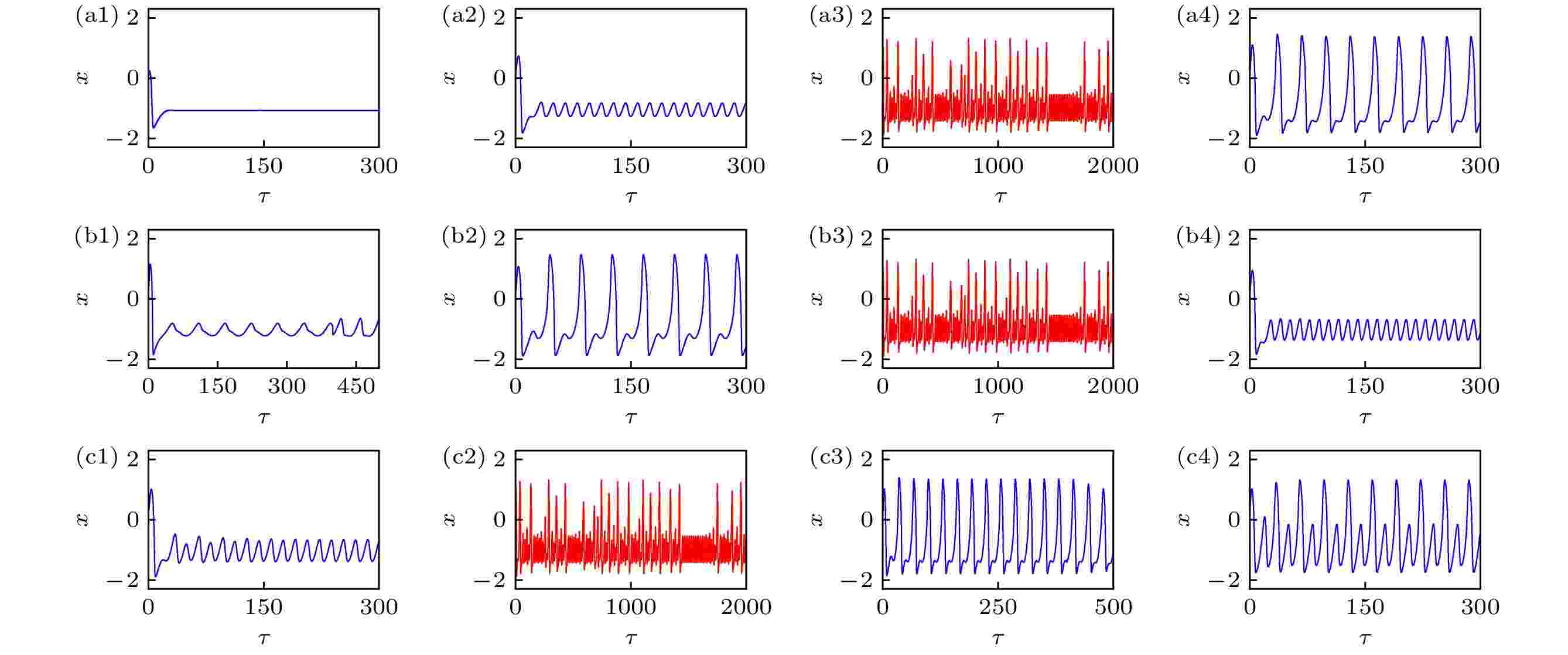图 7 不同分岔参数下的时间序列图, 其中固定参数ω = 0.4, ξ = 0.175, (a1) B₁ = 0.001, (a2) B₁ = 0.5, (a3) B₁ = 0.9, (a4) B₁ = 1.1; 固定参数B₁ = 0.8, ξ = 0.175时, (b1) ω = 0.11, (b2) ω = 0.31, (b3) ω = 0.4, (b4) ω = 0.5; 固定参数B₁ = 0.8, ω = 0.4时, (c1) ξ = 0.15, (c2) ξ = 0.175, (c3) ξ = 0.21, (c4) ξ = 0.45. 参数a = 0.7, b = 0.8, c = 0.1, 初始值为(x, y) = (0.2, 0.1).
Figure7. Firing patterns generated by applying different bifurcation parameters at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a1) B₁ = 0.001, (a2) B₁ = 0.5, (a3) B₁ = 0.9, (a4) B₁ = 1.1 with fixed parameters ω = 0.4, ξ = 0.175; (b1) ω = 0.11, (b2) ω = 0.31, (b3) ω = 0.4, (b4) ω = 0.5 with fixed parameters B₁ = 0.8, ξ = 0.175; (c1) ξ = 0.15, (c2) ξ = 0.175, (c3) ξ = 0.21, (c4) ξ = 0.45 with fixed parameters B₁ = 0.8, ω = 0.4.

当固定其他参数(ω = 0.4, ξ = 0.175), 随着参数B₁的增大, 系统经过静息放电、单周期放电过渡到混沌放电状态, 而后转变为尖峰放电状态(图7(a1)—(a4)). 若固定参数B₁ = 0.8, ξ = 0.175, 只改变参数ω, 系统经过单周期放电、尖峰放电过渡到混沌放电状态, 而后转为单周期放电(图7(b1)—(b4)). 固定参数B₁ = 0.8, ω = 0.4, 只改变参数ξ, 系统首先从单周期放电过渡到混沌放电状态, 而后继续呈现出不同的尖峰, 周期放电状态(图7(c1)—(c4)). 因此, 系统在不同的参数调制下有不同的通向混沌态的道路.
图5—7的结果集中反映出该神经元电路的膜电压可以在不同的外界刺激条件(振幅和频率)下呈现出不同的放电模式, 即静息放电态、尖峰放电态以及混沌放电态.
2 -->

3.2.系统(2)—电容C串联光电管的FHN神经元电路

对于动力系统(2)(第一类光敏神经元模型(10)), 在电容器所在支路接入光电管. 在神经元电路中引入光电管, 可以模拟感光神经元, 研究光照刺激对神经元动力学特性的影响. 特别地, 由于光电管的引入, 神经元电路拥有了更多可调参数. 为简单起见, 把光电管输出刺激视为周期性电压信号, 无量纲后即为u_g = B₂cosωτ, ω为外界刺激电压的角频率. 为了确定光电管对神经元电路的影响, 绘制该模型在改变参数B₂情况下的分岔图, 如图8所示, 其中FHN神经元的内禀参数选为与系统(1)中的参数相同的典型值, a = 0.7, b = 0.8, c = 0.1, B₁ = 0.8, B₂ = 0.2, ξ = 0.175.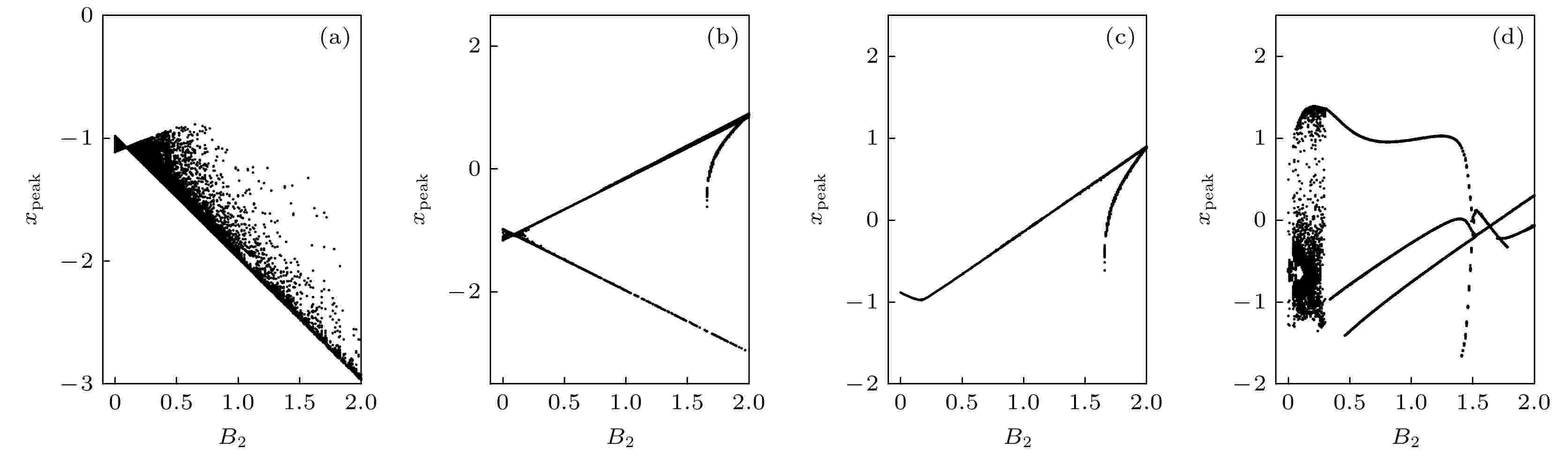
图 8 不同分岔参数ω下, 关于B₂的分岔图　(a) ω = 0.001; (b) ω = 0.01; (c) ω = 0.1; (d) ω = 0.4; 其中参数a = 0.7, b = 0.8, c = 0.1, B₁ = 0.8, ξ = 0.175, 初始值为(x, y) = (0.2, 0.1)
Figure8. Bifurcation diagram of B₂ calculated by changing the bifurcation parameter ω at a = 0.7, b = 0.8, c = 0.1, B₁ = 0.8, ξ = 0.175, initial parameters (x, y) = (0.2, 0.1): (a) ω = 0.001; (b) ω = 0.01; (c) ω = 0.1; (d) ω = 0.4.

从图8可以看出, 在其他参数确定的情况下, 当外界刺激的角频率$ \omega $小于1, 例如ω = 0.001, 0.01或0.1时, 在振幅范围内B₂∈(0, 2], 混沌被抑制. 当角频率ω增大到一定值后, 系统可以呈现出混沌放电状态, 例如当ω = 0.4时, 在区间B₂∈(0, 0.3]中系统为混沌放电状态. 由于光电管的引入, 神经元电路的可调参数空间维度增加. 为了说明维度增加的效应对动力学分岔的影响, 计算不同的参数组合下的分岔图(图9).
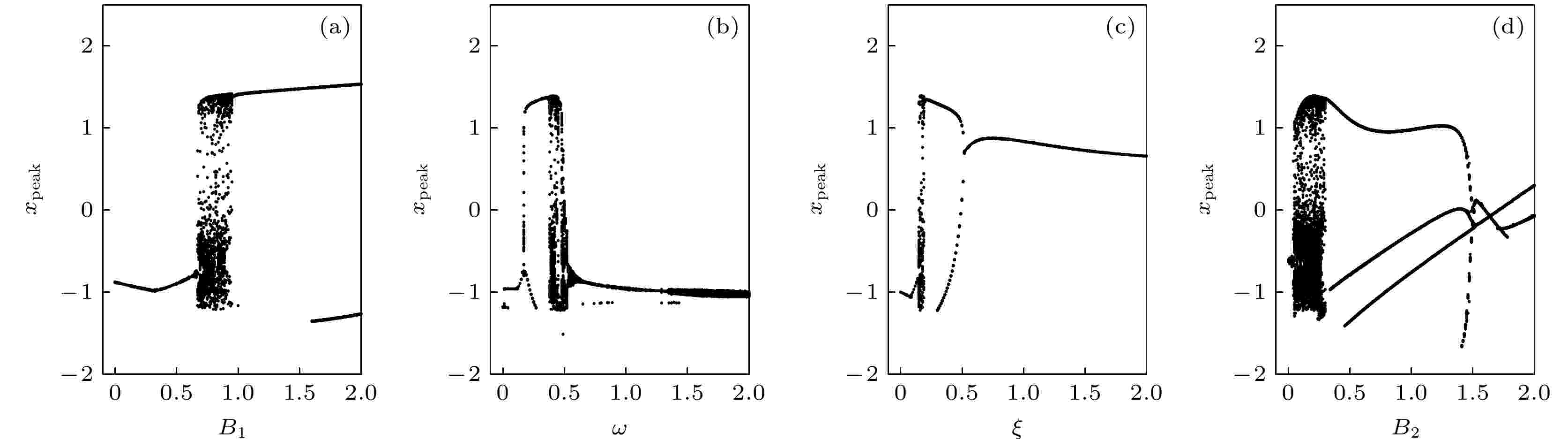图 9 不同分岔参数(B₁, ω, ξ, B₂)下的分岔图　(a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4; 其中参数 a = 0.7, b = 0.8, c = 0.1, 初始值为 (x, y) = (0.2, 0.1).
Figure9. Bifurcation diagram calculated by changing the bifurcation parameters (B₁, ω, ξ, B₂) at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4.

图9结果表明, 通过分别改变参数B₁, ω, ξ, B₂, 系统出现混沌态的参数区域分别为B₁∈[0.67, 0.94], ω∈[0.38, 0.5], ξ∈[0.15, 0.19], B₂∈(0, 0.3]. 与系统1无光电管耦合情况(图5)相比较, 当B₂ = 0.2, 参数ω, ξ的混沌区域并没有太大变化, 但是对于B₁, 出现混沌的区域明显缩小, 从B₁∈[0.81, 1.05]缩减至B₁∈[0.67, 0.94]. 此外, 为了验证混沌态的实现, 还计算了对应参数下的李雅普诺夫指数图. 如图10所示, 其结果和分岔图结果一致.
图 10 不同分岔参数(B₁, ω, ξ, B₂)下的李雅普诺夫指数图　(a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4; 其中参数 a = 0.7, b = 0.8, c = 0.1, 初始值为(x, y) = (0.2, 0.1).
Figure10. Distribution for the Lyapunov exponent spectrum calculated by changing the bifurcation parameters (B₁, ω, ξ, B₂) at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4.

对比图10(a)—(c)与图6(a)—(c)的结果可以发现, 当固定参数B₂ = 0.2时, 系统出现周期态的参数区域没有很大差异. 而图10(d)结果表明, 在改变参数B₂的情形下, 混沌态出现在较大的B₁所在区域内. 并且, 当B₂∈[0.3, 2.0]时, 系统可以有效诱发不同的放电状态.
为了更直观地描述光电模型(10)在不同参数下的动力学特征, 绘制了系统在不同参数设置下的时间序列图(图11). 由于光电管串联在电容所在支路上会使得新神经元系统具有更多的分岔参数, 与无光电管耦合的神经元电路相比, 存在新的通往混沌的路径和方式, 即参数B₂. 如图11(a1)—(a4)所示, 固定参数ω = 0.4, ξ = 0.175, B₂ = 0.2, 改变参数B₁, 系统经过静息放电过渡到混沌放电状态, 而后继续呈现出尖峰放电. 如图11(b1)—(b4)所示, 固定参数B₁ = 0.8, ξ = 0.175, B₂ = 0.2, 改变参数ω, 系统经过静息放电、多周期放电、尖峰放电过渡到混沌放电状态. 如图11(c1)—(c4) 所示, 固定参数B₁ = 0.8, ω = 0.4, B₂ = 0.2, 改变参数ξ, 系统经过静息放电过渡到混沌放电状态, 而后继续呈现出周期放电状态. 如图11(d1)—(d4)所示, 固定参数B₁ = 0.8, ω = 0.4, ξ = 0.175, 系统出现混沌放电状态后改变参数B₂取值, 系统可以出现不同的周期放电状态. 另一方面, 通过固定B₂以外的其他参数, 可以有效抑制混沌放电.
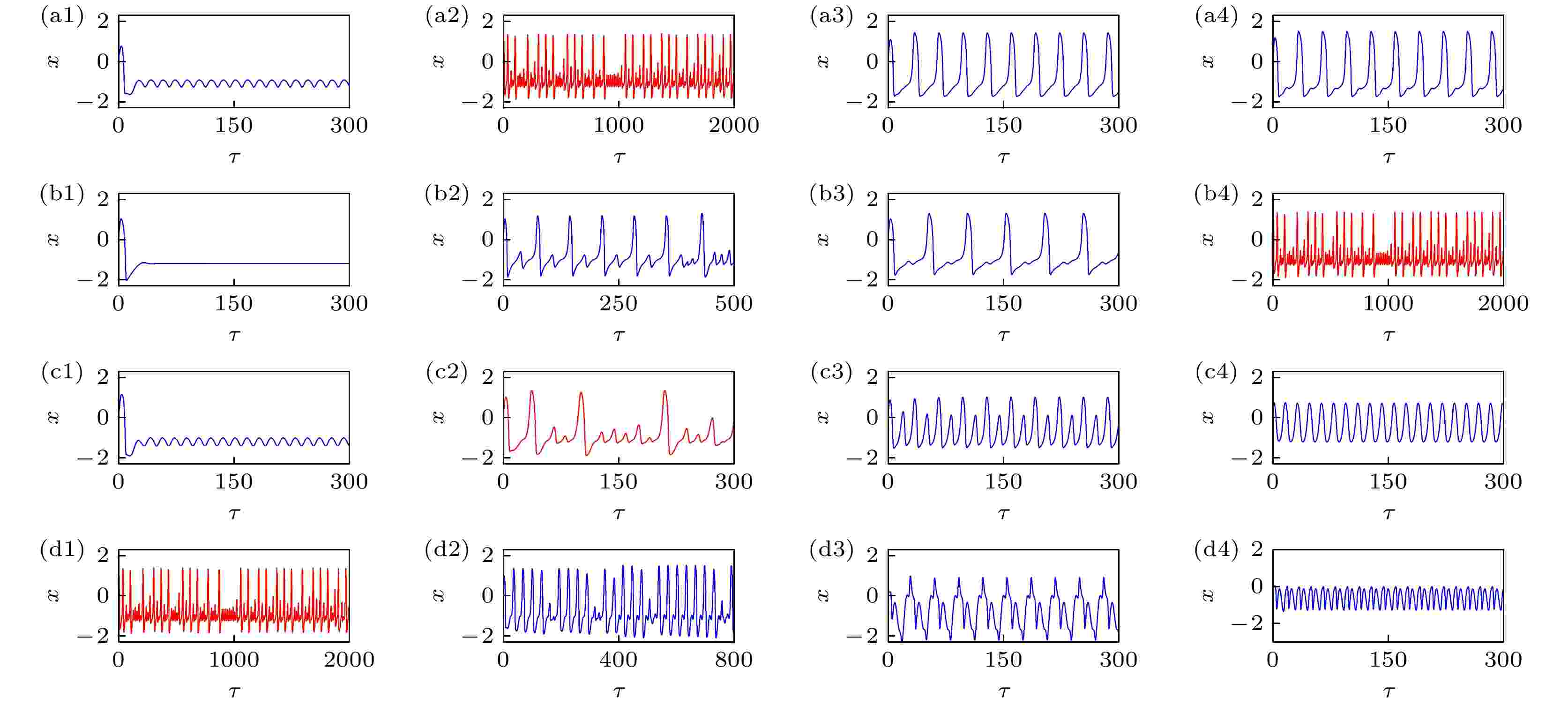图 11 不同分岔参数下的时间序列图, 其中固定参数ω = 0.4, ξ = 0.175, B₂ = 0.2时, (a1) B₁ = 0.1, (a2) B₁ = 0.8, (a3) B₁ = 1.2, (a4) B₁ = 1.75; 固定参数B₁ = 0.8, ξ = 0.175, B₂ = 0.2时, (b1) ω = 0.001, (b2) ω = 0.18, (b3) ω = 0.25, (b4) ω = 0.4; 固定参数B₁ = 0.8, ω = 0.4, B₂ = 0.2时, (c1) ξ = 0.005, (c2) ξ = 0.175, (c3) ξ = 0.5, (c4) ξ = 1.5; 固定参数B₁ = 0.8, ω = 0.4, ξ = 0.175时, (d1) B₂ = 0.2, (d2) B₂ = 0.28, (d3) B₂ = 1.0, (d4) B₂ = 1.6. 其中参数a = 0.7, b = 0.8, c = 0.1, 初始值为(x, y) = (0.2, 0.1).
Figure11. Firing patterns generated by applying different bifurcation parameters at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a1) B₁ = 0.1, (a2) B₁ = 0.8, (a3) B₁ = 1.2, (a4) B₁ = 1.75 with fixed parameters ω = 0.4, ξ = 0.175, B₂ = 0.2; (b1) ω = 0.001, (b2) ω = 0.18, (b3) ω = 0.25, (b4) ω = 0.4 with fixed parameters B₁ = 0.8, ξ = 0.175, B₂ = 0.2; (c1) ξ = 0.005, (c2) ξ = 0.175, (c3) ξ = 0.5, (c4) ξ = 1.5 with fixed parameters B₁ = 0.8, ω = 0.4, B₂ = 0.2; (d1) B₂ = 0.2, (d2) B₂ = 0.28, (d3) B₂ = 1.0, (d4) B₂ = 1.6 with fixed parameters B₁ = 0.8, ω = 0.4, ξ = 0.175.

2 -->

3.3.系统(3)—电感L串联光电管的FHN神经元电路

进一步讨论光敏神经元模型(12)对应的神经元电路输出特性, 即光电管与电感线圈串联. 为了对比系统(3)的动力学行为与系统(1)和系统(2)的不同, 选择与模型(10)同样的参数设置, a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, B₁ = 0.8, B₂ = 0.2, ω = 0.4. 图12为系统(3)在相应参数下的分岔图.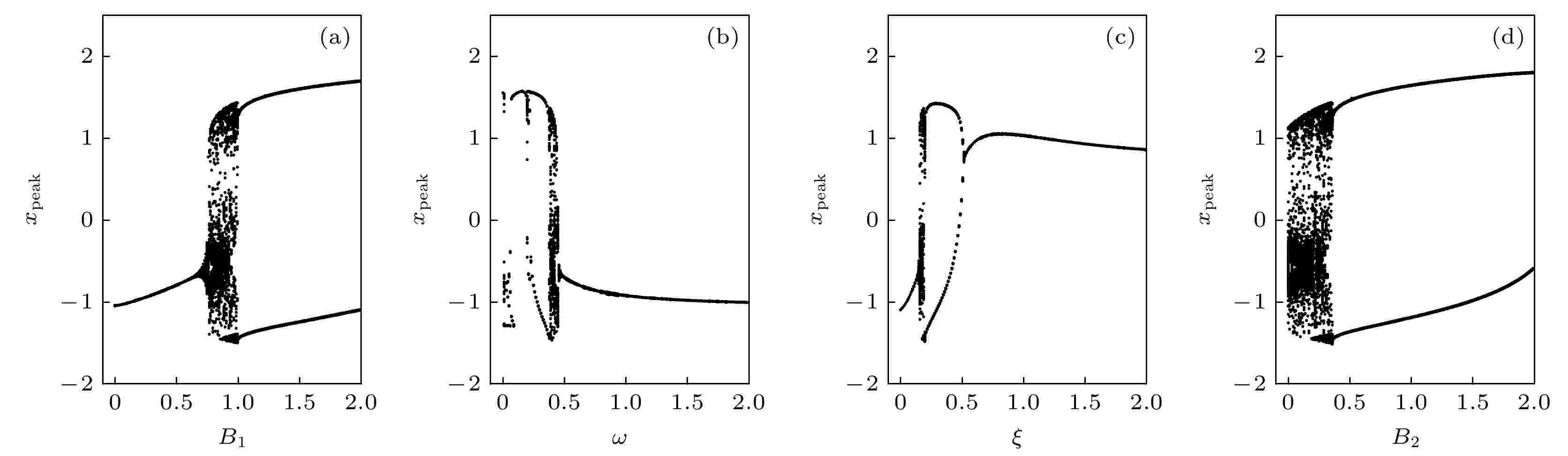
图 12 不同分岔参数(B₁, ω, ξ, B₂)下的分岔图　(a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4; 其中参数a = 0.7, b = 0.8, c = 0.1, 初始值为(x, y) = (0.2, 0.1)
Figure12. Bifurcation diagram calculated by changing the bifurcation parameters (B₁, ω, ξ, B₂) at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4.

图12的结果表明, 在保持与模型(10)相同的分岔参数条件下, 当光电管置于电感所在支路时, 同样可诱发不同的放电状态. 一方面, 比较图9(b)、图9(c)与图12(b)、图12(c), 发现两种光敏神经元模型和电路出现混沌的区域和各分岔点的位置没有发生太大变化, 且两类系统分岔图的结构也是相似的. 然而, 对比图9(a)—(d)和图13(a)—(d), 发现当固定其他参数而改变振幅B₁, B₂时, 两类神经元的分岔图具有明显的不同. 首先, 当光电管耦合到电感线圈所在支路上时, 出现混沌的参数区域变大, 为B₂∈(0, 0.39], 而B₁的范围确缩减至B₁∈[0.67, 0.94]. 其次, 两类系统通往混沌的路径也不同, 光电管与电感耦合时, 系统典型非混沌态为多周期; 而当光电管与电容器耦合时, 系统随着B₁的减小, 从单周期不断通过倍周期分岔通往混沌态.
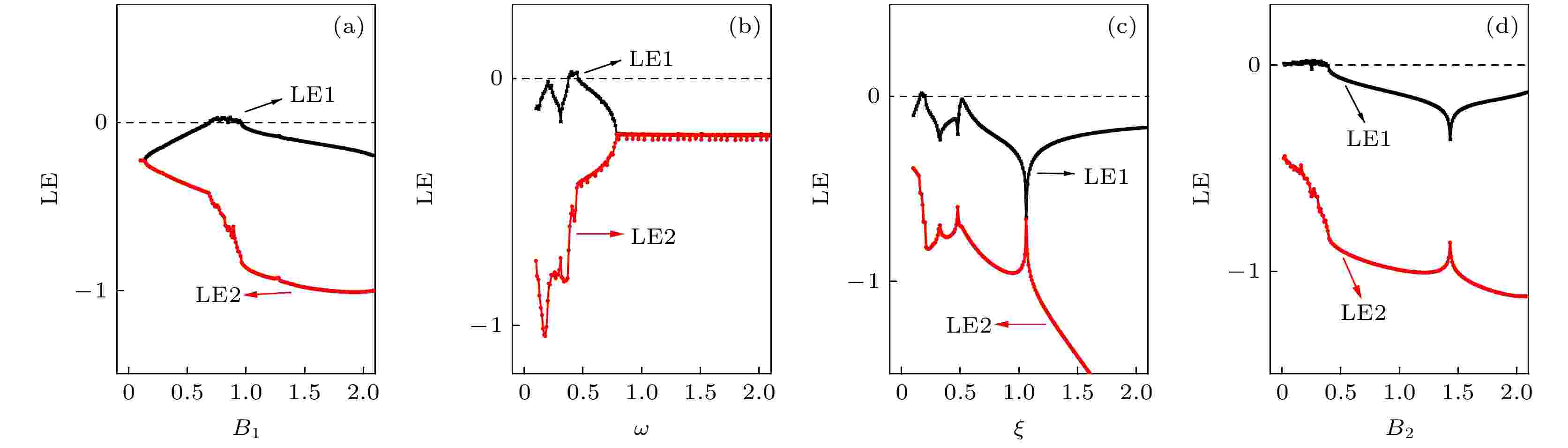图 13 不同分岔参数(B₁, ω, ξ, B₂)下的李雅普诺夫指数图　(a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4; 其中参数a = 0.7, b = 0.8, c = 0.1, 初始值为 (x, y) = (0.2, 0.1)
Figure13. Lyapunov exponent spectrum calculated by changing the bifurcation parameters (B₁, ω, ξ, B₂) at a = 0.7, b = 0.8, c = 0.1, initial parameters (x, y) = (0.2, 0.1): (a) B₂ = 0.2, ξ = 0.175, ω = 0.4; (b) B₂ = 0.2, B₁ = 0.8, ξ = 0.175; (c) B₂ = 0.2, B₁ = 0.8, ω = 0.4; (d) B₁ = 0.8, ξ = 0.175, ω = 0.4.

在图13中绘制了相应参数下的李雅普诺夫指数图, 李指数的正负切换与分岔图的动力学行为完全一致. 比较图10(a)—(c)和图13(a)—(c)之间可以看出, 两类系统李亚普诺夫指数谱的结构是相似的, 而图10(d)和图13(d)的Lyapunov指数谱的结构完全不同, 从而进一步验证了上述现象.
此外, 从非线性谐振子方面考虑, 对方程(4), (10)和(12)作如下变换, 即通过方程中的第1个式子得到y关于x的表达式, 然后代入第2个式子中得到二次非线性方程, 由此定义系统的有效幅值R. 无光电管驱动的神经元电路对应的神经元(4)可以表达为

$ \begin{split} &\ddot x - (1 - \xi )\dot x + {x^2}\dot x + cx - bcx(1 - \xi )\\ & - \frac{1}{3}bc{x^3} - bc\dot x + ac \\ =\,& - bc{u_S} + \xi {{\dot u}_S} \hfill = bc{u_S} + \xi {{\dot u}_S} \\ =\,& - \sqrt {{{(bc{B_1})}^2} + {{(\xi {B_1}\omega )}^2}} \sin (x + \varphi ) , \end{split} $

其对应的有效幅值定义为

$ {R}_{1}(\omega ,{B}_{1},{B}_{2})=\sqrt{{(bc{B}_{1})}^{2}+{(\xi {B}_{1}\omega )}^{2}}. $

为简单起见定义z = x + u_g, 对应的光敏神经元(10)可以表达为

$ \begin{split} & \ddot z - (1 - \xi )\dot z + cz - bc(1 - \xi )z + bc\dot z + ac \\ &\;\; +\;\frac{1}{3}bc{z^3} + {z^2}\dot z \hfill \\ &= \; - \sqrt {{{(\xi {B_1}\omega + bc{B_2}\omega )}^2} + {{(bc\xi {B_1} + {B_2}{\omega ^2})}^2}} \\ &\quad \;\, \times \;\sin (\omega \tau + \varphi ),\quad \hfill \\ \end{split} $

则其对应的有效幅值为

$\begin{split}&{R}_{2}(\omega ,{B}_{1},{B}_{2})\\=\;& \sqrt{{(\xi {B}_{1}\omega +bc{B}_{2}\omega )}^{2}+{(bc\xi {B}_{1}+{B}_{2}{\omega }^{2})}^{2}}. \end{split} $

同样地, 第二类光敏神经元(12)动力学等效表达为

$ \begin{split} & - (\ddot x - \dot x(1 - \xi ) + {x^2}\dot x + cx - bcx(1 - \xi ) \\& \;\;\; + \frac{1}{3}bc{x^3} + bc\dot x + ac) \hfill\\&= \sqrt {{{(\xi {B_1}\omega )}^2} + {{(bc\xi {B_1} + c{B_2})}^2}} \sin (\omega \tau + \varphi ) ,\end{split} $

其对应的有效幅值可以表达为

$ {R}_{3}(\omega ,{B}_{1},{B}_{2})=\sqrt{{(\xi {B}_{1}\omega )}^{2}+{(bc\xi {B}_{1}+c{B}_{2})}^{2}}. $

3类有效幅值的表达式表明, 此3类系统的动力学形式是等价的, 系统的动力学行为与R, ω之间具有直接联系. 在相同的驱动频率和其他固定参数下, 它们之间的主要不同体现在有效幅值上, 即有效幅值R_{1, 2, 3}对不同参数具有不同的函数依赖关系. 事实上, 从非线性动力学方程分析, 当光电管与电容器串联时, 只改变了系统的外在驱动; 而当光电管耦合电感线圈时, 方程(12)中两个等式中都存在正弦信号, 即系统除了有外在驱动, 还有参数驱动效应的参与, 而这个参数驱动也是周期性变化的. 另一方面, 从(14)式、(16)式、(18)式可以看出, R的改变会伴随着频率和幅值同时改变, 且3个系统与频率、振幅的函数关系也不一样.
以上结果表明, 在同一参数设定下, 3种神经元模型都能够诱发出不同的放电状态(静息、周期、混沌放电状态), 且有着不同的通向混沌放电的道路. 相比无光电管耦合的情形, 光敏神经元电路比一般的FHN神经元电路具有更丰富的神经元放电现象和更多可调参数. 一方面, 对于这3类神经元模型而言, 出现混沌态的分岔区域有相似之处, 即参数ω, ξ的分岔区间是相似的; 另一方面, 值得注意的是, 当光电管与电容串联时, 若外界刺激的角频ω小于1, 例如ω = 0.001, 0.01或0.1时, 在振幅范围内(B₂∈(0, 2]), 可以有效抑制混沌放电现象的出现. 此外, 在无光电管驱动的神经元中选择同样的参数时, 第1类光敏神经元(10)出现混沌放电状态的参数(B₂)区域为B₂∈(0, 0.3]; 不同于光电管串联电感的是, 当光电管在电容所在支路时, 系统对光电管信号的幅值更为敏感; 此外, 两种耦合方式都明显缩减了出现混沌放电状态下参数B₁的区间. 另外, 通过计算和对比3类连接方式所对应的二阶非线性方程, 发现在单个简谐信号驱动下, 3类系统的非线性动力学方程可以统一成相同的形式, 其区别在于等效驱动信号的有效幅值和频率的不同.

在被激活非线性电路中, 能量的释放和储存在很大程度上取决于物理变量和电子元件属性, 连续的能量流在感应线圈和电容器中传递和交换, 即非线性电路的每个分支将共享和贡献能量流. 本文构建并研究了两类光敏神经元电路模型在光电流驱动下膜电位的模式转换性质, 从生物物理的角度模拟了不同感光神经元细胞对光信号的响应. 基于简单的FHN神经元电路, 在不同支路中接入光电管来驱动神经元电路系统, 从而有效增强神经元电路的物理响应. 由于通道电流依赖于光电管信号输入与电路元件之间的相互作用, 其效应体现在信号特征的改变会引起不同类神经元电路的动力学分岔结果不同, 进而影响放电模式的输出差异. 特别地, 周期性输入信号的频率和幅值决定了神经元电活动的模式转换.
结果表明, 适当的周期性刺激可以观察到适当的神经元动力学响应, 即神经元的兴奋性受到外界光信号的调控, 可以使FHN神经元有效诱发神经元电路的不同放电模式. 并且, 在同一参数设定下, 3种神经元都能够诱发不同的放电状态, 且可以沿着不同路径产生混沌. 相比无光电管耦合的情形, 光敏神经元电路具有更好的可控性. 实际上, 当光电管与电容器串联时, 等同于光电管的输出电压直接作用于膜电位上; 而光电管与电感串联时, 等同于作用在通道电流上, 属于间接作用. 相比于第1类光敏神经元模型, 第2类光敏神经元在各参数下出现混沌的临界点均向后移动, 且其动力学对参数B₂的变化更为敏感. 另外, 计算3类神经元模型所对应的二阶非线性方程, 一定条件下3类系统的非线性动力学方程可以统一成相同的形式, 其区别仅在于等效驱动信号的有效幅值和频率的不同.
总而言之, 神经元电活动的模式选择依赖于外界光信号刺激对不同电路元件的刺激方式. 这些结果有助于进一步研究在光信号输入情况下功能性神经元网络的集体行为, 并为光敏神经元在人工眼、人机交互等方面的应用提供了理论依据.
课题组姚昭博士对本论文的数值计算结果进行仔细验证并修改笔误, 马军教授对修改稿的文字部分和结论给予的宝贵意见, 作者在此表示真诚感谢.