删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于弹性变分模态提取的时间相关单光子计数信号去噪

本站小编 Free考研考试/2021-12-29
摘要:单光子激光雷达的回波信号具有极低的信噪比, 有效地消除噪声和提取出回波信号特征是提升单光子激光雷达测距精度的关键, 变分模态分解算法需要使用者依据经验确定分解本征模态函数数量, 不具有适用性和通用性. 为此, 本文基于时间相关单光子计数信号特点, 提出了在变分模态分解中让信号按照指定频率进行聚类分解的变分约束条件, 并采用弹性网回归重构不适定问题的求解模型, 提出了弹性变分模态提取算法. 实验结果表明, 在波段850 nm、平均发射功率为25 nW、背景噪声平均功率为19.51 μW的条件下, 利用该方法, 得到了时间相关单光子计数信号重建精度的均方根误差为1.414 ns. 同时在不同的累积时间下, 能够稳定且快速地提取出回波信号特征, 有效地提高了算法的去噪能力和特征提取的性能.
关键词: 弹性变分模态提取/
时间相关单光子计数/
去噪/
特征提取

English Abstract


全文HTML

--> --> -->
1.引　言
时间相关单光子计数技术目前是激光雷达领域中前沿的研究方向之一. 该技术采用时间相关单光子计数器(time-correlated single photon counter, TCSPC), 对单光子探测器的输出信号进行统计分析, 将激光雷达的探测能力提升到了单光子级, 进一步提升了激光雷达的探测范围和测距精度. 本技术在天地目标识别[1]、水下目标探测[2]、非视域成像[3]、远距离激光三维成像[4]、生物学医疗[5]和大气观测[6]等众多领域都有广泛的应用前景.
近年来, 基于时间相关单光子计数技术的应用在各个领域逐步普及. Aurora等[2]实现了无背光环境下, 水下6.7个衰减长度的动态目标成像; David等[3]实现了对隐藏目标进行激光器到墙面的距离为1 m、分辨率为512 × 512的非视域成像, 累积时间长达50 min; Li等[4]实现了夜间对45 km外目标进行三维成像. 这些应用都是在弱噪声环境、长累积时间等理想条件下进行的. 这是由于时间相关单光子计数技术易受噪声干扰, 尤其是在白天强太阳背景光的情况下, TCSPC会受噪声光子堆积效应的影响, 有效信号完全被噪声淹没. 同时, 由于该技术采用的单光子探测器, 对回波信号的响应和器件本身的热噪声响应均服从泊松分布[7], 是典型的非平稳信号(时间序列), 由于非平稳信号稳定性差、随机性强、易与其他信息混叠[8], 从中提取出有效信号十分困难. 此外单光子探测器需要对回波信号进行累积, 累积时间与信号信噪比呈正相关, 而总累积时间直接影响探测过程的实时性, 很难平衡探测时间和信噪比之间的关系.
为了从被噪声污染的非平稳信号中提取有效信息, 可以采用图像后处理的方法, 文献[9]和文献[10]利用相邻像素之间的关系进行去噪, 但处理实时性差; 也可以采用信号分解的方法, 相关****已经取得了诸多研究成果, 获得较为广泛应用的方法有小波变换(wavelet transform, WT)[11]、希尔伯特振动分解(Hilbert vibration decomposition, HVD)[12]、经验模态分解(empirical mode decomposition, EMD)[13]和自适应噪声总体集合经验模态分解(complete ensemble empirical mode decomposition method based on adaptive noise, CEEMDAN)[14]等. WT算法构建了可随频率改变的窗口函数, 可以方便地分离出目标信息, 但需要人为地针对信号特征选取小波基, 且分解结果包含无意义的谐波成分[15]. HVD算法则采用的是希尔伯特变换和低通滤波的组合, 会产生端点效应[16]. EMD算法在分解过程中用包络线进行拟合, 会引起端点效应和模态混叠[17]; CEEMDAN算法作为EMD的改进, 减小了模态混叠, 但依然无法避免端点效应, 且计算复杂度大幅度增加[18].
鉴于上述方法存在的诸多问题, Dragomiretskiy等[19]提出了变分模态分解(variational mode decomposition, VMD)算法, 它是一种包含Wiener滤波和Hilbert变换的新型模态分解算法, 并将求解本征模态函数(intrinsic mode function, IMF)这一变分问题通过Parseval/Plancherel等距变换映射到频域. 因其具有完备的数学理论基础, 对非平稳信号进行VMD分解时, 克服了EMD类经验分解算法存在的端点效应和模态混叠问题, 从而对非平稳信号有着更强的适应性. 然而, VMD无法提取特定频率范围内的信号, 当其分解模态数量参数M确定了之后, VMD算法会按频率从低到高对信号进行分解, 而感兴趣的信号往往和其他频率的噪声信号混叠在一起, 要想将目标频段的信号分离出来, 只能手动调节分解模态数量, 不仅提升了计算复杂度, 也降低了算法的适用性[20]. 针对这些问题, 国内外****开展了更加深入的研究. 文献[21]在VMD算法基础上增加了新的迭代停止判定条件, 具有较高的收敛速度; 文献[22]提出采用神经网络优化VMD算法参数; 在文献[23]和文献[24]中则结合不同类型的群优化算法, 基于信号的特征, 确定最优的模态分解的层数. 这些改进方法仅考虑模态函数数量对分解效果的影响, 而忽略了底层不适定问题模型对迭代的影响, 从而导致分解效果不佳.
为了进一步提高非平稳信号的重建精度, 同时提升重建方法的通用性和适应性, 本文提出了一种新的非平稳信号的时频分解方法, 称为弹性变分模态提取(elastic variational mode extraction, EVME). 此方法对以时间相关单光子计数信号为例的非平稳信号进行分析, 增加了信号按照在指定频率进行聚类分解的变分约束条件, 并采用弹性网回归重构了变分模态分解中基于吉洪诺夫(Tikhonov)正则化的不适定问题的求解模型, 从而改进算法结构, 提升其性能. 利用本文所提出的方法对噪声条件下的时间相关单光子计数信号进行处理, 并与相关非平稳信号处理算法进行对比, 以验证本方法的性能.
2.弹性变分模态提取方法
2
2.1.理论基础
-->

2.1.理论基础

VMD算法通过迭代来搜索将实信号$ f\left(t\right) $分解为若干个本征模态函数的组合, 其本质是将时域上的不适定问题用Tikhonov正则化转换为适定问题, 再映射到频域上, 构建成变分约束问题进行求解. 求解出来的本征模态函数组在频域上从低频到高频分离, 每一个本征模态函数都需要估计其中心频率和带宽, 且所有本征模态函数的估计带宽之和最小. VMD算法对应的约束变分模型为:
$\begin{split} &\mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} \left\{ {\sum\limits_k {\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{{\rm{j}}}{{{\rm{\pi }}t}}} \right) * {u_k}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|_2^2} } \right\},\\& {\rm{s}}{\rm{.t}}\sum\limits_k {{u_k}} = f,\\[-20pt] \end{split}$
其中, $\left\{ {{u_k}\left( t \right)} \right\} = \left\{ {{u_1}\left( t \right), {u_2}\left( t \right), \cdots, {u_M}\left( t \right)} \right\}$是分解后的M个本征模态函数, $\left\{ {{\omega _k}} \right\} = \left\{ {{\omega _1}, {\omega _2}, \cdots, {\omega _M}} \right\}$为对应的中心频率, *为卷积运算, $\left\| \cdot \right\|$为范数, $\delta \left( t \right)$为单位冲激函数.
通过交替方向乘子法(alternating direction method of multipliers, ADMM)[19]将上述变分约束求极值问题转变成凸优化问题, 写出对应约束变分模型的增广Lagrange方程:
$\begin{split} & {\cal{L}}\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} \right) \\ =\; & \alpha \sum\limits_k {\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{{\rm{i}}}{{{\rm{\pi }}t}}} \right) * {u_k}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{i}}{\omega _k}t}}} \right\|_2^2} \\ & + \left\| {f\left( t \right) - \sum\limits_k {{u_k}\left( t \right)} } \right\|_2^2\\ & + \left\langle {\lambda \left( t \right),f\left( t \right) - \sum\limits_k {{u_k}\left( t \right)} } \right\rangle, \end{split} $
其中, λ为Lagrange乘子, $\alpha $为惩罚因子, $\left\langle, \right\rangle $代表两个向量的点积. 再利用对偶上升法求解出${u_k}, {\omega _k}$和$\lambda $在频域内的迭代算式.
利用VMD算法将信号分解成M个本征模态函数的步骤如下.
1) 初始化输入$\left\{ {\hat u_k^{\left( 1 \right)}} \right\}$, $\left\{ {\hat \omega _k^{\left( 1 \right)}} \right\}$, ${\hat \lambda ^{\left( 1 \right)}}$.
2) ${\hat u_k}\left( \omega \right)$和${\omega _k}$分别由(3)式和(4)式迭代得出:
$\begin{split} & \hat u_k^{\left( {n + 1} \right)}\left( \omega \right) \\= \;& \frac{{\hat f\left( \omega \right) - \displaystyle\sum\limits_{i = 1}^{k - 1} {\hat u_i^{\left( {n + 1} \right)}\left( \omega \right) -\displaystyle\sum\limits_{i = k + 1}^K {\hat u_i^{\left( n \right)}\left( \omega \right)} + \dfrac{{{{\hat \lambda }^{\left( n \right)}}\left( \omega \right)}}{2}} }}{{1 + 2\alpha {{\big( {\omega - \omega _k^{\left( n \right)}} \big)}^2}}},\end{split}$
$\omega _k^{\left( {n + 1} \right)} = \dfrac{{\displaystyle\int_0^\infty {\omega {{\left| {\hat u_k^{\left( {n + 1} \right)}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }}{{\displaystyle\int_0^\infty {{{\left| {\hat u_k^{\left( {n + 1} \right)}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }}. $
3) λ通过(5)式迭代更新确定,
${\hat \lambda ^{({n + 1})}}( \omega) \!=\! {\hat \lambda ^{(n)}}(\omega) \!+\! \tau \bigg({\hat f(\omega) - \sum\limits_K {\hat u_k^{({n + 1})}(\omega)} } \bigg). $
4) 重复运行步骤2)和步骤3)直到满足迭代的停止条件
$\sum\nolimits_K {\left\| {\hat u_k^{\left( {n + 1} \right)} - \hat u_k^{\left( n \right)}} \right\|} _2^2\bigg/\left\| {\hat u_k^{\left( n \right)}} \right\|_2^2 < \varepsilon . $
(3)式—(6)式中, 上标$ \wedge $代表傅里叶变换, 右上角标(n)和(n+1)为迭代次数, 右下角标k表明对应第k个分解模态, $ \tau $为更新参数, $ \varepsilon $为判别精度, 且有$\varepsilon > 0$.
5) 输出M个本征模态函数$\left\{ {{u_k}} \right\}$.
2
2.2.弹性变分模态提取原理
-->

2.2.弹性变分模态提取原理

本文提出的弹性模态提取算法是时频信号分解方法, 它相较于原始的变分模态分解算法, 增加了变分约束条件, 让信号按照在指定频率进行聚类分解, 通过得到模态中心频率的近似值, 可以提取出一个中心频率在预定模态附近的本征模态, 让信号按照预设中心频率进行聚类提取, 而无需人为地调节分解模态的个数. 同时, 本文方法采用弹性网回归重新构建不适定问题的求解模型, 从2-范数和1-范数结合的角度来对代价函数进行有偏分析, 克服了基于Tikhonov正则化的VMD算法带来的回归结果失真问题, 让信号分解更加精确.
弹性模态提取算法的推导过程如下.
首先构建本文提出的弹性模态提取算法的变分约束模型, 设输入信号$f\left( t \right)$被分解为两种信号: 期望模式${u_{\rm{d}}}\left( t \right)$和残差信号${f_{\rm{r}}}\left( t \right)$, 如下所示:
$f\left( t \right) = {u_{\rm{d}}}\left( t \right) + {f_{\rm{r}}}\left( t \right). $
本文提出的方法建立在以下基础上.
1) 所期望的模态应该紧凑地围绕其中心频率. VMD算法通过Tikhonov正则化将病态问题转化为适定问题, 再利用最小化准则来寻找最优解, 如(1)式中变分约束方程所示. 并对其进行扩充, 修改为弹性网回归, 则变分约束方程变为
$\begin{split}{J_1} =\; & \left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{{\rm{i}}}{{{\rm{\pi }}t}}} \right) * {u_{\rm{d}}}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{i}}{\omega _d}t}}} \right\|_2^2 \\ & + {\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{{\rm{i}}}{{{\rm{\pi }}t}}} \right) * {u_{\rm{d}}}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{i}}{\omega _d}t}}} \right\|_1},\end{split}$
其中${\omega _d}$是第d个模态的中心频率.
2) 残余信号${f_{\rm{r}}}\left( t \right)$与期望模态${u_{\rm{d}}}\left( t \right)$的频谱重叠应尽量小, 即在期望模态所在的频带内残余信号的能量应尽量小. 特别是${f_{\rm{r}}}\left( t \right)$在${\omega _d}$处的能量应为零, 以保证完全提取模态.
为了满足这些约束条件, 首先通过合适的滤波器提取出属于期望模态的${u_{\rm{d}}}\left( t \right)$分量, 然后将滤波后的${f_{\rm{r}}}\left( t \right)$的能量作为${f_{\rm{r}}}\left( t \right)$和${u_{\rm{d}} }\left( t \right)$谱重叠的指标. 为此, 使用滤波器的频率响应为
$\hat \beta(\omega) = {1}\big/{{\varphi {{\big( {\omega - \omega _d^{\left( n \right)}} \big)}^2}}}, $
其中, $\varphi $为滤波器$\hat \beta \left( \omega \right)$的系数, 滤波器$\hat \beta \left( \omega \right)$在$\omega = \omega _d^{\left( n \right)}$处具有无限增益, 在其他频率处可以近似为维纳滤波器. 因此, 为了使${f_{\rm{r}}}\left( t \right)$和${u_{\rm{d}}}\left( t \right)$的谱重叠最小, 在解中考虑如下惩罚函数:
${J_2} = \left\| {\beta \left( t \right) * {f_{\rm{r}}}\left( t \right)} \right\|_2^2, $
其中, $\beta \left( t \right)$是所使用滤波器的脉冲响应. 所以, 寻找期望模态的问题可以表示为一个(8)式和(10)式联合约束的最小化问题:
$\begin{split} &\mathop {\min }\limits_{{u_{\rm{d}}},{\omega _d},{f_{\rm{r}}}} \left\{ {\alpha {J_1} + {J_2}} \right\},\\ &{\rm{s}}{\rm{.t}}\;{u_{\rm{d}}}\left( t \right) + {f_{\rm{r}}}\left( t \right) = f\left( t \right),\end{split}$
其中, α是平衡${J_1}$和${J_2}$的参数.
由(7)式—(11)式所推导出的变分约束模型, 即是本文提出算法的理论模型. 然后就可以按照2.1节中的ADMM迭代优化算法[19], 将上述变分约束求极值问题转变成凸优化问题进行求解, 同时采用Parseval/Plancherel等距变换, 在频域上写出对应约束变分模型的增广Lagrange方程:
$\begin{split} & {\cal{L}}\left( {{u_{\rm{d}}},{\omega _d},\lambda } \right) \\ =\; & \alpha \left\| {{\rm{j}}\left( {\omega - {\omega _d}} \right)\left[ {1 + {\rm{sgn}} \left( \omega \right){{\hat u}_{\rm{d}}}\left( \omega \right)} \right]} \right\|_2^2 \\ & + \alpha {\left\| {{\rm{j}}\left( {\omega - {\omega _d}} \right)\left[ {1 \!+\! {\rm{sgn}} (\omega){{\hat u}_{\rm{d}}} (\omega)} \right]} \right\|_1} \!+\! \big\| {\hat \beta (\omega){{\hat f}_{\rm{r}}} (\omega)} \big\|_2^2\\ & + \left\| {\hat f\left( \omega \right) - {{\hat u}_{\rm{d}}}\left( \omega \right) - {{\hat f}_{\rm{r}}}\left( \omega \right)} \right\|_2^2 \\ & + \left\langle {\hat \lambda \left( \omega \right),\hat f\left( \omega \right) - {{\hat u}_{\rm{d}}}\left( \omega \right) - {{\hat f}_{\rm{r}}}\left( \omega \right)} \right\rangle,\\[-14pt] \end{split}$
其中, $\hat f\left( \omega \right) - {\hat u_{\rm{d}}}\left( \omega \right) - {\hat f_{\rm{r}}}\left( \omega \right)$为损失项.
再按照文献[19]中所提出的交替迭代方法, 该最小化问题可以通过一系列迭代优化来求解. 即第(n + 1)次迭代所需模态函数可以表述为(13)式—(15)式. 对(12)式求解以${\hat u_{\rm{d}}}\left( \omega \right)$为变量时, (12)式的变分最小值问题, 解得:
$\hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right) = \dfrac{{\hat f\left( \omega \right) \!-\! {{\hat f}_{\rm{r}}}\left( \omega \right) + \dfrac{{{{\hat \lambda }^{\left( n \right)}}\left( \omega \right)}}{2} \!-\! \alpha \left( {\omega \!-\! \omega _d^{\left( n \right)}} \right)}}{{2\alpha {{\left( {\omega - \omega _d^{\left( n \right)}} \right)}^2} + 1}}. $
同样, 分别对(12)式求解关于${\omega _d}$和${\hat f_{\rm{r}}}\left( \omega \right)$变分最小值问题, 可以得出:
$\begin{split} & \omega _d^{(n + 1)} \\=\;& \bigg[2\alpha \displaystyle\int_0^\infty \omega {{\left| {\hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right)} \right|}^2}{\rm{d}}\omega + \alpha \displaystyle\int_0^\infty {\omega \hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right){\rm{d}}\omega } \\& - \frac{2}{{{\varphi ^2}}}\displaystyle\int_0^\infty {\dfrac{1}{{{{\left( {\omega - \omega _d^{\left( n \right)}} \right)}^5}}}{{\left| {{{\hat f}_{\rm{r}}}\left( \omega \right)} \right|}^2}{\rm{d}}\omega} \bigg]\\ &\times \bigg({{\alpha \displaystyle\int_0^\infty {{{\left| {\hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }}\bigg)^{-1},\\[-12pt] \end{split}$
$\begin{split} & \hat f_{\rm{r}}^{\left( {n + 1} \right)}\left( \omega \right) \\ = \;& \frac{{{\varphi ^2}{{\left( {\omega - \omega _d^{\left( {n + 1} \right)}} \right)}^4}\left( {\hat f\left( \omega \right) - \hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right) + \dfrac{{{{\hat \lambda }^{\left( n \right)}}\left( \omega \right)}}{2}} \right)}}{{1 + {\alpha ^2}{{\left( {\omega - \omega _d^{\left( {n + 1} \right)}} \right)}^4}}}.\end{split}$
由于构建上述方程的目的是确定${\hat u_{\rm{d}}}\left( \omega \right)$和${\omega _d}$, 而不是计算${\hat f_{\rm{r}}}\left( \omega \right)$, 故对(13)式—(15)式进行重新迭代计算, 得到:
$\begin{split} & \hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right) =\\ \; & \frac{{\hat f\left( \omega \right) - {{\hat f}_{\rm{r}}}\left( \omega \right) + \dfrac{{{{\hat \lambda }^{\left( n \right)}}\left( \omega \right)}}{2} - \alpha \left( {\omega - \omega _d^{\left( n \right)}} \right)}}{{\left[ {1 + {\alpha ^2}{{\left( {\omega - \omega _d^{\left( n \right)}} \right)}^4}} \right]\left[ {1 + 2\alpha {{\left( {\omega - \omega _d^{\left( n \right)}} \right)}^2}} \right]}}.\end{split}$
对(13)式进行相同的推导操作. 在(13)式中, 因为系数α取值很大, 分子处的第三项远远小于第一项. 因此, 可以通过合理的近似对(13)式加以简化, 忽略其分子中的第三个子项, ${\omega _d}$更新表达式可近似表示为
$\omega _d^{\left( {n + 1} \right)} \!=\! \frac{{2\displaystyle\int_0^\infty\!\! {\omega {{\big| {\hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right)} \big|}^2}{\rm{d}}\omega \!+\! \!\displaystyle\int_0^\infty {\omega \hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right){\rm{d}}\omega } } }}{{\displaystyle\int_0^\infty {{{\big| {\hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right)} \big|}^2}{\rm{d}}\omega } }}. $
最后, 通过对偶上升法得到Lagrange乘子λ的迭代公式, 当滤波器$\hat \beta \left( \omega \right)$中的系数$\varphi $取值与增广Lagrange方程的惩罚因子α相等时, λ迭代公式得到最简形式:
${\hat \lambda ^{\left( {n + 1} \right)}}\left( \omega \right) = {\hat \lambda ^{\left( n \right)}}\left( \omega \right) + \eta \left\{ {\frac{{\hat f\left( \omega \right) - \hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right)}}{{1 + {\alpha ^2}{{\left( {\omega - \omega _d^{({n + 1})}} \right)}^4}}}} \right\}, $
其中, $ \eta $是更新参数. 综上所述(16)式—(18)式即是本文提出算法的最终迭代公式.
至此, 弹性模态提取算法已经介绍完成, 算法流程如算法1所示.
算法1: EVME
初始化$\hat u_{\rm{d}}^{\left( 1 \right)}$, ${\hat \lambda ^{\left( 1 \right)}}$, $n = 0$, $\omega _d^{\left( 1 \right)}$初始化为预测值
repeat
$n \leftarrow n + 1$
对于所有$\omega \geqslant 0$更新${\hat u_{\rm{d}}}$:
$\begin{split}& \hat u_{\rm{d}}^{(n + 1)}\left( \omega \right) = \bigg\{\hat f\left( \omega \right) + {\alpha ^2}{{\left( {\omega - \hat \omega _d^{\left( n \right)}} \right)}^4}\hat u_{\rm{d}}^{\left( n \right)}\left( \omega \right) \\&~~ + \dfrac{{{{\hat \lambda }^{(n)}}( \omega )}}{2} - {\alpha ^3}{{\left( {\omega - \hat \omega _d^{\left( n \right)}} \right)}^5}\bigg\}\times \\&~~ \bigg\{{\left[ {1 + {\alpha ^2}{{\left( {\omega - \hat \omega _d^{\left( n \right)}} \right)}^4}} \right]\left[ {1 + 2\alpha {{\left( {\omega - \hat \omega _d^{\left( n \right)}} \right)}^2}} \right]}\bigg\}^{-1}.\end{split}$
更新${\omega _d}$:
$\omega _d^{({n + 1} )} = \frac{{2\displaystyle\int_0^\infty {\omega {{\left| {\hat u_{\rm{d}}^{\left( {n + 1} \right)}( \omega )} \right|}^2}{\rm{d}}\omega + \displaystyle\int_0^\infty {\omega \hat u_{\rm{d}}^{( {n + 1})}( \omega){\rm{d}}\omega } } }}{{\displaystyle\int_0^\infty {{{\left| {\hat u_{\rm{d}}^{( {n + 1} )}( \omega)} \right|}^2}{\rm{d}}\omega } }}.$
对于所有$\omega \geqslant 0$进行对偶上升:
${\hat \lambda ^{\left( {n + 1} \right)}}\left( \omega \right) = {\hat \lambda ^{\left( n \right)}}\left( \omega \right) + \eta \left\{ {\frac{{\hat f\left( \omega \right) - \hat u_{\rm{d}}^{\left( {n + 1} \right)}\left( \omega \right)}}{{1 + {\alpha ^2}{{\left( {\omega - \omega _d^{\left( {n + 1} \right)}} \right)}^4}}}} \right\}.$
until 收敛:
$\left\| {\hat u_{\rm{d}}^{(n + 1)}\left( \omega \right) - \hat u_{\rm{d}}^{(n)}\left( \omega \right)} \right\|_2^2\bigg/\left\| {\hat u_{\rm{d}}^{(n)}\left( \omega \right)} \right\|_2^2 < \varepsilon .$

3.实验系统及测量结果
为了显示本文所提出方法的准确性和有效性, 搭建了时间相关单光子探测系统进行了实验验证. 时间相关单光子探测系统工作原理如图1所示, 信号发生器产生编码脉冲信号驱动激光器, 同时产生计时信号输入到TCSPC的计时通道2中作为计时参考. 发射激光脉冲通过发射光路进行调节, 并经过扫描镜照射到目标上. 目标物体反射激光脉冲, 接收光路收集到回波信号, 通过光纤耦合输入到单光子雪崩二极管(single photon avalanche photon diode, SPAD)中, 探测器将光信号转换为数字信号输入TCSPC的计时通道1中. 最后对通道1和通道2的信号进行互相关计算, 可以计算出单个像素的距离.
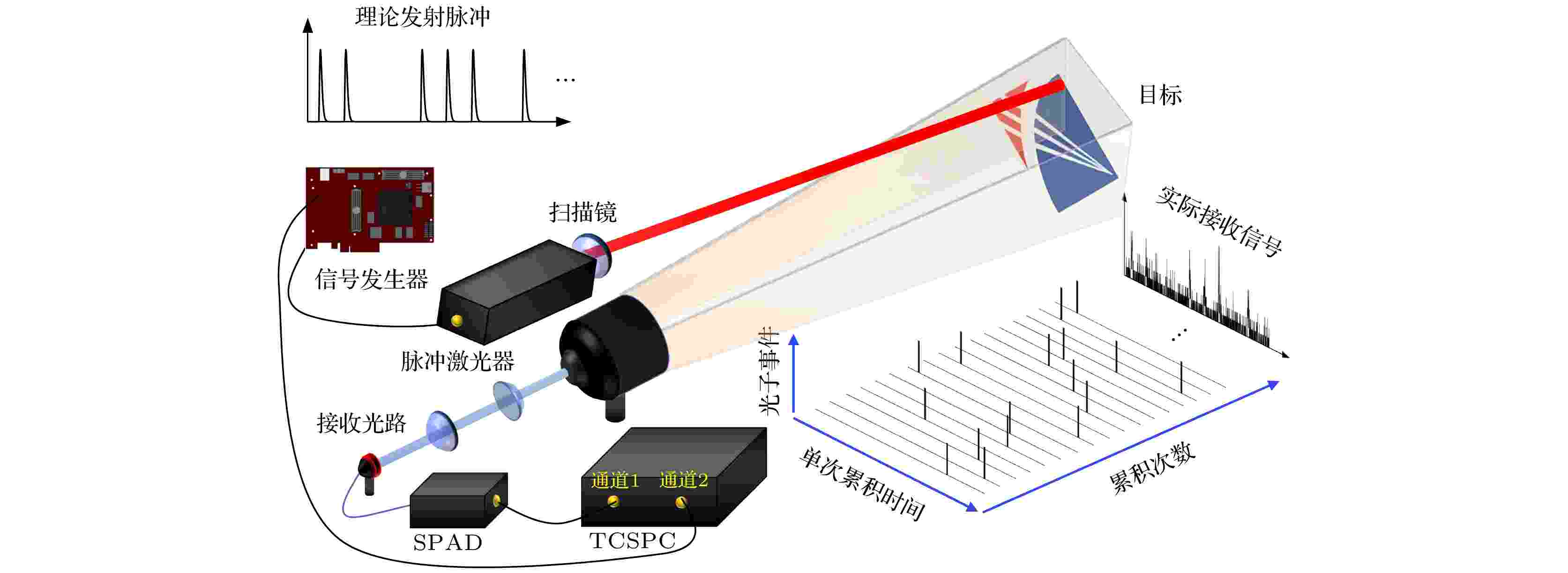图 1 系统工作原理图
Figure1. The principal components of the system.

实验系统实物图如图2所示, 激光器型号为PicoQuant LDH-D-C-850, 波段为850 nm, 最大脉冲发射频率为80 MHz, 平均功率为40 mW; TCSPC为PicoQuant PicoHarp 300, 最大时间分辨率为4 ps; 探测器是型号为EXCELITAS DTS_SPCM- AQRH-16-FC的SPAD, 量子效率 > 40% @850 nm, 暗计数率 < 20 cps; 采用型号为Xilinx KINTEX XC7 K325 T的现场可编程逻辑阵列(field programmable gate array, FPGA)作为信号发生器; 二维扫描镜型号为Thorlab GVS012; 带通滤波片型号为Semrock FF01-850, 通过带宽为 ± 10 nm.
图 2 实验系统实物图
Figure2. Experimental system.

2
3.1.强噪声条件下的信号去噪实验
-->

3.1.强噪声条件下的信号去噪实验

目标物体到接收光路物镜的距离为7.3 m, 扫描镜调整发射光束对准目标物体, 激光器实际输出编码脉冲频率为1 MHz, 脉宽为500 ps, 平均发射功率为0.11 mW(由OPHIR PD300-3W-v1 & VEGA光功率计测量, 下同), 带通滤波片用于滤掉除了850 nm以外的背景杂散光. 为了模拟远距离测试中的强衰减场景, 发射光路包含两个型号为Thorlab NE30B-B的衰减片, 衰减倍数为4296.51倍, 故系统平均发射功率为25.6 nW, 发射激光单个脉冲能量为25.6 fJ. 而接收光路中SPAD探测器前放置了一个衰减倍数为380.99的衰减片, 型号为Thorlab NE40B-B, 可以通过激光雷达方程计算出此时目标物体到接收光路物镜的等效距离约为3000 m. 同时实验在强噪声场景进行, 接收光路物镜处的850 nm波段背景噪声平均功率实测为19.51 μW. 所有数据是在基于Intel(R) Core(TM) i7-6700CPU和24GB 2133MHz DDR4的计算机平台上测得的.
进行累积时长为5 s的探测, 截取部分TCSPC输出探测信号段, 时间分辨率为16 ps, 截取的信号对应发射脉冲编码为“1 1 0 0 1 1 1 0 1 0”, 如图3(a)所示, 将其与经过不同算法处理后的信号进行对比.
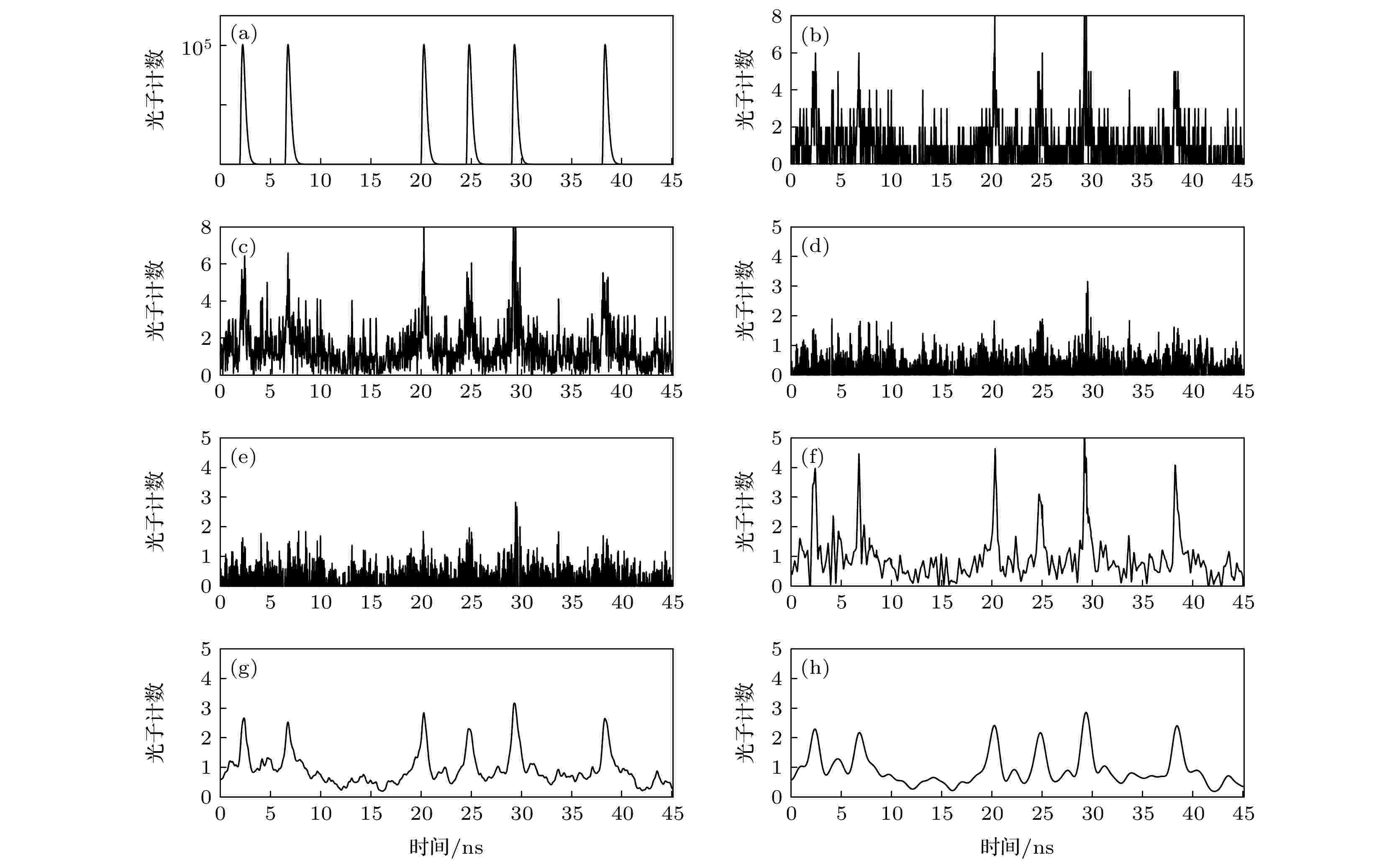图 3 时间相关单光子探测原始信号与6种方法对其重建的信号效果图　(a)激光器理论发射光信号; (b)实际接收信号; (c) Hilbert包络; (d) EMD; (e) CEEMDAN; (f) Haar小波软阈值法; (g) VMD; (h)本文方法
Figure3. The curves of time-correlated single photon single-photon signal and its six reconstruction algorithms: (a) Original signal; (b) theoretical output signal; (c) Hilbert envelope; (d) EMD; (e) CEEMDAN; (f) Haar wavelet; (g) VMD; (h) proposed method.

图3(a)理论发射信号由FPGA产生的实测输出脉冲信号结合激光器出厂报告中给出的实测发射脉冲波形曲线计算生成. 对比图3(b)实际接收信号和图3(a)理论发射信号, 可见本应有回波信号的地方, 由于系统发射平均发射功率为25.6 nW, 此时接收光路物镜处经过非协作目标物体漫反射的回波能量达到了10–18 W量级, 远远小于实测850 nm波段背景噪声平均功率19.51 μW, 这造成了大量的数据缺失, 无法重建出有效的信号波形图, 导致信号失真.
对图3(b)的实际接收信号进行Hilbert包络重建, 结果如图3(c)所示, 部分区域的噪声能量密度和峰值已经超过了信号段的平均水平, 可见对实际接收信号采用基于峰值、半高全宽、包络、能量密度、短时能量等常用信号特征提取手段无法直接提取出回波脉冲信号的准确位置信息.
图3(d), (e)分别采用的EMD和CEEMDAN方法对图3(b)信号进行处理, 均取分解后的本征模态函数1. 将其与图3(a)对比, 这两种方法处理效果很差, 无法将信号与噪声进行分离, 它们的信号特征相较于原始信号更差, 且随着模态分解数量提升后, 模态混叠效果越严重. 这是由于EMD和CEEMDAN方法都是利用信号自身统计特征, 在时域上对信号本身进行经验分解. 由于时间相关单光子计数技术所探测到的信号存在有效数据大量缺失、噪声功率远大于信号功率等问题, 造成信号自身的统计特征被破坏, 并不适用于这类以有效数据本身作为驱动的分解方法.
图3(f)为采用Haar小波软阈值(Haar wavlet, Haar WT)方法对原始信号进行重建的效果图. 将其与图3(a)进行对比, 可见此方法仅在一定程度上提取出回波信号的位置, 但重建出的信号波形仍然受到泊松噪声的影响, 重建出来的信号波形宽度不尽相同, 信号波形畸变程度大.
图3(g)是基于VMD方法进行重建后取其本征模态函数1的效果图, 模态分解数量为5. 将其与图3(a)进行对比, 可见此方法可以很好地提取出回波信号所在的位置, 但信号波形仍然存在明显畸变, 信号波形的峰值随机不固定. 且模态分解数量需要多次实验后确定.
图3(h)为本文所提出的弹性变分模态提取方法的重建效果图, 将其与图3(a)进行对比. 可以发现本方法不仅去除了泊松噪声的影响, 在有效数据大量缺失的情况下依然可以提取出回波信号, 且每一个信号波形形状基本相同, 畸变程度小, 信号峰值与图3(a)中的理论峰值位置误差在上述6种方法中最小.
为了进一步分析6种重建方法的重建效果, 采用均方根误差(root mean square error, RMSE)、平均绝对值误差(mean absolute error, MAE)和对称平均绝对百分比误差(symmetric mean absolute percentage error, SMAPE)这三种常用误差评价指标来比较经这6种方法重建出来的信号和理论真值之间的误差. 这三种指标是信号处理领域广泛使用的误差评价指标, 用来衡量信号的重建质量, 例如在本领域文献[14,15,25]中都有使用, 因此本文采用这三种评价指标来量化上述6种重建方法的性能. 计算公式见(23)式—(25)式. 6种方法重建图3(b)中的实际接收信号, 并以图3(a)激光器理论发射光信号波形作为参考真值, 分别选取峰值、半高全宽、短时能量(计算公式为(26)式)三种信号特征作为信号位置判断依据, 计算RMSE, MAE和SMAPE值, 结果见表1.
信号特征重建方法RMSE/nsMAE/nsSMAPE/%
峰值本文方法1.7791.1671.156
VMD2.4152.1672.100
Haar WT3.8293.0002.959
EMD4.2423.6673.599
CEEMDAN5.1474.1673.599
Hilbert包络4.1433.1673.104
半高全宽本文方法1.5281.3331.056
VMD1.9691.4171.115
Haar WT2.3692.2501.096
EMD8.5396.3335.060
CEEMDAN8.1506.0004.740
Hilbert包络10.005.3334.469
短时能量本文方法1.4141.0000.855
VMD1.8261.6671.402
Haar WT2.38112.0001.694
EMD4.1433.5002.962
CEEMDAN4.1633.6673.107
Hilbert包络4.2823.6673.140


表16种方法重建信号性能分析
Table1.Performance comparison among proposed method and previously published methods.

均方根误差计算公式为
${\rm{RMSE}} = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {\left( {{y_i} - {{\bar y}_i}} \right)} }, $
其中: ${\bar y_i}$为回波信号真值, ${y_i}$为回波信号测量值, m为回波信号样本数据数量.
平均绝对值误差计算公式为
${\rm{MAE}} = \frac{1}{m}\sum\limits_{i = 1}^m {\left| {{y_i} - {{\bar y}_i}} \right|}. $
对称平均绝对百分比误差计算公式为
${\rm{SMAPE}} = \frac{{100{\text{%}}}}{m}\sum\limits_{i = 1}^m {\frac{{\left| {{y_i} - {{\bar y}_i}} \right|}}{{\left( {\left| {{y_i}} \right| + \left| {{{\bar y}_i}} \right|} \right)/2}}} . $
短时能量的计算公式为
${E_i} = \sum\limits_{j = 0}^\infty {{{\left[ {s\left( j \right)w\left( {l - j} \right)} \right]}^2}},~~j = 0,1,2, \cdots, $
其中, ${E_i}$代表第i个时间窗内的短时能量, $s\left( \cdot \right)$为输入信号, $w\left( \cdot \right)$则为窗函数, l为窗函数的长度. 窗函数一般取矩形窗, 公式如下:
$w\left( n \right) = \left\{ \begin{aligned}& 1, \quad 0 \leqslant n \leqslant l - 1,\\& 0, \quad {\text{其他}}.\end{aligned} \right.$
由表1可见, 对于采用短时能量作为信号特征时, 在平均发射功率为25.6 nW、背景噪声平均功率为19.51 μW的强噪声条件下, 时间相关单光子计数信号重建精度的均方根误差为1.414 ns, 对应到单个脉冲测距时, 其重建误差为0.21 m; 而当采用脉冲伪随机编码方法时, 测距精度可提升至厘米级. 与之相对的, 在文献[1]中对天基非合作目标进行测距, 在激光脉冲重复频率为200 Hz、功率为40 W、脉冲宽度为5.5 ns的条件下, 测距精度约为1.6 m. 若采用本文去噪算法, 可以进一步提升测距精度.
2
3.2.不同累积时间下的信号实验
-->

3.2.不同累积时间下的信号实验

为了进一步验证本文提出方法的性能和普遍适应性, 在相同实验环境下, 分别进行了不同累积时间下的实验, 并采用上述6种方法对重建信号进行去噪, 进行比对. 本实验中, 调节发射光路衰减倍数为407.27倍, 故平均发射功率为270 nW, 单个脉冲发射能量的为270 fJ. 接收光路物镜处的850 nm波段背景噪声平均功率为40.61 μW, SPAD探测器前放置了一个衰减倍数为380.99的衰减片, 型号为Thorlab NE40 B-B. 采用3.1节中精度最高的短时能量信号特征作为信号位置判定依据, 采用RMSE作为衡量性能的指标.
由图4可见, 本文提出的方法明显优于其余5种方法, 其重建的时间相关单光子计数信号最为准确, 误差最小, 其次为VMD, Haar WT, Hibert包络, CEEMDAN, EMD. 由于噪声的功率远大于有效信号的功率, 随着累积时间的逐步增加, 噪声信号的增量也会大于有效信号的增量. 这6种算法达到一定累积时间后, 去噪效果均会达到极限, 其中Hibert包络、CEEMDAN、EMD这三种方法即使达到了极限, 其随机波动性依然很大. 而采用本文方法进行重建, 随着有效信号能量增强, 其重建信号误差逐步减小至收敛, 随机波动也逐步减小, 当累积时间达到10 s时, 信号重建精度的RMSE误差为0.408 ns.
图 4 6种方法在不同累积时间下去噪性能对比
Figure4. The line chart of the results comparison among proposed method and previously published methods.

表2给出了6种不同算法的计算耗时情况, 数据取自图4中累积时长为10 s的实验, 对应光子事件总数为17436个.
算法耗时/ms
Hilbert包络20
本文算法50
VMD1470
Haar WT75
EMD1100
CEEMDAN37060


表2本文方法耗时与其他方法的对比
Table2.Time consumption comparison among proposed method and previously published methods.

由表2可知, 本文提出的算法计算速度仅次于采用Hilbert包络方法, 略优于Haar WT算法, 相较于VMD算法有了大幅度的提升, 这是由于本文方法在构建变分约束条件的时候, 仅仅在信号感兴趣的中心频率附近进行模态提取, 而不需要逐次迭代生成信号在所有频段上的本征模态函数, 故而大幅度提升了计算速度.
4.结　论
本文分析了非平稳信号的特征, 深入研究了相关模态分解, 有针对性地在变分模态分解基础上增加了相关约束条件, 从而能够在指定中心频率附近提取出有效信号, 并采用弹性网回归来修改以Tikhonov正则化为基础的不适定问题求解模型, 提出了一种新的非平稳信号的时频分解方法—弹性变分模态提取, 并给出其推导过程. 经过理论分析与实测表明, 应用本文提出的方法对时间相关单光子计数信号进行去噪和特征提取, 在波段850 nm、系统平均发射功率为25 nW、背景噪声平均功率为19.51 μW的条件下, 得到的重建信号与理论信号之间的均方根误差为1.414 ns, 且不受模态混叠的影响. 与现有VMD, EMD, CEEMDAN等特征提取方法相比, 本文提出的方法去噪性能更好, 特征提取精度更高, 运算速度更快; 能够让基于时间相关单光子计数技术的远距离激光三维成像、非视域成像、水下目标探测等应用对复杂环境的适应性更强.
相关话题/信号 光子 实验 激光 计算
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 一种同步研究透明材料折射率和动力学特性的实验方法
    摘要:基于电磁加载装置CQ-4,建立了一种同步开展透明材料折射率和高压声速测量的实验方法.完成了聚甲基丙烯酸甲酯(PMMA)窗口材料14GPa斜波压缩实验,利用多点双光源外差位移干涉测速仪(duallaserheterodynevelocimetry,DLHV),获得了PMMA样品后表面的速度历史曲 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种基于束缚态的可调等离子体光子晶体窄带滤波器
    摘要:利用一维光子晶体和二维等离子体光子晶体构建了一种基于束缚态的可调窄带滤波器,滤波器的工作频率位于两个光子晶体的共同禁带内.使用COMSOLMultiphysics有限元仿真软件研究了一维光子晶体的几何参数和等离子体参数对滤波器性能的影响.研究发现两个禁带的中心频率和深度越接近,则滤波器的峰值透 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 金刚石/铝复合材料界面性质第一性原理计算及界面反应
    摘要:采用第一性原理计算和实验相结合的方法,研究了金刚石/铝复合材料的界面性质及界面反应.计算结果表明:金刚石(100)/铝(111)界面粘附功更大,相比金刚石(111)/铝(111)的界面粘附功4.14J/m2提高了41%.同时,金刚石(100)/铝(111)界面处形成Al—C键合的趋势更强.Al ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 新型双模式加权机制及其对网络计算的影响
    摘要:高效率的网络分析方法对于分析、预测和优化现实群体行为具有重要的作用,而加权机制作为网络重构化的重要方式,在生物、工程和社会等各个领域都有极高的应用价值.虽然已经得到越来越多的关注,但是现有加权方法数量还很少,而且在不同拓扑类型和结构特性现实网络中的效果和性能有待继续提高.本文提出了一种新型的双 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于直角锥面变形镜的薄管激光光束质量提升新方法
    摘要:针对大遮拦比窄环宽薄管激光光束质量提升需求,提出了一种基于直角锥面变形镜的薄管激光光束质量提升新方法.采用直角锥面实现薄管激光离轴像差的自校正,再利用驱动单元控制直角锥面变形镜的形变来进一步校正残余像差,进而实现对薄管激光光束质量的提升.以48单元直角锥面变形镜为例,利用有限元分析方法建立了直 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 激光烧蚀-吸收光谱测量铀同位素比实验研究
    摘要:铀同位素比(235U/238U)高精度测量在核能安全领域具有重要的研究意义和应用价值,本文基于高灵敏度可调谐吸收光谱技术,结合脉冲激光烧蚀产生等离子体的样品处理方式,实现了固体材料中235U和238U铀同位素比的高精度测量.实验测量选择λ=394.4884nm/394.4930nm(vacuu ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二极管叠阵侧面折返泵浦多边形薄片激光器
    摘要:本文报导了一种二极管叠阵侧面折返泵浦的多边形薄片Nd:YAG激光器,通过对其增益特性和光学特性的优化,得到了泵浦光耦合效率为97%,增益介质吸收效率达87%,增益介质内泵浦吸收分布均匀性为3.21%(rootmeansquare,RMS)的结果.实验测得与模拟数据吻合较好的增益介质荧光分布.在 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 用于激光等离子体中脉冲强磁场产生的电感耦合线圈
    摘要:脉冲强磁场装置是磁化激光等离子体实验的核心设备.本文研制了一种用于优化脉冲强磁场设备的电感耦合线圈,相对于单匝磁场线圈可以进一步提高磁场强度.通过实验和模拟研究了电感耦合线圈的初级螺线管匝数和直径对磁场强度的影响,发现对于2.4μF电容的放电系统,电感耦合线圈的初级螺线管在35匝、35mm直径 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • CdS/CdMnTe太阳能电池异质结界面与光电性能的第一性原理计算
    摘要:CdS/CdMnTe异质结是具有集成分立光谱结构的叠层电池的“核芯”元件,是驱动第三代太阳能电池发展的核心引擎,其界面相互作用对大幅度提高太阳能电池的转换效率至关重要.本文采用基于密度泛函理论的第一性原理计算构建CdS(002),CdMnTe(111)表面模型及Mn原子占据不同位置的CdS/C ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 有机铅碘钙钛矿太阳电池结构优化及光电性能计算
    摘要:甲胺铅碘(CH3NH3PbI3MAPbI3)和甲脒铅碘(CH(NH2)2PbI3FAPbI3)是目前最常用于太阳电池研究的有机铅碘钙钛矿材料.对于层状结构的钙钛矿太阳电池来说,每层薄膜的光学性质和厚度都影响着电池的光电转换效率.本文利用光学导纳法和严格耦合波分析法计算了金属氧化物透明导电薄膜掺 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.