摘要: 量子计算作为一种新兴的计算范式, 有望解决在组合优化、量子化学、信息安全、人工智能领域中经典计算机难以解决的技术难题. 目前量子计算硬件与软件都在持续高速发展, 不过未来几年预计仍无法达到通用量子计算的标准. 因此短期内如何利用量子硬件解决实际问题成为了当前量子计算领域的一个研究热点, 探索近期量子硬件的应用对理解量子硬件的能力与推进量子计算的实用化进程有着重要意义. 针对近期量子硬件, 混合量子-经典算法(也称变分量子算法)是一个较为合理的模型. 混合量子-经典算法借助经典计算机尽可能发挥量子设备的计算能力, 结合量子计算与机器学习技术, 有望实现量子计算的首批实际应用, 在近期量子计算设备的算法研究中具有重要地位. 本文综述了混合量子-经典算法的设计框架以及在量子信息、组合优化、量子机器学习、量子纠错等领域的研究进展, 并对混合量子-经典算法的挑战以及未来研究方向进行了展望.
关键词: 混合量子-经典算法 /
量子信息 /
量子计算 English Abstract Hybrid quantum-classical algorithms: Foundation, design and applications Chen Ran-Yi-Liu Zhao Ben-Chi Song Zhi-Xin Zhao Xuan-Qiang Wang Kun Wang Xin Institute for Quantum Computing, Baidu Research, Beijing 100193, China Received Date: 25 May 2021Accepted Date: 25 June 2021Available Online: 15 August 2021Published Online: 05 November 2021Abstract: Quantum computing, as an emerging computing paradigm, is expected to tackle problems such as quantum chemistry, optimization, quantum chemistry, information security, and artificial intelligence, which are intractable with using classical computing. Quantum computing hardware and software continue to develop rapidly, but they are not expected to realize universal quantum computation in the next few years. Therefore, the use of quantum hardware to solve practical problems in the near term has become a hot topic in the field of quantum computing. Exploration of the applications of near-term quantum hardware is of great significance in understanding the capability of quantum hardware and promoting the practical process of quantum computing. Hybrid quantum-classical algorithm (also known as variational quantum algorithm) is an appropriate model for near-term quantum hardware. In the hybrid quantum-classical algorithm, classical computers are used to maximize the power of quantum devices. By combining quantum computing with machine learning, the hybrid quantum-classical algorithm is expected to achieve the first practical application of quantum computation and play an important role in the studying of quantum computing. In this review, we introduce the framework of hybrid quantum-classical algorithm and its applications in quantum chemistry, quantum information, combinatorial optimization, quantum machine learning, and other fields. We further discuss the challenges and future research directions of the hybrid quantum-classical algorithm.Keywords: hybrid quantum-classical algorithms /quantum information /quantum algorithms 全文HTML --> --> --> 1.引 言 量子计算是基于量子力学与计算机科学的一门新兴学科, 被认为在人工智能、信息安全、生物制药、量子化学等领域能带来极具潜力的应用. 特别地, 通用量子计算机理论上可以高效地解决经典计算机无法高效解决的大数分解[1 ] 、数据搜索[2 ] 、量子模拟[3 ] 等问题. 随着学术界与工业界对量子计算技术研发力度的逐步加大, 量子计算硬件的技术在不断地进步[4 -7 ] . 尽管如此, 目前的技术离通用量子计算机要求的保真度、相干时间等条件还有一段距离. 因此, 从目前已实现几十量子位到未来实现通用量子计算这段时间, 如何利用好当前不断增强的有噪中规量子(noisy intermediate-scale quantum, NISQ)计算设备[8 ] , 是一个至关重要的问题, 也是当前量子计算领域的一个研究热点.[9 ] 、量子化学[10 ] 、量子物理[8 ] 、机器学习[11 ,12 ] 等诸多方向, 目标是尽可能利用NISQ设备的能力去完成特定的对于经典计算相对有挑战的任务.[13 ] 与求解基态能量问题的变分量子本征求解器(variational quantum eigensolver, VQE)[10 ,14 ] . 囿于目前对外开放的量子设备有限, 同时又涉及经典与量子设备之间的交互, 目前此类混合算法通常在模拟平台[15 -17 ] 上进行小规模开发, 然后通过硬件平台验证效果. 量桨[15 ] 是国内较为完善的混合算法开发平台, 借助技术领先的产业级深度学习框架飞桨[18 ,19 ] , 通过深度学习赋能量子计算领域的前沿研发.2 节介绍混合量子-经典算法中的基本概念与设计思想; 第3 节列举混合量子-经典算法在不同领域中具有代表性的若干应用; 第4 节讨论混合量子-经典算法目前面临的主要挑战; 第5 节进行总结.表1 所列.定义 符号 厄米特算符 H 含参数酉算符 ${\boldsymbol U}({\boldsymbol{\theta} }), {\boldsymbol V}({\boldsymbol{\theta} })$ 不含参数酉算符 W 可调参数 θ 量子态 ${\boldsymbol \rho}, {\boldsymbol \sigma}$ 量子比特数 n 电路层数 L 损失函数 $ C, C({\boldsymbol{\theta}})$ 能量 E 泡利算符 P 迹 Tr
表1 主要符号表Table1. Notations2.基本概念 混合量子-经典算法的核心在于将计算任务转化为优化问题. 以最具代表性的变分量子本征求解器(VQE)[10 ] 为例, VQE将求解哈密顿量H $ E_0 $ 问题转化为整个密度算符(量子态)集合上的优化问题:$ {\cal{D}} $ 表示所有与H $ {\rm{Tr}}[{\boldsymbol {H\rho}}] $ 可以通过对量子态的测量得到. 进一步地, 如果将量子态ρ $ {\boldsymbol \rho}_{\rm{in}} $ 出发, 经过一个参数化酉变$ {\boldsymbol U}({\boldsymbol{\theta}}) $ 演化之后的量子态$ {\boldsymbol \rho} = {\boldsymbol U}({\boldsymbol{\theta}}){\boldsymbol \rho}_{\rm{in}} {\boldsymbol U}({\boldsymbol{\theta}})^\dagger $ , 则VQE可以表示为一个参数空间上的优化问题:θ $ C({{\boldsymbol{\theta}}}) $ , VQE最终得到目标基态能量$ E_0 $ .C , 使得当C 取最小(或最大)值时可以实现计算任务. 随后, 混合量子-经典算法通过调整一个参数化酉变${\boldsymbol U}({\boldsymbol{\theta}})$ 最小(或最大)化损失函数, 从而实现计算任务. 值得注意的是, 由于损失函数实现了从实数(可调参数)到实数(测量结果)的映射, 混合量子-经典算法可以使用经典优化方法来优化可调参数θ 图1 所示.图 1 混合量子-经典算法流程Figure1. Diagram for hybrid quantum-classical algorithms.图1 可知, 实现一个混合量子-经典算法必须考虑如何设计损失函数将计算任务转化为优化问题, 以及如何构造一个参数化酉变(如果算法处理的任务涉及到经典数据, 则需要额外的编码过程将数据转换成量子数据. 详见3.4.1 节). 此外, 混合量子-经典算法中采用的经典优化方法往往会对算法的效率和准确度产生影响. 特别地, 相比于不基于梯度的优化方法, 解析梯度以及解析高阶导数因为需要运行更少的量子电路来决定优化方向成为混合量子-经典算法所关注的重点. 本节接下来将就这几个混合量子-经典算法中的基本概念展开讨论.2.1.损失函数 2.1.损失函数 损失函数是混合量子-经典算法设计的核心. 一般来说, 为保证函数值可以在量子设备上通过测量高效计算, 混合量子-经典算法中的损失函数具有如下形式:$ {\boldsymbol \rho}_j $ 是一组输入量子态, $ {\boldsymbol H}_j $ 是一组厄米特算符, $ \left\langle {{{\boldsymbol H}_j}} \right\rangle = {\rm{Tr}}\left[{\boldsymbol H}_{j} {\boldsymbol U}({\boldsymbol{\theta}}) {\boldsymbol \rho}_{j} {\boldsymbol U}^{\dagger}({\boldsymbol{\theta}})\right] $ 表示在电路末端进行$ {\boldsymbol H}_j $ 测量的结果, $ f_j $ 是一组经典函数, 表示对测量结果的经典后处理. 由混合量子-经典算法的框架可知, 损失函数的设计必须满足: 当且仅当损失函数达到全局最小时, 计算任务求得解. 这被称为混合量子-经典算法的忠实性条件[20 ] . 对于VQE算法, 由于其损失函数直接设为哈密顿量的测量值, 忠实性条件自然满足.$ {\boldsymbol H}_j $ 的种类, 计算损失函数的方法可大致分为以下几种:$ {\boldsymbol H}_j $ 是泡利算符. 此时损失函数可以直接通过对量子态的泡利测量得到. 特别地, 在许多常见的物理模型(如伊辛模型)中, $ {\boldsymbol H}_j $ 写成局部泡利算符的线性组合:${\boldsymbol{P}}_{j, k}$ 是泡利算符, 且只不平凡地作用在局部的量子比特上. 若每一个${\boldsymbol{P}}_{j, k}$ 最多只作用于m 个量子比特, 则称损失函数为m -局部的. 局部损失函数相较于全局损失函数在梯度消失问题上被认为更具有优势[21 ] (详见4.3 节).$ {\boldsymbol H}_j $ 是密度算符σ $ {\rm{Tr}}[{\boldsymbol {\rho\sigma}}] $ ), 或量子态的纯性($ {\rm{Tr}}[{\boldsymbol \rho}^2] $ ). 这类的损失函数可通过交换测试[22 ] 或其变种破坏性交换测试[23 ] 在量子设备上计算(电路实现分别如图2(a) 和图2(b) 所示). 同时, 由于密度算符之间的Frobenius距离可以写成如下形式:图 2 (a) 交换测试电路; (b)破坏性交换测试电路; (c) 哈达玛测试电路Figure2. (a) Swap test circuit; (b) destructive swap test circuit; (c) Hadamard test circuit.$ {\boldsymbol{H}}_j $ 中包含酉算符. 由于酉算符自身不是厄米特算符, 此时需要对酉算符进行变换, 常见的变换包括哈达玛测试[24 ] , 用于计算图2(c) 所示. 同时, 通过将哈达玛测试电路输入端的$ \left| 0 \right\rangle $ 替换为$1/\sqrt{2}(| 0 \rangle- $ $ {\rm i}| 1 \rangle )$ 即可计算${\rm{Im}}\left({\rm{Tr}}\left[{\boldsymbol{U\rho}}\right]\right)$ .2.2.参数化酉变 -->2.2.参数化酉变 作为典型的NISQ算法, 混合量子-经典算法实现的关键在于采用近期设备可实现的参数化酉变. 参数化量子电路(parameterized quantum circuit, PQC)是一种通用的参数化酉变实现方式. 在PQC中, 电路一般采用分层结构:L 被称为电路的层数. 由于设备噪声的存在, 近期设备所能提供的有效的电路宽度(量子比特数n )和深度(层数L )将受到限制. 同时, 为使电路能够在近期设备上高效实现, 在电路的每一层$ {\boldsymbol{U}}_l({\boldsymbol{\theta}}_l) = {\boldsymbol{V}}_l({\boldsymbol{\theta}}_l){\boldsymbol{W}}_l $ 中, 参数化的酉门${\boldsymbol{V}}_l({\boldsymbol{\theta}}_l) = $ $ \Pi_k{\rm e}^{-{\rm i}\theta_kA_k/2}$ 一般采用单比特旋转门或含参双比特门(ZZ门); 而不含参的酉门$ {\boldsymbol{W}}_l $ 作为连接层, 一般由临近量子比特间的CNOT或CZ两比特门构成, 为电路提供纠缠能力. 参数化电路的结构也常被称为拟设. 由于参数化量子电路的逻辑结构与设计思想和机器学习中的神经网络相似, 参数化量子电路又被称为量子神经网络(quantum neural network, QNN).[9 ] 等). 而在针对一般问题的电路结构设计中, 或当问题的解不存在先验信息时, 电路结构的每一层$ {\boldsymbol{U}}_l({\boldsymbol{\theta}}_l) $ 往往采用相同的结构, 即$ {\boldsymbol{U}}_l({\boldsymbol{\theta}}_l) = {\boldsymbol{U}}({\boldsymbol{\theta}}_l) = {\boldsymbol{V}}({\boldsymbol{\theta}}_l){\boldsymbol{W}} $ . 文献[25 ]列举了若干常见的硬件高效拟设. 此外, 文献[21 ]设计了一种交错分层拟设. 这样的拟设在宽度或深度增大时会面临电路可训练性变差等问题. 相对地, 一些每层结构各不相同的电路拟设在特定任务下拥有更好的表现. 下面介绍几种特殊的的电路拟设.[26 ,27 ] . 类比于经典神经网络中的感知机模型, 在量子感知机模型中, 每个神经元对应一个量子比特, 神经元之间的连接对应作用在两端的量子比特上的酉变. 量子感知机模型及其对应的量子电路模型如图3(a) 所示. 一种耗散量子感知机模型[27 ] 在节省量子比特数方面具有一定优势.图 3 (a) 量子感知机; (b)量子卷积神经网络; (c)影子电路Figure3. (a) Quantum perceptron; (b) quantum convolutional neural network; (c) shadow circuit.[28 ] . 在QCNN中, 电路各层被进一步分为卷积层和池化层. 卷积层电路由参数化的酉门构成, 而在池化层中, 电路通过测量部分量子比特减小系统的维度. 此外, 一种树张量网络[29 ] 也采用了类似的结构逐层减小系统的宽度. QCNN和树张量网络的结构如图3(b) 所示. 由于系统的有效宽度随层数快速减小, QCNN等技术有望避免梯度消失问题[30 ] .[31 ] . 受到经典影子学习[32 ] 的启发, 影子电路模型通过对多次局部酉变和局部测量结果的后处理学习目标特征. 在每一次影子电路的运行中, 参数化的酉门只作用在部分系统上, 然后对这部分系统进行测量, 这种部分系统的测量信息被称为“影子”; 最后, 将所有的“影子”进行经典后处理(例如全连接的经典神经网络)以提取特征. 影子电路模型如图3(c) 所示. 由于采用了局部的电路和测量, 影子电路模型在节约计算资源(需要训练的参数量)和可训练性方面更有优势.4 节将就这两个问题作进一步讨论.2.3.优化方法 -->2.3.优化方法 由于混合量子-经典算法将损失函数的优化任务“外包”给了经典计算机, 绝大多数经典优化方法都可以用于混合量子-经典算法中的优化步骤. 常用的混合量子-经典算法的经典优化方法中, 基于梯度的方法有批量梯度下降、ADAM优化、涉及多样本的随机梯度下降(stochastic gradient decent, SGD)、以及基于梯度估计的同步扰动随机逼近算法(simultaneous perturbation stochastic approximation, SPSA)等. 由于混合量子-经典算法中损失函数的解析梯度可以在量子设备上直接计算(详见2.4 节), SGD和ADAM被广泛应用于各类混合量子-经典算法, 特别是算法的经典模拟[33 ] 中; 同时, 非梯度的优化方法包括下山单纯形法、粒子群算法、贝叶斯估计等, 这些优化算法的详细内容可参阅优化理论相关教材[34 ] .[35 ] 优化. 相比于传统的梯度下降法, 量子自然梯度优化在每轮迭代中参数更新时需额外计算因子${\boldsymbol{g}}^+$ :g $ {\boldsymbol g}^+ $ 表示g g 2.4 节), 结合解析梯度$ \nabla C $ , 整个量子自然梯度优化的参数更新便可以在混合量子-经典算法的框架下实现. 相比于传统的梯度下降法, 量子自然梯度在一些VQE问题中具有更快的收敛速度.[36 -38 ] . 此类优化方法的关键在于利用了损失函数的如下性质: 当损失函数(3 )式中的后处理函数$ f_j $ 均为一次函数, 且参数化酉门${\boldsymbol{V}}_l({\boldsymbol{\theta}}_l) = \Pi_k{\rm e}^{-{\rm i}\theta_k{\boldsymbol{A}}_k/2}$ 中的生成元${\boldsymbol{A}}_k$ 满足${\boldsymbol{A}}_k^2 = {\boldsymbol{I}}$ 时, 固定其他参数, 损失函数C 是任一参数的周期为$ 2\pi $ 的正弦函数. 基于此, 量子序列最小优化方法在优化参数时, 可以选取一个或一组参数并固定其他参数, 直接将选取的参数调至当前最优, 随后对所有参数重复这一过程直至收敛. 相比于传统的梯度下降法, 量子序列最小优化在一些VQE问题中具有更快的收敛速度.2.4.解析梯度 -->2.4.解析梯度 混合量子-经典算法的一大优势在于其损失函数的梯度可以在量子设备上直接计算. 不失一般性, 假设损失函数不包含对测量结果的经典后处理:[39 ,40 ] 是计算混合量子-经典算法中解析梯度的基本工具. 该规则表明, 当参数化酉门${\boldsymbol{V}}_l({\boldsymbol{\theta}}_l) = \Pi_k{\rm e}^{-{\rm i}\theta_k{\boldsymbol{A}}_k/2}$ 中的生成元$ {\boldsymbol{A}}_k $ 满足$ {\boldsymbol{A}}_k^2 = {\boldsymbol{I}} $ 时, 形如(9 )式的损失函数对参数$ \theta_k $ 的偏导为$C(\theta_k\pm {\pi}/{2})$ 表示C 中参数$\theta_k\pm {\pi}/{2}$ 而其他参数保持不变. 因此, 通过改变目标参数后计算两次电路的输出, 可以得到损失函数关于目标参数的梯度值. 进一步地, 在一些基于梯度的优化算法中需要用到高阶导数信息(如黑塞矩阵等), 此时反复利用参数平移规则即可求解相应的高阶导数.[41 ] 将偏导式(10 )表示为$ {\boldsymbol{U}}_{-} ( {\boldsymbol{U}}_{+} )$ 表示参数$ \theta_k $ 对应的参数化酉门之前(之后)的电路, 即$ {\boldsymbol{U}}_{-} ={\boldsymbol{ U}}_l({\boldsymbol{\theta}}_l)\cdots {\boldsymbol{U}}_1({\boldsymbol{\theta}}_1) $ , ${\boldsymbol{U}}_+ = $ $ {\boldsymbol{U}}_L({\boldsymbol{\theta}}_L)\cdots {\boldsymbol{U}}_{l+1}({\boldsymbol{\theta}}_{l+1})$ . 因此, 当P P 2.1 节)计算得到.[35 ] . 文献[35 ]表明, Fubini-Study度量张量有分块对角矩阵近似 ${\boldsymbol g} = {\rm{diag}} ({\boldsymbol g}^{(1)}, $ $ {\boldsymbol g}^{(2)},\; \cdots,\; {\boldsymbol g}^{(L)})$ , 且对角子矩阵${\boldsymbol g}^{(l)}$ 的矩阵元满足2.5.计算精度 -->2.5.计算精度 本节的最后简单讨论混合量子-经典算法中计算损失函数时达到的精度与所需的测量次数. 不失一般性, 设待计算的损失函数为$ C = {\rm{Tr}}[{\boldsymbol{H\rho}}_{\rm{out}}] $ , 其中$ {\boldsymbol{\rho}}_{\rm{out}} $ 表示电路输出量子态. 由于量子力学的内禀随机性, 损失函数C 实际上通过测量结果估计得到. 为此, 首先将H ${\boldsymbol{H}} = \displaystyle\sum\nolimits_{j = 1}^{m}\mu_j{\boldsymbol{P}}_j$ . 随后, 损失函数C 可按如下方式估计:$ {\boldsymbol{P}}_j $ 上对$ {\boldsymbol{\rho}}_{\rm{out}} $ 进行T 次测量. 由于泡利测量只有两种测量结果, 记+1结果出现的次数为$ M_0 $ , –1结果出现的次数为$ M_1 $ , 记$X_j^{(1)} = $ $ (M_0-M_1)/T$ .S 次步骤1, 得到$X_j^{(1)}, X_j^{(2)}, \cdots, X_j^{(S)}$ .$X_j^{(1)}, X_j^{(2)}, \cdots, X_j^{(S)}$ 的中位数$ X_j^{\rm{median}} $ .$ j\in[1, m] $ 执行步骤1—3, 损失函数估计值为$\hat{C} = \displaystyle\sum\nolimits_{j = 1}^{m}\mu_jX_j^{\rm{median}}$ .$ \hat{C} $ 是损失函数C 的无偏估计: ${\mathbb{E}}[\hat{C}] = $ $ C$ . 进一步地, 根据文献[42 ]可知, 当估计测量总次数mTS 满足$ 1-\delta $ 的概率小于? , 即${\rm{Pr}}[|\hat{C}- C|\leqslant $ $ \epsilon]\geqslant1-\delta$ . 因此, 当$ m = O({\rm{poly}}(n)) $ 时, 损失函数可以通过测量在量子设备上以任意精度高效地估计.3.应用实例 23.1.谱信息估计 3.1.谱信息估计 由于物理粒子的密度算符、哈密顿量等物理量的矩阵描述都是厄米特矩阵, 粒子的各种特性往往能被对应物理量的谱信息(本征值)很好地描述; 另一方面, 量子电路模型也能直接处理密度矩阵(量子态)和哈密顿量(可观测量). 因此, 对厄米特矩阵的谱信息估计是混合量子-经典算法的一个重要也是直接的应用.3.1.1.子空间搜索-量子变分本征求解器 -->3.1.1.子空间搜索-量子变分本征求解器 子空间搜索-量子变分本征求解器(subspace search VQE, SSVQE)[43 ] 是VQE算法的一个直接拓展. SSVQE求解目标哈密顿量的基态以及前$ K-1 $ 个激发态能量, 亦即求解厄米特矩阵最小的K 个本征值. 在SSVQE中, 损失函数对K 个正交单位向量(通常选取计算基向量)经过参数化电路后的测量值加权求和:$ \{{\boldsymbol{\rho}}_k\}_{k = 1}^K $ 是互相正交的纯态, 通常取${\boldsymbol{\rho}}_k = | k - 1 \rangle $ $ \left\langle {k - 1} \right|$ , $ \omega_k $ 是严格单调减小的正实数序列. 通过排序不等式可以证明, 上述损失函数取到最小当且仅当$\left| {{e_k}} \right\rangle $ 为H k 小个本征值对应的本征向量, 即H k 激发态. 因此, 当损失函数优化到最小时, 测量得到${\rm{Tr}}\left[{\boldsymbol{H U}}({\boldsymbol{\theta}}) {\boldsymbol{\rho}}_k {\boldsymbol{U}}^{\dagger}({\boldsymbol{\theta}})\right]$ 即为厄米特矩阵第k 小个本征值, 亦即待求的基态或激发态能量.3.1.2.变分量子态对角化 -->3.1.2.变分量子态对角化 对混态的谱分解(对角化)有助于我们理解量子态的纠缠性质. 变分量子态对角化(variational quantum state diagonalization, VQSD)[44 ] 算法求解酉变U ρ ${\boldsymbol{U\rho U}}^\dagger = \displaystyle\sum\nolimits_j c_j \left| j \right\rangle \left\langle j \right|$ . 在VQSD中, 记${\boldsymbol{\widetilde{\rho}}} = {\boldsymbol{U}}({\boldsymbol{\theta}}) {\boldsymbol{\rho U}}^{\dagger}({\boldsymbol{\theta}})$ , 损失函数提供了两种设计:$ {\cal{D}} $ 表示整个输入量子态上的(完全)去极化信道, $ {\cal{D}}_j $ 表示仅对第j 个量子比特作用的(完全)去极化信道. 显然$ C_1 $ 和$ C_2 $ 等于0当且仅当$ \widetilde{\rho} $ 实现了对角化. 因此, 通过优化损失函数至0即可完成量子态的对角化. 同时, 文献[44 ]分别设计了两种电路用于计算两个损失函数. 文献[44 ]指出, 由于$ C_1 $ 拥有更简单的计算电路, 而$ C_2 $ 拥有更好的可训练性, 在实际训练中可以根据量子比特数对两种损失函数进行加权求和作为最终的损失函数.3.1.1 节SSVQE中对正交量子态加权求和的技巧也可用于量子态对角化, 如文献[20 ]就基于该技巧实现了量子态的本征值求解.3.1.3.变分量子奇异值分解 -->3.1.3.变分量子奇异值分解 奇异值分解作为谱分解的扩展, 在数据压缩、推荐系统等领域具有重要应用. 变分量子奇异值分解(variational quantum singular value decomposition, VQSVD)[45 ] 实现任意方阵M $ \{\left| k \right\rangle \}_{k = 1}^K $ 是一组互相正交的纯态, $ \omega_k $ 是严格单调减小的正实数序列. 文献[45 ]证明上述损失函数取到最大值当且仅当$ d_k $ 是M k 大的奇异值. 因此, 通过最大化损失函数即可完成方阵的奇异值分解. 由于M ${\boldsymbol M} = $ $ \displaystyle\sum\nolimits_jc_j{\boldsymbol{P}}_j$ , 损失函数 $C = \displaystyle\sum\nolimits_{k, j} \omega_{k} c_j {\rm{Re}}\left\langle k \right|{\boldsymbol U}({\boldsymbol{\theta}}_1)^{\dagger}\times $ $ {\boldsymbol{P}}_j {\boldsymbol V}({\boldsymbol{\theta}}_2)\left| k \right\rangle$ 中求和各项均可经哈达玛测试得到, 因此VQSVD可在混合量子-经典算法框架下实现.46 ]通过对优化两个局部参数化电路实现施密特分解. 本质上, 文献[46 ]和VQSVD相当于对待分解的矩阵采用了不同的编码方式: VQSVD将矩阵分解为酉算符的线性组合, 而文献[46 ]相当于将矩阵重排为两方量子态对应的向量.3.1.4.迹范数估计 -->3.1.4.迹范数估计 厄米特矩阵H $\|{\boldsymbol H}\|_1$ 定义为矩阵的奇异值之和, 即H [47 ] 、纠缠负性[48 ] 等. 文献[49 ]通过在单比特辅助系统R 上的测量估计厄米特矩阵的迹范数. 设$\widetilde{\boldsymbol H}_{AR} = {\boldsymbol U}({\boldsymbol{\theta}})_{AR} {\boldsymbol H}_A\otimes $ $ \left| 0 \right\rangle \left\langle 0 \right|_R {\boldsymbol U}_{AR}^{\dagger}({\boldsymbol{\theta}})$ , 其中$ {\boldsymbol H}_A $ 是A 系统上的厄米特矩阵, $ \left| 0 \right\rangle \left\langle 0 \right|_R $ 是R 系统上的基向量, $ {\boldsymbol U}({\boldsymbol{\theta}})_{AR} $ 是作用在联合系统上的参数化电路. 文献[49 ]指出, $ \widetilde{\boldsymbol H}_{AR} $ 满足:$ \widetilde{\boldsymbol H}_{R} = {\rm{Tr}}_A[\widetilde{\boldsymbol H}_{AR}] $ . 进一步地, 由于H 20 )式等号左边可以通过量子设备在辅助系统上测量得到. 因此, 可以通过两次优化迭代得到厄米特矩阵H $ \|\boldsymbol H\|_1 $ .3.2.距离估计 -->3.2.距离估计 在量子设备上制备特定的量子态是一项重要的基本能力, 例如在变分量子本征求解器中任务的目标即可认为是制备一个量子系统的能量基态. 在制备量子态后, 离不开验证和刻画的过程. 在这之中就会涉及到量子态之间距离估计的函数. 这里主要讨论常用的两种距离估计函数[47 ] , 即迹距离D F 3.2.1.迹距离估计 -->3.2.1.迹距离估计 由于对一般量子态间的迹距离的大小判断属于QSZK-complete复杂度类[50 ] , 而QSZK (quantum statistic zero knowledge)包括了BQP (bounded-error quantum polynomial time)复杂度类, 因此即使在量子计算机上迹距离的估计目前也不存在高效算法. 由于迹距离具有如下性质:P $0\leqslant $ $ {\boldsymbol P}\leqslant {\boldsymbol I}$ 的半正定矩阵), 文献[49 ]基于该性质, 并通过奈马克扩张定理引入一个辅助比特, 将POVM元的优化转化为酉矩阵上的优化, 证明迹距离满足${\cal{U}}_{A\rightarrow R}({\boldsymbol X}_A) = {\rm{Tr}}_A[{\boldsymbol U}({\boldsymbol X}_A\otimes\left| 0 \right\rangle \left\langle 0 \right|_R){\boldsymbol U}^\dagger]$ . 因此, 通过最大化损失函数$C = {\rm{Tr}}[\left| 0 \right\rangle \left\langle 0 \right|_R{\cal{U}}_{A\rightarrow R}({\boldsymbol{\rho}}-{\boldsymbol{\sigma}})]$ 即可得到${\boldsymbol{\rho}}, {\boldsymbol{\sigma}}$ 间的迹距离估计. 值得一提的是, 在文献[49 ]中, (24 )式由(20 )式令${\boldsymbol{H }}= 1/2({\boldsymbol{\rho}}-{\boldsymbol{\sigma}})$ 直接得到.3.2.2.保真度估计 -->3.2.2.保真度估计 用经典方法计算保真度F 需要先对量子态ρ σ 22 )式进行计算. 由于希尔伯特空间维度随着量子比特数呈指数增长, 这种方法通常认为是困难的. 随之而来的问题就是, 在量子设备上直接估算态保真度是否可行, 是否更高效. 这种思路下的主要问题在于保真度计算公式中涉及到对量子态的非整数幂的操作$\sqrt{{\boldsymbol{\rho}}}$ , 没有已知的量子算法可以精确完成这一任务. 针对这一问题, 文献[20 ]提出了一种混合量子-经典算法用于近似任意混合态σ ρ ρ σ 49 ]基于乌尔曼定理(Uhlmann’s theorem)给出了计算任意混合态之间保真度的方式. 通过纯化子程序, 先分别获得需要测量保真度的两个量子态$ {\boldsymbol \rho}_A $ 和$ {\boldsymbol \sigma}_A $ 的纯化态$ |\psi\rangle_{AR} $ 和$ |\phi\rangle_{AR} $ . 然后通过纯化中辅助量子比特的自由度以及经典优化算法去最大化两个纯化态之间的态重叠, 即可获得对保真度的估计:A 表示原始问题的空间, R 表示纯化子程序中引入的辅助量子比特的空间.3.3.组合优化问题 -->3.3.组合优化问题 组合优化问题是指从离散的可行解集合中找出最优的一个解, 如旅行商问题、最大割问题等著名的NP困难问题都属于组合优化问题. 这些问题都可以抽象为最小化(或最大化)一个目标函数$ D(x) $ , 其中x 为一组离散的二进制变量.$ D(x) $ 编码为哈密顿量${\boldsymbol H}_D$ , 使得该哈密顿量的基态对应原优化问题的解[51 ] . 这样, 组合优化问题就变成了求解哈密顿量基态的问题, 即找到一个量子态$ \left| \psi \right\rangle $ 使得$\left|{\psi({\boldsymbol{\theta}})}\right\rangle = {\boldsymbol U}({\boldsymbol{\theta}})\left| s \right\rangle$ , 其中量子态$ \left| s \right\rangle $ 为量子电路运行前的初始态, θ [13 ] 提供了一种设计参数化量子电路的思路, 该算法最初由Farhi等[52 ] 提出, 专门用于解决组合优化问题. 与量子绝热算法(quantum adiabatic algorithm, QAA)[52 ,53 ] 类似, QAOA受到绝热定理的启发, 构造类似绝热演化的参数化量子电路来求解哈密顿量$ {\boldsymbol H}_D $ 的基态. 根据绝热定理, 如果一个系统的哈密顿量随时间的演化由$ {\boldsymbol H}(t) = (1-t/T){\boldsymbol H}_{\rm B} + t{\boldsymbol H}_D/T $ 给出, 且初始时该系统处于哈密顿量$ {\boldsymbol H}_{\rm B} $ 的基态, 那么通常经过足够长的演化时间T , 系统最终会处于哈密顿量$ {\boldsymbol H}_D $ 的基态. 因此, 只需要准备一个基态易于制备的辅助哈密顿量$ {\boldsymbol H}_{\rm B} $ , 将其基态作为初始量子态借助Trotter乘积式来近似演化哈密顿量$ {\boldsymbol H}(t) $ , 最终便能得到哈密顿量$ {\boldsymbol H}_D $ 的基态, 也即原组合优化问题的最优解. 这个演化过程可以近似为如下的参数化酉变:$ {\boldsymbol U}_D(\gamma_j) = {\rm e}^{-{\rm i}\gamma_j {\boldsymbol H}_D} $ 和$ {\boldsymbol U}_{\rm B}(\beta_j) = {\rm e}^{-{\rm i}\beta_j {\boldsymbol H}_{\rm B}} $ 分别是哈密顿量$ {\boldsymbol H}_D $ 与哈密顿量$ {\boldsymbol H}_{\rm B} $ 对应的参数化酉变; ${\boldsymbol{\gamma}},\; {\boldsymbol{\beta}}$ 是可以优化的参数; p 则是参数化酉变的层数.[9 ] .3.4.量子机器学习 -->3.4.量子机器学习 量子机器学习就是量子算法和机器学习的有机结合. 经典的神经网络分为两部分: 神经网络和优化器. 而量子机器学习, 就是把经典的神经网络换成量子的神经网络并由量子计算设备执行, 并且在经典设备上进行量子神经网络的参数优化, 即使用经典的优化器去优化量子神经网络. 通常情况下, 量子神经网络是由参数化量子电路表达的. 量子机器学习有望利用量子的并行运算的特性对经典的机器学习算法进行加速. 下面讨论几种较为常见的量子机器学习问题: 量子分类器[31 ,39 ,41 ,54 ] 、量子生成对抗网络[55 ,56 ] 和量子自编码器[57 ,58 ] .3.4.1.量子分类器 -->3.4.1.量子分类器 在机器学习中, 分类问题是极其重要的监督学习问题. 分类过程实质上是一个给数据贴标签的过程, 当输入数据满足某个条件的时候, 就给该数据贴上相应的标签, 从而完成分类. 分类问题通常会给定一个训练包含N 个样本的数据集$ \{(x^{(k)}, $ $ y^{(k)})\}^N_{k = 1} $ , 其中$ x^{(k)} $ 是数据点, $ y^{(k)} $ 是数据的标签. 该任务的目的是通过训练数据集训练神经网络, 使得该神经网络在遇到没有处理过的数据时能够做出正确的分类. 在量子分类器的框架下, 量子神经网络主要表达形式为参数化量子电路, Mitarai等[39 ] 以及Farhi和Neven[41 ] 采用参数化量子电路的结构分别完成了二分类任务和手写数字的分类任务.$ x^{(k)}\rightarrow \left| \psi \right\rangle ^{(k)} $ . 下一步需要把参数化量子电路$ {\boldsymbol{U}}({\boldsymbol{\theta}}) $ 作用在编码后的量子态上, 由此得到$ {\boldsymbol{U}}({\boldsymbol{\theta}})\left| \psi \right\rangle ^{(k)} $ . 随后, 把损失函数定义为真实标签和某个可观测量O [59 ,60 ] 包括基态编码、振幅编码、角度编码和IQP编码. 关于神经网络表达能力将在4.2 节详细讨论.31 ]提出了影子量子学习方法, 利用作用在局部量子比特上的影子电路实现多分类任务. 数值实验结果表明, 相比于已有的量子分类算法, 该算法具有更强大的分类能力, 同时大幅减少了网络参数, 降低了训练代价. 此外, 量子核方法[59 ,61 -63 ] 也是实现量子分类器的可行方案. 和经典核方法一样, 量子核方法也是先通过特征映射把原始数据映射到特征空间里, 然后寻找超平面把数据分类. 从理论上来说, 相较于经典的核方法, 量子核方法在处理分类问题时有平方级的加速效果[64 ] .[65 ] 在光量子平台上实现了对MNIST数据集中的手写 “0” 和 “1” 进行分类, 三层结构的分辨准确率达98.58%, 五层结构的分辨准确率达99.10%. 在影子量子学习方法中, 本课题组使用35个参数使得MNIST的二分类任务准确率达到99.52%. 而在MNIST十分类任务中, 在使用928个参数的情况下, 准确率达到$ 87.39\% $ [31 ] .3.4.2.量子生成对抗网络 -->3.4.2.量子生成对抗网络 生成对抗网络(generative adversarial network, GAN)[66 ] 在经典学习中扮演着重要的角色. GAN通常由生成器和判别器两部分组成, 其中生成器接受随机的噪声信号, 以此为输入来生成期望得到的数据; 判别器判断接收到的数据是不是来自真实数据, 通常输出一个$ P(x) $ , 表示输入数据x 是真实数据的概率.[55 ,56 ,67 ] (quantum generative adversarial network, QGAN)的目的是利用量子计算设备加速经典生成对抗网络的训练. 相比于GAN, QGAN生成的是量子态, 而不再是经典数据. 在QGAN的框架下, 生成器G 和判别器D 分别对应着两个参数化量子电路$ {\boldsymbol{U}}_G $ 和$ {\boldsymbol{U}}_D $ . 生成器的目标是最小化损失函数, 从而达到生成的数据以假乱真的效果; 判别器的目标是最大化损失函数, 要尽可能地分辨出哪些是真实数据, 哪些是生成器生成的数据. 可以把训练过程视为博弈的过程, 训练的结果会使得生成器和判别器达到纳什均衡点, 即生成器具备了生成真实数据的能力, 而判别器也无法再区分生成数据和真实数据. 一般情况下, 量子对抗生成网络的优化函数都可以写成以下形式:C 根据任务的不同而相应变化. 值得注意的是, 实际过程中, 通常采用交替训练的方式, 即先固定G , 训练D , 然后再固定D , 训练G , 不断往复. 当两者的性能足够时, 模型会收敛, 两者达到纳什均衡.[68 ] 解决了GAN的缺陷. 相应地, 在量子领域, QWGAN (quantum Wasserstein GAN)[69 ] 的提出也提升了QGAN效果. 如今, 量子对抗生成网络的方法已经被应用到各种任务上, 比如概率分布的学习[70 -72 ] 、量子态的学习[56 ,73 ] 、量子电路的学习[69 ] 以及纠缠的探测[74 ] .3.4.3.量子自编码器 -->3.4.3.量子自编码器 量子自编码器和经典自编码器一样, 都是由编码器和解码器组成, 是用于压缩数据, 进行特征降维的一种算法. 在量子自编码器中, 输入的数据为复合量子系统AB 的量子态${\boldsymbol{ \rho}}_{AB} $ . 将编码器$ E = $ $ {\boldsymbol{U}}({\boldsymbol{\theta}}) $ (即参数化量子电路)作用在量子态上, 得到$ {\boldsymbol{U}}({\boldsymbol{\theta}}){\boldsymbol{\rho}}_{AB}{\boldsymbol{U}}^\dagger({\boldsymbol{\theta}}) $ . 该步骤将量子系统AB 的信息编码到量子系统A 上. 对于量子系统B , 只需要对他们进行测量并丢弃即可, 即$\tilde{{\boldsymbol{\rho}}}_A = {\rm{Tr}}_B({\boldsymbol{U}}({\boldsymbol{\theta}}) {\boldsymbol{\rho}}_{AB} $ $ {\boldsymbol{U}}^\dagger({\boldsymbol{\theta}}))$ . 至此, 已经完成了信息的压缩. 在进行解码时, 需要引入与系统B 维度相同的系统C , 并且固定其量子态${\boldsymbol{ \rho}}_C $ . 随后将解码器$ D = {\boldsymbol{U}}^\dagger({\boldsymbol{\theta}}) $ 作用在整个量子系统$ A+C $ 上, 得到还原后的量子态$\tilde{{\boldsymbol{\rho}}}_{AC} = {\boldsymbol{U}}^\dagger({\boldsymbol{\theta}})[{\boldsymbol{\rho}}_c\otimes {\rm{Tr}}_B({\boldsymbol{U}}({\boldsymbol{\theta}}) $ $ {\boldsymbol{\rho}}_{AB}{\boldsymbol{U}}^\dagger({\boldsymbol{\theta}}))]{\boldsymbol{U}}({\boldsymbol{\theta}})$ [57 ] .${\boldsymbol{ \rho}}_{\rm{out}} $ 和输入的量子态${\boldsymbol{ \rho}}_{\rm{in}} $ 尽可能地相似, 所以损失函数定义为两个量子态之间的保真度F , 即C , 与系统A 进行耦合. 相对应地, 压缩过程可以理解为量子系统A 和量子系统B 解耦的过程, 由此可以定义损失函数为压缩后的量子系统$ \tilde{{\boldsymbol{\rho}}}_B $ 和引入的量子系统$ {\boldsymbol{\rho}}_C $ 之间的保真度, 即$ {\boldsymbol{\rho}}_{AB} $ 含有的量子资源超过了量子系统A 所能容纳的上限, 那么量子自编码器必然会导致信息的损失. 文献[58 ]设计了一种可以在量子退火机上运行的绝热算法进行量子信息的压缩. 和其他的量子自编码器相比, 该算法充分利用了测量所得到的信息, 在一定程度上解决了信息损失的问题.3.5.量子纠错 -->3.5.量子纠错 量子纠错[75 -77 ] 可表示为如下过程: 1)编码信道$ {\cal{U}} $ 将k 个逻辑量子比特的量子态$ \left| \varPsi \right\rangle $ 编码到n 个物理量子比特, 得到逻辑量子态$ \left| \varPsi \right\rangle _{\rm L} $ ; 2)逻辑量子态$ \left| \varPsi \right\rangle _{\rm L} $ 经过噪声信道$ {\cal{N}} $ , 该噪声信道由具体硬件设备决定; 3)纠错信道$ {\cal{W}} $ 尝试纠正噪声对逻辑量子态的影响, 该信道使用辅助量子比特探测并纠正错误; 4)解码信道$ {\cal{U}}^\dagger $ (编码信道$ {\cal{U}} $ 的逆)从物理比特解码还原量子态. 整个过程如图4 所示. 编码信道$ {\cal{U}} $ 和纠错信道$ {\cal{W}} $ 决定该纠错方案的性能: 复合信道$ {\cal{U}}^\dagger\circ{\cal{W}}\circ{\cal{N}}\circ{\cal{U}} $ 和理想无噪信道越接近, 纠错效果越好. 然而设计高效的纠错方案是极具挑战性的任务. 近年来, 研究人员尝试利用经典机器学习技术提高量子纠错效率[78 -88 ] , 这类工作属于典型的混合量子-经典算法. 使用混合量子-经典算法实现量子纠错的优势在于构造参数化电路时可以综合考虑硬件设备的特点, 比如所支持的量子门类型以及拓扑结构等, 设计出更高效的硬件相关的纠错方案. 下面介绍两个具有代表性的探索工作.图 4 量子纠错基本框架: 量子态$\left| \varPsi \right\rangle $ 使用编码信道${\cal{U}}$ 编码, 经过噪声信道${\cal{N}}$ 后使用纠错信道${\cal{W}}$ 纠正错误, 最后使用解码信道${\cal{U}}^\dagger$ 解码, 还原输入量子态Figure4. Framework of quantum error correction. The quantum state $\left| \varPsi \right\rangle $ first is encoded by the encoding channel ${\cal{U}}$ , then passes the noise channel ${\cal{N}}$ , and then is corrected by the correction channel ${\cal{W}}$ , finally is recovered by the decoding channel ${\cal{U}}^\dagger$ .78 ]提出量子变分纠错算法QVECTOR (variational quantum error corrector). 该方法的基本思路是将如图4 所示的编码信道$ {\cal{U}} $ 和纠错信道$ {\cal{W}} $ 表示为参数化量子电路${\cal{{\boldsymbol{U}}}}(\cdot) = {\boldsymbol{U}}({\boldsymbol{\theta}}_1)(\cdot) $ $ {\boldsymbol{U}}^\dagger({\boldsymbol{\theta}}_1)$ 和$ {\cal{{\boldsymbol{W}}}}(\cdot) = {\boldsymbol{W}}({\boldsymbol{\theta}}_2)(\cdot){\boldsymbol{W}}^\dagger({\boldsymbol{\theta}}_2) $ . 我们期望复合信道$ {\cal{{\boldsymbol{U}}}}^\dagger({\boldsymbol{\theta}}_1){\cal{{\boldsymbol{W}}}}({\boldsymbol{\theta}}_2){\cal{{\boldsymbol{N}}}}{\cal{{\boldsymbol{U}}}}({\boldsymbol{\theta}}_1) $ 等效或者逼近理想无噪信道, 因此定义如下形式的平均保真度作为损失函数:$ \mu(\psi) $ 表示哈尔测度. 直观上而言, 该损失函数刻画了上述纠错方案在输入量子态上的平均表现行为. 当$ F({\boldsymbol{\theta}}_1, {\boldsymbol{\theta}}_2) = 1 $ 时, 对应的参数化量子电路$ {\boldsymbol{U}}({\boldsymbol{\theta}}_1) $ 和$ {\boldsymbol{W}}({\boldsymbol{\theta}}_2) $ 实现了对噪声信道$ {\cal{{\boldsymbol{N}}}} $ 的完全纠错. 可采用更高效的酉2-设计[89 ] 或近似酉2-设计[90 ] 进行随机采样量子态来估计损失函数(32 )式. 实验数据表明, 相对五比特量子纠错码[91 ,92 ] , QVECTOR算法在处理特定噪声时有更好的效果.图4 可知, 设计合适的编码信道$ {\cal{U}} $ 精确地制备逻辑量子态$ \left| \varPsi \right\rangle _{\rm L} $ 是量子纠错中的关键任务. 文献[79 ]提出使用混合量子-经典算法制备$ \left| \varPsi \right\rangle _{\rm L} $ , 其核心思想是分析$ \left| \varPsi \right\rangle _{\rm L} $ 的数学性质将之编码为某个哈密顿量H H H [93 ] 为例给出H S ${\boldsymbol{ S }}= \langle {\boldsymbol{g}}_1,\; \cdots, \;{\boldsymbol{g}}_K\rangle$ . 著名的例子包括五比特量子纠错码[91 ,92 ] 、Steane纠错码[94 ] 和Shor纠错码[95 ] . 由稳定子码定义可知, 对任意$ k = 1, \cdots, K $ 均有${\boldsymbol{g}}_k\left| \varPsi \right\rangle _{\rm{L}} = \left| \varPsi \right\rangle _{\rm{L}}$ . 令$ \left| \varPsi^\perp \right\rangle _{\rm{L}} $ 表示$ \left| \varPsi \right\rangle _{\rm{L}} $ 的正交态, 定义算符 $O_{\rm{L}}: = \left| \varPsi \right\rangle _{\rm{L}}\left\langle \varPsi \right|_{\rm{L}} - $ $ \left| \varPsi^\perp \right\rangle _{\rm{L}}\left\langle \varPsi^\perp \right|_{\rm{L}}$ , 易见$O_{\rm{L}}\left| \varPsi \right\rangle _{\rm L}= \left| \varPsi \right\rangle _{\rm L}$ . 算符$ O_{\rm L} $ 编码逻辑量子态$ \left| \varPsi \right\rangle _{\rm L} $ 的系数信息. 定义哈密顿量$ c_k, c_o > 0 $ . 由定义可验证$ \left| \varPsi \right\rangle _{\rm L}$ 是H $E_0 = - \bigg(c_o+ \displaystyle \sum\nolimits_{k = 1}^Kc_k\bigg)$ . 以五比特量子纠错码和Steane纠错码为例, 针对不同硬件设备上述方法均能给出量子门数量更少的逻辑量子态制备电路.3.6.其他应用 -->3.6.其他应用 本节介绍3种不直接属于上述分类但具有代表性的混合量子-经典算法. 选择这些算法的原因在于它们使用的技巧具有一定代表性和启发性.3.6.1.量子线性求解器 -->3.6.1.量子线性求解器 变分量子线性求解器(variational quantum linear solver, VQLS)[96 -98 ] 实现线性方程组$ {\boldsymbol{A}}{\boldsymbol{x}} = {\boldsymbol{b}} $ 的求解. 不失一般性, 假设b A ${\boldsymbol{A}} = $ $ \displaystyle\sum\nolimits_jc_j{\boldsymbol{A}}_j$ , 随后根据归一化向量b $ \left| b \right\rangle $ , 并将$ \left| 0 \right\rangle $ 态输入参数化电路得到$ \left| x \right\rangle = {\boldsymbol{U}}({\boldsymbol{\theta}})\left| 0 \right\rangle $ , 然后最小化损失函数:${\boldsymbol{A}} = \displaystyle\sum\nolimits_jc_j{\boldsymbol{A}}_j$ 代入损失函数后, 损失函数中求和各项可通过哈达玛测试计算. 显然, 当损失函数优化至$ C = 0 $ 时, 有$ {\boldsymbol{A}}\left| x^{\rm{opt}} \right\rangle \propto\left| b \right\rangle $ , 此时计算$ \left| x^{\rm{opt}} \right\rangle /|{\boldsymbol{A}}\left| x^{\rm{opt}} \right\rangle | $ 即完成线性方程组的求解.3.6.2.纠缠检测 -->3.6.2.纠缠检测 变分纠缠检测(variational entanglement detection, VED)[99 ] 利用了转置映射的准概率分解[100 ] . 对于密度矩阵${\boldsymbol{\rho}} = \displaystyle\sum\rho_{jk}\vert j\rangle\langle k\vert$ , 转置映射T 将其映射为$T({\boldsymbol{\rho}}) = \displaystyle\sum\rho_{jk}\vert k\rangle\langle j\vert$ . 对于两方量子态$ {\boldsymbol{\rho}}_{AB} $ , 量子纠缠存在的一个充分条件是$ {\boldsymbol{\rho}}_{AB} $ 在B 系统上部分转置后的最小本征值小于0, 这种方法被称为PPT准则(positive partial transpose criterion)[101 ] . 据此, VED通过估计${\boldsymbol{ \rho}}_{AB} $ 部分转置后的最小本征值检测两方纠缠. 由于转置映射不是完全正的, 不能在物理设备上直接实现, 文献[99 ]将转置映射分解为泡利门的线性组合, 随后基于准概率分解对电路进行随机采样得到相应损失函数的无偏估计. 文献[99 ]同样给出了其他纠缠判定条件对应映射的泡利门分解.3.6.3.吉布斯态制备 -->3.6.3.吉布斯态制备 吉布斯态是量子模拟、多体物理研究等诸多领域的关键步骤. 给定哈密顿量H $\beta = 1/(k_{\rm{B}}T)$ . 由于吉布斯态使得系统自由能最小:S 为量子态ρ $S({\boldsymbol{\rho}}) = -{\rm{Tr}}[{\boldsymbol{\rho}}\log{\boldsymbol{\rho}}]$ , 基于该性质可以设计混合量子-经典算法, 通过最小化自由能制备吉布斯态. 对于量子态的自由能在量子设备上的估计, 文献[102 , 45 ]分别提供两种方法: 文献[102 ]将冯诺依曼熵中的对数运算展开成三角级数并截断, 随后设计电路估计自由能; 而文献[45 ]直接将冯诺依曼熵展开成泰勒级数并截断, 随后利用交换测试计算态重叠和高阶态重叠(即$ {\rm{Tr}}[{\boldsymbol{\rho}}^2] $ 和$ {\rm{Tr}}[{\boldsymbol{\rho}}^3] $ ), 从而估计自由能.3.6.4.虚时演化 -->3.6.4.虚时演化 虚时演化[103 ] 是研究量子系统的工具, 被广泛应用在许多物理领域, 包括量子力学、统计力学和宇宙学. 在实时演化中, 一个哈密顿量为H $ {\rm{e}}^{-{\rm{i}}{\boldsymbol{H}}t} $ . 在虚时演化中, 由于时间$ \tau = {\rm{i}}t $ 为虚数, 该系统的传播函数为$ {\rm e}^{-{\boldsymbol{H}}\tau} $ . 显然, 演化的时间越长, 系统的能量也就越低, 最终会稳定在系统的基态能量$ E_0 $ , 即$ \tau \rightarrow \infty $ , $ E_{{\rm{sys}}}\rightarrow E_0 $ . 因此, 虚时演化算法可用于求解子系统的基态. 由于虚时演化过程是数学的而非物理的, 如何模拟演化过程是虚时演化算法的关键.104 , 105 ]提出了使用变分量子电路对虚时演化进行模拟, 并计算化学系统的基态能量. 首先, 需要制备一个追踪态$ \left| {\psi({\boldsymbol{\theta}}(\tau))} \right\rangle = {\boldsymbol{V}}({\boldsymbol{\theta}}(\tau)) \left| 0 \right\rangle $ , 其中, ${\boldsymbol{V}}({\boldsymbol{\theta}}(\tau)) = $ $ {\boldsymbol{U}}_N({\boldsymbol{\theta}}_N) \cdots {\boldsymbol{U}}_k({\boldsymbol{\theta}}_k)\cdots {\boldsymbol{U}}_1({\boldsymbol{\theta}}_1)$ 代表着一系列酉门, 这里可以把$ {\boldsymbol{V}}({\boldsymbol{\theta}}(\tau)) $ 当作参数化量子电路. 当$ \tau = 0 $ 时, 代表着量子系统的初始态. 随后, 对$ {\boldsymbol{V}}({\boldsymbol{\theta}}(\tau)) $ 的各个参数进行更新$ {\dot{\boldsymbol{\theta}}}(\tau) $ 是量子电路的自然梯度. 随后通过迭代$ N_T = \tau_{\rm totoal}/\text {δ}\tau $ 次, 来模拟虚时从$ \tau = 0\rightarrow \tau = \tau_{\rm total} $ 的演化过程. 当模拟的时间足够长时, 便能够得到系统哈密顿量H 4.挑 战 尽管混合量子-经典算法已经在理论和实践上被证明在求解特定问题时具有高效的表现, 该领域仍然存在若干开放性问题与挑战. 本节主要介绍3种对混合量子-经典算法效果的制约因素和潜在的解决思路, 分别为噪声影响、电路表达能力以及可训练性.4.1.噪声影响 4.1.噪声影响 作为一类NISQ算法, 噪声对混合量子-经典算法的影响值得深入研究. 大体上, 量子噪声可以分为相干噪声和非相干噪声. 相干噪声的产生可能是由于硬件校准的精度, 导致在执行一个量子门$ {\boldsymbol{U}}(\theta) $ 时实际执行的是$ {\boldsymbol{U}}(\theta + \delta) $ . 通常来说, 相干噪声对于经典优化方法来说并不构成很大的影响, 特别是SPSA这种本身就会对参数产生随机扰动的优化方法. 量子设备的非相干噪声往往会对损失函数的整体景观产生影响, 使其变得平坦或改变最值的位置, 如图5 所示. 文献[106 ]和文献[107 ]分别从数值和理论上研究了泡利噪声对QAOA算法的影响, 并指出QAOA算法对低强度泡利噪声具有一定抗性; 文献[108 ]进一步探究了QAOA算法的误差上界与噪声和量子Fisher信息相关; 文献[109 ]指出泡利噪声直接导致混合量子-经典算法的梯度消失问题; 文献[110 ]表明, 在一部分计算任务中(如变分量子编译), 尽管噪声使得损失函数整体变得平坦, 但不会影响最优参数的取值, 因此不影响算法最终结果的正确性; 文献[111 ]表明噪声会破坏参数空间的对称性, 导致部分全局最优解变为局部最优, 从而增加优化难度; 文献[112 ]对比了有噪条件下混合量子-经典算法和经典算法的复杂度, 证明了在大噪声条件下混合量子-经典算法相比于经典算法不再具有优势.图 5 无噪(左)与有噪(右)条件下损失函数景观对比Figure5. Comparison between noise-free (left) and noisy (right) cost function landscape.4.2.电路表达能力 -->4.2.电路表达能力 2.2 节曾提到, 在参数化量子电路的模型设计中, 为使参数空间能够对应尽可能多的酉变, 从而使优化过程覆盖尽可能大的解空间. 参数化量子电路的表达能力可直观地理解为电路取遍所有参数时能表达的酉变范围的大小. 一般来说, 更深的电路具有更强的表达能力, 但电路深度同时会带来更严重的噪声和可训练性问题. 因此, 如何权衡电路深度与表达能力, 以及如何设计表达能力更强的电路模型是混合量子-经典算法面临的重要一项挑战.$ {\boldsymbol{U}}({\boldsymbol{\theta}}) $ 表达能力进行量化:$ D_{\mathrm{KL}}(A\|B) $ 表示概率分布$ A, B $ 之间的K-L散度; $P({\boldsymbol{U}}, F)$ 表示电路U $ \left| 0 \right\rangle $ 且参数θ $ P_{\mathrm{Haar}}(F) $ 表示一对满足哈尔分布的随机量子态间的保真度的概率分布且有解析表示: $ P_{\mathrm{Haar}}(F) = (d-1)(1-F)^{d-2} $ ; d 是系统希尔伯特空间的维度. 由于$ P({\boldsymbol{U}}, F) $ 可以通过对电路参数采样后测量估计, 表达能力因此可以在近期设备上有效计算. 文献[25 ]首先定义并计算了若干常用参数化电路模型的表达能力; 文献[113 ]进一步比较了常见的硬件高效拟设与交错分层拟设的表达能力, 指出后者相较于前者, 在提供更强的可训练性的同时保留了几乎相当的表达能力. 文献[114 ]从理论角度证明了损失函数的梯度方差的上界与电路表达能力有关.25 ]基于梅尔-沃勒克度量定义了电路的纠缠能力, 即电路平均能提供多少纠缠. 电路纠缠能力在一些量子态制备任务中起到关键作用.4.3.可训练性 -->4.3.可训练性 目前混合量子-经典算法的可训练性主要指的是由贫瘠高原现象对优化过程造成的困难. 贫瘠高原(barren plateau)现象[115 ] 最早于2018年被提出, 当混合量子-经典算法所选取的非结构化的拟设电路$ {\boldsymbol{U}}({\boldsymbol{\theta}}) $ 进行随机参数初始化时, 算法对应损失函数$ C({\boldsymbol{\theta}}) $ 的梯度方差在采样的平均意义下$\text{Var}\Big[\dfrac{\partial C({\boldsymbol{\theta}})}{\partial \theta_k}\Big]$ 会随着问题规模n 的扩大呈现指数递减. 直观来看, 这种现象会使得问题的优化曲面变得非常平坦(故称贫瘠), 从而使得为了达到确定优化方向的计算精度所需的测量数变得非常巨大(如果无法达到测量精度要求, 电路的优化过程可能会接近于随机游走), 最终导致基于梯度或者非梯度的优化方法[116 ] 都很难找到全局最小值. 产生这种现象背后的数学原因在于非结构化的电路在随机初始化参数时满足酉2-设计的性质[117 ] . 相关证明和避免贫瘠高原现象的理论研究也是围绕这个核心性质展开的. 值得注意的是, 文献[115 ]中的结果部分表明了4.2 节中提到的电路表达能力和可训练性之间的权衡关系. 当电路的深度增加时相应的表达能力增强, 但同时梯度的方差(可训练性)也会逐渐减小.118 ]提出了一种初始化参数θ 119 ]进一步提出了分层训练的方案, 即使用若干初始层训练然后依次添加电路结构和层数. 除了上述通过设计初始化训练方案, 基于特定问题启发设计的电路结构[9 ,120 ] 通常认为对于大规模的问题依然是可以训练的. 此外, 3.1.2 节提到的通过重新设计损失函数将其表达为局部损失函数的形式(只同时测量部分量子比特)[21 ] 也被证明可以有效应对可训练性问题. 然而很多算法的损失函数是否存在这样的表达形式依然未定. 最后, 有研究表明噪声[109 ] 和过度的纠缠能力[121 ] 也会造成类似现象并阻碍训练过程. 可以说, 可训练性问题至今依然是混合量子-经典算法长远发展的一大挑战.5.总结与展望 本综述介绍了混合量子-经典算法的基本概念, 此类算法在量子化学、机器学习、组合优化、量子信息等领域的研究进展以及算法目前面临的主要挑战. 一方面, 可以看到混合量子-经典算法已为许多领域问题提供了有效且具备潜在优势的解决方案, 同时可以结合优化理论和机器学习中的现有技术, 尽可能在近期量子设备上发挥量子计算的能力, 推动量子计算与机器学习的融合创新. 另一方面, 我们也认识到混合量子-经典算法作为一个相对“年轻”的研究方向存在若干瓶颈, 包括对电路表达能力的理论分析工具不够完善, 对算法规模的可扩展性有限, 大部分算法的量子优势缺乏严格的理论和实验证明等. 如何克服这些混合量子-经典算法的瓶颈以及探索其在更多领域的应用, 将是混合量子-经典算法未来重要的发展方向. 此外, 张量网络作为连接经典与量子计算的数学模型, 已经从理论[122 ,123 ] 和应用[124 ,125 ] 层面启发了机器学习领域的许多研究方向. 因此, 这一工具在近期量子设备上的探索同样值得关注. 随着量子硬件能力的不断提升与混合量子-经典算法技术的不断发展, 相信具有量子优势的近期量子设备实用化应用将有望实现. 
图 1 混合量子-经典算法流程
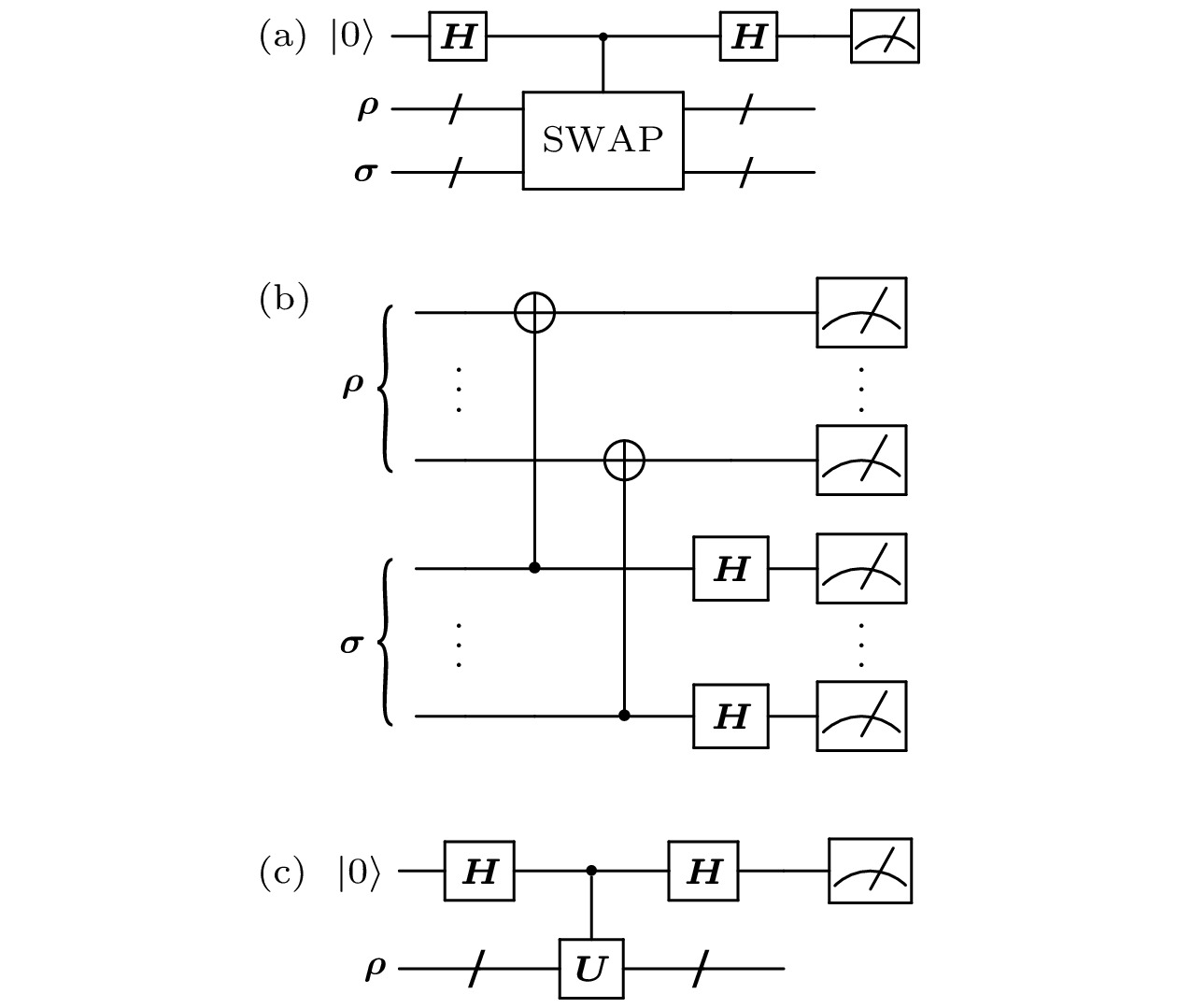图 2 (a) 交换测试电路; (b)破坏性交换测试电路; (c) 哈达玛测试电路
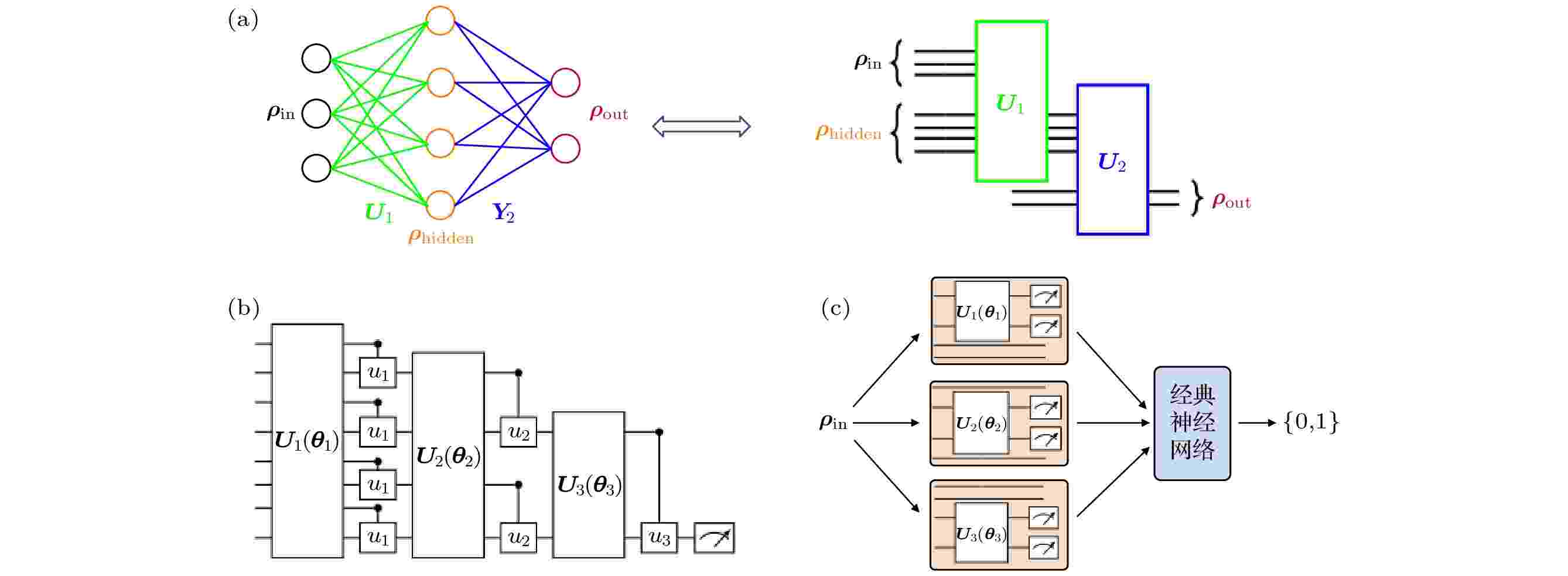图 3 (a) 量子感知机; (b)量子卷积神经网络; (c)影子电路
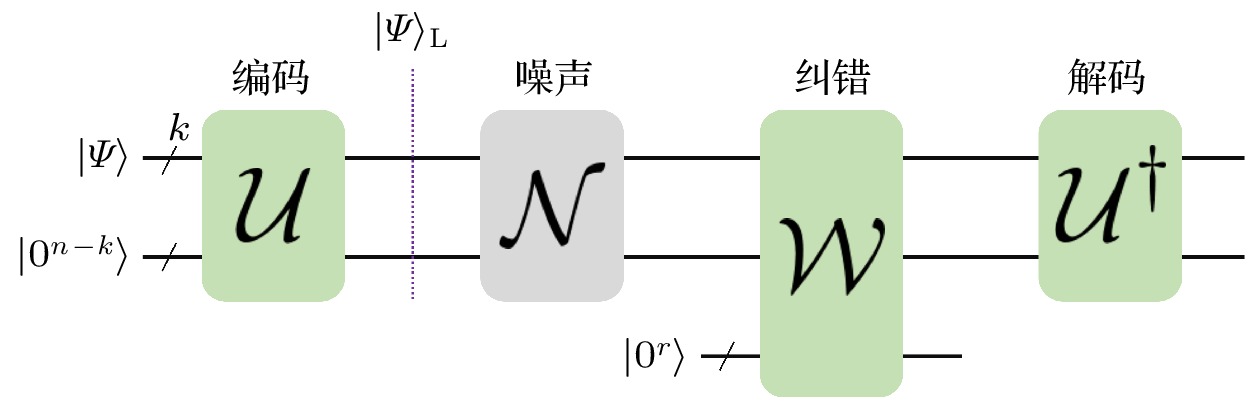图 4 量子纠错基本框架: 量子态
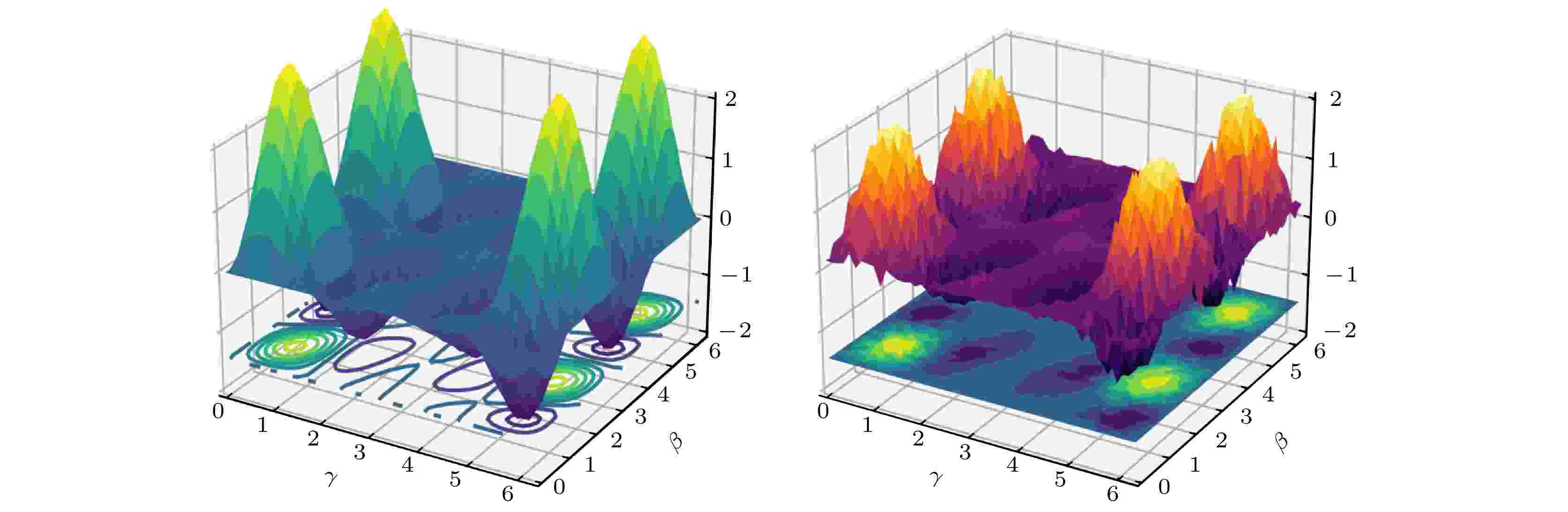图 5 无噪(左)与有噪(右)条件下损失函数景观对比
