摘要:碳纳米管晶体管作为新一代纳米器件, 由于缺乏成熟的阈值电压调控机制, 仍难以运用到实际逻辑电路中. 本文提出了一种简单易实现且能够大规模处理的表面掺杂方法, 通过AuCl₃的p型掺杂作用来实现对晶体管阈值电压的有效调控, 研究了不同掺杂浓度对碳纳米管电学性能的影响. 实验结果表明, 在低掺杂浓度条件下, 不仅实现了晶体管阈值电压稳定调控, 器件导电性能也大幅提高, 迁移率提升2—3倍. 更进一步地, 研究了退火对掺杂后器件的电学性能影响, 发现在同等掺杂条件下, 退火温度达到50 ℃时, p型掺杂效果最佳. 最后采用第一性原理计算方法, 验证了金离子对碳纳米管的掺杂调控机制. 这项研究为未来实现大面积低功耗逻辑电路以及高性能电子器件提供了重要指导.
关键词: 碳纳米管网络/
表面掺杂/
阈值电压调控/
密度泛函理论

English Abstract

全文HTML

--> --> -->

碳纳米管网络作为一种由一定数量的单壁碳纳米管相互连接构成的网状纳米薄膜, 由于其极好的电学性能以及良好的稳定性而被广泛研究^[1,2]. 近几年来, 基于碳纳米管晶体管的电子器件在大规模集成电路、太阳能电池以及新兴的神经计算领域发展迅速^[3-6]. 然而, 当前基于碳纳米管晶体管的集成电路仍存在诸多挑战, 其中实现有效稳定的阈值电压调控机制是目前亟待解决的问题^[7].
众所周知, 阈值电压作为场效应晶体管的关键电学参数, 它决定了晶体管的不同工作模式和开启电压, 对于控制功耗以及噪声容限具有重要作用^[8]. 因此, 晶体管阈值电压调控的问题一直是研究人员关注的重点. Zhong等^[7]在顶栅介质HfO₂表面依次沉积金属Pd和Sc作为顶栅电极, 通过改变Pd的厚度来实现对碳纳米管网络晶体管阈值电压的准确调控. 这种方式虽然可以实现对阈值电压连续准确调控, 但是结构设计复杂难以实时调控限制了其在实际应用中的发展. 除此之外, 研究人员提出含氟聚合物或自组装单分子层在栅极绝缘层表面诱导产生表面偶极子等一系列方式进行阈值电压控制^[9-12]. 但上述几种调控方式均存在一定缺点, 例如有限的调控能力、结构复杂以及难以大面积处理等.
表面掺杂作为一种调控晶体管电学性能的常用手段, 具有操作简单且易实现等优点, 推动了电子器件大规模处理的发展. 这种基于溶液的化学处理方式, 主要通过在功能层的表面沉积有机或者无机掺杂层, 利用掺杂剂和功能层之间的表面电荷转移实现对晶体管电学性能的调控^[13]. 相较于体掺杂需要将掺杂剂和半导体在溶液中混合的处理方式, 表面掺杂通过将掺杂剂直接沉积到已经形成的碳纳米管薄膜的表面, 很难引入结构缺陷或者散射中心, 因此基本不会导致晶体管迁移率降低^[14,15]. 作为表面掺杂中常用的p型掺杂剂, AuCl₃已经被广泛用于石墨烯基电子/光电子器件的电学性能调控, 并且被证明能够有效降低石墨烯与金属接触电阻以及调控器件的阈值电压^[16-19]. 近年来, Kim等^[20-22]深入研究了AuCl₃掺杂碳纳米管过程中金离子和氯离子的作用机制, 并且进一步研究了不同退火温度下碳纳米管的电学性能转换. 然而到目前为止, 针对AuCl₃对碳纳米管的电学性能调控研究, 特别是在阈值电压的稳定调控方面仍缺乏深入研究. 本文将充分利用AuCl₃对二维纳米器件电学性能调控上的优势, 对碳纳米管晶体管阈值电压进行有效调控并通过密度泛函理论进一步验证.
本文提出一种基于溶液的表面掺杂方式, 通过在碳纳米管表面旋涂p型掺杂剂AuCl₃, 利用金离子和碳纳米管网络之间表面电荷转移, 从而实现对阈值电压的有效控制. 采用拉曼光谱验证了AuCl₃对碳纳米管的p型掺杂效果, 并深入研究了不同掺杂浓度对碳纳米管晶体管阈值电压的调控作用. 实验结果表明在掺杂浓度小于50 μmol/L时, 晶体管阈值电压不断向右偏移, 同时器件导电性能大幅提升, 迁移率提升2—3倍. 更进一步研究了退火对晶体管电学性能的影响, 发现在浓度一定的情况下, 退火温度达到50 ℃时掺杂效果达到最佳. 最后利用密度泛函理论计算掺杂前后碳纳米管的能带结构, 态密度以及二次差分电荷密度图, 分析了金离子对碳纳米管的调控机制. 这项研究为未来高性能二维电子器件的阈值电压调控奠定了基础.

2

-->

2.1.材料和器件的制备

AuCl₃掺杂的碳纳米管晶体管的结构示意如图1所示. 具体制备过程如下: 首先, 本文中采用的碳纳米管, 管径分布1.2—1.8 nm, 碳管长度1.5—2.0 μm, 纯度大于99%. 溶剂为邻二甲苯. 将Si/SiO₂基片依次用丙酮、无水乙醇和异丙醇冲洗干净, 并用氮气枪吹干备用. 随后将多聚赖氨酸滴在Si/SiO₂衬底表面静置30 min, 对衬底表面功能化便于吸附碳纳米管, 然后用去离子水和异丙醇反复冲洗3次以便去除多余的多聚赖氨酸. 然后将Si/SiO₂基片完全浸没在碳纳米管的悬浮液中(浓度约为98%)2 h后, 依次用去离子水和异丙醇冲洗并用氮气枪烘干. 随后通过紫外光刻技术和电子束光刻设备在碳纳米管网络表面制备Cr/Au(10 nm/50 nm)电极, 并进一步采用光刻机技术和等离子体刻蚀工艺对碳纳米管网络沟道进行图形化. 最后, 将制备好的器件放在氩气气氛下200 ℃条件下退火30 min, 完成碳纳米管晶体管器件的制备.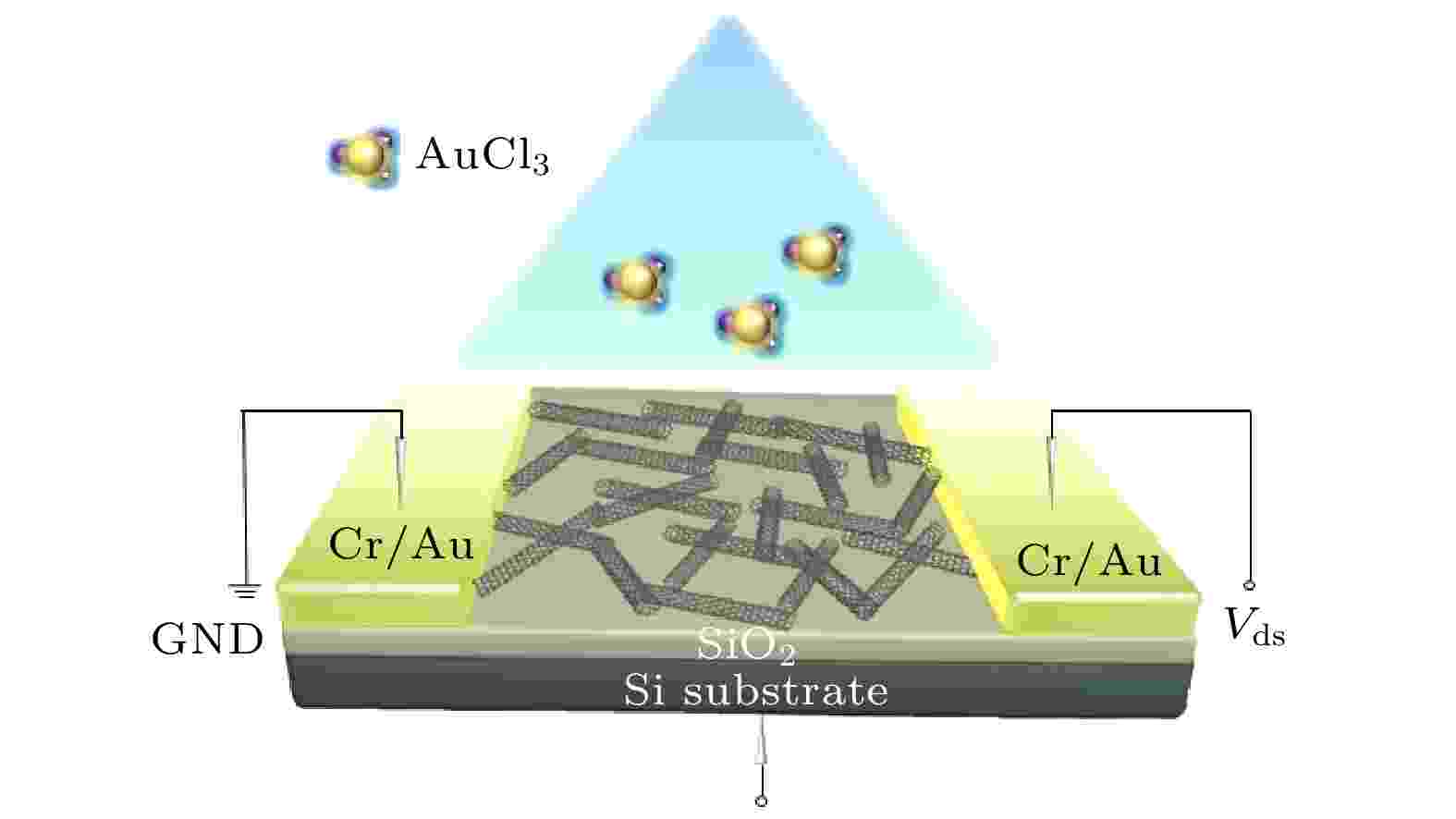
图 1 AuCl₃掺杂碳纳米管器件的结构示意图
Figure1. Schematic illustration of the AuCl₃-doped CNFET device.

2 -->

2.2.AuCl₃溶液的配备及旋涂工艺

将纯度99%的AuCl₃粉末溶于去离子水中分别配置了10, 20, 50, 100 μmol/L四种不同浓度的AuCl₃溶液. 随后, 利用移液枪取出100 μL AuCl₃溶液滴在器件沟道表面静置30 s, 然后通过匀胶机以5000 r/min的转速均匀旋涂在碳纳米管网络表面, 时间大约1 min. 随后, 将硅片转移至热板上, 在50 ℃条件下退火5 min. 需要特殊说明的是, 在探究AuCl₃浓度对碳纳米管晶体管电学性能的调控作用时, 退火温度和退火时间分别固定在50 ℃和5 min.
2 -->

2.3.结构和电学特性表征

采用原子力学显微镜(AFM, SPA 500, Seiko Instruments Inc)观察碳纳米管网络表面的形貌. 使用拉曼光谱仪(Renishaw, RM-1000 Invia)采集AuCl₃掺杂的碳纳米管的散射光谱, 以表征碳纳米管的结构特性. 利用Helios G4 CX型扫描电子显微镜获取X射线能谱来分析碳纳米管表面金元素的含量和分布. 晶体管的转移特性曲线以及输出特性曲线主要通过探针台和半导体分析仪(Agilent B1500A)进行测量.

2

-->

3.1.材料表面形貌以及元素分布表征

图2(a)给出了AuCl₃掺杂碳纳米管器件的光学照片, 沟道宽度和长度分别为50 μm和20 μm, 阴影部分为碳纳米管网络薄膜. 图2(b)给出了碳纳米管晶体管的AFM图, 图中可以清晰地看到均匀分布的碳纳米管网络以及附着在其表面的金颗粒. 由于金离子和碳纳米管之间存在氧化还原电势差, 因此两者之间会发生表面电荷转移^[20]. 碳纳米管中的电子由于电势差会被提取到金离子中, 金离子被还原成金原子. 图中一些比较亮的斑点是由于在退火过程中, 金颗粒融化形成的比较大的团簇. 为了进一步观察碳纳米管网络的形貌以及金元素的分布, 图2(c)和图2(d)给出了碳纳米管的SEM图以及对应的EDS图谱. SEM观测结果证明了碳纳米管致密均匀地排列在Si/SiO₂表面, 而图2(d)证实了分布在碳纳米管网络表面的金元素的存在.
图 2 AuCl₃掺杂碳纳米管的表面形貌及元素分析　(a) OM图; (b) AFM图; (c) SEM图; (d) EDS图谱
Figure2. (a) Optical image of the CNFET device; (b) AFM image; (c) SEM image of AuCl₃-doping CNT; (d) energy-dispersive X-ray spectroscopy (EDX) mappings of the Au element.

2 -->

3.2.AuCl₃对碳纳米管电学性能的调控作用

图3(a)给出了AuCl₃掺杂前后碳纳米管晶体管转移特性曲线的变化, 从图3(a)可以明显看出, 未掺杂碳纳米管晶体管具有明显的p型半导体特性. 这种p型特性是由于碳纳米管表面吸附空气中的氧气而产生的电子提取效应^[21]. 在旋涂AuCl₃溶液后, 碳纳米管晶体管转移特性曲线发生明显移动, 开关比保持在10⁵左右, 而阈值电压发生显著右移. 主要是因为金离子作为一种典型的p型掺杂剂, 相对于正常的氢电极具有1.5 V的还原电势, 明显高于碳纳米管的第一和第二范霍夫奇点, 因此碳纳米管中第一和第二范霍夫奇点电子会被提取用来还原金离子, 导致碳纳米管的费米能级向下移动, 因此AuCl₃对碳纳米管具有p型掺杂效果^[20,22]. 图3(b)给出了不同栅压下AuCl₃掺杂碳纳米管晶体管的输出特性曲线, 在低漏源电压下这种线性的输出特性证明了碳纳米管网络和铬/金电极之间典型的欧姆接触.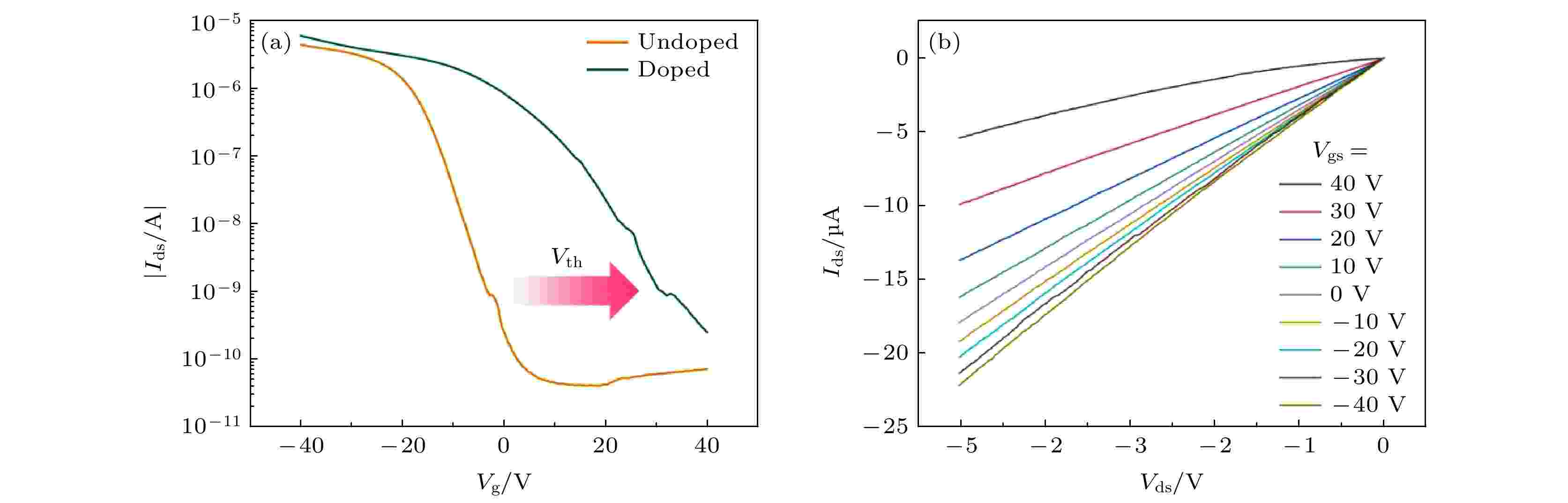
图 3 掺杂前后碳纳米管晶体管转移特性曲线以及掺杂后晶体管的输出特性曲线
Figure3. (a) Transfer curves (I_ds-V_g) of pristine and AuCl₃-doping CNFET; (b) output curves (I_ds-V_ds) of the AuCl₃-doping CNFET.

为了进一步探究AuCl₃浓度对碳纳米管晶体管电学性能的调控机制, 分别用10, 20, 50 和100 μmol/L浓度的AuCl₃溶液旋涂在碳纳米管晶体管表面, 并在50 ℃条件下退火5 min. 图4(a)给出了不同浓度AuCl₃掺杂下碳纳米管的拉曼光谱, 可以明显看到随着AuCl₃浓度提高, G带峰值明显右移, 从1591.12 cm^–1到1594.32 cm^–1再到1596.78 cm^–1. 这种拉曼峰明显右移的现象与p型碳纳米管和金离子之间发生的电子转移密切相关, 进一步证实了金离子对碳纳米管的p型掺杂效果. 同时G/D带峰值强度的比值可以用来表征缺陷的形成, 而掺杂前后没有观察到明显的D带峰以及G/D带峰值强度的比值基本没有变化, 说明在掺杂过程中碳纳米管基本没有结构缺陷产生. 图4(b)给出了碳纳米管晶体管的转移特性随AuCl₃掺杂浓度变化的曲线, 从图4(b)可以看出, 随着AuCl₃浓度提高, 碳纳米管的p型半导体特性越来越显著, 开关比逐渐减小, 由初始的10⁵减小到10左右趋于导体特性. 进一步使用线性外推法从转移特性曲线中提取晶体管的阈值电压. 由图3(b)可知, 在漏源电压V_ds为–1 V条件下, I_ds和V_gs的对应关系处在线性区域内, 故采用线性区计算公式提取阈值电压. 从转移特性曲线(I_ds-V_gs)中选取线性段进行数据拟合, 得到$ y=kx+b $, 其中
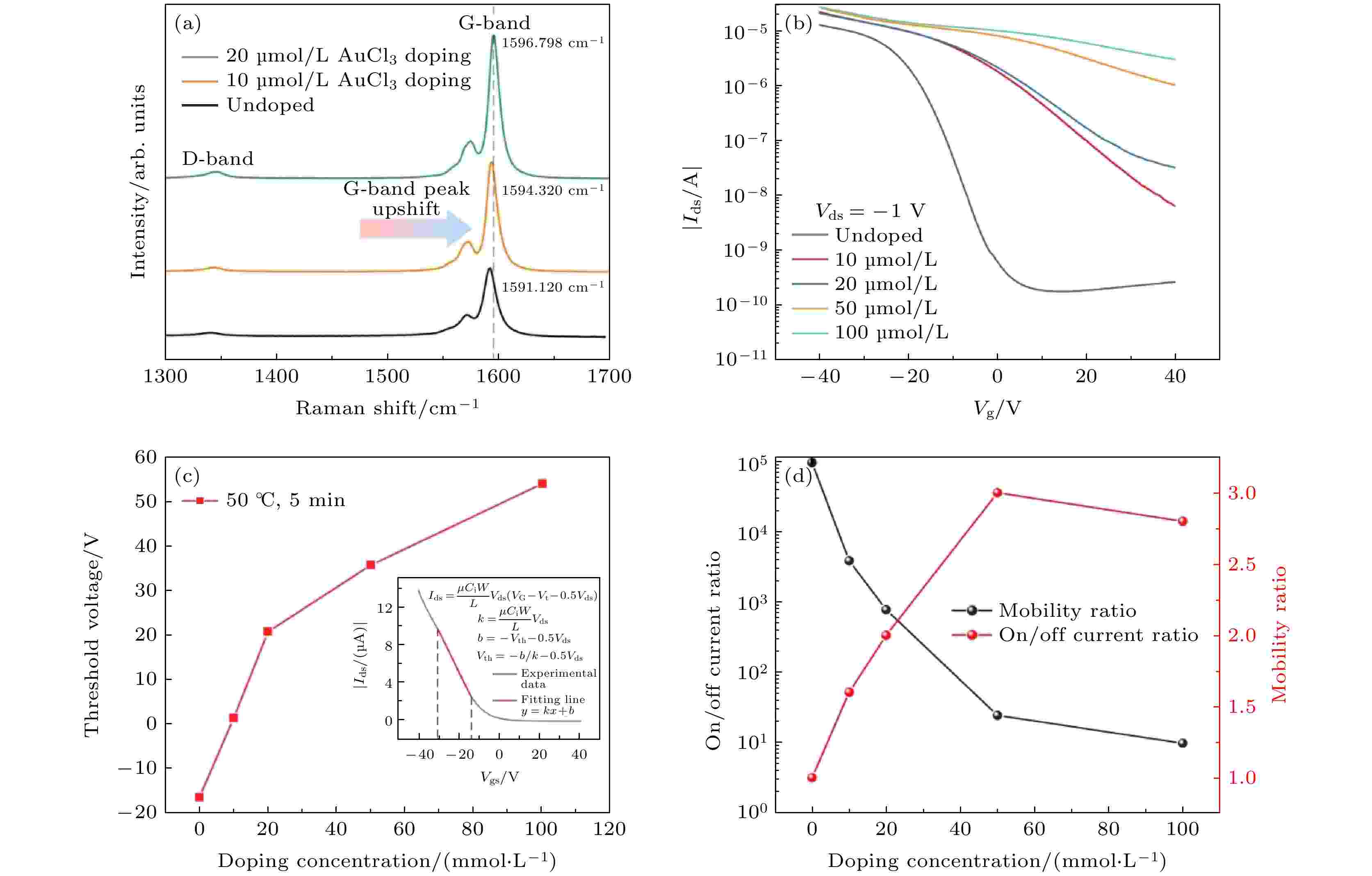图 4 (a) 不同掺杂浓度下碳纳米管的拉曼光谱; (b) 不同掺杂浓度下碳纳米管晶体管的转移特性曲线, 漏源电压V_ds被固定在–1 V; (c) 阈值电压随AuCl₃浓度的变化曲线, 插图为从转移特性曲线中提取阈值电压的计算方式; (d) 开关比以及迁移率随AuCl₃浓度的变化曲线
Figure4. Modulation of the AuCl₃ concentration on the electrical performance of CNFET: (a) Raman Spectra of the CNT under different doping concentrations; (b) the transfer curves (I_ds-V_g) of a CNFET device with different doping concentrations, with the drain-source voltage fixed at –1 V; (c) threshold voltage value of the doped CNFET device as a function of AuCl₃ concentration. The inset illustrates the calculation method of threshold voltage extracted from transfer curves; (d) ON/OFF current ratio (I_on/I_off) and the field-effect mobility ratio (μ_ratio = μ_doped/μ_pristine) as a function of the doping concentrations.

$ {I}_{\rm{ds}}=\dfrac{\mu {C}_{i}W}{L}{V}_{\rm{ds}}\times \left({V}_{\rm{gs}}-{V}_{\rm{th}}-0.5{V}_{\rm{ds}}\right), $

斜率$k=\dfrac{\mu {C}_{i}W}{L}{V}_{\rm{ds}}$ 和截距 $ b= -{V}_{\rm{th}}-0.5{V}_{\rm{ds}} $, 这里V_t代表晶体管阈值电压, μ代表晶体管迁移率, C_ox代表绝缘层的单位面积电容, V_gs代表栅源电压, W和L分别代表器件沟道的宽度和长度. 根据上述公式, 晶体管阈值电压可以被计算V_th = $-0.5{V}_{\rm{ds}} -b$, 如图4(c)插图所示.
图4(c)给出了晶体管阈值电压随AuCl₃浓度的变化曲线, 随着AuCl₃浓度提高, 阈值电压偏移逐渐增大. 因此, 通过调控掺杂浓度可以实现对阈值电压的有效调控. 相较于之前报道的阈值电压调控方法, 这种基于表面改性的掺杂方法在大规模处理, 结构简单以及更好地保持器件性能方面展现出巨大优势^[23]. 图4(d)给出了晶体管迁移率以及开关比随AuCl₃浓度的变化曲线. 随着掺杂浓度不断升高, 晶体管的迁移率提升2—3倍左右, 在AuCl₃浓度为50 μmol/L的条件下, 迁移率达到峰值, 是本征碳纳米管的3倍左右. 这种迁移率大幅提高的现象是由于在低掺杂条件下(小于50 μmol/L), 沉积在碳纳米管网络表面的金离子数量较少, 导致金离子对载流子产生的散射作用很小, 因此散射对迁移率所产生的负面影响很小. 另一方面, 在引入金离子后, 由于金离子强大的还原电势, 碳纳米管中的电子会不断被提取至金离子, 导致作为主要载流子空穴的浓度提高. 这种p型掺杂效果已经超过了散射所带来的负面影响, 成为迁移率增大的主要因素. 同时, 这种化学掺杂方式既有效调控了晶体管的阈值电压, 同时增强了晶体管的其他电学性能, 对于未来纳米器件的电学性能调控具有指导意义.
2 -->

3.3.退火温度对AuCl₃掺杂作用的影响

更进一步地研究了退火温度对AuCl₃掺杂碳纳米管的电学特性影响, 图5(a)给出了晶体管的开关比以及阈值电压随退火温度的变化曲线. 可以很明显看出退火温度在50 ℃以下, 随着温度升高, 开关比逐渐降低, 阈值电压逐渐增大, 这表明AuCl₃对碳纳米管的p型掺杂效果越来显著. 然而, 在退火温度从50 ℃开始逐渐升高时, 开关比和阈值电压逐渐恢复, p型掺杂效果被明显抑制. 这种现象的主要原因是由于沉积在碳纳米管表面金离子的数量在不断减小, 此外在温度超过50 ℃时, 带正电荷的碳纳米管CNT⁺和氯离子会形成具有n型掺杂特性的CNT—Cl键^[22], 从而导致p型掺杂效果退化. 图5(b)给出了迁移率随退火温度的变化曲线. 在50 ℃时出现拐点, 迁移率达到峰值. 由室温逐渐升高到50 ℃的过程中, 碳纳米管由于电子被不断抽取导致作为主要载流子的空穴浓度不断升高, 因此迁移率相较于本征碳纳米管有较大提升. 当退火温度继续升高时, 被还原的金颗粒逐渐融化形成大的团簇, 导致缺陷或散射中心的形成, 从而使得迁移率不断下降. 因此, 在50 ℃时掺杂效果达到最佳.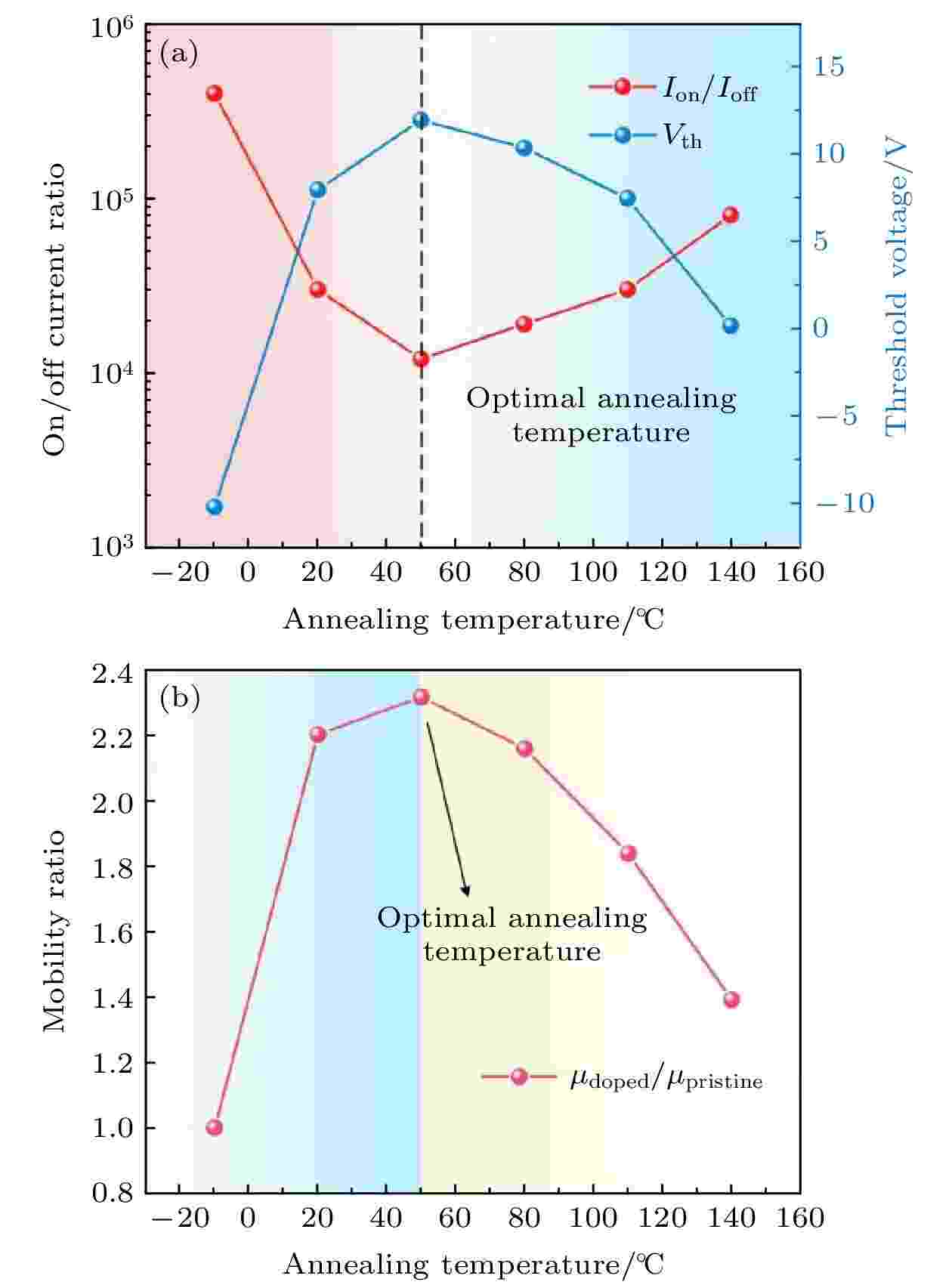
图 5 (a) 开关比以及迁移率随退火温度的变化曲线; (b) 迁移率的比值随退火温度的变化
Figure5. (a) ON/OFF current ratio (I_on/I_off) and threshold voltage value as a function of annealing temperature; (b) field-effect mobility ratio (μ_ratio = μ_doped/μ_pristine) as a function of annealing temperature.

2 -->

3.4.AuCl₃掺杂作用的机理分析

为深入分析AuCl₃掺杂对于碳纳米管电子结构的影响, 采用基于密度泛函理论的第一性原理计算方法对碳纳米管和金/碳纳米管系统进行了系统性的研究. 本文所采用的是p型半导体碳纳米管, 在进行建模时选择将碳纳米管的手性指数设置为(10, 0), 晶胞设置为六方晶胞, 为保证不同碳纳米管的碳原子之间的最小距离不低于10 ?, 晶胞参数设置为$a=b=20.06\;?, c=4.27\;?, \alpha =\beta =90°, \gamma = $$ 120°$, 如图6(a)所示. 对于金/碳纳米管的掺杂系统, 采用了$ 1\times 1\times 3 $的超胞, 每个超胞中有一个金原子, 晶胞结构如图6(b)所示. 为了对掺杂系统的能带结构进行更精确的描述, 采用GGA-PBE^[24,25]泛函描述电子的交换关联作用. 特别地, 为避免赝势对芯电子波函数的错误描述, 进一步采用了投影缀加波(PAW)方法^[26,27], 平面波截断能设置为$ 520\;{\rm{eV}} $. 通过Monkhorst-Pack方法对布里渊区^[28]进行采样, k 空间采样密度为$ 0.03\times 2{\text{π}} \;? $. 在计算电子结构前, 对于每个系统进行充分的结构优化, 收敛标准设置为每个原子受力不大于$1.5\times {10}^{-2}{\rm{eV}}/$?. 在计算二次差分密度时, 采用$\Delta \rho ={\rho }_{\rm{Au}/{\rm{CNT}}}-{\rho }_{\rm{Au}}- $$ {\rho }_{\rm{CNT}}$的定义, 计算的二次差分电荷密度图如图6(c)所示. 在计算能带结构时, 由于碳纳米管是一维结构, 高对称性路径只取$\varGamma \to Z$, 计算的能带结构与态密度如图6(d)—(f)所示. (10, 0)碳纳米管的能带结构是典型的p型半导体的能带结构, 计算得到的带隙为$ 0.509\;{\rm{eV}} $, 价带电子的有效质量为$ -0.128{m}_{0} $. 当引入金对碳纳米管进行掺杂后, 如图6(e)所示, 禁带中引入了一条金元素贡献的杂质能带, 由于金的还原电势为$ 1.5\;{\rm{V}} $, 碳纳米管价带的第一、第二甚至第三范霍夫奇点的电子都会被注入到禁带中的杂质能带中, 如图6(c)所示, 碳纳米管的电子会被局域在金原子附近, 从而有空穴被注入到碳纳米管中, 产生p型掺杂. 这项理论计算结果从电子结构角度验证了金离子对碳纳米管具有p型掺杂作用, 为AuCl₃掺杂对碳纳米管进行阈值电压调控提供理论基础.
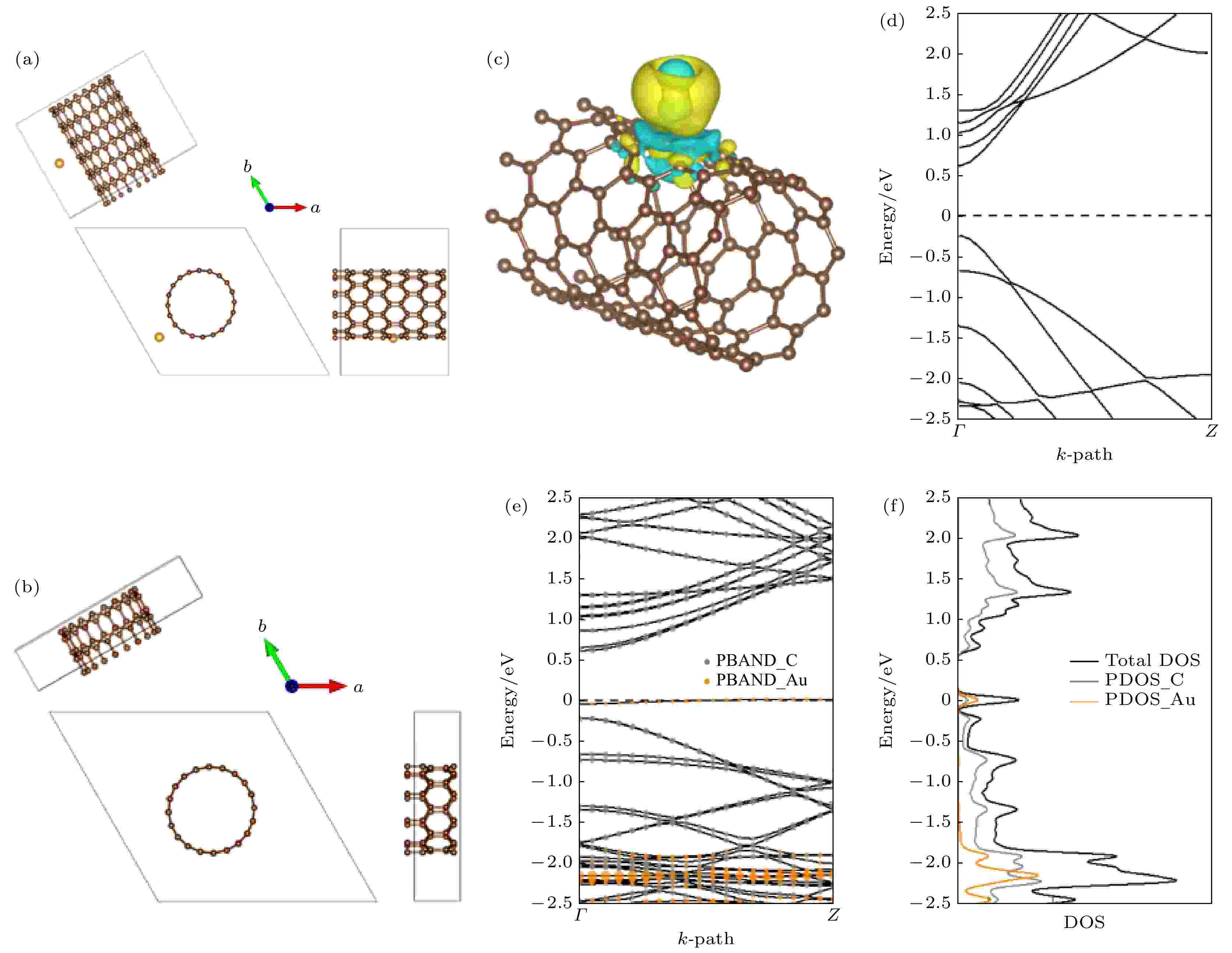图 6 　(a), (b) 碳纳米管与金/碳纳米管的晶胞结构; (c) 金/碳纳米管的二次差分密度图; (d) (10, 0)碳纳米管的能带结构图, 虚线为费米能级; (e) 金/碳纳米管系统的能带结构和投影能带, 灰色气泡为每个k点处碳元素的权重, 橙色气泡则为金元素对应的权重; (f) 金/碳纳米管系统的态密度和投影态密度, 黑色实线为总态密度, 灰色实线为投影到碳元素的态密度, 橙色实线为投影到金元素的态密度
Figure6. (a) (b) Crystal structures of CNT and Au/CNT are presented in; (c) Au/CNT difference charge density plot; (d) band structure of (10, 0) CNT, with dash line the Fermi energy; (e) band structure and projected band structure of each element, with solid line the total bands, gray bubble the projected weights of C, orange bubble the projected weights of Au; (f) total DOS and projected DOS, with black solid line the total DOS, gray solid line PDOS of C, orange solid line PDOS of Au.

本文提出了一种简单且能够大面积处理的表面掺杂方法, 通过在碳纳米管网络表面旋涂AuCl₃溶液并辅以退火处理, 利用金离子对碳纳米管的p型掺杂作用, 能够有效调控碳纳米管晶体管的阈值电压. 实验结果表明晶体管阈值电压可以通过调节AuCl₃浓度而被稳定调控. 同时在低于50 μmol/L的掺杂浓度下, 晶体管展现了极好的电学性能, 迁移率提升3倍左右. 更进一步地, 在同等掺杂条件下, 退火温度保持在50 ℃时, p型掺杂效果达到最佳. 最后通过密度泛函理论计算分析AuCl₃掺杂下碳纳米管的二次差分密度, 能带结构以及态密度, 从理论角度证明了金离子对碳纳米管具有p型掺杂作用, 为通过AuCl₃掺杂实现碳纳米管晶体管阈值电压的调控提供可行性保证. 这项通过掺杂实现阈值电压调控的研究为未来实现高性能电子器件及逻辑电路提供了一个新思路.