删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

超导动态电感单光子探测器的噪声处理

本站小编 Free考研考试/2021-12-29
摘要:噪声是影响弱信号检测器件性能指标的主要因素之一, 而最优滤波算法是白噪声背景中自适应提取弱有用信号的一种常见处理方法. 本文针对极低温环境下微波动态电感探测器(microwave kinetic inductance detector, MKID)光子弱信号响应的噪声特性, 在改进噪声模型的基础上利用最优滤波算法改进了探测信号的噪声处理. 结果表明, 经过改进噪声模型的算法处理, MKID的能量分辨(单光子探测器的主要性能指标之一)得到了15%左右的提升, 实现了0.26 eV的红外单光子能量分辨.
关键词: 最优滤波/
微波动态电感/
能量分辨/
噪声模型

English Abstract


全文HTML

--> --> -->
1.引　言
单光子探测器是光量子信息技术领域中的核心器件, 广泛应用于光量子保密通信[1]、线性量子光学计算[2]和光量子精密测量[3]等研究. 一般而言, 单光子探测器的主要性能指标包括: 光谱响应范围、死时间、暗计数率、探测效率、时间抖动、能量分辨或光子数分辨能力等[4]. 相比于目前常用的室温光电倍增管和半导体单光子探测器, 低温超导探测器在光通信波段单光子探测方面具有明显的优势, 例如: 探测器的系统效率高(可达95%以上)、暗计数率低(可以忽略不计), 响应频带宽(通过定制可实现对毫米波到伽马射线的探测[5])等. 尤其是, 目前几种主流的超导单光子探测器: 超导纳米单光子探测器(superconducting nanowire single photon detector, SNSPD)[6]、超导转边缘探测器(transition edge sensor, TES)[7]以及微波动态电感探测器(microwave kinetic inductance detector, MKID)[8]等都能以各种方式实现光子数分辨, 从而可应用于实现光场量子态非高斯操作[9]. 其中, MKID因其单元器件就具有的光子数分辨、并且结构相对简单易于实现大阵列集成而受到关注[10].
提高单光子探测器性能指标, 尤其是光子数分辨能力方面, 近年来主要关注于光敏材料的优化及其器件的制备工艺等探测器硬件本身, 包括: 寻找对单光子响应更灵敏的光敏材料、设计并制备具有快响应时间和噪声特性更好的器件及单光子响应信号读取线路等. 例如, 2008年Lita等[11]采用钨研制出的TES在1556 nm波长的探测效率达到了95%, 能量分辨达到了0.29 eV; 2013年, Lolli等[12]用Ti/Au合金制备的TES单光子探测器实现了最高可分辨29个光子, 能量分辨达到了0.113 eV. 由此, 具有较高光子数分辨水平的TES在量子光学实验中得到了推广应用. 在国内, 中国科学院上海微系统与信息技术研究所和南京大学等实现了高性能超导纳米线单光子探测器的研发和应用[13,14]; 中国科学院南京紫金山天文台等单位也实现了针对天文观测应用的TES单光子探测器[15]. 2017年, 通过和美国国家标准与技术研究院(NIST)合作, 西南交通大学课题组研发了光通信波段可分辨7个光子的光子数可分辨MKID探测器, 其能量分辨最高可达0.22 eV[16], 并实现了阵列探测器的集成[17]. 一般来说, 弱信号探测器件的性能主要取决于探测材料和器件制备工艺等硬件优化, 但与噪声背景中的信号提取也有很大关系. 本文将讨论在探测器芯片、测试线路等硬件条件一定的情况下, 如何通过探测数据中的噪声信号特性分析、建立更有效数据处理方法等, 进一步研究提高批量制备MIKD单光子探测器能量分辨的方法.
本文第2节简要介绍MKID单光子探测的工作原理、结合所测试的弱相干光脉冲特性阐明实验中数据的采集和处理方法. 将实验测量数据作为前置滤波信号, 在第3节中对噪声信号处理方法进行了改进, 针对理想化的白噪声模型和实测噪声的白化处理, 实现了噪声信号最优滤波算法处理, 将批量制备MKID单光子探测器的主要性能指标-能量分辨提升了15%左右. 第4节总结.
2.超导MKID的单光子探测原理及其能量分辨
2
2.1.实验测量系统
-->

2.1.实验测量系统

图1为实验所采用的测量系统简单示意图. 其中弱光脉冲由1550 nm激光二极管输出, 经衰减器后由光纤导入对准10 mK环境中由1/4波长超导谐振器构成的探测器芯片, 照射到探测器芯片上的光子能量拆散超导库珀对成为准粒子, 导致谐振器频率可检测的变化. 测试信号由微波信号产生器输入后一路作为本地信号, 另一路作为探测器的探测信号; 在输出端的IQ混频器实现本地信号和探测信号的混频, 经低通滤波器滤波、AD模数转换后由数据采集卡进行收集.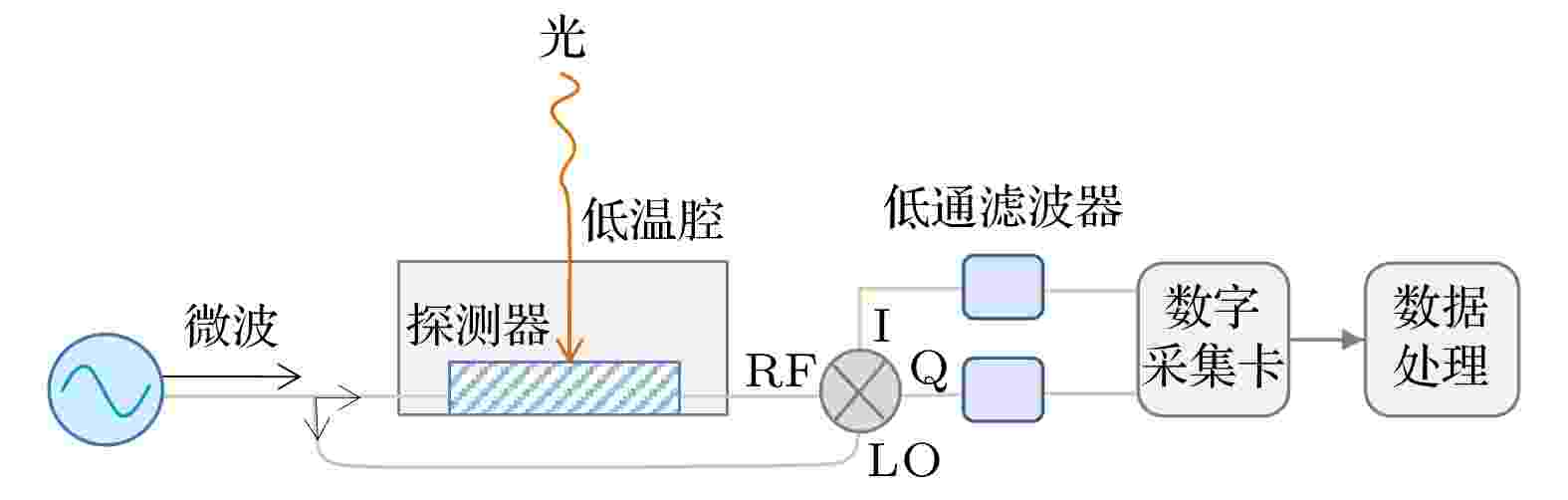
图 1 实验测量系统示意图
Figure1. Schematic diagram of the experimental system for single-photon detection.

图2为探测器的弱光信号的响应示意图. 其中, 蓝色的圆代表由频率扫描得到的无光照射时的IQ信号谐振圆; 红色箭头表示脉冲导致的信号上升沿, 该响应可以投影到沿谐振环切向的频率响应和沿谐振环法向的噪声响应; 绿色是实际测量中所得到的一个脉冲信号的整个响应. 在实际测量中信号主要沿频率方向响应且恢复至平衡点的时间更长, 因此主要对频率信号进行分析.
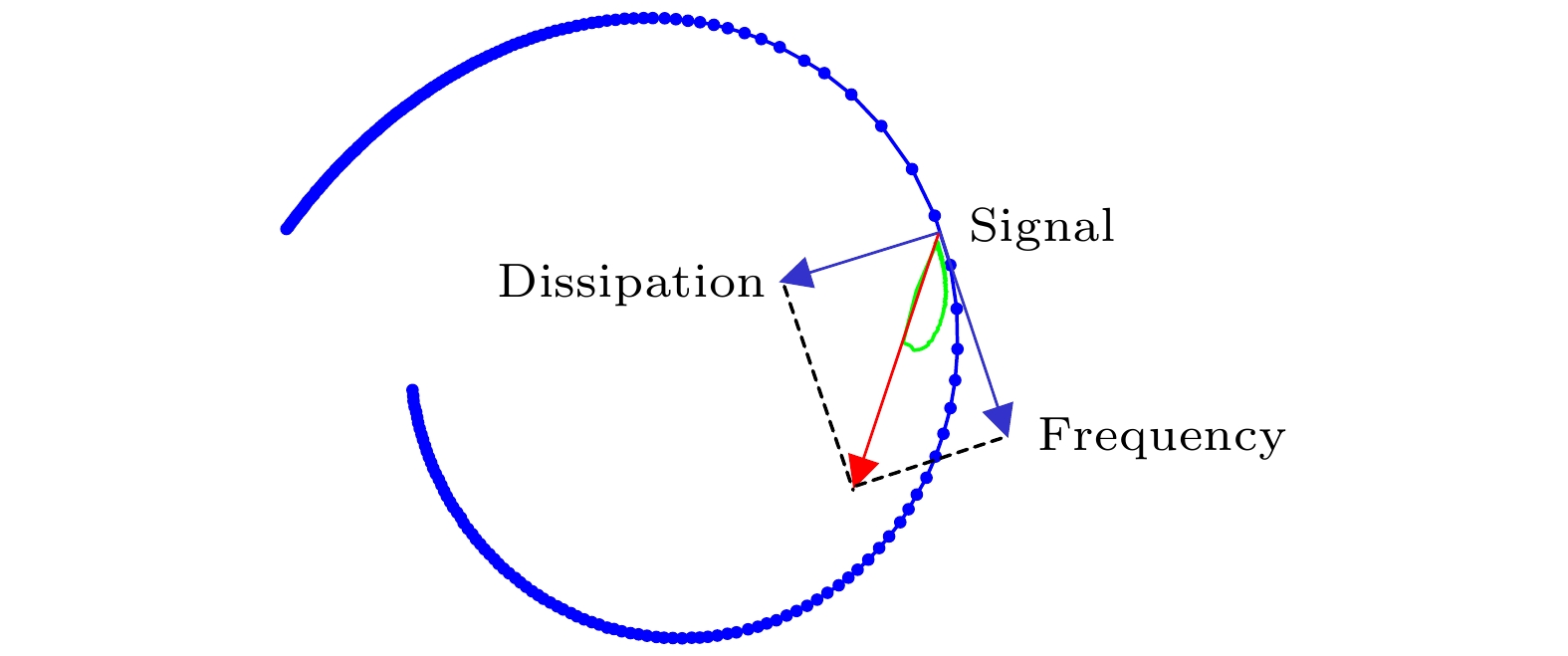图 2 复平面上的脉冲响应图
Figure2. Pulse response diagram.

图3简单表示了一个数据的采集时间操作序列. 其中, 蓝色为IQ信号输出; 红色代表200 ns宽的光脉冲; 黄色为信号产生器的120 Hz触发信号并同步至模数转换AD采集卡, 其采样率为2.5 MHz. 每次实验在触发模式下采集20000个脉冲, 并对脉冲前后各5000个(2 ms), 共10000个(4 ms)数据点进行记录分析. 在数据处理过程中, 取前5000个数据点用作噪声分析, 取2501—7500这5000个数据点进行幅值估计.
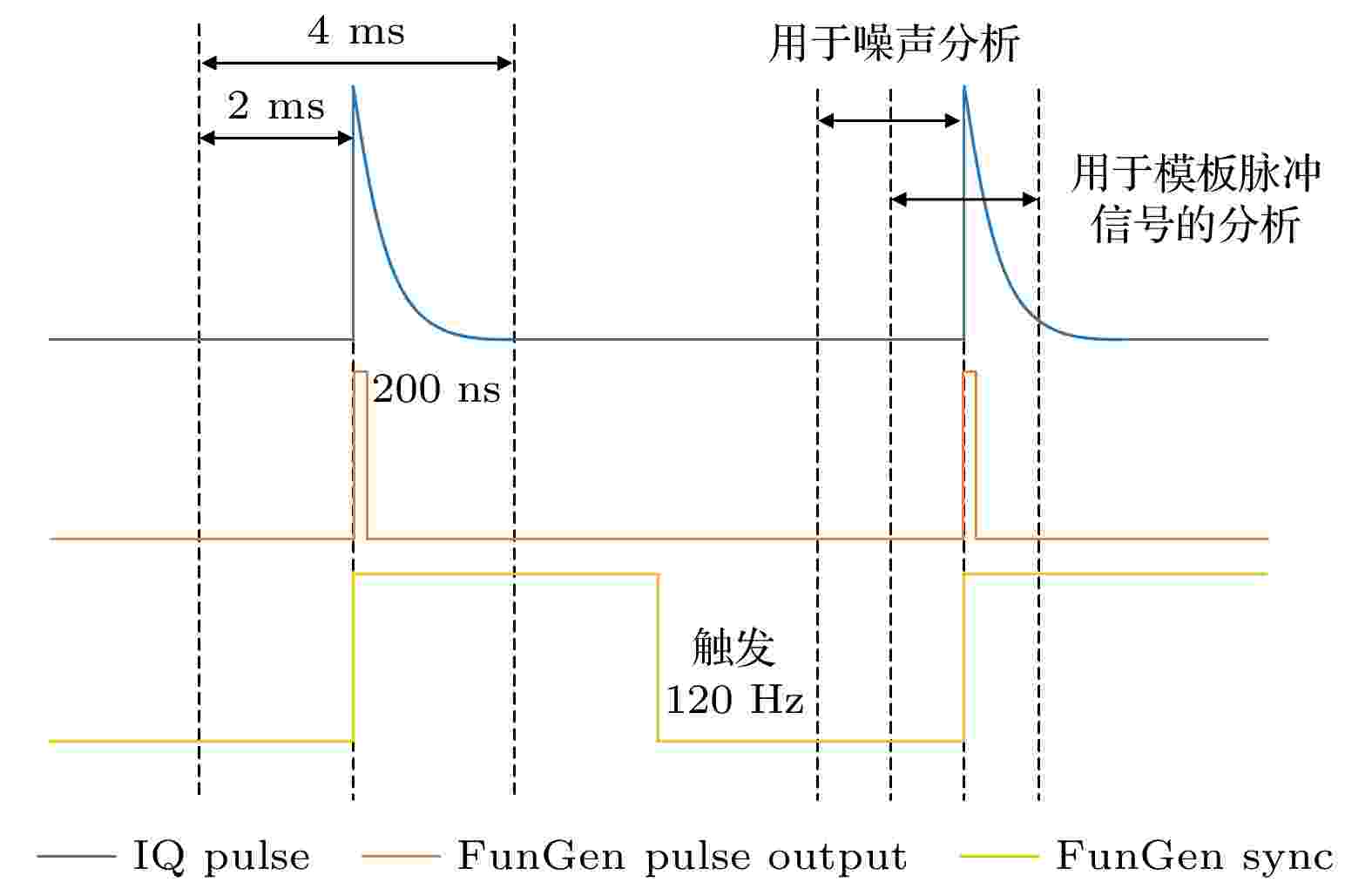图 3 触发模式记录时间序列信号的示意图
Figure3. Schematic diagram of the signal triggers and records in time domain.

2
2.2.MKID探测器的光子探测数据处理
-->

2.2.MKID探测器的光子探测数据处理

MKID探测数据的处理实际上是一个噪声信号与模板匹配的最优滤波过程[18,19]. 这里模板匹配指的是利用计算机计算探测器信号输出与模板信号之间的互相关程度. 模板信号的最简单提取方法就是多次脉冲信号取平均得到:
$s\left(t\right)=\frac{1}{n}\sum\limits _{k=1}^{n}{v}_{k}\left(t\right),$
其中, $ s\left(t\right) $代表平均求得的模板函数, $ n $代表总的脉冲信号次数, $ {v}_{k}\left(t\right) $是第$ k $次单脉冲的幅值函数.
对系统实测噪声的特性进行了分析, 如图4所示, 可以发现在极低温环境下, 系统的实测噪声比较接近于白噪声, 其自相关函数比较接近于冲激函数, 功率谱密度函数虽然在一个常数周围波动, 但不够平滑. 这必定会导致平均得到的模板函数与真实的脉冲相似波形存在误差. 尝试用此噪声模型进行滤波处理. 最优滤波算法中最优幅值倍数表达式为[20]
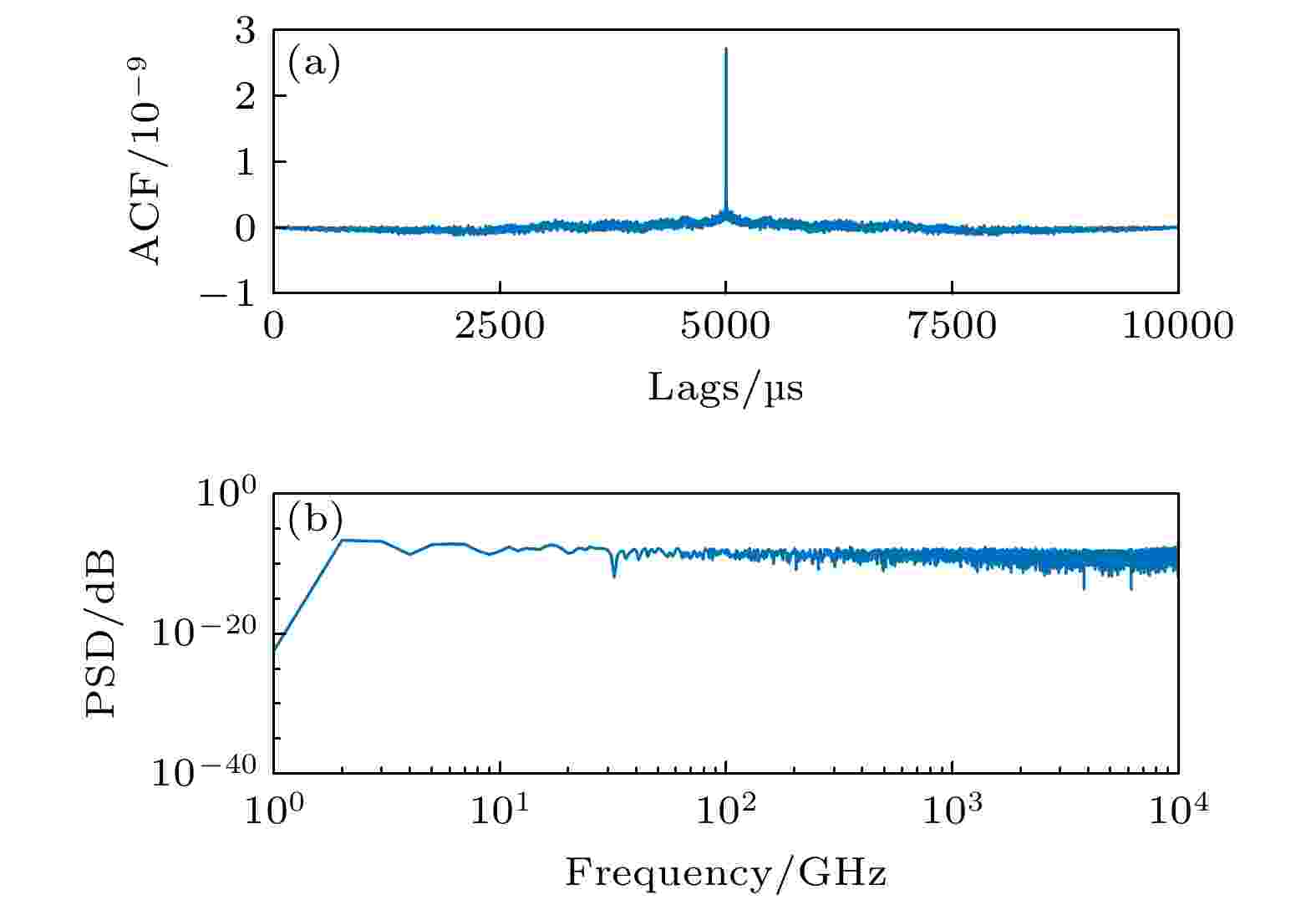图 4 实验测量的探测器噪声　(a)自相关函数; (b)功率谱密度$ J\left(f\right) $
Figure4. Autocorrelation function (a) and power spectral density(b) of detector noise measured experimentally.

$A=\frac{\displaystyle \int _{-\infty }^{+\infty }\mathrm{d}f\cdot \frac{V\left(f\right)\cdot {\tilde {S}}^{*}\left(f\right)}{J\left(f\right)}}{\displaystyle \int _{-\infty }^{+\infty }\mathrm{d}f\cdot \frac{{\big|\tilde {S}(f)\big|}^{2}}{J\left(f\right)}},$
式中$ , A $是单次脉冲和模板匹配的最优幅值倍数, $ V\left(f\right) $代表单次脉冲幅值函数的傅氏变换, $ \tilde {S}\left(f\right) $是模板函数的傅氏变换, 而$ J\left(f\right) $是实验测量得到的噪声功率谱密度. 探测器性能的标定是通过统计所有脉冲的最优幅值倍数$ A $的分布来实现的.
实验中的模板信号是对弱光脉冲照射下谐振频率为6.44 GHz的MKID探测器所探测到的20000次采样信号进行平均而得到的. 利用矩阵分析软件实现了最优滤波算法, 得到图5所示的两组MKID探测器光脉冲响应信号的幅值倍数统计分布及高斯拟合结果. 这里, 高斯拟合的表达式为
$f\left(x\right)=\sum _{n=1}^{N}{a}_{n}\frac{1}{\sqrt{2\mathrm{\pi }}{\sigma }_{n}}{\mathrm{e}}^{-\tfrac{{\left(x-{u}_{n}\right)}^{2}}{2{{\sigma }_{n}^{2}}}},$
其中, $ {a}_{n} $表示第$ n $个高斯峰的幅度, $ {u}_{n} $表示第$ n $个高斯峰的中心点, ${{\sigma }}_{n}^{2}$表示第$ n $个高斯峰分布的方差. 图5中, 蓝色手指峰部分为多次脉冲幅值倍数统计图, 红色曲线为高斯相加拟合的图像.
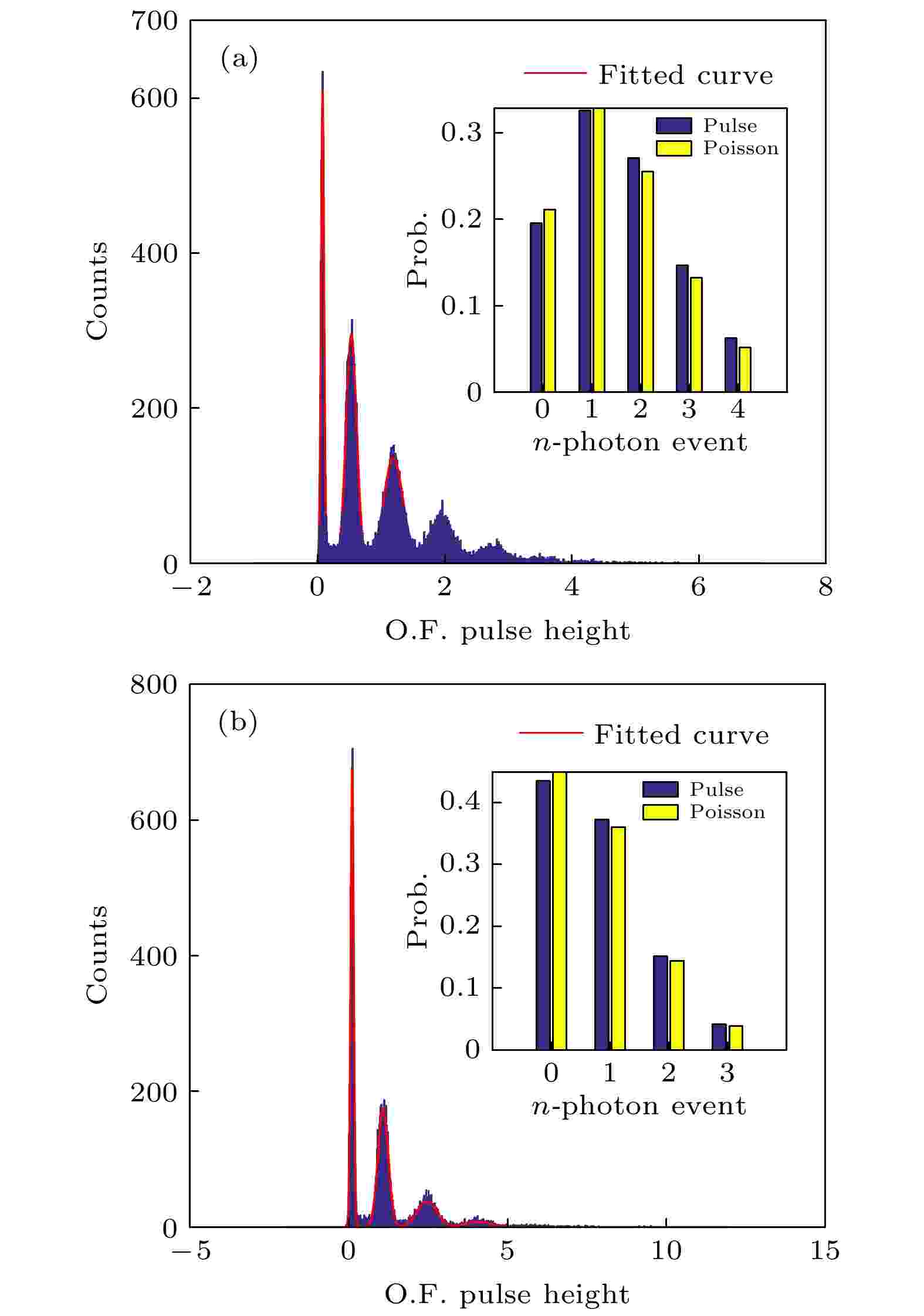图 5 光学衰减17 dB (a)和20 dB (b)下脉冲信号幅值统计的高斯拟合结果
Figure5. Gaussian fitting results of pulse signal amplitudes under optical attenuation of 17 dB (a) and 20 dB (b), respectively, for the experimental noises.

2
2.3.弱光脉冲的特性分析
-->

2.3.弱光脉冲的特性分析

实验中到达探测器芯片上的是一种通过强衰减所获得的相干光, 它并不是严格的单光子源, 而是一种平均光子数很少的弱相干光源: 每次脉冲所包含的光子数是以平均光子数为均值的一种泊松分布[21]. 因此, 在探测器端所探测到的信号也应该是某种对应的泊松分布. 实际上, 在短时间$ \mathrm{d}t $内, 得到光子计数的概率是: $ \Delta P\left(t\right)=\alpha \cdot I\left(t\right)\cdot \mathrm{d}t $, 其中, $ \alpha $代表探测器的灵敏度, 它取决于探测面积和入射光的光谱范围; $ I\left(t\right) $代表在某一时间光的辐射强度; 那么在这段时间内, 没有探测到光子的概率就是: $ 1-\Delta P\left(t\right) $. 由于在不同时间间隔内光子计数是独立的, 所以在时间间隔$ {t}_{0} $至$ {t}_{0}+T $ 内不发生光子计数事件的联合概率可用乘积表示为:
$\begin{split}\prod _{{t}_{0}}^{{t}_{0}+T}[1-\Delta P\left(t\right)]\approx\;& \prod _{{t}_{0}}^{{t}_{0}+T}{\mathrm{e}}^{-\Delta P\left(t\right)}={\mathrm{e}}^{-\sum _{{t}_{0}}^{{t}_{0}+T}\Delta P\left(t\right)}\;\;\;\\=\;&{\mathrm{e}}^{- \int _{{t}_{0}}^{{t}_{0}+T}\mathrm{d}P\left(t\right)}.\end{split}$
所以, 在$ {t}_{0} $至$ {t}_{0}+T $内探测到零光子的概率就是: $ {P}_{0}={\mathrm{e}}^{-\int _{{t}_{0}}^{{t}_{0}+T}\alpha I\left(t\right)\mathrm{d}t} $. 相应地, 在$ {t}_{0} $至$ {t}_{0}+T $内发生1个光子计数的概率是:
$ {P}_{1}= \left[\alpha \int _{{t}_{0}}^{{t}_{0}+T}I\left(t\right)\mathrm{d}t\right]{\cdot \mathrm{e}}^{-\alpha \int _{{t}_{0}}^{{t}_{0}+T}I\left(t\right)\mathrm{d}t}.\qquad\qquad\quad$
类似地, 这段时间内探测到2个光子的概率可表示为:
$\begin{split}{P}_{2}=\;&\left[\alpha \int _{{t}_{0}}^{{t}_{0}+T}\times I\left(t\right)\mathrm{d}t\right]\bigg/{2}\\&\times \left[\alpha \int _{{t}_{0}}^{{t}_{0}+T}I\left(t\right)\mathrm{d}t\right]\cdot {\mathrm{e}}^{-\alpha \int _{{t}_{0}}^{{t}_{0}+T}I\left(t\right)\mathrm{d}t}, \end{split}$
以此类推, 获得$ n $个光子计数的概率是:
$ {P}_{n}=\left[\alpha \int _{{t}_{0}}^{{t}_{0}+T}\times I\left(t\right)\mathrm{d}t\right]\bigg/{n!}^{n}\cdot {\mathrm{e}}^{-\alpha \int _{{t}_{0}}^{{t}_{0}+T}I\left(t\right)\mathrm{d}t},$
所以, 对恒定辐射强度的光弱相干光, 探测到的$ n $光子数事件的分布就是: ${P}_{n}={\dfrac{ \left\langle { \bar{n} } \right\rangle }{n!}}^{n}{\mathrm{e}}^{- \left\langle { \bar{n} } \right\rangle }$, 其中$\langle { \bar{n} } \rangle =\alpha IT$代表平均光子数, 这正是一种泊松分布.
将图5所示弱相干光的光子数标准泊松分布(黄色直方图)与实验数据拟合的高斯分布面积分布图(蓝色直方图)进行比较, 可以看出实测的弱光脉冲信号中的光子数分布与上述理论分析预期的标准泊松分布基本一致, 这说明照射到MKID探测器芯片上的光脉冲确实是一种弱相干信号. 图5中两组数据分别是探测器对光源衰减17 dB和衰减20 dB探测所得到的平均光子数分别为$\mu = $$ 1.55$和$ \mu =0.80 $的弱相干光信号响应.
2
2.4.MKID单光子探测器的能量分辨
-->

2.4.MKID单光子探测器的能量分辨

单光子探测器的一个重要性能指标是其光子数可分辨性. 由于探测器信号存在噪声, 所以每个光子数峰都不是严格的$ \mathrm{\delta } $函数而是近似的高斯峰. 由此, 把每个峰的半宽高值(full-width at half maximum, FWHM)定义为该光子数信号的探测器能量分辨[22], 例如$: $
$\Delta {E}_{0}= 2\sqrt{2\cdot \mathrm{l}\mathrm{n}2}\frac{{\sigma }_{0}}{{A}_{1}-{A}_{0}}\cdot hv,$
$\Delta {E}_{n}= 2\sqrt{2\cdot \mathrm{l}\mathrm{n}2}\frac{{\sigma }_{n}}{{A}_{n}-{A}_{n-1}}\cdot hv,~~ n=\mathrm{1,2},3,\cdots,$
分别为无光子探测事件和第$ n $个光子数峰的能量分辨. 其中, $ {\sigma }_{n} $为第$ n $光子数峰高斯拟合后的标准差, $ {A}_{n} $为第$ n $光子峰对应归一化脉冲的高度(高斯峰的均值), $ hv $为单光子能量. 可见, $ \Delta {E}_{n} $越小能量分辨率越高. 显然, 如果第$ n $个光子数峰的能量分辨满足条件$ \Delta {E}_{n}/\left(h\nu \right) < 1 $, 则称该光子数是可分辨的, 即它与$ (n-1) $光子数峰和$ (n+1) $光子数峰是可区分. 要实现1550 nm波段光信号的光子数可分辨探测, 要求探测器的能量分辨需小于$ hv=0.8\;\mathrm{e}\mathrm{V} $. 表1给出了图5中所示的探测器对两个弱相干光源探测所实现的少光子数峰的能量分辨. 可见, MKID单光子探测器是可以实现光子数分布的, 虽然少光子数峰的能量分辨仍有一定的改进空间.
能量分辨$ \Delta E_{{0}}{/{\rm{eV}}} $$ \Delta E_{{1}}{/{\rm{eV}}} $$ \Delta E_{2}{/{\rm{eV}}} $$ \Delta E_{3}{/{\rm{eV}}} $$ \Delta E_{4}{/{\rm{eV}}} $
衰减17 dB
的信号		0.10150.35260.43600.46910.6140
衰减20 dB
的信号		0.09550.32000.41990.4758—


表1光学衰减17 dB和20 dB下探测器的能量分辨
Table1.Energy resolution of detector under optical attenuation of 17 dB and 20 dB.

3.基于噪声模型改进的最优滤波算法提升探测器的能量分辨
最优滤波算法中的模板信号通常是通过对多次信号取平均的方式来获得的, 这实际上默认了背景噪声是一种均值可以抵消的随机分布, 即白噪声. 在以上所采用的噪声滤波算法, 即(2)式中, 噪声功率谱密度$ J\left(f\right) $取自实测的噪声数据, 但建立匹配模板时又简单地取为白噪声. 而由图4可见实测噪声并非严格的白噪声, 因而所通常所采用的最优滤波算法与实际的噪声特性实际上存在一定的失配现象. 解决这一问题的简单途径有两个: 要么根据实测的器件噪声特性, 采用大数据机器学习方法寻找更佳的模板信号[23]; 要么对实测噪声信号进行近似处理, 使之尽可能接近白噪声分布. 下面我们采用第二种途径来优化探测器的噪声处理, 其流程如图6所示.
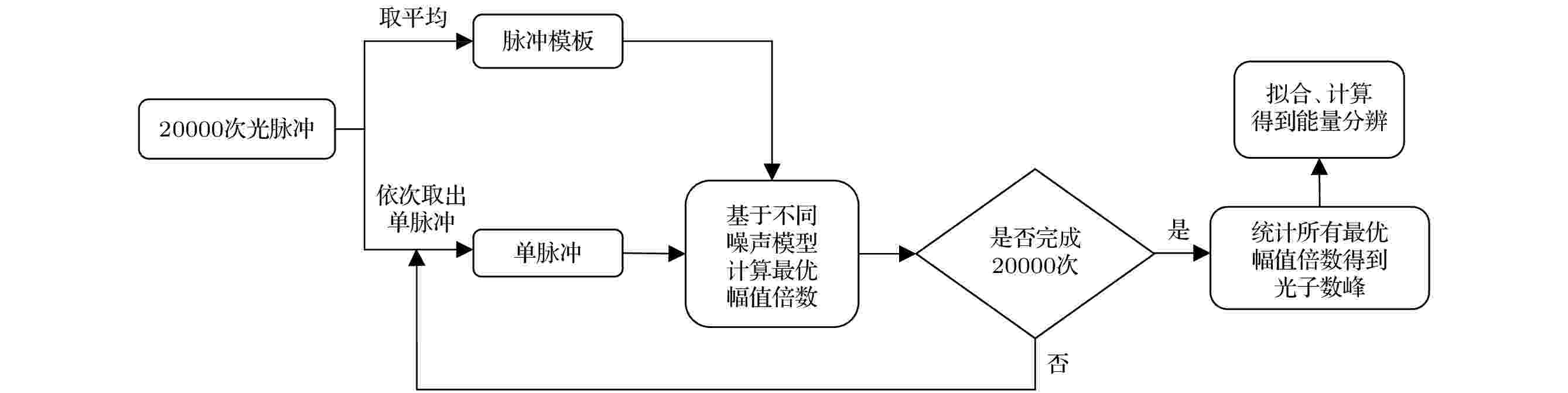图 6 信号处理的流程框图
Figure6. Flow diagram of the signal processing.

2
3.1.白噪声模型
-->

3.1.白噪声模型

从图4所示的实测噪声功率谱密度分布特性中, 我们看到探测器的噪声非常接近于白噪声, 所以我们首先对实测的噪声信号进行高斯白噪声拟合, 如图7所示. 对此拟合拟合的噪声模型, 通常的模板分析方法无疑是最佳的, 从而公式(2)可简化为
图 7 探测器噪声(点集)及其高斯分布函数拟合(红实线)
Figure7. Detector noise (point set) and Gaussian distribution function fitting (red solid line).

${A}'=\frac{\displaystyle\int _{-\infty }^{+\infty }\mathrm{d}f\cdot V\left(f\right)\cdot {\tilde {S}}^{*}\left(f\right)}{\displaystyle\int _{-\infty }^{+\infty }\mathrm{d}f\cdot {\left|\tilde {S}\left(f\right)\right|}^{2}} .$
这表明, 在白噪声情况下最优滤波算法本质上是一个利用最小二乘法进行最小方差拟合的过程. 这时, 最优幅值倍数$ \tilde {A} $可计算为未知脉冲和模板脉冲的互相关函数除以模板脉冲的自相关函数, 或者简单地说等于未知脉冲向量除以模板脉冲向量. 由此, 模板获取的方式大为简便, 从而极大减少算法的运算量. 图8给出了基于白噪声模型、光学衰减17 dB和20 dB下弱相关光脉冲响应的光子数峰及其高斯拟合结果. 对比于之前图5所示的数据处理结果, 光子数峰的分辨能力有所提升. 基于此拟合结果, 应用(4)式和(5)式可计算出相应的能量分辨, 如表2和表3所示.
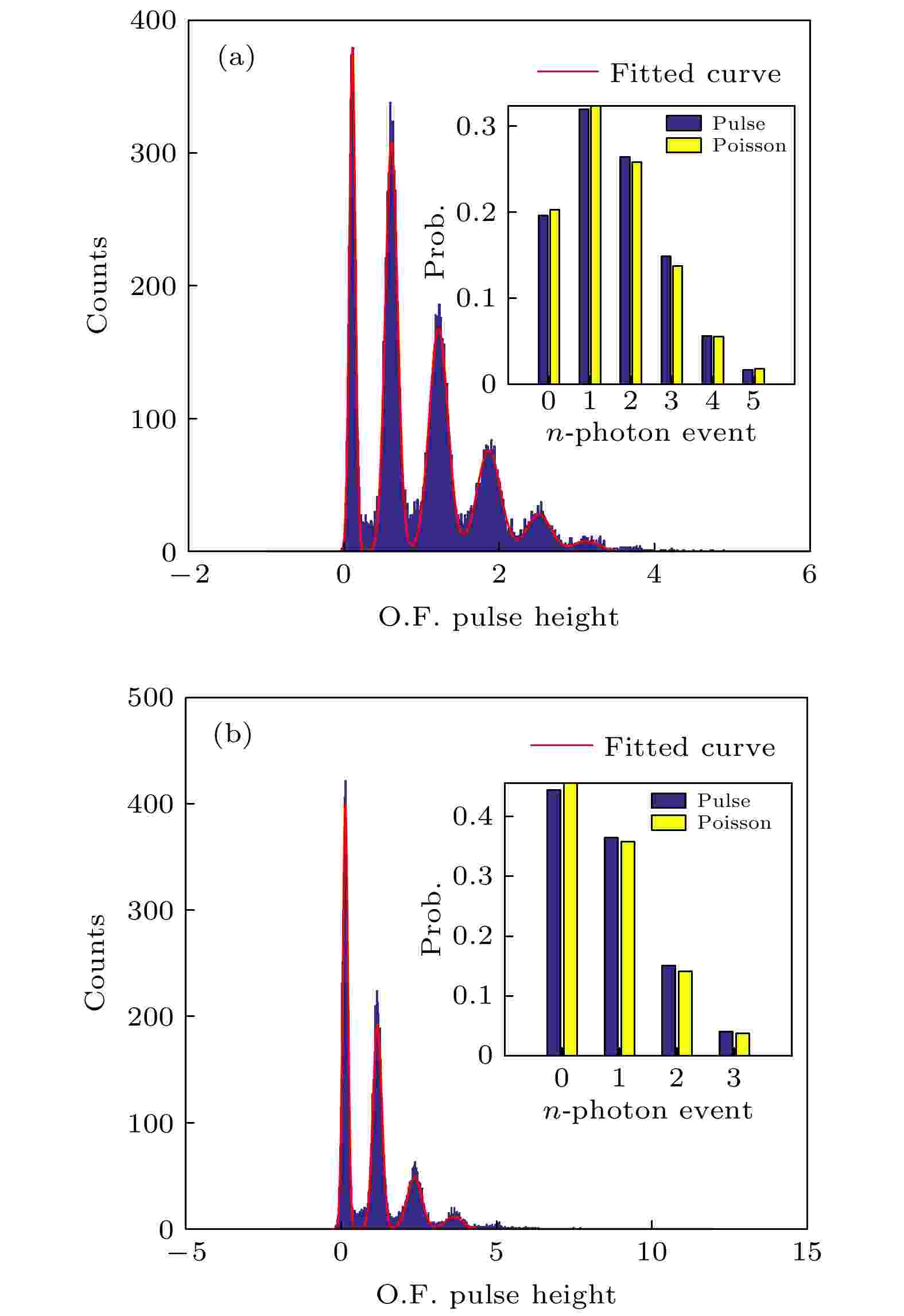图 8 采用白噪声模型后, 光学衰减17 dB (a)和20 dB (b)下的脉冲幅值统计分布以及拟合图像
Figure8. Gaussian fitting results of pulse signal amplitudes under optical attenuation of 17 dB (a) and 20 dB (b), respectively, for the ideal white noises.

能量分辨$ \Delta E_{{0}}{/{\rm{eV}}} $$ \Delta E_{{1}}{/{\rm{eV}}} $$ \Delta E_{2}{/{\rm{eV}}} $$ \Delta E_{3}{/{\rm{eV}}} $$ \Delta E_{4}{/{\rm{eV}}} $$ \Delta E_{5}{/{\rm{eV}}} $
实测噪声0.10150.35260.43600.46910.6140—
白噪声模型0.14890.29920.37720.43820.44480.5113
提高–31.83%+17.85%+15.59%+7.05%+38.04%—


表2光学衰减17 dB下使用实测噪声和白噪声模型处理后探测器能量分辨对比
Table2.Comparison of detector energy resolutions after processing with measured noise and white noise model under optical attenuation of 17 dB.

从表2和表3对比可以看出, 除了零光子峰外的其他光子峰的能量分辨都有所提高, 最高提高效率达到了38%. 而且, 从表2第2行数据可以看到, 对噪声模型的修改数据处理后, 可以分辨原来不能分辨的5光子峰响应. 尤其是, 从表3可以看到, 探测器的单光子能量分辨达到0.265 eV, 比之前的数据处理结果(0.32 eV)提高了17%左右.
能量分辨$ \Delta E_{{0}}{/{\rm{eV}}} $$ \Delta E_{{1}}{/{\rm{eV}}} $$ \Delta E_{2}{/{\rm{eV}}} $$ \Delta E_{3}{/{\rm{eV}}} $
实测噪声0.09550.32000.41990.4758
白噪声模型0.15530.26500.37480.4032
提高/%–62.61+17.19+10.74+15.26


表3光学衰减20 dB下使用实测噪声和白噪声模型处理后探测器能量分辨对比
Table3.Comparison of detector energy resolutions after processing with measured noise and white noise model under optical attenuation of 20 dB.

2
3.2.噪声白化模型
-->

3.2.噪声白化模型

现实情况下严格的白噪声是不存在的, 所以以上采用白噪声模型来实现最优滤波算法的数据处理过于理想化. 为此, 对实测噪声特性进行白化处理[24], 使之尽量接近最优滤波算法中约定的白噪声模型. 实测噪声的白化处理主要步骤是: 首先, 对噪声数组求自相关得到噪声的自相关函数$ {R}_{xx} $; 然后, 再对$ {R}_{xx} $进行toeplitz变换得到噪声的协方差矩阵$ {R} $; 其次, 将得到的矩阵进行Cholesky分解得到下三角矩阵$ {{{L}}} $; 最后, 将下三角矩阵求逆矩阵便可得到白化后噪声的自相关矩阵$ {{{W}}}={{L}}^{{-1}} $. 图9为实测噪声白化后的特性.
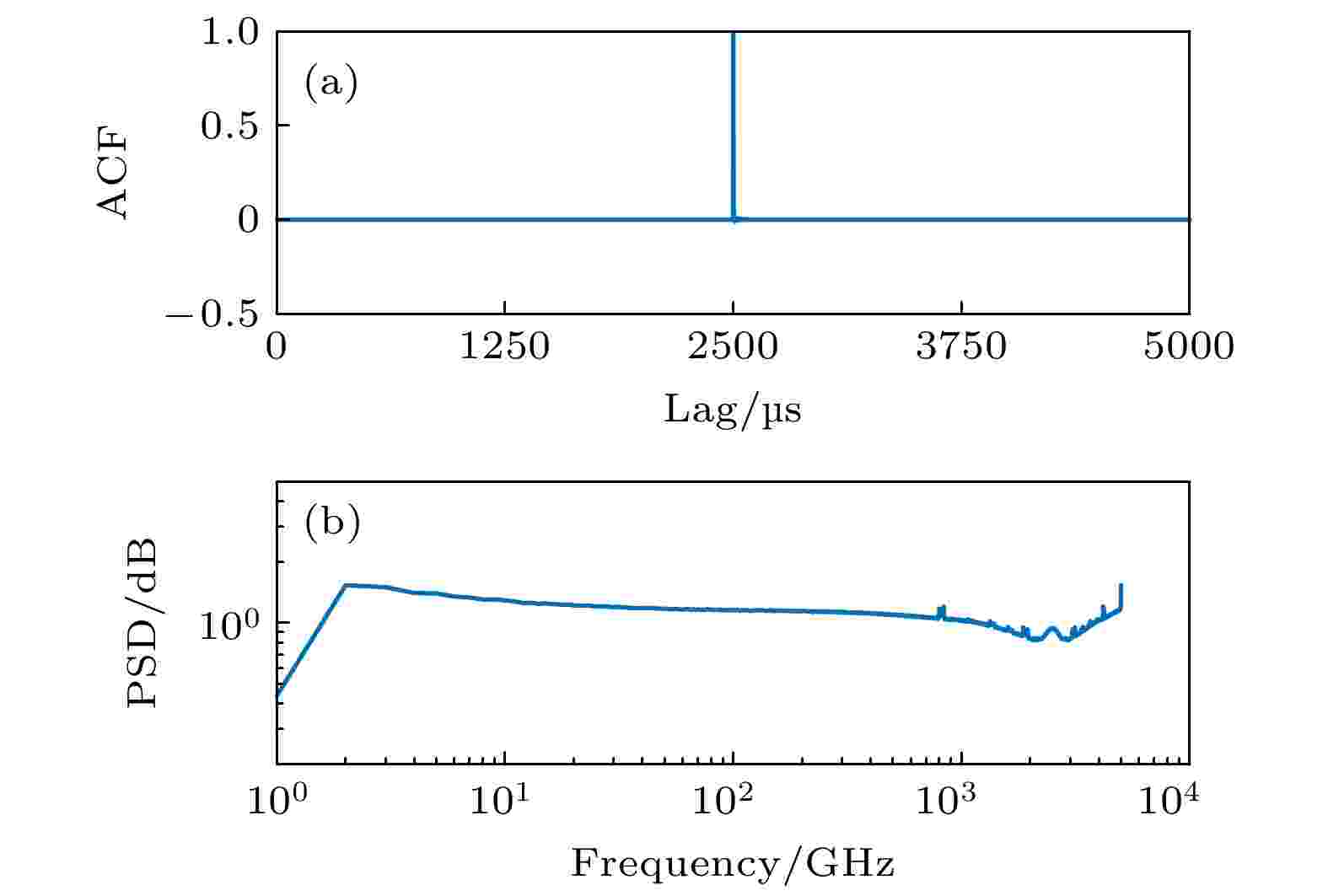图 9 白化后的探测器噪声　(a)自相关函数; (b)功率谱密度$ J{'}\left(f\right) $
Figure9. Autocorrelation function (a) and Power spectral density (b) of the whitened noise.

可以看出, 白化后的噪声相比于之前系统的实测噪声更加接近白噪. 因此, 相比于图4, 图9的自相关函数更接近于冲激函数, 并且功率谱密度函数更平滑. 将得到的白化后的噪声用于最优滤波幅值估计, 可得最优幅值倍数的矩阵形式[25]:
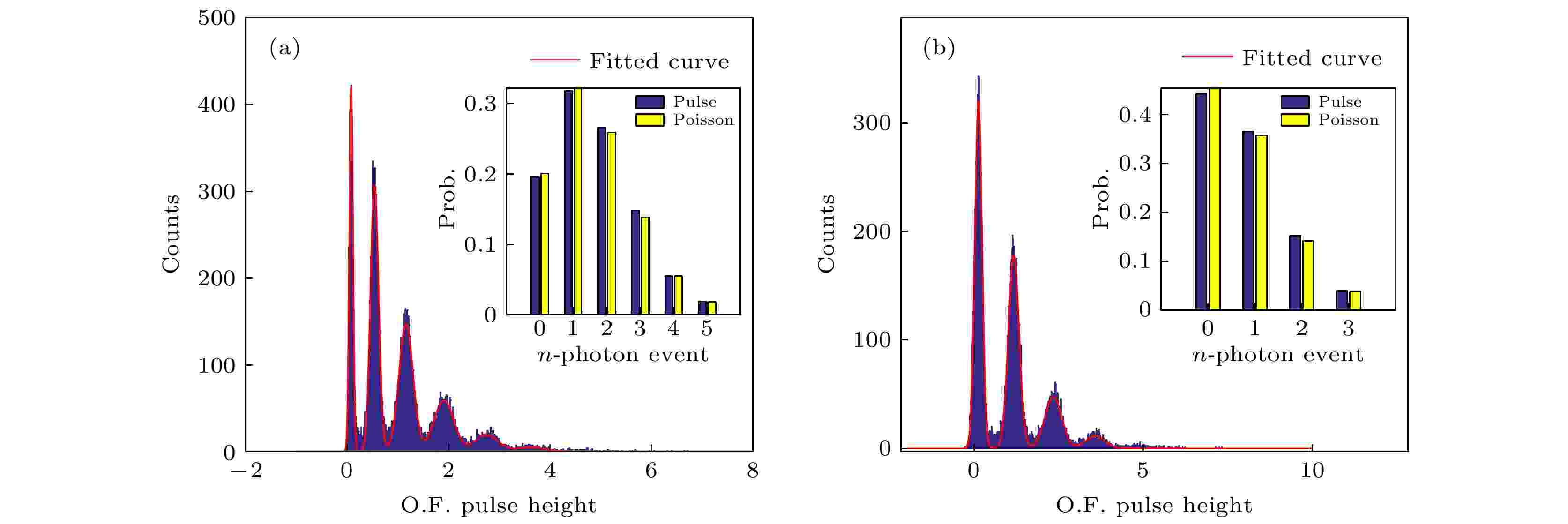${{A}}''=\frac{{{{{S}}}}^{\mathrm{T}}\cdot {{{{W}}}}^{-1}\cdot {{{d}}}}{{{{{S}}}}^{\mathrm{T}}\cdot {{{{W}}}}^{-1}\cdot {{{S}}}} ,$
其中S代表脉冲模板向量, d代表未知脉冲向量, W是白化后噪声自相关矩阵. 图10给出了白化噪声后的弱相干光脉冲的探测器光子数响应峰值拟合分布. 由此, 可计算出各光子数峰的能量分辨, 如表4和表5所示.
图 10 噪声白化后, 光学衰减17 dB (a)和20 dB (b)下探测器的光子数响应拟合
Figure10. Gaussian fitting results of pulse signal amplitudes under optical attenuation of 17 dB (a) and 20 dB (b), respectively, for the whitened noises.

能量分辨$ \Delta {{E}}_{{0}}{/{\rm{eV}}} $$ \Delta {{E}}_{{1}}{/{\rm{eV}}} $$ \Delta {{E}}_{2}{/{\rm{eV}}} $$ \Delta {{E}}_{3}{/{\rm{eV}}} $$ \Delta {{E}}_{4}{/{\rm{eV}}} $$ \Delta {{E}}_{5}{/{\rm{eV}}} $
实测噪声0.10150.35260.43600.46910.6140—
噪声白化0.14690.32740.42630.48970.50090.6216
提高/%–44.73+7.15+2.22–4.39+18.42—


表4光学衰减17 dB下实测噪声和噪声白化后处理得到的探测器能量分辨对比
Table4.Comparison of energy resolutions for the experimental noises and the whitening ones, where the optical pulse is attenuated 17 dB.

能量分辨$ \Delta {{E}}_{{0}}{/{\rm{eV}}} $$ \Delta {{E}}_{{1}}{/{\rm{eV}}} $$ \Delta {{E}}_{2}{/{\rm{eV}}} $$ \Delta {{E}}_{3}{/{\rm{eV}}} $
实测噪声0.09550.32000.41990.4758
噪声白化0.19320.28550.396490.4196
提高/%–100.02+10.78+5.60+11.81


表5光学衰减20 dB下实测噪声和噪声白化后处理得到的探测器能量分辨对比
Table5.Comparison of energy resolutions for the experimental noises and the whitening ones, where the optical pulse is attenuated 20 dB.

从表5可以看出, 通过噪声白化手段处理后, 相比于实测噪声的最优滤波处理, 能量分辨在除0光子峰之外的其他光子也峰略有提高, 但并不比直接使用白噪声模型处理的结果明显. 最后, 为比较方便起见, 表6给出了对光学衰减20 dB的弱相干光, 采用3种噪声模型处理所得到的探测器对1, 2, 和3光子数峰的能量分辨对比.
能量分辨$ \Delta {{E}}_{1}{/{\rm{eV}}} $$ \Delta {{E}}_{{2}}{/{\rm{eV}}} $$ \Delta {{E}}_{3}{/{\rm{eV}}} $
实测噪声0.32000.41990.4758
白噪声模型0.2650
(+17.19%)		0.3748
(+10.74%)		0.4032
(+15.26%)
噪声白化0.2855
(+10.78%)		0.39649
(+5.60%)		0.4196
(+11.81%)


表6光学衰减20 dB下原始滤波和改进噪声模型后探测器能量分辨对比(括号中是改进后相对于实测噪声处理所得到的能量分辨的提高百分比)
Table6.Comparison of energy resolutions of the detector for the experimental noise, white noise and withened noise, respectively. The improvemence is relative to the those for the experimental noise. Here, the optical pulse is attenuated 20 dB.

需要说明的是, 两种改进方法相比于之前使用实测噪声进行最优滤波处理所得的结果都有所提高. 这说明, 基于白噪声模型的最优滤波算法在探测器响应实验数据处理方面, 基本是可行的. 虽然实际噪声并不是白噪声, 但通过噪声白化处理后仍可利用最优滤波算法进行数据处理.
4.结　论
针对极低温环境下MKID弱信号响应的噪声特性, 在分析其影响探测器主要性能指标之一的能量分辨的基础上, 提出了基于噪声模型改进的最优滤波算法, 实现光子数探测的能量分辨数据拟合. 考虑到最优滤波算法与实测有色噪声的失配性, 首先采用理想化的白噪声模型对噪声数据进行了滤波分析及拟合, 实现了探测器能量分辨和光子数分辨性能的提升. 鉴于白噪声模型过于理想, 对实测噪声进行了白化处理, 并对数据进行滤波分析及拟合, 得到了与采用白噪声模型基本相当的结果. 相比于之前未对实测噪声做任何处理而强行匹配白噪声模板的滤波方案, 噪声改进后的两种最优滤波算法可将探测器的单光子能量分辨最高提高了17%左右、整体光子数峰的能量分辨提升15%左右, 相应地也提高了探测器的光子数分辨能力, 实现了之前未能分辨的四光子数峰响应的分辨.
本文工作是在噪声模型近似处理基础上利用最优滤波算法进行探测器噪声信号的处理. 由于最优滤波算法中模板的提取是以白噪声模型为基础的, 所以对实测噪声做白化处理是为了发挥最优滤波算法中模板提取相对容易的优势. 在以后的工作中, 有必要针对实测噪声(一般是有色噪声)利用大数据机器学习的方法来提取与实测噪声特性更为符合的脉冲模板, 再进行噪声滤波, 从而有望在数据处理环节进一步实现MIKD单光子探测器各种性能指标的提升.
感谢美国国家标准与技术研究院(NIST)高湔松博士的讨论和帮助.
相关话题/光子 信号 数据 实验 光学
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于剪切模量和热分析数据研究Zr<sub>50–</sub><i><sub>x</sub></i>Cu<sub>34
    摘要:非晶合金具有独特物理和力学性能,如何建立非晶合金微观结构非均匀性与物理/力学性能之间的关联是非晶固体的重要研究课题之一.微合金化是调控非晶合金微观结构有效手段之一.本研究以玻璃形成能力优异的Zr50–xCu34Ag8Al8Pdx(x=0,2)非晶合金为模型合金,借助差示扫描量热仪和电磁声转换设 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • L型步行通道内行人转弯行为的实验分析与仿真
    摘要:以L型步行通道内的单向行人流为研究对象,基于可控实验与微观仿真研究行人转弯行为.首先,构建转弯区无障碍物、障碍物沿转弯区对角线布局、以及障碍物垂直转弯区对角线布局三种实验场景,通过行人可控实验分析行人移动轨迹、速度分布等行为特征;然后,基于L型通道内的行人微观行为,改进基于Voronoi图的速 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 甚低频台站信号对地球内辐射带和槽区能量电子的散射效应分析
    摘要:人工地面甚低频台站发射的10—30kHz信号主要在地球—低电离层波导传播,部分能量会泄露进入内磁层,进而会影响近地空间中高能电子的动态变化过程.本文详细研究了NWC,NAA和DHO38三个人工甚低频台站信号对内辐射带和槽区高能电子的散射作用.基于准线性理论,分别计算了三个甚低频台站信号单独和共 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维冰相I的电子和光学性质
    摘要:二维冰是典型的原子制造技术获得的新型原子级材料,其结构和成核生长在材料科学、摩擦学、生物学、大气科学和行星科学等众多领域具有至关重要的作用.虽然二维冰的结构性质已被广泛研究,但对其电学和光学性质知之甚少.本文通过密度泛函理论和线性响应理论计算了二维冰相I在零温时的主要电学、光学、介电性质和红外 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于光学频率梳的超低噪声微波频率产生
    摘要:低噪声的微波频率在雷达,长基线干涉仪等领域有重要应用.基于光学频率梳产生的微波信号的相位噪声在1Hz频偏处低于–100dBc/Hz,在高频(>100kHz)处低于–170dBc/Hz,是目前所有的微波频率产生技术中噪声最低的.文章介绍了光学频率梳产生微波频率的基本原理,对基于光梳产生的微波频率 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高超声速三角翼上横流不稳定性的实验研究
    摘要:本文研究了三角翼迎风面边界层中的非定常横流不稳定性.实验在马赫6低噪声风洞中进行,模型为平板构型,攻角为5°和10°.通过温敏漆技术,观察到在远离头部的区域,边界层转捩阵面光滑且平行于前缘,通过Kulite高频脉动压力传感器得到的功率谱密度曲线中有明显的f≈10kHz的扰动波信号峰值.利用基于 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 液态金属软表面池沸腾传热的实验研究
    摘要:池沸腾是一种高效的传热方式,目前主要通过刚性固体表面改性强化沸腾传热.本文以乙醇为工质,实验研究了光滑铜表面和液态金属软表面池沸腾传热.发现液态金属软表面可有效降低沸腾起始点(ONB)壁面过热度,饱和沸腾时,ONB壁面过热度从光滑铜表面的约18℃降低到软表面的约6℃,沸腾传热系数最大提高了14 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 亚米级光学卫星影像邻近效应校正
    摘要:邻近效应是指卫星成像过程中目标物周围自然环境反射的太阳辐射对卫星入瞳处目标像元辐亮度的贡献.它会导致卫星图像清晰度、对比度和信息熵值降低,并且导致表观反射率卫星影像中目标像元反射率介于其真实反射率和背景像元平均反射率之间,严重影响定量遥感精度.背景各像元对邻近效应的贡献权重值主要取决于大气分子 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 层状磁性拓扑材料中的物理问题与实验进展
    摘要:层状磁性材料与拓扑材料的交汇点同时结合了二者的优势,形成了在最小二维单元下同时具有磁序和拓扑性的材料体系,即层状磁性拓扑材料.这类材料的电子结构中可能存在狄拉克点、外尔点、节线等具有螺旋性或手性的拓扑电子态,同时涵盖了绝缘体、半金属和金属等的材料分类,导致新物性、新现象成为可能,因此引起了广泛 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于光子晶体的有机太阳能电池研究进展
    摘要:随着近几年来光伏产业的迅速发展,有机太阳能电池因其成本低、重量轻、易于成批次生产、制作工艺简单和可制备成柔性器件等优点备受研究人员关注.目前,有机太阳能电池存在光电转换效率偏低、半透明器件显色性较差等问题,光子晶体的引入为解决上述问题提供了新思路.本文从光子晶体的结构特性和优化原理入手,系统性 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.