摘要:信息化对高速大容量光纤网络的需求日益强烈, 空分/模分复用是继波分复用之后可使通信容量翻倍的新一代光纤通信技术. 本文提出了一种双沟槽环绕型十三芯五模光纤, 以满足未来对高速大容量信息传输的需求. 针对空分-模分复用中降低串扰的目标设计优化光纤, 采用双沟槽环绕结构, 将光能量更好地限制在纤芯内, 从而减小芯间和模间串扰. 利用全矢量有限元法与功率耦合理论相结合计算并分析多芯光纤的串扰和传输特性. 经过优化结构参数, 可使光纤在1.3—1.7 μm波段内稳定传输LP₀₁, LP₁₁, LP₂₁, LP₀₂, 和LP₃₁ 5个模式; 信号在1.55 μm波长处传输60 km时, 对应于以上5个模式相邻纤芯的芯间串扰分别为–122.37, –114.76, –106.28, –100.68, –92.81 dB, 相邻模式之间的有效折射率差大于1.026 × 10^–3, 芯间和模间串扰可以被有效抑制; 5个模式对应的非线性系数分别为0.74, 0.82, 0.88, 1.26, 0.93 W^–1·km^–1, 均可保持低非线性传输. 该光纤结构简单紧凑, 可利用气相沉积法和堆叠法制备预制棒, 进一步拉制成具有低串扰低非线性的十三芯五模光纤, 可应用于长距离高速大容量光纤传输系统.
关键词: 空分-模分复用/
双沟槽/
低串扰/
低非线性系数

English Abstract

全文HTML

--> --> -->

随着社会信息传输量的猛烈增长, 传统光纤已经逼近其传输上限, 已无法满足通信容量的需求^[1]. 研制高速大容量传输光纤成为现在急需解决的问题, 基于空分-模分复用技术的多芯少模光纤传输容量在理论上可以高于传统光纤数十倍, 因此采用空分-模分复用的多芯少模光纤已成为解决此问题的方法之一^[2].
目前, 空分复用已成为国内外研究热点. 在文献[3]中, 提出了一种新型空气沟槽辅助异质十二芯四模光纤, 该光纤结构可以显著降低串扰, 相较于普通沟槽异质光纤串扰可降低–66 dB/km. 在文献[4]中优化了一种七芯六模光纤, 成功获得低串扰, 低损耗特性, 可用于构建长途密集的空分复用传输链路. 在文献[5]中, 设计并制备出了一种低差分群时延折射率渐变型沟槽光纤, 可在C + L波段保持小于124 ps/km的低差分群时延下稳定传输六种LP模式.
多芯少模光纤的发展主要受到串扰、非线性系数和色散等问题的限制^[6]. 其中芯间串扰和模间串扰对多芯少模光纤的限制最大, 过大的串扰会导致信号传输距离缩短和信号失真, 目前全世界的研究者都在致力于减小串扰以制造出实际可用的多芯少模光纤. 光纤的串扰可以通过设置结构差异来抑制, 例如控制相邻纤芯直径、纤芯间距、折射率分布及纤芯排布方式^[6-9]. 然而受制于光纤的尺寸, 光纤设计的可能性就大大减小. 为抑制串扰, 目前多芯光纤的设计方案主要分为三种: 沟槽环绕型^[10,11]、纤芯异质型^[12]和空气孔辅助型^[13]. 利用这三种结构可以将能量更好地限制在纤芯中从而减小纤芯之间的串扰. 三种结构相对比来说, 空气孔辅助型结构由于空气孔的存在, 在熔接时空气孔难以完全对准且拉制过程中空气孔容易塌陷造成光纤缺陷; 纤芯异质结构由于其纤芯各不相同在熔接问题上也较为困难; 沟槽环绕型结构在串扰抑制能力上具有一定的优势, 也利于优化光纤性能, 在制作工艺上也更为简单, 更符合实际应用. 对于采用模分复用的少模光纤, 单根纤芯中同时有多个独立且正交的模式, 为使光纤可以长距离稳定传输, 模式之间的串扰要求越小越好. 模式差分群时延(DMGD)是影响基于模分复用技术的少模光纤的重要因素之一^[14,15]. DMGD是在少模光纤中由于不同模式具有不同的有效折射率, 各模式在纤芯中的传播速度不相同, 传输一段距离后形成模式间的时延^[1]. 小DMGD的少模光纤模间串扰较大, 大DMGD的少模光纤模间串扰相对较小, 小的模间串扰能够保证模式间的相对独立, 而且较大的DMGD有利于接收端的解复用, 但DMGD不宜过大, 过大的DMGD不利于光纤长距离传输^[1,13-19]. 在光纤的设计过程中, 设置合适的DMGD大小, 从而使光纤获得更优的性能. 上述方法对于设计多芯少模光纤, 实现长距离大容量稳定传输具有一定的指导意义.
本文设计了一种双沟槽环绕型十三芯五模光纤, 为了实现设计目标, 光纤设置的参数必须要以模式的传输数量为依据^[6], 使得每个纤芯都可以稳定传输5个LP模式. 本文采用双沟槽辅助型结构, 相比于单沟槽结构可以将光能量更好地限制在纤芯中, 减小能量耦合; 优化双沟槽参数, 可以有效降低芯间串扰和模间串扰, 并利用最佳的DMGD减小模式间的相互影响. 仿真结果显示: 光纤在1.55 μm波长处传输60 km后, 对应于LP₀₁, LP₁₁, LP₂₁, LP₀₂, LP₃₁5个模式, 相邻纤芯间的串扰分别为–122.37, –114.76, –106.28, –100.68, –92.81 dB, 有效折射率差均大于1.026 × 10^–3, 芯间和模间串扰可被有效抑制; 5个模式的非线性系数可保持在1.6 W^–1·km^–1以下. 综合光纤性能, 本文所设计的光纤可以应用于长距离大容量传输系统.

2

-->

2.1.光纤结构

本文设计了一种双沟槽环绕型十三芯五模光纤, 其光纤截面图如图1所示. 该光纤基于空分-模分复用技术设计, 采用阶跃折射率分布结构, 光纤芯区使用掺锗石英材料提高芯区折射率, 沟槽包层采用掺氟石英材料降低沟槽折射率, 石英包层使用纯石英材料; 每一个芯区从内而外依次相间环绕2个石英包层和2个沟槽包层组成1个少模纤芯, 13个少模纤芯的参数相同.
图 1 双沟槽环绕型十三芯五模光纤结构
Figure1. Schematic structure of a double-trench assisted 13-core 5-LP mode fiber.

相邻两个纤芯的折射率分布如图2所示. 其中: a为芯区半径; b₁, b₂为石英包层宽度; c₁, c₂为沟槽宽度; Λ为纤芯间距; R为光纤半径; 以上物理量单位为μm. 芯区与石英包层的相对折射率差为Δ₁, 石英包层与沟槽包层的相对折射率差为Δ₂.
图 2 相邻纤芯折射率分布
Figure2. Refractive index profile of adjacent fiber-core.

2 -->

2.2.光纤参数设计

对于传统阶跃折射率光纤, 纤芯中传输的模式数量由归一化频率V决定^[1]:

$ V=\frac{2{\rm{\pi }}r}{\lambda }\sqrt{{n}_{\rm{co}}^{2}-{n}_{\rm{cl}}^{2}}{,} $

其中, r为纤芯有效半径, λ为工作波长, n_co为纤芯折射率, n_cl为包层折射率. 若想保证纤芯中能够稳定传输5个模式(LP₀₁, LP₁₁, LP₂₁, LP₀₂, LP₃₁), 归一化频率必须满足^[20]: 5.1 < V < 5.5, 在本文中利用该条件确定光纤的初始参数.
本文在参数设计过程中, 着重考虑了光纤抑制串扰的能力、有效模场面积大小和非线性系数. 对于多芯少模光纤, 抑制串扰的能力决定了光纤是否可以长距离稳定传输光能量, 非线性系数决定了光纤容量大小. 非线性系数与有效模场面积成反比, 通过增大有效模场面积可以有效降低非线性系数, 而增大有效模场面积最直接的方法就是增大纤芯直径, 因此本文会合理设置纤芯直径从而抑制非线性系数, 优化光纤参数使串扰达到目标水平. 表1给出了光纤初始参数.

a/μm	b1/μm	b2/μm	c1/μm	c2/μm	Λ/μm	R/μm	Δ1	Δ2
6	2	2	5	4	42	100	0.017	–0.01

表1光纤初始参数
Table1.The initial fiber parameters

本文使用基于全矢量有限元分析方法的Comsol Multiphysics仿真软件, 结合完美匹配层(perfectly matched layer, PML)边界条件对设计的光纤结构进行仿真分析. 控制光纤直径为200 μm, 优化调整光纤其他参数, 获得低串扰低非线性系数的双沟槽环绕型十三芯五模光纤.

2

-->

3.1.芯间串扰计算方法

芯间串扰是多芯少模光纤中必须要解决的问题, 特别是用于长距离大容量传输的多芯少模光纤, 串扰必须要足够低, 光纤才能稳定传输. 目前, 计算串扰的方法主要有模式耦合理论和功率耦合理论, 其中功率耦合理论更适用于多芯少模光纤的串扰计算^[2], 所以本文将采用功率耦合理论计算串扰, 并在仿真模拟时沿横向引入随机波动的传播常数, 以此更准确的计算纤芯之间的串扰. 图3给出了具有横向波动的两相邻纤芯之间的串扰计算模型.
图 3 具有横向随机波动的两相邻纤芯之间的串扰
Figure3. Crosstalk between two adjacent cores with random fluctuation along longitudinal direction.

相邻纤芯之间的串扰(XT, 单位为dB)计算表达式为^[2,6]:

$ {\rm{XT}}=10{\rm{lg}}\left( {{P}_{2}}/{{P}_{1}}\right){,} $

其中, P₁是纤芯1的输出功率, P₂是从纤芯1耦合到相邻纤芯2的功率. 只考虑相邻纤芯的串扰, 第i个纤芯的功率可表示为

$ \frac{{\rm{d}}{P}_{i}}{{\rm{d}}z}=\sum \nolimits_{j}{h}_{ij}[{P}_{j}\left(z\right)-{P}_{i}\left(z\right)]{,} $

其中, P_i和P_j分别是纤芯i和j的平均功率, h_ij是纤芯i和纤芯j之间的耦合系数, z是传输方向. 如果以功率P₁(0)输入中心纤芯1, 则中心纤芯1和相邻纤芯2中的的输出功率可表示为:

$ \frac{{P}_{1}}{{P}_{1}\left(0\right)}=\frac{1+6{\rm{\exp}}(-7{h}_{12}Z)}{7}{,} $

$ \frac{{P}_{2}}{{P}_{1}\left(0\right)}=\frac{1-{\rm{\exp}}(-7{h}_{12}Z)}{7}{,} $

其中, h₁₂是功率耦合系数, Z为传输距离. (2)式可变换为

$ {\rm{XT}}=10{\rm{lg}}\Big(\frac{{P}_{2}}{{P}_{1}}\Big)=10{\rm{lg}} \bigg(\frac{1-{\rm{exp}}(-7{h}_{12}Z)}{1+6{\rm{exp}}(-7{h}_{12}Z)}\bigg), $

其中,

$ {h}_{12}=\frac{2{\kappa }_{12}^{2}}{\pi \sqrt{{7} ({\delta }^{2}+{\kappa }_{12}^{2}})}{,} $

其中, δ是纤芯1和纤芯2的传播常数差$\dfrac{{{\beta _1} - {\beta _2}}}{2}$; κ₁₂是模式耦合系数. κ₁₂可由(8)式计算得出

$ {\kappa }_{12}=\dfrac{\omega {\varepsilon }_{0}\displaystyle\int _{-\infty }^{\infty }\displaystyle\int_{-\infty }^{\infty }({n}_{\rm{co}}^{2}-{n}_{\rm{cl}}^{2}){{E}}_{1}^{*} \cdot {{E}}_{2}{\rm{d}}x{\rm{d}}y}{\displaystyle\int_{-\infty }^{\infty }\displaystyle\int_{-\infty }^{\infty }{{u}}_{z} \cdot ({{E}}_{1}^{*}\times {{H}}_{1}+{{E}}_{1}\times {{H}}_{1}^{*}){\rm{d}}x{\rm{d}}y}{,} $

其中: ω是电磁场的角频率, ε₀是真空介电常数, u_z为单位矢量, E₁为纤芯1中分布的电场能量分布, E₂为纤芯1的电场能量在纤芯2中的分布, H₁为纤芯1的磁场能量分布.
由于光纤在制作过程中会不可避免地产生制造误差, 本文假设相邻纤芯制造的相对误差为δa/a = 1%^[10]; 由于次邻近纤芯间距较大, 次邻近芯间串扰足够小可以被忽略^[8], 所以本文只计算中间纤芯和相邻纤芯的串扰值.
2 -->

3.2.模间串扰的表征

模间串扰是影响光纤传输的重要参数之一. 对于微结构光纤, 纤芯与包层的折射率差要大于传统光纤, 这会使得微结构光纤的模间串扰小于传统光纤^[13]. 目前有效抑制模间串扰的方法主要有两种^[19]: 1)通过设计较大的有效折射率差, 减小模式间的能量耦合, 抑制模间串扰; 2)保持模式间的差分群时延足够小, 使用多输入多输出技术在光纤的接受端对信号进行补偿处理. 两种方法各有优劣, 本文将采用第一种方法控制模间串扰.
根据文献[1, 13]所述, 同一纤芯中各模式之间的有效折射率相差较大且大于10^–3时, 纤芯内的模间串扰可以被忽略, 而模式间的有效折射率差与MDGD关系密切, 具有较大的有效折射率差同时会具有较大的MDGD, 因此MDGD较大的少模光纤具有更低的模间串扰, 但是过大的MDGD会影响光纤的传输距离. 目前, 长飞公司制造出的通信用阶跃型少模光纤在1.55 μm处LP₃₁与基模的最大MDGD为15 ps/m. 本文将综合考虑光纤性能, 合理设计适宜的MDGD.
MDGD的计算公式为^[3]

$\begin{split}&{\rm{MDGD}}=\tau ({\rm{LP}}_{mn})-\tau ({\rm{LP}}_{{m}{'}{n}{'}})= \\\;&\frac{{n}_{{\rm{e}}{\rm{f}}{\rm{f}}mn}-{n}_{{\rm{e}}{\rm{f}}{\rm{f}}{m}^{'}{n}^{'}}}{c}-\frac{\lambda }{c}\left( {\frac{{\partial n}_{{\rm{e}}{\rm{f}}{\rm{f}}mn}}{\partial \lambda }-\frac{{\partial n}_{{\rm{e}}{\rm{f}}{\rm{f}}m{'}n{'}}}{\partial \lambda } } \right) ,\end{split}$

其中, τ为群时延, λ是波长, n_eff是模式的有效折射率, c为真空中的光速.
2 -->

3.3.沟槽结构对串扰的影响

首先本文对比了芯区外无沟槽、单沟槽和双沟槽三种结构对光纤芯间串扰的影响, 除沟槽数量外三种光纤的其他结构参数完全相同. 针对LP₀₁模式三种结构的芯间串扰如图4所示.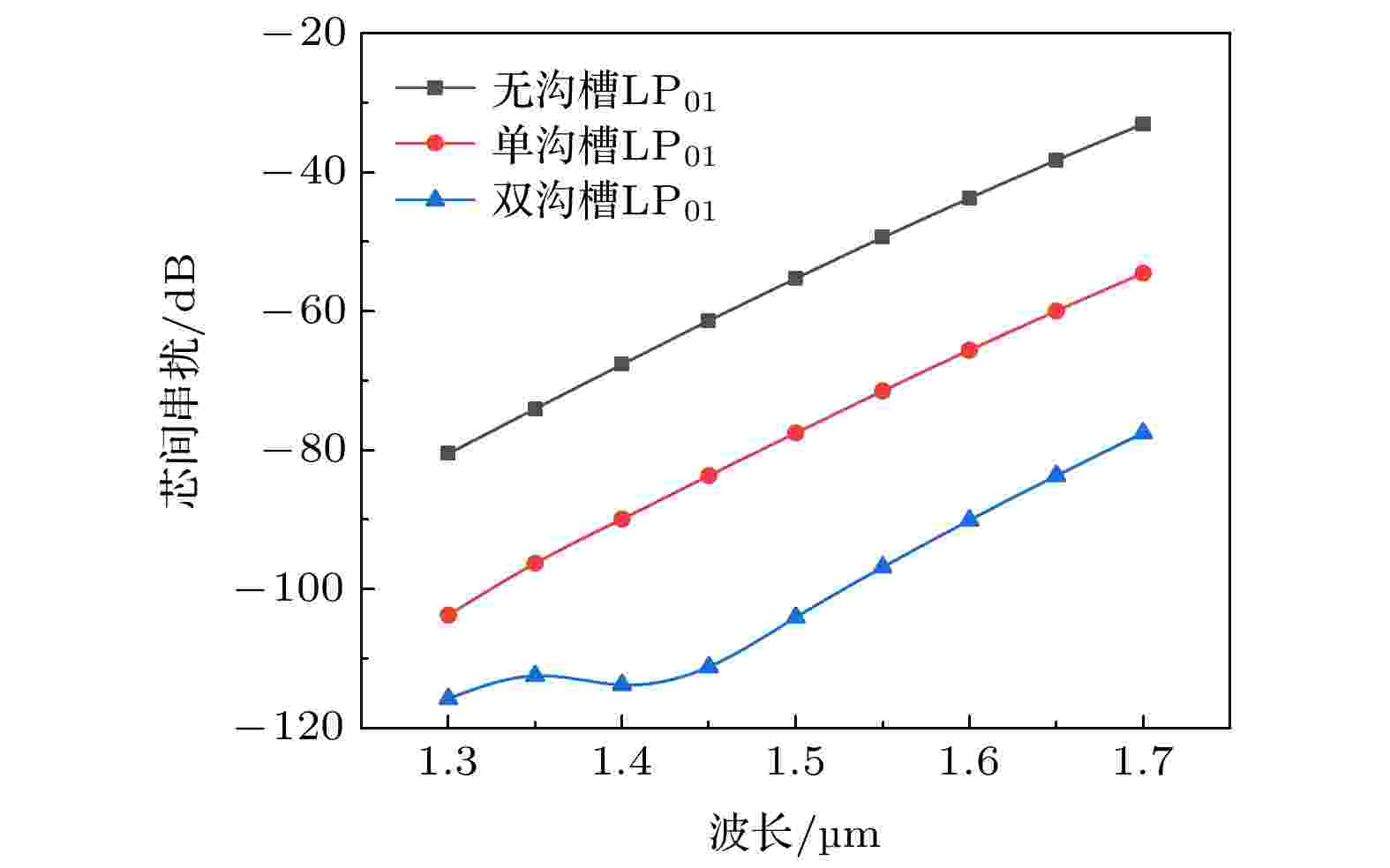
图 4 无/单/双沟槽结构中LP₀₁模式的芯间串扰对比
Figure4. No/single/double trench structure crosstalk contrast of LP₀₁ mode.

由图4可以看出, 单沟槽结构的串扰小于无沟槽结构, 双沟槽结构对串扰的抑制效果又明显优于单沟槽, 采用双沟槽结构可以增强光纤抑制串扰的能力. 确定双沟槽结构优势后, 继续研究了沟槽宽度和沟槽相对折射率差Δ₂对串扰的影响. 计算了光纤在1.55 μm处传输60 km, 串扰随沟槽宽度和Δ₂的变化趋势. 图5给出了Δ₂ = –0.01时芯间串扰与沟槽宽度的关系, 图6给出了沟槽宽度c₁和c₂都等于4 μm时, 串扰和Δ₂的关系.
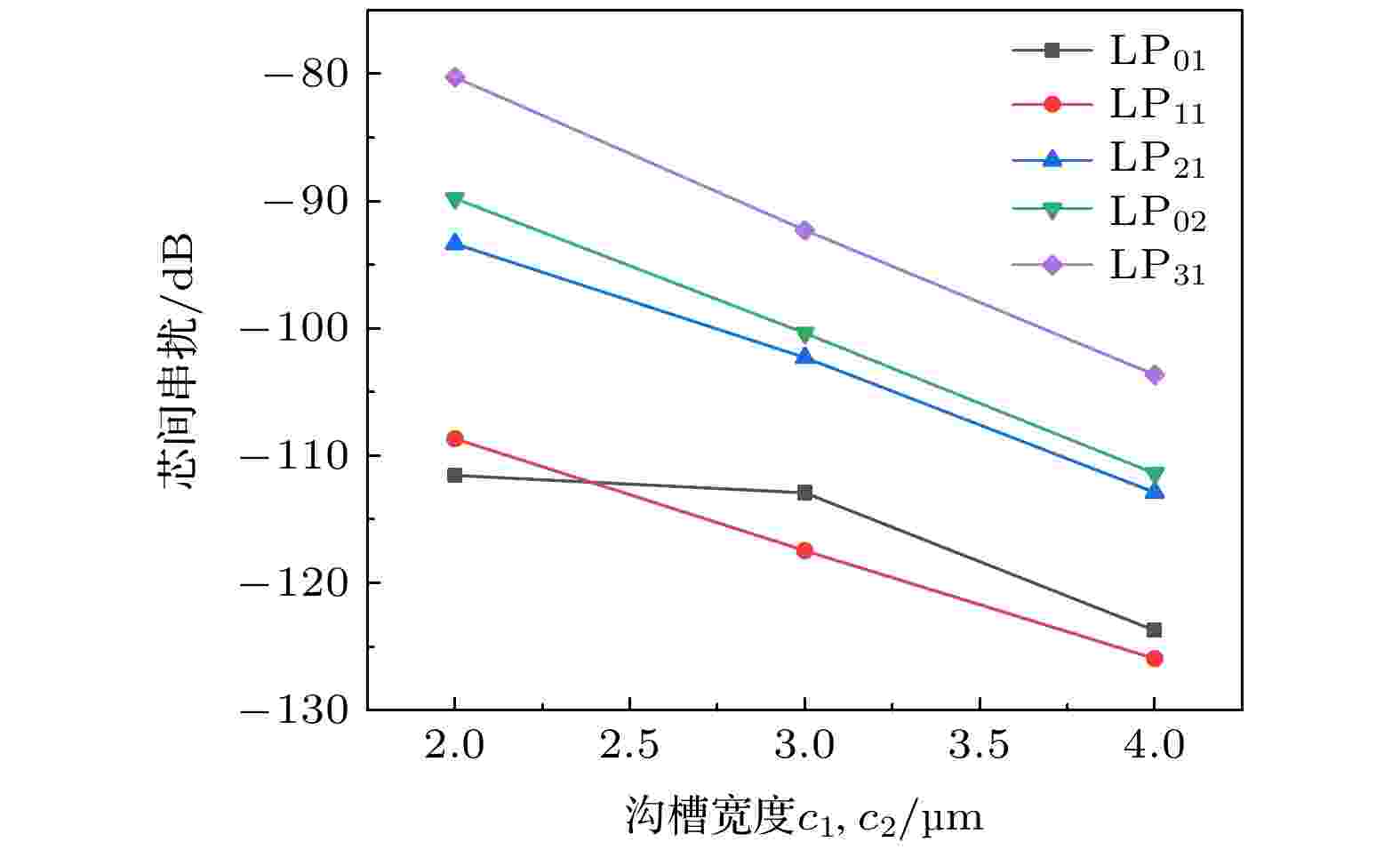图 5 Δ₂ = –0.01时芯间串扰与沟槽宽度的关系
Figure5. Relation between crosstalk and trench width at Δ₂ = –0.01.

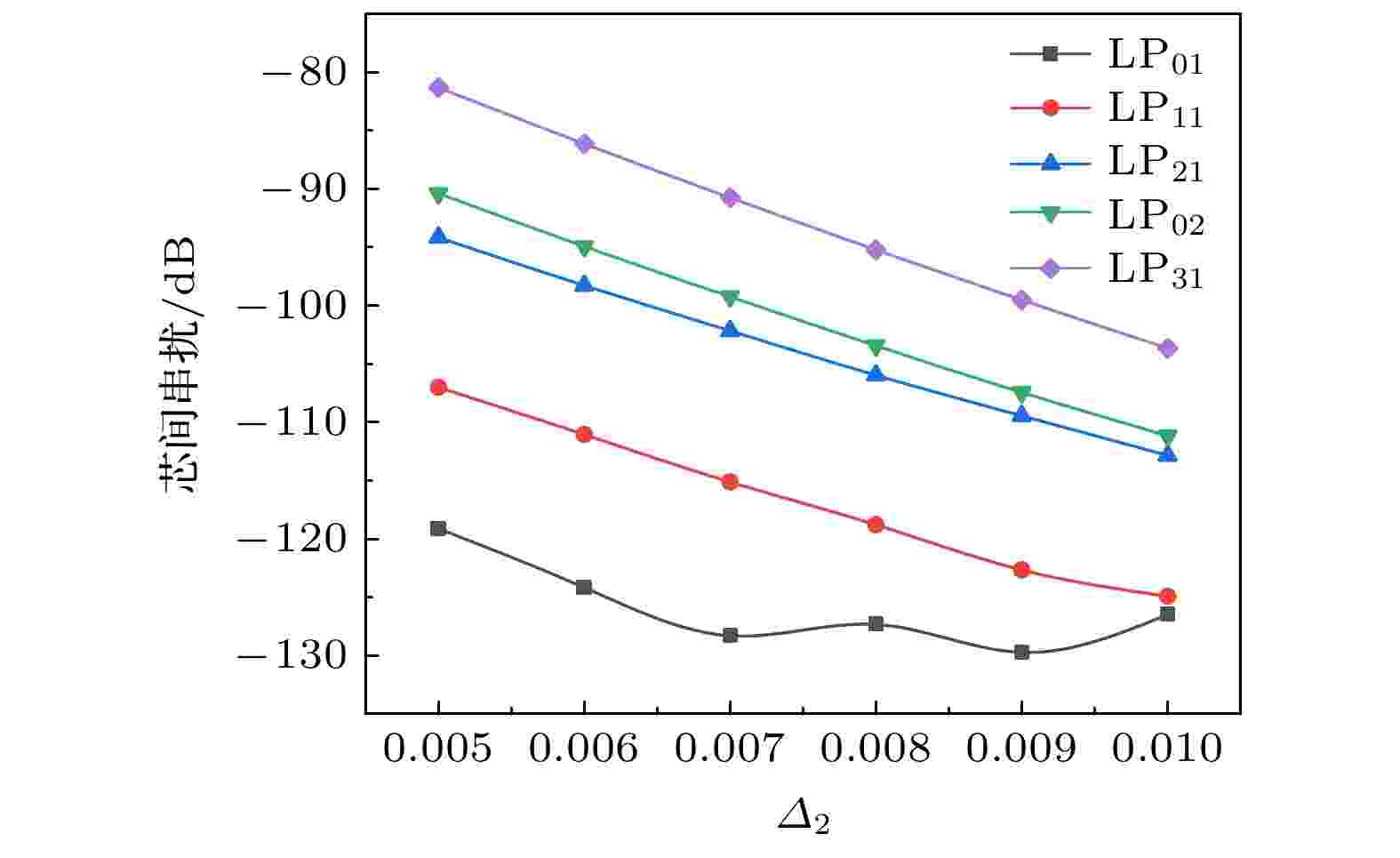图 6 c₁, c₂ = 4 μm时串扰和Δ₂的关系
Figure6. Relation between crosstalk and Δ₂ at c₁, c₂ = 4 μm.

由图5和图6可以得出芯间串扰随着沟槽宽度和Δ₂的增加不断减小, 增加沟槽的宽度和Δ₂可以有效的抑制串扰. 本文将选取最佳的沟槽宽度和Δ₂, 使双沟槽十三芯五模光纤具有最优的串扰抑制能力.
2 -->

3.4.纤芯分析

芯区半径对光纤的串扰和性能有着显著的影响, 分析芯区大小与光纤性能的关系是必不可少的步骤, 本文拟定对芯区半径a = 5—8 μm进行分析, 分析结果如图7所示.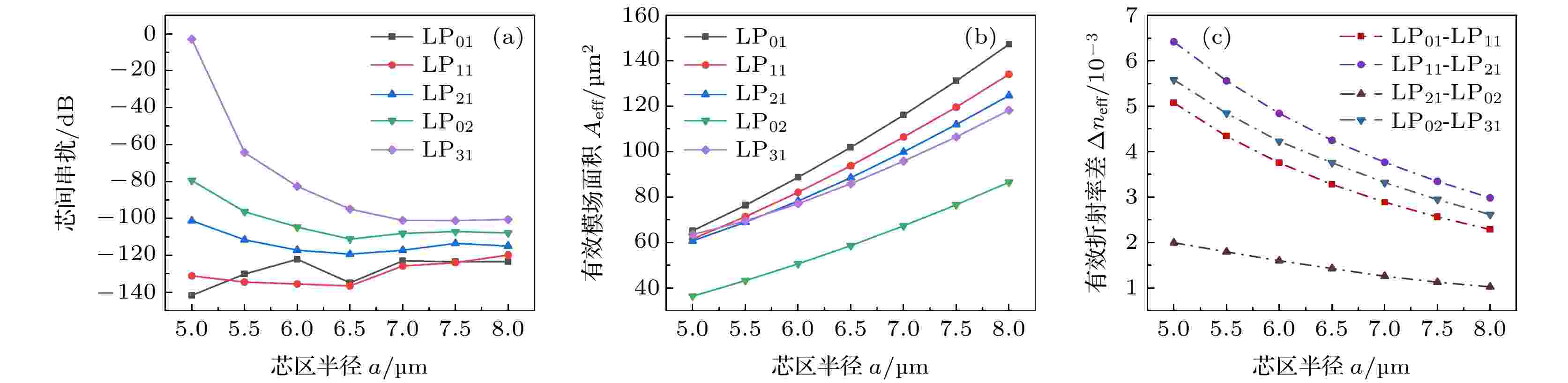
图 7 在?₁ = 0.015, 波长1.55 μm处5个模式的串扰、A_eff和Δn_eff与芯区大小的关系 (a)芯区大小和串扰的关系; (b)芯区大小和A_eff的关系; (c)芯区大小和模式折射率差的关系
Figure7. The relationship between crosstalk, A_eff, Δn_eff of five modes and core size at 1.55 μm: (a) The relationship between core size and crosstalk; (b) the relationship between core size and A_eff; (c) the relationship between core size and Δn_eff.

由图7(a)可以看出5个模式的芯间串扰呈现非线性变化, LP₀₁模式的串扰随芯区大小变化具有一定的波动性, 芯区较小时LP₀₁模式呈现低串扰特性, 但芯区半径超过7 μm后, LP₀₁模式的串扰只有微小的变化; LP₁₁模式的串扰呈现出随着芯区半径增大, 串扰缓慢增长的趋势; LP₂₁和LP₀₂两模式的串扰变化趋势基本相同, 但LP₂₁模式串扰低于LP₀₂, 随着芯区增大串扰在a = 6.5 μm处存在一最小值, 芯区半径超过7 μm后串扰变化趋于平缓; LP₃₁模式的串扰随芯区半径变化最为明显, 随着芯区增大串扰迅速降低, 在芯区半径超过7 μm后, 串扰变化趋于平缓. 图7(a)中的串扰变化规律可以从模式的电磁能量分布角度解释, 同一大小的芯区对不同模式的能量束缚能力不同, 高阶模式的能量更容易泄露到纤芯外, 且高阶模的能量主要分布在芯区外围更容易引起能量耦合, 通过增大芯区可以增强对高阶模能量的束缚能力以达到减小高阶模式的芯间串扰的目的, 当芯区增大到一定程度后, 芯区对模式的束缚能力增长程度不在明显. 综上分析, 5个模式的串扰均有一个相同的特点: 芯区半径超过7 μm后, 串扰均能保持在较低水平, 并且串扰随芯区半径变化很小; 若想保持5个模式的串扰均保持在较低水平, 芯区半径最佳的选择范围是7—8 μm.
由图7(b)可知, 光纤中各模式的A_eff均与芯区半径成正比, 5个模式的A_eff增长趋势基本形同, 但LP₀₂模式的A_eff大小却低于其他4个模式. 对于高折射率芯区, 其具有较强的集光能力, 光会被集中在芯区内传播, 当芯区半径较小时, 传输模式会被集中在小芯区内, 模式所占据的横向面积就会很小, 对应的有效模式面积也会较小; 当芯区半径增大时, 模式被集中在较大的芯区面积内, 模式的横向分布面积也会增大, 有效模式面积也会随之增大. 根据图7(b)分析, 若想获得较大的A_eff, 就要尽量扩大芯区半径.
图7(c)为相邻模式之间的有效折射率差, 随着芯区增大, 模式之间的有效折射率差减小. 从图7(c)中可以看出LP₂₁和LP₀₂模式之间的有效折射率很接近, 两者之间的差值相比于其他4个模式略低, 所以在考虑折射率差时应以LP₂₁–LP₀₂为标准. 根据上文所述, 各模式之间的有效折射率差大于10^–3便可忽略模间串扰, 但过大的折射率差将会引起较大的MDGD, 所以应选择适宜的芯区半径以获得最佳的模间折射率差值, 从而获得足够小的模间串扰.
除芯区半径外, 芯区的折射率大小对光纤也有着重要的影响. 现对芯区的相对折射率差Δ₁进行分析, 结果如图8所示.
图 8 在1.55 μm处5个模式的芯间串扰、A_eff和?n_eff与芯区相对折射率差Δ₁的关系 (a) Δ₁和芯间串扰的关系; (b) Δ₁和A_eff的关系; (c) Δ₁和模式折射率差的关系
Figure8. . The relationship between crosstalk, A_eff, ?n_eff of five modes and Δ₁ at 1.55 μm: (a) The relationship between Δ₁ and crosstalk; (b) The relationship between Δ₁ and A_eff; (c) The relationship between Δ₁ and ?n_eff.

由图8(a)所示, LP₀₁模式的芯间串扰在Δ₁ = 0.01–0.016区间内, 串扰在–110 dB上下波动, Δ₁超过0.016后, 串扰随着Δ₁的增大开始降低; LP₁₁模式在Δ₁为0.01—0.017范围内, 串扰呈现降低趋势, 但Δ₁大于0.017后串扰变化不在下降, 呈现平稳趋势; LP₂₁, LP₀₂和LP₃₁模式的串扰随着Δ₁的增加不断减小. 由图8(a)分析可得, 纤芯折射率越大对串扰的抑制能力越强. 但芯区折射率的增大要受实验上掺锗浓度的限制.
如图8(b)所示, 芯区的相对折射率Δ₁增大, 会减小模式的有效模式面积, 但减小程度并不强烈. 若想获得较大的模式面积, 需减小芯区的相对折射率Δ₁.
由图8(c)可知, 芯区的相对折射率Δ₁对模式之间的有效折射率差具有一定的影响, 模式之间的有效折射率差随着Δ₁增大而增大, 但相比芯区半径, 影响效果较小.
综上分析, 较大的Δ₁具有更优的串扰抑制能力, 但同时会降低模式的有效模式面积, 增大光纤的非线性系数.

经过模拟分析可知, 若想使十三芯五模光纤具有低串扰, 芯区半径需在7—8 μm范围内选择, 芯区折射率要尽量增大, 沟槽折射率要尽量减小, 沟槽宽度也应尽量增大; 若想获得大模场面积低非线性系数, 需要扩大芯区半径, 减小芯区折射率. 但这两种特性的调控方式相反, 只能在两者之间寻找最佳参数, 使光纤同时具有最优的串扰和低非线性特性. 经过大量仿真优化, 确定光纤结构, 优化后的参数如表2所示. 该结构可以稳定传输5个LP模式, 每个模式对应的芯间串扰、有效模式面积和MDGD如表3所示. 进一步利用Rsoft软件模拟了光纤优化参数后的模场分布, 图9给出了该光纤的5-LP模式的传输截面图, 结果表明13个纤芯可以保持低串扰稳定传输5个模式.

a/μm	b1/μm	b2/μm	c1/μm	c2/μm	Λ/μm	R/μm	Δ1	Δ2
8	2	2	4	4	42	100	0.015	–0.008

表2光纤优化参数
Table2.The optimal fiber performance.

Modes	Crosstalk/ (dB/60 km)	Aeff /μm2	MDGD/ (ps·m–1)
LP01	–122.37	147	0
LP11	–114.76	134	5.855
LP21	–106.28	125	13.452
LP02	–100.68	87	15.799
LP31	–92.81	118	22.314

表35个LP模式的串扰、有效模面积和MDGD(LP_mn–LP₀₁)
Table3.Estimated values of crosstalk, effective area and MDGD(LP_mn–LP₀₁) for 5-LP modes at 1.55 μm.

图 9 5-LP横向模式剖面
Figure9. Transverse mode profile for 5-LP modes.

芯间串扰受波长影响较大, 如图10所示, 在1.3—1.7 μm波段, 芯间串扰随着波长逐渐增大. 在1.3 μm处传输60 km, LP₃₁模式的芯间串扰可以保持在–140.61 dB左右, 但在1.7 μm处, LP₃₁模式的芯间串扰却达到了–66.75 dB, 若要在传输过程中保持低串扰, 应尽量选择在较低波段进行传输.
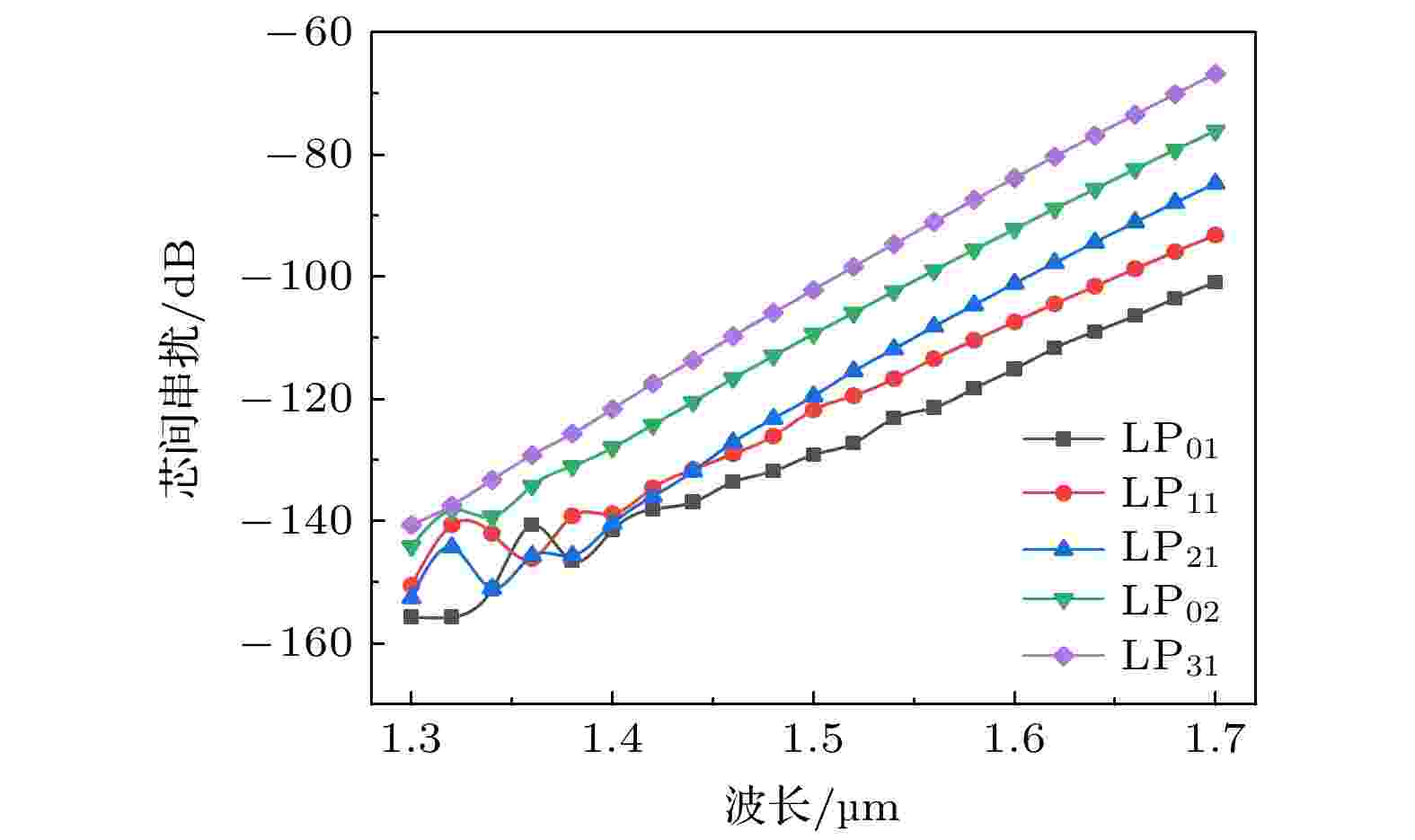图 10 双沟槽十三芯五模光纤芯间串扰与波长关系
Figure10. Relation between wavelength and core-to-core crosstalk for the double-trench assisted 13-core 5-LP mode fiber.

对于模间串扰, 根据图11分析, 优化后的光纤结构相邻模式之间可以保持较大的有效折射率差, 模式区分度大, 模间串扰可以被有效抑制, 当波长大于1.54 μm, 5个模式间的有效折射率差均大于10^–3, 可以忽略模间串扰. 相邻模式间的模式差分群时延也可保持在适宜大小, 可以在接收端解复用.
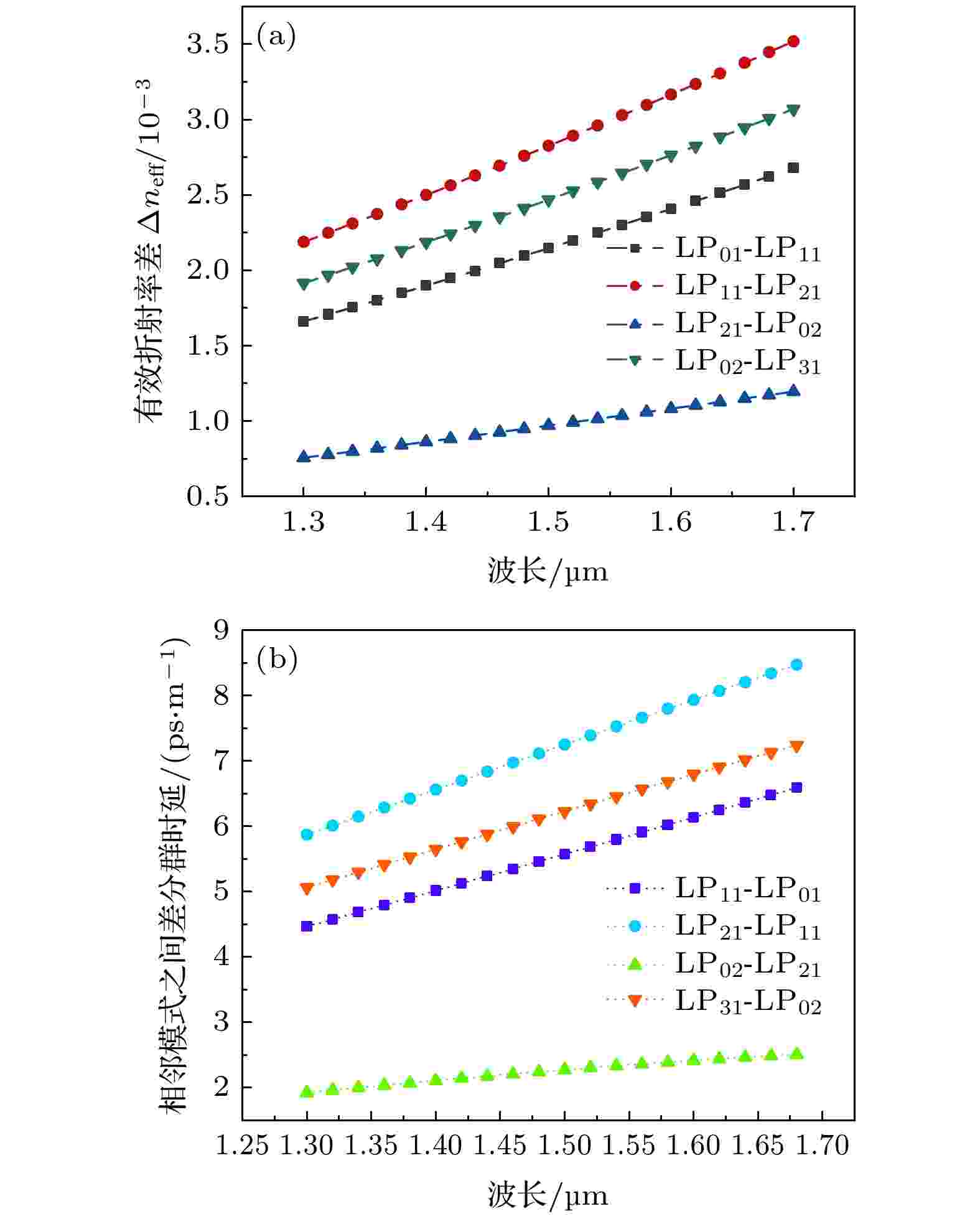图 11 5个LP模式之间的?n_eff和MDGD与波长的关系　(a) ?n_eff与波长的关系; (b)相邻模式之间差分群时延与波长的关系
Figure11. The relationship between ?n_eff, MDGD of five modes and wavelength: (a) The relationship between ?n_eff and wavelength; (b) the relationship between ?n_eff and wavelength.

通过仿真优化, 双沟槽十三芯五模光纤的芯间串扰和模间串扰均可以被有效抑制, 在长距离传输后, 串扰依旧可以保持在低水平.

2

-->

5.1.各模式非线性系数分析

非线性系数是衡量光纤容量的重要参数, 光纤的非线性系数的计算公式为^[21,22]:

$ \gamma = {2{\rm{\pi }}{n}_{2}}/({\lambda \cdot {A}_{{\rm{e}}{\rm{f}}{\rm{f}}}}){,} $

其中: n₂为材料的非线性折射率系数, 对于石英玻璃在此取n₂ = 2.7 × 10^–20 m²/W; A_eff为光场的有效模场面积.
光纤的非线性系数与有效模场面积成反比关系, 通过增大有效模面积可以有效降低非线性系数. 目前通信用的G.652和G.655光纤的有效模式面积在80 μm²左右, 长飞公司生产的同质七芯光纤的有效模场面积在100 μm²左右, 对于多芯少模光纤, 模式的有效面积最好保持大于100 μm^2[3,6,7,23]. 本文设计的光纤结构在1.55 μm波长处各模式的有效模面积如表3所示, 除LP₀₂模式的有效模面积为86.5 μm², 其他4个模式的有效模面积均保持在110 μm²以上, 可以使光纤保持低非线性系数.
图12(a)和图12(b)分别给出了光纤中各模式的有效模式面积A_eff和非线性系数与波长的关系. 从图12(b)可以看出, 非线性系数γ随着波长的增大逐渐减小, LP₀₂模式的非线性系数在5个模式中最大, 但也未超过1.6 W^–1·km^–1, 在1.55 μm波长处各模式的非线性系数为0.74, 0.82, 0.88, 1.26, 0.93 W^–1·km^–1, 5个模式均可以保持低非线性传输.
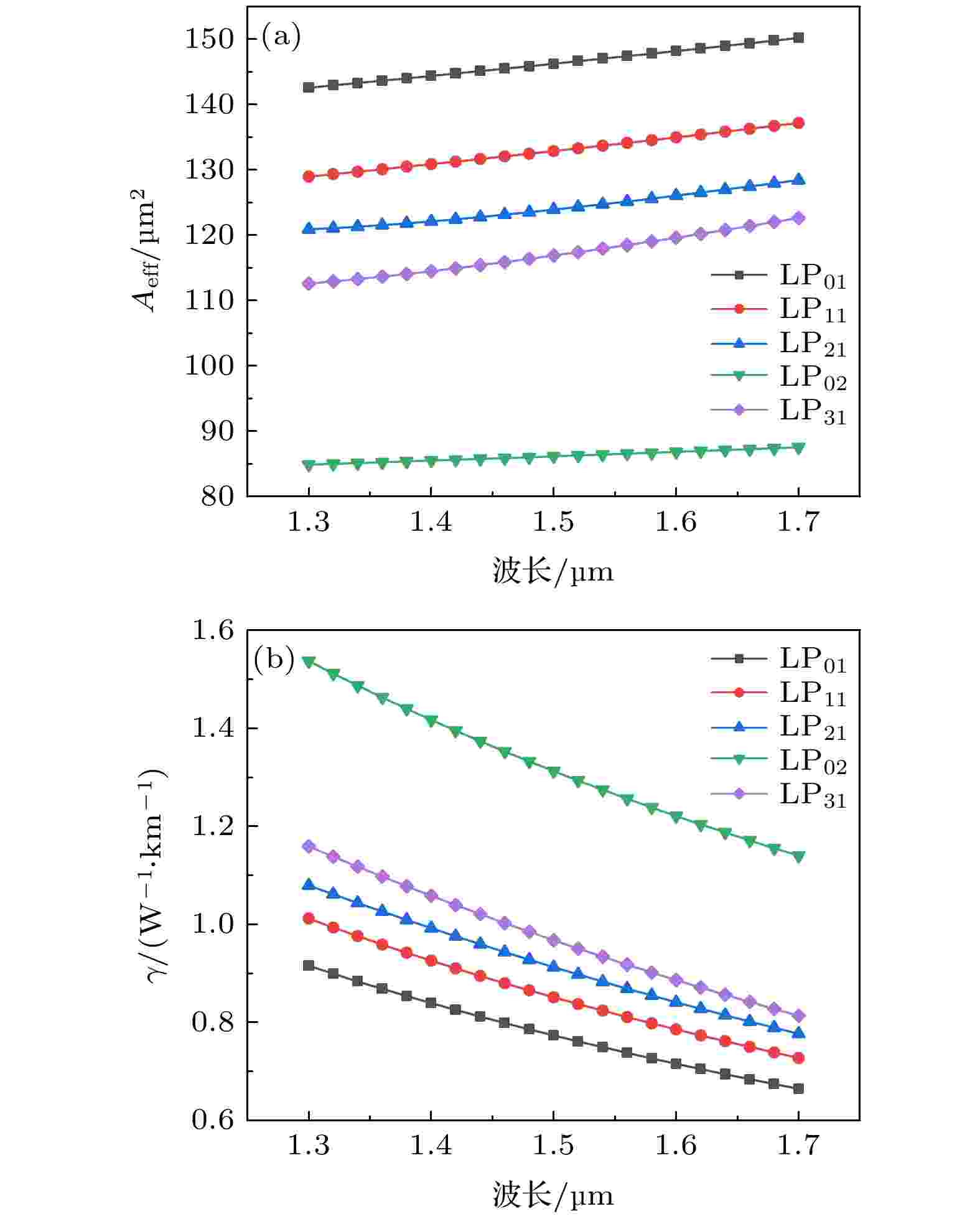图 12 5个LP模式的有效模面积A_eff和非线性系数γ与波长的关系　(a) 有效模面积A_eff与波长的关系; (b)非线性系数γ与波长的关系
Figure12. The relationship between A_eff, γ of five modes and wavelength: (a) The relationship between A_eff and wavelength; (b) the relationship between γ and wavelength.

2 -->

5.2.色散分析

通过增大模场面积减小非线性系数会对光纤的色散产生影响, 在设计时必须要考虑到光纤传输的色散问题^[10], 折射率高掺杂也会对色散有明显的影响. 色散(D)与有效折射率相对于波长的二阶导数成正比, 通常由(11)式表示^[3,6]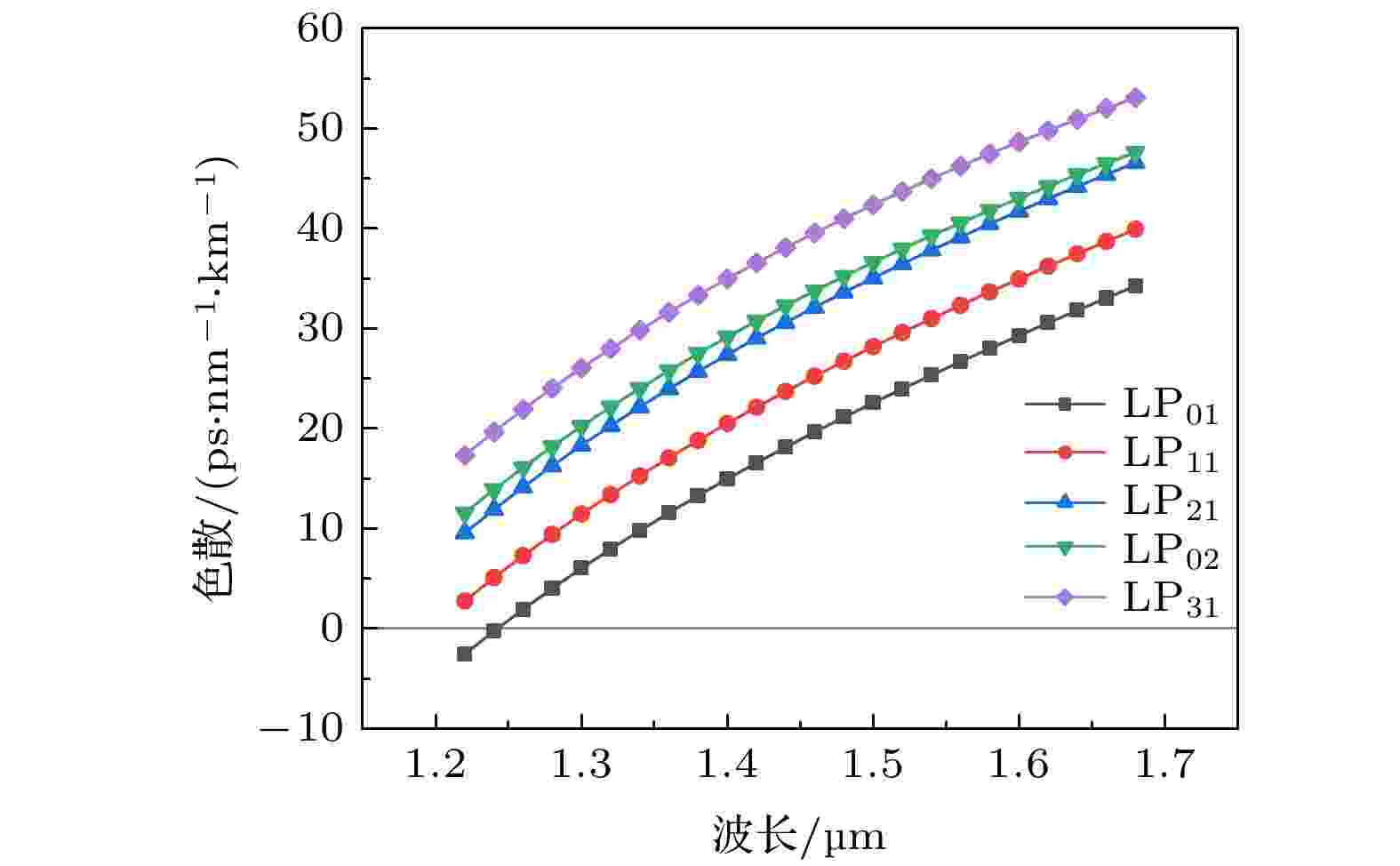

$ D = - \frac{\lambda }{c}\frac{{{{\rm{d}}^2}Re\left[ {{n_{{\rm{eff}}}}} \right]}}{{{\rm{d}}{\lambda ^2}}}{\rm{ps}}/({\rm{nm}} \cdot {\rm{km}}), $

其中, c是真空中的光速, Re[n_eff]是有效折射率的实部, λ是波长. 由(11)式计算出中间纤芯5个模式的色散随波长变化的曲线, 如图13所示. 从计算结果分析可得, 双沟槽环绕型十三芯五模光纤的色散随波长呈增长趋势, 相比于文献[3]中所设计的光纤, LP₀₁的色散增大了5 ps/(nm·km)左右. 5个模式的色散仍处于可控范围内, 且增长趋势相同.
图 13 5-LP的色散与波长的关系
Figure13. Relation between dispersion and wavelength for 5-LP modes.

2 -->

5.3.纤芯复用因子分析

纤芯复用因子(F_CM)是多芯少模光纤的一个重要参数, 可利用表3中各模式的有效模式面积估算纤芯复用因子, 同质多芯光纤的纤芯复用因子的计算公式为^[6]:

${F_{{\rm{CM}}}} = \left[ {N\sum\limits_m^l {{A_{{\rm{eff}} - m}}} } \right]\bigg/\left[ {\frac{\pi }{4}{R_{{\rm{CD}}}}^2} \right],$

其中, N是纤芯数, l是每个纤芯的空间模数(对于5-LP模, l = 8), A_eff是特定模的有效面积, R_CD是多芯光纤的包层直径. 此外, 相对纤芯复用因子(F_RCM)被定义为多芯少模光纤的F_CM值与传统单模光纤(R_CD和A_eff分别为125 μm和80 μm²)的F_CM值之比, F_RCM可表示为^[6]

${F_{{\rm{RCM}}}} = {F_{{\rm{CM}}}}\Big/\left[ {80/\left( {\frac{\pi }{4}{{125}^2}} \right)} \right],$

本文所设计的双沟槽十三芯五模光纤的F_CM和F_RCM分别为0.41和62.9.

为实现低串扰特性, 本文使用芯区高掺杂和双沟槽环绕结构抑制芯间串扰, 利用模式间的大有效折射率差抑制模间串扰, 对一些重要的影响参数进行了分析, 如沟槽宽度、折射率大小、芯区直径和波长. 对于芯间串扰, 基模(LP₀₁)的串扰可以被有效控制, 而高阶模式具有高串扰特性, 通过扩大芯区可以有效抑制高阶模串扰, 经过优化串扰可以保持在较低水平. 若想保持每个的模式的低芯间串扰, 可以通过增加沟槽宽度和减小沟槽折射率及控制芯区半径的方式有效减小串扰. 在光纤实际制备中, 纤芯和沟槽高掺杂会增加光纤的制备难度, 受限于掺氟技术, 沟槽掺氟的相对折射率差一般为–0.007, 且沟槽宽度不宜过大, 过高的氟掺杂和过大的沟槽宽度会导致光纤在制造或使用过程中容易断裂; 本文设计的沟槽相对折射率为–0.008, 宽度为4 μm, 在实际制备中可以通过增加沉积时间和沉积面积略微提高掺杂浓度以达到设计值; 由图5和图6分析可知, 制备参数达不到设计值时光纤的性能会下降, 但下降幅度在可接受范围内, 光纤性能依旧可保持在较好范围内. 限制损耗是一种出现在微结构光纤中的损耗类型, 可以衡量纤芯限制光信号的能力, 对于多芯少模光纤的设计, 限制损耗的大小是有必要计算的^[24-26], 本文优化后的光纤结构的限制损耗均保持在10^–10以下, 保持在低水平内, 便不再详细讨论.

本文提出一种新型的双沟槽环绕型十三芯五模光纤. 为了获得低串扰特性, 采用高掺杂和双沟槽环绕的方式增大芯包折射率差, 并将光纤外径控制在200 μm. 通过有限元法和功率耦合理论计算得出高掺杂和双沟槽环绕的方式可以有效降低串扰, 优化光纤参数可以获得低串扰特性. 计算结果表明: 在1.3—1.7 μm波长范围内, 可以实现LP₀₁, LP₁₁, LP₂₁, LP₀₂, LP₃₁ 5个模式稳定传输; 在1.55 μm波长处光纤传输60 km, 相邻纤芯中5个模式串扰分别为–122.37, –114.76, –106.28, –100.68, –92.81 dB, 通过对模间有效折射率差的分析, 同一纤芯中模间串扰也可被忽略; 5个模式的非线性系数不超过1.6 W^–1·km^–1. 利用现有的气相沉积法和光纤堆叠拉丝工艺便可制作本文设计的光纤, 该光纤可用于大容量信息传输, 以满足未来对高速大容量光纤传输系统的需求.