全文HTML
--> --> -->微波无线能量收集系统(图1(a))可通过微波接收天线捕获环境中的射频信号, 系统中的整流电路利用核心元件肖特基二极管(Schottky barrier diode, SBD)对射频信号能量整流, 并将直流能量供应给接收负载, 是实现上述应用的理想系统. 然而, 在2.45 G 弱能量密度RF信号输入条件下, 基于SBD的微波射频无线能量收集系统整流效率偏低, 尚无法真正实现商业应用[3-5]. 目前, 工程师们主要开展基于Ge半导体肖特基二极管整流电路的优化研发工作, 通过外围电路被动开启优化, 以提升2.45 G弱能量密度无线能量收集系统整流效率, 但收效甚微[6-8].
图 1 (a) 微波无线能量传输系统; (b) 典型肖特基二极管示意图Figure1. (a) Microwave wireless energy transmission system; (b) schematic diagram of a typical Schottky diode.
SBD作为2.45 G弱能量密度Wi-Fi波段无线能量收集系统整流电路的核心器件(图1(b)), 其性能决定了系统整流效率的上限. 因此, 欲进一步提升目前2.45 G弱能量密度Wi-Fi波段无线能量收集系统整流效率, 对该核心元器件-肖特基二极管予以设计优化势在必行[9-11]. 有鉴于此, 我们拟提出一种2.45 G弱能量密度无线能量收集用Ge基肖特基二极管, 旨在解决2.45 G弱能量密度无线能量收集系统整流效率低的问题.
基于器件物理相关原理, 首先推导建立了SBD开启电压模型. 依据文献, SBD从半导体到金属的电子流所形成的电流密度是
根据SBD器件金半接触的能带关系[13], 上式可进一步化简为
金属一侧的势垒高度不随外加电压变化, 从金属到半导体的电子流所形成的电流密度
综合以上模型, 可以发现, SBD开启电压与器件反向饱和电流密切相关. 同等条件下, 反向饱和电流越大, SBD开启电压越低. 反向饱和电流不仅仅与金半接触区域半导体电子有效质量、金属功函数有关, 还与半导体掺杂浓度和半导体的亲和能有关. 对于Ge SBD, 目前要想增大其反向饱和电流达到显著降低开启电压的目的, 只有通过材料设计想办法增大器件层结构材料中金半接触区域半导体电子有效质量与亲和能这条途径, 其他的方法已无法进一步实现优化.
2
2.1.大有效质量高迁移率设计
一方面, 我们希望增大SBD层结构材料中金半接触区域半导体电子有效质量, 以达到降低SBD开启电压的目的. 然而, 电子有效质量的增加会显著降低半导体的电子迁移率, 进而导致SBD串联电阻增大, 整流效率降低. 即增大半导体电子有效质量有利于SBD在弱能量密度信号情况下开启工作, 但低整流效率下SBD仍然无法实用.我们知道, Ge半导体电子有效质量具有各向异性, 沿不同的晶向电子电导率有效质量数值不同. 利用kp微扰理论, 图2建立了极坐标系下(001), (101), (111)剖面任意晶向Ge电子电导率有效质量模型(建模过程详见我们发表的文献[14]). 由图2可见, 沿各晶面典型高对称晶向, [100]晶向Ge电子电导率有效质量0.95m0, 数值最大. 其他依次为, [111]晶向0.64m0,
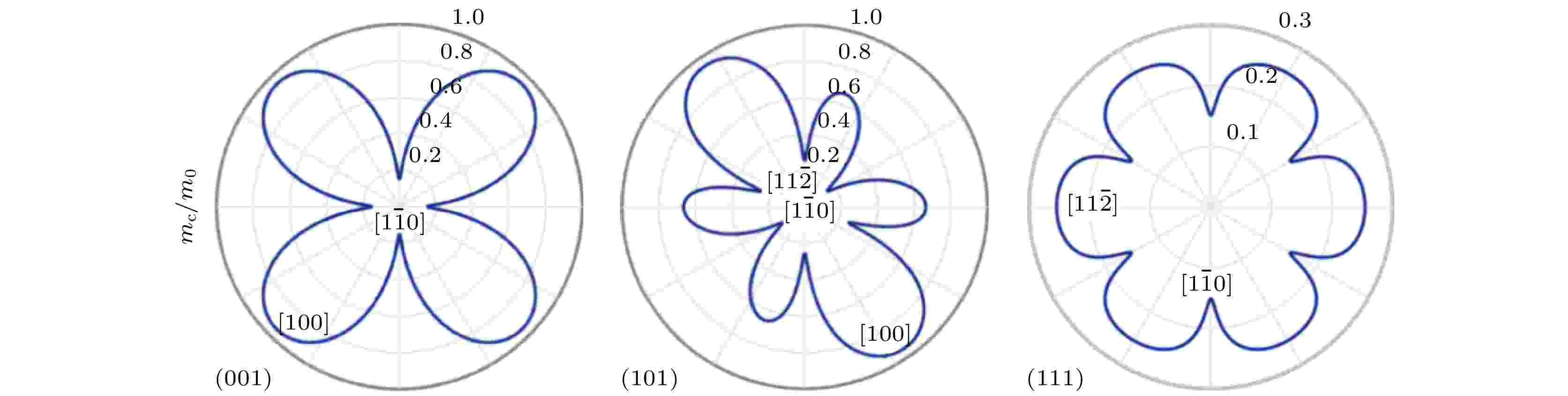图 2 (001), (101), (111)剖面任意晶向电子电导率有效质量(极坐标系下)[14]Figure2. (001), (101), (111) cross-section arbitrary crystal orientation electron conductivity effective mass (in polar coordinate system)[14].
据此, 我们提出, 一方面优化选用
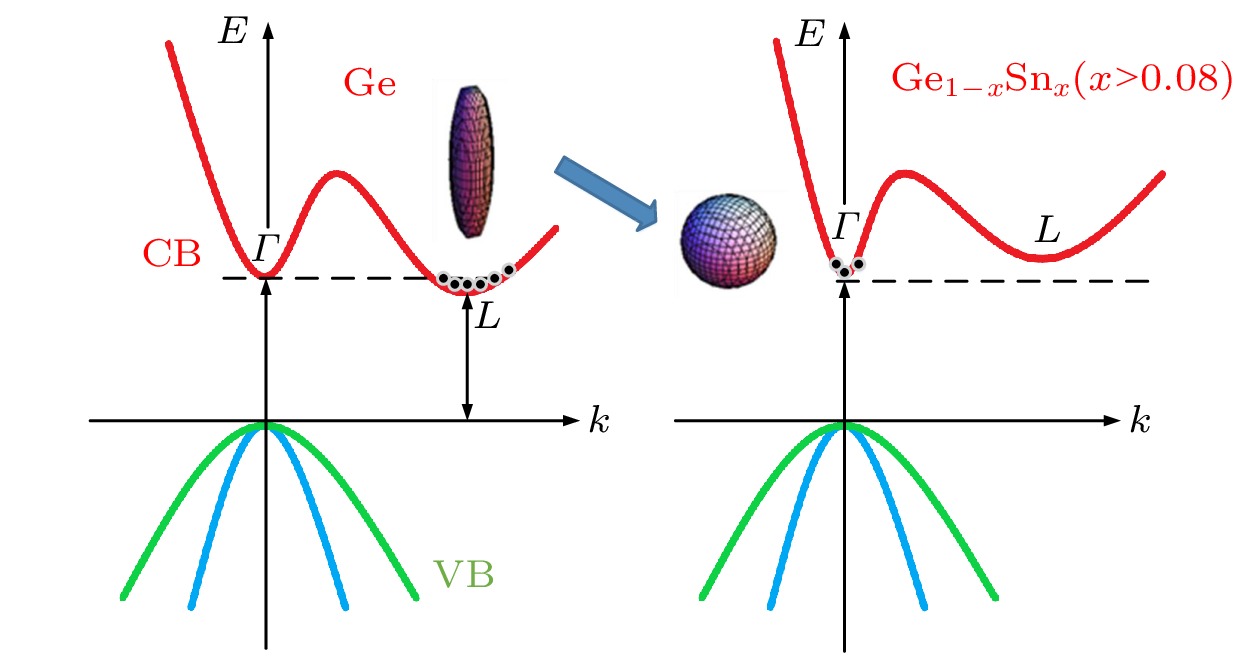图 3 Sn合金化致Ge带隙类型转变示意图[19]Figure3. Schematic diagram of Ge band gap type transition caused by Sn alloying[19].
2
2.2.亲和能设计
进一步讨论Ge半导体电子亲和能各向异性问题, 第一性原理仿真结果如图4所示(详见我们的工作[20]). 结果表明, [100]晶向Ge功函数为4.604 eV, [110]晶向为4.495 eV, [111]晶向为4.55 eV.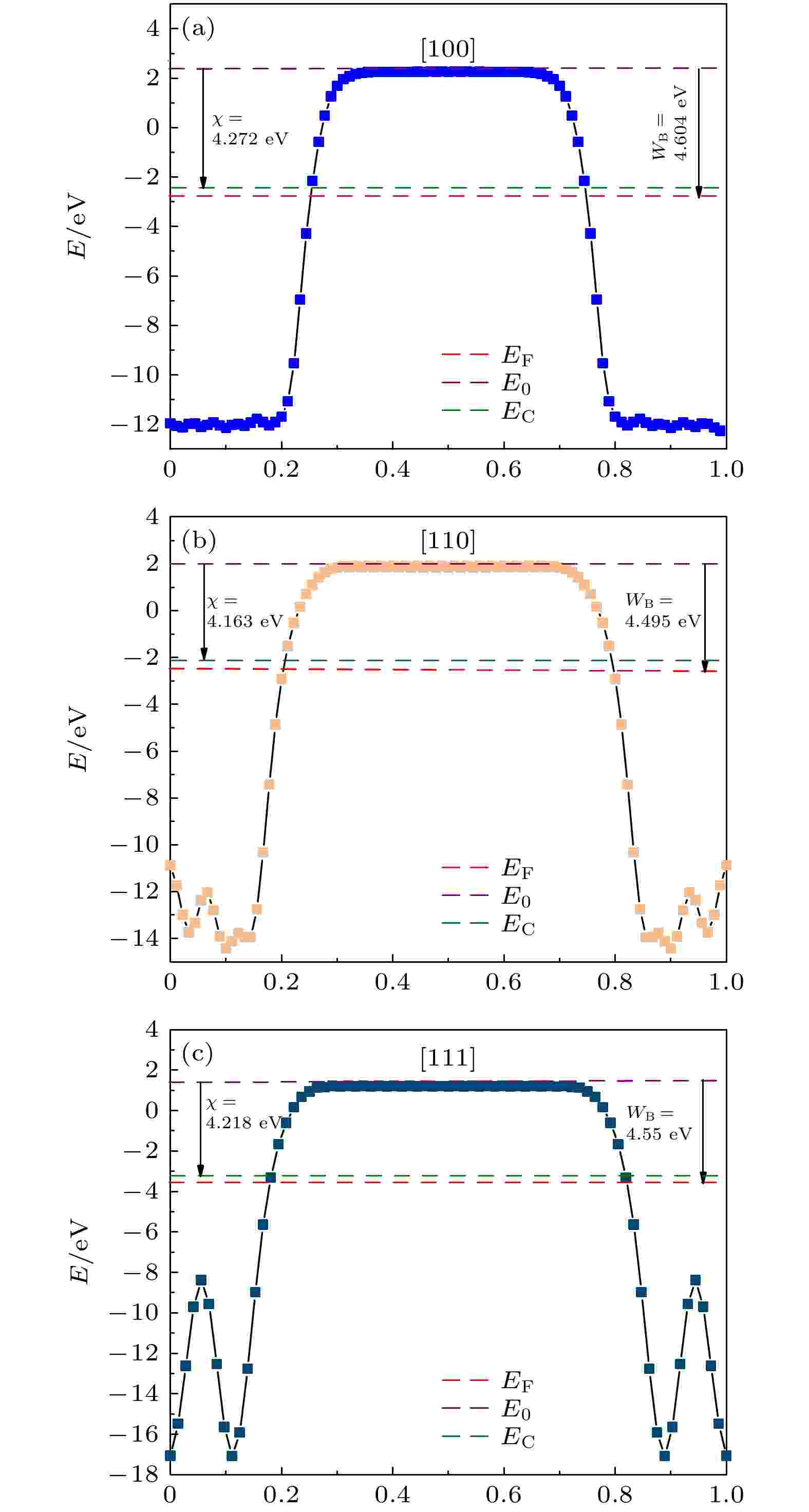
图 4 (100), (110), (111)晶面Ge半导体功函数[18,19]Figure4. (100), (110), (111) crystal plane Ge semiconductor work function[18,19].
利用半导体亲和能与功函数之间的关系[20], 可进一步解得, [100]晶向Ge亲和能为4.272 eV, [110]晶向为4.163 eV, [111]晶向为4.218 eV. 与(110)高电子迁移率晶面相比, 选用(100)晶面Ge作SBD的金半接触面, 可增大半导体亲和能, 有利于进一步降低SBD开启电压, 这与前述为增大电子电导率有效质量而选用(100)晶面方案不产生矛盾.
图 5 (a) 新型SBD器件剖面示意图含层结构材料物理参数和几何结构参数; (b)传统SBDFigure5. (a) The cross-sectional schematic diagram of the new SBD device contains the physical parameters and geometric structure parameters of the layered structure material; (b) the traditional SBD.
肖特基结采用金属W, 欧姆结采用金属Al, 且阴极设置于在n+ DR-GeSn层, 能够避免n+ DR-GeSn与Si衬底之间界面差致器件性能退化的问题; 轻掺杂n–区域, 包括
图6为Silvaco软件器件仿真结构和网格设置图, 这里要补充说明两点: 1) 考虑器件软件仿真收敛效率, 仿真结构中去掉了Si衬底和Ge缓冲层, 但不会影响仿真结果; 2) 网格设置过程中, Ge帽层与n– GeSn层之间、n– GeSn层与n+ GeSn层之间网格相对于其他区域更加密集, 以保证仿真结果收敛.
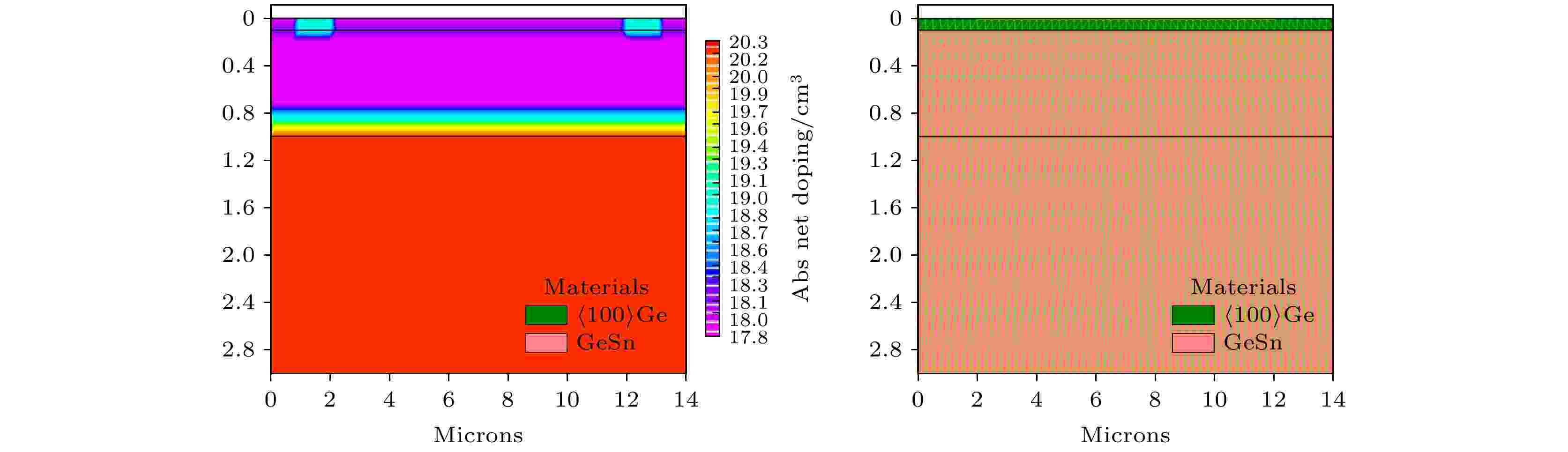图 6 新型SBD器件Silvaco仿真结构和网格设置截图Figure6. A screenshot of the Silvaco simulation structure and grid settings of the new SBD device.
从有效质量和亲和能两个材料物理指标设计出发, 提出引入
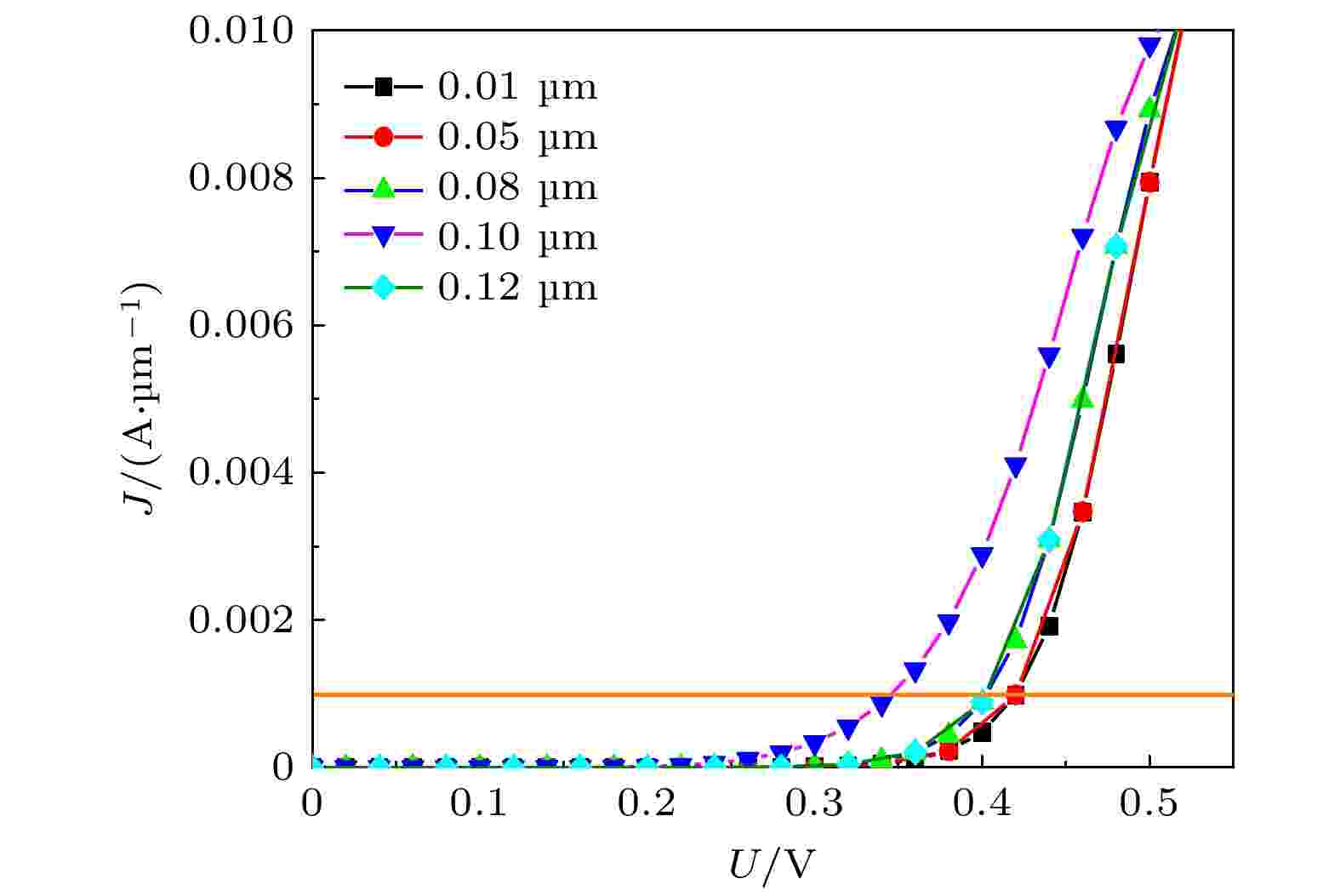图 7 不同厚度
Figure7. Forward V-J characteristic curve of new SBD device with different thickness
图8(a)和图8(b)中Ge, GeSn和Ge_on_GeSn三条曲线分别对应传统Ge SBD, GeSn SBD以及带Ge帽层新型GeSn SBD的伏安特性、电容特性器件仿真结果, 由图8(a)可见, 相对于传统Ge基SBD器件, 带Ge帽层新型GeSn SBD开启电压明显降低. 同时, 器件仍然保持了优异的整流非线性特性.
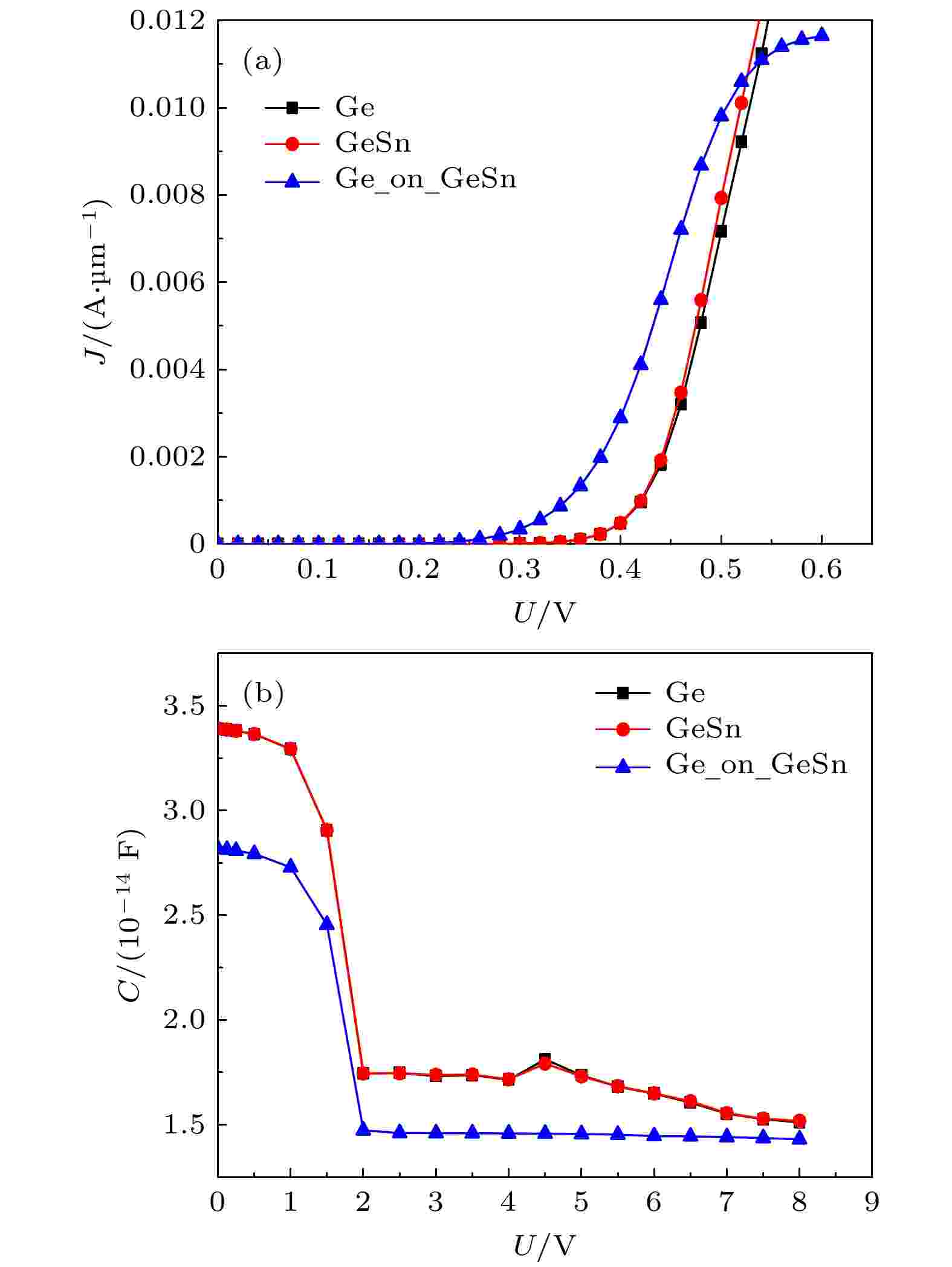图 8 三种Ge基SBD器件伏安特性、电容特性仿真结果Figure8. volt-ampere characteristic Capacitance-voltage characteristic simulation results of three Ge-based SBD devices.
如前所述, 带Ge帽层新型GeSn SBD低开启电压、非线性优异主要源于大有效质量、大亲和能、高迁移率的复合材料设计, 符合前期设计预想. 电容特性方面, 由图8(b)可见, 相对于传统Ge基SBD器件, 带Ge帽层新型GeSn SBD电容有一定程度降低, 这有利于后续对2.45 G弱能量密度RF信号整流效率的提升[21,22]. 依据器件物理相关知识, SBD电容与材料亲和能等物理参数相关, 其下降的原因也主要是因为新型复合材料的引入所致.
图9为带Ge帽层新型GeSn SBD的器件击穿特性仿真结果, 由图可见, 当所施加电压达到约11.4 V时, 器件会发生反向击穿, 反向饱和电流的增大导致器件更容易被击穿, 但是击穿电压的变化在后续仿真中对弱能量密度区域的整流效率影响并不大.
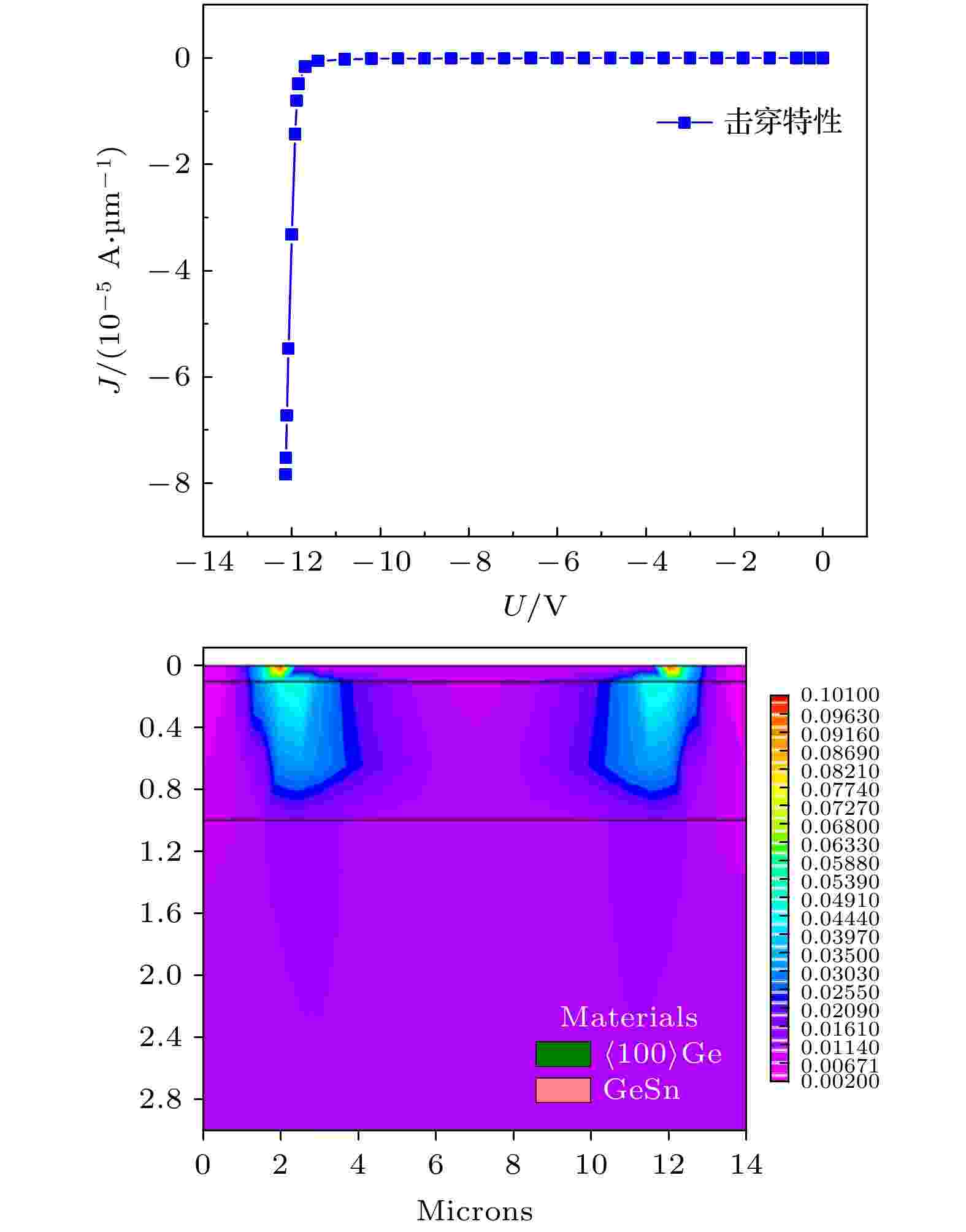图 9 新型Ge基SBD器件击穿特性仿真结果Figure9. Simulation results of the breakdown characteristics of the new Ge-based SBD device.
将所设计的带Ge帽层新型GeSn SBD、传统Ge SBD以及GeSn SBD正向伏安特性曲线、反向伏安特性曲线以及在2.45 GHz频率下的电容特性曲线带入Cadance Model Editor软件中, 提取器件的SPICE参数如表1所列.
| 参数 | $ {B}_{v}/ $V | $ {C}_{j0} $/fF | $ {E}_{\rm{G}} $/eV | $ {I}_{\rm{S}} $/A | N | $ {R}_{\rm{S}} $/${\Omega }$ | M |
| Ge | 18.9 | 36 | 0.69 | 9.6235 × 10–11 | 0.999 | 2.9 | 0.5072 |
| GeSn | 19 | 36.2 | 0.69 | 9.628 × 10–11 | 0.999 | 2.8 | 0.5073 |
| Ge_on_GeSn | 11.4 | 30 | 0.69 | 1.0437 × 10–8 | 1.106 | 11.6 | 0.4037 |
表1三种Ge基SBD器件SPICE参数表
Table1.SPICE parameter table of three Ge-based SBD devices.
将所设计的肖特基二极管SPICE参数带入ADS仿真软件中, 采用图10所示仿真电路, 使用阻抗自匹配模型, 对整流电路进行优化.
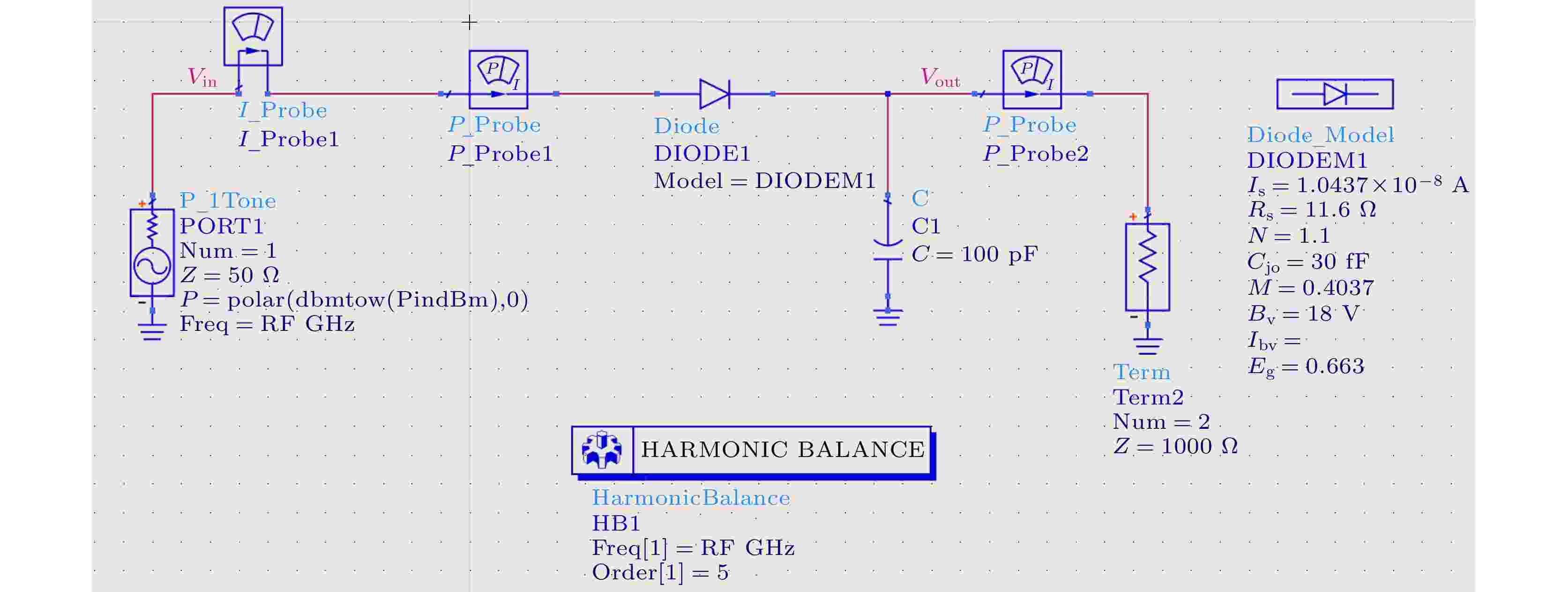图 10 新型Ge基SBD器件整流测试电路Figure10. New Ge-based SBD device rectification test circuit.
图11为仿真结果, 将电路匹配在–10 dBm附近, 匹配结果良好. 在输入能量为–10 dBm时, 能量转换效率达到了35.1%; 在输入能量为–20 dBm时, 能量转换效率达到了7.7%. 与传统Ge肖特基二极管相比, 该新型Ge基肖特基二极管在输入能量为–10 — –20 dBm的弱能量工作区域, 能量转换效率整体提升约10%.
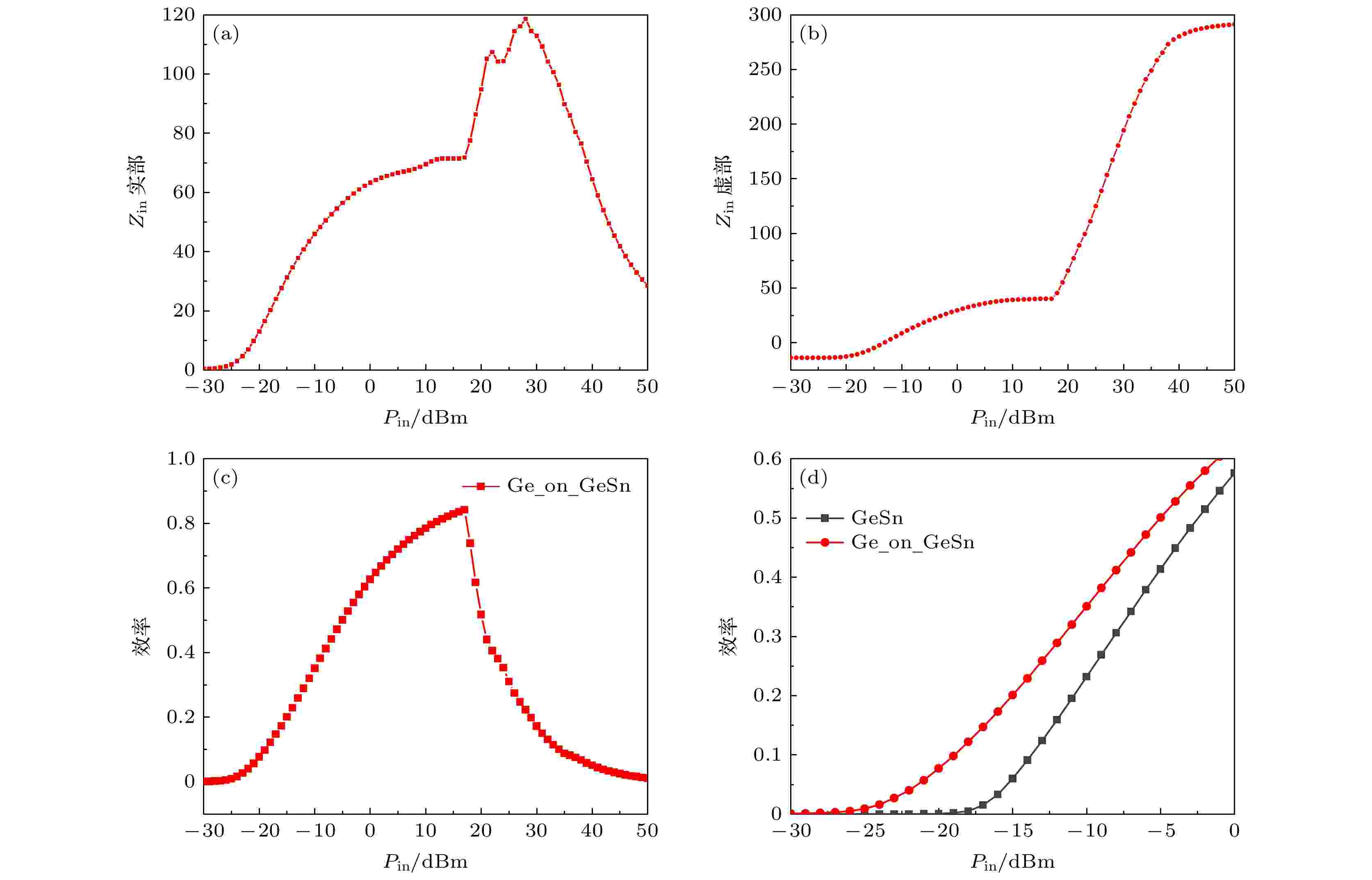图 11 整流电路的仿真结果, 输入能量与 (a)阻抗实部、(b)阻抗虚部、(c)整流效率以及(d)弱能量区域整流效率的关系Figure11. Simulation results of the rectifier circuit, the relationship between the input energy and (a) the real part of the impedance (b) the imaginary part of the impedance (c) the rectification efficiency (d) the rectification efficiency in the weak energy region.
