摘要:频率分辨光学开关(frequency-resolved optical gating, FROG)法是目前测量超短激光脉冲的主要方法之一. 针对其常用的主成分广义投影重构(principal component generalized projections, PCGP)算法在处理大矩阵FROG谱图时速度会减慢及存在噪音时准确度下降的缺点, 本文提出一种基于搜寻者优化算法的FROG算法. 该算法在直接测量脉冲光谱分布的基础上, 通过搜索脉冲频域相位的几个色散系数, 从而恢复脉冲的结构. 由于新算法主要在频域上进行运算, 流程比PCGP算法简便很多, 收敛速度和准确性都有明显改善. 通过数值模拟方法重构了多个不同结构的超短脉冲, 分析讨论了无噪音和在不同噪音水平下该算法的准确度. 计算结果充分展示了该算法重构脉冲的速度快、准确度高的特点, 在无噪音条件下其准确度比PCGP提升了3个数量级以上.
关键词: 频率分辨光学开关法/
超短脉冲/
实时测量/
优化算法

English Abstract

全文HTML

--> --> -->

频率分辨光学开关(frequency-resolved optical gating, FROG)法是目前常用的超短激光脉冲测量技术^[1-3], 它可以完整地恢复脉冲信息. 其中二次谐波频率分辨光学开关(second-harmonic generation FROG, SHG-FROG)法因灵敏度高, 可测量较弱能量的脉冲而应用广泛^[4-6]. FROG方法的输出信号是一个二维光谱图, 需要采用迭代逼近算法来重构脉冲的形状. 为了提高脉冲重构的速度和准确性, 达到实时测量脉冲的目的, 人们不断地对FROG重构算法进行改进^[7-10]. 其中广义投影(generalized projections, GP)算法^[7-11]适用于各种结构的FROG技术的脉冲重构, 其收敛性能和鲁棒性都很好. 在GP算法基础上, Kane^[8,12-14]提出了主成分广义投影(principal component generalized projections, PCGP)算法, 它通过脉冲的外积矩阵构建FROG谱图, 然后用奇异值分解(singular value decomposition, SVD)或者幂方法选择主成分因子的方法, 代替GP算法的最小化搜寻方式, 计算速度比GP算法快了2倍以上^[8]. 目前, GP和PCGP算法作为主流的FROG算法, 被应用于各种超短脉冲的测量^[15-17]. 利用全局搜索算法实现的FROG算法也分别被提出, 例如利用模拟退火(simulated annealing, SA)算法^[9]和遗传算法(genetic algorithm, GA)^[10]实现FROG技术的脉冲重构.
然而, GP算法的脉冲重构速度相对较慢^[8]; PCGP算法处理存在噪音的FROG谱图时重构出来的脉冲相位与强度不能很好吻合^[12], 用单一矩阵构建的FROG谱图与实际图像存在偏差^[14,18], 以致重构脉冲的误差较大^[12]. 在恢复复杂脉冲时, PCGP算法的收敛性通常不太理想, 尽管Hause等^[19]通过修改标准的PCGP算法流程降低了较差收敛的概率, 但没有彻底解决这个问题. Kane^[20]在2017年提出一种基于PCGP的改进算法, 利用多个外积矩阵之和来构造FROG谱图, 在不影响收敛速度的情况下算法的鲁棒性可提升50%. 基于SA和GA的FROG算法则受经典SA和GA收敛速度的限制, 它们重构脉冲的速度比较慢.
总之, GP和PCGP算法未能同时兼顾重构脉冲的准确性和实时性, 其他基于全局搜索算法的重构方法也只能牺牲速度以保证重构脉冲的准确性. 这意味着在实时并准确地重构超短脉冲的需求方面, 现有FROG算法的表现未能令人满意.
针对以上问题, 我们提出了一种新的FROG算法. 该算法在实验上记录待测脉冲的FROG谱图和光谱分布, 利用搜寻者优化算法(seeker optimization algorithm, SOA)^[21-23]搜索脉冲的色散系数, 这些色散系数可决定脉冲的光谱相位曲线. 知道了光谱分布和光谱相位曲线即可确定脉冲的形状. 理论模拟结果显示, 基于SOA的FROG算法具有搜索速度快, 收敛准确度高和鲁棒性强的特点; 与PCGP算法比较, 其迭代速度稍快一些, 重构脉冲的准确度更高, 尤其对具有高阶色散的脉冲重构有较为突出的优势, 如在无噪音条件下其准确度比PCGP提升了3个数量级以上.

超快激光脉冲的结构可分别采用电场振幅的时域表示E(t)和频域表示E(ω)两种形式:

$E\left( t \right) = \sqrt {I\left( t \right)} \exp \left\{ {{\rm{i}}\left[ {{\omega _0}t - \phi \left( t \right)} \right]} \right\},$

$E\left( \omega \right) = \sqrt {S\left( \omega \right)} \exp \left[ {{\rm{i}}\varphi \left( {\omega - {\omega _0}} \right)} \right],$

其中, I(t)和?(t)分别是脉冲在时域上的强度包络和相位曲线, ω₀是中心圆频率, S(ω)和φ(ω)是脉冲的光谱强度和光谱相位分布. E(t)和E(ω)满足傅里叶变换关系, 只要测得其中一个, 脉冲的结构就唯一地确定了.
由锁模激光振荡器和超快激光放大器输出的超短脉冲, 其光谱相位φ(ω)通常展现为一条平滑曲线, 可在中心频率ω₀处作泰勒级数展开

$\varphi \left( \omega \right) = \sum\limits_{k = 0}^\infty {\varPhi ^{\left( k \right)}}\left( {{\omega _0}} \right)\frac{{{{\left( {\omega - {\omega _0}} \right)}^k}}}{{k!}},$

式中$ {\varPhi }^{\left(k\right)}\left({\omega }_{0}\right)\!=\!{\left.\dfrac{{\partial }^{k}\varphi \left(\omega \right)}{\partial {\omega }^{k}}\right|}_{\omega ={\omega }_{0}} $为第k阶色散系数. 其中0阶色散系数称为载波包络相位, 1阶系数为群延迟, 这二者对脉冲结构的影响不大. 2—5阶系数分别为群延迟色散(group-delay dispersion, GDD)、3阶色散(3^rd order dispersion, TOD)、4阶色散(4^th order dispersion, FOD)和5阶色散(5^th order dispersion, FVOD), 它们对脉冲的形状结构起着主要的决定作用.
由(2)式和(3)式可知, 如果脉冲光谱S(ω)已知, 则只要测出光谱相位φ(ω)的各阶色散系数, 即可确定脉冲的结构. 由此, 我们提出一种新的FROG算法, 在直接用光谱仪测量S(ω)的基础上, 选择一种优化算法搜索φ(ω)的各阶色散系数(特别是2—5阶系数), 使之相对应的SHG-FROG谱图与实验测得的谱图基本相符即可.
我们考察或尝试了包括SA, GA, 进化算法和粒子群算法等多种优化算法, 最终选择了SOA用于FROG的脉冲重构.
SOA是一种新型智能的全局搜索算法, 它模仿人类的经验、记忆、不确定性推理和彼此合作互通信息等搜索行为, 能够根据情况的变化不断调整多个参数的搜索方向和搜索步长, 因而兼具全局搜索和局部优化的特点, 能够有效地避免在搜索过程中陷于局部极小的境地, 目前它在多种应用上表现出优越的性能^[21-24]. 该算法要设定S个搜寻者, 每个搜寻者有M个搜索维度. 每个搜寻者各个维度的搜索方向被自己的利己行为、预动行为和他人的利他行为所决定, 而每次搜索的步长则由基于模糊推理规则的不确定性推理所决定.
基于SOA的FROG重构算法(SOA-FROG)的具体流程如下:
1) 用实验方法记录待测脉冲的SHG-FROG谱图I_frog(ω, τ)(为N × N矩阵), 同时用光谱仪记录脉冲的光谱分布S(ω), 并设定FROG迭代算法的容许误差ε.
2) 根据SOA规则选定S个搜寻者Ψ_n(n = 1, 2, ···, S), 每个搜寻者包含M个色散系数, 其随机初始位置为Ψ_n (GDD₀, TOD₀, FOD₀, FVOD₀, ···).
3)对每个搜索者Ψ_n, 结合已知的S(ω)可导出对应的猜测脉冲的频域表示E(ω). 对E(ω)作傅里叶变换可得到时域表示E(t), 即可利用(4)式求出相应的SHG-FROG谱图I_calc(ω, τ)(亦为N × N矩阵):

${{{I}}_{{\rm{calc}}}}\left( {\omega ,\tau } \right) = {\left| {\int E\left( t \right)E\left( {t - \tau } \right){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t} \right|^2}. $

4)利用(5)式计算各个搜寻者当前所对应的误差函数G:

$G = \sqrt {\frac{1}{{{N^2}}}\sum\limits_{i,j = 1}^N {{\left[ {{I_{{\rm{calc}}}}\left( {{\omega _i},{\tau _j}} \right) - {I_{{\rm{frog}}}}\left( {{\omega _i},{\tau _j}} \right)} \right]}^2}} . $

5) 判断是否其中一个搜寻者已满足迭代终止条件G ≤ ε. 若还没有, 则由SOA搜索规则去确定每个搜寻者各个维度新的搜索方向和步长, 从而得到下一轮循环的色散系数组合Ψ_n(GDD, TOD, FOD, FVOD, ···).
6) 重复3)—5)的循环迭代过程, 直至其中一个Ψ_n满足终止条件G ≤ ε即可停止搜索, 然后输出其对应的脉冲结构E(ω)和E(t)作为脉冲重构结果.
可以看出, SOA-FROG算法的迭代运算主要在频域上进行, 其流程步骤要比PCGP算法简便很多; PCGP算法则要对FROG谱图作时域-频域的反复转换及相应的SVD运算等一系列矩阵操作. 估计在PCGP算法一个迭代循环的时间内, 新算法已经循环搜索了5次以上. 这对于处理大数据阵列如512 × 512, 1024 × 1024以上的情形尤其有利. 另外, 由于光谱分布S(ω)已知, 该算法只需要搜索几个色散系数, 理应比PCGP算法具有更快的收敛速度.

采用数值模拟的方法, 分析SOA-FROG算法分别在无噪音和有噪音条件下的准确度及达到收敛的速度, 并与PCGP算法作对比.
为方便起见, 设定要重构的所有待测脉冲具有相同的高斯分布的光谱强度S(ω)(如图1所示), 不同的待测脉冲只是色散系数有差异. 其中脉冲的中心圆频率为ω₀ = 2π × 375 THz, 光谱宽度为Δω = 2π × 25 THz. 脉冲SHG-FROG谱图的时间抽样点数为N = 256, 抽样间隔为1.5 fs.
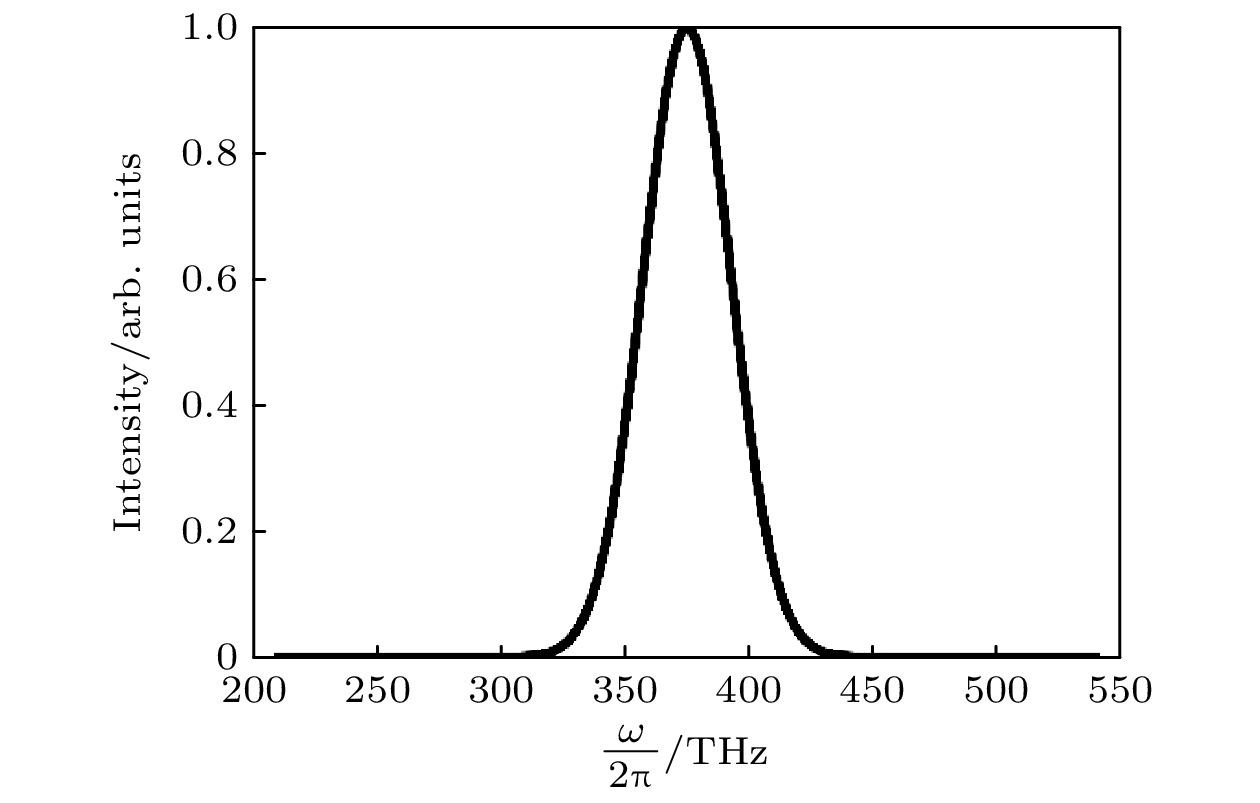图 1 所有待测脉冲的光谱强度分布
Figure1. Spectral intensity of all the test pulses in context.

2

-->

3.1.脉冲重构的准确度

3 -->

3.1.1.无噪音的情形

设定SOA-FROG算法的迭代次数为1500次. 考察两类待测脉冲的结构: 一是脉冲的色散系数只有GDD和TOD是主要的, 而更高阶的系数较小可以忽略. 这时可设置搜寻者数目S = 3, 空间维度M = 2, 即只搜索GDD和TOD. 我们对100个色散系数落在$\left| {{\rm{GDD}}} \right| < 200\;{\rm{f}}{{\rm{s}}^2}, \;\left| {{\rm{TOD}}} \right| < 2500\;{\rm{f}}{{\rm{s}}^3}$, $ \left| {{\rm{FOD}}} \right| < 10\;{\rm{f}}{{\rm{s}}^4}$和$\left| {{\rm{FVOD}}} \right| < 100\;{\rm{f}}{{\rm{s}}^5}$范围内的随机脉冲进行了重构计算. 数值模拟的结果为当算法收敛时误差G值均小于10^–4, 其中G < 10^–6的脉冲有28个, 10^–6 < G < 10^–5的脉冲70个, 而10^–5 < G < 10^–4的只有2个, 误差平均值$ \bar{G}=2.30\times {10}^{-6} $(如图2灰柱所示). 另一类脉冲是既有一定量的GDD和TOD色散, 更高阶色散FOD和FVOD也不可忽略, 这时就需要增加搜索维度. 我们设定搜寻者数目S = 3, 空间维度M = 4, 即搜索GDD, TOD, FOD和FVOD. 对100个色散系数落在$ \left| {{\rm{GDD}}} \right| < 200\;{\rm{f}}{{\rm{s}}^2} $, $\left| {{\rm{TOD}}} \right| < 2500\;{\rm{f}}{{\rm{s}}^3}$, $\left| {{\rm{FOD}}} \right| < $$ 5000\;{\rm{f}}{{\rm{s}}^4} $ 和$ \left| {{\rm{FVOD}}} \right| < 10000\;{\rm{f}}{{\rm{s}}^5}$范围内的随机脉冲进行了重构计算. 模拟结果为重构脉冲的误差平均值$ \bar{G}=2.54\times {10}^{-5} $, 其中FROG误差G < 10^–6的脉冲有66个, 10^–6 < G < 10^–4的脉冲有31个, 而G > 10^–4的脉冲只有3个(如图2黑柱所示).
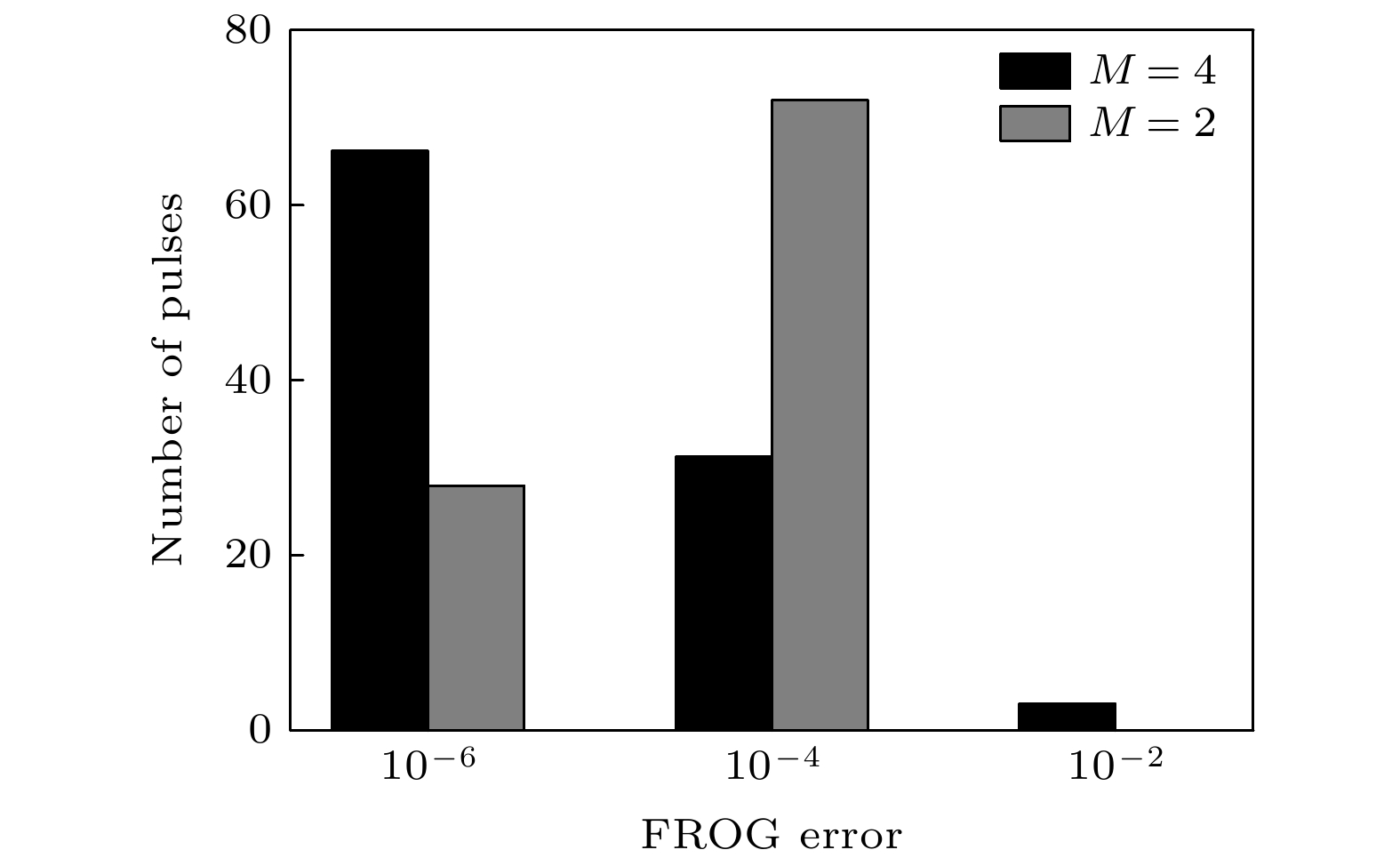图 2 两类色散结构的随机脉冲经过SOA迭代运算1500次后的误差分布
Figure2. Distributions of FROG error at three levels for random ultrashort pulses of two chirped features after 1500 circles of iteration with SOA.

根据FROG算法的规则, 在无噪音时G ≤ 10^–4代表所用算法能严格收敛. 所以在FOD及以上色散系数可忽略时, 本文提出的SOA-FROG算法在迭代1500次以内完全达到了严格收敛的条件; 而当脉冲的FOD和FVOD不可忽略, 但落在上述限定范围时, 绝大部分脉冲在迭代1500次后也实现了算法的严格收敛. 个别脉冲可能需要更多的迭代次数或者设定不同的初始随机色散系数进行搜索应能达到严格收敛条件.
表1列出了上述运算中处理过的3个脉冲的原始色散系数, 以及分别对它们随机设定初始色散系数然后进行30次重构运算后所得到的平均结果. 可以看出SOA的平均误差$ \bar{G} $基本上低于10^–5, 重构得到的色散系数值甚至可准确到个位数(忽略时间方向上的模糊). 作为对比, 利用基于文献[13]的PCGP算法标准程序对这3个脉冲在相同条件下进行了重构, 其平均误差就比较大. 从表1可看出SOA的准确度比PCGP算法提升了至少3个数量级.

脉冲编号	原始脉冲色散系数					SOA-FROG计算结果						PCGP结果
	GDD/fs2	TOD/fs3	FOD/fs4	FVOD/fs5		GDD/fs2	TOD/fs3	FOD/fs4	FVOD/fs5	$ \bar{G} $		$ \bar{G} $
1 (M = 2)	150	–2000	5	80		150	–2000	0	0	4.0 × 10–6		1.1 × 10–2
2 (M = 4)	50	30	520	600		50	30	520	600	6.4 × 10–9		7.2 × 10–3
3 (M = 4)	100	–500	–3652	8000		100	–500	–3652	7999	1.2 × 10–5		9.8 × 10–3

表1无噪音情形下几个脉冲的重构结果
Table1.Reconstructed results of three test pulses in cases without noise.

FROG误差G越小, 恢复的色散系数就越准确. 以表1中的脉冲3为例, 其中一次重构结果为G = 9.2 × 10^–5, 对应的色散系数为(100, –492, –3628, 6212), 前3个系数与原始脉冲比较相近; 另一次重构误差为G = 2.2 × 10^–6时, 恢复的色散系数为(100, –500, –3652, 7962), 4个系数与原始脉冲相差不多; 还有一次重构结果为G = 4.2 × 10^–8, 恢复的色散系数与原始脉冲完全一样. 这个结果比文献[25, 26]的结果好很多, 其中文献[25]在相干自相关上使用GA与保证优化相结合的算法, 文献[26]在相干自相关上使用进化算法, 它们模拟恢复的色散系数与原始值差别都比较大.
图3展示了重构脉冲3时采用SOA和PCGP算法的误差分别为G = 4.2 × 10^–8和G = 9.8 × 10^–3时所对应的脉冲结构在时域上的差异. 可以看出SOA的表现非常好, 它重构的脉冲准确还原了原始脉冲的结构, 而PCGP算法的结果明显偏离真实情况.
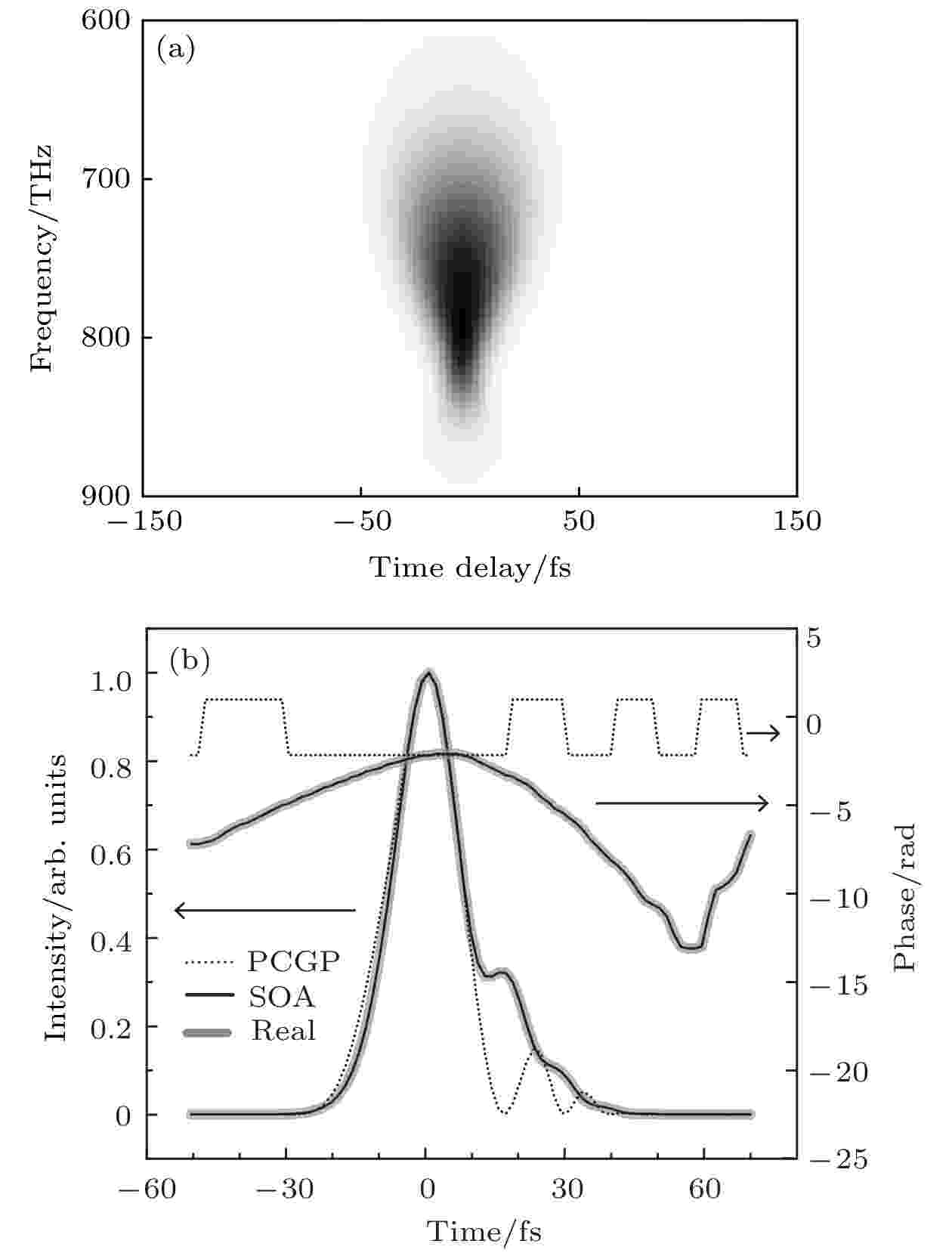图 3 (a)脉冲3的原始SHG-FROG谱图; (b) SOA和PCGP两种算法重构出的脉冲3的时域强度和相位
Figure3. (a) Original SHG-FROG trace of pulse 3#; (b) reconstructed intensities and phases in time domain of the pulse by SOA and PCGP algorithm, respectively.

3 -->

3.1.2.有噪音的情形

由于泊松噪音可以模拟暗电流等真实的实验噪音, 因此利用泊松噪音作为加性噪音, 并设其泊松分布的均值为5. 可将不同程度的噪音量添加在SHG-FROG谱图上, 即:

$\begin{split}I_{{\rm{frog}}}^{{\rm{noise}}}\left( {{\omega _i},{\tau _j}} \right) =\;& {I_{{\rm{frog}}}}\left( {{\omega _i},{\tau _j}} \right) + {\rm{noise}}\left( {{\omega _i},{\tau _j}} \right) \\&\times {\rm{max}}\left\{ {{I_{{\rm{frog}}}}\left( {{\omega _i},{\tau _j}} \right)} \right\}. \end{split}$

为了直观地了解SOA-FROG算法在FROG谱图有噪音下的表现, 考察对脉冲1的重构情况, 其中噪音平均值分别取FROG谱图最大值的1%, 5%, 10%和20% (加入噪音之后应对谱图做归一化处理). 在使用SOA-FROG算法重构脉冲前, 要先对FROG图进行预处理. 计算角落60个点的平均值作为背景噪声, 然后让整个FROG谱图扣除这个背景噪声; 扣掉背景噪音之后, 必要时还可对FROG谱图做3 × 3的均值滤波处理.
在每个噪音水平下运行SOA-FROG算法100次, 设置最大搜索次数为300. 图4为不同噪音水平下利用SOA对脉冲1进行重构的结果. 其中图4(a)展示了只扣除背景噪音、扣除背景噪音加3 × 3均值滤波与未扣除背景噪音时获得的FROG误差G的对比. 可知扣除背景噪音后的误差G小了约50%, 加上均值滤波后效果要稍好一些.
图 4 不同噪音水平下用SOA对脉冲1进行重构所对应的　(a) FROG误差、(b)强度误差和(c)相位误差
Figure4. (a) FROG error, (b) intensity error, and (c) phase error of test pulse 1# reconstructed by SOA with different noise levels.

脉冲重构的准确性通常用时域上的强度误差GI和相位误差GP来表征, 具体定义请参看文献[27]. 由图4(b)和图4(c)可知, 在1%和5%的噪音水平下GI和GP均较小; 而在10%和20%的噪音水平下, 虽然收敛时的FROG误差比噪音水平低得多, 且统计偏差也不大, 但是强度误差和相位误差的平均值增大; 且随着噪音的增大, 统计偏差也在变大.
经过滤波处理后, 在较大噪音条件下, GI和GP比未滤波时要小很多; 而在噪音较小时滤波反而恶化了重构结果, 原因是均值滤波可能会滤掉一些脉冲结构的细节, 特别是关于高阶色散的一些信息.
在不同噪音水平下用SOA-FROG算法重构脉冲1的模拟结果见图5. 第1列是原始FROG谱图加上噪音后的图像, 第2列和第3列分别是为重构出来的FROG谱图及I(t)和?(t)曲线. 其中噪音水平为1%和5%的重构结果是只扣本底但未做均值滤波的条件下得到的; 而10%和20%的结果是扣本底且实施均值滤波下得到的. 可以看出, 重构脉冲与原始脉冲在时域的强度包络和相位曲线的偏差也随着噪音的增加而增大.
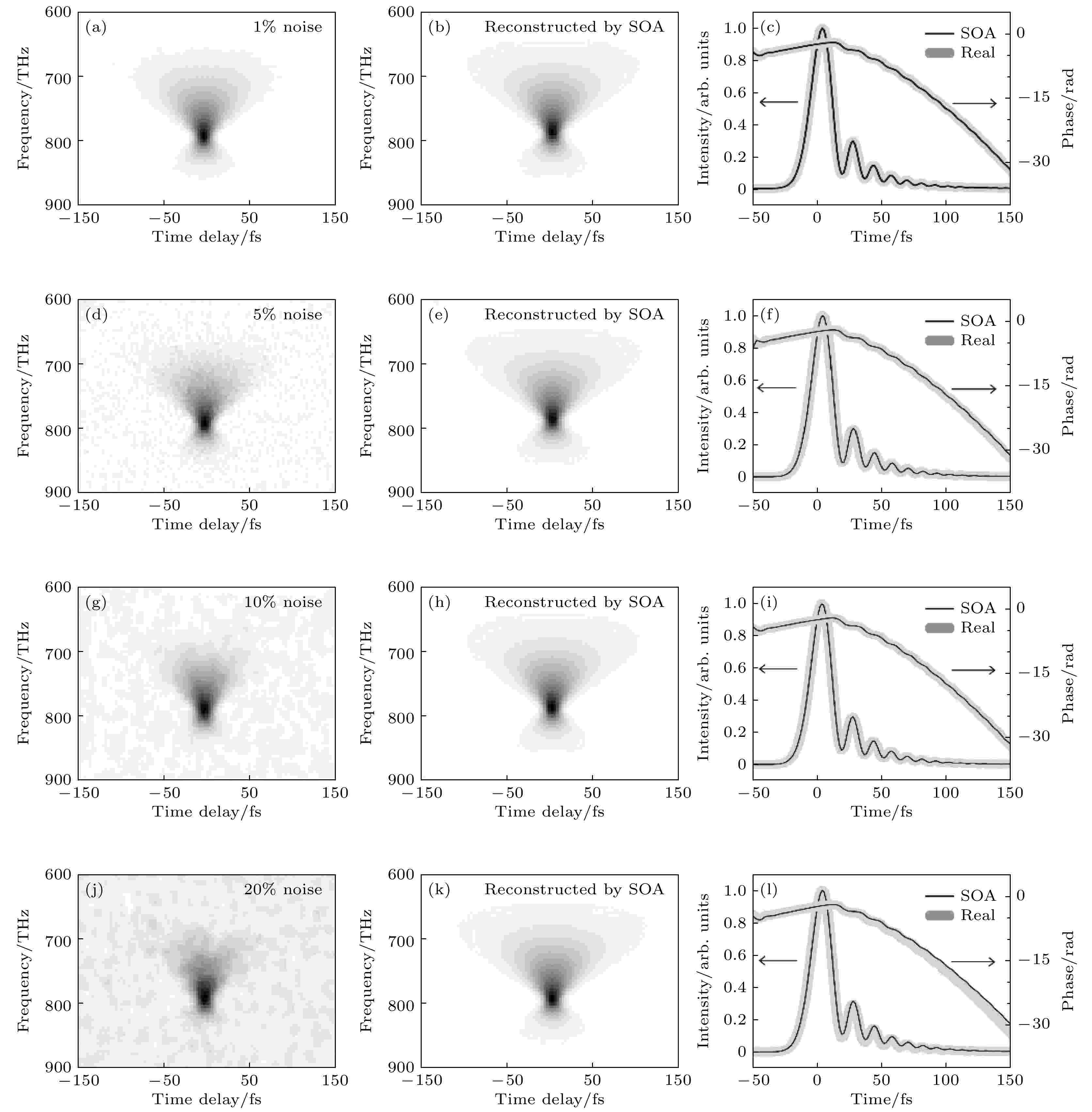图 5 不同噪音水平下重构脉冲1得到的FROG谱图和时域曲线
Figure5. Reconstructed FROG traces, intensities and phases in time domain of test pulse 1# by SOA algorithm with different noise levels.

作为对比, 也计算了相同噪音条件下采用PCGP算法的重构结果, 其中对FROG谱图也作了相同的扣除背景和滤波处理. 两种算法在不同噪音水平下的重构准确度的比较见表2. 可以看出噪音的增加导致SOA重构出来的色散系数偏离原始值, 噪音越大偏离越远. 但总体而言, SOA-FROG算法对噪音不是太敏感, 即使FROG谱图存在一定的噪音, SOA仍能达到较高的准确度, 要比PCGP算法优越许多. 原因在于用光谱仪直接测量脉冲的光谱分布S(ω), 其噪音水平应远低于利用二阶非线性光学效应测量到的SHG-FROG谱图, 而SOA算法只是搜索几个色散系数, 搜索循环过程中所构建的各个猜测脉冲都并非来源于有噪音的FROG谱图, 因而该算法对噪音的耐受度较高. 可以认为实测的光谱分布S(ω)对脉冲重构的误差具有强力的抑制作用, 大大提高了噪音条件下脉冲重构的准确性. 相比之下, 用PCGP算法在同等噪音水平下得到的重构误差GI和GP远大于SOA的数值, 是由于在迭代循环过程中所构建的各个猜测脉冲都来源于有噪音的FROG谱图, 这样重构出来的脉冲在时域上的强度包络和相位曲线通常会出现不规则的毛刺, 噪音越大重构准确度就越差. 至于表2中两种算法得到的误差G的差别并不大, 原因在于它是重构出来的FROG谱图与有噪音的谱图逐点相减得到的平均误差(见(5)式), 因而其数值大小与噪音水平直接相关, 不足以准确反映两种算法在脉冲重构准确度上的明显差异.

噪音水平/%	SOA-FROG的重构结果					PCGP的重构结果
	GDD/fs2	TOD/fs3	GI/%	GP/%		G/%	GI /%	GP/%	G/%
1	–150	2002	0.01	0.08		0.33	4.44	16.3	0.87
5	154	–2105	1.95	0.78		1.31	14.0	20.1	1.88
10	153	–1940	0.02	2.61		2.01	13.2	13.6	3.46
20	193	–2651	1.52	5.77		3.77	20.0	22.3	4.62

表2不同噪音水平下用SOA和PCGP算法重构脉冲1的结果比较
Table2.Comparison of reconstructed results of pulse 1# by SOA and PCGP algorithms with different noise levels.

实际上, 还对色散系数范围在$\left| {{\rm{GDD}}} \right| < 200\;{\rm{f}}{{\rm{s}}^2}, $$ \; \left| {{\rm{TOD}}} \right| < 2500\;{\rm{f}}{{\rm{s}}^3}$, $\left| {{\rm{FOD}}} \right| < 5000\;{\rm{f}}{{\rm{s}}^4}$, 以及$\left| {{\rm{FVOD}}} \right| < $$ 10000\;{\rm{f}}{{\rm{s}}^5}$的100个随机脉冲进行了有噪音条件下的重构. 其中SOA取S = 3和M = 4, 重构的结果与脉冲1的情况基本相似, 其中误差GI和GP的变化趋势分别与图4(b)和图4(c)一致, 误差水平也与图4差不多; 而同样噪音水平下PCGP的误差变化趋势也与SOA基本相似.
2 -->

3.2.脉冲的实时重构

本文SOA-FROG算法的迭代速度是很快的, 可以实现大多数脉冲的实时重构. 上述模拟计算工作的运行环境为Inter? Core^TM i5-4570 CPU(4s) @ 3.20 GHz. 当SHG-FROG谱图的尺寸为256 × 256时, SOA在设置S = 3和M = 4条件下每秒可进行100.8次迭代, 迭代1500次不超过15 s, 迭代300次仅需3 s. 且从该算法的原理上来说搜索维度M越少, 搜索速度会越快. 如果待测脉冲的高阶色散不太大, 显然取M = 2和M = 3时的收敛速度要比M = 4快很多.
如前所述, 在无噪音情形, 若以G ≤ 10^–4作为算法的终止条件, SOA-FROG算法对100个随机啁啾脉冲进行重构, 除去在1500次迭代过程中不能达到终止条件的2个脉冲, 其余98个脉冲的重构平均时间为3.5 s, 其中71个脉冲能在4 s以内完成, 见图6(a).
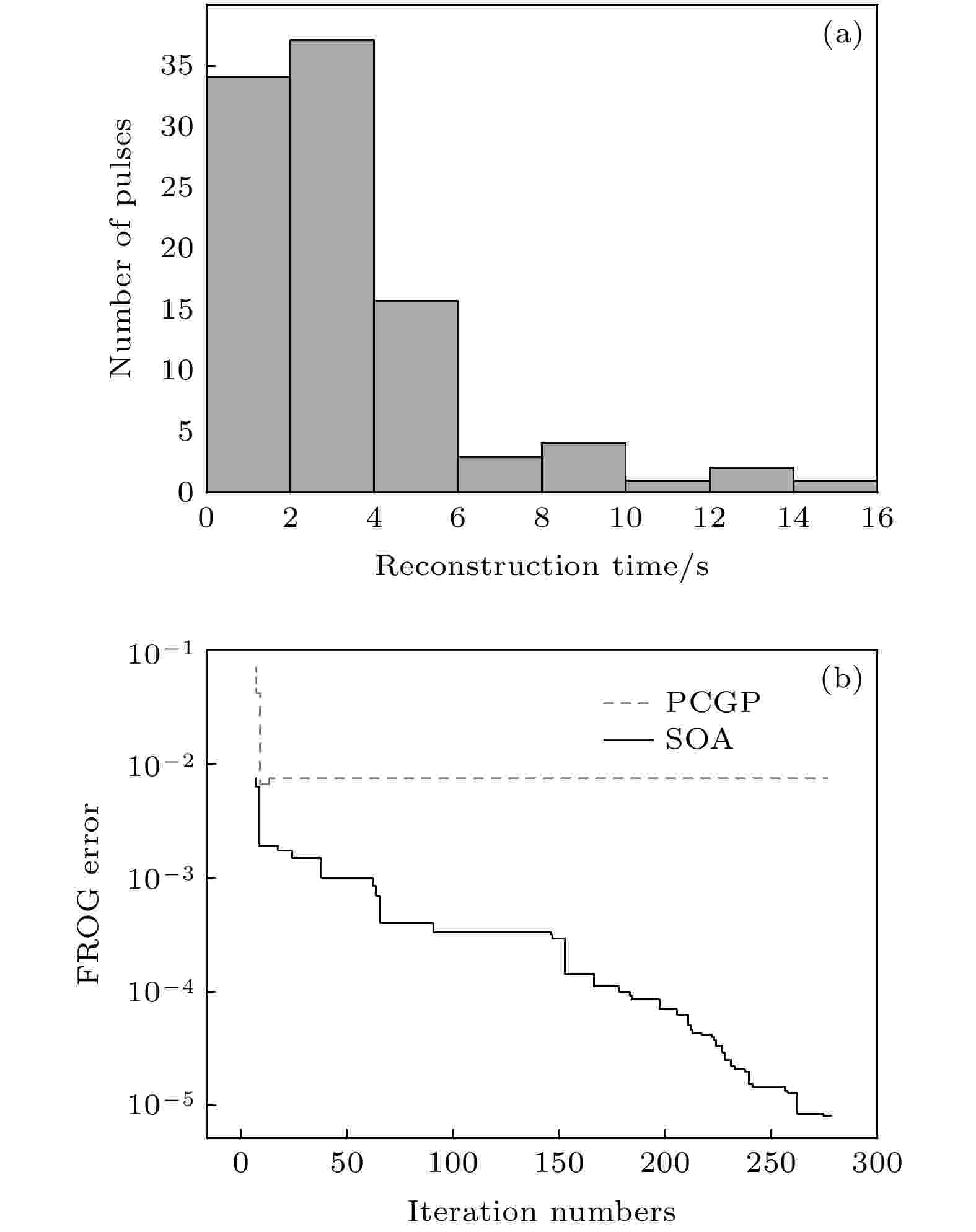图 6 (a)无噪音条件下用SOA重构随机色散脉冲的收敛时间范围; (b)两种算法对脉冲1重构迭代300次情形下其误差的演化过程
Figure6. (a) Distributions of pulse numbers via reconstruction time for SOA in cases without noise; (b) evolutions of FROG error for pulse 1# in 300 circles of iteration with SOA and PCGP algorithm, respectively.

比较而言, 在脉冲的重构过程中PCGP算法的迭代速度是GP算法的两倍左右, 且大多数时候能在100次迭代内收敛, 被认为可以实现超短脉冲的实时重构^[8]. 在本文的模拟运算环境下, PCGP算法每秒的迭代次数为21.5次(与SOA相差约5倍), 它的收敛时间约4—5 s. 即取M = 4时SOA重构脉冲的收敛速度比PCGP算法稍快一点, 但实际上两者在收敛时的脉冲重构准确度有着很明显的差别. 图6(b)给出了两种算法对表1中脉冲2的迭代运算情况. 尽管该脉冲具有较大的TOD, 用SOA迭代300次后误差G仍可降到10^–5以下; 而PCGP算法在迭代过程中误差G先是快速下降并很快达到平稳状态(从而可认为已经收敛), 但G值一直维持在7 × 10^–3附近, 远未达到严格收敛条件. 因此, 如果不对比脉冲重构准确度而只是比较PCGP算法与SOA的收敛速度, 并没有太大的意义.
而在有噪音情形下, 由于通常设置的重构容许误差ε要大一些(与噪音水平接近), 因而收敛会相对容易达到. 用SOA算法进行300次迭代(时间3 s左右)之后, 绝大部分脉冲都可完成重构流程, 并有较高的重构准确度, 详见上文的模拟结果.

本文提出了一种基于SOA的FROG算法, 它通过直接测量待测脉冲的光谱分布, 然后用SOA算法搜索该脉冲光谱相位曲线的色散系数来实现脉冲的重构. 利用数值模拟方法, 分析了在无噪音和存在几种噪音水平条件下SOA算法的重构准确度. 计算结果表明, 相较于PCGP算法, SOA-FROG算法得到的结果会更准确. 在无噪音情形下SOA-FROG算法准确度比PCGP算法提升了3个数量级以上; 在有噪音情形下, 重构的脉冲形状基本上与原始脉冲吻合. 由于该算法的迭代运算过程主要在频域上进行, 流程要比PCGP算法简便很多, 省去了许多矩阵运算和时域-频域转换的操作, 因而迭代速度和搜索速度都很快.
总之, SOA-FROG算法在重构超短脉冲方面既快速又准确, 可为超短脉冲的实时测量提供一种新的解决方案. 它不仅适于SHG-FROG, 也能用于其他基于三阶非线性光学效应的FROG方法. 当然该算法目前还存在一些限制. 例如要比PCGP算法多测量一个脉冲光谱, 另外它只适用于测量光谱相位曲线连续可微分的超短脉冲. 若要处理光谱相位存在跳变或者光谱分段等更为复杂的超短脉冲, 需要对算法作进一步的优化改进, 或者选择更为合适的优化算法. 相关研究工作有待继续.