摘要: 基于激光尾场加速的全光汤姆孙散射能够提供高质量X射线束并大大减小装置的尺寸. 与分光式相比, 自反射式的构架可以降低实验的时空同步难度, 但是由于激光尾场电子加速和汤姆孙散射过程耦合, X射线优化难度大, 目前缺乏参数优化的相关报道. 本文用数值模拟修正解析理论的方法, 定量分析了激光尾场电子加速和汤姆孙散射过程中激光和电子束的焦斑、脉宽、能量等参数变化情况, 并给出了激光在等离子体镜上的反射率, 从而实现了用解析公式计算而非数值模拟跟踪参数变化, 在保证精度的同时节约了计算时间. 另外, 利用修正后的公式优化了给定激光条件下的自反射式全光汤姆孙散射X射线, 通过改变等离子体密度和等离子体镜位置这两个参数给出了最优X射线亮度和光子产额, 该方法为将来结合人工智能优化控制全光汤姆孙散射光源提供了理论基础.
关键词: 激光尾场加速 /
汤姆孙散射 /
自反射 /
X射线 English Abstract Parameter optimization of self-reflecting all-laser-driven Thomson scattering based on laser wakefield acceleration Ye Han-Sheng 1,2 ,Gu Yu-Qiu 1,3 ,Huang Wen-Hui 2 ,Wu Yu-Chi 1 ,Tan Fang 1 ,Zhang Xiao-Hui 1 ,Wang Shao-Yi 1 1.Key Laboratory of Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, China Fund Project: Project supported by the National Key Research and Development Program of China (Grant No. 2016YFA0401100) and the Science Challenge Project, China (Grant No. TZ2018005)Received Date: 22 March 2021Accepted Date: 03 April 2021Available Online: 14 April 2021Published Online: 20 April 2021Abstract: All-laser-driven Thomson scattering based on laser wakefield acceleration can provide high quality X-ray and greatly reduce the source size. Compared with two-pulse setting, the self-reflecting setting can reduce the requirement for temporal and spatial synchronization in experiment. However, it is difficult to optimize X-ray because Thomson scattering is coupled with laser wakefield acceleration in this process. In this paper, we correct theory formula through numerical simulation, and analyze the parameters quantitatively in laser wakefield acceleration and Thomson scattering, such as spot size, duration and energy of laser and electron beam, and reflectivity of plasma mirror. Then we can trace the parameters by using the modified formula rather than the numerical simulation with similar accuracy and less time. The modified formula is also used to optimize the self-reflecting all-laser-driven Thomson scattering X-ray under the given laser conditions. The optimal X-ray luminance and photon number can be obtained by changing the plasma density and the position of the plasma mirror.Keywords: laser wakefield acceleration /Thomson scattering /self-reflecting /X-ray 全文HTML --> --> --> 1.引 言 基于X射线的高光子能量、高穿透、生物杀伤特性, 高质量的X射线源被广泛应用于放射医疗、核物理研究、材料无损检测等领域[1 ] . 如今产生X射线的方式主要包括同步辐射、韧致辐射、Betatron辐射、自由电子激光和汤姆孙散射[1 -3 ] 等, 其中基于高能电子束与激光对撞产生的汤姆孙散射可以在获得更高光子能量的同时具备单能性、准直性、高亮度等特性, 是一种优良的高能X射线产生方式. 传统的汤姆孙散射X射线源需要用到庞大的传统加速器, 从而限制了其广泛应用. 近十年来, 激光尾场电子加速得到了飞速发展[4 ,5 ] , 将拥有高加速梯度的激光尾场加速(laser wakefield acceleration, LWFA)而非传统加速器得到的电子束作为汤姆孙散射的注入电子, 可以大幅度降低汤姆孙散射X射线源装置的尺寸, 具有极大的应用推广价值. 由于在电子加速和激光对撞整个过程中只用一束激光驱动, 被称为全光汤姆孙散射[6 ] .图1 所示. 自反射式与分光式相比实验难度要低很多, 但是由于激光加速过程和汤姆孙散射耦合, 独立可控的参量更少, 优化难度较大. 近年来两种方法都有所发展, Nebraska大学对分光式进行了多年的研究[7 -9 ] , 得到了能量可调的准单能MeV量级X射线, 并探究了高阶非线性的全光汤姆孙散射[10 ] . Sarri等[11 ] 也通过分光式得到了亮度高达1019 photons/(s·mm2 ·mrad2 ·0.1%BW)的MeV量级X射线. Ta Phuoc等[12 ] 于2012年开展了最早的自反射汤姆孙散射X射线源输出, 随后Texas大学也多次实现了自反射式实验, 得到了能量可调的高质量的X射线并探讨了过程中PM的反射作用[13 ,14 ] . 但是他们对自反射式全光汤姆孙散射的优化研究也很少提及, 优化条件往往在实际实验中摸索. 近年也有文章通过改变激光条件优化汤姆孙散射X射线并实现荧光成像[15 ] , 但没有给出给定激光条件下的优化方案. 本文的目的便是希望通过解析理论分析和数值模拟, 用简单的解析公式计算来得到各个过程的物理参量的变化关系, 并利用这些公式计算探究给定激光条件下自反射式全光汤姆孙散射X射线的优化条件.图 1 自反射全光汤姆孙散射示意图Figure1. Schematic of self-reflecting all-laser-driven Thomson scattering.2.研究方法 本文的研究方法是结合数值模拟与解析计算, 首先利用推导的理想公式给出定性的变化趋势, 使公式符合基本的物理规律, 然后结合数值模拟给出定量的参量大小, 使公式更贴合实际. 在确定解析公式时, 由于LWFA过程中的不稳定性会给运算带来很强的非线性, 为避免复杂运算, 对于一些不好确定的结果会用分段线性处理.[16 ] 模拟, 模拟参数为激光能量1 J, 功率45 TW, 波长800 nm, 焦斑$ {w}_{0}=10\;\text{μ}\mathrm{m} $ , 激光强度参数${a}_{0}\approx $ $ 3.64$ , 激光聚焦在等离子体入口处. 空泡加速能够提供稳定的加速梯度, 得到高质量电子束, 此时等离子体密度应满足$ {k}_{\mathrm{p}}{w}_{0}\approx 2\sqrt{{a}_{0}} $ [17 ] , 即${n}_{\mathrm{p}0}=4\times $ $ {10}^{18}\;{\mathrm{c}\mathrm{m}}^{-3}$ , 故选择等离子体密度$ {n}_{\mathrm{p}} $ 为2 × 1018 — 6 × 1018 cm–3 , 长度为7 mm, 采用单一气体自注入的注入方式. 以光速移动的模拟窗口大小为76.32 μm × 50.88 μm, 网格大小为25.44 nm × 84.80 nm, 时间步长为0.07632 fs, 网格和时间步长满足克朗条件, 使模拟结果能够收敛. 反射后的激光与电子束进行汤姆孙散射过程使用蒙特卡罗程序cain[18 ] 模拟, 模拟使用非线性汤姆孙散射模型, 其中激光参数根据osiris模拟结果拟合成高斯脉冲, 电子束参数由从osiris选出能量大于10 MeV的电子直接导入.3.全光汤姆孙散射参数变化 23.1.激光参数变化 3.1.激光参数变化 一般LWFA中只关心加速电子参数而不用考虑加速后的激光参数, 但自反射式全光汤姆孙散射却不一样, LWFA过后的激光不仅要经过PM反射, 还要与加速电子进行汤姆孙散射, 故需要得知加速后的激光参数. 模拟得出激光在LWFA过程中焦斑、脉宽、能量随传播距离d 之间的变化关系如图2 所示. 从图2(a) 看出, 激光焦斑总体上变化不大, 当满足$P > {P}_{\mathrm{c}}=17\dfrac{{n}_{\mathrm{c}}}{{n}_{\mathrm{e}}}\left(\mathrm{G}\mathrm{W}\right)$ 时, 等离子体对于激光如同一面凸透镜, 激光表现出强烈的自聚焦效应, 与自然散焦效应相抵消, 从而维持焦斑不变[17 ] . 注意到虽然模拟密度范围内都满足$ P>{P}_{\mathrm{c}} $ , 但是密度增大时自聚焦效果变强, 激光焦斑能够在更长距离内保持不变; 而密度较小时激光仍然有散开现象, 焦斑整体上更大[19 ] . 故可对于自聚焦效应做更加精确的标定, 取中间密度为${n}_{\mathrm{p}0}=4\times $ $ {10}^{18}\;{\mathrm{c}\mathrm{m}}^{-3}$ , 密度小于$ {n}_{\mathrm{p}0} $ 时激光在研究距离范围内的整体焦斑随密度线性增大, 密度大于$ {n}_{\mathrm{p}0} $ 时激光焦斑维持不变.图 2 LWFA中激光的参量的变化 (a) 焦斑; (b) 脉宽; (c) 能量(图中能量低于能量截止线时包含激光能量和尾场能量); (d) 激光能量衰减长度Figure2. Evolution of laser parameters in LWFA: (a) Laser spot size; (b) laser duration; (c) laser energy (energy in figure contains laser parts and wakefield parts when it is below dashed line); (d) pump depletion length.图2(c) )看出, 激光能量随距离近似线性衰减, 这可以理解为激光能量随距离均匀地传递到了尾场中. 到了虚线以下的部分偏离线性是因为图中实际上统计了整个窗口的电磁场能量. 激光能量较大时统计能量即为激光能量, 但当激光能量较小时尾场能量与激光能量可以比拟, 统计能量为尾场能量和激光能量之和, 故在虚线以下部分并不是真正的激光能量. 在虚线处将激光能量线性外推可得激光损失全部能量对应的长度, 如图2(d) 散点所示. 文献中描述过激光能量损失速度${v}_{\mathrm{e}\mathrm{t}\mathrm{c}\mathrm{h}}=\dfrac{{\omega }_{\mathrm{p}}^{2}}{{\omega }_{\mathrm{L}}^{2}}$ [20 ] , 则激光能量衰减长度为${k}_{\mathrm{p}}{L}_{\mathrm{p}\mathrm{d}}=\dfrac{{k}_{\mathrm{p}}c\tau }{{v}_{\mathrm{e}\mathrm{t}\mathrm{c}\mathrm{h}}}\times c=\dfrac{{\omega }_{\mathrm{L}}^{2}}{{\omega }_{\mathrm{p}}^{2}}{\omega }_{\mathrm{p}}\tau$ , 拟合曲线为绿色, 与模拟点差距较大, 这可能是因为推导过程中只考虑了一维的影响. 将公式修改为${k}_{\mathrm{p}}{L}_{\mathrm{p}\mathrm{d}}=2\dfrac{{\omega }_{\mathrm{L}}^{2}}{{\omega }_{\mathrm{p}}^{2}}{\omega }_{\mathrm{p}}\tau$ , 即衰减长度为之前的2倍, 拟合曲线为红色, 符合较好. 激光脉宽衰减与能量衰减类似, 衰减关系也可以按照$ {L}_{\mathrm{p}\mathrm{d}} $ 来对标, 如图2(b) 所示. 根据模拟结果可以总结为距离小于$ {0.5 L}_{\mathrm{p}\mathrm{d}} $ 时脉宽线性衰减, 距离大于$ {0.5 L}_{\mathrm{p}\mathrm{d}} $ 时激光头部几乎完全耗尽, 脉宽衰减到原脉宽的1/3并保持不变. 这说明激光能量损失过程为开始峰值电场不变而脉宽减小, 后来脉宽不变峰值电场减小.3.2.电子束参数变化 -->3.2.电子束参数变化 LWFA产生的电子束品质很大程度上决定了X射线的品质, 在以前的文献中有过对各个参量的推导计算[3 ,17 ] , 但是由于推导条件的局限性, 我们很难跟踪整个过程中的电子参量变化. 有的过程如电子注入、beam loading效应等也难以定量描述, 只能在实验中观察得出[21 -23 ] , 因此结合数值模拟给出电子参量的变化过程至关重要. 图3 是LWFA过程窗口内能量大于10 MeV的电子束的参量变化. 图3(a) 是电子束平均能量$ {E}_{\mathrm{e}} $ 随激光传播距离的变化曲线, 第一个空泡内的电子在失相长度$ {L}_{\mathrm{d}} $ 内受到尾场加速, 能量线性增大. 达到$ {L}_{\mathrm{d}} $ 时由于第二个空泡内的电子开始注入, 且注入的电荷量与第一个空泡的相近, 把电子平均能量拉低到了之前的一半. 然后第一个空泡内的电子开始减速, 第二个空泡的电子开始加速, 两者速度梯度和电荷量相近, 导致电子平均能量直到$ {L}_{\mathrm{p}\mathrm{d}} $ 保持不变. $ {L}_{\mathrm{p}\mathrm{d}} $ 之后激光能量耗尽, 尾场变得不稳定, 电子能量变化不再考虑. 失相长度随等离子体密度的变化关系如图3(b) 所示, 按照${k}_{\mathrm{p}}{L}_{\mathrm{d}}= $ $ \dfrac{4}{3}\frac{{\omega }_{\mathrm{L}}^{2}}{{\omega }_{\mathrm{p}}^{2}}\sqrt{{a}_{0}}$ [17 ] 拟合结果(绿线)所示, 根据模拟数据可进一步修正为${k}_{\mathrm{p}}{L}_{\mathrm{d}}=0.93\dfrac{{\omega }_{\mathrm{L}}^{2}}{{\omega }_{\mathrm{p}}^{2}}\sqrt{{a}_{0}}$ , 如红线所示, 该结果与理论公式仅相差0.7倍. 从图3(a) 还可以看出, 在失相长度之前, 等离子体密度较低时电子加速梯度符合$ {E}_{\mathrm{w}}(\mathrm{e}\mathrm{V}/\mathrm{m})\approx 96\sqrt{{n}_{\mathrm{p}}\left({\mathrm{c}\mathrm{m}}^{-3}\right)} $ [24 ] , 但当密度进一步增大, 电子能量并不增加. 为了解释这一现象, 模拟了0.5 mm处的轴线上纵向电场分布, 如图3(c) 所示, 其中黑色三角形的位置即为电子束所处的位置. 可以看出, 随着密度的增加, 虽然尾场的峰值场强在增大, 但是电子束所处的场强由于beam loading效应并没有一直增大, 而是趋于某一数值达到饱和. 模拟饱和点对应的密度即为$ {n}_{\mathrm{p}0}=4\times {10}^{18}\;{\mathrm{c}\mathrm{m}}^{-3} $ , 故将加速电场处理为密度小于$ {n}_{\mathrm{p}0} $ , 电子能量${E}_{\mathrm{e}}\leqslant {E}_{\mathrm{e}}\left(\mathrm{e}\mathrm{V}\right)\approx 96\sqrt{{n}_{\mathrm{p}}\left({\mathrm{c}\mathrm{m}}^{-3}\right)} \times $ $ d\left(\mathrm{m}\right)$ , 密度大于$ {n}_{\mathrm{p}0} $ , 电子能量不随密度变化.图 3 LWFA中电子的参量变化 (a)电子平均能量; (b)失相长度; (c) 0.5 mm处轴线上的纵向尾场分布; (d)电子电荷量; (e)密度为4 × 1018 cm–3 时电子束焦斑和脉宽; (f) 密度为4 × 1018 cm–3 时电子束发散角Figure3. Evolution of electron parameters in LWFA: (a) Average energy; (b) dephasing length; (c) longitudinal electric field on axis when d = 0.5 mm; (d) charge; (e) spot size and duration when n p = 4 × 1018 cm–3 ; (f) divergence angle when n p = 4 × 1018 cm–3 .图3(d) 是不同密度下单位长度电荷量随距离的变化, 从激光刚传播0.1 mm处电荷的突然抬升可以看出, 电荷注入过程十分迅速, 因此不需要考虑电荷注入所需的距离. 0—1 mm内单位长度电荷量几乎不随密度变化是因为尾场注入电荷已经达到饱和, 饱和时电荷量约为5 pC/μm, 这与图3(c) 中的尾场畸变都指向beam loading效应. 观察电荷量陡增的位置发现与$ {L}_{\mathrm{d}} $ 对应, 这也与图3(a) 中电子能量陡降相符合. 多段的电荷陡增则是由于多个空泡的注入, 而每个空泡的电荷量都为饱和电荷量, 即5 pC/μm. 但由于第二个之后的空泡加速较晚, 品质不高, 前两个空泡部分信息, 故只考虑前两已经包含了电子束大部分信息, 故只考虑前两个空泡的注入情况. 随着激光传播距离进一步增大, 高密度时距离超过$ {L}_{\mathrm{p}\mathrm{d}} $ 激光损失殆尽, 低密度时激光自聚焦不够强, 两种条件下都会使电子束受到的横向聚焦力不够, 电子跑出探测窗口导致电荷量减小.18 cm–3 时电子焦斑和脉宽随距离的变化关系如图3(e) 所示, 其他密度条件下电子变化情况相似. 单个空泡内的电子脉宽大约等于一个空泡的尺寸$ {r}_{\mathrm{b}} $ , 而空泡尺寸又, 而空泡尺寸又约等于激光焦斑w 0 , 即$ {\sigma }_{z, \mathrm{e}}\approx {r}_{\mathrm{b}} $ . 电子脉宽在2.3 mm处的陡增是因为多个空泡的处的陡增是因为多个空泡的注入在空间上拉长了电子的脉宽. 而电子焦斑远比文献中$ {\sigma }_{r, \mathrm{e}}\approx {r}_{\mathrm{b}} $ 要小, 大约为$ {\sigma }_{r, \mathrm{e}}\approx {r}_{\mathrm{b}}/5 $ . 这是因为电子在空泡尾部注入,. 这是因为电子在空泡尾部注入, 具体注入位置则由电势决定, 只有电子场相速度的速度时才会被捕获. 注入对应位置的归一化电势要小于–1[25 ] , 这部分的横向尺寸约为$ {r}_{\mathrm{b}}/5 $ . 由电子束焦斑和单位长度电荷量可以得到电子束的总电荷量$Q=\dfrac{5~\mathrm{p}\mathrm{C}}{\text{μm}}\dfrac{{r}_{\mathrm{b}}}{5}= $ $ 10\;\mathrm{p}\mathrm{C}$ . 然而文献描述电子数$N=2.5\times {10}^{9}\dfrac{\lambda \left({\text{μm}}\right)}{0.8} $ $ \sqrt{\dfrac{P\left(\mathrm{T}\mathrm{W}\right)}{100}}$ [17 ] , 约为模拟的25倍. 公式推导时是将空, 约为模拟的25倍. 公式推导时是将空泡内全部电磁场能量除以每个电子最大能量得到的, 而实际上电子并不会消耗全部电磁场能量, 存在一个吸收比例, 约为1/25 = 4%. 因此公式计算结果比模拟结果大1个数量级, 这在许多实验中都有所印证[5 ,9 ,13 ,14 ,26 -28 ] . 电子束发散角的变化如图3(f) 所示, 约为20 mrad, 在2.5和4.0 mm附近增大是电子能量降低导致. 绿线是电子在尾场中的betatron振荡的估计值, ${\theta }_{\mathrm{e}}\left(\mathrm{r}\mathrm{a}\mathrm{d}\right)\approx \dfrac{1.33\times {10}^{-10}\sqrt{\gamma {n}_{\mathrm{e}}\left({\mathrm{c}\mathrm{m}}^{-3}\right)}\times {\sigma }_{r, \mathrm{e}}\left({\text{μm}}\right)}{\gamma }$ [2 ] , 公式与模拟符合得很好.3.3.PM反射 -->3.3.PM反射 激光经过LWFA过程后与PM的反射也由二维osiris模拟, 得到不同激光强度下反射率如图4 所示. 模拟和文献都表明经过LWFA过程后激光仍处于非线性状态($ {a}_{0}>1 $ ), 在此强度范围内PM反射率并没有明显变化[14 ] , 只会随着激光强度增大而缓慢降低. 图4 中统计的激光能量是PM一侧的总能量, 包括反射激光能量和杂散的能量. 当激光强度增大时, 激光与PM作用更加剧烈, 杂散能量所占比例增大, 导致a 0 = 5时反射率反常偏高. 故在计算中取反射率为75%. 在自反射式全光汤姆孙散射中激光先加速电子, 预脉冲已经在形成尾场过程中消耗掉了, 故无需考虑预脉冲对PM的损伤. 激光与PM作用还会产生高次谐波, 但是谐波强度大约只有入射激光强度的10–4 , 远小于汤姆孙散射光的强度, 故可以忽略不计[29 ] .图 4 PM反射率Figure4. Reflectivity of PM.3.4.汤姆孙散射 -->3.4.汤姆孙散射 自反射式全光汤姆孙散射的构架决定了激光与电子的作用角度为$ \alpha =180° $ , 当密度为$ {n}_{\mathrm{p}0} $ , PM位置为2.5 mm时X射线能谱和角分布如图5 所示. 图5(a) 显示X射线能谱呈现出明显的非线性特性, 且在不同接收角$ \theta $ 下X射线能谱不同, 随着接收角度不断增大, 能谱趋于包含全部立体角内的总光谱. 能谱图曲线不够平滑、相对误差较大是因为每个能量间隔内的宏粒子数较少. 为了适当减小osiris输出文件大小, 一般只输出模拟宏电子数的1%, 因此cain输入的宏电子数一般为2000个. 汤姆孙散射若将相对误差按照$ 1/\sqrt{N} $ 来估计, 取100能量间隔时相对误差约为20%. 但是本文主要衡量X射线总体性质, 这时相对误差为2%, 而且解析计算与模拟符合较好, 故该误差的影响可以忽略不计. 从图5(b) 可以看出, X射线发散角小于20 mrad. 对于X射线的各项参数, Esarey等[30 ,31 ] 进行了详细的阐述, 例如X射线能量${E}_{\mathrm{X}}= $ $ \dfrac{2 n\left(1-\beta \mathrm{c}\mathrm{o}\mathrm{s}\alpha \right){\gamma }^{2}}{1+{\gamma }^{2}{\theta }^{2}+{a}_{0}^{2}/2}\times \hslash {\omega }_{0}$ 、焦斑$ {\sigma }_{x, y}\approx {\sigma }_{r, \mathrm{e}} $ 、发散角$ {\theta }_{x, y}=\sqrt{{\left({a}_{0}/\gamma \right)}^{2}+{\left({\theta }_{\mathrm{e}}\right)}^{2}} $ 、脉宽${\sigma }_{T}=\dfrac{{\sigma }_{\mathrm{e}z}}{c}$ 、光子数${N}_{\mathrm{\gamma }}=\dfrac{\sigma {N}_{\mathrm{e}}{N}_{\mathrm{l}}}{2\mathrm{\pi }\sqrt{{\sigma }_{\mathrm{e}z}^{2}+{\sigma }_{\mathrm{l}z}^{2}}\sqrt{{\sigma }_{\mathrm{e}r}^{2}{+\sigma }_{\mathrm{l}r}^{2}}}$ ($ \sigma $ 为汤姆孙散射微观截面, 为$\dfrac{8}{3}\mathrm{\pi }{r}_{\mathrm{e}}^{2}$ ; $ {N}_{\mathrm{l}} $ 为激光光子数)等. 由于该过程不稳定性较少, 因此模拟结果与计算结果符合得很好. 对于X射线亮度计算, 可以用$B\left(\omega \right)= $ $ \dfrac{{N}_{\mathrm{\gamma }}K\left(E\right)}{{\left(2\mathrm{\pi }\right)}^{5/2}{\sigma }_{\mathrm{T}}{\sigma }_{x}{\sigma }_{y}{\theta }_{x}{\theta }_{y}}$ 计算, 其中$ K\left(E\right) $ 为光子能量E 附近0.1%内带宽内的光子数占比. 设能谱为$ f\left(E\right)(\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{s}/\mathrm{k}\mathrm{e}\mathrm{V}) $ , 则图 5 汤姆孙散射X射线参数 (a) 能谱; (b) 角分布Figure5. X-ray from Thomson sacttering: (a) Energy spectrum; (b) angle divergence distribution.$K\left(E\right)=0.2\%\times \dfrac{E}{{E}_{\mathrm{c}}}\left(1-\dfrac{E}{{E}_{\mathrm{c}}}\right)$ , $ K\left(E\right) $ 最大可以取到$ 5\times {10}^{-4} $ . 实际上能谱低能段光子更多, 故计算时一般取$ K\left(E\right)=2\times {10}^{-4} $ .4.自反射式全光汤姆孙散射优化 综上所述, 我们修正了公式得到了与数值模拟一致的结果, 如表1 所列. 接下来可以用公式计算的方式代替模拟进行X射线优化. 在给定激光条件下, 等离子体密度几乎成为LWFA过程的唯一调控手段, 也是自反射式全光汤姆孙散射的第一个调控手段. 第二个调控参数是PM位置: 距离太远, 激光能量大幅度损失, 产生X射线亮度低; 距离太近, 电子束能量低, 发散角大, X射线亮度也低, 故存在最优的PM位置. 因此对X射线的优化主要考虑这两个参数. 通过前文总结的公式, 对X射线数值上优化的结果如图6 所示, 横坐标是等离子体密度, 纵坐标是PM位置, 颜色表示各项数值大小. 从图6 可以发现两条明显的曲线, 分别对应$ {L}_{\mathrm{d}} $ 和$ {L}_{\mathrm{p}\mathrm{d}} $ , 这是由于距离大于$ {L}_{\mathrm{d}} $ 会导致第二个空泡注入和电子平均能量降低, 而距离大于$ {L}_{\mathrm{p}\mathrm{d}} $ 则激光耗尽, 两者均会引起数值突变. 实际优化时可以先根据实际需要选择X射线能量范围, 在能量范围对应的优化参数范围内找到最佳的X射线亮度或光子数. 对于图6 给出的结果, 等离子体密度在1 × 1018 —6 × 1018 cm–3 范围内, PM在1—10 mm范围内时最佳亮度对应的等离子体密度为4 × 1018 cm–3 , PM位置2 mm, 此时X射线亮度1.7 × 1018 photons/(s·mm2 ·mrad2 ·0.1%BW), 光子数4.8 × 107 , 能量460 keV. 根据公式可知, 要想进一步增加X射线的亮度或者光子数, 最为直接的方法便是增大驱动激光的功率产生更多的电子.方法 经过LWFA的激光 电子束 X射线 焦斑/μm 脉宽/fs 能量损失/(%·mm–1 ) 能量/MeV 焦斑/μm 发散角/mrad 光子数/107 亮度/(1018 photons·s–1 ·–2 ·mrad–2 ·–1 ) 修正公式 10 7 17 460 2.0 18 4.1 1.3 数值模拟 10 6 17 450 1.8 16 4.0 1.6
表1 等离子体密度4 × 1018 cm–3 , PM位置2.5 mm时修正后的公式计算和数值模拟的部分参数比较Table1. Comparison of modified formula calculation and numerical simulation when plasma density is 4 × 1018 cm–3 and PM position is 2.5 mm away.图 6 X射线优化结果 (a) 亮度; (b) 光子数; (c) 光子能量Figure6. Optimization results of X-ray: (a) Brightness; (b) photon number; (c) photon energy.5.总 结 本文通过数值模拟分别分析了LWFA和汤姆孙散射中激光、电子和X射线的变化关系, 提出了一些较为简单的解析公式用于逼近数值模拟的结果. 这些公式是在纯理论推导出的公式的基础上得到的, 在保留了一些物理规律的同时比起理论公式更贴合实际, 能够帮助我们更加准确快速地预测参数品质. 利用这些公式优化了自反射式全光汤姆孙散射产生的X射线, 通过改变等离子体密度和PM位置这两个参数给出了最佳的X射线亮度和光子数. 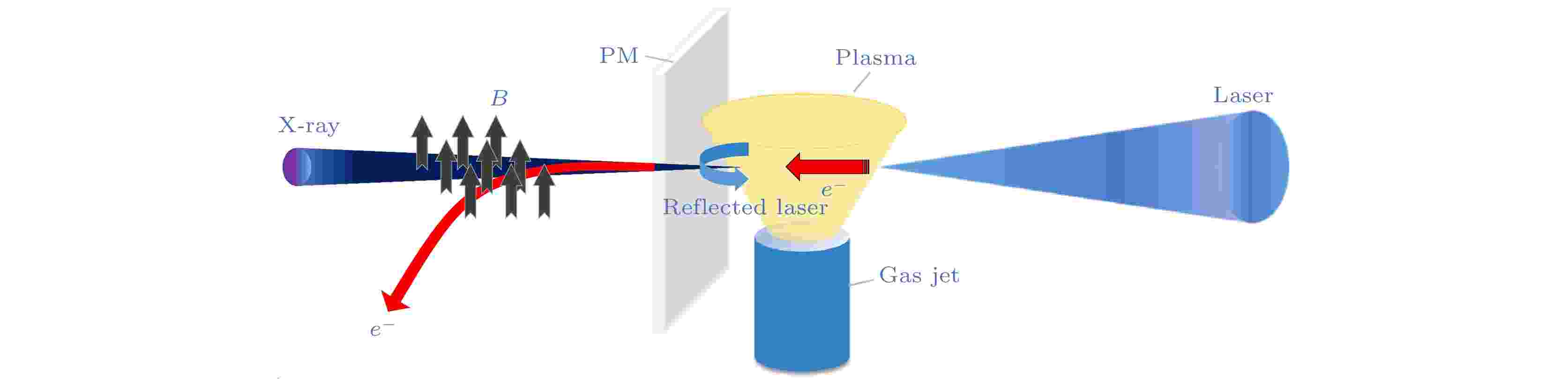 图 1 自反射全光汤姆孙散射示意图
图 1 自反射全光汤姆孙散射示意图














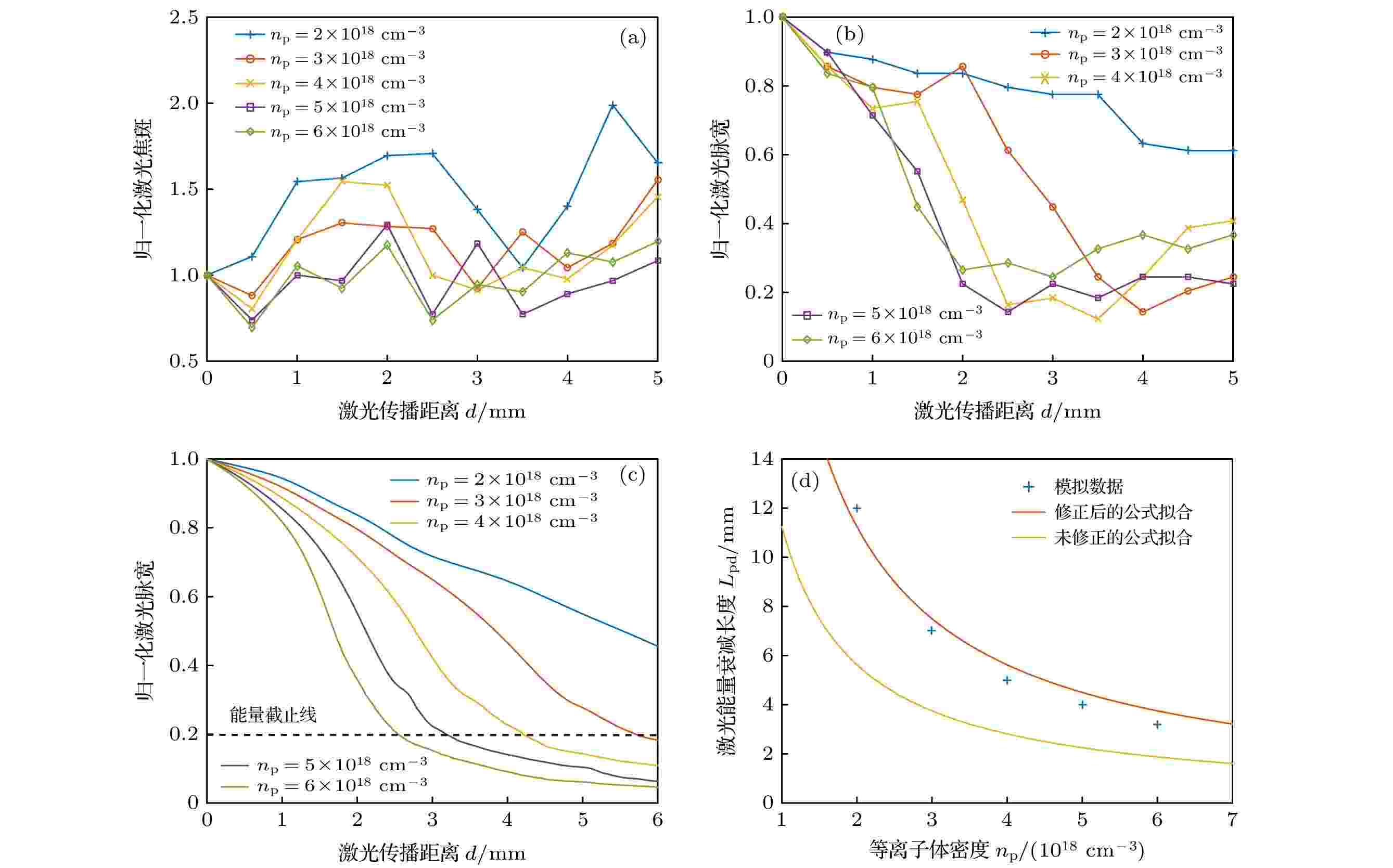 图 2 LWFA中激光的参量的变化 (a) 焦斑; (b) 脉宽; (c) 能量(图中能量低于能量截止线时包含激光能量和尾场能量); (d) 激光能量衰减长度
图 2 LWFA中激光的参量的变化 (a) 焦斑; (b) 脉宽; (c) 能量(图中能量低于能量截止线时包含激光能量和尾场能量); (d) 激光能量衰减长度



























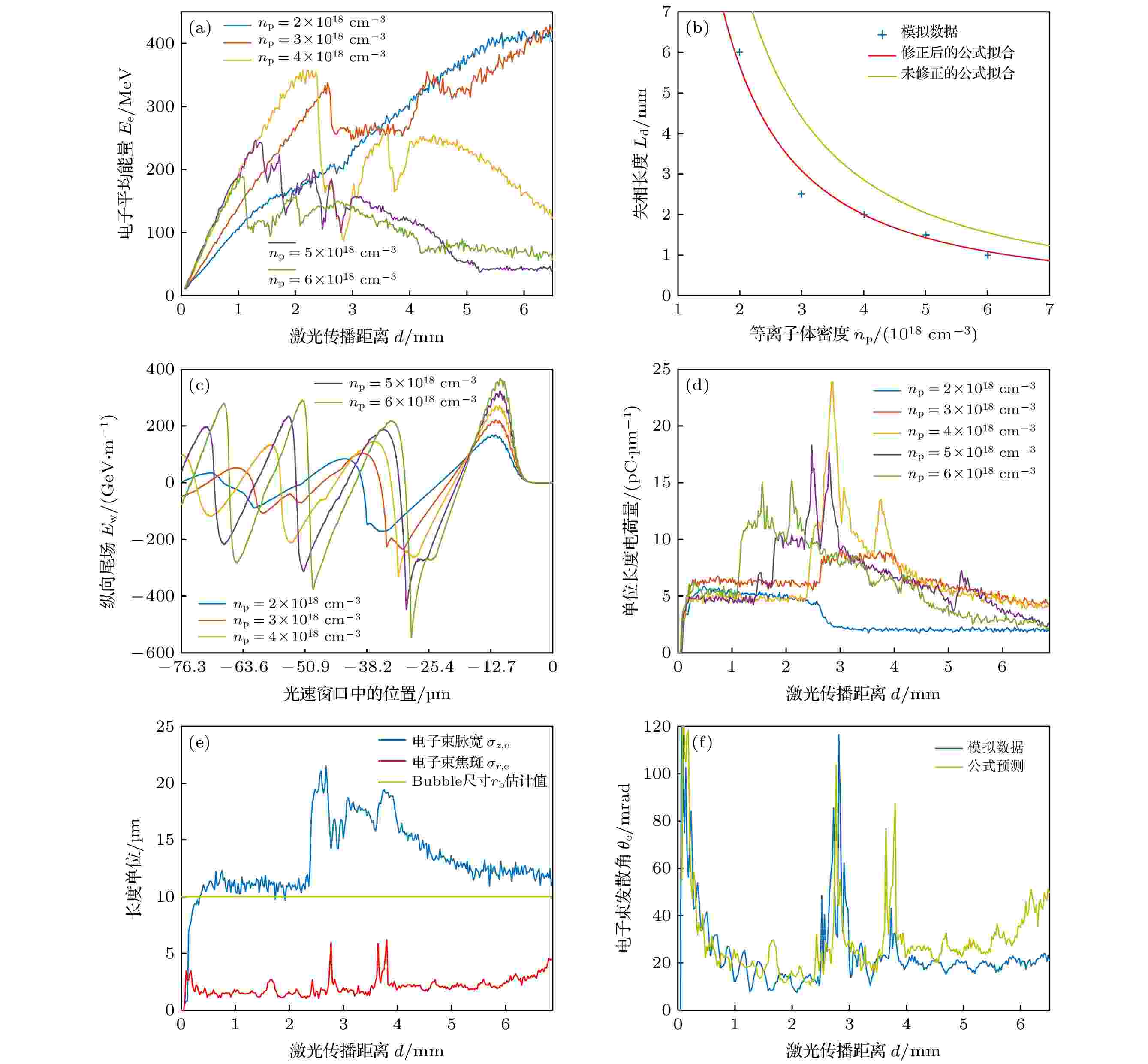 图 3 LWFA中电子的参量变化 (a)电子平均能量; (b)失相长度; (c) 0.5 mm处轴线上的纵向尾场分布; (d)电子电荷量; (e)密度为4 × 1018 cm–3时电子束焦斑和脉宽; (f) 密度为4 × 1018 cm–3时电子束发散角
图 3 LWFA中电子的参量变化 (a)电子平均能量; (b)失相长度; (c) 0.5 mm处轴线上的纵向尾场分布; (d)电子电荷量; (e)密度为4 × 1018 cm–3时电子束焦斑和脉宽; (f) 密度为4 × 1018 cm–3时电子束发散角












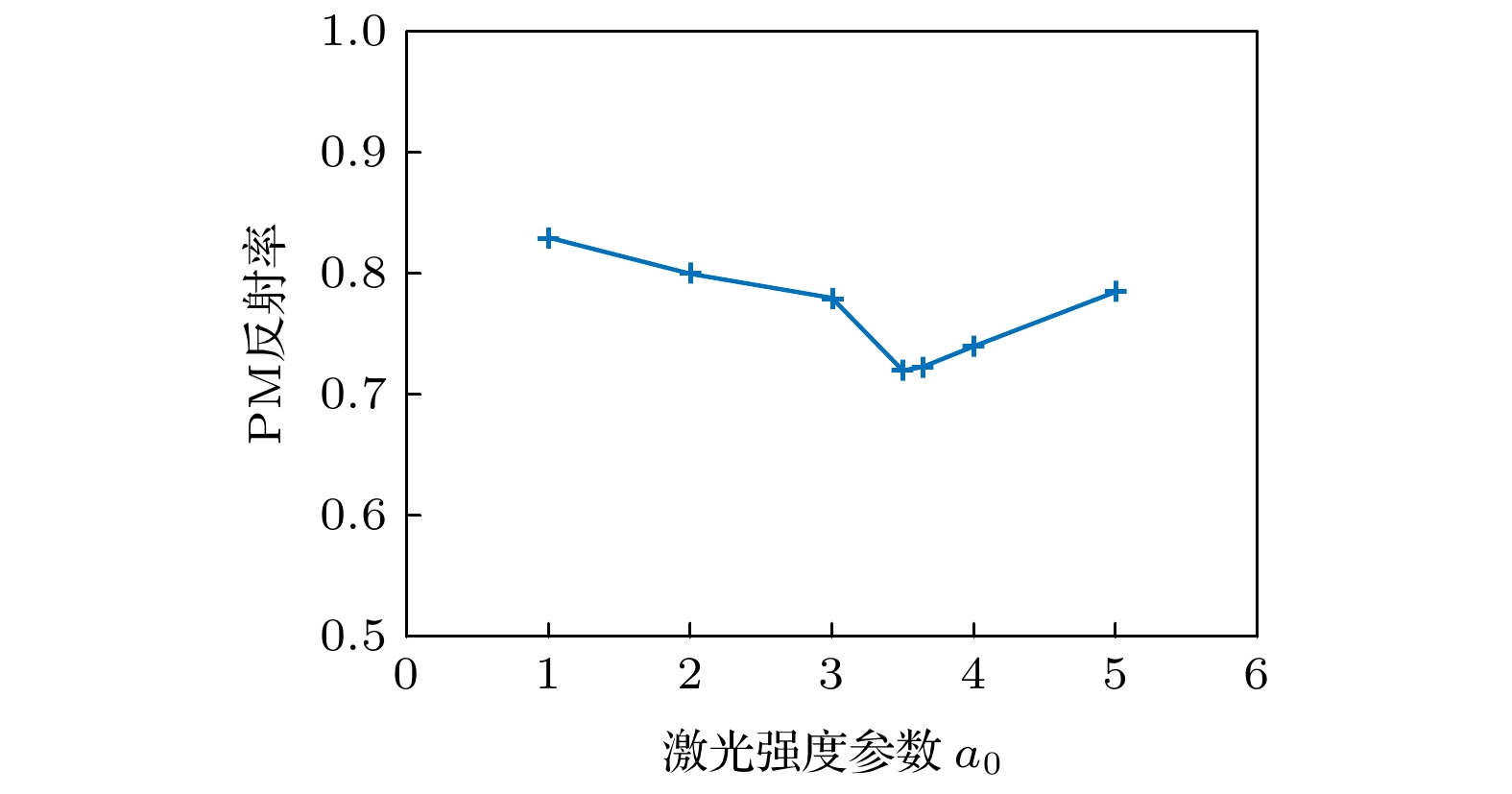 图 4 PM反射率
图 4 PM反射率
















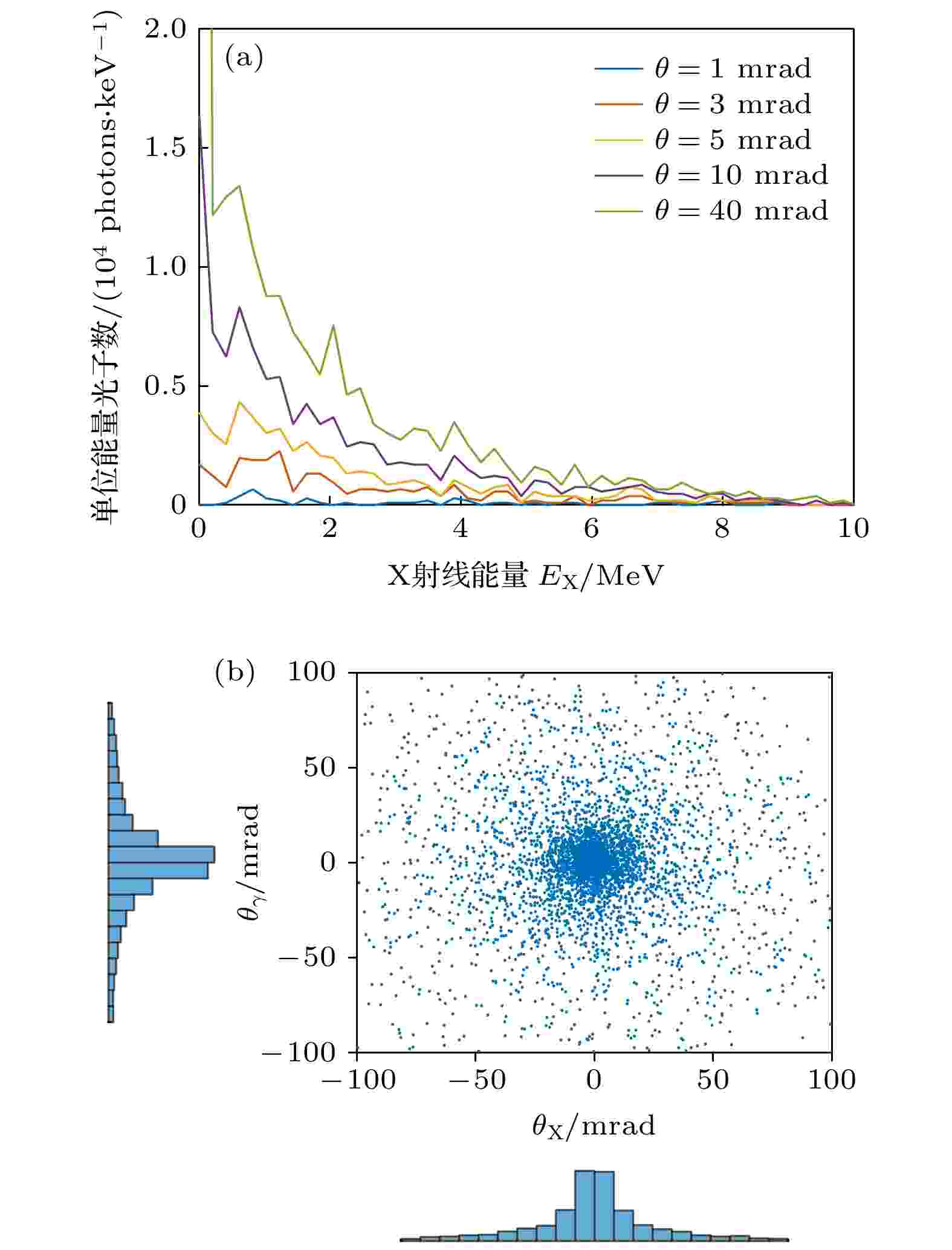 图 5 汤姆孙散射X射线参数 (a) 能谱; (b) 角分布
图 5 汤姆孙散射X射线参数 (a) 能谱; (b) 角分布











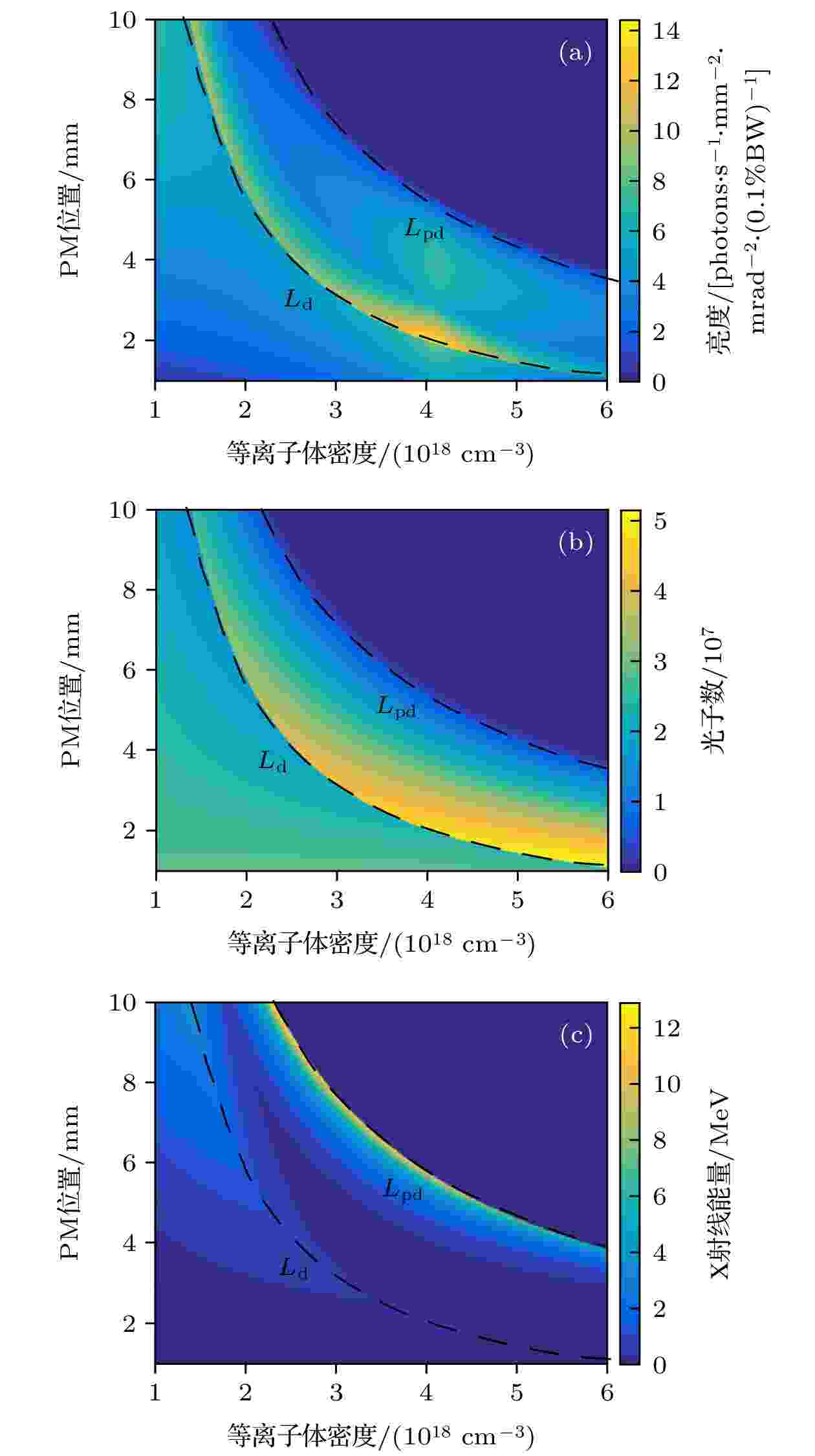 图 6 X射线优化结果 (a) 亮度; (b) 光子数; (c) 光子能量
图 6 X射线优化结果 (a) 亮度; (b) 光子数; (c) 光子能量