摘要: 本文提出并研究了“单队列-双参数”光电延时反馈控制条件下的激光局域网络的混沌控制及串联的动力学行为的并行队列“交叉驱动-反馈”网络同步实现, 建立了该光学局域网络的数学物理控制模型. 通过含时延超越方程理论的分析, 预言了该光学局域网络是可以实现混沌控制的, 且网络两路结点队列是可以实现实时引导控制到多个类周期状态上的, 并通过并行队列同步方程理论证明并行串联队列同步是可以获得的. 结果发现在可控的激光局域网络两个并行串联队列光路上, 分别实现了网络队列结点的混沌控制并能够实现多个类周期的网络结点的并行串联队列同步, 实现了络网结点激光器的2周期、3周期、4周期等状态的并行队列同步, 以及其他多个类周期的队列并行同步和动态同步. 还发现了两个类周期并行队列网络同步控制区域. 本文还给出了激光局域网络“并行多点混沌载波同步发射及其在光学超宽带通信中应用”的一个案例并成功实现. 这是一种新型的激光混沌局域网络控制系统, 具有光局域网络光传送与光联接核心控制技术要素, 具有复杂动力学系统与网络的多变量、多空间维度及并行两路不同队列混沌控制技术特点, 还具有光网络超宽带通信功能等. 其研究结果对局域网络、光网络的控制与同步、激光技术以及混沌的研究具有重要的参考价值.
关键词: 混沌 /
控制 /
同步 /
局域网络 /
激光网络 /
周期 English Abstract Chaos-control and parallel queue synchronization of laser local area network Yan Sen-Lin School of Electronic Engineering, Nanjing Xiaozhuang University, Nanjing 211171, China Received Date: 03 August 2020Accepted Date: 10 October 2020Available Online: 02 April 2021Published Online: 20 April 2021Abstract: In this work, we study the chaos-control and parallel queue synchronization of a laser local area network (LAN). We present and study specifically a “single-queue-double-parameter” method of the parallel series queue dynamic behavior synchronization of the controlled laser LAN under two optoelectronic delay feedback controllers, and establish the mathematical and physical model of the controlled laser LAN. The LAN node is composed of two space coupled lasers with different parameters and other two single lasers, where two lasers series produce two different parallel queues, which results in two different chains of LAN nodes. Optical LAN links are composed of two optical parallel-crossing paths and two photoelectric delay feedback controllers setting in two lasers of LAN, which creates a method of double-parameter control of LAN. Through the analysis of the stability theory of differential equation and the dynamic characteristic equation of coupled lasers of LAN, our mathematical theory demonstrates that the chaos-control of laser LAN can be achieved by two photoelectric delay feedback controllers adjusting photoelectric feedback levels and feedback delay time of one of the two coupled laser and another single laser, respectively. Making analysis of the stability theory of differential equation and the dynamic characteristic equation of LAN nodes in two queue chains, we demonstrate theoretically how to obtain synchronization in network nodes of the controlled LAN on two queue chains by controlling optical feedback levels, and by the photoelectric delay feedback controllers adjusting photoelectric feedback levels and feedback delay time, respectively. Using our numerical calculation of parallel queue synchronization, the node laser’s waveform and its phase space trajectory, we find that very lasers of network nodes of the controlled LAN can lead to the parallel queue synchronization of a double-period, a three-period, a four-period and other quasi-periods while these quasi-periodic synchronizations and dynamic synchronizations are controlled in two queue chains of LAN nodes when we let the photoelectric feedback level and the delay time shift on some parameters. We find also two controlled quasi-periodic parallel queue synchronization regions. This paper also presents an application case of laser LAN multi-point chaotic carrier synchronous emission and ultra-wideband communication. This is a new type of controlled laser LAN system, which has the core elements of optical LAN and the characteristics of multi-variable, multi-dimension and parallel queue chaos-control techniques of complex dynamic networks. It also has the function of optical network ultra-wideband communication. The results have important reference value for studying the LAN, optical network and its synchronization and control, laser technology and chaos.Keywords: chaos /control /synchronization /local area network /laser network /period 全文HTML --> --> --> 1.引 言 混沌一直是非线学科学、复杂动力学网络与系统研究领域中一个重要学科. 混沌动力学变化规律难以预测, 其信号具有随机变化等特性并被广泛应用在多个领域[1 -11 ] . 自从20世纪90年代Ott等[12 ] 发现“OGY”混沌控制方法以来, 混沌控制作为控制科学的一个重要的研究领域得到了广泛重视, 有微扰法、自适用控制法、线性反馈控制法、偶然正比反馈控制法等[13 -15 ] . 激光混沌控制作为一个重要研究领域也一直受到人们的广泛关注并获得许多重要研究成果[16 -25 ] , 其控制技术有电流微扰法、光反馈法、相移调制法、双劈双反馈方法等. 复杂动力学网络与系统在人工智能、通信系统与网络工程等方面具有重要的研究价值. 高维多节点网络混沌同步及超混沌同步、时空混沌同步、星形网络同步、链式同步、多通道混沌通信等有了广泛的应用研究成果[26 -36 ] . 为了深入开展激光混沌控制与应用研究[37 -41 ] , 本文基于网络混沌同步及激光混沌控制的思想方法[26 -41 ] , 针对光网络光传送、激光电流驱动与光电放大与时间调控等技术的特点, 开展了激光局域网络(LAN)的混沌控制研究, 提出“单队列-双参数”激光LAN的混沌控制新方法, 建立了一个新的“单队列-双参数”光电延时反馈控制条件下的激光LAN的混沌控制系统, 以及并行队列同步的光学局域网络及其数学物理控制模型; 证明了网络利用光“交叉驱动-反馈”光发送与光联接方法能够实现并行串联队列同步; 提出光电时延双参数可调控的激光LAN“并行多点混沌载波同步发射及其在光学超宽带通信中应用”的一个案例, 此案例也可进行交替发射或联合通信的推广. 我们研究发现, 对该激光网络单结点激光器的混沌控制难以实现对整个网络系统的混沌控制, 为了克服这个困难, 提出并研究了对一个队列的激光器控制的“单队列-双参数”光电延时反馈的混沌控制方法, 其中单队列多维度结点被控制演化为无限维度, 该方法实现了对整个网络系统的混沌控制的目标, 即实现对网络全部结点激光器的混沌控制, 并实现网络的并行队列同步. 由此, 给出关于含时延的超越方程理论的分析式及系统可控的理论预言; 还给出两组并行队列同步方程理论公式及分析. 研究发现: 虽然是单队列激光器的混沌控制, 但是仍然可以实现两链路队列所有结点激光器的混沌控制, 因为本网络存在着“交叉驱动-反馈”作用影响能够引导控制另外一链路激光器动力学行为; 如有两种不同类型周期状态同时被控制出现在两链路上, 这种混沌控制具有“两态”物理现象呈现, 能够实现并行两路队列的激光器动力学行为同步. 这是一种新构建的可调控的激光LAN系统, 具有局域光网络光传送与光联接核心可控制技术要素, 具有取得并行两路不同队列混沌控制及同步特点. 本网络物理结构主要特点是: 该系统与传统上的星形网络仅有一个中心结点结构相比较具有不同的结构特点, 激光LAN具有双中心结点结构特点, 其中激光混沌发送源有两个异激光器系统耦合构成组成双中心产生双光输出, 两中心联结串联了两个路径; 由于两个路径由两不同种类激光器组成(两个不同路径由两类不同系统构成结点), 这与传统上高维多节点网络混沌同步的结点(如通常全部结点有相同系统构成或异系统构成同样结点)还是有区别的; 而且本系统“交叉驱动-反馈”网络结构与全局耦合网络、最邻近耦合网络(主要特点是“耦合”)等也是有区别的. 在网络物理状态呈现上, 由于结构不同, 传统上网络系统同步通常呈现的是某个态的同步, 本系统物理动力学状态变化特点是可呈现出并行的“两态”同步, 还可以实现网络混沌动态控制及同步. 为了进一步开展激光混沌通信应用研究, 还对该系统进行了激光LAN并行多点混沌载波同步发射及在激光混沌超宽带通信应用等研究. 传统上激光混沌通信通常是两个或多个混沌激光器发收通信或多信道通信, 本系统特点是可以进行并行网络通信以及交替发射或网络组合联合通信的推广, 具有光网络组合与联合超宽带光通信功能特点. 研究发现该激光LAN可以被控制引导到1周期、2周期、3周期和其他类周期上, 并能在两条链路上分别实现网络结点队列多种类周期同步. 在此基础上, 我们发现该受控的LAN的两个类周期同步区, 成功实施了激光LAN并行多点混沌载波同步发射与激光混沌超宽带通信. 所以本研究对局域网络、光学网络、复杂动态系统、控制科学、混沌及同步等方面的研究有一定的参考价值.2.激光局域网络的控制与并行队列同步的网络结构及数学物理模型 基于我们曾经提出的2N 维激光两路串联同步系统[41 ] , 并主要为了说明 LAN控制科学问题, 这里简化该系统为双路四结点并行串联队列同步激光LAN. 并针对激光LAN控制思想, 进一步提出激光LAN“单队列-双参数”光电延时反馈控制下的并行队列同步的数学物理网络模型, 如图1 所示.图 1 激光局域控制网络图, ⊕表示光电转换控制器Figure1. A controlled laser local area network. Signal ⊕ is the photoelectric controller.图1 中LAN有4个激光器分别构成网络结点. 其中, 两个空间耦合激光器t1和t2 构成混沌信号发生器网络结点[23 -26 ] , 其余两个独立激光器r1 和r2 为网络信号接收网络结点. 激光器t1和r1串联为一队列, 激光器t2和r2串联为另外一个队列, 即形成两个并行队列. 同时, 激光器t1驱动激光器r2, 激光器t2驱动激光器r1, 为了实现LAN两路网络结点并行队列同步, 网络结点r1 和r2 激光器都有一光学反馈回路. 由此形成“交叉驱动-反馈”网络并行队列同步结构. 原则上, 队列激光器r1与t1有相同的参数, 队列激光器r2与t2有相同的参数. 为了控制该激光LAN动力学行为, 设计出激光器t1和r1都增加一个光电延时反馈控制回路, 其中光电转换控制器能够把激光器t1和r1部分光转换成为光电流并放大反馈到它们各自激光器驱动电路上. 由此形成t1和r1队列的“单队列- 双参数”光电延时反馈控制(存在着时间延迟和反馈水平两参数的变化调控)下并行队列同步的激光LAN, 这样得到可控的激光LAN的数学方程组[17 -27 ] :E , φ 和N 分别表示激光振幅、相位和载流子数. 激光器t1和r1的腔长是激光器t2和r2腔长的2倍, 由此导致两个光学光路是由两组不同参量激光器串联成两个不同队列组合构成. 载流子非线性损耗速率和模式增益分别是v g , 模式体积是V p = V /Г , 激光在透明时的载流子数和密度分别是N th = n th V 与n th , γ p = v g α m 表1 . 物理量ρ 和τ 是光电延时与放大反馈调控参量, 其数值变化可由光电转换控制器等控制设施完成. 其中, ρ 表示反馈水平(即光电转换放大与反馈)参量, τ 是延迟时间.参量 值 参量 值 腔长 L /μm 350 俄歇复合因子C /(cm6 ·s–1 ) 3.5 × 10–29 腔宽 w /μm 2 饱和光子场振幅|E s |/m–3/2 1.6619 × 1011 腔厚 d /μm 0.15 增益常数 α /cm2 2.3 × 10–16 压缩和限制因子Γ 0.29 光线宽增强因子 β c 6 群速度折射率n g 3.8 耦合驱动系数 k 0.055 光子损耗系数 α m / cm–1 49 频率差 Δω /(Rad·s–1 ) 2π × 10–9 非辐射复合速率 A nr /s–1 1.0 × 108 激光透明时载流子密度 n th /cm–3 1.2 × 1018 辐射复合因子 B /(cm3 ·s–1 ) 1.2 × 10–10 光在腔内来回一周的时间 τ L 8.8667 × 10–12 驱动电流 I t1, t2 / mA 34, 30 光反馈系数 k r 0.15
表1 激光器参量Table1. Laser parameters.3.理论分析 23.1.控制理论分析 3.1.控制理论分析 取j 代表激光器 t1, t2, r1和 r2; 脚标0表示激光器稳定点. 并有G j 0γ ej 0 是激光器增益和载流子非线性损耗速率在稳定点所对应的物理量. 可控LAN中的空间耦合激光器t1和t2的动力学稳定性方程是:8 )式的特征值ζ 方程是:$\hat {{I}}$ 是单位矩阵. 由于系统动力学稳定性主要由特征值实部决定. 当驱动电流不是远大于门限电流时, 激光动力学特性可以由特征值谱来描述, 即通常可取一级近似分析. 所以这里可近似取控制关联项a 31 中的${{\rm{e}}^{\zeta \tau }} \approx 1 + \zeta \tau $ . 这样可由(9 )式得到特征值的近似解, 其中控制关联项a 31 中的物理控制参量ρ 和τ 决定了(9 )式的特征值. 如不采取近似, 由于关联项a 31 中的指数项${{\rm{e}}^{\zeta \tau }}$ 存在, (9 )式将是一个超越方程, 可以进行数值求解. 如最大特征值实部具有负值, 系统不动点就是渐近稳定的, 说明LAN系统是可以控制到稳定点的; 如最大特征值的实部是零值, 说明激光器存在着周期解, 即LAN系统是可以控制到周期态. 所以, 只要选择合适的物理控制参量ρ 和τ , 就有可能获取到最大特征值实部具有零值或负值的数学解, 进而控制激光LAN耦合系统到周期态或稳定态.3.2.可控的并行队列同步理论分析 -->3.2.可控的并行队列同步理论分析 对于可控的LAN结点激光器t2 和 r2链路, 可以获得该链路队列同步方程及相关的特征值λ 的方程, 分别是:10 )式和(11 )式中b 11 和b 22 中的物理参量k r 以获取(11 )式的最大特征值实部具有负值的变化. 当最大特征值实部有负值时, LAN网络结点激光器t2 和 r2队列可以获得渐近稳定性同步.η 方程, 分别是:12 )式和(13 )式中c 11 和 c 22 中的物理参量k r 获取(13 )式的最大特征值实部具有负值的变化. 当最大特征值实部具有负值时, LAN网络结点激光器t1 和 r1队列可以获得渐近稳定性同步.4.结果和讨论 图2 和图3 是激光LAN并行串联混沌同步结果. 其中, 图2 是激光器t1 与r1 已呈现出相同的混沌波形变化(E r1 已向上平移0.12), 图3 是激光器t2 与r2 输出相同混沌光波的结果(E r2 已向上平移0.09). 为了实现该激光LAN混沌控制, 施加光电延时反馈控制, 发现可以控制激光LAN两链上各个结点队列分别处在多种类周期状态上, 并能取得两个链路上网络结点的类周期状态队列同步. 在数值计算中, 对光电转换放大与反馈参量进行归一化处理, 形式上改写为ρ × 112.782.图 2 激光器t1与r1链路混沌同步Figure2. Chaotic laser t1 synchronizes with the laser r1.图 3 激光器t2与r2链路混沌同步Figure3. Chaotic laser t2 synchronizes with the laser r2.τ = 0.2 ns, ρ = 0.01时, 激光LAN一个链路上的网络两结点队列激光器t1与r1能够被有效控制到9周期态, 并能够取得9周期同步, 结果见图4 . 其中, 两个插图是激光器t1与r1在其相空间上的9周期轨迹变化图, 同步用了约10 ns(其中用$E_{{\rm{t}}1}^2 -E_{{\rm{r}}1}^2=0 $ 表示同步). 图5 是另一个链路上的网络两结点队列激光器t2与r2 被控制6周期状态并取得同步(其中用$E_{{\rm{t}}2}^2 -E_{{\rm{r}}2}^2=0 $ 表示同步)的结果. 由此可见, 激光LAN两链上网络结点队列可以分别被有效控制在9周期、6周期状态上, 且两个链路的网络结点队列能够分别取9周期状态与6周期状态的同步. 所以我们成功地实现了激光LAN的混沌控制与两个链路的并行队列同步.图 4 激光器t1与r1取得9周期同步Figure4. The laser t1 synchronizes with the laser r1 at a 9-periodic state.图 5 激光器t2与r2取得6周期同步Figure5. The laser t2 synchronizes with the laser r2 at a 6-periodic state.τ = 0.2 ns, ρ = 0.038时, 激光LAN一个链路上的网络结点队列激光器t1与r1能够被有效控制到4周期态上, 并能够取得4周期同步, 而另一个链路上的网络结点激光器t2与r2 队列被控制3周期状态上, 并取得3周期同步的结果, 即实现了激光LAN的混沌控制与两个链路队的并行队列的两个不同周期同步. 同时我们也注意到, 当τ = 0.2 ns条件下, ρ 取较小值时(如ρ = 0.01), 网络能够控制到多周期态, ρ 取较大值时(如ρ = 0.038、ρ = 0.09时), 网络能够控制到低周期态区域, 如会呈现2, 3, 4周期.τ = 0.2 ns, 当ρ = 0.04时, 在激光LAN的混沌控制下可以实现两个链路队并行队列的两个同级周期(2周期但变化轨道不同)同步. 发现一个链路上的网络结点队列激光器t1与r1能够被有效控制到2周期态上, 取得2周期同步; 另一个链路上的网络结点队列激光器t2与r2 被控制到另外一个2周期状态上, 取得该链路上的2周期同步, 这两个结果见图6 和图7 . 还进一步发现可控的两个队列2周期并行同步分布区域是ρ 从0.04到0.06.图 6 激光器t1与r1取得2周期同步Figure6. The laser t1 synchronizes with the laser r1 at a 2-periodic state.图 7 激光器t2与r2取得2周期同步Figure7. The laser t2 synchronizes with the laser r2 at another 2-periodic state.ρ = 0.065时, 激光LAN一个链路上的激光器t1与r1能够被控制到3周期态, 并能够取得3周期同步. 另一个链路上的激光器t2与r2可被控制到4周期状态上并能取得4周期同步. 当分别有ρ = 0.07与ρ = 0.09时, 激光器t1与r1能够取得3周期同步; 与此同时, 激光器t2与r2能够取得4周期同步, 即LAN两个链路队列结点的3周期与4周期队列控制同步已分别实现.τ = 0.5 ns, ρ = 0.2时, 可以控制实现两个链路队并行队列的两个同级周期(都是3周期但变化轨道不同)同步. 其中激光器t1与r1能够被有效地控制到3周期态, 并能获得同步. 而激光器t2与r2 能被有效地控制在另外一个3周期状态上并能取得同步.τ = 0.8 ns和ρ = 0.06时, 图8 显示激光LAN一个链路上的激光器t1与r1能够被有效地控制到一个4周期态上, 并取得4周期同步. 图9 是另一个链路上的激光器t2与r2 被有效地控制到另外一个4周期状态上并取得同步的结果. 双参数变化改变了周期轨道. 当τ = 1.2 ns, ρ = 0.07时, 激光LAN控制的结果是两个链路上的各个网络结点队列激光器都能够分别被控制在两个不同的2周期状态上并能够取得并行队列同步.图 8 激光器t1与r1取得4周期同步Figure8. The laser t1 synchronizes with the laser r1 at a 4-periodic state.图 9 激光器t2与r2取得4周期同步Figure9. The laser t2 synchronizes with the laser r2 at another 4-periodic state.τ = 1.6 ns, ρ = 0.12时, 图10 显示, 在经过约80 ns后, LAN一个链路上的激光器t1与r1能够被控制到6周期态上, 并能够取得6周期同步. 图11 是另一个链路上的激光器t2与r2 被控制到5周期状态上并取得了该5周期同步的结果.图 10 激光器t1与r1取得6周期同步Figure10. The laser t1 synchronizes with the laser r1 at a 6-periodic state.图 11 激光器t2与r2取得5周期同步Figure11. The laser t2 synchronizes with the laser r2 at a 5-periodic state.τ = 1.6 ns, 对于控制参量ρ 其他的取值, 还会有另外一些控制结果. 如当ρ = 0.14时, 一个队列激光器t1与r1能够控制实现5周期同步. 另一个队列激光器t2与r2 能够控制实现6周期同步. 如当ρ = 0.1时, 两个链路上的网络结点激光器t1与r1以及t2与r2 能够被控制, 并能够分别获得3周期、2周期的并行队列同步.τ = 1.6 ns不变, 前70 ns时取ρ = 0.14, 后70 ns时取ρ = 0.1. 控制结果是: 前70 ns, 激光器t1与r1能够有效地控制到5周期同步(变化波形相同); 当70 ns时参数ρ 改变后, 激光器t1与r1也同时发生状态改变, 并能够有效地控制到3周期同步(变化波形相同), 其中物理状态改变时间$ t_{\rm r} $ 大约为2.5 ns, 但整个控制过程仍然是同步的(且计算有$E_{{\rm{t}}1}^2 -E_{{\rm{r}}1}^2=0 $ ), 见图12 (E r1 已向上平移0.18). 另一个队列激光器t2与r2 的动态控制结果见图13 (E r2 已向上平移0.1). 前70 ns, 激光器t2与r2能够有效地控制到6周期同步(变化波形相同), 当70 ns时参数ρ 改变后, 激光器t2与r2同时发生状态改变并能够有效地控制到2周期同步(变化波形相同), 其中状态改变时间t r 大约为2.5 ns, 但整个过程也都是同步的(且计算有$E_{{\rm{t}}2}^2 -E_{{\rm{r}}2}^2=0$ ).图 12 激光器t1与r1取得类周期动态同步Figure12. The laser t1 synchronizes dynamically with the laser r1 in quasi-periodicity.图 13 激光器t2与r2取得类周期动态同步Figure13. The laser t2 synchronizes dynamically with the laser r2 in quasi-periodicity.τ 和ρ 调控下, 激光器t1和激光器r1可以进行两点混沌载波同步发射与超宽带通信. E t1 和E r1 可以作为超宽带载波同步发射, 在两个位置分别被调制向外传送两个信息号, 也可以进行交替发射, 或还可以设想推广为光网络组合联合超宽带通信, 这与传统上混沌通信是由两个同步混沌激光器实施信息的发收与解调是有区别的. 其系统实施光网络组合超宽带通信主要是利用网络功能, 如激光器t1向激光器r2发射信息, 激光器r2与激光器t2同步解调; 或激光器t2向激光器r1发射信息, 激光器r1与激光器t1同步解调. 这里仅给出激光器t1与t2超宽带通信结果, 如图14 和图15 所示, 其中取τ = 1 ns和ρ = 0.01调控系统到混沌态, 并实现两点混沌载波同步发射(见图16 , 两个相同混沌吸引子轨迹相同且$E_{{\rm{t}}1}^2 =E_{{\rm{r}}1}^2 $ ). 图14 是激光器t1超宽带通信过程, 通信速率是0.5 GHz, 信息信号振幅是0.4, 其中图14(a) 是混沌载波被信息信号调制后的载波和信号的包络变化, 其中信号强度远大于载波且可识别, 这是混沌超宽带通信的基本要求. 图14(b) 是从包络上恢复出来的信息信号. 图15 通信速率是0.25 GHz, 信号振幅是0.4. 这样两点混沌载波同步发射与超宽带通信完成. 同样, 激光器t2和激光器r2也可以进行两点混沌载波同步发射与超宽带通信. 这样该网络系统可以完成并行多点混沌载波同步发射与超宽带光通信.图 14 激光器t1超宽带通信Figure14. The laser t1 performs an ultra-wideband communication.图 15 激光器r1又一个超宽带通信Figure15. The laser r1 performs another ultra-wideband communication.图 16 激光器t1与r1取得混沌同步发射Figure16. The lasers t1 and r1 emit synchronously two same chaotic carriers.5.结 论 本文成功研究并实现了激光局域网络的混沌控制与并行队列同步. 具体提出“单队列-双参数”光电延时反馈控制激光LAN系统及可控的“交叉驱动-反馈”并行队列同步网络的数理模型. 通过超越方程理论预言了该LAN是可以实现混沌控制的, 通过并行队列同步方程理论证明了并行串联队列同步是可以获得的. 数值结果和理论分析取得了完美统一. 发现在两个并行串联队列光路上, 可分别实现网络各结点的混沌控制并能够实现类周期的网络结点的并行队列同步, 实现了2周期、3周期、4周期等状态的并行队列同步及其他多个类周期网络结点的激光并行队列同步及动态同步, 发现了2个类周期等并行队列同步控制区域. 最后给出两点混沌载波同步发射与光超宽带通信的实例, 阐述了交替发射、网络组合联合超宽带通信的设想等. 简言之, 本激光LAN特点是异系统耦合双中心生成串联并行队列网络, “交叉驱动-反馈”基本网络结构实现并行队列同步, “单队列-双参数”控制实现网络全部结点激光器物理状态的“两态”控制, 具有光网络联合超宽带通信功能等. 这种新型的激光LAN混沌控制系统, 具有局域光网络光传送与光联接核心控制技术要素, 具有复杂动力学网络系统的多变量、多空间维度以及并行两路不同队列混沌控制技术特点. 研究结果对局域网络、光网络的控制与同步、激光技术以及混沌的研究具有重要的参考价值. 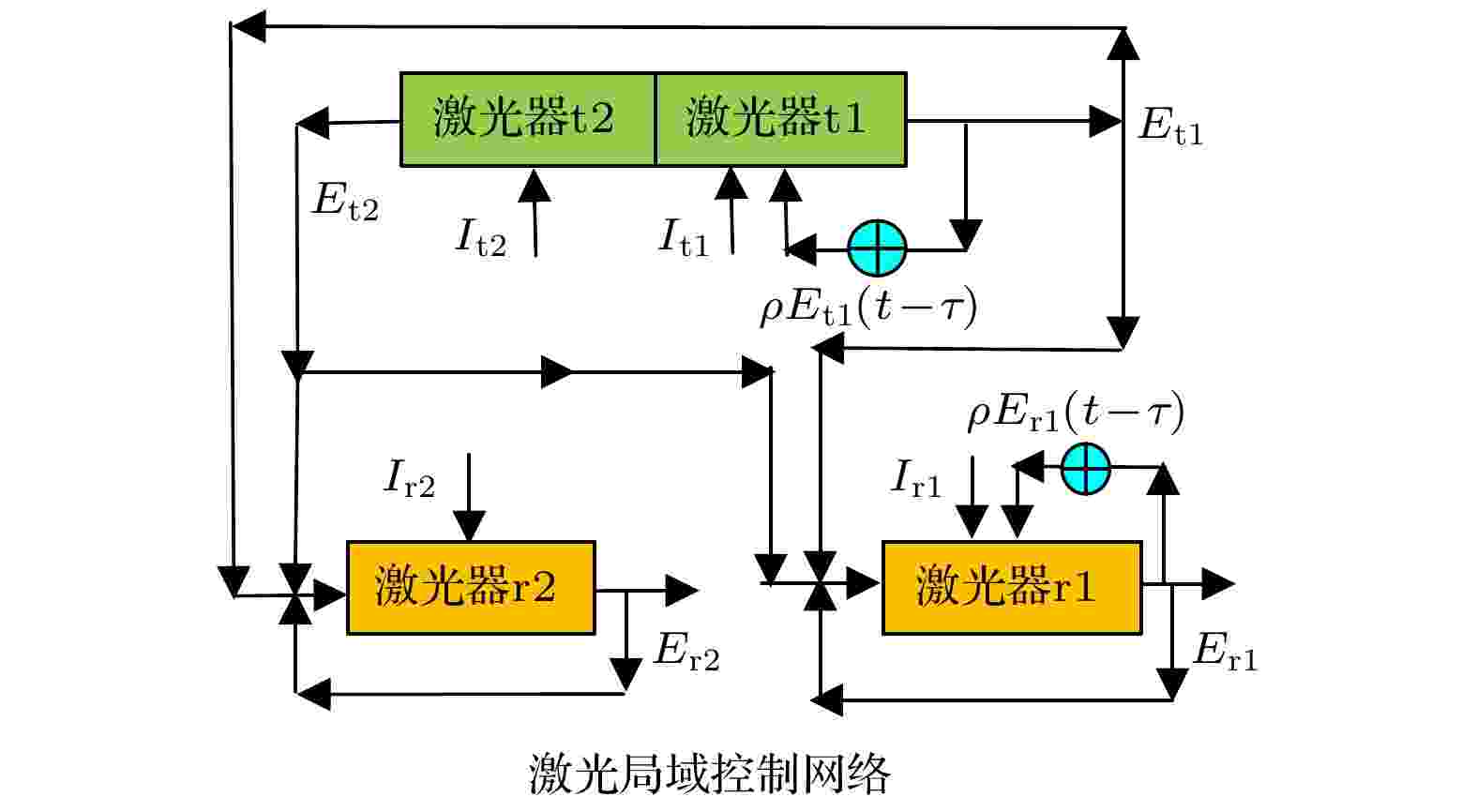 图 1 激光局域控制网络图, ⊕表示光电转换控制器
图 1 激光局域控制网络图, ⊕表示光电转换控制器


 图 2 激光器t1与r1链路混沌同步
图 2 激光器t1与r1链路混沌同步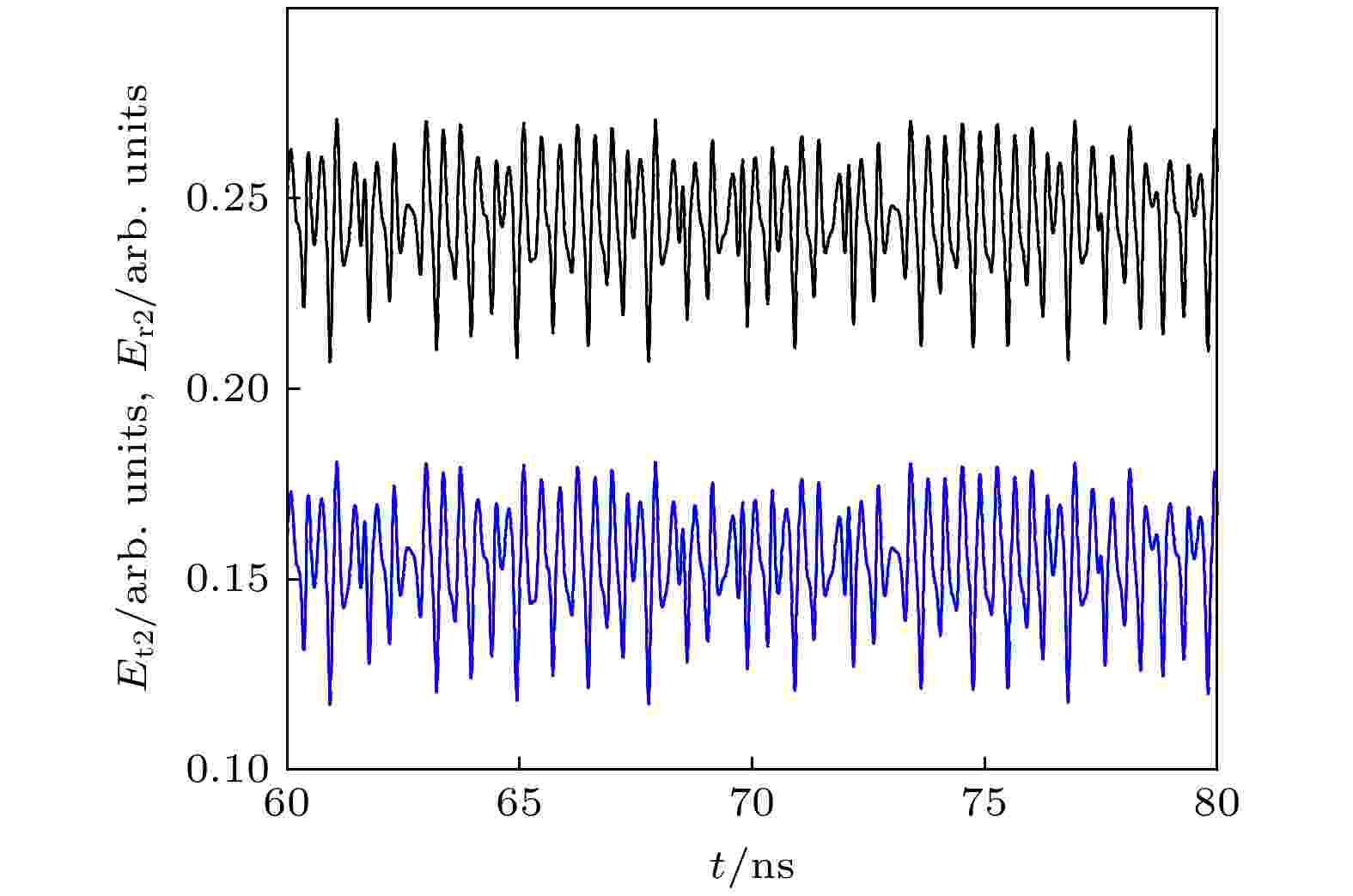 图 3 激光器t2与r2链路混沌同步
图 3 激光器t2与r2链路混沌同步

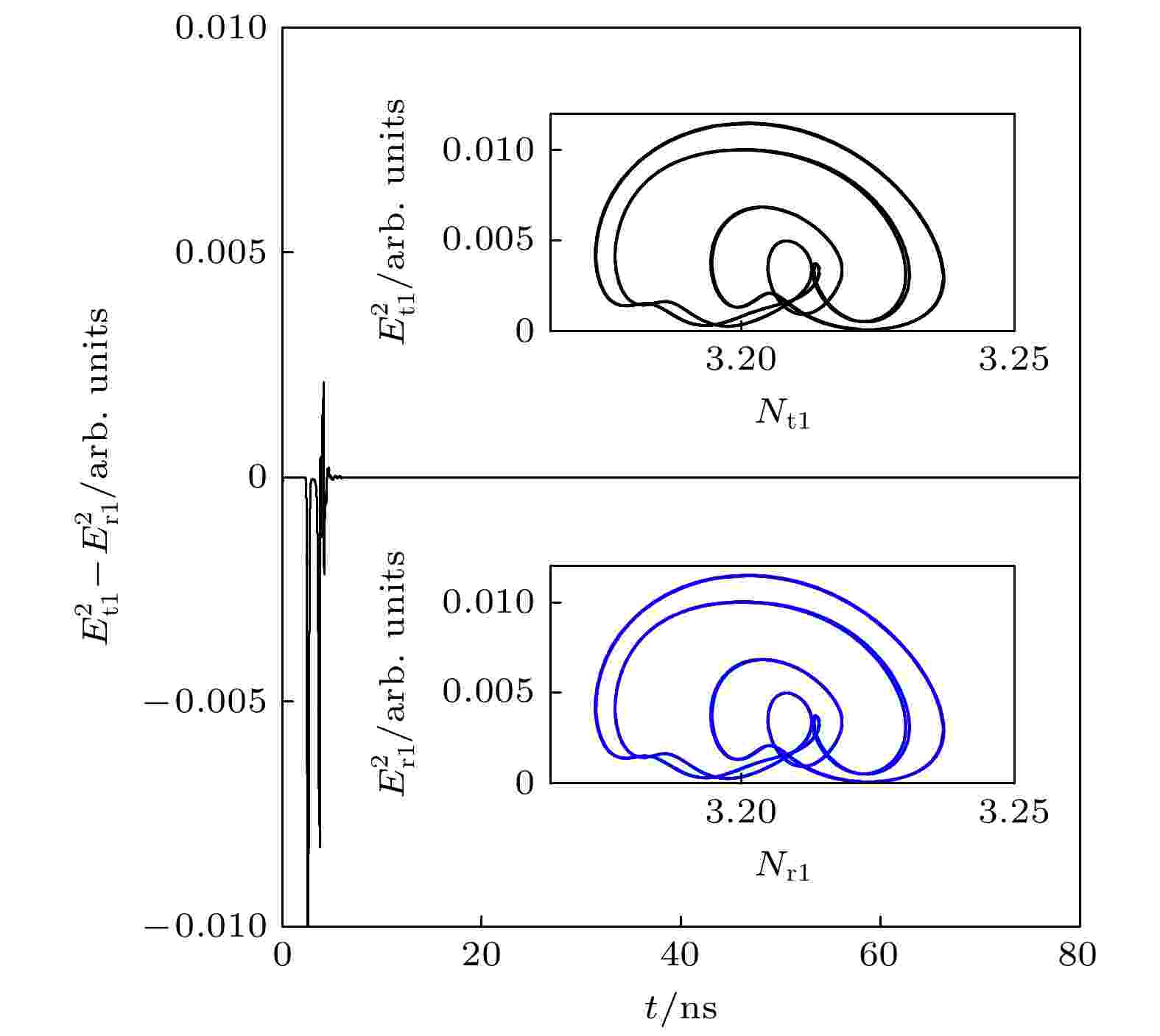 图 4 激光器t1与r1取得9周期同步
图 4 激光器t1与r1取得9周期同步 图 5 激光器t2与r2取得6周期同步
图 5 激光器t2与r2取得6周期同步 图 6 激光器t1与r1取得2周期同步
图 6 激光器t1与r1取得2周期同步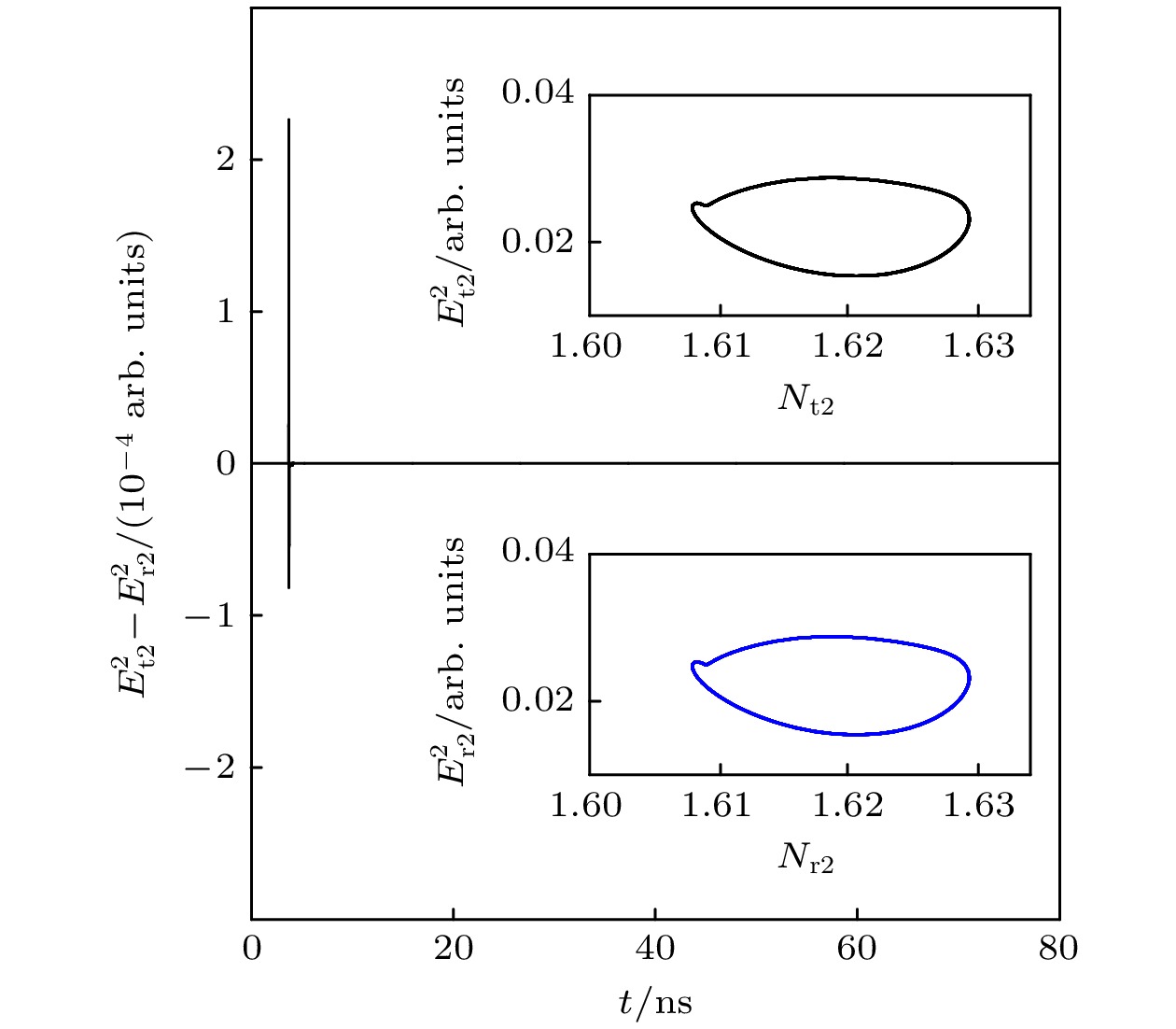 图 7 激光器t2与r2取得2周期同步
图 7 激光器t2与r2取得2周期同步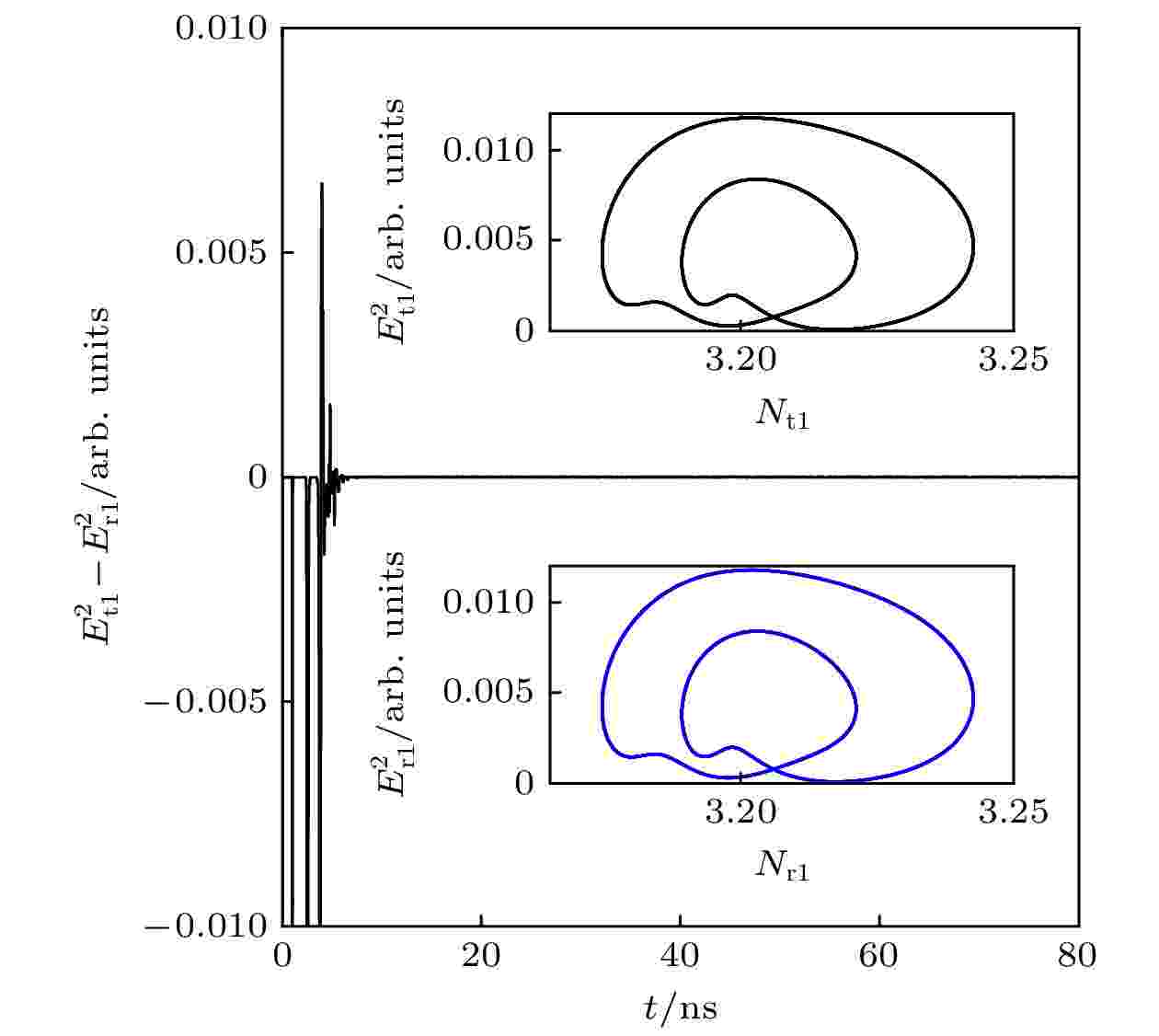 图 8 激光器t1与r1取得4周期同步
图 8 激光器t1与r1取得4周期同步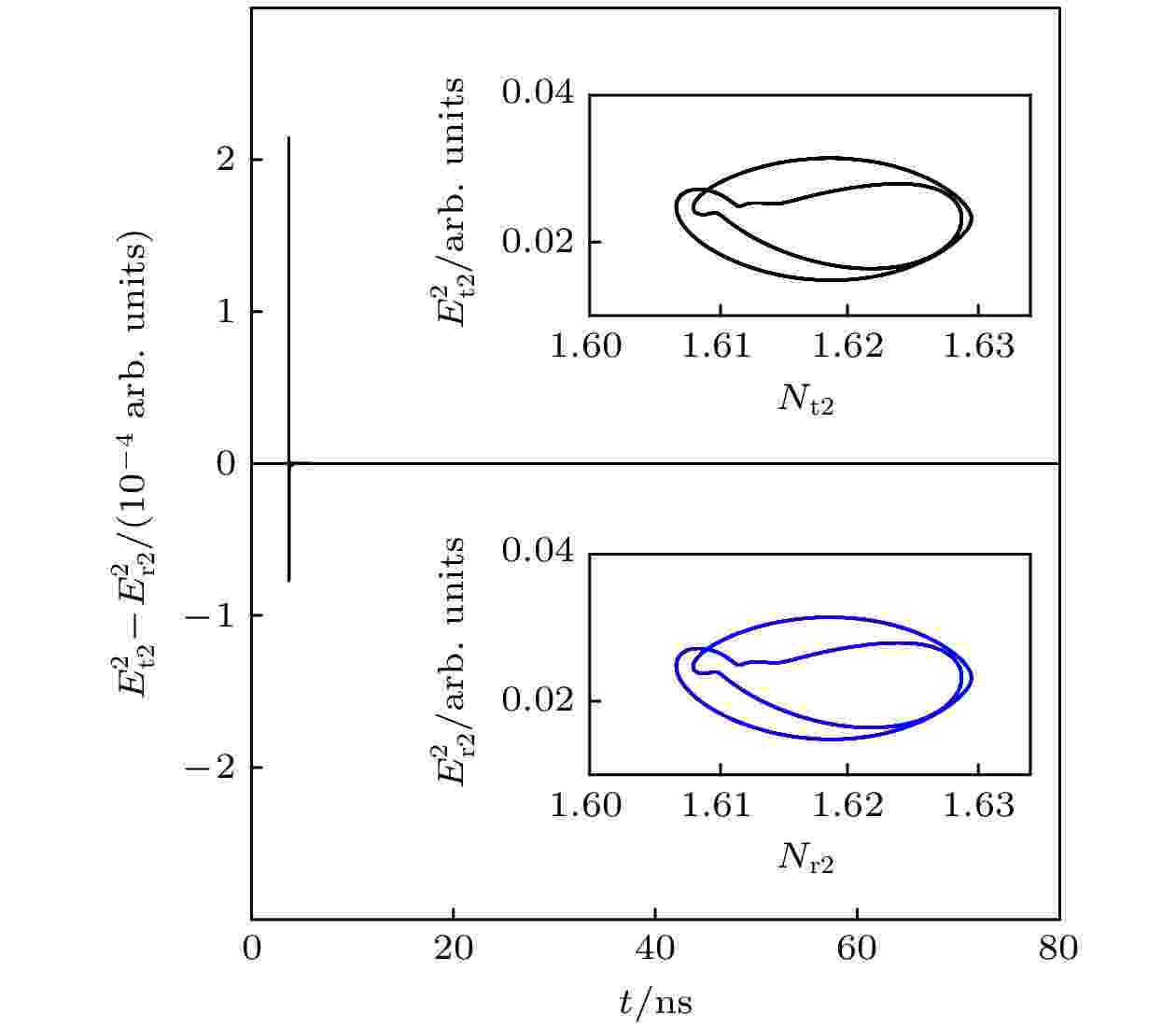 图 9 激光器t2与r2取得4周期同步
图 9 激光器t2与r2取得4周期同步 图 10 激光器t1与r1取得6周期同步
图 10 激光器t1与r1取得6周期同步 图 11 激光器t2与r2取得5周期同步
图 11 激光器t2与r2取得5周期同步


 图 12 激光器t1与r1取得类周期动态同步
图 12 激光器t1与r1取得类周期动态同步 图 13 激光器t2与r2取得类周期动态同步
图 13 激光器t2与r2取得类周期动态同步
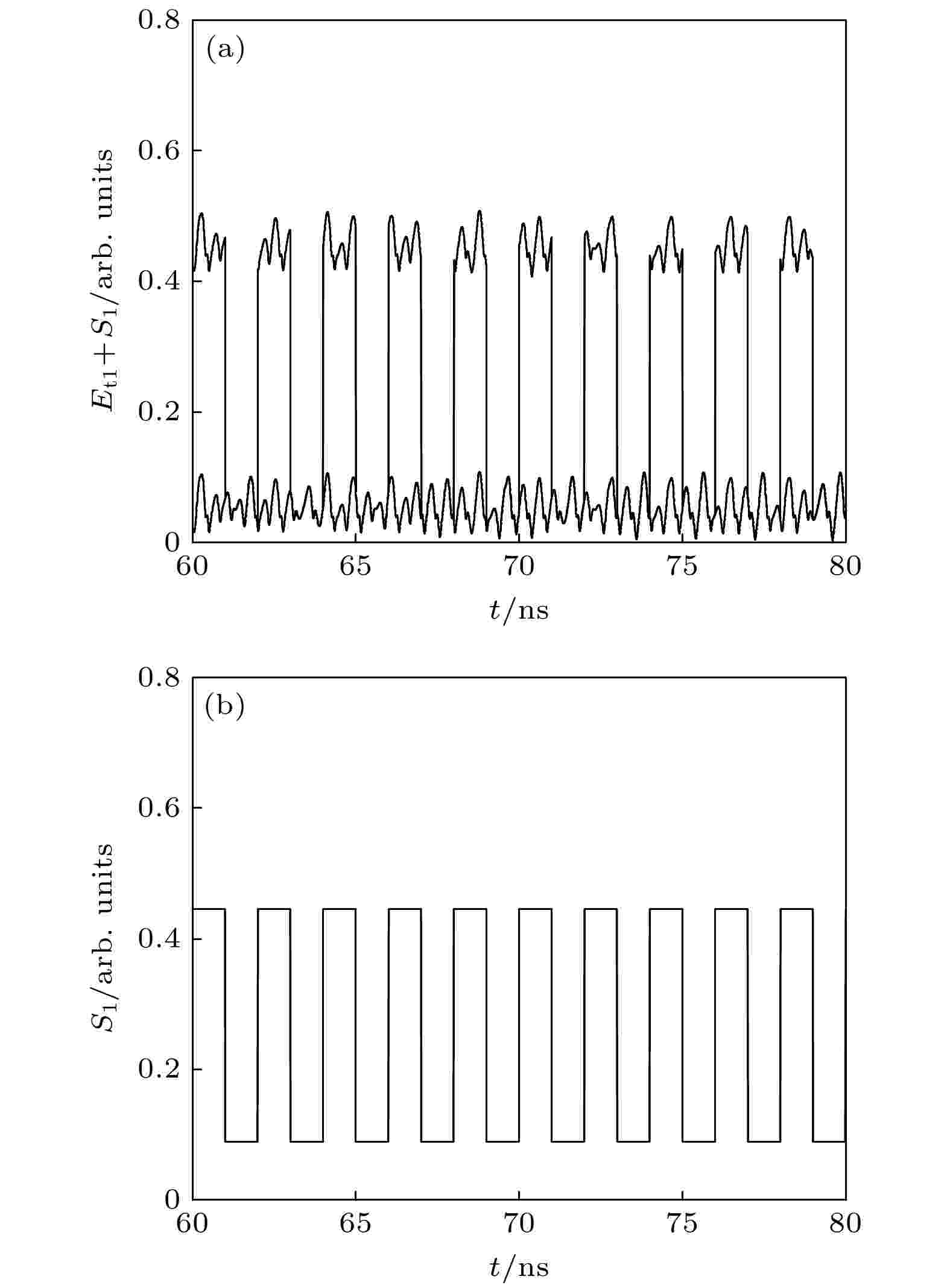 图 14 激光器t1超宽带通信
图 14 激光器t1超宽带通信 图 15 激光器r1又一个超宽带通信
图 15 激光器r1又一个超宽带通信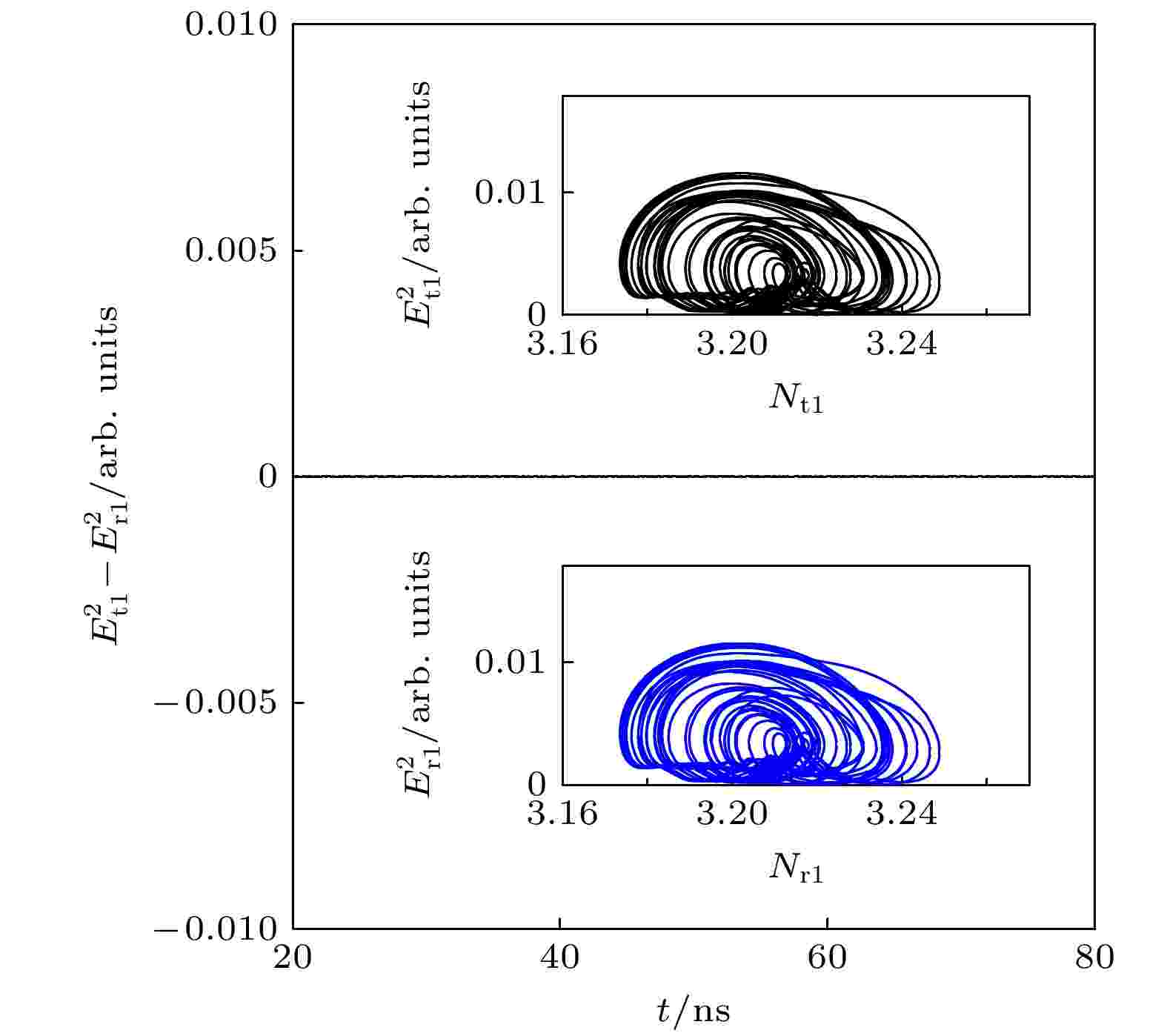 图 16 激光器t1与r1取得混沌同步发射
图 16 激光器t1与r1取得混沌同步发射