摘要:基于外部光注入的光泵浦自旋垂直腔表面发射激光器(vertical cavity surface-emitting laser, VCSEL)的两个混沌偏振分量, 提出了对两个复杂形状目标中的多区域精确测距方案. 这里, 两个混沌偏振探测波具有飞秒量级快速动态并且被双极性sinc波形调制, 使它们具有时空不相关特性. 利用这些特性, 通过计算多束延时反馈混沌偏振探测波形和与之相对应的参考波形的相关性, 实现了对两个复杂形状目标多区域位置矢量精确测量. 研究结果表明, 对多区域小目标的测距具有非常低的相对误差(低于0.94%). 当光电探测器的带宽足够大时, 其测距的分辨率达到0.4 mm, 并具有很强的抗噪声能力. 本文的研究结果在复杂形状目标的精确测距方面具有潜在应用.
关键词: 光泵浦自旋垂直腔表面发射激光器/
混沌偏振雷达/
多区域目标测距

English Abstract

全文HTML

--> --> -->

随着人工智能的飞速发展, 激光雷达在自动驾驶、无人机、机器视觉和目标跟踪测量等领域发挥着重要作用^[1-5]. 通过感知周围环境, 激光雷达有望实现以下功能: 目标精确测距、高质量三维(3D)成像、目标跟踪和识别、自动定位和地图绘制. 目前, 大多数激光雷达测距方案^[6-8]都使用脉冲激光器和连续波激光器作为光源, 以获得更好的信噪比和测量范围. 然而, 基于脉冲激光器和连续波激光器的雷达测距具有分辨率低、拦截概率高、抗干扰能力弱、成本高等缺点. 具有光反馈或光注入的半导体激光器产生的光混沌信号, 经天线发射后容易形成混沌激光雷达(chaotic lidar, CLR). 与使用脉冲激光器和连续波激光器进行测距相比, CLR对目标测距具有许多优势^[9-13], 例如拦截概率低、抗干扰能力强和成本低. 此外, 由于受益于光学混沌的宽带宽, 因而具有高分辨率. 最后, 由于CLR对激光参数的敏感性, 很容易生成和控制.
已报道的关于CLR测距的工作主要关注的是通过发射的混沌信号(参考信号)和从目标反射回来的延迟信号的相关性来实现测距^[14-20]. 在最近报道的工作中, 通过使用不同装置, 基于互相关理论的CLR测距取得了一些进展. 例如, 2014年, Zhang等^[18]实验论证了一种基于微波光子混沌信号生成和光纤分布的超宽带雷达远程测距系统. 2015年, Wang等^[19]利用损耗介质研究了混沌雷达系统对目标检测与测距的性能. 同年, Yao等^[21]演示了一种基于波分复用技术的分布式多输入多输出混沌雷达. 2017年, 利用两个混沌外腔半导体激光器的外差产生的宽带白混沌雷达, Wang等^[16]理论探索了一个测距分辨率和抗干扰能力得到加强的雷达系统. 2018年, Cheng等^[22]利用自零差和时间门控技术产生一个脉冲外差混沌激光雷达, 以提高混沌激光雷达能量利用效率, 结果实现了目标测距的精度达到毫米量级水平, 目标检测范围达到100 m以上. 最近, 利用驱动-响应垂直腔面发射激光器(vertical cavity surface-emitting laser, VCSEL)系统的同步混沌偏振探测信号, 我们实现了两个目标的实时测距^[23,24]. 此外, 利用三节点VCESLs网络中的6个同步混沌偏振探测信号, 我们探索了6个方位目标测距^[25].
据我们所知, 相关CLR测距的分辨率在很大程度上受到混沌激光器带宽的限制. 测距分辨率的进一步提高需要具有大调制带宽的超快速混沌激光器. 最近提出的光泵浦自旋VCSEL^[26]具有吸引人的特性, 例如, 激光输出的灵活自旋控制、飞秒量级的快速动态和大的调制带宽. 光注入或光反馈的光泵浦自旋VCSEL发射的超快混沌探测信号有望用于提高目标测距的分辨率和精度. 此外, 在己报道的关于CLR测距的工作^{[14,19,22,27,28]}中, CLR通常用于目标中的固定点. 另外, 这些工作没有使用多束CLR, 测距目标数量受限于少量目标. 文献[27-29]提出的相关CLR测距的方案和方法不能完全检测目标中不同区域的距离, 不适合复杂形状目标中整个区域的精确测距, 基于相关CLR的探测波形在目标测距前没有被设计, 这影响了目标测距的分辨率和精度的进一步提高. 为了克服这些问题, 复杂形状目标中多区域CLR测距的理论和物理机理需要进一步探索, 实现的新方案和方法也需要进一步探讨. 因此, 本文基于外部光注入的光泵浦自旋VCSEL, 通过利用双极性sinc波形调制的两个混沌偏振波形, 提出了一种新颖的方案来实现两个复杂形状目标中的多区域精确测距. 在这个方案中, 两个调制的混沌偏振波形具有时间和空间上不相关的特性, 以及飞秒量级的快速动态特性. 利用这些特性, 通过计算多束延时反馈混沌偏振探测波形和与之相对应的参考波形的相关性, 探讨了两个复杂形状目标中的多区域测距的机理和实现方法. 最后论述了两个复杂形状目标中多区域的测距分辨率和相对误差.

图1给出了基于外部光注入的光泵浦自旋VCSEL的两个混沌偏振波形对两个复杂形状目标的多个区域进行精确测距的实现方案. 其中, DFB(distributed feedback laser)是外部注入激光器. 下标为1, 2的光学隔离器(optical isolator, OI)用于确保光波的单向传播. 中密度滤波器(neutral density filter, NDF)用于控制来自DFB的外部光场的注入强度. 为了确保将DFB的偏振光平行注入到光泵浦自旋VCSEL(spin-VCSEL)的x偏振分量和y偏振分量中, 来自DFB输出的偏振光需要通过偏振控制光路(polarization control optical circuit, PCOC)进行分离和调整为x偏振分量(x polarization component, x-PC)和y偏振分量 (y-PC). PCOC 的偏振控制功能相关的描述详见文献[30]. 在PCOC中, 一些无源器件, 如光纤偏振器(fiber polarizer, FP)、光纤偏振控制器(fiber polarization controller, FPCO)、光纤消偏器(fiber depolarizer, FD)、光纤偏振耦合器(fiber polarization coupler, FPC), 被用来实现x偏振分量和y偏振分量之间的转换. 目标1 (target 1, T₁)和目标2 (target 2, T₂)是被测量的复杂形状目标. PD (photodetector)是光电探测器. AM (amplitude modulator)是振幅调制器. EA (electric amplifier)是电放大器. TA (transmitting antenna)和RA(receiving antenna)分别是发射天线和接收天线. 光注入光泵浦自旋VCSEL产生的混沌光波通过光纤偏振分束器(fiber polarization beam splitter, FPBS)分为两个偏振分量, 其中x偏振分量被1 × 1光纤分束器1 (fiber beam splitter 1, FBS₁)进一步分成两束光波. 其中一束光被考虑为参考信号, 另外一束光被用来作为探测信号, 为了便于讨论, 它们分别被定义为x偏振参考信号和x偏振探测信号. 同时, FBS₂将y偏振分量进一步分离为两束光, 其中一束光作为参考信号, 另一束光考虑为探测信号, 分别被命名为y偏振参考信号和y偏振探测信号. 针对复杂形状目标T₁的测距, x偏振探测信号通过1 × N FBS₁分为N束探测波形. 利用带有下标为11—1N的振幅调制器, 这些探测波形被双极性sinc波形调制. 这些调制后的探测波形被下标为11—1N的光电探测器PD转换为N条支路探测电流信号, 接着被下标为1—N的电放大器EA₁ 放大. 利用下标为11—1N的发射天线, 这些放大的电流信号被发射为N束雷达波, 之后到达目标T₁的多个区域目标. 当N束雷达波被目标T₁中的多个目标小区域反射或散射之后, 首先被延时, 然后被接收天线RA₁ 接收, 最后被电放大器EA₂ 放大. 另一方面, x偏振参考信号被1 × N FBS₂分成N束参考波形. 利用下标依次为21—2N的振幅调制器, 这些参考波形被双极性sinc波形调制. 这些调制后的参考波形被下标依次为21—2N 的光电探测器PD 转换为N条支路参考电流信号. 探测电流信号与对应的参考电流信号之间的相关性可通过相关函数计算模块(correlation function calculation module, CFCM)进行计算. 通过观察相关性最大期望值的时间位置, 使用目标测距计算模块(target ranging calculation module, TRCM), 进一步计算目标T₁中的多个区域目标的位置矢量. 使用相同的方法, 可以获得目标T₂中的多个区域的目标位置矢量.
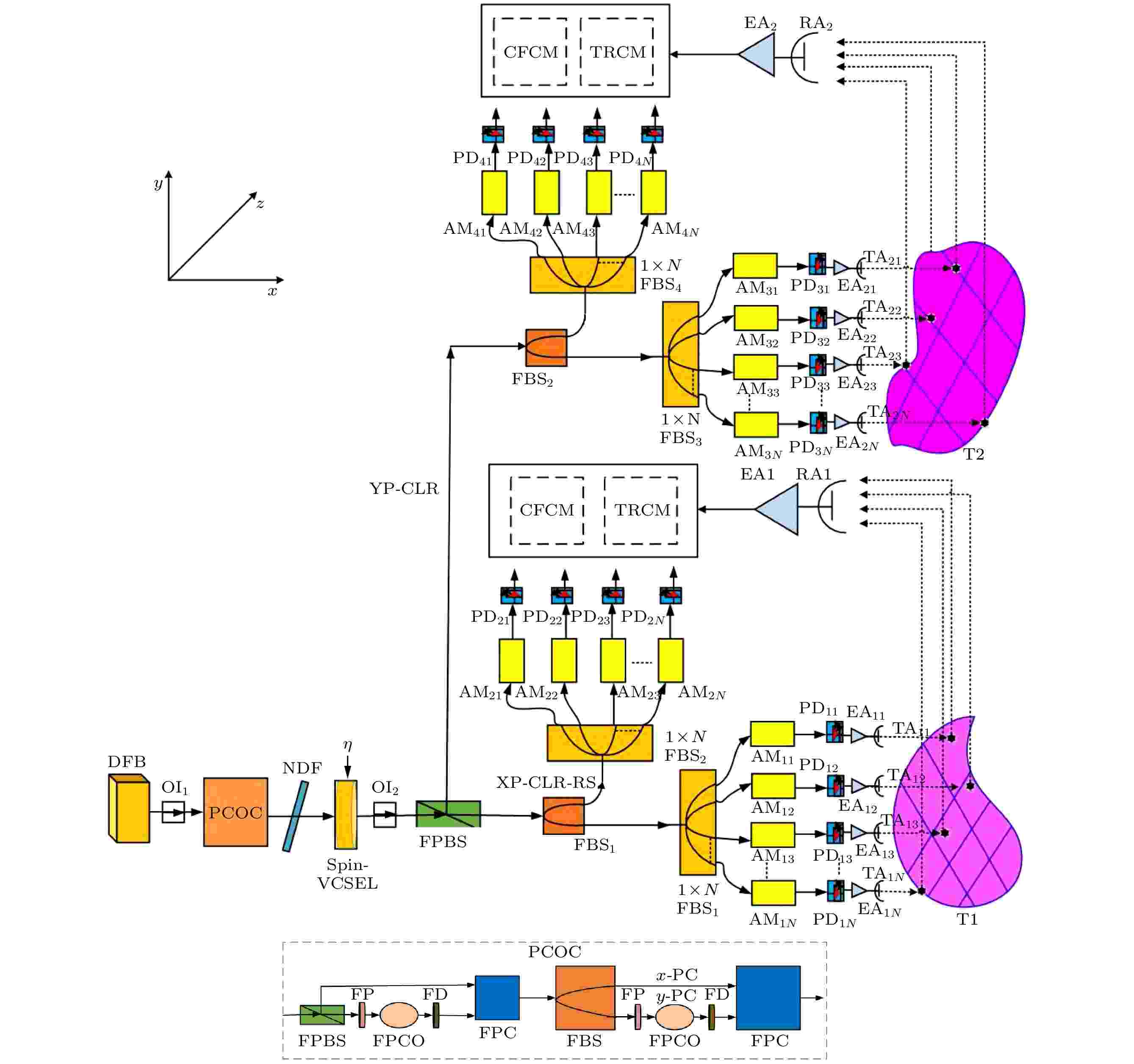图 1 基于外部光注入的光泵浦自旋VCSEL的两个混沌偏振波形对两个复杂形状目标中多个区域的精确测距方案. 这里, DFB: 分布式反馈激光器; OI: 光学隔离器; NDF: 中密度滤器; PCOC: 偏振控制光路; FP: 光纤偏振器; FPCO: 光纤偏振控制器; FD: 光纤消偏器; FPC: 光纤偏振耦合器; PD: 光电探测器; AM: 振幅调制器; Spin-VCSEL: 自旋VCSEL; FPBS: 光纤偏振分束器; FBS: 光纤分束器; EA: 电放大器; TA: 发射天线; RA: 接收天线; T₁ 和T₂: 两个待测目标; CFCM: 相关函数计算模块; TRCM: 目标测距计算模块; x-PC: x偏振分量; y-PC: y偏振分量; $ \eta $: 泵浦光的归一化总泵浦功率
Figure1. Schematic diagram of the precise ranging for the multi regions of two complex-shape targets by using two chaotic polarization radars in the optically pumped spin-VCSEL with optical injection. Here, DFB, distributed feedback laser; OI, optical isolator; NDF, neutral density filter; PCOC, polarization control optical circuit; FP, fiber polarizer; FPCO, fiber polarization controller; FD, fiber depolarizer; FPC, fiber polarization coupler; PD, photodetector; AM, amplitude modulator; Spin-VCSEL, spin vertical cavity surface emitting laser; FPBS, fiber polarization beam splitter; FBS, fiber beam splitter; EA, electric amplifier; TA, transmitting antenna; RA, receiving antenna; T₁ and T₂, two targets to be measured; CFCM, correlation function calculation module; TRCM, target ranging calculation module; x-PC, x polarization component; y-PC, y polarization component; $ \eta $, total normalized pump power.

针对自旋VCSEL, 光场的左旋和右旋圆偏振分量改写为正交线性分量, 即

$ E_{x} = \frac{{E_+}(t)+{E_-}(t)}{\sqrt{2}},\; E_{y} = -{\rm i}\frac{{E_+}(t)-{E_-}(t)}{\sqrt{2}}, $

其中, $ E_{+} $和E_–分别为是左右圆偏振分量的复振幅, $ E_{x} $和$ E_{y} $分别为两个正交线性分量(x-PC和y-PC)的复振幅. 基于方程(1), 利用修正的自旋相关模型^[31], 可以获得外部光注入的光泵浦自旋VCSEL的四个耦合速率方程如下:

$ \begin{split} \frac{{\rm d}{E_x}(t)}{{\rm d}t} =\;& \kappa (1+{\rm i}\alpha) \big[(M(t)-1){E_x}(t)+{\rm i}n{E_y}(t)\big]\\&-(\gamma_{\rm a}+{\rm i} \gamma_{\rm p}){E_x}(t)+\xi_1{\sqrt{\beta \gamma \big[M(t)+n(t)\big]}} \\ &-{\rm i}\Delta \omega {E_x}(t)+k_{xinj}E_{xinj}(t),\\[-10pt] \end{split} $

$ \begin{split} \frac{{\rm d}{E_y}(t)}{{\rm d}t} =\;& \kappa (1+{\rm i}\alpha) \big[(M(t)-1){E_y}(t)-{\rm i}n{E_x}(t)\big]\\&-(\gamma_{\rm a}+{\rm i} \gamma_{\rm p}){E_y}(t)+\xi_2{\sqrt{\beta \gamma \big[M(t)+n(t)\big]}}\\ &-{\rm i}\Delta \omega {E_y}(t)+k_{yinj}E_{yinj}(t), \\[-10pt]\end{split} $

$ \begin{split} \frac{{\rm d}M(t)}{{\rm d}t} = \;&\gamma \big[\eta-(1+|{E_x}(t)|^2+|{E_y}(t)|^2)\big]M(t)\\&-{\rm i}n\big({E_y}(t){E_x^*}(t)-{E_x}(t)E_y^{*}(t)\big), \end{split} $

$ \begin{split}\frac{{\rm d}n(t)}{{\rm d}t} =\;& \gamma P\eta-n(t)\big[\gamma_s+\gamma+(|{E_x}(t)|^2+|{E_y}(t)|^2)\big]\\&-{\rm i}\gamma M(t)\big({E_y}(t)E_x^{*}(t)-{E_x}(t)E_y^{*}(t) \big),\\[-10pt] \end{split} $

这里, 下标x和y分别表示x-PC和y-PC; 圆偏振电场分量被晶体双折射耦合, 其中, 用速率$ \gamma_{\rm p} $和二向色性$ \gamma_{\rm a} $来描述晶体双折射的特征; 在方程(2)—(5)中, 归一化的载流子变量M和n 分别定义为$M = ( n_{+} + n_{-} )/2$和$n = ( n_{+} - n_{-} )/2$, 其中$ n_{+} $和$ n_{-} $分别是相应的归一化上旋和下旋电子密度; $ \kappa $是腔衰减速率; $ \alpha $是线宽增强因子; $ \gamma $是电子密度衰减速率; $ \gamma_{\rm s} $ 是自旋弛豫速率; $ \eta = \eta_{+} + \eta_{-} $是泵浦光的归一化总泵浦功率, 其中, $ \eta = 1 $表示泵浦阈值. $ \eta_{+} $和$ \eta_{-} $是无量纲圆极化偏振泵浦分量, 用来描述极化偏振光光泵浦功率; 泵浦椭圆极化率P定义为^[32]$P = ( \eta_{+} - \eta_{-} )/( \eta_{+} + \eta_{-} )$; $ k_{xinj} $和$ k_{yinj} $分别是x-PC 和y-PC 的注入强度; $ \beta $ 是自发散射系数, 也称为噪声强度. $ \xi_1 $和$ \xi_2 $都是均值为0, 方差为1 的独立高斯白噪声, 其中$\langle \xi_i (t) \xi^{*}_j (t) \rangle = $$ 2 \delta_{ij} \delta (t-t')$. $ \Delta\omega $ 是DFB 的中心频率和Spin-VCSEL的参考频率之间的失谐.

如图1所示, 通过使用N束混沌偏振雷达探测波, 待测区域T₁和T₂中的任何一个小区域能同时被检测. 在小区域目标处反射或散射后, 具有不同延时的N束混沌偏振雷达探测波形同时被接收天线RA接收. 在这种情况下, 根据相关理论^[33], 为了容易地探测每个小区域的位置矢量, 混沌激光雷达需要满足时间正交不相关和时间空间不相关. 尽管N束x偏振和y偏振混沌激光雷达探测信号容易满足时间正交性, 但很难实现空间正交性, 这是因为它们在空间上波形是相同的. 为了满足这些条件, N束探测信号需要具有高质量自相关函数进行调制, 例如, 在–1和1之间变化的双极性sinc波形. 下面以Spin-VCSEL输出的x偏振探测信号对目标T₁测距为例, 阐述其测距原理. 当用双极性sinc波形对N束x偏振探测信号进行调制时, 可以获得调制后波形为

$ \begin{split}&S_{{1x}_j}(j,t) = s_{{1x}_j}(t)A_{\rm m}\{ {\rm {sinc}} (t) \}_{j},\\&j = 1,\;2,\;3,\;\cdots,\;N \quad ({\text{下同}}); \end{split} $

同理, 当用双极性sinc波形对N束x偏振参考信号进行调制时, 调制后的波形可以表达为

$ S_{{2x}_j}(j,t) = s_{{2x}_j}(t)A_{\rm m}\{ {\rm {sinc}} (t) \}_{j}, $

其中, A_m为双极性sinc波形的幅值; $\{ {\rm {sinc}} (t) \}_{j}$代表第j个sinc波形, 当j取不同整数值时, 有不同的sinc波形; 下标1和2分别表示探测信号和参考信号; $ s_{{1 x}_j, {2 x}_j} = |E_{{1 x}_j, {2 x}_j}|/\max ( |E_{{1 x}_j, {2 x}_j}|) $, 其中$ {E_{1 x}}_j $和$ {E_{2 x}}_j $分别为第j束x偏振探测信号和第j束x偏振参考信号的复振幅. 根据方程(6)—(7), N束x偏振探测信号在空间上彼此正交, 其互相关可以表达为

$ \begin{split} &R_{{\rm P}x} = \int S_{{1x}_j}(t)S_{{1x}_l}^{*}(t){\rm d}t = \delta(j-l),\\ &l, j = 1,\; 2,\;3,\;\cdots,\;N \quad ({\text{下同}}), \end{split} $

这里, $ S_{{1 x}_j} $和$ S_{{1 x}_l} $分别为第j束和第l束雷达探测信号. 当j = l时, $ R_{{\rm P}x} $ = 1; 当j ≠ l时, $ R_{{\rm P}x} $ = 0, 这意味着空间上不同束的雷达探测信号是互不相关的. 此外, 对于同一束x偏振探测信号, 在不同时刻是不相关的, 但在同一时刻, 它是自相关的. 因此, 对于第j束x偏振探测信号, 其时间自相关可以描述为

$ T_{{\rm P}x} = \int S_{{1x}_j}(t-{t_1})S_{{1x}_j}^{*}(t-{t_2}){\rm d}t = \delta ({t_1}-{t_2}), $

式中$ S_{{1 x}_j}(t-{t_1}) $和$ S_{{1 x}_j}(t-{t_2}) $分别为第j束雷达探测信号在不同时间上的波形. 当$ t_1 = t_2 $时, $ T_{{\rm P}x} $ = 1; 假如 $ t_1 \neq t_2 $, $ T_{{\rm P}x} $ = 0. 此外, 第j束x偏振雷达探测信号与第l束x偏振参考信号的空间互相关可以表达为

$ R_{{\rm PR}x} = \int S_{{1x}_j}(t)S_{{2x}_l}^{*}(t){\rm d}t = \delta (j-l), $

式中$ S_{{1 x}_j}(t-{t_1}) $和$ S_{{1 x}_j}(t-{t_2}) $分别为第j束雷达探测信号在不同时间上的波形. 当$ t_1 = t_2 $时, $ T_{{\rm P}x} $ = 1; 假如 $ t_1 \neq t_2 $, $ T_{{\rm P}x} $ = 0. 此外, 第j束x偏振雷达探测信号与第l束x偏振参考信号的空间互相关可以表达为

$ T_{{\rm {PT}}x} = \int S_{{1x}_j}(t-{t_1})S_{{2x}_j}^{*}(t-{t_2}){\rm d}t = \delta ({t_1}-{t_2}), $

这里, 当$ t_1 = t_2 $时, $ T_{{\rm PT}x} $ = 1; $ t_1 \neq t_2 $时, $ T_{{\rm {PT}}x} $ = 0. 由方程(8)—(11), 可以得出第j束x偏振雷达探测信号与第l束x偏振雷达探测信号在时间和空间上的相关函数为

$ \begin{split}C_{{\rm {RT}}_1}(j,l;{t_1},{t_2}) =\;& \int S_{{1x}_j}(t-{t_1})S_{{1x}_l}^{*}(t-{t_2}){\rm d}t \\=\;& \delta ({t_1}-{t_2})\cdot\delta(j-l). \\[-10pt]\end{split} $

同时, N束x偏振雷达探测信号与第l束x偏振参考信号在时间和空间上的相关函数可以表示为

$ \begin{split}C_{{\rm {RT}}_2}(j,l;{t_1},{t_2}) =\;& \int S_{{1x}_j}(t-{t_1})S_{{2x}_l}^{*}(t-{t_2}){\rm d}t\\=\;& \delta ({t_1}-{t_2})\cdot\delta(j-l). \\[-10pt] \end{split} $

如图2所示, 分别考虑调制的N束x偏振雷达信号用于探测目标T₁中的小区域中任意目标点A, 并通过其反射或者散射后, 被天线RA₁接收. 该天线接收信号可以表达为
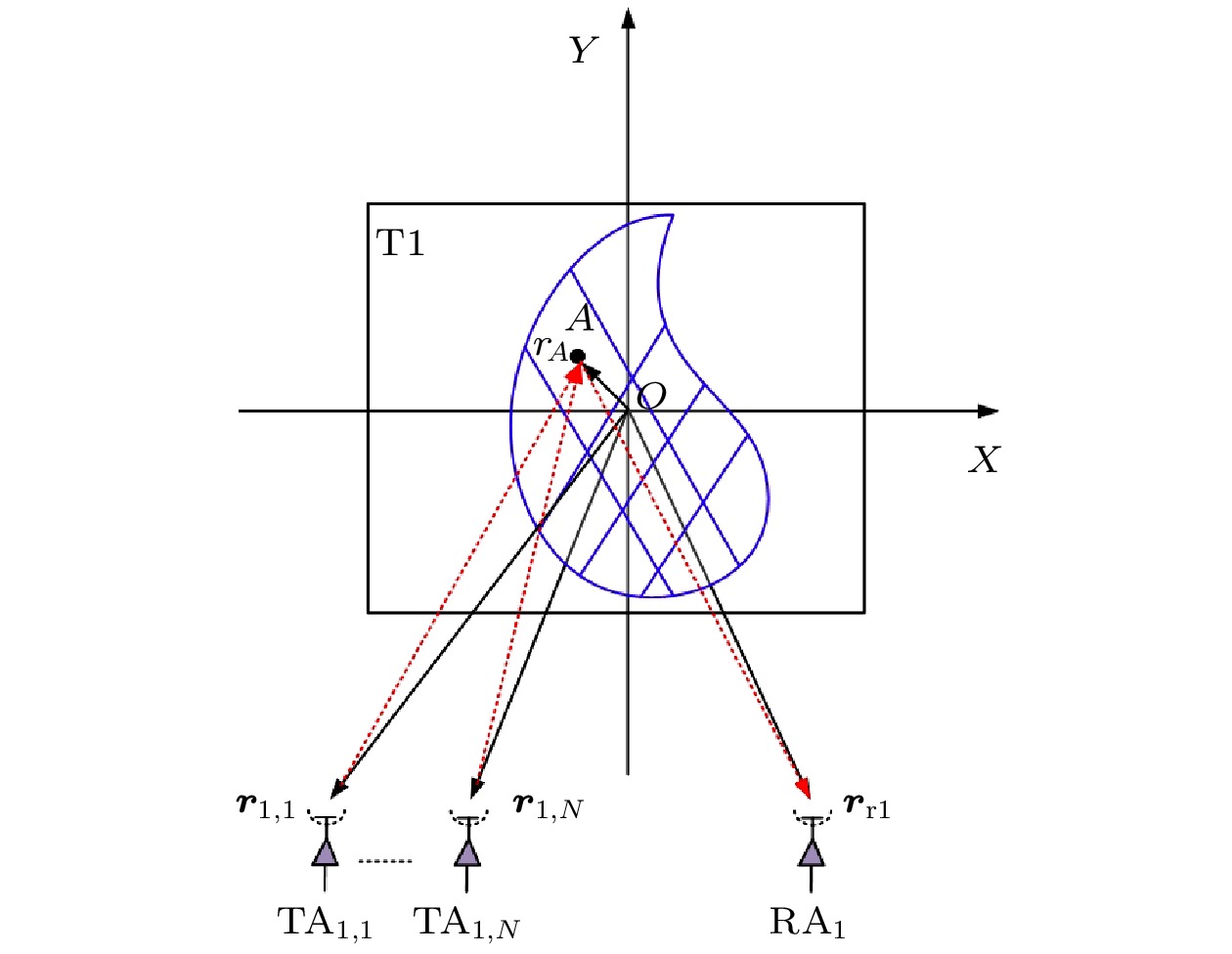图 2 复杂形状目标T₁中的任意小区域测距的几何图. 图中, ${{\mathit{\boldsymbol{r}}}}_{{{A}}}$: A点的实际位置矢量; ${{\mathit{\boldsymbol{r}}}}_{{1}, {1}}—{{\mathit{\boldsymbol{r}}}}_{{1}, {{{N}}}}$: 发射天线TA_{1, 1}—TA_{1, N}的位置矢量; $ {{\mathit{\boldsymbol{r}}}}_{{{\rm r}}1}$: 接收天线的位置矢量; 红色点线: 天线发射的雷达探测信号指向目标点A的方向, 以及由目标点A反射或散射的雷达探测信号指向接收雷 达RA₁的方向
Figure2. Geometry diagram of the ranging for arbitrary small area of the target T₁. Here, $ {{\mathit{\boldsymbol{r}}}}_{{{A}}} $, the actual position vector of the point-A; $ {{\mathit{\boldsymbol{r}}}}_{{1}, {1}}–{{\mathit{\boldsymbol{r}}}}_{{1}, {{{N}}}} $, the position vectors for the transmitting antennas TA_{1, 1}–TA_{1, N} ; Red dotted lines, the direction of the radar probe signals transmitted by the antennas toward the point-A, as well as the direction of the radar probe signals reflected or scattered by the point-A toward the receiving antenna RA₁.

$ R_{x}(t) = \sum\limits_{j = 1}^{N} S_{{1x}_j}(t-{\tau_{{1},{j}}}), $

其中, $ \tau_{{1}, {j}} $是从发射天线TA_{1, j}到接收天线RA₁的时间延迟. 因此, 根据方程(13)和方程(14), 可以得到来自RA₁的接收信号和第j束x偏振参考信号的互相关函数为

$ \begin{split}CC_{{1},{j}} =\;& \int_{0}^{T_{\rm {int}}}S_{{2x}_j}(t)R_{x}(t){\rm d}t \\=\;& \int_{0}^{T_{\rm {int}}}S_{{2x}_j}(t)S_{{1x}_j}^{*}(t-\tau_{1j}){\rm d}t, \end{split} $

式中$ T_{\rm {int}} $是有效的相关时间. 时间延迟$ \tau_{1 j} $可以估计为最大相关性对应的时间值, 表示为

$ \tau_{{1},{j}} = \mathop{\rm {Max}}\limits_{\tau} \Big | \varepsilon \big [ CC_{{1,{j}}}(\tau) \big ] \Big |, $

其中, $ \varepsilon $是期望值. 如图2所示, 将A点的实际位置矢量设为$ {{\mathit{\boldsymbol{r}}}}_{{{A}}} $, 用第j束x偏振雷达探测信号对A点目标测量所得到位置矢量设定为${{\mathit{\boldsymbol{r}}}}_{{{A_j}}}$. 第j个发射天线TA_1,j的位置矢量设置为$ {{\mathit{\boldsymbol{r}}}}_{{1}, {{{j}}}} $. 接收天线RA₁的位置矢量设为$ {{\mathit{\boldsymbol{r}}}}_{{{r}}1} $. 根据A点的几何关系, 可以得到

$ \tau_{{1},{j}} = {\big | {{\mathit{\boldsymbol{r}}}}_{{{A_j}}}-{{\mathit{\boldsymbol{r}}}}_{{1},{{{j}}}} \big |}/{c}+ {\big | {{\mathit{\boldsymbol{r}}}}_{{{A_j}}}-{{\mathit{\boldsymbol{r}}}}_{{{r}}1} \big |}/{c}. $

由方程(17), 可以通过求解$ C_{N}^{2} $个方程, 得到$ C_{N}^{2} $个A点的位置矢量. 取这些位置矢量值的平均值作为A点的精确位置矢量, 表达式为

$ \overline{{{\mathit{\boldsymbol{r}}}}}_{{{A}}} = \frac1{C_{N}^{2}}{\sum \limits_{k = 1}^{C_{N}^{2}}{{\mathit{\boldsymbol{r}}}}_{{{A}}_k}}. $

表1列出了下面用于计算的系统参数值. 这里使用四阶Runge-Kutta方法对方程(1)—(5)进行数值计算, 其中, 时间步长h为1 ps, 时间离散采样点总数L = 100000. 双极性sinc波形的抽样周期$ T_{\rm s} $为0.1 ns, 对应的抽样点数$N_{\rm s}$为100. 双极性sinc波形的抽样周期数$K_0 = L/ N_{\rm{s}} = 1000$. 于是, 第j个调制信号离散化的表达式为${{\rm {sinc}} (t)}_{j}$, 离散化的表达式为

符号	参数	值
$ \alpha $	线宽增益因子	4
$ \eta $	总归一化泵浦功率	9
$ \kappa $	场衰减率	300
p	泵浦极化椭圆率	1
$ \beta $	自发耦合因子	$ 10^9 $
$ \gamma $	电子密度衰减率	$1\; {\rm {ns}}^{-1} $
$\gamma_{\rm a}$	线性二向色性	$10\; {\rm {ns}}^{-1} $
$\gamma_{\rm p}$	线性双折射效应	$60\; {\rm {ns}}^{-1} $
$\gamma_{\rm s}$	自旋弛豫率	$120\; {\rm {ns}}^{-1} $
$ k_{xinj} $	x-PC的光注入强度	$10\; {\rm {ns}}^{-1} $
$ k_{yinj} $	y-PC的光注入强度	$10\; {\rm {ns}}^{-1} $
$ \Delta \omega $	频率失谐	30 × 109 rad/s

表1用于计算的系统参数值
Table1.Parameter values of the system for calculations

$ y(k)=\sum\limits_{k = 1}^{K_{0}}{\rm {sinc}}\{h [(k-1)N_{\rm s}+1]:hkN_{\rm s}\}{\rm{sgn}}[c_{j}(k)] , $

其中,

$ \begin{split}&{\rm {sinc}}(kh) = \sin(2\pi kh/T_{\rm s})/(2\pi kh/T_{\rm s}),\\&k = 1,\;2,\;3,\;\cdots,\;L, \end{split}$

并且

$ {\rm{sgn}} = \left\{ \begin{aligned} &+1, \;\;\; {\text{假如}} \; c_{j}(k) = 0 \\&-1, \;\;\; {\text{假如}} \; c_{j}(k) = 1 \end{aligned}, \right. $

这里, $ c_{j}(k) $为数值0和1的随机分布序列. 当j取不同的整数值时, $ c(k) $有不同随机分布序列, 从而获得不同的sinc波形. 如图3(a)和图3(b)所示, 当j = 1和3时, ${{\rm {sinc}} (t)}_{1}$和${{\rm {sinc}} (t)}_{3}$的时间轨迹是不同的, 它们的值以不同的分布状态介于–1和1之间. 图3(c)和图3(d)给出了来自Spin-VCSEL输出的第1束和第3束x偏振探测信号的时间轨迹. 可以看出, x偏振探测信号时间轨迹呈混沌状态. 这两束x偏振探测信号被双极性sinc波形调制后的时间轨迹($ S_{1 x_{1}}(t) $和$ S_{1 x_{3}}(t) $)分别如图3(e)和图3(f)所示. 从图中可以发现, 它们的时间轨迹也呈混沌状态和飞秒量级的快速动态特征. 表明从天线发射的雷达探测信号的时间轨迹是混沌的, 具有快速动态特征, 以及满足时间和空间上的不相关性(见方程(12)和方程(13)). 为了方便讨论, 让N束x偏振雷达探测信号放置在一条水平线上. 这里以第5束x偏振混沌激光探测信号为例, 计算它们的时间自相关($ T_{{\rm P}x} $)以及空间互相关($ R_{{\rm P}x} $), 计算结果如图4所示. 可以看出, $ T_{{\rm P}x} $的最大值出现在t = 0处. 除t = 0外, $ T_{{\rm P}x} $在其他时间上的值几乎都为0. $ R_{{\rm P}x} $的峰值出现在j = 5处, 在除5之外的其他j值上都等于0. 根据方程(12)和方程(13), 图5(a)给出了10束x 偏振雷达探测信号的相关函数$ C_{{\rm {RT}}_{1}} $的时空演变. 可以看出, 针对第N束x偏振雷达探测信号, $ C_{{\rm {RT}}_{1}} $的最大值发生在t = 0和j = N处(N = 1, 2, 3, ···, 10, 以下相同). 图5(b)进一步给出了10 束x 偏振雷达探测信号与10束x偏振参考信号的相关函数$ C_{{\rm {RT}}_{2}} $的时空演变. 从图5(b)可以发现, 第N束x偏振雷达探测信号和第N束x偏振参考信号的相关性$ C_{{\rm {RT}}_{2}} $的最大值出现在t = 0和j = N处. 图5所示的结果表明, 在经过调制的N束x偏振雷达探测信号中, 两两之间具有时间和空间不相关的特性. 同时, 经过调制的N束x偏振雷达探测信号与其相应的参考信号也具有时空不相关特性. 下面, 利用它们的时空不相关性, 以复杂形状目标T₁中12个小区域目标为例, 讨论对它们的测距.
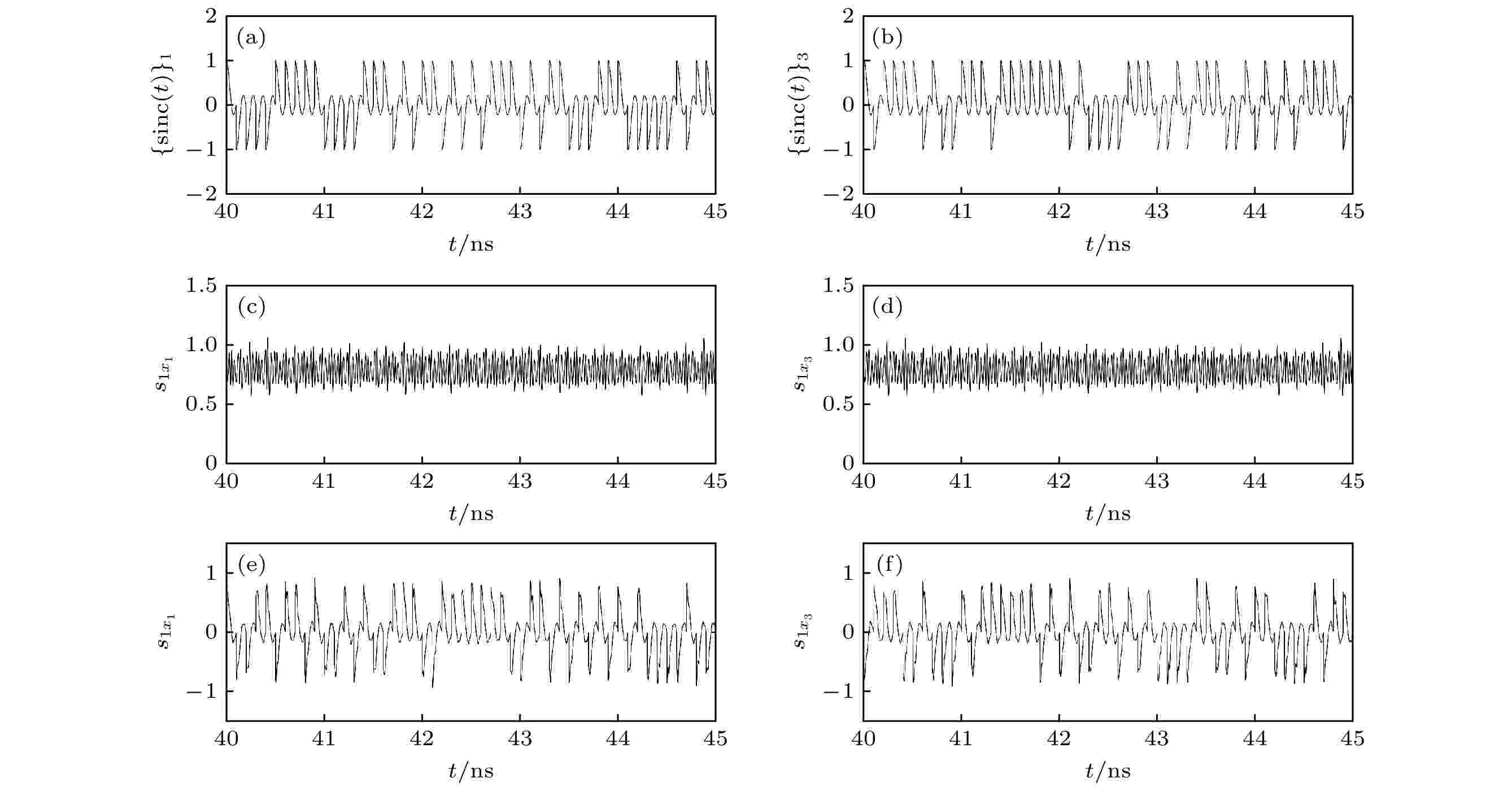图 3 (a)用于调制第1束x偏振探测信号的sinc波形的时间轨迹; (b)用于调制第3束x偏振探测信号的sinc波形的时间轨迹; (c)第1束x偏探测信号($ s_{1 x_1} $)的时间轨迹; (d)第3束x偏振探测信号($ s_{1 x_3} $)的时间轨迹; (e)调制后的第1束x偏振雷达探测信号的时间轨迹; (f)调制后的第3束x偏振雷达探测信号的时间轨迹
Figure3. (a) Temporal traces of the sinc waveform which are used to modulate the first beam of the x-polarization probe signal; (b) temporal traces of the sinc waveform which are used to the third beam of the x-polarization probe signal; (c) temporal traces of the first beam of the x-polarization probe signal ($ s_{1 x_1} $); (d) temporal traces of the third beam of the x-polarization probe signal ($ s_{1 x_3} $); (e) temporal traces of the modulated first beam of the x-polarization probe signal; (f) temporal traces of the modulated third beam of the x-polarization probe signal.

图 4 (a)第5束x偏振雷达探测信号的时间自相关($ T_{{\rm P}x} $); (b)第5束x偏振雷达探测信号和数量为10束的x偏振雷达探测信号的空间互相关($R_{{\rm P}x}$), 变量j表示第j束x偏振雷达探测信号
Figure4. (a) Time autocorrelation ($T_{{\rm P}x}$) of the fifth beam of the x-polarization radar probe signal; (b) space autocorrelation ($ R_{{\rm P}x} $) between the fifth beam of the x-polarization radar probe signal and ten beams of ones. Variable j denotes the j th x-polarization radar probe signal.

图 5 (a)在10束x偏振雷达探测信号中, 两两之间的时空相关性($ C_{RT_1} $); (b)10束x偏振雷达探测信号与10束x偏振参考信号的时空相关性($ C_{RT_2} $); 这里, 变量j表示第j束x偏振雷达探测信号或第j束x偏振雷达参考信号
Figure5. (a) Time-space correlation $ C_{RT_1} $ among ten beams of the x-polarization radar probe signals; (b) Time-space correlation $ C_{RT_2} $ of ten beams of the x-polarization radar probe signals with ten beams of the x-polarization radar reference signal. Here, the variable j denotes the jth x-polarization radar probe signal or the jth x-polarization radar reference signal.

图6给出了复杂形状目标T₁中12个小区域的测距几何图. 为了方便讨论, T₁中12个小区域被定义为$ A_1—A_{12} $, 在每个小区域中, 测量3—4个目标点. 如图6所示, $ A^{(\iota)}_1—A^{(\iota)}_{12} $ ($ \iota $ = 1, 2, 3或1, 2, 3, 4)的位置矢量被依次设定为${{\mathit{\boldsymbol{r}}}}_{A^{(\iota)}_{{1}, {1}}} - {{\mathit{\boldsymbol{r}}}}_{{{A}}^{(\iota)}_{{1}, {12}}}$. 发射天线(TA_1,1—TA_1,10)被排列成一条直线, 位置矢量依次设定为$ {{\mathit{\boldsymbol{r}}}}_{{1}, {1}}$—$ {{\mathit{\boldsymbol{r}}}}_{{1}, {10}} $, 具体如表2所列. 另外, 两相邻的发射天线之间的距离为0.5 m. 这些发射天线发射的10束x偏振雷达探测信号依次用于探测目标$ A^{(\iota)}_1— A^{(\iota)}_{12} $的距离. 为了验证对这些目标测距的可行性, 目标$ A^{(\iota)}_1—A^{(\iota)}_{12} $的实际位置矢量分别假定为$ {{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{{1}}}—{{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{{12}}} $, 具体表达式如表3所列. 为了进一步描述这些目标点($ A^{(\iota)}_1—A^{(\iota)}_{12} $)的准确度, 引进相对误差(relative error, RE)如下:
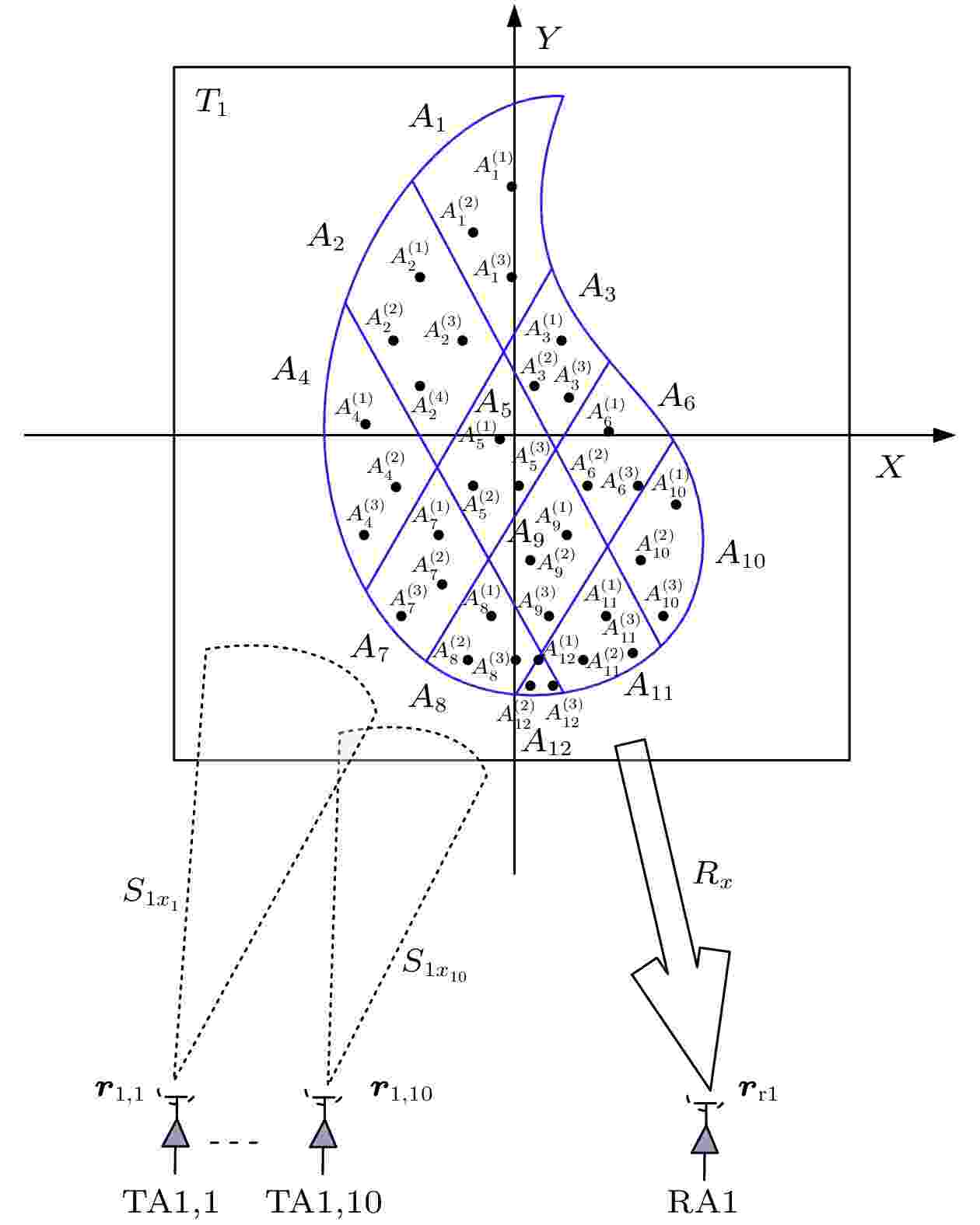图 6 复杂形状目标T₁中12个小区域目标测距的几何图. A₁—A₁₂: 12个小区域目标; TA_1,1—TA_1,10: 10个发射天线; $ {{\mathit{\boldsymbol{r}}}}_{{1}, {1}}—{{\mathit{\boldsymbol{r}}}}_{{1}, {10}}$: 发射天线(TA_1,1—TA_1,10)的位置矢量; RA₁: 接收天线; $ S_{1 x_1}—S_{1 x_{10}} $: 10束x偏振雷达探测信号; R_x: 接收的雷达探测信号
Figure6. Geometry diagram of the ranging for twelve small areas in the complex-shape target T₁. A₁—A₁₂, twelve small area targets; TA_1,1—TA_1,10, ten transmitting antennas; $ {{\mathit{\boldsymbol{r}}}}_{{1}, {1}}—{{\mathit{\boldsymbol{r}}}}_{{1}, {10}} $, position vectors for the transmitting antennas (TA_1,1—TA_1,10); RA₁, receiving antenna; $ S_{1 x_1}—S_{1 x_{10}} $, ten beams of the x-polarization radar probe signals; R_x, received radar probe signals.

${{\mathit{\boldsymbol{r}}}}_{{1}, {{{j}}}}$	位置矢量		${{\mathit{\boldsymbol{r}}}}_{{1}, {{{j}}}} $	位置矢量
$ {{\mathit{\boldsymbol{r}}}}_{{1}, {1}} $	$-5 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $		$ {{\mathit{\boldsymbol{r}}}}_{{1}, {6}} $	$-2.5 {{\mathit{\boldsymbol{e}}}}_{{x}} -3{{\mathit{\boldsymbol{e}}}}_{{y}} $
$ {{\mathit{\boldsymbol{r}}}}_{{1}, {2}} $	$ -4.5 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $		$ {{\mathit{\boldsymbol{r}}}}_{{1}, {7}} $	$-2 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $
$ {{\mathit{\boldsymbol{r}}}}_{{1}, {3}} $	$-4 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $		$ {{\mathit{\boldsymbol{r}}}}_{{1}, {8}} $	$ -1.5{{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $
$ {{\mathit{\boldsymbol{r}}}}_{{1}, {4}} $	$-3.5 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $		$ {{\mathit{\boldsymbol{r}}}}_{{1}, {9}} $	$-1 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $
$ {{\mathit{\boldsymbol{r}}}}_{{1}, {5}} $	$-3 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $		$ {{\mathit{\boldsymbol{r}}}}_{{1}, {10}} $	$-0.5 {{\mathit{\boldsymbol{e}}}}_{{x}} -3 {{\mathit{\boldsymbol{e}}}}_{{y}} $

表2发射天线(TA_1,1—TA_1,10)的位置矢量
Table2.Position vectors of the transmitting antennas (TA_1,1—TA_1,10)

小区域$ A_{j} $	目标点$ A^{(\iota)}_{j} $	$ {{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{j}} $	$ \overline{{{\mathit{\boldsymbol{r}}}}}_{{{A}}^{(\iota)}_{j}} $	$ RE^{(\iota)}_{j} $
$ A_1 $	$ A^{(1)}_1 $	0$ {{\mathit{\boldsymbol{e}}}}_{x}$ + 0.2$ {{\mathit{\boldsymbol{e}}}}_y$	–0.0001$ {{\mathit{\boldsymbol{e}}}}_{x}$ + 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0.04%
	$ A^{(2)}_1 $	–0.05$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.17$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0498$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.17$ {{\mathit{\boldsymbol{e}}}}_y $	0.14%
	$ A^{(3)}_1 $	0$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0002$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.13%
$ A_2 $	$ A^{(1)}_2 $	–0.1$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0999$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.07%
	$ A^{(2)}_2 $	–0.12$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	–0.1199$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.05%
	$ A^{(3)}_2 $	–0.05$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0499$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.1001$ {{\mathit{\boldsymbol{e}}}}_y $	0.09%
	$ A^{(4)}_2 $	–0.1$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.03$ {{\mathit{\boldsymbol{e}}}}_y $	–0.1002$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.03$ {{\mathit{\boldsymbol{e}}}}_y $	0.19%
$ A_3 $	$ A^{(1)}_3 $	0.05$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.0501$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.06%
	$ A^{(2)}_3 $	0.02$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.03$ {{\mathit{\boldsymbol{e}}}}_y $	0.0197$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.03$ {{\mathit{\boldsymbol{e}}}}_y $	0.88%
	$ A^{(3)}_3 $	0.06$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.02$ {{\mathit{\boldsymbol{e}}}}_y $	0.0597$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0.02$ {{\mathit{\boldsymbol{e}}}}_y $	0.49%
$ A_4 $	$ A^{(1)}_4 $	–0.16$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.01$ {{\mathit{\boldsymbol{e}}}}_y $	–0.1599$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.01$ {{\mathit{\boldsymbol{e}}}}_y $	0.08%
	$ A^{(2)}_4 $	–0.12$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	–0.1197$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0.21%
	$ A^{(3)}_4 $	–0.16$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	–0.1602$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.11%
$ A_5 $	$ A^{(1)}_5 $	–0.02$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0198$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0$ {{\mathit{\boldsymbol{e}}}}_y $	0.94%
	$ A^{(2)}_5 $	–0.05$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	–0.05$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0
	$ A^{(3)}_5 $	0$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0.0001$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0.19%
$ A_6 $	$ A^{(1)}_6 $	0.1$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0$ {{\mathit{\boldsymbol{e}}}}_y $	0.1003$ {{\mathit{\boldsymbol{e}}}}_{x} $ + 0$ {{\mathit{\boldsymbol{e}}}}_y $	0.31%
	$ A^{(2)}_6 $	0.08$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0.0796$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0.4%
	$ A^{(3)}_6 $	0.13$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.05$ {{\mathit{\boldsymbol{e}}}}_y $	0.1301$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.0$ {{\mathit{\boldsymbol{e}}}}_y $	0.05%
$ A_7 $	$ A^{(1)}_7 $	–0.08$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0803$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.4%
	$ A^{(2)}_7 $	–0.07$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.12$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0705$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.12$ {{\mathit{\boldsymbol{e}}}}_y $	0.38%
	$ A^{(3)}_7 $	–0.12$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	–0.1204$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.21%
$ A_8 $	$ A^{(1)}_8 $	–0.03$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	–0.0299$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.05%
	$ A^{(2)}_8 $	–0.07$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	–0.07$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0
	$ A^{(3)}_8 $	0$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0.0001$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0.04%
$ A_9 $	$ A^{(1)}_9 $	0.06$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.0599$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.1$ {{\mathit{\boldsymbol{e}}}}_y $	0.08%
	$ A^{(2)}_9 $	0.02$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.12$ {{\mathit{\boldsymbol{e}}}}_y $	0.0203$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.12$ {{\mathit{\boldsymbol{e}}}}_y $	0.24%
	$ A^{(3)}_9 $	0.04$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.0401$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.02%
$ A_{10} $	$ A^{(1)}_{10} $	0.18$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.07$ {{\mathit{\boldsymbol{e}}}}_y $	0.18$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.0701$ {{\mathit{\boldsymbol{e}}}}_y $	0.02%
	$ A^{(2)}_{10} $	0.13$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.12$ {{\mathit{\boldsymbol{e}}}}_y $	0.1297$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.12$ {{\mathit{\boldsymbol{e}}}}_y $	0.18%
	$ A^{(3)}_{10} $	0.15$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.1501$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.07%
$ A_{11} $	$ A^{(1)}_{11} $	0.0 $ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.0898$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.15$ {{\mathit{\boldsymbol{e}}}}_y $	0.12%
	$ A^{(2)}_{11} $	0.06$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0.0598$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.25$ {{\mathit{\boldsymbol{e}}}}_y $	0.07%
	$ A^{(3)}_{11} $	0.13$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.19$ {{\mathit{\boldsymbol{e}}}}_y $	0.1302$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.19$ {{\mathit{\boldsymbol{e}}}}_y $	0.09%
$ A_{12} $	$ A^{(1)}_{12} $	0.02$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0.0197$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.2$ {{\mathit{\boldsymbol{e}}}}_y $	0.15%
	$ A^{(2)}_{12} $	0.03$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.22$ {{\mathit{\boldsymbol{e}}}}_y $	0.0297$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.22$ {{\mathit{\boldsymbol{e}}}}_y $	0.16%
	$ A^{(3)}_{12} $	0.05$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.22$ {{\mathit{\boldsymbol{e}}}}_y $	0.0501$ {{\mathit{\boldsymbol{e}}}}_{x} $ – 0.22$ {{\mathit{\boldsymbol{e}}}}_y $	0.02%

表3目标T₁的每个小区域中3—4个目标点的实际位置矢量($ {{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{j}} $)和测量的位置矢量 ($ \overline{{{\mathit{\boldsymbol{r}}}}}_{{{A}}^{(\iota)}_{j}} $)及它们的相对误差
Table3.Actual position vectors ($ {{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{j}} $) of 3–4 target points in each small area of target T₁ and the measured position vectors ($ \overline{{{\mathit{\boldsymbol{r}}}}}_{{{A}}^{(\iota)}_{j}} $), as well as their relative errors.

$ RE^{(\iota)}_{j} = \frac{\big |{{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{j}}-\overline{{{\mathit{\boldsymbol{r}}}}}_{{{A}}^{(\iota)}_{{j}}}\big |}{\big |{{\mathit{\boldsymbol{d}}}}_{{{A}}^{(\iota)}_{j}}\big |}\times 100{\text{%}}, $

其中, j = 1, 2, 3, ···, 12.
根据方程(16)给出的相关函数CC₁的最大期望值, 可以得到一组延迟时间($ \tau_{{1}, {1}} $—$ \tau_{{1}, {10}} $). 在此基础上, 使用方程(17)和方程(18), 可以获得目标T₁中任意1个目标点的测量位置矢量的平均值. 下面以目标点$ A^{(1)}_2 $为例, 讨论其测距过程. 当来自天线RA₁接收的雷达探测信号(包括来自TA_1,1—TA_1,10发射天线的10束x偏振雷达探测信号)用于探测目标$ A^{(1)}_2 $时, 计算来自天线RA₁接收的雷达探测信号与10束x偏振参考信号的时空互相关($ CC_{{1}, {1}}—CC_{{1}, {10}} $), 结果如图7(b)所示. 可以看出, 互相关的最大期望值依次位于10个不同的延迟时间处. 观察图7(c)可以得到10个延迟时间如下: $ \tau_1 $ = 34.149 ns; $ \tau_2 $ = 32.770 ns; $ \tau_3 $ = 31.443 ns; $ \tau_4 $ = 30.182 ns; $ \tau_5 $ = 29.004 ns; $ \tau_6 $ = 27.932 ns; $ \tau_7 $ = 26.994 ns; $ \tau_8 $ = 26.222 ns; $ \tau_9 $ = 25.652 ns; $ \tau_{10} $ = 25.316 ns. 基于这10个时间延迟, 使用方程(17)和方程(18), 计算得到测量的目标点$ A^{(1)}_2 $的平均位置矢量为$ \overline{{{\mathit{\boldsymbol{r}}}}}_{{{A}}^{(1)}_{{2}}} = -0.0999 {{\mathit{\boldsymbol{e}}}}_x +0.15 {{\mathit{\boldsymbol{e}}}}_y $. 用同样的方法, 可以得到目标T₁中其他目标点测量的平均位置矢量, 结果列于表3中. 因此, 根据方程(22), 可获得目标T₁中目标点$ A^{(\iota)}_1—A^{(\iota)}_{12} $的测距相对误差, 结果如表3所列. 从表3可以看出, 目标点$ A^{(\iota)}_1—A^{(\iota)}_{12} $的测距相对误差在0% 和0.94% 之间. 这些结果表明, 针对复杂形状目标的多区域的测距, 本文所提供的方案具有较小的相对误差(小于0.94%).
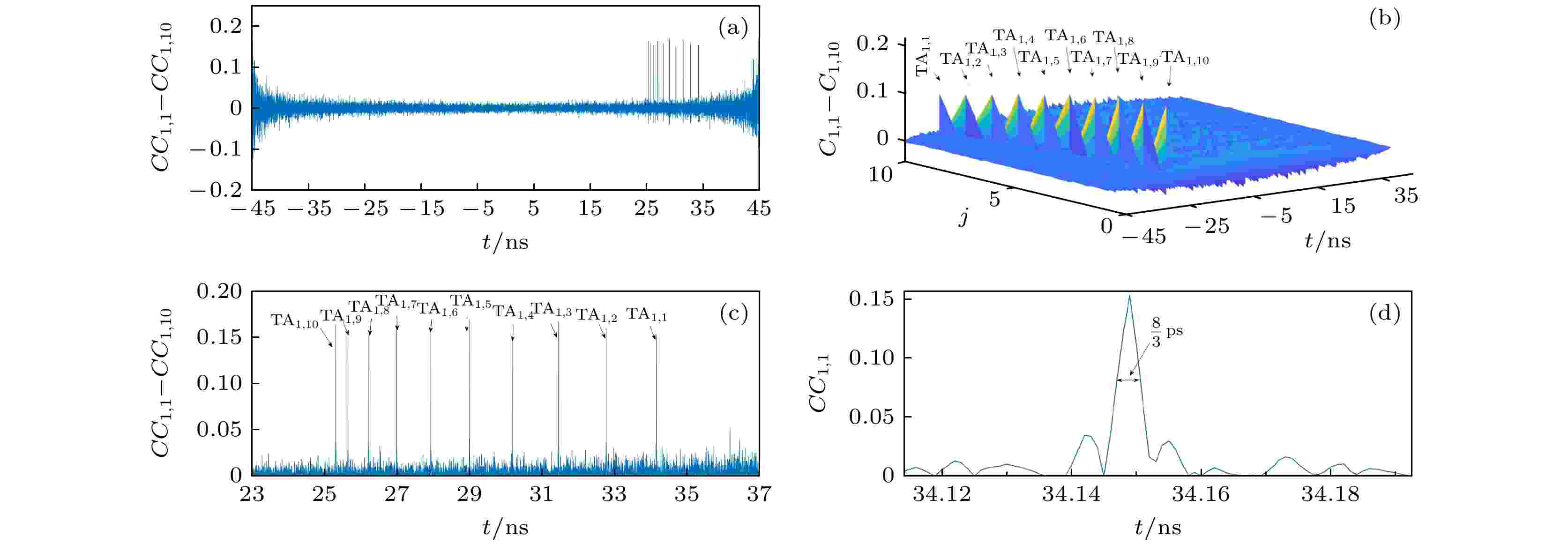图 7 (a)针对目标点$ A^{(1)}_2 $, 从天线RA₁接收的雷达探测信号与10束x偏振参考信号的时间互相关; (b)针对目标$ A^{(1)}_2 $, 从接收天线RA₁接收的雷达探测信号与10束x偏振参考信号的时空互相关; (c)图(a)的局部放大图; (d)针对目标点$ A^{(1)}_2 $, 从天线RA₁接收的雷达探测信号与第1束x偏振参考信号的互相关
Figure7. (a) For the target point-$ A^{(1)}_2 $, the time autocorrelations of the radar probe signals received by the antenna RA₁ with ten beams of the x-polarization radar probe signals; (b) for the target point-$ A^{(1)}_2 $, the space autocorrelations of the radar probe signals received by the antenna RA₁ with ten beams of the x-polarization radar probe signals; (c) local enlarged plot of panel (a); (d) for the target point-$ A^{(1)}_2 $, the time autocorrelation of the radar probe signals received by the antenna RA₁ with the first beam of the x-polarization radar probe signal.

根据文献[34], 相关峰的半极大处全宽(full width at half maximum, FWHM)通常用于描述测距分辨率(ranging resolution, RR). 从图7(d)可以看出, 相关函数$ CC_{{1}, {1}} $的FWHM为8/3 ps. 根据RR = (c × FWHM)/2, 得到RR为0.4 mm, 其中, c为真空中的光速. 从图7(c)可以观察到: $ CC_{{1}, {1}}—$$ CC_{{1}, {10}} $的FWHM均为8/3 ps. 这表明10束x偏振雷达探测信号对目标点$ A^{(1)}_2 $的测距分辨率均能达到0.4 mm. 用同样的计算方法, 可以得到目标T₁中的其他目标点的测距分辨率均为0.4 mm. 为了观察一些关键参数(如注入强度、自发辐射噪声强度、目标点与雷达探测信号源的距离、光电探测器的带宽、sinc波形的振幅)对测距分辨率的影响, 下面以目标$ A^{(1)}_2 $为例来阐述它们的依赖关系. 图8给出了上述参数对目标点$ A^{(1)}_2 $的测距分辨率的依赖关系. 这里, 参数$ d_1 $是第1束x偏振雷达探测信号源与目标点$ A^{(1)}_2 $之间的距离. 由于这些雷达探测信号源被排列在水平线上, 且相互之间的距离不发生改变, 因此, 当$ d_1 $在一定范围内变化时, 其他的x偏振雷达探测信号源与目标点$ A^{(1)}_2 $ 之间的距离也发生相应的变化, 但它们之间的距离不发生变化. $ \Delta f_1 $是光电探测器PD₁₁和PD₂₁的带宽. 从图8可以看出, 目标点$ A^{(1)}_2 $的测距分辨率独立于注入强度、自发辐射噪声强度、目标点与探测信号的距离、sinc波形的振幅. 当这些参数在一定范围内变化时, 它们的范围分辨率始终保持0.4 mm. 其他目标点的测距分辨率同样与这些参数无关, 且都为0.4 mm. 然而, 目标点$ A^{(1)}_2 $ 的测距分辨率严重依赖于光电探测器(PD₁₁和PD₂₁)的带宽. 如图8(c)所示, 当带宽$ \Delta f_1 $从10 GHz增大到100 GHz时, 测距分辨率从11.8 mm快速地减小到1 mm. 当带宽$ \Delta f_1 $进一步从100 GHz增大到250 GHz 时, 测距分辨率从1 mm慢慢地减小到0.4 mm. 当带宽$ \Delta f_1 $在250—300 GHz之间变化时, 分辨率保持在0.4 mm. 当其他光电探测器的带宽发生改变时, 与其相应的其他目标点的测距分辨率有相同的变化. 这些结果表明, 当光电探测器的带宽足够大时, 利用由双极性sinc波形调制的x偏振雷达探测信号对复杂形状目标的多区域测距分辨率可达到0.4 mm. 它们具有出色的强抗噪声性能和稳定性. 另外计算了第一束x偏振雷达探测信号与目标T₁中的任意目标点之间的距离d对测距相对误差的影响, 结果如图9所示. 可以看出, 当d在5.56—5.95 m之间变化时, 目标T₁中任意目标点的测距相对误差RE在0—0.94%之间变化. 这说明x偏振雷达探测信号源与目标点的距离对测距相对误差有很小的影响.
图 8 目标点$ A^{(1)}_2 $的测距分辨率(RR)对一些关键系统参数的依赖关系　(a) RR与注入强度$ k_{xinj} $的依赖关系; (b) RR与第一束x偏振雷达探测信号和目标点$ A^{(1)}_2 $之间的距离$ d_1 $的依赖关系; (c) RR与光电探测器(PD₁₁和PD₂₁)带宽$ \Delta f_1 $的依赖关系; (d) RR与sinc波形的振幅$ A_{\rm m} $的依赖关系; (e) RR与自发辐射噪声强度$ \beta $的依赖关系. 此外, $ k_{xinj} $ = $ k_{yinj} $, 除上述讨论参数之外的其他参数值见表1
Figure8. Dependences of the range resolutions (RR) for the target point-$ A^{(1)}_2 $ on some key system parameters: (a) Dependence of the RR on the injection strength $ k_{xinj} $; (b) dependence of the RR on the distance between the first beam of the x-polarization radar probe signal and the target point-$ A^{(1)}_2 $; (c) dependence of the RR on the bandwidths $ \Delta f_1 $ of the photo detectors (PD₁₁ and PD₂₁); (d) dependence of the RR on the amplitude of sinc waveform; (e) dependence of the RR on the spontaneous emission noise intensity $ \beta $. Moreover, $ k_{xinj} $ = $ k_{yinj} $, values of other parameters are shown in Tab. 1.

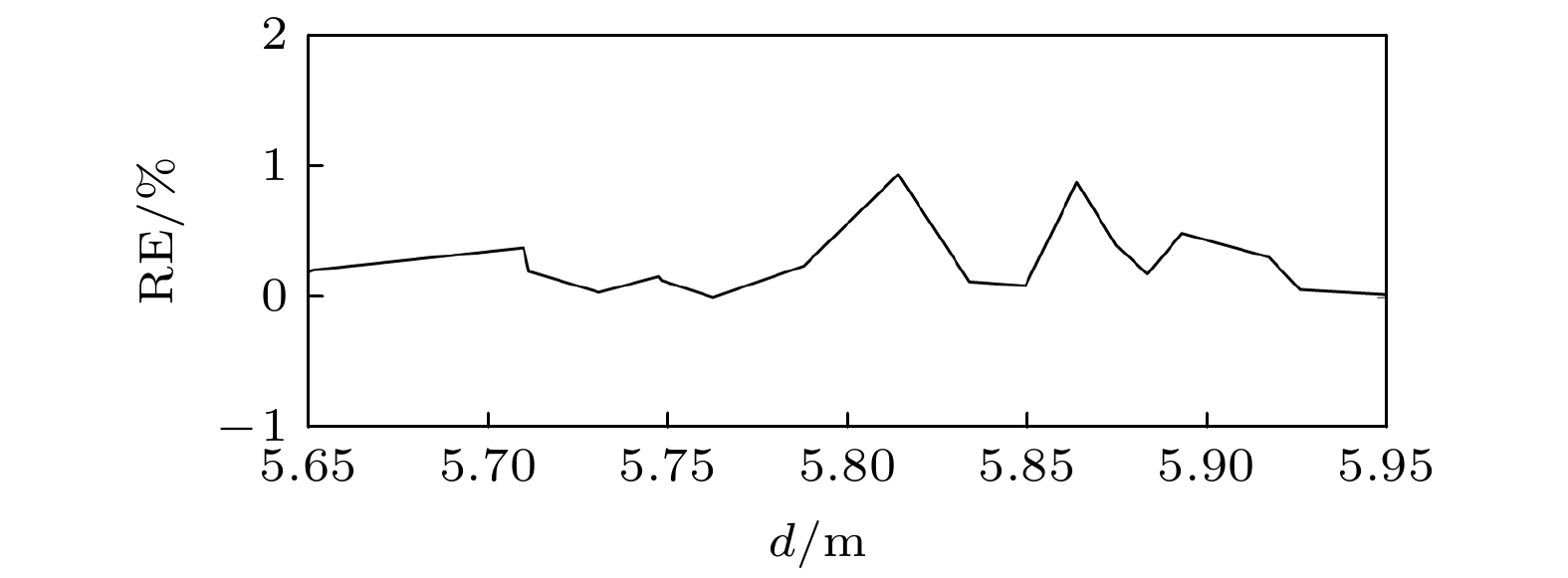图 9 测距相对误差RE与目标T₁中任意目标点与第1束x偏振雷达探测信号源之间的距离d的依赖关系
Figure9. Dependence of the ranging relative error RE on the distance d between the arbitrary target point and the first beam of the x-polarization radar probe signal source.

需要特别注意的是, 由于x偏振和y偏振雷达探测信号对目标T₁和T₂分别独立测量, 并且测距原理相同, 因此, 在本文提出的方案中, y偏振雷达探测信号对目标T₂的测距结果(包括测距分辨率和测距相对误差)与x 偏振雷达探测信号对目标T₁的测距结果是几乎相同的. 另外, 本文提出的测距方案能够实现0.4 mm分辨率的关键现实条件是: 1)需要具有飞秒量级快速动态的激光光源; 2)需要用高质量自相关函数对激光器输出的探测光波进行调制, 使其具有时空不相关特性; 3)方案中涉及的相关光路中的光器件带宽要足够宽, 例如, 光电探测器的带宽约100 GHz.

总之, 利用外部光注入的光泵浦自旋VCSEL产生的两个混沌偏振分量, 提出了对两个复杂形状目标中多区域精确测距的新颖方案. 在此方案中, 两个混沌偏振雷达探测信号被双极性sinc波形调制. 调制混沌偏振雷达探测信号具有时空不相关和飞秒量级的快速动态的独有特性. 利用这些特性, 通过观察混沌偏振探测信号及相应的参考信号之间互相关的最大期望值对应的时间位置, 获得来自多区域目标的延迟时间. 基于这些延迟时间, 复杂形状目标中多区域的位置矢量可以被精确测量. 研究结果表明, 多区域目标的测距相对误差很低, 小于0.94%. 当光电探测器带宽足够大时, 它们的测距分辨率非常稳定, 可以达到0.4 mm, 并且具有很强的抗噪声能力. 本文提出的多区域目标测距方案具有如下吸引人的优势: 具有稳定且高的测距分辨率、很强的抗噪声能力、非常低的相对误差. 这些特性能够迎合复杂形状目标中多区域位置矢量测量的需要.