摘要:为了深入认识α-Fe中氦泡冲出位错环的微观机制, 有必要研究α-Fe中氦泡冲出位错环时的极限压强特性. 本文建立金属-氦泡的立方体型代表性体积单元模型, 针对8种不同初始半径的球形氦泡, 以初始氦空位比为变量, 开展分子动力学模拟, 得到了各模型中位错环开始形成时的氦泡极限压强和临界氦空位比. 研究结果表明: 对于无量纲半径介于2—10的氦泡, 冲出位错环时的氦泡极限压强和临界氦空位比均随着氦泡初始半径的增大而非线性减小; 基体中氦泡冲出位错环时的临界氦空位比具有明显的尺寸效应; 初始时刻(0 ps), 在经过立方体型模型中心的横截面上, 氦泡周围Fe原子阵列的剪应力集中和最大剪应力出现在对角线与氦泡边界交点(即45°)处, 并且关于横截面上平行于边的两条对折线对称分布, 剪应力集中区的范围和最大剪应力均随着初始氦空位比的增大而增大; 位错环冲出方向对应最大剪应力方向. 本文的研究加深了对金属中氦泡物理特性的认识, 为后续分析氦泡对材料宏观物理和力学性质的影响奠定了有益的基础.
关键词: α-Fe/
氦泡/
初始氦空位比/
极限压强

English Abstract

全文HTML

--> --> -->

核反应堆中第一壁和储氚压力容器是核工业中典型的涉氚涉氦结构. 被引入到金属材料中的氦, 几乎不溶于金属基体材料, 会在金属材料中聚集, 形成纳米级的氦泡, 从而引起氦效应, 如使金属材料的韧性降低、延伸率下降等^[1-5], 并最终改变结构的承载能力, 影响结构的安全性. 因此, 氚在金属基体材料中的渗透与扩散及其引起的氚和氦浓度的时空变化、氦泡在基体材料中的形核长大及其对材料力学性能的影响成为核材料和核技术领域的研究焦点^[1-10].
在氦泡形核与长大过程中, 氦泡压强是氦泡的主要物理特性指标, 也是氦泡影响金属宏观物理与力学性能的重要参数. 因此, 氦泡的压强特性受到了越来越多的研究者关注^[11-15]. 由于金属中氦泡尺寸大多为纳米量级, 因此氦泡压强很难通过实验手段直接测量. 现行做法是先采用电子能量损失谱方法(electron energy-loss spectroscopy, EELS)测量氦泡中的He原子密度, 再利用氦泡的状态方程, 计算得到氦泡压强^[11,12]. 因基体材料存在机械稳定极限^[2,13], 就内部含有高压氦泡的金属基体而言, 当氦泡施加在金属基体上的作用强度超过基体的机械稳定极限时, 氦泡将会通过冲出位错环机制而长大, 此时的氦泡压强为其极限压强^[2]. 由于氦泡极限压强可达数十GPa量级, 因此它不仅是金属基体中氦泡长大机制的特征参数, 而且也是研究氦泡引起的金属材料微观损伤机理的重要物理参数. 氦泡冲出位错环现象是快速发生的^[14], 且无明显的临界特征, 采用现有技术条件还难以精确掌握冲出位错环时的临界点, 因此对于氦泡冲出位错环时的临界He原子密度, 也难以采用EELS方法进行准确测量, 相应地, 也就难以准确计算氦泡极限压强.
Trinkaus^[13]和Wolfer^[15]分别通过解析理论建模和求解, 给出了单个氦泡冲出位错环时的极限压强公式. 与Trinkaus的公式相比, Wolfer的公式更为简洁, 即氦泡冲出位错环时的极限压强为基体材料剪切模量的0.2倍. 随着计算软硬件技术的发展, 分子动力学(molecular dynamics, MD)方法成为有力的工具, 已用于诸多的模拟研究中. Zhang等^[16]利用微观-细观-宏观3个尺度的实验信息, 校准MD模拟的模型系统, 研究了氢对HR-2钢弹性性能的影响, 深化了对氢脆机理的认识. Deng等^[17]采用MD方法模拟了α-Fe中氦团簇在块体和晶界的扩散特性. Gao等^[18]模拟了α-Fe中氦浓度和辐照温度对He原子与移位级联相互作用的影响. 关于金属中的氦泡压强, Zhang等^[19]采用MD方法, 对钛中初始氦空位比为2 (He原子数与初始孔洞空位数的比值n_He/n_V = 2)的氦泡进行模拟, 得到了在不同温度时, 4种不同初始半径氦泡的压强, 并通过数据拟合, 给出了氦泡的状态方程; Hetherly等^[20]通过在MD模型中先用1个He原子替换掉原位置的Fe原子, 然后采用每2 ps向体系中加入1个He原子的方式, 不断添加He原子进行模拟, 结果表明: 当He原子数为99时, 氦泡冲出位错环现象发生, 而冲出位错环后, 氦泡的压强下降到局部最小值27.20 GPa; Caro等^[21]通过MD模拟得到了Fe和FeCr中氦泡压强随He原子数增加的变化过程, 并观察到了氦泡冲出位错环现象; Xie等^[22]采用MD方法, 模拟了钨中初始半径为1.00 nm的氦泡, 结果表明: 当位错演化成棱形位错环并离开氦泡时, 氦泡压强从40.50 GPa下降到35.60 GPa, 氦泡半径从1.16 nm增大到1.18 nm.
如前所述, 通过MD模拟研究, 文献[20-22]观察到了冲出位错环现象和相应氦泡压强的变化, 但是并没有关注和讨论氦泡极限压强及其与初始氦空位比和氦泡尺寸的关联特性等问题. 同时, 根据文献[23-25], 非热形成时, 氦泡的平均半径为2.50 nm或更小. 目前, 对该尺寸范围内氦泡的压强特性, 包括氦泡极限压强, 还有待进一步研究. 本文采用MD方法构建含氦泡的模拟模型, 运用LAMMPS^[26]软件进行模拟, 研究不同初始氦空位比下氦泡的压强特性. 由于涉核结构和压力容器以铁基合金为主, 故本文以α-Fe为基体材料, 构建基体材料内含球形氦泡的立方体型代表性体积单元模型(representative volume element, RVE). 为了分析球形氦泡的尺寸效应, 分别考虑了初始半径为0.50, 0.81, 1.00, 1.31, 1.50, 2.00, 2.12, 2.50 nm的8种情况, 这些尺寸跨越了氦泡的形核阶段(氦泡半径 < 1.00 nm)和非理想气体阶段(1.00 nm ≤ 氦泡半径 < 100.00 nm)^[13]. MD模拟结果表明: 对于初始半径介于0.50—2.50 nm的氦泡, 冲出位错环时的氦泡极限压强和临界氦空位比都随着氦泡初始半径的增大而非线性减小. 基于MD模拟结果, 拟合得到了冲出位错环时的氦泡极限压强和临界氦空位比随氦泡初始半径变化的关系式, 与Wolfer的解析分析结果吻合. 本文的研究深化了对金属中氦泡物理特性的认识, 为后续分析氦泡对材料宏观物理和力学性质的影响奠定了有益的基础.

2

-->

2.1.分子动力学模型

MD建模和模拟均采用软件LAMMPS实施. 本文对含氦泡的α-Fe采用如下方法建模: 首先建立尺寸为45a₀ × 45a₀ × 45a₀的α-Fe原子阵列模型, Fe原子总数为182250个, 这里a₀为其晶格常数, a₀ = 2.86 ? (1 ? = 0.1 nm); 然后以模型中心为球心, 删除一定半径范围内的Fe原子, 形成球形孔洞; 最后在孔洞中填入不同数量的He原子, 即可形成氦泡. 该建模方法在文献[19,27]中也有运用. 建立的金属-氦泡的立方体型RVE模型如图1所示. 图1所示模型中, Fe-Fe, He-He和Fe-He之间的相互作用势, 分别采用Ackland等^[28]、Aziz等^[29]和Gao等^[30]开发的势函数. RVE模型的3个晶向[100]、[010]和[001]分别对应于图1中直角坐标系的x, y和z轴, 且3个方向均施加周期性边界条件, 模拟温度保持在300 K, 选用NPT系综, 模拟时间步长为1 fs.
图 1 含氦泡的α-Fe计算模型(图中He → He泡, Fe → Fe基体)
Figure1. Model of α-Fe with helium bubble (In Fig. He → helium bubble, Fe → Fe matrix).

2 -->

2.2.氦泡压强计算方法及其有效性

氦泡压强的计算表达式为^[31]

$P = - \frac{1}{{3V}}\sum\limits_i^n {[{\sigma _{11}}(i) + {\sigma _{22}}(i) + {\sigma _{33}}(i)]}, $

式中: n是氦泡中的He原子个数; ${\sigma _{11}}(i)$, ${\sigma _{22}}(i)$和${\sigma _{33}}(i)$为第i个He原子的原子应力分量, 由LAMMPS中的原子应力^[32]模块计算; V是氦泡体积, 使用Voro++软件包^[33], 采用Voronoi算法计算得到.
Mills等^[34]通过实验手段测量了液氦的压强, 拟合得到了温度区间为$75\;{\rm{K}} < T < 300\;{\rm{K}}$、压强区间为$0.20\;{\rm{GPa}} < P < 2.00\;{\rm{GPa}}$的状态方程, 根据其状态方程得到温度为300 K时的压强(GPa)-原子密度(at./?³)曲线, 如图2中黑色实线所示. 根据Mills等的实验条件, 建立与半径为0.50 nm的球形氦泡体积相同的立方模拟盒子, 施加周期性边界条件, 设定模拟温度为300 K, 在NVT系综下进行MD模拟, 所得纯氦的压强随He原子密度的变化情况如图2中红点所示. 比较图2中的MD模拟结果和实测结果可见, 6种He原子密度下的模拟结果都与实验结果有很好的吻合. 目前, 在没有直接针对α-Fe中氦泡压强实验结果的情况下, 这一对比情况, 能够作为对α-Fe中氦泡压强计算方法的降级检验, 能够一定程度地支持对计算方法有效性的认定. 需说明的是, 图1中氦泡中He原子与基体Fe原子之间存在相互作用势, 而本节立方模拟盒子中的纯氦则只有He原子与He原子之间的相互作用势, 因此说前者还缺乏实验检验, 而后者是对前者的降级检验.
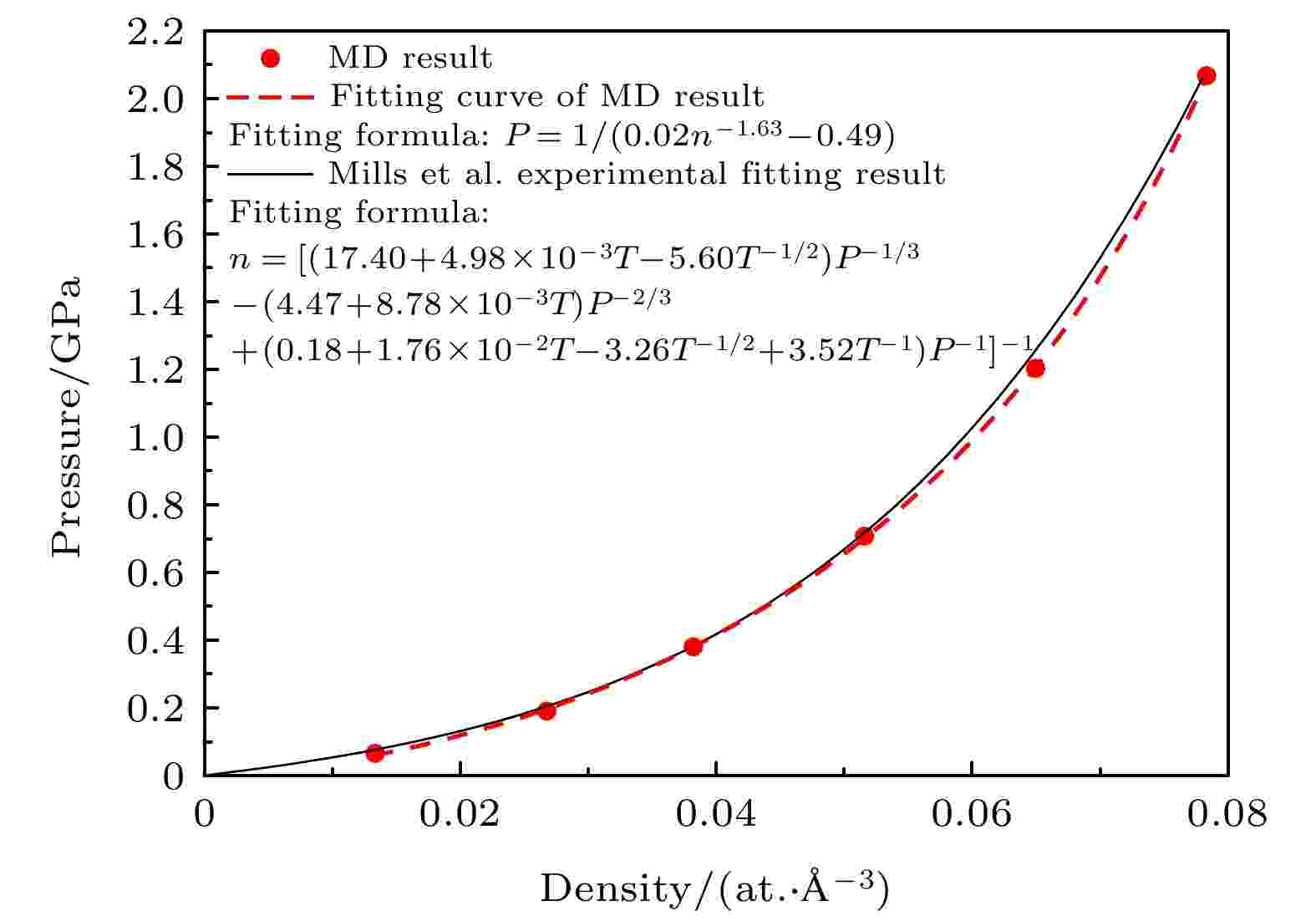图 2 MD模拟结果与Mills等^[34]的实验结果对比(300 K)
Figure2. Comparison of MD simulation results with experimental results of Mills et al.^[34] (300 K).

2 -->

2.3.计算与数据处理过程

对含有不同初始半径氦泡的各RVE模型, 以初始氦空位比为变量, 开展MD模拟. 首先对各RVE模型弛豫100 ps; 然后继续模拟30 ps, 并在此过程中每间隔0.30 ps, 以0.002 ps的频率提取一次氦泡压强, 连续提取100次, 总计提取6000次; 最后将6000次的算术平均值作为最终的氦泡压强.
模拟结束后利用可视化软件OVITO^[35]中的Dislocation Extraction Algorithm (DXA)^[36]模块, 分析各模型中位错形成情况.

2

-->

3.1.位错环冲出与氦泡极限压强

MD模拟所得氦泡压强-初始氦空位比曲线如图3所示. 图中氦泡压强峰值点用实心标识符表示, 其他数据点用空心标识符, 红色实线是基于各模型的模拟数据点的拟合曲线. 图3表明: 对于金属基体中8种不同初始半径的氦泡, 各自的氦泡压强随初始氦空位比的变化规律总体上是相同的, 都具有类抛物线特征. 在压强峰值点之后, 存在小幅度的波动现象, 该现象的产生归因于金属基体材料存在机械稳定极限, 当氦泡压强即孔洞内压超过基体材料的机械稳定极限时, 氦泡周围的基体材料就产生局部塑性变形和破坏, 从而造成了这些波动. 这在Zhang等^[19]、Hetherly等^[20]和Caro等^[21]的研究中也有所揭示.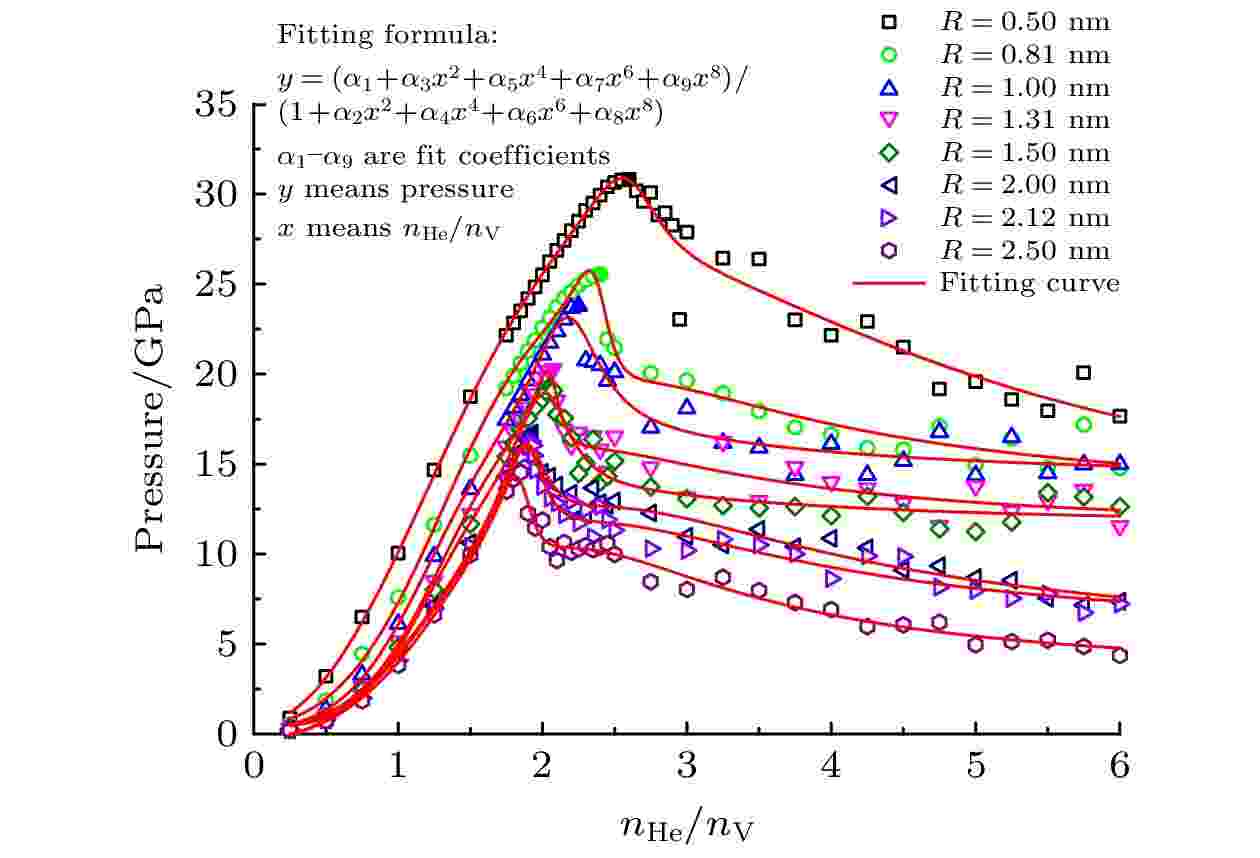
图 3 氦泡压强随初始氦空位比的变化
Figure3. Changes of pressure of helium bubble with initial helium-to-vacancy ratio.

文献[2]的研究表明, 当氦泡压强超过基体材料的机械稳定极限时, 基体材料将发生局部塑性变形和破坏, 最有可能的情况是在基体中冲出位错环. 而一旦冲出位错环, 氦泡体积就会明显长大而压强下降. 因此将氦泡冲出位错环时的压强定义为氦泡极限压强. 但值得注意的是, 图3中的氦泡压强是在RVE模型弛豫后提取的, 而弛豫过程中可能会发生冲出自间隙原子或位错环现象. 因此图3中各条曲线上的氦泡压强峰值点是基体材料内未发生冲出位错环现象时的最大氦泡压强, 而并非冲出位错环时的极限压强. 根据图3中各条曲线的峰值点, 可以得到对应的初始氦空位比, 按氦泡初始半径由0.50 nm依次增大到2.50 nm的顺序, 它们分别是2.60, 2.40, 2.25, 2.08, 2.05, 1.93, 1.92和1.84. 通过对MD模拟过程中的各RVE模型进行DXA分析, 可以得到氦泡在基体中冲出位错环时的初始氦空位比—临界氦空位比, 同样按氦泡初始半径由0.50 nm依次增大到2.50 nm的顺序, 所得结果依次是2.95, 2.45, 2.30, 2.10, 2.08, 1.94, 1.93和1.85. 对比可见, 氦泡压强峰值点对应的初始氦空位比与冲出位错环时的临界氦空位比相比有一定偏差, 后者比前者大. 已有研究表明, 高压氦泡在基体中冲出的位错环由基体材料的自间隙原子组成^[21,22,37]. 对于形核初期或中期的氦泡(如氦泡初始半径为0.50 nm的氦泡), 由于其外表面积较小, 因此在氦泡压强峰值点所对应的初始氦空位比时, 氦压作用下冲出的自间隙Fe原子数目较少, 还不足以形成位错环; 而要形成位错环则需更大的初始氦空位比, 以便形成更高的初始氦压, 冲出更多的自间隙Fe原子; 对于初始半径为0.50 nm的氦泡, 其冲出位错环所需的临界氦空比比其压强峰值点对应的初始氦空位比约大13.46%. Caro等^[21]的研究也得到了类似结果. 但对于形核后期的氦泡(如氦泡初始半径为0.81 nm的氦泡)和非理想气体阶段的氦泡(如氦泡初始半径为1.00—2.50 nm的氦泡), 各氦泡压强峰值点对应的初始氦空位比与冲出位错环时的临界氦空位比应当相同, 前述偏差产生的原因主要在于: 本模拟中建立的氦泡, 其初始氦空位比采用间隔取值, 因而受到取值间隔精度的影响, 且在图3中给出的氦泡压强是在弛豫过后再采样提取的, 未能反应出冲出位错环时的极限压强和临界氦空位比. 初始半径为0.50 nm的氦泡与其他7种尺寸的氦泡, 在冲出位错环时所需临界氦空位比的不同, 正是氦泡尺寸效应的具体表现.
对于特定初始半径的氦泡, 初始氦空位比越大, 初始氦压也就越高. 因此可知氦泡冲出位错环时的极限压强肯定高于图3中峰值点的氦泡压强. 氦泡冲出位错环时, 氦泡体积长大而压强下降, 因而可以通过MD模拟提取得到模拟过程中不同时间点的氦泡压强, 特别是氦泡冲出位错环前后的压强值. 在本文的模拟条件下, 为了获得各模型冲出位错环时的氦泡极限压强, 可由DXA分析得到冲出位错环时的临界氦空位比, 提取模型在该临界氦空位比下氦泡压强的最大值, 作为冲出位错环时的极限压强.
2 -->

3.2.氦泡极限压强、临界氦空位比随氦泡初始半径的变化关系

根据DXA分析结果得到临界氦空位比, 提取氦泡极限压强, 绘制它们随氦泡初始半径的变化曲线, 如图4所示. 通过拟合数据点, 得到氦泡极限压强${P_{{\rm{ultimate}}}}$和临界氦空位比(n_He/n_V)_cr与$\bar R$的关系式分别为:
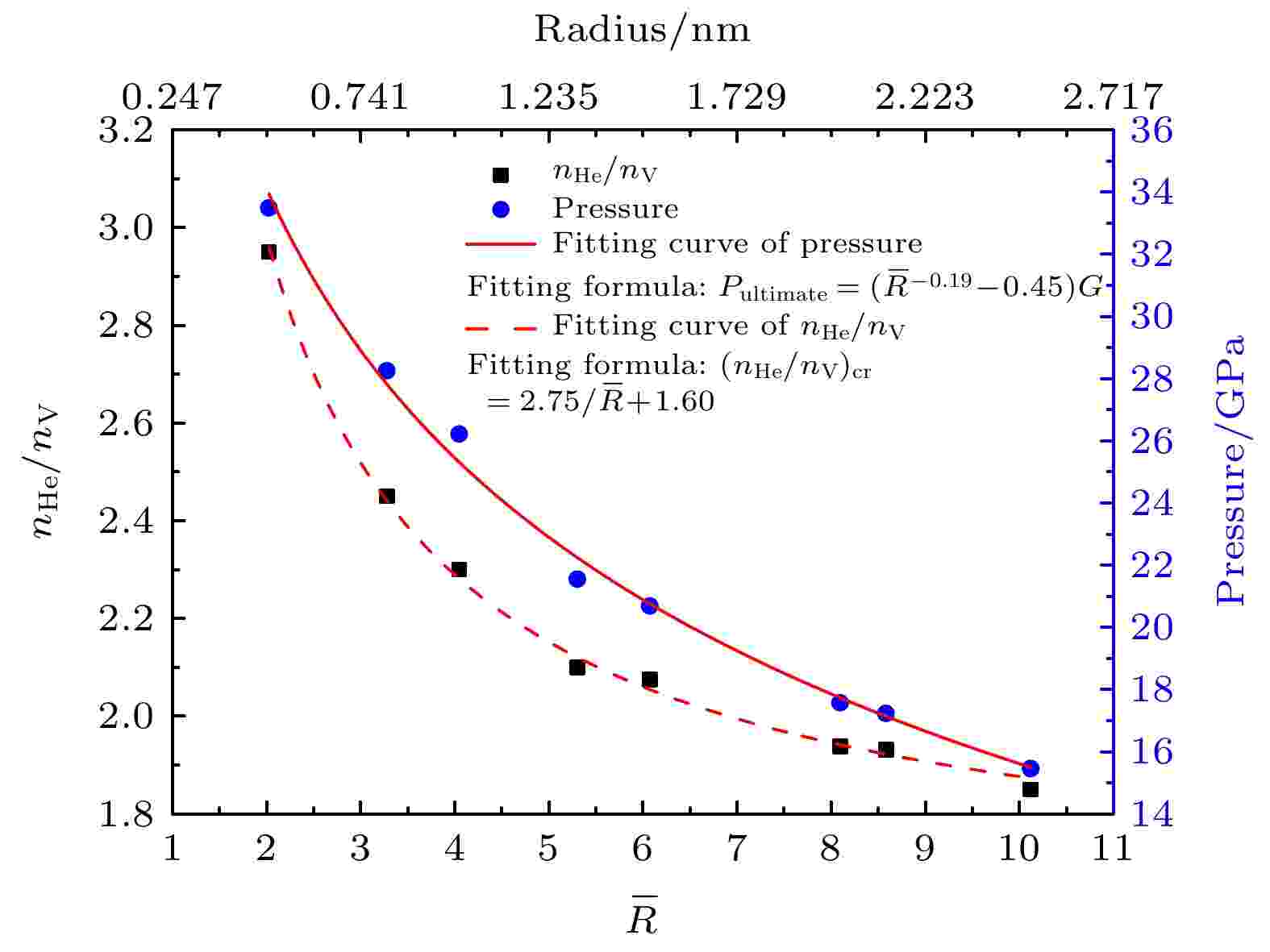图 4 氦泡极限压强、临界氦空位比随氦泡初始半径的变化
Figure4. Changes of ultimate pressure and critical helium-to-vacancy ratio of helium bubble with initial radius of helium bubble.

${P_{{\rm{ultimate}}}} = \left[ {{{\left( { {1}/{{\bar R}}} \right)}^{0.19}} - 0.45} \right] \cdot G\;,$

${({n_{{\rm{He}}}}/{n_{\rm{V}}})_{{\rm{cr}}}} = \left[ {2.75\left( { {1}/{{\bar R}}} \right) + 1.60} \right],$

式中: $\bar R$是无量纲量, $\bar R = R/b$, R为氦泡初始半径, b为Burgers矢量a₀/2$ \left\langle {111} \right\rangle $的模, b = 0.25 nm; G是α-Fe的剪切模量, G = 80.40 GPa^[38].
由图4、(2)式和(3)式可知, 氦泡极限压强和临界氦空位比均随氦泡初始半径的增大而非线性减小, 其中前者与Trinkaus^[13]和Wolfer^[15]的研究结果一致, 后者与Wolfer^[15,39]的研究结果吻合.
2 -->

3.3.氦泡周围Fe基体的原子应力分析

在氦泡压强驱动下, 基体中产生了冲出自间隙原子及位错环的现象^[21,22,37]. 因此, 这里对氦泡周围Fe原子阵列的原子应力进行研究, 以便从应力角度理解冲出位错环的机制. 图5给出了经过氦泡初始半径为1.31 nm的MD模型中心横截面上的原子剪应力分布, 图中紫色代表He原子, 其余为基体Fe原子. 图5(a)—(c)3幅分图依次对应初始氦空位比小于、等于和大于临界氦空位比2.10的情况, 每幅分图包括模拟时间为0 ps和100 ps时基体Fe原子的应力分布图. 由图5可知: 在图1所示MD模型坐标系中, 氦泡压强使其周围Fe原子阵列的剪应力集中和最大剪应力出现在45°处, 并且关于横截面上平行于边的两条对折线对称分布, 这与Xie等^[22]研究钨时的结果一致. 当初始氦空位比分别小于、等于和大于临界氦空位比时, 与0 ps时的氦泡形状相比, 100 ps时的氦泡形状依次是基本保持球形、近似椭球体和多面体, 并且氦泡的体积也依次长大. 这种氦泡形状的变化原因在于当初始氦空位比大于等于临界氦空位比时, 氦泡周围的Fe原子被冲出点阵位置而成为自间隙原子, 而冲出方向是沿特定的晶面和晶向进行, α-Fe为bcc晶体结构, 其密排面为{110}、{112}和{123}, 密排方向为$ \left\langle {111} \right\rangle $, 因此密排面上沿密排方向的Fe原子被冲出而成为自间隙原子, 而氦泡中的He原子则占据相应空位, 使得100 ps时氦泡的形状呈多面体或近似椭球体. 初始氦空位比小于临界氦空位比时, 氦泡压强不足以将点阵位置的Fe原子冲出, 或者冲出的数量少, 因而100 ps时氦泡的形状基本与0 ps时相同, 仍保持为球形. 结合图5(a)—(c)可知, 与0 ps时的原子剪应力分布相比, 100 ps时, 氦泡周围的应力集中情况变得缓和, 原因是高压氦泡将应力集中区域的部分Fe原子冲出, 成为自间隙原子, 氦泡内的空位数增多, 氦泡长大, 氦泡压强得以释放, 进而氦泡周围的Fe原子应力集中得到消散. 同时, 由图5(a)—(d)可知, 在0 ps时, 基体Fe原子的最大剪应力和剪应力集中区的范围均随着初始氦空位比的增大而增大.
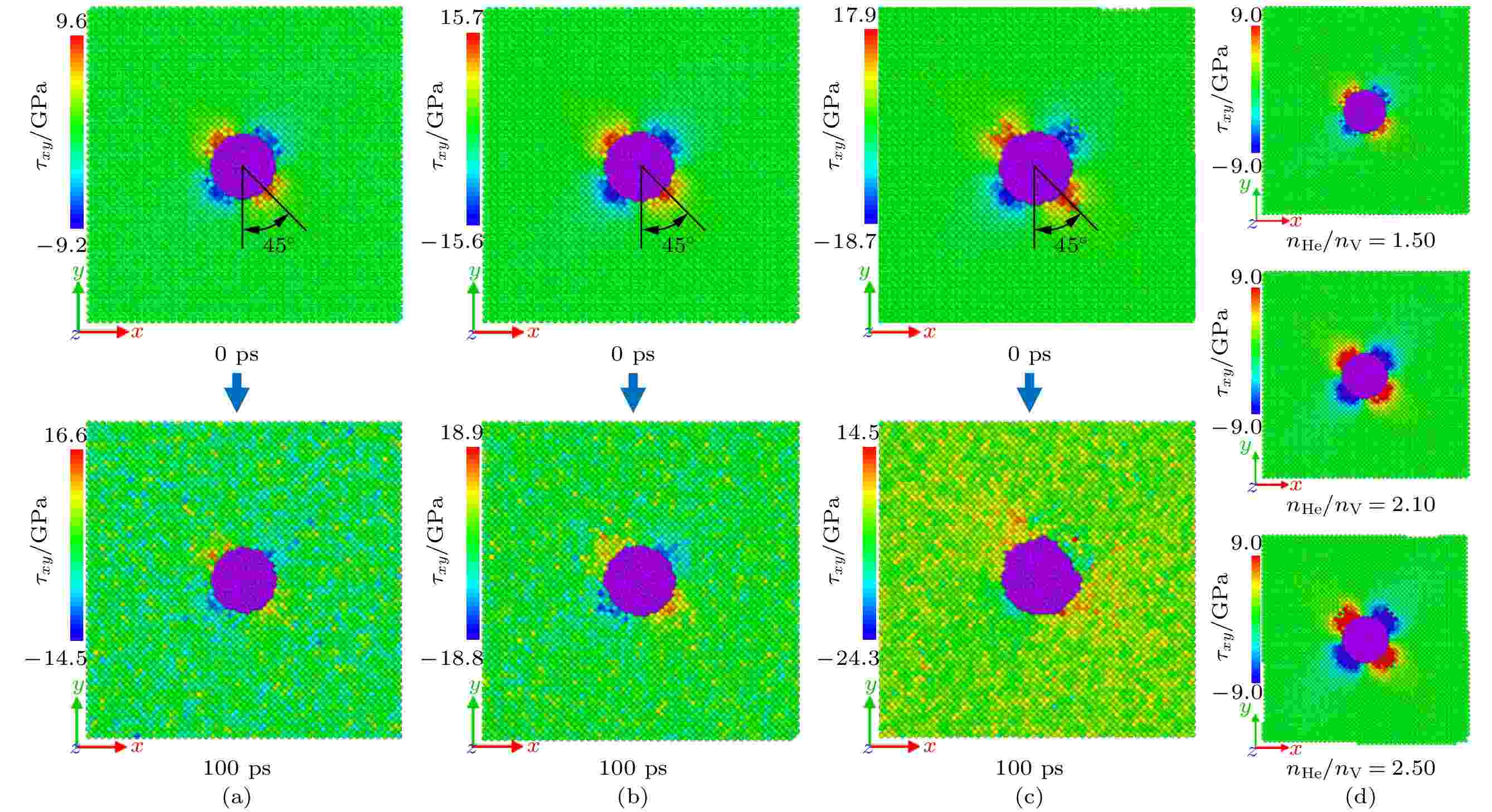图 5 氦泡周围Fe原子阵列的剪应力分布　(a) n_He/n_V = 1.50; (b) n_He/n_V = 2.10; (c) n_He/n_V = 2.50; (d) 上下限相同时0 ps处的原子应力分布
Figure5. Shear stress distribution of Fe atom array around helium bubble: (a) n_He/n_V = 1.50; (b) n_He/n_V = 2.10; (c) n_He/n_V = 2.50; (d) atomic stress distribution at 0 ps with the same upper and lower limit.

图6为氦泡在基体中冲出的位错环在xy平面上的投影, 其中红色箭头表示Burgers矢量方向, 红绿蓝色表示离氦泡表面距离不同的Fe原子, 显示时隐去了完美晶格状态的Fe原子. 包绕在氦泡周围的Fe原子由两部分组成, 一部分是经氦泡压强冲出点阵的自间隙Fe原子, 另一部分则是紧邻氦泡的Fe原子. 由图6可见, 位错环起、止都在氦泡表面, 位错环的冲出方向与图5中Fe原子阵列的最大剪应力出现位置吻合. 由图7进一步分析可知, 剪应力分布沿$ \left\langle {111} \right\rangle $方向最大, 这种剪应力分布与图6(d)中冲出的Burgers矢量为1/2$ \left\langle {111} \right\rangle $型的位错相吻合. 这表明当氦泡压强足够大时, 就会使其周围Fe原子阵列的应力达到极限, 从而相应的Fe原子就被冲出点阵位置而成为自间隙原子, 而随着自间隙原子的不断累计增多, 就形成间隙型位错环, 如图6(a)—(c)所示. 这与文献[40]针对钨中氦泡冲出位错环现象的分析结果一致.
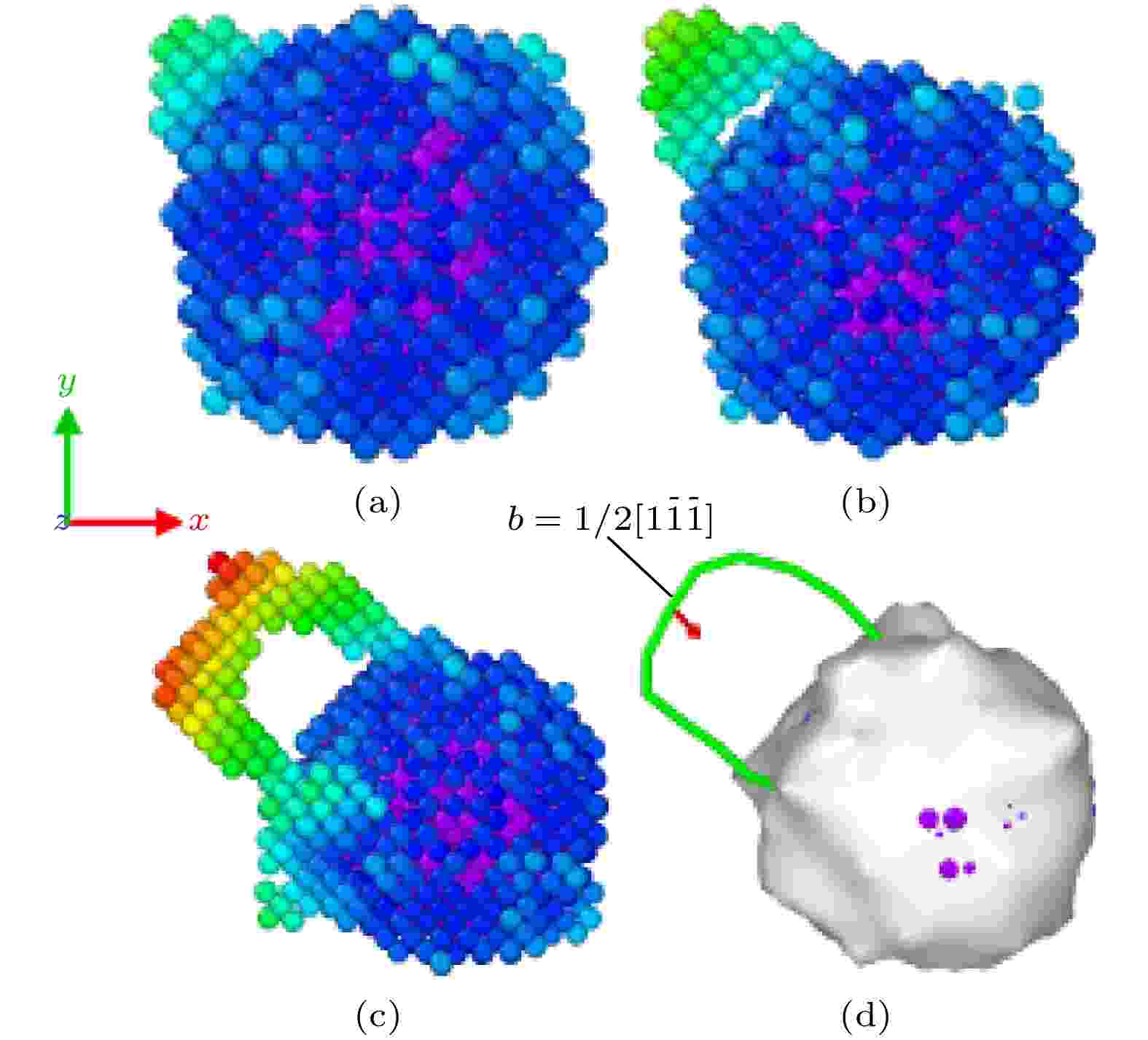图 6 初始半径为1.31 nm, n_He/n_V = 2.10时氦泡冲出的位错环在xy平面投影　(a) 88 ps; (b) 92 ps; (c) 100 ps; (d)删除图6(c)中Fe原子后带缺陷网格的位错图
Figure6. Projection of dislocation loops produced by helium bubbles in xy plane, when initial radius of helium bubble is 1.31 nm, n_He/n_V = 2.10: (a) 88 ps; (b) 92 ps; (c) 100 ps; (d) a dislocation picture with a defect mesh after removing the Fe atoms in Fig. 6(c).

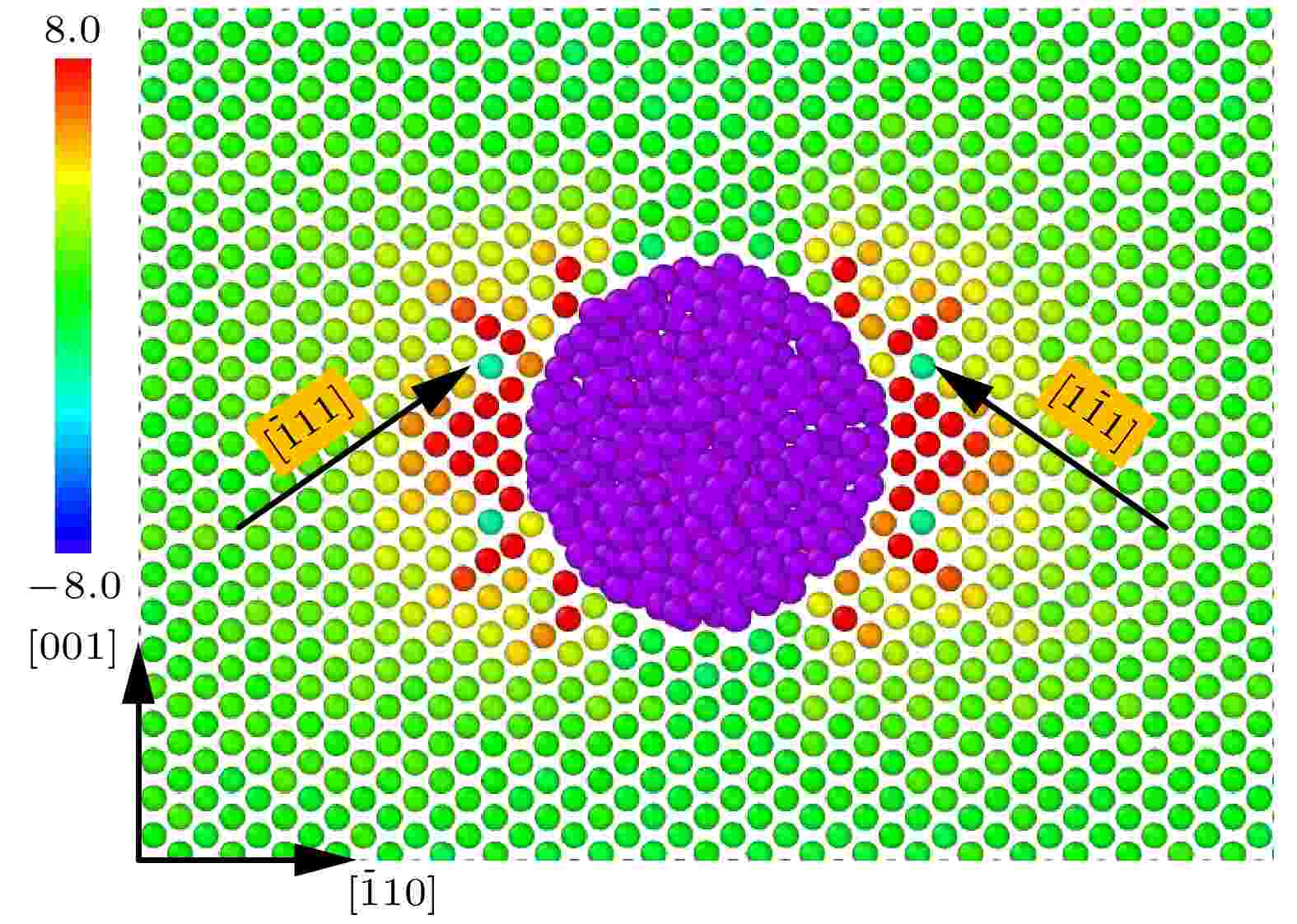图 7 (110)面原子剪应力分布(氦泡初始半径为1.31 nm, n_He/n_V = 2.10)
Figure7. (110) Surface atomic shear stress distribution (initial radius of helium bubble is 1.31 nm, n_He/n_V = 2.10).

2 -->

3.4.高压氦泡冲出位错环时的极限压强对比分析

Trinkaus^[13]根据基体材料的机械稳定极限, 给出了氦泡冲出位错环时极限压强的理论估算公式:

${P_{{\rm{ultimate}}}} = {{2\gamma }}/{R} + {{Gb}}/{R}, $

式中, γ是表面自由能, 单位为Pa·m. 对于α-Fe, 取表面自由能γ = 1.65 Pa·m^[38]. Donnelly^[41]指出(4)式的适用范围为$2 < \bar R < 10$.
Wolfer^[15]分别基于Helmholtz自由能和基体材料弹性理论解, 得到氦泡冲出位错环时的极限压强公式为

${P_{{\rm{ultimate}}}} = 0.20G. $

Trinkaus、Wolfer和本文MD的结果对比, 如图8所示. 由Wolfer^[15]的研究可知, (5)式只适用于$\bar R > 10$的情况; 但Wolfer的研究中给出了$3 < $$ \bar R < 10$范围内的极限压强数据, 如图8中蓝色实线所示. Wolfer^[15,39]指出对于小氦泡其极限压强甚至可达到0.50G, 接近于发射自间隙原子所需压力, 这与Trinkaus在文献[42]中指出的极限压强应该为0.20G—0.50G的结论相吻合. 值得注意的是虽然图8中Wolfer^[15]的数据是以Ni为例, 基于Helmholtz自由能得出的, 但其在随后的研究中指出氦泡压强(初始氦空位比)才是影响位错环冲出与否的主要因素, 金属材料间的差异为次要因素^[39].
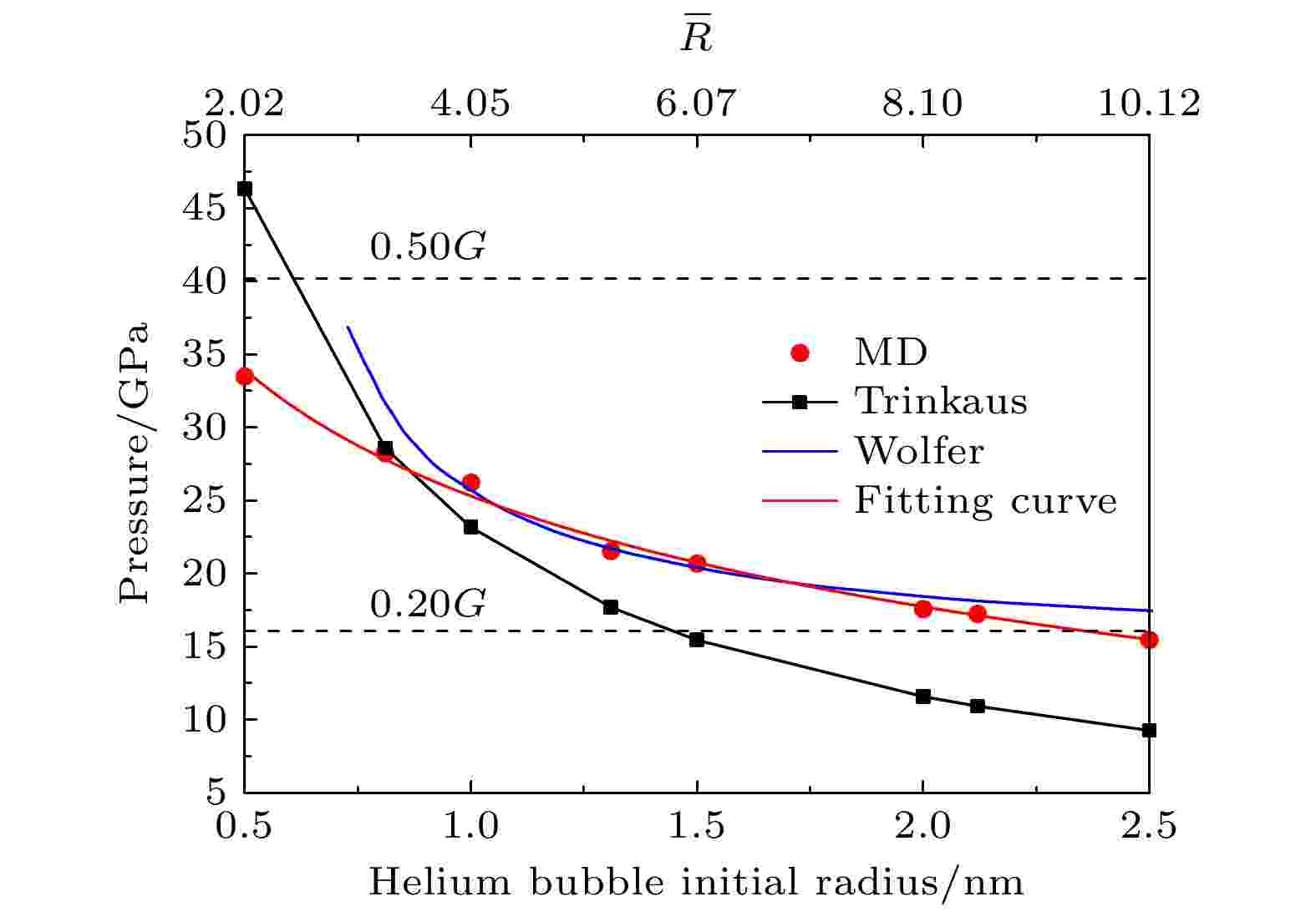图 8 氦泡极限压强与氦泡初始半径关系
Figure8. Ultimate pressure vs. initial radius of helium bubble.

由图8可见, 对于$2 < \bar R < 10$的氦泡, 氦泡极限压强随着氦泡初始半径的增大而非线性减小. 对于$2 < \bar R < 3$的氦泡(如氦泡初始半径为0.50 nm的氦泡), MD模拟值相对Trinkaus和Wolfer的结果偏低, 但是按照Trinkaus^[13]的划分, 初始半径为0.50 nm的氦泡, 属于形核阶段的氦泡, 从冲出位错环所需临界氦空位比(n_He/n_V =2.95)角度来分析, MD模拟值与Wolfer^[39]的研究结果吻合. 在$3 < \bar R < 10$的范围内, Trinkaus的计算值相对偏低, 而本文MD的模拟值与Wolfer的结果比较接近. 并且结合文献[2,15]可知, 在$\bar R > 10$时, 氦泡极限压强${P_{{\rm{ultimate}}}} \leqslant $$ 0.20 G$, 因此本文通过MD模拟得到的初始半径为2.50 nm氦泡的极限压强在合理范围内, 并且所需临界氦空位比也与Wolfer^[15,39]的研究结果吻合.
本文采用的氦泡压强计算方法的准确性已经在2.2节加以检验, 可认为在临界氦空位比下计算得到的氦泡极限压强是合理的. 不可否认的是, 本文中8种不同初始半径的氦泡, 冲出位错环时的临界氦空位比, 受到初始氦空位比取值间隔精度影响, 进而影响氦泡极限压强的确定. 由3.1节的分析可知, 各尺寸的氦泡均是在图3氦泡压强峰值点之后开始出现冲出位错环现象, 如果进一步细化峰值点之后的初始氦空位比, 可以得到更为精确的临界氦空位比, 进而确定不受取值间隔精度影响的氦泡极限压强.

采用分子动力学方法, 建立金属-氦泡的立方体型代表性体积单元模型, 针对8种不同初始半径的球形氦泡, 以初始氦空位比为变量, 开展MD模拟, 获得了各RVE模型中位错环开始形成时的氦泡极限压强和临界氦空位比. 通过对MD模拟结果的分析, 得到如下结论:
1)基于MD模拟给出了冲出位错环时的氦泡极限压强和临界氦空位比随氦泡初始半径非线性变化的公式, 可用于估算α-Fe中$2 < \bar R < 10$的氦泡极限压强和临界氦空位比.
2)对于$2 < \bar R < 10$的氦泡, 在金属基体中冲出位错环时的氦泡极限压强和临界氦空位比随着氦泡初始半径的增大而非线性减小.
3)基体中氦泡冲出位错环时的临界氦空位比具有明显的尺寸效应, 对于形核后期的氦泡(如氦泡初始半径为0.81 nm的氦泡)和非理想气体阶段的氦泡(如氦泡初始半径为1.00—2.50 nm的氦泡), 其冲出位错环时的临界氦空位比与各自氦泡压强峰值点对应的初始氦空位比相同, 而对于形核初期或中期的氦泡, 如初始半径为0.50 nm的氦泡, 其冲出位错环所需的临界氦空比比其压强峰值点对应的初始氦空位比约大13.46%.
4)初始时刻(0 ps), 在经过RVE中心的横截面上, 氦泡周围Fe原子阵列的剪应力集中和最大剪应力出现在对角线与氦泡边界交点(即45°)处, 并且关于横截面上平行于边的两条对折线对称分布, 剪应力集中区的范围和最大剪应力均随着初始氦空位比的增大而增大; 位错环冲出方向对应于最大剪应力方向.
本文的研究深化了对金属中氦泡物理特性的认识, 为后续分析氦泡对材料宏观物理和力学性质的影响奠定了有益的基础.