摘要:霍尔天平材料中层间耦合作用易于调控, 基于此可以实现多组态磁存储模式, 其区别于当前基于自旋阀或者磁性隧道结的传统二组态磁存储原理. 与此同时, 还可以在存储单元中实现信息的逻辑运算从而提高器件整体的运算效率. 这一设计有利于自旋电子学器件的微型化、集成化, 有望从物理原理上解决当前基于自旋阀或者磁性隧道结的传统二组态自旋电子学材料器件的技术瓶颈, 进一步提高磁存储密度, 为推动新型自旋电子学材料的研究开辟了一条新的研究思路. 首先, 本综述将介绍基于霍尔天平材料的磁存储器件的研究背景; 其次, 重点介绍霍尔天平存储逻辑器件一体化设计的提出与发展历程; 再次, 介绍霍尔天平材料关键指标—霍尔电阻比值的界面调控及物理机理探索; 随后详细阐述霍尔天平体系中磁性斯格明子的产生与多场调控等动态行为. 最后, 简单介绍霍尔天平结构在其他相关材料中的扩展、应用, 并展望其在未来器件应用中的前景.
关键词: 霍尔天平/
多组态存储/
磁性斯格明子/
倾斜磁结构

English Abstract

全文HTML

--> --> -->

20世纪中叶, 以操控电子电荷属性为基础的传统微电子技术取得了飞速发展, 为人类的生活带来了极大便利. 随着人类对产品性能的要求越来越高, 对于微电子产品而言, 由于晶体管数量的不断增加而带来的散热、兼容等一系列的问题, 使得微电子技术的发展受到了严重的制约^[1]. 为了解决上述瓶颈和挑战, 科学家们始终孜孜不倦地探索新材料、新原理和新技术, 在尝试优化结构和改进工艺的同时也在寻求利用新材料中的新奇物理效应来实现信息技术的革新.
自旋电子学作为凝聚态物理学与材料科学及微电子技术的新兴交叉学科, 伴随着巨磁电阻效应(GMR)的发现成为近代磁学的里程碑, 揭开了人类利用电子自旋这一电子所具有的另一个本征属性来进行信息存储和读写的序幕^[2]. 随着材料制备和微纳米加工技术的日益成熟, 更多新型功能材料及器件被设计和制备出来, 为科学家们深入研究其中的物理机理提供了良好的基础. 过去20多年中, 自旋电子学材料、物理及相关器件的研究得到了突飞猛进的发展, 极大地推动了信息产业的变革式发展, 尤其是磁存储密度的量级提升^[3-5]. 以信息存储产业需求为先导, 进一步降低器件尺寸和提高磁信息存储密度是科学家们普遍关注的热点问题之一. 科学家们首先利用两组态的GMR^[6]、隧穿磁电阻(TMR)^[7]自旋电子学材料, 通过降低其单元尺寸和减少薄膜厚度来提高这类器件的存储密度等物理性能指标. 经过十余年的基础研究, 基于TMR的磁性隧道结(MTJ)作为磁随机存储器单元得到了迅速发展. 特别是, 利用自旋转移矩^[8]可以实现MTJ磁化翻转, 加速其作为磁随机存储器单元的实用化进程, 解决磁场诱导MTJ磁化翻转中磁场难以微型化的技术瓶颈. 随着研究的不断深入, 科学家们也逐步尝试利用新的物理效应^[9] (例如自旋轨道矩(SOT))推动TMR存储器件的继续发展. 与此同时, 随着TMR材料制备工艺的不断成熟, 基于TMR的自旋电子学器件也逐步进入大规模信息存储产业中并得到实际应用. 需要指出的是, 科学家们发现当磁性器件的尺寸降低到一定程度时(如纳米级别), 量子尺寸效应和热效应使得存储单元无法长时间正常工作甚至失效, 这让数据保存的时间大幅度缩短, 数据稳定性也随之降低. 随着对自旋电子学器件微型化、集成化的需求不断提高, 以GMR和TMR效应为基础的二组态自旋电子学材料遇到了前所未有的技术瓶颈, 受到了摩尔定律和超顺磁极限的严重制约. 与此同时, 过去数十年中科学家们为了优化提高磁存储单元的核心指标—磁电阻比值而呕心沥血, 但是在磁电阻比值经历了一段快速提升过程, 室温下达到604%之后, 便无法进一步提升. 此外, TMR的最高比值仍未达到理论预期值^[10-12], 且与半导体二极管的开关比存在一定程度的差距, 这也为磁信息存储的进一步发展蒙上一层阴影.
从应用的角度来看, 国家集成电路长远规划(2019—2026年)的蓝图中, 高集成密度(3D (three dimensional)存储模式)、低能耗和高运算效率的电路模式将占据最高的优先级并成为产业化和商业化的首选. 虽然科学家们也在不断探索利用多场调控等手段提高信息磁存储关键性指标, 优化原有的二组态磁存储构架^[13-17], 但是仍无法完美地弥补二组态的固有短板. 为了从根本上突破这一技术瓶颈, 适应未来信息产业发展的需要, 人们将研究的重点集中在新型自旋电子学材料的设计和基础物理问题的探索上. 目前, 主要的研究方向集中在两条主线上: 1)继续探索新型磁性功能材料和具有新自旋结构的材料体系(例如基于畴壁运动的赛道存储器^[18]、磁性斯格明子^[19]等), 优化二组态存储模式, 提高存储密度; 2)突破传统二组态存储模式, 寻找具有空间多组态存储的新结构、新材料从而实现3D存储模式^[20]. 基于这两大主要研究方向, 科学家们做出了大量原创性的理论和实验工作, 并在物理原理、材料设计和器件加工等多方面取得了重要性突破, 一系列研究成果将进一步促进自旋电子学的蓬勃发展, 同时为实现高密度新型信息磁存储奠定坚实基础. 其中, 霍尔天平是利用垂直磁性多层膜材料的反常霍尔效应所设计的新型自旋电子学材料, 其核心为垂直铁磁层/隔离层/垂直铁磁层所构成的三明治结构. 接下来, 本文将重点介绍近期霍尔天平材料在新型信息存储器件中的现状、应用和未来可能的发展方向.

传统磁信息存储主要利用GMR和TMR效应等实现高、低二组态存储模式(即“1”和“0”), 其核心单元是一个由两层铁磁薄膜和中间隔离层所组成的三明治结构. 当隔离层为金属薄膜时, 如Cu和Cr, 体系具有GMR效应; 而当隔离层为绝缘体时, 如Al₂O₃和MgO, 体系具有TMR效应. 通常两种铁磁性薄膜的矫顽力不同, 其中矫顽力低、容易翻转的那一层称为自由层; 另外一个磁性层的矫顽力较大, 在器件中常利用反铁磁薄膜通过交换耦合原理对其进行钉扎来提高矫顽力, 被称为钉扎层. 上述三明治结构工作的物理原理是采用外加磁场、外加电流产生的奥斯特磁场、自旋极化电流等手段来控制磁性多层膜结构中自由层和钉扎层磁矩的相对取向. 例如, 当两层处于平行排列时, 体系处于低电阻状态; 当两层处于反平行排列时, 体系处于高电阻状态. 高低电阻状态对应于信息存储的“1”和“0”两态, 如图1(a)所示^[21]. 从器件架构设计的角度来看, 如果要在基于GMR和TMR的信息存储器件中实现多组态信息存储, 那么一种可行的方法是增加铁磁层的个数. 基于这一思路, 人们尝试通过设计双势垒隧道结器件以求实现多组态信息存储^[22]. 但是, 双势垒隧道结对磁性多层膜材料的制备和器件微纳加工工艺提出了更高的要求, 特别是超薄铁磁层的脱耦合和磁性层矫顽力的精确控制十分具有挑战性. 因此, 这方面的研究工作仍然任重而道远. 与此同时, 人们也在尝试利用磁性功能薄膜中的新奇物理效应设计具有不同功能的高密度存储材料及原理型器件. 其中, 利用磁性多层膜中的反常霍尔效应制备具有高存储密度的新型磁性存储材料逐步受到了人们的关注, 其典型输出曲线如图1(b)所示.
图 1 (a)磁性隧道结Fe(25)/MgO(3)/Fe(10)/IrMn(10) (厚度单位均为纳米)中的R-H输出曲线^[21]; (b)霍尔天平CoO(10)/[Co(0.3)/Pt(1)]₃/NiO(1.1)/Pt(0.6)/[Co(0.3)/Pt(1)]₃/CoO(10) (厚度单位均为纳米)中的R-H输出曲线
Figure1. (a) R-H loops for the magnetic tunnel junction with the structure of Fe(25)/MgO(3)/Fe(10)/IrMn(10) (in nm)^[21]; (b) R-H loop for Hall balance with the structure of CoO(10)/[Co(0.3)/Pt(1)]₃/NiO(1.1)/Pt(0.6)/[Co(0.3)/Pt(1)]₃/CoO(10) (in nm).

反常霍尔效应是磁性材料所特有的一种超大霍尔效应, 由美国实验物理学家Edwin Hall于19世纪末在铁磁金属中首次观测到. 与图2(a)所示的正常霍尔效应不同的是, 反常霍尔效应是一种自旋相关的物理效应, 具有不同自旋方向的载流子在自旋轨道耦合作用下向着相反的方向运动, 从而在垂直于外加电流方向的两端积累并形成电势差. 图2(b)是反常霍尔效应原理图, 它是磁性材料所特有的不需要外加磁场就可以观测的霍尔效应. 但是, 利用外磁场等手段可以改变磁性材料的磁矩方向, 从而可以调控反常霍尔电压的方向, 即磁矩向上(下)对应于反常霍尔电压为正(负), 这就为利用反常霍尔效应来设计信息存储器件提供了可能.
图 2 (a)正常霍尔效应和(b)反常霍尔效应原理图
Figure2. Schematic of (a) ordinary Hall effect and (b) anomalous Hall effect.

通常情况下, 反常霍尔效应的大小不仅与磁性材料的磁化强度成正比, 还和磁性多层膜中的界面状态息息相关, 这也为后续调控基于反常霍尔效应的自旋电子学器件性能提供了一条有效的途径. 早期的关于反常霍尔效应的研究主要集中在揭示其物理起源和内在机制上, 研究体系也相对单一, 主要发现了与自旋轨道耦合作用相关的内禀机制以及与杂质散射相关的外禀机制^[23-26]. 近些年来, 随着材料制备工艺的发展、微观结构的精细表征以及理论计算方法的完善, 关于反常霍尔效应的研究体系也逐渐从单一铁磁金属体系扩展到稀磁半导体、稀土过渡金属合金、铁磁合金和磁性复合多层膜结构等^[27-30]. 多元、复合的纳米结构使得反常霍尔效应中不同的物理机理相互竞争, 其反常霍尔信号也受到了纳米薄膜材料本身晶体结构、组分、微观缺陷、界面结构等一系列因素的影响^[31-38]. 随着研究的进一步深入, 人们对于磁性多层膜中反常霍尔效应的物理起源和调控机理有了更加清晰的认知, 这也为后续设计不同功能性的反常霍尔器件奠定了物理和材料基础. 基于前期大量的研究工作, 国内多个团队先后利用超薄复合多层膜结构设计开发了具有高灵敏度的反常霍尔线性磁传感器材料^[39-41], 为反常霍尔效应材料及器件设计拉开了帷幕.
近期, 一种新型多组态磁存储材料概念—霍尔天平^[42]被国内****首次提出. 霍尔天平的核心结构为铁磁层1/隔离层/铁磁层2的三明治结构, 其中铁磁层1和铁磁层2均具有垂直磁各向异性, 且两个铁磁层之间具有较强的层间交换耦合作用. 隔离层可以为绝缘材料(例如氧化镍NiO, 氧化镁MgO等), 也可以为金属材料(例如钌Ru, 铂Pt, 铜Cu, 钽Ta等). 霍尔天平可以具有多种状态: 反向平行、反平行和正向平行, 如图1(b)中所示的“0”, “1”, “1′”和“2”状态. 与基于GMR和TMR效应的二组态信息存储器件不同的是, 霍尔天平可以有效地区分磁矩平行的两种状态, 即正向平行态和反向平行态. 以图3(a)中基于NiO隔离层的霍尔天平为例^[42], 该体系的霍尔电阻输出曲线显示了三个稳定的状态: 1)两个磁性层的磁矩处于正向平行时, 反常霍尔电压等于他们各自的反常霍尔电压之和, 称为高阻态; 2)两个磁性层的磁矩在低场下处于反平行状态, 体系的反常霍尔电压等于两者反常霍尔电压之差, 如果两个磁性层的反常霍尔效应大小完全相同, 那么此时的总霍尔电压为零, 即中间阻态; 3)当两个磁性层的磁矩处于反向平行时, 反常霍尔电压等于两者的反常霍尔电压之和, 大小与正向平行时的数值相同, 却具有相反的方向, 此时为低阻态. 利用霍尔天平设计的新型自旋电子学器件可以实现三组态甚至多组态, 进而实现高密度3D信息存储阵列, 如图3(b)所示^[42]. 这就为新型高密度3D存储模式提供了有效的途径, 为后续的多功能磁存储材料及相关器件设计提供了可能的发展方向.
图 3 (a)基于NiO的霍尔天平R-H曲线; (b)基于霍尔天平的3D存储阵列示意图^[42]
Figure3. (a) R-H loop for Hall balance based on NiO spacer; (b) schematic of 3D storage based on Hall balance^[42].

利用霍尔天平进行信息存储的同时, 科研工作者也尝试在单一霍尔天平存储单元内实现信息布尔逻辑运算, 从根本上解决信息存储和逻辑运算分离的限制, 从而实现可编程的存算一体化器件设计. 对于大多数可编程的逻辑运算而言, 逻辑操作均需要在实际运算发生前对基本的布尔逻辑进行预选择, 这将极大地限制信息运算处理的速度. 为了实现可编程的逻辑门计算操作, 研究者首先设计了一种结构简单的霍尔天平存储器件^[42], 其核心结构为两层具有垂直磁各向异性的[Co/Pt]_n多层膜, 中间用超薄的NiO隔离层隔开, 通过材料结构的优化, 最终实现了具有稳定三组态的对称霍尔电压输出曲线. 在此基础上进行了可编程的逻辑门运算操作.
图4给出了单一霍尔天平存储单元进行可编程布尔逻辑门运算操作^[42]. 对于一个具有三组态的霍尔天平器件单元而言, 经过简单操作输出三元代码就可以实现所有的布尔逻辑运算. 为了实现多种可编程的基本布尔逻辑运算, 选取两个垂直于薄膜表面的磁场A和B (也可以采用两个电流I_A和I_B产生的磁场)作为输入值, 反常霍尔电压(V)作为输出值, 如图4(a)所示. 对于输入值磁场A和B而言, 预先设定正向磁场(负向磁场)为逻辑输入值1(0). 需要注意的是, 磁场A和B幅值相等, 且单个磁场(A或者B)无法实现薄膜磁矩的翻转. 例如, 对于结构优化后的三组态霍尔天平而言, 磁场A和B幅值均为200 Oe; 同时设定霍尔电压作为输出值. 只有当磁场A和B同向时, 才能实现薄膜磁矩的翻转, 即A, B = (0, 0), (1, 1)分别对应于霍尔天平中的“↓↓”, “↑↑”状态, 电压绝对值为最大值, 即输出值记为1. 对于磁场A和B反向时, 其输入值为(0, 1)和(1, 0), 对应霍尔天平中的“↓↑”或“↑↓”状态, 即霍尔电压绝对值接近零, 即输出值记为0. 基于上述的操作关系, 单一霍尔天平存储单元中可以实现XNOR逻辑门运算, 即当输入值A和B相同对应输出值为1, 反之输出值为0, 具体真值表如图4(b)所示.
图 4 基于霍尔天平存储单元的基本布尔逻辑运算输出曲线及真值表^[42]
Figure4. Boolean logic operation in storage cell based on Hall balance and truth table ^[42].

为了在同一霍尔天平单元内实现可编程的逻辑门运算, 可以引入两个辅助操作变量, 即霍尔天平器件中的纵向电流方向(沿着霍尔条的方向)和横向偏置电压方向(膜面内沿着垂直于纵向电流方向), 如图4(c)—图4(f)所示. 在图4(b)的霍尔电压输出曲线基础上, 横向偏置电压的引入使得霍尔电压输出曲线将偏离X轴, 如图4(c)和图4(d)所示. 此时, 霍尔电压为正(负)值对应于逻辑门输出值的1(0). 图4(c)给出了利用霍尔天平结构实现OR逻辑门运算. 当磁场A和B均为负值(输入值为(0, 0)), 此时对应于霍尔电压为负值(输出值为0); 当磁场A和B不同号(输入值为(1, 0)或者(0, 1)), 由于正的横向偏置电压的存在, 对应于霍尔电压为正值(输出值为1); 当磁场A和B均为正值(输入值为(1, 1)), 对应于霍尔电压为正值(输出值为1). 因此, 利用霍尔天平就可以实现OR逻辑门运算操作. 此外, 利用负的横向偏置电压可以在同一霍尔天平单元中实现AND逻辑门运算操作, 如图4(d)所示. 接下来在图4(c)和图4(d)的基础上, 可以将纵向电流的方向从正向变为负向, 同时改变横向偏置电压的方向, 那么霍尔天平的输出响应曲线分别如图4(e)和图4(f)所示. 图4(e)和图4(f)中的真值表显示该器件还可以分别实现NOR和NAND逻辑门运算操作. 根据上述结果可知, 利用单一霍尔天平存储单元可以进行基本的布尔逻辑运算, 进而实现可编程的逻辑操作.
因此, 利用霍尔天平单元不仅实现了多组态信息磁存储, 还可以完成存算一体化设计. 基于霍尔天平结构的磁存储逻辑计算一体化器件突破了当前自旋电子学领域的技术瓶颈, 给出了一种解决当前磁随机存储器所面临问题的有效途径, 符合未来3D存储模式的发展需求^[42,43]. 此外, 基于这种具有两个铁磁层的霍尔天平器件的设计理念, 一种多组态存储材料—自旋算盘^[44]也被科研工作者提出, 并且相应的原理型器件也被成功制备出来. 科研工作者受到中国古代算盘技术思想的启发, 设计了一种多磁性层的薄膜材料, 利用材料中各个磁性层磁矩逐层翻转, 从而实现了多进制计数的功能, 如图5所示^[44]. 随后, 科研人员通过对NiO和[Co/Pt]_n多层膜之间的界面耦合和层间耦合作用的精确调控, 实现了外磁场驱动下磁性层磁矩逐层翻转, 从而实现了多组态信息磁存储, 极大地拓展了存储器件的单位存储密度.
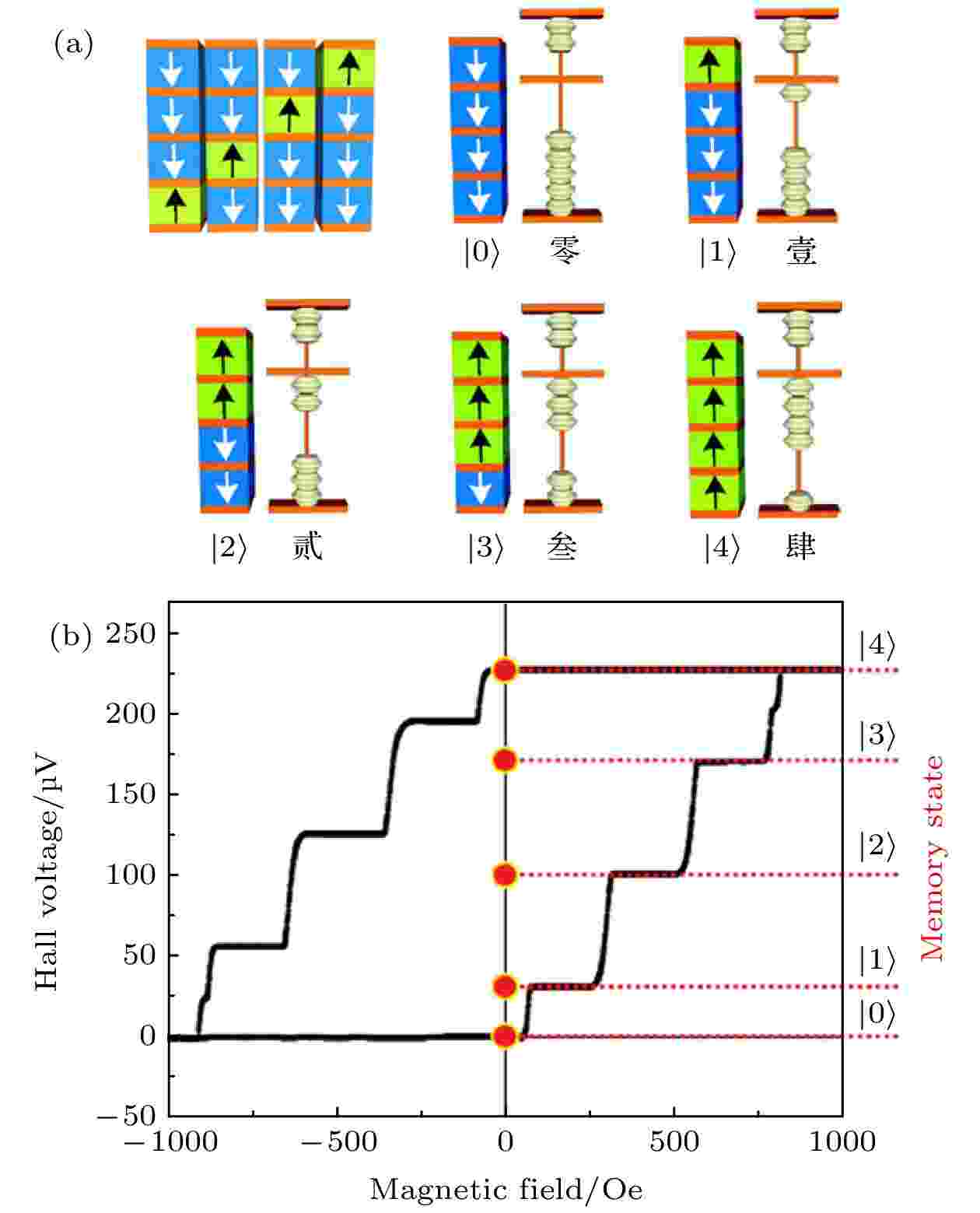图 5 (a)自旋算盘设计示意图; (b)基于NiO隔离层的自旋算盘霍尔输出曲线^[44]
Figure5. (a) Schematic of magnetic abacus memory; (b) Hall loop for the magnetic abacus based on NiO spacer^[44].

正如前文所述, GMR和TMR比值分别是自旋阀和磁性隧道结的核心指标, 其数值大小影响着以自旋阀或者隧道结为信息存储单元的综合性能, 尤其是灵敏度和信噪比. 以TMR效应为例, 目前室温下MR比值(如CoFeB/MgO/CoFeB磁性隧道结)最高值可达604%, 低温下高达1144%^[10], 且近十余年来该比值没有进一步提高. 受限于材料制备技术和物理原理的内在限制, 隧道结中TMR比值的量级仍无法与半导体二极管的开关比相媲美. 鉴于这一现状, 科学家们在霍尔天平结构的磁性多层膜中提出了霍尔电阻比值这一指标^[42]. 霍尔电阻比值(Hall resistance ratio, HRR)是霍尔天平材料及器件的核心关键指标, 代表了霍尔天平结构中的磁电阻开关比, 其表达式为

$ {\rm{H}}{\rm{R}}{\rm{R}}= ({{R}_{{\rm{p}}}-{R}_{{\rm{a}}{\rm{p}}}})/{{R}_{{\rm{a}}{\rm{p}}}}\times100 {\text{%}}\text{,}$

其中R_p和R_ap分别代表正向平行态霍尔电阻和反平行态霍尔电阻.
通常情况下, HRR主要受到两方面因素的影响: 1)霍尔天平的组态数; 2)霍尔天平中各组态电阻的大小. 对于一个仅具有两组态的霍尔天平磁性多层膜而言, 体系不具备HRR值; 只有当霍尔天平具有多组态时, 衡量体系的HRR比值才具有物理涵义. 此外, HRR值的大小由R_p和R_ap两部分决定, 其中R_p和R_ap取决于霍尔天平中两个铁磁层的反常霍尔效应的大小. 通常情况下, 为了获得更高的HRR值, 可以采用降低R_ap同时提高R_p的方法来实现. 研究发现: 磁性多层膜中的自旋输运性质不仅与铁磁层本身的磁化强度有关, 同时还受到磁性层间耦合作用、界面化学状态、界面粗糙度、铁磁层的晶化程度以及界面缺陷浓度等多方面的影响^[41,45-47]. 因此, 深入研究并澄清磁性多层膜材料设计对霍尔天平HRR效应调控内在机理, 实现高HRR值的霍尔天平材料及器件制备是当前亟待解决的热点问题之一.
首先, 采用超高真空多靶磁控溅射镀膜系统制备了以铁磁层/氧化物/铁磁层([Co/Pt]_n/oxide spacer/[Co/Pt]_n)为核心结构的霍尔天平材料. 核心铁磁层选用[Co/Pt]_n多层膜, 主要是由于[Co/Pt]_n多层膜具有较强的自旋轨道耦合作用和易于调控的垂直磁各向异性(PMA); 氧化物选择磁性隧道结中常用的MgO作为隔离层, 其具有一定的晶体结构, 易于调控磁性薄膜的层间耦合. 图6(a)给出了样品[Co/Pt]_n/MgO/[Co/Pt]_n的霍尔输出曲线^[42]. 从霍尔输出曲线不难看出, 该样品的两个垂直磁性层的磁化方向是分步翻转的, 具有明显的多组态特性. 样品的R_p和R_ap分别为650和70 mΩ, 其HRR值达到850%, 该数值高出了目前报道的TMR室温下最高值^[10]. 在此基础上, 科学家尝试利用NiO作为隔离层, 经过材料结构优化, 成功制备出结构为NiO/[Co/Pt]_n/NiO/[Co/Pt]_n的霍尔天平, R_p和R_ap分别为630和2 mΩ, 其HRR值达到31400%, 如图6(b)所示^[42].
图 6 (a)样品NiO(20)/[Co(0.4)/Pt(1.2)]/MgO/[Co(0.4)/Pt(1.2)]/NiO(1) (nm)的霍尔输出曲线; (b)样品NiO(50)/Pt(0.6)/[Co(0.3)/Pt(1)]/NiO/[Co(0.4)/Pt(1.2)] (单位: nm)的霍尔输出曲线^[42]
Figure6. (a) Hall loop for the sample NiO(20)/[Co(0.4)/Pt(1.2)]/MgO/[Co(0.4)/Pt(1.2)]/NiO(1) (in nm); (b) Hall loop for the sample NiO(50)/Pt(0.6)/[Co(0.3)/Pt(1)]/NiO/[Co(0.4)/Pt(1.2)] (in nm) ^[42].

以NiO作为隔离层的霍尔天平为基础, 科学家们进一步对材料进行结构优化, 重点研究了铁磁层、隔离层对HRR的调控作用. 图7(a)—图7(c)给出了不同NiO厚度(t_NiO)的霍尔天平Pt(0.6)/[Co(0.4)/Pt(1)]₃/Co(0.4)/Pt(0.3)/NiO(t_NiO)/Pt(0.3)/[Co(0.4)/Pt(1)]₄ (厚度单位为纳米)的霍尔输出曲线^[48]. 从图中可以看出, 两个[Co/Pt]_n多层膜的耦合状态强烈地依赖于NiO层厚度, 例如, 当t_NiO = 1 nm 或者1.1 nm时, 霍尔天平中的铁磁层处于反铁磁耦合状态. 此时, 霍尔天平具有多个组态: 1) 铁磁层的磁矩方向反平行排列对应于中间阻态(如图中状态“1”或者“1'”), 状态“1”或者“1'”的出现是由反铁磁耦合作用强度和铁磁层/氧化物界面结构共同决定的; 2)铁磁层的磁矩方向正向平行和反向平行分别对应于高阻态和低阻态(如图中状态“2”和“0”). 根据前面的霍尔天平中HRR值的计算公式可知, 图7(a)和图7(b)中霍尔天平HRR值分别为1122%和1089%. 继续增加NiO层厚度至1.2 nm时, 霍尔天平的两个铁磁层变成铁磁耦合状态, 如图7(c)所示. 对于铁磁耦合的霍尔天平而言, 两个铁磁层的磁矩将一致翻转, 那么就没有中间状态, 因此就没有HRR值. 在图7(d)的基础上改变上层铁磁多层膜[Co/Pt]_n中Pt的厚度(t_Pt), 制备出结构为Pt(0.6)/[Co(0.4)/Pt(1)]₃/Co(0.4)/Pt(0.3)/NiO(1.1)/Pt(0.3)/[Co(0.4)/Pt(t_Pt)]₄(厚度单位均为纳米)的样品, 其霍尔输出曲线如图7(d)—图7(f)所示. 随着上层[Co/Pt]_n多层膜中t_Pt降低, 该结构的霍尔天平中两个铁磁层始终保持着反铁磁耦合状态. 当t_Pt = 0.8 nm时, 霍尔天平中的“1”或者“1'”对应的电阻值基本相同, 所以霍尔天平形成稳定的三组态. 此时, 霍尔天平的R_p和R_ap分别为1050和6 mΩ, 其HRR值达到17400%. 上述结果表明, 改变霍尔天平中的铁磁层和隔离层的厚度可以有效地调控阻态的个数和HRR比值, 这主要是由霍尔天平的耦合状态强烈依赖于材料结构所导致的.
图 7 (a)?(c)样品Pt(0.6)/[Co(0.4)/Pt(1)]₃/Co(0.4)/Pt(0.3)/NiO(t_NiO)/Pt(0.3)/[Co(0.4)/Pt(1)]₄ (厚度单位为纳米)的霍尔曲线; (d)?(f)样品Pt(0.6)/[Co(0.4)/Pt(1)]₃/Co(0.4)/Pt(0.3)/NiO(1.1)/Pt(0.3)/[Co(0.4)/Pt(t_Pt)]₄ (厚度单位均为纳米)样品的霍尔输出曲线^[48]
Figure7. (a)?(c) Hall loops for the sample Pt(0.6)/[Co(0.4)/Pt(1)]₃/Co(0.4)/Pt(0.3)/NiO(t_NiO)/Pt(0.3)/[Co(0.4)/Pt(1)]₄ (in nm); (d)?(f) Hall loops for the sample Pt(0.6)/[Co(0.4)/Pt(1)]₃/Co(0.4)/Pt(0.3)/NiO(1.1)/Pt(0.3)/[Co(0.4)/Pt(t_Pt)]₄ (in nm)^[48].

利用金属/氧化物界面工程设计可以提高载流子的自旋相关散射进而提高R_p值, 为进一步优化霍尔天平的HRR比值提供了一条有效的途径. 以上述样品结构为基础, 在霍尔天平核心结构的两侧引入CoO/[Co/Pt]_n和[Co/Pt]_n/CoO界面, 研究其相关物性. 这里需要特别说明的是: 考虑到CoO层的引入会提高CoO和[Co/Pt]_n之间的界面耦合作用, 从而会影响到霍尔天平的磁性层间耦合状态. 因此, 在引入CoO的同时还需要对[Co/Pt]_n多层膜的厚度进行细微调制. 图8(a)—图8(d)是结构为CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(t_NiO)/[Co(0.4)/Pt(0.6)]₄/CoO(3)(厚度单位为纳米)霍尔天平的霍尔输出回线^[48]. 从图中可以看出, 随着NiO层厚度的增加, 霍尔天平的耦合状态和阻态个数也发生了明显的变化. 这就导致了该霍尔天平结构中HRR值随着NiO厚度变化呈现非线性变化. 例如, 当t_NiO = 1 nm时, 霍尔天平的R_p和R_ap分别为2590和3.7 mΩ, 其对应的HRR比值达到69900%, 这是目前报道的室温下最高的霍尔电阻比值, 和没有CoO包覆的霍尔天平(图7(f))结构相比较, HRR比值提高了302%.
图 8 (a)?(d)样品CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(t_NiO)/[Co(0.4)/Pt(0.6)]₄/CoO(3)(厚度单位为纳米)的霍尔回线^[48]
Figure8. (a)?(d) Hall loops for the sample CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(t_NiO)/[Co(0.4)/Pt(0.6)]₄/CoO(3) (in nm)^[48].

为了阐明CoO层调控霍尔天平HRR比值的内在原因, 研究者们选取了HRR比值为69900%的样品进行微结构表征. 图9给出了该样品的低倍明场像透射电镜照片和选区电子衍射照片^[48], 其中图9(a)中的低倍明场像透射电镜照片表明了该霍尔天平结构的磁性多层膜具有良好的连续平整的层状结构. 选区电子衍射照片中的衍射环(如图9(b)所示)表明, [Co/Pt]_n多层膜为多晶结构. 同时, 图9(b)也显示了NiO和CoO的(111)取向的电子衍射环. 进一步对该样品进行高分辨透射电镜表征, 如图10所示^[48]. 通过高分辨透射电镜照片可以看出, 霍尔天平材料整体呈现晶化状态, 其中面间距0.242, 0.22和0.245 nm分别对应于CoO(111), CoPt(111)和NiO(111)晶面, 说明了霍尔天平具有{111}CoO// {111}CoPt//{111}NiO//{111}CoPt//{111}CoO局部的外延生长关系. 正是由于这种较好的晶体结构和局部外延关系的存在, 使得金属/氧化物界面上的电子自旋相关散射得到增强, 因此通过界面调控在霍尔天平中实现了超高的HRR比值.
图 9 (a)样品CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]₄/CoO(3)(厚度单位均为纳米)低倍透射电镜照片; (b)上述样品的选区电子衍射花样照片^[48]
Figure9. (a) Transmission electron microscope (TEM) image and (b) electron diffraction pattern for the sample CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]₄/CoO(3) (in nm)^[48].

图 10 样品CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]₄/CoO(3)(厚度单位均为纳米)高分辨透射电镜照片^[48]
Figure10. High resolution TEM image for the sample CoO(3)/[Pt(0.6)/Co(0.4)]₄/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]₄/CoO(3) (in nm)^[48]

此外, 关于NiO与[Co/Pt]_n之间的界面氧迁移调控霍尔天平HRR比值的相关研究也相继展开. 为了分别研究[Co/Pt]_n/NiO界面和NiO/[Co/Pt]_n界面对霍尔天平HRR比值的调控作用, 研究者设计并利用超高真空多靶磁控溅射镀膜系统制备了两组磁性多层膜样品: S1: CoO/[Co/Pt]₃/Co/Pt(t_B)/NiO(1.1)/[Co/Pt]₄/CoO;S2: CoO/[Co/Pt]₄/NiO(1.1)/Pt(t_T)/[Co/Pt]₄/CoO(厚度单位为纳米). 图11是系列样品S1的霍尔输出回线^[49], 可以看出, 当t_B = 0时, 霍尔天平呈现标准的铁磁耦合状态, 即二组态, 此时没有HRR比值. 当t_B = 0.3 nm时, 霍尔天平结构呈现明显的反铁磁耦合状态, 即多组态, 此时霍尔天平的R_p和R_ap分别为2480和8 mΩ, 对应的HRR比值达到30900%. 继续增加t_B到0.6 nm时, 霍尔天平保持了反铁磁耦合状态, 但R_p和R_ap分别为2325和139 mΩ, 对应的HRR比值降低到1570%. 进一步增加t_B到0.9 nm时, 随着中间状态的消失, 霍尔天平的HRR比值也随之消失. 图12是系列样品S2的霍尔输出回线^[49], 可以看出, 随着t_T的增加, 霍尔天平的HRR比值呈现了非线性的变化规律. 具体而言, t_T = 0时, 霍尔天平的HRR比值达到1570% (R_p和R_ap分别为2325和139 mΩ); t_T = 0.3 nm时, 霍尔天平HRR比值提高至18700% (R_p和R_ap分别为2257和12 mΩ); t_T = 0.6 nm时, 霍尔天平HRR比值变化至5410% (R_p和R_ap分别为2094和38 mΩ); t_T = 0.9 nm时, 霍尔天平没有HRR比值. 从上述结果不难看出的是, 随着NiO两侧Pt厚度的变化, 霍尔天平的阻态个数和HRR比值得到显著的调控, 这主要是由中间状态和R_ap变化所导致, 也说明界面处的Pt层可以有效地调控霍尔天平的耦合状态和HRR比值.
图 11 (a)?(d)样品CoO/[Co/Pt]₃/Co/Pt(t_B)/NiO(1.1)/[Co/Pt]₄/CoO(厚度单位为纳米)的霍尔回线^[49]
Figure11. (a)?(d) Hall loops for sample CoO/[Co/Pt]₃/Co/Pt(t_B)/NiO(1.1)/[Co/Pt]₄/CoO (in nm)^[49]

图 12 (a)?(d)样品CoO/[Co/Pt]₄/NiO(1.1)/Pt(t_T)/[Co/Pt]₄/CoO(厚度单位为纳米)的霍尔回线^[49]
Figure12. (a)?(d) Hall loops for the sample CoO/[Co/Pt]₄/NiO(1.1)/Pt(t_T)/[Co/Pt]₄/CoO (in nm)^[49].

为了进一步探索界面调控氧迁移对霍尔天平HRR比值的调控机制, 可以利用X射线光电子能谱(X-ray photoelectron spectroscopy, XPS)来精确探测界面原子状态, 对上述两个系列样品S1和S2进行界面元素电子结构表征. 关于XPS表征技术原理及相关实验细节, 可以参考之前的相关文献[30,50]. 为更直观地表征界面元素状态、氧迁移行为等, 通常利用界面氧含量比率来标定. 界面氧含量比率(ε)是根据XPS能谱中元素各种价态的峰面积比值定义的, 计算公式为

$\varepsilon =\frac{{S}_{{\rm{o}}{\rm{x}}{\rm{i}}{\rm{d}}{\rm{e}}}}{{S}_{{\rm{m}}{\rm{e}}{\rm{t}}{\rm{a}}{\rm{l}}}}\text{,}$

其中S_oxide和S_metal分别代表元素氧化态和金属态XPS峰面积值. 图13(a)和图13(b)分别是霍尔天平中Co/NiO界面和NiO/Co界面的高分辨Co 2p_3/2 XPS谱图^[49]. 当Co/NiO界面没有Pt插层时, XPS能谱中峰位位于777.8, 779.1和781.3 eV, 分别对应于Co⁰, Co²⁺和Co³⁺价态, 该结果说明在Co/NiO界面处存在Co的氧化物或者说Co—O键的形成. 随着Pt插层厚度的不断增加, Co 2p_3/2的峰位并没有发生改变, 但是峰面积比率发生了显著的变化. 当Pt的厚度为0, 0.3, 0.6和0.9 nm时, ε值分别为1.7∶1, 2.2∶1, 2.9∶1和1.5∶1, 如图13(c)所示^[49]. 与此同时, 界面Pt插层的Pt 4f_7/2 XPS峰位随着Pt层厚度的增加向着低结合能方向移动并始终高于块材Pt中的Pt 4f_7/2 XPS峰位(70.8 eV), 如图13(d)所示^[49]. 类似的情况也发生在NiO/Co界面上, 如图13(b)所示^[49]. 对于NiO/Co界面而言, 无论是否有Pt插层的引入, Co 2p_3/2 XPS峰始终位于777.8, 779.1和781.3 eV. 当Pt的厚度为0, 0.3, 0.6和0.9 nm时, ε值分别为3.3∶1, 2.3∶1, 2.9∶1和0.81∶1, 如图13(c)所示^[49]. 与之相对应的Pt 4f_7/2峰也随着Pt厚度的增加而进一步向着低结合能移动, 如图13(d)所示^[49]. 根据上述结果可知, 界面超薄的Pt插层可以有效地改变界面处的氧迁移状态. 这是因为Pt插层的厚度都在亚纳米量级, 与纳米颗粒的性质相类似, 其表面具有较多的活性位点, 有利于界面处的电子轨道杂化和原子成键. 例如, 在Co/NiO界面上引入厚度为0.3 nm的Pt层时, 非连续的Pt具有十分高的活性能, 将促进Pt—O—Co键的增加; 进一步增加Pt层厚度至0.6 nm时, 会导致Pt—O—Co键的进一步增加; 当Pt层厚度达到0.9 nm时, Pt层已经逐渐形成连续的层状结构, 这时Pt将会阻隔Co和O之间键合的形成, 从而导致Pt—O—Co键的显著降低. 界面上Pt—O—Co键的多少反映了界面氧迁移的情况. 需要特别说明的是, Co/NiO界面和NiO/Co界面的调控作用还是有一些不同的, 这主要是铁磁层和氧化物层的生长顺序不同所导致的. 从霍尔天平HRR值的调控结果来看, 只有当Pt层为0.3 nm时, 其HRR比值为极大值. 此时, 其界面处的氧含量比率约为2.3∶1, 这就说明了只有适度氧迁移下界面Pt—O—Co键形成时才有利于超高HRR比值的获取. 过度氧化或者欠氧化的状态(氧含量比率过高或者过低)都会导致霍尔天平中的HRR比值显著降低.
图 13 (a), (b)Co/NiO界面和NiO/Co界面上高分辨Co 2p XPS图谱; (c)界面CoO_x/Co比率随Pt厚度变化规律; (d)界面Pt 4f结合能随界面Pt厚度变化规律^[49]
Figure13. (a), (b) High resolution XPS Co 2p spectra at Co/NiO interface and NiO/Co interface; (c) interfacial CoO_x/Co content and (d) Pt 4f binding energy as a function of the Pt thickness at interfaces^[49].

过去一段时间, 科学家们利用磁性多层膜中的均一化磁化状态作为信息存储的基础进行新材料、新结构和新原理型器件的设计开发. 近些年来, 非共线的自旋结构(局域磁化状态)由于具有拓扑保护等诸多物理特性而逐步得到了人们广泛的关注. 磁性斯格明子是一种具有拓扑保护特性非共线手性自旋结构, 由材料体系中多种能量相互竞争所导致, 具有丰富的物理内涵^[51]. 特别是, 磁性斯格明子的尺寸通常为纳米尺度, 且具有较低的临界翻转驱动电流密度(约 10² A/cm²)远低于当前磁性隧道结的临界翻转电流密度^[19], 这一系列的物理特性使其在磁性随机存储器件设计中展现了巨大的潜在应用前景. 因此, 磁性材料中磁性斯格明子的多场调控及相关原理型器件研究是近年来自旋电子学领域的研究热点之一.
近期的研究结果显示最近邻交换作用、Dzyaloshinskii-Moriya interaction(DMI)作用、磁偶极能和磁各向异性对磁性斯格明子的形成具有重要影响^[52]. 其中, 磁性材料中由空间对称性破缺引入的手性相互作用(例如DMI作用)促使自旋倾向于非平行排列, 是形成非共线自旋结构的重要起因之一. 通常情况下, 磁性斯格明子分为两大类: 布洛赫型磁性斯格明子和奈尔型磁性斯格明子. 关于磁性斯格明子的研究也逐渐从二元合金、复杂氧化物单晶扩展到多元合金、磁性纳米复合结构、磁性多层膜体系等, 从低于室温向室温发展. 多元、复合纳米结构使得磁性斯格明子中不同的物理机理相互竞争, 其形成和动力学过程也受到了纳米薄膜材料本身结构、组分、界面等一系列因素的影响^[53-59], 而针对上述内容, 科学家们相继开展了一系列的研究工作^[60-63]. 目前, 观察磁性斯格明子的技术手段主要包括洛伦兹透射电镜(Lorentz TEM, L-TEM)、自旋极化扫描隧道显微镜(SP-STM)、磁力显微镜(MFM)、磁光克尔显微镜(MOKE)和光发射电子显微镜(PEEM)等. 其中, L-TEM技术的发展为磁性斯格明子的实空间表征提供了快速和有效的实验平台. 例如, Yu等^[64]利用L-TEM首次在Fe_0.5Co_0.5Si单晶体系中观察到二维磁性斯格明子拓扑自旋结构, 为磁性斯格明子的实空间观察提供了一条有效途径. 随后, 磁性斯格明子相继在FeGe^[65], Cu₂OSeO₃^[66]等多个体系中被观察到. 对于磁性斯格明子新物态的调控也逐步得到人们的重视^[67-69]. 与此同时, 国内外的专家****们将目光转向磁性薄膜中的斯格明子探索, 并在理论和实验上取得了许多可喜的研究成果^[70-74]. 大量的研究使得人们对于铁磁材料中的磁性斯格明子观察和调控有了一定程度的认识, 但是利用磁性斯格明子薄膜材料设计新型的磁信息存储器件的研究仍有大量工作需要开展. 关于磁性斯格明子的研究进展可以参考相关综述文章^[75-80].
随着磁性斯格明子相关研究的逐步开展, 人们在理论和实验上均发现铁磁多层膜中的斯格明子在外部激励(电流或者电压)下沿着电流方向运动的同时, 还会向横向漂移并在侧向发生积累和湮灭. 这一物理现象和大家熟知的霍尔效应相类似, 因此被命名为斯格明子霍尔效应(Skyrmion Hall effect, SkHE)^[81]. 由于SkHE的存在, 磁性斯格明子作为存储单元的赛道存储器件无法有效地进行信息存储和传递, 这使得肩负着未来希望的基于斯格明子赛道存储器件的进一步实用化蒙上了一层阴影.
为了突破当前铁磁薄膜中磁性斯格明子所面临的困境, 人们也在不断寻找能够降低或者完全消除SkHE的新材料. 随着研究的不断深入, 具有两套自旋晶格的亚铁磁和反铁磁材料逐步得到了人们的关注. 2017年, Zhang等^[82]利用微磁学模拟研究了人工反铁磁体中斯格明子的动力学过程, 模拟结果显示上下两铁磁层中出现一对磁性斯格明子, 且它们受到大小相等、方向相反的马格努斯力, 可以实现电流驱动下的直线运动. 2018年, Akosa等^[83]从理论上提出了反铁磁体中的斯格明子在电流驱动下可以完全消除SkHE, 这主要是由于反铁磁体中两套完全相反的自旋晶格受到的马格努斯力完全抵消所导致的. 随后不久, 一些相关的理论工作也相继被报道^[84,85], 这些研究成果为科学家们在实验上寻找新的斯格明子材料指明了一条极具希望之路. 但是, 相关实验工作并不顺利, 探索道路十分坎坷.
众所周知, 反铁磁体中的两套自旋结构在严格意义上是成反平行排列的, 宏观净磁矩为零, 这就导致反铁磁体的自旋结构观察和探测极具挑战性, 这也是当前自旋电子学领域的一大难题. 而亚铁磁体中两套自旋晶格部分补偿抵消, 宏观上具有较弱的净磁矩, 这就为自旋状态和磁畴结构的观察提供了可能. 随后, 一系列的理论和实验研究成果显示SkHE在亚铁磁多层膜材料中可以被有效地抑制, 同时斯格明子的动力学过程也可以得到调制^[86,87]. 但是, 如何在反铁磁体中实现斯格明子的观察和多场调控仍然是人们普遍关注的热点问题之一.
鉴于目前磁性斯格明子研究所遇到的挑战, 我国科学家利用洛伦兹透射电镜技术在具有反铁磁耦合的霍尔天平结构中首次发现了高密度的磁性斯格明子并实现了对磁性斯格明子的多场调控. 图14(a)给出了霍尔天平的结构示意图^[88]. 这里选择的霍尔天平与前文所述的在结构上稍微有所不同, 主要是Pt底层为后续调控霍尔天平的磁畴状态提供了自旋流. 图14(b)给出了两种典型的具有铁磁耦合(t_NiO = 1 nm)和反铁磁耦合(t_NiO = 1.3 nm)霍尔天平结构的磁滞回线^[88]. 从磁滞回线可以看出, 霍尔天平结构中的反铁磁耦合状态下剩余磁矩接近于0, 主要是因为霍尔天平中两个铁磁层的磁矩反平行排列且大小几乎相等. 图14(c)给出了霍尔天平结构中交换耦合场随隔离层NiO厚度的变化规律曲线. 随着NiO厚度的增加, 霍尔天平的耦合状态在铁磁耦合和反铁磁耦合间呈现振荡变化规律. 但是, 霍尔天平的饱和磁化强度并不随着NiO厚度的改变而变化, 如图14(d)所示.
图 14 (a)霍尔天平的结构示意图; (b)具有铁磁耦合和反铁磁耦合霍尔天平的垂直膜面方向的磁滞回线; (c)霍尔天平的交换耦合场和(d)饱和磁化强度随NiO厚度变化规律^[88]
Figure14. (a) Schematic of Hall balance in L-TEM measurement; (b) normalized M-H loops for the sample with ferromagnetic coupling and antiferromagnetic coupling, respectively; (c) shifted field and (d) saturation magnetization as a function of NiO thickness^[88].

图15(a)和图15(b)分别是铁磁耦合和反铁磁耦合状态下霍尔天平结构在基态时的洛伦兹透射电镜照片^[88]. 这里的基态是指对霍尔天平材料施加垂直于膜面磁场至正向饱和后再撤掉磁场的状态. 洛伦兹透射电镜照片表明: 基态下霍尔天平结构无论是在铁磁耦合或反铁磁耦合状态下, 视野中基本上看不到明显的磁畴结构. 在此基础上, 对霍尔天平施加外部激励(垂直磁场和面内脉冲电流), 然后撤掉外部激励, 再利用洛伦兹透射电镜对霍尔天平进行观察, 如图15(c)和图15(d)所示^[88]. 可以看出, 具有铁磁耦合和反铁磁耦合的霍尔天平结构中均发现了高密度的磁性斯格明子, 其密度约为7.5 μm^–2.
图 15 (a), (b)铁磁耦合和反铁磁耦合霍尔天平基态下的洛伦兹透射电镜照片; (c), (d)铁磁耦合和反铁磁耦合霍尔天平激励后的洛伦兹透射电镜照片^[88]
Figure15. L-TEM images for Hall balance at ground state with (a) ferromagnetic coupling and (b) antiferromagnetic coupling, respectively. High density of skyrmions in a Hall balance after drawing excitation with (c) ferromagnetic coupling and (d) antiferromagnetic coupling, respectively^[88].

随后, 研究者们利用洛伦兹透射电镜的样品与电子束角度可调功能进一步研究霍尔天平中磁性斯格明子的性质. 图16(a)—图16(c)分别是不同角度下的霍尔天平中的斯格明子磁结构^[88]. 当角度为0°时, 无法观察到磁性斯格明子; 当角度为 ±15°时, 霍尔天平中的磁性斯格明子的黑白衬度发生翻转, 这一研究结果也说明了霍尔天平中的磁性斯格明子为奈尔型斯格明子. 研究人员选取其中一个斯格明子在角度为 ± 15°下的图像, 进行了斯格明子尺寸的标定, 显示霍尔天平中的磁性斯格明子大小为180 nm左右. 综上所述, 室温下霍尔天平结构可以形成零场下的高密度奈尔型磁性斯格明子, 这为后续基于霍尔天平磁性斯格明子的存储器件提供了材料基础.
图 16 (a), (b)和(c)分别是不同角度下的霍尔天平中的磁性斯格明子^[88]
Figure16. (a), (b), (c) Magnetic skyrmions in a Hall balance with various tilting angle^[88].

为了进一步阐明霍尔天平中磁性斯格明子形成和调控机制, 对霍尔天平磁结构进行精确表征就显得尤为重要. 幸运的是中国散裂中子源(CSNS)在近期投入运行, 它是国家“十一五”期间重点建设的国家大科学装置, 是发展中国家拥有的第一台散裂中子源, 是国际前沿的高科技多学科应用的大型研究平台, 与正在运行的美国、日本和英国散裂中子源一起构成世界四大散裂中子源. 该实验平台为我国在物理学、化学、生命科学、材料科学、纳米科学、医药、国防科研和新型核能开发等学科前沿领域的研究提供了一个先进、功能强大的科研平台. 特别指出的是, 中子散射技术在确定磁性材料的原子结构和磁结构方面具有得天独厚的优势, 可以为材料结构优化和物理机理研究提供强有力的微结构表征技术支持.
针对磁性多层膜样品而言, 国内科学家们相互合作, 利用极化中子反射技术(polarized neutron reflectometry, PNR)对面内磁矩的高敏感特性, 从而定量分析磁性多层膜中的磁矩分布情况. 当具有不同极化方向的中子束流入射到磁性多层膜样品表面时, 通过收集测量不同极化方向的反射中子束流强度随动量转移矢量Q的变化关系, 可获得磁性多层膜中磁性深度分布信息. 通常情况下, PNR技术具有无损穿透的特性的同时, 还可实现超高的空间分辨率和极低的磁性探测. 因此, PNR技术在磁性多层膜中磁结构深度分布的精准测量具有独特的技术优势, 为研究非共线磁结构等复杂自旋结构提供了有效途径. PNR技术的应用已在解决自旋电子学领域热点问题中发挥了重要作用. 关于中子散射技术在磁性材料中的应用可以参考朱涛研究员撰写的综述及相关文章, 这里不再赘述^[89-91].
图17(a)和图17(b)分别是低场下和高场下具有反铁磁耦合霍尔天平的极化中子反射谱图^[88]. 当施加外磁场(9000 Oe, 如图17(b)所示)远大于霍尔天平饱和场时, 薄膜样品的磁矩均在面内方向, 不同极化方向的中子反射曲线呈现明显的差别; 当施加外磁场接近零(20 Oe, 如图17(a)所示)时, 薄膜样品的磁矩基本为剩余磁化状态, 不同极化方向的中子反射曲线基本重合. 通过对自旋不对称(spin asymmetry, SA)曲线的拟合, 研究者们发现低场下具有反铁磁耦合的霍尔天平呈现了一个非常小的面内磁矩分量. 根据拟合结果可知, 具有反铁磁耦合的霍尔天平具有倾斜的界面磁结构, 靠近NiO隔离层的Co层呈现7°的倾斜角, 如图17(c)所示^[88]. 根据相同的方法, 研究者们发现具有铁磁耦合的霍尔天平也具有4°的倾斜角, 中子结果和磁结构解析如图17(d)—图17(f)所示. 界面倾斜磁矩的实验验证有助于人们更加深入地理解霍尔天平结构中斯格明子的形成机制, 同时为多场调控霍尔天平中的磁性斯格明子提供了一条思路.
图 17 (a)和(b)分别是低场下和高场下具有反铁磁耦合霍尔天平的极化中子反射谱图; (c)具有反铁磁耦合的霍尔天平自旋结构示意图; (d)和(e)分别是低场下和高场下具有铁磁耦合霍尔天平的极化中子反射谱图; (f)具有铁磁耦合的霍尔天平自旋结构示意图^[88]
Figure17. PNR spectra as a function of Q measured with in-plane (a) low and (b) high magnetic fields for the Hall balance with antiferromagnetic coupling; (c) schematic of the magnetic structure of the Hall balance with antiferromagnetic coupling; PNR spectra as a function of Q measured with in-plane (d) low and (e) high magnetic fields for the Hall balance with ferromagnetic coupling; (f) schematic of the magnetic structure of the Hall balance with ferromagnetic coupling^[88].

微磁学模拟有助于加深对霍尔天平中磁性斯格明子形成与调控机制的理解, 相关的研究工作围绕霍尔天平中的耦合强度(E_IEC)和易磁化轴方向(θ)与磁性斯格明子之间的内在关系展开. 首先, 研究者设定易磁化轴为90°, 同时改变耦合强度. 图18(a)是基态下具有不同反铁磁耦合强度的霍尔天平中的磁性斯格明子^[88]. 因为霍尔天平中的磁性斯格明子是成对出现的, 这里只给出了下层[Co/Pt]_n多层膜中的磁结构信息. 当E_IEC < –1.4 mJ/m²时, 霍尔天平结构无法形成稳定的磁性斯格明子; 当E_IEC = –1.5 mJ/m²时, 霍尔天平中的磁性斯格明子密度达到100 μm^–2; 继续增加E_IEC至–2.4 mJ/m²时, 磁性斯格明子的密度显著降低. 图18(b)给出了霍尔天平中磁性斯格明子密度随E_IEC和θ变化的相图^[88]. 从相图可知, 只有当反铁磁耦合强度达到一定值时, 霍尔天平中才会形成稳定的磁性斯格明子. 同时, 对不同的易磁化轴角度θ而言, 形成磁性斯格明子的耦合强度阈值呈现明显的变化. 当反铁磁耦合强度在–1.5 mJ/m²附近时, 磁性斯格明子密度达到极大值. 即使在反铁磁耦合强度较大的情况下, 霍尔天平中的磁性斯格明子的密度仍然可以保持较高的水平(25 μm^–2). 图18(c)和图18(d)是在霍尔天平基态的基础上施加外部激励并撤除后不同耦合强度下的霍尔天平中磁结构信息^[88]. 不难看出的是, 外部激励施加过后霍尔天平中的斯格明子的个数明显增加. 即使在耦合强度很低的情况下, 霍尔天平中仍然存在着数目相当的磁性斯格明子. 这也说明了外部激励促使出现磁性斯格明子对应的耦合强度能量范围变宽了. 外部激励的施加对霍尔天平中磁畴结构产生了显著的影响, 并且脉冲电流在Pt底层中产生了自旋流注入到霍尔天平核心结构中, 上下两层[Co/Pt]_n多层膜受到自旋流影响并不相同, 从而导致了上下铁磁层中不同的磁畴结构. 上述微磁学模拟结合实验结果可以让人们更好地理解霍尔天平中的拓扑磁性及调控机制, 为后续的原理型器件的设计打下坚实的基础.
图 18 (a)具有不同层间耦合强度的霍尔天平中的基态和激励后的磁性斯格明子; (b)基态下霍尔天平中磁性斯格明子密度随E_IEC和θ变化的相图; (c)外部激励撤除后霍尔天平中磁性斯格明子个数随层间耦合强度的变化规律曲线^[88]
Figure18. (a) Simulated skyrmions in a Hall balance with various E_IEC; (b) contour map of the skyrmion density as a function of E_IEC and θ without external excitation; (c) the skyrmion number as a function of E_IEC in Hall balance with drawing excitation^[88].

与此同时, 研究者们也开展了电流驱动霍尔天平中斯格明子运动的动力学研究. 鉴于该结构的霍尔天平中磁性斯格明子尺寸较小以及较强的钉扎作用, 利用电流驱动斯格明子的实验十分具有挑战性. 为了更好地理解霍尔天平中磁性斯格明子的动力学过程, 研究者利用微磁学模拟的方法对其进行了系统研究. 结果发现, 具有铁磁耦合的霍尔天平中磁性斯格明子在电流驱动作用下向前运动的同时发生显著偏转. 然而, 具有反铁磁耦合霍尔天平中的磁性斯格明子会在电流驱动作用下沿着直线向前运动, 展现了较强的器件实用性. 因此, 对于霍尔天平中磁性斯格明子动力学的相关实验仍然在进行中.

随着霍尔天平材料及相关器件设计的研究不断深入, 基于霍尔天平的高密度存储逻辑器件逐步受到了人们的普遍关注^[92-98]. 基于霍尔天平材料的概念, 人们也将这一理念推广到其他材料体系中, 并且获得了一系列可喜的研究进展.
荷兰代尔夫特理工大学Caviglia团队^[97]利用脉冲激光沉积技术制备了一种全氧化物的霍尔天平材料, 其核心结构为SrRuO₃/SrTiO₃/SrRuO₃(SRO/STO/SRO)三明治结构. 该团队利用原子级厚度控制可以实现霍尔天平中两个磁性层的霍尔输出信号的调控, 进而实现霍尔天平多组态的功能化. 与此同时, 研究还发现SRO/STO/SRO霍尔天平中的反常霍尔效应具有很强的温度依赖特性. 图19给出了不同温度下SRO/STO/SRO霍尔天平的反常霍尔输出曲线, 并对霍尔天平中双铁磁层的反常霍尔信号进行解析^[97]. 研究结果表明, 随着测试温度的不断提高, 霍尔天平的反常霍尔信号在特定温度区间发生符号翻转, 这主要是由STO层反常霍尔效应的内禀贡献与相转变温度息息相关所导致的. 对于具有不同厚度的STO层的磁相变温度并不相同. 因此, 利用对不同厚度的STO层的温度调控可以实现其反常霍尔效应的调控, 从而实现霍尔天平多组态功能.
图 19 (a)不同温度下SRO/STO/SRO霍尔天平的反常霍尔曲线; (b)霍尔信号符号翻转温度附近的输出曲线放大图; (c) SRO/STO/SRO霍尔天平双通道霍尔电阻贡献解析图^[97]
Figure19. (a) Hall loops for the SRO/STO/SRO Hall balance under various temperature; (b) enlarged Hall loops in the vicinity of the sign reversal temperature; (c) Hall resistance in SRO/STO/SRO Hall balance^[97].

近期, 德国科隆大学的Vrejoiu研究团队^[98]利用脉冲激光沉积技术制备了霍尔天平SrRuO₃/SrIrO₃/SrRuO₃(SRO/SIO/SRO)多层膜, 并利用磁电输运性质测试对该材料体系中拓扑霍尔效应和反常霍尔效应进行深入研究并探讨异常的霍尔回线形成机理, 澄清了拓扑霍尔效应与磁性斯格明子探测之间的内在关系. 虽然近期的多数工作都是利用磁性多层膜中的拓扑霍尔效应来表征并探测磁性斯格明子的形成^[99,100], 但该研究结果表明霍尔天平SRO/SIO/SRO中反常霍尔输出曲线是铁磁层反常霍尔电压符号的不同所导致的. 该材料体系中的反常霍尔效应与磁性层厚度、温度和界面化学势等诸多因素相关. 因此, 该研究结果表明不能只利用反常霍尔回线来探测并表征磁性斯格明子的存在.

鉴于丰富的物理内涵以及在信息磁存储器件设计中巨大的潜在应用前景, 霍尔天平自提出之后就受到了人们的广泛关注. 以霍尔天平结构为核心的磁存储原理型器件的提出, 突破了传统二组态信息存储模式, 实现了信息多组态磁存储的同时, 也可以完成多种布尔逻辑运算. 这种新型的存算一体化器件构架设计, 解决了当前基于GMR, TMR的传统二组态自旋电子学材料器件的技术瓶颈, 其超高霍尔电阻比值突破了当前磁电阻与半导体电阻开关比相差甚远的窘境. 霍尔天平提出之初, 人们普遍认为具有垂直磁各向异性的霍尔天平的磁矩应该垂直于薄膜平面. 国内****利用中国散裂中子源这一大科学装置优势平台获得了突破性进展, 首次证实了垂直霍尔天平材料中具有角度可控的倾斜磁矩, 这也为霍尔天平中拓扑磁性相关研究的开展提供了强有力的实验依据. 基于这一重要研究结果, 利用洛伦兹透射电镜技术结合多场调控手段在霍尔天平材料中成功观察到高密度室温奈尔型磁性斯格明子. 从实验和微磁学模拟两个角度深入研究发现, 霍尔天平的层间耦合作用和界面磁矩倾斜程度都极大地影响着磁性斯格明子的形成, 为下一步设计基于磁性斯格明子的霍尔天平原理型器件提供了有力的理论和实验依据. 此外, 还利用微磁学模拟的方法揭示了霍尔天平中磁性斯格明子的动力学过程, 研究结果显示, 具有反铁磁耦合的霍尔天平中磁性斯格明子在电流驱动过程中斯格明子霍尔效应可以被完全抑制, 磁性斯格明子可以在电流驱动下沿直线运动, 这对设计基于斯格明子的赛道存储器件有着重要的指导意义. 这些研究成果为推动新型自旋电子学材料的研究开辟了一条新的研究思路. 目前, 利用原位多场调控技术在霍尔天平材料中可以实现磁性斯格明子的产生、湮灭和密度调制等多种状态转换. 但是, 利用电流驱动霍尔天平中磁性斯格明子运动的实验工作却遇到了一些困难. 这主要是因为磁性多层膜中较大的钉扎作用导致了驱动电流密度居高不下, 同时霍尔天平材料中磁性斯格明子尺寸较小, 克服钉扎势垒进行运动所需要的能量较高. 因此, 霍尔天平材料中磁性斯格明子动力学的相关实验研究将是下一步关注的一个十分重要的问题. 针对这一问题, 后续的工作将重点通过优化磁性多层膜的生长质量降低缺陷等钉扎位点, 寻找合适的磁性层和功能层, 从材料、物理和器件设计多角度综合考虑, 力图深入研究多场调制下磁性斯格明子动力学过程.
与此同时, 霍尔天平的概念已经扩展到氧化物多层膜结构、二维范德华异质结等低维结构中. 但是, 如何实现基于霍尔天平结构的磁存储逻辑计算一体化器件的全电场调控, 如何设计基于霍尔天平结构的磁性斯格明子赛道存储器件, 如何深入理解霍尔天平中拓扑磁性调控的物理机理, 如何解决当前霍尔天平材料与半导体工艺器件的兼容等一系列科学问题的解决仍然面临挑战. 这些问题的澄清需要更加深入的理论分析与实验验证相结合. 随着国内外对霍尔天平材料及原理型器件关注度逐步升温, 结合先进的技术手段和大科学装置的投入使用, 基于霍尔天平的信息磁存储器件及多场调控物理机理的相关研究将会取得更多突破性研究成果.
感谢中国科学院物理研究所蔡建旺研究员、孙阳研究员、张颖研究员、于国强研究员在磁性材料表征方面予以的帮助与指导; 感谢中国科学院半导体所王开友研究员在自旋输运表征方面予以的帮助与指导; 感谢中国散裂中子源朱涛研究员在极化中子反射谱仪表征方面予以的帮助与指导; 感谢四川师范大学赵国平教授在微磁学模拟理论方面予以的帮助与指导.