摘要:混杂复合材料是一种新型复合材料, 其复杂的细观结构导致预测其等效热传导性能极富挑战性. 本文结合渐近均匀化方法、小波变换方法和机器学习方法发展了一种新的可以有效预测混杂复合材料等效热传导性能的小波-机器学习混合方法. 该方法主要包括离线多尺度建模和在线机器学习两部分. 首先借助渐近均匀化方法通过离线多尺度建模建立了混杂复合材料的热传导性能材料数据库, 然后利用小波变换方法对离线的材料数据库进行预处理, 接下来分别运用人工神经网络和支持向量回归方法建立混杂复合材料等效热传导性能预测的在线机器学习模型. 最后通过对周期和随机混杂复合材料进行数值实验, 验证了小波-机器学习混合方法的有效性, 数值实验结果表明小波-神经网络混合方法具有最优的预测效果和抗噪能力. 此外, 需要强调的是对于具有高维大规模数据特征的随机混杂复合材料, 小波-机器学习混合方法不仅可以提取离线材料数据库的重要特征, 还可以显著减少在线监督学习的输入数据规模并提高机器学习模型的训练效率及抗噪性能. 本文建立的小波-机器学习混合方法不仅适用于混杂复合材料等效热传导性能的预测, 还可进一步推广应用于复合材料等效物理、力学性能的预测.
关键词: 混杂复合材料/
等效热传导性能/
机器学习方法/
小波变换

English Abstract

全文HTML

--> --> -->

混杂复合材料是一种在同一基体或多个基体中增加两种或两种以上夹杂材料制成的新型复合材料^[1], 如碳纤维-玻璃纤维混杂复合材料、碳纤维-芳纶纤维混杂复合材料等, 若混杂得当可使得混杂复合材料具备优异的热学、力学性能. 近年来, 随着航天、航空工业的快速发展, 混杂复合材料由于具有良好的热稳定性和抗疲劳性被广泛应用于制造飞行器的机身、机翼、隔热结构等. 总之, 混杂复合材料的应用正处于蓬勃发展的阶段, 但是有关混杂复合材料基础性的理论研究还比较少, 为了给新型飞行器的隔热结构设计和性能优化提供坚实的基础理论和高性能算法, 研究混杂复合材料热传导性能的有效预测方法具有重要的应用价值和理论意义.
相比传统的复合材料, 混杂复合材料的组成成分和微观结构更加复杂, 预测其等效热传导性能需要发展更加高精度、高效率的方法. 为了预测复合材料的等效热传导性能, 数学家和工程师已经发展出了多种解析方法^[2-4]来研究其等效热传导性能, 但是这些解析方法仅仅能够预测具有简单微观结构的复合材料的热传导性能, 无法分析具有复杂微观结构的混杂复合材料. 此外, 研究人员还提出了预测复合材料等效热传导系数的数值方法^[5-9], 使得具有复杂微观结构的复合材料的等效热传导性能能够得到精确的预测和分析. 其中, 渐近均匀化方法具有严格的数学基础, 且能够很好地与有限元方法结合^[10], 在实际工程应用中得到了广泛的应用. 渐近均匀化方法通过建立周期单胞(unit cell, UC)或者代表体积元(representative volume element, RVE)来精细刻画复合材料的微观构造, 之后通过求解UC或RVE上的辅助单胞问题得到捕捉复合材料微观振荡信息的辅助单胞函数. 最后, 通过在UC或RVE上做积分得到复合材料的宏观等效材料参数和宏观均匀化问题, 渐近均匀化方法可以有效预测复合材料的宏观等效性能^[10]. 但是对于混杂复合材料, 不同的微观结构导致需要重新计算辅助单胞问题, 然后重新计算混杂复合材料的等效材料参数, 这导致了计算资源的极大耗费, 因此有必要发展一种高效率、可避免重复计算的混杂复合材料等效热传导性能预测方法.
近年来, 随着计算机科学技术的迅猛发展, 机器学习方法被广泛应用到各个工程领域. 在材料科学领域, Sundararaghavan和Nicholas^[11]采用支持向量机方法实现了三维复合材料的分类和重构. Liu等^[12]基于支持向量机方法预测了高对比三维复合材料弹性应变场的分布. Sun等^[13]利用支持向量机方法预测和理解块体非晶合金的玻璃形成能力. Kondo等^[14]借助卷积神经网络方法建立了陶瓷材料微观结构和离子导电率之间的映射关系. Cang等^[15]发展了形态感知生成模型并借助图像数据和卷积神经网络方法预测了复合材料的物理性质. Bessa等^[16]基于数据驱动建立了分析复合材料力学响应和设计复合材料微观结构的计算框架. Benyelloul和Aourag^[17]采用混合的遗传算法和人工神经网络方法预测了奥氏体不锈钢的体积模量. 基于图像建模和深度学习, Li等^[18]成功地预测了页岩复合材料的有效力学性质. Balokas等^[19]结合神经网络方法和多尺度分析预测了三维编织复合材料的弹性性能. Liu和Wu^[20]研究了数据驱动的多尺度力学中深度材料网络的三维结构. Rong等^[21]结合二维截面图像和卷积神经网络预测了三维复合材料的有效热传导系数. 但是, 对于预测混杂复合材料等效热传导性能的高精度、高效率的机器学习方法缺乏充分的研究.
本文主要研究了预测具有周期型或随机型微观结构的混杂复合材料等效热传导性能的机器学习方法. 混杂复合材料通常由两种以上的不同成分组成, 其热传导性能与各组成材料的性能及其微观结构密切相关, 要建立混杂复合材料宏观等效热传导性能与各组成材料的性能以及微观结构之间的显式关系或公式十分复杂. 本文通过结合渐近均匀化方法、小波变换方法和机器学习方法各自的优势, 建立了一种新的有效预测混杂复合材料等效热传导性能的机器学习框架. 本研究的主要创新点有三方面: 第一, 借助于渐近均匀化方法建立了混杂复合材料的材料数据库, 该材料数据库可以准确提取混杂复合材料各组分的材料参数和微观结构信息, 并包含准确计算的混杂复合材料等效热传导系数. 第二, 基于人工神经网络(artificial neural network, ANN)方法和支持向量回归(support vector regression, SVR)方法对建立的混杂复合材料的材料数据库进行了数据挖掘和监督学习, 建立了能够有效预测混杂复合材料等效热传导系数的机器学习模型. 第三, 借助小波变换方法解决了具有复杂微观结构的随机混杂复合材料的材料数据库在线机器学习的困难. 基于小波变换方法的预处理策略不仅可以大大减少机器学习模型的输入数据规模, 保证机器学习模型的成功训练, 而且可以提取原始材料数据库中的主要特征并自动过滤原始数据中的噪声. 最后, 本文成功建立了可以有效预测混杂复合材料等效热传导性能的小波-机器学习混合方法, 所建立的机器学习框架具有极强的扩展性, 可以应用于混杂复合材料其他物理、力学性能的预测和分析.

本节首先给出三种代表性混杂复合材料的微观结构的计算机建模. 随后基于建立的混杂复合材料微观几何结构, 利用渐近均匀化方法建立其热传导问题的多尺度模型, 得到混杂复合材料等效热传导系数的计算公式. 最后选取混杂复合材料的特征数据, 并将计算得到的等效热传导系数值作为用于机器学习的数据标签, 建立混杂复合材料的材料数据库, 完成混杂复合材料的离线多尺度建模.
2

-->

2.1.混杂复合材料计算机模型及其热传导问题的渐近均匀化方法

本文主要研究三种混杂复合材料, 包括两种周期型混杂复合材料和一种随机型混杂复合材料, 三种混杂复合材料的微观结构计算机模型如图1所示.
图 1 混杂复合材料计算机模型　(a) 周期混杂复合材料I; (b) 周期混杂复合材料II; (c) 随机混杂复合材料
Figure1. Computer geometric models: (a) Periodic hybrid composite material I; (b) periodic hybrid composite material II; (c) random hybrid composite material.

对于这三种混杂复合材料, 其计算机几何模型具体生成算法如下:
1) 对于周期型混杂复合材料I和II, 如图1(a)和图1(b)所示, 首先生成混杂复合材料的内部夹杂边界和整个材料的外部边界, 然后建立该混杂复合材料的有限元网格.
2) 对于随机型混杂复合材料, 如图1(c)所示, 采用文献[22, 23]中的概率分布模型和网格生成算法来创建其微观结构.
需要说明的是, 本文研究的所有混杂复合材料的微观结构均基于Freefem++软件二次开发生成. 基于上述算法, 我们成功地建立了周期型和随机型混杂复合材料的计算机几何模型和有限元计算网格.
基于建立的混杂复合材料微观结构计算机几何模型, 建立混杂复合材料热传导问题的渐近均匀化方法, 得到混杂复合材料等效热传导系数的计算公式. 首先考虑如下的混杂复合材料的热传导问题:

$ \left\{ \begin{aligned} &-\frac{\partial }{\partial {x_i}}\left( {k_{ij}^{{{\varepsilon}}}({{{x}}})\frac{\partial T^{{{\varepsilon}}}({{x}})}{\partial {x_j}}} \right) = h({{x}}),\;\;\text{in}\;\;{\varOmega},\\ &T^{{{\varepsilon}}}({{x}}) = \widehat T({{x}}),\;\;\;\text{on}\;\;\partial {\varOmega_T},\\ &{k_{ij}^{{{\varepsilon}}}({{{x}}})\frac{\partial T^{{{\varepsilon}}}({{x}})}{\partial {x_j}}}{n_i} = \bar q({{x}}),\;\;\;\text{on}\;\;\partial {\varOmega_q}, \end{aligned} \right. $

其中$ \varOmega $是一个$ {\mathbb{R}}^{\cal N}({\cal N} = 2, 3) $中的有界凸区域并具有边界$ \partial\varOmega = \partial\varOmega_{T}\cup\partial\varOmega_{q} $; 小参数$ {{\varepsilon}} $代表混杂复合材料的周期单胞(UC) 或代表体积元(RVE)的特征尺寸; $ T^{{{\varepsilon}}}({{x}}) $是待求解的温度场; $ k_{ij}^{{{\varepsilon}}}({{{x}}}) $代表二阶热传导系数张量; $ h({{x}}) $是混杂复合材料的内部热源; $ \widehat{T}({{{x}}}) $是边界$ \partial\varOmega_{T} $上的温度场; $ \bar{q}({{{x}}}) $是边界$ \partial\varOmega_{q} $上的热流场. 此外, 我们强调所有周期型和随机型混杂复合材料都用RVE来统一描述其微观结构.
根据渐近均匀化方法的理论^[10], 令${{y}} = {{{x}}}/{{{\varepsilon}}}$为代表体积元$ Q = (0, 1)^{\cal N} $的微观坐标, 于是可以得到如下的链式法则:

$ \frac{\partial}{\partial x_i}\rightarrow\frac{\partial}{\partial x_i}+\frac{1}{{{\varepsilon}}}\frac{\partial}{\partial y_i}. $

对于(1)式的多尺度热传导问题, 假设其精确解$T^{{{\varepsilon}}}({{x}})$具有如下的渐近展开形式:

$ T^{{{\varepsilon}}}({{x}}) = {T^{(0)}}({{x}}) + {{\varepsilon}} M_{{\alpha _1}}({{{y}}})\frac{\partial {T^{(0)}({{x}})}}{\partial {x_{{\alpha _1}}}}+ {\rm O}({{{\varepsilon}}^2}). $

接下来, 将(3)式代入(1)式, 并借助链式法则(2)式, 可以得到用于求解辅助单胞函数$ M_{\alpha _1}({{{y}}}) $的具有齐次狄利克雷边界条件的辅助单胞问题如下所示:

$ \begin{cases} \dfrac{\partial }{\partial y_i}\Big( k_{ij}({{{y}}})\dfrac{\partial {M_{\alpha _1}({{{y}}}})}{{\partial y_j}} \Big) = -\dfrac{\partial k_{i\alpha_1}({{{y}}})}{\partial y_i}, & {{{y}}} \in {Q},\\ M_{{\alpha _1}}({{{y}}}) = 0, & {{{y}}} \in \partial {Q}. \end{cases} $

然后在代表体积元Q上做积分并利用高斯定理, 得到混杂复合材料的宏观均匀化热传导问题为

$ \left\{ \begin{aligned} &- \frac{\partial }{{\partial {x_i}}}\left( {\widehat k_{ij}\frac{{\partial {T^{(0)}}({{{x}}})}}{{\partial {x_j}}}} \right) = h({{x}}),\;\;\text{in}\;\;\varOmega,\\ &T^{(0)}({{x}}) = \widehat T({{x}}),\;\;\;\text{on}\;\;\partial {\varOmega_T},\\&{\widehat k_{ij}\frac{\partial T^{(0)}({{x}})}{\partial {x_j}}}{n_i} = \bar q({{x}}),\;\;\;\text{on}\;\;\partial {\varOmega_q}. \end{aligned} \right. $

这里宏观的均匀化热传导系数$ \widehat k_{ij} $的计算公式为

$ {\widehat k_{ij} = \frac{1}{{\left| {{Q}} \right|}}\int_{{Q}} {\left( {{k_{ij}}({{{{ y}}}}) + {k_{i{\alpha _1}}}({{{{ y}}}})\frac{{\partial {M_j}({{{{ y}}}})}}{{\partial y_{{\alpha _1}}}}} \right){\rm d}{Q}}}. $

(6)式被应用于预测研究的三种混杂复合材料的等效热传导性能.
2 -->

2.2.混杂复合材料的材料数据库

针对所研究的三种混杂复合材料, 首先建立其计算机几何模型和有限元计算网格. 然后采用渐近均匀化方法计算其等效均匀化材料参数. 通过离线多尺度建模, 可以得到混杂复合材料包含数据特征和数据标签的材料数据库. 该材料数据库的数据特征包括混杂复合材料组成成分的材料参数和微观结构几何参数, 该数据库中的数据标签为混杂复合材料的等效热传导系数, 数据库的建立对在线机器学习建立预测混杂复合材料等效热传导性能的机器学习模型至关重要.
假设本文研究的混杂复合材料的夹杂材料和基体材料都是各向同性的. 对于图1(a)和图1(b)所示的周期型混杂复合材料I和II, 数据特征设置为夹杂材料的热传导系数$ kc_1 $和$ kc_2 $, 基体材料的热传导系数$ km $和夹杂物1的半径$ r_1 $与夹杂物2的半径$ r_2 $. 为便于建模分析, 采用归一化的思想, 将代表体积元Q的边长设置为1, 热传导系数$ kc_1 $, $ kc_2 $和$ km $均在(0, 1)中随机生成并服从均匀分布, 夹杂物半径$ r_1 $和$ r_2 $均在(0, 0.25)中随机生成并服从均匀分布. 对于图1(c)所示的随机型混杂复合材料, 数据特征的选择比周期型混杂复合材料更为复杂. 为了解决这一问题, 引入了等间距矩形网格作为背景网格来提取机器学习需要的数据特征. 需要强调的是, 用于提取材料特征的背景网格与渐近均匀化方法中的有限元计算网格不同. 然后定义随机型混杂复合材料的夹杂材料的热传导系数$ kc_1 $, $ kc_2 $和基体材料的热传导系数$ km $仍在(0, 1)中服从均匀分布随机生成. 随后, 选取背景网格上各个节点的热传导系数$ k_{x_1 x_2}^i $为随机型混杂复合材料的数据特征. 需要注意的是, 背景网格法也可以应用于周期型混杂复合材料. 但是周期型混杂复合材料的数据特征十分明显, 没有必要采用这种方法. 将所有混杂复合材料的数据标签统一设定为利用渐近均匀化方法计算得到的混杂复合材料等效热传导系数$ \widehat k $.
据此, 建立周期型和随机型混杂复合材料的材料数据库, 具体的材料数据库构成详见表1和表2.

样本编号	数据特征					数据标签
样本1	$kc_1$	$kc_2$	$km$	$r_1$	$r_2$	$\widehat k$
$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$
样本n	$kc_1$	$kc_2$	$km$	$r_1$	$r_2$	$\widehat k$

表1周期型混杂复合材料的材料数据库
Table1.Database for periodic hybrid composite material

样本编号	数据特征				数据标签
样本1	$k^1_{x_1 x_2}$	$k^2_{x_1 x_2}$	$\cdots$	$k^m_{x_1 x_2}$	$\widehat k$
$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$
样本n	$k^1_{x_1 x_2}$	$k^2_{x_1 x_2}$	$\cdots$	$k^m_{x_1 x_2}$	$\widehat k$

表2随机型混杂复合材料的材料数据库
Table2.Database for random hybrid composite material

本节首先介绍小波变换方法的理论基础及其在我们建立的小波-机器学习混合方法中的应用. 然后介绍我们建立的混杂复合材料等效热传导性能预测的小波-机器学习混合方法. 需要强调的是, 新引入的小波预处理策略对于保证机器学习模型的成功训练至关重要, 而且可以在很大程度上提高学习的效率, 此外小波预处理具有自动过滤噪声的功能.
2

-->

3.1.小波变换方法

训练过程是成功建立机器学习模型至关重要的部分, 但是如果训练集中输入数据规模较大会对机器学习模型的结构产生很大影响, 并导致训练效率降低和监督学习难度增加, 因此我们创新地采用小波变换方法对具有大规模数据特征的混杂复合材料的材料数据库进行数据预处理. 已有研究表明, 小波变换方法是信号和图像处理领域中数据压缩和特征提取的强有力工具^[24-27].
小波变换方法的一个主要优点是能够从输入数据中提取多尺度信息. 通过对输入数据递归使用, 小波变换会得到输入数据的多层小波分解^[25,28]. 接下来给出三层小波分解过程的示意图, 如图2所示, 原始数据经一次小波分解后得到近似系数$ CA_1 $和细节系数$ CD_1 $两部分; 然后将近似系数$ CA_1 $作为输入进行下一次小波分解, 得到近似系数$ CA_2 $和细节系数$ CD_2 $; 最后将$ CA_2 $作为输入进行下一次小波分解, 得到近似系数$ CA_3 $和细节系数$ CD_3 $. 三层小波分解得到的最终结果为$ [CA_3, CD_3, CD_2, CD_1] $. 针对原始数据特征进行多层小波分解的主要优点有两点: 1) 从小波分解得到的结果中选取合适的小波系数作为新的监督学习输入数据, 能显著减小用于机器学习模型训练的输入数据规模, 保证机器学习模型的成功训练并提高训练效率; 2) 通过小波分解可以过滤原始数据中的噪声, 提高训练得到的机器学习模型的准确率. 此外, 需要强调的是, 通常选取小波近似系数和最高层次的小波细节系数作为新的输入数据, 这样选择的根本原因是较低层的细节系数包括来自原始数据特征的噪声和小的数据波动.
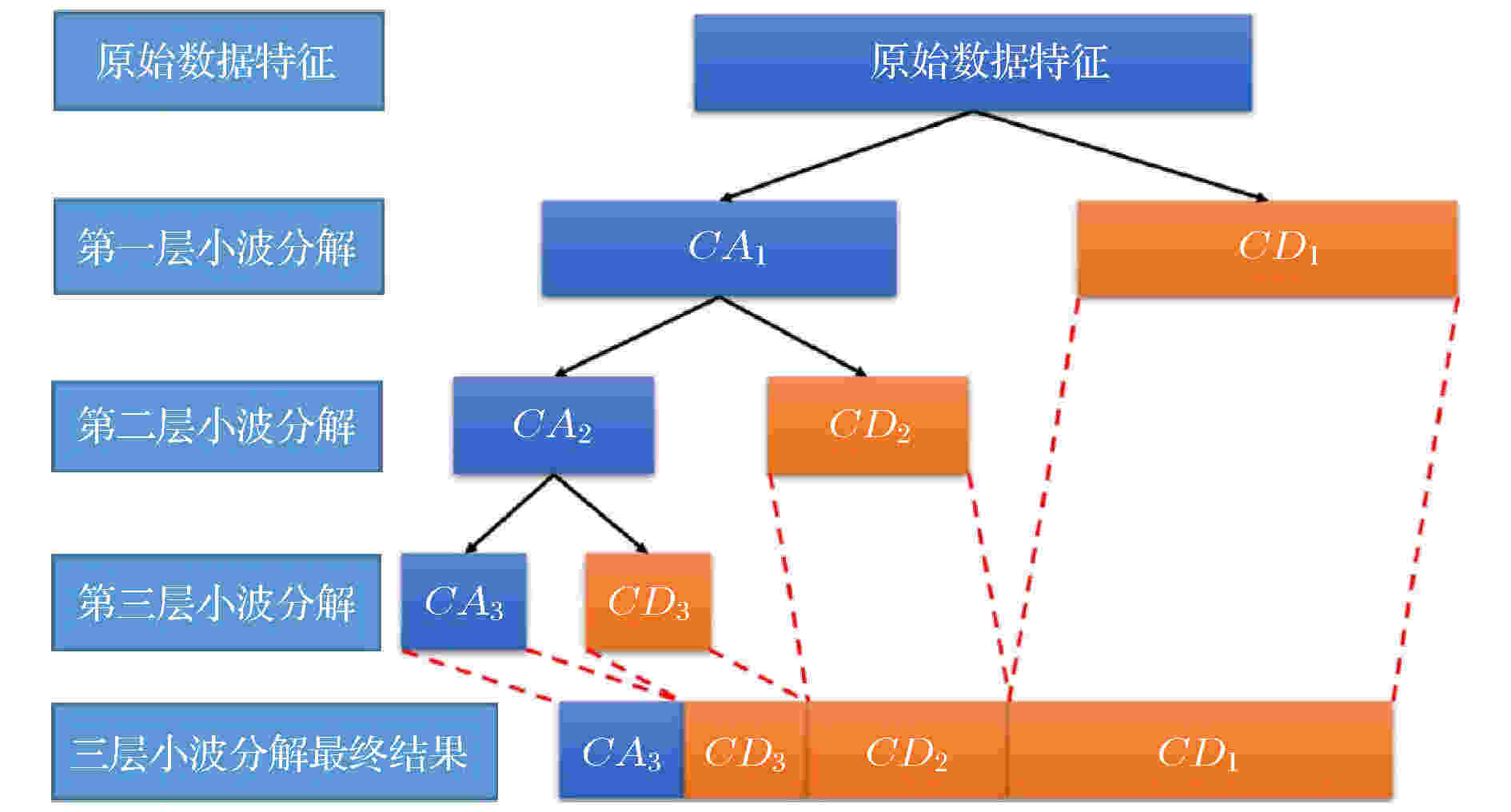图 2 三层小波分解示意图
Figure2. Schematic of three-level wavelet decomposition.

在随后的数值实验中, 针对随机型混杂复合材料, 采用99 × 99的背景网格提取样本各节点的材料参数$ k^i_{x_1 x_2} $作为原始数据集样本的特征. 在此背景网格下, 总共有10000个节点, 即10000个原始数据特征, 若直接采用如此大规模的数据特征作为机器学习模型输入数据, 要保证机器学习模型的成功训练相对困难, 因此采用上述小波变换方法对原始数据进行预处理, 以减小输入数据的特征规模. 选用小波函数“db1”, 对原始数据特征进行三层小波分解, 将得到的1250个小波系数$ CA_3 $作为新的输入数据特征, 建立随机型混杂复合材料新的材料数据库, 如表3所列.

样本编号	数据特征	数据标签
样本1	$CA_3$	$\widehat k$
$\cdots$	$\cdots$	$\cdots$
样本n	$CA_3$	$\widehat k$

表3随机型混杂复合材料新的材料数据库
Table3.New database for random hybrid composite material.

2 -->

3.2.小波-机器学习混合方法

在机器学习领域, ANN方法和支持向量机(support vector machine, SVM)方法是两种广泛应用的经典方法. 首先对ANN方法的基本原理做简单介绍. ANN是一种应用类似于大脑神经突触连接的结构进行信息处理的数学模型, ANN方法中最基本的组成单元是神经元^[29], 图3(a)给出了一个神经元模型. 多个神经元按一定的层级结构连接起来就得到了神经网络模型, 多层前馈神经网络模型是一种常用的ANN模型, 其基本构架如图3(b)所示. 通常, ANN的第一层为输入层, 最后一层为输出层, 中间可包含若干隐藏层, 每一层中的每一个圆圈代表一个神经元.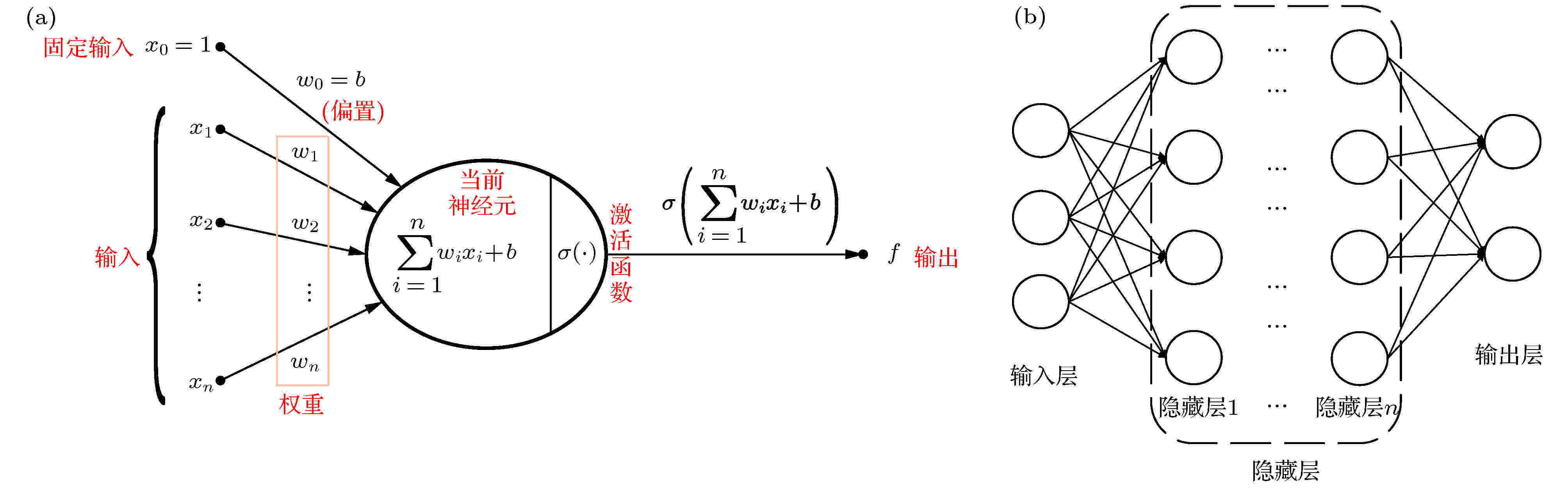
图 3 人工神经网络方法示意图　(a) 神经元模型; (b) 多层前馈神经网络模型
Figure3. Schematic of artificial neural network: (a) The neuron model; (b) the multilayer feedforward ANN model.

在神经元模型中, 来自其他n个神经元的输入信号$ x_i $分别和权重$ {w_i} $相乘后传递至当前神经元, 神经元接收到的总输入叠加求和后再加上一个偏置b, 然后用激活函数$ \sigma(\cdot) $对其进行作用产生当前神经元的输出f, 其中偏置b可等效为一个固定输入$ x_0 = 1 $和权重$ w_0 = b $相乘后传递至当前神经元. 从数学上讲, ANN方法的最终目标是学习得到一个最佳的映射函数$ \varphi\left(\cdot\right) $, 以便在给定输入$ {{x}} $时能够获得其对应标签$ {{y}} $的近似值^[29], 即:

$ \varphi \left(\cdot\right):{{{x}}}\to {{y}}, $

通常ANN采用链式结构, 映射$ \varphi\left(\cdot\right) $由函数f层层嵌套生成, 即:

$ \varphi \left({{{x}}}\right) = {f^n}\left( { \cdots {f^1}\left( {{f^0}\left({{{x}}}\right)} \right)} \right), $

式中, 函数${f^i}\left({{{x}}}\right) = \sigma \left( {{{{W}}^i}{{{x}}} + {{{b}}^i}} \right), i = 0,\;1,\; \cdots,\; n,$ 其中$ {{{W}}^i} $为权重矩阵, $ {{{b}}^i} $为偏置, $ \sigma \left(\cdot\right) $为激活函数. ANN方法的本质即通过不断学习, 更新权重和偏置参数求解如下极值问题, 使得$ \varphi\left(\cdot\right) $能够更好地模拟输入数据和输出数据之间的关系.

$ \mathop{\text{min}}\limits_{{{\theta}}}{\cal L}\big(\varphi \left({{{x}}}\right),{{y}}\big)+\sum\limits_{i = 1}^{n}\psi(\theta^i), $

其中$\theta^k \!=\! ({{{W}}}^k, {{{b}}}^k)$, ${{\theta}} \!=\! (\theta^0, \cdots, \theta^n)$, $ {\cal L} $为损失函数, $ \psi $为正则函数. ANN方法训练过程中常用的激活函数有ReLU函数: $\sigma \left( z \right) = {\rm {max}} \left( {0, z} \right)$和Sigmoid函数: $\sigma \left( z \right) = 1/\left( {1 + {{\rm e}^{ - z}}} \right)$, 常用的损失函数有均方误差(mse) 和绝对误差(mae) 等, 常用的优化算法有随机梯度下降算法(SGD)、自适应梯度算法(AdaGrad)和自适应矩估计算法(Adam)等.
SVR方法是基于SVM方法发展而来的一种回归方法, 在实际应用中, 许多问题都不是线性可分的, SVR通过使用核函数把不能够线性可分的原始样本空间映射到一个新的高维的样本空间, 使得新得到的高维样本空间可能是线性可分的, 一些数学家已经证明了对于一个有限维样本空间, 必然存在一个高维的特征空间使得样本可分^[30]. SVR方法的具体数学模型^[30]为给定训练集${ D} \!=\! \left\{ {({{{{x}}}_1}, {y_1}), ({{{{x}}}_2}, {y_2}),\; \cdots, ({{{{x}}}_m},\;{y_m})} \right\}$, 其中${{{x}}}_i \in {\mathop{\mathbb{R}^n}\nolimits}$和${y_i} \in {\mathop{\mathbb{R}}\nolimits}$, 定义相似性函数$ \phi(\cdot) $和核函数$ \kappa ({{{{x}}}_i}, {{{{x}}}_j}) $, $\kappa ({{{{x}}}_i}, {{{{x}}}_j}) = \left\langle {\phi ({{{m{x}}}_i}), \phi ({{{{x}}}_j})} \right\rangle = \phi {({{{{x}}}_i})^{\rm{T}}}\phi ({{{{x}}}_j})$, 其中$ \left\langle {\cdot, \cdot} \right\rangle $为高维特征空间中的内积. 然后得到$ \phi({{x}}) $为原始向量$ {{x}} $经过映射后得到的特征向量, SVR方法的数学模型就是确定一个函数$F({{{x}}}) = {{\bf{\theta}}^{\rm T}}{\phi({{x}})} + b$, 该函数满足如下极值问题:

$ \mathop {\min }\limits_{{\bf{\theta}},b} \frac{1}{2}{\left\| {\bf{\theta}} \right\|^2}{\rm{ + }}C\sum\limits_{i = 1}^m {{\ell _\varepsilon }} \left( {{{F(}}{{{{x}}}_i}{\rm{) - }}{{{y}}_i}} \right), $

其中$ {\bf{\theta}} $和b为模型参数, C为正则化参数, $ \ell _\varepsilon $为$ \varepsilon $-insensitive损失函数并满足如下的关系式:

$ {\ell _\varepsilon }(z) = \left\{ \begin{aligned} &0,\;\;\;\;\;\;\;\;\; \;\;\left| z \right| < \varepsilon,\\ &\left| z \right| - \varepsilon,\;\;{\text{其他}}. \end{aligned} \right. $

需要强调的是, SVR模型的数值精度取决于核函数选择的合适程度, 然而如何选择一个SVR模型最优的核函数仍是一个开放性的问题.
通过离线多尺度建模, 建立了周期型和随机型混杂复合材料的材料数据库. 接下来, 对随机型混杂复合材料的材料数据库应用小波变换方法得到新的材料数据库. 然后利用经典的ANN方法和SVR方法对周期型和随机型混杂复合材料的材料数据库进行在线机器学习, 具体的小波-机器学习混合方法预测混杂复合材料等效热传导性能的流程图如图4所示.
图 4 机器学习混合方法流程图
Figure4. Flowchart of hybrid wavelet-based learning method.

本节通过数值实验来验证提出的小波-机器学习混合方法的有效性和可行性. 通过数值实验, 成功训练了三种混杂复合材料等效热传导系数预测的ANN模型和SVR模型. 三种混杂复合材料的材料数据库均由1000组样本数据构成, 在每种材料的数据库中随机选取800组样本数据作为训练集, 剩下的200组作为测试集用来评估训练得到的机器学习模型.
首先给出三种混杂复合材料的1000个随机样本等效热传导系数分布图, 如图5所示. 图5(a)为周期混杂复合材料I的1000个随机样本无量纲等效热传导系数分布图, 其中最小和最大等效热传导系数分别为0.001114和0.989869. 图5(b)为周期混杂复合材料II的1000个随机样本无量纲等效热传导系数分布图, 其中最小和最大等效热传导系数分别为0.001331和0.989154. 图5(c)为随机混杂复合材料的1000个随机样本无量纲等效热传导系数分布图, 其中最小和最大等效热传导系数分别为0.034763和0.986564.
图 5 三种混杂复合材料1000个随机样本的等效热传导系数分布图　(a) 周期混杂复合材料I; (b) 周期混杂复合材料II; (c) 随机混杂复合材料
Figure5. Effective thermal conductivity distribution of 1000 RVE samples of three kinds of hybrid composite materials: (a) Periodic hybrid composite material I; (b) periodic hybrid composite material II; (c) random hybrid composite material.

本节数值实验中提到的验证(集)误差、训练(集)误差和测试(集)误差均为平均绝对相对误差.
2

-->

4.1.小波-神经网络混合方法

用小波-神经网络混合方法对三种混杂复合材料的等效热传导性能进行预测, 在训练过程中, 用于训练的损失函数被设定为均方误差函数(mse), 应用Adam优化算法来更新所有权重并进行迭代, 激活函数采用ReLU函数. 为了避免过拟合现象的发生, 采用十折交叉验证(cross-validation, Cv)的方法对神经网络的过拟合行为进行抑制. 在十折交叉验证中将训练集随机分为10份, 并且分别以这10份中的1份为验证集, 其余9份为训练集进行10次训练, 最后以这10次训练中验证集误差的平均值作为神经网络模型过拟合程度的判断标准, 十折交叉验证过程如图6所示.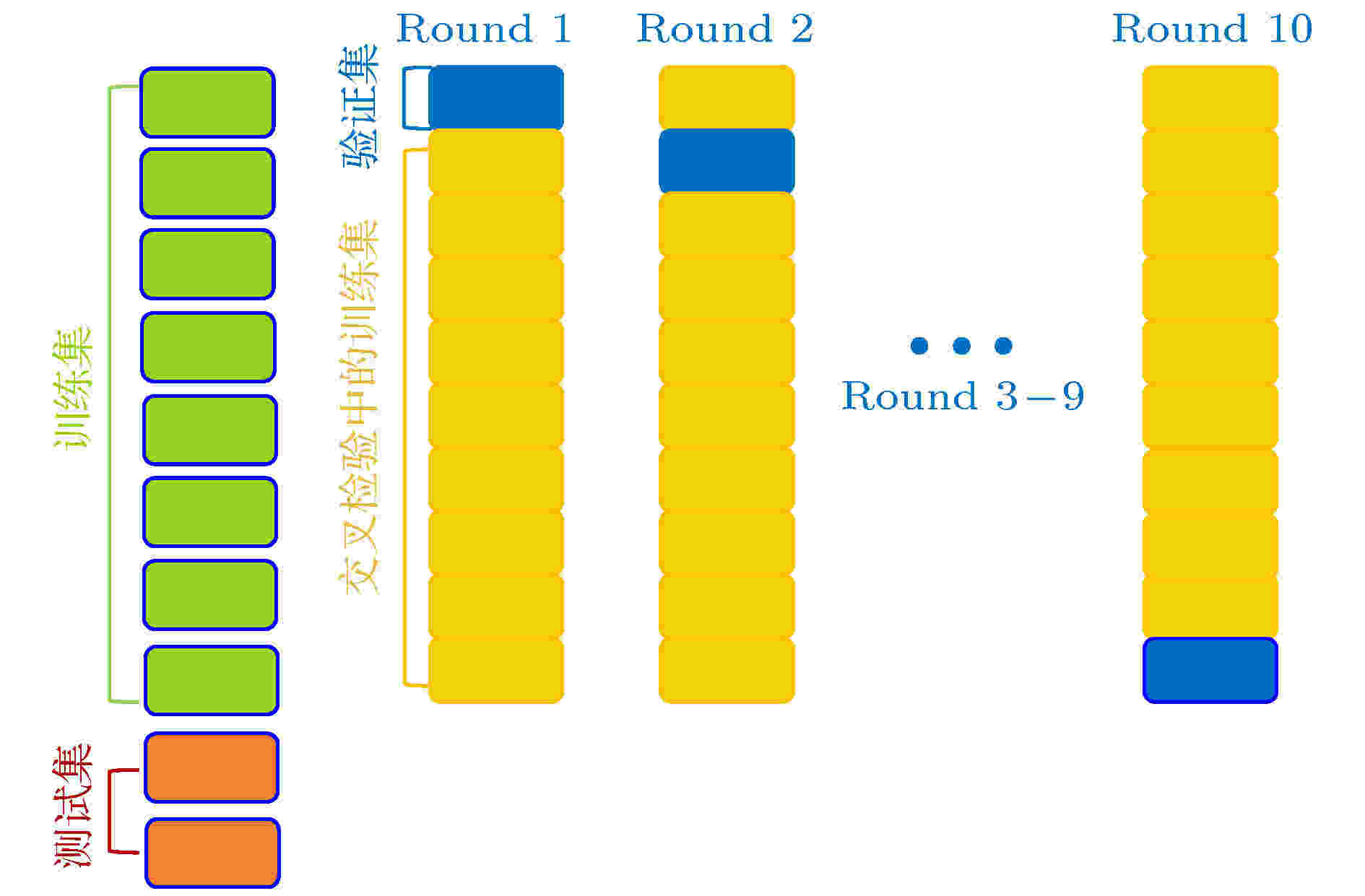
图 6 十折交叉验证过程示意图
Figure6. Schematic of 10-fold cross-validation.

最终将整个训练集输入调试好的模型进行训练, 并在测试集上对模型进行评估, 给出建立的模型在整个训练集和测试集上的相对误差分布图及其平均值. 对周期型混杂复合材料I和II, 将其材料数据库中的$ kc_1 $, $ kc_2 $, $ km $, $ r_1 $和$ r_2 $定义为神经网络输入层的5个神经元, 等效热传导系数$ \widehat k $作为输出层的1个神经元, 对周期混杂复合材料I建立5-128-128-1的前馈ANN模型, 设定迭代次数为250次; 对周期混杂复合材料II建立5-128-64-32-1的前馈ANN模型, 设定迭代次数为500次; 对随机型混杂复合材料以材料数据库中原始数据特征经三层小波分解后得到的1250个小波系数$ CA_3 $作为神经网络输入层的1250个神经元, 等效热传导系数$ \widehat k $作为输出层的1个神经元, 对随机混杂复合材料建立1250-1024-512-512-256-1的前馈ANN模型, 设定迭代次数为500次.
数值实验完成后, 给出最终的数值结果如图7和图8所示.
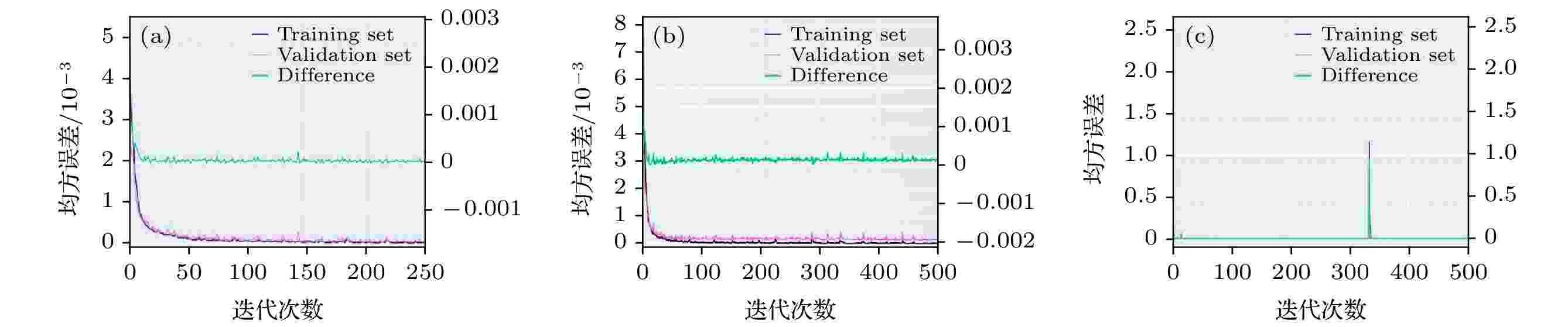图 7 三种混杂复合材料训练集误差和验证集误差随迭代次数变化曲线图　(a) 周期混杂复合材料I; (b) 周期混杂复合材料II; (c) 随机混杂复合材料
Figure7. Training error and cross-validation error descend as the training iteration increases for three kinds of hybrid composite materials: (a) Periodic hybrid composite material I; (b) periodic hybrid composite material II; (c) random hybrid composite material

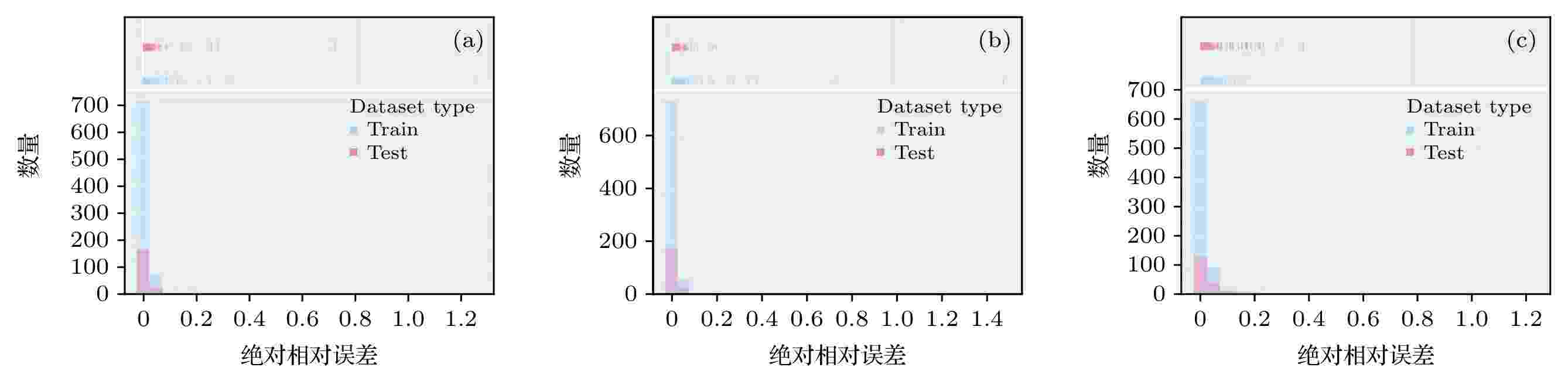图 8 三种混杂复合材料训练集和测试集上的相对误差分布图　(a) 周期混杂复合材料I; (b) 周期混杂复合材料II; (c) 随机混杂复合材料
Figure8. Frequency distribution of training error and test error of three kinds of hybrid composite materials: (a) Periodic hybrid composite material I; (b) periodic hybrid composite material II; (c) random hybrid composite material.

图7(a)—(c)分别给出了三种混杂材料的训练集误差和验证集误差随迭代次数的变化. 从图7可以清楚地看到, 由于权重和偏置的初始值是随机生成的, 因此刚开始迭代的训练误差很大. 随着迭代的进行, 权重和偏置会根据Adam算法逐渐更新, 训练误差和验证误差均迅速下降, 趋于收敛. 最终, 周期混杂复合材料I经10折交叉验证得到的训练集误差为1.7656%, 验证集误差为3.2645%; 周期混杂复合材料II经10折交叉验证得到的训练集误差为1.6503%, 验证集误差为4.1921%; 随机混杂复合材料经10折交叉验证的训练集误差为1.7080%, 验证集误差为5.7597%. 说明对于研究的三种混杂复合材料, 训练过程中没有出现明显的过拟合情况, 因此可以将训练得到的网络进一步在测试集上进行评估. 重新将800组训练集作为已经确定网络构架的ANN模型的输入, 用训练得到的ANN模型对测试集中每个样本的等效热传导系数进行预测, 并与用渐近均匀化方法计算得到的数据标签进行对比, 最终三种混杂复合材料的3个模型在整个训练集和测试集上的相对误差分布分别如图8(a)—(c)所示. 在图8(a)和图8(b)中, 周期混杂复合材料I和II的训练集和测试集中绝大部分样本的相对误差都小于2%. 最终, 材料I的ANN模型在训练集和测试集上的误差分别为1.4954%和2.2164%; 材料II的ANN模型在训练集和测试集上的误差分别为1.4745%和1.4533%. 在图8(c)中, 随机混杂复合材料的训练集和测试集中绝大部分样本的相对误差都小于 3%. 最终, 随机混杂复合材料训练集和测试集的误差分别为1.3596%和3.9731%. 总而言之, 我们建立的小波-神经网络方法可以高精度、高效地预测周期型和随机型混杂复合材料的等效热传导性能.
2 -->

4.2.小波-支持向量混合方法

用小波-支持向量混合方法对三种混杂复合材料的等效热传导性能进行预测, 训练过程中, 将SVR方法的核函数设置为高斯核函数并通过调节另外两个参数C和$ \varepsilon $来确定最优的SVR模型, 并且仍采用十折交叉验证的方法来避免过拟合现象的发生. 为了确定SVR模型中参数C和$ \varepsilon $的值, 在十折交叉验证的基础上结合了网格搜索的方法. 在网格搜索过程中, 将不同参数值C和$ \varepsilon $进行组合, 然后进行十折交叉验证, 最后比较不同组合下十折交叉验证的结果, 以最小误差对应的参数值作为最终选择的参数值, 三种材料的网格搜索的误差结果与最终选择的参数组合如图9所示.
图 9 三种混杂复合材料参数网格搜索示意图, 其中标记√处为最终确定的最优参数组合　(a) 周期混杂复合材料I; (b) 周期混杂复合材料II; (c) 随机混杂复合材料
Figure9. Grid search diagram of three kinds of hybrid composite materials’ parameters, where the final optimal combination of parameters is marked with √: (a) Periodic hybrid composite material I; (b) periodic hybrid composite material II; (c) random hybrid composite material.

在图9(a)中, 对周期混杂复合材料I, 确定了最优参数组合为C = 1500和$ \varepsilon = 10^{-5} $, 此时训练集误差为0.20%, 验证集误差为2.7018%; 在图9(b)中, 对于周期混杂复合材料II, 确定了参数组合为C = 10和$ \varepsilon = 10^{-3} $, 此时训练集误差为1.7727%, 验证集误差为2.7741%; 在图9(c)中, 对于随机混杂复合材料, 确定了参数组合为C = 1和$ \varepsilon = 10^{-2} $, 此时训练集误差为2.6578%, 验证集误差为9.2572%. 上述结果表明, 对周期型混杂复合材料均没有出现明显的过拟合行为, 对随机型混杂复合材料出现了一定程度的过拟合行为. 接下来将800组训练集作为已经确定参数的SVR模型的输入, 再用训练后的SVR模型预测测试集中每个样本的等效热传导系数, 并与用渐近均匀化方法计算得到的等效热传导系数进行对比, 最终三种混杂复合材料的训练集和测试集的相对误差分布如图10所示.
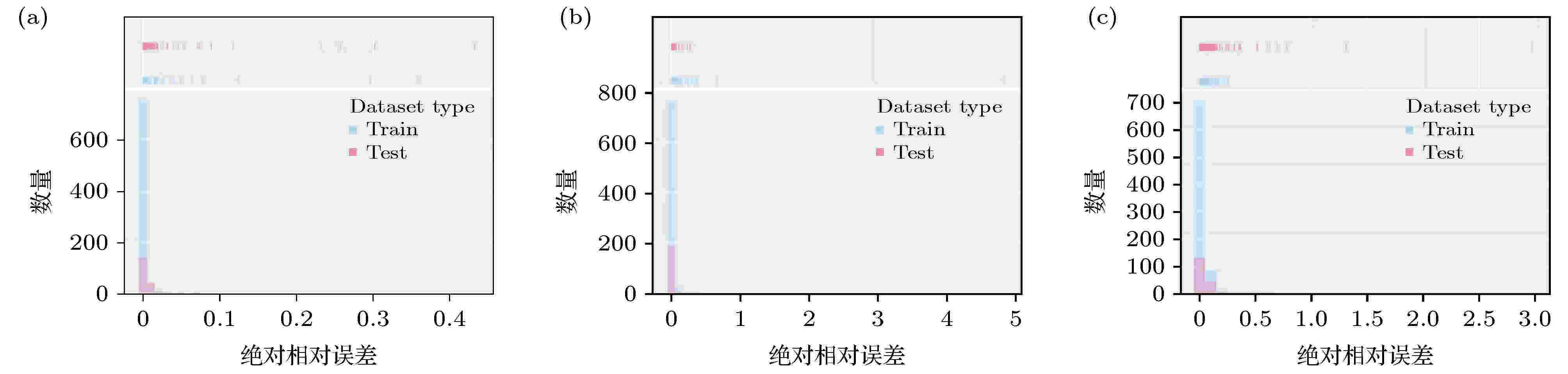图 10 三种混杂复合材料训练集和测试集上的相对误差分布图　(a) 周期混杂复合材料I; (b) 周期混杂复合材料II; (c) 随机混杂复合材料
Figure10. Frequency distribution of training error and test error of three kinds of hybrid composite materials: (a) Periodic hybrid composite material I; (b) periodic hybrid composite material II; (c) random hybrid composite material.

从图10可以发现, 对周期混杂复合材料I和II的训练集和测试集中除个别样本的相对误差高于10%外, 绝大部分样本的相对误差都小于2%. 材料I最终的训练集和测试集的误差分别为0.2462%和1.2712%, 材料II最终的训练集和测试集的误差分别为1.4252%和1.7516%. 而对随机混杂复合材料的训练集和测试集中绝大部分样本的相对误差都小于8%, 且其最终的训练集和测试集误差分别为2.6636%和8.1561%. 总而言之, 对于周期型混杂复合材料, 小波-支持向量混合方法是高精度、高效率的, 但对于随机型混杂复合材料, 该方法的预测精度没有周期型混杂复合材料高.
2 -->

4.3.小波-机器学习混合方法抗噪性能分析

在实际工程应用中, 各种各样的噪声无法避免, 小波方法天然地具有一定的去噪能力, 接下来对我们建立的小波-机器学习混合方法的抗噪性能进行分析. 由于随机型混杂复合材料的原始数据特征是由背景网格中每个节点的材料参数$ k_{x_1 x_2}^i $定义, 因此通过分别向背景网格各节点随机添加三种不同强度的高斯噪声$ N(0, 0.001^2) $, $ N(0, 0.01^2) $和$ N(0, 0.1^2) $, 再分别应用建立的小波-神经网络混合方法和小波-支持向量混合方法对加噪后的随机混杂复合材料的等效热传导性能进行预测分析. 数值实验完成后, 对不同强度的噪声最终的预测效果见表4, 其中ANN和SVR代表没有噪声时两种小波-机器学习混合方法的预测结果, ANN-I, ANN-II, ANN-III和SVR-I, SVR-II, SVR-III分别代表添加噪声$ N(0, 0.001^2) $, $ N(0, 0.01^2) $, $ N(0, 0.1^2) $时两种小波-机器学习混合方法的数值实验结果.

方法	模型参数	Cv训练误差	Cv验证误差	训练误差	测试误差	训练时间/s	测试时间/s
ANN	1250-1024-512-512-256-1	1.708%	5.760%	1.360%	3.973%	100.345	0.061
ANN-I	1250-1024-512-512-256-1	1.516%	5.948%	1.671%	4.496%	100.517	0.089
ANN-II	1250-1024-512-512-256-1	1.349%	5.404%	1.683%	4.427%	101.160	0.071
ANN-III	1250-1024-512-512-256-1	1.550%	5.862%	1.285%	4.810%	100.270	0.059
SVR	C = 1和$\varepsilon=10^{-2}$	2.658%	9.257%	2.664%	8.156%	0.780	0.171
SVR-I	C = 1和$\varepsilon=10^{-2}$	2.664%	9.268%	2.660%	8.160%	0.710	0.187
SVR-II	C = 1和$\varepsilon=10^{-2}$	2.659%	9.265%	2.673%	8.150%	0.696	0.159
SVR-III	C = 1和$\varepsilon=10^{-2}$	2.677%	9.124%	2.675%	8.099%	0.694	0.166

表4两种小波-机器学习混合方法抗噪性能分析
Table4.Anti-noise performance analysis of two kinds of hybrid wavelet-based learning methods.

由表4可知, 小波-神经网络混合方法和小波-支持向量混合方法对于三种不同强度的噪声都是不敏感的, 不同强度的噪声不会对两种方法的精度造成较大的影响. 此外, 相比小波-支持向量混合方法, 小波-神经网络混合方法在噪声干扰下表现出更好的数值精度, 训练集和测试集的误差精度均控制在5%以内, 同时样本测试时间很短, 这对于实际工程应用具有重要的意义. 从表4还可以看出, 小波-支持向量混合方法对于无噪声污染和有噪声污染的随机型混杂复合材料等效热传导性能预测均出现了一定程度的过拟合现象, 因为该方法交叉验证得到的训练集误差很小而验证集误差偏大. 综上所述, 在实际工程应用中采用小波-神经网络混合方法来预测随机型混杂复合材料的等效热传导系数更为有效, 不仅预测精度高而且预测效率高.

为了有效预测混杂复合材料的等效热传导性能, 本文结合多尺度分析提出了一种新的小波-机器学习混合方法. 在该方法中, 基于Freefem++软件二次开发, 建立了三种典型混杂复合材料的计算机几何模型. 利用渐近均匀化方法离线计算得到了三种混杂复合材料的等效热传导系数, 然后以混杂复合材料组成成分的微观结构参数和材料参数作为数据特征, 其等效热传导系数作为数据标签, 建立混杂复合材料的离线材料数据库. 对于随机型混杂复合材料, 创造性地利用小波变换方法对其建立在背景网格上的数据特征进行预处理, 建立了新的材料数据库. 最后, 利用神经网络方法和支持向量回归方法对周期型和随机型混杂复合材料的材料数据库进行在线监督学习, 得到混杂复合材料等效热传导性能预测的机器学习模型.
本文建立的新的小波-机器学习混合方法充分利用了小波变换方法的数据压缩、特征提取和去噪能力, 以及机器学习方法优异的数据拟合能力. 数值实验表明, 在无噪声的情形下, 对于周期型混杂复合材料, 小波-神经网络混合方法和小波-支持向量回归混合方法均表现出很高的数值精度, 并且稳定高效; 对于随机型混杂复合材料, 小波-神经网络混合方法的预测精度高于小波-支持向量回归混合方法. 在加入噪声的情形下, 两种混合方法均表现出很好的抗噪能力, 其中小波-神经网络混合方法数值精度更高, 样本测试时间更短, 小波-支持向量混合方法的数值精度较低, 且表现出一定程度的过拟合行为. 综上所述, 本文建立的小波-机器学习混合方法可以有效预测混杂复合材料的等效热传导性能, 特别是小波-神经网络方法具有高精度、高效率的预测能力和优异的抗噪性能. 本文建立的统一的小波-机器学习混合框架可以很容易地扩展到预测混杂复合材料的其他物理、力学性能, 为新型复合材料的开发提供了坚实的基础理论和高性能算法. 在未来, 希望能够进一步利用我们建立的小波- 机器学习混合框架对混杂复合材料的其他非线性物理、力学性能进行深入研究.
感谢阿尔伯塔大学数学与统计科学系Yaushu Wong教授和Yile Zhang博士的讨论.