摘要:超顺磁性氧化铁纳米粒子与造影剂微泡结合形成磁性微泡, 用于产生多模态造影剂, 以增强医学超声和磁共振成像. 将装载有纳米磁性颗粒的微泡包膜层看作由磁流体膜与磷脂膜组合而成的双层膜结构, 同时考虑磁性纳米颗粒体积分数α对膜密度及黏度的影响, 从气泡动力学基本理论出发, 构建多层膜结构磁性微泡非线性动力学方程. 数值分析了驱动声压和频率等声场参数、颗粒体积分数、膜层厚度以及表面张力等膜壳参数对微泡声动力学行为的影响. 结果表明, 当磁性颗粒体积分数较小且α ≤ 0.1时, 磁性微泡声响应特性与普通包膜微泡相似, 微泡的声频响应与其初始尺寸和驱动压有关; 当驱动声场频率f为磁性微泡共振频率f₀的2倍(f = 2f₀)时, 微泡振动失稳临界声压最低; 磁性颗粒的存在抑制了泡的膨胀和收缩但抑制效果非常有限; 磁性微泡外膜层材料的表面张力参数K及膜层厚度d也会影响微泡的振动, 当表面张力参数及膜厚取值分别为0.2—0.4 N/m及50—150 nm时, 可观察到气泡存在不稳定振动响应区.
关键词: 磁性微泡/
非线性振动/
功率谱/
分岔图

English Abstract

全文HTML

--> --> -->

将超声造影剂微泡(microbubble, MB)与超顺磁性氧化铁纳米粒子(superparamagnetic iron oxide nanoparticles, SPIOs)结合形成的混合剂-磁性微泡(magnetic microbubble, MMB)^[1], 是一个将对现代医学诊断产生深远影响的新概念^[2]. MMB兼具MB和SPIOs两者各自特性, 可同时用作超声造影(ultrasound imaging, UI)与磁共振成像(magnetic resonance imaging, MRI)对比剂. 在临床诊断中, UI与MRI是两种互补的病理鉴别技术, 使用MMB这种多模态造影剂, 单次注射可同时用于多个造影增强成像技术, 快速获取UI的组织灌注及MRI的器官结构信息用以对病情快速诊断. 多模态对比剂的开发正成为提供更有价值的诊断信息和治疗方案的重要途径. 另一方面, 自Stride等^[3]证实MMBs在磁声共同作用相比于单独应用可获得更高的基因转染率后, 将MMBs用于生物发光标记物、核酸治疗试剂及药物递送的活体和离体实验也分别取得成功^[4,5]; 磁声组合的磁性微泡血栓溶解^[6-8]和癌症治疗^[9]等方面近年也取得很好的效果. MMB作为集诊断与治疗于一体的新型微泡制剂所展现出的巨大应用潜力而成为研究热点.
无论作造影剂还是辅助治疗, MMB在可变压力场作用下的动力学不仅是其诊疗应用的基础, 也是进行功能优化结构设计及拓展应用的前提. MMB生产制备中, MB膜层与SPIOs的结合一般通过静电吸附、化学键连或物理镶嵌等方式, 不同结合方式形成的包膜结构和物理特性不同. Sciallero等^[10]对SPIOs与外壳共价连接及被束缚在外壳中两类MMB的声特性进行了实验表征, 认为两者都是有效的超声造影剂, 但壳结构对成像过程中的回声强度和探测灵敏度有明显影响. Gu等^[11]对MMB的谐波响应和空化活性进行了实验研究, 发现SonoVue微泡的稳定空化阈值和惯性空化阈值与SPIOs浓度为某一定值时的MMB测量值相似, 表明欲提高MMB的诊疗性能, 需对其壳层如厚度及颗粒体积分数等进行合理设计. Marlies等^[12]在对MMB的声压阈值测试中, 发现其共振曲线随声压增大明显倾斜, 非线性振动特性增强. 这些实验从不同程度上有助于认识MMB的声特性, 但MMB作为一种新型造影剂, 在超声成像和药物输送中的动态特性尤其是非线性振动行为仍缺乏全面的了解.
为更好地了解MMB的声响应特性及SPIOs的影响, Mulvana等^[13]利用数值方法在洞察微泡动力学机制方面的优势, 如可提供详细、非破坏性且高效的在体或离体很难观察到的力学过程^[14-16], 假设MMB膜层为均匀分布有球形磁性纳米颗粒的疏水性黏性流体, 在Church^[17]模型基础上, 发展了较为简单的磁性单层膜微泡动力学理论模型, 分析了MMB在声场中的体振荡特性, 认为SPIOs主要影响微泡的谐波响应. 然而, Mulvana等在发展MMB模型过程中, 仅考虑颗粒介入引起的包膜材料密度的变化. 按照磁流体理论, SPIOs不仅改变磁流体密度, 同时还改变了磁流体的黏度及弹性. 膜结构和特性是影响泡动力学的关键, 随制备技术的发展MMB出现多种结构, 常见的有SPIOs分散在内壳油层内、嵌入在脂质膜层壳上及非共价结合在微泡外表面等^[18], 因此发展能够更为适当地描述多层膜结构MMB声响应的数学模型, 通过理论方法探讨颗粒的存在对微泡振荡的影响, MMB在超声作用下的运动以及其与普通MB是否存在显著差异等问题不仅有趣且极为重要.
MMB的另一个重要特性就是因SPIOs的存在具有磁性及磁场响应. 磁声场同时存在时, 因多场叠加及耦合作用使MMB行为极为复杂化, 为使问题简化Malvar等^[19]采取磁流体力学方法, 将泡的磁场响应问题转化为磁流体中气泡动力学来研究, 发现足够强的磁场对气泡振动有一定抑制作用. Mo等^[20]也发现在相同驱动声场作用下, 磁场对水中泡的振动影响很小.因此研究泡的径向振动特性时可暂时不考虑磁性以及磁场的影响.
本文目的是在不考虑外磁场条件下, 构建具有双层膜结构的MMB动力学理论模型, 通过数值方法研究其声响应及SPIOs含量对泡的动力学的影响. 在考虑MMB基本结构基础上, 建立图1所示双层膜模型, 同时考虑磁性颗粒对流体膜层密度和黏度的影响, 构建双层膜磁性微泡动力学方程. 使用微扰法对磁性微泡的动力学方程进行一阶线性化, 并用数值方法分析驱动声场参数、SPIOs体积分数、表面张力和膜层厚度等对MMB振动非线性的影响.
图 1 磁性微泡几何模型. 1-空气, 2-磁流体层, 3-磷脂薄层
Figure1. The geometric model of MMBs. 1-air, 2-magnetic fluid, 3-thin layer of phospholipid regardless of thickness.

图1所示MMB双层膜结构模型. 气核1被双层膜包裹; 内层膜2为磁流体层, 其基液为疏水性油酸, SPIOs均匀分散其中; 外层膜为疏水性磷脂层, 泡外为无限大液体. 假设磁泡初始内、外半径分别为R₁₀和R₂₀, 磁流体膜层2厚度为d, 磷脂薄层3厚度很小可忽略, 于是微泡膜层厚度即为磁流体层厚度. 膜层磁流体和泡外无限大液体均为不可压缩牛顿流体, 磁流体密度和黏度分别为ρ_s和η_s, 由疏水性油酸基液和所载磁性纳米颗粒密度和黏度共同决定, 基液密度和黏度分别用ρ_o和η_o表示. 密度为ρ_np的SPIOs均匀分散在基液中, 为避免颗粒团聚需对其体积分数进行控制, 参照MMB相关制备文献数据^[21]估计, α值一般不超过0.1, 此时颗粒间相互作用可忽略不计. 磁流体密度ρ_s与α间存在关系ρ_s = (1–α)ρ_o + αρ_np, η_s满足Einstein方程η_s = η_o(1 + 2.5α)^[22]. 无限大液体的密度和黏度分别为ρ_l和η_l, 磷脂薄层黏度为η_s0, 不考虑膜层内外质量交换, 磁泡仅作径向振动且在膨胀、收缩期间始终保持球形.
设磁流体膜层厚度$d \ll {R_1}$, 微泡振荡过程中d变化很小可视为常量, 同时在振荡过程中壳层体积V_S始终保持不变, 即

${V_{\rm{S}}} = \frac{4}{3}\pi (R_{20}^3 - R_{10}^3) = {\rm{const}}, $

则

$R_2^3 - R_1^3 = R_{10}^3 - R_{20}^3,R_1^2{\dot R_1} = R_2^2{\dot R_2},$

其中${\dot R_1} $(ν₁)和${\dot R_2} $(ν₂)分别为振动微泡内、外壁的速度.
考虑连续介质动力学方程为^[23]

$\rho \left( {\frac{{\partial {{v}}}}{{\partial t}} + {{v}} \cdot \nabla {{v}}} \right) = - \nabla p + \nabla \cdot {{\sigma}}, $

其中ρ, ν, p, σ分别是介质密度, 质点速度, 压强, 黏性应力张量, 在球坐标系下, 只考虑径向振动, 此时速度v_r = v, v_θ = v_φ = 0, 故径向动力学分量式为

$\rho \left( {\frac{{\partial v}}{{\partial t}} + v\frac{{\partial v}}{{\partial r}}} \right) = - \frac{{\partial p}}{{\partial r}} + \frac{{\rm{1}}}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}{\sigma _{rr}}} \right) - \frac{{{\sigma _{\theta \theta }} + {\sigma _{\phi \phi }}}}{r}, $

式中, σ_rr, σ_θθ, σ_φφ分别是黏性应力张量在球坐标系下的径向、切向及φ角方向分量.
对于不可压缩黏性流体, 其黏性应力张量满足如下关系^[24]:

${\sigma _{rr}} + {\sigma _{\theta \theta }} + {\sigma _{\phi \phi }} = 0.$

则不可压缩黏性流体的径向黏性应力张量可表示为

${\sigma _{rr}} = - {\sigma _{\theta \theta }} - {\sigma _{\phi \phi }}.$

将(6)式代入(4)式得

$\rho \left( {\frac{{\partial v}}{{\partial t}} + v\frac{{\partial v}}{{\partial r}}} \right) = - \frac{{\partial p}}{{\partial r}} + \frac{{\partial {\sigma _{rr}}}}{{\partial r}} + \frac{{3{\sigma _{rr}}}}{r}.$

由边界处压力的平衡条件, 在边界r = R₁处, 作用在内表面膜层一侧的压力为

${p_S}\left( {{R_1},t} \right) = {P_S}\left( {{R_1},t} \right) - {\sigma _{S,rr}}\left( {{R_1},t} \right) + \frac{{2{\sigma _1}}}{{{R_1}}}, $

由于泡内气体压力等于包膜层一侧的压力, 得到边界条件:

${P_G}( {{R_1},t} ) = {P_S}( {{R_1},t} ) - {\sigma _{S,rr}}( {{R_1},t} ){\rm{ + }}\frac{{{\rm{2}}{\sigma _{\rm{1}}}}}{{{R_1}}} \;\;( {r = {R_1}} ).$

在r = R₂处, 因包膜层外包裹一层不计厚度的磷脂分子薄层, 磷脂分子数对R₂处外表面的影响包含两部分, 分别为引起外侧膜层黏性及表面张力的影响, 具体定量关系如下^[13]:

$F = 4{\eta _{s0}}\frac{{{{\dot R}_2}}}{{R_2^2}} + \frac{{2K}}{{{R_2}}}\bigg[ {1 - {{\left( {\frac{{{R_{{\rm{20}}}}}}{{{R_2}}}} \right)}^2}} \bigg].$

η_s0和K分别为引起边界R₂处表面黏性项和表面张力项变化的比例常数, 同理由膜层内外压力相等的条件可以得到边界条件:

$\begin{split}&{P_{\rm{s}}}\left( {{R_2},t} \right) - {\sigma _{S,rr}}\left( {{R_2},t} \right) \\ =& {P_L}\left( {{R_2},t} \right) - {\sigma _{L,rr}}\left( {{R_2},t} \right) + \frac{{2{\sigma _{\rm{2}}}}}{{{R_2}}} + 4{\eta _{s0}}\frac{{{{\dot R}_2}}}{{R_2^2}} \\ & + \frac{{2K}}{{{R_2}}}\bigg[ {1 - {{\left( {\frac{{{R_{{\rm{20}}}}}}{{{R_2}}}} \right)}^2}} \bigg], \;\;(r = {R_2}), \end{split}$

其中$ P_{\rm G}(R_1, t) = P_{\rm G0}(R_{10}/R_1)^{3\gamma} $, P_G(R₁, t)是内部气体压力, P_G0是泡内初始平衡气压; P₀是外界静压; σ₁和σ₂分别为内外表面张力系数; γ为气体多方指数; P_S(R₁, t), P_S(R₂, t)分别是R₁, R₂处膜层侧的压力; σ_{S, rr}, σ_L, _rr分别为包膜内、外流体黏性应力分量.
结合边界条件, 对(7)式从R₁到∞积分得:

$\begin{split} & {R_1}{{\ddot R}_1}\left[ {1 + \left( {\dfrac{{{\rho _l} - {\rho _s}}}{{{\rho _{\rm{s}}}}}} \right)\dfrac{{{R_1}}}{{{R_2}}}} \right] \\ & + \dot R_1^2\left[ {\dfrac{3}{2} + \left( {\dfrac{{{\rho _l} - {\rho _{\rm{s}}}}}{{{\rho _{\rm{s}}}}}} \right)\left( {\dfrac{{4R_2^3 - R_1^3}}{{2R_2^3}}} \right)\left( {\dfrac{{{R_1}}}{{{R_2}}}} \right)} \right] \\ =\; & \dfrac{1}{{{\rho _s}}}\!\bigg\{ {P_{{\rm{G}}0}}{{\!\left(\! {\dfrac{{{R_{10}}}}{{{R_1}}}} \!\right)}^{3\gamma }}\! -\! {P_\infty } \!-\! \dfrac{{2{\sigma _1}}}{{{R_1}}} \!-\! \dfrac{{2{\sigma _2}}}{{{R_2}}} \!-\! \dfrac{{4{\eta _{{\rm{s}}0}}{{\dot R}_2}}}{{R_2^2}}\! \\ & - \!\dfrac{{2K}}{{{R_2}}}\!\bigg[\! {1 - {{\!\left(\! {\dfrac{{{R_{{\rm{20}}}}}}{{{R_2}}}} \right)}^2}} \bigg] + 3\displaystyle\int_{{R_1}}^{{R_2}} \dfrac{{{\sigma _{{\rm{S}},rr}}}}{r}{\rm d} r \\ & + 3\displaystyle\int_{{R_2}}^\infty \dfrac{{{\sigma _{{\rm{L}},rr}}}}{r}{\rm{d}}r \bigg\} ,\\[-12pt]\end{split} $

式中,

$3\int_{{R_1}}^{{R_2}} {\frac{{{\sigma _{{\rm{S}},rr}}}}{r}} {\rm{d}}r = - 4\left( {1{\rm{ + 2}}{\rm{.5}}\alpha } \right){\eta _{\rm{o}}}\frac{{{V_{\rm{S}}}{{\dot R}_1}}}{{R_2^3{R_1}}},$

$3\int_{{R_2}}^\infty {\frac{{{\sigma _{{\rm{L}},rr}}}}{r}} {\rm{d}}r = \frac{{ - 4{\eta _l}R_1^2{{\dot R}_1}}}{{R_2^3}},$

其中P_G0 = P₀ + 2σ₁/R₁₀ + 2σ₂/R₂₀, P_∞ = P₀ + P_d(t) = P₀ + P_asin(2πft), P_a是声压幅值, f是驱动频率.
于是, MMB动力学方程可表示为

$\begin{split}& {R_1}{{\ddot R}_1}\left[ {1 + \left( {\dfrac{{{\rho _l} - {\rho _{\rm{s}}}}}{{{\rho _{\rm{s}}}}}} \right)\left( {\dfrac{{{R_1}}}{{{R_2}}}} \right)} \right] \\& + \dot R_1^2\left[ {\dfrac{3}{2} + \left( {\dfrac{{{\rho _l} - {\rho _{\rm{s}}}}}{{{\rho _{\rm{s}}}}}} \right)\left( {\dfrac{{4R_2^3 - R_1^3}}{{2R_2^3}}} \right)\left( {\dfrac{{{R_1}}}{{{R_2}}}} \right)} \right] \\ =\;& \dfrac{1}{{{\rho _{\rm{s}}}}} \bigg\{ P_{{\rm{G}}0} {{\left( {\dfrac{{{R_{10}}}}{{{R_1}}}} \right) }^{3\gamma }} - {P_d}\left( t \right) - {P_0} - \dfrac{{2{\sigma _1}}}{{{R_1}}} \\ & - \dfrac{{2{\sigma _2}}}{{{R_2}}} - \dfrac{{4{\mu _l}{{\dot R}_1}R_1^2}}{{R_2^3}} - \dfrac{{4{\eta _{\rm{o}}}\left( {1{\rm{ + 2}}{\rm{.5}}\alpha } \right){{\dot R}_1}{V_S}}}{{R_2^3{R_1}}} \\ & - \dfrac{{4{\eta _{s0}}{{\dot R}_2}}}{{R_2^2}} - \dfrac{{2K}}{{{R_2}}} \bigg[ {1 - {{\left( {\dfrac{{{R_{{\rm{20}}}}}}{{{R_2}}}} \right) }^2}} \bigg] \bigg\}.\\[-18pt]\end{split}$

将(15)式进行线性化近似, 此时微泡内、外半径可表示成如下关系:

${R_1} = {R_{10}} + \xi \left( t \right),~{R_2} = {R_{20}} + \frac{{R_{10}^2}}{{R_{20}^2}}\xi \left( t \right).$

式中, $\left| \xi \right| \ll {R_{10}}$. 将(16)式代入(15)式得

$\ddot \xi + \delta \dot \xi + \omega _0^2\xi = - \frac{{{P_{\rm{d}}}\left( t \right)}}{{{\rho _{\rm{s}}}\beta {R_{10}}}}, $

其中$\beta = 1 + \left( {\dfrac{{{\rho _l} - {\rho _s}}}{{{\rho _s}}}} \right)\dfrac{{{R_{10}}}}{{{R_{20}}}}$,

$\begin{split}\delta =\;&\frac{4}{{{\rho _{\rm{s}}}\beta {R_{10}}}}\left( {\eta _l}\frac{{R_{10}^2}}{{R_{20}^3}} \right. \\&\left.+ {\eta _{\rm{o}}}\frac{{\left( {1{\rm{ + 2}}{\rm{.5}}\alpha } \right)\left( {R_{20}^3 - R_{10}^3} \right)}}{{{R_{10}}R_{20}^3}}+ {\eta _{{\rm{s}}0}}\frac{{R_{10}^2}}{{R_{20}^4}} \right), \end{split}$

${{\omega _0} \!=\! \frac{1}{{{R_{10}}\sqrt {{\rho _{\rm{s}}}\beta } }}{\left\{ {3\gamma {P_{G0}} \!-\! \frac{{2{\sigma _1}}}{{{R_{10}}}} \!-\! \frac{{2{\sigma _2}R_{10}^3}}{{R_{20}^4}} \!+\! \frac{{4KR_{10}^3}}{{R_{20}^4}}} \right\}\!^{\tfrac{1}{2}}}} .$

(17)式即为小振幅驱动声场下、线性化后的MMB动力学方程. 其中δ表示振动系统阻尼系数, ω₀为固有圆频率. 从它们各自的表达式可以间接看出, 磁性颗粒的存在增大了振动系统的阻尼, 降低了微泡的固有频率f₀ (f₀ = ω₀/2π).
从(15)式和(17)式可看出, 在周期性外声场驱动下的磁性微泡, 其振动特性不仅受声场参数包括声压幅值P_a和驱动频率f的影响, 还与微泡本身参数有关, 包括微泡初始半径R₂₀、包膜层上磁性颗粒的体积分数和膜层材料等. 由ω₀表达式可以看出, 初始半径相同的磁性微泡, α引起的膜层密度及黏度变化、K值及膜层厚度d共同决定磁性泡的固有频率. 磁性颗粒的结合增大了膜的密度和黏度, 因而导致磁性微泡的共振频率下降. 同时, 磁性微泡膜壳黏弹性一定程度增加了振动阻尼, 也会对磁性泡振动系统特性产生影响, 所以有必要去分析声场条件及微泡自身参数对微泡振动的影响.

以水为工作介质, 利用龙格-库塔法求解磁性微泡动力学方程. 微泡振动非线性方程的解在经过初始的暂态过程达到稳定, 采用分岔图、振动相图、功率谱图及庞加莱截面图描述声场中磁性微泡振动特性. 数值分析中所涉及的基本参数为:σ₁ = 0.04 N/m, σ₂ = 0.005 N/m, γ = 4/3, ρ_l = 10³ kg/m³, ρ_np = 5.1 × 10³ kg/m³, ρ_o = 0.7 × 10³ kg/m³, P₀ = 10⁵ Pa, η_l = 10^–3 Pa·s, η_o = 8 × 10^–3 Pa·s, η_s0 = 4.5 × 10^–9 kg/s.
2

-->

3.1.声场参数响应

超声诊疗应用中驱动声压是重要控制参数之一. 通过MMB在大范围声压幅值内所表现出的混沌运动及非线性运动以及所引起的谐波成分, 能更多更全面了解其声响应特性. 控制MMB基本结构参数d = 100 nm, α = 0.1, K = 0.3 N/m保持不变, 分析驱动声压幅值从0—500 kPa连续变化, R₂₀ = 5 μm (f₀ = 0.85 MHz)微泡分别在 f₀/2, f₀, 2f₀声频激励下, 微泡R₂/R₂₀随驱动压P_a变化规律, 结果见图2(a)—(c). 随着驱动压幅值增加, 微泡振动由周期1过渡到周期2、再进入周期4, 随后进入混沌, 也就是说微泡经由倍周期分岔发展为混沌运动. 对比图2(a)、图2(b)及图2(c)发现, 倍周期分岔所对应的临界声压随驱动声频率变化有所不同, f = f₀时最大而f = 2f₀时最小. 另外, f = f₀/2时声压阈值介于f = f₀和f = 2f₀两者之间, 但此时微泡混沌响应最为强烈且在混沌区域微泡振幅急剧增大.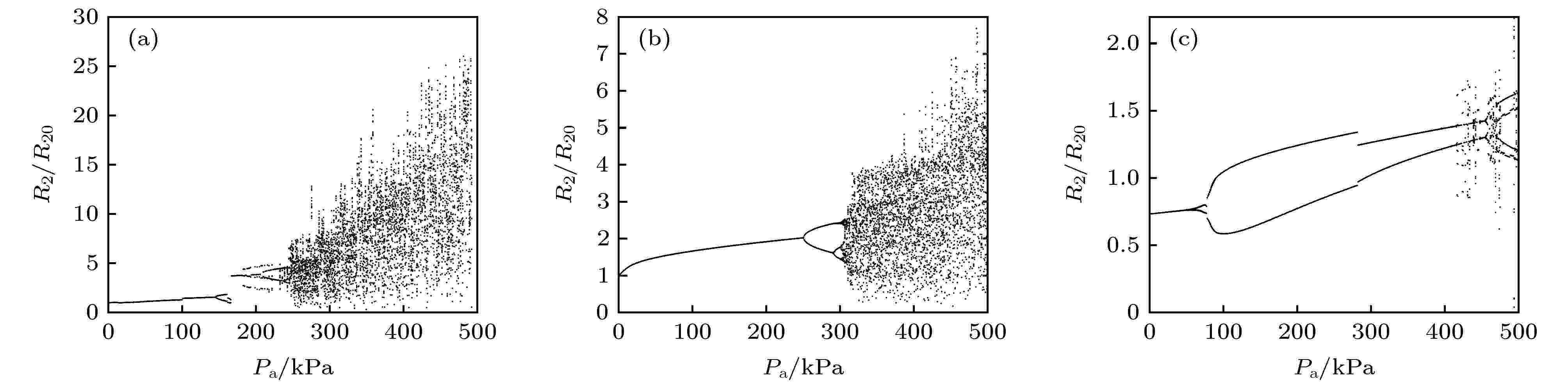
图 2 声压响应分岔图 (R₂₀ = 5 μm)　(a) f = f₀/2; (b) f = f₀; (c) f = 2f₀
Figure2. Bifurcation diagram of an MMB with pressure amplitude for R₂₀ =5 μm: (a) f = f₀/2; (b) f = f₀; (c) f = 2f₀.

微泡作为一个非线性受迫振动系统, 当驱动声压连续变化到某个临界值时系统出现分岔, 振动图出现分岔意味着系统全局性态突变、展示出非线性特性, 该临界声压可能与磁性微泡的空化阈值相关.f = f₀时稳定振荡区域最宽, f = f₀/2更容易发生混沌, f = 2f₀发生振动失稳临界声压最低但混沌临界压最大, 普通微泡在2f₀驱动下具有最小的次谐波阈值的结论已得证实^[25], 可见磁性微泡有与一般包膜泡相似的声压响应规律.
对任意一个非线性振动系统, 超谐波响应总是或多或少存在, 而次谐波行为仅在驱动压超过某阈值时才存在, 因此次谐波分量出现被认为空化发生的重要标志^[11], 为此, 通过功率谱和庞加莱截面分析上述微泡在共振激励下的运动细节, 当P_a分别取100, 255和350 kPa时结果分别对应图3(a)—(c)和图3(d)—(f).对比功率谱发现, 从开始仅有f₀和2f₀两个分立谱(图3(a)), 到P_a = 255 kPa时除了f₀和2f₀又增添了f₀/2及其他谐波成分(图3(b)), 最后P_a = 350 kPa时又出现新的f₀/5, 2f₀/5等多个分谐波成分(图3(c)). 随着驱动压增大分谐波成分增多, 对应庞加莱截面图上的离散点也从1到2再到有限个点集. 功率谱图和庞加莱截面联合判定, 微泡从开始的稳定周期振荡到不稳定周期振荡、最后进入到混沌运动. P_a = 255 kPa时f₀/2的出现表明此时可能发生不稳定空化; 随着声压的继续增大、更多无规律分布的频率成分出现, 在庞加莱截面表现为一定层次结构有限点密集分布, 运动呈现混沌特性. Sciallero等^[10]实验表明: MMB线性振荡区间为50—100 kPa, 非线性区域为120—450 kPa, 与本文理论预测结果一致.微泡诊疗应用中可根据需求设置声参数, 实现在输运过程中微泡处于稳态振动以辅助超声诊断, 或在微泡到达目标位置后调节驱动声波压力促使微泡处于混沌态促进载药体释放或治疗.
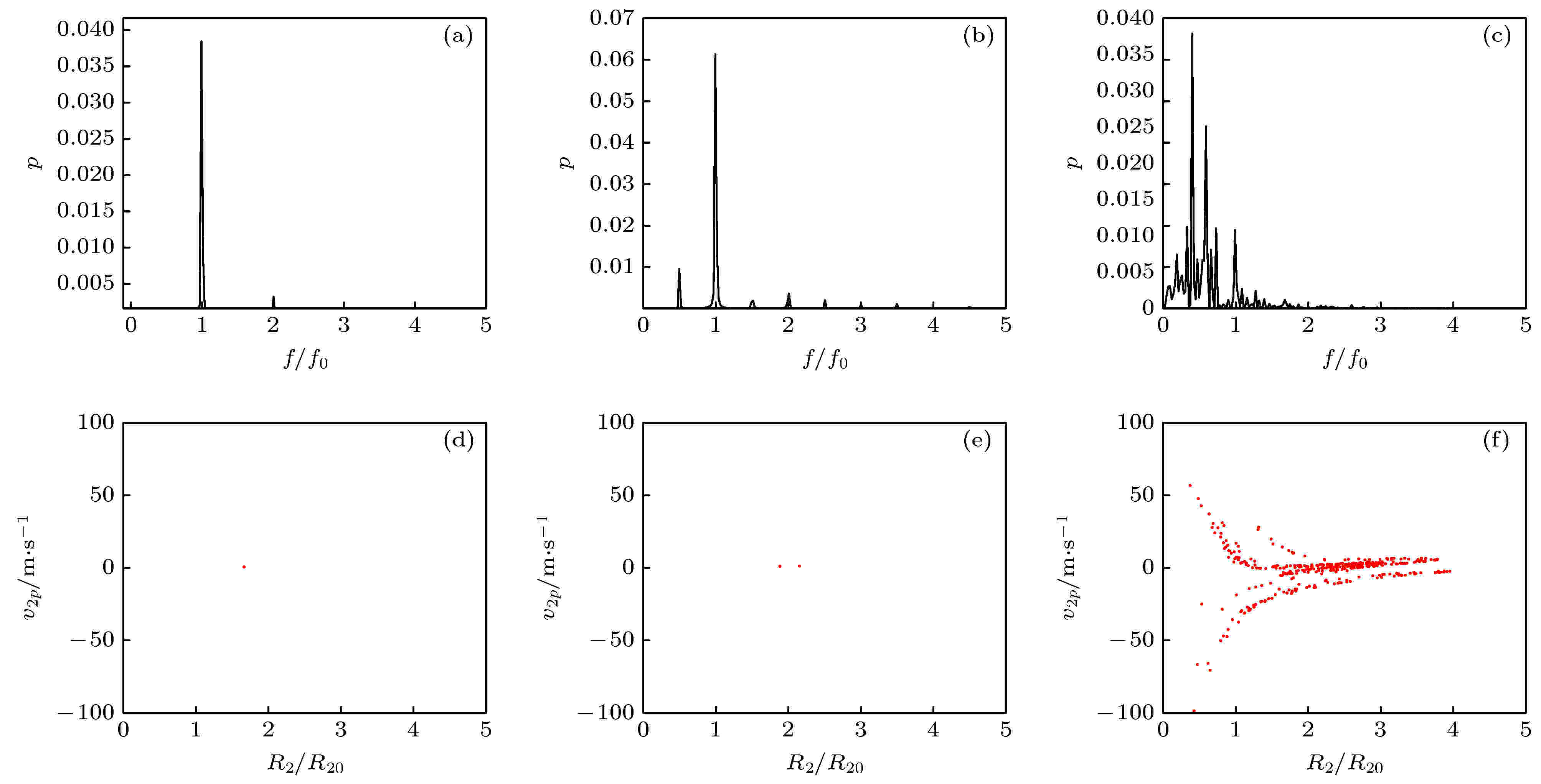图 3 基频激励时MMB频谱图　((a)—(c))和庞加莱截面图((d)—(f)) (R₂₀ = 5 μm)　(a), (d) P_a = 100 kPa; (b), (e) P_a = 255 kPa; (c), (f) P_a = 350 kPa
Figure3. Spectra diagram and Poincaré cross-section of an MMB at f = f₀ (R₂₀ = 5 μm): (a), (d) Pa = 100 kPa; (b), (e) Pa =255 kPa; (c), (f) Pa = 350 kPa

微泡大小是其诊疗应用的关键参数之一.驱动压一定且P_a = 150 kPa时, 初始半径分别为3, 4及5 μm磁性微泡(其本征频率依次为1.60, 1.11及0.85 MHz)频响曲线见图4(a)—(c).在低于微泡共振频率的低频区存在不稳定频响区, 此时驱动声波频率的微小变化将引起R₂/R₂₀的跳跃, 跳跃的幅度一定程度上反映微泡振动过程中能量转换能力的强弱, 是振动非线性及谐波共振叠加的综合体现. 特别地, 当R₂₀ = 5 μm时沿着频率增大方向, 微泡从混沌经倍周期最后进入稳定周期1运动, 呈现倒分岔特性(图4(c)), 表明微泡混沌运动发生在低频区域, 在该区域选择声频率参数可提高超声治疗效果. 对比图4(a)、图4(b)及图4(c)发现, 随初始半径增大, 跳跃点增多且跳跃幅度增大、振动非线性更为强烈, 一般磁性微泡的尺寸都在5 μm以下^[26]; 对初始尺寸一定的微泡可通过控制声波频率使其做稳定周期振动或混沌运动.
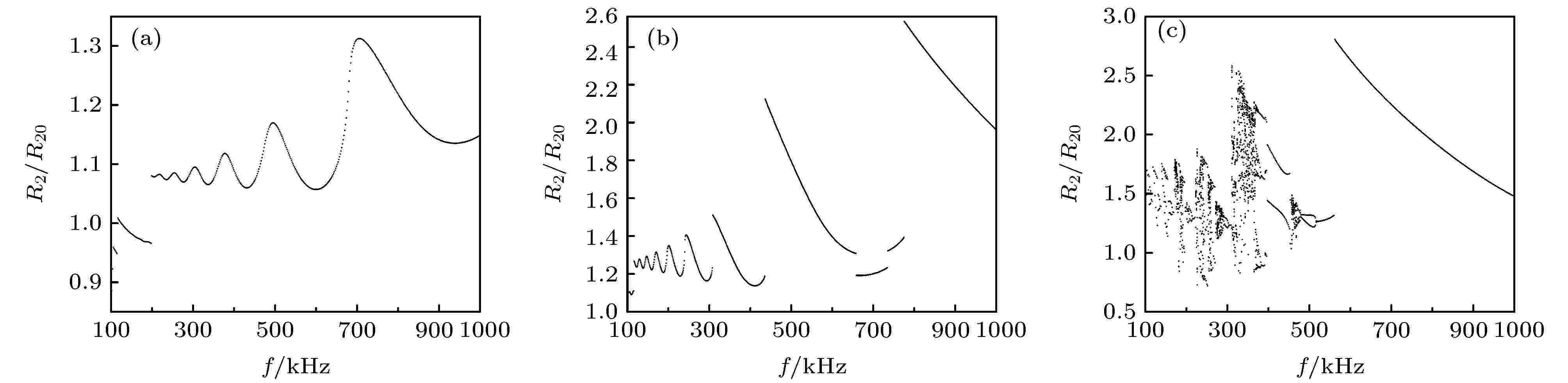图 4 不同尺寸MMB频响曲线(P_a = 150 kPa)　(a) R₂₀ = 3 μm; (b) R₂₀ = 4 μm; (c) R₂₀ = 5 μm
Figure4. Bifurcation diagrams of an MMB with driving frequency as the control parameter at P_a = 150 kPa: (a) R₂₀ = 3 μm; (b) R₂₀ = 4 μm; (c) R₂₀ = 5 μm.

值得注意的是, 图4(c)所展示出的微泡在驱动压一定条件下的倒分岔频率响应特性, 与图2所展示的在固定声波频率时响应是截然不同的, 表明磁性微泡对驱动频率响应具有复杂性. 经对图4(c)混沌区观察发现, 该区域呈现出一定准周期性且每个周期的局部似乎都有与整体相似的倒分岔结构. 若局部与整体有自相似结构, 则表明混沌区是无限多个倍周期分岔的结果^[27]. 为进一步考察微泡频率响应的细节, 在图4(c)中令f在一个小范围取值如取f分别为350, 381 及550 kHz, 图5(a)—(c)给出所相应的振动相图. 当f = 350 kHz时, 相图上存在无数条相轨迹且这些轨迹疏密不均匀, 奇点数目(速度、加速度均为零的点)众多, 表现出强烈的混沌运动特性(图5(a)); 当f =381 kHz时, 奇点数目迅速减少, 极限环中出现近邻轨迹跳跃现象, 其原因主要应归于微泡倍周期振动的非线性(图5(b)); 当f = 550 kHz时, 微泡相轨迹是一曲线环仅有2个奇点(图5(c)), 此时微泡做线性等幅振动.可见, 驱动频率在一个非常小的变化范围, 微泡的运动也是从混沌按倍周期分岔途径、向单极限环过渡的过程, 呈现出与整体相似的倒分岔特性, 证实混沌区是无限多个倍周期分岔的结果.
图 5 混沌态微泡振动相图 (P_a = 150 kPa, R₂₀ = 5 μm)　(a) f = 350 kHz; (b) f = 381 kHz; (c) f = 550 kHz
Figure5. MMB phase diagram in chaotic motion (P_a = 150 kPa, R₂₀ = 5 μm): (a) f = 350 kHz; (b) f = 381 kHz; (c) f = 550 kHz.

2 -->

3.2.颗粒体积分数$ \alpha$的影响

前面讨论了装载有确定体积分数磁性颗粒(α = 0.1)微泡的振动特性, 另一个更为有兴趣的问题是, SPIOs的数量如何影响微泡的振动行为, 同样声场条件下载磁和无磁微泡振动特性的差别. 以磁性纳米颗粒体积分数α = 0作为参照组进行对比, 分析微泡(R₂₀ = 5 μm, d = 100 nm, K = 0.3 N/m)在P_a = 150 kPa, f = 500 kHz时对α的响应, 结果见图6所示. 图6中两条黑色实线代表微泡做周期2运动, 线条附近的点代表在特定频率下微泡振动出现小的扰动.从两条线的变化趋势看, R₂/R₂₀在α = 0时有最大值, 随着α增加R₂/R₂₀线性的缓慢的下降, 表明颗粒的存在一定程度上抑制了泡的振动, 但这种影响总体来看比较小.另外, 在α的一些离散取值点R₂/R₂₀出现波动且α较大处波动稍显密集, 可能与微泡振动的随机不稳定性有关.
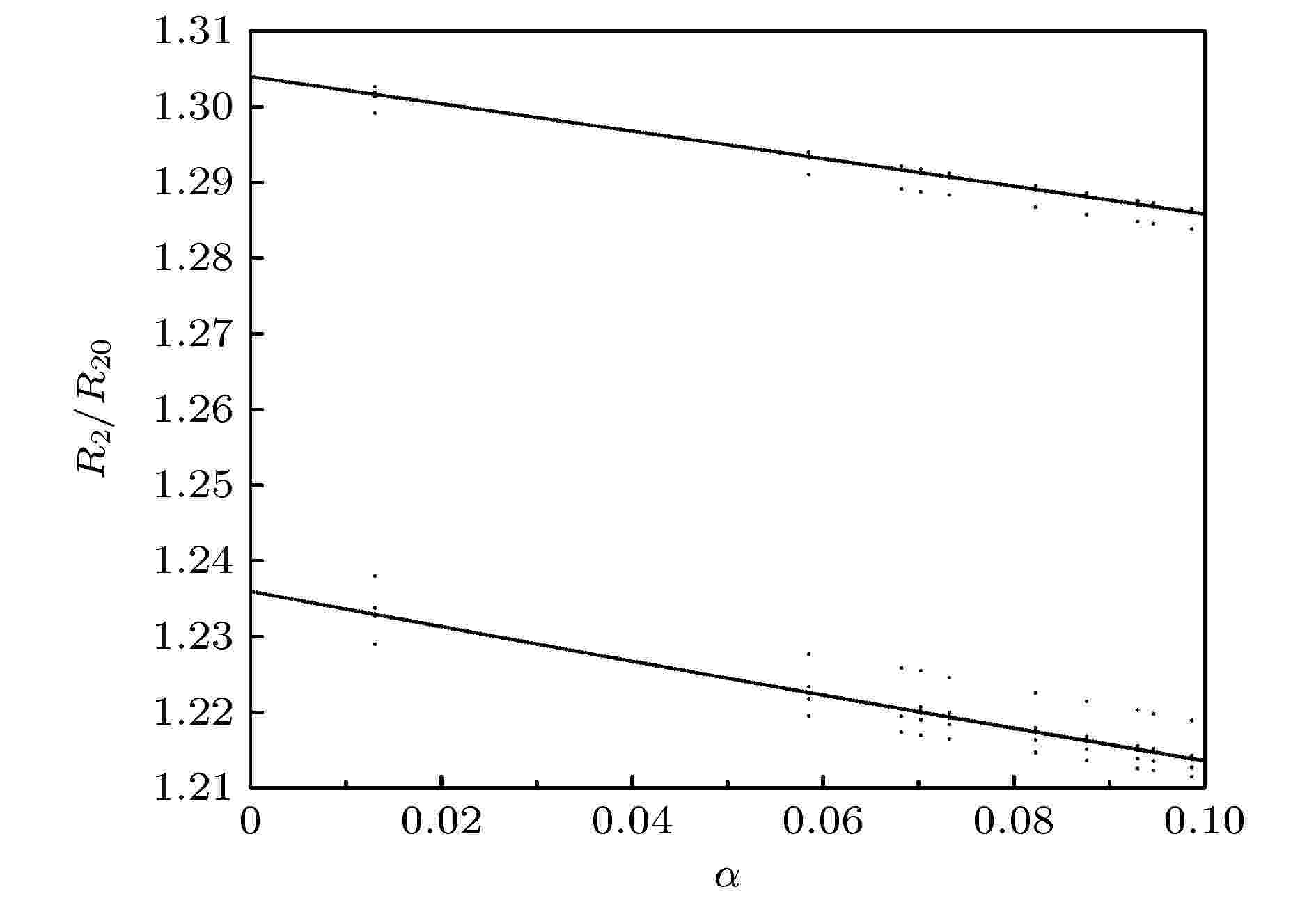图 6 α对R₂/R₂₀的影响
Figure6. R₂/R₂₀ responses to α.

2 -->

3.3.K值的影响

与磷脂膜张力相关的常数K的取值取决于膜层材料特性, (15)式中虽未考虑磷脂薄层厚度, 但却考虑了其所引起的外表面张力变化的影响并通过控制K值体现. 图7显示P_a = 150 kPa, f = 350 kHz, K在0—2 N/m范围内变化时R₂/R₂₀响应分岔图. K在0.2—0.4 N/m之间磁性微泡存在一个不稳定响应区, 大于0.4 N/m或小于0.2 N/m其影响较小. 对油基磁流体为内膜层的磁性微泡, 可通过选择合适的外膜层材料控制其声响应.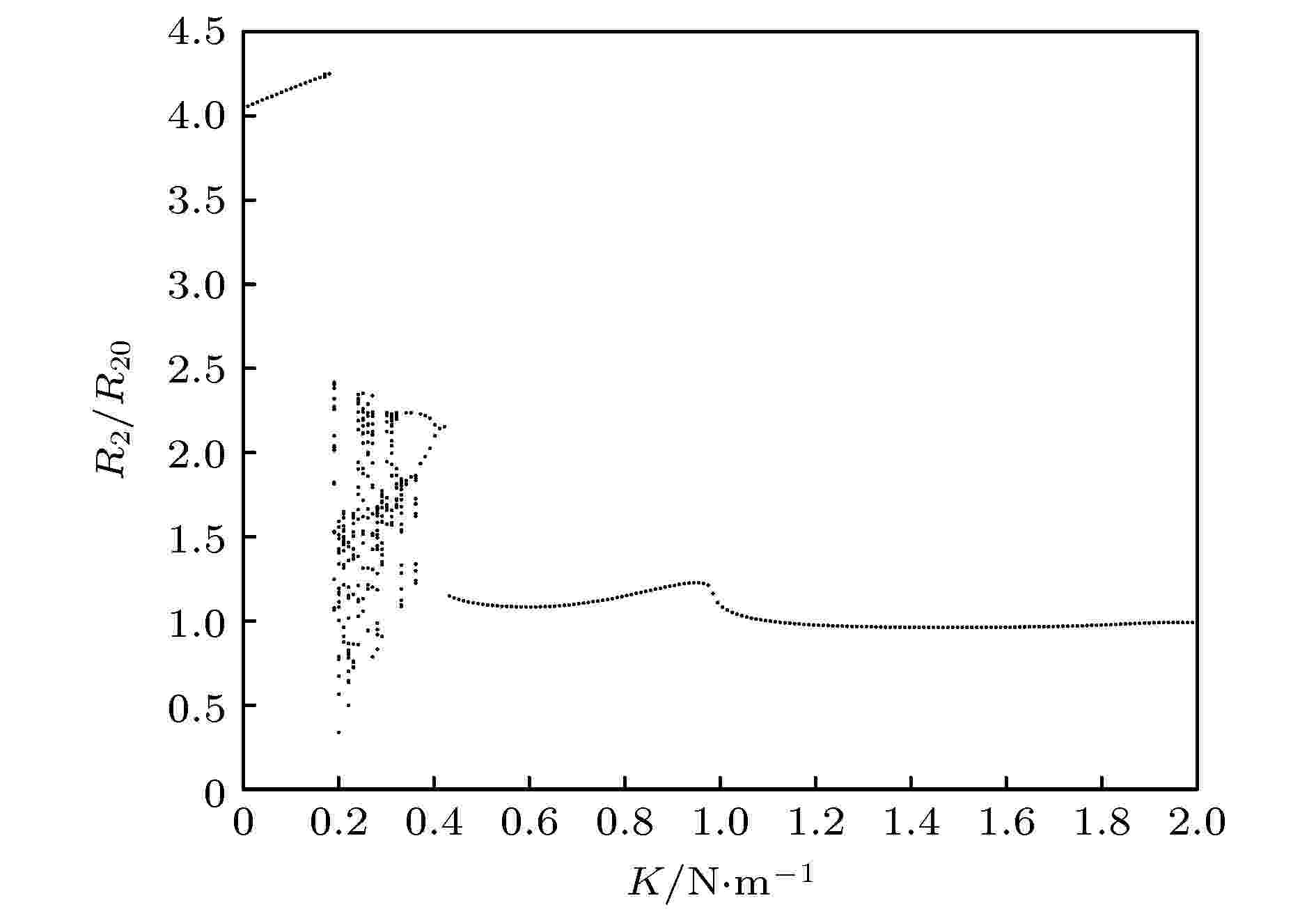
图 7 K值响应
Figure7. MMB responses to K.

2 -->

3.4.膜层厚度的影响

微泡膜层厚度也会对其振动产生影响, 图8给出 f = 350 kHz, P_a = 150 kPa, R₂₀ = 5 μm, α = 0.1, K = 0.3 N/m时微泡的R₂/R₂₀–d变化规律.当d在17 nm以下时泡做稳定的周期1振荡, 随着d逐渐增大振荡失稳进入混沌运动, 在300 nm附近通过倍周期分岔返回稳定周期运动, 可见膜层厚度在50—150 nm附近有利于微泡的谐波响应.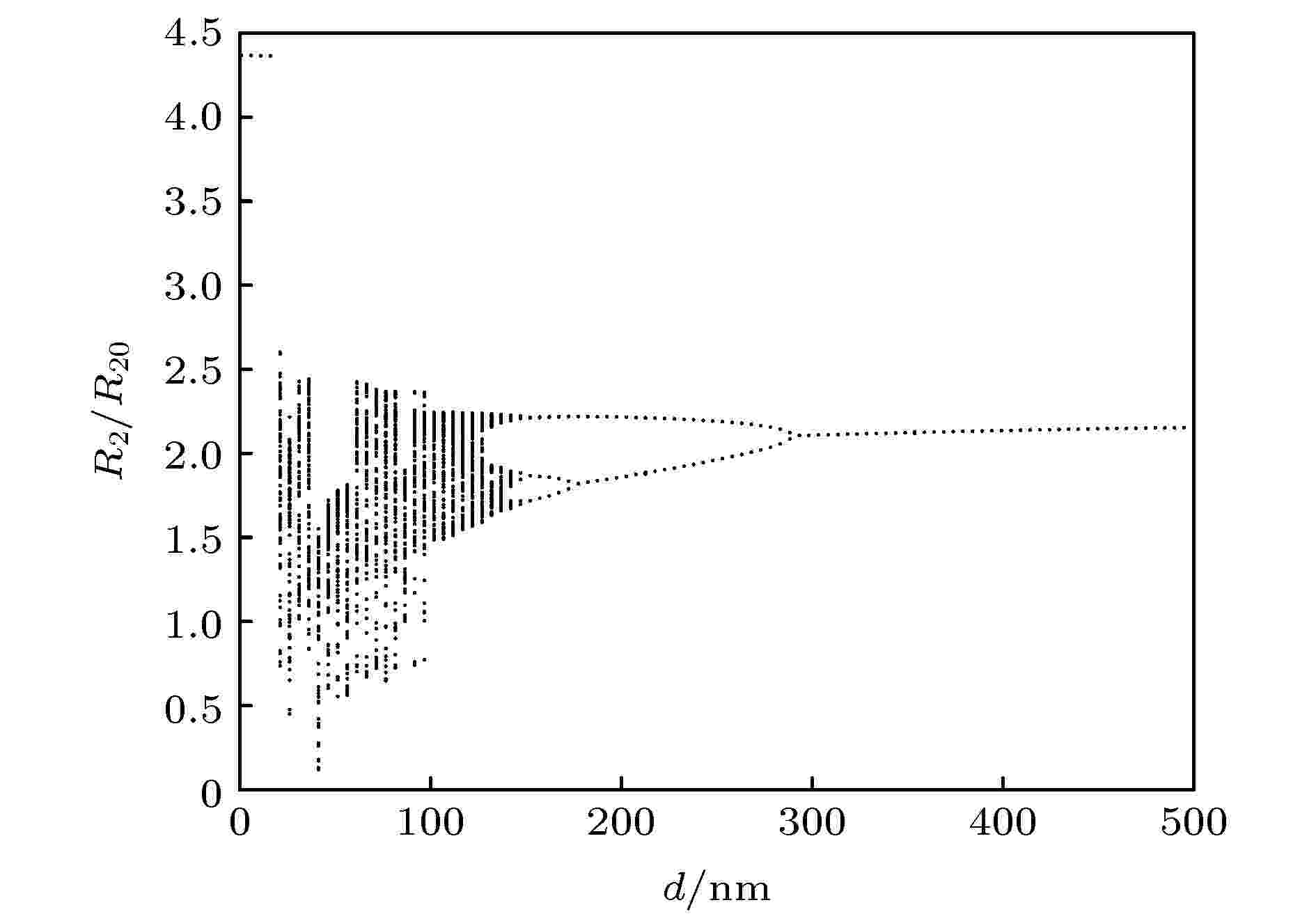
图 8 膜厚响应
Figure8. MMB responses to film thickness.

磁性微泡声响应是进行微泡功能设计、制备组装及超声成像的基础, 以磷脂层为外膜、装载有超顺磁性纳米颗粒的磁流体为内膜, 构建了一种新型双膜层磁性微泡动力学理论模型. 通过数值方法探究了声场参数(压力和频率)、磁性纳米颗粒体积分数及膜层参数(厚度、材料特性)等对微泡振动的影响.得到以下结论: 1) 磁性颗粒的体积分数不超过0.1时, 磁性微泡与一般包膜泡具有相似的声特性, 2f₀驱动下具有最小的谐波阈值, 对驱动声波频率的响应与微泡初始尺寸和驱动压有关; 2) 磁性颗粒的存在抑制了微泡的膨胀和收缩, 但这种抑制作用非常弱; 3) MMB外膜层材料表面张力参数K及膜层厚度d也会影响应泡的行为, K在0.2—0.4 N/m、磁性微泡膜层厚度在50—150 nm附近有利于谐波响应. 以上结论可为功能化磁性微泡的设计和诊疗应用提供有益支持和参考, 同时该理论模型还可用于磁性微泡空化阈值及谐频响应预测. 本研究主要关注单个MMB对时间尺度在($ \sim $1—10 μs)附近超声的响应动力学, 理论模型忽略了液体流动时泡的平移及声辐射力, 同时假设没有外磁场作用, 然而在发展基于磁性微泡的治疗方案中, 在声场和磁场共同作用下磁性微泡可同时保持磁性和声学特性, 而磁场作用下对磁流体膜层产生磁压缩, 定量分析磁场对MMB的振动行为正是我们目前正在进行的工作, 后续将对其进行更详细的讨论.