摘要:金纳米粒子表面修饰剂的组分和形貌影响其物理化学性质. 本文采用隐式溶剂耗散粒子动力学模拟的方法, 研究了金纳米棒、溴化十六烷基三甲基铵和二肉豆蔻酰磷脂酰胆碱的自组装形貌. 结果表明, 复合体组装形貌主要与溴化十六烷基三甲基铵和二肉豆蔻酰磷脂酰胆碱这两种修饰剂的摩尔比有关, 而金纳米棒与修饰剂的相互作用强度以及金纳米棒的直径对形貌的影响不明显. 当作用强度和直径一定时, 随着摩尔比增加, 修饰剂在金纳米棒表面会形成完整的双层膜、有裂痕的双层膜、长片状胶束、以及以螺旋形式缠绕在金纳米棒上的蠕虫状胶束. 进一步分析发现, 金纳米棒直径越小、摩尔比越大、或作用强度越大时, 金纳米棒两端的覆盖程度越高, 同时修饰剂吸附层的厚度越薄. 这些结果直接表征了溴化十六烷基三甲基铵和二肉豆蔻酰磷脂酰胆碱混合物在金纳米棒表面的形态, 在分子水平上加深了对金纳米棒自组装行为的理解, 有助于实现金纳米棒的可控自组装.
关键词: 耗散粒子动力学/
金纳米棒/
磷脂/
表面活性剂

English Abstract

全文HTML

--> --> -->

金纳米棒(gold nanorods, GNRs)作为可溶性贵金属(Au, Ag, Cu等)纳米粒子的一个重要成员^[1-3], 因具有独特的物理化学性质^[4-6]在生物医学领域有巨大的应用潜力, 可用于光热疗法^[7-9]、生物传感^[10-12]、分子成像^[13-15]和癌症治疗的基因传递^[16,17]等. 合成GNRs的方法众多, 主要包括多孔铝模板法^[18]、电化学法^[19]、光化学法^[20]和晶种生长法^[21]. 在这些方法中, 晶种生长法由于历史悠久、能灵活控制GNRs的长宽比、产率较高等特点而被广泛使用. 在用晶种生长法合成GNRs的过程中, 经常使用溴化十六烷基三甲基铵(cetyltrimethylammonium bromide, CTAB)这种阳离子表面活性剂来提高GNRs的产率, 这里的CTAB不仅是诱导剂也是封装剂. CTAB封装的GNRs一般对细胞无害, 但是溶液中游离的CTAB分子具有显著的毒性. 实验表明随着CTAB浓度的增加, 细胞的存活率从100%逐渐下降到20%^[22], 这使得GNRs难以应用到临床. 为了降低毒性, 使GNRs在生物医学领域有更好的应用, 对GNRs进行表面修饰显得尤为重要. 目前主要有三类分子用于GNRs的表面修饰: 聚合物、小分子化合物、无机硅. 在众多修饰剂中, 磷脂作为生物膜的主要成分, 是生命的物质基础, 在解决生物兼容性和稳定性方面^[23]具有明显的优越性. 将GNRs放入含有磷脂的氯仿溶液, 磷脂与GNRs表面的CTAB可以发生交换; 通过测量Zeta电位发现, GNRs表面的CTAB虽然没有被完全替换掉, 但溶液中游离CTAB的毒性已降低到可忽略的程度^[24].
近年来, 金纳米粒子表面修饰剂丰富的斑图引起了众多研究者的兴趣. Galati等^[25]将聚苯乙烯末端接枝在不同形状的金纳米粒子上时, 发现了一个十分有趣的现象: 当纳米粒子的曲率和聚合物接枝密度等条件改变时, 聚合物在纳米粒子表面将形成不同的图案. 对于金纳米立方体来说, 聚合物贴片优先在具有高曲率的12个边缘和8个顶点区域形成; 当金纳米立方体逐渐转变为金纳米球时, 聚合物贴片在其表面均匀分布. 而对于GNRs而言, GNRs表面的聚苯乙烯聚合物贴片呈现出有趣的螺旋分布^[26], 但螺旋形图案仅在特定的聚合物接枝密度和特定的聚合物长度/GNRs直径比条件下才能形成, 超出这些特定范围, 贴片将随机分布在GNRs表面. Tao等^[27]通过改变两种互不相溶的聚苯乙烯和聚乙二醇的摩尔比, 在GNRs表面得到了均匀的和不均匀的聚苯乙烯壳、无规律分布的聚苯乙烯贴片、以及有趣的螺旋形图案. 另外, Wang等^[28]通过简单的分子模板法获得了一种新的手性混合结构, 即离散的短GNRs在CTAB/磷脂混合纳米带中呈现螺旋排列.
实验上可通过光谱或者电子显微镜等技术研究修饰剂分子和GNRs的结构. 例如, 通过核磁共振^[24]、红外光谱^[24]、表面增强拉曼^[29]、局域表面等离子体共振^[29]等方法, 可间接得到溶液中CTAB的含量以及磷脂/CTAB与GNRs表面的结合方式, 但是磷脂与CTAB交换的动力学过程以及结合强度需要进一步的探索. 扫描电子显微镜^[30]和透射电子显微镜^[31]可直接观察到GNRs的一维、二维、三维自组装结构, 如CTAB和乙二胺四乙酸的静电相互作用诱导的头碰头组装^[32]、半胱氨酸分子间的静电相互作用诱导的头碰头组装^[33]、抗原和抗体相互竞争引起的肩并肩组装^[34]. 尽管电子显微镜能够较为快速、直接地观察到GNRs的组装结构, 但由于在制样过程中进行了干燥处理, 显微镜观察到的结构可能并不是GNRs在溶液中的真实结构.
分子动力学模拟可以在原子级别研究GNRs组装和生长过程的形貌和机制. 2003年, Wang和Dellago^[35]对含有1000—10000个金原子的GNRs进行了模拟, 发现GNRs在加热至融化前会经历形貌转变和结构转变, 他们提出了转变机制用来解释实验观察到的GNRs在激光加热过程中的中间产物和内部缺陷. 然而, 该模拟中没有溶液环境和修饰剂. da Silva等^[36]基于Gromos 54a7力场参数^[37]发展了CTAB的全原子模型, 准确地还原了CTAB的胶束特征以及CTAB在金表面的吸附模式. 他们采用该模型研究了溴离子浓度对GNRs表面CTAB胶束结构的影响^[38]及不同曲率的表面在GNRs各向异性生长中的作用^[39]. 但这些研究只模拟了局部GNRs表面, 没有考虑GNRs的整体形貌. 通过采用粗粒化的办法可以模拟完整的GNRs, 例如Oroskar等^[40]研究了聚乙二醇包覆的GNRs跨越二棕榈酰磷脂酰胆碱双层膜的机制. 然而, 该模拟采用了带有周期性边界条件的双层膜, 可能会影响结果的准确性. 为了突破体系尺寸的限制, 可以将水的自由度忽略, 即采用隐式溶剂方法. Horschs等^[41]用粗粒化布朗动力学模拟了模型化的聚合物绳子和GNRs的自组装, 不仅可以重现实验上已经观察到的形貌, 还可以预测新的形貌. 我们小组采用隐式溶剂粗粒化方法, 研究了二肉豆蔻酰磷脂酰胆碱(dimyristoylphosphatidylcholine, DMPC)和GNRs的自组装行为^[42], 发现GNRs之间以头碰头或肩并肩的方式进行组装, 而且DMPC头部和GNRs表面的相互作用强度是决定GNRs吸附的DMPC丰度的一个重要因素, 所吸附的DMPC丰度反过来也会影响DMPC和GNRs的形貌. 根据DMPC和GNRs的摩尔比的不同, 我们还预测了多种DMPC和GNRs组装的形貌, 如环状、树枝状、蠕虫状等. 但是由于当时没有适用于CTAB的力场, 体系中没有加入CTAB分子. 系统中同时存在GNRs, DMPC和CTAB的理论模拟鲜有报道.
本文采用我们新发展的隐式溶剂耗散粒子动力学模拟方法对GNRs-CTAB-DMPC复合体的自组装行为进行了系统研究. 结果表明, 当CTAB含量较低时, CTAB和DMPC的混合物在GNRs表面形成双层膜, 符合实验所推测的结构^[24]; 而当CTAB含量较高时, 二者的混合物在GNRs表面却不再是完整的双层膜. 双层膜的完整程度与CTAB/DMPC摩尔比有关: 随着摩尔比的增加, CTAB和DMPC在GNRs表面先后形成完整双层膜、有裂痕的双层膜、长片状贴片、以及螺旋缠绕GNRs的蠕虫状胶束, 这对实验推测进行了重要的补充和修正. 通过对体系的各项性质进行深入分析, 能够非常直观地了解不同修饰剂组装行为的差异以及不同因素对组装体结构的影响, 为实现GNRs的可控自组装提供了指导.

2

-->

2.1.分子结构和力场

采用隐式溶剂耗散粒子动力学方法(implicit solvent dissipative particle dynamics, Im-DPD)模拟了GNRs-CTAB-DMPC的自组装复合体. 各分子的粗粒化模型如图1所示. 一根GNR由10个珠子连成的硬棒表示; 1个CTAB分子由含有5个珠子的线性链表示, 其中1个H₁珠子代表头部, 其余4个T珠子代表尾巴; 1个DMPC分子含有10个珠子, 其中2个H珠子代表头部, 剩余8个珠子代表尾巴. 在CTAB分子中, 每个H₁珠子带1个单位正电荷; DMPC的H₁和H₂珠子按照偶极子处理, 不带电荷.
图 1 粗粒化模型　(a) GNRs; (b) CTAB; (c) DMPC
Figure1. Coarse-grained model of (a) GNRs, (b) CTAB, and (c) DMPC

在DPD力场中, 当任意两个珠子i和j之间的距离r_ij小于r₀时, 它们之间存在3个成对的两体作用力: 保守力$ {{F}}_{ij}^{\rm{C}} $、耗散力$ {{F}}_{ij}^{\rm{D}} $、随机力$ {{F}}_{ij}^{\rm{R}} $.

${{F}}_{ij}={{F}}_{ij}^{\rm{C}}+{{F}}_{ij}^{\rm{D}}+{{F}}_{ij}^{\rm{R}},r<1.0{r}_{0}{,}$

${{F}}_{ij}^{\rm{C}}={a}_{ij}\left(1-{{r}_{ij}}/{{r}_{0}}\right){\hat{{r}}}_{ij},$

${{F}}_{ij}^{\rm{D}}=-{\gamma }_{ij}{\left(1-{{r}_{ij}}/{{r}_{0}}\right)}^{2}\left({\hat{{r}}}_{ij}.{{v}}_{ij}\right){\hat{{r}}}_{ij},$

${{F}}_{ij}^{\rm{R}}=\sqrt{2{r}_{ij}{k}_{B}T}\left(1-{{r}_{ij}}/{{r}_{0}}\right){\zeta }_{ij}{\hat{{r}}}_{ij}{,}$

这里的r_ij = |r_ij|是位置向量r_ij = r_i－r_j的模; $\hat{{{r}}}_{ij }$ = r_ij/r_ij是向量r_ij的单位向量; r₀是截断半径, 也是DPD的长度单位, r₀ = 0.71 nm; a_ij是DPD排斥力参数(单位为k_BT/r₀, k_B是玻尔兹曼常数, T是约化温度), 描述最大排斥力的强度, a_ij的取值见附录表A1及文献[43]; 向量v_ij = v_i － v_j是粒子i和j之间的速度差; γ_ij (以(k_BTm₀/r₀²)^1/2为单位, m₀是珠子的质量, 在DPD中均为1)是摩擦系数, ζ_ij是对称且均匀分布的随机数.

aij	ION	H1	H2	M	T
ION	100	98	98	102	130
H1	98	110	100	102	130
H2	98	100	110	102	130
M	102	102	102	100	110
T	130	130	130	110	100

表A1DPD力场中a_ij参数的取值(ION, H₁, H₂, M, T珠子分别和文献[43]中的W, Q₀, Q_a, N_a, C珠子一一对应)
TableA1.Values of parameters a_ij in DPD Force field. The ION, H₁, H₂, M, and T beads correspond to the W, Q₀, Q_a, N_a, and C beads in Ref [43], respectively.

为了加快模拟速度, 本文将溶剂进行隐式处理^[44-46]. 该方法通过对保守力添加一段高斯形式的吸引力来体现溶剂的效果, 并对耗散力和随机力进行相应的修正. 这三种力成对地施加在2个珠子上, 使得体系的总动量守恒.

$\begin{split}{{{F}}_{ij}^{\rm{C}}\left({r}_{ij}\right)}^{{\rm{i}}{\rm{m}}}=\;&{{F}}_{ij}^{\rm{C}}\left({r}_{ij}\right)-\frac{2\left({s}_{i}{c}_{i}\right){(s}_{j}{c}_{j})}{{{\kappa }_{\rm{H}}{\rm{\pi }}^{\frac{3}{2}}\left({{\sigma }_{i}}^{2}+{{\sigma }_{j}}^{2}\right)}^{\frac{5}{2}}}\\& \times \left({\rm{e}}^{\frac{-{{r}_{ij}}^{2}}{{{\sigma }_{i}}^{2}+{{\sigma }_{j}}^{2}}}\right){\hat{{r}}}_{ij}{,} \end{split}$

$ \begin{split} {{{F}}_{ij}^{\rm{D}}\left({r}_{ij}\right)}^{{\rm{i}}{\rm{m}}}=\;&{{F}}_{ij}^{\rm{D}}\left({r}_{ij}\right)+{\gamma }_{ij}^{{\rm{i}}{\rm{m}}}{\left({\rm{e}}^{\tfrac{-{{r}_{ij}}^{2}}{{{\sigma }_{i}}^{2}+{{\sigma }_{j}}^{2}}}\right)}^{2} \quad \\& \times\left({\widehat{{r}}}_{ij}\cdot {{v}}_{ij}\right){\widehat{{r}}}_{ij}{,}\end{split}$

$\begin{split} {{{F}}_{ij}^{\rm{R}}\left({r}_{ij}\right)}^{{\rm{i}}{\rm{m}}}=\;&{{F}}_{ij}^{R}\left({r}_{ij}\right) -\sqrt{2{\gamma }_{ij}^{{\rm{i}}{\rm{m}}}{k}_{\rm{B}}T} \qquad\qquad \\&\times\left({\rm{e}}^{\tfrac{-{{r}_{ij}}^{2}}{{{\sigma }_{i}}^{2}+{{\sigma }_{j}}^{2}}}\right){\zeta }_{ij}^{{\rm{i}}{\rm{m}}}{\hat{{r}}}_{ij}{,}\end{split}$

其中, σ_i是扩展宽度; c_i是场和珠子的耦合强度; s_i是缩放参数; κ_H是Helfand系数, 设置为19.69. 上角标im表示和显式溶剂DPD力场采用不同的热浴. σ_i, c_i, s_i的取值见附录表A2及文献[46]. Im-DPD力的截断半径设置为2.5r₀.

	ION	H1	H2	M	T
c	0	19.37	19.37	20.02	24.56
σ	0.5385	0.536	0.536	0.541	0.566
s	0.625	0.625	0.625	0.7135	0.7135

表A2Im-DPD力场中c, σ和s参数的值
TableA2.Values of c, σ, s in Im-DPD Force field.

在之前模拟纯的磷脂体系时^[44-46], 长程处也施加了耗散力((6)式的第二项)和随机力((7)式的第二项). 但在模拟纯的CTAB时, 发现体系的温度会比设定值偏高20%. 这是因为长程的疏水吸引力是用来代替和水有关的作用力, 已经考虑了涨落耗散效应, 不应该再额外施加耗散力和随机力. 当重复施加耗散力和随机力之后, 对于较为凝聚的体系影响较小(例如纯DMPC的体系), 却会使较分散的体系(例如含有离子和CTAB的体系)温度偏高. 在本工作中, 为了更准确地控制温度, 不再对长程(r > r₀)施加(6)式和(7)式中第二项的耗散随机力, 但需要对s_i进行修正, 来还原DMPC磷脂的性质, 详见附录B.
为了维持分子的骨架, 采用二体的键长约束E₂(r)和三体的键角约束E₃(r)来描述成键相互作用能:

$ {E}_{2}\left(r\right)=\frac{1}{2}{K}_{2}{\left(r-{L}_{0}\right)}^{2}, $

$ \left.{E}_{3}\left(r\right)={K}_{3}[1-{\rm{cos}}\left(\theta -{\theta }_{0}\right)\right], $

其中, K₂和K₃分别是描述键强度和角刚度的弹簧系数, L₀和θ₀分别是平衡键长和键角. GNRs, CTAB, DMPC的成键参数见附录表A3.

bond	L0/r0	K2/kBT·r0–2	angle	θ0/(o)	K3/kBT
GN—GN	d/0.71	512	GN—GN—GN	180	600
H1—T	0.47	512	H2—M—M	120	6
H1—H2	0.47	512	H2—M—T	180	6
H2—M	0.47	512	M—T—T	180	6
M—M	0.31	512	T—T—T	180	6
M—T	0.59	512
T—T	0.59	512

表A3Im-DPD力场中的键长、键角和对应的力参数(d是以纳米为单位的金纳米棒的直径)
TableA3.Equilibrium bonds, angles, and corresponding force constants in Im-DPD Force field. d is the diameter of GNRs in unit of nanometer.

为了更准确地描述粒子之间的静电作用, 需要考虑长程静电相互作用. 由于DPD中的作用单元是软珠子, 为了避免珠子间强烈的粒子耦合, 不宜直接采用库仑定律, 这里采用由格点求和法推导的解析形式^[47]:

$\begin{split}& F\left( r \right) = \\& \left\{\begin{aligned}&{1.6\left( {\frac{r}{{r_{\rm{e}}^3}} - \frac{{{r^3}}}{{r_{\rm{e}}^5}}} \right) + 0.699\frac{{{r^{4.145}}}}{{{{r}}_{\rm{e}}^{6.145}}},~~r < {r_{\rm{e}}},}\\&{\frac{1}{{{r^2}}} - \frac{{9.63}}{{r_{\rm{e}}^2}}{{\left( {1 - \frac{r}{{2{r_{\rm{e}}}}}} \right)}^5},~~{r_{\rm{e}}} < r < 2{r_e},}\\&{\frac{1}{{{r^2}}},~~\;2{r_{\rm{e}}} < r < 3.125{r_{\rm{e}}},}\end{aligned}\right.\end{split}$

其中, r_e是静电拖尾半径, 设为r_e = 1.6, r₀ = 1.136 nm.
由于GNRs尺寸远大于修饰剂分子, 不宜采用软球DPD势, 采用Lennard-Jones (L-J)硬球势来描述修饰剂以及离子和GNRs之间的体积排斥势:

${U}_{{\rm{L}}-{\rm{J}}}\left(r\right)=4\varepsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^{6}\right],\;\;\;\;r<{2}^{1/6}\sigma {.}$

这里, ε是势阱深度, 设置为5k_BT. σ是L-J势为0处的距离, 2^1/6σ是L-J力为0处的距离. 截断半径设置为2^1/6σ, 即只采用L-J力的排斥部分. 2^1/6σ反映了珠子的物理尺寸, 等于两个珠子直径的平均值. 对于两个不同的金珠子的作用, 2^1/6σ的值从2 nm设置到5 nm, 来模拟GNRs有不同直径d. 对于金珠子和其他小珠子的作用, 2^1/6σ等于(d + 0.5)/2 nm, 0.5 nm近似为这些小珠子的直径. 需要注意到, 这里没有采用DPD软珠子的直径0.71 nm, 而是采用了Martini力场^[48]中硬珠子的直径0.47 nm的近似值.
为了描述GNRs对CTAB/DMPC的头部H珠子的吸附作用, 采用了Morse势^[42].

$\begin{split}{U}_{\rm{Morse}}\left(r\right)=\;& D\left[{\rm{e}}^{-2\alpha \left(r-{r}_{{\rm{m}}{\rm{b}}}\right)}-2{\rm{e}}^{-\alpha \left(r-{r}_{{\rm{m}}{\rm{b}}}\right)}\right], \\ & r<3.2{r}_{{\rm{m}}{\rm{b}}}{,}\end{split}$

式中, r_mb是Morse势的平衡位置, 设置为(d + 0.5)/2 nm; α用来描述Morse势的势阱深度, 设置为1.25; D是Morse势的强度, D越大则GNRs和修饰剂头部之间的相互作用越强. 实验上可以通过改变盐浓度调节作用强弱, 本文中D的取值从1k_BT到4k_BT, 和之前模拟的GNRs-DMPC体系^[42]一致.
附录A中进一步讨论了该工作中势能函数和参数的选择依据.
2 -->

2.2.模拟设置

下面分别对CTAB-DMPC和GNRs-CTAB-DMPC两个体系进行了模拟. 在不含GNRs的体系中, CTAB和DMPC的总数目N设置为1000, 1500, 2000, 2500个, 摩尔比选择1∶1, 3∶2, 4∶1, 8∶1, 16∶1, 1∶0, 其中1∶0代表只有CTAB. 在含有GNRs的体系中, GNRs的直径d设置为2, 3, 4和5 nm. 根据比表面积换算出, 修饰剂分子数量N需要满足2∶3∶4∶5的比例关系, 即N分别选为1000, 1500, 2000和2500, 才能保证GNRs被基本包覆. CTAB/DMPC摩尔比的取值范围和第一个体系相同. GNRs和修饰剂头部的相互作用强度D的取值从1k_BT到4k_BT. 为了保持体系的电中性, 在两个体系中均加入了和CTAB数目相同的1价阴离子, 介电常数设置为15.
使用本课题组开发的耗散粒子动力学程序模拟复合体的自组装. 模拟采用正则系综和周期性边界条件, 模拟盒子的3个边长均为50 nm, 温度设置为298 K, 时间步长Δt设置为0.02τ (τ = τ₀(m₀/k_BT)^1/2). 每个体系进行400000 τ的模拟, 后一半轨迹用来计算性质. 使用VMD^[49]软件可视化所有的模拟样本.

2

-->

3.1.CTAB-DMPC的组装形貌

如图2所示, 在无GNRs的体系中, CTAB-DMPC的组装形貌只取决于二者的摩尔比, 而与N无关. 具体来看, 当摩尔比为1∶1和3∶2时, 混合体系形成稳定的椭球囊泡; 当摩尔比增加至4∶1时, 囊泡破裂成多个片状胶束; 继续增加摩尔比至8∶1时, 一部分片状胶束分离开来, 形成蠕虫状; 当摩尔比增加至16∶1时, 蠕虫状胶束占体系的多数; 当体系中只有CTAB时, 体系呈现多个短的蠕虫状胶束, 这与Illa-Tuset等^[50]使用Dry-Martini力场模拟1000个CTAB分子组装所观察到的现象类似.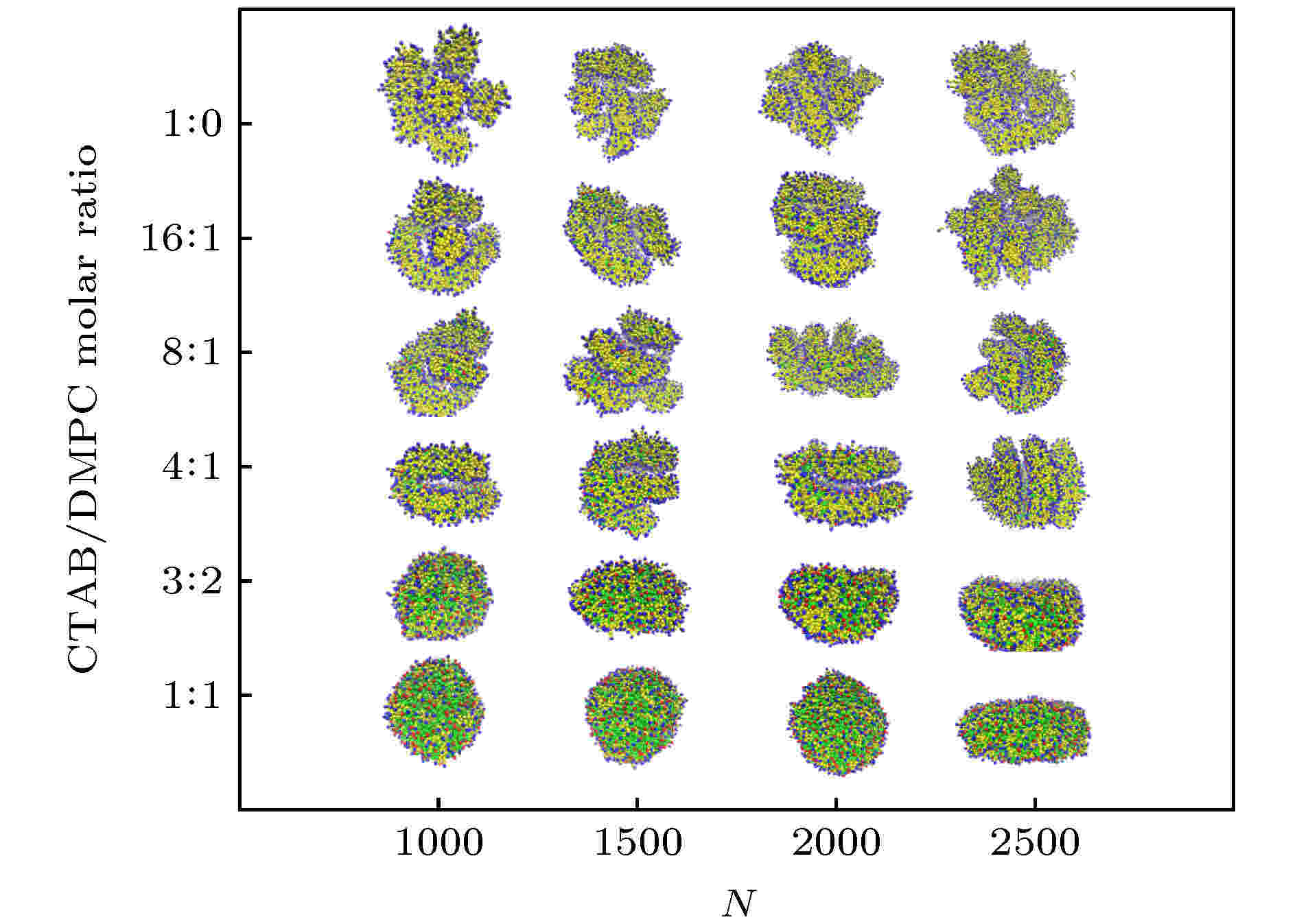
图 2 CTAB和DMPC混合物的形貌图(CTAB的头部H和尾巴T珠子分别用蓝色和黄色表示, 而DMPC的H和M/T珠子分别用红色和绿色表示)
Figure2. Morphology of a mixture of CTAB and DMPC. The H and T beads of CTAB are colored in blue and yellow, while the H and M/T beads of DMPC are in red and green, respectively.

2 -->

3.2.GNRs-CTAB-DMPC的组装形貌

为了研究GNRs-CTAB-DMPC的组装形貌, 需要设置合适的金纳米棒直径d和Morse势D参数. 我们在前期工作^[42]中将d设置为4 nm, 本工作将d设置为2—5 nm来研究d对组装行为的影响. Morse势的D反映了修饰剂和GNRs之间的相互作用强度, D越大表示结合越强. 当D ≤ 0.75k_BT时, 磷脂囊泡无法封装GNRs; 当D ≥ 5k_BT时, 磷脂和GNRs组装成致密的堆积结构, 磷脂膜的双层结构被破坏^[42]. 所以本研究将D设置为1k_BT — 4k_BT. 当D = 1k_BT — 4k_BT, d = 2—5 nm时, 还对GNRs-DMPC体系进行了模拟(相当于CTAB/DMPC摩尔比为0∶1, 详见附录C), 发现纯DMPC均以双层膜的形式包覆GNRs, 这与前期工作的结果^[42]一致, 进一步说明了D和d的取值在合理的范围之内.
如图3所示, 以d = 4 nm和D = 4k_BT为例, 可以看出随着CTAB/DMPC摩尔比从1∶1逐渐增加到1∶0时, CTAB和DMPC在GNRs表面依次形成完整的双层膜(摩尔比为1∶1和3∶2), 不完整的双层膜(4∶1), 长的片状胶束(8∶1), 短的蠕虫状胶束(16∶1、1∶0). 其中, 部分蠕虫会以一定的螺旋缠绕住GNRs. 这些形貌与Tao等^[27]改变GNRs表面两种互不相溶的高分子聚合物的摩尔比形成的形貌十分相似. 本文还绘制了GNRs表面修饰剂分布的投影展开图, 来更好地观察这些形貌, 见附录D中的图D1.
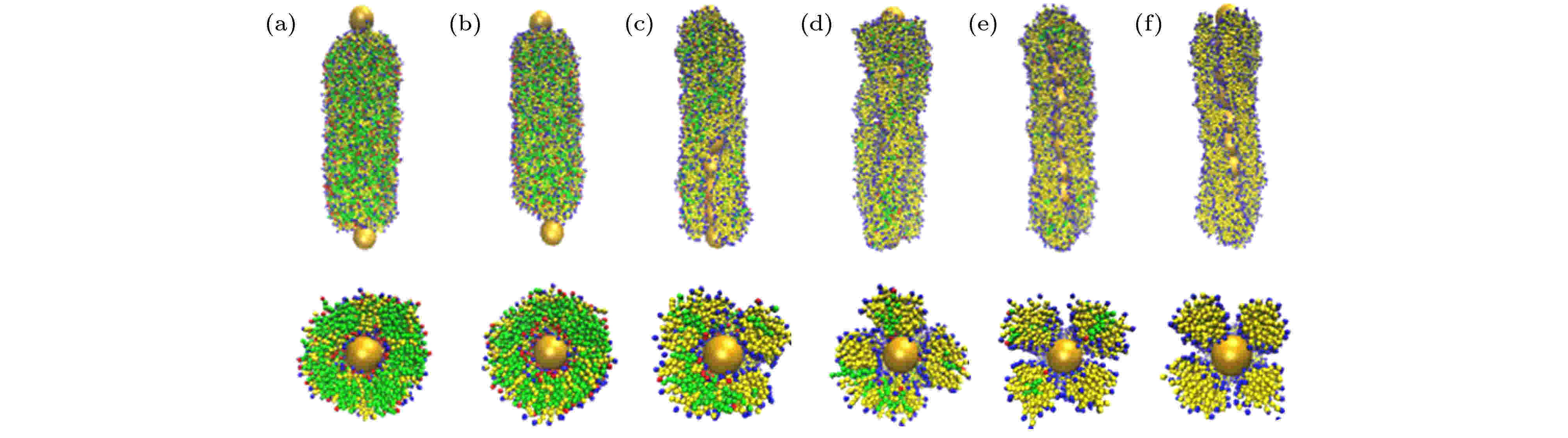图 3 GNRs-CTAB-DMPC复合体在d = 4 nm, D = 4k_BT时的组装形貌, 其中CTAB/DMPC摩尔比分别为(a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0
Figure3. Morphology of assembled GNRs-CTAB-DMPC complex with d = 4 nm and D = 4k_BT. The CTAB/DMPC molar ratio is (a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0, respectively.

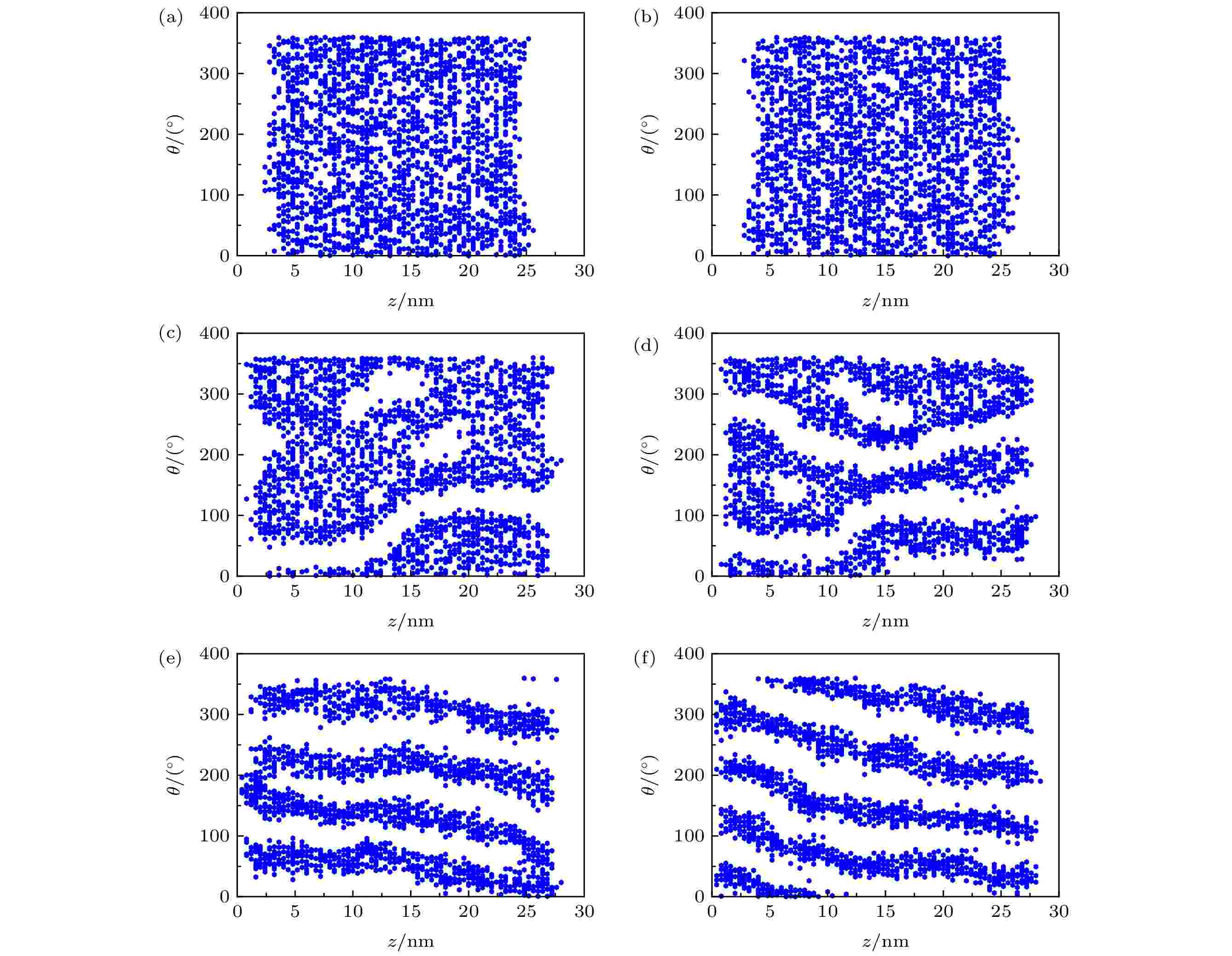图 D1 d = 4 nm和D = 4 k_BT时GNRs表面修饰剂的投影展开分布图, 其中摩尔比分别为(a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0
FigureD1. Projected expansion map of coating agents distributing on the surface of GNRs. Data is obtained at d = 4 nm and D = 4 k_BT. The CTAB/DMPC molar ratio is (a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0.

与图2中不含GNRs的形貌相比, 图3中CTAB和DMPC变得更加有序. 例如, 当摩尔比等于1∶1和3∶2时, CTAB和DMPC不再是变形的椭球形囊泡, 而是均匀地包裹住GNRs; 当摩尔比为4∶1时, CTAB和DMPC不再以片状胶束分散在盒子中, 而是均匀地包覆上GNRs, 并留下一道和GNR的轴线近似平行的裂缝; 当摩尔比更大时, CTAB和DMPC不再是随机分散的蠕虫, 而是大致沿一个方向缠绕住GNRs.
尽管GNRs对CTAB和DMPC的组装有很强的诱导作用, 但不会严重破坏它们的内部结构. 当摩尔比小于等于3∶2时, GNRs表面的CTAB和DMPC呈现完整的双层膜, 这与实验推测一致^[24]. 但是, 当摩尔比大于等于4∶1时, CTAB和DMPC不再是完整的双层膜, GNRs表面也有不同程度的裸露, 这一现象是实验没有注意或无法观测到的.
图4(a)和图4(b)展示了不同D和d下组装形貌随CTAB/DMPC摩尔比的变化趋势. 可以看出, 组装形貌受到D(d)的影响较小, 主要与摩尔比有关. 在每一种D和d的情况下, 形貌随着摩尔比变化的规律与图3非常相似.
图 4 (a) 当金纳米棒直径d = 4 nm时, GNRs-CTAB-DMPC复合体在不同CTAB/DMPC摩尔比及D下的组装形貌; (b) 当Morse势参数D = 4k_BT时, GNRs-CTAB-DMPC复合体在不同CTAB/DMPC摩尔比及d下的组装形貌
Figure4. (a) Morphology of assembled GNRs-CTAB-DMPC complex at various CTAB/DMPC molar ratio and D with given GNR diameter d = 4 nm; (b) morphology of assembled GNRs-CTAB-DMPC complex at various CTAB/DMPC molar ratio and d with given Morse potential parameter D = 4k_BT.

2 -->

3.3.CTAB和DMPC在蠕虫或双层膜内部的分布

为了更好地理解CTAB和DMPC在GNRs表面组装的细节, 定义了修饰剂分子的骨架和GNRs形成的夹角α, 来区分蠕虫和双层膜. 如图5(a)和图5(b)所示, α角是H₁-GN和H₁-T两条向量之间的夹角. 根据α角大小可判断修饰剂分子所处的位置: 当0° < α < 40°时, 修饰剂分子分布在远离GNRs的一侧(称之为外层); 当140° < α < 180°时, 修饰剂分子分布在靠近GNRs的一侧(称之为内层); 当40° < α < 140°时, 修饰剂分子分布在中间区域(称之为中间层).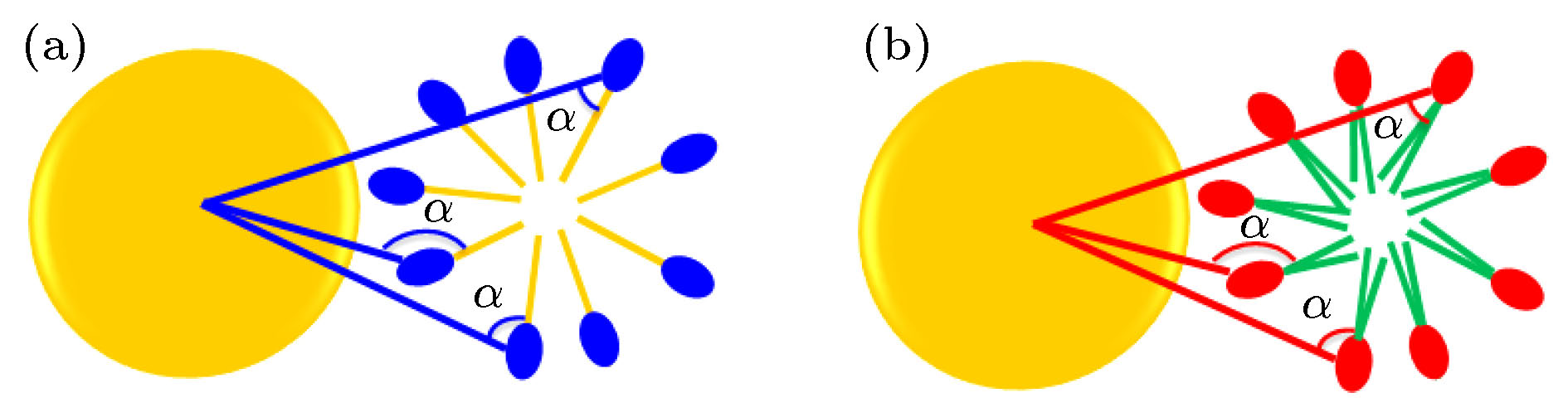
图 5 (a) CTAB和(b) DMPC的$ \alpha $角的定义示意图
Figure5. Schematic diagram of definition of $ \alpha $ for (a) CTAB and (b) DMPC.

在游离的蠕虫形貌中, α角在0 —180°之间均匀分布. 假设蠕虫被GNRs吸附以后不会发生严重的变形(图6(a)中F_worm与D无关从侧面证实了这一点), 那么中间层的修饰剂百分比近似为(140－40)/180 = 56 %. 而对于平整的双层膜来说, 修饰剂分子会更多地分布在内外两层. 据此, 通过对所有吸附的修饰剂分子的α角进行统计, 可以分析体系中蠕虫和双层膜的含量. 为了方便分析, 定义了蠕虫系数F_worm:
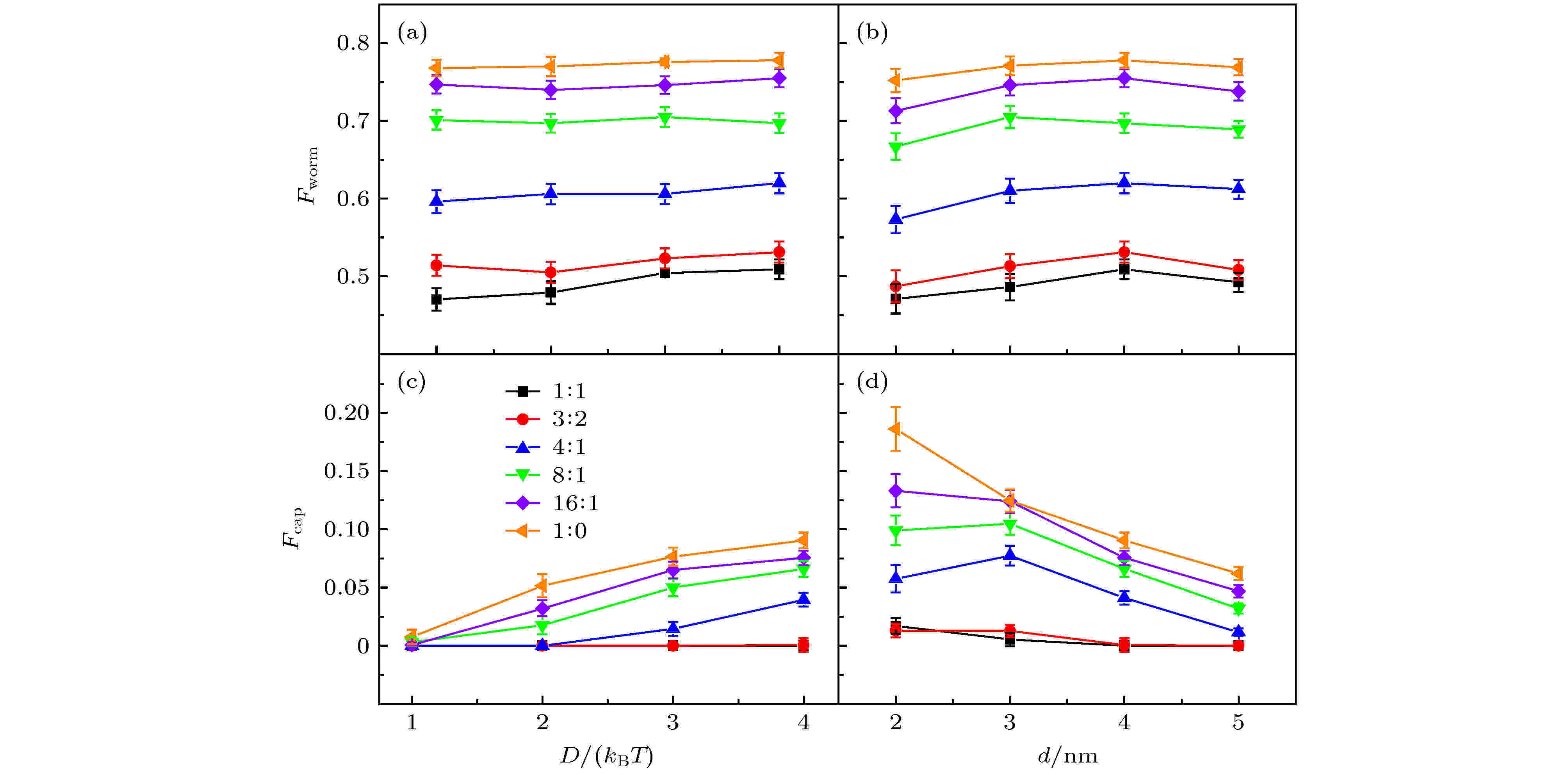图 6 (a) 修饰剂的蠕虫系数F_worm与D的关系图; (b) F_worm与d的关系图; (c) GNRs的覆盖率F_cap与D的关系图; (d) F_cap与d的关系图; 不同颜色的直线代表不同的摩尔比
Figure6. (a) Worming coefficient F_worm of coating agents as a function of D; (b) F_worm as a function of d; (c) capping rate F_cap of GNRs as a function of D; (d) F_cap as a function of d. Results are obtained at various CTAB/DMPC molar ratios, shown in different colors.

${F_{{\rm{worm}}}} = \left\langle {\frac{{ \displaystyle\sum\nolimits_{40^\circ < {\alpha _i} < 140^\circ } {\alpha _i}}}{{\displaystyle\sum\nolimits_{0^\circ < {\alpha _i} < 180^\circ } {\alpha _i}}}} \right\rangle ,$

(13)式的分母是对所有被GNRs吸附的修饰剂按照α角进行的求和; 分子是对被GNRs吸附的中间层修饰剂按照α角进行的求和, $ \left\langle \cdot \right\rangle $代表求系综平均. F_worm值越大, 说明体系中蠕虫的比例越高, 双层膜的比例越低.
如图6(a)和图6(b)所示, 当D和d不变时, 摩尔比越大, 修饰剂的F_worm越大, 说明体系中出现了更多的蠕虫; 增加D或d, 修饰剂的F_worm几乎保持不变. 这些结果和图4中的形貌一致, 同时说明影响蠕虫的主要因素是CTAB/DMPC的摩尔比, 而与GNRs的直径大小或者GNRs对修饰剂的吸附力强弱无关.
当摩尔比增加时, 体系中CTAB的比例增加, CTAB的增多使得体系的蠕虫化程度提高, 这一现象和CTAB的结构有关. CTAB的头部大而尾巴小, 侧面投影呈现倒三角的形状, 使得它们更容易组装成胶束, 在金纳米棒表面以多角度吸附, 形成蠕虫. 而DMPC的头部比CTAB略小, 并且多了一条尾巴, 侧面投影呈现梯形的形状, 易于形成平面双层膜, 在金纳米棒表面以垂直于轴的角度吸附, 不易形成蠕虫. 这一现象提示我们, 在实验室制备GNRs时, 可以根据需要选择合适形状的修饰剂分子.
2 -->

3.4.CTAB和DMPC沿GNRs轴向的分布

在图4(a)和图4(b)的形貌中, GNRs的两端存在较大程度的裸露. 为了定量地研究这一问题, 定义了GNRs表面的覆盖率:

${F_{{\rm{cap}}}} = \left\langle {1 - \frac{{{N_{2 - 9}}}}{{{N_{1 - 10}}}}} \right\rangle ,$

这里, N_2—9和N_1—10分别是第2—9和第1—10个GN珠子吸附的修饰剂分子个数. 覆盖率描述了两端的GN珠子吸附的修饰剂占总吸附的修饰剂的比例, 反映了修饰剂朝两端迁移的程度. 理想情况下, 覆盖率为2/10=0.2.
如图6(c)和图6(d)所示, 当CTAB/DMPC摩尔比为1∶1和3∶2时, GNRs的覆盖率几乎为0, 对应的GNRs两端有着非常大程度上的裸露(图4). 这些形貌的共同特点是修饰剂的吸附层非常完整. 完整的膜被拉长需要克服很高的能量, 所以不容易包覆住GNRs的两端. 当CTAB/DMPC摩尔比大于等于4∶1时, GNRs的覆盖率逐渐增加. 此时, 修饰剂形成了片状的胶束或者蠕虫(图4), 相比于完整的双层膜来说, 它们更容易延展, 只需要克服很少的能量就可以移动到GNRs的两端.
在相同的摩尔比下, 随着相互作用强度D的增加, GNRs两端的覆盖率逐渐增大(图6(c)). 覆盖率和D的正相关说明了修饰剂的吸附需要一定的吸附力来维持, 换句话说, GNRs的两端是吸附的不稳定区域. 而当GNRs直径d增加时, GNRs两端的覆盖率逐渐减小. 可能的原因是, 随着d的增加GNRs表面的曲率减小, 吸附层变得更加平整, GNRs和吸附层之间的接触面积更大, 需要克服更多的能量来覆盖GNRs的两端.
我们注意到, d = 2 nm处覆盖率明显偏低. 为了找到覆盖率异常的原因, 对d = 2, 3, 4 nm, 摩尔比为4∶1的体系各补充了2个平行样. 在对3个样本进行平均以后, 发现覆盖率仍然在d = 2 nm处存在异常的极小值(数据未列出). 事实上, 摩尔比为8∶1, 16∶1的体系中也存在这一现象. 可能原因是饱和吸附的修饰剂个数和GNRs的直径(比表面积)之间并不是严格的线性关系, 但在制备初始结构时却按照线性的比例关系来添加总修饰剂个数, 使得d = 2 nm的体系中总修饰剂个数不足, 从而让覆盖率偏低. 对于摩尔比为1∶0, 3∶2, 1∶1的体系, 在d = 2 nm处没有发现覆盖率异常. 这是因为纯CTAB蠕虫(摩尔比1∶0)的延展性最强, 可以弥补修饰剂个数不足带来的影响; 而完整的双层膜(摩尔比3∶2, 1∶1)很难被拉伸至GNRs两端, 使得覆盖率对d的依赖关系不明显. 不管怎样, 图6中覆盖率和d的整体依赖关系仍然存在, 实验可以参考该规律来添加修饰剂, 让GNRs两端刚好被包覆.
实验室在制备GNRs时, 最后一步常常进行离心分离操作, 这一步很可能会将吸附较弱的修饰剂分子从GNRs上剥离. 从模拟中能够发现, GNRs两端被修饰剂覆盖的程度较底, 吸附较弱, 这些修饰剂分子(尤其是DMPC)会被优先分离掉. 这样, 两端的金珠子很可能裸露出来, 这和实验上猜测的修饰剂完全包覆GNRs的结构有所不同. GNRs的裸露部位和程度还可以解释实验上看到的CTAB和DMPC不同的组装行为^[24]: 对于DMPC和GNRs组装的双层膜包覆形貌, 由于金纳米棒的两端裸露得多, 静电排斥作用使它们不易头碰头相连, 而是在侧面以肩并肩的方式组装; 但当CTAB较多时, 修饰剂以蠕虫缠绕, 金纳米棒的中间部位有更大程度的裸露而使侧面之间的排斥更强, GNRs倾向以头碰头的形式相连. 另外, 多个GNRs在进行头碰头组装时, 表面的蠕虫很可能发生融合, 这也许可以解释Wang等^[28]观察到的GNRs较大规模的手性螺旋形态.
2 -->

3.5.CTAB和DMPC在GNRs表面的径向分布

3.4节中计算了GNRs的覆盖率, 它反映了修饰剂的吸附层在GNRs表面的铺展面积. 为了定量地研究吸附层的厚度, 还计算了径向分布函数(radial distribution function, RDF). 图7给出了在不同CTAB/DMPC摩尔比及不同D下, GNRs表面的CTAB与DMPC的H₁珠子与金珠子之间的RDF. 当D ≤ 2 k_BT时, RDF曲线在3和6 nm附近会出现2个峰(位置记作r₂, r₃), 分别对应靠近GNRs的内层和远离GNRs的外层. 当D ≥ 3 k_BT时, RDF曲线在2.5 nm附近还会出现1个额外的峰(位置记作r₁), 对应的H₁珠子陷入相邻GN珠子之间的缝隙里(附录E中的图E1). 在RDF曲线上, 对r₂和r₃作差, 可以近似得到蠕虫或双层膜厚度L_mem. 不同D及CTAB/DMPC摩尔比下, GNRs表面CTAB与DMPC的H₁珠子的r₁, r₂, r₃和L_mem的值见附录E中的表E1.
图 7 CTAB与DMPC的H₁珠子和金珠子在不同D及CTAB/DMPC摩尔比下的RDF, 其中摩尔比分别为(a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0
Figure7. RDF between H₁ bead of CTAB and DMPC and gold bead at various D and CTAB/DMPC molar ratios. The molar ratio is (a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0, respectively.

Molar ratio	D = 1kBT				D = 2kBT				D = 3kBT					D = 4kBT
	r2	r3	Lmem		r2	r3	Lmem		r1	r2	r3	Lmem		r1	r2	r3	Lmem
1∶1	2.88	6.33	3.45		2.72	6.11	3.39			2.62	5.82	3.2		2.24	2.68	5.78	3.1
3∶2	2.93	6.42	3.49		2.72	5.95	3.23			2.64	5.71	3.07		2.25	2.66	5.63	2.97
4∶1	2.89	6.1	3.21		2.8	5.75	2.95		2.32	2.73	5.62	2.89		2.29	2.67	5.36	2.69
8∶1	2.75	6.06	3.31		2.74	5.71	2.97		2.3	2.74	5.52	2.78		2.24	2.70	5.36	2.66
16∶1	2.87	6.09	3.22		2.71	5.74	3.03		2.23	2.70	5.58	2.88		2.26	2.74	5.46	2.72
1∶0	2.75	5.89	3.14		2.79	5.60	2.81		2.29	2.67	5.42	2.75		2.29	2.77	5.36	2.59

表E1不同D及CTAB/DMPC摩尔比下的r₁, r₂, r₃和L_mem
TableE1.r₁, r₂, r₃ and L_mem at different combinations of D and CTAB/DMPC molar ratio.

如图8所示, 无论是增加D还是增加摩尔比, L_mem都是整体降低. 进一步分析发现, 这两种方式减小膜厚的原因不同. 当D逐渐增加时, r₂, r₃明显降低, 并且r₃降低的幅度更大, 使得修饰剂的吸附层变薄. 而增加摩尔比时, r₂没有发生明显的变化, r₃明显降低, 这是由CTAB分子本身比DMPC分子更短造成的.
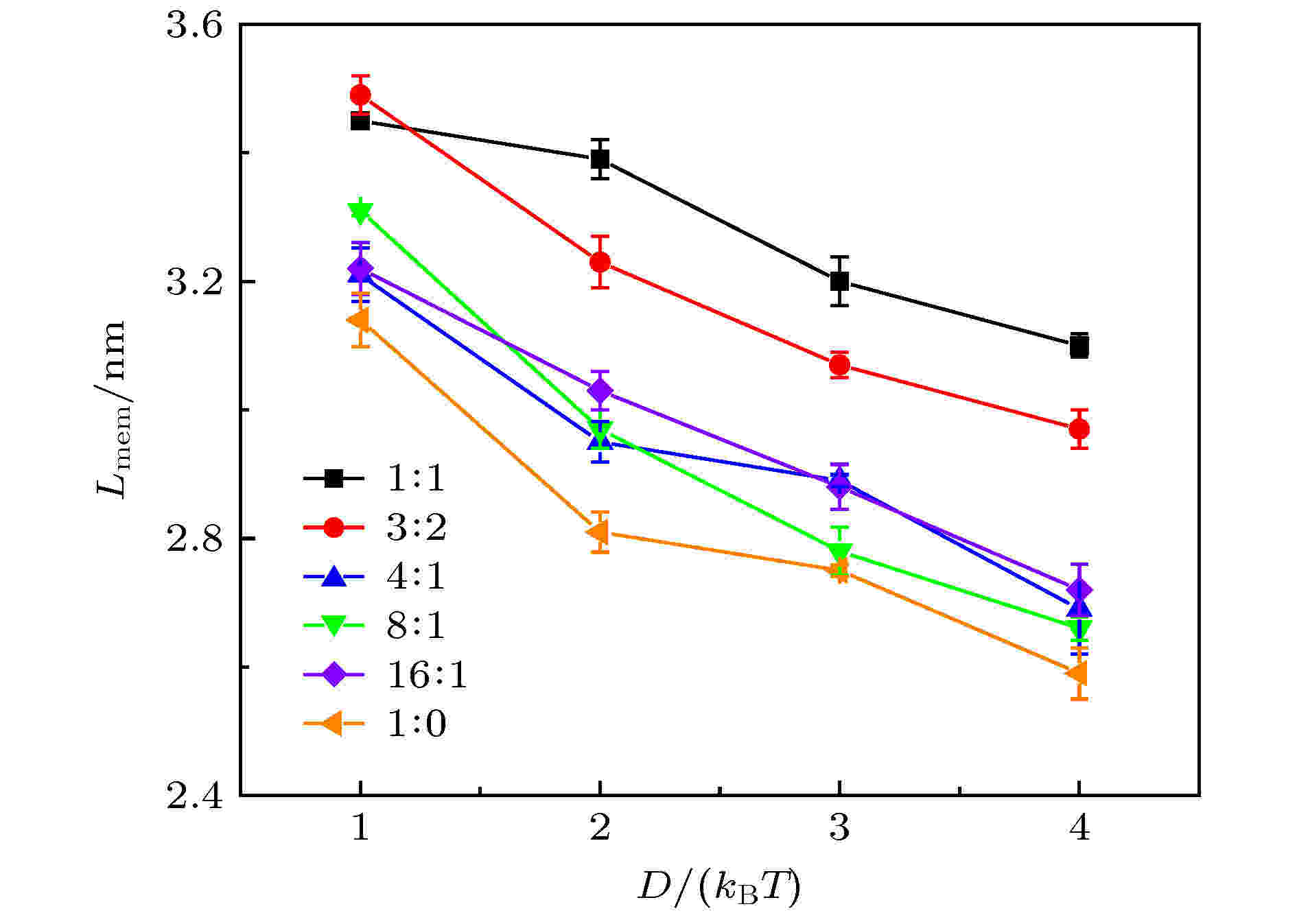图 8 不同CTAB/DMPC摩尔比下得到的膜厚度L_mem与D的关系图.
Figure8. Membrane thickness L_mem as a function of D. Results are obtained at various CTAB/DMPC molar ratios.

2 -->

3.6.蠕虫状胶束的螺旋形貌

一个有趣的发现是, 当CTAB/DMPC的摩尔比为16∶1和1∶0时, 修饰剂形成的蠕虫在GNRs表面以一定的倾斜角沿同一方向缠绕(图4和图D1), 形成了特殊的螺旋形貌. 为了定量估算蠕虫的倾斜程度, 绘制了修饰剂在GMRs表面的位置分布图, 以极角θ和坐标z来标识(详见附录D), 称为投影展开分布图. 对θ(z)做线性拟合得到的斜率可用于衡量螺旋程度(图9). 可以看到, 随着D的增加, 拟合斜率不断减小, 蠕虫的倾斜程度也逐渐降低, 说明在较强的吸附作用下螺旋形貌不易维持. 当D给定时, 在摩尔比为1∶0的体系中, 蠕虫斜率更大, 螺旋更加明显, 这意味着DMPC对螺旋的形成起到了一定的阻碍作用.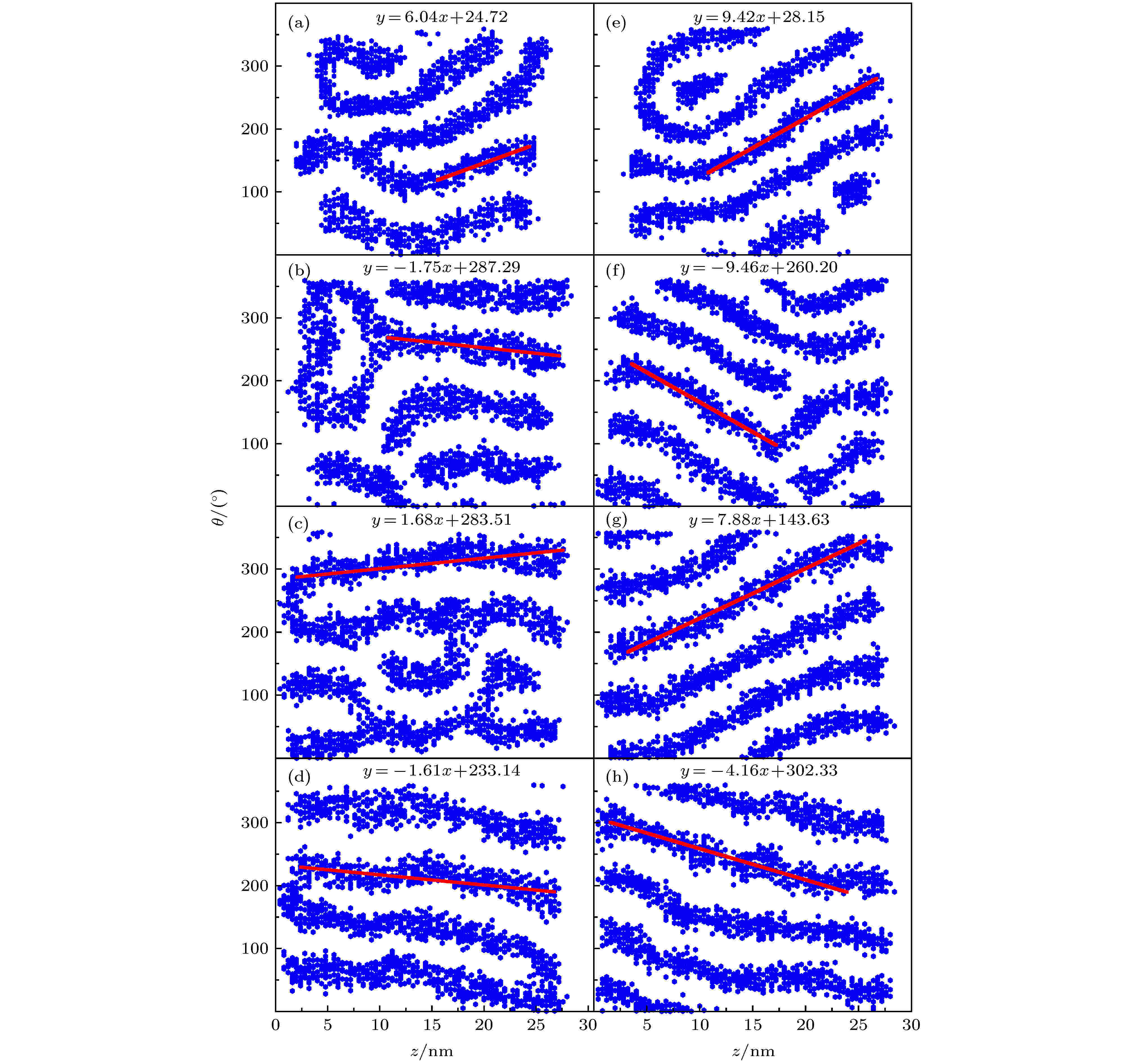
图 9 不同D下得到的GNRs表面修饰剂的投影展开分布图(GNRs直径d = 4 nm), 其中, 线性拟合斜率代表螺旋程度; 左图是CTAB/DMPC摩尔比为16∶1的结果, (a) D = 1k_BT, (b) D = 2k_BT, (c) D = 3k_BT, (d) D = 4k_BT; 右图是CTAB/DMPC摩尔比为1∶0的结果, (e) D = 1k_BT, (f) D = 2k_BT, (g) D = 3k_BT, (h) D = 4k_BT
Figure9. Projected expansion map of coating agent distributing on the surface of GNRs with d = 4 nm. The slope of the linear fitting represents the spiral degree. The left panels are results at CTAB/DMPC molar ratio of 16∶1 with (a) D = 1k_BT, (b) D = 2k_BT, (c) D = 3k_BT, (d) D = 4k_BT. The right panels are results at CTAB/DMPC molar ratio of 1∶0 with (e) D = 1k_BT, (f) D = 2k_BT, (g) D = 3k_BT, (h) D = 4k_BT.

2 -->

3.7.GNRs-CTAB-DMPC复合体形貌的形成机制

GNRs-CTAB-DMPC复合体的多种形貌可以通过考察吸附在固体表面的膜的形状能来定性解释. 膜的形状能ε = (σ－|W|)A = (2κm²－|W|)A由表面张力σ和黏附能密度|W|决定^[51], 其中σ与膜的弯曲刚度κ和自发曲率m的平方成正比; |W|与本文中修饰剂头部和GNRs表面的作用强度D有关; A是膜面积. 当σ > |W|时, 膜可以从固体表面解吸附, 形状发生变化, 其变化趋势与自由膜的自发曲率有关. 当CTAB/DMPC摩尔比较小时, 修饰剂组装成平面双层膜或囊泡, 自发曲率较小甚至为零, 膜易于以完整双层膜的形式吸附在固体表面. 当CTAB/DMPC摩尔增加时, 修饰剂组装成片状胶束, 自发曲率增加, 膜与固体表面吸附能力降低, 倾向于以裂片形式黏附在固体表面; 进一步增加CTAB, 修饰剂组装成类球状或蠕虫状胶束, 自发曲率更大, 不易吸附到固体表面, 而是倾向于以蠕虫状附着. 该能量公式成立的条件是假设固体表面是平面, 对于弯曲固体表面, 还要考虑其本身的曲率. 对于柱形的GNRs, 它和胶束(相对于GNRs的轴心)具有反向曲率, 这使得胶束不易吸附到(特别是半径小、曲率高的) GNRs的表面, 因而修饰剂呈现明显裂痕和螺旋. 另外, CTAB质量比DMPC小, 对D的变化更加敏感; CTAB带电荷, 彼此之间存在排斥, 而DMPC的加入会减弱胶束间的排斥, 使胶束融合逐渐形成比较规则的蠕虫、裂片. 简而言之, GNRs的固有曲率、CTAB/DMPC混合膜或胶束的自发曲率以及黏附能之间通过协同和竞争, 最终使修饰剂在GNRs的表面形成了各种有趣的形貌.

本文采用隐式溶剂耗散粒子动力学模拟的方法研究了GNRs-CTAB-DMPC复合体的自组装. 结果表明, CTAB/DMPC摩尔比是影响形貌的最主要因素, 随着摩尔比的增加, 修饰剂会在GNRs表面先后经历完整的双层膜、不完整的双层膜、长片状胶束、以及螺旋缠绕GNRs的蠕虫状胶束. 完整双层膜的形貌验证了实验上的一个猜测, 而其他三种形貌则是全新的发现. 另外, 通过减小GNRs的直径、增加修饰剂中CTAB的含量、或增加修饰剂和GNRs之间的作用强度, 可以让GNRs的表面尤其是两端被完整包裹, 同时让包覆层变薄. 以上的分析结果使得能够在分子水平上深刻地理解修饰剂对GNRs自组装形貌的影响, 弥补了实验表征手段的不足, 有助于实现GNRs的可控自组装. 在后续工作中, 我们会进一步分析GNRs的刚度和修饰剂的弹性性质, 深入研究不同修饰剂的交换动力学以及更大尺度的组装行为.

本文采用了隐式溶剂耗散粒子动力学力场. 事实上, 从模拟体系大小和物质种类的角度出发, 也可以采用Dry Martini力场^[52]. 然而, Dry Martini力场无法灵活地添加自定义的势能函数. 另外, 本文中的金珠子尺寸过大, 需要设置较大的截断半径, 严重影响了模拟效率. 为了可以灵活地自定义势能函数, 并对不同的相互作用设置不同的截断半径, 使用了本课题组自写的程序, 该程序目前支持显式和隐式耗散粒子动力学力场^[43,46].
为了保证模拟体系的合理性和性质的准确性, 需要根据相互作用的类型以及珠子的特点选择合适的势能函数并设置参数. 1)对于磷脂, 采用了最近发表的DPD力场参数^[43,46], 这些参数很好地重现了磷脂的结构性质和弹性性质. 对于CTAB, 直接沿用了磷脂的相关参数. 附录B中DMPC和CTAB的性质测试结果确认了这套参数的合理性. 2)为了提高模拟速度, 将直径2—5 nm的金原子团簇作为一个粗粒化珠子. 此时, 如果采用较为柔软的DPD势能函数, 会让金珠子和其他珠子发生非物理交叠. 因此采用硬球L-J势来描述与金珠子有关的体积排斥作用. 在设置L-J势的参数时, 参考的是文献值^[48]和珠子的尺寸. 3)为了体现不同修饰剂头部和GNRs相互作用的差异性, 采用了Morse势. Morse势的D越大, 相互作用强度越强, D取值的范围参考了我们上一个工作^[42]. 4)在最近发表的DPD力场参数的文章中^[43,46], 将DMPC的两个头部珠子作为总电量为零的偶极子来加快模拟速度. 由于采用了该力场的大部分参数, 为了不影响性质的准确性, 该工作沿用了这种处理头部珠子的方式. a_ij的取值见表A1.σ, c, s的取值见表A2. GNRs, CTAB, DMPC的成键参数见表A3.

为了更好地控制温度, 不施加长程处(r > r₀)的耗散随机力, 这需要对文献[46]中的s = {0.46, 0.46, 0.46, 0.734, 0.734}进行调整, 来重现DMPC的性质. 对s重新进行了参数化^[46], 最终得到s = {0.625, 0.625, 0.625, 0.7135, 0.7135}. 在这套新的s下, DMPC在大盒子中可组装成囊泡. 还测试了DMPC双层膜的性质(计算细节见文献[43, 46]): 在表面张力为零处的膜面积为0.6996 nm² = 1.39r₀², 双层膜厚度为4.07 nm, 抗弯刚度为19.8k_BT = 0.82 × 10^–19 J. 与显式溶剂DPD模拟的结果^[43] (膜面积为1.355r₀², 膜厚为3.56 nm, 抗弯刚度为0.5 × 10^–19 J)相比, 新的控温系综结合新的s参数模拟的结果在可以接受的范围之内.
为了测试Im-DPD力场下CTAB的性质, 进行了纯CTAB的模拟, 体系中含有72个CTAB分子和72个1价阴离子, 其他模拟条件与CTAB/DMPC体系相同. 表B1列出了CTAB胶束的胶束直径、离心率、电离度等性质, 并列出了全原子、有水Martini和无水Martini模拟的结果. 结果显示, CTAB在这些不同的力场下的性质非常接近.

Force Field	D/nm	e	α
All-atomic	4.79	0.29	0.63
Martini	4.54	0.14	0.78
Dry Martini	4.42	0.12	0.73
Im-DPD	5.13	0.16	0.68

表B1单个CTAB胶束的模拟结果, 其中, D是胶束的直径, e是离心率, α是CTAB分子的电离度(更多细节详见文献[50]), 表格中的前3行数据来自文献[50], 用作对比分析
TableB1.Simulations results of the single CTAB micelle. D is the diameter of the micelle, e is the eccentricity, and α is the degree of ionization of CTAB molecules (see Ref. [50] for details). The data in the first three lines are taken from Ref. [50] for comparison.

由于Im-DPD比其他力场模拟速度更快, 所以在本文中采用该力场. 需要注意, 本文关心的是GNRs和CATB/DMPC修饰剂之间的相互作用, 所以目前的s参数能够满足模拟需要, 尽管它仍然有较大的提升空间.

图C1为纯DMPC和d = 4 nm, D = 4k_BT时GNRs-DMPC的组装形貌, 可以看出, 单纯的DMPC会形成囊泡, 加入GNRs以后磷脂(d = 4 nm, D = 4k_BT, CTAB/DMPC摩尔比为0∶1)会以双层的形式包裹住GNRs, 这和我们前期工作观察到的现象一致^[42]. 结合图C1和图3可以发现, 摩尔比小于3∶2时修饰剂均以完整双层膜的形式对GNRs包覆. 当d和D等于其他值时, 观察到类似的现象. 由于本文重点研究CTAB对形貌的影响, 所以不对摩尔比为0:1的体系做过多介绍.
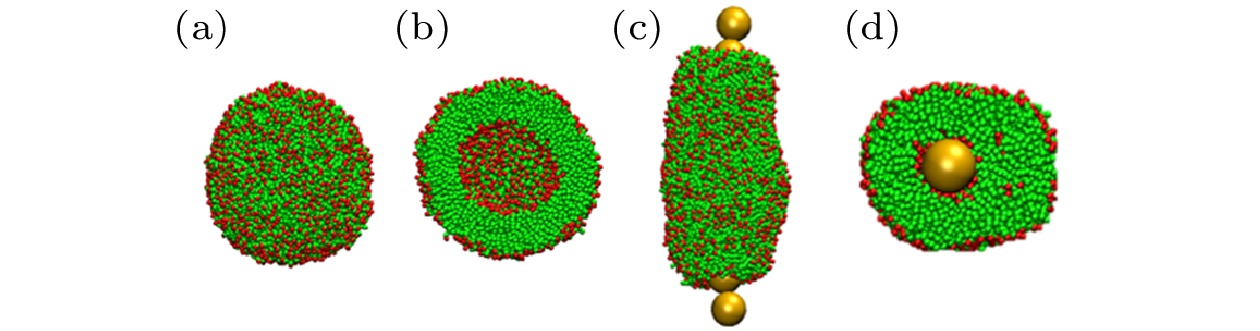图 C1 纯DMPC和d = 4 nm, D = 4k_BT时GNRs-DMPC的组装形貌　(a) DMPC的形貌及(b)切面图; (c) GNRs-DMPC的形貌及(d)切面图
FigureC1. Morphology of the pure DMPC lipids and assembled GNRs-DMPC complex with d = 4 nm and D = 4k_BT: (a) Morpohology and (b) cross-sectional view of DMPC; (c) morpohology and (d) cross-sectional view of GNRs-DMPC

图D1给出了摩尔比分别为 (a) 1∶1, (b) 3∶2, (c) 4∶1, (d) 8∶1, (e) 16∶1, (f) 1∶0情况下, d = 4 nm和D = 4 k_BT时GNRs表面修饰剂的投影展开分布图.

图E1为RDF峰的位置示意图. 表E1列出了不同D及CTAB/DMPC摩尔比下的r₁, r₂, r₃和L_mem.
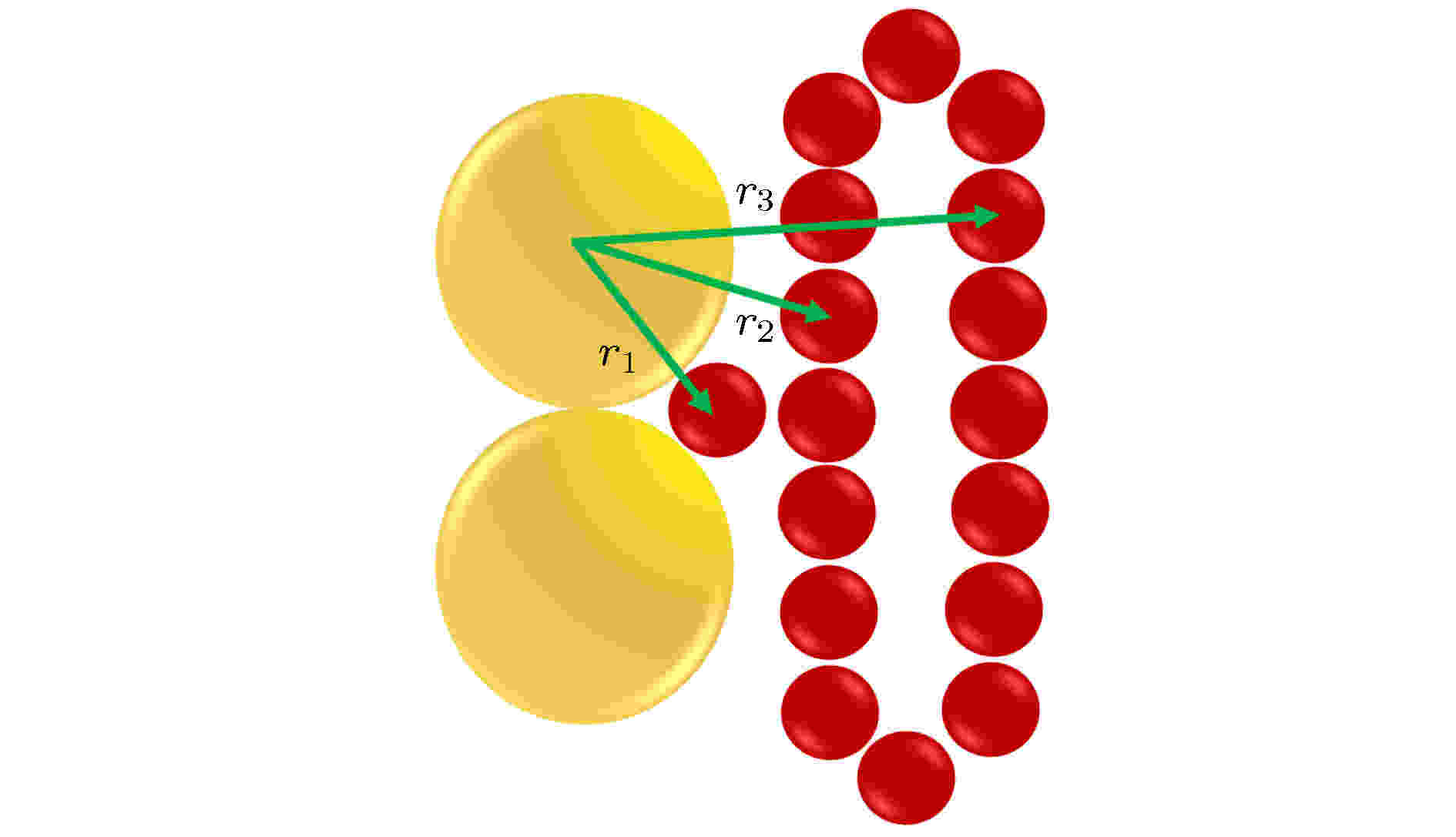图 E1 RDF峰的位置示意图, 其中金珠子用黄色表示, CTAB和DMPC的H₁珠子用红色表示
FigureE1. Schematic diagram of RDF. The GN bead is shown in yellow, the H₁ head beads of CTAB and DMPC were shown in red.