摘要:微尺度系统传热具有较小的热惯性和较快的热响应, 在控制传热方面具有独到的优势. 本文利用分子动力学方法研究了纳米通道中壁面温度及壁面润湿性不同时, 静态流体和动态流体下界面热阻的变化规律. 结果表明, 在静态流体中, 壁面润湿性的增强会显著降低界面热阻, 对于温度不同的壁面, 当润湿性较弱时, 可以观察到高温壁面处的界面热阻高于低温壁面处, 反之, 当润湿性较强时, 壁面温度对界面热阻的影响较小; 对流体区域施加外力使流体流动, 结果显示外力的增加能有效提高系统的热通量, 流体温度升高. 当润湿性较弱时, 外力的增大能显著减低界面热阻, 而随着壁面润湿性增强, 外力对界面热阻的影响逐渐减小. 此外, 本文将界面热阻与壁面吸附流体分子数量相联系, 发现在静态流体中, 界面热阻值与壁面吸附流体分子的数量呈负相关; 而在动态流体中, 外力的变化对吸附分子数量的影响较小, 壁面润湿性的强弱是影响壁面吸附流体分子的主要影响因素.
关键词: 润湿性/
外力/
界面热阻/
分子动力学

English Abstract

全文HTML

--> --> -->

近年来, 航天、生物、医学等高端领域的发展使得科技微型化成为目前研究的重点^[1]. 然而, 虽然科技微型化所涉及的电子器件尺寸越来越小, 但是需要满足的热通量和功率却越来越大, 因此, 研究微尺度下的传热特性与相关机理十分必要. 纳米技术的快速发展有利于深入了解润湿性与物质运输及传热机理^[2], 但由于微尺度下存在层流效应、快速热传导效应、扩散效应及壁面滑移效应等微尺度效应^[3], 大大提高了实验研究的难度, 也降低了实验所得数据的精度. 因此, 利用分子动力学等计算机模拟技术成为研究微尺度流动与传热的主要方式^[4].
界面热阻是研究纳米级系统热传递的关键物理因素, 它反映了两种物质接触界面间的传热性能, 这使得界面热阻成为目前研究微尺度传热的重点^[5-7]. 近年来, 国内外众多****在该研究领域取得了不同程度的研究成果. 葛宋和陈民^[8]利用分子动力学模拟研究了固液势能强度对界面热阻的影响, 发现固液势能强度增强可以有效地减小界面热阻, 同时, 该研究还发现, 改变固体原子间的相互作用强度也会影响界面热阻的变化. 周璐和马红和^[9]利用非平衡分子动力学方法, 以铜-氩纳米流体为模型, 研究了固液势能强度对界面热阻的影响, 发现增大铜粒子与流体氩间的作用强度可增强粒子吸附流体原子的能力, 促进纳米粒子与流体间的传热, 降低界面热阻. Chiloyan等^[10]研究发现当纳米尺度下固液界面接触时, 声子成为主要的热载流子. 张龙艳等^[11]采用非平衡分子动力学方法研究了界面热阻与模拟微通道尺寸间的关系, 结果表明, 在小尺寸通道内, 流体原子受到壁面影响较大, 固液原子间的声子失配程度较低, 界面热阻减小; 而在大尺度通道中, 只有近壁区流体原子受到壁面影响, 固液原子间的声子失配程度不变, 导致界面热阻不再随着通道尺寸变化而变化. Shi等^[12]以及Baresik和Beskok^[13]利用分子动力学方法分析了纳米通道中壁面温度对界面热阻的影响, 发现壁面温度越高, 界面热阻值越大. 同样研究壁面特性对传热的影响, 张程宾等^[14]重点分析了粗糙壁面结构表面对流体流动与传热的影响, 结果表明, 粗糙壁面的存在使得流体在流动过程中更加容易与壁面间产生摩擦粘性热, 导致近粗糙壁面一侧的流体温度高于光滑壁面一侧, 并且粗糙壁面处的速度滑移和温度跳跃均小于光滑壁面处. Li^[15]利用分子动力学模拟研究了摩擦诱导流体加热的机理, 通过施加外力使近壁处流体与壁面间产生明显的速度差, 从而产生摩擦. 结果表明随着外力的增大, 流体温度逐渐增高, 作者将这一现象解释为由于界面摩擦而产生的粘性耗散热. 但这些文献中并没有提及摩擦诱导粘性热与界面热阻之间的关系, 因此, 需要进一步模拟分析.
综上所述, 目前在研究微尺度界面热阻方面仍存在一些疑问, 例如界面摩擦诱导的粘性耗散热对界面热阻的影响, 以及相同条件下, 静态流体与动态流体下界面热阻的区别. 为更深一步地探究微尺度下的传热机理, 本文拟构建非对称纳米通道模型(壁面润湿性和温度不同), 通过改变冷热壁面润湿性, 观察界面热阻与壁面润湿性之间的关系, 总结壁面温度对界面热阻的影响. 并统计计算模拟工况中流体的平均温度, 对每个平均温度下对应的热导率进行验证, 确定模拟的可靠性. 同时, 通过给流体施加外部驱动力, 重点研究外力诱导的界面摩擦粘性热与界面热阻之间的关系, 并将静态流体与动态流体下的界面热阻值进行比较, 总结规律.

纳米系统物理模型如图1所示, 由两个平行的固体铜壁和限制在壁面间的液态氩分子构成. 其中红色和蓝色代表温度不同的铜分子, 绿色代表氩分子. 模拟系统的尺寸为x × y × z = 10.21 nm × 3.67 nm × 3.67 nm, 其中流体区域在x方向上的长度为6.61 nm. 由于流体的密度参数直观展示了分子的填充紧密程度, 对计算纳米系统热物理参数有很大的影响, 本文取氩的无量纲晶格常数为0.7, 流体区域总共包括有1774个氩分子, 密度ρ_l = 1.32 g/cm³. 沿x方向壁面厚度为1.80 nm, 每个壁面共由10层铜层构成, 每层间距0.20 nm, 且每层包括220个铜分子, 壁面分子的密度ρ_s = 4.53ρ_l. 为了保持模拟系统的体积不变, 将壁面最外层的两层壁面固定, 如图1中的区域1和区域5, 其余原子均可自由移动. 所有原子的初始结构均按照面心立方结构(FCC)排列, 周期性边界条件应用于y和z方向.
图 1 物理模型结构示意图
Figure1. The diagram of physical model structure.

Lennard-Jones (12-6) 势能模型应用于流体原子间以及固液原子间, 其表达式为

$U({r}_{ij})=4\varepsilon \left[{\left( {\frac{\sigma }{{r}_{ij}}} \right)}^{12}-{\left( {\frac{\sigma }{{r}_{ij}}} \right)}^{6}\right],\;\;\;\;\;\;{r}_{ij} < {r}_{\rm{c}}, $

式中, r_ij为分子间的距离, ε和σ分别为能量参数和尺寸参数, r_c为截断半径. 流体氩分子间的参数为ε = 1.65 × 10^–21 J, σ = 0.3405 nm, 氩分子的质量为m = 6.63 × 10^–26 kg. 铜与氩分子间的势能参数由Lorentz-Berthelot混合法则^[16]求解, 需要注意的是, 只有当配对分子具有相同形式的势函数时, 该混合法则才能使用^[17], 因此, 本文研究壁面铜原子之间的势函数也是采用Lennard-Jones (12-6)势能模型.
界面热阻与温度跳跃ΔT密切相关, 即满足关系ΔT = R_K·Q, 其中Q为热通量. 界面处的温度跳跃为壁面温度与界面流体温度之差(T_wall–T_fluid), 但由于界面处流体温度分布往往会出现很大的波动, 导致统计温度跳跃时会出现很大误差. 因此, 本文利用Navier型边界条件来研究界面热传导^[12], 即利用连续热传导方程来预测纳米通道界面处流体的温度. 预测方式如图2所示, 通过拟合延长通道主流区的温度分布直至壁面处, 将预测得到的流体温度作为界面处流体温度.
图 2 固液界面处流体温度的预测
Figure2. Prediction of fluid temperature at the solid-liquid interface.

在分子动力学模拟中, 固液界面处的温度跳跃可表示为^[12]

$\Delta T = \alpha ({T_{\rm{w}}}){\left( {\frac{{{\omega _{\rm{w}}}}}{{{\omega _{\rm{f}}}}}} \right)^4}\exp \left( { - 1.85\frac{{{\varepsilon _{{\rm{wf}}}}}}{\varepsilon }} \right)\frac{{\partial {T_{\rm{f}}}}}{{\partial n}},$

其中, α(T_w)是与壁面温度相关的系数, ω_w和ω_f分别是壁面原子与流体原子的热振动频率, ε_wf为固液分子间的势能强度, ?T_f/?n为流体区域内的温度梯度. 本文主要研究了固液势能强度及外力对界面温度跳跃及界面热阻的影响.
模拟系统中壁面温差会诱导通过固液界面的热通量Q_x, 其计算公式如下^[18]:

$ \begin{split}{Q_x} =\;& \frac{1}{V}\sum\limits_i {\left( {\frac{1}{2}{m_i}v_i^2 + {\varphi _i}} \right)} \\&+ \frac{1}{2}\sum\limits_i {\sum\limits_{i < j} {\left[ {{F_{ij}} \cdot ({v_i} + {v_j}){r_{ij}}} \right]} } \end{split}$

式中V为流体区域的体积, ${\varphi _i}$为分子的总势能. 等式右边第一项为原子i的动能与势能之和, 右边第二项为原子i与周围原子间相互作用而传递的能量.
为了获得更加精确的模拟结果, 每个分子的性质应该接近于真实的分子, 即在初始时刻, 需要给每个分子设定随机速度以及位置. 确定系统的系综为正则系综(NVT), 采用Nose-Hoover恒温器使系统中的所有原子在100 K的温度下随机运动, 速度大小遵循高斯随机分布^[19], 公式表示为

$\frac{1}{{{N_{{\rm{argon}}}}}}\sum\limits_{i = 1}^{{N_{\operatorname{}{\rm{argon}}}}} {\frac{1}{2}} m\left| {v_i^2} \right| = \frac{3}{2}{k_{\rm{B}}}T,$

式中, k_B为玻尔兹曼常数, k_B = 1.38 × 10^–23 J/K, N_argon为流体分子数量, v_i为分子i的速度.
模拟计算时利用共轭梯度法使系统能量最小化, 即迅速使系统达到相对合理的状态, 减少模拟计算成本, 设置时间步长为2 fs, 计算100万步(2 ns)使系统驰豫稳定. 随后取消NVT系综, 利用微正则系综(NVE)对系统进行模拟. 为诱导系统产生一恒定的热通量, 需要给壁面设置一个恒定的温度, 分别作为热源和冷源, 如图1所示, 红色代表热壁面, 蓝色代表冷壁面. 采用Langevin恒温器将壁面温度恒定为140和90 K. 在不施加外力的条件下, 控制壁面温度后, 进行200万步(4 ns)的平衡计算, 系统平衡后, 再运行100万步(2 ns)将所需要的数据进行统计, 最后将这些数据进行时间平均. 此外, 还研究了驱动力对界面热阻的影响, 以Poiseuille流动为研究对象, 控制壁温后, 对每一个氩分子施加沿y正方向的驱动力, 运行200万步(4 ns)实现动态平衡, 系统平衡后, 运行计算100万步(2 ns)将所需要的数据进行统计, 最后将这些数据进行时间平均. 本文模拟采用LAMMPS程序编写^[20].

本节主要研究静态流体中固液势能强度变化对界面热阻的影响, 同时以静态流体为基础, 施加外部驱动力使流体流动, 分析外力诱导的摩擦粘性热对界面热阻的影响. 通道中设置冷热壁面使系统产生热流及温度梯度, 其中热、冷壁面温度分别设定为140和90 K, 共分析了两种工况, 如表1所列.

模拟工况	壁面温度	固液势能强度εwf/ε
工况1	热壁面(140 K)	6.0	1.5	1.0	0.75	0.5
	冷壁面(90 K)	6.0	6.0	6.0	6.0	6.0
工况2	热壁面(140 K)	6.0	6.0	6.0	6.0	6.0
	冷壁面(90 K)	6.0	1.5	1.0	0.75	0.5

表1模拟工况
Table1.Simulated conditions

壁面润湿性由固液原子间的作用强度决定, 流体在壁面铺展得越充分, 接触角越小, 可认为润湿性越好, 对于光滑壁面而言, 润湿性与固液势能强度之间的关系为

$\cos \theta = 2\frac{{{\varepsilon _{{\rm{wf}}}}}}{\varepsilon } - 1,$

式中, θ为壁面接触角, 当cosθ ≥ 1时, 认为θ = 0°, 即亲水状态. 模拟得到的工况中固液势能强度与接触角关系如表2所列.

εwf/ε	6.0	1.5	1.0	0.75	0.5
θ/(°)	0	0	0	60	90

表2不同固液势能强度下对应的接触角
Table2.Corresponding contact angle under different solid-liquid potential energy intensity

2

-->

3.1.静态流体中的界面热阻

图3(a)和图3(b)分别展示了工况1和工况2中液态氩的温度分布. 可以发现流体温度分布是从热壁面侧向冷壁面侧逐渐递减, 并且近壁面处的温度波动和预测得到的壁面附近流体温度显示了流体温度与壁面温度之间的不连续性. 对于工况1, 如图3(a)所示, 当ε_wf/ε = 6.0时, 近壁面附近流体温度波动最大, 而在x = 2.11 nm到x = 8.16 nm之间, 可以观察到温度分布呈线性分布. 随着固液势能强度的减弱, 热壁面附近流体温度也逐渐趋向于线性. 同样在工况2中, 如图3(b)所示, 通道主流区域温度分布呈线性分布, 而随着冷壁面固液势能强度的减弱, 冷壁面附近流体温度波动逐渐减缓, 并趋向于线性分布. 这是由于壁面润湿性的减弱会降低近壁面处的流体密度波动, 如图4所示, 其中图4(a)和图4(b)分别表示ε_wf/ε = 6.0和ε_wf/ε = 0.75时, 工况1和工况2下近热壁面和近冷壁面处的流体数密度分布. 可以发现, 当ε_wf/ε = 6.0时, 冷、热壁面附近液态氩的密度波动很大, 相邻两层中密度的巨大变化可能导致两个层中相应的温度变化; 而ε_wf/ε = 0.75时. 冷、热壁面附近流体密度波动较小, 对应的温度分布较为均匀. 此外, 对应于图3(a)和图4(a), 当ε_wf/ε = 6.0时, 可以发现在x = 2.0 nm位置处流体的数密度接近于零, 说明该位置上存在极少或不存在液体分子, 导致在该位置上统计流体温度时会出现很大的误差, 为了避免该现象, 本节并没有显示该位置上流体的温度分布.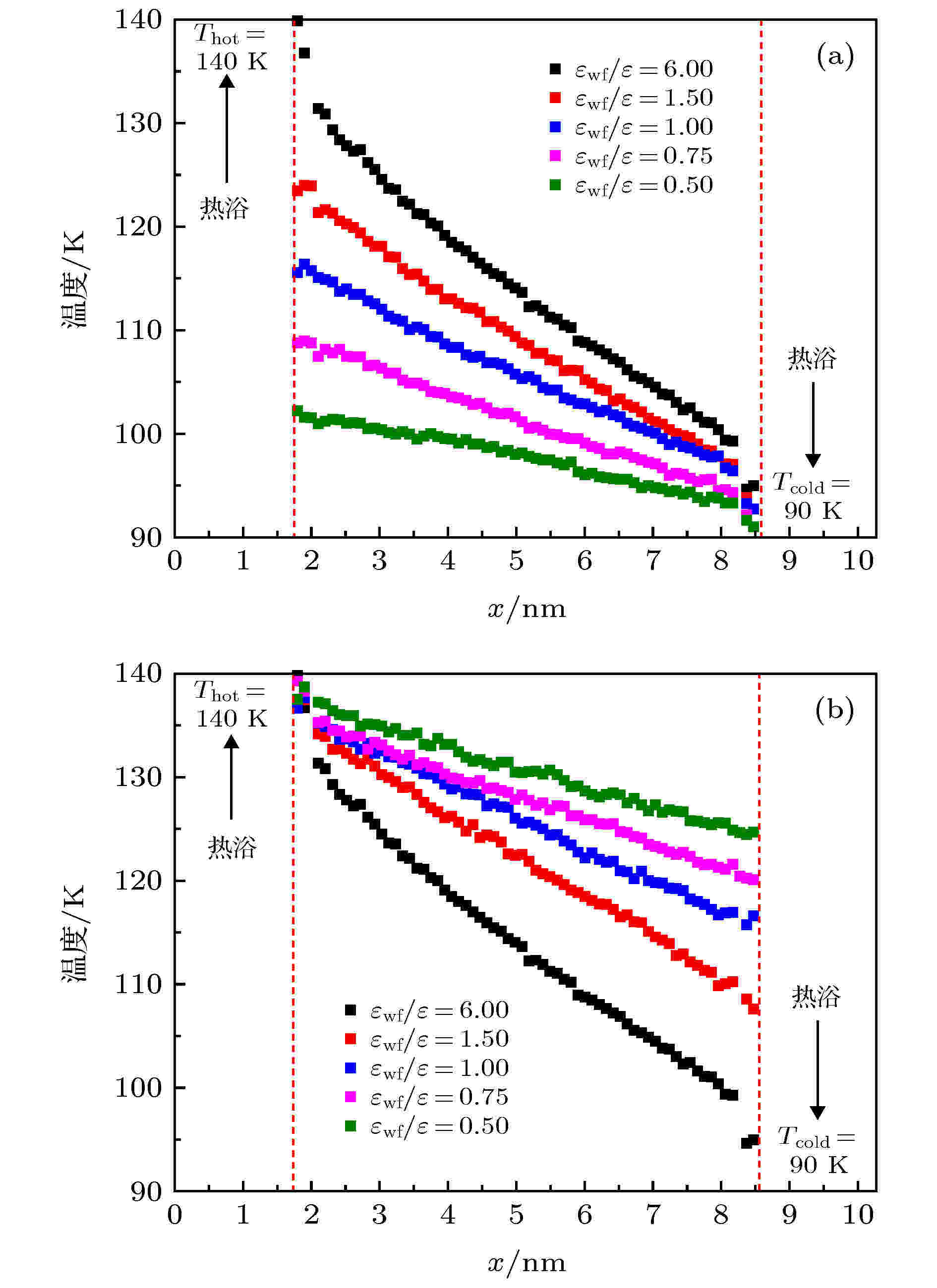
图 3 液态氩在不同固液势能强度ε_wf/ε下的温度分布　(a)工况1; (b)工况2
Figure3. Temperature distribution of liquid argon at different solid-liquid potential energy ε_wf/ε: (a) Condition 1; (b) condition 2.

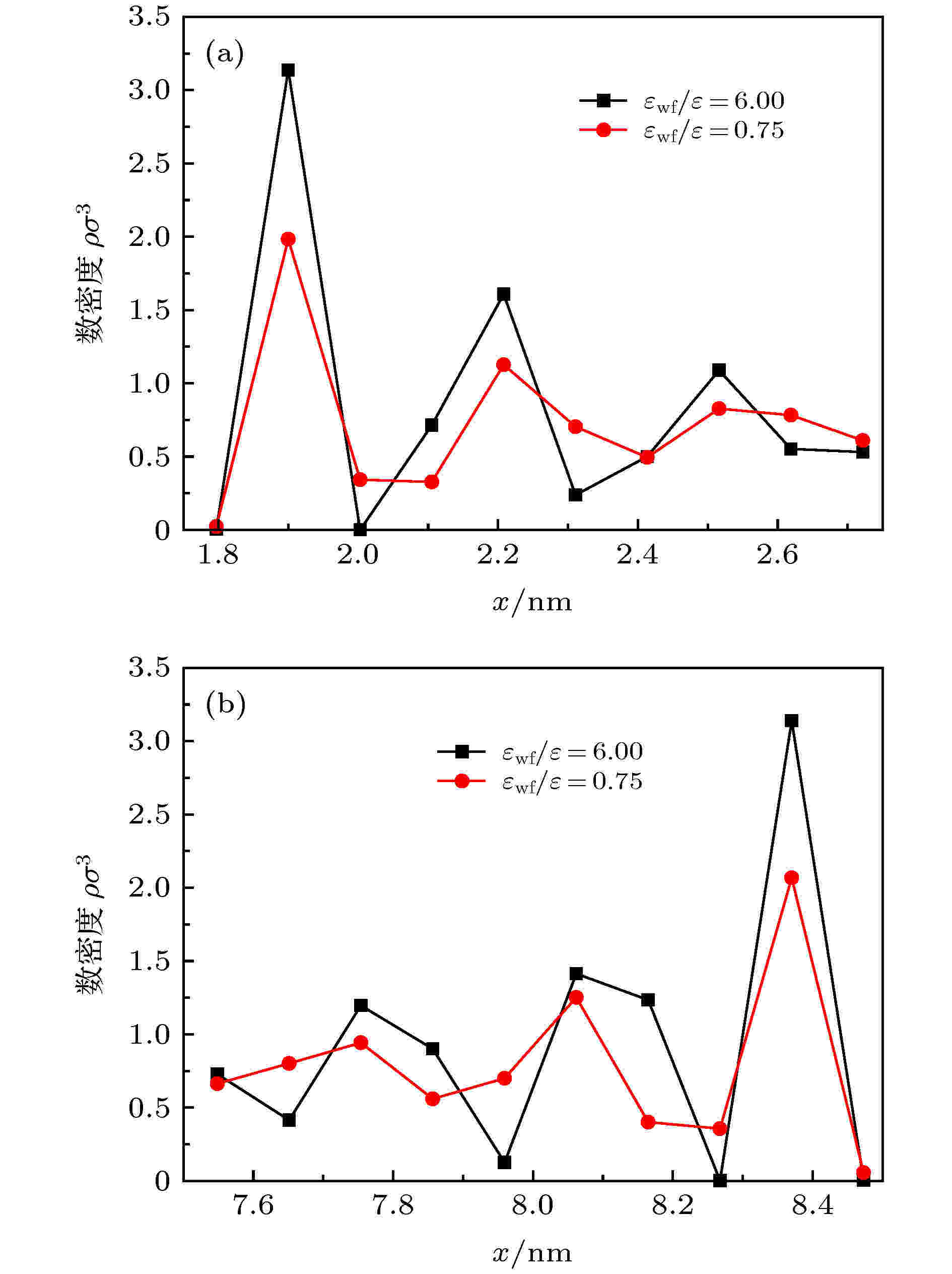图 4 (a)工况1中近热壁面附近流体数密度分布; (b)工况2中近冷壁面附近流体数密度分布
Figure4. (a) Number density distribution near the hot wall surface in condition 1; (b) number density distribution near the cold wall surface in condition 2.

为准确地计算出图3中冷热壁面附近的温度跳跃, 利用连续性热传导方程进行推算, 结果如图5所示. 对于工况1, 随着固液势能强度的增强, 热壁面处的温度跳跃逐渐减小, 而冷壁面处的温度跳跃却略有些增大, 这是因为热壁面润湿性的增强会增大整体流体温度分布的梯度, 由(2)式可知, 冷壁面润湿性不变的情况下, 温度梯度的增大会增大冷壁面处的温度跳跃. 同样, 工况2中随着冷壁面处温度跳跃的降低, 热壁面处温度跳跃略有增大. 同时, 可以发现工况1中热壁面处的温度跳跃比工况2中冷壁面处的温度跳跃高, 且随着壁面润湿性的增强, 这种差异逐渐减小, 说明壁面温度也可以影响界面温度跳跃, 但影响力随着润湿性的增强而减弱.
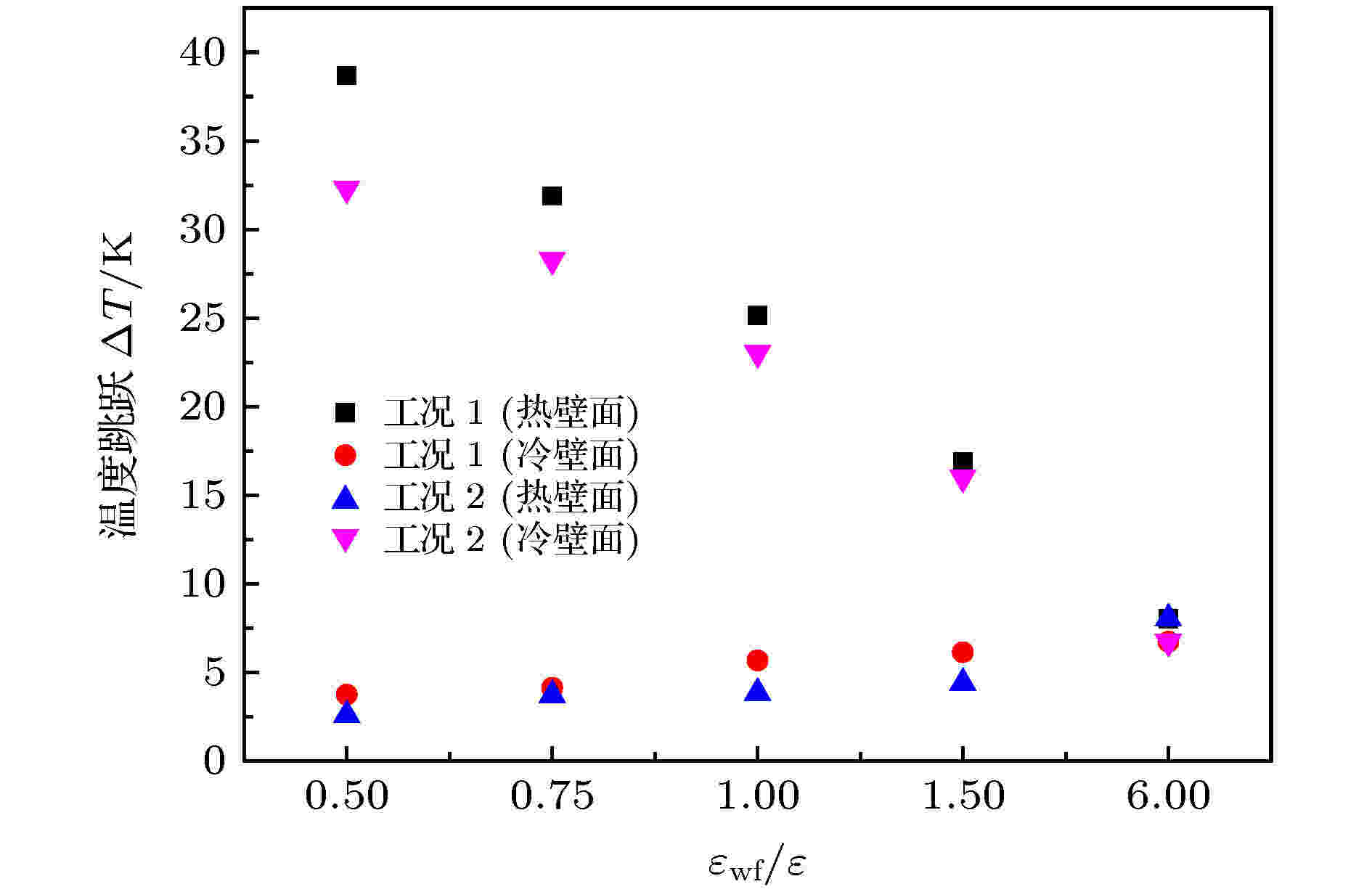图 5 固液势能强度对温度跳跃的影响
Figure5. Effect of solid-liquid potential energy on temperature jump.

计算系统的热通量是求解界面热阻的关键, 图6展示了图3中各个条件下计算的热通量. 可以看出, 随着固液势能强度的增大, 两种工况下的热通量均有所增大, 且增大的趋势近似为线性. 这是因为壁面润湿性的增强会强化壁面与流体间的热量传递. 同时, 除 ε_wf/ε = 6.0和0.5, 工况1中的热通量要略高于工况2中的热通量, 说明壁面温度对系统热通量也有一定的影响, 但效果不明显.
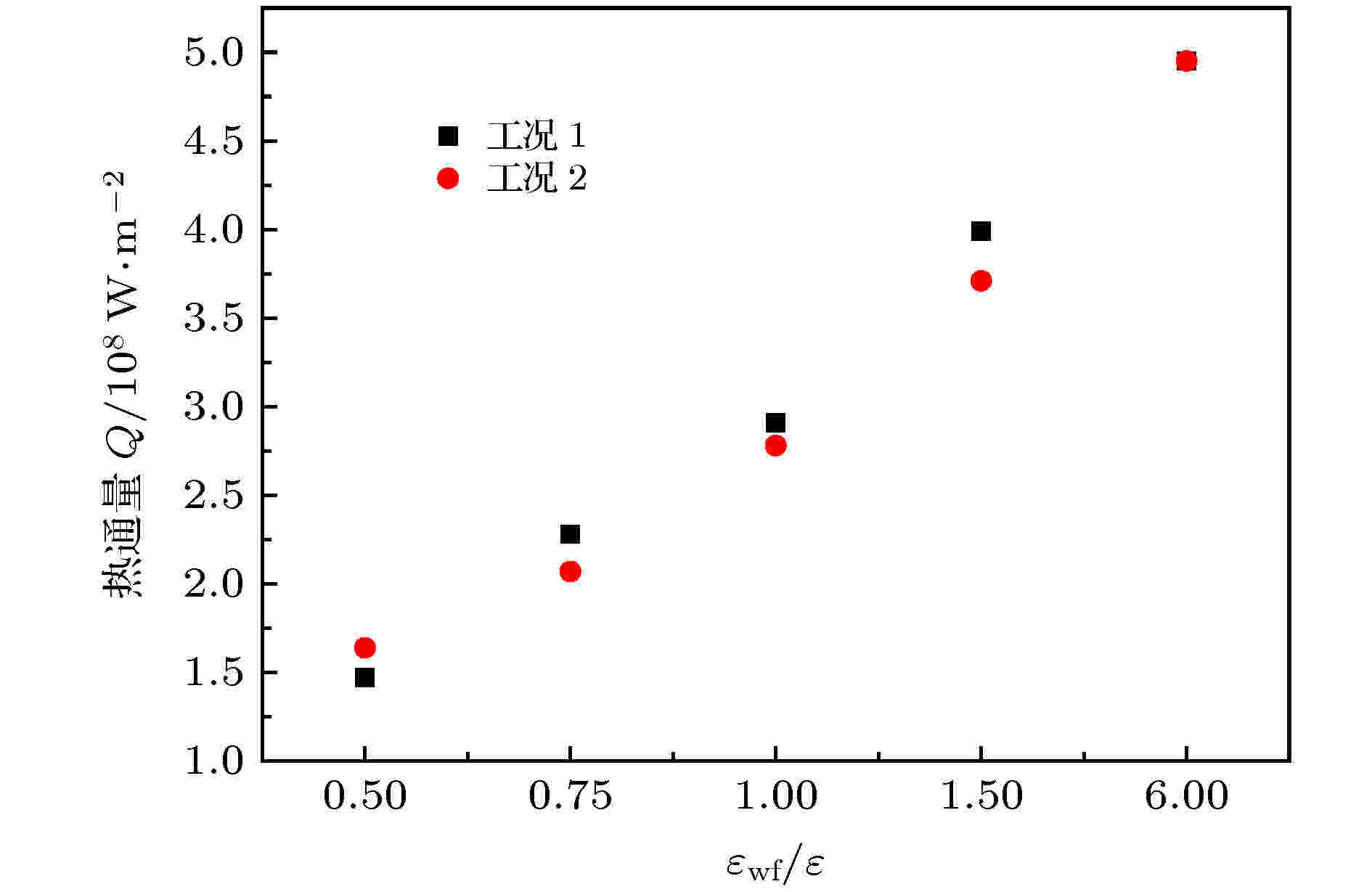图 6 固液势能强度对系统热通量的影响
Figure6. Effect of solid-liquid potential energy on heat flux of system.

界面热阻为温度跳跃与热通量的比值, 图7显示了固液势能强度对界面热阻的影响. 结果显示, 随着固液势能强度的增强, 工况1中热壁面的界面热阻与工况2中冷壁面的界面热阻均减小, 该趋势与温度跳跃的变化一致. 需要注意的是, 在本文模拟的条件下, 仅当固液势能强度最弱时(ε_wf/ε = 0.5), 才可以明显观察到工况1中热壁面处的界面热阻要高于工况2中冷壁面处的界面热阻, 在其他条件下, 壁面温度对界面热阻的影响基本可以忽略. 由于工况1中冷壁面和工况2中热壁面润湿性始终不变, 其对应的界面热阻值也基本处于恒定. 由此可以得出结论, 壁面温度对界面热阻的影响受到壁面润湿性的限制.
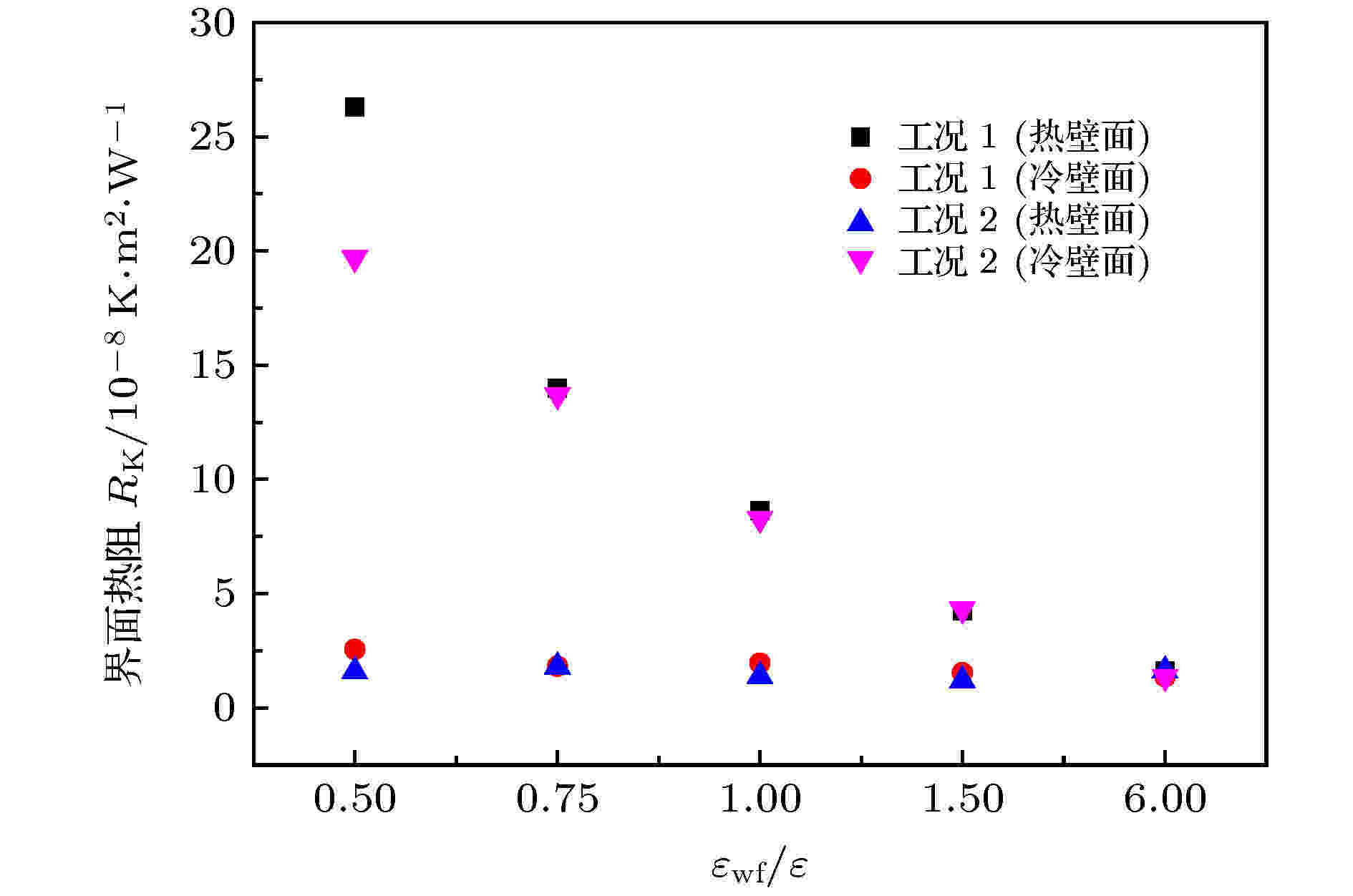图 7 固液势能强度对界面热阻的影响
Figure7. Effect of solid-liquid potential energy on interface thermal resistance.

固体壁面与近壁面流体间的传热决定了界面热阻的大小^[21,22], 特别是对于近壁区第一层液体原子而言, 其排列方式及数量分布能够很好地反映界面热阻. 图8展示了工况1中热壁面和工况2中冷壁面上吸附流体分子的快照图. 可以明显发现, 固液势能强度的增大能有效吸附更多的流体分子, 且流体分子的排列更加规整, 当ε_wf/ε ≥ 1.5时, 流体分子的排列形式逐渐接近于固体壁面, 即“类固体”行为. 壁面吸附流体分子越多, 越规整, 有利于固液界面间的传热, 降低界面传热的阻力. 同时, 将图8中吸附流体分子的数量具体化, 以观察壁面温度对界面热阻影响的本质, 结果如图9所示. 当ε_wf/ε ≤ 1.5时, 工况1中热壁面上吸附的流体分子数低于工况2中冷壁面上吸附的分子数量, 从分子运动角度来分析, 吸附在高温壁面上的氩分子具有更高的动能, 脱离壁面束缚的可能性更大. 壁面吸附流体分子的减少可能是导致热壁面处界面热阻值大于冷壁面处热阻值的原因.
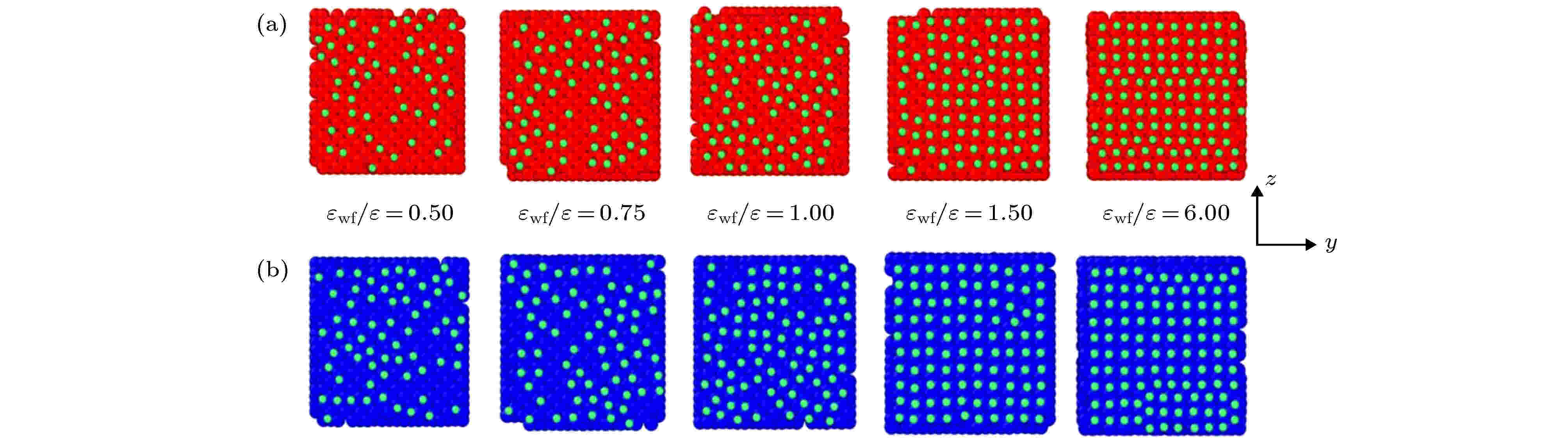图 8 壁面吸附流体分快照图
Figure8. Snapshot of wall adsorbed fluid molecules.

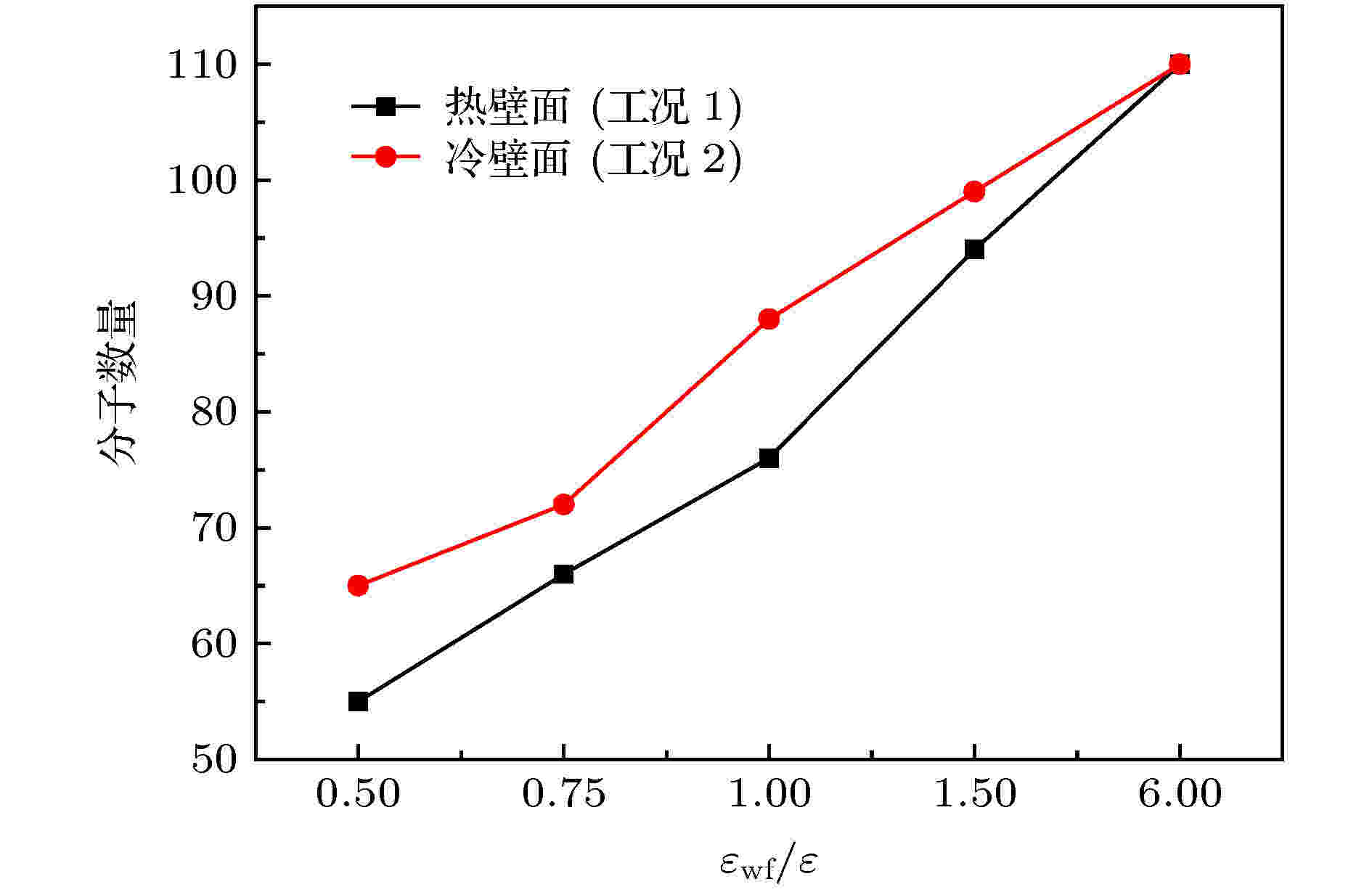图 9 固液势能强度对壁面吸附流体分子数的影响
Figure9. Effect of solid-liquid potential energy on the number of fluid molecules adsorbed on the wall surface.

2 -->

3.2.液态氩的热导率验证

为验证静态流体中计算导热的正确性, 以及进行更深一步的研究, 本节主要就图3中每个模拟工况下对应的氩的热导率进行验证. 图10统计了图3中所有条件下液态氩的平均温度(T_ave), 可以发现, 随着固液势能强度的增大, 工况1中流体的平均温度逐渐增大, 而工况2中流体的平均温度逐渐减小, 总的变化区间在97.54—130.82 K范围内. 利用傅里叶定律$\left(Q = - k\dfrac{{\partial T}}{{\partial n}}\Big| {_{{\rm{liquid}}}} \right)$计算各个平均温度下的热导率k, 结果如图11所示. 与高温条件下相比, 低温下液态氩的热导率变化幅度较大, 且平均温度较低时对应的热导率较高. 本模拟中氩的热导率数据与实验数据^[23,24]以及其他文献中的模拟数据^[12]具有很好的一致性. 因此, 可认为本文所采用的计算方法和所得数据具有可靠性.
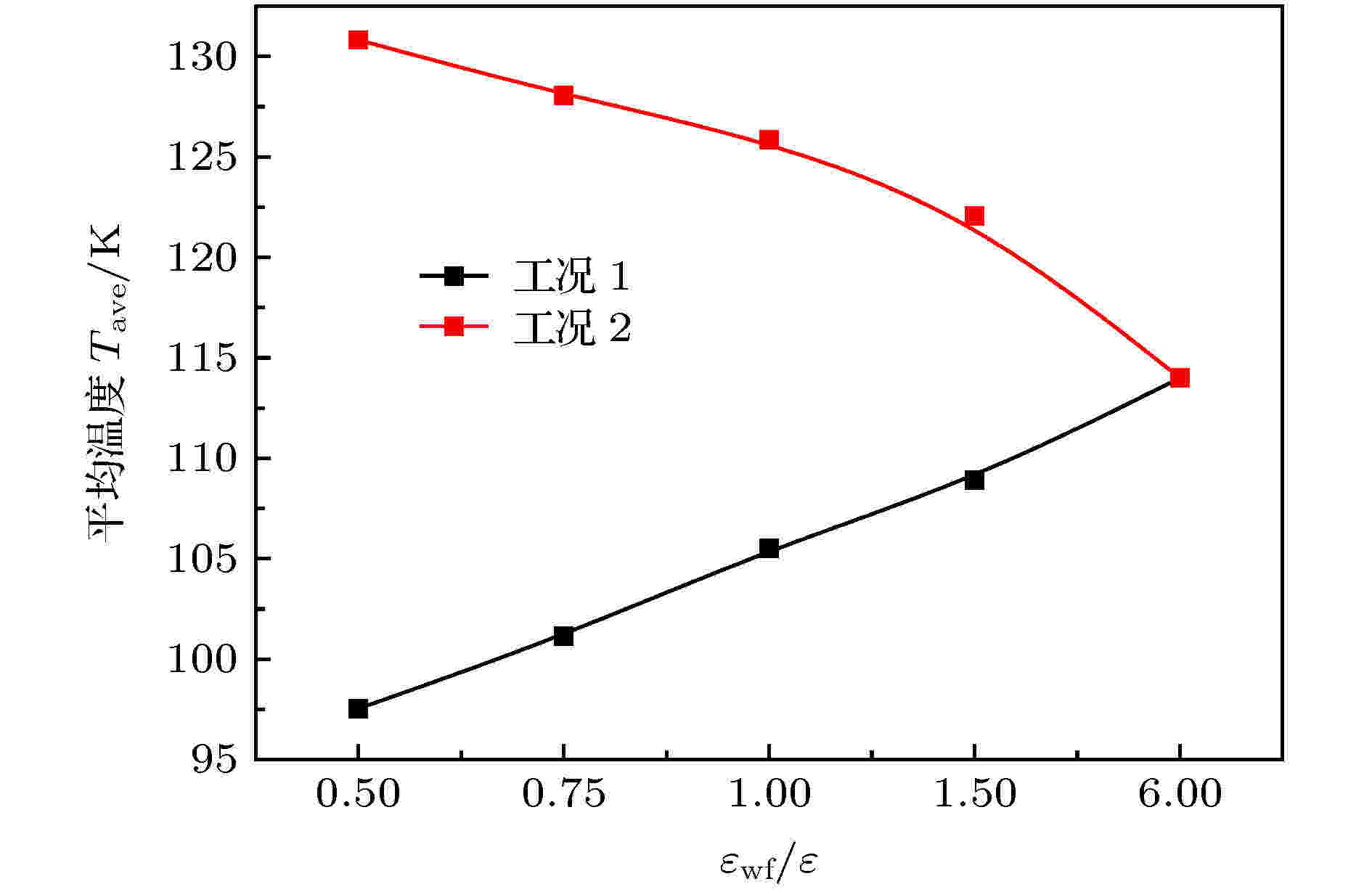图 10 液态氩的平均温度分布
Figure10. Average temperature distribution of liquid argon.

图 11 液态氩的热导率验证
Figure11. Thermal conductivity verification of liquid argon.

2 -->

3.3.动态流体中的界面热阻

本节主要以工况1为研究对象, 施加外部力形成Poiseuille流动, 并通过设置不同外部力来研究动态流体下固液界面热阻的变化趋势, 并与静态流体下的界面热阻相比, 总结相关规律.
图12显示了不同外力(F)作用下纳米通道内的流体速度分布, 包括(a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ. 结果显示, 在相同外力作用下, 随着热壁面固液势能强度的减弱, 流体流动速度逐渐增大, 且流体分布的对称性逐渐减弱, 流体速度的峰值由通道中心位置逐渐向热壁面侧偏移. 随着外力的不断增大, 流体速度大小也有明显的上升, 但速度分布的趋势基本一致. 图12中显示速度变化主要集中在热壁面侧, 而冷壁面侧由于固液势能强度不变, 速度分布变化很小.
图 12 工况1中液体氩在不同外力作用下的速度分布　(a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ
Figure12. Velocity distribution of liquid argon under different external forces in condition 1: (a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ

通过上述对流体速度场的介绍, 可以更好地理解通道内的流动情况. 进一步分析了不同外力作用下液氩的温度场分布, 结果如图13所示. 由图可知, 液态氩的温度分布依然是从高温壁面向低温壁面处递减, 但随着外力的增大, 温度分布形式明显变化. 如图13(a)所示, 当外力较小时(F = 0.01ε/σ), 流体温度分布与静态流体温度分布相似, 通道主流区温度场变化呈线性分布. 随着外力的增大, 主流区温度场逐渐偏离线性, 温度偏离线性分布的部分为靠近热壁面的一端, 这是因为冷壁面的润湿性恒定且较强, 外力的变化对壁面润湿性较强时的温度分布影响较小, 相反地, 随着热壁面润湿性的减弱, 外力的增大会明显提高近热壁面区域的流体温度, 如图13(b)—(d)所示. 同时可以发现, 随着固液势能强度的减弱, 热壁面附近流体温度偏离线性区域的范围也越大, 当固液势能强度较弱时(ε_wf/ε = 0.5), 该偏离位置距离壁面约1.19 nm. 这是由于壁面润湿性较弱时界面处更容易产生摩擦粘性热, 使得近热壁面处出现温度升高以及局部脱离线性分布的现象. 且从图13中可以看出, 随着外力的增大, 不同固液势能强度下的流体温度分布差距逐渐减小, 特别是图13(d)中, ε_wf/ε = 0.5时对应的流体温度与ε_wf/ε = 0.75和ε_wf/ε = 1.0时对应的温度分布基本重合.
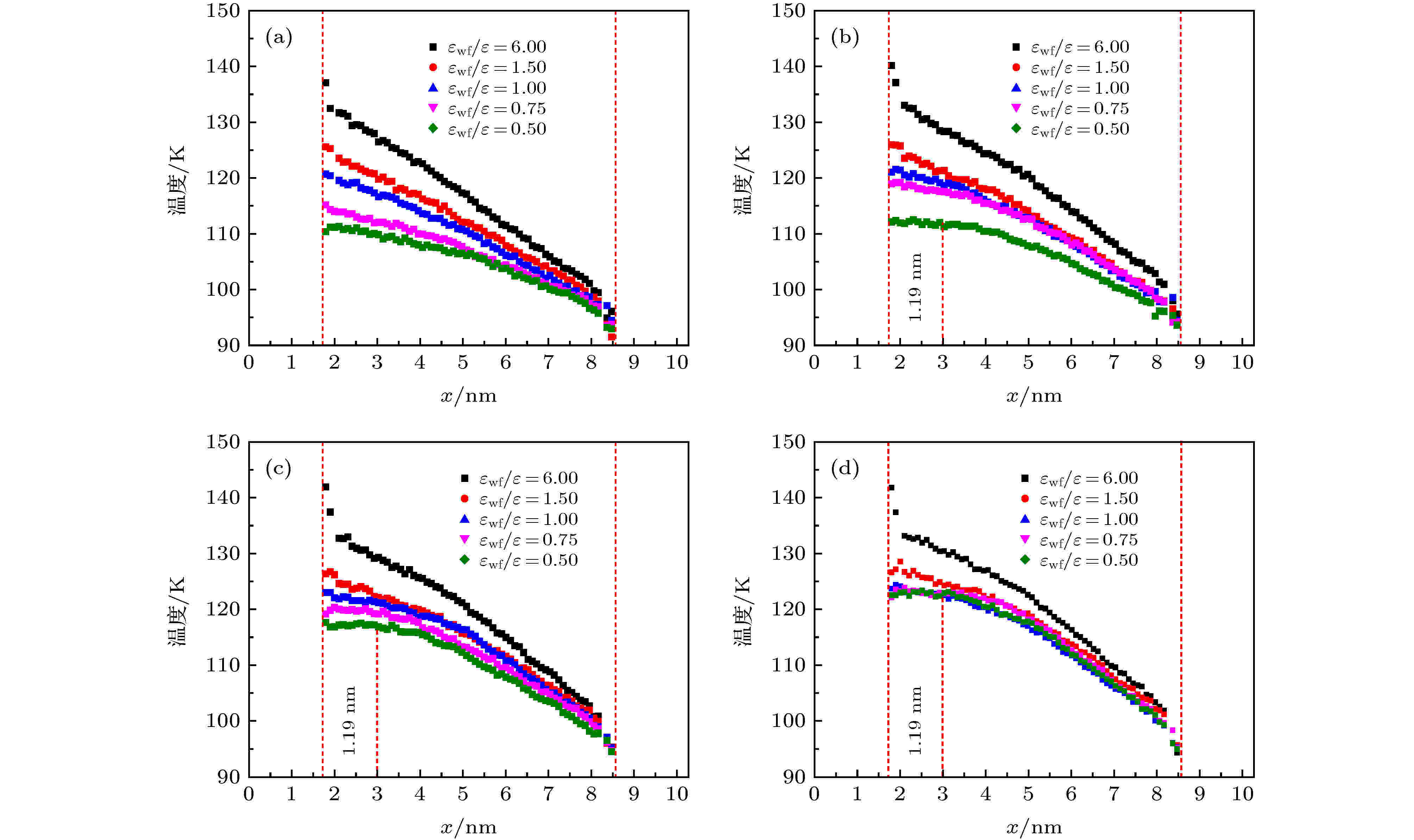图 13 工况1中液体氩在不同外力作用下的温度分布　(a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ
Figure13. Temperature distribution of liquid argon under different external forces in condition 1: (a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ.

图14直观展示了相同固液势能强度下, 不同外力作用对流体温度分布的影响. 包括(a) ε_wf/ε = 6.0; (b) ε_wf/ε = 1.5; (c) ε_wf/ε = 1.0; (d) ε_wf/ε = 0.75; (e) ε_wf/ε = 0.5. 结果显示, 无论固液势能强度取值多大, 流体温度随着外力的增大均有着不同程度的上升. 当固液势能强度较强时(ε_wf/ε = 6.0), 外力的增大使流体温度略有上升, 且分布形式有偏离线性分布的趋势. 随着固液势能强度的减弱, 外力对流体温度分布的影响逐渐明显, 即不同外力间温度分布差距越来越大, 且温度分布偏离线性的现象越来越明显. 特别是当固液势能强度较弱时(ε_wf/ε = 0.5), 随着外力的增大, 距离壁面1.19 nm范围内的流体温度分布明显脱离线性, 这是由于较弱固液势能强度下, 固液界面处更容易产生摩擦粘性热导致的. 为了定量地描述1.19 nm范围内界面摩擦对局部温度的贡献, 图15显示了ε_wf/ε = 0.5时, 不同外力作用下1.19 nm范围内局部平均温度分布. 结果显示, 随着外力的增大, 局部区域流体平均温度逐渐上升, 上升幅度分别为9.37%, 10.68%, 15.81%和21.35%.
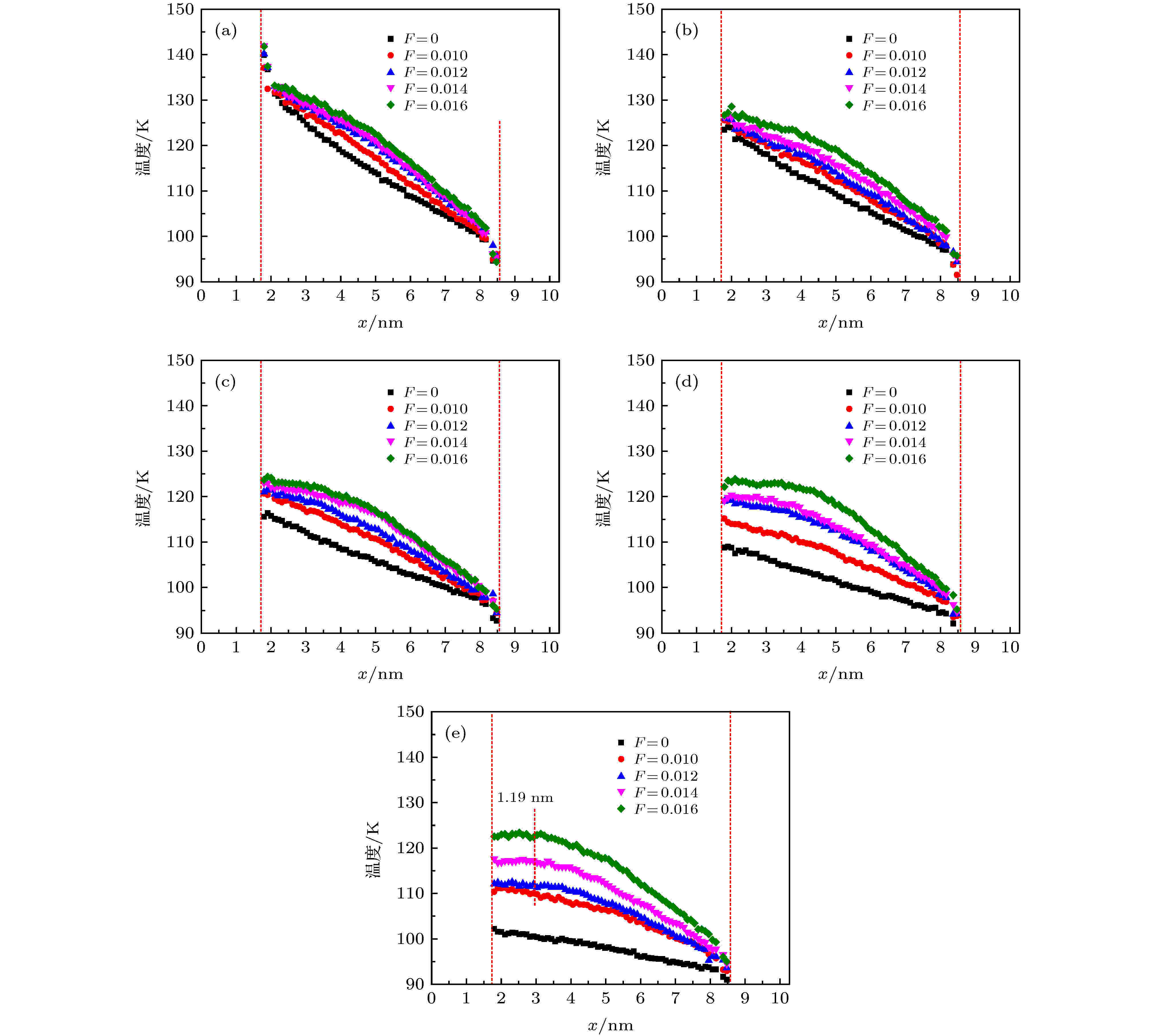图 14 工况1中液体氩在不同固液势能强度下的温度分布　(a) ε_wf/ε = 6.0; (b) ε_wf/ε = 1.5; (c) ε_wf/ε = 1.0; (d) ε_wf/ε = 0.75; (e) ε_wf/ε = 0.5
Figure14. Temperature distribution of liquid argon under different solid-liquid potential energy intensity: (a) ε_wf/ε = 6.0; (b) ε_wf/ε = 1.5; (c) ε_wf/ε = 1.0; (d) ε_wf/ε = 0.75; (e) ε_wf/ε = 0.5.

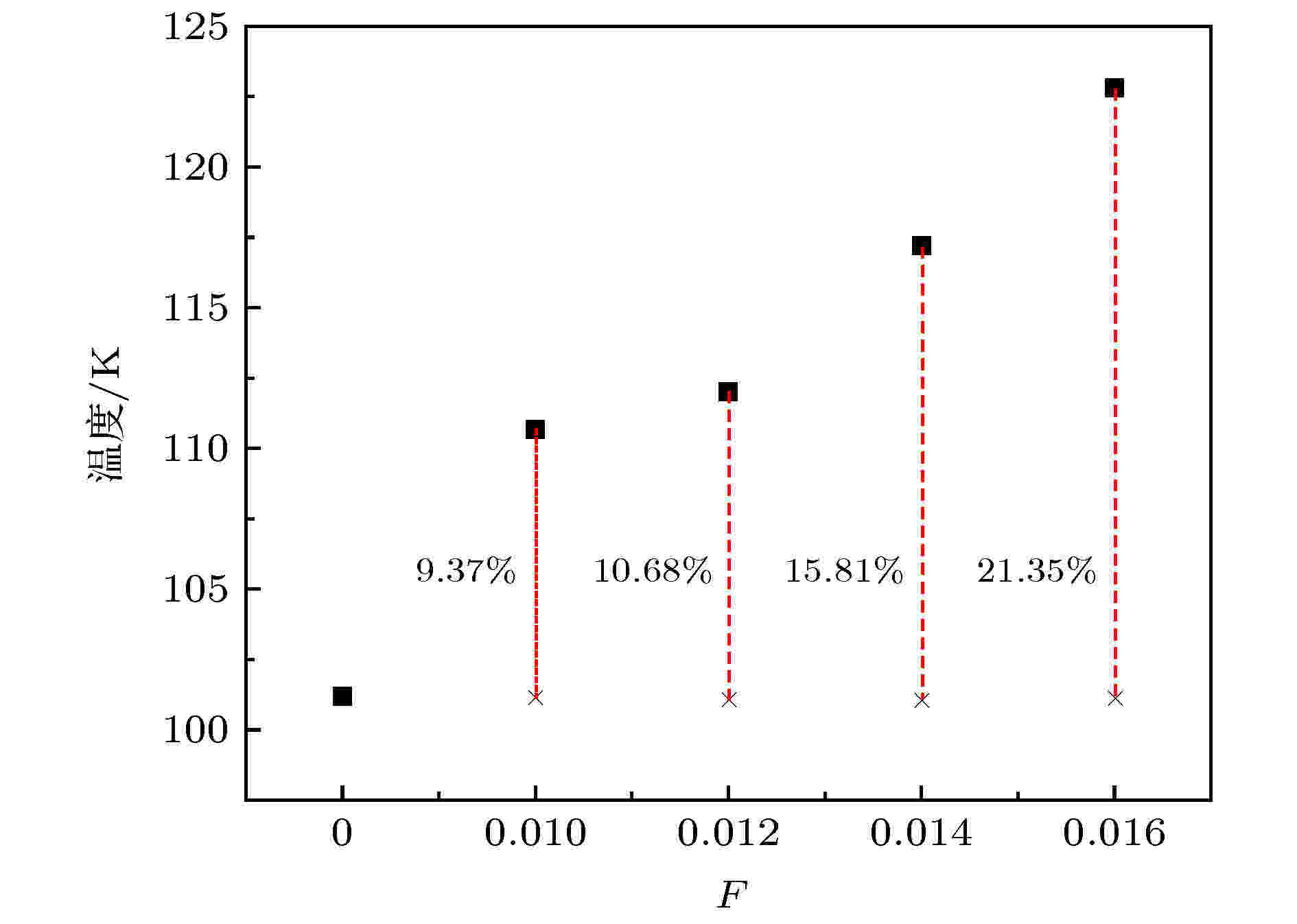图 15 不同外力作用下近热壁面局部(1.19 nm)平均温度分布
Figure15. Local (1.19 nm) average temperature distribution near the hot wall under different external forces.

为了说明产生上述温度分布的原因, 本节计算了工况1中热壁面附近液态氩的速度分布, 目的是为了比较不同外力和固液势能强度下产生的滑移现象, 结果如图16所示. 图中仅显示了距离壁面厚度为0.4 nm的流体区域内速度分布, 结果表明, 当固液势能强度ε_wf/ε < 1.5时, 随着外力的增大, 近热壁面处流体的速度逐渐增大, 即产生了明显的界面滑移, 并导致界面处产生摩擦粘性热. 而在较强的润湿性下, 由于壁面分子与流体分子间较强的作用力, 使得近热壁面处流体的速度极小, 甚至为零, 即在界面处没有速度滑移, 说明此时在界面处没有产生额外的粘性热或产生的粘性热极少. 这与图14中观察到的现象一致, 即壁面润湿性较弱时, 外力的增大会明显增大界面滑移, 产生明显的温度上升现象, 而在润湿性较强时, 外力的增大不会带来界面滑移, 同时界面处温度变化幅度也不再明显.
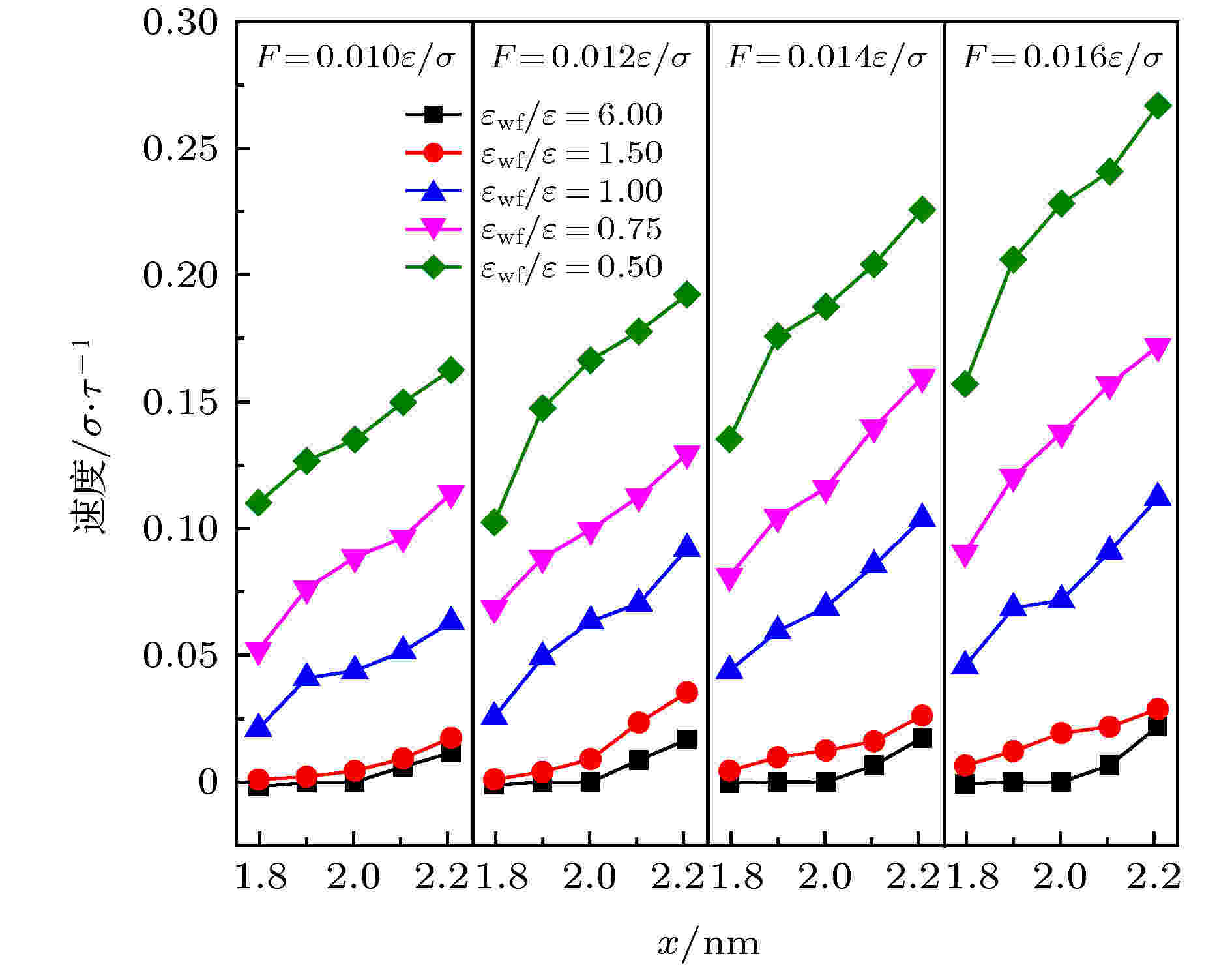图 16 近热壁面处液态氩的速度分布
Figure16. Velocity distribution of liquid argon near the hot wall surface.

图17为工况1中, 不同外力与固液势能强度对系统热通量的影响. 如图所示, 随着外力的增大, 每个固液势能强度下对应的热通量均有所上升, 因为在较高外力作用下, 系统产生了较大的额外能量, 流体分子获得了较大的动能, 固液界面处产生的摩擦粘性热使系统温度升高. 此外可以发现, 随着固液势能强度的增大, 外力对热通量的影响逐渐减小, 这是由于热壁面与流体之间较高的势能强度限制了界面处流体分子的运动, 从而降低或消除了流体与壁面间的摩擦粘性热.
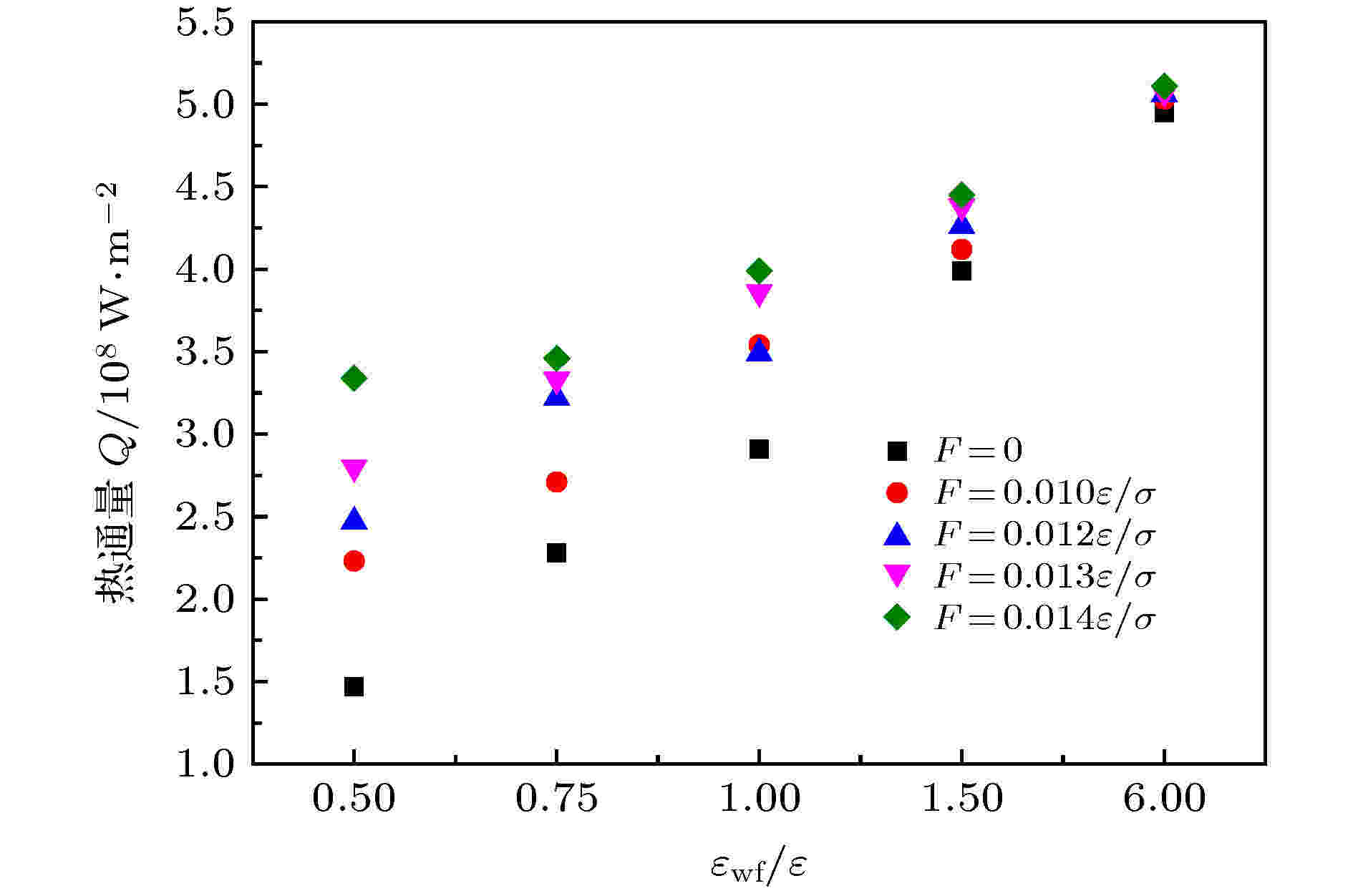图 17 外力作用下固液势能强度比对系统热通量的影响
Figure17. Effect of solid-liquid potential energy on system heat flux under external force

图18为工况1中, 不同外力与固液势能强度对温度跳跃的影响. 图18(a)显示了热壁面处的温度跳跃(ΔT_hot), 结果表明, 随着外力的增大, 热壁面处的温度跳跃逐渐减小, 这是因为在所选取的外力范围内, 由Navier型温度边界条件预测的界面处的流体温度均未超过热壁面的温度(140 K), 因此, 外力越大, 界面处的流体温度越接近壁面温度, 并导致温度跳跃的减小. 与静态流体中相同的是, 在固液势能强度较强的条件下, 呈现出较低的温度跳跃. 这是因为虽然在较弱润湿性下, 外力的存在更容易产生摩擦粘性热, 但其产生的额外热量始终小于较强润湿性下壁面与流体间导热产生的热量, 说明了纳米尺度下, 固液原子间作用力是决定界面传热的主导因素. 图18(b)显示了工况1中冷壁面侧的温度跳跃(ΔT_cold), 结果表明, 随着壁面润湿性的增强, 冷壁面侧的温度跳跃略有增大; 而随着外力的增大, 冷壁面侧的温度跳跃也有所增大, 但幅度很小, 这可能是由于流体分子内部碰撞而产生了少量的热量, 使得近冷壁面流体温度也略有上升, 增大了与冷壁面间的温度差异.
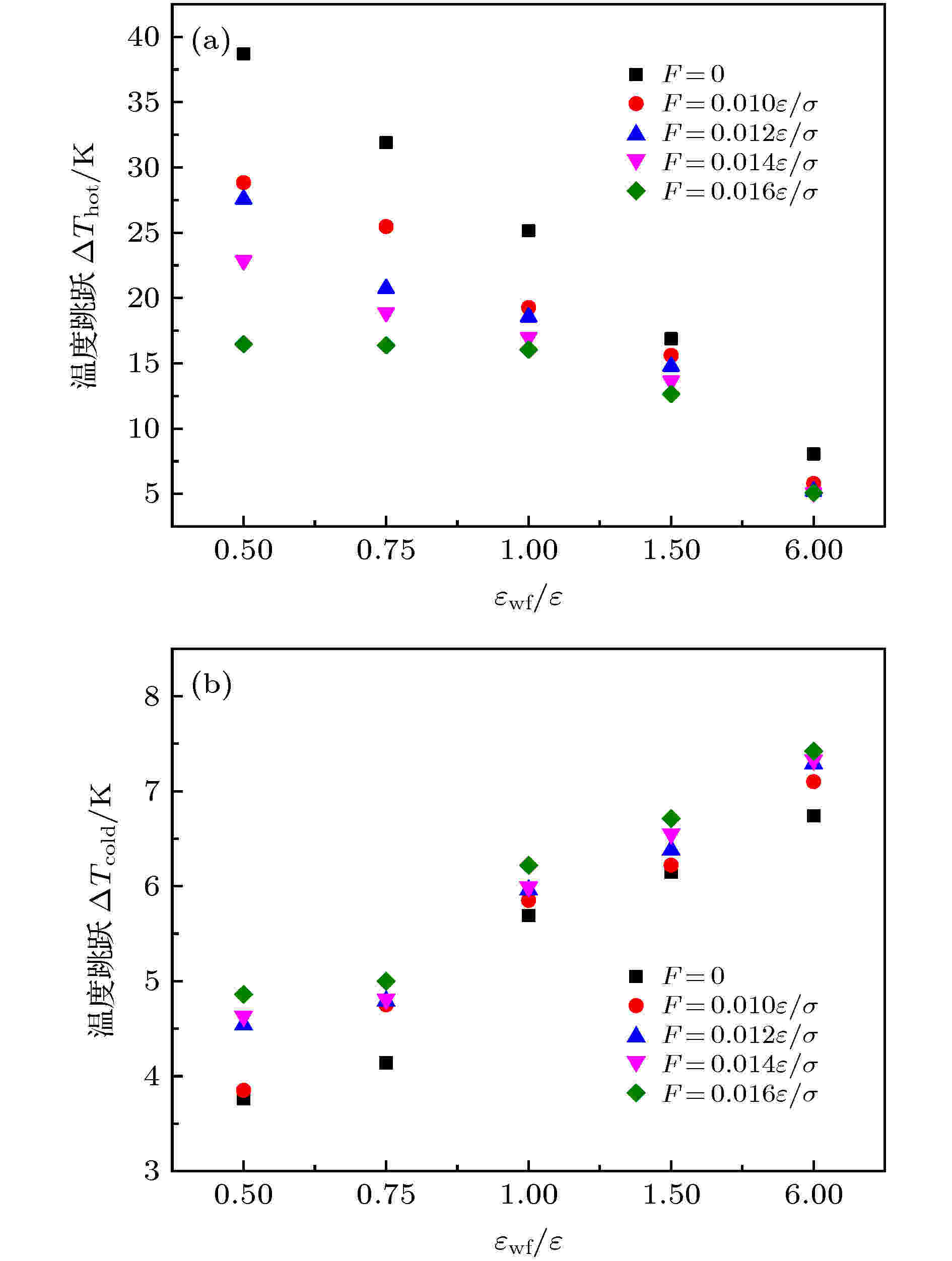图 18 工况1中不同外力作用下固液势能强度对温度跳跃的影响　(a) 热壁面; (b) 冷壁面
Figure18. Effect of solid-liquid potential energy on temperature jump under different external forces in condition 1: (a) Hot wall surface; (b) cold wall surface.

根据上述对系统热通量及温度跳跃的分析, 得到了不同外力作用及固液势能强度对界面热阻的影响规律, 结果如图19所示. 其中图19(a)表示热壁面侧界面热阻的变化规律, 可以看出, 随着外力的增大, 热壁面处界面热阻在每个对应的固液势能强度下均有所降低; 同时固液势能强度的增大也有利于降低界面热阻. 当固液势能强度较强时, 各个外力下对应的热阻值趋于一致, 说明在较强壁面润湿性条件下, 外力对界面热阻的影响较小. 图19(b)为冷壁面侧界面热阻的变化规律, 从图中可以发现, 冷壁面侧的界面热阻变化幅度很小, 且规律性较差.
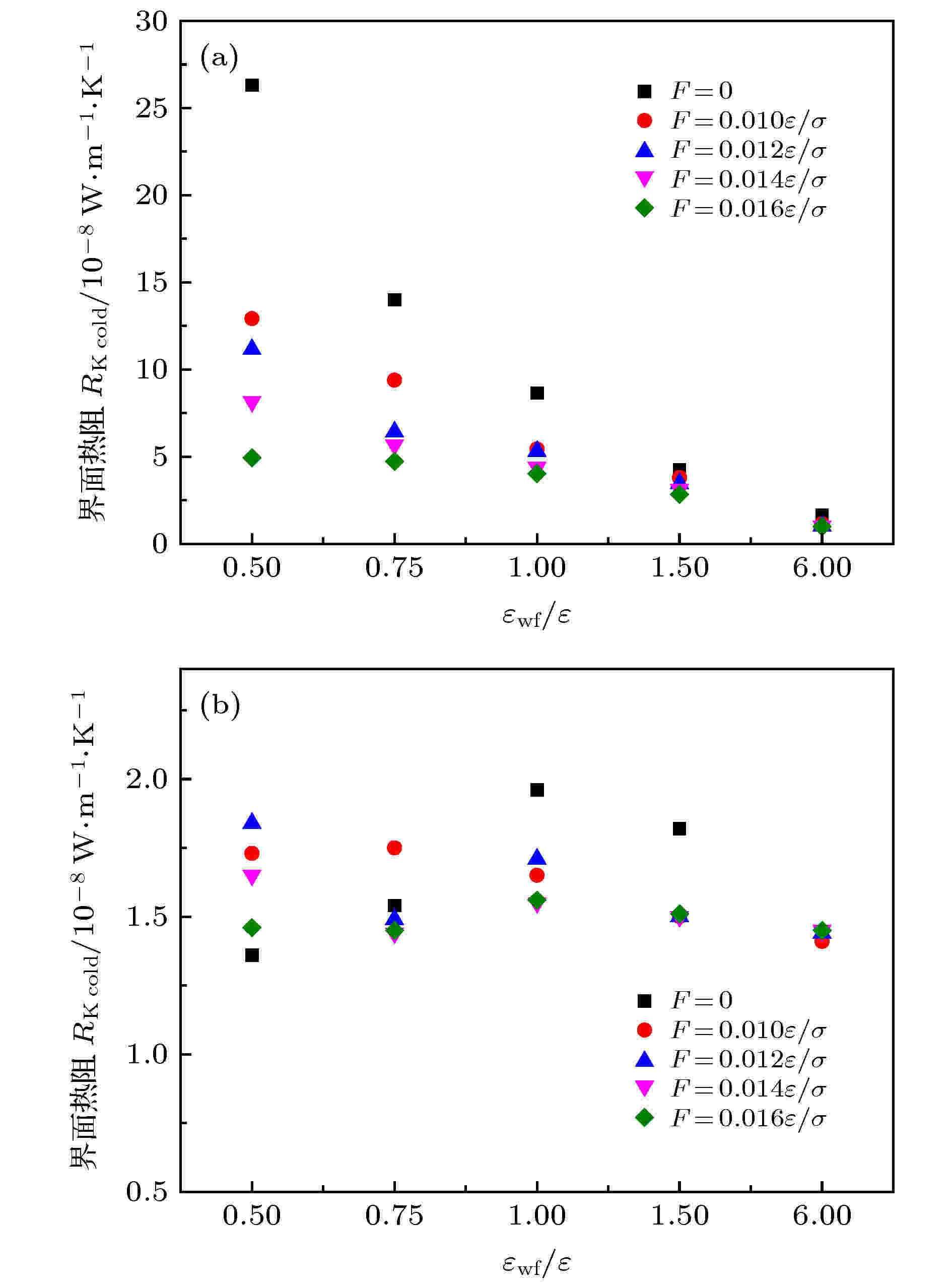图 19 工况1中不同外力作用下固液势能强度对界面热阻的影响　(a) 热壁面; (b) 冷壁面
Figure19. Effect of solid-liquid potential energy on interface thermal resistance under different external forces in condition 1: (a) Hot wall surface; (b) cold wall surface.

为了探究在外力存在条件下, 壁面吸附流体分子数量对界面热阻的影响, 计算了不同外力下热壁面上吸附的氩分子数量, 结果如图20所示. 从图中可以看出, 固液势能强度的增大可以增加壁面吸附流体分子的数量, 从而导致界面热阻减小, 这与之前所得结论一致. 而外力的变化对壁面吸附流体分子数量的影响较小, 这是因为壁面吸附流体分子数量主要是由固液势能强度决定的. 当固液势能强度较强时, 外力作用很难使界面流体分子脱离壁面的束缚, 界面滑移现象不明显; 当固液势能强度较弱时, 外力作用可能使流体分子脱离壁面束缚, 并获得一定的动能, 但其运动位置始终在固液界面处, 导致固液界面处流体分子数量基本不变, 同时产生明显的滑移现象.
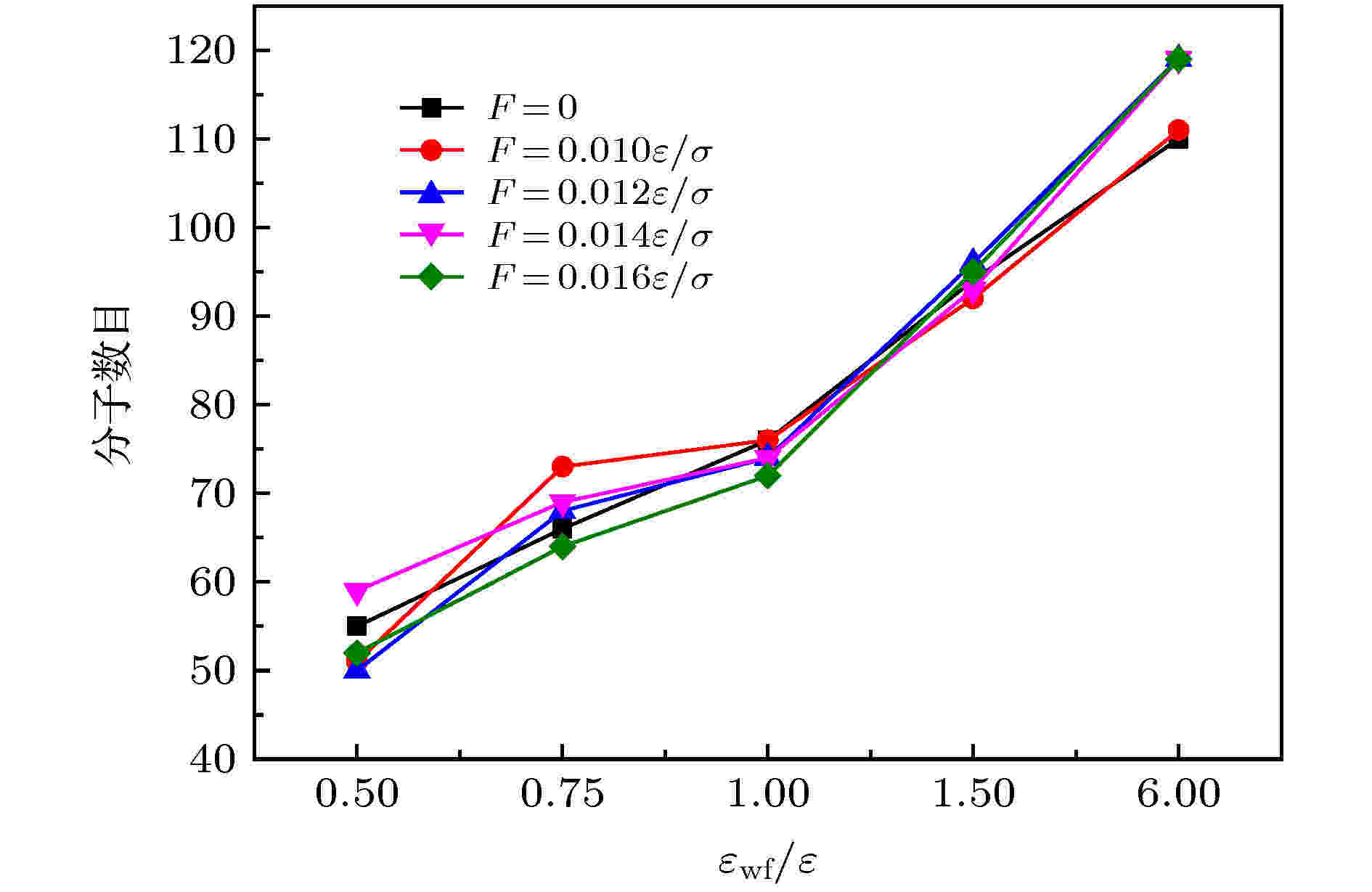图 20 动态流体中热壁面吸附流体分子数
Figure20. The number of adsorbed fluid molecules on the hot wall in flowing fluid.

本文利用分子动力学方法对非对称纳米通道中固液界面处的界面热阻进行研究. 分析了固液势能强度变化, 以及高、低温壁面对界面热阻的影响. 随后, 通过添加外部驱动力, 使流体流动, 研究了外部驱动力大小对界面热阻的影响, 并将静态流体下的界面热阻与动态流下的热阻值进行比较, 得到如下结论.
1)静态流体中, 固液势能强度的增大能够有效降低界面温度跳跃, 提高系统热通量, 从而降低界面热阻. 壁面温度对界面热阻的影响是受限的, 当固液势能强度较弱时, 可以观察到热壁面处的界面热阻要高于冷壁面处的界面热阻; 而当固液势能强度较强时, 壁面温度对界面热阻的影响很小.
2)动态流体中, 外力对界面热阻的影响也是受限的. 当固液势能强度较弱时, 外力的增大会导致界面处产生滑移现象, 使流体温度升高, 界面热阻值逐渐减小; 而当固液势能强度较强时, 外力的作用很难使界面产生滑移, 对界面热阻的影响也很小.
3)将界面热阻与壁面吸附流体分子数量相联系. 结果表明, 静态流体中, 界面热阻与壁面吸附流体分子数相关, 吸附分子数量越多, 越有利于传热, 界面热阻越小; 在动态流体中, 外力的变化对壁面吸附流体分子数影响很小, 影响流体分子数量的主要因素是固液势能强度.