摘要:针对霍尔效应对高超声速磁流体力学控制的影响问题, 考虑高超声速流动过程中高温化学反应、气体分子热力学温度激发(即平动、转动、振动以及电子温度能量模态之间的激发与松弛过程)及多电离组分等离子体霍尔系数分布, 通过耦合求解各向异性霍尔电场泊松方程和带电磁源项的高温热化学非平衡流动控制方程组, 建立了高超声速流动磁流体力学控制霍尔效应数值模拟方法, 开展了多种条件下高超声速流动磁流体力学控制数值模拟, 分析了霍尔效应“漏电”与“聚集”现象原理及其对气动力/热特性的影响机制, 详细探讨了不同空域、速域和飞行器特征尺度条件下霍尔效应的作用机理和影响规律. 研究表明: 1)霍尔效应改变了流场等离子体洛伦兹力分布, 削弱了整体的力学效果, 使整体的磁阻特性降低; 2)霍尔效应对高超声速磁流体力学控制的影响, 与壁面导电性和壁面附近漏电层的“漏电”现象紧密相关, 要增强磁控效果, 必须抑制壁面附近的“漏电”现象; 3)霍尔效应对磁控热防护效果的影响较为复杂, 受“漏电”现象和电流“聚集”现象共同作用; 4)基于本文基准状态, 当高度高于67 km或速度高于5.7 km/s或特征尺度大于0.5 m时, 霍尔效应使磁控热防护效果增强, 电流“聚集”现象对气动热环境的影响占主导; 反之, 则霍尔效应使磁控热防护效果减弱, “漏电”现象对气动热环境的影响占主导.
关键词: 磁流体动力学/
霍尔效应/
等离子体/
数值模拟

English Abstract

全文HTML

--> --> -->

20世纪90年代以来, 随着高超声速飞行技术的蓬勃发展, 人们对磁流体力学(magnetohydrodynamic, MHD)控制在高超声速领域的研究投入了极大的热情. 通过磁场发生装置向高超声速流动注入适当的动量和能量, 可以有效地控制和改善飞行器的气动环境与性能. 这种涉及多学科交叉融合的高超声速磁流体控制技术, 可广泛应用于飞行器气动热防护与管理、气动力操控、电磁通信与隐身、磁流体发电等多个方面, 受到世界各航天大国的高度重视^[1], 例如国外很早就提出了高超声速巡航飞行器AJAX概念, 拟将MHD控制技术应用于高超声速飞行器控制系统, 其中涉及了磁流体流动控制技术的多种应用形式.
由于流体中带正、负电荷的载流子迁移率的差异, 高超声速电磁流动过程中会出现霍尔效应^[2] (Hall effect), 例如在飞行高度为75 km时, 激波波后气体的相对霍尔系数可达10² T^–1量级, 霍尔效应有可能使磁阻力效果下降50%以上. 霍尔效应不仅受磁场强度影响, 而且与流体介质物理特性紧密相关. 在高超声速领域, 其有效评估较为困难. 一方面是由于高超声速流动介质一般为含多种电离组分的等离子体混合气体, 它的霍尔系数存在较多的不确定性, 与高超声速流动过程的热化学非平衡现象紧密相关; 另一方面霍尔效应导致的各向异性特性, 会极大地增加数值模拟的复杂度和难度, 尤其是在大霍尔系数条件下, 电导率系数矩阵“病态程度”大大增加, 会导致强烈的刚性问题和收敛性问题^[3]. 因此, 国内外在开展高超声速MHD数值模拟时, 常常忽略霍尔效应的影响, 或者采用简化方法进行处理, 如采用完全气体模拟、定霍尔系数方法或均变霍尔系数方法(全场各区域霍尔系数相等, 为可变的人为给定值)等.
对于高超声速MHD控制来说, 霍尔效应的影响较为复杂. 为了探讨霍尔效应对高超声速MHD控制的影响, 国外近十多年来针对霍尔效应开展了不少研究. 2003年, Borghi等^[4]开展尖锥体飞行高度为50 km下的磁流体数值模拟时, 采用完全气体模型和定霍尔系数方法, 人为给定全流场相对霍尔系数${\beta _{\rm{e}}}$ = 50 T^–1, 发现霍尔效应在一定程度上削弱了磁场对压力系数和摩阻系数的影响; 2005年, Otsu^[5]采用定霍尔系数方法(${\beta _{\rm{e}}}$为20 T^–1)开展了钝柱体飞行器飞行高度为69 km的磁控热防护系统的数值模拟, 发现霍尔效应的作用效果受壁面导电性影响, 对于绝缘壁面, 霍尔效应的影响几乎可以忽略, 而对于导电壁面, 霍尔效应一定程度上削弱了磁控热防护的效果; 2006和2007年, Fujino等^[6,7]针对钝体飞行器OREX开展了飞行高度为59.6 km时不同导电壁面条件下霍尔效应对磁控热防护影响的研究, 发现当壁面的导电性低于某个限度时, 霍尔效应的影响可以忽略; 2009年, Boettcher^[8]采用完全气体模型, 开展了导电球头模型磁流体数值模拟, 发现霍尔效应在一定程度上削弱了磁场对激波脱体距离的影响; 2012年, Nagata等^[9]采用完全气体模型和均变霍尔系数(${\beta _{\rm{e}}}$变化范围为0—100 T^–1)方法开展了倾斜磁场条件下钝柱体磁流体数值模拟, 发现霍尔效应一定程度上会影响飞行器气动特性的磁控效果; 2013年, Fujino和Ishikawa^[10]又开展了二维大钝头沿再入轨道的低磁雷诺MHD流动, 他们的主要结论之一是霍尔效应对激波脱体距离和磁控热防护效果的影响基本可以忽略; 2015年, Takahashi等^[11]开展了典型火星探测器60 km时MHD控制数值模拟, 发现霍尔效应对于磁控热防护和磁控增阻特性的影响很小, 基本可以忽略. 同年, Masuda^[12]在Fujino研究的基础上进一步开展了非零攻角或倾斜磁场条件下霍尔效应对钝锥体MHD控制的影响, 发现霍尔效应会导致环形电流扭曲, 进而产生非对称的气动力作用.
国内也有高超声速磁流体霍尔效应方面的研究, 得到一些有价值的结论. 2010年, 吕浩宇和李椿萱^[13]采用定霍尔系数方法, 开展了霍尔效应对压缩管道磁流体流动影响的研究, 发现霍尔效应将导致磁流体发生器的性能下降; 2011年, 胡海洋等^[3]采用完全气体流场计算霍尔系数, 开展大霍尔系数下电离气体与磁场相互作用规律数值研究, 分析了圆管绕流大霍尔系数条件下的收敛情况及其磁控效果; 2017年, 李开等^[14]采用均变霍尔系数方法, 开展了高超声速飞行器磁控热防护霍尔电场的数值计算方法研究, 探讨了步进因子的取值方法及其对计算收敛性影响.
从国内外的发展可以看出, 尽管国内外对高超声速磁流体霍尔效应进行了不少研究, 但霍尔效应的影响及其定性/定量规律, 仍存在很大的不确定性: 霍尔效应的研究大多采用简化模型或方法, 如完全气体模型、均变霍尔系数方法等, 这些研究与真实的飞行热化学非平衡等离子体环境存在差异; 霍尔效应的影响仍有待进一步探索, 霍尔效应通常表现为对磁场控制效果的某种弱化, 但这种“弱化”效果差异较大, 尚未有明确的作用范围和界限, 缺乏较为系统的认识. 在某些情况下, 霍尔效应甚至表现为对磁控效果的增强, 例如2015年, Masuda^[12]的研究表明霍尔效应明显增强了钝锥体头部磁控热防护效果; 2017年, 李开等^[15]发现在不同磁感应强度下霍尔效应对绝缘壁面热流的影响规律不同, 当磁场特征磁感应强度为0.2 T时, 霍尔效应增强了磁控热防护效果, 他认为这种现象是由于这一条件下霍尔效应使附面层洛伦兹力增加, 流体减速作用占主导造成的. 但这一研究采用的是假设的均变霍尔系数方法, 霍尔系数的分布没有考虑真实等离子体环境影响, 同时只开展了特定飞行器单个飞行状态(高度63 km、马赫数20)的研究, 没有进行霍尔效应在不同飞行空域、速域和尺度效应方面的研究.
作者所在研究团队对高超声速飞行器非平衡等离子体流场及磁流体控制, 进行了较为广泛的研究^[16-19]. 本文考虑高温热化学非平衡效应模拟高温气体等离子体生成机制, 得到多电离成分混合气体霍尔系数, 通过耦合求解各向异性霍尔电场泊松方程和带电磁源项的高温非平衡流动控制方程组, 建立高超声速流动MHD控制霍尔效应数值模拟方法, 采用典型算例对数值模拟方法进行校验, 同时结合壁面导电特性, 分析霍尔效应“漏电”现象机理和影响. 在此基础上, 考虑热化学非平衡流场等离子体霍尔系数分布, 开展多种计算条件(速域、空域、尺度)下高超声速流动MHD控制数值模拟, 探讨霍尔效应对MHD控制的作用机制及影响规律.

2

-->

2.1.高温化学反应模型和热力学温度模型

为了较为真实地模拟高温气体流场多种电离成分等离子体环境, 选用11组分(O₂, N₂, NO, O, N, NO⁺, e, ${\rm{O}}_2^ + $, ${\rm{N}}_2^ + $, O⁺, N⁺)空气电离模型, 其中考虑高温空气离解、电离、置换和复合等化学反应, 模拟高超声速流动过程中的高温气体化学反应非平衡过程. 气体第j个组分的化学非平衡源项^[18]可写为${W_j} = {M_j}\displaystyle\sum\nolimits_{i = 1}^{N_{\rm r}} {\left( {\gamma _{ij}^* - {\gamma _{ij}}} \right)} {Q_i}$, 这里$N_{\rm r}$为化学反应数, ${Q_i}$为第i个化学反应的生成源项, ${M_j}$为第j组分分子量, ${\gamma _{ij}}$和$\gamma _{ij}^*$分别第i个化学反应的反应物和生成物中第j组分的系数. 通过化学反应非平衡过程的模拟, 可得到流场中各气体组分分布, 为准确计算气体电导率和霍尔系数分布提供基础数据.
高超声速流动等离子体鞘中, 热力学振动非平衡松弛过程及其与化学离解反应耦合影响, 通过热力学双温度模型和振动-离解耦合模型模拟. 热力学非平衡源项^[19,20]可写为${W_{\rm{V}}} \!=\!\sum [{\rho _i}(e_{i, {\rm{V}}}^ * \!-\! {e_{i, {\rm{V}}}})/{\tau _{{\rm{V}}i}} +\! {e_{i, {\rm{V}}}}{W_i}]$, 这里${\rho _i}$为第i组分密度, ${W_i}$是第i组分的化学生成源项, $e_{i, {\rm{V}}}^ * $, $e_{i, {\rm{V}}}$和${\tau _{{\rm{V}}i}}$分别为第i组分的平衡振动能、非平衡振动能和松弛特征时间. 通过热力学非平衡过程的模拟, 可为计算电导率和霍尔系数提供较为准确的平动-转动温度和振动-电子温度分布.
2 -->

2.2.气体霍尔系数及电导率计算模拟

霍尔系数存在多种形式^[2,3,11]. 一般认为, 对于高超声速流动, 霍尔系数$\beta $正比于电子迁移率, 即$\beta = {\mu _{\rm{e}}}\left| {{B}} \right|$, 这里${\mu _{\rm{e}}}$和${{B}}$分别为电子迁移率和磁感应强度. ${\mu _{\rm{e}}}$可由气体电导率给出^[12], 即${\mu _{\rm{e}}} \!=\! \sigma /(e{n_{\rm{e}}})$, 这里$\sigma $, e和${n_{\rm{e}}}$分别为气体电导率、电子电荷和电子数密度. 气体电导率$\sigma $的计算方法很多^[17], 如无特别说明, 本文采用基于电子/离子/中性粒子扩散、碰撞与迁移的原理计算电导率, 该方法综合考虑了强/弱电离导电机理和不同气体成分碰撞截面的差异, 能较好地适用于多组分电离气体. 因此, 霍尔系数$\beta $、相对霍尔系数${\beta _{\rm{e}}}$和电导率$\sigma $可写为

$ \beta ={\beta }_{\rm{e}}\left|{{B}}\right|, \; {\beta }_{\rm{e}}= \dfrac{\sigma}{ e{n}_{\rm{e}}}, \;\sigma = \dfrac{{n}_{\rm{e}}{e}^{2}}{{m}_{\rm{e}}{\displaystyle\sum\nolimits_{s\ne \rm{e}}{\upsilon }_{{\rm e},s}^{\rm{m}}}}, $

这里$\upsilon _{{\rm{e}}, s}^{\rm{m}}$为电子与混合气体第s组分有效动量传输碰撞频率, 与气体成分和热力学松弛紧密相关. 当s为离子组分, 其表达式可写为^[16,17]

$\begin{split}\upsilon _{{\rm{e}},s}^{\rm{m}} =\;& 6{\rm{\pi }}{\left( {\frac{{{e^2}}}{{12{\rm{\pi }}{\varepsilon _0}{k_{\rm{b}}}{T_{\rm{e}}}}}} \right)^2}\ln \left[ {12{\rm{\pi }}{{\left( {\frac{{{\varepsilon _0}{k_{\rm{b}}}}}{{{e^2}}}} \right)}^{1.5}}\sqrt {\frac{{{T_{\rm{e}}}^3}}{{{n_{\rm{e}}}}}} } \right]\\&\times{n_s}\sqrt {\frac{{8{k_{\rm{b}}}{T_{\rm{e}}}}}{{{\rm{\pi }}{m_{\rm{e}}}}}},\\[-20pt]\end{split}$

当s为中性组分, 其表达式为^[16,17]

$\upsilon _{{\rm{e}},s}^{\rm{m}} = \dfrac{4}{3}\sigma _{{\rm{e}},s}^{\rm{m}}{n_s}\sqrt {\dfrac{{8{k_{\rm{b}}}{T_{\rm{e}}}}}{{{\rm{\pi }}{m_{\rm{e}}}}}},$

这里${k_{\rm{b}}}$和${\varepsilon _0}$分别为玻尔兹曼常数和真空介电常; ${T_{\rm{e}}}$, e, ${m_{\rm{e}}}$, ${n_{\rm{e}}}$和${n_s}$分别为电子温度、电子电量、电子质量、电子数密度和气体组分s的数密度; $\sigma _{{\rm{e}}, s}^{\rm{m}}$为电子与气体中性组分s的有效碰撞截面, 一般为温度的函数, 由试验拟合曲线计算得到.
2 -->

2.3.控制方程及处理方法

高超声速飞行器高温气体流场中混合气体的电导率一般较低, 通常满足低磁雷诺数假设, 这里采用低磁雷诺数MHD方法, 流动控制方程形式为

$\begin{split}&\frac{{\partial {{Q}}}}{{\partial t}} + \frac{{\partial {{F}}}}{{\partial x}} + \frac{{\partial {{G}}}}{{\partial y}} + \frac{{\partial {{H}}}}{{\partial z}} \\=\;& \frac{1}{{Re}}\left( {\frac{{\partial {{{F}}_{\rm{V}}}}}{{\partial x}} + \frac{{\partial {{{G}}_{\rm{V}}}}}{{\partial y}} + \frac{{\partial {{{H}}_{\rm{V}}}}}{{\partial z}}} \right) + {{W}} + {{{W}}_{{\rm{MHD}}}}. \end{split}$

这里${{Q}}$为守恒变量; ${{{F}}_{\rm{V}}}, {{{G}}_{\rm{V}}}, {{{H}}_{\rm{V}}}$和${{F}}, {{G}}, {{H}}$分别为3个方向的黏性向量与无黏向量; 等离子体分布及热力学非平衡效应的模拟通过热化学非平衡源项^[21]${{W}} = {({W_j}, {W_{\rm{V}}}, 0, 0, 0, 0, 0)^{\rm{T}}}$表达, ${W_j}$和${W_{\rm{V}}}$由2.1节模型计算得到. 流场控制方程(4)迭代求解过程中, 电磁场对流场动量/能量的输运, 通过电磁源项${{{W}}_{{\rm{MHD}}}} = [{0_j},\; 0, {({{J}} \times {{{ B}}})_x}, {({{J}} \times {{B}})_y}, {({{J}} \times {{B}})_z}, {{J}} \cdot {{E}}, \gamma {{J}} \cdot ({{E}} + {{U}} \times {{B}})]^{\rm{T}}$表达. 这里${{J}}$为电流密度矢量, ${{E}}$为电场强度矢量, $\gamma $为焦耳热振动能量配比, ${{U}}$为速度矢量. 为了保证计算精度和稳定性, (4)式对流项的空间离散采用AUSMPW+(advection upstream splitting method by pressure-based weight functions)格式, 时间离散是采用全隐式全耦合的LUSGS (lower-upper symmetric Gauss Seidel)方法. 流场边界处理见文献[22, 23].
(4)式的电磁源项${{{W}}_{{\rm{MHD}}}}$中电流${{J}}$和电场${{E}}$, 通过数值耦合求解电场泊松方程得到, 其形式为

$\partial \phi /\partial t + \nabla \cdot \left\{ {{\tilde{ \sigma }}\left[ {\nabla \phi - ({{U}} \times {{B}})} \right]} \right\} = 0,$

其中$\phi $为电势, 电场$E=-\nabla \phi$, 电流${{J}} = \tilde \sigma ({{E}} + {{U}} \times {{B}})$. $\partial \phi /\partial t$为人工虚拟项, 不具有实际的物理意义. 引入人工虚拟项的主要目的是类比流体力学CFD (computational fluid dynamics)定常流场计算方法, 便于采用隐式时间离散迭代求解. 其优点在于可根据矩阵的谱半径计算虚拟的当地时间步长, 从而避免了歩进因子等人工参数, 自动达到快速收敛的目的. 对于定常状态, 当(5)式迭代收敛时, 需满足“电势$\phi $的分布与时间无关”的收敛判据条件, 即$\partial \phi /\partial t \to 0$. 此时(5)式等价于$\nabla \cdot \left\{ {{\tilde{ \sigma }}\left[ {\nabla \phi - ({{U}} \times {{B}})} \right]} \right\} = 0$, 即定常条件下电荷守恒方程$\nabla \cdot {{J}} = 0$.
霍尔效应通过电场泊松方程(5)影响电流${{J}}$和电场${{E}}$分布, 进而影响电磁场对流场动量/能量的输运过程, 即影响流动控制方程(4)中的电磁源项${{{W}}_{{\rm{MHD}}}}$. 不考虑霍尔效应时, (5)式中电导率张量${\tilde{ \sigma }} = \sigma {{I}}$, ${{I}}$为单位矩阵. 考虑霍尔效应时, 张量${\tilde{ \sigma }}$可写为

$ \begin{split}&{\tilde{ \sigma }} = \sigma {{A}},\qquad{{A}} = \dfrac{1}{{1 + {\beta ^2}}}\left[ {\begin{array}{*{20}{c}}{1 + \beta _{}^2b_x^2}&{\beta ( - {b_z} + \beta {b_x}{b_y})}&{\beta ({b_y} + \beta {b_x}{b_z})}\\{\beta ({b_z} + \beta {b_x}{b_y})}&{1 + \beta _{}^2b_y^2}&{\beta ( - {b_x} + \beta {b_y}{b_z})}\\{\beta ( - {b_y} + \beta {b_x}{b_z})}&{\beta ({b_x} + \beta {b_y}{b_z})}&{1 + \beta _{}^2b_z^2}\end{array}} \right],\end{split}$

这里$ (b_x,b_y,b_z) = B/| B| =(B_x,B_y,B_z)/| B|. $电导率$\sigma $和霍尔系数$\beta $由(1)—(3)式计算得到, 其中流场气体组分密度、平动-转动温度和振动-电子温度等参数分布, 由(4)式结合热化学反应模型和热力学温度模型计算得到.
由(6)式可以看出, 当${\beta ^2} \gg 1$时, 系数矩阵A非对角线元素与对角线元素之比近似为${B_i}/{B_j}$, 这里i和j代表$x, y, z$三个坐标方向, 且$i \ne j$. 可见, 由于实际物理磁场方向的“任意性”, 很容易出现系数矩阵A的对角线元素不占优的情况, 使矩阵出现“病态”, 这在一定程度上导致了数值模拟的刚性. 为了保证数值模拟的收敛性和稳定性, (5)式时间离散采用AF (approximate factorization)隐式处理, 结合局部时间步长方法保证泊松方程三对角阵对角线元素占优, 在右端项空间离散过程中严格保证网格守恒性. 由于全场霍尔系数变化较大, 在大霍尔系数区采用松弛渐进的方法, 使霍尔系数随计算歩数增加逐渐趋近于目标值, 保证霍尔效应的有效模拟. (5)式求解过程中, 绝缘边界满足电流无穿透条件${{n}} \cdot {{J}} = 0$, 代入广义欧姆定律得到${{n}} \cdot ({\tilde{ \sigma }}\nabla \phi ) = {{n}} \cdot [{\tilde{ \sigma }}({{U}} \times {{B}})]$; 导电壁面和远场条件采用常电势边界条件$\phi = {\phi _{\rm{C}}}$, ${\phi _{\rm{C}}}$为某一给定电势. 由于电势是个相对概念, 必须存在一个基准电势, 因此边界条件中必须包含至少一个常电势边界(可以某一个点).
(4)式和(5)式的耦合采用以下步骤: 1)不考虑霍尔效应及霍尔电场, 结合欧姆定律计算电磁源项, 迭代计算(4)式至残差下降约2个量级, 得到初场; 2)结合磁感应强度、流场速度、电导率以及霍尔系数等参数分布, 迭代(5)式至霍尔电场基本收敛(残差降低一个量级或残差较小), 迭代步数不少于100步; 3)根据(5)式得到的电流${{J}}$和电场${{E}}$, 进而得到新的${{{W}}_{{\rm{MHD}}}}$, 逐渐松弛替换(4)式中旧的${{{W}}_{{\rm{MHD}}}}$并迭代(4)式至流场基本稳定, 迭代步数不少于100歩; 4)反复迭代步骤2和步骤3, 直至完全收敛.

采用球头柱体外形, 头部半径1.0 m, 柱体长10.0 m. 模拟飞行高度为69.0 km, 来流速度6500.0 m/s, 等温壁面条件. 外加偶极子磁场, 磁场磁感应强度${{B}} = {B_0}\dfrac{({{r}}\cos \alpha + 0.5{{\alpha }}\sin \alpha )} {(r/{r_0})^3}$, 这里(${{r}}, {{\alpha }}$)为极坐标单位矢量, 偶极子中心位于坐标原点, 即头部球心; ${B_0}$为极轴上距离偶极子中心${r_0}$处的磁感应强度. 磁偶极子的参考长度${r_0}$为1.0 m, 参考点的磁感应强度${B_0} = 0.2$—0.3 T, 磁场极轴与球柱轴线的夹角$ \theta ={0}^{\circ }, {45}^{\circ }$和${90}^{\circ }$, 如图1(a)所示. 流场计算条件及气体电导率和霍尔系数处理方法, 与文献[5, 9]方法相同: $\sigma= {\sigma _0}{(T/{T_0})^2}$, ${\sigma _0} =$ 250 S/m, ${T_0} =$ 25000 K, 均变相对霍尔系数${\beta _{\rm{e}}}= 0.0\text{—} {{100}}{{.0 }}\;{{\rm{T}}^{ - 1}}$, 采用绝缘和导电两种壁面条件. 由于远场边界的设定在一定程度上会影响霍尔电场分布, 因此计算网格远场边界设定原则为: 到壁面的最近距离大于30倍的球头半径.
图 1 磁场配置示意图和网格无关性分析　(a)磁场配置; (b)表面压力; (c)表面热流
Figure1. Magnetic field configuration and anlysis of indepence of grids: (a) Magnetic field configuration; (b) surface pressure; (c) surface heat flux.

为了排除网格对数值计算结果的影响, 图1(b)和图1(c)给出了两套网格计算得到的表面压力和热流分布, Grid 1为稀网格计算结果, 壁面网格第一层法向间距0.01 mm; Grid 2为密网格计算结果, 壁面第一层法向间距0.001 mm. 可以看出, 两套网格计算结果几乎完全重合, 数值计算得到的驻点热流与Fay-Riddell公式计算结果符合较好, 这说明两套网格均能满足数值模拟要求. 为了保证流场的分辨率更高, 这里采用密网格Grid 2开展数值模拟.
图2给出了考虑霍尔效应时钝柱体气动特性计算结果与文献[9]比较, 轴向力系数和侧向力系数分别为体轴坐标系下, X方向和Z方向的气动力系数. 可以看出, 霍尔效应会削弱磁场对轴向力系数的影响, 霍尔系数越大, 削弱作用越强; 磁场倾斜角度对磁流体气动力控制具有一定意义, 磁场倾斜角$\theta $越小, 磁场作用下阻力系数越大; 在计算条件和磁场配置X-Y平面对称的情况下, 磁场倾斜时霍尔效应作用会引入非对称的侧向力, 其大小受磁场倾斜角度和霍尔系数共同影响; 本文计算结果与文献[9]结果符合良好, 说明本文考虑霍尔效应的磁控气动特性模拟具有较好的可信度.
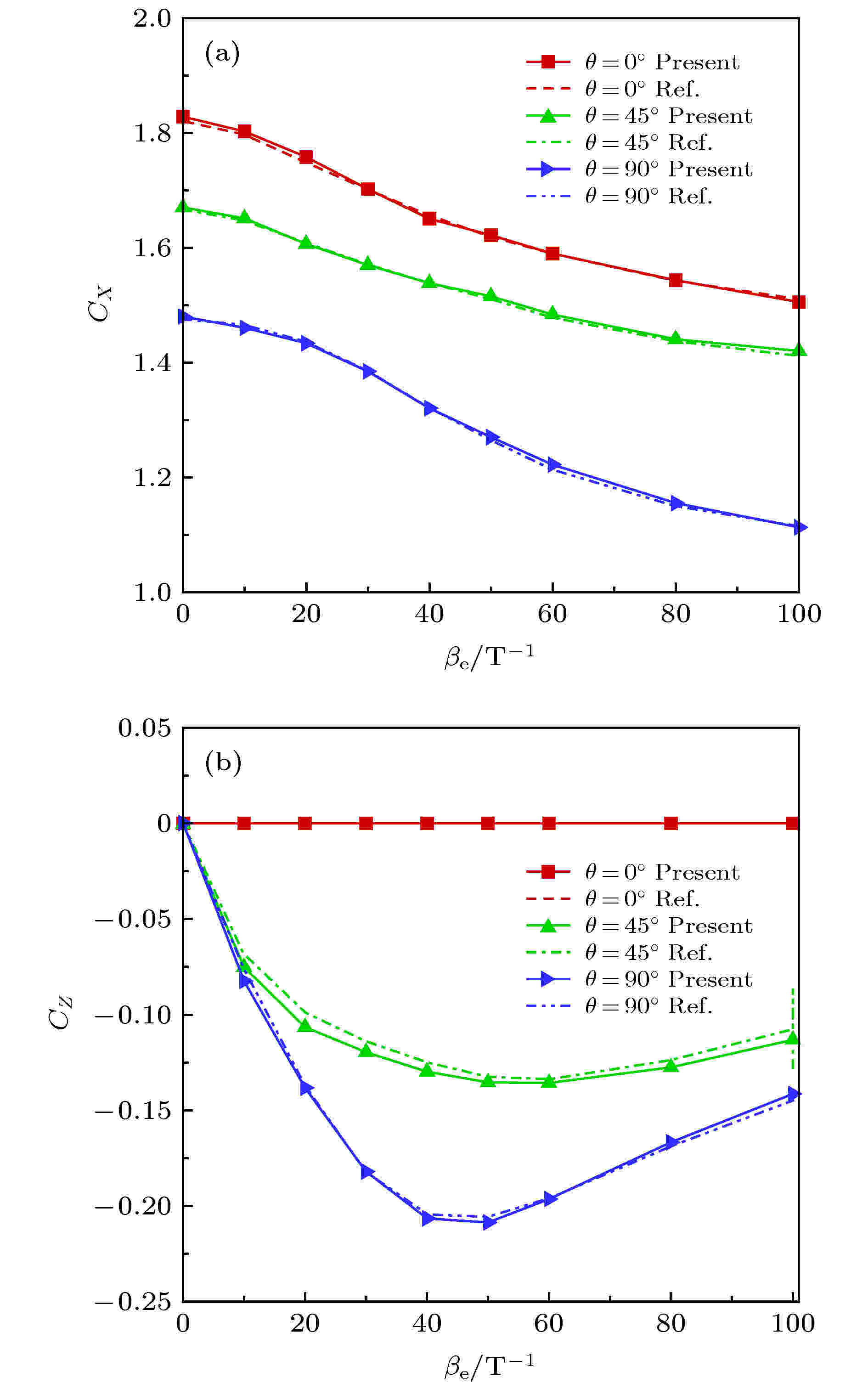图 2 不同霍尔系数条件下钝柱体气动特性　(a)轴向力系数; (b)侧向力系数
Figure2. Aerodynamic coefficent using different Hall parameter: (a) Axial force coefficent; (b) side force coefficent.

图3给出了不同壁面导电性与霍尔系数条件下表面热流分布, 文献[5]结果中beta_0, phi和Heat Flux分别对应本文的相对霍尔系数${\beta _{\rm{e}}}$、偏转角$\psi $和表面热流Q. 可以看出, 绝缘壁面条件下霍尔效应对磁控热防护效果的影响较小, 随霍尔系数的增大, 驻点热流略有上升; 导电壁面条件下, 霍尔效应明显削弱了磁控热防护效果, 但在霍尔系数较大时, 磁场作用反而使部分表面区域热流增大; 本文计算的热流结果与Fay-Riddell公式符合较好(图1(b)), 其受霍尔效应影响的变化规律与文献[5]结果一致, 这说明本文采用的计算方法能较为准确地捕捉霍尔效应对气动热环境的影响特征.
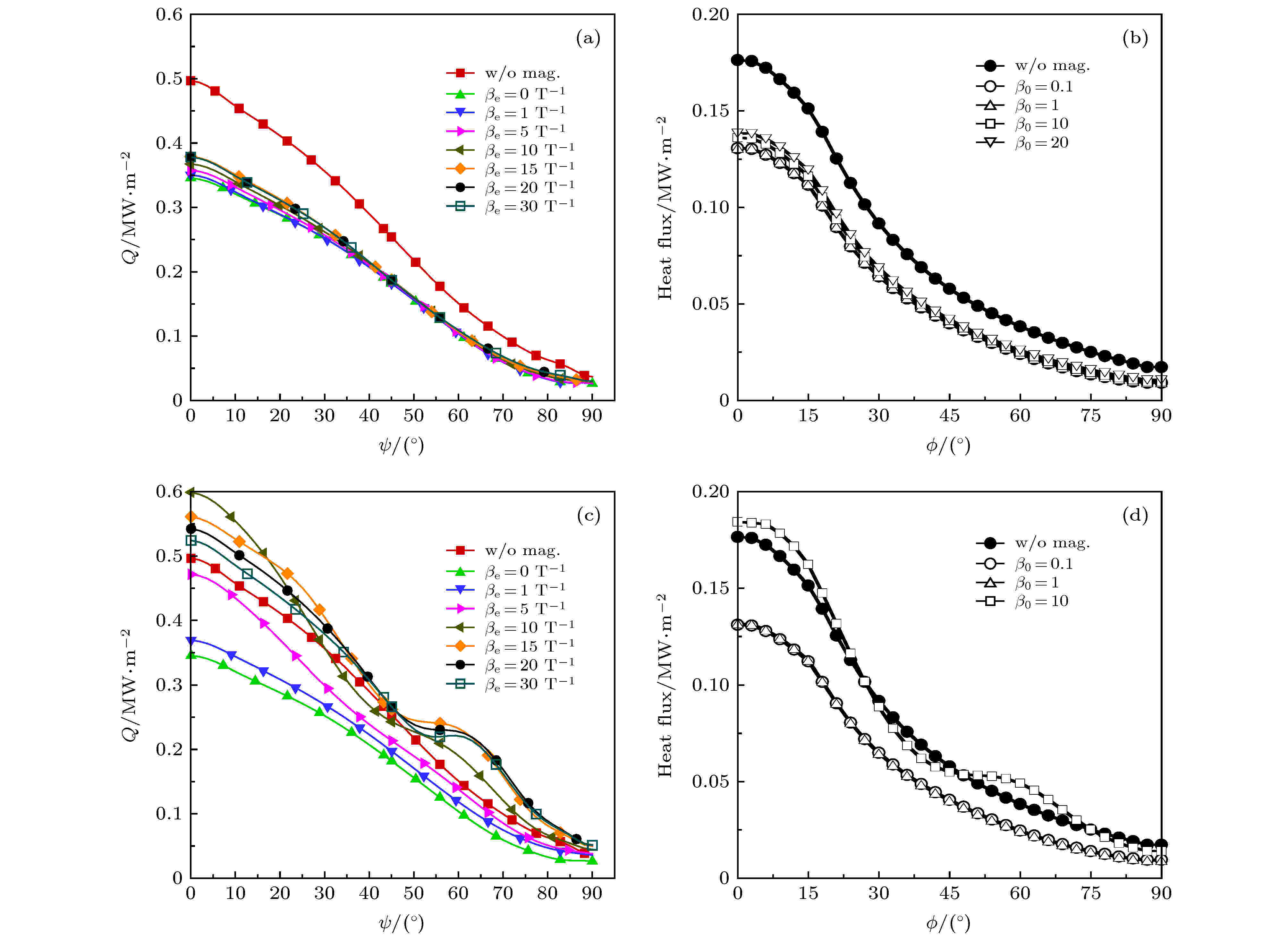图 3 不同条件下钝柱体表面热流　(a)本文绝缘壁; (b)文献绝缘壁^[5]; (c)本文导电壁; (d)文献导电壁^[5]
Figure3. Heat flux under different conditions: (a) Insulating wall of this work; (b) insulating wall^[5]; (c) conductive wall of this work; (d) conductive wall^[5].

$ {J}_{\varphi }\!\approx\! \dfrac{\sigma }{1\!+\!{\beta }^{2}}[\beta {({ E}\times { B})}_{\varphi }/\left|{ B}\right|+{({ U}\!\times \!{ B})}_{\varphi }],\;\beta ={\beta }_{\rm{e}}\left|{ B}\right|.$

另外还可以看出, 霍尔效应的影响与壁面导电性存在一定关联. 为了进一步分析霍尔效应对磁控效果“削弱”作用产生的机理, (7)式给出了流场中环形电流${J_\varphi }$的近似数学表达式, $\varphi $为球柱周向. 由${J_\varphi }$产生的洛仑兹力, 是球柱电磁流动有效动量和能量输运的主体, 因此可在一定程度上表征磁流体控制的效果. 图4给出了对不同壁面条件下霍尔电场变化以及霍尔效应原理示意图. 图4(a)和图4(b)分别为本文和文献绝缘壁面${\beta _{\rm{e}}} = 20 \;{{\rm{T}}^{ - 1}}$时电势等值线与感应电流流线分布; 图4(c)为流场最大电势差${\rm{d}}\phi $随霍尔系数变化; 图4(d)为霍尔效应原理示意图.
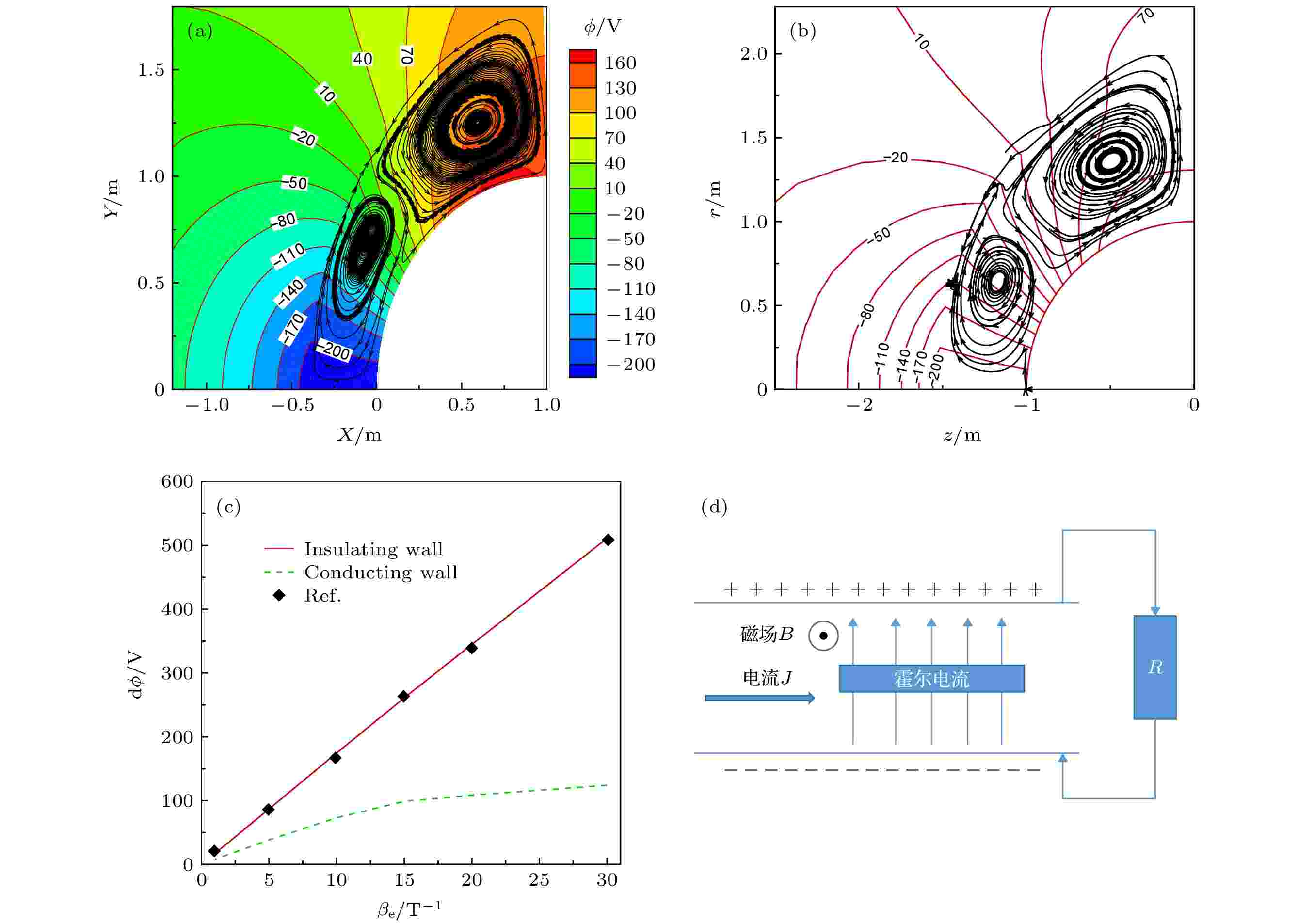图 4 不同条件下霍尔电场分析　(a)本文结果; (b)文献结果^[5]; (c)最大电势差; (d)霍尔效应示意图
Figure4. Analysis of Hall electric field under different conditions: (a) This work; (b) Ref. [5]; (c) maximum of potential difference; (d) sketch of Hall effect.

可以看出, 在X-Y平面内, 感应电流形成涡状结构; 流场中形成霍尔电势差, 在驻点附近区域电势较低, 而在肩部区域电势较高; 在本文计算条件下, 随霍尔系数增大, 绝缘壁面条件下流场中最大电势差呈线性上升趋势, 这一结果与文献[5]符合; 而导电壁面条件下流场中最大电势差明显小于绝缘壁面结果, 其上升趋势逐渐平缓.
也就是说, 绝缘壁面条件下, 随着霍尔系数的增大, 流场中的霍尔电场E呈线性比例增大, 即$\left| {{E}} \right| \propto \beta $; 而在导电壁面条件下, 霍尔电场被显著削弱. 结合(5)式可以看出, 随着霍尔系数的增大, $\beta {({{E}} \times {{B}})_\varphi }/\left| {{B}} \right|$逐渐占据主导, 而绝缘壁面$\left| {{E}} \right| \propto \beta $, 因此${J_\varphi }$趋于定值, 磁控效果变化相对较小; 而导电壁面条件下, 霍尔电场E被大幅削弱, 因此磁控效率的削弱幅度较大.
采用导电壁面, 电势差小于绝缘壁面的原因, 可结合霍尔效应的原理图(图4(d))进行解释. 电流通过与其垂直的磁场时, 会在同时垂直于电流和磁场的方向产生霍尔电势差. 如果外部电阻R为无穷大(对应球柱体表面绝缘壁), 此时洛伦兹力与电场力平衡, 霍尔电势将达到最大, 电流不发生偏转, 霍尔电流为零, 水平电流(对应球柱体的环形电流${J_\varphi }$)不被削弱; 如果外部电阻R接近于零(对应球柱体表面导电壁), 霍尔电势差减小, 电流发生偏转, 霍尔电流分量不为零, 形成霍尔电流回路, 电流的水平分量(对应球柱体的环形电流${J_\varphi }$)减小, 有效的洛仑兹力做功减小, 同时电磁流动相互作用的能量, 也将通过外部电阻产生消耗, 削弱了磁场整体的控制作用效果, 即出现“漏电”现象.
事实上, 采用绝缘壁也会出现“漏电”现象, 如图4(a)和图4(b)中涡型电流的产生就是一种典型的“漏电”现象, 其中由阴极(低电势区域)流向阳极(高电势区域)的电流主要对应霍尔电流分量, 而由阳极流向阴极的电流主要对应漏电电流. 产生这一现象的原因在于流场各区域流动速度、气体性质以及磁场分布存在差异, 导致了各区域霍尔效应强度的差异; 在霍尔效应较强区域, 霍尔感生电势差较大, 而在霍尔效应较弱区域, 霍尔感生电势差较小; 霍尔电势差的差异, 导致了涡型电流的产生, 在霍尔效应相对较弱的区域出现“漏电”现象(或者称“漏电”效应). “漏电”现象削弱了整体的磁控效果, 图2(a)、图3(a)和图3(b)给出的气动力/热特性的磁控效果变化规律体现了这一点.

第3节主要开展了均变霍尔系数(即全场相对霍尔系数相等)的数值模拟, 本节将尽量真实地考虑等离子体环境霍尔系数的分布, 开展高超声速热化学非平衡流动MHD控制霍尔效应影响的数值模拟研究.
为了便于理论分析, 仍采用球头外形开展数值计算分析, 以“球头半径为1.0 m, 飞行高度为65.0 km, 来流速度为7.0 km/s”为基准状态, 开展不同空域(55.0—75.0 km)、速域(5.0—8.0 km/s)、尺度(半径0.05—1.0 m)的数值对比分析, 磁相互作用数(N)的变化范围约为0.5—40, Hartmann数(${H_a}$)的变化范围约为40—1000. 这里, $N = {\sigma _{0}}B_0^2 L/{\rho _0}{u_0}$${\sigma _{0}}$, ${H_a} = {B_0}L\sqrt {{\sigma _{0}}/{\mu _0}} $, 其中$B_0$, L, ${\rho _0}$, ${u_0}$, ${\mu _0}$分别为电导率、磁感应强度、磁场作用区域尺度、流体密度、流体速度和流体黏性的特征量.
磁场配置与第3节类似, 采用常见磁偶极子磁场, 偶极子中心位于球心, 磁场特征长度与球头半径相同, 磁偶极子方向为直角坐标横轴负方向, 磁场特征感应强度为0.2 T. 为了增强磁控效果, 应尽量采用绝缘壁面条件, 因此本节重点分析绝缘壁面条件下霍尔效应的影响.
2

-->

4.1.基准状态下霍尔效应对磁流体力学控制影响分析

为了分析霍尔效应对MHD控制的影响, 开展三种情况下的高超声速流动数值对比计算. 标识如下: 无磁场, 记为Case 1; 有磁场但不考虑霍尔效应, 记为Case 2; 有磁场同时考虑霍尔效应, 记为Case 3.
图5给出了基准状态驻点线温度和表面热流分布. 表1列出了基准状态阻力系数. 这里${C_{\rm{D}}}$为总阻力系数, ${C_{{\rm{D1}}}}$为压力和黏性应力造成的阻力分量, ${C_{{\rm{D2}}}}$为洛仑兹力造成的阻力分量. 可以看出, 磁场使激波脱体距离增大, 考虑霍尔效应时, 激波脱体距离略微减小, 这说明霍尔效应削弱了整体的磁控效果. 这与气动力系数的磁控变化规律一致: 磁场使阻力系数增大, 主要是由于洛仑兹力造成的, 霍尔效应削弱了整体的洛仑兹力阻力效果, 使磁控增阻效果降低, 这符合第3节“漏电效应”影响的分析. 但对于气动热环境, 考虑霍尔效应, 磁场使驻点附近区域热流下降幅度增大, 也就是说霍尔效应反而使磁控热防护效果增强, 这与第3节的分析(图2(a)和图2(b))不一致.

Case	${C_{\rm{D}}}$	${C_{{\rm{D1}}}}$	${C_{{\rm{D2}}}}$	磁控增阻百分比
Case1	0.9239	0.9239	—	—
Case2	1.1679	0.9462	0.2217	26.4%
Case3	1.1167	0.9375	0.1792	20.9%

表1基准状态的阻力系数
Table1.Drag coefficient of refference state.

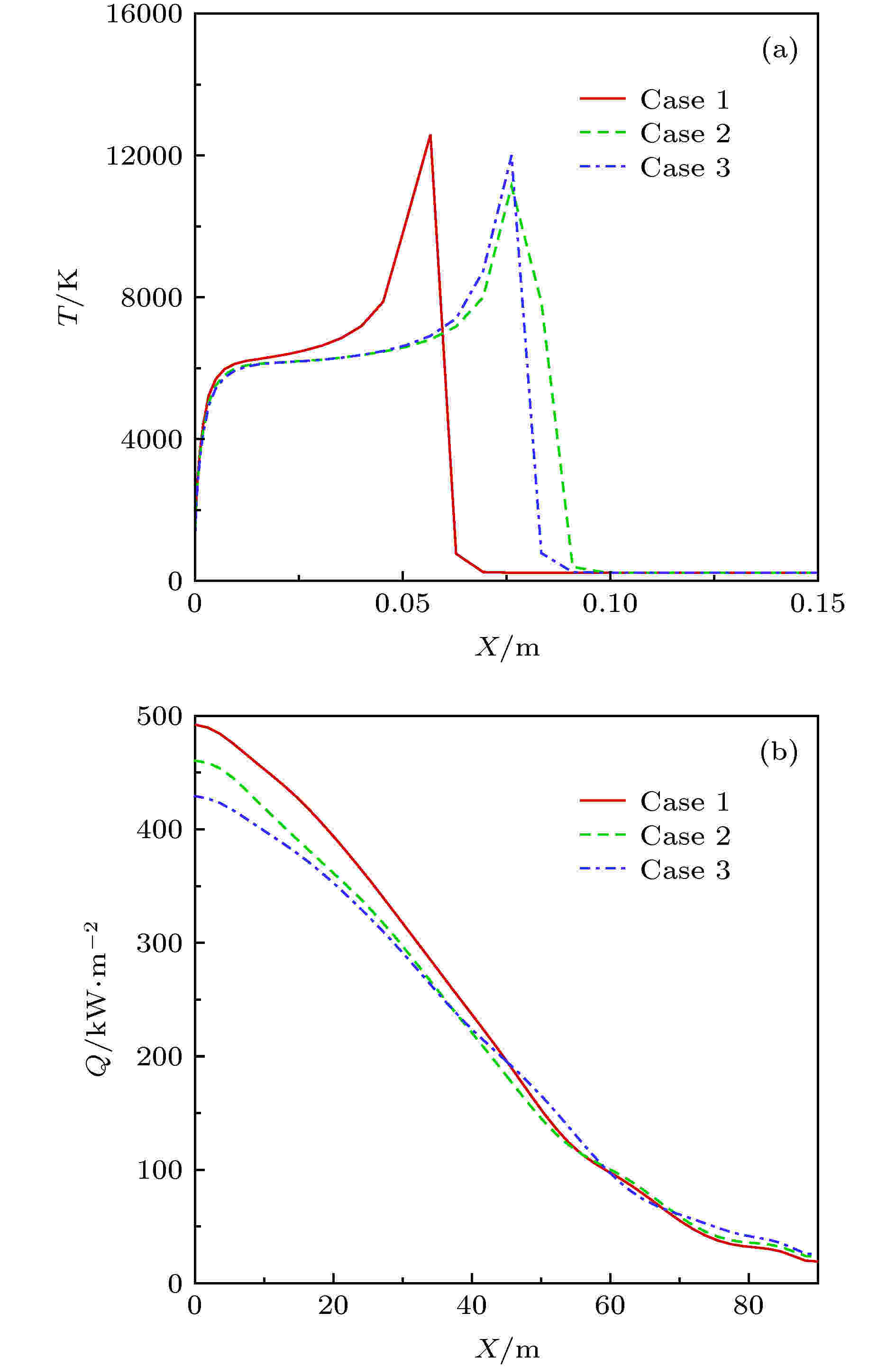图 5 基准状态部分流场参数分布　(a)驻点线温度; (b)表面热流
Figure5. Partical flow field parameters of refference state: (a) Temperatrue along stagnation line; (b) surface heat flux.

为了分析这一现象产生的机理, 图6给出了流场中环形电流${J_\varphi }$强度和洛伦兹力矢量${F_{\rm{L}}}$ (黑色线段, 其长度代表洛伦兹力大小). 图7给出了流场中电导率和相对霍尔系数. 可以看出, 霍尔效应使环形电流分布发生变化, 宏观上表现为环形电流向壁面附近“聚集”, 进而改变洛伦兹力分布, 使壁面附近Z2区域洛仑兹力增大, 激波间断附近Z1区域洛仑兹力减小. 这种电流“聚集”现象(或称电流“聚集”效应)可结合(5)式和图7进行分析: 激波间断附近Z1区域霍尔系数较大、电导率较高且流速较快, 霍尔效应产生较强的霍尔电势差; 该霍尔电势差高于壁面附近Z2区域气体(霍尔系数小、壁面附近速度较低)霍尔效应所应该产生的霍尔电势差; 由于这两个区域电势场整体上是“连通”的, 从而使壁面附近部分区域霍尔电场得到增强, 其环形电流${J_\varphi }$增大, 导致壁面区域受到洛伦兹力增大, 提升了该区域洛伦兹力对局部流体的外推与减速作用, 使热流下降的幅度增大; 同时这种不同区域电势差的差异性还导致了“漏电”现象的产生(见图3和图4分析), 从整体上削弱了霍尔电场强度, 尤其是激波间断附近的电场强度, 因而使该区域的环形电流减小, 洛伦兹力减弱, 降低了整体的磁控激波外推及磁阻力效果.
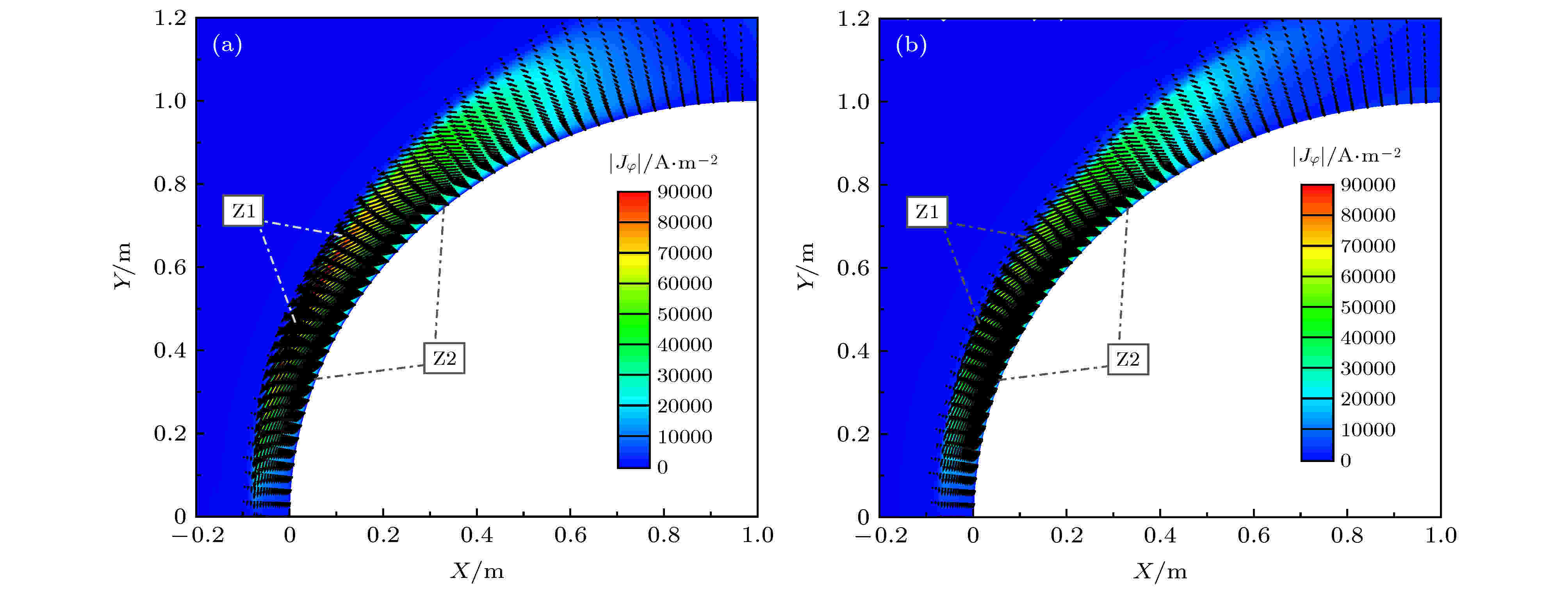图 6 基准状态环形电流和洛伦兹力矢量分布　(a) Case 2; (b) Case 3
Figure6. Annular electric current and Lorentz force: (a) Case 2; (b) Case 3

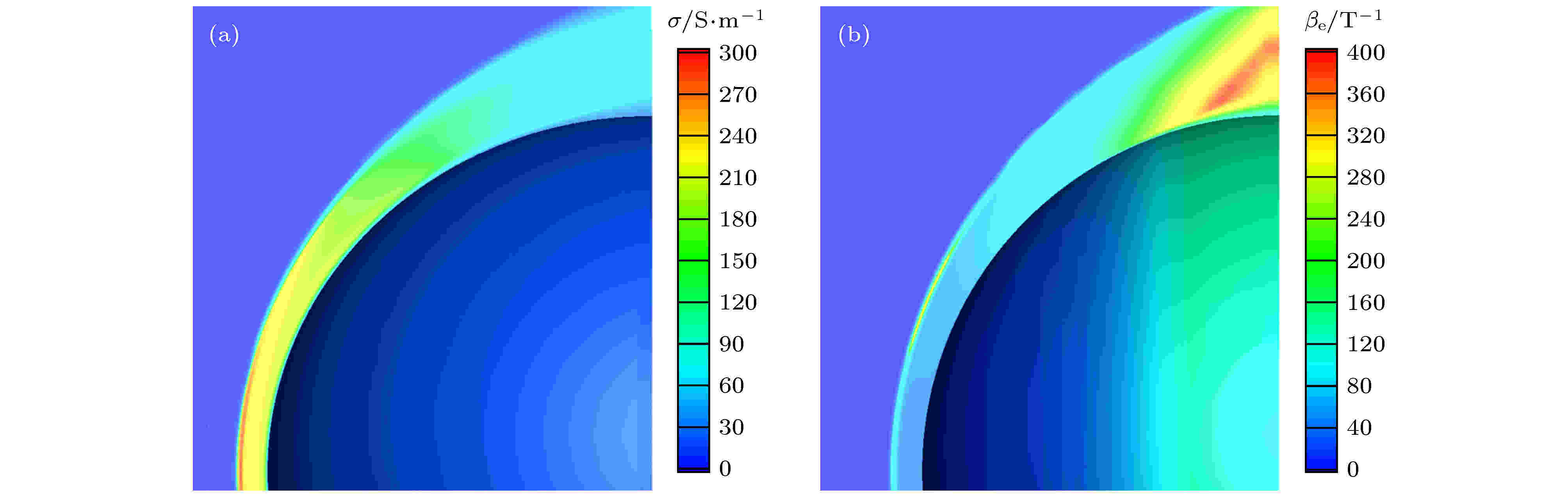图 7 基准状态电导率和相对霍尔系数分布　(a)$\sigma $; (b)${\beta _{\rm{e}}}$
Figure7. Distribution of electronic conductivity and Hall parameter: (a)$\sigma $; (b)${\beta _{\rm{e}}}$.

2 -->

4.2.不同飞行高度条件下(空域)霍尔效应的影响分析

飞行高度的变化主要带来气体压力和密度的变化, 飞行高度每上升10 km, 大气压力约下降为原来的1/4, 在温度变化不大的情况下气体密度也约下降为原来的1/4. 这会造成两方面的影响: 一方面气体密度减小, 磁相互作用数增大, 提升了磁场的作用效率; 另一方面气体分子碰撞频率减小, 化学反应和热力学松弛特征时间变长, 改变流场非平衡特性和电子迁移率, 进而影响等离子体分布及其电导率和霍尔系数分布. 这里主要开展飞行高度为55—75 km的磁流体数值模拟, 其他计算条件与基准状态一致: 球头半径为1.0 m, 来流速度为7 km/s, 绝缘壁面条件, 偶极子磁场特征磁感应强度为0.2 T.
图8和图9分别给出了不同飞行高度下霍尔效应对驻点热流和阻力系数的磁控效果分析. 可见, 对于气动热环境, 55—65 km时, 霍尔效应使磁控热防护(热流下降或减缓)效果增强, 这说明此时电流“聚集”效应(结合图6和图7分析)对气动热环境的影响占主导, 霍尔效应使壁面附近环形电流增强, 提升了局部洛伦兹力对流体的减速和外推作用, 从而使热流下降幅度增大; 而对于70—75 km, 霍尔效应使磁控热防护效果减弱, 这说明此时“漏电”效应(结合图3和图4)对气动热环境影响占主导, 整体霍尔电场的削弱, 使洛仑兹力整体上减小, 激波脱体距离减小, 进而使磁控热防护效果减弱. 而对于阻力特性来说, 霍尔效应降低了磁控增阻效果, 高度越高越明显, 尤其是75 km时, 磁控增阻率由不考虑霍尔效应(Case 2)时的95%, 降至考虑霍尔效应(Case 3)时的18%.
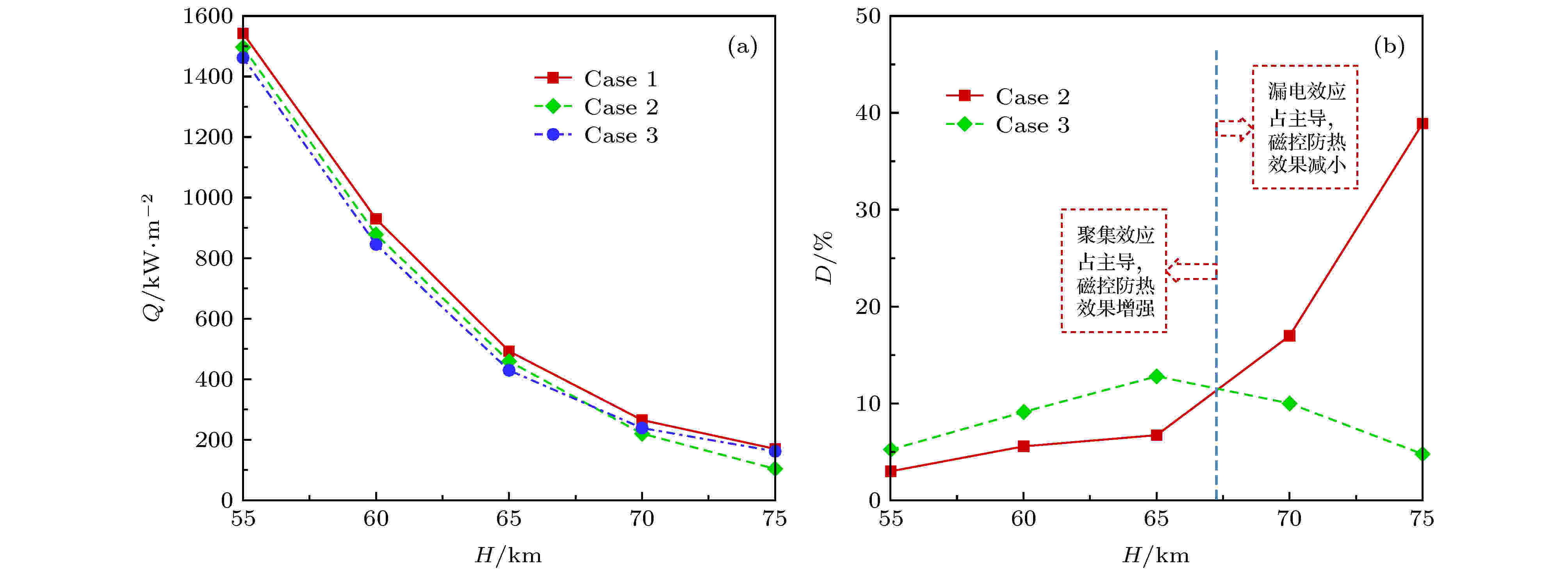图 8 不同飞行高度下驻点热流及其磁控效率　(a)驻点热流; (b)磁控热防护效率
Figure8. Heat flux at stagnation point and its control efficiency at different altitudes: (a) Heat flux; (b) control efficiency.

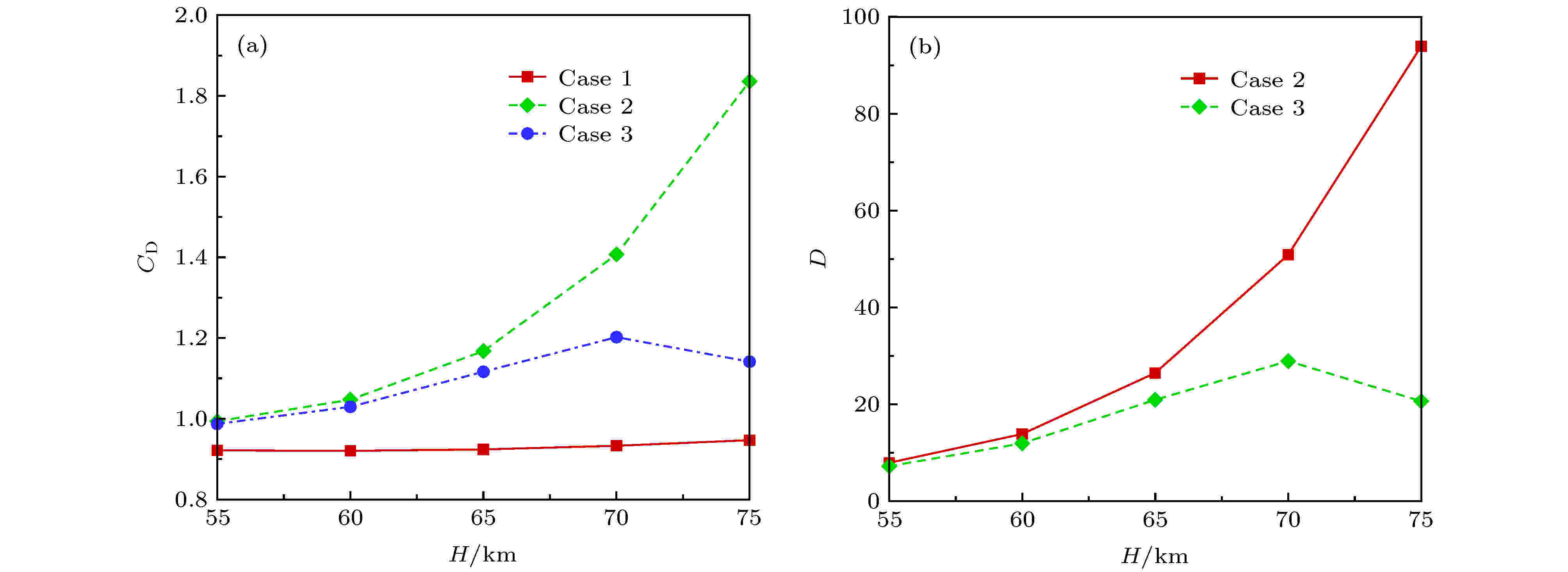图 9 不同飞行高度下阻力系数及其磁控效率　(a)阻力系数; (b)磁控增阻效率
Figure9. Darg coefficient and its control efficiency at different altitudes: (a) Darg coefficient; (b) control efficiency.

还可以看出, 霍尔效应对于气动力特性和气动热环境磁控效果的影响, 存在明显差异. 这主要是由于气动力特性需考虑全场的积分, 更倾向于整体的效果; 而表面热流更关注流场的局部特性, 因此不仅需要综合考虑整体的变化, 而且需要考虑局部效应的影响.
为了分析不同飞行高度下霍尔效应影响差异产生的原因, 图10给出了不同飞行高度下驻点线电导率和霍尔系数分布, 图11给出了不同飞行高度下激波后较大区域的相对霍尔系数${\beta _{\rm{e}}}$和流场最大霍尔电势差${\rm{d}}\phi $. 由图10和图11可以看出, 不同飞行高度, 流场中电导率分布存在一定差异, 但整体上差异不大, 没有本质差别; 而霍尔系数受飞行高度影响十分明显, 随飞行高度上升, 霍尔系数的急剧增大, 从55 km到75 km, 波后驻点线区域大范围内相对霍尔系数由10 T^–1左右上升至120 T^–1以上; 与图4(c)不同, 绝缘边界条件下, 流场中的霍尔电势差不再与相对霍尔系数呈近似线性比例关系, 这说明随高度上升, 霍尔电场被“削弱”的幅度增大, 尤其是75 km时, 霍尔电势差被明显地削弱. 由(5)式可知, 这将大幅削弱环形电流${J_\varphi }$, 使洛仑兹力有效动量和能量输运减小, 大幅削弱磁控效果.
图 10 不同高度下流场驻点线电导率和相对霍尔系数　(a)$\sigma $; (b)${\beta _{\rm{e}}}$
Figure10. Electronic conductivity and Hall parameter along stagnation line at different altitudes: (a)$\sigma $; (b)${\beta _{\rm{e}}}$.

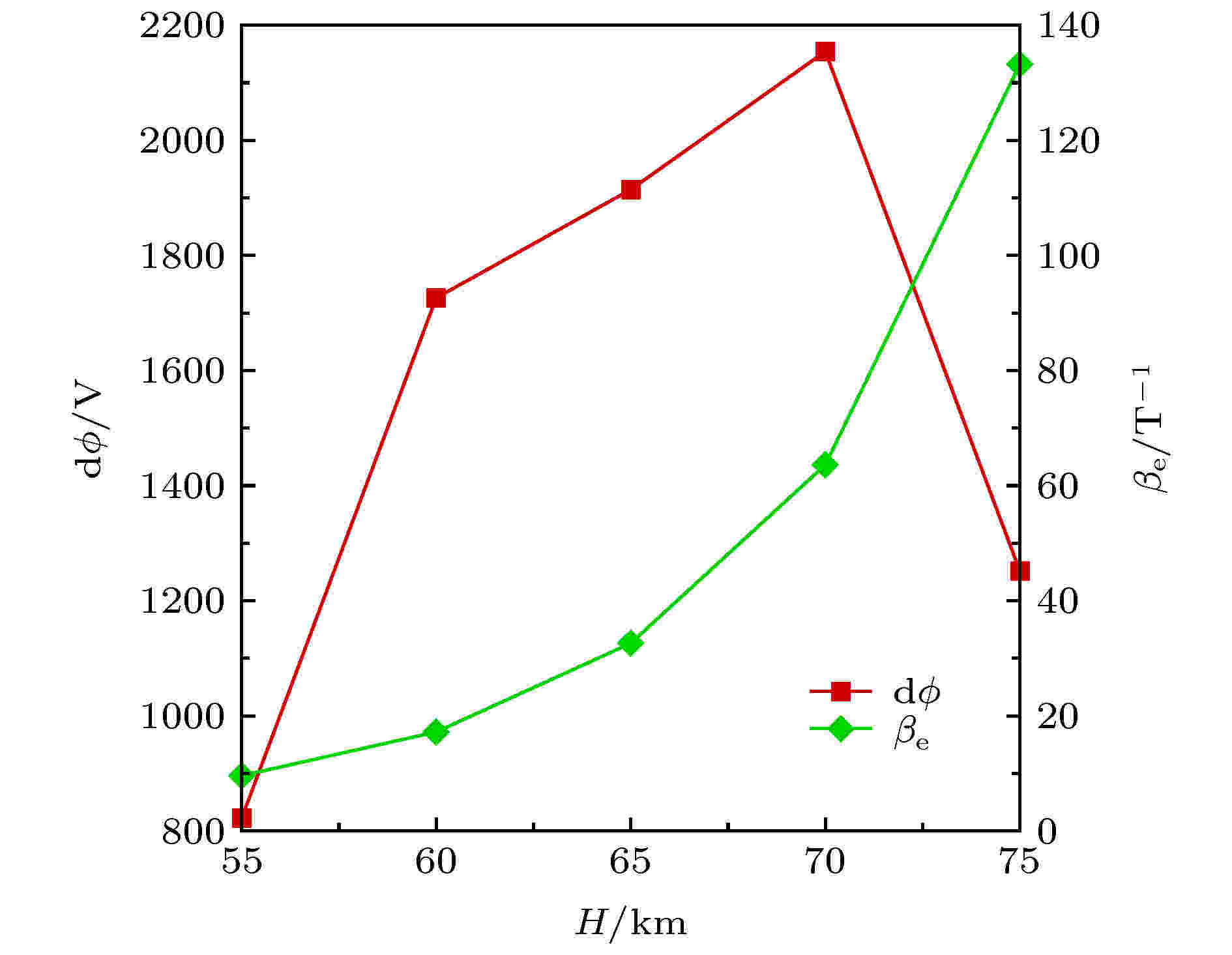图 11 不同飞行高度下流场最大电势差和激波后较大区域的相对霍尔系数
Figure11. Potential difference maximum and Hall parameter after shock wave at different altitudes.

为了进一步分析随高度上升霍尔电场被“削弱”幅度增大的原理, 图12给出了驻点附近近壁面区域的相对霍尔系数和电导率分布. 可以看出: 与波后霍尔系数相比, 在壁面附近, 相对霍尔系数明显降低, 也就是说, 壁面附近存在霍尔系数大幅度下降的“霍尔效应较弱”的气流层. 波后其他区域产生的霍尔电势差将高于该气流层产生的霍尔电势差, 这不仅导致了环形电流${J_\varphi }$向壁面附近聚集, 即电流“聚集”现象, 而且导致了“涡型电流”产生, 出现“漏电”现象. 因此该气流层是霍尔效应作用差异的主要区域之一, 本文称为“漏电层”.
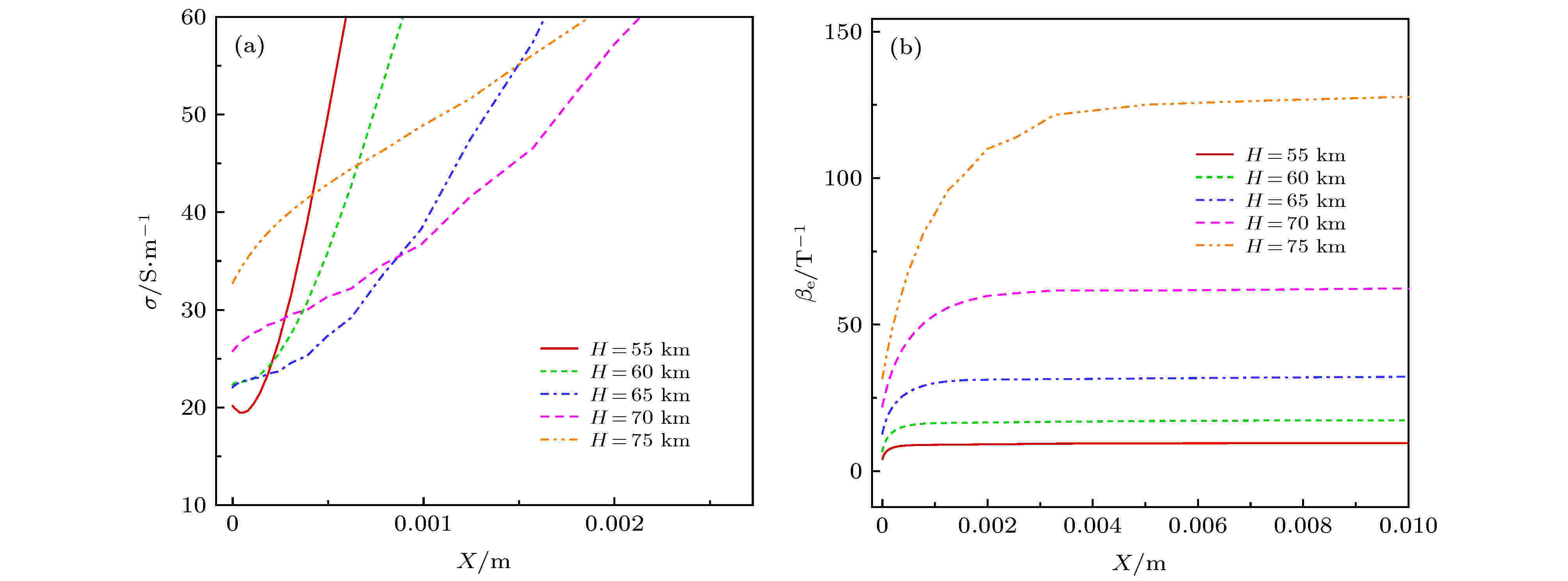图 12 不同高度下流场壁面附近电导率和相对霍尔系数　(a)$\sigma $; (b)${\beta _{\rm{e}}}$
Figure12. Electronic conductivity and Hall parameter near wall at different altitudes: (a)$\sigma $; (b)${\beta _{\rm{e}}}$.

飞行高度越高, “漏电层”低霍尔系数区域越宽, 其霍尔系数下降幅度越大, 相比于波后的大范围的${\beta _{\rm{e}}}$, 飞行高度为75 km时“漏电层”${\beta _{\rm{e}}}$减小了约75%, 而55 km时仅减小了50%. 同时, 随着飞行高度上升, 漏电层的电导率上升, 由55 km时的20 S/m, 上升至75 km时的32 S/m. 这说明, 飞行高度较高时, 壁面附近“漏电层”的厚度较大且电导率较高, 其“漏电”现象将更加显著, 效果类似于壁面的导电性增大. 图13(a)为75 km时电场和电流流线分布, 图13(b)为本文第3节导电壁面条件下的结果. 通过对比可以看出, 二者壁面附近电流流线的分布变化规律相似, 这说明75 km时, 壁面处的“漏电层”效果类似于导电壁面, 这大幅地削弱整体的霍尔电场, 使${J_\varphi }$整体减小, 从而极大地削弱了气动力/热磁控效果.
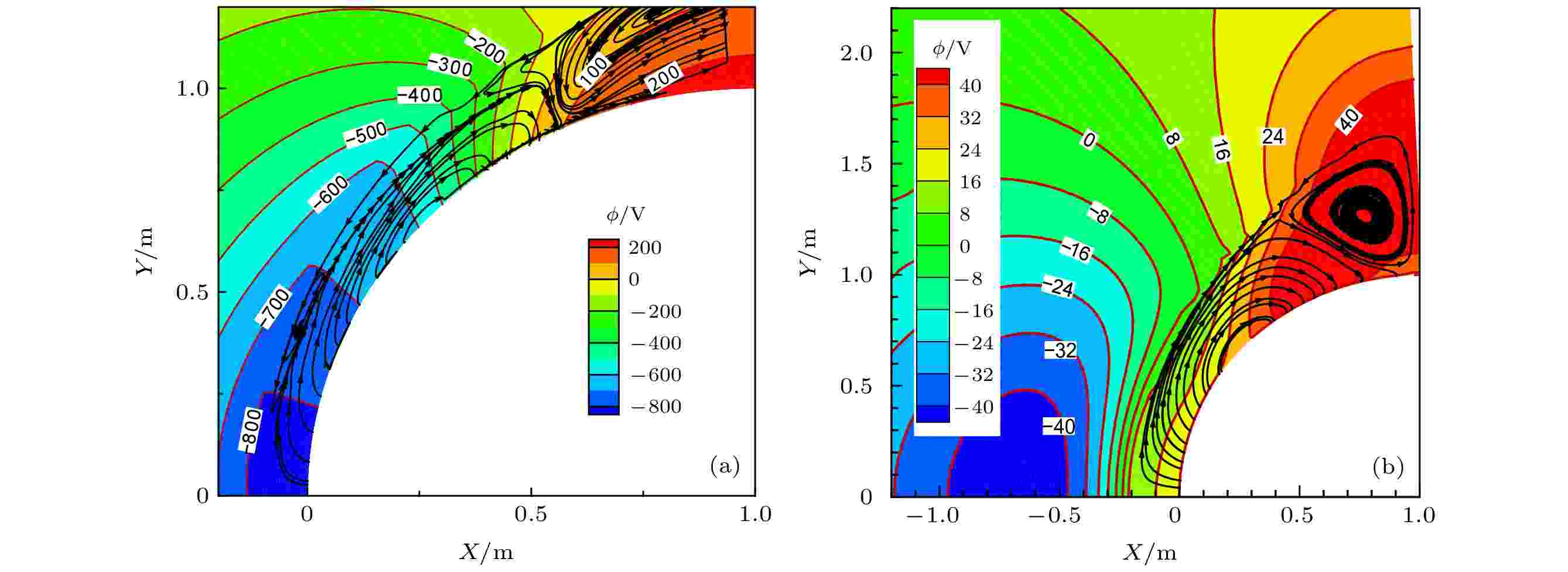图 13 霍尔电场及电流流线分布　(a)绝缘壁, 飞行高度为75 km; (b)导电壁, 本文第3节状态
Figure13. Hall electric field and electric current streamline: (a) Insulating wall at 75 km; (b) conductive wall at the state of the 3rd part in this paper.

由此可见, 壁面附近“漏电层”的厚度和电导率大小, 直接影响了霍尔效应“漏电”现象的强弱, 进而影响气动力/热的磁控效果. 随飞行高度增大, “漏电层”的厚度和电导率增大, “漏电”现象逐渐占据主导, 因此霍尔效应对磁控气动热防护效果的影响, 由增强逐渐转为削弱.
2 -->

4.3.不同飞行速度条件下(速域)霍尔效应的影响分析

飞行速度升高, 气流的动量和能量增大, 波后压力升高, 温度上升, 化学电离和离解等反应更加剧烈. 一方面增加了气流的密度和电离度, 影响气体电导率和霍尔系数; 另一方面流场中气体流速增大, 这相当于磁相互作用数的分母增大, 影响磁场作用效果. 这里主要开展飞行速度为5—8 km的磁流体数值模拟, 其他计算条件与基准状态一致: 球头半径为1.0 m, 飞行高度为65 km, 绝缘壁面条件, 偶极子磁场特征磁感应强度为0.2 T.
图14和图15分别为不同飞行速度下霍尔效应对驻点热流和阻力系数的磁控效果分析. 可以看出, 对于气动热环境来说, 飞行速度为5 km/s时, 霍尔效应削弱了磁控热防护效果, 这说明此时整体漏电效应占主导; 飞行速度为6—8 km/s时, 霍尔效应使磁控热防护效果增强, 且速度越高, 增强的幅度越大, 这说明随飞行速度上升, 局部电流聚集效应逐渐占据主导. 对于气动力来说, 霍尔效应整体上体现为漏电效应影响, 削弱了磁控增阻效果, 且飞行速度越低, 削弱幅度越大.
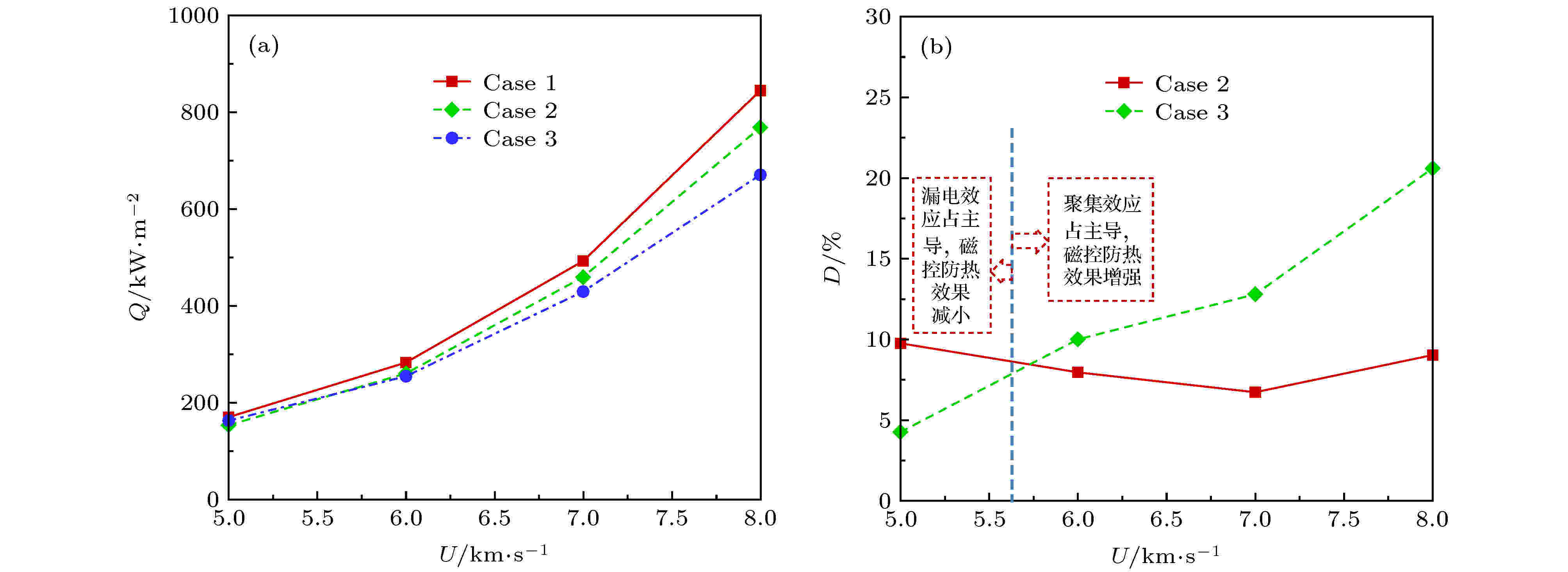图 14 不同飞行速度下驻点热流及其磁控效率　(a)驻点热流; (b)磁控热防护效率
Figure14. Heat flux at stagnation point and its control efficiency at different velocities: (a) Heat flux; (b) control efficiency.

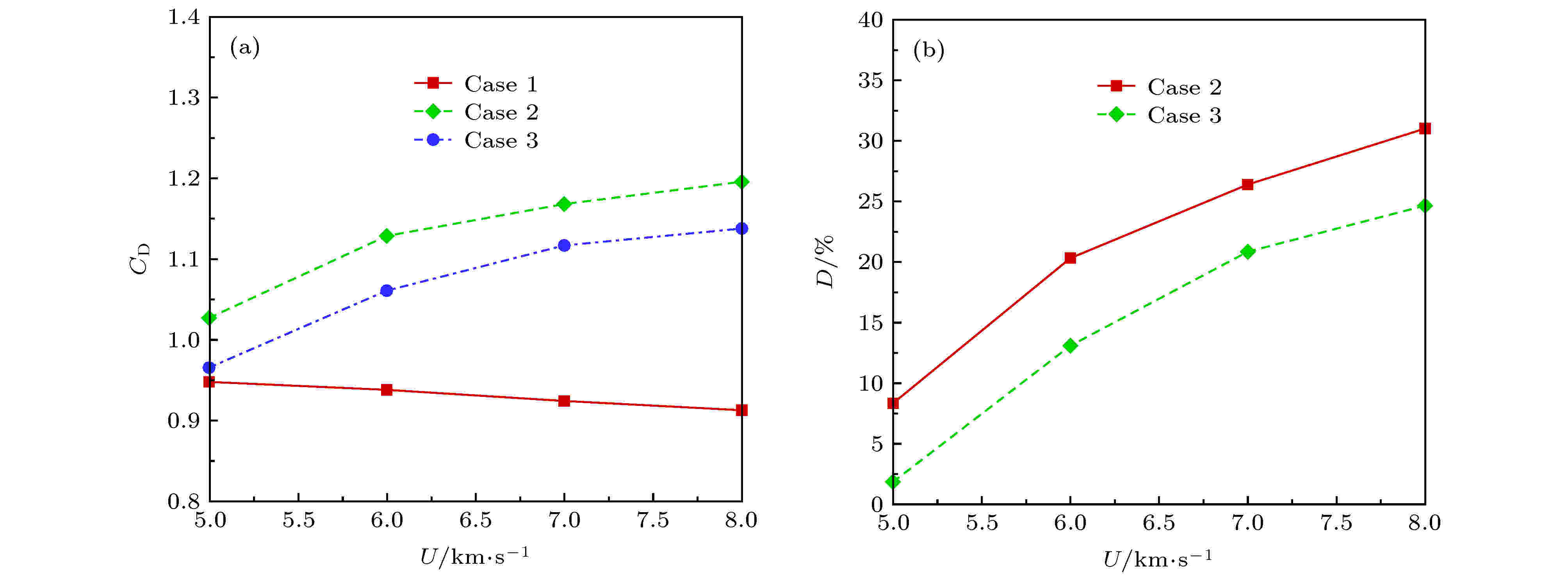图 15 不同飞行速度下阻力系数及其磁控效率　(a)阻力系数; (b)磁控增阻效率
Figure15. Darg coefficient and its control efficiency at different velocities: (a) Darg coefficient; (b) control efficiency.

为了进一步分析不同飞行速度条件下磁控效果以及霍尔效应变化产生的原因, 类似于图10和图12, 图16和图17分别给出了不同飞行速度条件下驻点线和壁面附近的电导率与霍尔系数分布, 对漏电层进行分析.
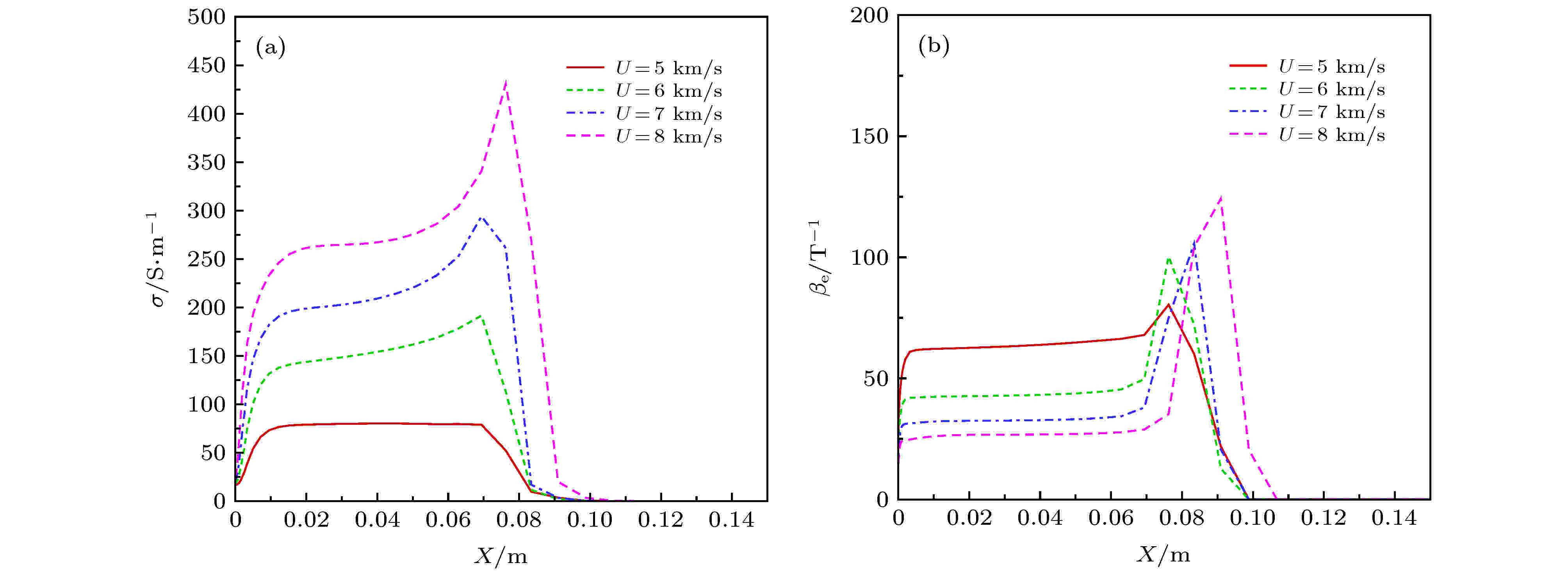图 16 不同速度下流场驻点线电导率和相对霍尔系数　(a) $\sigma $; (b) ${\beta _{\rm{e}}}$
Figure16. Electronic conductivity and Hall parameter along stagnation line at different velocities: (a) $\sigma $; (b) ${\beta _{\rm{e}}}$.

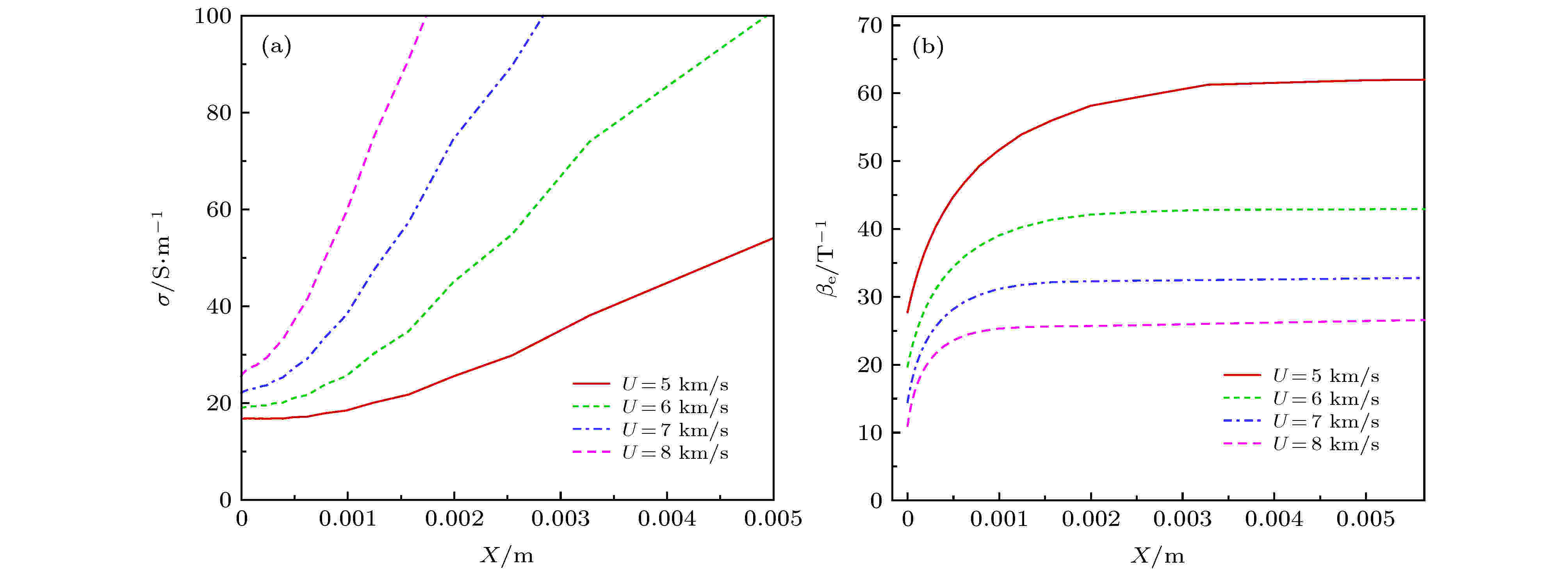图 17 不同速度下流场壁面附近电导率和相对霍尔系数　(a) $\sigma $; (b) ${\beta _{\rm{e}}}$
Figure17. Electronic conductivity and Hall parameter near wall at different velocities: (a) $\sigma $; (b) ${\beta _{\rm{e}}}$.

从图16和图17可以看出, 随飞行速度升高, 气体电导率显著增大, 波后相对霍尔系数显著减小, 壁面附近“漏电层”变薄, 且漏电层电导率下降幅度增大. 气体电导率增加, 会增强磁控效果; 霍尔系数减小, 将导致霍尔效应随飞行速度升高而减弱; 而“漏电层”变薄, 漏电效应减弱, 会进一步减小霍尔效应“整体的削弱”的影响, 使电流聚集的局部影响逐步凸显. 这在一定程度上解释和印证了图14和图15的结果.
2 -->

4.4.不同特征尺寸条件(尺度)下霍尔效应的影响分析

飞行器以及磁控系统特征尺寸的变化, 主要带来高温气体效应作用区域以及等离子体流场与磁场相互作用区域的变化. 随着特征尺寸的增大, 一方面高温气体热化学反应区域增大, 化学反应与热力学松弛有效时间增长, 气体状态逐渐偏向于平衡态, 这会导致等离子体温度和组分变化, 改变气体电导率和霍尔系数; 另一方面, 磁场与流场相互作用区域增大, 磁场向流动注入动量和能量的总量增加, 磁相互作用数和Hatrmann数增大, N约由0.5增大到10, ${H_a}$约由45增大到900, 磁场作用效果增强. 这里主要开展球头半径$R \!=\! 0.05—1.0$ m(磁场特征长度与球头半径相等)的磁流体数值模拟, 其他计算条件与基准状态一致: 飞行高度为65 km, 速度为7 km/s, 绝缘壁面条件, 偶极子磁场特征磁感应强度为0.2 T.
图18和图19分别给出了不同特征尺度条件下霍尔效应对驻点热流和阻力系数的磁控效果分析. 可以看出, 不考虑霍尔效应时, 驻点热流的磁控热防护效果(热流下降或减缓幅度)随特征尺度的增大而增强, 但其变化趋势逐渐平缓; 考虑霍尔效应时, 磁控热防护效果与特征尺度呈近似线性关系; 当半径较小时(R < 0.5 m), 霍尔效应削弱了磁控热防护效果, 这说明此时漏电效应占主导; 而当半径较大时(R > 0.5 m), 霍尔效果增强了磁控热防护效果, 这说明此时电流聚集效应占主导. 对于气动力特性, 半径越大, 磁控增阻效果越强; 霍尔效应整体上表现为磁控增阻效果的削弱, 半径越小, 削弱的相对幅度越大.
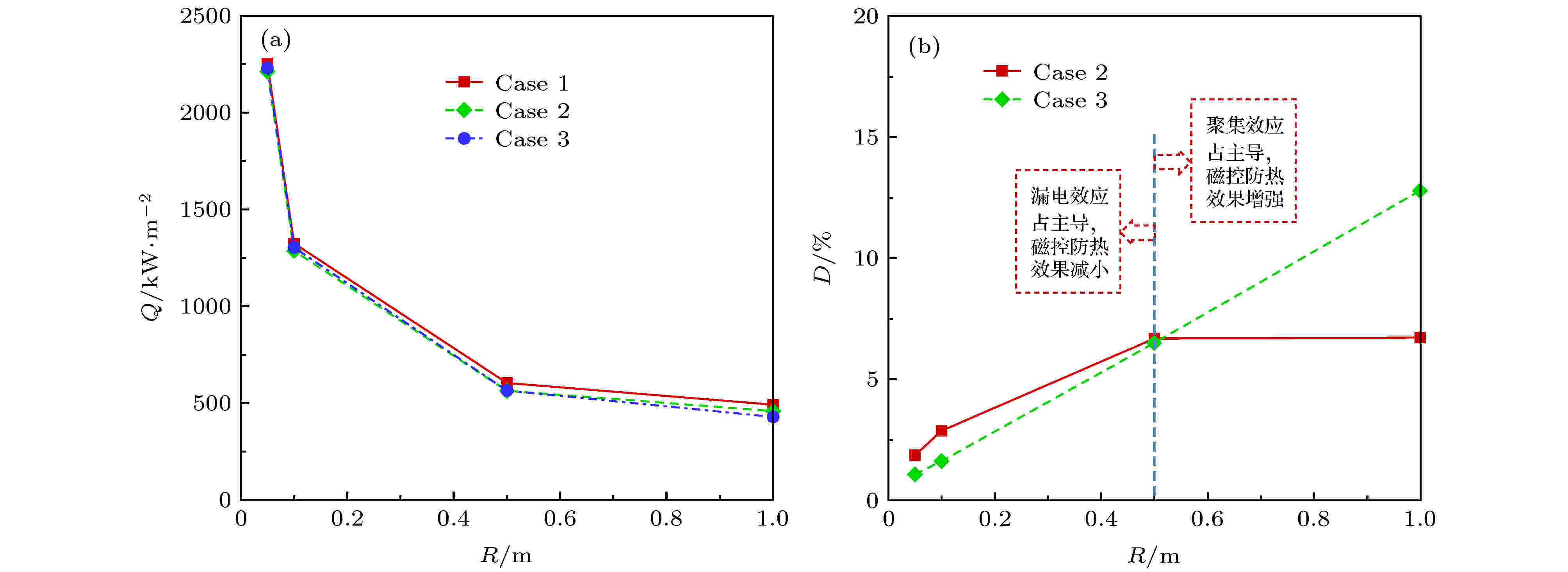图 18 不同尺度下驻点热流及其磁控效率　(a)驻点热流; (b)磁控热防护效率
Figure18. Heat flux at stagnation point and its control efficiency using different scales: (a) Heat flux; (b) control efficiency.

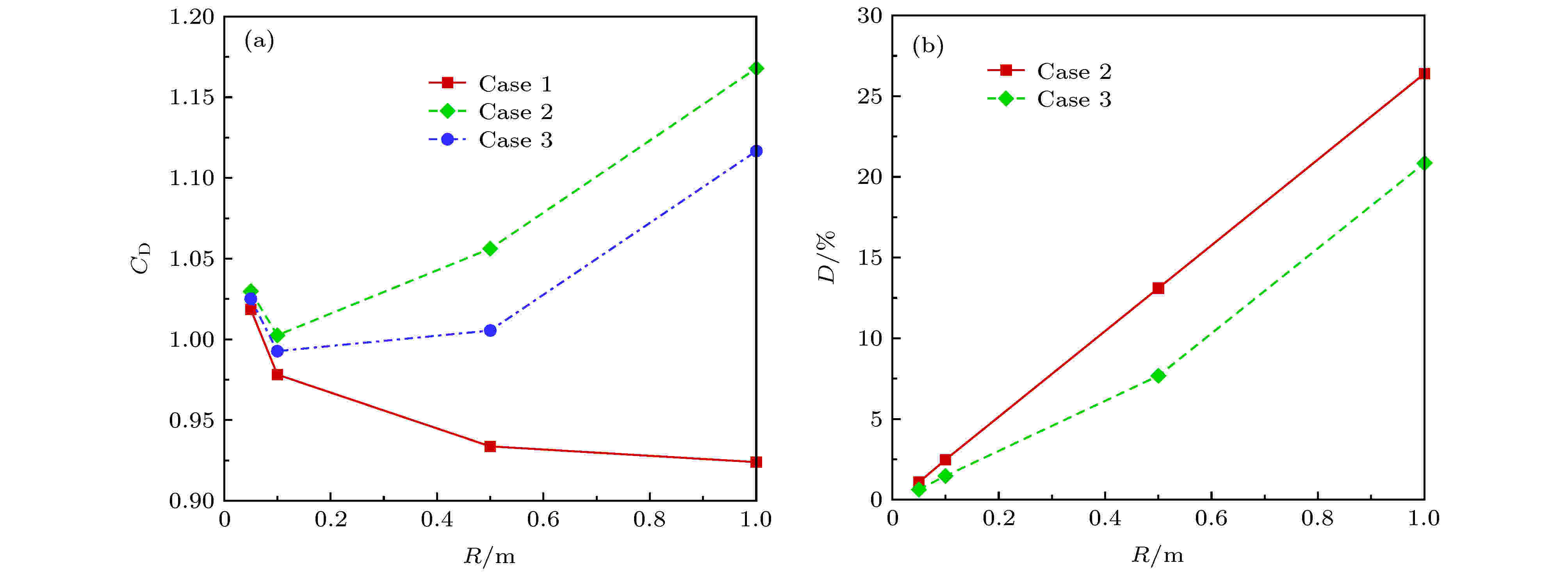图 19 不同尺度阻力系数及其磁控效率　(a)阻力系数; (b)磁控增阻效率
Figure19. Darg coefficient and its control efficiency using different scales: (a) Darg coefficient; (b) control efficiency.

为了进一步分析不同特征尺度条件下磁控效果以及霍尔效应变化产生的原因, 类似于图10和图12, 图20和图21分别给出了不同特征尺度条件下驻点线和壁面附近的电导率与霍尔系数分布.
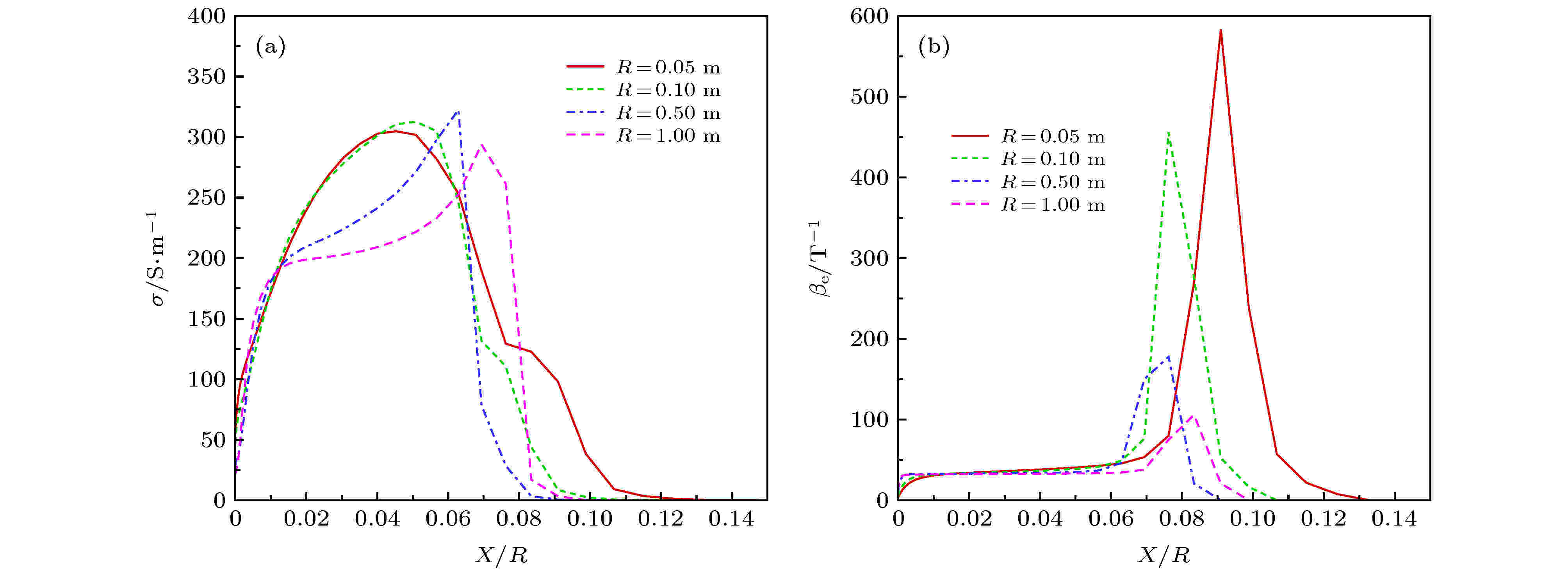图 20 不同尺度下流场驻点线电导率和相对霍尔系数　(a) $\sigma $; (b) ${\beta _{\rm{e}}}$
Figure20. Electronic conductivity and Hall parameter along stagnation line using different scales: (a) $\sigma $; (b) ${\beta _{\rm{e}}}$.

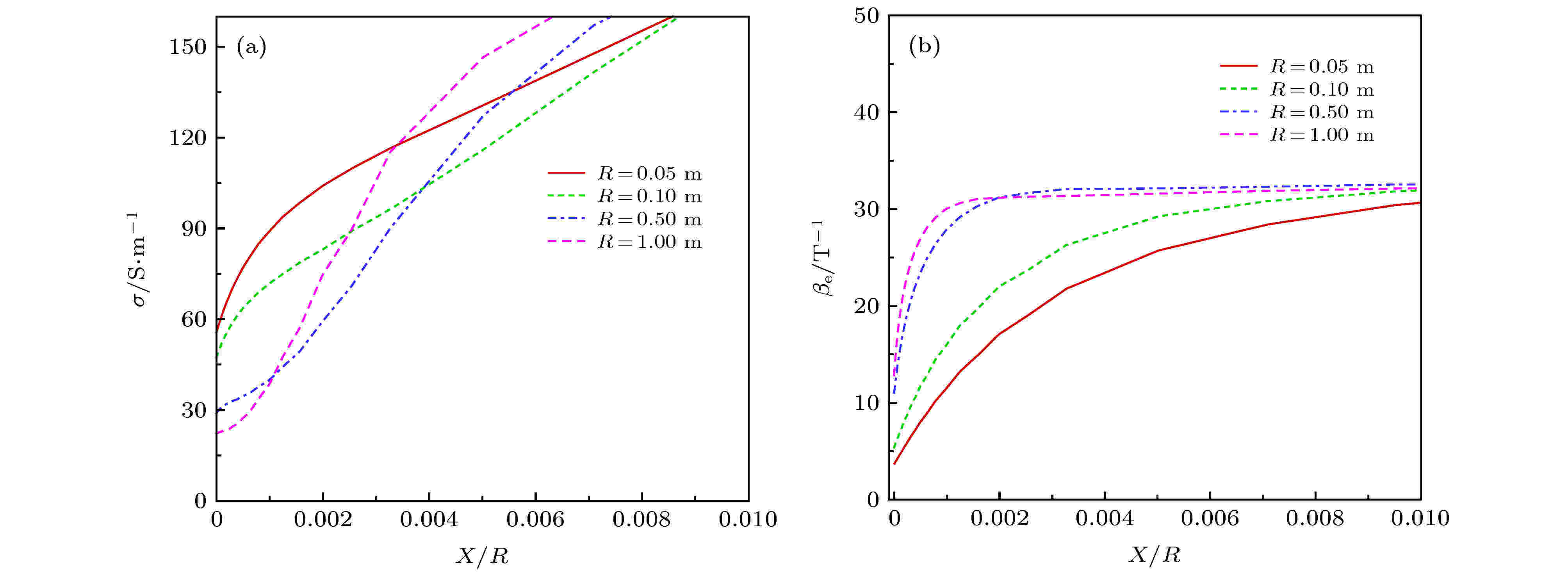图 21 不同尺度下壁面附近电导率和相对霍尔系数　(a) $\sigma $; (b) ${\beta _{\rm{e}}}$
Figure21. Electronic conductivity and Hall parameter near wall using different scales: (a) $\sigma $; (b) ${\beta _{\rm{e}}}$.

由图20和图21可以看出, 不同特征尺度下, 整体电导率和霍尔系数分布存在一定差别, 但其峰值差别不大; 特征尺度越小, 壁面附近的低霍尔系数“漏电层”厚度相对越大, 电导率越高.
取峰值电导率为特征电导率计算磁相互作用数, 在特征速度、密度(取来流值)等参数相同的情况下, 磁相互作用数将正比于特征尺度, 因此特征尺度越大, 磁控效果越显著; 波后较大区域的相对霍尔系数受特征尺度影响较小, 但漏电层变化明显: 随着特征尺度的增大, 其漏电层相对厚度显著减小、电导率明显降低, 这会使“漏电”效应逐渐减弱, 霍尔效应“整体的削弱”作用减弱, 同时使局部电流“聚集”效应逐渐凸显, 从而增强磁控热防护效果. 这在一定程度上解释和印证了图18和图19的结果.

通过耦合求解各向异性霍尔电场泊松方程和带电磁源项的高温热化学非平衡流动控制方程组, 建立了高超声速流动MHD控制霍尔效应数值模拟方法, 考虑热化学非平衡流场等离子体霍尔系数分布, 开展了多种计算条件(壁面导电性、速域、空域、尺度)下高超声速流动MHD控制数值模拟, 探讨霍尔效应“漏电”与“聚集”现象机理及其对MHD控制的作用机制和影响规律. 研究结果表明:
1)霍尔效应改变了流场等离子体洛伦兹力分布, 削弱了整体的力学效果, 使整体的磁控增阻特性降低; 霍尔效应对高超声速MHD控制的影响, 与壁面导电性和壁面附近漏电层的“漏电”现象紧密相关, 要增强磁控效果, 必须抑制壁面附近的“漏电”现象; 霍尔效应对磁控热防护效果的影响较为复杂, 在某些条件下, 反而使磁控热防护效果增强, 这与环形电流向表面附近“聚集”有关.
2)飞行高度越高, 波后霍尔系数越大, 霍尔效应越强, 壁面附近“漏电层”越厚且电导率高, “漏电”效应越显著, 整体的霍尔电场削弱幅度越大, 在一定程度上抵消了局部电流“聚集”效应的作用效果; 在本文基准条件下, 飞行高度低于67 km时, 霍尔效应使磁控热防护效果增强, 电流聚集效应占主导; 飞行高度高于67 km时, 霍尔效应使磁控热防护效果削弱, 漏电效应逐渐占据主导.
3)飞行速度越大, 波后霍尔系数越小, 霍尔效应整体上越弱, 同时壁面附近“漏电层”越薄, “漏电”效应越弱, 整体的霍尔电场削弱幅度越小, 局部电流“聚集”效应的作用效果逐渐凸显; 本文基准条件下, 飞行速度高于5.7 km/s时, 霍尔效应使磁控热防护效果增强, 电流聚集效应占主导; 飞行速度低于5.7 km时, 霍尔效应使磁控热防护效果削弱, 漏电效应逐渐占据主导.
4)飞行器尺寸越小, 壁面附近“漏电层”厚度越大且电导率高, “漏电”效应越显著, 整体的霍尔电场削弱幅度越大, 在一定程度上抵消了局部电流“聚集”效应的作用效果. 本文基准条件下, R > 0.5 m时, 霍尔效应使磁控热防护效果增强, 电流聚集效应占主导; R < 0.5 m时, 霍尔效应使磁控热防护效果削弱, 漏电效应逐渐占据主导.