摘要: 高速流体以一定角度冲击壁面可以简化为斜驻点流动, 包括正驻点流动分量和剪切流动分量. 以往研究集中在不可压缩的斜驻点流动, 本文针对高速可压缩的斜驻点流动模型, 给出了新的自相似求解方案. 通过与数值结果对比验证, 发现该模型能很好地模拟高超声速再附产生的均匀剪切层撞击壁面流动. 通过对比流动中能量输运项和做功项的贡献, 发现斜驻点流动的剪切分量带来较强的压缩效应和耗散效应, 造成流动具有显著的流向对流传热, 表现为再附后近壁流体温度迅速升高, 最终产生壁面上的高热流值. 参数分析表明壁面热流系数与无量纲壁面温度梯度和边界层厚度相关, 前者主要受斜驻点剪切分量参数控制, 后者与驻点分量参数呈负相关.
关键词: 斜驻点流动 /
再附流动 /
剪切层 /
壁面热流 English Abstract Heat transfer characteristics of shear layer impinging on wall based on oblique stagnation-point model Fang Fang Bao Lin Tong Bing-Gang School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11572319) and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences, China (Grant No. XDB22040202)Received Date: 28 June 2020Accepted Date: 11 July 2020Available Online: 22 October 2020Published Online: 05 November 2020Abstract: Hypersonic reattachment flow usually causes extremely high wall heat flux, which is of great concern in engineering. The flow can be modeled as a high-speed shear layer impinging on a wall at a certain angle, which forms an oblique stagnation-point flow in the vicinity of the stagnation point, including stagnation-component and shear-component. Previous work focused on incompressible oblique stagnation-point flow, while in the present study a semi-analytical-semi-numeric solution is given via the self-similar method for compressible oblique stagnation-point flow. Through the comparison and validation with the numerical results, it is found that the flow model can well simulate the heat transfer near the wall in the flow of uniform shear layer impinging on the wall caused by hypersonic reattachment. With the analysis of the contribution of the energy transport and the heat production in the flow model, it is found that the compression effect and dissipation effect are mainly caused by the shear-component, leading to a significant convective heat transfer in the flow direction, which is different from the case of the classic boundary layer. Then the temperature of the flow near the wall rises rapidly after reattachment, resulting in a high heat flux to the wall. Parameter analysis indicates that the wall heat-transfer coefficient is related to the dimensionless wall temperature gradient and the thickness of the boundary layer. The former is mainly controlled by the shear-component parameter $H_{\zeta}$ , and the latter is negatively correlated with the stagnation-component parameter $H_{\beta}$ . Further analysis shows that the wall heat-transfer coefficient has a linear relationship with $H_{\zeta}$ and is proportional to $\sqrt{H_{\beta}}$ when $H_{\beta}$ is small. This work provides a theoretical basis and solution for studying on the hypersonic reattachment flow, and it is also an extension of the asymmetric stagnation boundary layer theory.Keywords: oblique stagnation-point /reattachment /shear layer /heat transfer 全文HTML --> --> --> 1.引 言 高速流动撞击壁面不仅带来冲击力的作用, 而且由于流体靠近壁面时快速滞止, 其巨大的动能转化为内能, 导致流体温度急遽升高, 并向固壁输入大量能量, 这是高超声速流动及相关工程领域特别关注的问题[1 ] . 这类流动引发能量交换和能量转换问题较为复杂, 流体动能向内能转换其实是流体内应力做功的结果, 可分为压力做功和剪切力做功. 压力做功体现为高速流动的可压缩效应; 剪切力做功即流体内摩擦的耗散生热, 体现为剪切效应. 因此, 流体流动伴随有热传导、对流传热、压缩以及耗散等多种物理作用.[2 ] , Lees[3 ] 以及Fay和Riddell[4 ] 等逐步建立了高超声速驻点边界层理论, 这些研究发现流动经过正激波压缩而产生极高的温度, 这些能量一部分沿着驻点边界层法向传输, 最终传入壁面, 这是一个相对简化的问题. 他们由此给出的驻点热流公式至今仍在广泛使用.[5 ] 首次利用斜驻点简化模型求解了高超声速再附流动, 提出了解决这类问题的一个新途径, 但其能量方程过于简化, 未能讨论其中的流动传热机制.[6 ] 首先得到不可压缩斜驻点流动的解, Tamada[7 ] , Dorrepaal[8 ] 以及Tooke和Blyth[9 ] 对其做了扩展和修正, 但均未考虑流动的传热. Lye[10 ] 假设不可压缩斜驻点流动的温度分布与速度分布类似, 即由驻点分量叠加上剪切分量, 给出了该假设下驻点局部区域的温度分布. 尽管低速不可压缩斜驻点理论取得了较多进展, 但是求解高速可压缩的斜驻点流动面临热力学和动力学耦合的挑战, 迄今尚缺乏系统的研究. 而高速斜驻点流动中同时存在较强的压缩过程和剪切耗散过程, 它们如何影响流体与固壁的传热规律也是一个尚未明确的问题.2.高超声速再附流动与可压缩斜驻点剪切层流动模型 在高超声速分离流动中, 边界层分离后成为自由剪切层, 流过一段距离后再次撞击到壁面, 则形成了再附流动. 不同的流动模型, 如压缩拐角流动[11 ,12 ] 、激波入射边界层流动[13 ,14 ] , 均可以产生再附流动. 这些再附流动在再附局部区域是相似的[15 ,5 ] , 对该区域的研究具有一定的普适性.图1 为高超声速压缩拐角流动的数值模拟结果, 可以看出, 再附区域流动非常接近于剪切层撞击壁面的流动, 其再附流动局部区域与斜驻点流动极为类似. 图2(a) 是斜驻点流动的示意图, 平板壁面处于笛卡尔坐标系$ y = 0 $ 处, 流体处在壁面上方$ y > 0 $ 区域, $ \theta $ 为斜驻点的倾斜角, 即零流线与平板的夹角. 流动在边界层外缘的流函数可写为[6 -8 ] 图 1 压缩拐角流动速度云图(横坐标和纵坐标分别为距前缘点的水平和垂直距离)Figure1. Flow field of a ramp flow (The abscissa and the ordinate are the horizontal and vertical distances from the leading edge, respectively)图 2 经典不可压缩斜驻点流动示意图 (a) 斜驻点流动; (b) 驻点流动与剪切流动的叠加Figure2. Sketch of incompressible oblique stagnation-point flow: (a) Oblique stagnation-point flow; (b) stagnation-point flow and shear flow.图2(b) 所示. 易知$ \beta $ 为流向速度梯度, $ \zeta $ 为涡量. 斜驻点流动形成的边界层厚度可以用相应的正驻点流动边界层厚度$ \delta_0 $ 估计,$ \rho_{\rm{e}} $ 和$ \mu_{\rm{e}} $ 分别为外缘的密度和黏性系数. 例如不可压缩斜驻点边界层的位移厚度为$ 0.65 \delta_0 $ [6 ] , 所以斜驻点边界层厚度仍是一个小量.图3 所示. 紧邻壁面为黏性斜驻点边界层, 中间是无黏有旋的剪切层流动, 外部则是无黏势流, 黏性层和剪切层厚度相对流向尺度均为小量. 因此, 再附流动可视为均匀的自由剪切层以一定角度撞击壁面而形成的斜驻点流动, 为方便区分, 将其称为“斜驻点剪切层流动”. 由于流动是非对称的, 本文仅关注再附下游一侧(图3 中右侧)的流动, 因为壁面热流最大值发生在此区域内.图 3 高速剪切层撞击壁面形成的斜驻点流动模型Figure3. The model of compressible oblique-stagnation-point flow induced by impinging shear-layer.3.斜驻点剪切层流动的自相似解及其验证 23.1.控制方程 3.1.控制方程 斜驻点剪切层流动内的边界层厚度为小量, 经量级分析, 可给出斜驻点边界层的控制方程$ h = c_p T $ , $ c_p $ 为定压比热容. k 为导热系数. $ \mu $ 为黏性系数, $ \left(\mu / \mu_{\rm{e}}\right) = \left(T / T_{\rm{e}}\right)^n $ , n 为黏性幂次律的幂指数. $ \varPhi $ 为耗散函数,[16 ] 的思想. 由于无黏有旋的剪切层流动与底层黏性流动的特征相同, 都分为驻点分量和剪切分量, 可认为控制方程(4 )适用的区域包括黏性边界层和无黏剪切层两部分. 黏性边界层和无黏剪切层整体的厚度为$ \delta_{\rm{e}} $ , 定义无量纲厚度为3.2.自相似解法 -->3.2.自相似解法 斜驻点黏性流动方程组(4 )中的动量方程和能量方程与经典边界层相应的方程不同, 需要引用新的流场和温度场自相似概念, 给出方程组(4 )的数学求解方案.$ {C_{\rho}} = {\rho_{\rm{e}}}/{\rho} $ . 并假设$ \rho_{\rm{e}} $ , $ T_{\rm{e}} $ 等外缘物理量沿流向的变化可以忽略, 均看作常量, 因而$ \delta_0 $ 也是常量. 该变换类似Howarth-Dorodnitsyn变换[17 ,18 ] , 可以将可压缩的动量方程从形式上变成不可压缩的形式. 其次, 参考Tooke和Blyth[9 ] 的不可压缩斜驻点流动解法, 假设黏性层内流函数具有驻点分量加剪切分量的形式, 即$ T_{\rm{w}} $ 为壁温, $ T_{\rm{aw}} $ 为恢复温度, $T_{\rm aw} = [1 + 0.5\times \sqrt{Pr} (\gamma-1) M_{\rm e}^2 ] T_{\rm e}$ , $ M_{\rm{e}} = u_{\rm{e}}/\sqrt{\gamma R T_{\rm{e}}} $ 为外缘马赫数, $ {Pr} = {\mu {c_p}}/{k} $ 为普朗特数. 最后, 考虑到边界层位移厚度的影响, 斜驻点流动中剪切层要与底层边界层相匹配, 将外缘流函数与速度分别修正为$ c_{\delta} {\delta _0} $ 为边界层位移厚度. 对于不可压缩流动, $ c_{\delta} \approx 0.65 $ [6 ] . 对于可压缩流动, 类比于平板边界层的做法[19 ,20 ] , 得$ C^* = \left({\rho^* \mu^*}\right) / \left({\rho_{\rm{e}}}{\mu_{\rm{e}}}\right) $ . 上标$ * $ 表示使用参考温度法[21 ,22 ] 进行计算, 即8 )式—(10a )式代入到方程(4 )中, 并按(7 )式进行坐标变换, 在原点附近可得11a )—(13 )中出现的无量纲参数定义为$ {\bar T}_{\rm{aw}} = T_{\rm{aw}}/T_{\rm{e}} = 1 + 0.5\sqrt{{Pr}}(\gamma-1) M_{\rm{e}}^2 $ 为无量纲的恢复温度, $ C = \left({\rho \mu}\right) / \left({\rho_{\rm{e}}}{\mu_{\rm{e}}}\right) $ 为Chapman-Rubesin数, $ \eta_{\rm{e}} $ 是经过坐标变换的边界层的厚度.11a )各函数和边界条件(13 )均与$ \xi $ 无关, 也即斜驻点流动在驻点局部是自相似的, 然而这里的自相似与经典的边界层自相似又有所不同. 方程(11a )和方程(11b )说明流动是两个自相似流动叠加而成, 方程(11c )—(11e )则表明能量传输是3个自相似过程的耦合结果.11a )无法直接解析, 使用数值打靶法求解方程(11a ), 可给出无量纲壁面温度梯度$ \varTheta_0^{\prime}\left(0\right) $ , 那么传入壁面的热流为$ C_{\rm{w}} = \left({\rho_{\rm{w}} \mu_{\rm{w}}}\right) / \left({\rho_{\rm{e}}}{\mu_{\rm{e}}}\right) $ . 本文仅考虑理想气体, 在计算中, 取比热比$ \gamma = 1.4 $ , 普朗特数$ {Pr} = 0.72 $ , 黏性幂次$ n = 0.76 $ .3.3.数值验证 -->3.3.数值验证 使用直接模拟蒙特卡罗(direct simulation of Monte Carlo, DSMC)方法进行了一系列的压缩拐角分离-再附流动[11 ] 的数值模拟. DSMC方法在中低雷诺数高超声速流动中是公认可靠的, 已在相当多的研究当中得到应用[23 ,24 ] . 根据实际流动的参数范围, 本文选取了不同拐角角度和来流参数的压缩拐角算例进行了系统的计算, 具体参数见表A1 . 提取再附流动的外缘参数, 包括剪切层撞击壁面的倾斜角$ \theta $ 、剪切层厚度$ \delta_{\rm{e}} $ 、外缘速度$ u_{\rm{e}} $ 、温度$ T_{\rm{e}} $ 、压强$ p_{\rm{e}} $ 以及峰值压强$ p_{\rm{pk}} $ , 使用峰值压强作为剪切层外缘压强, 根据(14a )式和(6 )式可计算出无量纲参数$ M_{\rm{e}} $ , $ H_{\beta} $ , $ H_{\zeta} $ , $ D_{\rm{e}} $ , $ {\bar T}_{\rm{w}} $ , 作为斜驻点剪切层流动的外缘边界条件. 各参数范围为$ M_{\rm{e}} = 4.6—7.1 $ , $ H_{\beta} = (0.3 —1.8)\times 10^{-4} $ , $ H_{\zeta} = (0.2—1.3)\times 10^{-2} $ , $ D_{\rm{e}} = 16—33 $ , $ {\bar T}_{\rm{w}} = 0.3—2.1 $ , 具体数值见表A2. 通过求解方程组(11a )得到流场内的温度分布以及壁面热流值, 再与DSMC的数值结果进行对比, 验证斜驻点模型解的有效性.Case No. $ M_\infty $ $ {Re}_L / 10^4 $ $ \theta /(^{\circ}) $ $ T_\infty $/K $ T_{\rm{w}} $/K L /mA1 9 1 25 60 300 1 B1 9 2 25 60 300 1 B2 11 2 25 60 300 1 C1 9 5 25 60 300 1 C2 11 5 25 60 300 1 C3 13 5 25 60 300 1 C4 15 5 25 60 300 1 D1 13 10 25 60 300 1 D2 15 10 25 60 300 1 E1 11 5 21 60 297 1 E2 11 5 24 60 297 1 E3 11 5 27 60 297 1 E4 11 5 30 60 297 1 F1 15 2 30 60 300 1 G1 15 5 24 60 300 1 G2 15 5 27 60 300 1 H1 11 2 25 100 300 1 H2 11 2 25 150 300 1 H3 11 2 25 200 300 1 H4 11 2 25 250 300 1 I1 11 5 25 60 100 1 I2 11 5 25 60 200 1 I3 11 5 25 60 250 1 I4 11 5 25 60 350 1 I5 11 5 25 60 450 1
表A1 DSMC模拟压缩拐角分离-再附流动的流动参数TableA1. Flow conditions of the compression ramp flow in DSMC simulations.Case No. $ M_{\rm{e}} $ $ H_{\beta} \times 10^4 $ $ H_{\zeta} \times 10^3 $ $ D_{\rm{e}} $ $ {\bar T}_{\rm{w}} $ $ \theta $ A1 4.82 1.79 12.25 15.2 1.64 13.6 B1 4.60 1.60 10.27 16.4 1.51 14.0 B2 5.57 1.16 6.45 19.9 1.43 15.0 C1 4.69 0.97 5.21 23.1 1.57 15.3 C2 5.44 0.78 3.89 25.6 1.37 15.8 C3 6.15 0.66 3.22 27.5 1.23 16.0 C4 6.55 0.68 3.10 27.7 1.04 16.5 D1 6.00 0.51 2.32 32.4 1.18 16.6 D2 6.28 0.51 2.17 32.9 0.96 17.0 E1 5.90 0.57 4.93 23.0 1.56 12.1 E2 5.60 0.71 4.07 25.1 1.42 14.8 E3 5.18 0.93 3.86 25.4 1.25 17.2 E4 4.71 1.28 3.99 24.5 1.07 19.7 F1 5.71 1.75 5.17 21.0 0.82 20.2 G1 7.05 0.50 2.61 30.4 1.19 15.5 G2 5.99 0.90 3.40 26.1 0.88 18.0 H1 5.48 1.17 6.40 18.9 0.83 15.1 H2 5.38 1.22 6.52 18.2 0.54 15.3 H3 5.46 1.12 5.90 18.9 0.41 15.4 H4 5.08 1.36 7.29 16.8 0.36 15.3 I1 5.35 0.90 3.88 23.4 0.45 16.9 I2 5.50 0.78 3.53 25.7 0.93 16.6 I3 5.50 0.75 3.57 26.1 1.17 16.2 I4 5.43 0.80 4.10 25.5 1.59 15.6 I5 5.45 0.73 4.06 27.1 2.07 15.0
表A2 再附点后局部的无量纲流动参数TableA2. Dimensionless parameters of the vicinity behind the reattachment point图4 所示. 由于壁面热流值取决于在壁面附近的温度分布, 因此准确模拟壁面邻域的温度分布是关键. 图4 中的结果表明, 在紧邻壁面处两温度剖面基本一致, 本文主要关注壁面热流, 从温度剖面可以推测, 斜驻点模型预测的热流与数值热流解是相符的, 可以准确地模拟壁面邻域的流动和传热. 另一方面, 在远离壁面的地方, 斜驻点模型得到的温度比数值解有明显的偏低. 近壁面流动是剪切层撞击壁面后发展出的边界层流动, 远离壁面的地方则主要是剪切层附着于壁面后的流动. 理论模型描述的是近壁面边界层的流动特征, 而对远离壁面的剪切层描述有一定简化, 主要是并未考虑实际压缩拐角流动中, 剪切层的形成来自于上游边界层的分离, 其本身经历分离和再附激波压缩后, 有一定温升, 即携带有较高的内能, 因此理论结果较数值结果偏低.图 4 理论结果与DSMC结果的温度剖面对比(横坐标为温度, 纵坐标为距壁面的法向距离)Figure4. Comparision of temperature profile between theoretical results and DSMC simulations.$ St_{\rm{e}} $ , 如图5 所示. 其中横坐标为数值计算中提取的结果, 纵坐标表示理论计算得到的结果, 两条虚线为$ \pm 10 $ %的相对误差线. 结果表明, 理论给出的峰值热流系数与DSMC结果的最大相对误差小于10%. 这也进一步证实了上节中的论断, 即斜驻点理论模型预测的壁面热流值与DSMC数值模拟给出的结果是相符的.图 5 理论结果与DSMC结果的当地热流系数对比Figure5. Comparision of the local heat-transfer coefficient (Stanton number) between theoretical results and DSMC simulations.4.斜驻点流动中的传热机制 24.1.斜驻点流动的能量方程 4.1.斜驻点流动的能量方程 为深入探讨斜驻点流动中流体对固壁传热的物理机理, 需要对能量方程进行细致分析. (16 )式表明在$ x = 0 $ 邻域无量纲的壁面热流率与无量纲温度$ \varTheta_0 $ 的梯度有关. 因此, 本节基于能量方程(11c )重点分析该区域流动的传热机制. 流动中的动能与内能转换包括压缩、耗散过程, 流动还伴随对流传热和热传导, 这些共同构成了流动中的能量交换和转换现象. 将方程(11c )改写为8 ), f 和$ g^{\prime} $ 分别为法向和流向速度, $ f^{\prime} $ 和$ (f^{\prime})^2 $ 分别为法向速度的梯度及其对应的耗散, $ g^{\prime\prime} $ 和$ (g^{\prime\prime})^2 $ 分别为流向速度的梯度及其对应的耗散, 因此, 在方程(17 )中分别用$ (\xi) $ 和$ (\eta) $ 表示流向和法向的对流传热, 以及流向速度的梯度和法向速度的梯度产生的耗散, 为了方便, 以下简称为流向耗散和法向耗散.17 )中各项在斜驻点剪切层内的分布, 分析各项作用的强弱. 可选取一组典型的流动参数进行理论计算. 参考上节的流动参数范围, 不失一般性, 取$ M_{\rm{e}} = 5.0 $ , $ H_{\beta} = 3 \times 10^{-3} $ , $H_{\zeta} = 3 \times 10^{-3}$ , $ D_{\rm{e}} = 20 $ , $ {\bar T}_{\rm{w}} = 0.5 $ , 结果如图6 所示. 图中纵坐标为无量纲法向坐标, 横坐标为能量方程(17 )中的各项的数值, 为正值时表示相应的物理过程增加当地的内能, 反之则减少.图 6 能量方程(17 )中的各项在剪切层内的分布Figure6. Profiles of the items in Equation (17 ).图6 明确显示了这个特点. 因此, 斜驻点边界层温度剖面沿流向是变化的, 无法采用原始的自相似解法, 但在斜驻点附近区域内可以假设流动和传热具有局域自相似性, 即温度、温度流向梯度分别具有自相似性, 这也是我们提出的温度变换式(8 )的物理含义. 图6 还表明, 在远离壁面的地方, 对流传热起主导作用, 且流向对流传热数值为正, 法向对流传热数值为负, 意味着上游的高焓流体通过流向对流将大量的热量输入至当地, 并通过法向对流向近壁区域的流体传热. 同时远离壁面的流体有较大的流向速度, 压缩作用也不可忽略. 另一方面, 在紧邻壁面处, 情况更为复杂, 由于靠近壁面的剪切力较大, 因此耗散作用很强, 尤其是流向剪切耗散产生的热量不可忽略, 再叠加上对流传热从上层带来的大量能量, 使得近壁处产生一个高温区, 法向热传导作用非常强, 导致流体向壁面的导热率非常大.17 )中压缩项和法向耗散项的大小与无量纲流动参数$ H_{\zeta} $ 有关, 流向耗散项与参数$ H_{\beta} $ 有关, 因此, 还需要继续探索这些参数影响壁面热流的物理规律.4.2.剪切分量和驻点分量传热的物理机理和规律 -->4.2.剪切分量和驻点分量传热的物理机理和规律 根据控制方程(11a ), 与斜驻点流动密切相关的参数是$ H_{\beta} $ 和$ H_{\zeta} $ , 分别与$ \beta $ 和$ \zeta $ 有关. 由(1 )式可知, 在斜驻点流动中, $ \beta $ 和$ \zeta $ 分别为流函数中驻点分量和剪切分量的系数. 因此, $ H_{\beta} $ 和$ H_{\zeta} $ 以动能与焓差之比的形式分别表征了斜驻点流动驻点分量和剪切分量的相对大小. 本节主要探讨这两个参数对传热的影响.图7 为不同$ H_{\beta} $ 和$ H_{\zeta} $ 下的无量纲温度剖面. 可以看出, 提高$ H_{\beta} $ 和$ H_{\zeta} $ 的值均可以增大剪切层内的温度, 从而增大壁面传热, 并且$ H_{\zeta} $ 的影响更为显著. 根据能量方程(11c ), 提高$ H_{\zeta} $ 主要影响了压缩效应和流向耗散效应. 由于斜驻点流动受压缩波系作用, 压缩效应强, 增大$ H_{\zeta} $ 可显著提高剪切层内的温度. $ H_{\beta} $ 主要影响了法向速度梯度的耗散效应, 然而该部分耗散效应对提高内能的贡献较小, 对温度剖面的影响也较小. 图8 给出了壁面上无量纲温度法向梯度$ \varTheta_0^{\prime}(0) $ 随$ H_{\beta} $ 和$ H_{\zeta} $ 的变化趋势, 可见$ H_{\beta} $ 从$ 10^{-4} $ 增大到$ 2\times 10^{-3} $ 仅使$ \varTheta_0^{\prime}(0) $ 增大约$ 10\% $ , 所以$ \varTheta_0^{\prime}(0) $ 主要与$ H_{\zeta} $ 有关. 因此, 在斜驻点剪切层流动中, 剪切分量是影响内能和能量传递的主要因素.图 7 $ H_{\beta} $ 和$ H_{\zeta} $ 对温度剖面的影响 (a) 不同$ H_{\beta} $ 下的温度剖面; (b) 不同$ H_{\zeta} $ 下的温度剖面Figure7. Influences of $ H_{\beta} $ and $ H_{\zeta} $ on heat transfer: (a) Temperature profiles under different $ H_{\beta} $ ; (b) temperature profiles under different $ H_{\zeta} $ .图 8 $ H_{\beta} $ 和$ H_{\zeta} $ 对$ \varTheta_0^{\prime}(0) $ 的影响规律Figure8. Influences of $ H_{\beta} $ and $ H_{\zeta} $ on $ \varTheta_0^{\prime}(0) $ .$ H_{\zeta} $ 对应的压缩效应和剪切分量耗散作用是影响流动中能量输运的主要因素, 这其实与高速斜驻点流动特性具有密切关联. 斜驻点流动在再附过程中受到一系列压缩波系作用(在图3 中已有说明), 压缩波对剪切层产生了显著的压缩作用, 使得流体压强和温度升高, 同时产生了较强的流向对流传热. 而在近壁区, 剪切分量带来的速度梯度非常大, 产生的黏性耗散作用强, 进一步增大了流场内的温度, 甚至高于剪切层外缘的温度. 这些现象与图6 中能量方程各项大小的对比是完全一致的. 直至压缩波系末端, 压强达到最大值, 流体压缩效应消失, 开始转变为膨胀效应, 此时流动已远离斜驻点, 开始向传统意义上的边界层流动发展.图9 为$ H_{\beta} $ 和$ H_{\zeta} $ 对壁面热流系数的影响. 可以看出, $ H_{\beta} $ 和$ H_{\zeta} $ 对壁面热流均有显著的影响. 而根据前面得到的结果, 剪切层内温度的大小主要与$ H_{\zeta} $ 相关, 受$ H_{\beta} $ 的影响很小, 这说明$ H_{\beta} $ 和$ H_{\zeta} $ 对壁面热流的影响机制并不相同. 由(16 )式, 壁面热流系数$ {St}_{\rm{e}} \propto \varTheta_0^{\prime}(0) \sqrt{H_{\beta}} $ .图 9 参数$ H_{\beta} $ 和$ H_{\zeta} $ 对壁面热流系数的影响 (a) $ H_{\beta} $ 的影响; (b) $ H_{\zeta} $ 的影响.Figure9. Influences of $ H_{\beta} $ and $ H_{\zeta} $ on the wall heat-transfer coefficient: (a) Influence of $ H_{\beta} $ ; (b) influence of $ H_{\zeta} $ .$ \varTheta_0^{\prime}(0) $ 受$ H_{\beta} $ 的影响很小, 可以近似认为$ {St}_{\rm{e}} \propto \sqrt{H_{\beta}} $ . 从流动物理角度可以解释该式代表的规律, 即驻点分量主要影响了剪切层内的边界层厚度. 根据(3 )式和(14b )式, 当$ \beta $ 变化时, 有$ \sqrt{H_{\beta}} $ 呈反比. 因此,$ \varTheta_0^{\prime}(0) $ 主要与$ H_{\zeta} $ 有关. 增大$ H_{\zeta} $ 将提高剪切层内的温度, 从而增大了$ \varTheta_0^{\prime}(0) $ , 最终增大了壁面热流系数$ {St}_{\rm{e}} $ . 从图9(b) 还能发现$ {St}_{\rm{e}} $ 与$ H_{\zeta} $ 具有很好的线性关系. 事实上, 假设能量方程(11c )的右端项与$ \varTheta_0 $ 为弱耦合关系, 即忽略$ \varTheta_0 $ 对方程右端各项的影响, 则方程(11c )为线性方程, 其解有如下的形式:$ H_{\beta} $ 对能量方程的影响较小, 忽略与之相关的项后不难发现$ S_0, S_1, S_2 \propto H_{\zeta} $ , 同时关于$ \varTheta_1 $ 的方程为线性齐次方程, 因而有$ \varTheta_1 \propto H_{\zeta} $ . 根据(20 )式易得$ {\varTheta_{0, {\rm{sp}}}} \propto H_{\zeta} $ , 从而$B_{\varTheta_0} \!\propto\! H_{\zeta}$ . 不妨令$B_{\varTheta_0} \!=\! {\tilde B}_{\varTheta_0} H_{\zeta}$ , $ {\tilde B}_{\varTheta_0} $ 是一个与$ H_{\zeta} $ 无关的函数, 则(21 )式可以改写为$ {St}_{\rm{e}} \propto {\varTheta_0}^{\prime}\left(0\right) $ , (22 )式解释了壁面热流系数$ {St}_{\rm{e}} $ 与$ H_{\zeta} $ 之间的线性关系.$ H_{\zeta} $ 即剪切分量主要影响剪切层内的无量纲温度剖面分布, 而$ H_{\beta} $ 即驻点分量主要影响剪切层内边界层的厚度, 最终壁面热流系数$ {St}_{\rm{e}} $ 受两者共同作用. 进一步地, 结合(16 )式和(22 )式可得,$ {St}_{\beta} $ 与剪切分量无关, 可认为是由驻点分量引起的壁面热流系数, 而$ \phi_{\zeta} $ 则是由剪切分量引起的壁面热流系数增量. 当剪切层撞击壁面的角度逐渐增大, 流动从斜驻点转变为正驻点流动时, 剪切分量为零, 即$ H_{\zeta} = 0 $ , 则有$ \phi_{\zeta} = 0 $ , 由(23 )式得到壁面热流为[2 ] 是一致的. 本文的斜驻点剪切层流动模型可以退化到正驻点流动且与经典理论相符, 说明本论文的理论分析在大角度的剪切层撞击壁面流动中仍然是合理的.$ H_{\beta} $ 的影响较小, 表明在能量转换和输运过程中, 流动驻点分量产生的耗散作用相比压缩效应和剪切分量的耗散作用是比较弱的. 还要注意到, 上面的分析中, $ H_{\beta} $ 和$ H_{\zeta} $ 是同一量级的, 而在大部分实际再附流动中, 如附录中表A2 所列, $ H_{\beta} $ 比$ H_{\zeta} $ 要小一个量级, 因此, 可认为能量方程中与$ H_{\beta} $ 相关的项可以忽略不计. 相当于有量纲的原能量方程可以简化为$ H_{\beta} $ 很小, 那么其能量方程与经典边界层方程[22 ] 基本相同, 重要差别仅在于压缩梯度项为(5 )式. 经过进一步检验, 当$H_{\beta} < 4.5 \times 10^{-4}$ 时, 采用简化方程计算得到的壁面热流与完整斜驻点流动方程结果相比, 偏差不超过5%.5.结 论 本文研究了可压缩斜驻点剪切层流动模型, 利用自相似变换法, 得到了完整的流场和温度场解, 并详细分析了其中对流、热传导、压缩以及耗散等现象的物理机理. 得到如下结论:$ H_{\zeta} $ 可表征两效应作用的强弱, 也是壁面热流系数的主要影响参数之一.$ H_{\beta} $ 表征.附录A DSMC模拟算例中的来流参 数以及再附点局部流动参数 本文采用DSMC方法数值模拟压缩拐角分离-再附流动, 以考察不同来流参数和拐角角度的压缩拐角流动, 展示再附区流动的特性. 表A1 列出了DSMC模拟的压缩拐角流动参数, 其中, A–D组为马赫数和雷诺数变化, E–G组为拐角角度变化, H组和I组分别为来流温度和壁面温度变化. 表A2 列出了对应各个算例中, 模拟得到的气流再附于壁面时的局部流动参数, 作为斜驻点剪切流动模型的外缘条件, 以验证该模型的有效性. 


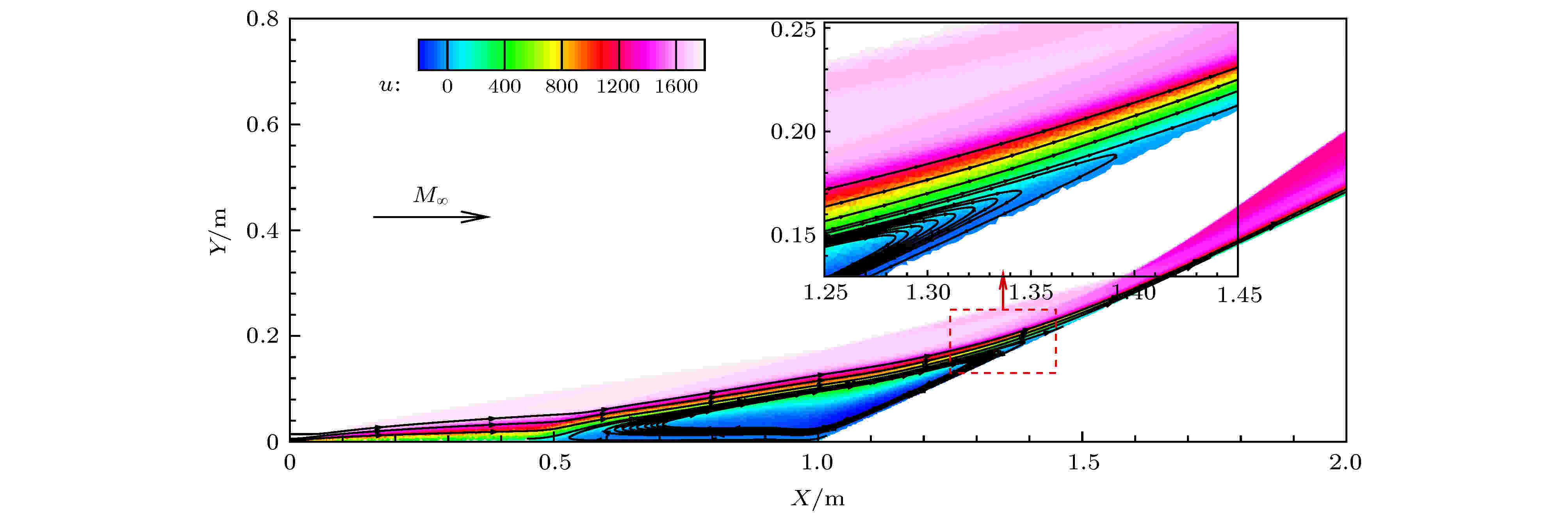 图 1 压缩拐角流动速度云图(横坐标和纵坐标分别为距前缘点的水平和垂直距离)
图 1 压缩拐角流动速度云图(横坐标和纵坐标分别为距前缘点的水平和垂直距离) 图 2 经典不可压缩斜驻点流动示意图 (a) 斜驻点流动; (b) 驻点流动与剪切流动的叠加
图 2 经典不可压缩斜驻点流动示意图 (a) 斜驻点流动; (b) 驻点流动与剪切流动的叠加





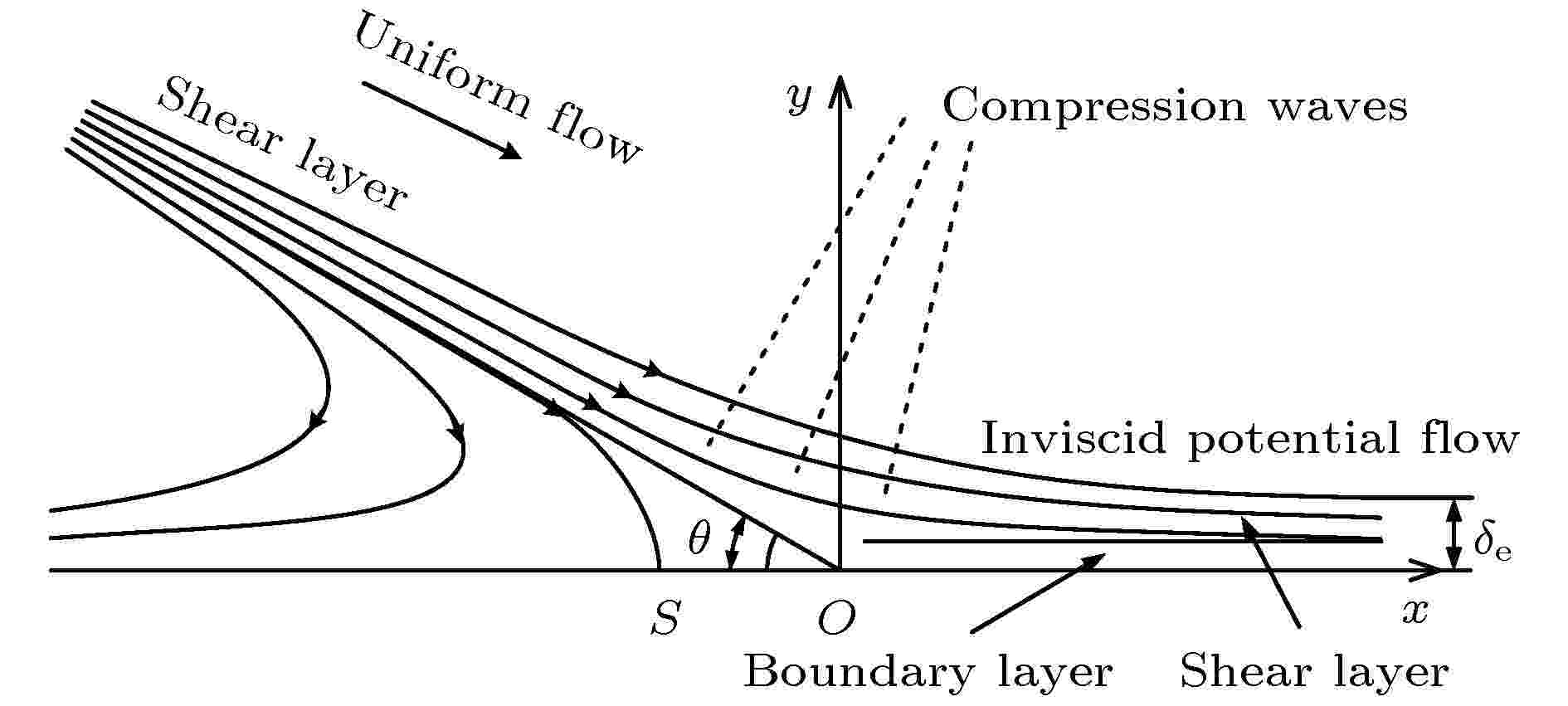 图 3 高速剪切层撞击壁面形成的斜驻点流动模型
图 3 高速剪切层撞击壁面形成的斜驻点流动模型











































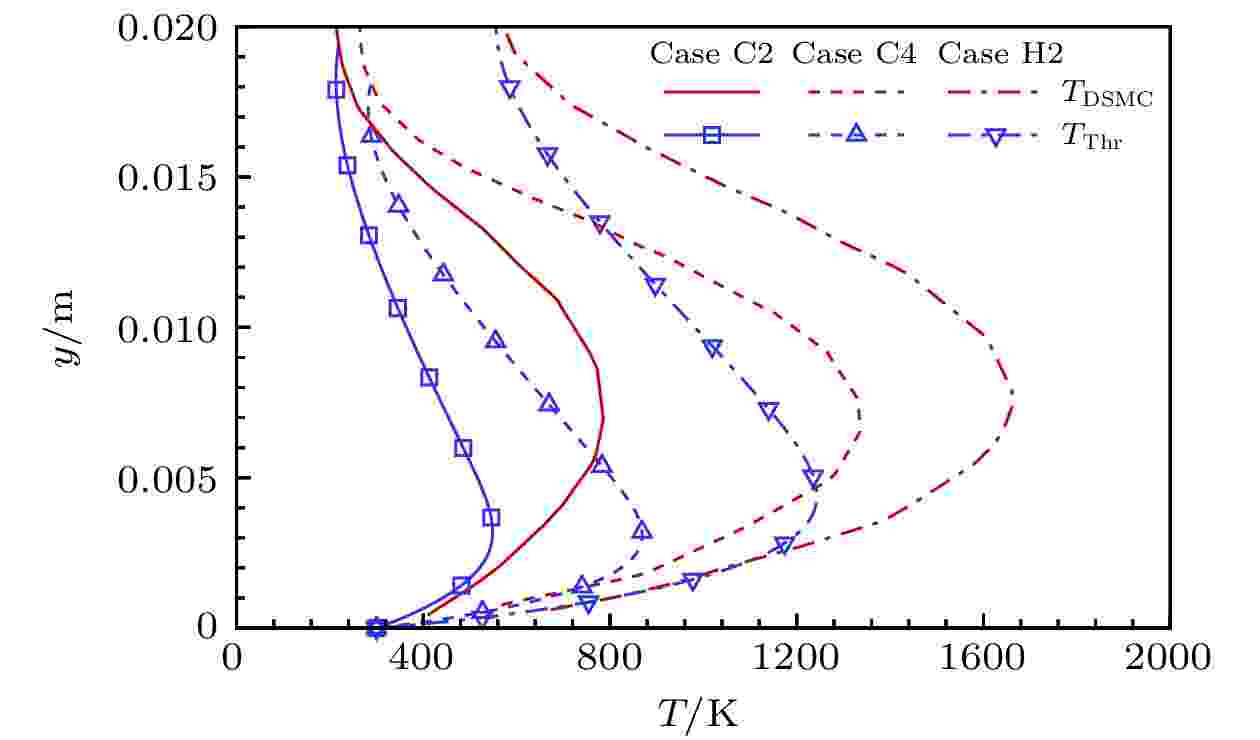 图 4 理论结果与DSMC结果的温度剖面对比(横坐标为温度, 纵坐标为距壁面的法向距离)
图 4 理论结果与DSMC结果的温度剖面对比(横坐标为温度, 纵坐标为距壁面的法向距离)

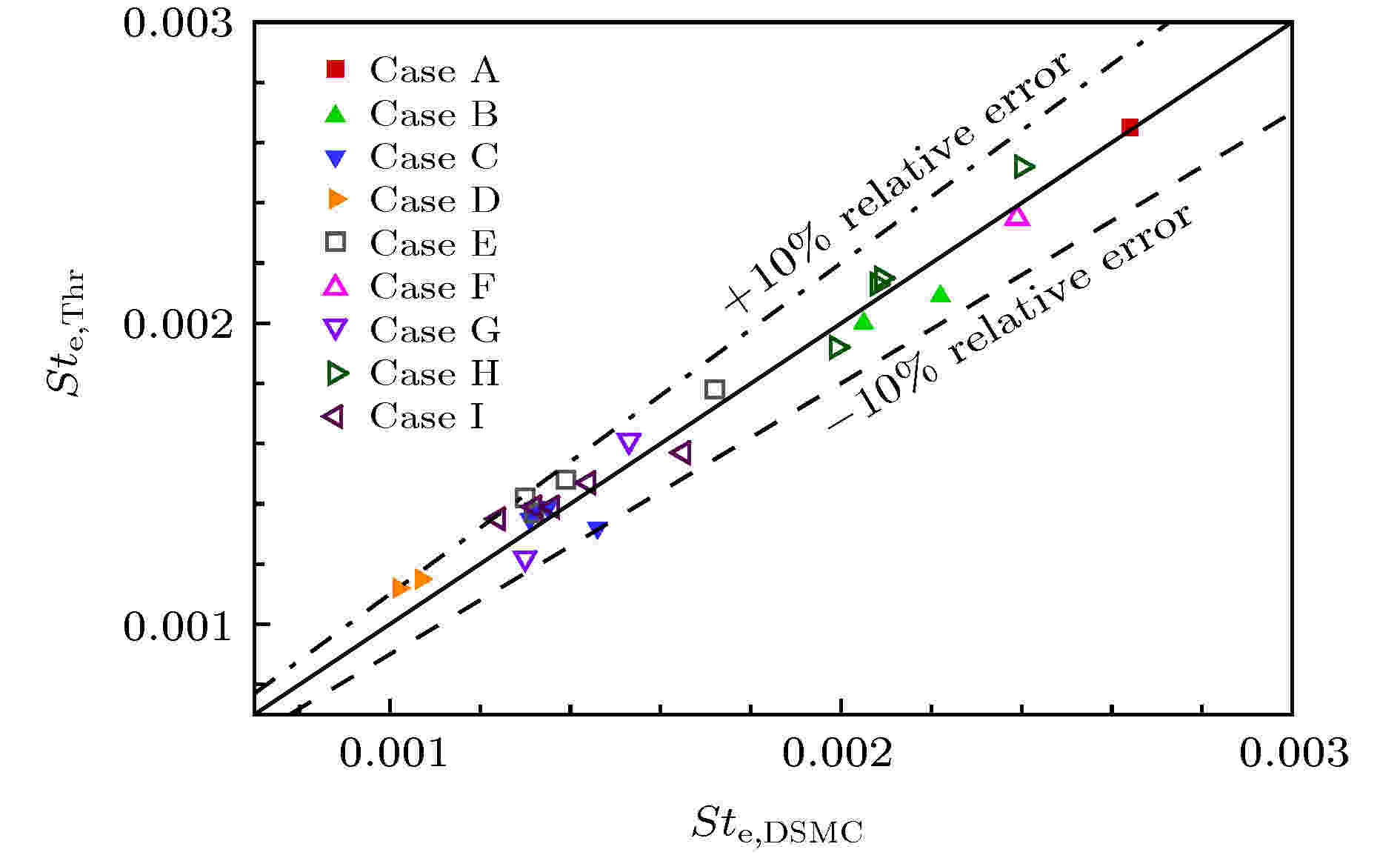 图 5 理论结果与DSMC结果的当地热流系数对比
图 5 理论结果与DSMC结果的当地热流系数对比













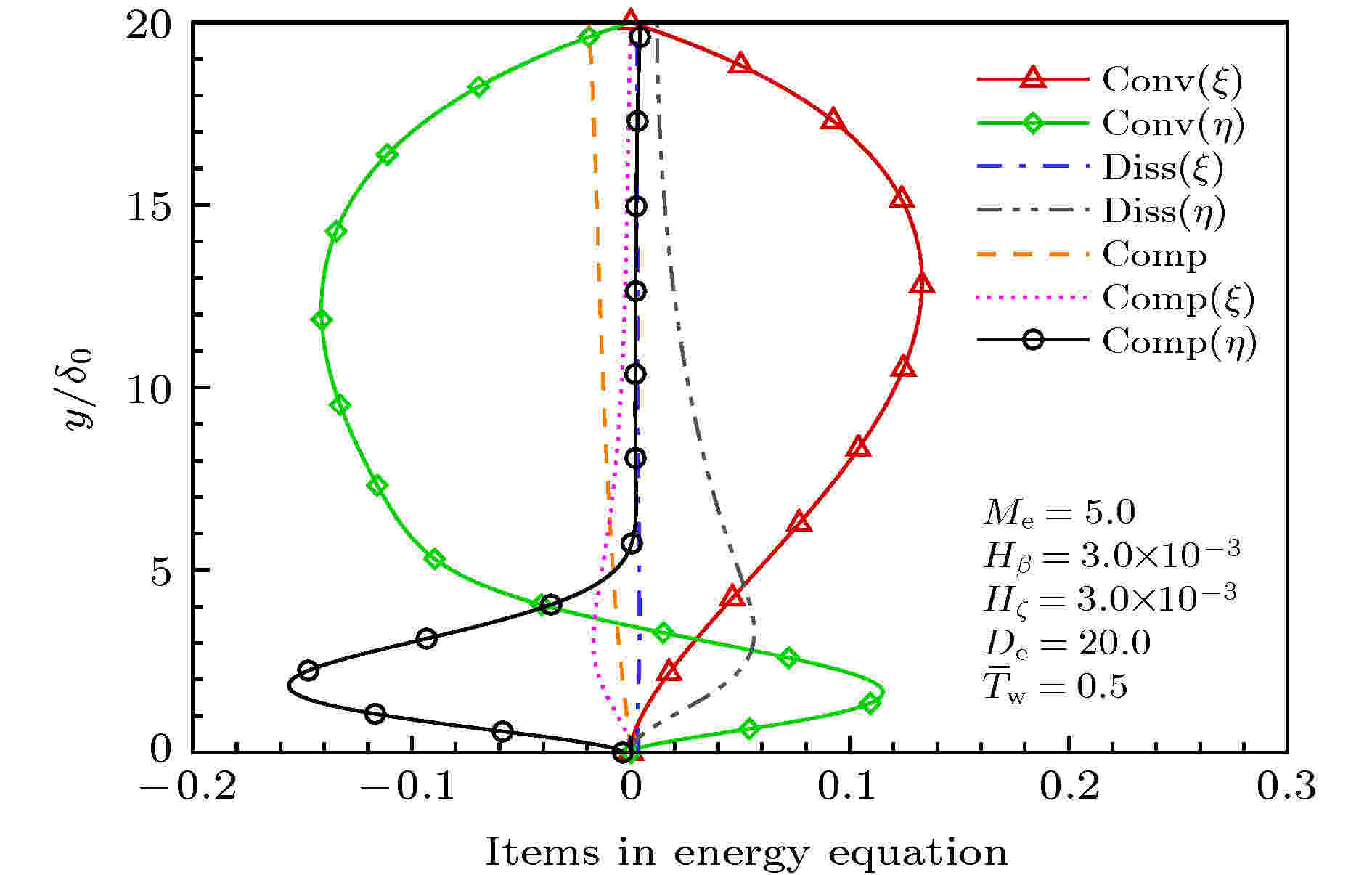 图 6 能量方程(17)中的各项在剪切层内的分布
图 6 能量方程(17)中的各项在剪切层内的分布







































































































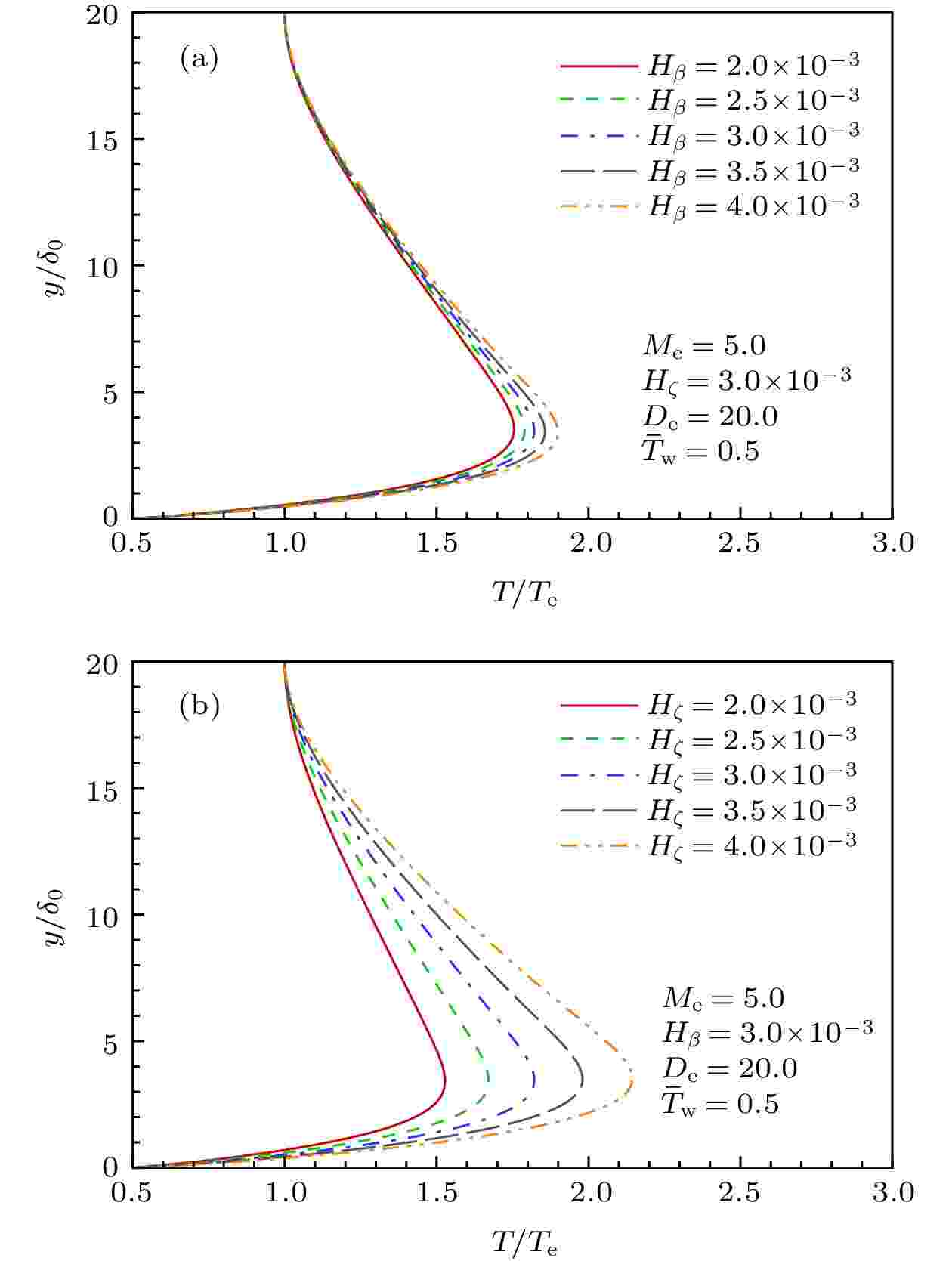 图 7
图 7 















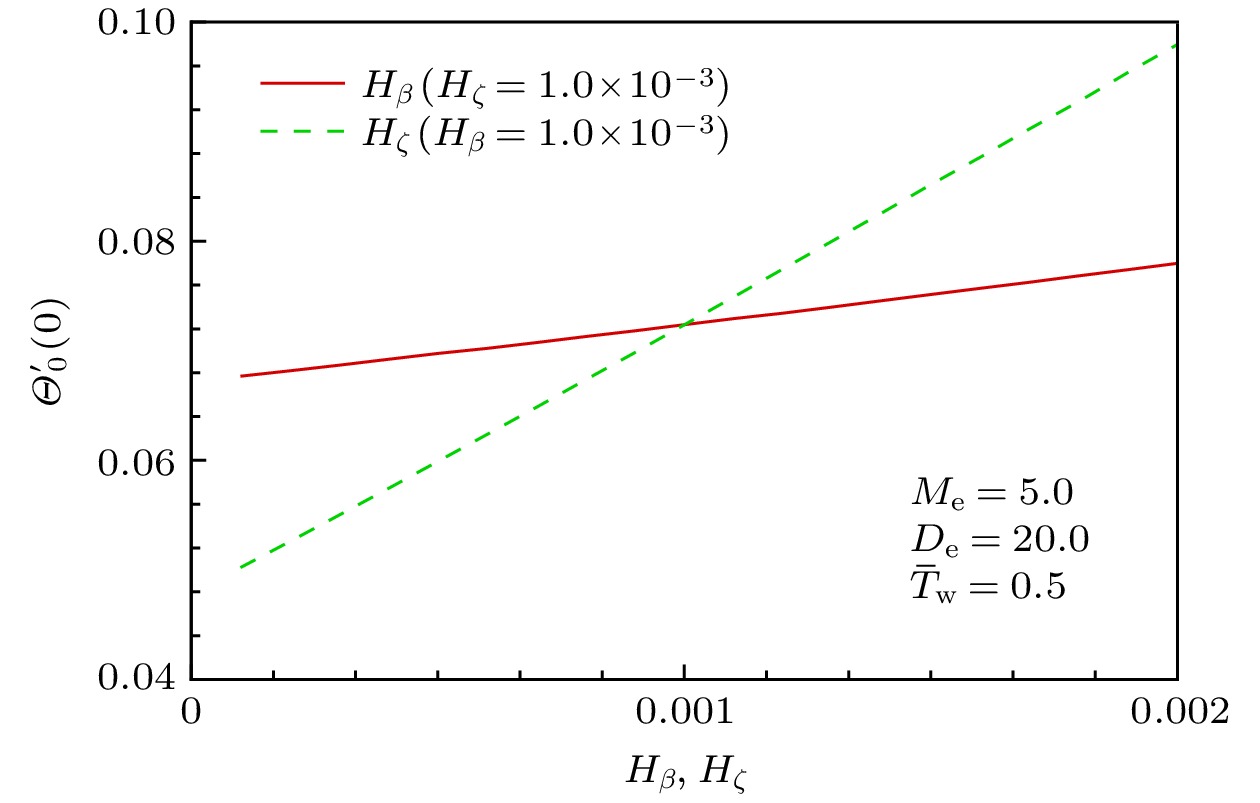 图 8
图 8 







































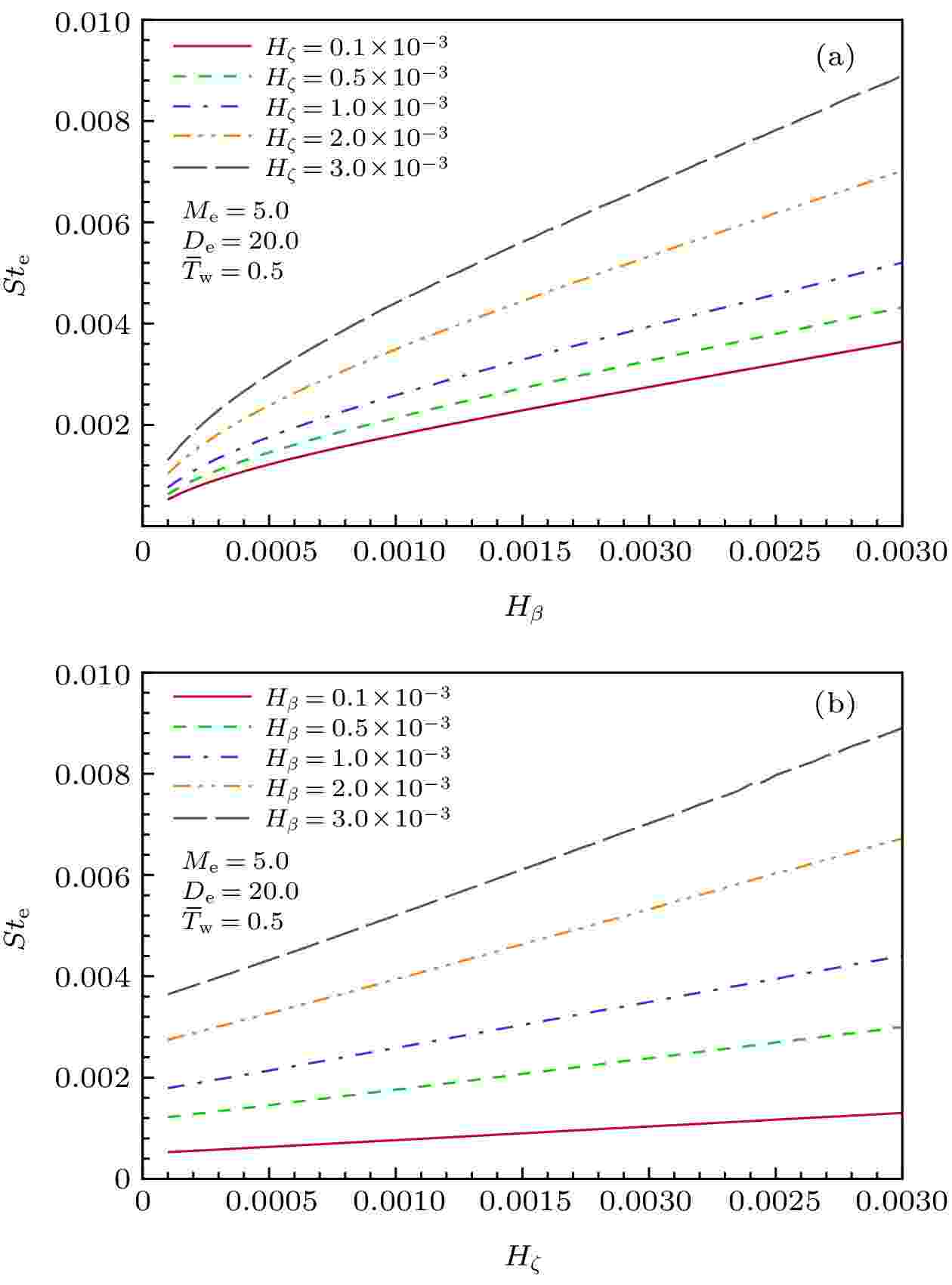 图 9 参数
图 9 参数























































































