全文HTML
--> --> -->虽然分子电子学的研究目标是在分子层次上构建功能电子器件并组装逻辑电路, 但是伴随分子电子学发展起来的单分子结制备技术为人们在单原子/分子层次上理解体系的物理过程、物理性质及其相互作用机理提供了强有力的技术手段[35]. 在分子电子学实验中需要组装单分子结并对其电输运性质进行测量, 因此获取到的是单分子层次的电输运信号, 这是分子电子学实验的独特优势. 尽管测量到的单分子电流信号不一定是满足功能器件特定要求的电输运信号, 但信号中包含了丰富的单分子、电极界面结构及其相互作用的丰富信息[8,36-38]. 到目前为止, 在分子电子学的研究中已经对各种不同类型的分子进行了测量, 从分子骨架上看有共轭分子[37-40]、非共轭分子[41-43]等, 从末端连接基团上分类有硫醇/酚末端分子[43-47]、氨基末端分子[6,45-48]、吡啶末端分子[47,49-54]等. 不同的分子, 特别是不同末端连接基团的分子, 与电极之间存在不同的相互作用, 并且表现出不同的电输运特征[47,50,53,55]. 因此, 从理论上探索分子结体系的电输运特性跟体系结构特别是体系结构变化过程之间的对应关系, 可以为实验探测和理解分子体系的结构及其物理过程提供理论与数据支持.
从近二十几年的实验测量文献报道中发现, 以吡啶基为末端的分子是一类非常值得关注的分子. 实验中在拉伸两末端为吡啶基的金电极-分子-金电极体系并对体系电导进行测量时发现, 此类分子的拉伸电导曲线一般会出现高低电导转换现象, 这是一般分子很少出现的比较特殊的一种现象[47-54]. 弄清产生这一现象的物理过程和内在物理机制, 对于利用含吡啶末端分子构建分子开关、分子存储器、分子传感器等功能分子器件具有十分重要的意义. 为了理解这一现象, 一些课题组通过输运性质计算探讨了体系高低电导可能对应的几何结构. 这些探索性的设计与计算虽然在一定程度上可以说明高低电导的差异, 但未与分子结的拉伸过程相联系, 因此这些研究结果既无法合理地理解分子结拉伸过程中体系高低电导间的突变式转换过程, 更无法发现分子结拉伸过程中界面结构的变化以及界面原子的移动过程. 为了解决这些问题, 真正解决末端为吡啶基的分子结拉伸过程中的高低电导之谜, 发展了基于第一性原理计算的分子结绝热拉伸模拟技术[30,37], 对4, 4′-二吡啶分子结的拉伸过程进行了计算模拟. 计算结果不仅破解了4, 4′-二吡啶分子与金电极构成的分子结在拉伸过程中出现的双电导平台之谜, 而且进一步证明了, 通过理论计算并结合相关实验测量, 可以很好地在单原子/分子层次上有效识别电极尖端几何结构以及分子-电极间的界面连接方式.
图 1 STM-BJ技术中分子结形成原理示意图Figure1. The schematic structure of the forming principle of molecular junction in STM-BJ technique.
在分子体系拉伸过程的每一步几何结构计算中, 两电极的最外层金原子固定, 内层金原子及分子的坐标完全放开进行几何结构优化, 其中两电极最外层金原子之间的垂直距离定义为电极距离(D) (如图2(a)所示). 分子结的拉伸是在上一步优化好的几何结构基础上, 将电极的最外层金原子向外移动一小段距离后固定, 然后再次对其他金原子和分子进行几何结构优化. 这样通过逐步结构优化, 完成基于第一性原理计算的分子结绝热拉伸过程模拟. 体系结构优化基于杂化的密度泛函理论, 计算采用B3LYP杂化交换关联泛函, 选用LanL2DZ为基矢, 在Gaussian09程序包上进行[56].
图 2 分子体系在拉伸过程中的结构演化 (a)?(d) 吸附在基底电极表面金原子上的4, 4′-二吡啶分子结(体系I)的拉伸与结构演化过程; (e)?(g) 吸附在基底电极表面上的4, 4′-二吡啶分子结(体系II)的拉伸与结构演化过程; (h)?(k) 吸附在基底电极表面金原子上的4, 4′-二氨基联苯分子结(体系III)的拉伸与结构演化过程Figure2. Configuration evolutions in the stretching processes of molecular junctions: (a)?(d) Stretching and configuration evolution process of 4, 4′-bipyridine molecular junction, in which the 4, 4′-bipyridine molecule is adsorbed on the surface Au atom of substrate electrode (denoted as System I); (e)?(g) stretching and configuration evolution process of 4, 4′-bipyridine molecular junction, in which the 4, 4′-bipyridine molecule is adsorbed on the surface of substrate electrode (denoted as System II); (h)?(k) stretching and configuration evolution process of 4, 4′-diaminobiphenyl molecular junction, in which the 4, 4′-diaminobiphenyl molecule is adsorbed on the surface Au atom of substrate electrode (denoted as System III).
由于实验中测量体系电导所用的偏压为不超过0.3 V的较低偏压, 在这一偏压下, 体系的共振输运通道尚未开通, 因此体系的电导主要来源于电子的非共振输运贡献. 非共振输运的特点是电子以波动的形式由一电极进入分子后, 在分子所产生势场的散射与衍射作用下进入另一电极. 因此电流的计算采用笔者前期发展的基于分子非共振输运机制的一维透射结合三维修正近似(OTCTCA)方法[57], 即
3.1.4, 4′-二吡啶分子结与众不同的拉伸过程
利用STM-BJ技术构建分子结, 探针与基底接触时容易拉出孤立的表面金原子, 另外基底本身也会存在缺陷或者表面金原子. 计算表明吡啶环中的N原子极易吸附到基底表面的孤立金原子上, 因此计算中在基底平面电极上放置了一个孤立的表面金原子, 设计了探针电极尖端为三棱锥形、基底电极含有孤立表面金原子的4, 4′-二吡啶分子结(体系I, 如图2(a)—(d)所示). 同时为了比较, 计算中也设计了基底电极表面相对平整的没有表面金原子的4, 4′-二吡啶分子结(体系II, 如图2(e)—(g)所示). 另外, 为了与吡啶末端分子进行对比, 还计算了4, 4′-二氨基联苯分子结的拉伸过程, 其中基底电极采用了含有孤立表面金原子的结构模式(体系III, 图2(h)—(k)).图2(a)—(d)显示的是体系I的拉伸过程. 初始, 4, 4′-二吡啶分子末端的氮原子吸附在表面金原子上. 一般情况下, 探针探测到分子时, 分子在π电子的作用下斜靠在探针电极旁边(图2(a)). 随着探针电极逐渐抬高, 由于基底电极的表面金原子对分子具有较强的吸附作用, 分子的上端在探针表面逐渐向下滑移. 当电极距离大约为2.0 nm时, 分子上端的N原子开始吸附到探针尖端的第二层金原子上. 由于初始为侧面吸附, 氮原子和金原子的吸附强度很弱, 其吸附作用力仅为0.1 nN左右. 特别值得关注的是, 当电极距离拉伸到2.04 nm时, 分子上端的氮原子与第二层金原子之间的吸附作用迅速加强, 并对尖端的金原子产生明显的侧向推动作用, 把尖端的金原子向一侧推移约0.15 nm, 从而使分子末端正面吸附到第二层金原子上(如图2(b)所示). 目前根据对含各种常见末端的分子结进行第一性原理拉伸模拟计算发现, 这是含吡啶末端分子所特有的一种现象[6,8,30,37-39]. 继续将电极距离拉伸到2.24 nm, 4, 4′-二吡啶分子上端的氮原子从探针电极第二层金原子上断开, 迅速连接到探针顶端的金原子上(图2(c)), 这时顶端金原子也回到原来正常的晶格位置上. 可以发现, 4, 4′-二吡啶分子从吸附到探针电极第二层金原子到吸附到尖端金原子, 电极距离拉伸了约为0.21 nm, 这与实验测量结果完全一致[52-54]. 而当电极距离拉伸到2.47 nm, 4, 4′-二吡啶分子从探针电极尖端的金原子上断下来(图2(d)).
图3给出了分子体系拉伸过程中能量、作用力以及电导随电极距离的变化曲线, 其中正作用力表示分子与电极间为吸引作用, 负作用力表示分子与电极间为挤压作用. 图3(a)显示, 当体系I中4, 4′-二吡啶分子上端的N原子刚吸附到第二层金原子时, 体系仍处于高能量状态, 特别是当分子上端刚从侧面吸附变为正面吸附时, 分子与电极间存在着较强的约为0.85 nN的挤压作用. 尽管分子与电极间有较强的挤压作用, 但是分子正面吸附到第二层金原子上具有更低的能量. 从图中可以看出, 在2.04 nm附近分子从侧面吸附到第二层金原子上转变为正面吸附到第二层金原子上(即从图2(a)构型转变为图2(b)构型)的过程中, 体系能量明显降低了大约0.1 eV. 另外, 从体系几何结构的优化过程中发现, 电极距离为2.04 nm时, 探针尖端的金原子受到持续的背向氮原子的作用力, 在尖端金原子侧向移动的0.15 nm距离内, 其中大约0.1 nm的距离受力接近或超过0.1 nN. 因此在分子结拉伸过程中, 分子可以自动地由侧面吸附转变为正面吸附. 分子正面吸附到第二层金原子上的最低能量状态发生在2.11 nm的电极距离下. 当电极距离处于2.04—2.11 nm之间时, 分子与电极间一直保持为相互挤压作用, 在这一过程中, 体系能量降低约0.2 eV. 而电极距离在2.11—2.23 nm之间变化时, 分子与第二层金原子之间则表现为相互吸引作用, 因此在这一范围内增大电极距离需要对电极施加一定的拉力作用, 而体系能量在这一过程中也因拉力主动做功提高了约0.5 eV. 当电极距离为2.23—2.24 nm时, 拉力达到约1.2 nN, 这时拉力达到分子与第二层金原子相互作用的极限, 分子上端从第二层金原子上断开并迅速连接到尖端金原子上, 同时体系能量迅速降低大约0.4 eV. 当分子刚刚连接到尖端金原子上时, 分子与电极间表现出约0.8 nN的挤压作用. 而当电极距离为2.35 nm时, 体系I达到分子与尖端金原子相连接的最低能量状态, 与分子连接到第二层金原子上的稳定状态相比, 体系能量降低了约0.25 eV. 分子与尖端金原子之间能够承受的最大拉力是0.8 nN, 对应电极距离是2.43 nm. 可以发现, 4, 4′-二吡啶分子与探针电极第二层金原子正面连接能够承受的最大拉力明显高于其与尖端金原子相连接能够承受的拉力. 这不仅与实验观察到的高电导状态的断裂力明显高于低电导状态的断裂力一致, 而且与实验测量到的断裂力的数值也完全符合[54]. 目前技术上还无法观察到分子结拉伸过程中分子与电极界面结构的具体变化细节, 因此基于第一性原理的绝热拉伸计算方法不仅可以模拟分子结的拉伸过程、而且是理解并识别分子结界面特殊物理过程和分子体系特殊物理现象的非常有效的手段.
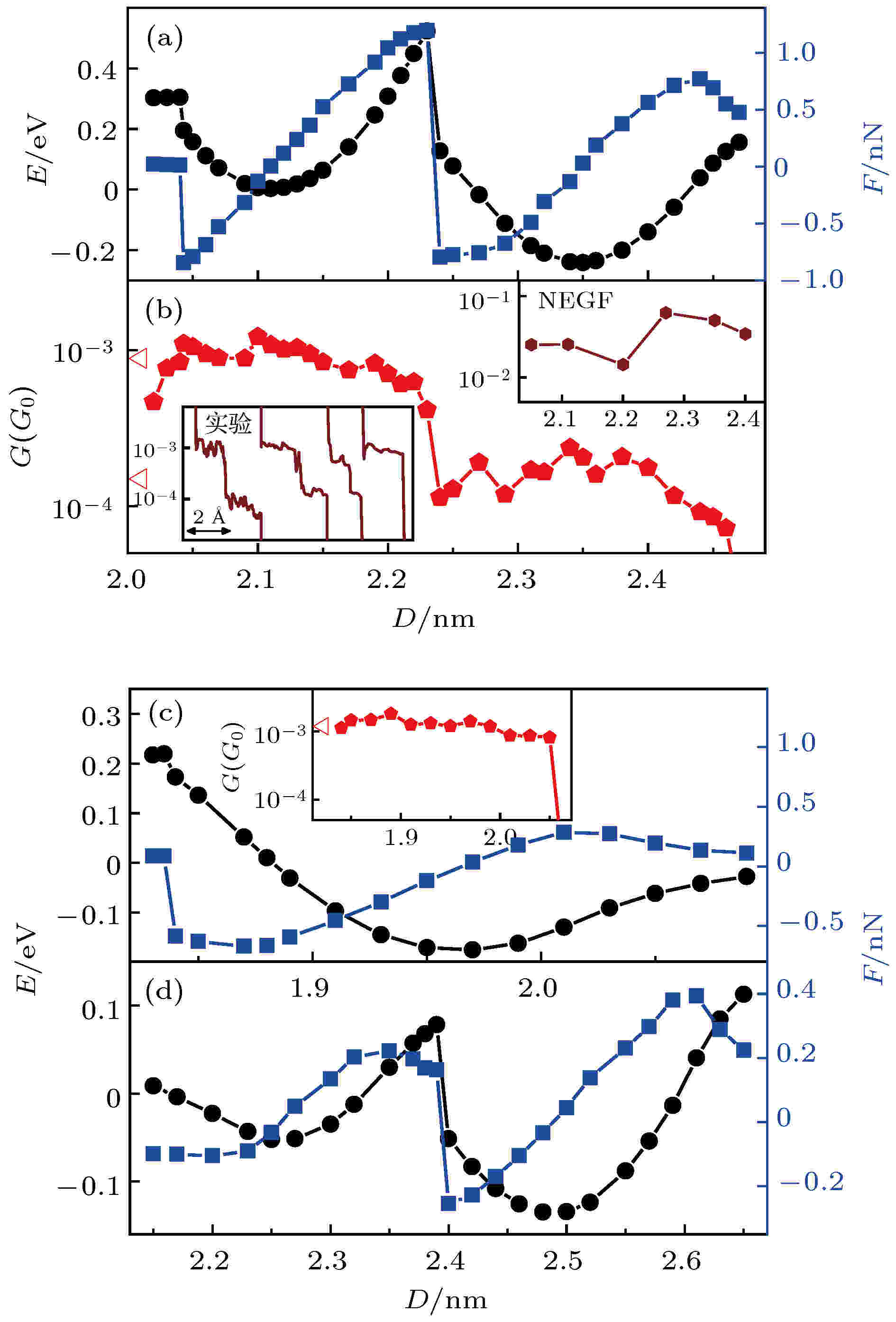图 3 分子体系拉伸过程中的能量、作用力和电导变化曲线 (a) 体系I拉伸过程中的能量、作用力随电极距离的变化曲线及其(b) 电导变化曲线, 其中左下插图为文献[53]中实验测量结果, 右上插图为非平衡格林函数(NEGF)方法计算结果; (c) 体系II 和 (d) 体系III的能量、作用力随电极距离的变化曲线, (c)中插图为体系II拉伸过程中电导变化曲线Figure3. Energy, force, and conductance traces of the molecular junctions in the stretching processes: (a) Energy, force and (b) conductance traces as functions of electrode distances for the stretching process of system I. The bottom-left inset in (b) is the experimental conductance traces that are reported in Ref. [53], and the top-right inset in (b) is the results calculated by applying NEGF method. (c) Energy and force traces as functions of electrode distances for the stretching process of system II and (d) system III. The inset in (c) is the conductance traces of system II.
为了进一步证明在分子结拉伸过程中, 4, 4′-二吡啶分子能够从侧面吸附自动转换成正面吸附到探针电极的第二层金原子上, 同时说明表面金原子在分子结拉伸过程中的作用, 进一步计算了基底电极无表面金原子的分子体系II的拉伸过程. 图2(e)—(f)显示在体系II的拉伸过程中, 当电极距离拉伸到1.84 nm时, 分子上端同样由侧面吸附变为正面吸附到探针电极的第二层金原子上, 而且探针尖端的金原子由于分子的侧向推动作用移到了一侧. 与体系I的拉伸过程不同的是, 当继续增大电极距离时, 分子没有从探针电极第二层金原子上移动到尖端金原子, 而是整个分子在第二层金原子的牵引下向上移动, 并将分子下端拉离基底电极. 由此可见, 基底电极上的表面金原子不仅能够将分子由探针电极第二层金原子上拉到尖端金原子上, 而且在整个分子结拉伸过程中保持分子不离开基底电极具有至关重要的作用. 这一点可以从分子结不同拉伸过程中作用力的差别上很明显的表现出来. 由图3(c)可以发现, 对于体系II, 当电极距离拉到2.1—2.3 nm, 分子逐渐被拉离基底表面时, 所需的最大拉力只有约0.3 nN, 明显小于体系I中将分子由探针电极第二层金原子拉到尖端金原子上的1.2 nN作用力. 由此可见4, 4′-二吡啶分子与平面金电极的吸附最大只能承受约0.3 nN的拉力作用, 而如果4, 4′-二吡啶分子吸附到表面金原子, 则能够承受大于1.2 nN的拉力作用. 所以表面金原子对于4, 4′-二吡啶分子具有很强的固定作用.
根据已计算的各种末端基团单分子结的拉伸过程发现, 只有含吡啶末端的分子在吸附到锥型电极第二层金原子上时才能自动由侧面吸附转换成正面吸附, 并同时产生较强的对尖端金原子的侧向推动作用. 图2(h)—(k)是 4, 4′-二氨基联苯分子结的拉伸过程, 从图中可以很明显地看出, 在分子结拉伸过程中, 上面的氨基可以很平稳地由探针电极第二层金原子滑移到尖端金原子上. 氨基末端分子结的拉伸过程及相应的电输运特性, 在文献[6]中已做过系统的报道.
2
3.2.破解4, 4′-二吡啶分子结拉伸过程中的高低电导转换之谜
特别值得关注的是4, 4′-二吡啶分子结拉伸过程中独特的高低电导转换现象. 图3(b)是基于OTCTCA方法计算得到的体系I在拉伸过程中电导随电极距离的变化曲线. 从图中可以看出, 4, 4′-二吡啶分子结在拉伸过程中表现出明显的双电导平台现象. 其中2.02—2.22 nm之间的高电导平台对应于4, 4′-二吡啶分子正面吸附于探针电极第二层金原子上, 而2.23—2.45 nm之间的低电导平台对应于4, 4′-二吡啶分子吸附在探针电极的尖端金原子上. 高电导与低电导之间相差约5—8倍, 这一差别与文献报道的实验测量结果完全一致[50,53,54]. 另外, 从文献[53]报道的实验测量结果发现, 分子结拉伸过程中还存在只有高电导平台、没有低电导平台的电导曲线(图3(b)插图)[53], 这与OTCTCA方法计算得到的体系II拉伸过程的电导变化曲线是一致的(图3(c)插图). 对于体系II, 由于基底电极上没有表面金原子, 当分子正面吸附到第二层金原子上后, 继续增大电极距离, 分子直接被拉离基底表面, 从而导致低电导平台缺失. 比较体系I和体系II的拉伸过程和电导变化情况可以发现, 有两个关键因素导致了4, 4′-二吡啶分子结在拉伸过程中出现高低电导转换现象: 1)分子的吡啶末端具有较强的趋向于正面吸附到探针电极第二层金原子上的独特性质, 并且由此产生对尖端金原子的侧向推动力; 2)基底电极表面金原子对分子的吡啶基末端具有更强的吸附作用, 可以将分子由探针电极第二层金原子拉至尖端金原子上. 根据以上分析, 若4, 4′-二吡啶分子结在拉伸过程中出现高低电导转换现象, 则可以判断出基底电极一定存在表面金原子, 且分子末端一定吸附在表面金原子上. 这表明, 利用单分子结拉伸过程中测量到的电导曲线, 可以有效识别电极尖端构型以及分子与电极间的连接方式.至于分子的两种吸附状态为什么会产生差别很大的高低电导, 可以从OTCTCA方法中得到非常好的解释[57]. 在OTCTCA理论框架中, 电子在外加偏压作用下由一端电极进入分子, 由于存在波动性, 电子受到分子所在空间势场的散射后, 注入另一端电极, 从而形成电流. 从三维角度来说, 分子中的每一个原子都是电子波的一个散射中心, 由于原子核附近的势场对于电子来说相当于势阱, 因此可以看作电子波的小孔. 所以电子波经过每一个原子时同时发生散射和衍射, 导致的结果是电子只有一部分能够通过原子, 而另一部分将返回源电极. 另外, 由于在电子传播路径上电势是起伏变化的, 即传播路径上既有势垒也有势阱, 因此根据量子力学一维势垒/势阱的透射与反射理论, 电子波在传播路径上既有透射又有反射. 综上可见, 电子在传输过程中遇到原子时, 三维效应导致电子在传播过程中出现散射和衍射, 而一维效应导致电子在传输路径上发生一定概率的反射. 在OTCTCA方法中计算电子透过率时分别从一维和三维角度考虑了分子中各原子对电子的反射、散射和衍射效应, 有效解决了低偏压下的电子输运问题[57].
基于OTCTCA方法可以发现, 与分子吸附到探针电极第二层金原子上相比, 4, 4′-二吡啶分子吸附到尖端金原子上时, 尖端金原子增加了对电子的散射、衍射与反射, 导致电子的透射概率降低, 从而产生了低电导. 根据计算经验, 电子在输运路径上每经过一个原子, 透射概率将降低大约3/4, 即只有大约1/4的电子波可以继续向前传播. 另外分子与电极的耦合强度会影响界面电势分布, 并在一定程度上影响透射概率. 这里需要指出的是, 在OTCTCA理论中没有考虑扩展分子轨道进入偏压窗而产生的共振透射的贡献. 由于实验是在低偏压下测量的, 所有轨道均未开通, 即共振透射可以忽略, 因此本工作发展的OTCTCA方法不仅能给出与实验符合很好的结果, 而且给出了容易理解的物理图像. 对4, 4′-二吡啶分子结的高低电导现象, 同时采用NEGF方法进行了计算, 计算基于密度泛函理论, 采用广义梯度近似(GGA)下的PBE (Perdew-Burke-Ernzerhof)泛函、截止能(mesh cut-off energy)为200 Ry, k点取样为(5, 5, 100), 总能量收敛标准为
2
3.3.影响体系高低电导差异的其他因素
除了探针电极尖端金原子的散射、衍射和反射作用影响体系高低电导的差异外, 分子与电极之间轨道耦合程度的不同也在一定程度上加大了体系高低电导之间的差异. 这一点可以从扩展分子轨道的多少上很直观地发现体系高低电导状态之间的差异. 图4给出了同时扩展到探针电极和分子上的所有分子轨道的空间分布图. 从图中可以看出, 当分子正面连接到第二层金原子上时, 有16条分子轨道同时扩展到探针电极和分子上(图4体系I (b)所示轨道); 而当分子移动到电极尖端金原子上时, 只有8条分子轨道同时扩展到探针电极和分子上(图4体系I (c)所示轨道). 扩展分子轨道数目的差异表明, 当分子正面吸附到第二层金原子时, 分子与电极间具有更好的耦合作用. 因此尽管低偏压下这些轨道离偏压窗很远, 但分子与电极间较强的轨道耦合仍然可以有效提高电子在分子与电极间非共振转移的概率. 这是因为这些轨道可以通过影响分子与电极界面处电势的空间分布来影响电子的输运性质.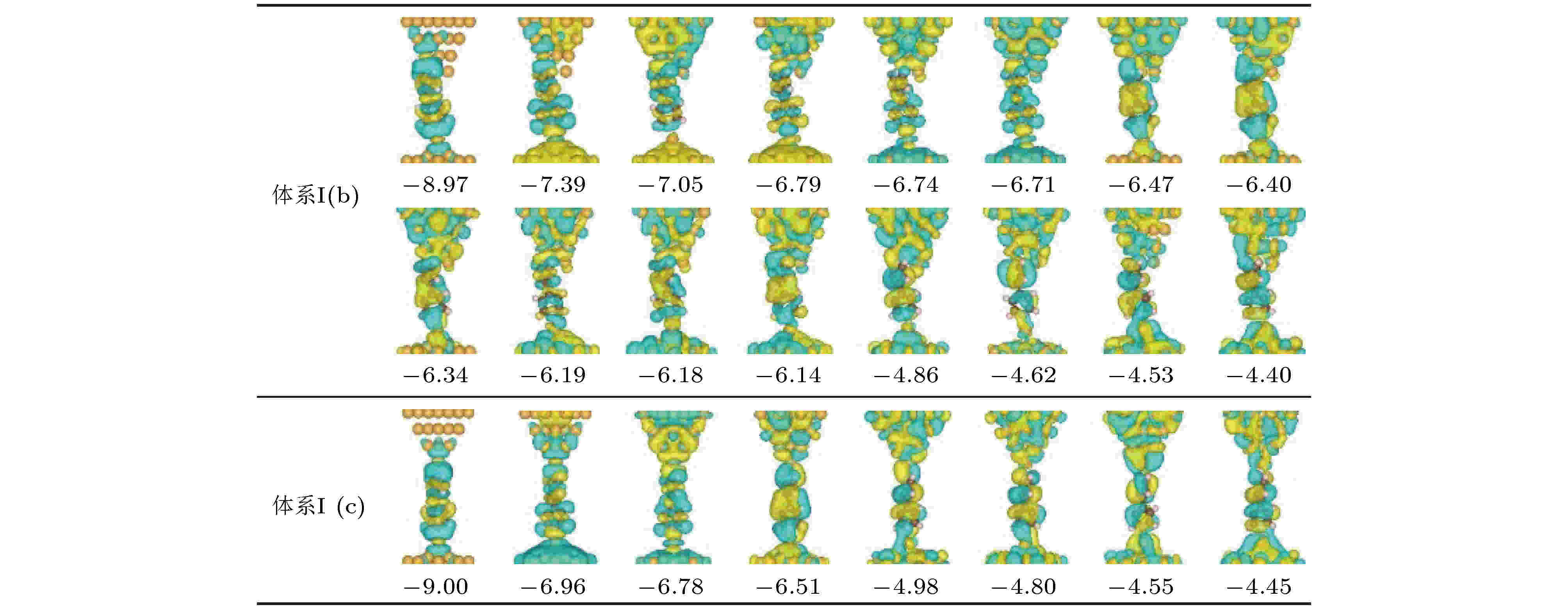
图 4 图2体系I (b)和体系I (c)中同时扩展到分子与探针电极上的所有占据分子轨道空间分布图, 图中数字为各轨道相对于费米能级的能量(单位: eV)Figure4. Spatial distributions of occupied molecular orbitals of System I (b) and System I (c) in Fig. 2 that are delocalized on the molecule and probe electrode simultaneously. The numbers in the figures are the orbital energy relative to the Fermi level (the unit is eV)
图5对分子吸附到探针电极第二层金原子上和分子吸附到探针电极尖端金原子上体系所在空间的电势分布进行了比较, 图中的蓝色虚线框内是分子与探针电极连接区域的势阱通道. 从图中可以看出分子连接到第二层金原子上后, 由于分子与电极的耦合增强, 电子在电极与分子之间转移的势阱通道(黑色实线内侧区域)明显比分子连接到电极尖端金原子上的势阱通道宽. 根据量子力学理论和OTCTCA计算, 电子在势垒中是以衰减波的形式传输, 即电子的透射概率随着势垒在输运方向长度的增大而迅速衰减; 而电子在势阱中则是以平面波或者球面波的形式传播, 传播过程中会因势阱的起伏发生一定的反射, 但不会因势阱在输运方向长度的增大而衰减. 因此在低偏压没有共振输运通道开通的情况下, 电子通过势阱通道的非共振传输便成为体系电流的主要来源. 因此与分子连接到探针电极的尖端金原子上相比, 分子连接到探针第二层金原子上拓宽了电子在分子与电极间转移的势阱通道, 所以必然提高电子在分子与电极间的转移概率和体系的导电能力. 另外从体系结构上还可以发现, 4, 4′-二吡啶分子正面连接到第二层金原子后, 有4个金原子与分子近邻, 且电极距离更短, 而分子连接到尖端金原子上时, 与分子近邻的金原子只有1个, 这也在一定程度上影响着电子的透射概率.
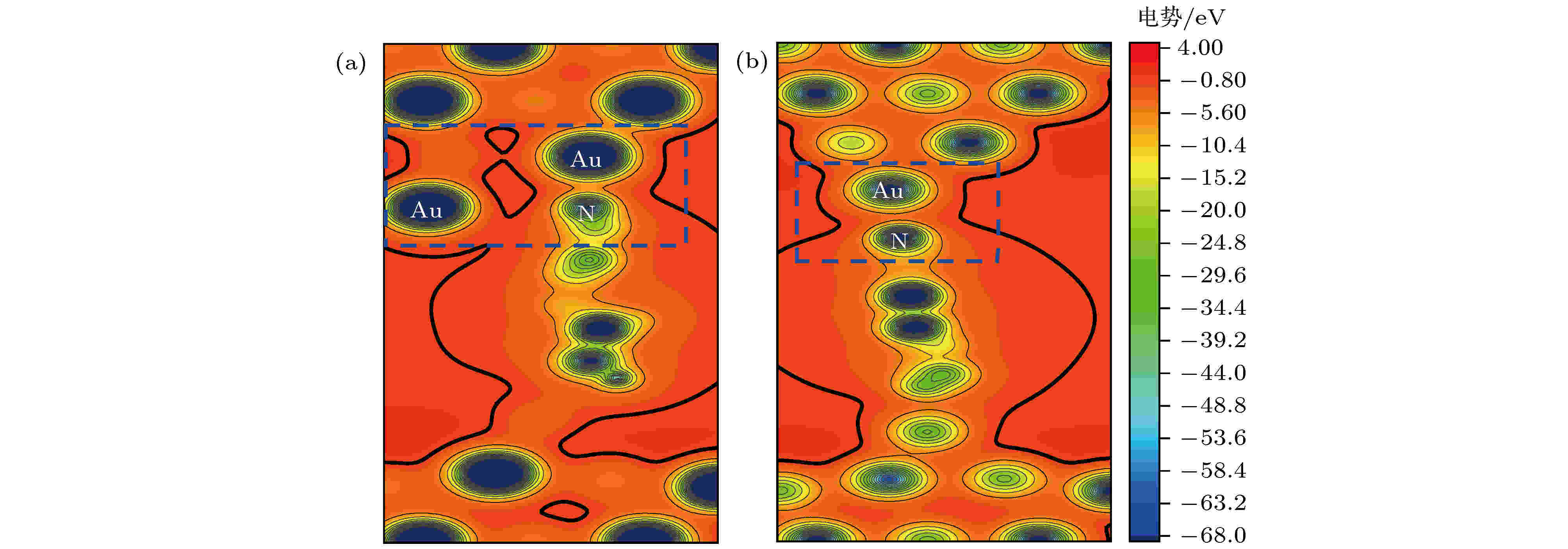图 5 (a) 分子吸附到探针电极第二层金原子上(图2中体系I (b))和 (b) 分子吸附到探针电极尖端金原子上(图2中体系I (c))体系所在的空间的电势分布图Figure5. (a) Spatial distributions of potential of the system that the molecule adsorbs on the second gold layer of prob electrode (system I (b) in Fig. 2) and (b) the system that the molecule adsorbs on the top gold of prob electrode (system I (c) in Fig. 2).
