摘要:相比于传统基于毛细管或针孔的 X 射线成像系统, 编码孔径成像系统具有结构简单、灵敏度高、扩展性强等优势，使其在 X 射线荧光成像中极具潜力. 本工作应用新型编码孔径成像计算模型, 设计了一种基于可分离编码的X射线成像系统. 利用Geant4蒙特卡罗仿真对系统的性能进行了研究, 并根据快速迭代收缩阈值算法进行了图像重建. 模拟及分析结果显示, 近场成像时, 与传统基于卷积模型的成像系统不同, 该系统的性能不受准直效应的影响. 成像系统的空间分辨率约为65 μm, 并能够准确地重建出不同能量的线源和形状复杂物体的图像. 重建图像的质量受校准时所用X射线能量和物体发射X射线能量的影响, 两者差异越小, 重建图像的质量越高. 三维重建结果显示, 系统能够从单次获取的二维投影图像, 正确地重建出物体与系统的距离, 轴向空间分辨率约为1.1 mm.
关键词: 编码孔径/
X射线荧光成像/
蒙特卡洛模拟/
图像重建

English Abstract

全文HTML

--> --> -->

基于X射线的分析技术是非常重要的材料表征方法, 它们被广泛用于元素空间分布、化学状态和质构特性等的测量^[1]. 其中, X射线荧光(XRF)技术因其具有对多元素样品进行无损分析的能力在许多科学领域和工业应用中得到了迅速发展^[1-4]. 在很多情况下, 获得高质量的X射线图像非常困难^[5]. 因此, 如何提高图像质量一直是相关****研究的热点^[6]. 类似于可见光成像, X射线图像的质量在很大程度上取决于所采用的光学系统. 但是不同于可见光, X射线穿透性强且折射率近似为1, 对其进行反射、折射或聚焦都非常困难; 用于X射线成像的光学器件, 如反射镜或透镜等, 必须满足非常严格的要求, 而且造价非常昂贵^[7].
最简单的实现X射线成像的方法是利用小孔成像原理, 设计基于单孔准直器的针孔成像系统. 针孔的直径越小, 成像系统的空间分辨率越好; 但直径越小, 系统的光收集效率越低, 图像的信噪比(SNR)也越差. 为了解决上述问题, Dicke^[8]和Ables^[9]分别独立提出了采用多开孔的准直器(编码孔径)取代单一开孔的准直器; 编码孔径技术使系统在保留小孔径对应的高空间分辨率的同时, 大幅提高系统的光收集效率(正比于开孔个数), 从而提高图像信噪比. 编码孔径技术提出之后得到了极大的发展, 并广泛用于X射线和γ射线成像, 包括天文观测、医学成像和辐射防护等^[10-12].
传统上, X射线荧光成像采用基于全反射原理制成的多毛细管作为光学聚焦器件, 但是此类系统能够收集的X射线的角度范围过小. 为提高系统的数值孔径, Haboub等^[13]探索将编码孔径技术用于X射线荧光成像, 获得了几种标准样品的实验图像, 初步验证了该技术的可行性. Kulow等^[14]进一步研究了近场成像时的图像重建算法, 并通过实验证明了采用编码孔径技术可以大幅提高采集到的光子通量, 降低成像时间. 另外, 相比于小孔或多毛细管方案, 编码孔径技术的一个很重要的优势是扩展性更强, 系统可以在不牺牲分辨率的前提下, 通过增加编码准直器的编码数和面积, 增大成像视野范围.
目前, 编码孔径技术应用于X射线荧光成像已显示出良好应用前景, 但仍存在采用传统的卷积成像模型时, 近场成像伪影大、图像分辨率较低等不足. 近年来, 得益于计算机视觉算法的进步, 编码孔径成像技术在光学成像领域取得了一些值得关注的进展. DeWeert^[15]和Asif^[16]分别提出采用可分离编码矩阵的编码孔径成像模型, 可以极大地降低计算的复杂度, 从而实现高编码数下的高分辨成像. 基于上述工作, Adams和Boominathan进一步提出了Texas Two-Step(T2S)模型^[17], 获得了高帧频、分辨率达微米级的近场可见光图像. T2S模型已被证明可用于近场高分辨γ射线成像^[18]. 本研究基于可分离编码的T2S模型, 进一步对编码孔径技术应用于X射线荧光成像进行详细的理论分析和模拟计算, 期望为将来的实验研究和实际应用提供参考依据和分析数据.

编码孔径成像系统通常由编码准直器和位置灵敏探测器组成, 两者相互平行. 编码准直器为多开孔结构, 其上的开孔是按照某种规则排列, 开孔部分允许射线通过而非开孔部分阻挡射线. 如图1所示, 编码孔径成像过程可以分为两部分: 编码投影和图像重建. 编码过程即物体发射的射线经过准直器在探测器平面进行投影, 对于准直器上的每一个开孔, 其均会在探测器平面上产生一个一定比例的物体的倒立投影; 编码孔径的多开孔, 使探测器平面上记录的是若干倒立投影的退化叠加像. 图像重建即计算机对探测器输出的原始投影图像进行图像解码, 以获得物体的重建图像.
图 1 编码孔径成像示意图
Figure1. Schematics diagram of coded aperture imaging

假设物体X, 探测器测量的投影图像Y均为M × N的二维矩阵. 对于任意的编码准直器, 编码孔径成像可以用广义线性模型表示为

${{y}} = {{\varPhi}} {{x}} + e, $

其中, x和y为分别将X和Y的列连接并矢量化后的一维向量(长度为MN); ${{\varPhi}} $为传递矩阵(大小为MN × MN), 表示物体和投影图像之间的线性关系; e是测量噪声. 对于任意给定的编码准直器和探测器, 可以通过模拟射线从物体传输到探测器或通过校准过程来获得不同几何条件下的传递矩阵. 但当成像系统分辨率或编码数较高时, 传递矩阵${{\varPhi}} $将非常大, 很难通过估算或校准计算得到${{\varPhi}} $, 同时, 进行图像重建时的反问题求解也非常困难. 比如, 当物体图像和探测器的分辨率均为300 × 300时, 传递矩阵${{\varPhi}} $将包含(9 × 10⁴) × (9 × 10⁴) = 8.1 × 10⁹个元素.
为减少从物体到测量投影的线性映射的复杂性, 一般将编码矩阵设计为可分离的, 即二维编码准直器的图样由两个一维序列的外积构造而来^[16,17]. 此时, 可以将式(1)中的成像模型重写为

${{Y}} = {{PX}}{{{Q}}^{\rm{T}}} + E, $

其中, P和Q分别为表示物体行和列的一维卷积的矩阵; E是测量噪声和模型失配. 当物体图像和探测器的分辨率均为300 × 300时, P和Q各只有9 × 10⁴个元素, 而${{\varPhi}} $中有8.1 × 10⁹个元素.
在T2 S模型中, 考虑到近场效应的影响, 探测器投影被进一步分解为两个可分离函数的叠加^[17]. 对于一个二维的物体X_d, 设其距离成像系统的距离为d, 探测器的测量投影满足

${{Y}} = {{{P}}_{od}}{{{X}}_d}{{Q}}_{od}^{\rm{T}} + {{{P}}_{cd}}{{{X}}_d}{{Q}}_{cd}^{\rm{T}}, $

其中, ${{{P}}_{od}}$和${{Q}}_{od}^{}$为无准直器时探测器响应的传递矩阵; ${{{P}}_{cd}}$和${{Q}}_{cd}^{}$为准直器编码对应的传递矩阵(下标“o”代表开孔, “c”代表编码, “d ”代表不同距离d ).
对于三维物体X_D, 可以将其离散为D个距离成像系统d的二维物体X_d, 则测量投影满足

${{Y}} = \sum\limits_{d = 1}^D {{{{P}}_o}_d{{{X}}_d}{{Q}}_{od}^{\rm{T}} + {{{P}}_{cd}}{{{X}}_d}{{Q}}_{cd}^{\rm{T}}}, $

其中, {P_od, Q_od, P_cd, Q_cd}^{{d = 1, 2…D}}是D个距离为d时的传递矩阵. 上述传递矩阵取决于距离d, 可以通过在不同距离校准给定系统来获得.
为了减小各种噪声源项对重建图像的影响, 同时避免过拟合, 可以通过求解正则化的总体最小二乘问题来进行图像重建. 采用FISTA(快速迭代阈值收缩算法)^[19]求解Lasso问题对应方程, 可以得到重建的物体图像${\widehat {{X}}_D}$:

$\begin{split}{\widehat {{X}}_D} \!= & \arg \mathop {\min }\limits_{{{{X}}_D}} \!\left\|\! {\left(\!\sum\limits_{d = 1}^D {{{{P}}_{od}}{{{X}}_d}{{Q}}_{od}^{\rm{T}} \!+\! {{{P}}_{cd}}{{{X}}_d}{{Q}}_{cd}^{\rm{T}}}\! \right) \!-\! {{Y}}} \right\|_2^2 \\ & + {\lambda _1}{\left\| {{{{X}}_D}} \right\|_1}.\\[-10pt]\end{split}$

2

-->

3.1.成像系统参数设计

本工作基于Geant4软件包^[20], 选用QGSP_BIC物理模型, 通过设计基于可分离编码准直器的X射线成像模拟程序, 验证T2S模型用于高分辨X射线成像的有效性. 编码准直器采用修正均匀冗余阵列(modified uniformly redundant arrays, MURA), 选择高编码数(N = 463)以使成像系统具有较高的分辨率. 如图2所示, 选取原编码排布中心区域的90 × 90个像素设计编码准直器, 黑色部分为重金属(铂), 白色部分为开孔, 单位像素尺寸为25 μm × 25 μm. 编码准直器的厚度应能够阻挡大部分垂直入射的X射线, 考虑到准直效应可能影响重建图像的质量, 准直器厚度设为25—200 μm. 参考目前pnCCD所用探测器^[2], 本工作模拟的探测器材料设置为硅, 灵敏体积为2 mm × 2 mm × 0.5 mm, 单位像素尺寸为25 μm × 25 μm, 总像素数为80 × 80. 探测器与编码准直器的距离设置为固定值2 mm. 模拟程序记录入射X射线在探测器上的沉积能量及对应像素编号生成不同情况对应的投影图像.
图 2 模拟选用的可编码准直器图样
Figure2. The mask pattern used in the simulation.

2 -->

3.2.模型校准

对于给定的成像系统, 成像模型中的传递矩阵可以通过建立射线经准直器到探测器的模型求解或经过校准来得到. 本工作通过模拟校准过程, 计算所需的所有传递矩阵. 当物体与系统之间距离固定为任一d时, 若物体平面仅第i行对应的像素分布着放射源, 即物体图像可表示为${{{X}}_i} = {{{e}}_i}{1^{\rm{T}}}$. 此时探测器测量到的投影图像为

${{{Y}}_i} = {{{P}}_o}{{{e}}_i}{({{Q}}_{\rm{o}}^{}1)^{\rm{T}}} + {{{P}}_{\rm{c}}}{{{e}}_i}{({{{Q}}_c}1)^{\rm{T}}} = {p_{{\rm{o}}i}}q_{\rm{o}}^{\rm{T}} + {p_{{\rm{c}}i}}q_{\rm{c}}^{\rm{T}}, $

其中, ${p_{{\rm{o}}i}}$和${p_{{\rm{c}}i}}$分别为${{{P}}_{\rm{o}}}$和${{{P}}_{\rm{c}}}$的第i列; $q_{\rm{o}}^{}$和$q_{\rm{c}}^{}$分别为${{Q}}_{\rm{o}}^{}$和${{{Q}}_{\rm{c}}}$的列的和. 由于${p_{{\rm{o}}i}}$和${p_{{\rm{c}}i}}$是正交的, 因此可以进行截断奇异值分解(truncated singular value decomposition, TSVD)投影${{{Y}}_i}$, 仅保留最大的两个奇异值, 分别赋值给${p_{{\rm{o}}i}}$和${p_{{\rm{c}}i}}$. 通过逐行扫描物体平面的每一行, 可以计算出${{{P}}_{\rm{o}}}$和${{{P}}_{\rm{c}}}$的所有元素. 类似地, 再通过逐列扫描物体平面的所有列, 可以计算出${{Q}}_{\rm{o}}^{}$和${{{Q}}_{\rm{c}}}$的所有元素. 通过改变物体与系统之间距离d, 重复上述扫描过程, 可以获得不同d对应的传递矩阵.
对于上述成像系统, 采用长度为2 mm, 宽度为0.001 mm的线状X射线源模拟校准过程. 参考相关研究工作^[13,14], 本文研究的荧光X射线能量范围设置为5—20 keV, 因此计算了线源能量为6、8、10和16 keV时对应的传递矩阵. 如果系统的参数保持不变, 只需执行一次校准过程, 对应的传递矩阵可重复使用.
2 -->

3.3.重建图像评价

本工作主要采用2个二维平面物体测试系统的成像能力. 一是长度为0.4 mm, 宽度为0.001 mm的线源; 二是形状为“180”的物体, 考察系统对复杂物体的成像能力. 两个物体均设置在平行于成像系统, 且距离为10 mm的平面上.
为了比较不同条件下的重建图像, 选用均方根误差(root mean square error, RMSE)和通用图像质量指标(universal quality index, UQI)2个指标定量评价图像质量. RMSE的定义为:

${\rm{RMSE}} = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^N {{{[P(i) - {P^{'}}(i)]}^2}} }}{N}} $

其中, P(i)为原始物体图像的像素值; P^’(i)为重建图像的像素值; N是图像总的像素数. RMSE值越大, 表明重建图像与原始图像的差异越大.
UQI的定义为^[21]:

${\rm{UQI}} = \dfrac{{2{\rm{cov}} (\bar x,\bar y)}}{{\sigma _{\bar x}^2 + \sigma _{\bar y}^2}} \cdot \dfrac{{2\bar x \cdot \bar y}}{{{{(\bar x)}^2} + {{(\bar y)}^2}}}$

其中, cov是协方差函数; $\bar x$和$\bar y$分别是原始图像和重建图像的均值; $\sigma _{\bar x}^2$和$\sigma _{\bar y}^2$分别是原始图像和重建图像的方差. UQI的动态范围为[0, 1], UQI的值越接近1, 表明重建图像与原始图像越相似.

2

-->

4.1.准直器厚度的影响

采用传统的卷积成像模型进行近场成像时, 由于编码准直器厚度引起的准直效应会使重建图像质量严重下降^[14]. 因此, 本节研究采用T2S模型时, 准直器厚度对重建图像的影响. 将X射线能量设置为10 keV, 编码准直器的厚度设置为25、50、100和200 μm等4个厚度. 图3(a)所示为0.4 mm线源的重建图像, 由于系统的空间分辨率有限, 重建图像在横纵向均有一定程度的模糊. 虽然线源沿横向均匀分布, 但其重建图像沿横向并不是均匀分布, 且与准直器厚度无关(图3b). 准直器的厚度从25 μm增加到200 μm, 系统沿纵向的分辨率并无明显变化(图3c). 通过进一步模拟点源(10 keV)成像, 计算得到准直器的厚度为25、50、100和200 μm时, 系统的空间分辨率(半高全宽, FWHM)分别为66.5、65.8、64.9和64.2 μm. 可以看出, 随着准直器厚度的增加, 空间分辨率缓慢减小. 作为对比, Haboub等人基于20 μm准直器研制的成像系统的空间分辨率约为72 μm^[13]. 因此, 相比于传统的卷积模型, 采用T2 S模型时分辨率略优.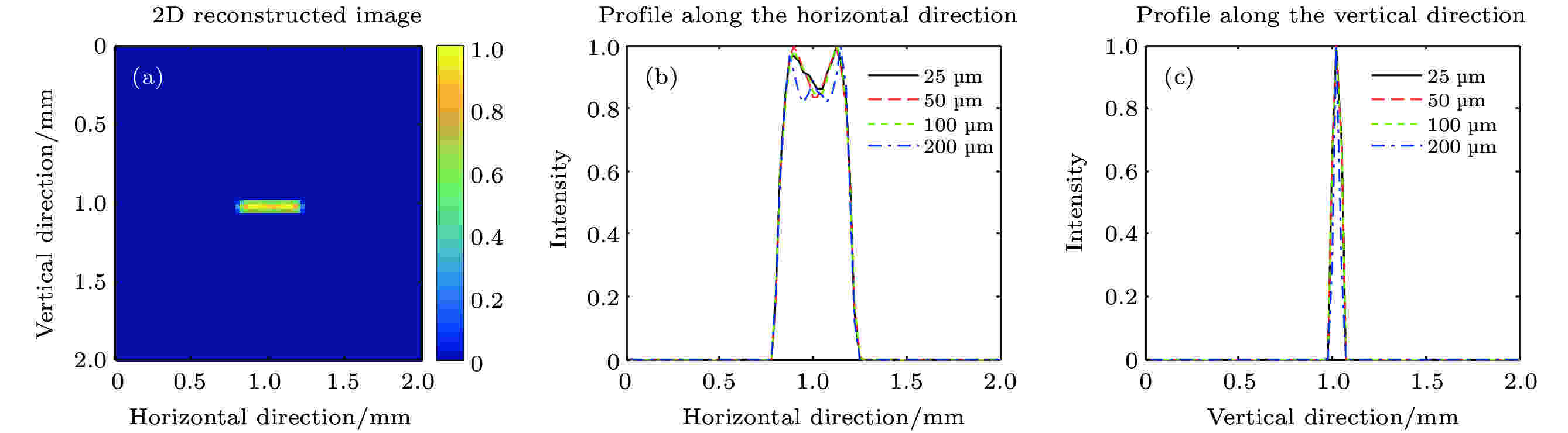
图 3 线源二维重建图像及其沿横纵向分布　(a)准直器厚度25微米时的线源重建图像; (b)不同准直器厚度时的横向分布; (c)不同准直器厚度时的纵向分布
Figure3. 2 d reconstructed image of the line source and its horizontal and vertical distribution: (a) Reconstructed image of the line source when the mask thickness was 25 micron; (b) horizontal distribution for different mask thickness; (c) vertical distribution for different mask thickness.

对于形状复杂的成像物体, 采用T2S模型时, 重建图像比较准确地还原了物体的原始分布情况(图4b). 而采用传统的卷积模型近场成像时, 重建图像通常存在较强的伪影^[13,14]. 当准直器厚度从25 μm增加到200 μm, 重建图像无明显变化. 在后两节的模拟中, 准直器的厚度设置为固定值25 μm.
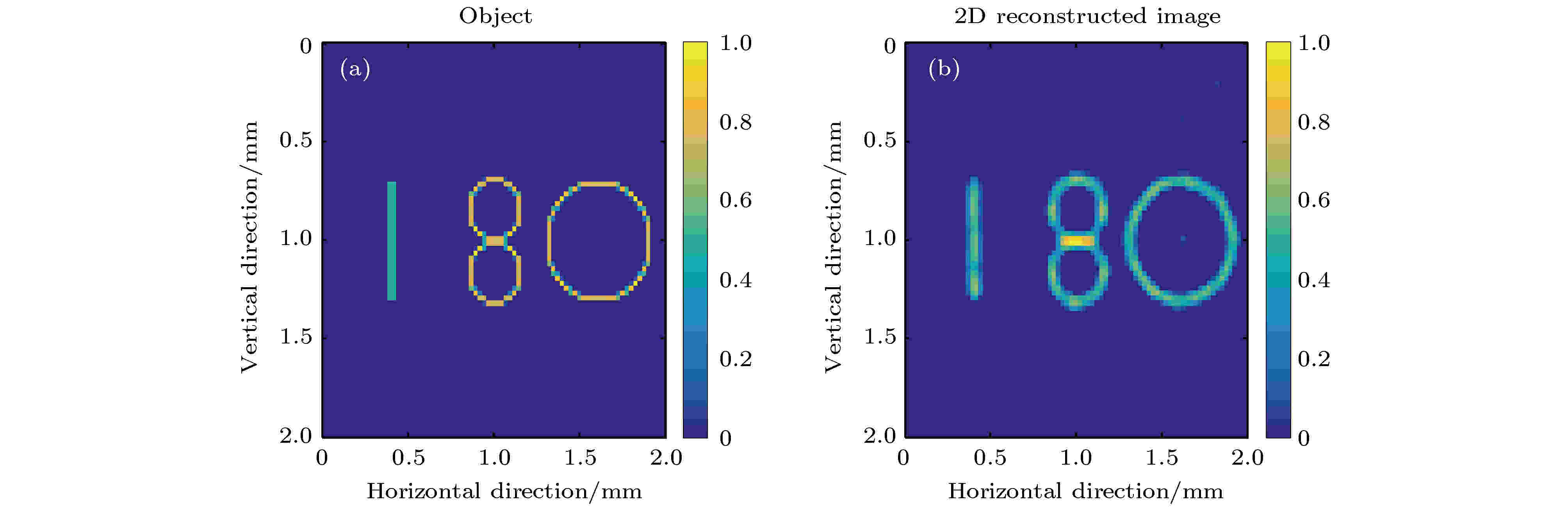图 4 物体的原始图像及重建图像　(a)原始图像; (b)准直器厚度25微米时的重建图像
Figure4. Original image and reconstructed image of the object: (a) Original image; (b) reconstructed image when the mask thickness was 25 micron.

2 -->

4.2.X射线能量的影响

X射线的能量越高, 穿透能力越强, 散射也越严重; 物体发射的X射线能量不同时, 产生的投影图像不同. 同样, 校准时采用的X射线能量不同, 计算得到的传递矩阵也不同. 因此, 本节研究物体发射的X射线能量和校准时采用的X射线能量对成像结果的影响.
如图5所示, 当校准能量为10 keV时, 物体发射的X射线能量为6和8 keV对应的重建图像质量较好; 而当物体能量增大为16 keV时, 重建图像的质量明显变差. 如图6所示, 当校准能量为16 keV时, 物体能量为16 keV对应的重建图像的质量较好, 而物体能量为6和8 keV时, 重建图像均有一定程度的畸变. 图7展示了形状为“180”的物体的重建图像质量的定量评价结果随物体能量和校准能量的变化情况. 可以看出, 物体能量不同时, 不同校准能量对应的重建图像的质量所能达到的最佳值相近, 且均出现在校准能量和物体能量相同时; 校准能量和物体能量不同时, 重建图像的质量均有不同程度的变差. 整体而言, 校准能量为10 keV时, 重建图像质量受物体能量变化的影响最小.
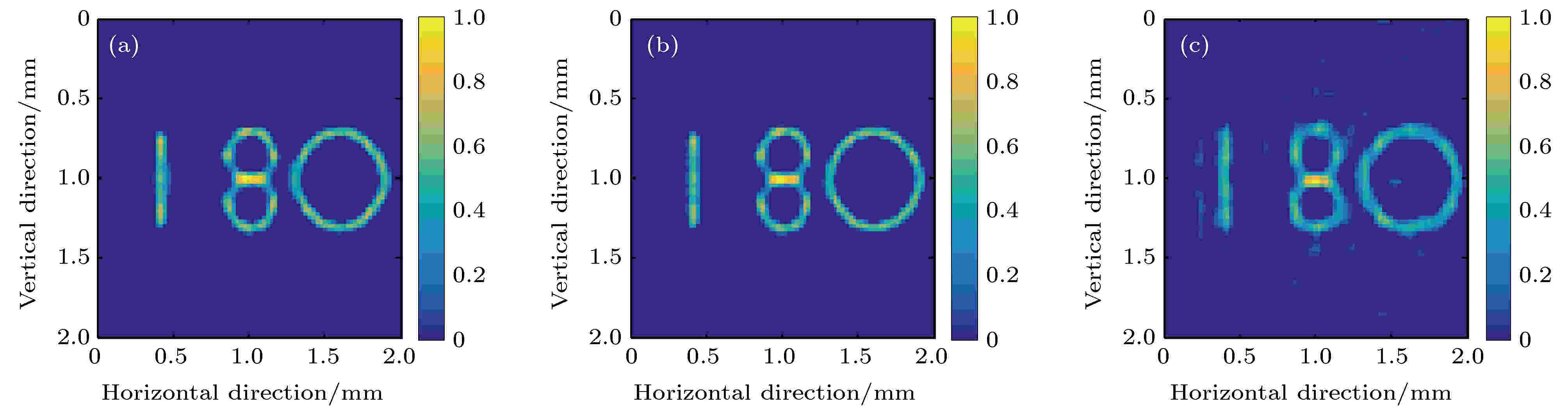图 5 校准能量10 keV情况下物体不同能量时的重建图像　(a) 6 keV; (b) 8 keV; (c) 16 keV
Figure5. Reconstructed images of the object with different energies at a calibration energy of 10 keV: (a) 6 keV; (b) 8 keV; (c) 16 keV.

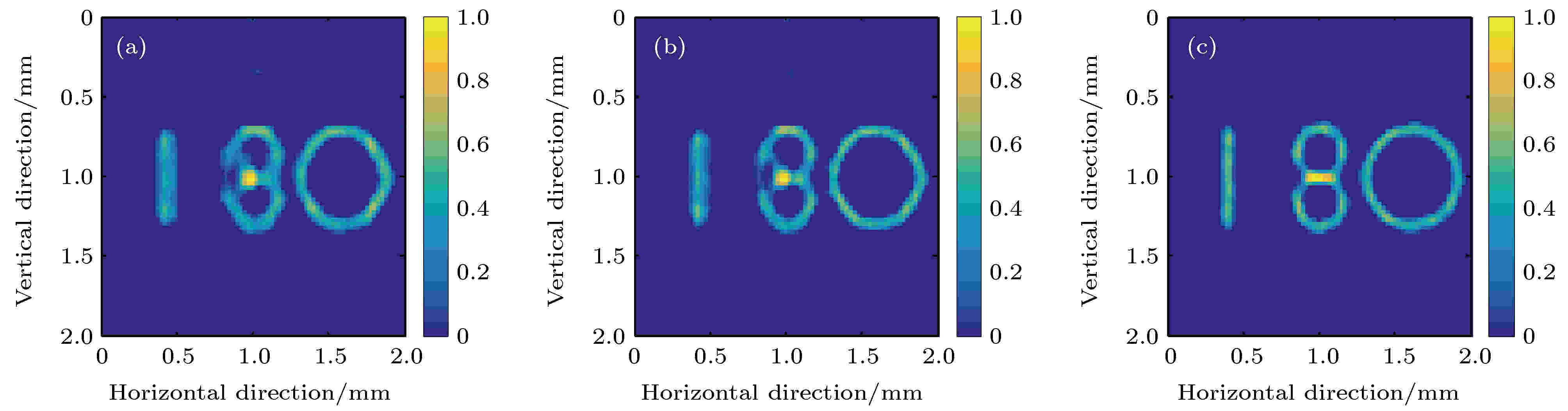图 6 校准能量16 keV情况下物体不同能量时的重建图像　(a) 6 keV; (b) 8 keV; (c) 16 keV
Figure6. Reconstructed images of the object with different energies at a calibration energy of 16 keV: (a) 6 keV; (b) 8 keV; (c) 16 keV.

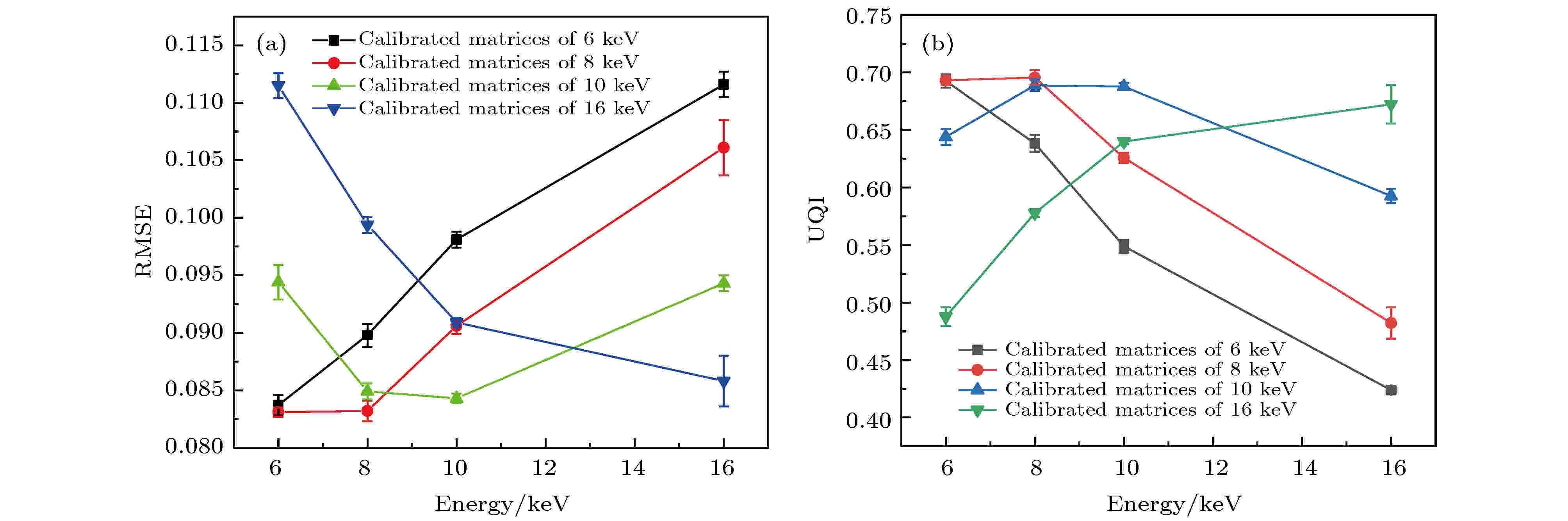图 7 重建图像质量的定量评价结果随物体能量和校准能量的变化情况　(a) RMSE; (b) UQI
Figure7. Quantitative evaluation results of reconstructed images change with the object energy and calibration energy: (a) RMSE; (b) UQI

2 -->

4.3.三维成像结果

在近场条件下, 编码孔径成像系统可以在二维成像的基础上提取三维和重聚焦信息. 为了考察系统的三维成像能力, 将两个成像物体的能量设为10 keV, 并放置于与系统距离为d = 10.0 mm的平面上. 如图8所示, 虽然模拟的线源是平面物体, 但重建的线源出现在不同的轴向切片上, 极大值出现在真实距离(d = 10.0 mm)附近; 成像系统的轴向分辨率较差(FWHM = 1.1 mm). 图9是形状为“180”的物体的三维重建图像. 类似于线源的重建结果, 重建物体出现在不同的轴向切片上, 并且在真实距离(d = 10.0 mm)附近最清晰. 因此, 相比于传统基于卷积模型的成像系统仅能实现二维成像, 采用T2S模型的成像系统可以很容易地实现距离d的估算.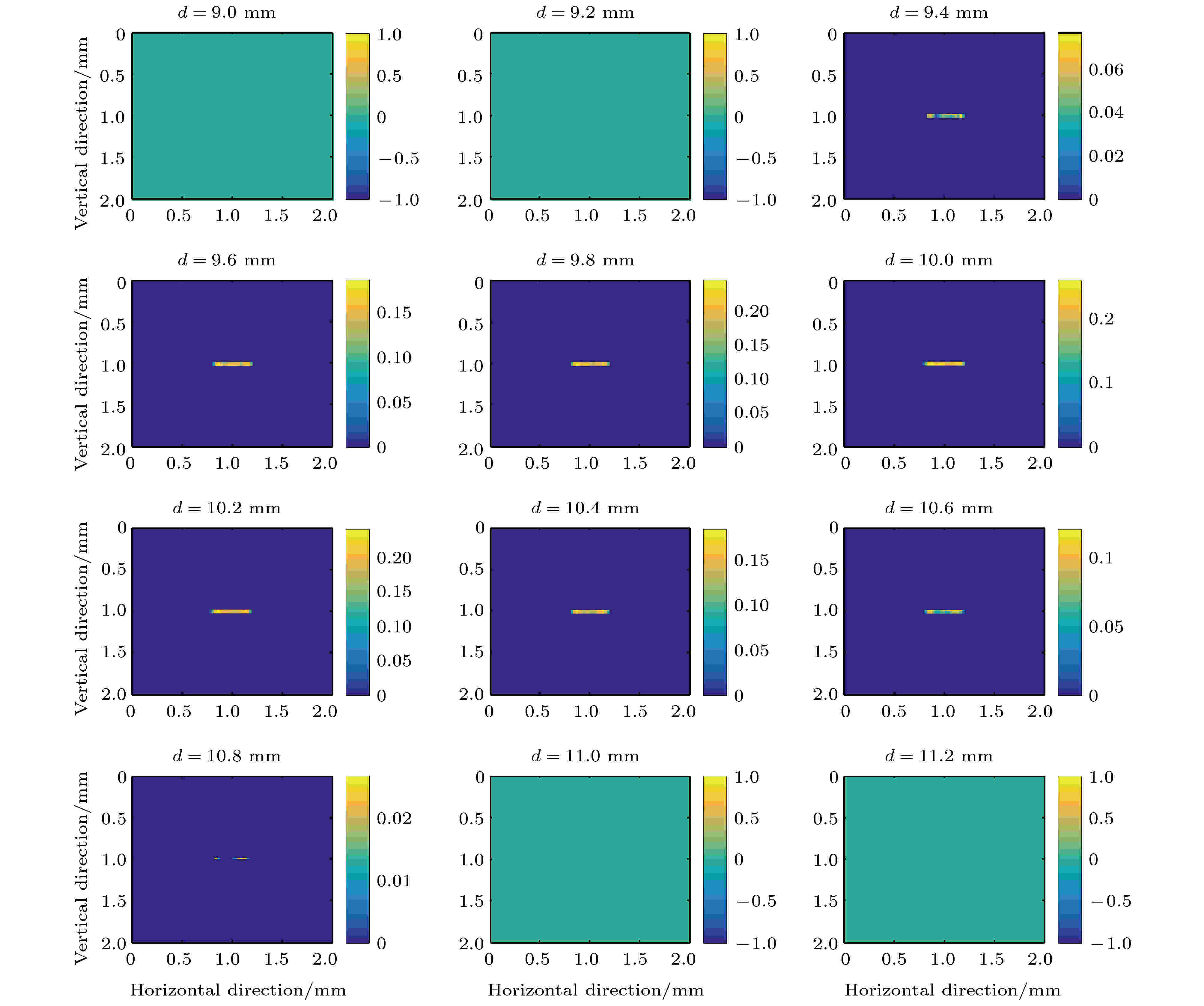
图 8 线源的三维重建图像
Figure8. 3D reconstructed image of the line source.

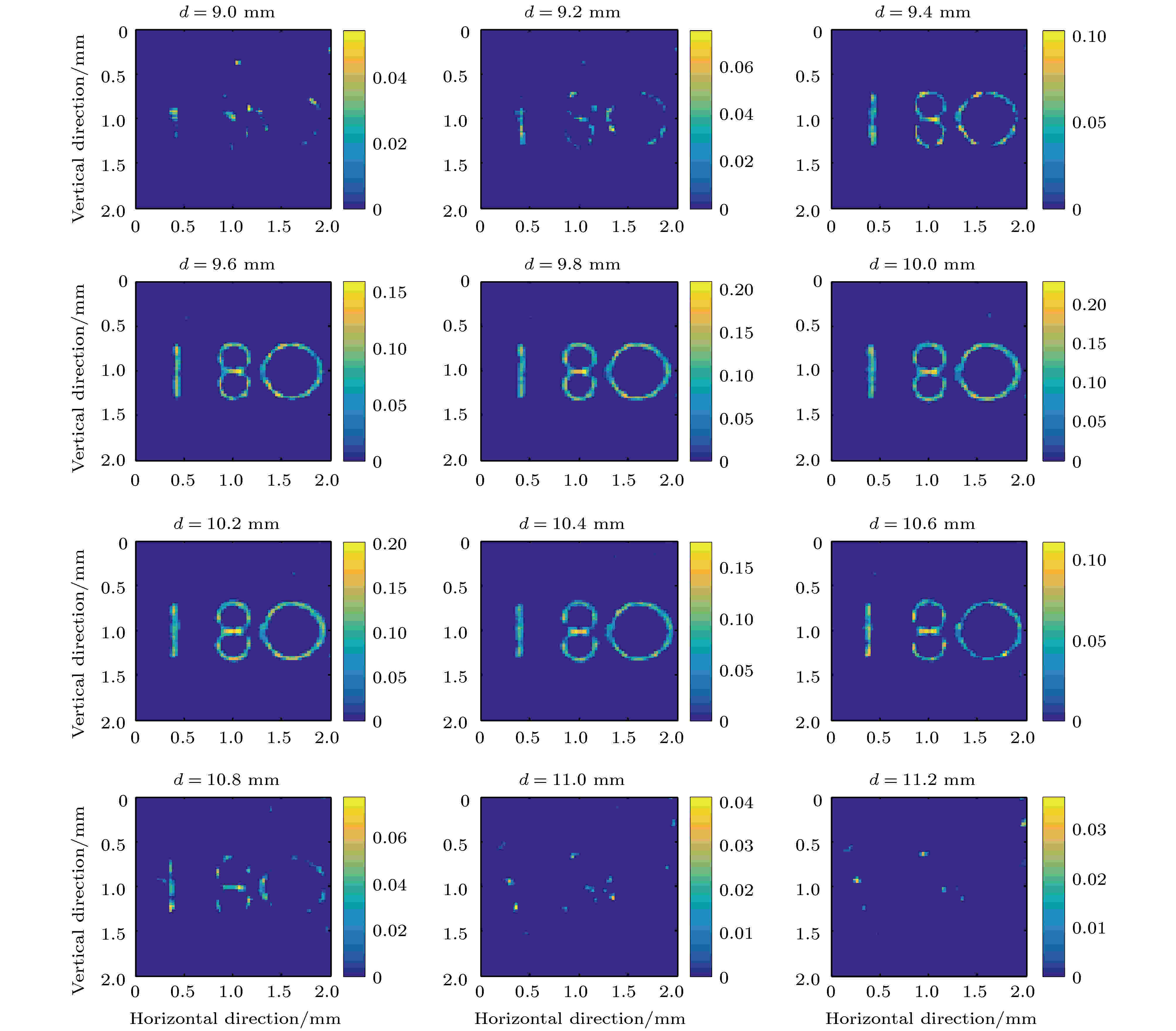图 9 复杂物体的三维重建图像
Figure9. 3D reconstructed image of the complex object.

本文利用Geant4蒙特卡罗仿真, 研究了基于可分离编码的新型编码孔径成像计算模型用于高分辨X射线荧光成像的可行性. 模拟结果表明, 基于该模型的成像系统能够实现对线源和形状复杂物体的高质量成像, 系统的空间分辨率约为65 μm. 与采用传统卷积模型的成像系统不同, 该系统的性能在近场成像时并不受准直效应的影响. 重建图像的质量同时受物体能量和校准能量的影响, 两者差异越小, 重建图像的质量越高. 系统能够从单次测量的二维投影图像, 正确地重建出物体与系统的距离, 轴向空间分辨率约为1.1 mm.
成像系统的空间分辨率受多个因素的影响, 包括编码准直器和探测器的像素尺寸、物体的放大倍数(取决于物体到编码准直器的距离与编码准直器到探测器的距离之比)、图像重建算法等. 提高系统空间分辨率的途径包括减小编码准直器和探测器的像素尺寸、增大物体的放大倍数以及采用更复杂的图像重建算法等. 未来的工作将集中于优化系统设计并开发新的重建算法, 以进一步提高系统的空间分辨率.