全文HTML
--> --> -->操控单个DNA分子, 将其有效导入、引导其穿越微纳通道是实现DNA生物芯片众多功能的必备条件. 通常, 将DNA分子顺利导入微通道的方法有: 流体力学进样[10](虹吸进样法、微通道端加压法、微通道末端抽真空法)、扩散进样[11]、电动力进样以及电渗驱动的流体进样[12]等方法. 流体力学进样法对所用设备有严格要求、装置复杂、设备体积大、成本高, 同时不利于分析黏度较大的样品; 扩散进样法引导样品进入通道内是被动的、且难以控制; 而电动力进样法相对容易控制, 附加设备少、成本低, 在毛细管电泳分析中普遍采用.
目前, 电动力进样法将DNA分子导入微纳通道仍存在尚未解决的关键问题. 例如, 随着外加电场强度的改变, DNA分子在管口附近的动力学特性、速度分布以及DNA本身的构象变化等不明确[13,14]; 而且, 电场力引导DNA分子进入微纳通道时, 不断有新现象、新问题被发现.
Wang等[15]曾利用可视化技术研究DNA分子在微米通道内的电动力学特性, 发现DNA分子从trans端口进入内径为30 μm通道时, 存在阈值电场强度.Yang等[16]研究发现DNA分子在外电场力作用下穿越5和10 μm的通道时, 其运动方向会发生反转, 并且, 微米通道管径越小, DNA分子运动方向发生反转时的阈值电场强度越大. 最近, Jones等[17]发明了一种微管收缩分选DNA分子的装置, 采用电场力驱动DNA分子运动, 通过改变电压的大小与频率调控DNA分子在通道出口处的偏转方向, 成功实现了不同大小DNA分子的筛选; 但是, 实验发现一部分分离后的DNA分子吸附在通道的管壁上, 非常不利于芯片的持久运行.
本文利用单分子荧光成像可视化技术, 实时观察研究了λ-DNA分子在外加电场力作用下进/出微米通道端口的电动力学特性, 并基于微流体电动力学理论, 对DNA分子在进入通道端口时的不同运动状态的物理机制进行了初步分析.
2.1.实验装置
实验装置如图1所示, 主要包括: 倒置荧光显微镜(IX-70, 奥林巴斯, 日本); EMCCD相机(iXon+885, Andor, 美国); 石英玻璃圆形微米通道(邯郸市鑫诺光纤色谱有限公司), 长度为5 mm, 直径为50 μm; 铂丝电极(上海捷昱电子科技有限公司); 外接高压电源(PS 8000 2U, EPS, 德国). 实验中, 电压调节范围为: 0—100 V. 图像数据采集、分析处理均用Image软件(
图 1 实验装置示意图Figure1. Schematic diagram of experimental set-up.
图1所示为实验的装置示意图. 实验具体步骤: 1) 导入缓冲液, 在cis端口处滴入10 μl的缓冲液, 2 s左右缓冲液将充满整个微米通道; 2) 导入DNA分子, 将10 μl浓度为0.455 mg/L的DNA/YOYO-1样品溶液滴在trans端口, 样品通过毛细力作用进入微通道内; 3) 待溶液处于稳定状态, 调整电压, 确定电场强度大小与方向.
实验中, EMCCD实时记录DNA样品进入端口以及在微通道内运动情况, 其曝光时间设定为100 ms, 拍摄间隔为100 ms, 每次连续拍摄持续为5 min; EMCCD一次可以连续拍摄1000张照片.
2
2.2.样品液、微芯片的制备
实验使用的是λ-DNA分子(富酶泰斯生物技术公司, 深圳,中国), 用染料YOYO-1分子进行标记. 为了保证最好的荧光效率, YOYO-1染料分子插入λ-DNA分子的配置比例为DNA碱基对: YOYO-1分子 = 10 : 1.样品溶液的制备过程如下所述: 1) 用移液枪移取100 μl的Bis-tris (pH=8) 和1000 μl的Tris-Hcl (pH = 8), 分别滴入标记为A和B的牛角管中; 2) 取0.411 μl的DNA原液和0.1 μl的YOYO-1原液分别加入A和B中, 摇匀A和B中的两种溶液使其充分混合, 置于暗室孵育30 min; 3) 从B中取200 μl的YOYO-1稀释液加入A中充分混合, 在暗室中孵育30 min. 最终得到DNA/YOYO-1的混合溶液, DNA浓度为0.455 mg/L, 储藏在暗室中备用.
微通道芯片核心部分的制备, 简述如下: 1) 将经过PLL(20)-g(3.6)-PEG溶液改性后的实验用微米通道烘干; 2) 将聚甲基丙烯酸甲酯(PMMA)颗粒与氯仿溶液按照1∶1进行充分混合, 制备2个样品池, 10 mm × 10 mm × 3 mm, 它们中间通过微米通道进行连接; 铂丝电极正对微通道端口处; 3) 将聚酰胺树脂与环氧树脂按1∶1混合后均匀涂抹在样品池的外围, 以加固结构; 将芯片系统放入烤箱, 温度60 ℃下烘烤两小时. 实验研究中, 为了避免DNA分子被通道内壁表面吸附, 采用改性液PLL(20)-PEG(2)-PEG(3.4)对微米通道内壁进行改性处理. 本文所涉及的缓冲液pH值都大于3, 当溶液与二氧化硅通道壁面接触时, 其表面的硅烷醇(Si—OH)基团因去质子化而产生负电荷, 带正电的PLL(多聚赖氨酸)通过静电作用与去质子化的硅烷醇基团相结合, 吸附在通道壁面; 不带电的亲水性聚合物PEG(乙二醇), 有效阻止生物分子非特异性吸附到管道内壁上[18], 从而可以有效减小管壁对DNA吸附. 实验所用改性混合液PLL与PEG的质量比 PLL∶PEG = 1∶3.6.
2
3.1.DNA分子顺利穿越微米通道的电场强度阈值
微米通道两端施加电压, 实验发现: 当电场强度E < 1.875 × 103 V·m–1时, 距离trans端口大约为100 μm范围内的样品池内未捕捉到DNA分子, 表明DNA分子很难靠近trans端口; 当电场强度E = 1.875 × 103 V·m–1时, 样品池内的DNA分子开始缓慢靠近trans端口, 但未进入trans端口; 当电场强度增大到E = 2.5 × 103 V·m–1时, DNA分子开始进入trans端口; 随后, 逐渐增大电场强度, DNA分子能够进入trans端口并顺利穿越通道, 并从cis端口顺利离开; 当E > 7.5 × 103 V·m–1时, 从trans端口进入通道的DNA分子迁移至cis端口附近时, 部分DNA分子发生反转运动, 即, DNA分子的运动方向发生逆转, 由cis端向trans端运动, 不能够从cis端口穿出. 可见, DNA分子能够从trans端口进入并且顺利穿越微通道, 电场强度大小有合适范围, 存在阈值: Emin = 2.5 × 103 V·m–1, Emax = 7.5 × 103 V·m–1.如图2所示, 当电场强度E = 3.75 × 103 V·m–1时, DNA分子从trans端口进入微米通道并在管内的迁移.
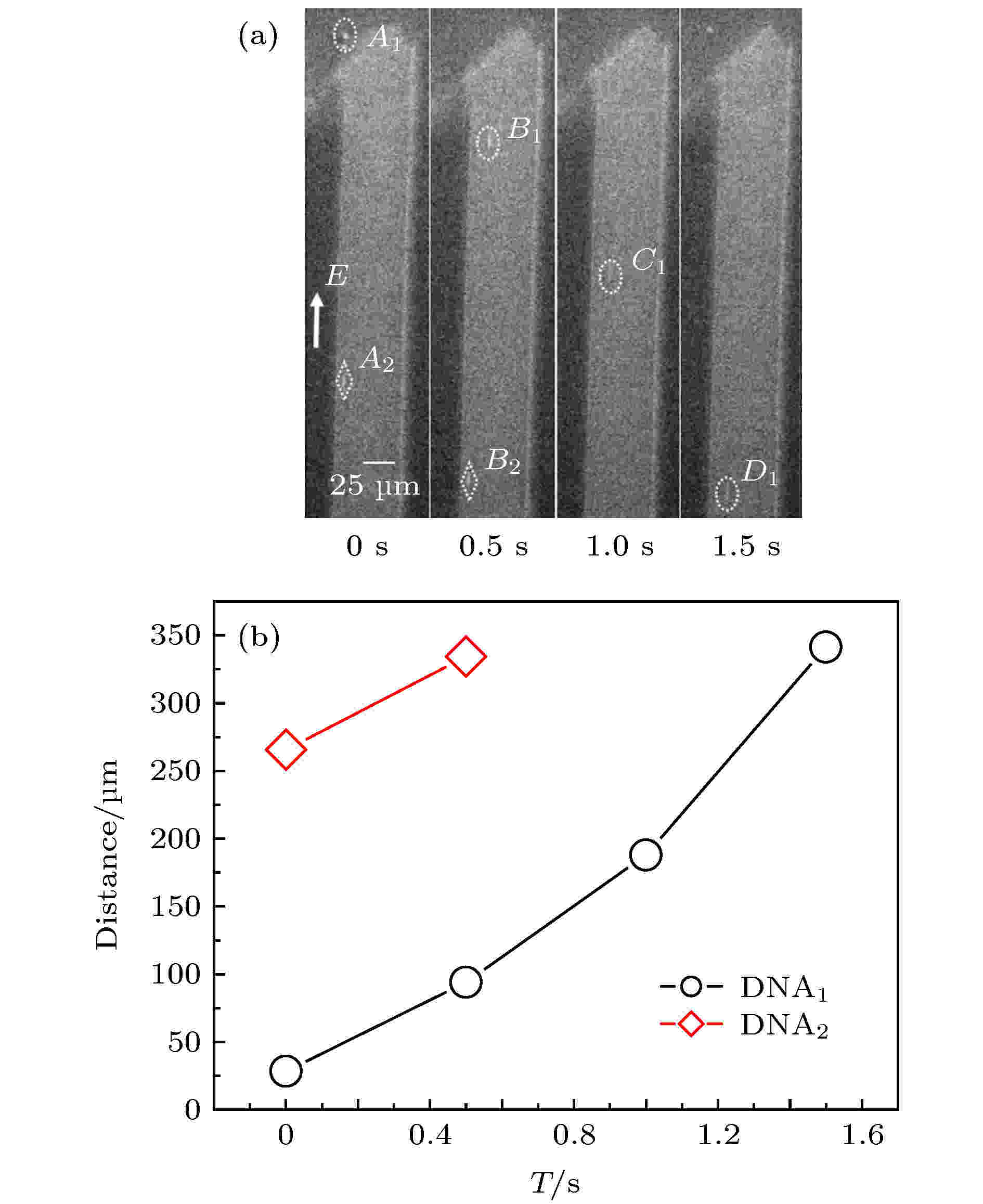图 2 DNA分子从trans端口进入微米通道并在内部迁移(E = 3.75 × 103 V·m–1) (a) 不同时间下的CCD照片; (b) DNA分子位置随时间的变化曲线Figure2. DNA molecules enter the microchannel from the trans port and migrate inside (E = 3.75 × 103 V·m–1): (a) CCD photographs; (b) DNA molecular position.
由图2(a)可见, 当外加电场在阈值电场强度内, DNA分子能够顺利进入trans端口, 其中有2个DNA分子进入观察视野范围内, 分别用虚线椭圆和虚线菱形标识; A1~D1和A2~B2分别对应DNA1和DNA2分子在不同时刻出现在微米通道内的位置, 可以发现: 1) DNA分子在通道内运动时, DNA1和DNA2分子到微米通道中心轴向的距离L1 < L2, 其大小基本不变; 2) DNA1分子在trans端口附近运动时(从A1位置到B1位置), 进入trans端口之前是纠缠蜷缩的(A1位置), 进入通道内, 渐渐被拉伸, 长度增大, 但在微米通道内拉伸长度变化不大; 3) 图2(b)是DNA分子在通道内迁移时位置的改变, DNA1分子在0—0.5 s内移动距离为65.5 μm, 0.5—1.0 s内移动距离为94.0 μm, 1.0—1.5 s内移动距离为153.0 μm, 其平均速度逐渐增大; 而DNA2分子在被捕捉时已经进入到微通道内, 0—0.5 s内移动距离为70.0 μm, 与DNA1分子刚进入端口时运动的距离几乎相同.
实验中, 还观察到DNA分子进入trans端口后, 其速度会逐渐增大, 而DNA分子穿出cis端口时的速度逐渐减小等现象. 图3所示为DNA分子进入trans端口和穿出cis端口时的速度随时间的变化曲线.
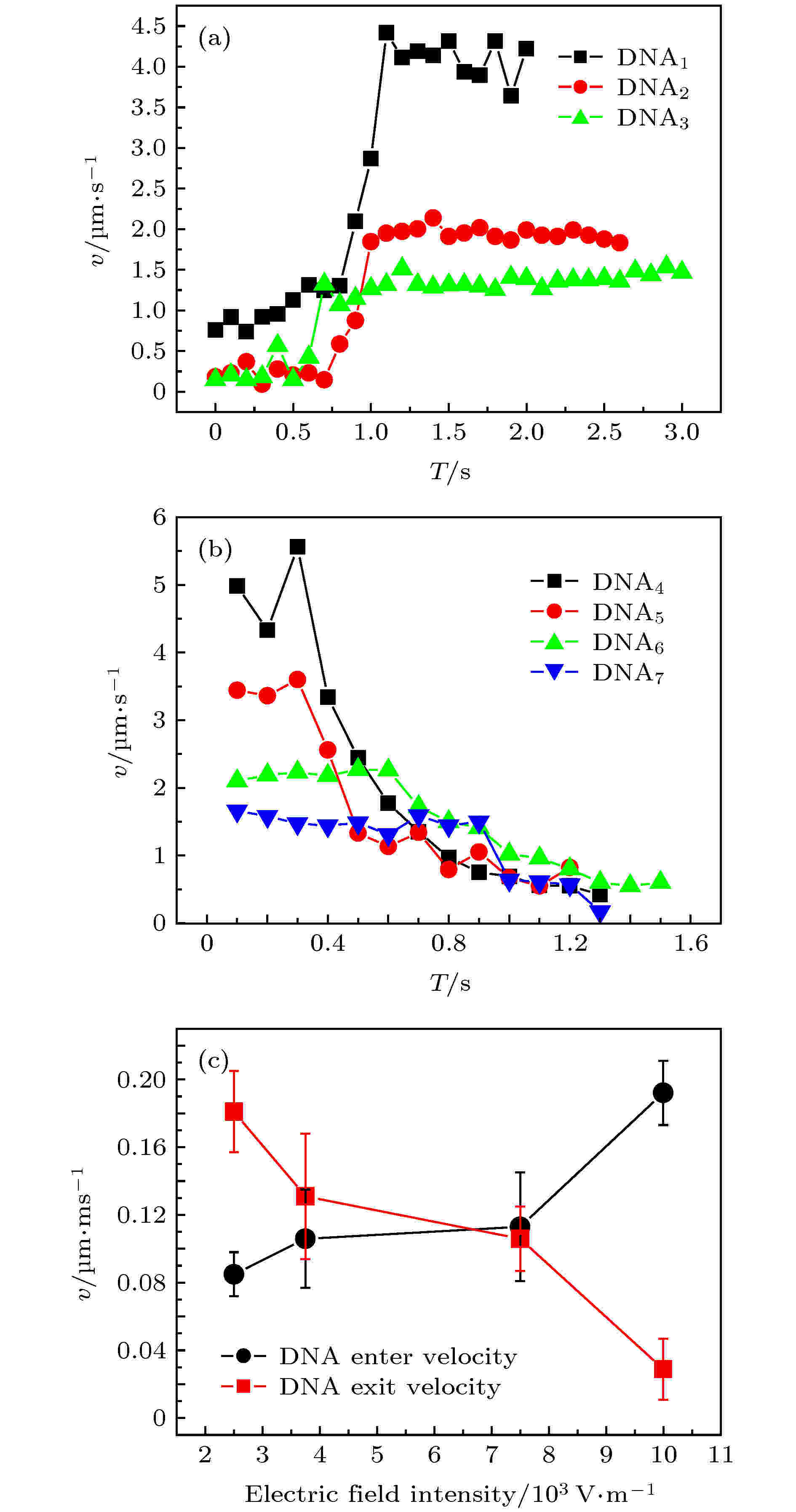图 3 DNA分子进出端口的速度随时间的变化(E = 3.75 × 104 V·m–1) (a) 进入trans端口; (b) 穿出cis端口; (c) 速度随外加电场强度的变化关系Figure3. The velocity of DNA molecules entering and leaving the port (E = 3.75 × 103 V·m–1): (a) Entering the trans port; (b) leaving the cis port; and (c) velocity versus electric intensity.
图3(a)为DNA分子进入trans端口的速度随时间的变化. 其中DNA1, DNA2和DNA3分子分别表示距离中心轴线不等的三个DNA分子, 距中心轴线的距离为L1 < L2 < L3, 速度关系为v1 > v2 > v3. 可见, DNA分子从样品池进入trans端口之前的速度较小, 一旦进入trans端口开始加速, 进入微米通道中部后速度比较平稳; 轴线附近的DNA分子速度大于管壁附近的DNA分子速度. 图3(b)为DNA分子流出cis端口时的速度随时间的变化特性, 实验数据是从DNA分子距离cis端口大约为100 μm的位置处开始记录的, DNA分子距离中心轴线的距离为L4 < L5 < L6 < L7, 测量轴向的速度v4 > v5 > v6 > v7.
对比图3(a)和图3(b), DNA分子进入trans端口与DNA分子流出cis端口的速度变化几乎是两个反对称的过程. 在通道端口附近的同一横截面处, 中心轴线附近的DNA分子速度变化快, 而管壁附近的DNA分子速度变化慢. DNA分子进入trans端口时, 速度逐渐增大, 最后保持不变; 穿出cis端口时, 速度逐渐减小, 最终进入样品池中的速度大小基本相同, 其主要原因是DNA分子在样品池中的运动主要受布朗运动的影响.
图3(c)为DNA分子在进入端口和离开端口处的速度随着外加电场变化的曲线图, 规定DNA分子逆着电场方向的运动为正方向. 图3(c)所示是在不同的电场强度下, 分别对通道进/出端口随机捕捉的30—50个DNA分子的平均速度, DNA分子距离中心轴线的范围为0—14 μm. 其中, 黑色曲线为DNA分子刚好进入端口的平均速度随着外加电场强度的变化关系, 红色曲线为DNA分子刚好离开端口处的平均速度随着外加电场强度的变化关系. 由图3(c)可知, 当电场强度2.5 × 103 V·m–1 < E ≤ 7 × 103 V·m–1时, DNA在入端口速度小于出端口速度; 当外加电场强为7 × 103 V·m–1 < E ≤ 1 × 104 V·m–1时, DNA在入端口的速度大于出端口速度.
2
3.2.DNA分子的反转运动
继续增大电场强度, 当电场强度E > 7.5 × 103 V·m–1时, 发现DNA分子从trans端口进入微米通道内, 运动至cis端口附近时将出现部分DNA分子反转运动, 即, 运动方向发生改变, 如图4所示.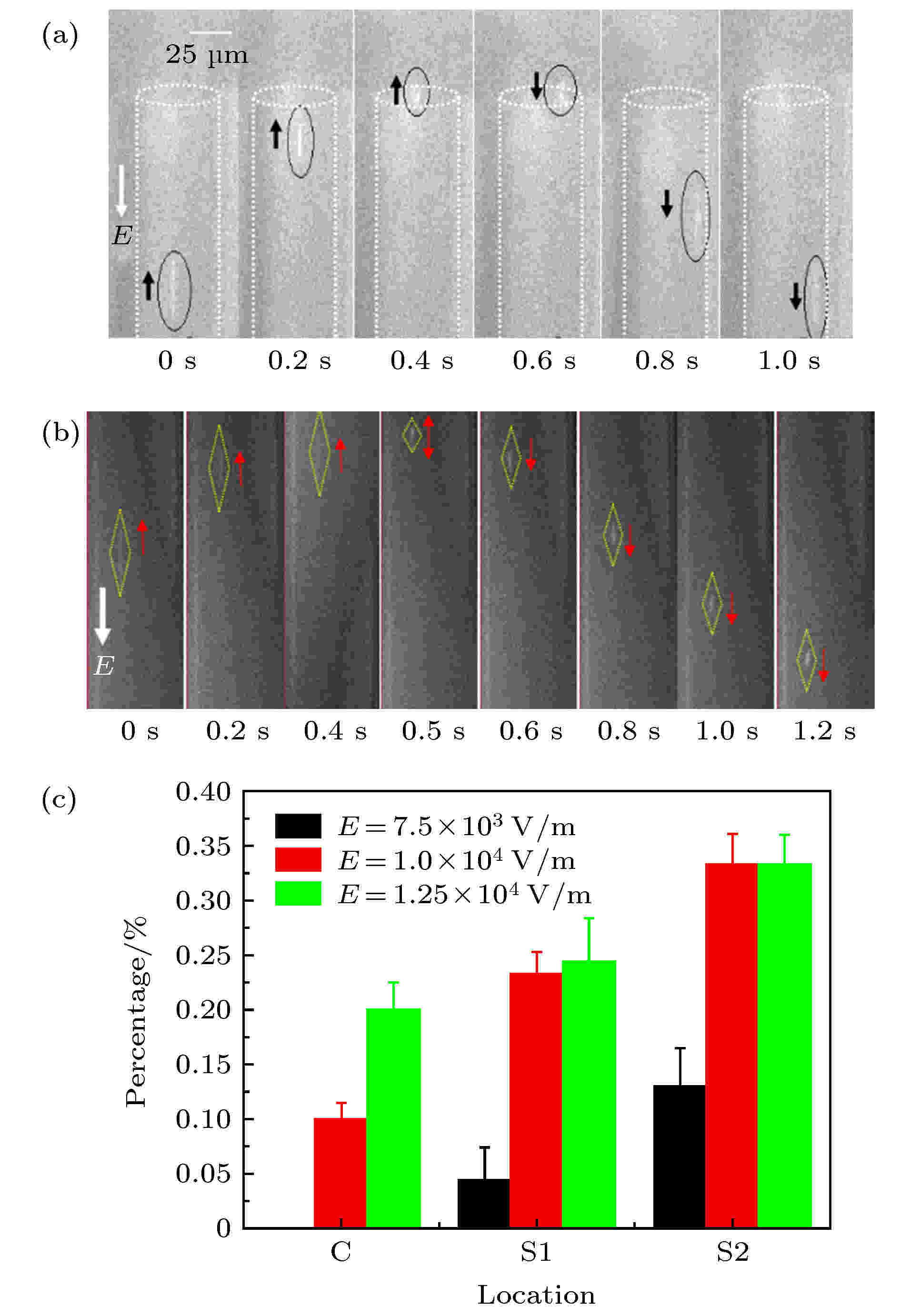
图 4 DNA分子在微通道内的反转运动 (a) E = 8.125 × 103 V·m–1; (b) E = 9.375 × 103 V·m–1; (c) 不同电场强度下, 在cis端口不同区域内的DNA分子反转数占总数的百分比Figure4. Reversed motion of DNA molecules within micro channel under different electric intensity: (a) E = 8.125 × 103 V·m–1; (b) E = 9.375 × 103 V·m–1; (c) percentage of DNA molecules with reversal motion direction in different regions of the cis port under different electric intensity.
图4所示为DNA分子在不同电场力作用下穿越微米通道时, 其运动方向发生反向的情况. 如图4(a)所示, 当外加电场强度E = 8.125 × 103 V·m–1时, DNA分子首先在通道内沿trans→cis方向运动(0—0.4 s内), 速度逐渐减小; 当DNA分子运动至cis端口处时, 将在径向上迁移, 而在轴向上近似静止(0.4—0.6 s内); 最后, DNA分子运动方向发生反转, 沿cis→trans方向运动(0.6—1.0 s内), 速度逐渐增大. 如图4(b)所示, 当电场强度继续增大至E = 9.375 × 103 V·m–1, DNA分子未到达cis端口的边界处就开始反转, 即, 在0—0.5 s内, DNA分子沿trans→cis方向运动, 逆着电场方向运动; 0.5—1.2 s内, DNA分子沿cis→trans方向运动, 顺着电场方向运动.
为了详细研究在不同的电场强度下DNA分子的反转运动沿管径方向的变化, 对微通道进行了划分, r为距离中心轴线的距离, C区域为0 ≤ r1 < 14 μm, S1区域为14 μm ≤ r3 < 20 μm, S2区域为20 μm ≤ r2 ≤ 25 μm. 同一电场强度下, 当DNA分子运动稳定后统计10 min. 在不同外加电场强度下重复实验, 发现每次实验捕捉到的各个分区域内DNA分子数目占DNA分子总数的百分比分布基本相同, 例如, 当电场强度为7.5 × 103 V·m–1时, DNA分子分布在C, S1和S2各区域内的平均百分比分别约为68%, 23%和9%. 图4(c)所示是随机的3次实验, 外加不同电场强度时, 发生在不同区域的反转DNA分子数占所捕捉的DNA分子总数的百分比. 由图4(c)可知, 在不同的外电场强度下, DNA分子流出端口不同区域的反转数占流出总数的百分比不同. 随着电场强度的增大, DNA分子反转的几率增大, 在相同的电场强度下, C区域内DNA分子的反转概率最小, 其次是S1区域, S2区域内DNA分子的反转概率最大.
随着电场强度的继续增大, DNA分子运动方向发生反转的位置距离cis端口越来越远, 离trans端口越来越近; 当E = 1 × 104 V·m–1时, 通道trans端口附近的内壁上会吸附DNA分子; 当E > 1 × 104 V·m–1时, 部分DNA分子刚进入trans端口内就发生反转运动, 返回到trans端的样品池中, 或者被吸附到管壁上.
DNA分子的反转运动方式可以分为基本的两种类型: 1) DNA分子首先逆着电场的方向运动至cis端口; 然后, DNA分子在反转点的位置径向迁移, 轴向上静止; 最后, DNA分子开始反转, 朝向trans端口运动; 2) DNA分子首先逆着电场的方向运动, 在未到达cis端口时收缩成一个紧凑的小球, 似乎停止在通道中; 最后, DNA分子直接反转运动. 其中, 距离中心轴线较远的DNA分子容易发生第一种类型的反转运动; 而中心轴线附近、或者管壁附近的DNA分子, 或者当电场强度大于9.375 × 103 V/m时, DNA分子容易发生第二种类型的反转运动.
2
3.3.DNA分子的往复运动以及旋转运动
当电场强度增大至E > 9.375 × 103 V·m–1时, 在trans端口附近, 发现DNA分子具有周期性往复运动的现象.如图5(a)所示, 当电场强度E > 9.375 × 103 V·m–1时, 在trans端口附近, 单个DNA分子在一个周期内的往复运动, 周期约为3.0 s, 其中, 红色箭头表示DNA分子的运动方向.
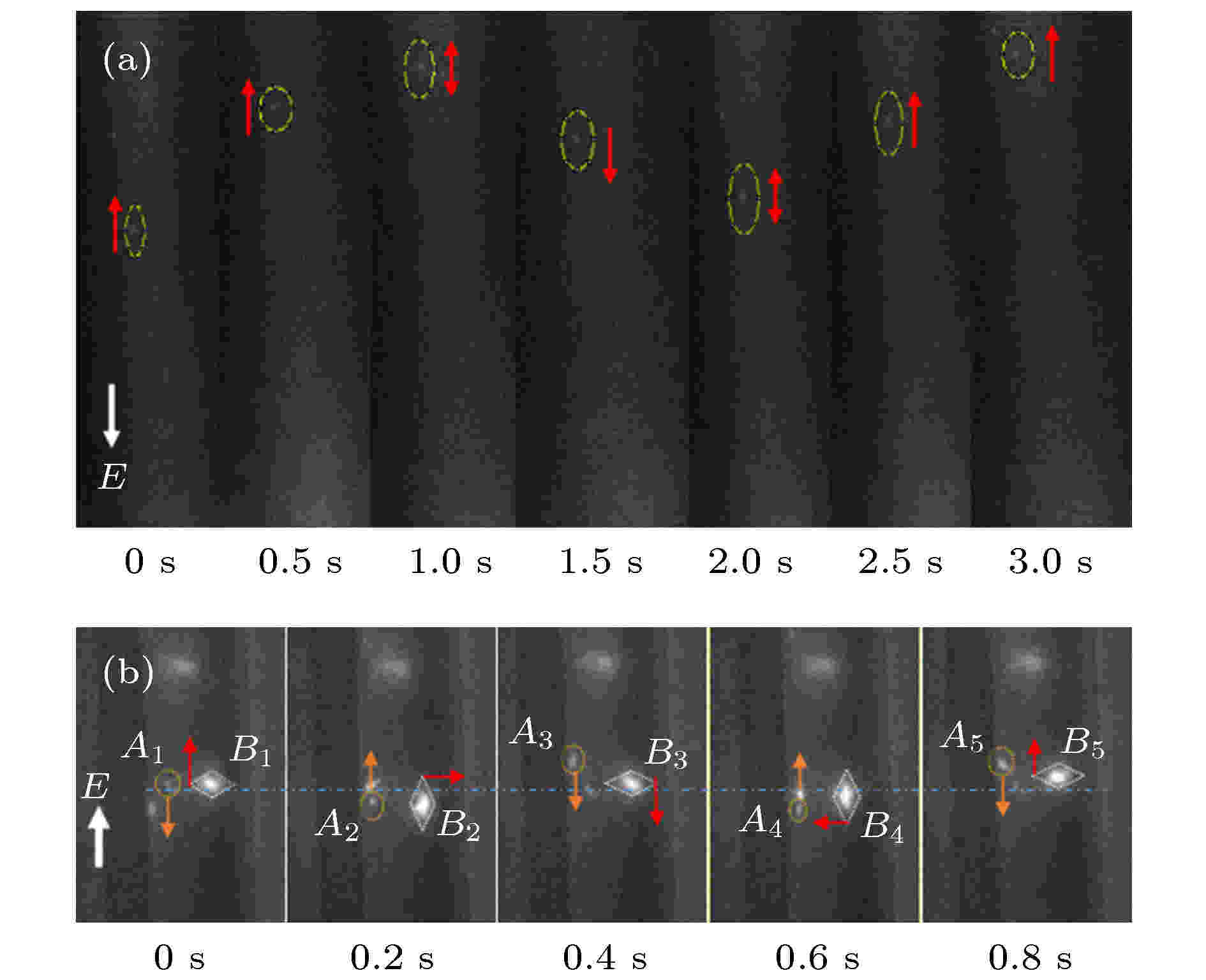图 5 DNA分子在trans端口附近沿轴向的运动 (a) 往复运动; (b) 旋转运动Figure5. The motion of DNA molecules near the trans port: (a) Reciprocating along the axis; (b) rotating.
如图5(b)所示, 当电场强度E = 1×104 V/m时, 捕捉到多个DNA分子的往复运动, 分别用圆形虚线、菱形虚线标记. 其中, 黄色箭头表示单个DNA分子(圆形虚线标记)在轴向上往复运动的方向, A1—A5表示DNA分子在不同时刻的位置, 它在轴向上的运动距离较大, 自身无旋转; 红色箭头表示团聚在一起的多个DNA分子(菱形虚线标记)绕着自身旋转的方向, 其方向指向管壁(顺时针旋转), B1—B5表示DNA分子在不同时刻的位置, 团聚的DNA分子在轴向上往复运动的距离较小, 蓝色虚线表示DNA做往复运动时的平衡位置.
图6是图5(b)中团聚的DNA分子在10 s内往复运动的轨迹. 其中, 蓝色曲线为DNA分子运动的轨迹, 红色虚线为DNA分子在运动过程中平衡位置的拟合曲线, 图中两点之间的时间间隔为0.1 s.
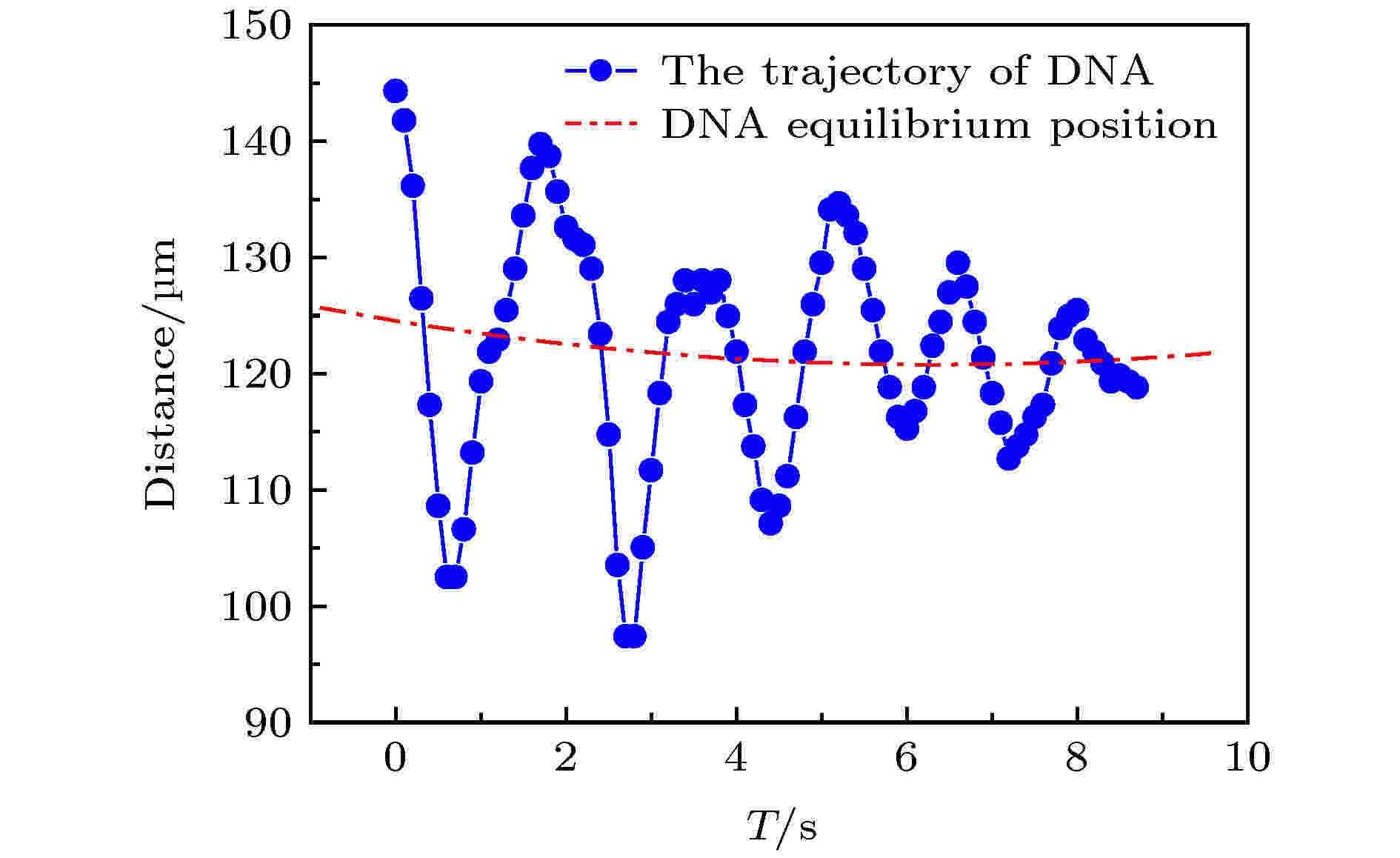图 6 DNA分子在trans端口附近的往复运动(E = 9.375 × 103 V·m–1)Figure6. The track of DNA molecules reciprocating near the trans port (E = 9.375 × 103 V·m–1).
图7所示为通道trans端口附近的内壁上吸附DNA分子的情形, 图7(a)和图7(b)的电场强度分别为7.5 × 103和1 × 104 V·m–1, 由图7可知, 随着电场强度的增大, 吸附在内管壁的DNA分子数量增多.
图 7 不同电场强度下的trans端口附近通道内壁团聚有DNA分子 (a) E = 7.5 × 103 V·m–1; (b) E = 1 × 104 V·m–1Figure7. Aggregates of DNA molecules on the wall of microchannel near the trans port; (a) E = 7.5 × 103 V·m–1; (b) E = 1 × 104 V·m–1.
2
3.4.DNA分子进/出微通道端口机制
图8所示是流体在通道内的速度分布以及DNA分子的受力和运动示意图. 由于微米通道端口处存在反压差, 通道内流体速度是电渗流和反压差流的叠加, 流体的流速不再是理想的塞状分布[19].
图 8 缓冲液在微米通道内的流速分布以及DNA受力和速度示意图 (a)受力; (b)速度Figure8. Schematic diagram of buffer velocity distribution in microfluidic channel and the infromation of DNA: (a) Force; (b) velocity.
图8中, 灰色带箭头的线段表示流体的速度分布, 流体在通道trans/cis端口的速度是顺着电场方向的电渗流流速与逆着电场方向的泊肃叶(Poiseuille)抛物线流速的叠加. 流体在径向上存在速度梯度; 另外, 由于端口处存在明显的反压差作用以及可能存在的污染、管口不平整等因素, 缓冲液沿轴向也存在速度梯度.
如图8(a)所示, DNA分子在trans/cis端口处沿轴向的受力为
当DNA分子与壁面之间的距离很近时存在静电作用, 其大小为[20]
由(1)式和(2)式可知, DNA分子所受合力的大小与外加电场强度、缓冲液速度、DNA分子大小、DNA电泳速度、管径大小等因素有关.
图8(b)是流体和DNA分子在通道中的运动示意图. 实验中使用的缓冲液pH > 3, 与管壁接触时管壁带负电; 当微米通道两端施加电场时, 微通道内的缓冲液将形成电渗流, 其移动方向为cis→trans; 由于DNA分子显负电性, DNA分子电泳的方向与电渗流方向相反, 为trans→cis. 理想状态下, DNA分子等带电粒子在微米通道中运动的速度是电泳[21,22]和电渗流[23,24]的叠加. 规定DNA分子电泳速度方向为正, 则DNA分子在微通道中运动的有效速度veff为
实验中, 样品池的边长(L = 10000 μm)相对于微通道的内径(D = 50 μm)以及DNA分子的回转半径(Rg = 0.7 μm), 几乎是一个三维无限大的储液池. DNA分子在样品池内将处于纠缠状态, 当其从trans端口进入通道, 是逆着流体流动的方向迁移, DNA分子进入以及穿越微米通道的过程中始终受到一个逆向流体的作用力[26].
研究发现[15], 电场力驱动DNA分子从trans端进入并顺利穿越内径为30 μm的通道时, 最小阈值电场强度为Emin = 7 × 103 V·m–1. 本研究发现, DNA分子从trans端口进入并顺利穿越内径为50 μm通道时的最小阈值电场强度Emin = 2.5 × 103 V·m–1. 即, 通道内径越小, 电场强度阈值越大. 这种现象符合电渗流压力同湿周长度C与通道截面积A的比值成正比的规律[27].
由(6)式与(7)式可得, DNA分子在微米通道内同一横截面上的有效速度:
图9所示是DNA分子在流出端口同一截面不同位置处沿轴向速度的实测数值与理论计算值. 其中, 横坐标为DNA分子距离中心轴线的距离, dp/dx = 0.04 Pa/m, μ = 1.011 × 10–3 Pa·s, y2 = 4.5, 13.5, 22.5 μm,
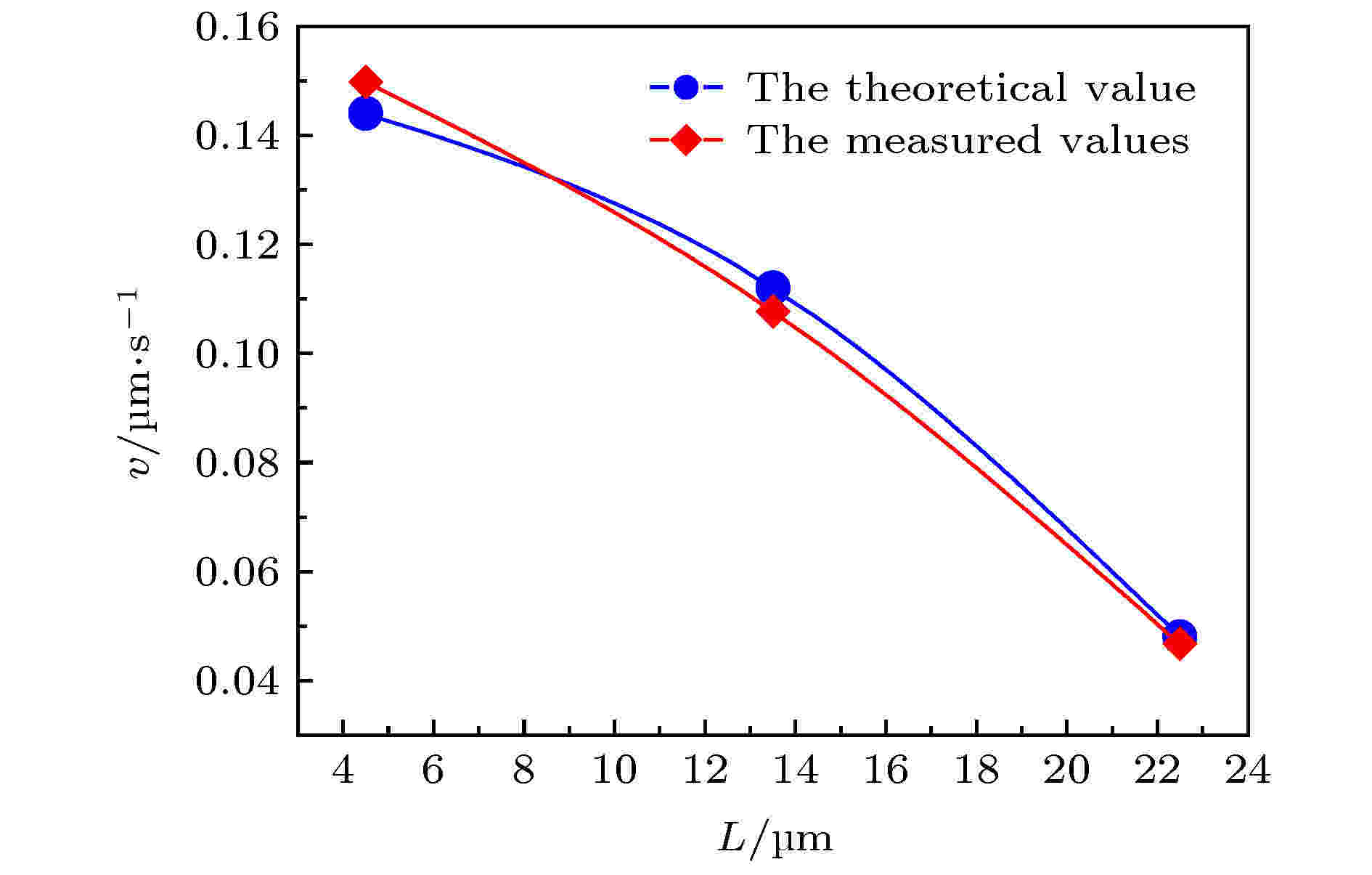图 9 DNA分子在端口同一截面不同位置的实测速度与理论速度Figure9. Measured and theoretical velocities of DNA molecules at different positions on the same cross section of near the microchannel port.
外加电场不同, DNA分子在通道内出现不同的运动状态, DNA的反转运动主要出现在cis端口, 往复运动和旋转运动出现在trans端口.
图10所示为DNA分子从trans端口进入微米通道, 并随着电场强度的改变, 在端口附近其反转运动发生位置点变化示意图. 图10(a)和图10(b)为DNA分子在不同电场强度下的反转运动过程. 其中, 图10(a)的电场强度范围为7.5 × 103 V·m–1 ≤ E ≤ 1 × 104 V·m–1, 图10(b)的电场强度范围为E > 1 × 104 V·m–1.
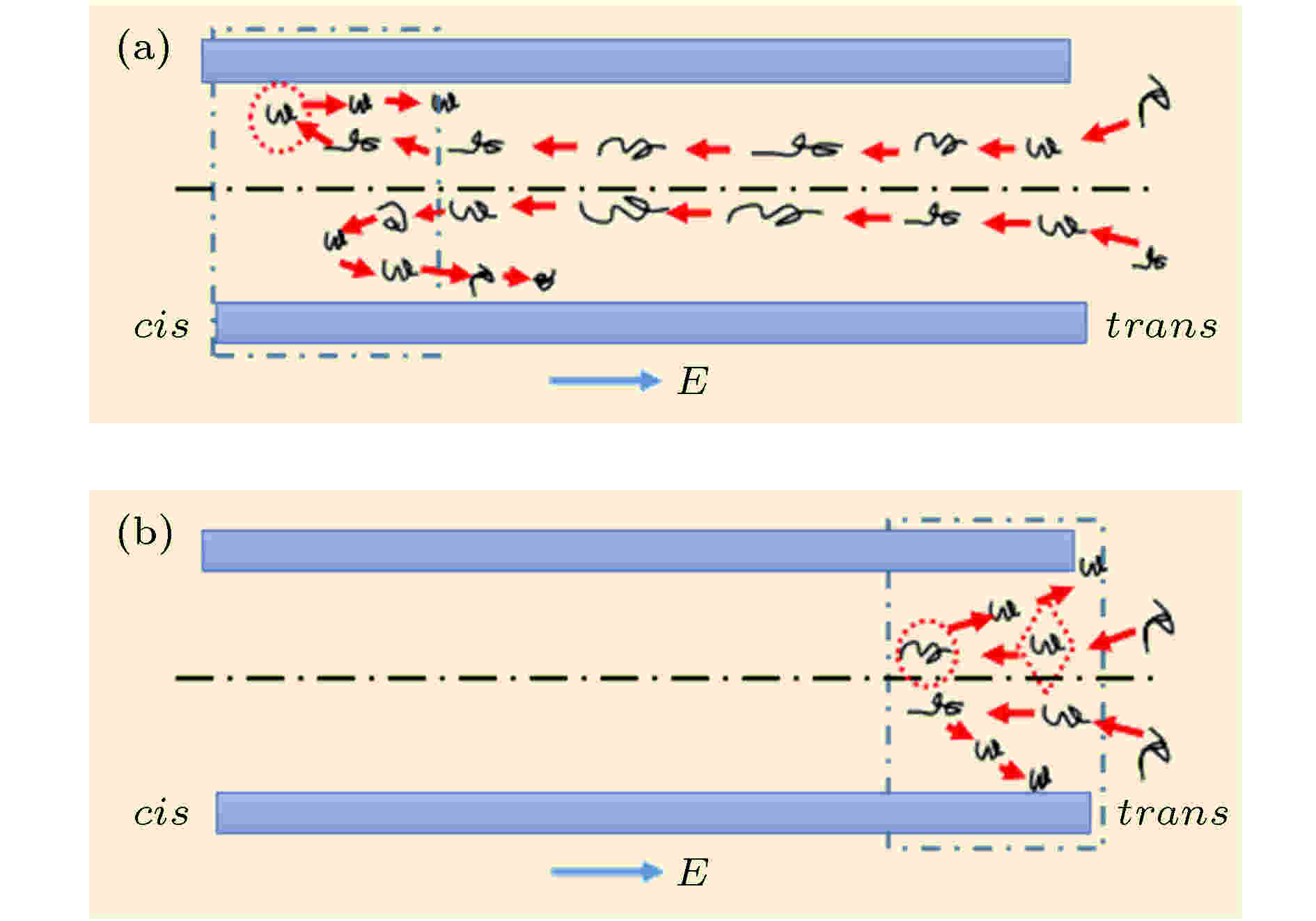图 10 DNA分子在微米通道内端口附近处的反转运动示意图 (a) DNA分子在cis端口处反转, 反转后的DNA分子容易吸附在微米通道内管壁上, 7.5 × 103 V·m–1 ≤ E ≤ 1 × 104 V·m–1; (b) DNA分子在trans端口附近的反转运动, E > 1 × 104 V·m–1Figure10. Schematic diagram of DNA molecules moving near the port of microchannel: (a) reversing near the cis port, and the reversed DNA molecule is easy to be adsorbed onto the inner wall, 7.5 × 103 V·m–1 ≤ E ≤ 1 × 104 V·m–1; (b) reversing near the trans port, E > 1 × 104 V·m–1.
由图10(a)可知, DNA分子是逆着流速靠近cis端口. DNA靠近cis端口, 其电泳力和电渗流阻力几乎不变, 流体的阻力虽然逐渐减小, 但压强梯度力却逐渐增大, 导致DNA分子的运动速度逐渐减小. 图10(a)中用虚线圆标记了一个在cis端口将要反转的DNA分子所处的位置, 此时, 压强梯度力与DNA分子表面的电渗流阻力之和大于DNA分子所受电泳力, 使得DNA开始反转运动.
电场强度的大小能够影响DNA分子反转点的位置. 当外电场达到反转电场强度时, 电场强度越大, DNA分子速度减小越快, 反转运动之前沿trans→cis方向运动的距离越小, 距离cis端口处越远. 如图10(b)所示, 外加电场强度E > 1 × 104 V·m–1, 菱形标记的一个DNA分子靠近trans端口, 此时, DNA分子受力满足条件:
另外, 电场强度越大对DNA分子构象的影响较明显, 使其表面电荷分布发生改变. 如图5(a)所示, DNA分子在构象上高度压缩, 其表面电荷密度将发生改变; 图5(b)所示, 电场强度超过1 × 104 V/m, DNA分子收缩成一个相当紧凑的小球, 导致DNA分子表面电荷密度分布发生改变, 各向同性增强[28], 表面电势(ζDNA)发生变化将导致DNA分子电泳力发生改变[29]. 图5(a)中, DNA分子逆着流体的方向进入通道, 在1.0 s时刻, DNA分子未到达cis端口, 但是其有效速度已减小为零. 由于在该电场强度下, DNA分子的电渗流淌度大于电泳淌度, 使得DNA分子不能保持静止状态, 因此下一刻DNA分子的运动方向开始反转, 转向cis→trans运动. 当到达trans端口附近时, 有效速度再次减小为零(2.0 s时刻), 此时DNA分子的受力为
电场强度继续增大, 并不能促使DNA分子在电泳的主导下向着cis端管口迁移, 反而加快DNA分子往复运动的频率. DNA分子在往复运动的过程中, 偏向管壁运动时速度减小. 由图6可以看出, DNA分子在往复运动的过程中逐渐地靠近管壁, 同时DNA分子往复运动的轴向距离逐渐减小. 当电场强度E > 7.5 × 103 V·m–1时, DNA分子明显偏向管壁运动, 主要原因是在trans端口附近, 反压差的作用使得DNA分子周围的流体存在速度梯度, 受到萨夫曼力的作用[30], 方向指向管壁. 关于DNA分子的旋转运动, 则主要是由于DNA分子周围的缓冲液在径向和轴向上都存在速度梯度. 当团聚的DNA分子质量较大时, 就有可能出现径向位置变化较小的旋转运动. 如图5(b)所示, 中心轴线右侧团聚的DNA分子周围的流体存在速度梯度, 距离中心轴线越近流体速度越小, 此时DNA分子向着管壁处旋转; 当DNA分子的旋转角速度矢量与运动的速度矢量不重合时, 在与旋转角速度矢量和平动速度矢量组成的平面相垂直的方向上将产生一个径向力, 即, 马格努斯力[31]. 萨夫曼力和马格努斯力之间存在互动性; DNA分子将在以上多种力的共同作用下做复杂的旋转运动.
