全文HTML
--> --> -->
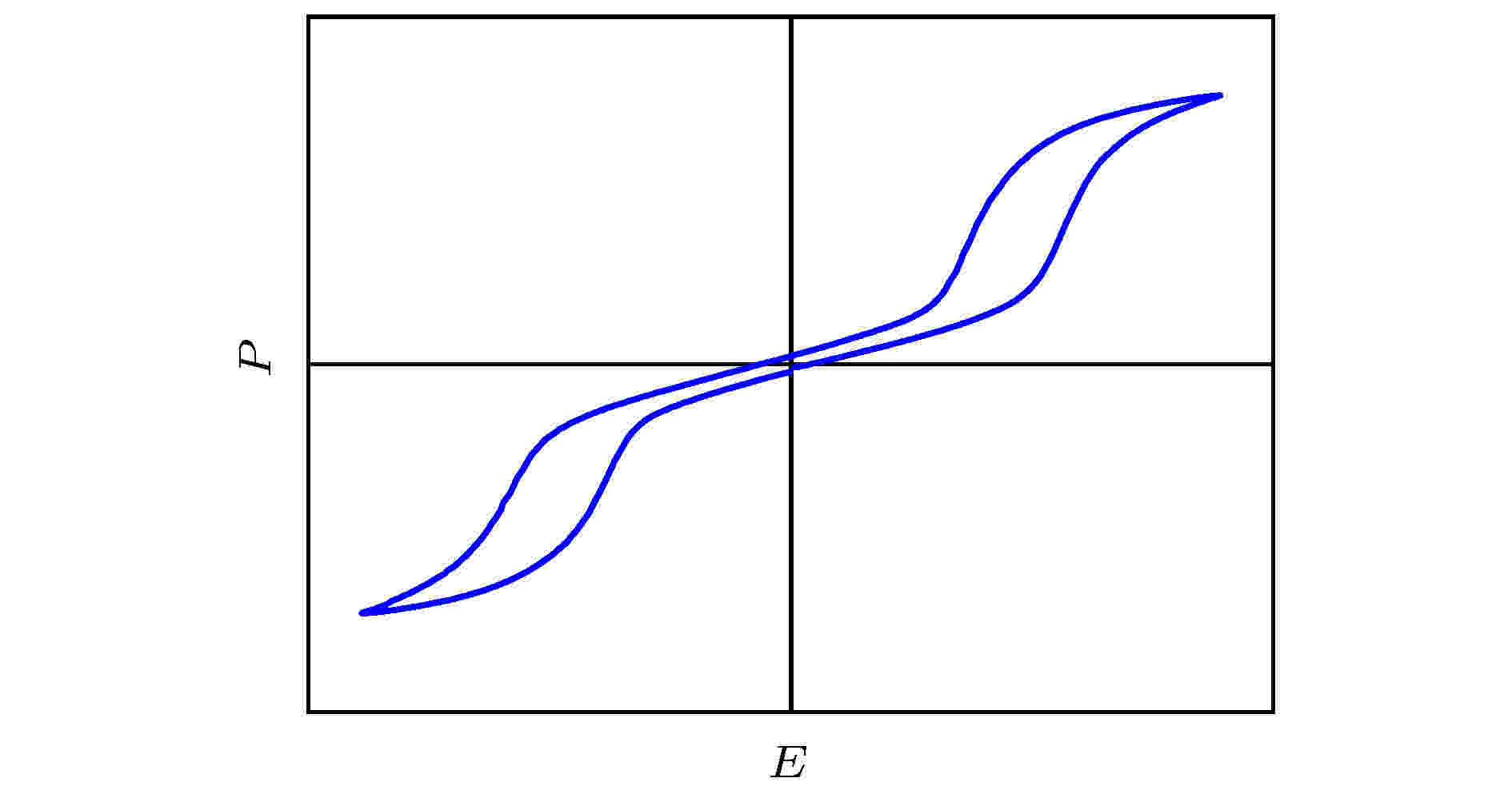图 1 反铁电材料的双电滞回线Figure1. Double P-E loop of antiferroelectrics.
由于此特殊的相变行为, 反铁电材料在多种工程应用方面具有巨大的潜力. 目前, 反铁电材料的研究热点是在储能电容器方面的应用. 研究人员一方面通过组分调节、微量元素掺杂等手段调控反铁电材料的相变特性, 增强其反铁电性和减小电滞, 以获得细长的电滞回线, 实现高储能密度和高能量效率[3,4]; 另一方面改进反铁电陶瓷制备工艺, 如采用轧膜成型、热压烧结等手段获得致密的陶瓷, 提高其击穿场强, 从而获得更高的能量密度[5,6]. 除去储能电容器外, 反铁电材料在电压调节器[7]、阴极材料[8-10]等方面也具有良好的应用前景.
反铁电材料实现上述应用的关键在于其特殊的极化和相变行为. 例如, 反铁电在电场诱导下的相变是实现高储能密度的关键, 其相变电场和极化强度决定了它的储能密度. 反铁电材料的极化和相变行为可通过电滞回线来表征. 根据电滞回线可得知其极化强度、相变电场、电滞宽度等参数, 并可进一步计算得到微分介电常数、储能密度、效率等参数. 对于陶瓷体材料, 电滞回线的测试频率一般在100 Hz以内[11]. 对于薄膜材料, 由于其测试电压较低和电极面积较小, 测试频率可更高, 但也无法达到100 kHz的水平. 因此, 介质上所施加的电场变化速率较慢, 上升或下降时间基本在毫秒量级. 然而, 在许多实际应用中, 铁电/反铁电材料均处于快速变化的瞬态电场中. 例如, 脉冲电容器工作时一般经历较慢的充电过程, 将电能以静电能的形式储存, 然后再迅速释放. 放电过程可达μs甚至ns量级[3,5]. 因此, 反铁电材料作为电容器介质时, 在放电过程中必然会经历快速的反向“铁电-反铁电”(FE-AFE)的相变过程. 此相变过程为电荷和能量释放的过程. 反铁电材料的FE-AFE相变若能在短时间内完成, 将有利于电荷和能量的快速释放. 反铁电材料用于其他场合时, 如电压调节器和阴极材料, 也处于快速变化的电场中[7-10].
在上述应用中, 反铁电材料所处电场的变化速率远大于一般电滞回线测量时所施加的电场. 因此, 研究反铁电材料在瞬态电场下的极化过程具有重要的实用价值. 事实上, 研究人员对反铁电材料在快速瞬变电场下的极化和相变特性也越来越重视. 大量研究结果表明测试频率对反铁电材料的电滞回线具有显著的影响, 反铁电材料的极化强度、相变电场和电滞损耗都与电滞回线的测试频率直接相关[12,13]. 而测试频率的增大意味着所施加的电场变化更快, 但现有电滞回线测试所施加的电场变化速率与实际应用的要求仍相距甚远.
电滞回线的测量一般基于Sawyer-Tower电路[11], 其电路示意图如图2所示.
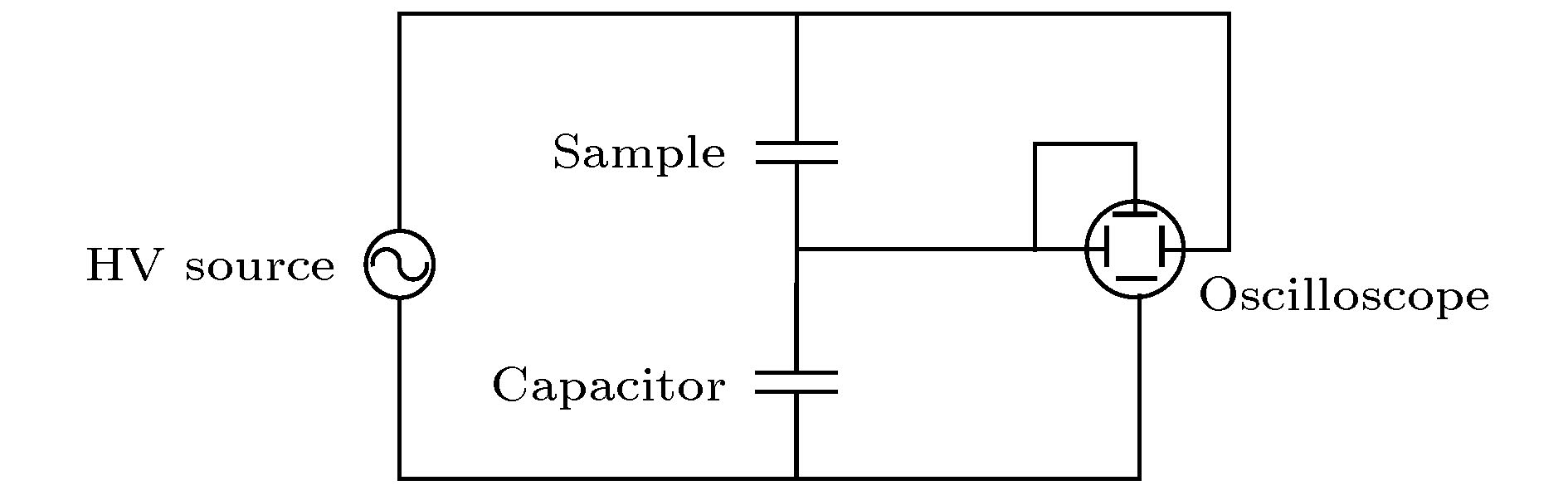图 2 Sawyer-Tower电路示意图Figure2. Sawyer-Tower circuit.
为了便于分析, 可将标准电容和测试样品串联回路简化为一个电容性负载C, 在正弦交变电压
早在1989年, Pan等[14]即通过放电电流曲线研究反铁电材料的相变特性, 结果表明反铁电材料的反向FE-AFE相变可在2 μs的时间内发生. 之后, Xu等[15]亦进行了相似的工作, 在PbLa(Zr, Sn, Ti)O3 (PLZST)反铁电薄膜材料中发现了反向相变时间可达6 ns. Zhang等[16]也发现反铁电的相变会导致其放电流的非线性增长, 通过放电电流的突增可大致判断反向相变时间在数百ns的时间范围. 但通过电流曲线仅能大致判断反铁电材料的相变时间, 其他关键参数如相变电场、极化曲线等无法获得.
2001年, Gundel等[17]将上升和下降时间为百ns级的脉冲方波施加在反铁电材料上, 对电流数值积分得到了极化强度, 然后通过电压和极化强度数据获得了铁电/反铁电材料的脉冲电滞回线, 直接证明了反铁电材料在快速脉冲电压下可以发生相变. 之后, 本研究组的李红刚等[18]利用相似的原理, 测得了PLZST反铁电陶瓷在脉冲电场下的电滞回线, 证明其AFE-FE和FE-AFE相变可在百ns量级时间内发生. 2016年, 本研究组进一步分析了测试频率对反铁电相变电场等参数的影响, 获得了μs量级的脉冲电滞回线, 结果表明反铁电在脉冲电场下的相变电场和极化强度发生了显著变化[11].
上述研究结果表明, 反铁电材料在快速变化的电场下, 极化和相变特性会发生显著变化, 这对反铁电材料的应用带来影响. 因此, 本文将进一步系统地研究反铁电材料在脉冲电场下的极化过程和相变行为, 并获得其在脉冲电场下的电滞回线. 利用脉冲电滞回线可得到反铁电材料在瞬态强电场下的极化强度、相变电场、相变时间等参数及储能密度的变化规律, 为反铁电材料的实际应用提供依据.
脉冲电滞回线的测试采用自行研制的实验平台[11], 如图3所示. 其基本工作原理为: 利用脉冲电压发生器产生一个单极性高电压脉冲, 将此脉冲注入反铁电陶瓷样品; 利用高压探头和罗氏线圈, 并结合示波器, 分别测得电压波形u(t)和电流波形i(t), t为时间.
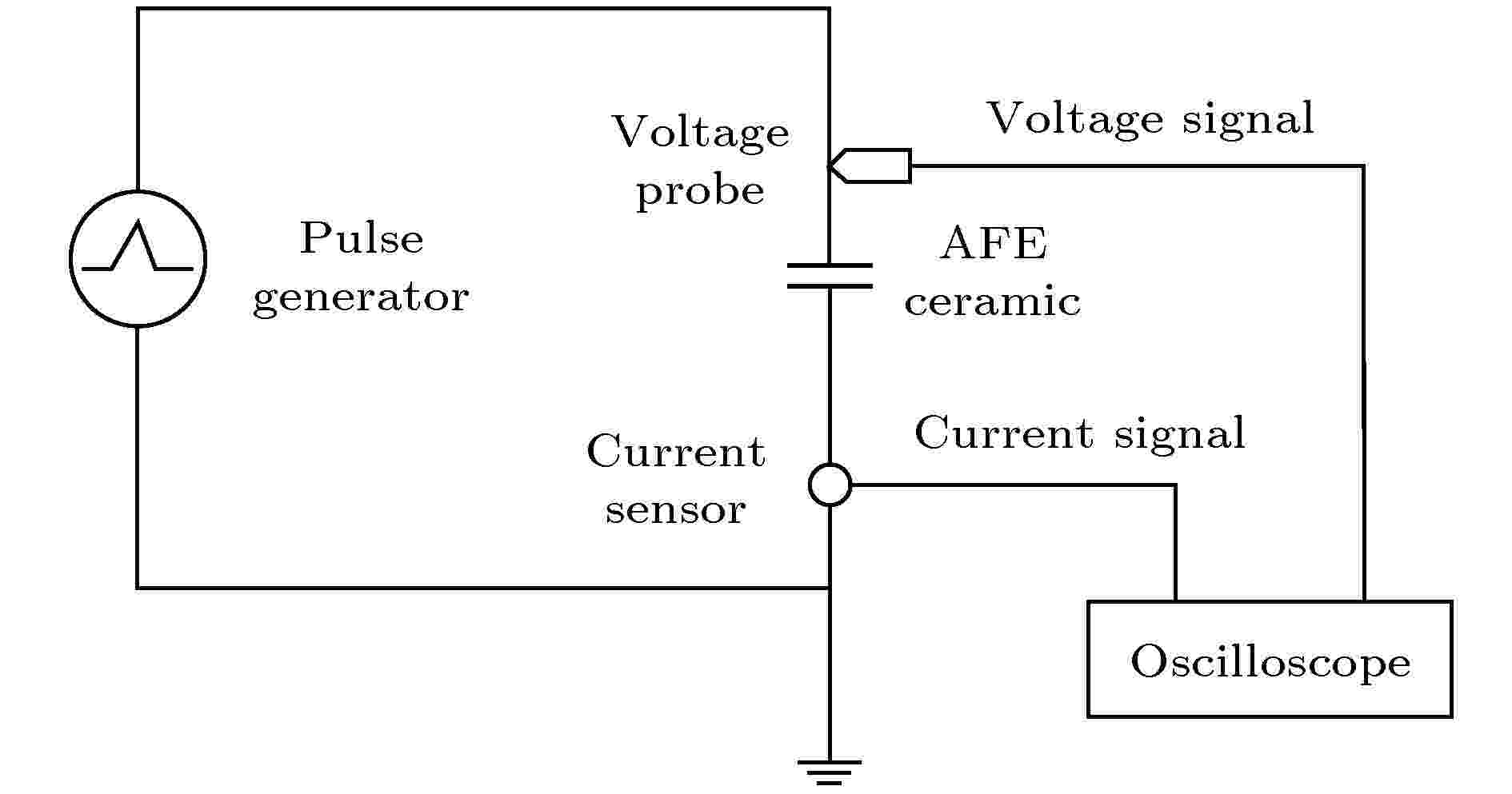图 3 脉冲电滞回线测试平台的电路原理图Figure3. Circuit diagram of the experimental setup for pulse hysteresis loop.
因此, 可获得反铁电陶瓷样品的电场数据E(t)和极化强度数据P(t):
3.1.反铁电陶瓷在μs脉冲下电滞回线
利用脉冲电滞回线测试平台对PLZST反铁电陶瓷进行脉冲电场下极化行为的研究. 首先测得脉冲电压和对应的电流波形, 然后根据电压波形获得电场曲线, 对测得的电流曲线进行积分获得极化强度曲线. 实验时脉冲电压幅值从200 V增加至2400 V, 间隔为200 V, 脉冲宽度保持在微秒级范围内, 部分结果如图4所示.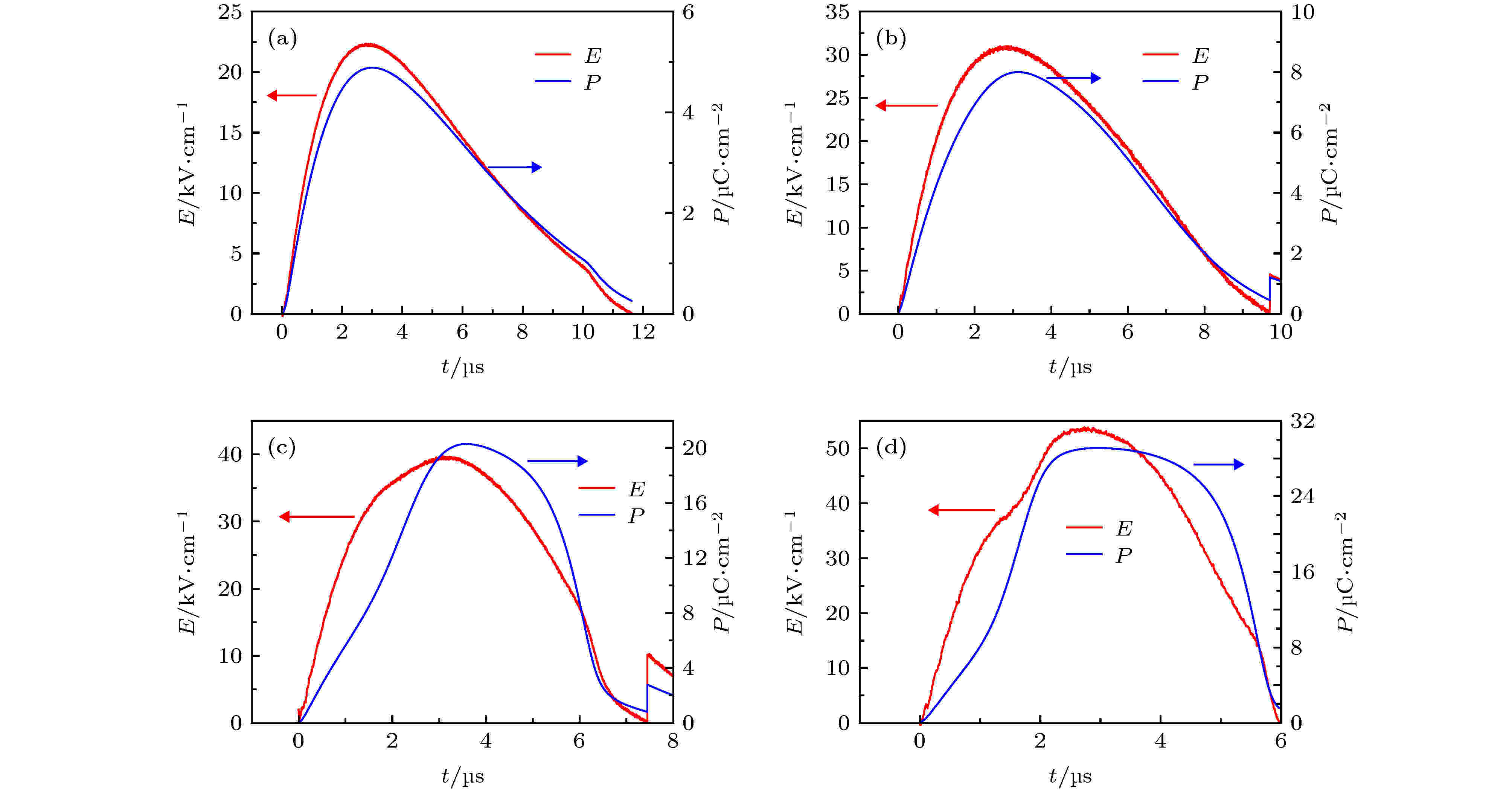
图 4 PLZST在不同电场幅值下极化强度曲线 (a) 22.22 kV·cm–1; (b) 31.11 kV·cm–1; (c) 40 kV·cm–1; (d) 53.33 kV·cm–1Figure4. P(t) curves of PLZST under electric field with different amplitudes: (a) 22.22 kV·cm–1; (b) 31.11 kV·cm–1; (c) 40 kV·cm–1; (d) 53.33 kV·cm–1.
由图4可知, 在低场下(31.11 kV·cm–1以下), 极化强度曲线与电场曲线形状基本一致, 无滞后现象. 此时极化强度较低, 且与外电场线性相关, 表现出线性介质的特征. 当电场增大至40 kV·cm–1以上时, 反铁电陶瓷发生电场诱导下的AFE-FE相变, 此时的极化强度突增, 极化强度与电压曲线出现了显著的滞后现象, 表现出非线性极化的特征.
由图4中电场和极化强度曲线可得到反铁电陶瓷在脉冲电压下的电滞回线, 同时测得了反铁电在10 Hz三角波电压下的电滞回线作为对比, 如图5所示.
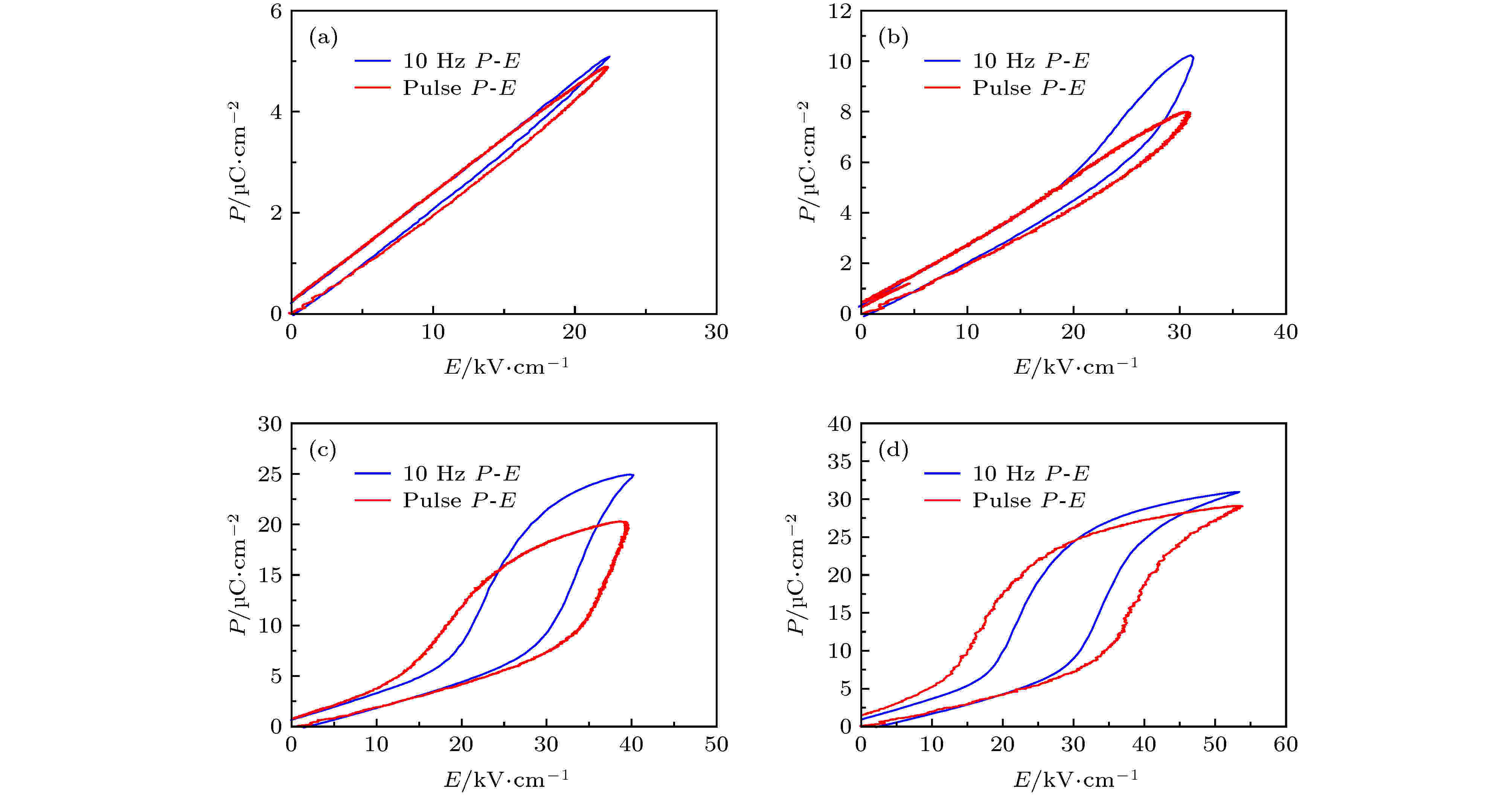图 5 PLZST的10 Hz和脉冲电滞回线 (a) 22.22 kV·cm–1; (b) 31.11 kV·cm–1; (c) 40 kV·cm–1; (d) 53.33 kV·cm–1Figure5. 10 Hz and pulse P-E curves of PLZST: (a) 22.22 kV·cm–1; (b) 31.11 kV·cm–1; (c) 40 kV·cm–1; (d) 53.33 kV·cm–1.
由图5可知: 当电场幅值为22.22 kV·cm–1时, 反铁电陶瓷的10 Hz与脉冲P-E曲线基本重合, 均为直线型; 电场提升至31.11 kV·cm–1时, 反铁电陶瓷的10 Hz P-E曲线表现出电场诱导AFE-FE相变的特征, 脉冲电场下P-E曲线仍然为直线型, 且脉冲电场下的极化强度低于10 Hz电场下对应的极化强度最大值; 电场增大至40.00 kV·cm–1时, 反铁电陶瓷的10 Hz和脉冲P-E曲线都表现出显著的AFE-FE相变特征, 极化强度出现突增, 但脉冲电场下对应极化强度较低, 且电滞损耗更大; 当电场为53.33 kV·cm–1时, 反铁电陶瓷的10 Hz和脉冲P-E曲线均接近饱和, 但相比10 Hz P-E曲线, 脉冲P-E曲线的极化强度仍较低, 正向相变电场EAFE-FE较大, 反向相变电场EFE-AFE较低, 电滞宽度ΔE和电滞损耗较大.
PLZST反铁电陶瓷在10 Hz电场下的极化强度记为P10 Hz, 在脉冲电场下的极化强度为Ppulse. 由图5的分析结果可知, 反铁电陶瓷在10 Hz和脉冲电场下极化强度幅值存在显著的差异, 定义其差值为ΔP = P10 Hz – Ppulse, 则ΔP随电场幅值的变化曲线如图6所示.
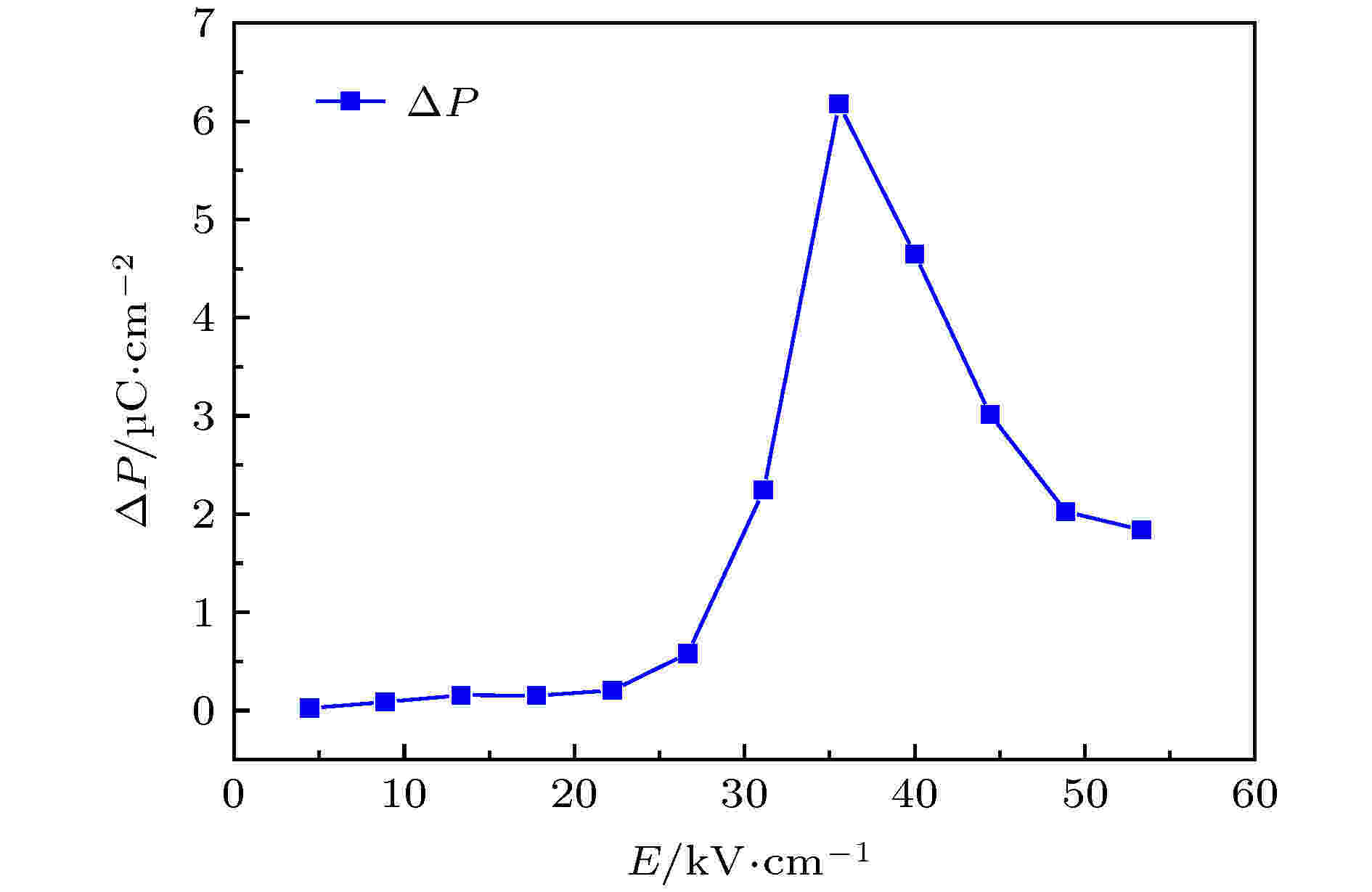图 6 PLZST在10 Hz与脉冲电场下极化强度差值ΔPFigure6. ΔP of PLZST under 10 Hz and pulse electric field.
如图6所示: 在低电场(低于25 kV·cm–1)下, PLZST在10 Hz和脉冲电场下的极化强度差别不大; 而当电场大于30 kV·cm–1后, 反铁电陶瓷在10 Hz电场下的极化强度显著大于其在脉冲电场下极化强度; 且随着电场的增大, 二者差值增大, 在35.56 kV·cm–1时二者的差值ΔP达到最大; 而电场超过35.56 kV·cm–1后, 极化强度的差值减小. 因此反铁电陶瓷在脉冲电场下要获得相同的极化强度, 所施加的脉冲电场幅值要高于10 Hz电场. 电场进一步提高, 反铁电陶瓷在10 Hz与脉冲电场的极化强度均趋于饱和, 导致二者的差值减小.
图5(d)的脉冲电滞回线表明反铁电陶瓷在相应的脉冲电场诱导下能发生相变, 且与准静态场下结果表现出显著的不同: 正向相变场EAFE-FE增大, 反向相变场EFE-AFE减小. 为定量地分析PLZST陶瓷相变电场的变化, 此处采用微分介电常数峰值确定相变场强. Feng等[19]在研究PLZST反铁电陶瓷的介电行为时, 提出利用微分介电常数判断其相变电场, 其定义为
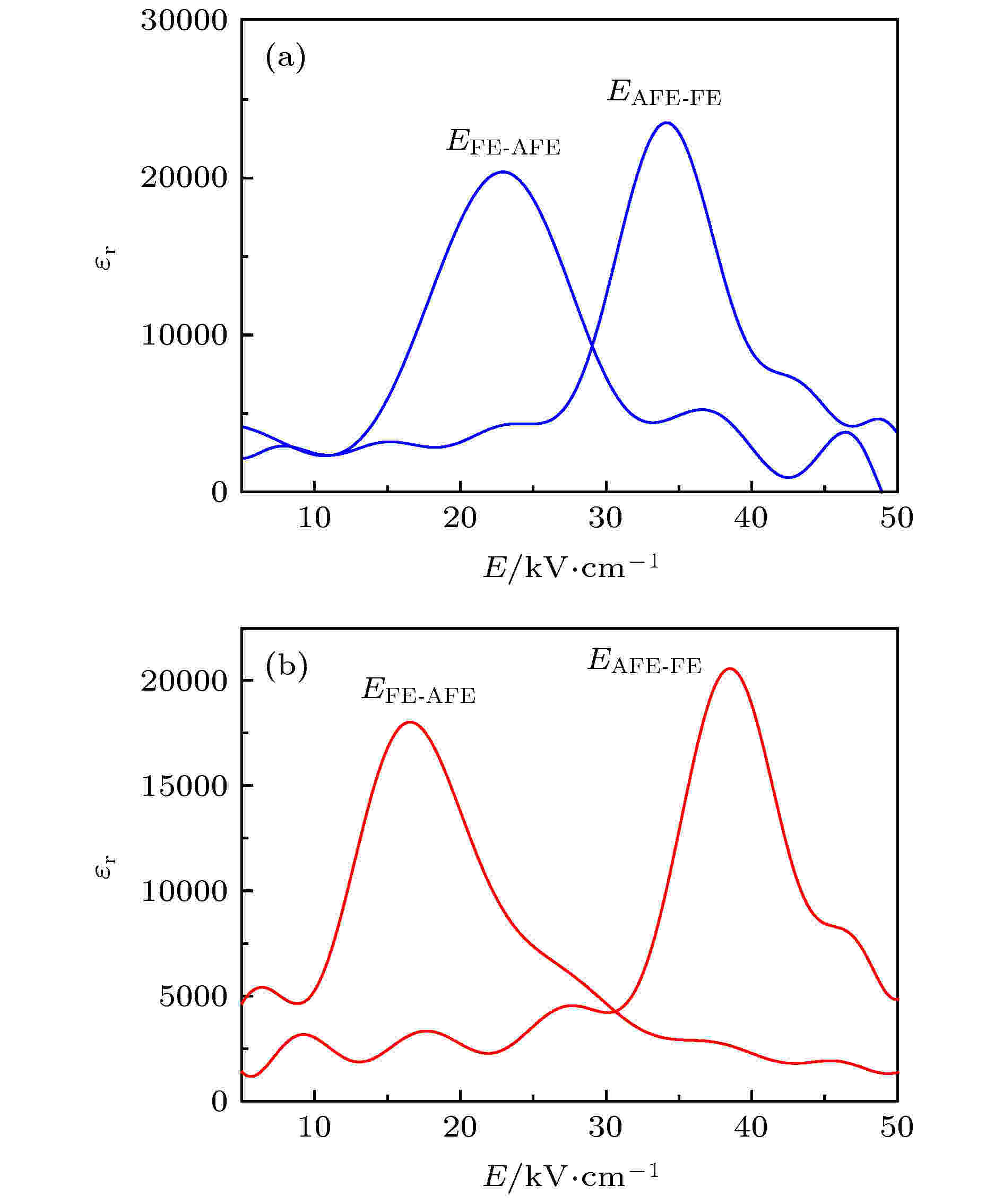图 7 PLZST在(a) 10 Hz与(b)脉冲电场下的微分介电常数Figure7. Differential permittivity of PLZST under (a) 10 Hz and (b) pulse electric field.
如图7所示, 在10 Hz电场和脉冲电场下, 微分介电常数曲线均具有两个显著的特征峰, 分别对应反铁电陶瓷的正向AFE-FE和反向FE-AFE相变, 对应相变电场值如表1所列.
| 电场类型 | EAFE-FE/ kV·cm–1 | EFE-AFE/ kV·cm–1 | ΔE/ kV·cm–1 |
| 10 Hz | 34.07 | 22.80 | 11.27 |
| 脉冲电场 | 38.48 | 16.53 | 21.95 |
表1PLZST在10 Hz与脉冲电场下相变电场
Table1.Phase transition fields of PLZST under 10 Hz and pulse electric field.
如表1所列, 在脉冲电场下, 反铁电陶瓷正向相变电场EAFE-FE由10 Hz电场下的34.07 kV·cm–1增大至38.48 kV·cm–1, 这表明在脉冲电场下, 要诱导反铁电陶瓷为铁电相, 需要更高幅值的电场; 在电压降低过程中, 样品由铁电相回到初始反铁电相所需电场值更低. 电滞宽度ΔE由10 Hz电场下的11.27 kV·cm–1 增大至21.95 kV·cm–1, 增大了约95%, 因此反铁电陶瓷在脉冲电场下的极化滞后效应更显著.
根据表1中相变电场值, 由极化电压波形可推知反铁电陶瓷发生相变的时间, 如图8所示.
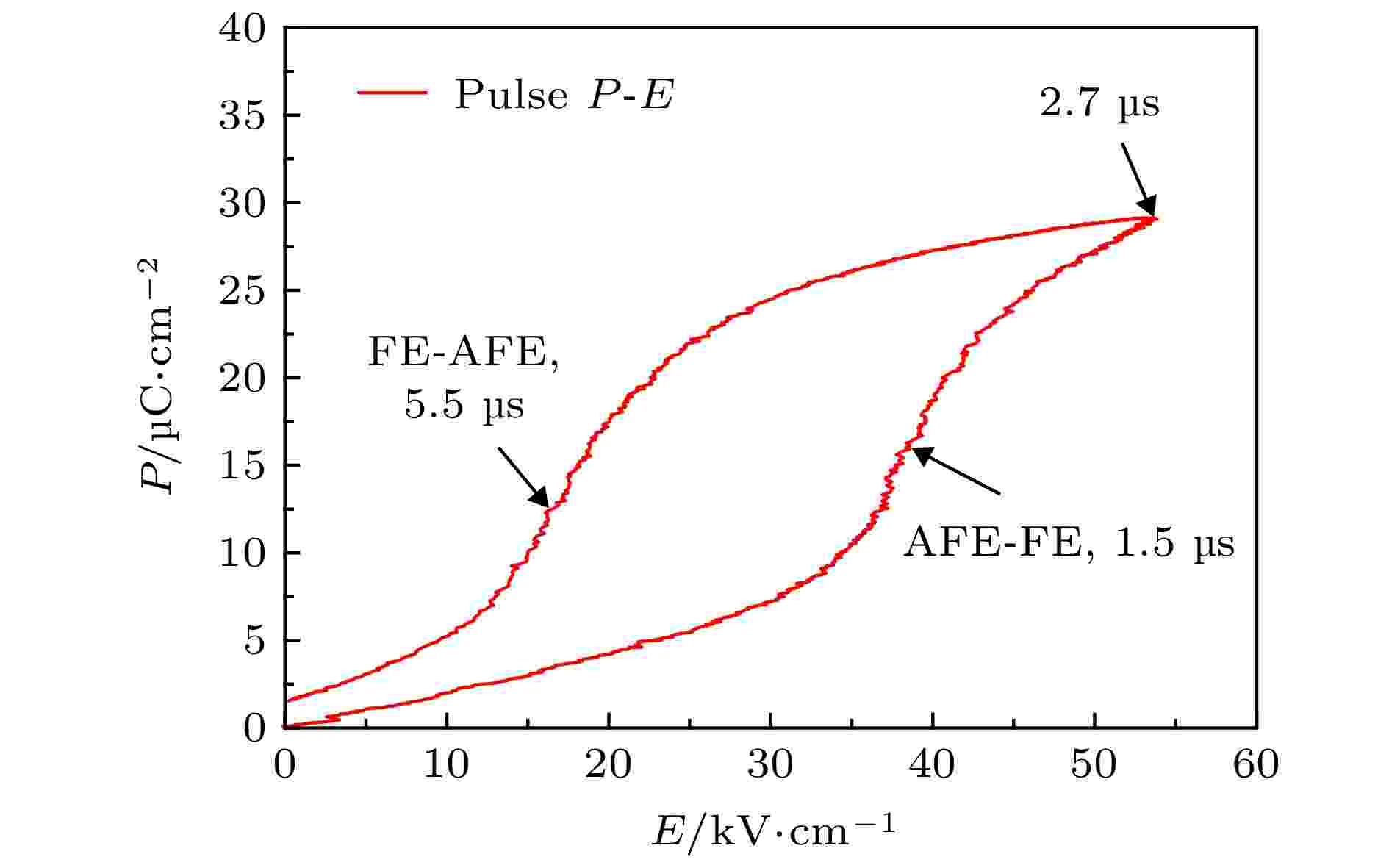图 8 PLZST在脉冲电场下相变时间Figure8. Phase transition time of PLZST under pulse electric field.
如图8所示, 反铁电正向相变发生在1.5 μs处, 反向相变发生在5.5 μs处. 因此反铁电陶瓷能在微秒时间范围内发生正向和反向相变. 此结论为反铁电陶瓷应用于快放电脉冲电容器、电压调节器等提供了依据.
2
3.2.反铁电陶瓷在脉冲电场下储能特性
如3.1节中所述, 反铁电陶瓷在脉冲电场下的电滞回线发生了显著变化, 包括相变电场、极化强度和电滞宽度等参数. 而上述参数的变化必然会导致其储能参数的变化, 包括充电过程中储存能量密度Wst、可恢复能量密度Wre和能量效率η. 实验中测试了不同电场下0.1, 1, 10, 50 Hz和脉冲电滞回线, 通过电滞回线可计算得Wst, Wre, η参数[11], 其中Wst在不同测试条件下随电场变化曲线如图9所示.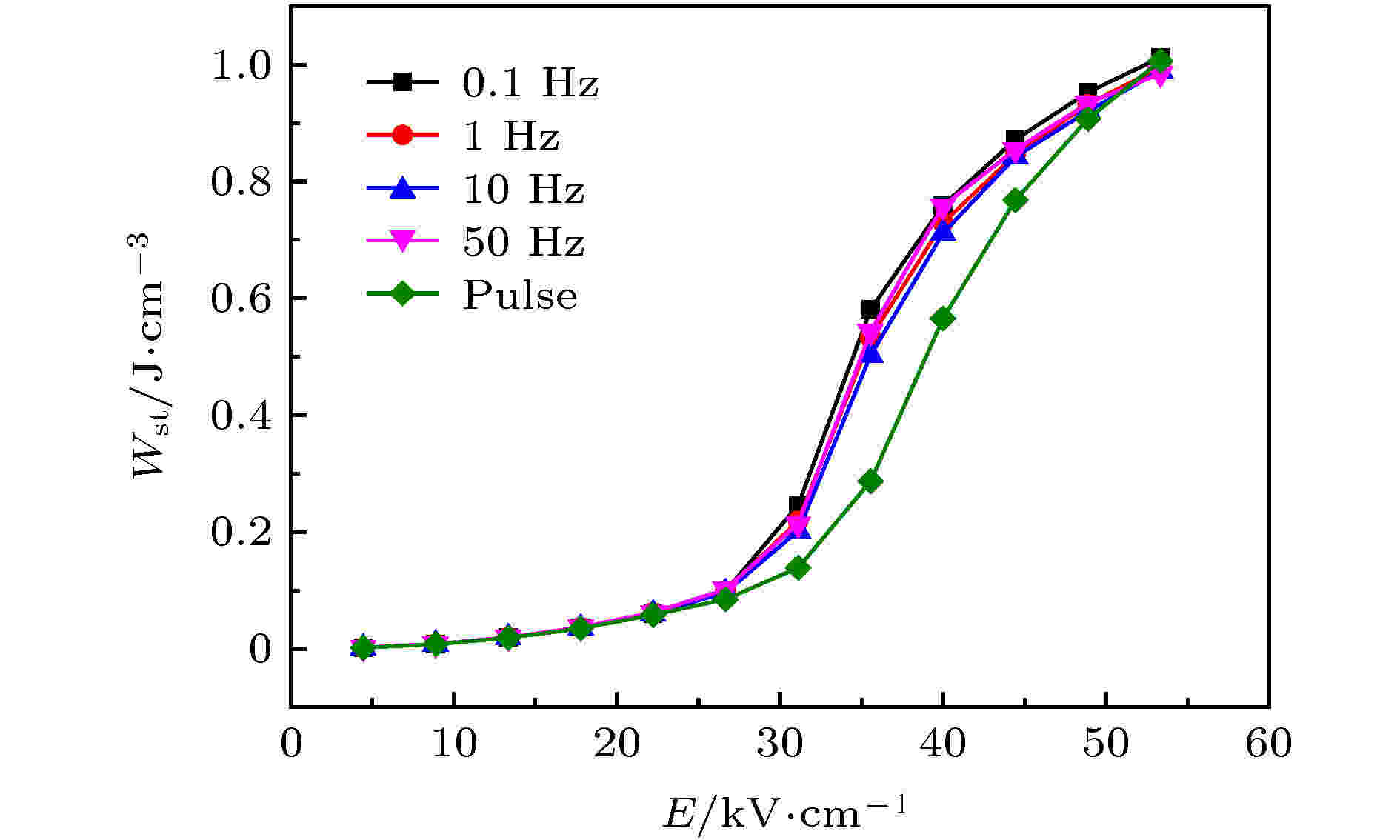
图 9 PLZST在0.1—50 Hz及脉冲电场下WstFigure9. Wst of PLZST under 0.1–50 Hz and pulse electric field
从图9可以看出, 反铁电陶瓷在充电过程中储存的能量密度Wst在0.1—50 Hz的范围内并无显著的变化, 而利用脉冲电滞回线计算得到的Wst与50 Hz以内Wst存在显著的差异: 低场下(低于22.22 kV·cm–1)脉冲Wst与0.1—50 Hz的Wst基本一致, 这是与图5(a)所示的两种电滞回线重合相符合; 相变场附近(22.22—35.56 kV·cm–1)时, 反铁电陶瓷在脉冲场下的极化强度显著低于其在0.1—50 Hz电场下极化强度, 极化强度差值ΔP在35.56 kV·cm–1时最大, 此阶段脉冲场下Wst显著低于0.1—50 Hz的Wst, 且在35.56 kV·cm–1时二者差值最大; 在高电场下(高于35.56 kV·cm–1), 反铁电陶瓷在0.1—50 Hz电场和脉冲电场下均能被诱导为铁电相, 且极化强度趋于饱和, 极化强度差值ΔP逐渐降低, 然而反铁电陶瓷在脉冲场下的正向相变场EAFE-FE显著高于其在10 Hz电场下的值, 这对提高Wst是有利的. 此时反铁电陶瓷在脉冲电场和0.1—50 Hz电场下储存的能量密度Wst逐步接近, 当电场为53.33 kV·cm–1时, 二者已经基本一致.
反铁电陶瓷在0.1—50 Hz和脉冲电场下的可恢复能量密度Wre变化曲线如图10所示.
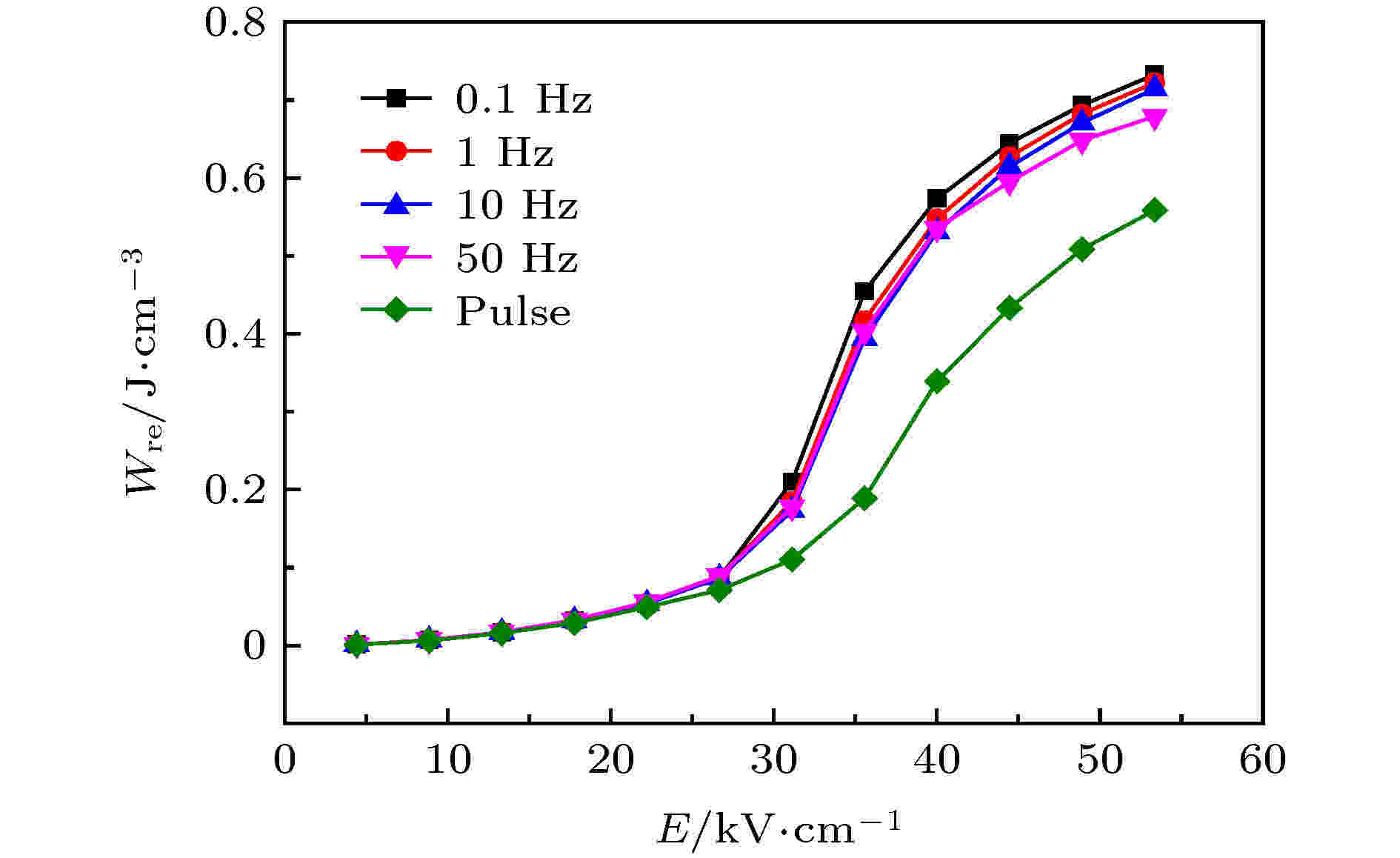图 10 PLZST在0.1—50 Hz及脉冲电场下WreFigure10. Wre of PLZST under 0.1–50 Hz and pulse electric field
如图10所示, 随着测试频率的提高, PLZST反铁电陶瓷的Wre-E曲线向下移, 特别在高场下Wre降低的程度更为显著. 在53.3 kV·cm–1电场下, 由0.1 Hz和50 Hz电滞回线计算所得Wre分别为0.73 J/cm3和0.68 J/cm3, 降低了约7%. 因此, 在0.1—50 Hz电场下, 反铁电相变场和极化强度受电场变化速率的影响, 其储能特性也会发生变化.
PLZST在脉冲与0.1—50 Hz电场下的Wre差距则更为显著, 且随着电场的提高, 差异逐渐变大. 这是因为反铁电陶瓷在脉冲场下最大极化强度Pmax和反向相变电场EFE-AFE均低于其在0.1—50 Hz电场下的值. 而Pmax和EFE-AFE的降低均会导致Wre的降低, 因此, 脉冲场下Wre显著低于0.1—50 Hz的Wre. 电场幅值为53.33 kV·cm–1时, 10 Hz电场下Wre为0.68 J/cm3, 脉冲电场下Wre为0.56 J/cm3, 降低了约20%.
为了衡量反铁电陶瓷在实际应用中的放电能量密度, 我们进一步测试了在53.33 kV·cm–1下反铁电陶瓷的脉冲放电电流曲线i(t), 如图11所示.
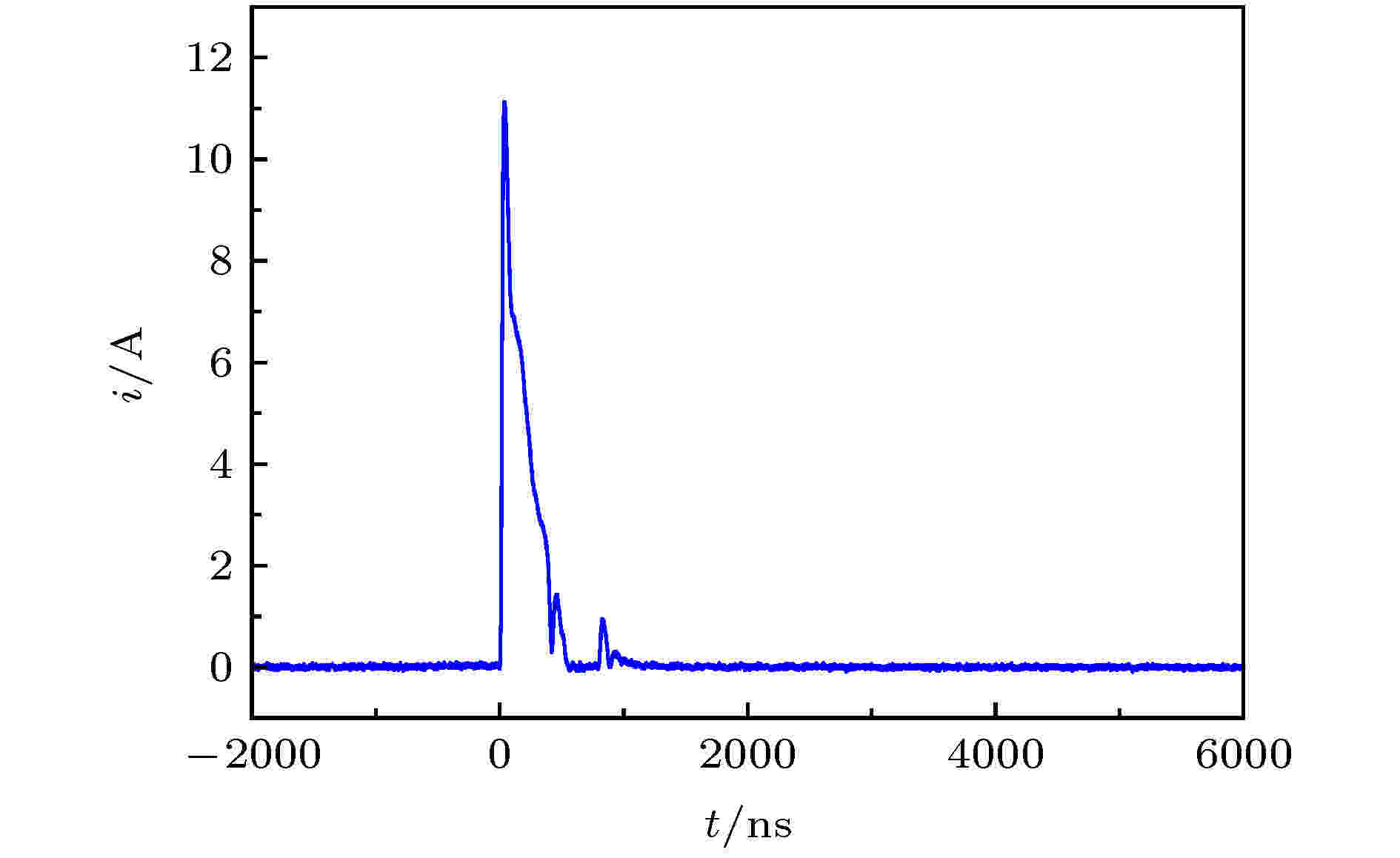图 11 PLZST脉冲放电电流(放电电阻100.4 Ω, 充电电场53.33 kV·cm–1)Figure11. Pulse discharge current curve of PLZST (with a load resistor of 100.4 Ω and charging electric field of 53.33 kV·cm–1)
利用图11中脉冲放电电流曲线, 通过(6)式可计算得到放电能量密度Wdis:
| 计算方法 | Wst/J·cm–3 | Wre 或 Wdis/J·cm–3 | η/% |
| 10 Hz电滞回线 | 0.99 | 0.71 (Wre) | 72.3 |
| 脉冲电滞回线 | 1.00 | 0.56 (Wre) | 55.5 |
| 放电电流 | 0.39 (Wdis) |
表2不同方式计算得PLZST反铁电陶瓷的储能参数(53.33 kV·cm–1)
Table2.Energy storage properties of PLZST calculated via different methods (53.33 kV·cm–1).
从表2可以看出, 电场变化快慢对储存的能量密度Wst影响不大, 但是对释放的能量密度Wre、放电能量密度Wdis和能量效率η有显著的影响. 10 Hz电滞回线中, 电场从最大值降为零的过程为0.025 s; 脉冲电滞回线中, 电场降为零的过程约为3 μs; 脉冲放电中, 电场降为零的过程不到1 μs. 结合Wre随测试频率增高而降低的事实, 可推断: 对反铁电陶瓷, 电场降低过程的快慢对其释放的能量有关键的影响, 此过程越快, 以电能形式释放的能量越小. 因此, 利用低频下的电滞回线来衡量反铁电材料的储能特性具有一定的局限性, 可恢复能量密度Wre并不能代表其在脉冲放电中能快速释放的能量密度Wdis, 本实验中Wdis仅为10 Hz下Wre的54.9%. 此外, 由于脉冲电场下电滞宽度ΔE变大, 导致其电滞损耗增大, 能量效率η由10 Hz电场下的72.3%降低为脉冲电场下的55.5%.
当前电滞回线最大的问题是测试频率较低, 这给研究铁电/反铁电材料极化、相变等随电场变化的时间响应带来很大的困难. 铁电/反铁电材料的极化、电滞、矫顽场或相变电场等均会随电滞回线测试频率的变化而变化, 其本质反映了铁电/反铁电材料极化反转、相变的时间响应[2,20], 这也是铁电物理学中的重要现象. 而上述参数对相关材料的实际应用也有重要的意义. 目前, 电滞回线测试频率一般在1000 Hz以内, 仅能反映上述物理过程在毫秒时间范围内的响应. 因此, 获取更高频率如MHz或GHz的电滞回线具有重要的物理意义和工程价值.
由于高频电滞回线测试的困难, ****也尝试通过其他的方法来研究上述物理过程在更短时间范围内的响应, 其中脉冲电学测量手段是一种有效的手段. 例如, ****通过测试钛酸钡铁电晶体的脉冲极化电流, 研究其极化反转以及电畴生长的过程, 该方法已经成为了铁电物理学中一种经典的实验手段[2,20]. 2017年, Chen等[21]为解决PMN-PT压电单晶高频矫顽场的测量难题, 通过脉冲法测得了等效频率高达5 MHz的结果, 为PMT-PT压电单晶在高频下的应用提供了重要参考. 对于反铁电材料, ****也通过脉冲放电电流, 定性地分析了陶瓷体材料相变时间大致在μs范围[14]. 但上述方法均未获得铁电/反铁电材料的电滞回线, 获取的物理信息有限, 对部分结果只能定性的分析.
本文所采用的方法与上述方法在本质上是相似的, 均采用脉冲电学测量的手段, 达到研究反铁电材料极化、相变随电场时间响应的目的. 更进一步地, 本研究通过测试方法的改进, 获取了电滞回线, 提取出更丰富的物理信息. 直接证明了反铁电材料在微秒时间范围内的极化、相变的时间响应, 并与毫秒范围内的时间响应进行了对比, 获得了相变电场、相变时间等关键参数的变化规律.
由图5中的结果可知, 反铁电到铁电相变的物理过程需要一定的时间, 当电场变化速率过快时, 反铁电有可能无法完成到铁电相的转变. 例如图5(b)中所示, 反铁电材料在低频下已经表现出相变的特征, 而在脉冲电场下依然表现线性介质的特征. 同时, 与铁电材料的矫顽场和测试频率相关的现象类似, 反铁电材料的相变场也受电场变化速率的影响. 本研究中受限于脉冲功率电源的限制, 仅能初步证明反铁电在微秒量级的相变, 且相变参数发生了变化. 若能缩短脉冲电源的电压上升、下降时间到ns甚至更短时间, 则能更深入地研究反铁电相变的动态行为. 同时, 反铁电的相变过程也会受样品厚度、温度等物理条件的影响, 它们对反铁电的相变速度也会产生影响, 这也是后期需要进一步进行的工作.
本研究中脉冲电源周期不可调, 因此仅获得了单一等效频率的电滞回线. 若能获得系列化等效频率, 如10 kHz, 100 kHz, 1 MHz到1 GHz范围内的电滞回线, 将会弥补这一频段研究的空白, 同时也会验证反铁电相变动力学的一些物理模型. 例如, Kim等[12]在研究反铁电电滞回线的频率特性时, 建立了电滞面积与测试频率的关系式, 但其实验中最大测试频率仅为1000 Hz, 其建立的物理模型是否能满足更高频率还未得到验证.
因此, 脉冲电滞回线对反铁电的极化、相变等物理现象的研究具有重要的作用, 它使上述物理过程的研究拓展至微秒甚至纳秒时间范围, 对其实际应用也有重要参考价值. 同时, 本方法也可推广至铁电、压电材料的研究, 对铁电动力学等的研究也有重要的参考价值.
