摘要:过渡金属轻元素化合物是高硬度材料的潜在候选. 以往研究多集中在二元过渡金属硼化物、碳化物和氮化物, 三元相的研究则相对较少. 本文通过提炼和堆垛已知相Nb₃B₃C (Ta₃B₃C)和Nb₄B₃C₂ (Ta₄B₃C₂)的结构基元, 构建不同组分的Nb-B-C和Ta-B-C三元相结构模型, 采用第一性原理计算方法, 计算所建结构的形成焓、声子谱和弹性常数, 通过判断其热力学、动力学和力学稳定性, 绘出了三元Nb-B-C和Ta-B-C相图, 成功预测了5种Nb-B-C和6种Ta-B-C三元稳定相. 力学和电学性能计算结果显示Nb-B-C和Ta-B-C三元稳定相均为高硬度导电材料, 硬度大约为25 GPa.
关键词: 硬质材料/
相图/
第一性原理计算/
稳定性

English Abstract

全文HTML

--> --> -->

硬质材料拥有高硬度、抗高压、耐摩擦磨损等优异的力学性能, 同时又具有良好的电学、光学和热学性能, 在众多工业领域都发挥着重要的作用^[1]. 高硬度材料通常可以分为两类: 第一类材料是轻元素B, C, N, O结合所形成的强共价键化合物, 比如金刚石、立方BN、立方BC₂N、立方BC₅、B₆O、不同成分C-N材料等^[2-8]. 这一类材料往往是超硬材料(维氏硬度H_v > 40 GPa), 硬度比较高, 但是合成条件比较苛刻, 一般需要高温高压才能合成. 另一类高硬度材料存在于过渡金属(transition metals, TM)的轻元素化合物, 比如硼化物、碳化物和氮化物. 过渡金属硼化物体系的研究主要集中在TMB₂组分, 比如2005年 H_v超过20 GPa的OsB₂被成功制备^[9], 2007年Chung等^[10]采用电弧方法成功合成出了RuB₂和ReB₂. 过渡金属碳化物体系的研究较多集中在TiC, ZrC, HfC, VC, NbC, TaC等TMC组分, 这些化合物往往通过常压合成方法均可制备得到. 在过渡金属氮化物体系中, OsN₂, IrN₂和PtN₂化合物采用对顶砧高压技术被成功合成^[11,12], 这些材料均为极难压缩材料, 但合成条件比较苛刻, 合成所需压力很高. 关于过渡金属硼化物、碳化物和氮化物的研究现状, 可参阅综述文献[2,13,14].
过渡金属轻元素化合物的研究主要集中于二元过渡金属硼化物、碳化物和氮化物, 三元相的研究则相对较少. 由于硼、碳、氮三种元素在元素周期表中毗邻, 三种元素原子大小差不多, 其核外电子排布也相近, 因此可推理, 三元过渡金属轻元素化合物的存在是完全有可能的. 2001年德国科学家Hillebrecht和Gebhardt^[15]以Nb, B和C三种单质作为反应原料, 以Al-Cu金属合金作为助熔剂, 成功制备了Nb₃B₃C和Nb₄B₃C₂晶体, 并给出了其晶体结构. 考虑到类质同晶效应, 我们以Nb₃B₃C和Nb₄B₃C₂晶体结构为模板, 用28种其他过渡金属元素分别替代两种结构中Nb原子位置, 理论计算了这些新构建化合物的结构稳定性, 找到了Ta₃B₃C和Ta₄B₃C₂两种稳定新相^[16]. 由于Hillebrecht和Gebhardt所合成的晶体尺寸较小, 所以实验未能测得其性能^[15]. 采用第一性原理计算了实验合成的Nb₃B₃C和Nb₄B₃C₂相、以及理论预测稳定的Ta₃B₃C和Ta₄B₃C₂相的力学和电学性能, 显示这4种化合物都是导电的高硬度材料^[16].
根据材料基因组学, 晶体材料最基本的结构基元是中心原子与周围原子所组成的配位多面体. 结构基元按照一定的空间排列方式进行周期排列, 从而构成晶体. 结构基元内的成键方式决定了晶体材料的本征物理化学性质, 因此从这个角度说, 结构基元就是材料的基因. 例如, Wang等^[17]和Xiao等^[18]以“无机类苯环”或“无机类苯环芳香性”作为功能结构基元, 设计了一系列锂电池正极材料.
本文通过分析Nb₃B₃C和Nb₄B₃C₂ (Ta₃B₃C和Ta₄B₃C₂)结构, 得出其结构基元, 通过裁剪和堆垛结构基元, 构建不同组分的Nb-B-C和Ta-B-C结构模型, 采用第一性原理计算方法, 计算所建结构的形成焓、声子谱和弹性常数, 判断其热力学、动力学和力学稳定性, 基于所得Nb-B-C和Ta-B-C三元相图, 得出稳定的Nb-B-C和Ta-B-C化合物, 并研究稳定相的力学和电学性能.

计算采用基于密度泛函理论的第一性原理平面波赝势方法, 由VASP软件包^[19]完成. 结构优化过程中, 采用全优化方式, 即原子位置和晶格常数未做任何限制. 电子间交换关联能采用广义梯度近似下的PBE泛函. 平面波截断能E_cut设置为600 eV. 赝势采用全电子投影缀加平面波方法^[20]. Nb原子的价电子为4p⁶4d⁴5s¹, Ta原子的价电子为5p⁶5d³6s², B原子的价电子为2s²2p¹, C原子的价电子为2s²2p². 第一布里渊区积分采用Monkhorst-Pack形式的特殊K点方法, K点精度设置为2π × 0.03 ?^–1. 优化过程中能量迭代收敛标准为1 × 10^–5 eV/atom. 弹性常数的计算采用应力应变方法^[21]. 声子谱的计算采用有限位移法, 由PHONOPY软件^[22]计算完成.

2

-->

3.1.构建结构

由于Nb₃B₃C和Ta₃B₃C, Nb₄B₃C₂和Ta₄B₃C₂结构相同, 所以在以下讨论中以Ta₃B₃C和Ta₄B₃C₂为例进行说明. 图1给出了Ta₃B₃C和Ta₄B₃C₂的晶体结构. 可以看出Ta₃B₃C和Ta₄B₃C₂都具有层状的堆垛方式, 堆垛的单元为Ta-C区和Ta-B区. 在Ta-C区中, C原子(Ta原子)处于周围6个Ta原子(C原子)所形成的八面体的中心, 组成岩盐矿型晶体结构, 所以Ta原子和C原子的配位数均为6. 在Ta-B区中, Ta原子和B原子形成AlB₂型结构, B原子位于6个Ta原子所形成的三棱柱中心. 每个B原子除了与这6个Ta原子成键以外, 还与相邻的3个B原子成键, 因此其配位数为9. 通过分析结构, 可以得知Ta₆C八面体和Ta₆B三棱柱就是这两个结构的结构基元. Ta₃B₃C和Ta₄B₃C₂两相的区别就在于具有不同的结构基元层数.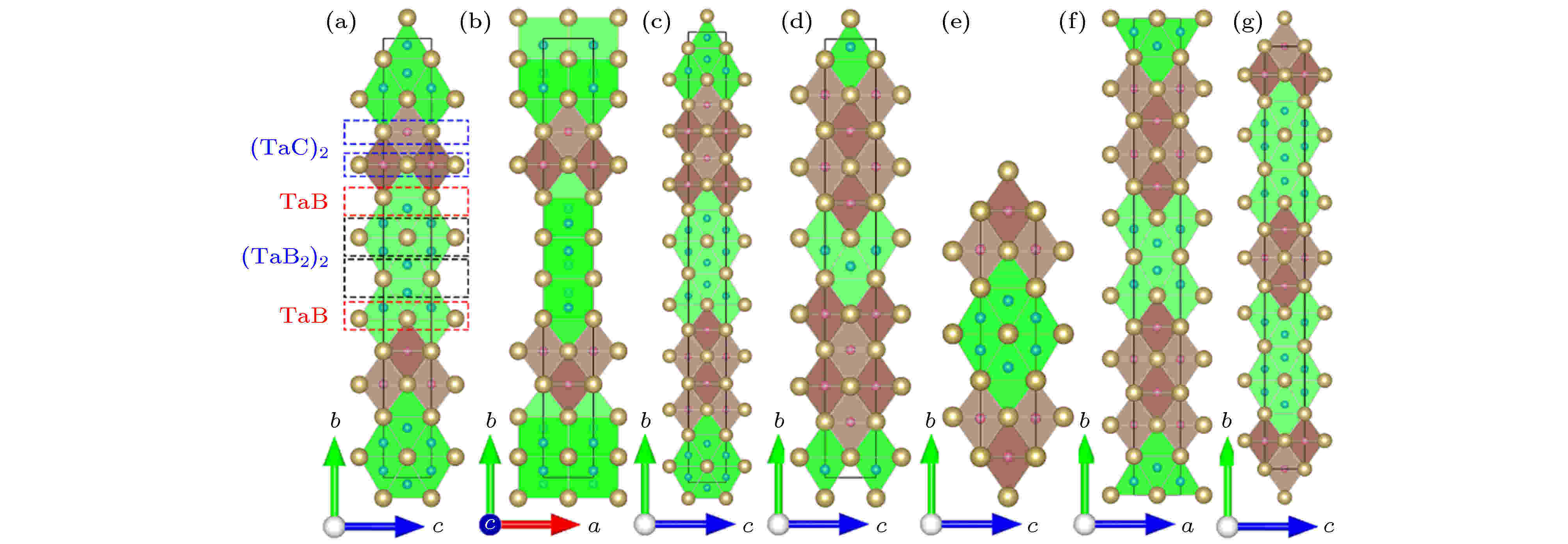
图 1 (a), (b) Ta₃B₃C; (c) Ta₄B₃C₂; (d) Ta₃BC₂; (e) Ta₆B₄C₃; (f) Ta₇B₄C₄; (g) Ta₇B₆C₃的晶体结构. 棕球: Ta原子; 蓝球: B原子; 粉球: C原子. Ta₆B三棱柱和Ta₆C八面体分别用绿色和褐色表示
Figure1. The crystal structures of (a), (b) Ta₃B₃C; (c) Ta₄B₃C₂; (d) Ta₃BC₂; (e) Ta₆B₄C₃; (f) Ta₇B₄C₄; (g) Ta₇B₆C₃. The light brown, blue and pink spheres represent Ta, B, and C atoms, respectively. The Ta₆B triangular prisms and Ta₆C octahedrons are painted green and dark brown.

通过调整Ta₆C八面体和Ta₆B三棱柱的数量, 可以构造一系列以Ta₆C八面体和Ta₆B三棱柱为结构基元的三元Ta-B-C化合物. 通过分析图1中所示Ta₃B₃C和Ta₄B₃C₂结构, 可以得出该系列Ta-B-C化合物结构式为TaB(TaB₂)_mTaB(TaC)_n, 化学式为Ta_{(m + n + 2)}B_{(2m + 2)}C_n. 对于Ta₃B₃C相来说, m = 2, n = 2; 对于Ta₄B₃C₂相来说, m = 2, n = 4. 在本文中限定m取值范围为0 ≤ m ≤ 4, n取值范围为1 ≤ n ≤ 4. 因此通过m和n数值的排列组合, 可以分别构建20种三元Nb-B-C化合物和20种三元Ta-B-C化合物, 如表1中所列. 部分Ta-B-C化合物晶体结构见图1中所示.

m	n	空间群	模型	晶格参数/?			模型	晶格参数/?
				a	b	c		a	b	c
0	1	Cmmm	Nb3B2C	3.254	13.808	3.141	Ta3B2C	3.240	13.697	3.127
0	2	Cmcm	Nb2BC	3.235	18.330	3.153	Ta2BC	3.220	18.165	3.140
0	3	Cmmm	Nb5B2C3	3.225	22.903	3.153	Ta5B2C3	3.199	22.659	3.138
0	4	Cmcm	Nb3BC2	3.214	27.376	3.156	Ta3BC2	3.198	27.132	3.150
1	1	Pmmm	Nb4B4C	3.290	18.994	3.145	Ta4B4C	3.277	18.878	3.127
1	2	Immm	Nb5B4C2	3.267	23.600	3.150	Ta5B4C2	3.248	23.377	3.138
1	3	Pmmm	Nb6B4C3	3.243	28.028	3.154	Ta6B4C3	3.225	27.872	3.141
1	4	Immm	Nb7B4C4	3.242	32.545	3.158	Ta7B4C4	3.224	32.315	3.147
2	1	Cmmm	Nb5B6C	3.302	24.414	3.134	Ta5B6C	3.289	24.208	3.122
2	2	Cmcm	Nb3B3C	3.284	28.877	3.144	Ta3B3C	3.267	28.688	3.133
2	3	Cmmm	Nb7B6C3	3.264	33.364	3.148	Ta7B6C3	3.246	33.164	3.136
2	4	Cmcm	Nb4B3C2	3.257	37.874	3.153	Ta4B3C2	3.243	37.609	3.141
3	1	Pmmm	Nb6B8C	3.309	14.889	3.137	Ta6B8C	3.298	14.788	3.122
3	2	Immm	Nb7B8C2	3.290	34.247	3.144	Ta7B8C2	3.276	34.007	3.131
3	3	Pmmm	Nb8B8C3	3.276	19.350	3.148	Ta8B8C3	3.258	19.235	3.135
3	4	Immm	Nb9B8C4	3.268	43.255	3.151	Ta9B8C4	3.252	42.977	3.138
4	1	Cmmm	Nb7B10C	3.312	35.192	3.131	Ta7B10C	3.299	34.990	3.116
4	2	Cmcm	Nb4B5C	3.296	39.694	3.139	Ta4B5C	3.280	39.441	3.125
4	3	Cmmm	Nb9B10C3	3.281	44.206	3.142	Ta9B10C3	3.263	43.924	3.130
4	4	Cmcm	Nb5B5C2	3.273	48.729	3.145	Ta5B5C2	3.257	48.400	3.134

表1不同成分Nb_{(m + n + 2)}B_{(2m + 2)}C_n和Ta_{(m + n + 2)}B_{(2m + 2)}C_n晶体的结构参数
Table1.Structural parameters of Nb_{(m + n + 2)}B_{(2m + 2)}C_n and Ta_{(m + n + 2)}B_{(2m + 2)}C_n crystals.

表1给出了构建的20种三元Nb-B-C化合物和20种三元Ta-B-C化合物的空间群及其结构优化后的晶格参数. 全部结构均为正交晶系. 当m为偶数、n为奇数时, 对称性为Cmmm; m为偶数、n为偶数时, 对称性为Cmcm; m为奇数、n为奇数时, 对称性为Pmmm; m为奇数、n为偶数时, 对称性为Immm. 各个结构在a和c轴方向排布相同, 只是沿b轴层数不同, 所以各个结构的晶格参数a和c大小很接近.
2 -->

3.2.热力学稳定性

鉴于Nb₃B₃C, Nb₄B₃C₂, Ta₃B₃C和Ta₄B₃C₂皆为稳定相^[16], 因此构造的其他组分三元Nb-B-C和Ta-B-C体系中也可能存在稳定结构. 一个热力学稳定的三元化合物, 意味着其不能分解成单质、二元相以及其他三元相的任意组合, 也就是其能量要小于相应单质、二元相以及其他三元相的任意组合. 首先判断所构建的三元Nb-B-C化合物和三元Ta-B-C化合物相对于单质的稳定性, 计算公式如下:

$\begin{split}\Delta {H_{{\rm{elements}}}} =\; & [(x + y + z) {H_{{\rm{TM}} _x{\rm{B}}_y{\rm{C}}_z}} - x {H_{{\rm{TM}}}} \\ &- y {H_{\rm{B}}} - z {H_{\rm{C}}}]/(x + y + z).\end{split}$

式中$ \Delta {H_{{\rm{elements}}}} $表示TM_xB_yC_z (TM = Ta或Nb)相对其三种单质的形成焓(eV/atom), ${H}_{{\rm{T}}{\rm{M}}_x{\rm{B}}_y{\rm{C}}_z}$, $ {H}_{{\rm{T}}{\rm{M}}} $, $ {H}_{{\rm{B}}} $和$ {H}_{{\rm{C}}} $分别是三元TM_xB_yC_z相、单质TM、单质硼以及石墨的焓值(eV/atom). 如果$ \Delta{H}_{\rm{elements}} > 0$, 则意味着三元相是不稳定的; 否则就说明三元相相对其三种单质材料来说是稳定的. 三元Nb-B-C化合物和三元Ta-B-C化合物相对单质的形成焓列于表2中. 可见所有化合物相对单质的形成焓均为负值, 这说明相对单质, 所构建的Nb-B-C化合物和Ta-B-C化合物都是稳定的.

Phases	$ \Delta{H}_{\rm{elements}} $	$ \Delta{H}_{\rm{comp}} $	最稳定竞争组合	Phases	$ \Delta{H}_{\rm{elements}} $	$ \Delta{H}_{\rm{comp}} $	最稳定竞争组合
Nb3B2C	–0.620	0.070	Nb3B4 + 6NbB + Nb6C5 = 5Nb3B2C	Ta3B2C	–0.651	0.086	Ta3BC2 + 3TaB = 2Ta3B2C
Nb2BC	–0.619	0.029	Nb3B4 + NbB + Nb6C5 = 5Nb2BC	Ta2BC	–0.664	0.035	Ta3BC2 + TaB = 2Ta2BC
Nb5B2C3	–0.586	0.036	3Nb3B4 + Nb7B4C4 + 4Nb6C5 = 8Nb5B2C3	Ta5B2C3	–0.655	0.021	3Ta3BC2 + TaB = 2Ta5B2C3
Nb3BC2	–0.586	0.019	Nb3B4 + 3Nb7B4C4 + 4Nb6C5 = 16Nb3BC2	Ta3BC2	–0.660	–0.002	TaB + 2TaC = Ta3BC2
Nb4B4C	–0.679	0.030	3Nb3B4 + Nb7B4C4 = 4Nb4B4C	Ta4B4C	–0.691	0.044	Ta7B4C4 + 3Ta3B4 = 4Ta4B4C
Nb5B4C2	–0.668	0.006	Nb3B4 + Nb7B4C4 = 2Nb5B4C2	Ta5B4C2	–0.694	0.019	Ta7B4C4 + Ta3B4 = 2Ta5B4C2
Nb6B4C3	–0.645	0.005	Nb3B4 + 3Nb7B4C4 = 4Nb6B4C3	Ta6B4C3	–0.693	0.004	3Ta7B4C4 + Ta3B4 = 4Ta6B4C3
Nb7B4C4	–0.632	–0.006	3Nb3B4 + 2C + 2Nb6C5 = 3Nb7B4C4	Ta7B4C4	–0.685	–0.017	3Ta3B4 + 4TaC = Ta7B4C4
Nb5B6C	–0.697	0.015	3Nb3B4 + C + 2Nb3B3C = 3Nb5B6C	Ta5B6C	–0.697	0.024	C + Ta5B6 = Ta5B6C
Nb3B3C	–0.685	–0.001	3Nb3B4 + C + 3Nb4B3C2 = 7Nb3B3C	Ta3B3C	–0.699	0.010	3Ta7B4C4 + 9Ta3B4 + 4C = 16Ta3B3C
Nb7B6C3	–0.664	0.0005	Nb3B3C + Nb4B3C2 = Nb7B6C3	Ta7B6C3	–0.695	0.0008	5Ta7B4C4 + 7Ta3B4 + 4C = 8Ta7B6C3
Nb4B3C2	–0.648	–0.001	5Nb3B4 + 4C + 7Nb7B4C4 = 16Nb4B3C2	Ta4B3C2	–0.684	0.002	7Ta7B4C4 + 5Ta3B4 + 4C = 16Ta4B3C2
Nb6B8C	–0.695	0.019	2Nb3B4 + C = Nb6B8C	Ta6B8C	–0.685	0.034	2Ta3B4 + C = Ta6B8C
Nb7B8C2	–0.683	0.008	3Nb3B4 + 2C + 4Nb3B3C = 3Nb7B8C2	Ta7B8C2	–0.686	0.020	Ta7B4C4 + 7Ta3B4 + 4C = 4Ta7B8C2
Nb8B8C3	–0.665	0.008	C + 8Nb3B3C = 3Nb8B8C3	Ta8B8C3	–0.684	0.012	Ta7B4C4 + 3Ta3B4 + 2C = 2Ta8B8C3
Nb9B8C4	–0.651	0.008	C + 5Nb3B3C + 3Nb4B3C2 = 3Nb9B8C4	Ta9B8C4	–0.675	0.013	3Ta7B4C4 + 5Ta3B4 + 4C = 4Ta9B8C4
Nb7B10C	–0.693	0.021	C + 2Nb2B3 + Nb3B4 = Nb7B10C	Ta7B10C	–0.677	0.030	TaB2 + 2Ta3B4 + C = Ta7B10C
Nb4B5C	–0.684	0.011	2C + Nb3B3C + 3Nb3B4 = 3Nb4B5C	Ta4B5C	–0.679	0.026	Ta7B4C4 + 19Ta3B4 + 12C = 16Ta4B5C
Nb9B10C3	–0.668	0.012	C + 2Nb3B3C + Nb3B4 = Nb9B10C3	Ta9B10C3	–0.677	0.019	3Ta7B4C4 + 17Ta3B4 + 12C = 8Ta9B10C3
Nb5B5C2	–0.655	0.011	C + 5Nb3B3C = 3Nb5B5C2	Ta5B5C2	–0.670	0.018	5Ta7B4C4 + 15Ta3B4 + 12C = 16Ta5B5C2

表2不同成分Nb-B-C相和Ta-B-C相的形成焓 (单位: eV/atom), $ \Delta{H}_{\rm{elements}} $表示单质为反应物, $ \Delta{H}_{\rm{comp}} $表示最稳定竞争组合为反应物
Table2.Calculated formation enthalpies of different Nb-B-C and Ta-B-C phases (in eV/atom).$ \Delta{H}_{\rm{elements}} $ represents the elements as the reactants, and $\Delta{H}_{\rm{comp}}$ indicates the most stable composite as the reactants.

但是除了单质, 三元相还有可能分解成单质、二元相和其他三元相的任意组合. 在所有各种可能任意组合中, 焓值总和最低的那一组合定义为该三元相的最稳定竞争组合. 对Nb-B-C和Ta-B-C来说, 通过在ICSD数据库搜索其各种单质、二元相和三元相结构, 计算其焓值. 三元相相对最稳定竞争组合的热力学稳定性可用下列公式进行计算:

$\Delta{H}_{\rm{comp}}={H}_{{\rm{T}}{\rm{M}}x{\rm{B}}y{\rm{C}}z}{-H}_{\rm{comp}}, $

式中$ \Delta{H}_{\rm{comp}} $是TM_xB_yC_z (TM = Ta或Nb)相对最稳定竞争组合的形成焓(eV/atom), $ {H}_{{\rm{T}}{\rm{M}}x{\rm{B}}y{\rm{C}}z} $和$ {H}_{\rm{comp}} $分别是三元相TM_xB_yC_z和最稳定竞争组合的焓值(eV/atom). 如果$ \Delta{H}_{\rm{comp}} > 0$, 则意味着三元相TM_xB_yC_z会分解成最稳定竞争组合; 否则就说明相对所有可能分解产物, 三元TM_xB_yC_z化合物都能稳定存在.
基于Nb-B-C和Ta-B-C体系中二元相和三元相相对单质的形成焓, 分别绘出了Nb-B-C和Ta-B-C的三元成分相图, 如图2所示. 表2列出了三元Nb-B-C相和三元Ta-B-C相的形成焓及其最稳定竞争组合. 从图2和表2中, 可以清楚地看出各相的稳定性. 相对最稳定竞争组合来说, Nb系三元相中有Nb₃B₃C, Nb₄B₃C₂和Nb₇B₄C₄是稳定的, 这与这三相已被成功合成的实验结果^[15]是一致的, 这也证明了计算结果的可靠性. Ta系中有Ta₃BC₂和Ta₇B₄C₄两相是稳定的. 之前的计算文献[16]报道Ta₃B₃C和Ta₄B₃C₂两相是稳定的, 是因为没有考虑Ta₃BC₂和Ta₇B₄C₄的原因, 这一点从Ta₃B₃C和Ta₄B₃C₂最稳定竞争组合中均包括Ta₇B₄C₄相可看出.
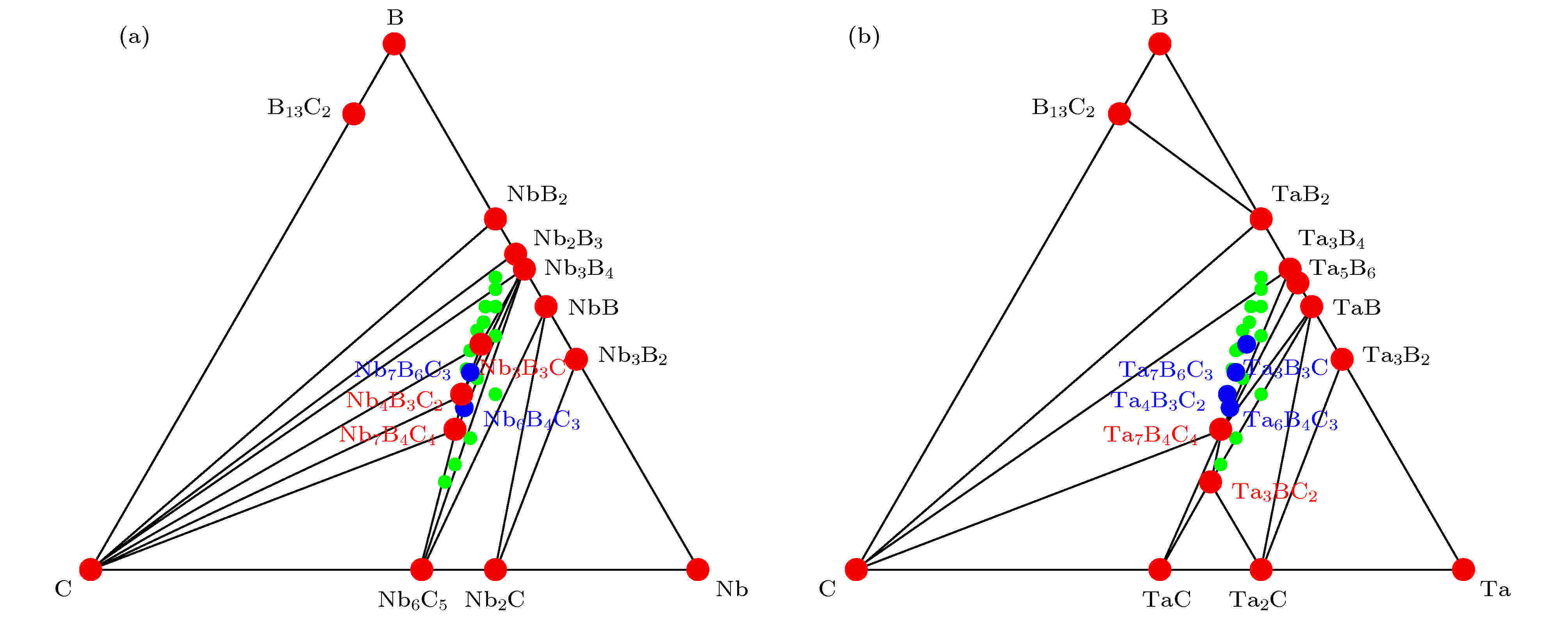图 2 (a) Nb-B-C和(b) Ta-B-C三元相图. 红色, 稳定相; 蓝色, 亚稳相; 绿色, 不稳定相
Figure2. Ternary phase diagrams of (a) Nb-B-C and (b) Ta-B-C. Red, stable; blue, metastable; green, unstable.

除了上述4种稳定相以外, 表2中还有一些化合物的形成焓虽为正值, 但却很接近零值. 把$0 < \Delta {H}_{\rm{comp}} \leqslant 0.005\;{\rm{eV}}/{\rm{atom}}$的化合物定义为亚稳相. 基于此标准, Nb-B-C体系中的Nb₆B₄C₃, Nb₇B₆C₃和Ta-B-C体系中的Ta₆B₄C₃, Ta₇B₆C₃, Ta₃B₃C和Ta₄B₃C₂皆为亚稳相. 第一性原理计算所得能量为绝对零度下物质的基态能量, 因此如果加以考虑温度作用, 亚稳相的形成能是有可能变成负值的. 采用准谐近似方法^[22,23]计算了Nb-B-C和Ta-B-C体系中三元稳定相和三元亚稳相及其最稳定竞争组合相在0—2000 K下的自由能, 计算结果如图3所示. 在Nb-B-C体系中, 考虑零点振动能之后, 亚稳相Nb₇B₆C₃变成了稳定相, 这与之前实验合成得到该相的结果^[15]相一致. 在1730 K, 亚稳相Nb₆B₄C₃形成能由正转负, 意味着该相变成了稳定相. 在Ta-B-C体系中, 考虑零点振动能之后, 亚稳相Ta₇B₆C₃变成了稳定相. 亚稳相Ta₆B₄C₃, Ta₄B₃C₂和Ta₃B₃C分别在210, 360和1100 K转变成了稳定相. 但同时注意到, 基态稳定相Ta₃BC₂在130 K转变成了不稳定相. 综上所述, 在温度高于室温条件下, 在Nb-B-C和Ta-B-C体系中存在Nb₃B₃C, Nb₄B₃C₂, Nb₆B₄C₃, Nb₇B₄C₄, Nb₇B₆C₃和Ta₃B₃C, Ta₄B₃C₂, Ta₆B₄C₃, Ta₇B₄C₄, Ta₇B₆C₃ 10种稳定相. 除此之外, 还预测了一种基态稳定相Ta₃BC₂. 目前除了Nb₃B₃C, Nb₄B₃C₂, Nb₇B₄C₄, Nb₇B₆C₃已经在实验上合成以外, 我们期待其他新相在未来可以实验合成.
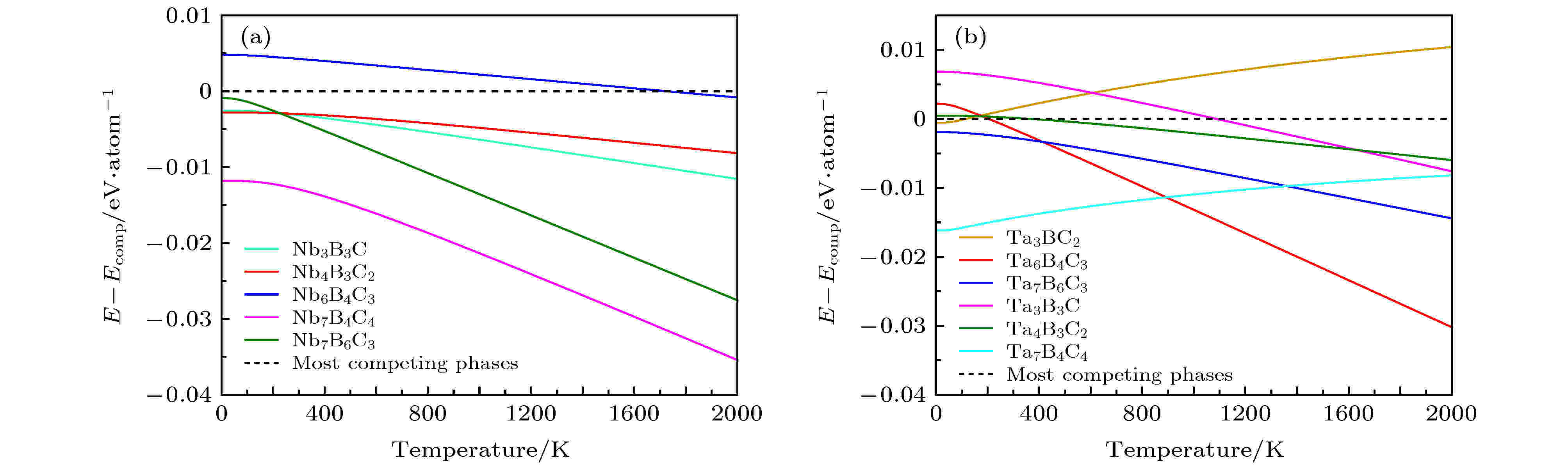图 3 不同温度下　(a) Nb-B-C和(b) Ta-B-C三元相分别和其相应最稳定竞争组合相的自由能之差
Figure3. Energy differences of (a) Nb-B-C and (b) Ta-B-C ternary phases with respect to their most competing phases as a function of temperature.

2 -->

3.3.动力学和力学稳定性

通过计算声子谱可以判断一个结构的动力学稳定性. 图4给出了本文预测的Nb-B-C和Ta-B-C体系中三元稳定相的声子谱. 可以看出所有结构都没有声子虚频存在, 从而表明这些结构在动力学上是稳定的.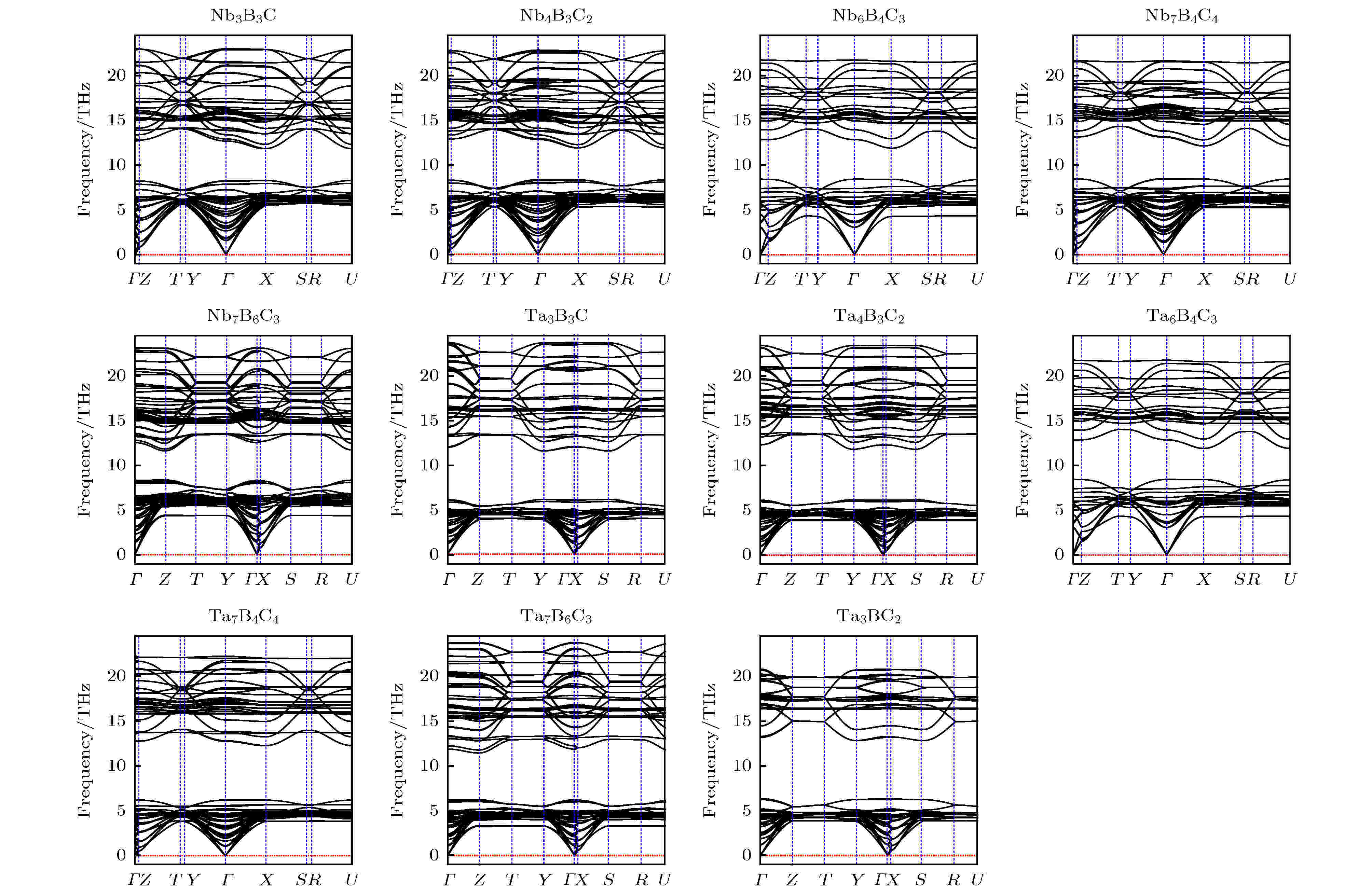
图 4 Nb-B-C和Ta-B-C三元相的声子色散曲线
Figure4. Phonon dispersion curves of Nb-B-C and Ta-B-C ternary phases.

材料结构的力学稳定性可以通过检验其弹性常数是否满足“波恩-黄”稳定判据^[24]来判断. 所预测的热力学稳定相都属于正交晶系. 对于正交晶系晶体来说, 其稳定结构的9个独立弹性常数需满足如下条件^[24]: $ {C}_{11}>0, {C}_{44}>0, {C}_{55}>0, {C}_{66}>0, $ ${C}_{11}{C}_{22}>{C}_{12}^{2}, {C}_{11}{C}_{22}{C}_{33}+2{C}_{12}{C}_{13}{C}_{23}-{C}_{11}{C}_{23}^{2}- $ ${C}_{22}{C}_{13}^{2}-{C}_{33}{C}_{12}^{2}>0 $. 预测的Nb-B-C和Ta-B-C体系中三元稳定相的弹性常数列于表3中. 经过计算, 表3中所列结构的弹性常数都满足上述判据, 说明这些相都是力学上的稳定相.

结构	弹性常数										力学性能a				硬度
	C11	C22	C33	C44	C55	C66	C12	C13	C23		B	G	B/G		HChen	HTian
Nb3B3C	544.3	479.8	522.8	181.5	171.9	245.3	170.9	132.9	162.2		275.3	189.7	1.45		24.8	24.7
Nb4B3C2	551.5	499.2	548.5	184.0	175.1	257.1	183.2	132.7	157.8		282.9	195.8	1.44		25.5	25.4
Nb6B4C3	533.3	493.8	548.1	174.9	161.3	255.2	175.4	138.9	151.7		278.5	189.5	1.47		24.4	24.3
Nb7B4C4	535.9	505.9	526.4	172.2	161.3	259.1	184.0	142.8	152.6		280.6	188.3	1.49		23.9	23.8
Nb7B6C3	553.1	494.5	563.2	188.7	179.6	255.6	176.4	132.1	157.7		282.5	198.9	1.42		26.3	26.2
Ta3B3C	569.6	514.4	563.5	194.1	180.0	261.8	187.1	147.3	173.9		295.9	200.8	1.47		25.3	25.3
Ta4B3C2	581.1	535.3	602.1	197.3	185.1	275.8	200.3	146.0	170.2		305.7	209.0	1.46		26.2	26.2
Ta3BC2	550.0	547.7	550.0	159.8	159.5	292.1	216.7	160.0	149.2		299.6	191.8	1.56		22.7	22.9
Ta6B4C3	584.7	539.6	614.2	203.0	189.9	279.9	195.5	168.0	144.1		305.9	213.9	1.43		27.4	27.3
Ta7B4C4	563.1	547.5	571.5	183.6	170.4	281.4	200.2	162.0	164.3		303.9	200.8	1.51		24.4	24.5
Ta7B6C3	584.7	540.0	614.2	203.0	190.0	280.0	195.5	168.0	144.1		305.9	213.9	1.43		27.4	27.3
TaB2											302	200	1.51		24.4	24.5
NbB2											287	195	1.47		24.8	24.8
TaC											324	215	1.51		25.6	25.9
NbC											239	161	1.48		21.6	21.4
SiC											213	187	1.14		33.6	32.2
Al2O3											232	147	1.58		18.7	18.7
TiN											259	180	1.44		24.3	24.0
注: a二元相力学性能数据来自Materials Project网站.

表3Nb-B-C和Ta-B-C三元相的弹性常数C_ij、体模量B、剪切模量 G和维氏硬度H_v (单位: GPa)
Table3.Elastic constants C_ij, bulk modulus B, shear modulus G, Vickers hardness H_v of Nb-B-C and Ta-B-C ternary phases (in GPa).

2 -->

3.4.力学和电学性能

多晶材料的体模量B和剪切模量G可以通过以下公式^[25]计算:

$B = 1/2\left( {{B_{\rm{V}}} + {B_{\rm{R}}}} \right),G = 1/2\left( {{G_{\rm{V}}} + {G_{\rm{R}}}} \right),$

其中下标V和R分别代表Voigt和Reuss方法.
正交晶系晶体的B_V, B_R, G_V和G_R可由弹性常数通过以下公式计算得出:

$\begin{split}{B_{\rm{V}}} =\;& 1/9\left[ {{C_{11}} + {C_{22}} + {C_{33}} + 2\left( {{C_{12}} + {C_{13}} + {C_{23}}} \right)} \right],\\{G_{\rm{V}}} =\;& 1/15[{C_{11}} + {C_{22}} + {C_{33}} + 3({C_{44}} + {C_{55}} + {C_{66}}) - ({C_{12}} + {C_{13}} + {C_{23}})],\\{B_{\rm{R}}} =\;& [{C_{11}}\left( {{C_{22}} + {C_{33}} - 2{C_{23}}} \right) + {C_{22}}\left( {{C_{33}} - 2{C_{13}}} \right) - 2{C_{33}}{C_{12}} + {C_{12}}\left( {2{C_{23}} - {C_{12}}} \right) + {C_{13}}\left( {2{C_{12}} - {C_{13}}} \right) \\& +{C_{23}}\left( {2{C_{13}} - {C_{23}}} \right){]^{ - 1}} \times [{C_{13}}\left( {{C_{12}}{C_{23}} - {C_{13}}{C_{22}}} \right) + {C_{23}}\left( {{C_{12}}{C_{13}} - {C_{23}}{C_{11}}} \right) + {C_{33}}\left( {{C_{11}}{C_{22}} - {C^2}_{12}} \right)],\\{B_{\rm{R}}} =\;& [{C_{11}}\left( {{C_{22}} + {C_{33}} - 2{C_{23}}} \right) + {C_{22}}\left( {{C_{33}} - 2{C_{13}}} \right) - 2{C_{33}}{C_{12}} + {C_{12}}\left( {2{C_{23}} - {C_{12}}} \right) + {C_{13}}\left( {2{C_{12}} - {C_{13}}} \right) \\& +{C_{23}}\left( {2{C_{13}} - {C_{23}}} \right){]^{ - 1}} \times \varDelta ,\\{G_{\rm{R}}} =\;& 15\{ 4[{C_{11}}\left( {{C_{22}} + {C_{33}} + {C_{23}}} \right) + {C_{22}}\left( {{C_{33}} + {C_{13}}} \right) + {C_{33}}{C_{12}} - {C_{12}}\left( {{C_{23}} + {C_{12}}} \right) - {C_{13}}\left( {{C_{12}} + {C_{13}}} \right) \\ & -{C_{23}}\left( {{C_{13}} + {C_{23}}} \right)]/\varDelta + 3[\left( {1/{C_{44}}} \right) + \left( {1/{C_{55}}} \right) + \left( {1/{C_{66}}} \right)]{\} ^{ - 1}},\\[-10pt]\end{split}$

其中Δ = C₁₃(C₁₂C₂₃ – C₁₃C₂₂) + C₂₃(C₁₂C₁₃ – C₂₃C₁₁) + C₃₃(C₁₁C₂₂ – C₁₂²).
计算的Nb-B-C和Ta-B-C体系中三元稳定相的体模量B和剪切模量G列于表3中. 所得三元相体模量B位于275—306 GPa的狭小数值范围内, 剪切模量G位于190—214 GPa的狭小数值范围内. 这说明无论是Nb-B-C三元相, 还是Ta-B-C三元相, 它们的力学性能很相似, 这与它们具有相同的结构基元有关. Ta-B-C化合物的B和G值均稍大于同一成分的Nb-B-C相, 这是因为Ta原子半径稍小于Nb原子, Ta—B和Ta—C键长要比Nb—B和Nb—C键长稍短. 这一点也可以从表1中所列两体系的晶格常数看出来.
体模量和剪切模量的比值可以用来判断一个材料是脆性还是韧性. 根据Pugh经验判据^[26], 如果B/G > 1.75, 则该材料属于韧性; 反之则为脆性. 根据表3中B/G比值, 可知Nb-B-C和Ta-B-C体系中所有三元相均为脆性材料.
硬度是本文所计算材料的重要性能. 硬度计算采用陈星秋公式^[27]和田永君公式^[1]:

$ {H}_{\rm{Chen}}=2{\left({k}^{2}G\right)}^{0.585}-3, $

$ {H}_{\rm{Tian}}=0.92{k}^{1.137}{G}^{0.708}. $

(5)式和(6)式中, H_Chen和H_Tian是维氏硬度, k为G/B的比值.
Nb-B-C和Ta-B-C体系中三元稳定相的硬度数值列于表3中. 可看出, 两种计算公式所得硬度数值很接近, 误差小于0.2 GPa. Ta-B-C三元相的硬度稍高于Nb-B-C三元相. 所有三元相的硬度值很接近, 位于23.8—27.4 GPa范围内, 均小于40 GPa, 这说明均不是超硬材料, 但也属于高硬度材料. 这些三元相和已知常见的二元相硬质材料硬度相当, 因此未来可被作为硬质材料来使用.
为了探索Nb-B-C和Ta-B-C体系中三元稳定相的电学性能, 计算了其态密度, 结果如图5所示. 由于结构的相似性, 各个结构的态密度也很相似. 为了表示更加清楚, 把Ta₃BC₂相的态密度图放大加以显示. 所示态密度图中, 虚线所示费米面处没有带隙存在, 电子态不为零, 这说明这些三元相均为导体. 通过图中所示不同电子的部分态密度可知, 费米面处的电子态主要来源于d电子, 这说明这些三元相的导电性主要来源于结构中过渡金属原子的d电子, 这和之前文献^[16]中对Ta₃B₃C和Ta₄B₃C₂态密度的分析结果是一致的.
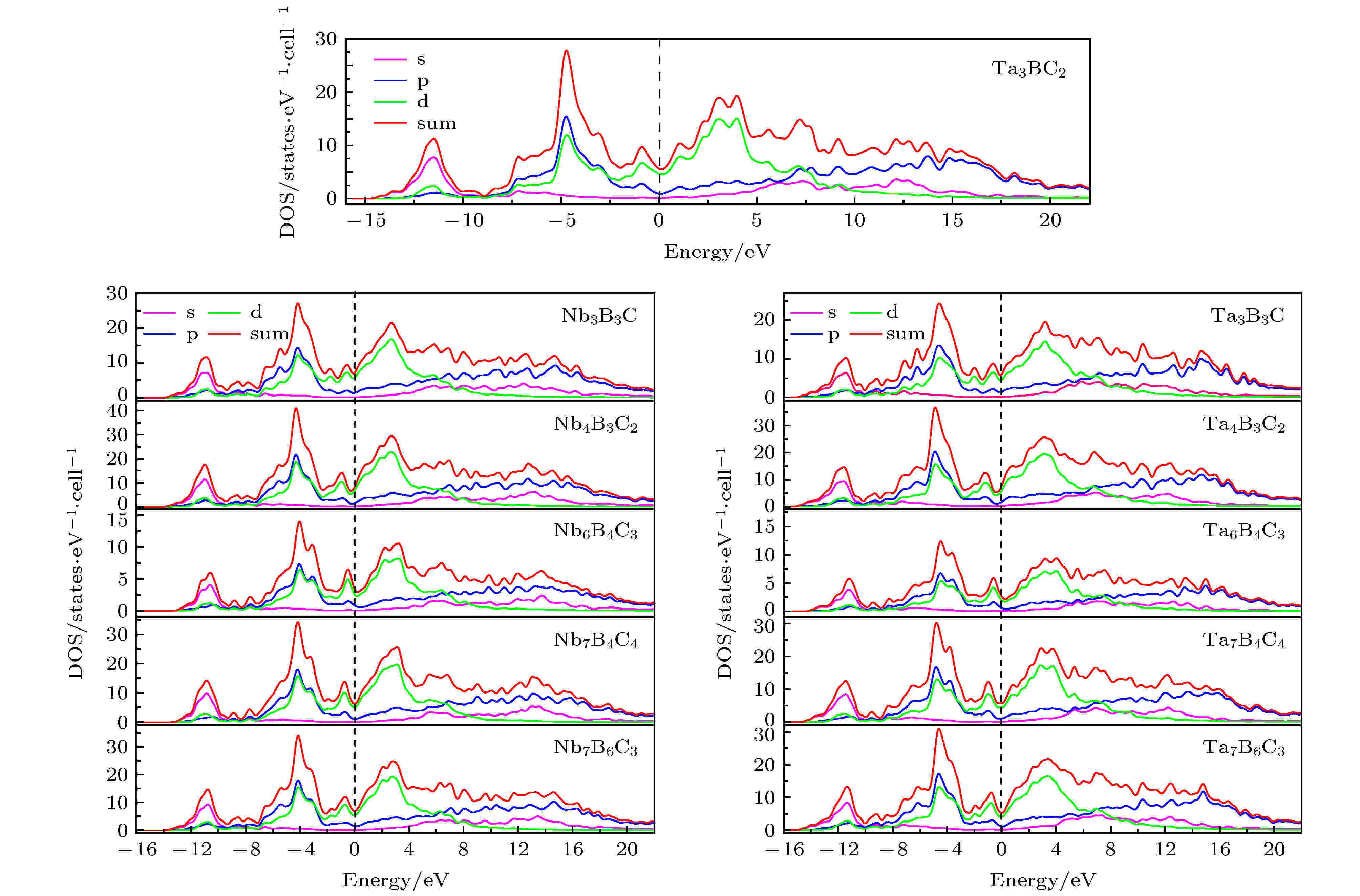图 5 Nb-B-C和Ta-B-C三元相的态密度图
Figure5. Density of states of Nb-B-C and Ta-B-C ternary phases.

本文通过分析实验合成的Nb₃B₃C和Nb₄B₃C₂结构, 得出其结构基元为Nb₆C八面体和Nb₆B三棱柱. 通过调整Nb₆C (Ta₆C)八面体和Nb₆B (Ta₆B)三棱柱的数量, 构建了20种三元Nb_{(m + n + 2)}B_{(2m + 2)}C_n化合物和20种三元Ta_{(m + n + 2)}B_{(2m + 2)}C_n化合物, 采用基于密度泛函理论第一性原理计算方法, 通过分析这些化合物的热力学、动力学和力学稳定性, 成功预测了Nb₃B₃C, Nb₄B₃C₂, Nb₆B₄C₃, Nb₇B₄C₄, Nb₇B₆C₃, Ta₃B₃C, Ta₄B₃C₂, Ta₆B₄C₃, Ta₇B₄C₄, Ta₇B₆C₃, Ta₃BC₂等11种三元稳定相. 其中Nb₆B₄C₃, Ta₆B₄C₃, Ta₄B₃C₂和Ta₃B₃C分别在1730, 210, 360和1100 K温度以上才能稳定存在. 而Ta₃BC₂相只能在130 K温度以下才能稳定存在. 这11种稳定相皆为导电的脆性硬质材料, 其硬度值位于23.8—27.4 GPa范围内. 目前除了Nb₃B₃C, Nb₄B₃C₂, Nb₇B₄C₄, Nb₇B₆C₃已经在实验上合成以外, 我们期待其他7种新相在未来的实验合成.