全文HTML
--> --> -->传统物理真随机数发生器主要基于电路热噪声[7,8]、压控振荡器[9]、混沌电路[10,11]等物理熵源, 但受限于这些物理信号的带宽, 产生的随机数速率多处于Mbit/s级别, 很难满足现代通信系统对高速随机数的要求. 近年来利用混沌激光作为物理熵源, 得到了离线速率高达100 Gbit/s[12], 300 Gbit/s[13]和实时速率达到14 GBit/s[14], 20 GBit/s[15]的随机数. 但混沌激光系统复杂, 成本高, 且需要外部反馈, 涉及电-光和光-电双重转换, 容易受到外界因素的干扰, 因此混沌激光随机数发生器无法小型化集成到保密通信设备之上.
超晶格(superlattices, SLs)是用两种晶格匹配度很好的半导体材料周期性交替生长而成的全固态电子器件, 最早由IBM公司的Esaki和Chang[16]提出. 中科院张耀辉团队[17-19]在国际上率先发现GaAs/Al0.45Ga0.55As SLs在液氮温区及室温条件下直流偏置电压的自发混沌振荡现象. 国内外诸多****通过对GaAs/Al0.45Ga0.55As SLs的结构[20]以及自发混沌振荡现象[21,22]的研究, 证实了SLs是理想的混沌噪声源, 可以产生真随机数, 其随机数产生速率可达80 Gbit/s[23].
本文提出了一种基于SLs芯片的实时高速物理真随机数发生器. 首先, 以SLs物理熵源为核心, 搭建了SLs高速物理真随机数产生装置. 通过对信号的混沌特性进行分析选择合适的直流偏置电压, 随后使用采样速率为2 GHz的12位高速模数转换器(analog-to-digital converter, ADC)对SLs信号进行采集量化得到随机比特. 接着使用现场可编程逻辑门阵列(field programmable gate array, FPGA)从12位随机比特中抽取最低4位作为有效位进行比特反转. 最终获得了实时速率为8 Gbit/s的随机数, 并且该随机数具有良好的统计随机特性, 可满足现代通信系统对高速率随机数的需求.
2.1.SLs结构
为方便实验调试, 本文使用的SLs封装成双列直插式, 如图1(a)所示, 其尺寸大小约为1.5 mm × 1.5 mm(圆圈内). 图1(b)为SLs的结构示意图, SLs由50周期的弱耦合势阱(GaAs)和势垒(Al0.45Ga0.55As)组成[23], 夹于两个300 nm硅基GaAs层中形成了n+-n-n+的二极管结构[19]. Al0.45Ga0.55As势垒层厚度为4 nm, GaAs势阱层总厚度为7 nm, 其中掺杂硅基GaAs层两侧各有2 nm厚的无掺杂GaAs层, 以防止硅原子扩散到相邻Al0.45Ga0.55As势垒层. 虽然这些结构是周期性的, 但是在生长过程中, 其层厚、掺杂浓度等不可避免地存在随机涨落, 因此构成了一个极大自由度的随机非线性系统. 交替生长的GaAs和Al0.45Ga0.55As材料具有不同的禁带宽度, 它们分别构成了量子阱的阱和垒, 其能带结构示意图如图1(c)所示. 在弱耦合SLs中, 电荷被局限在各个量子阱中, 电荷的输运通过各个相邻量子阱间的共振隧穿实现. 图1(d)为SLs电子运输过程中的级联共振隧穿模型, SLs加上特定的直流偏置电压, 会使相邻量子阱的子能级间发生级联共振, 即第n阱中基态能级与第n+1阱中第一激发态子能级相等, 形成共振隧穿. 电荷在外加偏置电压的驱动下, 可以形成电荷的单极子, 即电荷畴. 电荷畴有多种运动方式, 可以朝电场方向或者反方向运动, 产生自发的周期性电流振荡, 这种自发周期振荡被试验验证为是由高低电场畴边界的高频振荡造成的[24]. 弱耦合SLs的级联共振隧穿效应引入了负微分电导效应, 使电场中电子的行为具有非线性特性, 电子失去自身的相位信息, 形成一个非常复杂的随机过程, 因此SLs可以被看成是多个互相串联耦合的共振隧穿器件, 即由多个非线性系统互相耦合而成的复杂系统. 共振隧穿效应的强非线性特性引起了SLs芯片的自发混沌振荡, 但混沌振荡在理论上仍有待进一步研究[23].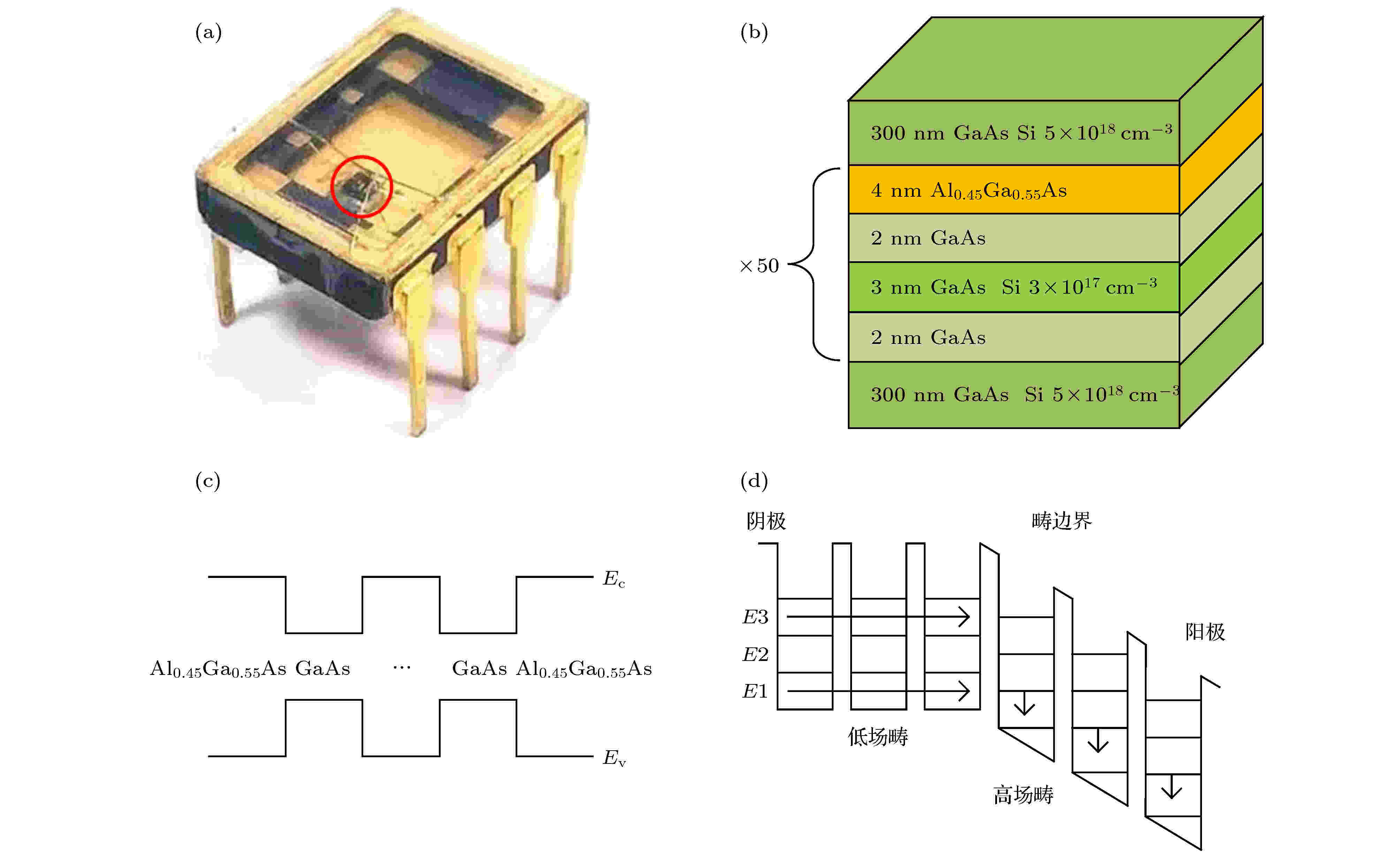
图 1 超晶格 (a)芯片实物图; (b)结构示意图; (c)能带; (d)高低场畴和级联隧穿模型Figure1. (a) Picture of SLs chip; (b) schematic representation of the SLs device; (c) energy band diagram of SLs; (d) the models of high and low field domain and sequential tunneling of SLs.
2
2.2.SLs高速物理随机数产生装置
根据SLs产生混沌信号的机理, 设计图2所示的SLs随机数发生器装置. 该系统分为两个部分: SLs物理熵源部分和随机数提取部分. 物理熵源部分通过选取合适的直流偏置电压产生混沌信号, 随机数提取部分对物理熵源信号采样数字化最终生成随机比特. GaAs/Al0.45Ga0.55As SLs具有多个能产生自发混沌振荡的直流偏置电压区间, 但是范围较窄, 通常只有几十mV左右, 对偏置电压较为敏感[25], 稍有变化就会使输出混沌信号的基本特性发生变化. 高精度可调直流电源(high accuracy power supply, HAPS)可以实时调节输出的电压与电流, 因此本文使用Keithley 2280S的HAPS进行SLs随机数实验. 为避免寄生电容对高频信号带来的影响[26], 直流偏置需要先经过一个Bias-Tee偏置器(BT), 它由超带宽、接近理想化的电感L和电容C组成, 其中电感用于隔离交流信号防止高频信号泄露到直流供电系统, 电容用于阻隔直流防止直流电压泄露到高频电路和测量仪器中. 物理熵源部分之间的连线均使用带宽为6 GHz的SMA高频同轴电缆, SLs通过SMA同轴电缆连接BT获得供电, 再经50 Ω的SMA铜镍同轴负载实现电阻匹配后接地. 从BT的电容端引出两路SLs信号C1和C2, 第一路信号C1供示波器(OSC, Lecroy, HDO 9404-MS, 40 GS/s)和矢量网络分析仪(VNA, Rohde & Schwarz, ZNL6, 5 kHz—6 GHz)观察和测量SLs信号的波形和功率谱, 然后对信号C2使用采样频率为2 GHz的12-bit高速ADC进行采样量化, 送至FPGA(Virtex-7 XC7VX690T)进行后处理. FPGA控制高速ADC对SLs混沌信号进行采样, 并抽取其中低4位作为有效位, 将两个4 bit数据合成8 bit后进行比特反转, 再将原始序列与经过比特反转的序列再进行异或处理, 最终得到可以输出的随机序列.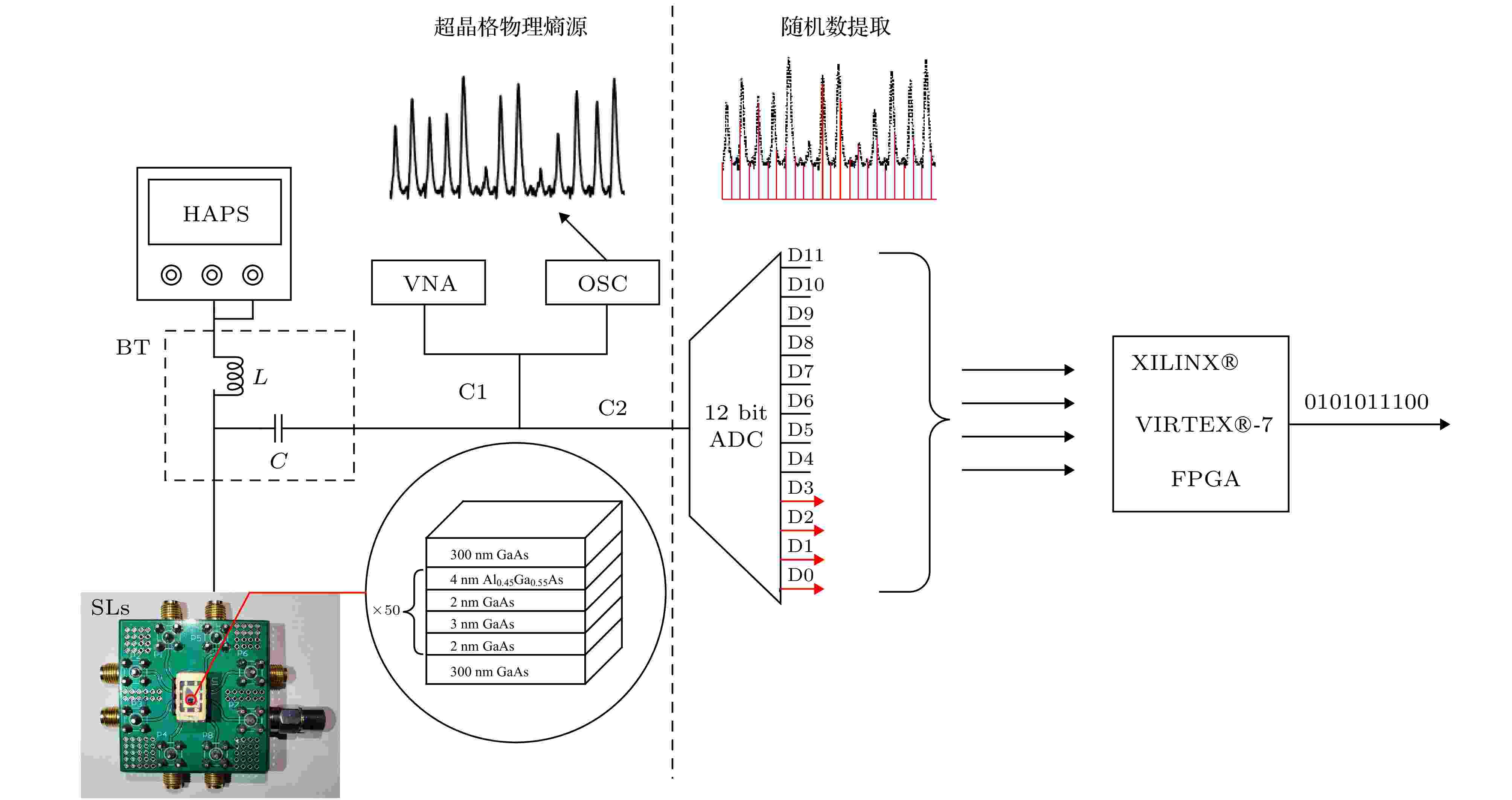
图 2 超晶格高速物理随机数产生装置(HAPS, 高精度电源; BT, T型偏置器; SLs, 超晶格; L, 电感; C, 电容; OSC, 示波器; VNA, 矢量网络分析仪; ADC, 模数转化器; FPGA, 现场可编程逻辑门阵列)Figure2. Schematic for high speed physical random number generator of SLs (HAPS, high accuracy powersupply; BT, Bias-Tee; SLs, superlattices; L, inductance (unit Lenz); C, capacitance; OSC, oscilloscope; VNA, vector network analyzer; ADC, analog digital converter; FPGA, field programmable gate array).
3.1.SLs信号基本特征
GaAs/Al0.45Ga0.55As SLs在不同的直流偏置电压下输出的信号具有不同特征, 因此对SLs的I-V特性进行测试, 得到如图3所示的I-V特性曲线图. 根据不同电压区间产生的信号的特征, 将电压区间分为A, B1, B2和C四个区间.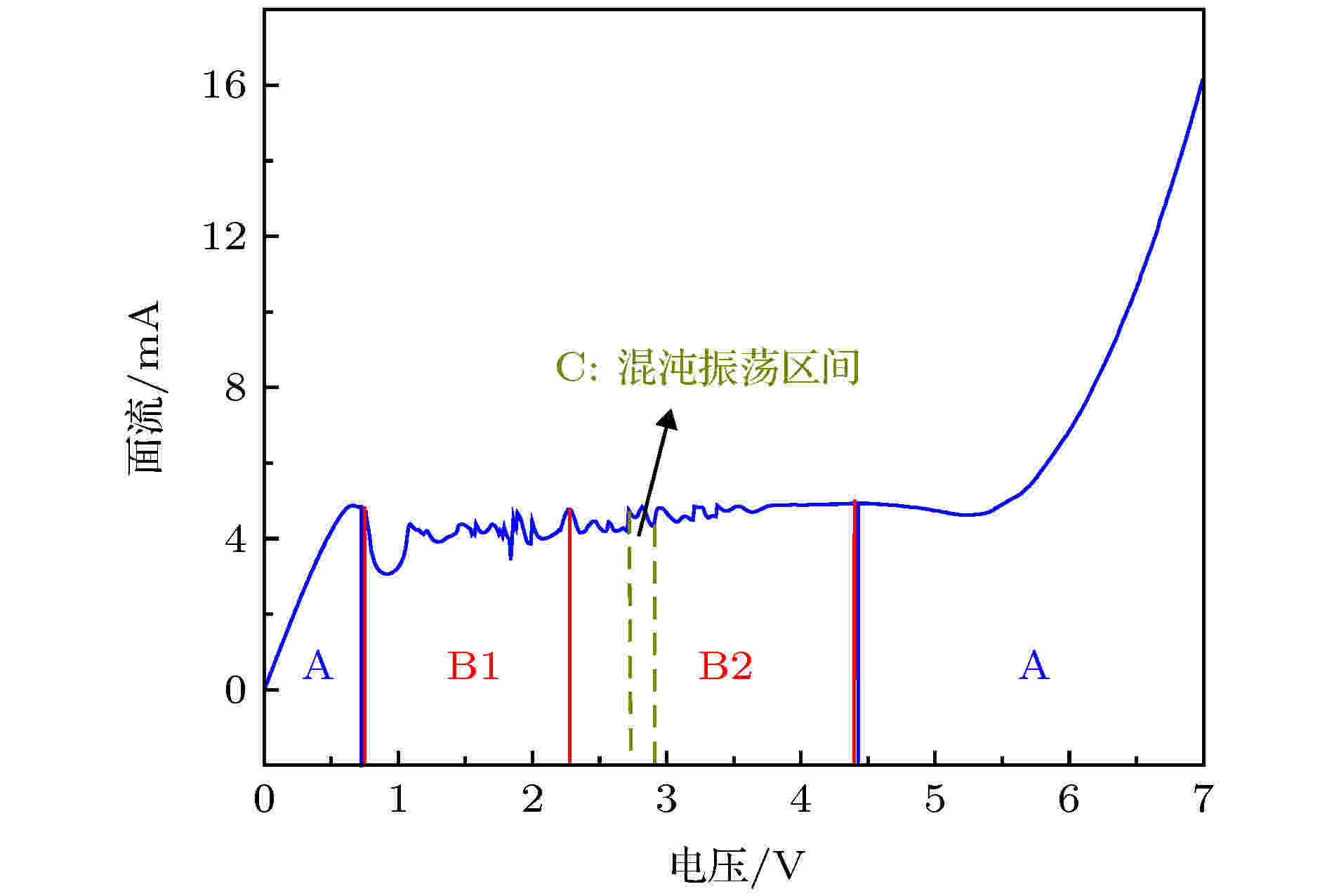
图 3 超晶格I-V特性曲线Figure3. I-Vcharacteristic curve of SLs.
当实验所用SLs处于电压区间A(0—0.74 V和4.40—7.00 V)时, 几乎无输出信号. 当给SLs施加B1区间(0.75—2.27 V)电压时, 输出单峰周期性信号, 尽管电压幅值随着电压发生变化, 但是其形状在该区间内基本保持一致, 当选取该区间内任一电压值(如1.89 V)时, 可得到该电压下的时序图, 如图4(a)所示, 对应电压下的峰峰值在108 mV左右. 当SLs处于区间B2(2.28—4.39 V)时(除混沌振荡区间), 幅值随电压变化, 但信号形状仍然基本保持一致, 为一大一小双峰周期性信号, 选择该区间的任一电压值(如2.42 V)可得时序图4(b), 对应的峰峰值在69 mV左右. 这两种电压区间下采集的信号不仅在时域上表现出明显的周期性, 在功率谱(图4(d)和图4(e))上也表现出明显非正弦周期性信号的特征, 即高次谐波处出现功率高峰值. SLs主要的载流子输运是从一个势阱通过势垒隧穿到相邻的势阱, 当加外加偏置电压从低到高逐渐增加时, 特定的电压会使相邻阱间的子能级发生从非共振到共振再到非共振的过程, 从而产生负微分电导效应. 因此除前面提到的几种电压区间, 还存在着一些特殊的负微分电压区间, 电流随电压变大反而变小, 并且在这些电压区间内的SLs信号具有非周期信号特征[22,24]. 选择混沌振荡区间C(2.71—2.90 V)的负微分区间的某一电压(如2.8 V)时得到时序图4(c), 其幅度随时间变化并无明显规律出现, 此电压下的SLs信号峰峰值在100 mV左右, 功率谱(图4(f))展现的频谱缓而宽, 无高次谐波, 为非周期信号特征[27]. 半导体中的不稳定现象和混沌行为从宏观上来看通常是由于负微分电导特性引起的[28]. 正常情况下半导体中的电流随电压的增大而增大, 而由于SLs电子的共振隧穿效应, 导致负微分电导效应, 在负微分电压区间电流随电压增大反而减少, 因此在某些特殊的负微分电导区间(混沌振荡区间内), 只需给予SLs合适直流偏置电压, 便可观察到持续不断的自激振荡混沌信号.
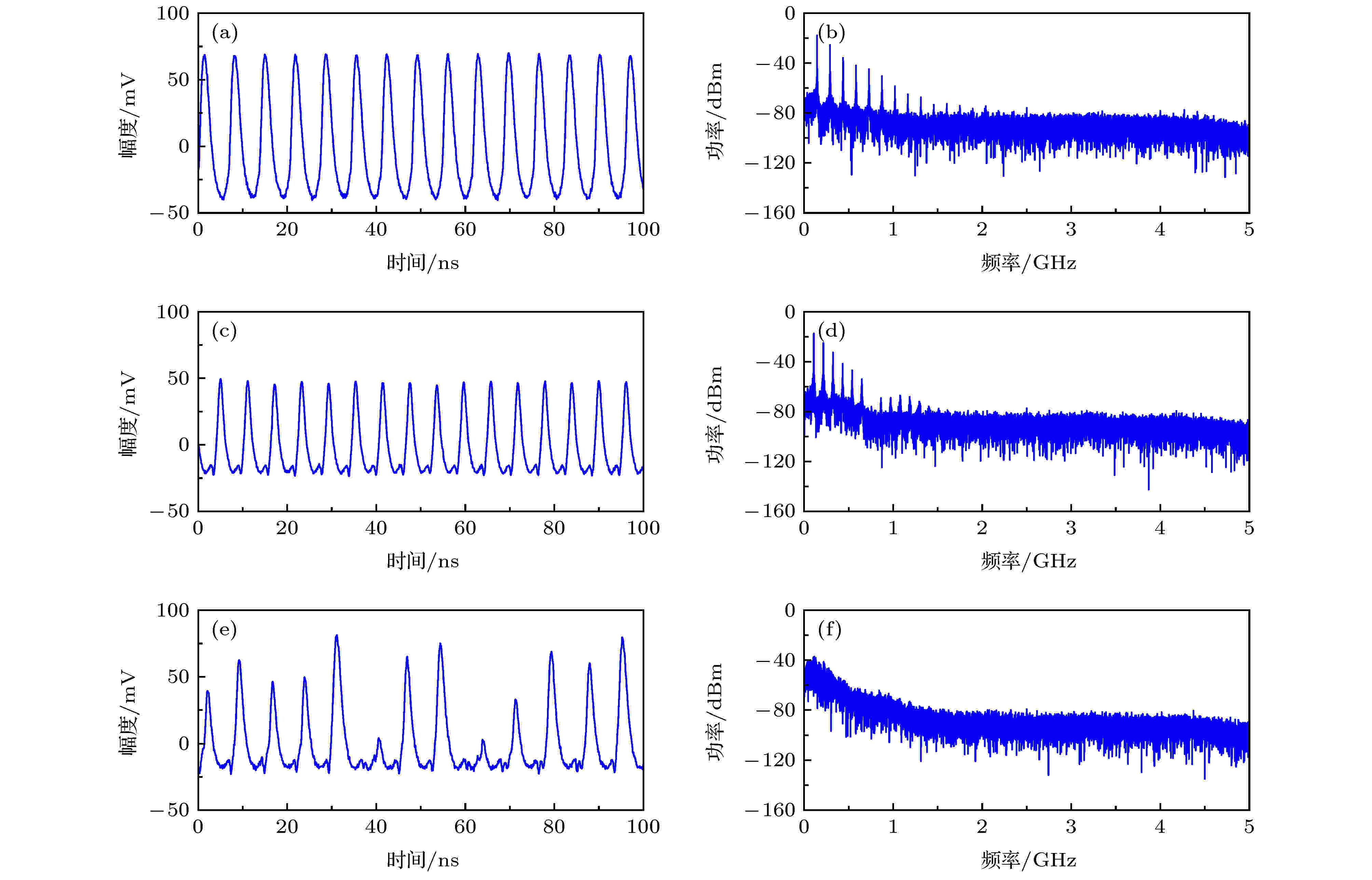图 4 超晶格 (a)单峰信号时序图; (b)双峰信号时序图; (c)非周期信号时序图; (d) 单峰信号功率谱; (e)双峰信号功率谱; (f)非周期信号功率谱Figure4. Superlattices: (a) Temporal waveform of single peak signal; (b) temporal waveform of bimodal signal; (c) temporal waveform of non-periodic signal; (d) power spectrum of single peak signal; (e) power spectrum of single bimodal signal; (f) power spectrum of single non-periodic signal.
对处于混沌振荡区间的SLs信号进行自相关系数计算, 得到其自相关曲线, 如图5所示, 经过零时刻峰值处时, 自相关性迅速衰减, 在2.23 ns内自相关系数首次衰减至0.01, 而后逐渐稳定在0.01以下, 表明该信号几乎没有自相关性, 说明SLs信号没有可检测的周期性[13], 可作为产生随机数的熵源.
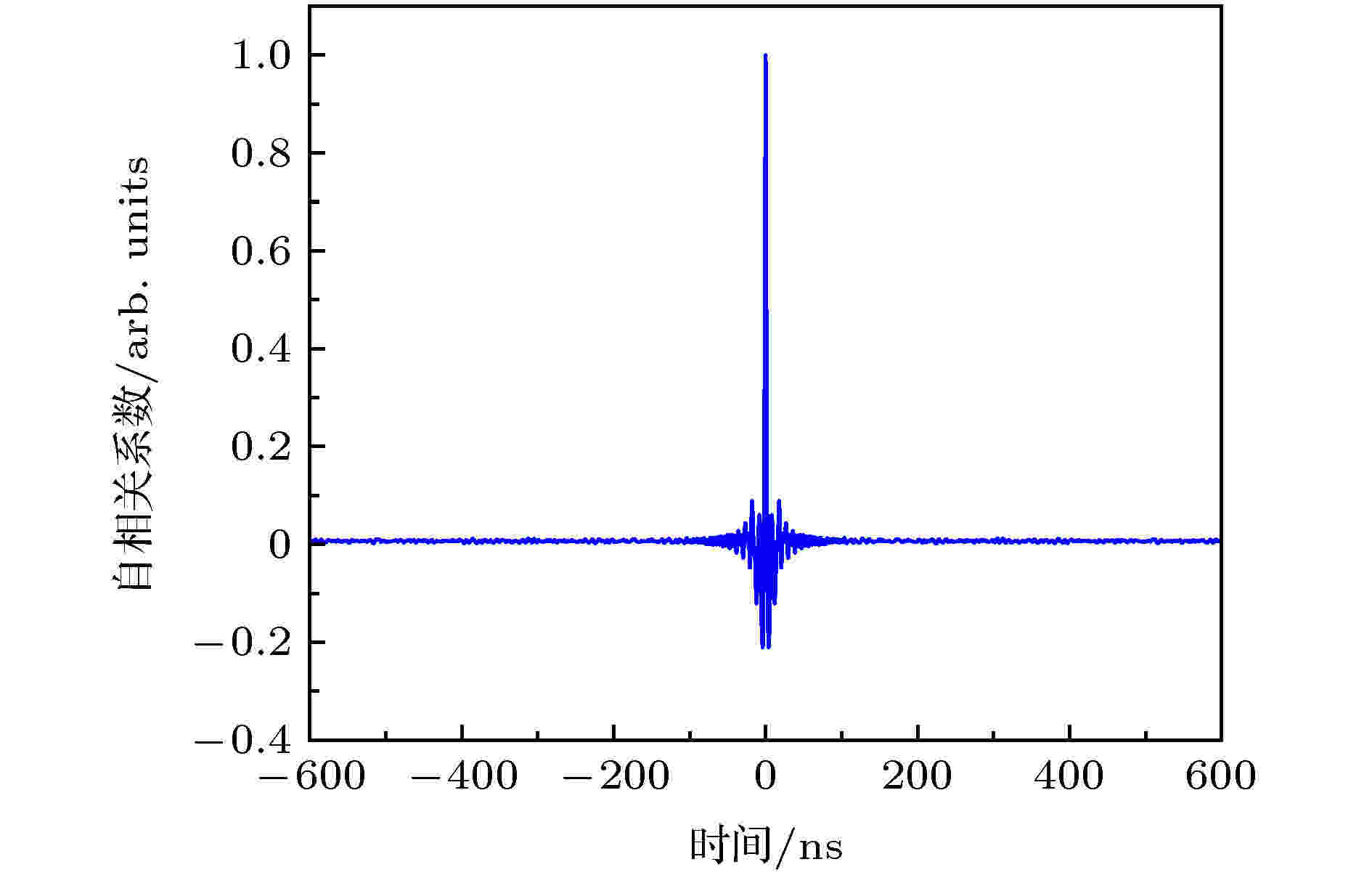图 5 超晶格信号自相关曲线Figure5. Autocorrelation curve of SLs.
2
3.2.SLs信号混沌特性分析
随机数的质量取决于SLs产生的混沌信号, 而SLs在不同电压下输出的混沌信号特征具有很大不同, 因此, 对不同电压下SLs混沌信号的分析显得尤为重要[29,30]. 混沌系统的基本特点就是对运动初始条件的极端敏感性[31], 两个靠得很近的初值所产生的轨线, 随着时间的推移, 将按指数方式分离(或接近)[32]. 李雅普诺夫指数[33] (Lyapunov exponents, LEs)是衡量系统动力学特性的一个重要定量指标, 它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率. 利用时间延迟τ和嵌入维m进行相空间重构而后利用wolf法[33]计算LEs. 时间延迟τ和嵌入维m的选择在相空间重构中至关重要, 直接决定了相空间重构后对其以吸引子的特征描述的不变量的准确度. 本文使用Masayuki Otani等提出的自动算法, 该方法利用平均位移法和Г-test[34]联合算法计算时间延迟τ和嵌入维m. 计算混沌振荡区间(2.71—2.90 V)SLs混沌信号的最大LEs, 绘制如图6(a)所示的曲线. 对于系统是否存在动力学混沌, 只要最大LEs大于零, 就可以确定存在混沌[35]. 为了能够使用混沌程度更高的信号产生随机数, 测试在不同LEs的SLs信号最终生成随机数的结果, 下文中会给出不同LEs的信号生成随机数的测试结果. 图6(a)中曲线最高点对应的直流偏置为2.803 V, 使用该电压下的SLs信号进行相空间重构, 并选取其中三个维度绘制如图6(b)所示的三维空间曲线图, 从图6(b)可以观察到奇异吸引子[36]的存在. 综上所述, SLs信号中存在非周期的无规律运动形态, 并且本文所用SLs在2.803 V电压下具有更强的混沌信号特征.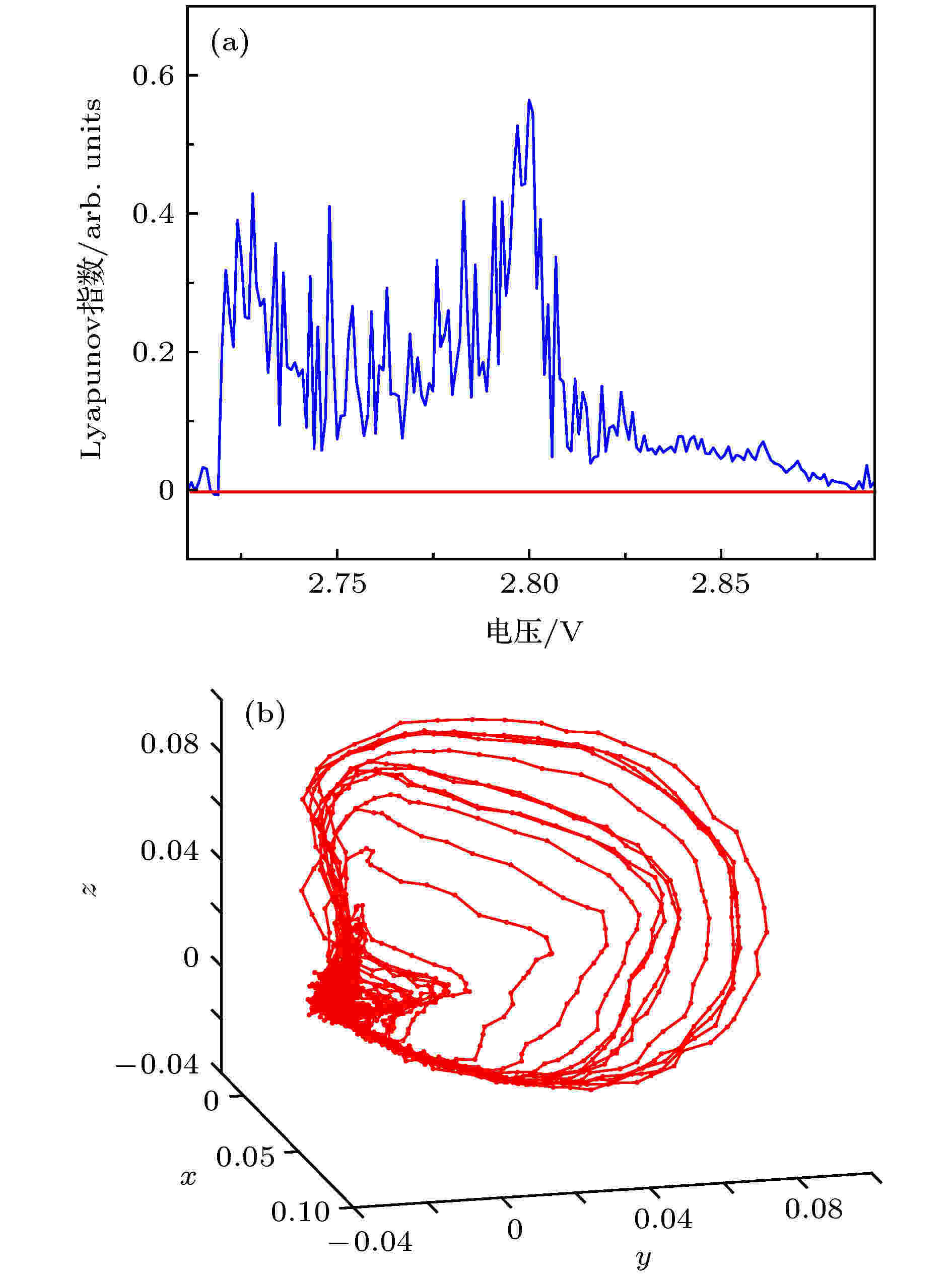
图 6 (a)不同电压下超晶格信号的最大Lyapunov指数; (b)重构相空间Figure6. (a) The maximum Lyapunov exponents of the superlattices signal at different voltages; (b) the phase space of the superlattices signal.
图 7 选取低m位有效的概率密度分布 (a) m = 8; (b) m = 6; (c) m = 5; (d) m = 4Figure7. M-bit effective probability density distribution: (a) m = 8; (b) m = 6; (c) m = 5; (d) m = 4.
值得注意的是, 使用上述方法选择低4位所获得的随机比特并不能通过所有的随机性统计检验, 这是因为在生成的随机比特中仍然存在明显的偏差或相关性[38]. 有效位抽取可在一定程度上消除偏差和相关性[37,38], Sciamanna和Shore[43]提出除使用mLSB方法还需结合其他后处理, 如异或、求导或者比特反转等方法才能最终生成理想随机数. 此前文献[13, 23, 38]大多采用离线生成真随机数, 将采集的数据先经过差分后进行一定延迟后与原始数据进行异或, 该方法可以降低随机比特的偏差和相关性, 然后得到优质随机数. 但是使用12 bit高速ADC得到的超大数据流会导致很难实时完成多阶差分以及延迟等运算处理, 因此无法直接使用离线处理中所使用的方法. 为了进一步提高随机性, 采用比特反转[38]的方法, 量化采集方案如图8(a)所示, SLs混沌信号采样量化之后得到12位的随机比特, 抽取最低4 bit作为有效位, 将相邻周期的两个4 bit数据拼接为8 bit进行比特反转, 最后将原始比特与反转后比特进行异或输出真随机数. 图8(b)给出了比特反转和异或的具体操作. FPGA内部无需对比特反转进行额外运算, 能高速处理ADC采集的数据, 实时生成随机数. 使用比特反转的方法可以进一步消除偏差和相关性, 极大地提高了随机比特的生成速度[44], 同时解决了高速数据处理的问题.
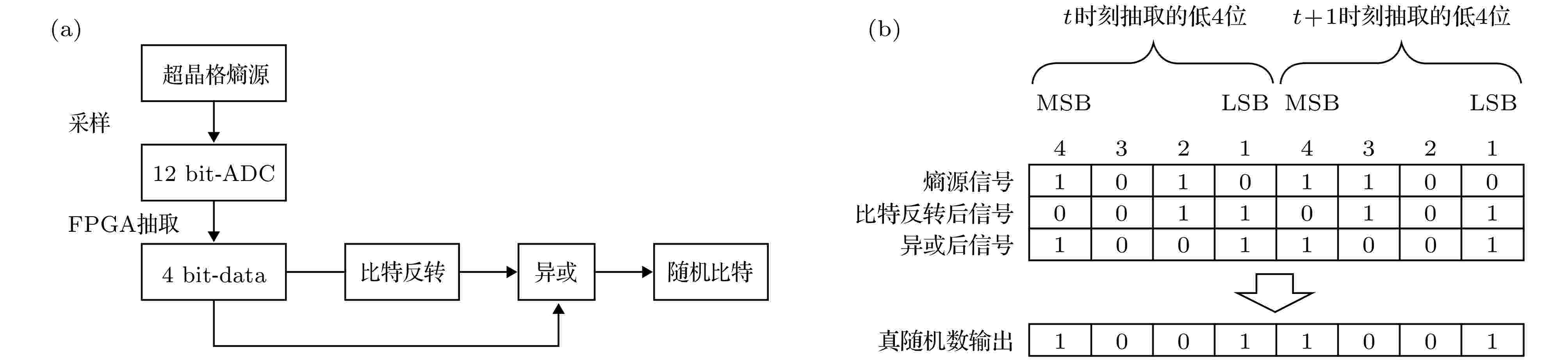图 8 超晶格量化采集方案 (a)采集转化原理图; (b)后处理方案示意图Figure8. acquisition scheme of SLs: (a) Schematic diagram of acquisition conversion; (b) schematic diagram of postprocessing.
采用随机数国际行业测试标准(NIST SP 800-22)对生成的随机数进行测试. 该随机数标准测试包含15个子项, 每个子项都会有一个P值作为其单项测试的结果, 若P值大于显著水平0.01, 则说明该随机数序列通过了相应的测试项, 并且该值越接近1说明该项测试中的结果越好. 前文中, 只是计算出了不同电压下SLs信号的最大LEs, 并未经过实际检验说明LEs越大的信号可能更适合用于随机数产生. 选取多组不同LEs的SLs信号, 每个LEs的信号分成1000组1 Mbits的随机数进行测试, 本文给出三组不同LEs (分别为0.2, 0.4, 0.56)信号生成的随机数进行随机数标准测试, 其测试对应的P值如图9所示, 横坐标轴上的数字1—15代表NIST测试的15个测试项(具体见表1). 可以观察到, 不同LEs在随机数测试中的P-value值具有明显差异, LEs为0.2和0.4时的测试结果相差不大, 但仍然可以观察到LEs = 0.4时的曲线有更多点位于LEs = 0.2的曲线上方, 而LEs = 0.56曲线的大多数项测试结果点处于最上方, 从一定程度上反映了LEs越大的SLs信号, 生成的随机数质量越好. 表1为2.803 V (LEsmax = 0.56)电压下生成的随机数的NIST详细测试结果, 包含P值和通过测试项的百分比和结果. 从测试结果来看, 本文的随机数发生器产生的随机序列能够通过15项随机性测试, 说明通过SLs信号产生的随机数具有良好的统计随机性, 其中块内频率测试(1 Mbit子块中0, 1比例均衡程度)和近似熵测试(序列的无规则性)测试结果几乎达到了1, 并且整体通过率均大于0.9806[45], 本文使用SLs信号生成的随机数通过了NIST SP 800-22的全部15项测试.
| 统计测试 | P 值 | 通过百分比 | 结果 |
| 频率测试 | 0.514124 | 0.995 | 通过 |
| 块内频率测试 | 0.966244 | 0.990 | 通过 |
| 累加和测试 | 0.981609 | 0.993 | 通过 |
| 游程测试 | 0.782040 | 0.993 | 通过 |
| 块内长游程测试 | 0.657933 | 0.996 | 通过 |
| 二进制矩阵秩测试 | 0.379555 | 0.992 | 通过 |
| 离散傅里叶变换测试 | 0.196920 | 0.985 | 通过 |
| 非重叠模块匹配测试 | 0.938463 | 0.988 | 通过 |
| 重叠块比配测试 | 0.224821 | 0.987 | 通过 |
| 全局通用统计测试 | 0.513309 | 0.989 | 通过 |
| 近似熵测试 | 0.955835 | 0.998 | 通过 |
| 随机游动测试 | 0.637119 | 0.985 | 通过 |
| 随机游动变量测试 | 0.324180 | 0.986 | 通过 |
| 串行测试 | 0.637119 | 0.982 | 通过 |
| 线性复杂度测试 | 0.414525 | 0.995 | 通过 |
表1NIST随机特性测试结果
Table1.Results of NIST statistical test.
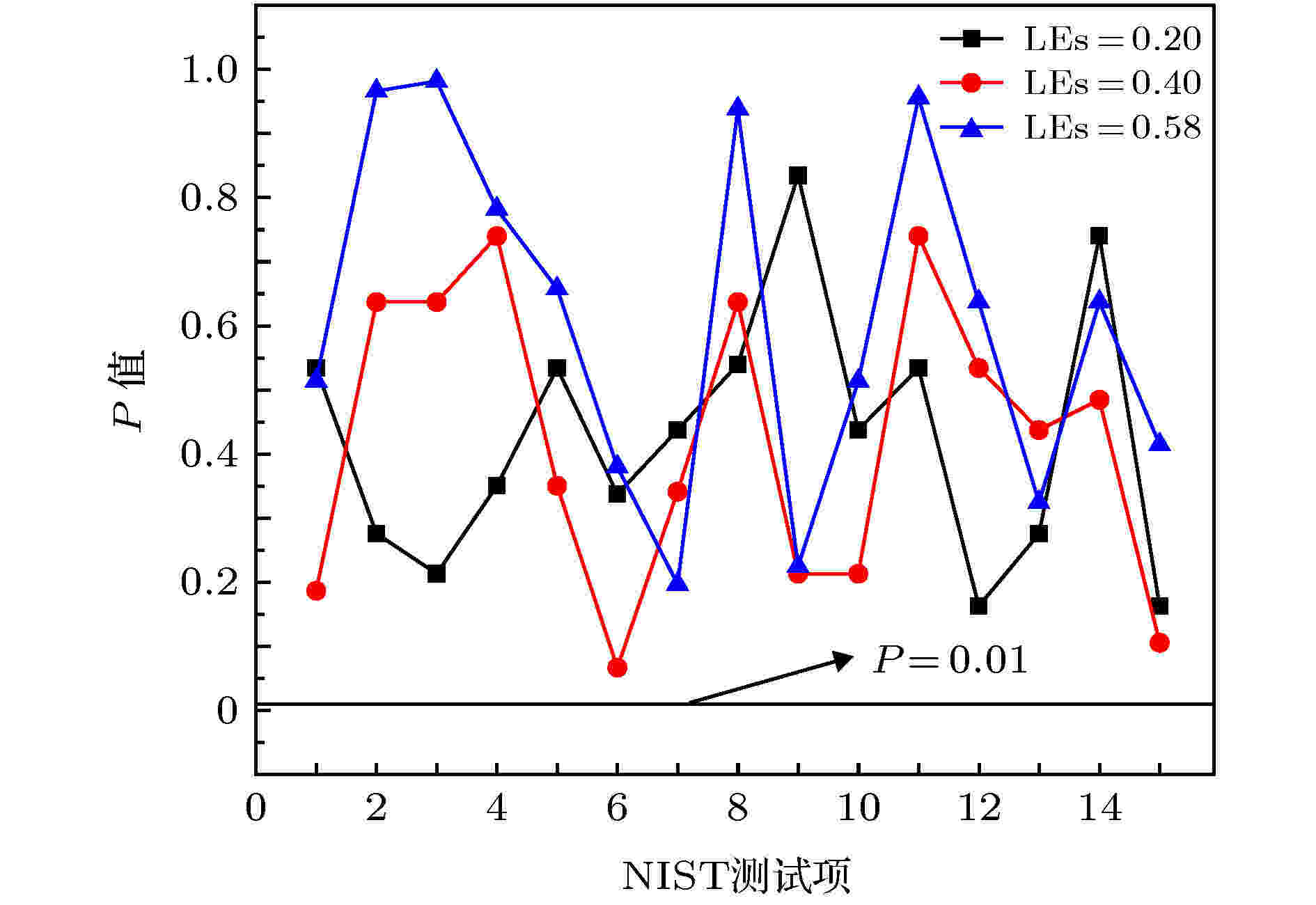图 9 不同LEs的超晶格随机数的NIST测试结果Figure9. Results of NIST for superlatticesrandom numbers at different Les.
感谢中国科学院苏州纳米所张耀辉团队为本文提供的SLs器件及理论帮助.
