摘要:工作于TE_01δ模式的金属谐振腔法是评价低损耗材料微波介电性能的通用方法. 微波介质谐振器均为多模式谐振器, 故正确识别TE_01δ模式是微波介电测试的基础. TE_01δ模式的识别可通过预测谐振频率及其随谐振器尺寸的变化、根据激励条件排除寄生模式等手段实现, 但已有方法存在复杂、易识别错误等缺点. 为此, 本文发展了一种准确识别TE_01δ模式的简单方法. 这种方法引入了介电性能已知的低损耗参考试样, 通过测试金属谐振腔中只放置参考试样及同时放置参考试样和待测试样时TE_01δ模式的谐振频率, 利用有限单元分析计算出待测试样的粗略介电常数, 并进一步预测只放置待测试样时TE_01δ模式的谐振频率. 此谐振频率的预测值与测试结果相差1%以内, 因此很容易将TE_01δ模式与其他寄生模式区分开, 进而实现TE_01δ模式的准确识别.
关键词: 微波介电测试/
TE_01δ模式/
模式识别/
有限单元分析

English Abstract

全文HTML

--> --> -->

低损耗微波介质材料被广泛应用于微波电路中的介质谐振器、滤波器、双工器、微波基板及电容器等元器件, 是现代微波通信技术的关键材料之一^[1-3]. 表征微波介质材料介电性能的基本参数为介电常数(ε_r)、Qf值(介电损耗tanδ与频率f的乘积)及谐振频率温度系数(τ_f )^[1-3], 对这3个性能指标的精确评价是微波介质材料研究领域的基础课题之一. 根据测试原理的不同, 可将评价材料微波介电性能的方法分为传输线法及介质谐振法两大类^[4]. 出于测试精度的考虑, 低损耗微波介质材料的性能应采用介质谐振法进行评价, 而其中应用最为广泛的则是工作于TE₀₁₁模式下的平行板法^[5-7]及工作于TE_01δ模式的金属谐振腔法^[5,8,9]. 对这两种方法而言, 所用试样一般均为圆柱体, 典型尺寸为直径10 mm、厚度5 mm. 平行板法具有结构简单、有解析解、易分析等优点, 但由于金属壁与试样接触、引起的损耗较大, Qf值的测试精度较低^[7,10]. 而在金属谐振腔法中, 金属壁远离试样、引起的损耗大幅降低, 故Qf值的测试精度显著提升^[9,10]. 但由于谐振系统结构较平行板法复杂, 这种方法不存在解析解、分析复杂、需较大计算量. 因此, 从各参数的精度考虑, 传统上通常用平行板法测试ε_r及τ_f、用谐振腔法测试Qf. 近年来, 随着电子计算机计算能力的大幅提升及数值分析方法的迅速发展, 谐振腔法测试ε_r的精度已接近平行板法, 可满足绝大多数场合下的测试要求^[11,12]. 虽然用其评价τ_f时仍存在一些问题^[13], 但谐振腔法在精确评价低损耗材料微波介电性能中的作用已变得越来越重要.
所有微波介质谐振器均具有无数种谐振模式, 故准确识别金属谐振腔法中的TE_01δ模式对微波介电测试而言具有非常重要的意义. 如果将其他谐振模式误判为测试所需模式, 由此得到的待测试样的微波介电性能显然是完全错误的. 实际上, 自微波介质材料的相关研究开展几十年来, 始终有一些文献中报道的微波介电性能无法重复, 一个重要原因即为测试时谐振模式的误判. 一般而言, ε_r越低, TE_01δ谐振峰附近的寄生模式峰越多, 也就越容易出现模式识别的错误. 通常可采用以下两类方法进行TE_01δ模式的识别^[5]. 1)根据激励条件排除寄生模式. 如使用探针进行电场耦合时, 需要电场有沿探针方向的分量; 而使用耦合环进行磁场耦合时, 则需要磁场有垂直于环面的分量. 对TE_01δ模式而言, 电流仅有环向分量, 而磁场则只有径向和轴向分量, 故可根据这一特点进行模式识别. 但这种方法较复杂, 且一些寄生模式具有与TE_01δ模式相似的电磁场结构, 无法排除. 2)估计待测试样的ε_r, 预测谐振频率及其随谐振器尺寸的变化. 当谐振器及待测试样的尺寸固定时, TE_01δ模式的谐振频率由试样的ε_r决定, 故可先在较低频率(如1 MHz)下测试材料的ε_r, 并将其作为微波频段下的ε_r用于预测TE_01δ模式的谐振频率. 但由于材料的介电性能在宽频率范围内普遍存在介电驰豫, 用这种方法估计的微波ε_r与真实值可能有较大偏差, 故会造成模式识别的错误. 此外, 可将金属谐振腔的上盖设计成可调节式的^[14], 通过计算上盖位置改变时TE_01δ模式谐振频率的变化并与测试结果对比, 即可用于模式识别. 但这种方法增加了谐振腔体的复杂性, 且使用时会磨损腔体内壁, 导致测试精度的降低.
另一方面, 将性能不同的两种材料制备成层状结构, 形成所谓的“叠层介质谐振器”, 是调控低损耗微波介质陶瓷性能的一种新型方法^[15-23]. 本课题组之前的工作已证明, 可以使用有限单元分析等数值方法, 根据两终端材料的性能精确预测叠层介质谐振器的性能^[18-20]. 受此启发, 本课题组发展了评价高损耗材料微波介电性能的改进型金属谐振腔法^[24-28]. 在此方法中, 采用尺寸较小(直径3 mm左右, 厚度小于1 mm)的高损耗待测试样, 同时引入尺寸较大(直径10 mm左右, 厚度1—5 mm)、微波介电性能已知的低损耗参考试样, 以保证能够观测到TE_01δ模式的谐振峰. 根据谐振腔中只放置参考试样及同时放置参考试样与待测试样时TE_01δ谐振峰的不同, 即可以利用有限单元分析得到待测试样的微波介电性能, ε_r的测试误差小于4%^[24,26]. 这一计算过程恰好为叠层介质谐振器的研究中根据终端材料的性能预测谐振器性能的逆过程. 实际上, 改进型金属谐振腔法同样可用于低损耗材料微波介电性能的粗略测量. 由于不存在高损耗导致谐振峰消失的问题, 采用典型尺寸低损耗待测试样即可, 通过此法得到的粗略介电常数的测试误差与高损耗待测试样相比可明显降低. 而将这一粗测的介电常数用于预测只放置待测试样时TE_01δ模式的谐振频率, 同样具有较小的误差, 从而可用于精确测试时TE_01δ模式的准确识别.

采用双端口圆柱形金属谐振腔, 底部放置具有低介电常数和超低介电损耗的石英单晶柱作为支撑物^[29]. 金属谐振腔法中引入支撑物是为了使待测试样远离金属壁, 从而减小金属壁的损耗、提高介电损耗的测试精度^[9,10]. 由于支撑物的介电常数及介电损耗很低、直径较小, 其对谐振系统的影响很小, 且可通过数值计算扣除. 使用Agilent E8363B矢量网络分析仪测试谐振系统在1—20 GHz频率范围内的散射参数S₂₁, 并采用有限单元分析进行数值计算, 具体过程见文献[18-20, 24, 30]. 谐振系统具有轴对称的物理结构, TE_01δ模式中电场也仅有呈轴对称分布的环向分量E_θ, 因此可将三维问题简化为半横截面内的二维问题, 并将待分析区域划分为若干个以节点相连接的三角形单元. 由于任何位置处的E_θ均满足Helmoltz方程, 可利用一阶近似构建每个单元的矩阵方程. 引入金属壁及对称轴处E_θ为零的边界条件后, 可将所有单元的矩阵方程组合为整体矩阵方程. 通过求解整体矩阵方程, 即可由谐振器的尺寸、内部所有介质材料的尺寸及介电常数计算出TE_01δ模式对应的谐振频率及E_θ的分布. 反过来, 当TE_01δ模式对应的谐振频率已知时, 也可利用迭代法求出谐振器内介质材料的介电常数.
图1为用金属谐振腔法评价待测试样微波介电性能时准确识别TE_01δ谐振模式的三个步骤. 第一步, 将直径10 mm左右、厚1—2 mm、具有已知较高介电常数的低损耗参考试样放置在谐振腔中的支撑物上. 由于参考试样的介电常数已知, 可利用有限单元分析精确计算TE_01δ模式的谐振频率, 并根据S₂₁随频率的变化对此模式进行准确识别. 记录此时TE_01δ模式的谐振频率f_0,1, 并利用有限单元分析计算参考试样的准确介电常数ε_r,ref. 第二步, 将具有典型尺寸(直径10 mm左右、厚5 mm左右)的待测试样缓慢放置于参考试样之上, 观测放置过程中TE_01δ模式谐振峰的变化, 记录最终的谐振频率f_0,2. 利用有限单元分析, 根据ε_r,ref及f_0,2计算出待测试样粗略的介电常数ε_r,rou. 第三步, 仅将待测试样放置在谐振腔中. 利用有限单元分析, 根据ε_{r, rou}计算此时TE_01δ模式的谐振频率f_0,3. 测试S₂₁随频率的变化, 并且在f_0,3附近准确识别TE_01δ模式的谐振峰, 记录测试的谐振频率f_0,4, 并利用有限单元分析计算待测试样的精确介电常数ε_r,sam.
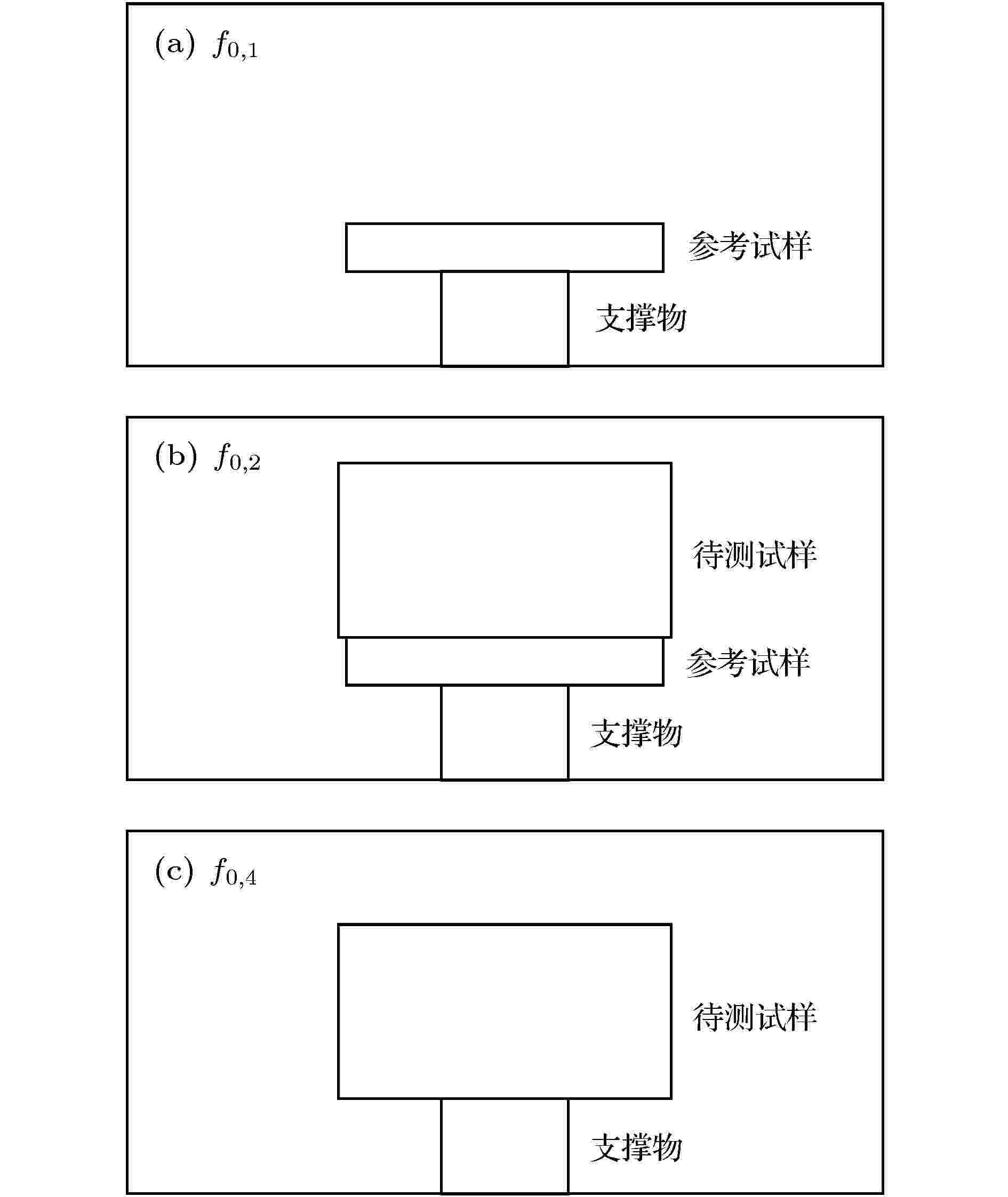图 1 识别待测试样TE_01δ模式谐振峰的三个步骤
Figure1. Three steps for identifying TE_01δ-mode resonant mode of to-be-measured sample.

表1列出了当前工作中所用参考试样(R1—R4)及待测试样(S1—S5)的尺寸与介电常数. 需要注意的是: 在测试之前, 参考试样的介电常数已知, 但认为待测试样的介电常数未知. 使用的参考试样R1—R4分别为Ca_1.15Nd_0.85Al_0.85Ti_0.15O₄^[31], Ba₂Ti₉O₂₀^[32], Ba_1.85Sm_4.1Ti₉O₂₄^[33], Ag(Nb_0.5Ta_0.5)O₃^[34]陶瓷, 而待测试样S1—S5则分别为H₃BO₃陶瓷^[35]、0.18B₂O₃-0.72SiO₂-0.1TiO₂复合材料^[36]、Al₂O₃单晶^[29]、Ca_1.15Nd_0.85Al_0.85Ti_0.15O₄陶瓷^[31]及Ba₂Ti₉O₂₀陶瓷^[32]. 待测试样的直径和厚度分别为9.90—12.03 mm及4.67—6.51 mm, 均为低损耗材料微波介电性能测试时所用的典型尺寸, 介电常数则在2.7—40之间. 参考试样则具有相近的直径及较小的厚度(1.04—1.64 mm), 这是由于支撑物、参考试样及待测试样的总厚度须小于腔体高度. 参考试样的介电常数较高(19.3—434), 是为了保证第一、二步中TE_01δ模式的谐振峰远离寄生模式, 易于识别.

类型	编号	直径/mm	厚度/mm	εr
参考试样	R1	10.17	1.64	19.3
	R2	10.86	1.48	39.4
	R3	10.75	1.49	77.2
	R4	9.36	1.04	434
待测试样	S1	12.03	6.51	2.79
	S2	9.90	5.10	4.78
	S3	10.00	5.00	9.50
	S4	10.12	4.67	19.4
	S5	10.83	5.44	39.2

表1参考试样及待测试样的尺寸与介电常数
Table1.Dimension and permittivity of references and to-be-measured samples.

图2为第三步中、谐振腔中仅放置待测试样时S₂₁的模随频率的变化. 对每个试样而言, 均可在1—20 GHz的频率范围内观测到多个谐振峰. 因此若缺少对待测试样介电常数及TE_01δ模式谐振频率的可靠估计, 难以准确识别出TE_01δ谐振模式. 图3给出了当前工作三个步骤中S₂₁的模随频率变化的一个例子, 其中参考试样及待测试样分别为R3和S2. 在第一步中仅放置参考试样R3时, TE_01δ模式的谐振频率f_0,1 = 5.224 GHz. 而在第二步中将待测试样S2放置于参考试样R3上时, 谐振频率降至f_0,2 = 5.160 GHz. 显然, f_0,2相对于f_0,1的降低是由S2的介电常数所决定的. 通过有限单元分析, 可求得待测试样S2的粗略介电常数ε_r,rou = 4.68, 并且进一步计算得到第三步中仅放置待测试样S2时TE_01δ模式的谐振频率f_0,3 = 13.862 GHz. 离f_0,3最近的两个峰对应的谐振频率分别为f_0,4 = 13.736 GHz及f_0,5 = 14.958 GHz. 显然, 两者分别对应TE_01δ模式及最近邻寄生模式, 从而可准确识别出TE_01δ模式.
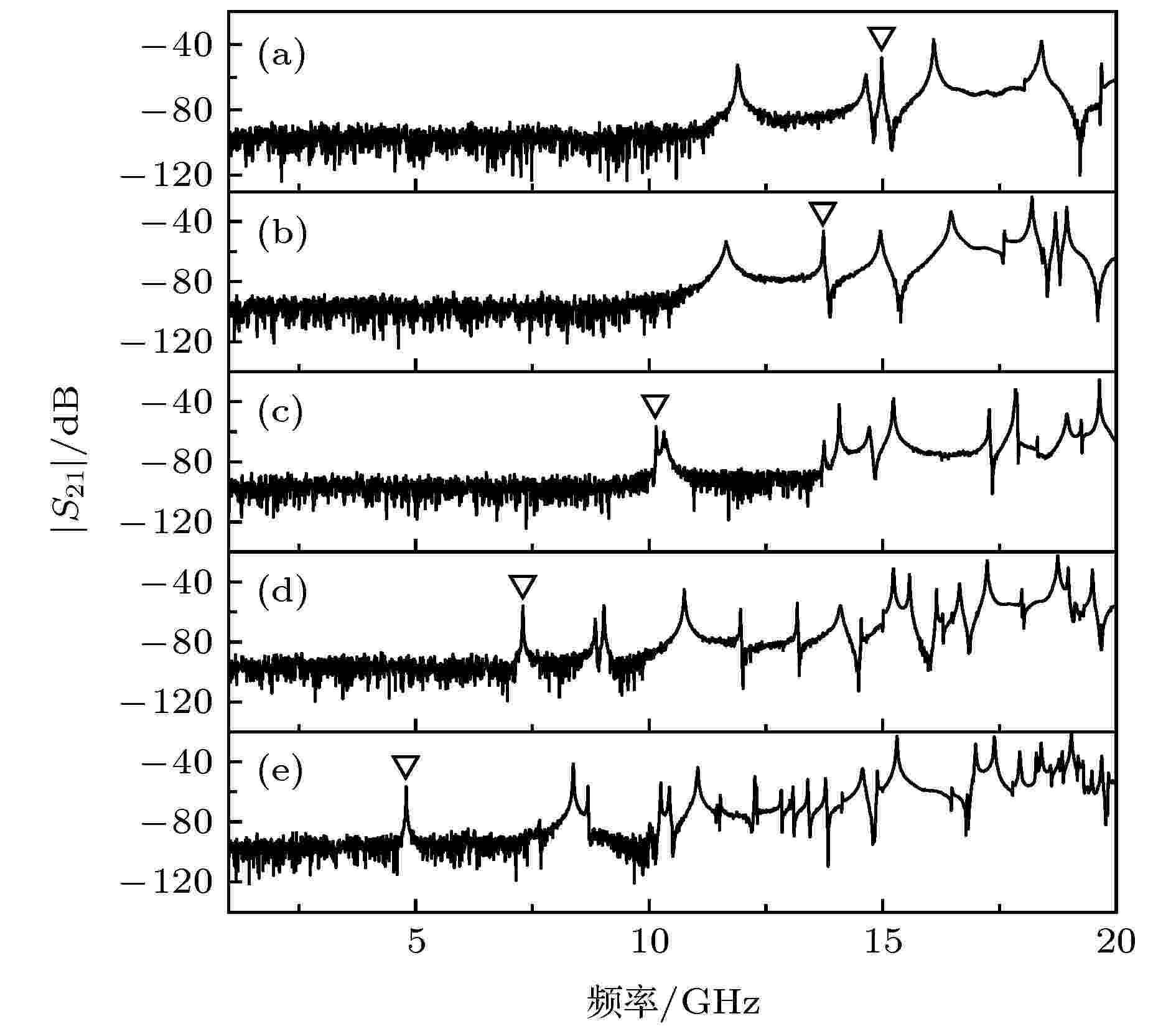图 2 待测试样(a) S1, (b) S2, (c) S3, (d) S4及(e) S5的|S₂₁|随频率的变化
Figure2. |S₂₁| as a function of frequency for to-be-measured samples: (a) S1; (b) S2; (c) S3; (d) S4; (e) S5.

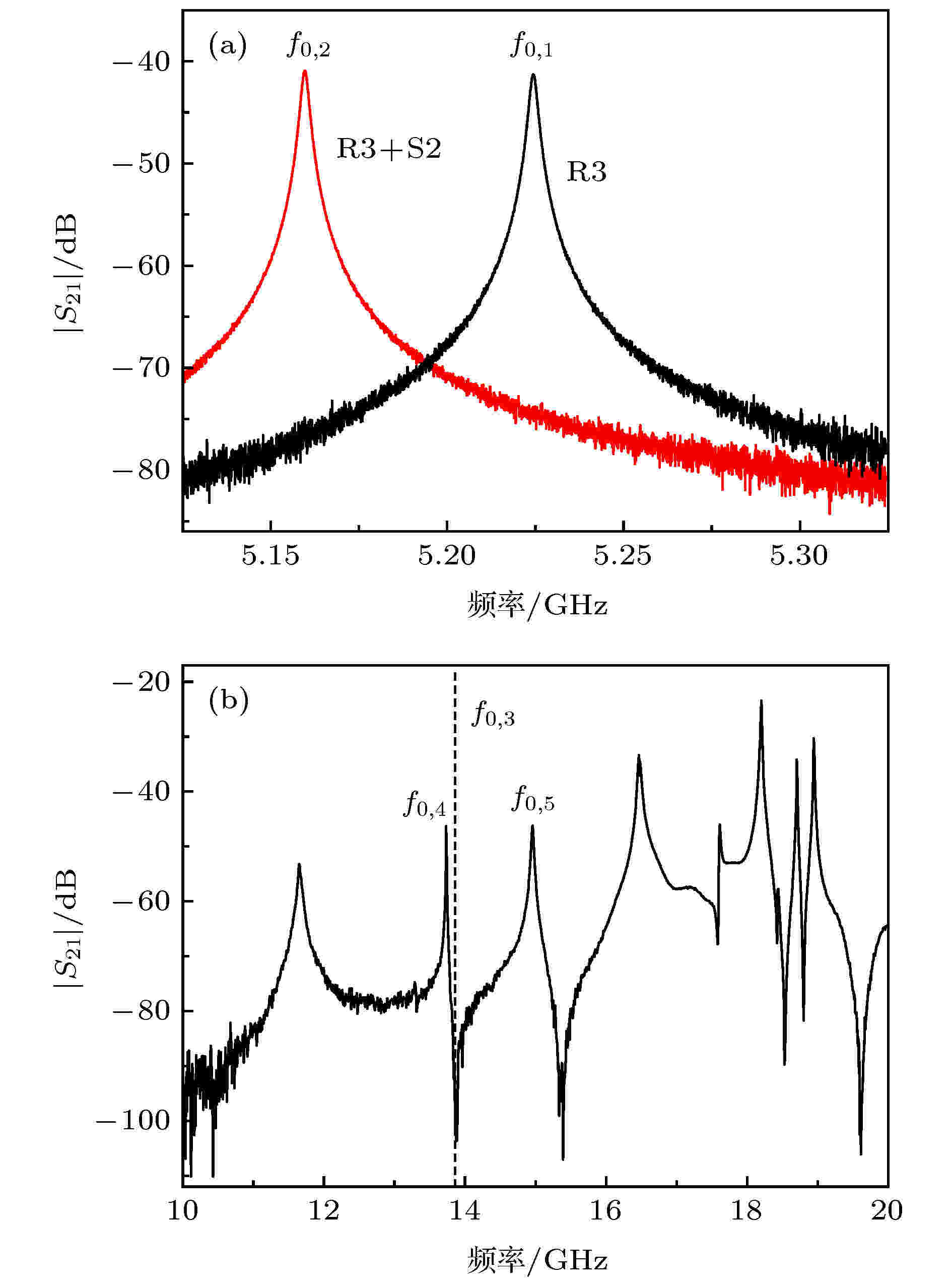图 3 (a) 谐振腔中放置R3及R3 + S2时TE_01δ模式的谐振峰; (b) 谐振腔中仅放置S2时|S₂₁|随频率的变化
Figure3. (a) TE_01δ-mode resonant peaks for R3 and R3 + S2 in the cavity; (b) |S₂₁| as a function of frequency for only S2 in the cavity.

为了进一步验证当前方法的可靠性, 表2列出了不同参考试样及待测试样进行组合时(R3/S1—S5及R1/S2, R2/S2, R4/S2)各谐振频率的测试及预测结果(其他组合的结果类似, 限于篇幅未列出). 显然, 对R3/S3之外的每种组合而言, 预测的谐振频率f_0,3附近仅有一个距离很近的谐振峰(对应f_0,4), 而次近邻峰(对应f_0,5)则相距较远, 因此可直接将f_0,4对应的谐振峰判定为TE_01δ模式、完成模式识别(见图2(a)、图2(b)、图2(d)、图2(e), 下三角符号表示识别出的TE_01δ模式谐振峰). 而在少数情况下, 当试样的介电常数较低且与尺寸满足一定关系时, 寄生模式与TE_01δ模式的谐振峰相距很近基至重叠, 难以区分. 这是由于各模式的谐振频率随着试样介电常数的升高而降低, 但TE_01δ模式谐振频率的降低速度却明显比较低频率下的寄生模式快(如图2所示), 而两者之间的对比同时还与试样尺寸相关. 例如, 对R3/S3的组合而言, f_0,4与f_0,5均与f_0,3相差较小, 故无法直接判定哪一个谐振峰对应TE_01δ模式, 而相距更远的其他谐振峰则可排除(见图2(c)). 这种情况下, 需改变待测试样的尺寸, 使寄生模式远离TE_01δ模式, 或者结合上文所述其他方法进行TE_01δ模式的最终识别^[5,14].

参考 试样	待测 试样	f0,1/GHz	f0,2/GHz	f0,3/GHz	f0,4/GHz	f0,5/GHz
R3	S1	5.224	5.184	15.107	14.988	14.642
R3	S2	5.224	5.160	13.862	13.736	14.958
R3	S3	5.224	5.067	10.216	10.158	10.360
R3	S4	5.224	4.849	7.358	7.298	9.035
R3	S5	5.224	4.217	4.830	4.800	8.376
R1	S2	10.046	9.498	13.807	13.736	14.958
R2	S2	7.215	7.028	13.789	13.736	14.958
R4	S2	2.760	2.752	13.830	13.736	14.958

表2不同参考试样/待测试样组合时各谐振频率的测试及计算结果
Table2.Measured and calculated resonant frequencies for different reference/to-be-measured sample combinations.

待测试样TE_01δ模式的准确识别归因于其谐振频率的精确预测. 表3列出了第三步中TE_01δ模式谐振频率的预测值与测试结果的相对误差((f_0,3 – f_0,4)/f_0,4). 对每一种组合而言, 这一相对误差均较小(0.38%—0.92%), 故在大多数情况下可轻易排除寄生模式, 实现TE_01δ模式的准确识别. 而第三步中TE_01δ模式谐振频率的精确预测又取决于第二步中计算所得待测试样粗略介电常数ε_r,rou的可靠性. 对采用类似步骤、测试高损耗材料微波介电性能的改进型金属谐振腔法而言, 待测试样的直径通常为3 mm左右、厚度小于1 mm, 介电常数的相对误差在4%以内^[24,26]. 而在本文中, 低损耗待测试样的尺寸大得多, 故粗略介电常数的相对误差((ε_r,rou – ε_r,sam)/ε_r,sam)有所降低, 为–2.2%至–0.8% (见表3). 这一误差对低损耗材料微波介电性能的精确测试来说是比较高的, 但对于当前工作中预测TE_01δ模式的谐振频率而言已经足够低, 故可轻易将TE_01δ模式从干扰模式中识别出来, 并进一步测试出试样的介电常数ε_r,sam及介电损耗tanδ (见表3). 本文发展的方法同样可用于其他介质谐振法中特定谐振模式的识别.

Reference	Sample	(f0,3 – f0,4)/ f0, 4	εr,rou	εr,sam	(εr,rou – εr,sam)/εr, sam	tanδ
R3	S1	0.80%	2.73	2.79	–2.2%	1.08 × 10–4
R3	S2	0.92%	4.68	4.78	–2.1%	2.75 × 10–4
R3	S3	0.58%	9.38	9.50	–1.3%	2.56 × 10–5
R3	S4	0.83%	19.1	19.4	–1.5%	7.63 × 10–5
R3	S5	0.62%	38.7	39.2	–1.3%	1.21 × 10–4
R1	S2	0.51%	4.72	4.78	–1.2%	2.75 × 10–4
R2	S2	0.38%	4.74	4.78	–0.8%	2.75 × 10–4
R4	S2	0.68%	4.70	4.78	–1.8%	2.75 × 10–4

表3TE_01δ模式谐振频率、粗略介电常数的相对误差及介电性能测试结果
Table3.Relative errors of TE_01δ-mode resonant frequency and rough permittivity, and measured results of dielectric properties

在叠层介质谐振器及改进型金属谐振腔法相关工作的启发下, 本文发展了低损耗材料微波介电性能测试中识别TE_01δ模式的新方法. 这种方法引入微波介电性能已知的低损耗参考试样, 通过在谐振腔内只放入参考试样及同时放入参考试样及待测试样时TE_01δ模式谐振频率的变化, 利用有限单元分析求出待测试样的粗略介电常数, 并进一步预测只放入待测试样时TE_01δ模式的谐振频率. TE_01δ模式谐振频率的预测值与测试结果的相对误差低于1%, 因此可轻易排除寄生模式, 实现TE_01δ模式的准确识别. 与已有模式识别方法相比, 本文发展的方法具有简单、可靠的特点, 并可用于其他介质谐振法中特定谐振模式的识别.