全文HTML
--> --> -->隐身, 在汉语词汇中指不露身份、隐蔽身体、隐匿身形. 因此, “隐身”的方式不仅限于人们最直观理解的物体透明化. 物体能被探测发现, 是由于物体的散射光进入人眼或探测器内成像. 因此, 通过调节物体的散射光, 人眼或探测器无法感知被隐身物体的信息, 就可以实现物体的隐身.
根据对散射光调控的方式, 隐身大体可以如下分为4类.
一是吸波或定向散射隐身: 通过吸收电磁波, 或设计特殊外形来调节物体的雷达散射截面, 降低探测器所接收的散射能量. 在空间中无背景场, 或背景场不作为测量对象而被忽略时, 该方法具有一定的效果. 但是, 一旦背景场的信息不可被忽略时, 所隐身的物体反而可能会更快暴露.
二是使物体在被观测者看来是透明的: 通过抑制物体的散射, 使物体在任意方向均不散射也不吸收探测波, 即散射为零. 这种方式是物理意义上的完美隐身, 但对材料电磁参数要求非常苛刻, 实现难度很大.
三是拟态隐身: 调节物体的散射光与背景类似, 使其融入背景环境中. 这种隐身方式在自然界中广泛存在. 静态的拟态隐身只能在特定的背景环境下有效, 受制于背景环境. 理想的拟态隐身设备应该具有一定的自适应能力.
四是干扰欺骗隐身: 相对于调节物体的散射光类似背景, 干扰欺骗隐身方式不以物体融入背景而隐身为目的, 而是将该物体的散射光调节至一个与被隐身物体信息无关的, 对探测器产生欺骗性的幻觉图像, 起到隐匿身形的效果.
除了将入射波吸收, 还可以将其反射至其他方向, 这也是避免反射电磁波进入探测器的方法之一. 世界上第一款隐身战机—著名的美国F117A隐身战机, 就采用了这一原理, 如图1所示. 雷达探测的原理是通过向目标区域发射电磁波, 如果电磁波遇到目标则会被反射, 雷达接收到该反射信号, 就会探测到该目标. F117A隐身战机具有完全不同于传统战斗机的非常奇特的外观, 其目的是为了把雷达反射波集中于4个窄波束内, 减少反射回雷达站的部分, 即减小雷达散射面积(radar cross section, RCS). 但是, 隐身飞机只能在机首正对雷达波发射源的方向才会有很小的雷达散射面积. 在其他方位, 尤其是腹部或者背部对准雷达波时, 其散射截面将会很大. 因此, 如果采用多站雷达进行探测, 即将发射机与接收机分布在不同位置, 隐身飞机的隐身效果将会大打折扣.
图 1 吸波或定向散射隐身, 美国空军F117A隐身战机的独特外观可以针对单基站雷达系统有效隐身Figure1. Examples of absorbing or directional scattering cloaking methods: The unique appearance of U.S. Air Force F117A stealth fighter enables it to be effectively cloaked under the single-based station radar system
如前文所述例子, 通过吸收探测电磁波, 使其尽可能少地返回探测器而实现隐身, 是针对现代战争设备、物资等“隐匿身形”需求的直接产物. 这种隐身方式也多被称为电磁波屏蔽隐身, 一般适用于微波频段或红外频段. 在微波频段, 常见的屏蔽方法是使用一些吸波材料, 如碳纳米管化合物、石墨烯化合物等[1-3], 而一种新型的人工材料— Metamaterial (也被译为超构材料、超材料、异向介质、新型人工电磁材料等)也被广泛地用于电磁吸波等领域. 超构材料是具有超越传统材料电磁特性的新型人工电磁材料, 其主体由周期性或者非周期性排列的人工电磁元件构成, 可等效地看作人造“原子”和“分子”, 当这些元件被组合在一起时, 便可在宏观上展现出独特的电磁特性. 这些特性可以用来设计多种多样的新型电磁设备, 如负折射[4-7], 逆切伦科夫辐射[8-11], 负古斯汉森位移[12-14], 滤波器[15], 调节偏振[16,17], 能量收集[18,19]等. 超构材料在理论和工程领域都有着巨大的应用前景, 也被广泛地用于实现电磁吸波与电磁隐身.
2008年, 美国波士顿学院的Landy等[20]首次设计了一种吸波结构, 这种材料由顶层的谐振结构、中间介质与底层的窄金属丝构成, 在11.5 GHz处可以近乎完美地吸收反射波, 实现隐身. 随后, 他们又与美国波士顿大学的Tao等[21]合作, 设计并实验实现了太赫兹频段的吸波超构材料. 同年, 湖南大学的Zou等[22]设计了在频率为4—9 GHz范围内可以显著地减弱反射的超构材料/表面. 2009年, 美国爱荷华州立大学Wang等[23]实现了一种手性吸波结构, 在入射波角度在一定范围内变化的情况下, 可在7.7 GHz左右对横电(transverse electric, TE)和横磁(transverse magnetic, TM)入射波实现吸波隐身. 东南大学Shen等[24]设计了一种多环形结构的吸波结构, 可以在三个频点上获得吸收峰, 拓宽隐身器件的工作频带. 2011年, 浙江大学Huang和Chen[25]提出了一种对极化不敏感的吸波超构材料, 能在多个频带上实现超过93.3%的吸收率. 2012年, 浙江大学Cui等[26]提出了一种锯齿形吸波结构, 这一设计可以对波长3—5.5 μm宽频范围内的入射波实现95%以上效率的吸波隐身. 浙江大学的Ding等[27]设计了一种金属-电介质多层锥体结构的超宽带吸收设备, 可以在7.8—14.7 GHz的频带内用于吸波隐身. 同年, 空军工程大学的Xu等[28]设计了一种二维人工传输线结构, 使用传输线理论设计谐振点, 实现了在三个频点上隐身的效果. 2014年, 美国德州大学奥斯汀分校的Soric等[29]设计了一种天线罩隐身衣, 这种天线罩可以灵活调整接收天线的散射, 以起到隐蔽或欺骗目标的作用. 2016年, 武汉理工大学Li等[30]提出了用于0.2— 7.6 GHz频段的铁氧体-超构材料复合吸波材料. 2017年, 新加坡南洋理工大学Mou和Shen[31]设计了一种非福斯特(Non-Foster)电路的吸波设备, 可以应用于160 — 1000 MHz的低频吸波隐身. 在红外频段屏蔽隐身方面, 如图2, 在2011年, 美国宾夕法尼亚州立大学Jiang等[32]设计了一种可以吸收中红外电磁波的表面遮罩; 2018年, 美国威斯康星大学麦迪逊分校Moghimi等[33]通过在超薄固体硅中植入银纳米线, 实现了热信号屏蔽/幻觉设备.
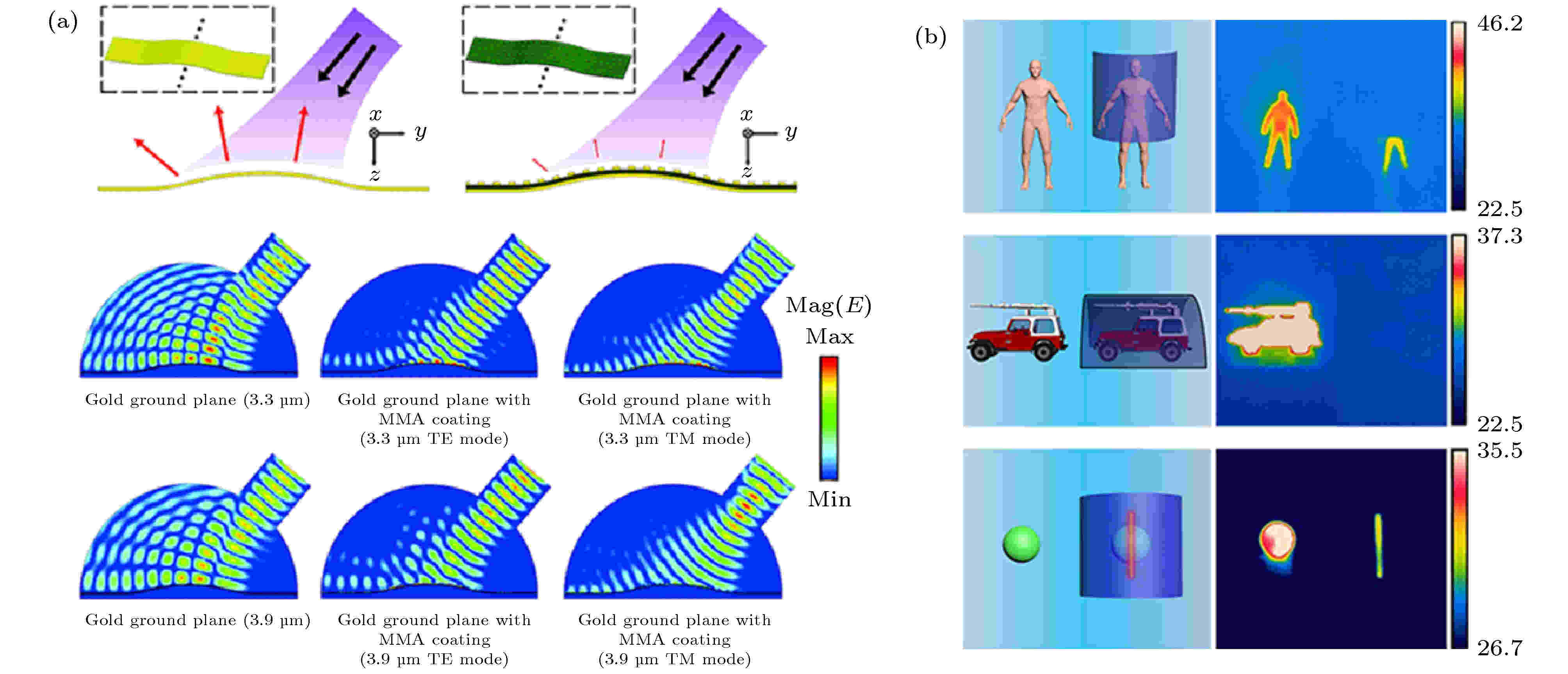图 2 吸收式隐身举例 (a)中红外波段吸收型表面遮罩[32], 若被隐身物体放置遮罩下方, 则反射波会被吸收而不会进入任何探测器; (b)红外隐身/幻觉对热成像图像的影响[33]Figure2. Examples of absorption cloaking. (a) A mid-infrared absorption cloaking sheet[32]. Most of the reflected wave will be absorbed without entering any detector. (b) Effect of infrared cloaking/illusion on thermal images[33].
由F117A隐身战机得到启发, 隐身设备即使向某些特定角度的散射不够小, 但只要能减弱后向散射, 就能够实现一定的隐身效果. 2018年, 复旦大学的Xu等[34]利用聚焦相位分布的单元结构阵列, 实验实现了一种宽频带, 极化无关的扩散散射设备, 这种设备向各个方向具有均匀且较低的散射. 随后, 他们利用波数分裂超构表面来实现扩散散射, 可以在宽角度入射波下实现双极化通道和多频通道的扩散散射隐身[35].
以吸收电磁波为原理的隐身衣具有概念简单、设计思路直接、在特定需求下隐身效果显著的优点, 但其缺点也较为明显. 例如, 在可见光的实际应用场景下, 由于昼间可见光的成分极其复杂, 若尝试让所设计的隐身设备吸收全部入射波, 除了探测仪器主动发出的探测波外, 本该入射于探测器中的一部分背景场也会被该隐身设备吸收, 探测器上会显示一个黑色物体. 虽然被隐身物体本身的信息可以不被探知, 但由吸波设备产生的与背景场的不协调仍会暴露该物体的存在, 故该方法在可见光隐身方面的应用有限. 利用这种方法实现的隐身衣不是物理概念上的完美隐身, 只适用于一些特殊情况下的隐身需求, 例如针对单雷达站探测隐身等, 使用中具有一定的局限性.
图 3 “完美隐身”示意[37] (电磁波在通过所设计的各向异性隐身球体后, 仍然沿着原来的方向传播)Figure3. “A perfect cloak”[37]. The electromagnetic wave still propagates in the original direction after passing through the designed anisotropic cloaking sphere.
2
3.1.通过自隐身方式达到透明隐身效果
空气的介电常数与磁导率均可以被近似视为1, 而若将材料本身制作成介电常数与磁导率均为1的材料, 那么此材料本身便可以实现完美隐身. 2016年, 浙江大学Ye等[39]提出了一种电磁参数与空气一致的光子晶体结构. 如图4所示, 这种特殊结构由金属与塑料复合材料构成, 在频率为10 GHz左右的等效介电常数与磁导率均为1. 在工作频率下, 该种结构对任意方向的探测电磁波均不会产生散射, 因此对于探测波是透明的, 可以实现隐身的效果. 由于该结构对所制成器件的形状和大小都没有限制, 也不需要任何其他隐身工具辅助, 因此它可以被看作一种“自隐身材料”. 由于其工作频段被限制在一个非常窄的范围内, 这种光子晶体结构适用于某些预先设计好的电子器件中, 如天线罩等. 2018年, 土耳其TOBB经济与技术大学Hayran等[40]提出了一种基于各向同性电介质的自隐身设备, 通过对原物体的介电常数分布进行微调优化来抑制物体对入射电磁波的散射, 实现了10.5—12.9 GHz频段内的自隐身效果.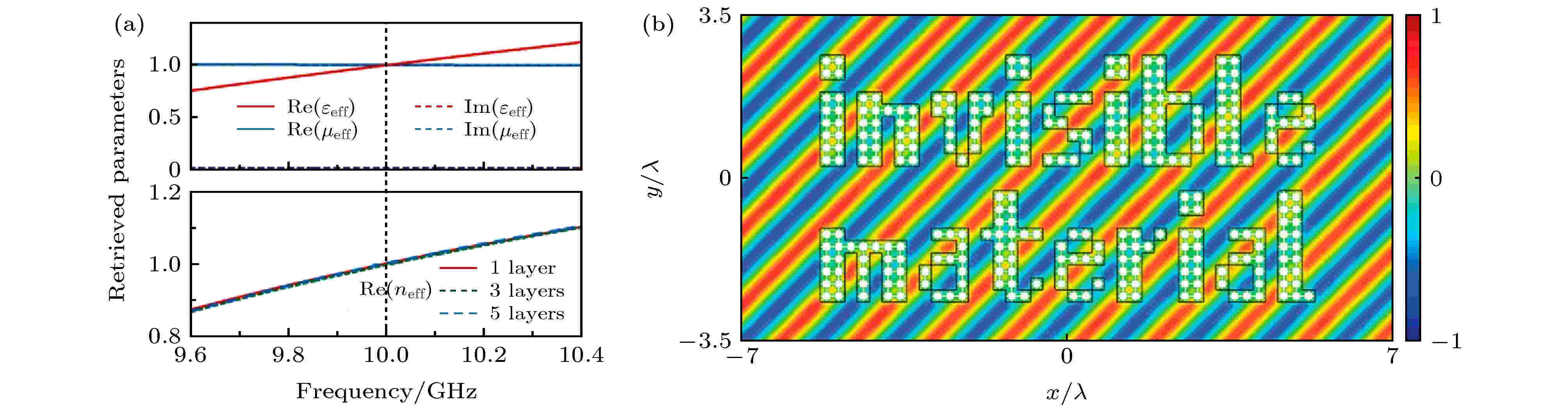
图 4 “自隐身材料”的工作原理及效果示意[39] (a)不同层数金属线谐振结构的等效电磁参数; (b) 自隐身结构在10 GHz斜入射平面波作用下的电场分布Figure4. The working principle and effect of “self-cloaked material”[39]: (a) Effective parameters of the solid slab composed of closely arranged corrugated wires with different layer thickness; (b) steady-state electric field distribution under an oblique plane-wave incidence at 10 GHz upon such self-cloaked material.
2
3.2.通过物理场相消达到透明隐身效果
2005年, 美国宾夕法尼亚大学Alù和Engheta提出了一种基于散射相消(scattering cancellation)的隐身设计理论[41]. 当探测波照射到任一物体时会产生散射, 若存在两个物体, 其中一个物体的散射可以被另一物体的散射相抵消, 就可以达到零散射的效果, 即二者组成的整体在探测波下是隐身的. 如图5所示, 通过在一个规则的电介质球外部添加一层相对介电常数小于真空(空气)的介质, 二者的组合体会呈现“透明”的效果.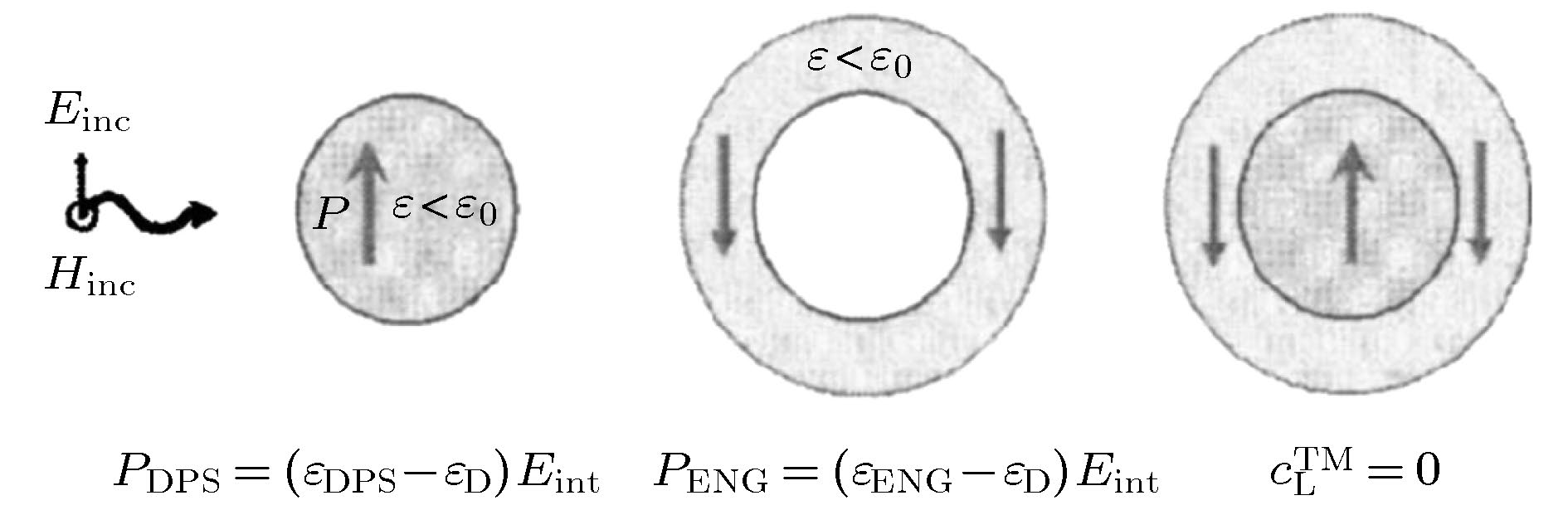
图 5 散射相消法的基本原理[41]Figure5. Schematic of the scattering cancellation cloaking method[41].
2009年, 美国宾夕法尼亚大学Edwards等[42]首次报道了由超构材料实现的等离子体隐身衣. 将金属鱼鳍阵列浸泡在高介电常数的液体中, 并控制阵列的数量、大小以及液体的介电常数, 便可以控制整个外壳材料的等效介电常数. 微波段实验证明, 这种等离子体隐身衣使物体的总散射减少了75%. 2012年, 浙江大学的Xu等[43]实验实现了一种各向异性材料层状结构隐身衣, 可以在2 GHz频率左右对较大尺寸物体隐身, 并实现一定的宽频效果. 同年, 美国德州大学奥斯汀分校的Rainwater等[44]进一步实现了探测波为斜入射情况下的隐身衣. 2013年, 该课题组Soric等[45]又基于散射相消实现了工作于微波频段的超薄隐身衣.
在这种调节散射的基础上, 研究者们又发现, 如果不将两个物体的散射匹配消除至零, 而是调节为某个值, 便可以实现幻觉光学. 使用散射相消模型实现幻觉光学的基本原理是, 对某一被隐匿物体A, 选择另一特殊定制的物体B进行配对来调节散射, 将二者组成的整体的散射波调整至只有物体C时相同, 这样就可以认为物体B与被隐匿物体A共同组成了物体C的幻觉. 2008年, 上海交通大学Yang等[46]提出, 将负折射率材料的外壳覆盖于完美电导体圆柱上, 便可以实现散射增强至远大于物体本身的超散射现象. 2015年, 兰州大学Yang等[47]从理论上推导了使用简单结构的各向同性材料实现散射相消光学幻觉的可行性, 并与Chen等[48]在热传导场中进行了实验验证.
随后, 受散射相消法启发, 有研究者将“相消”的基本原理从电磁波推广至静磁场. 在静磁场中, 磁场并无“散射”的概念, 但磁场线会受到物体的影响而产生偏移, 因此也可以通过物体的组合来控制磁场的路径. 斯洛伐克科学院与西班牙巴塞罗那自治大学G?m?ry等[49]提出, 一个圆柱形的磁介质圆柱壳会使得磁场线向内侧偏移, 而超导体会使得磁场线向外偏移, 因此适当调整介质壳的半径, 将二者合为整体, 便可以还原入射的静磁场的“扭曲”, 起到屏蔽和完美隐身的作用. 2018年, 该小组Mach-Batlle等[50]成功实验证明了该理论. 由于静磁场满足拉普拉斯方程, 对其波方程分离变量十分简便, 只需要均匀各向同性材料便可以满足要求, 这一简单的双层结构使得其得到了研究者们的关注. 2015年, 浙江大学Zhu等[51]根据双层隐身衣的原理, 设计并实验证明了宽频带下的双层球形静磁隐身衣. 在低温超导环境下, 该装置的宽频效应可以躲避金属探测器的探测. 2017年, 该课题组Jiang等[52]对此设备进行了改良, 以室温铁氧体代替了低温超导体, 使得该静磁隐身衣可以在室温下工作.
通过物理场相消取得隐身效果的方法局限在于, 相对于尺寸和波长相比拟的物体, 当物体尺寸较大时, 高次分量对散射场的影响增大, 会使得微结构的设计与制作非常困难.
2
3.3.通过变换光学法实现透明隐身
2006年, 英国圣安德鲁斯大学Leonhardt[53]提出了使用保角变换法实现隐身衣的构想, 通过对整个复平面进行坐标变换[54-56]来控制光线的路径. Leonhardt巧妙地选择了黎曼叶和支路的位置和大小, 以此实现对大部分光线的隐身效果. 但保角变换法理论有两个缺陷, 一是基于几何光学推导, 对于波长与隐身区域可比的情况不甚适用; 二是变换后产生的介电常数较为极端, 需要在一个大区域内连续变化, 相应的材料难以设计和制备. 同年, 英国帝国理工学院的Pendry等[37]提出了变换光学(transformation optics)这一概念. 由于麦克斯韦方程组在不同坐标系统下存在形式不变性[57-59], 故研究者可以通过坐标变换, 设计隐身衣材料的电磁参数, 从而在实空间中创造一个“隐身区域”. 电磁波在传播时将会绕过这个区域, 并保持各项电磁参数(幅度、相位、方向等)均不变. 在设计散射相消法或自隐身法的隐身设备时, 被隐身物体需要满足一定的电磁参数, 而利用变换光学法得到的隐身衣能够针对任意物体实现隐身. 由于电磁波在绕过这一隐身区域时不会产生散射, 因此放置在区域内的物体无法被外界探知, 实现隐身的效果. 在这种坐标变换下, 隐身衣外壳的电磁参数往往会随着半径的变化而变化, 需要自然界中不存在的非均匀各向异性材料来实现.在2006年, 美国杜克大学Cummer等[60]对Pendry等[37]提出的变换光学法进行了有限元数值分析, 证明了其可行性. 不久后, 杜克大学Schurig等[61]首次实验实现了微波频段的圆柱形隐身设备, 如图6所示. 由于电磁参数的完全渐变比较困难, 他们将理论推导的柱体隐身衣分为10层, 每层都由不同结构的单元结构阵列组成. 每个单元结构由覆铜的开口谐振环构成, 通过控制开口谐振环的几何参数, 等效介电常数和等效磁导率不同的介质便可以被构造出来. 将这些单元结构按照一定的方式排布, 便可以得到要求隐身参数的结构. 随后, 变换光学隐身衣开始了快速发展. 2007年, 美国普渡大学Cai等[62]提出了一种无磁化的光频段隐身衣设计方法, 基于柱体隐身衣的设计参数, 在只针对TM波的情况下对参数进行进一步简化, 并进行无磁化处理, 最终得到易于实现的参数. 2008年, 美国马里兰大学Smolyaninov等[63]利用二维等离子体超构材料实现了对TM极化波的简化参数隐身衣, 并在500 nm的工作波长处验证了其隐身特性. 但是, 由于工作在较高频率, 光频段隐身衣多处于微观尺度, 非均匀的各向异性介质有着较大的加工难度, 导致器件尺寸难以扩大至宏观尺度, 为光频段隐身衣实用化带来了一定困难.
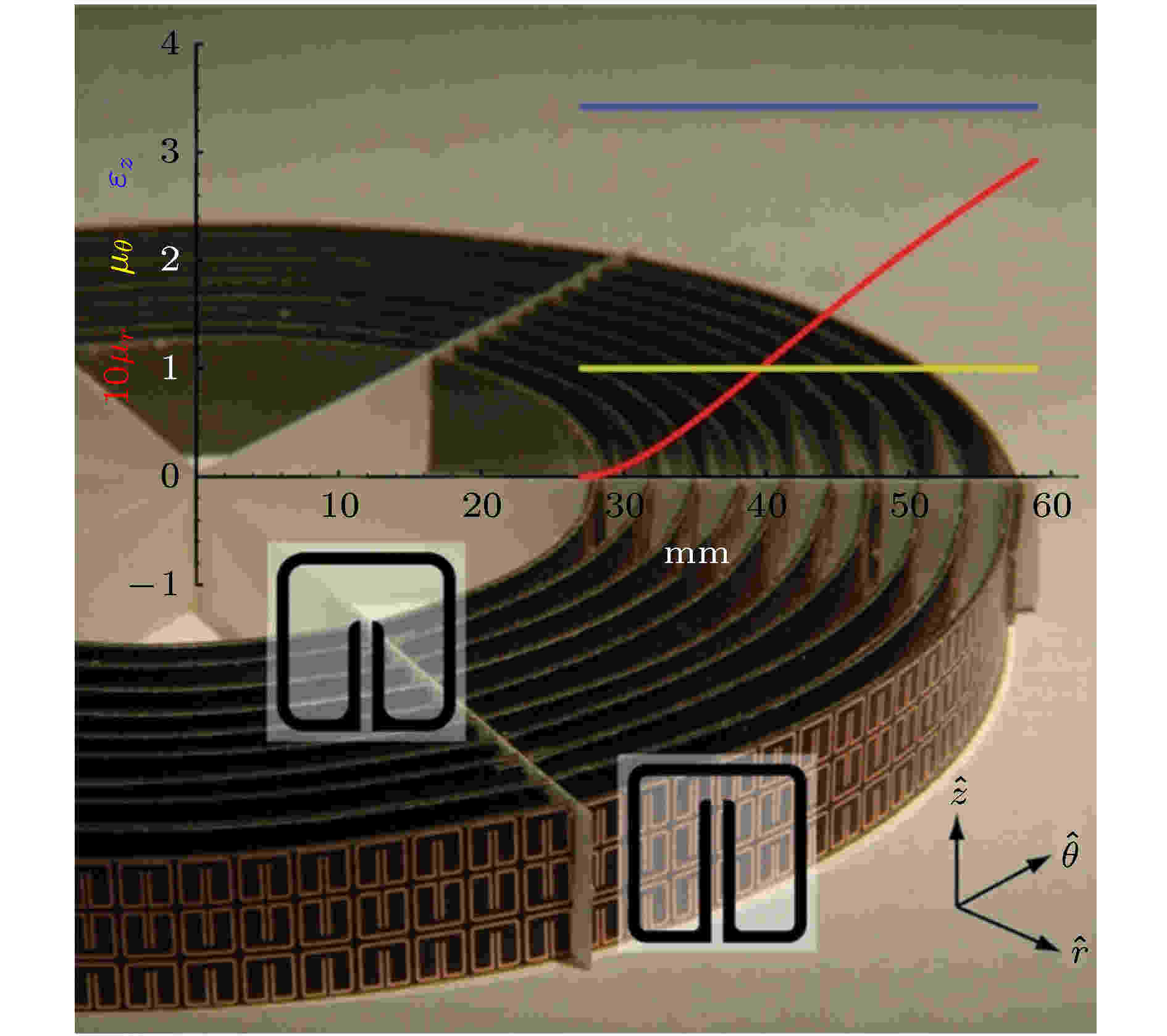图 6 基于变换光学的隐身衣实例[61]Figure6. Photo of cloak based on transformation optics[61].
早期利用变换光学法设计的隐身衣, 具有非均匀且各向异性的电磁参数, 实现起来较为困难. 针对此问题, 2009年, 浙江大学Xi等[64]提出了一种均匀变换光学的方法, 利用这种变换所得到的隐身衣具有均匀的电磁参数. 如图7(a)和图7(b), 通过在直角坐标系中三角形区域进行空间压缩或拉伸, 可以得到参数均匀的隐身参数. 将其参数进行进一步的对角化处理, 可以在三个选定的正交基方向呈现各向异性, 从而可以通过均匀的层状材料实现, 如图7(c)所示. 基于这一理论, 2013年, 美国杜克大学Landy和Smith[65]设计实现了微波频段一维隐身器件. 进一步地, 若取这一隐身设备的一半, 放置在全反射的地面, 便可以实现均匀变换光学的地毯式隐身衣[66]. 2019年, 浙江大学的Sun等[67]实现了一种宽入射角度的一维隐身衣.
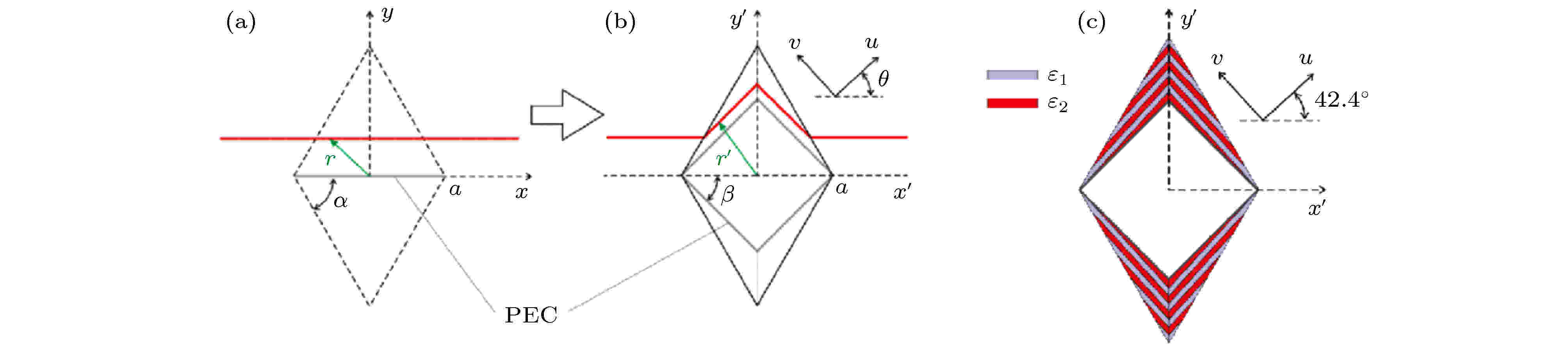图 7 利用均匀光学变换设计的一维方向隐身衣[64] (a)变换的原始虚空间, 红色场线代表某条光线; (b)变换后的实空间, 红色场线代表该条变换后的光线; (c)用周期性层状结构实现的该一维方向隐身衣示意图Figure7. Invisibility cloak designed by homogeneous transformation optics[64]: (a) The original virtual space of the transform; the red line represents a selected ray; (b) real space after transformation; the red line represents the transformed ray; (c) layered system for modeling the one-directional cloak.
一维均匀光学变换方法可以拓展到二维均匀光学变换. 浙江大学Chen和Zheng[68]设计并实现了对TM极化波的可见光频段柱体隐身器件. 如图8所示, 隐身器件由天然各向异性材料方解石构成, 可以实现TM极化波多个方向的隐身.
图 8 利用均匀光学变换原理设计的由方解石所构成的TM波可见光隐身器件[68]Figure8. A TM wave visible light invisibility cloak composed of calcite under natural light designed by homogeneous transformation optics[68].
实际上, 生活中简单易得的光学设备—镜子, 就是一种朴素的操控可见光的工具. 2014年, 美国罗切斯特大学Howell等[69,70]使用光学反射镜组, 利用简单的射线光学原理, 令可见光线多次反射, 将结构后面的物体呈现在视角范围内, 实现了光的绕行隐身效果. 他们称其为“宽频的、仅幅度调制”的隐身衣, 其意为该种隐身衣不包含对入射波的相位调制. 不同于微波天线对微波波段电磁波相位很敏感的特性, 在可见光隐身中, 由于可见光的波长较短, 人眼对可见光的相位并不敏感. 因此, 可以摒弃透射波相位保持一致性的条件来进行自然光隐身器件设计. 在这种情况下, 该种隐身衣可以使用各向同性材料来设计制造. 通过这一方法, 2013年, 浙江大学Chen等[71]实现了自然光大尺寸物体隐身器件, 如图9所示. 2015年, 该课题组把此模型拓展到了远红外波段, 实现了远红外波段的大尺寸隐身器件[72]. 随后, 该课题组进一步将这一模型延伸至三维, 设计实现了三维可见光隐身器件[73].
图 9 利用均匀光学变换原理, 舍弃相位一致性后制作的自然光大尺寸物体隐身器件示意图[71] (a), (b) 水中型自然光大尺寸物体隐身器件对一条鱼的隐身效果; (c), (d) 陆上型自然光大尺寸物体隐身器件对一只猫的隐身效果Figure9. Schematics of a nature light cloak for large objects when the phase consistency is ignored[71]: (a), (b) Dynamic monitoring of a fish swimming through the aquatic ray cloak; (c), (d) experimental observation of a cat in the terrestrial ray cloak.
2
3.4.地毯式隐身
2008年, 英国帝国理工学院的Li和Pendry[74]提出了一种利用准保角变换设计隐身衣的方法, 去除了变换后存在的奇点. 在坐标变换中, 由于真实空间是由虚空间压缩而成的, 此类隐身衣的电磁参数多呈各向异性. 在准保角变换中, 研究者通过选取某些特殊的坐标变换, 使得隐身衣整体的各向异性参数达到最小. 由此简化后, 此类隐身衣便可以通过各向同性的参数来实现, 大大降低了隐身材料设计制备的难度, 也让全极化电磁波的隐身成为了可能. 这类隐身衣通常放置在一个全反射平面上, 并覆盖于被隐身物体上方, 因此被称为地毯式隐身衣. 当电磁波入射到地毯式隐身衣后, 能够被全反射, 仿佛被隐身物体不存在于平面上, 从而起到隐身的效果, 如图10所示.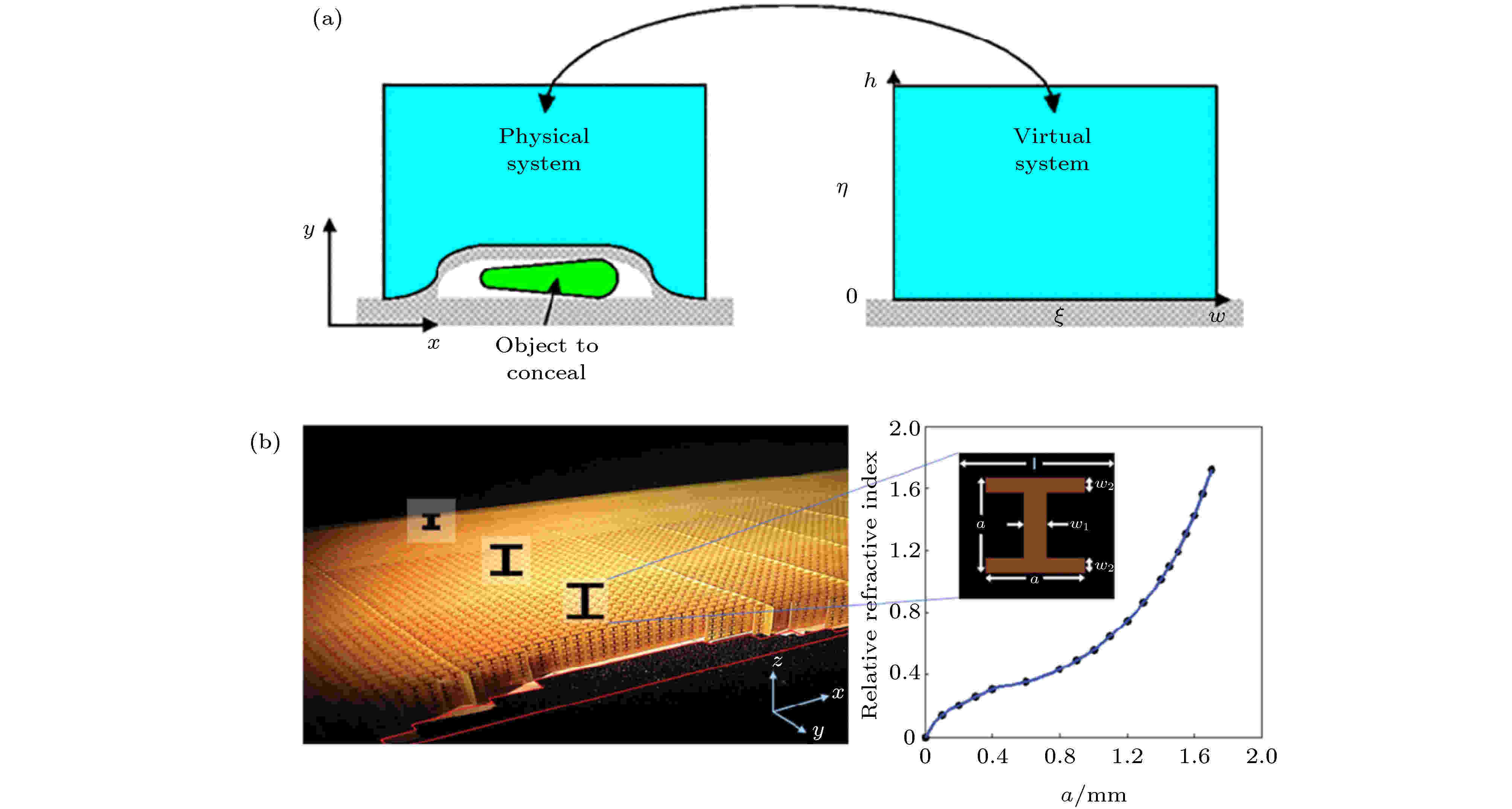
图 10 地毯式隐身衣 (a)地毯式隐身衣的设计方法[74], 通过对虚空间的压缩, 右侧子图的蓝色区域被变换至左侧子图中的蓝色区域, 从而隐藏实空间中的绿色物体; (b)首次实验实现的地毯式隐身衣及工字型单元结构[75]Figure10. Carpet invisibility cloak: (a) The design of carpet invisibility cloak[74], through the compression of virtual space, the blue region of right sub-figure is transformed to the blue region in the left sub-figure, thus concealing the green objects existing in the real space in figure (a); (b) experimentally realized carpet invisibility cloak and I-shaped unit structure by Liu et al[75].
2009年, 美国杜克大学Liu等[75]首次实验实现了地毯式隐身衣. 这种隐身衣由工字型的单元结构构成, 经由改变工字型单元的各项尺寸参数, 可以得到不同的等效折射率, 从而得到空间上渐变折射率分布的材料, 用于实现所需的参数. 由于使用的单元结构是非谐振的, 这一隐身衣可以在13—16 GHz实现宽频的隐身效果.
在近红外频段方面, 2009年, 美国加州大学伯克利分校的Valentine等[76]设计了二维近红外频段地毯式隐身衣. 该种隐身衣使用在硅片上打孔的方式调节折射率的大小. 随后, 美国科罗拉多大学Lee等[77]通过控制硅纳米棒的直径, 美国康奈尔大学Gabrielli等[78]通过控制硅纳米棒的密度, 也实现了近红外频段的地毯式隐身衣. 2011年, 美国西北大学Zhou等[79]利用当时逐渐兴起的3D打印技术制作实现了0.3—0.6 THz的地毯式隐身衣. 在可见光频段方面, 2011年, 德国卡尔鲁斯厄理工学院的Fischer等[80]利用基于受激发射损耗的激光直写技术, 将光子晶体的所有结构缩小了2倍以上, 实现了能够工作在可见光频段下的三维全极化地毯式隐身衣. 同年, 美国加州大学伯克利分校的Gharghi等[81]通过在氮化硅波导上刻蚀不同直径的亚波长的孔, 从而控制介质的等效折射率, 也实现了可见光频段的地毯式隐身衣.
准保角变换使用的各向同性参数是一种近似, 从理论上分析, 其实际隐身效果会有一部分瑕疵[82]. 早期的地毯式隐身衣是对被隐身物体上方的一段空间进行变换, 这种三维形式的结构存在体积大、不易加工、损耗严重等问题. 美国哈佛大学Capasso课题组[83]于2011年9月提出, 将超构材料二维平面化, 可以得到其平面形式—metasurface (也被译为超表面、超构表面等). 超构表面基于相位突变和极化控制思想设计、遵守广义斯涅耳折射/反射定律, 是一种以人工微结构单元为核心构成的新型材料, 其厚度一般都远小于工作波长, 具有尺寸薄、加工精确、易于共形等优势, 在实际应用特别是对可覆盖物体的应用中有着巨大的优势, 是未来一个重要发展方向. 鉴于上述优势, 已有的地毯式隐身衣设计思路可以被优化. 如图11(a)所示, 2013年, 兰州大学Zhang等[84]提出了使用广义斯涅耳定律实现地毯式隐身衣的可能性. 美国德州大学奥斯汀分校Estakhri和Alu[85]应用纳米谐振结构在太赫兹和毫米波频段上设计了隐身器件. 2015年, 美国加州大学伯克利分校的Ni等[86]设计了以金与氟化镁基底的纳米天线, 如图11(b)所示, 实现了可见光频段的地毯式隐身. 西班牙纳瓦拉公立大学Orazbayev等用一个环形谐振器表面结构在太赫兹[87]和毫米波[88]频段上设计了隐身器件, 如图11(c)所示. 在2016年, 美国东北大学Cheng等[89]提出了532 nm的可见光波段的地毯式隐身, 同年华中科技大学Tao等[90]提出了光频段全极化电磁地毯式隐身器件. 浙江大学Yang等[91]提出了一种超薄的表面隐身衣理论, 除可以作用于电磁波以外, 还可以作用于声波、水波等物理场. 随后, 他们通过使用C4对称的闭口谐振环, 在8 GHz左右实现了微波段全极化的地毯式隐身衣[92], 如图11(d)所示. 在2017年, 天津大学Wei等[93]将梯度超构表面应用在太赫兹波段, 实现了地毯式隐身. 在2018年, 浙江大学Wang等[94]、中国科学院光电技术研究所的Yang等[95]分别对既有表面隐身理论进行了改良, 使用多级结构将单频点工作的表面隐身衣扩展至多个频率.
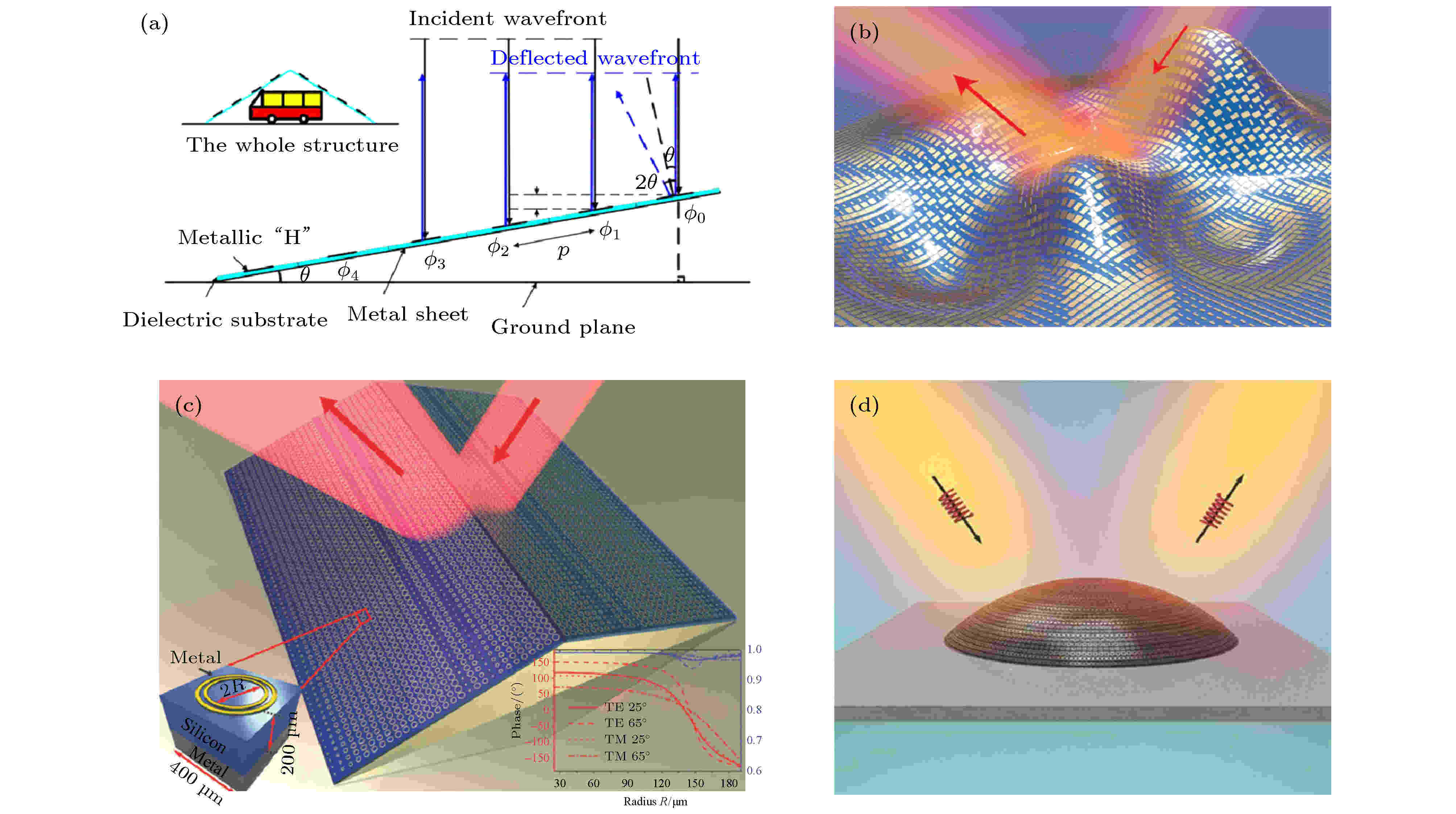图 11 (a)地毯式隐身效果的原理图[84]; (b)可见光频段隐身衣[86]; (c)使用环形谐振器结构在太赫兹和毫米波频段上设计的隐身器件[88]; (d)使用闭口谐振环实现的全极化表面隐身衣[92]Figure11. (a) A schematic of carpet cloak[84]; (b) schematic view of a visible spectrum invisibility cloak[86]; (c) cloaking devices designed at terahertz and millimeter wave frequencies by applying ring resonators to metasurfaces[88]; (d) a full-polarization carpet cloak by applying closed-loop resonators[92].
2
3.5.非接触式透明隐身
目前已经被实验实现的电磁波隐身器件, 大部分都是封闭式的. 所设计的隐身器件需要包围整个隐身区域, 隐身器件材料也将与隐身区域或者被隐身物体接触. 这使这类隐身器件在实际应用中面临一定的限制: 由于隐身区域内的物体与外界环境完全隔绝, 因而无法与外界进行交流; 针对大尺寸物体, 隐身器件需要包围比其更大的隐身区域, 实现难度和成本将会非常大. 2009年, 空军工程大学Ma等[96]基于变换光学提出了一种开放隐身衣模型, 允许传统的封闭式隐身衣有开口. 但该种隐身衣仍然需要将隐身物体放在隐身设备内部.2009年, 香港科技大学Lai等[97]提出了“补偿介质”的概念, 如图12(a)所示, 针对特定物体, 可以设计一个相应的“补偿物体”来消除该物体的散射, 从而能够通过隐身器件远距离地隐藏该特定物体. 随后, 基于这一方法的光学设备开始涌现, 如光学幻觉[98]、弯曲波导[99]等. 由于这一方法对物体和隐身器件的相对位置没有限制, 因此为远距离隐身的实现打开了一条通道. 但是, 不同于以往变换光学的隐身衣可以在隐身区域内隐藏任何物体, 这些远距离隐身器件和幻觉器件需要提前知道被隐身物体的形状、材料及位置, 设计相应的“补偿物体”来消除原有物体的散射, 因而只能针对特定的物体有效. 如果被隐身物体的形状、材料及相对位置发生改变, 将会影响整个器件的散射场分布, 从而破坏器件的整体隐身效果.
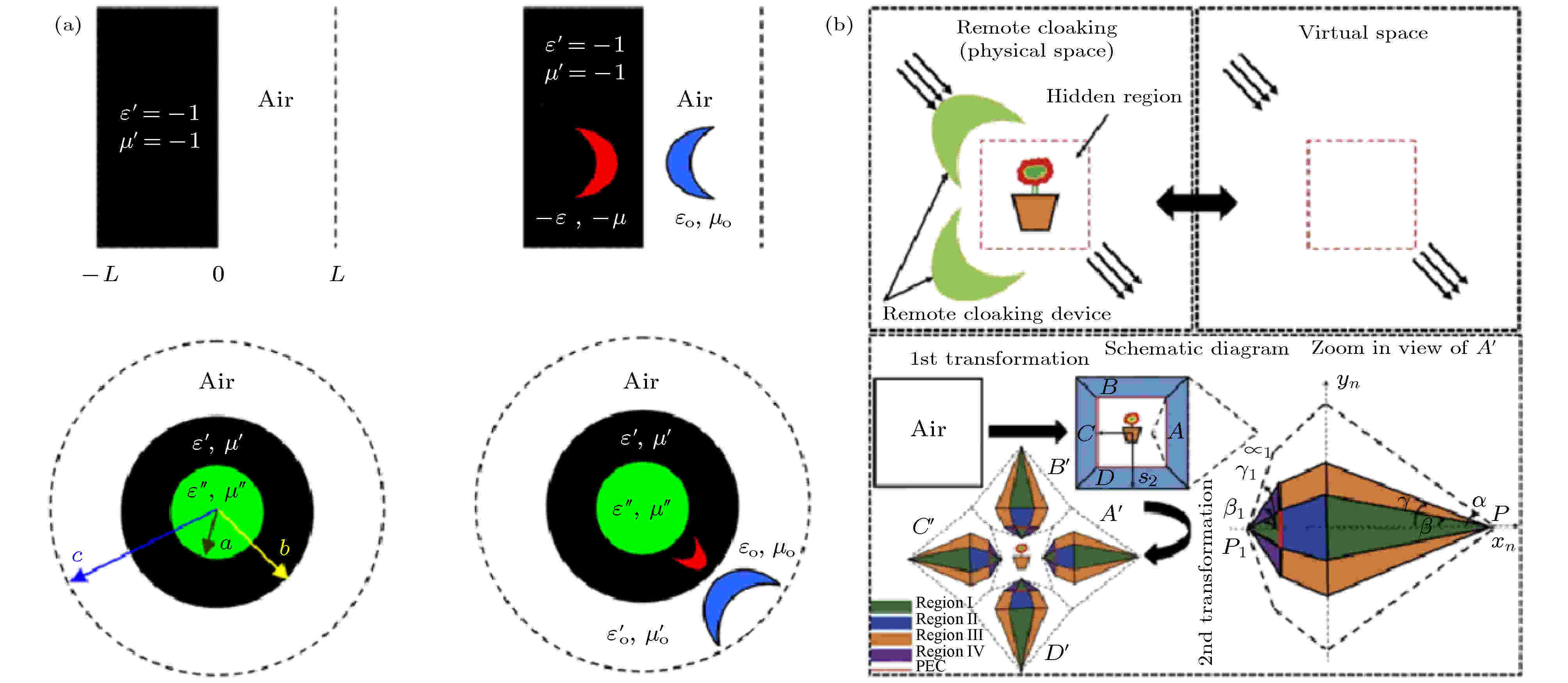图 12 (a) 基于“补偿介质”的隐身[97]; (b) 基于多重变换光学的远程非接触式隐身[100]Figure12. (a) Cloaking by designing a “complementary media” [97]; (b) remote cloaking based on multi-folded transformation optics[100]
2016年, 浙江大学Zheng等提出了一种针对任意物体有效的非接触式隐身器件, 如图12(b)所示[100]. 该器件利用了一种多重变换光学的方法, 通过对空间进行多次变换, 在隐身器件的一定距离外创造一个隐身区域, 入射电磁波将无法进入隐身区域, 而整个器件的远场散射仍然保持与没有物体时一致, 且保持被隐身物体与外界环境的连通. 不同于之前提出的远距离隐身器件, 用这种方式设计的非接触式隐身器件不需要针对被隐身物体设计相应的“补偿物体”, 因而具有更广泛的应用前景. 而且, 针对隐身区域内的任何物体, 无论其形状、材质以及相对位置的移动有何不同, 将有着同样的隐身效果. 研究者也基于该种多重均匀变换光学的方法进行了一些延伸工作, 如远程地毯式隐身[101]、光学幻觉[98]和微波集中器[102]等.
2
3.6.使用有源器件实现透明隐身
基于散射相消或变换光学的隐身衣已经获得了良好的隐身效果, 但上述的隐身衣多数存在一些共性短板, 例如, 隐身衣的尺寸一般大于被隐身区域, 一些设计甚至大于隐身区域数倍; 隐身衣多数是静态的, 一旦制造完成, 功能上就难以调整; 设计隐身衣所需要的实际材料会有一定损耗等. 因此在被动式、静态的隐身衣之外, 一些主动式的、有源的隐身衣的设计被提出. 使用主动源控制物理场隐身的概念最早在声学中就有提出[103]. 2006年, 美国斯坦福大学Miller[104]首次指出, 若在隐身区域外围放置成对的传感器与源, 实时对入射波的信息进行采集并计算还原, 便可以实现有源隐身. 2008年, 浙江大学的Zhang等[105]分析了隐身衣内部有电磁场源时的解, 进一步论证了隐身衣可以隐藏源. 2009年, 美国犹他大学Vasquez等[106,107]提出, 可用三个或多个有源设备在中央形成一个没有场的“静默区域”. 在隐身理论的基础上, 2010年, 香港科技大学Zheng等[108]计算了有源元件实现光学幻觉的方法. 2012年, 加拿大多伦多大学Selvanayagam等[109]使用等效原理推导了应用这类有源元件隐身的情况, 并在2013年实验实现了在1.5 GHz频段附近的有源微波隐身, 如图13(a)所示[110]. 这类有源隐身方法随后被扩展至其他物理场, 2015年, 兰州大学Ma等[111]使用36个电极(直流电源), 在稳恒电流场实现了有源隐身与幻觉, 如图13(b)所示. 同年, 新加坡南洋理工大学Nguyen等[112]使用24个半导体散热片作为“热极”, 实现了热传导场的有源隐身, 如图13(c)所示.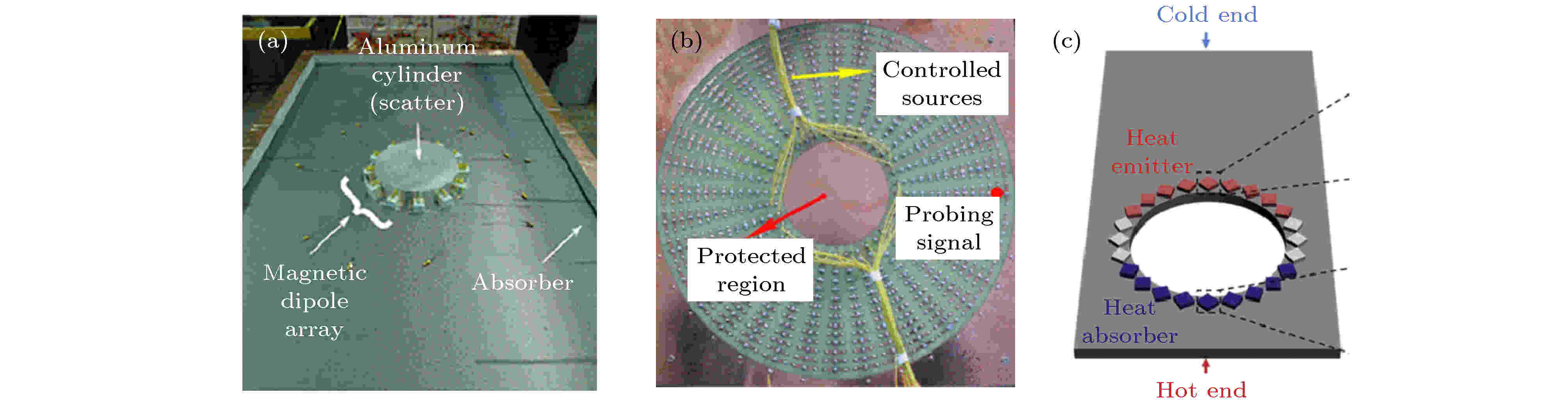
图 13 有源隐身的实现 (a) 微波电磁场有源隐身衣[110]; (b) 稳恒电流场有源隐身衣[111]; (c) 热传导场有源隐身衣[112]Figure13. Experimental realization of active cloaking: (a) Active invisibility cloak at microwave frequency[110]; (b) active direct current field invisibility cloak[111]; (c) active heat conduction field invisibility cloak[112].
以上所述的有源隐身方法均具有设备体积小、无需特殊介质材料、动态控制灵活等优势. 但针对电磁波, 此类有源隐身均需事先获知入射场源的信息才能进行正确匹配, 以发挥正常的隐身效果.
2
3.7.针对其他物理场的透明隐身
随着研究的进一步发展, 隐身也从电磁波领域拓展到了其他物理场领域. 对于区域内不存在源的情况, 很多标量扩散物理场的波方程都可以被转化为拉普拉斯方程, 除与电磁学相关的静电场、静磁场、以及稳恒电流场以外, 浓度分布场、温度分布场、不可压缩流体场等物理场也都满足要求. 类比于上述在电磁波领域的研究, 对于其他物理场的隐身, 仍然可以用透明隐身方式实现.对稳恒电流场, 即直流电的隐身是隐身发展史中较有特色的分支之一. 不同于电磁波隐身衣需要同时调节介电常数与磁导率, 对于作用于稳恒电流场的隐身衣, 可以通过只调节一个电磁参数——电导率来实现. 由前文可知, 基于变换光学的隐身衣, 需要各向异性介质, 制备极其繁琐. 在2012年, 兰州大学Yang等[113]提出了一种适用于稳恒电流场的隐身设备, 他们使用电阻网络和印制电路板来搭建背景介质与各向异性介质, 实验实现了经典的二维柱体隐身衣. 随后, 他们也提出了利用电阻网络呈现直流幻觉的实验验证[114]. 同年, 他们设计并实现了基于电阻网络的地毯式隐身衣[115]. 2013年, 他们又根据补偿介质理论[97], 使用等效电路设计了负电阻, 实现了对特定物体的远程隐身[116]. 2013年, 他们根据有源隐身模型提出并实验实现了稳恒电流场有源隐身[111]. 2015年, 东南大学Jiang等[117]使用光敏电阻实现了可调电流隐身/幻觉器件. 2018年, 新加坡国立大学Qiu与西南大学Han等[118]合作, 提出并验证了基于均匀变换光学的光敏直流可调隐身/幻觉器件. 2019年, 浙江大学Chen等[119]指出, 在不含负电导率的变换光学设计中, 变换前后网格元素的个数是不变的, 故可以利用这种方式简化一些稳恒电流场下各向异性材料的制作, 他们以此实验验证了较为复杂的直流远程隐身器件. 使用电阻网络模拟导体的方法较为灵活, 且实验与预测结果往往完全一致, 但此种方法与现实中的材料差距较大. 针对电流在块体材料的隐身研究较少, 如在2014年, 新加坡国立大学Han等[120]实验实现了直流电流下二维块体物体的隐身. 对于三维的块体材料的隐身, 主要实现难点在材料制备和测量方面, 可能是稳恒电流场隐身衣的下一个突破口.
热传导场(稳恒温度分布场)的隐身也是近年来被研究者们关注的话题. 2008年, 复旦大学Fan等[121]与台湾成功大学Chen等[122]分别提出了热学隐身的雏形并做了初步探讨. 2012年, 美国哈佛大学Narayana和Sato[123]使用层状结构设计了传热学上的各向异性材料, 并分别实验实现了热集中器、热旋转器与热隐身衣. 次年, 德国卡尔鲁斯厄理工大学Schittny等[124]使用在铜上嵌入PDMS格子的方式制作各向异性材料, 实现了经典的二维变换光学热学柱状隐身衣. 2014年, 新加坡南洋理工大学Xu等[125]使用机械加工工艺, 实验实现了简单结构下的三维块体材料热学隐身衣. 同年, 基于晶体热导率和电导率的高度相关性, 浙江大学Ma等[126]设计了一种可以同时调节稳恒电流场与稳恒温度场的多功能隐身衣. 新加坡国立大学Han等[127]使用均匀各向同性材料实现了柱状热学隐身衣. 随后, 他们类比光学中的光学幻觉, 提出并实现了热学幻觉[128]. 2015年, 新加坡南洋理工大学Nguyen等[112]设计并实现了有源热传导场隐身衣. 该年年底, 复旦大学Li等[129]提出了一种“热二极管”设备, 他们使用形状记忆合金作为热流通道, 实现了热流的单向流动, 并且所涉及的介质参数可以匹配隐身衣. 2016年, 西北工业大学Hou等[130]基于变换光学, 经由将热源所在的空间变换至其他位置, 实现了对热源位置的幻觉器件. 2018年, 新加坡国立大学Li等[131]提出了一种新型隐身结构, 这种结构能巧妙地同时对热传导和热辐射实现隐身. 随后, 他们又使用高速转动的水模拟热传导上的“零折射率材料”, 实现了基于零折射率材料模型的热学隐身衣[132]. 近来, 类比于超构表面, 对热流[133]、辐射[134]等在物体表面的操作也开始被研究者们关注. 这类材料可以在物体表面实现热学隐身、热学幻觉或热学全息等效应, 有望在信息学领域得到进一步应用.
图 14 拟态隐身效果实例 (a)捷蛙的保护色使得其与草原环境融为一体; (b)身着吉利服士兵的散射波与草原背景的散射波大体一致, 很难被观察者发现Figure14. Examples of imitation cloaking methods: (a) The protective color of a frog (Rana dalmatina) makes it difficult to be distinguished from the grasslands environment; (b) the scattering wave of soldiers in ghillie suit is almost the same as that of grasslands background, which is difficult to be spotted by enemy observers.
尽管此种隐身方式简单有效, 其劣势也显而易见: 只能静态调整材料的散射, 无法适应不同背景环境所带来的变化. 捷蛙的栖息地在林地、田野附近, 若在其他环境下, 其保护色将失效而暴露自己; 同样地, 吉利服在非林地区域就不再有效, 甚至会在隐匿方面带来劣势, 士兵需要换用其他种类的作战服来调整散射波, 以重新适应新的背景环境.
在自然界中, 也有一类动物具有“智能”的隐匿身形的能力. 变色龙、章鱼一类的动物, 可以随着背景环境的变化, 动态地调节自身表面的散射. 以变色龙为例, 变色龙的皮肤是一种自然界中的“光子晶体”, 其真皮细胞中含有色素, 且皮肤内有叠加层, 表面有一层虹细胞(iridophores), 通过改变这一细胞层内部鸟嘌呤纳米晶体的排列结构, 变色龙就可以实现颜色的变化[135]. 变色龙的隐身方式给予研究者以启示: 通过某种可调节的、动态变化的材料, 可以获得适应性更好的隐身效果. 随着隐身理论与材料科学的进一步发展, 另一种有源隐身方式—可调隐身也引起了研究者们的关注. 不同于上述隐身衣注重于“适配”, 可调隐身衣注重于在人工主动调节下, 实现某种特殊的隐身功能. 2012年, 韩国延世大学Shin等与美国杜克大学Smith提出并实现了一种可调网状结构, 通过调整材料不同的泊松比, 来控制地毯式隐身衣的工作频率[136]. 2015年, 东南大学Jiang等[117]提出了一种光控稳恒电流场隐身设备, 该设备使用光敏电阻, 可以在给定环境光弱时实现隐身, 给定环境光强时呈现电流场的幻觉效应. 2017年, 清华大学Peng等[137]使用钛酸锶材料重构了经典均匀变换光学的一维温控隐身衣. 由于钛酸锶材料的电磁参数可以随温度变化, 因此该隐身衣可以通过温度变化来调控工作频率, 如图15(a)所示. 2014年东南大学Liu等[138]应用了可调二极管设计并实验实现了一种可重构隐身衣, 其工作频率可以在2.3—3.7 GHz之间调节. 随后, 该组成员又提出了可编程超构表面的概念, 即利用计算机设备控制带有可重构单元的微波序构材料, 来实现对电磁波的编程式控制[139]. 如图15(b)所示, 2017年, 中国科学院光电技术研究所的Huang等[140]应用这一理论实现了地毯式隐身衣/光学幻觉. 2018年, 东南大学Zhao等[141]又提出了一种针对时谐场相位编程操作的表面设备, 这种设计可以实现针对速度的隐身或幻觉, 即多普勒隐身/幻觉, 见图15(c). 在2020年, 浙江大学Qian等[142]提出基于衍射神经网络的光学逻辑计算, 在物理层面使用高效介质超表面来模拟隐含层, 实验了多功能逻辑计算单元. 随后, 他们实现了一种基于机器学习的新型智能隐身, 在不依赖任何人为操作的情况下, 快速地动态适应变化的背景环境和外界刺激, 实现自适应隐身, 如图15(d)所示[143]. 东南大学Zhang等[144]应用光电二极管设计了一种光驱动的反射微波相位控制设备, 并实现了光学隐身、幻觉等效果.
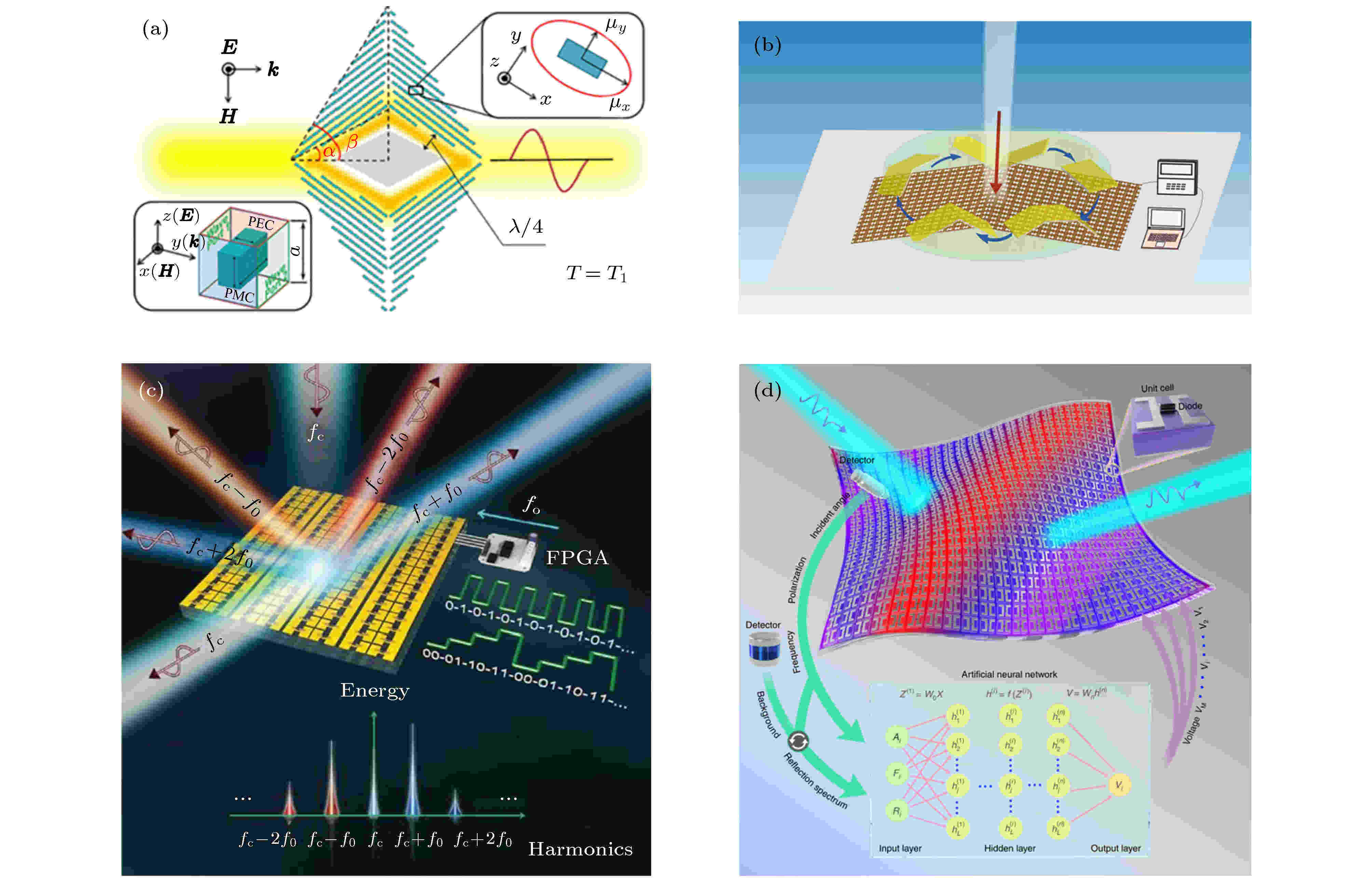图 15 可调隐身衣 (a)一维温控变换光学隐身衣[137]; (b) 基于可调超构表面设计的地毯式隐身/幻觉设备[140]; (c)针对时谐电磁波的数字可调超构表面, 可以用来人为制造多普勒相移, 即物体移动速度的光学幻觉[141]; (d)基于人工神经网络模型的自适应微波段隐身设备[143]Figure15. Tunable invisibility cloak: (a) Temperature tunable one-dimensional transformation optics invisibility cloak[137]; (b) carpet cloaking/illusion device based on tunable metasurface[140]; (c) the time-domain digital-coding metasurface which is able to create the analogue of Doppler shift, or velocity illusion[141]; (d) deep learning-enabled self-adaptive microwave cloak[143].
只要选取适当的坐标变换形式, 变换光学法同样可以实现光学幻觉. 相比于经典的变换光学隐身, 变换光学在幻觉光学中更注重出射光光路在目标幻觉物体边界的情况, 2010年, 香港科技大学Li等[145]对“隐形闸门”进行了验证, 该“闸门”利用变换光学, 将实际联通的空间变换得看起来像“阻拦”电磁波的效果. 2011年, 东南大学Jiang和Cui[146]以开口谐振环为单元结构作为外壳, 实验实现了将导体柱的散射波呈现出介质柱体散射波的像. 2013年, 伊朗K.N.图什理工大学Shoorian和Abrishamian[147]基于变换光学设计了一种针对布拉格光栅作用的开关, 当幻觉器件启用时, 光栅中的电磁波传播会被阻止.
超散射[144,148-150]也可以作为产生光学幻觉的工具. 在变换光学产生超散射现象方面, 2008年, 上海交通大学Yang等[46]使用负折射率来实现超散射现象. 2009年, 上海交通大学Luo等[151]计算仿真证明了可以使用超散射的概念隐藏一道物理空间上的开口, 实现了理论上的“穿墙术”等.
预期隐身将向可视化、便携化和智能化的方面发展. 可视化是指突破关键技术, 在工业上可以对微纳结构进行更细节、更复杂的操控, 以提升较高频率尤其是可见光频段的隐身衣的整体尺寸和精度; 便携化是指隐身器件更加灵活, 将不必拘泥于传统隐身器件体积大、厚度厚、需近距离有效等局限, 而是可以实现相对于被隐身物体小尺寸、超薄以及远程隐身器件. 智能化是指隐身衣工作在动态开放的环境中, 可以被计算机等设备灵活地编程调控, 并具有一定的自适应能力. 可以预见, 随着材料学和工业加工手段的进一步完善, 新型隐身技术也将迈上新的台阶.
