基于相变材料超表面的光学调控

全文HTML

--> --> -->

1.引　言

传统的光学器件如透镜、反射镜、滤色片和光栅等利用了光的折射、反射、吸收或衍射效应以实现光波振幅、相位或偏振的改变. 古人使用冰透镜聚焦阳光来生火即利用了光学器件改变光波相位传播的原理. 但传统光学器件体积庞大, 难以满足当代光学系统日益增长的微型化和集成化的需求. 超材料因其亚波长尺寸以及独特的光学性质而备受青睐^[1].
超材料一般由周期性的具有亚波长尺度的金属或电介质结构组成, 能与光波相互作用从而产生自然界不存在的电磁响应^[2]. 超材料在过去的十几年中引起了广泛关注, 并产生了很多突破性的电磁或光学现象, 如负折射^[3]、近零介电常数^[4]、超分辨光学成像^[5]、电磁隐身^[6]和信息编码^[7]等. 体材料的有效介电常数、磁导率等参数的改变很大程度上依赖于复杂的三维微纳加工技术^[8], 加工困难较大. 二维平面上的超材料, 又称为超表面, 可以较容易地使用现有微纳加工技术实现, 如光刻、电子束刻蚀或纳米压印等, 是当前的研究热点之一^[9]. 为方便理解光与超表面的作用, 超表面通常被认为是厚度近似为零的二维平面, 因此研究者不再对其有效体介电常数和磁导率感兴趣. 相反, 表面或界面上的反射、透射以及相位变化变得尤为重要^[10]. 此外, 超薄的厚度使得沿光传播方向的能量损耗大大降低, 这也很大程度上为超材料在实际产品中的推广应用提供了解决途径. 早期的光学超表面采用了类似微波领域中反射、透射阵列的设计, 多由周期性排列的金属微纳结构组成. 金属微纳结构与光相互作用形成等离激元共振, 能把远场的电磁波强烈地局域到结构表面, 形成近场电磁场增强^[11]. 同样, 微纳结构又可以作为散射体把近场倏逝波传输至远场, 充当天线的角色, 故超表面单元常被称为光学天线^[12]. 改变天线的材料、形状、尺寸、排列间隔和方向以及周围的介质环境, 就能对光传播的振幅和相位进行定量调控^[13]. 哈佛大学Yu等^[14]与上海复旦大学Sun等^[15]发现利用界面相位不连续性的概念可实现对透射光与反射光的任意控制, 为基于超表面的光学设计提供了理论依据.
二维空间和亚波长尺度使得超表面很适合做动态调控和可重构光学元件, 如利用衬底形变改变天线排列周期^[16], 利用光热效应^[17]、电注入载流子^[18]或相变材料^[19]改变衬底的介电常数(折射率)等. 相比于机械、温度或液晶调控, 相变材料在外部激励下能改变其晶格结构. 由于不同相态之间较大的电学和光学性质差异, 相变材料已广泛应用于商业存储^[20,21]. 近几年相变材料在前沿纳米光子学领域受到越来越多的关注, 被应用于各类光学器件的动态调控中. 比如利用相变材料纳米薄膜在不同相态下的反射率和吸收率的显著差异, 研究人员实现了可见光波段的电致变色薄膜^[22], 以及中红外波段的多级动态可调热辐射器^[23]. 另外把相变材料集成到波导结构中, 研究人员实现了对波导输出信号的光致调控, 进而应用于光学储存和光子计算^[24,25]. 与此同时, 基于相变材料的超表面动态光学调控也在持续研究. 一方面, 借助介电常数的改变, 相变材料薄膜能够对金属等离激元超表面的光谱响应进行大幅度的调节^[26,27]. 另一方面, 相变材料微纳结构自身可构成超表面的结构单元, 对入射光场进行局域和增强, 由此获取较高的光调制效率^[28]. 现今, 通过把相变材料引入到超表面, 研究人员实现了对超表面透射与反射光谱^[27,29-33], 及光场空间分布的动态调控^[34-37], 用于光束偏转器、透镜和热辐射器等诸多光学器件.
本综述主要讨论超表面对光波的调控原理及应用, 特别是基于相变材料GeSbTe (GST)的动态光调控, 分为六个部分: 第一部分引言; 第二部分介绍超表面光调控的相关原理及典型应用; 第三部分介绍相变材料的光学性质; 第四部分介绍相变材料进行动态光调控的相关原理; 第五部分介绍相变材料超表面在动态光调控上的具体应用; 最后一部分给出总结和展望.

-->

2.1.超表面光调控原理

2.1.1.振幅调控

-->

2.1.1.振幅调控

如图1(a)所示, 假设超表面处于介电常数为$ {\varepsilon }_{\mathrm{m}} $

的同种均匀介质之中, 位于$ xy $

平面且坐标$ z=0 $

处并忽略衬底. 考虑定态光沿z轴传播且电场偏振沿x轴方向. 电磁波在$ z < 0 $

和$ z>0 $

两个半空间的表达式可写为^[38]

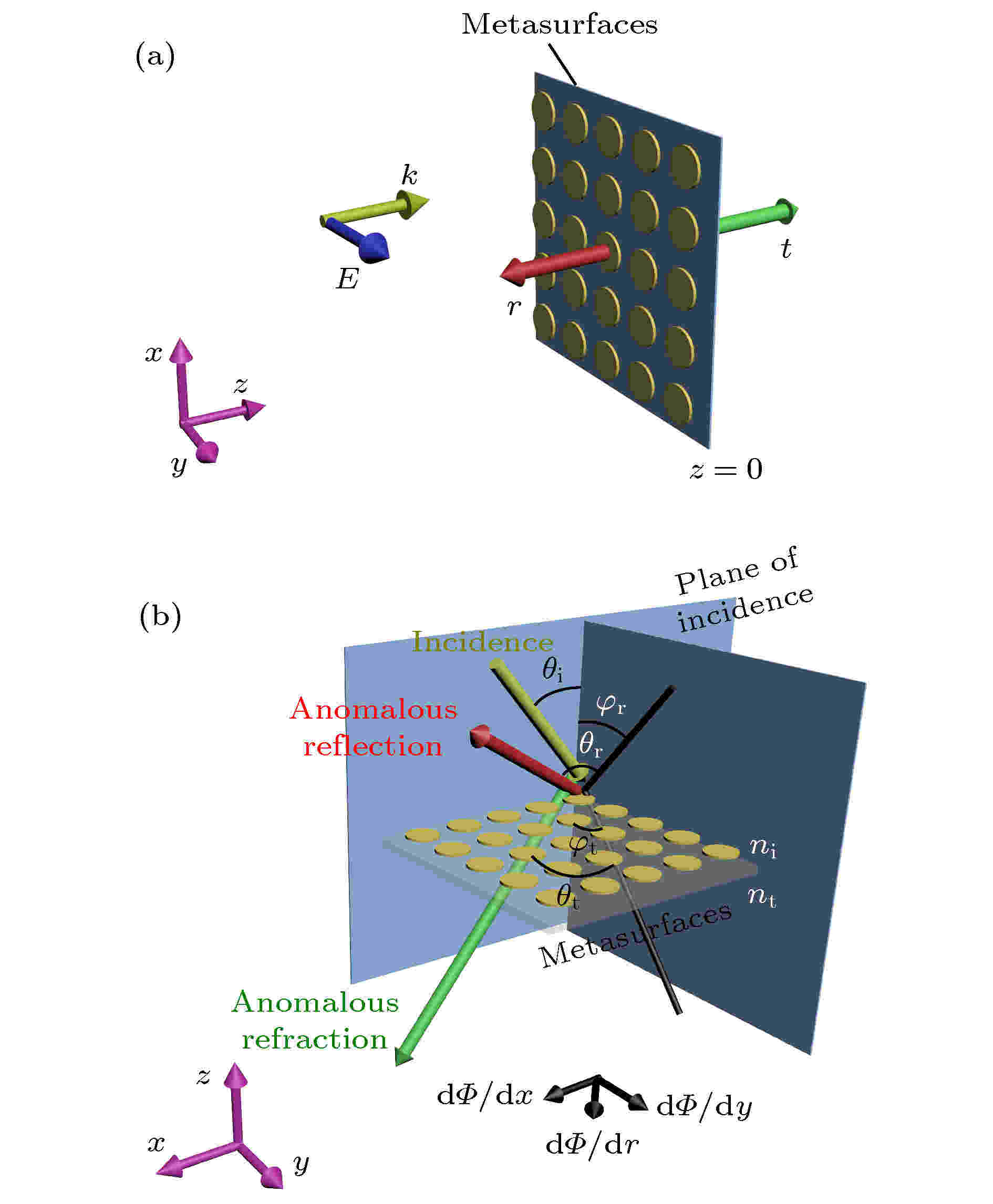图 1 超表面光调控的原理　(a)光通过超表面后透射(t, 绿色箭头)和反射系数(r, 红色箭头)的计算模型; (b)广义的折射和反射公式; 其中棕色、红色和绿色箭头分别表示入射、反射和折射波矢方向, 黑线表示波矢在与入射平面相垂直的平面的投影
Figure1. Principle of light modulation with metasurfaces: (a) Light transmission (green arrow) and reflection (red arrow) through a metasurface; (b) the generalized Snell’s law of reflection and refraction. Brown, red and green arrows represent the propagation directions of incident, reflected and refracted light, respectively. Black lines represent the projections of wavevectors of reflected and refracted light onto the surface perpendicular to the plane of incidence.

$ \left\{ \begin{aligned} &{{{E}}}_{-}\left(z\right)={E}_{0}\left({\mathrm{e}}^{\mathrm{i}kz}+r{\mathrm{e}}^{-\mathrm{i}kz}\right)\widehat{{x}},\\ &{{H}}_{-}\left(z\right)={E}_{0}{\eta }^{-1}({\mathrm{e}}^{\mathrm{i}kz}-r{\mathrm{e}}^{-\mathrm{i}kz})\widehat{{y}},\\ &{{{E}}}_{+}\left(z\right)={tE}_{0}{\mathrm{e}}^{\mathrm{i}kz}\widehat{{x}},\\ &{{H}}_{+}\left(z\right)={tE}_{0}{\eta }^{-1}{\mathrm{e}}^{\mathrm{i}kz}\widehat{{y}},\end{aligned} \right. $

其中$ k=\omega \sqrt{{\varepsilon }_{\mathrm{m}}{\mu }_{0}} $

是波数, $ \eta =\sqrt{{\mu }_{0}/{\varepsilon }_{\mathrm{m}}} $

是介质阻抗, r和t分别是反射和透射系数. 结合边界条件

$\hat {{z}} \times \left( {{{{E}}_ + } - {{{E}}_ - }} \right) = 0,\;\hat {{z}} \times \left( {{{{H}}_ + } - {{{H}}_ - }} \right) = {{{J}}_{\rm{s}}},$

其中$ {{J}}_{\mathrm{s}} $

是超表面引入的表面感应电流. 假设超表面单元面积为A, 电极化率为$ \alpha $

, 且仅考虑电偶极矩作用, 则:

${{J}}_{\mathrm{s}}=-\mathrm{i}\omega {A}^{-1}\alpha {{{E}}}_{av}, $

其中$ {{{E}}}_{av}=({{{E}}}_{+}+{{{E}}}_{-})/2 $

. 结合(1)—(3)式, 整理可得

$ \left.\begin{aligned} r=\dfrac{\mathrm{i}C}{1-\mathrm{i}C}, ~~~~ t=\dfrac{1}{1-\mathrm{i}C},\end{aligned}\right. $

其中$ C=\omega \alpha \eta /(2A) $

是一个无量纲参数.
从(4)式可以看出, 光波的透射系数和反射系数受超表面电极化率的影响, 而电极化率又取决于超表面结构单元形状、尺寸和材料等参数. 改变这些参数, 就可以定量地对光波的透射和反射进行调控. 由于(4)式仅考虑了电偶极矩作用, 故适用于超表面结构单元结构的尺寸在亚波长尺度内, 且材料相对磁导率$ \left|\mu \right|\approx 1 $

的情形, 如表面等离激元超表面. 表面等离激元超表面多采用贵金属, 特别是金与银, 与光作用产生自由电子集体共振, 即表面等离激元共振(surface plasmonic resonance, SPR), 对光波的吸收或散射产生较强的增强作用. 这里以周期为d正方晶格排列的金属球超表面为例, 超表面的电极化率$ \alpha $

可以近似表示为^[39]

$\alpha \approx \dfrac{1}{{\alpha }_{0}^{-1}-\dfrac{g}{{d}^{3}{\varepsilon }_{\mathrm{m}}}+\dfrac{\mathrm{i}{k}^{3}}{6\mathrm{{\text{π}} }{\varepsilon }_{\mathrm{m}}}}, $

式中$ {\alpha }_{0}=4\mathrm{{\text{π}} }{a}^{3}{\varepsilon }_{\mathrm{m}}\dfrac{{\varepsilon }_{\mathrm{s}}-{\varepsilon }_{\mathrm{m}}}{{\varepsilon }_{\mathrm{s}}+2{\varepsilon }_{\mathrm{m}}} $

是准静态近似下单个金属球的极化率, a和$ {\varepsilon }_{\mathrm{s}} $

分别表示球的半径和介电常数, $ g\approx 0.36$

表征了不同金属球之间的静电作用. 对于单个金属球, 当满足Fr?hlich条件$ \mathrm{R}\mathrm{e}\left[{\varepsilon }_{\mathrm{s}}\left(\omega \right)\right]= -2{\varepsilon }_{\mathrm{m}} $

时, $ {\alpha }_{0} $

达到峰值, 形成局域表面等离激元共振(localized surface plasmonic resonance, LSPR), 表现为在消光截面或吸收截面光谱上出现一个陡峭的波峰^[13]. 对于超表面, 由于结构单元之间的相互作用, Fr?hlich条件修正为$\mathrm{R}\mathrm{e}\left[\varepsilon \left(\omega \right)\right]= -2{\varepsilon }_{\mathrm{m}}+ 4\mathrm{{\text{π}}}g \left(\mathrm{R}\mathrm{e}\left[{\varepsilon }_{\mathrm{s}}\left(\omega \right)\right]-{\varepsilon }_{\mathrm{m}}\right)$

, 因此LSPR的谐振频率向长波长方向偏移. 当入射光频率处于LSPR的谐振频率时, 超表面的透射系数的幅度达到最小值, 而反射系数的幅度则达到最大值. 可见借助于LSPR的激发, 超表面可以对透射光与反射光的幅度实现调控.
对光的振幅进行调控, 人们通常关注于超表面的透射率$ {\left|t\right|}^{2} $

和反射率$ {\left|r\right|}^{2} $

. 金属超表面由于存在较大的欧姆损耗, 光波经金属超表面后不可避免地会损耗部分能量^[40], 成为限制其在很多光学实际应用的瓶颈. 而电介质超表面由于损耗较小, 对光波的吸收较小. 然而, 为了能够支持谐振模式, 电介质超表面结构单元的尺寸通常大于光在电介质材料中的衍射极限, 因此对光场的局域能力受限. 使用高折射率的电介质材料, 比如硅锗等, 可以减小衍射极限, 是破解这个问题的常用手段.
在前面的理论分析中, 忽略了结构单元的磁极化. 如果把磁偶极矩作用考虑在内, (4)式可改写为^[38]

$ \left\{\begin{aligned}& r=\dfrac{\mathrm{i}(C-D)}{(1-\mathrm{i}C)(1-\mathrm{i}D)},\\ & t=\dfrac{1+CD}{(1-\mathrm{i}C)(1-\mathrm{i}D)},\end{aligned}\right. $

其中$ D=\omega \beta /\left(2 A\nu \right) $

, $ \beta $

是磁极化率. 从(6)式可以看出, 忽略磁偶极矩作用($ D=0 $

)时, (6)式就转化为(4)式. 同时可以看出, 当$ C=D $

时, $ r=0 $

即实现完美透射; 当$ C=-1/D $

时, 可实现零透射. 值得注意的是, 条件$ C=D $

与$ \alpha =\beta $

等效, 后者又称为Kerker条件. 在这种条件下, 光波只会向前传播而没有反射, 这样的超表面又被称作惠更斯超表面. 实验中, 光通过惠更斯超表面的透过率普遍提高至42.3%^[40].
以上讨论均建立在极化强度与外电场成线性关系的基础之上, 从物理的角度看, 光与物质作用过程中一次仅吸收一个光子. 当激发阶段一次吸收多个光子时, 如二次谐波^[41,42]、双光子吸收^[42,43]、四波混频^[44]等, 就涉及到了非线性光学的相关理论知识, 我们会在应用部分通过具体案例做相应的阐述.
3

2.1.2.相位调控

-->

2.1.2.相位调控

与前述的振幅调控类似, 借助超表面结构单元的谐振现象同样可以对反射光和透射光的相位进行有效调控. 以正方晶格排列的金属球超表面为例, 将超表面电极化(5)式代入(4)式可以推知, 在以LSPR谐振频率为中心的频谱内, 透射系数与反射系数的相位变化剧烈, 并有180°的相位差. 因此, 通过控制超表面结构单元的谐振频率即可实现对反射光和透射光相位的有效调控. 此外, 光波相位还可以通过超表面结构单元波导模式的传播相位^[45]或具有拓扑性的几何相位^[46]来实现定量调节.
近几年, 调控光波相位的任意空间分布是超表面研究的一大热点. 为了理解光波相位的空间分布对光传播的影响, 这里考虑一束光入射到位于x-y平面的超表面上, 光的入射平面设为x-z平面. 假设超表面不同的结构单元给予入射光一个$ \varPhi (x, y) $

的空间相位分布, 如图1(b)所示. 基于广义的折射和反射公式, 入射角$ {\theta }_{\mathrm{i}} $

、折射角$ {\theta }_{\mathrm{t}} $

和反射角$ {\theta }_{\mathrm{r}} $

有如下关系^[1,14]:

$ \left\{\begin{aligned} &{n}_{\mathrm{t}}\sin {\theta }_{\mathrm{t}}-{n}_{\mathrm{i}}\sin {\theta }_{\mathrm{i}}=\dfrac{1}{{k}_{0}}\dfrac{\partial \varPhi }{\partial x},\\ & \cos {\theta }_{\mathrm{t}}\sin {\phi }_{\mathrm{t}}=\dfrac{1}{{n}_{\mathrm{t}}{k}_{0}}\dfrac{\partial \varPhi }{\partial y},\end{aligned}\right. $

$ \left\{\begin{aligned} & {n}_{\mathrm{i}}\sin {\theta }_{\mathrm{r}}-{n}_{\mathrm{i}}\sin {\theta }_{\mathrm{i}}=\dfrac{1}{{k}_{0}}\dfrac{\partial \varPhi }{\partial x},\\ & \cos {\theta }_{\mathrm{r}}\sin {\phi }_{\mathrm{r}}=\dfrac{1}{{n}_{\mathrm{i}}{k}_{0}}\dfrac{\partial \varPhi }{\partial y},\end{aligned}\right. $

其中$ {n}_{\mathrm{i}} $

和$ {n}_{\mathrm{t}} $

分别是入射光和折射光所在介质的折射率, $ {k}_{0} $

是光在真空中的波数, $ \partial \varPhi /\partial x $

和$ \partial \varPhi /\partial y $

分别称为平行和垂直于入射平面的相位梯度. 当界面处不存在超表面时, 相位梯度为零, (7)式和(8)式就简化成了经典的折、反射公式. 故超表面对相位的调控, 可理解为超表面的存在破坏了界面处光波的连续性, 产生了相位梯度, 进而改变反射光与透射光的传播方向. 如目前研究最为广泛的平面透镜, 超表面将在界面处引入相位:

$ \varPhi =k\big(\sqrt{{x}^{2}+{y}^{2}+{f}^{2}}-f \big), $

其中k是波数, f是平面透镜的焦距, 通过调节超表面单元的形状尺寸或空间分布满足其相位.
解释了超表面对界面相位的影响后, 其对光偏振的调控就不难理解. 与传统波片类似, 对入射光偏振的调控就是对o光和e光两者相对相位延迟的定量控制, 如半波片, 两者经过单轴晶体后相位差为π. 复合偏振态的调控可借助琼斯矩阵进行定量计算, 这里不再赘述.
2

2.2.超表面光调控应用

-->

2.2.超表面光调控应用

2.2.1.振幅调控

-->

2.2.1.振幅调控

超表面对光波振幅的调控大多体现在改变超表面的LSPR以达到调节光的吸收、散射或透射光谱, 在有机太阳能电池、生物传感、热辐射管理以及表面增强光谱(拉曼、荧光和非线性信号等)等领域已得到了广泛应用. 研究表明, 通过激发超表面太阳能电池的LSPR, 能有效增加电子-空穴对量子产率以及电子或空穴的平均散射光程, 大幅度提高了光能转换效率^[47]. 如图2(a)所示, 将有机半导体P3HT颗粒加工到金纳米颗粒的热点处, 其局域电磁场增强系数高达数十倍, 可有效提高光能利用率. 此外, 图2(a)所示的各向异性超表面结构由于对不同线性极化的光有不同的响应, 还可用于实现极化转换、滤波等功能^[48-50].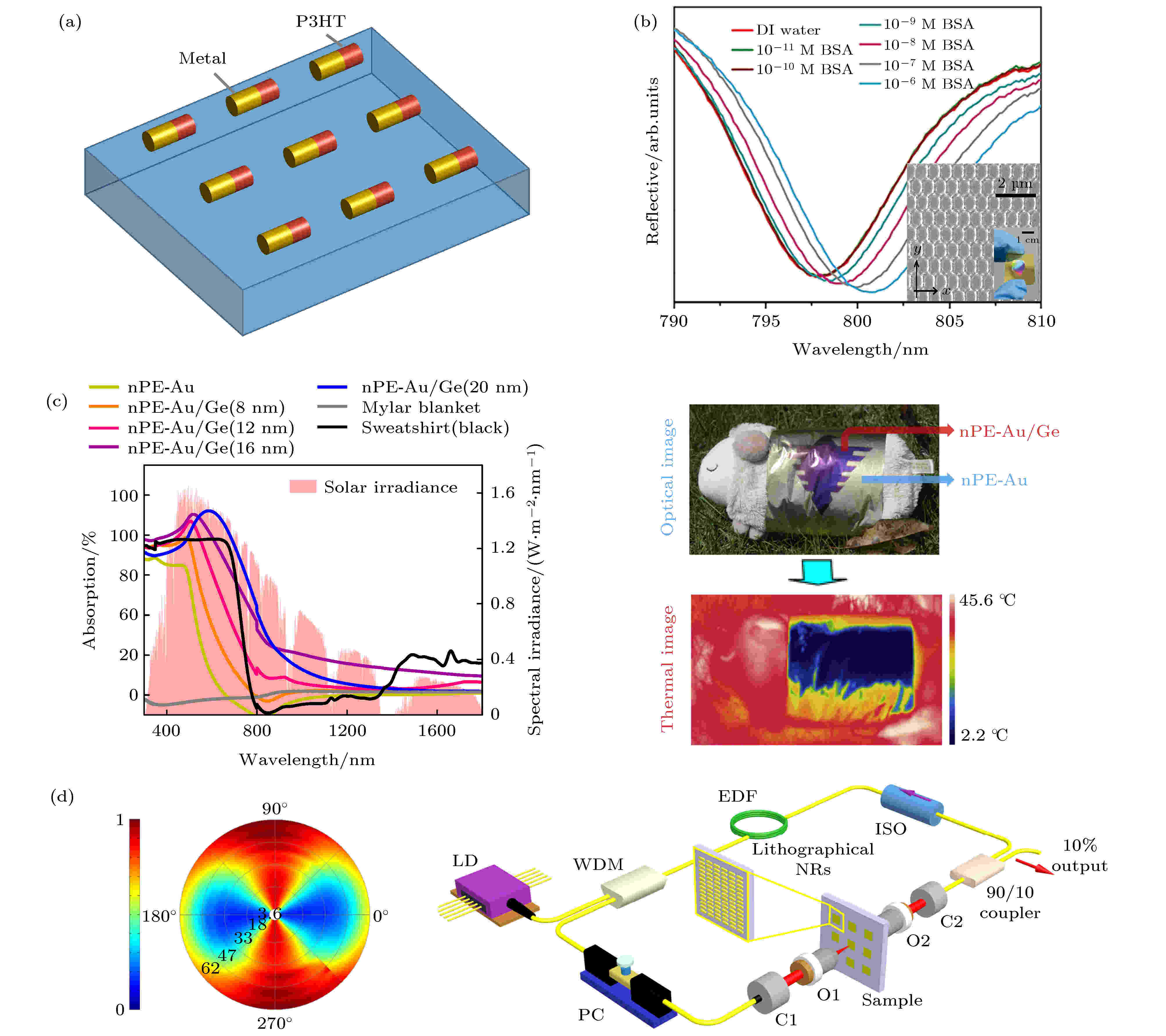

图 2 超表面在调控光波振幅上的前沿应用　(a)等离激元超表面增强的有机太阳能电池^[47]; (b)基于等离激元超表面的液体浓度传感器, 右下角是正六边形金超表面的扫描电子显微镜图片和实物图(1 M = 1 mol/L)^[51]; (c)超表面多层带孔薄膜保暖织物^[52]; 左侧: 不同镀膜厚度nPE-Au/Ge超表面的吸收光谱, 右侧: 带有nPE-Au/Ge超表面的一实物在可见(上)和红外(下)波段的成像; (d)基于等离激元超表面的孤子锁模激光器^[53]; 左侧: 金纳米棒超表面在1550 nm激发光下的光学透过率随激发光功率和偏振变化的实验数据伪彩图, 径向表示激光功率, 方位角表示偏振方向, 颜色表示光透过率; 右侧: 电子束刻蚀的纳米金棒超表面用作可饱和吸收体集成于超短脉冲光纤激光器谐振腔中; LD, 激光二极管; WDM, 波分复用器; EDF, 掺铒光纤; ISO, 光频隔离器; PC, 偏振控制器; C1, C2, 准直器; O1, O2, 物镜
Figure2. Applications of metasurfaces based on modulation of light in amplitude. (a) Efficiency improvement of organic solar cell by exploiting plasmonic metasurfaces^[47]. (b) Liquid concentration sensor based on plasmonic metasurfaces^[51]. Inset: scanning electron microscope (SEM) and optical images of a gold hexagonal-lattice metasurface. (c) Ultra-thin colored textile with simultaneous solar and passive heating abilities^[52]. Left: measured absorptivity of different textiles from visible to near infrared wavelength; Right: optical and thermal images of a toy sheep partly wearing a colored textile. (d) Ultrafast pulsed fiber laser using lithographically-defined plasmonic metasurfaces as saturable absorbers^[53]. Left: experimental excitation power and polarization dependent nonlinear transmittance of a gold nanorod metasurface; Right: sketch of the home-built ultrafast fiber laser integrating lithographical plasmonic metasurfaces as saturable absorbers; laser diode (LD), wavelength-division multiplexing (WDM), erbium-doped fiber (EDF), optical isolator (ISO), polarization controller (PC), collimators (C1, C2) and objectives (O1, O2).

从(5)式可以看出, LSPR对周围介质环境非常敏感, 当环境的介电常数发生改变, LSPR随之发生频移以满足Fr?hlich条件. 根据这一特性, 超表面可用于检测液体环境的浓度、折射率等. Liu等^[51]利用正六边形纳米金超表面获取半峰宽小于8 nm的LSPRs, 光谱范围可从600 nm延伸至960 nm. 如图2(b)所示, 此超表面用于检测血清蛋白浓度, 精度可达10^–10 mol/L.
除了应用于科学研究, 超表面在实际生活中也展现出较大的应用潜力. Luo等^[52]将带有超表面材料的多层带孔薄膜应用到了保暖纺织衣物上, 实现了主动和被动的个人热量管理优化. 如图2(c)所示, 利用不同nPE-Au/Ge (镀金、锗的聚乙烯微孔结构)超表面对太阳光吸收率的不同, 定量设计锗镀层厚度以达到同时减小人体热辐射(低至10%, 右上图)和增大外界太阳光热转换效率(平均最高至50%, 左图)的效果. 相比于2 mm的传统黑色体恤衫, 他们使用厚度仅为16 μm的超表面薄膜就可以将个体温度在室内提高3.8 ℃, 在室外提高6.3 ℃.
目前有关超表面的应用研究大多局限在线性光学范畴内. 在非线性光学领域, 尽管存在利用超表面材料实现二次谐波、三次谐波、多光子吸收或四波混频的相关报道, 但展示实际应用的案例并不常见, 主要原因包括: 1)相比于非线性晶体, 超表面常用材料的非线性极化系数普遍较小, 同等激发条件下产生的非线性光学信号几乎可以忽略不计; 2)超表面微纳结构的熔点普遍较低, 强光激发过程中易发生热变形甚至热损伤从而失去独特的光学性质. 所以, 充分挖掘超表面材料非线性光学应用价值的关键在于, 既要保证强激发条件下对多光子的有效吸收, 又要避免热量在电子驰豫阶段的过度累积. Wang等^[53]首次利用电子束刻蚀的纳米金棒超表面用作可饱和吸收体实现了中心波长在1550 nm、脉宽仅为729 fs的孤子锁模, 如图2(d)所示. 他们首先通过设计纳米结构的尺寸和排列周期, 将超表面LSPR定量调节至1550 nm, 然后将此超表面放入由掺铒增益光纤组成的光纤激光器谐振腔中. 使用980 nm的抽运光, 增益光纤首先在谐振腔中产生1550 nm的连续激光. 随着抽运强度的逐步提高, 等离激元超表面优先在1550 nm波段发生饱和吸收, 在时域上产生对应于电子驰豫时间的超短脉冲. 饱和吸收是一种非线性光学过程, 在等离激元超表面中受LSPR影响较大, 取决于激发光的波长、偏振和入射强度等多种因素. 与其他材料可饱和吸收体不同, 通过定量设计超表面的LSPR, 可实现中心波长和脉冲宽度定量调控的超短激光脉冲, 在光学领域特别是超快超强激光领域, 具有广阔的应用前景.
3

2.2.2.相位调控

-->

2.2.2.相位调控

在相位调控应用中, 平面透镜是目前研究最多的超表面光学器件. 利用超表面单元引入的相位梯度, 从整体上改变波前, 以获取聚焦或散焦的光学效果. 以聚焦透镜为例, 平面透镜中每个单元引起的相位变化可用(9)式计算. 从(9)式可以看出, 此相位与波长相关, 即不同波长的光经聚焦后的焦距不尽相同. 为了解决因色散引起的像差问题, 一般需在(9)式基础上添加额外的色散补偿相位. 补偿相位一般与波长成反比, 换言之, 与波数呈线性关系, 这就要求超表面单元在给定测试波长范围内的电磁场相位与波数近似呈线性关系^[54,55]. 如图3(a)所示, Wang等^[54]使用金纳米柱结构组成的超表面获取了波长1200—1680 nm范围内的色散补偿平面透镜, 整体聚焦效率达到12%. 与此同时, 最新研究把超表面与微机电系统结合, 朝着变焦平面透镜的方向发展^[56]. 此外, 将超表面透镜制备在柔性衬底上, 通过机械拉伸衬底改变相邻超表面结构单元的间距, 也是实现变焦透镜的有效方法. 如图3(b)所示, Ee等^[16]把纳米金棒组成的超表面制备在聚二甲硅氧烷柔性衬底上, 通过机械拉伸衬底以改变纳米金棒之间的排列周期, 最终获得焦距在150—250 μm范围连续可调的平面透镜.

图 3 超表面在调控光波相位上的前沿应用　(a)具有色散校正功能的平面透镜^[54]; 左侧: 扫描电子显微镜镜图像(比例尺是1 μm); 右侧: 平面透镜在不同波长下的聚焦光斑; (b)柔性超表面透镜^[16]; 左侧: 微机械拉伸柔性衬底上的平面透镜以实现变焦; 右侧: 拉伸量在100%, 115%和130%时平面透镜的焦距分别为150, 200和250 μm; (c)超表面将圆偏振光转变为线偏振^[57]; (d)超表面把线偏振光转变成螺旋光^[60]
Figure3. Applications of metasurfaces based on modulation of light in phase. (a) Broadband achromatic metalens^[54]. Left: SEM image of the metalens (scale bar, 1 μm); Right: measured light intensity profiles for the achromatic metalens at various incident wavelengths. (b) Zoom metalens on a stretchable substrate^[16]. Left: sketch of a metasurface on a stretched PDMS membrane; Right: measured longitudinal beam profiles generated on the transmission side of the zoom metalens with stretch factor s = 100% (top), 115% (middle), and 130% (bottom). (c) Ultrathin quarter-wave meta-plate for circular-linear polarization conversion^[57]. (d) Dielectric-metasurface enabled optical vortex beam converter^[60].

除了在改变波前上的应用, 超表面在光偏振调控上也取得了长足的发展, 有望在微纳光子器件上取代传统光学波片. 以传统1/4波片为例, 它可以把线性偏振光转换成圆偏振光, 把圆偏振光转换成线偏振光, 广泛应用于光学设计之中. 如图3(c)所示, Zhao和Alù^[57]使用两个相互垂直的银纳米棒组成超表面的基本单元, 使得两个正交偏振方向的相位差成π/2, 实现了传统1/4波片的功能. 除了常规的半波片和1/4波片外, 把波片与透镜两种功能相结合^[58,59], 以及一些产生复杂偏振态的波片如涡旋、螺旋同样可以通过超表面实现^[60]. 如图3(d)所示, Shalaev等^[60]使用硅块把超表面平均分为8个区域, 相邻两个区域的相位差设计为π/4, 光通过超表面后就形成了面包圈状的涡旋光. 把涡旋光束和一高斯光束进行干涉, 进而获得了螺旋光束.

3.相变材料

超表面的光学性能主要由两个因素决定: 1)结构单元的几何形状与尺寸; 2)材料的介电常数. 当器件制备后, 结构的几何形状与尺寸就难以改变, 因此需要通过改变材料的介电常数以实现器件光学性能的调控或重构. 常用的方法包括: 载流子注入—通过改变载流子浓度来改变材料的介电常数, 适用的材料包括半导体、石墨烯等; 热光效应—通过温度的变化来改变材料介电常数, 常用的材料包括硅、氮化硅等; 泡克耳斯效应—介电常数随着外加电场的增大而增大, 适用的材料如铌酸锂、钽酸锂等. 上述方法虽已被广泛应用与研究, 但它们存在一个共同缺点: 介电常数改变幅度较小. 而相变材料通过在外加激励(如热、激光、外加电压)下改变物质内部的晶格, 可以大幅度地改变介电常数. 因此, 相变材料为动态调控超表面的光学性能提供了一种新方案^[61-64]. 而GST, VO₂作为常用的相变材料, 近几年在纳米光子学领域受到了广泛关注, 本章将重点介绍这两种相变材料的光学特性.
2

3.1.GST

-->

3.1.GST

GST由锗(Ge)、锑(Sb)和碲(Te)三种元素组成, 在可重写光盘技术上被广泛应用. 固态GST有晶态和非晶态两种相态, 两态的介电常数存在较大的差别. 晶态与非晶态GST之间可相互转换, 如图4(a)所示, 当非晶态GST温度超过结晶温度(约160 ℃)时, 非晶态会首先相变为亚稳态的面心立方晶体结构, 类似于NaCl. 如果温度继续升高, 亚稳态晶体结构会变为稳态的六方结构. 非晶态到晶态的相变过程可通过把GST放置于加热板上加热、使用激光脉冲照射、外加电压等手段来实现. 相反地, 把晶态GST加热超过其熔点(约640 ℃)并液化, 后经急速冷却可形成非晶态GST. 整个冷却凝固过程需要在10 ns内急速完成, 如果凝固时间过长, 液态GST有充足时间重组为晶态结构. 在应用激光的情况下, GST从晶态到非晶态的相变往往需要较大功率的短脉冲(脉宽 < 10 ns)激光. 当GST晶态或非晶态的相变过程一旦完成, 即使撤去外部激励并回到室温环境, GST仍可长时间保持相变后的晶态或非晶态, 这个性质常被称为非易失.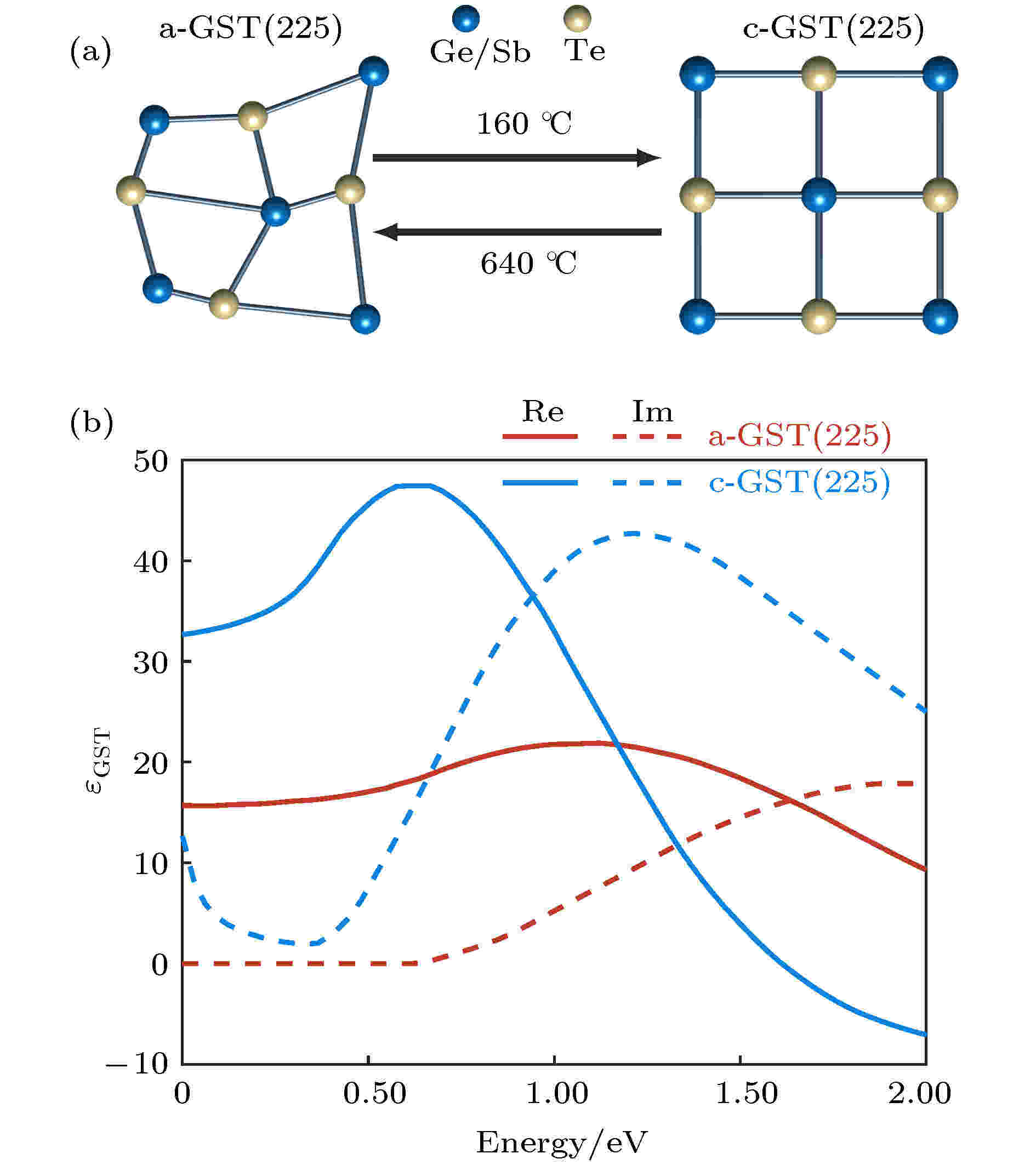

图 4 (a)晶态与非晶态GST-225的相变过程; 当温度超过结晶温度160 ℃, 非晶态GST (a-GST)相变为晶态GST (c-GST); 当温度升至熔点640 ℃, c-GST液化, 后经快速冷却可形成a-GST; (b)晶态与非晶态GST-225的介电常数^[65,66]
Figure4. (a) Sketch of phase transitions between crystalline and amorphous phases of GST-225; (b) dielectric permittivity of crystalline and amorphous GST-255^[65,66].

根据含锗、锑和碲的比例不同, GST存在多个稳定的化学构成, 最常见和应用最广泛的是Ge₂Sb₂Te₅ (GST-225)和Ge₃Sb₂Te₆ (GST-326). 以GST-225为例, 非晶态和晶态有着显著不同的介电常数^[65,66], 如图4(b)所示. 非晶态GST-225的光学带隙约位于0.77 eV (1.6 μm). 当光频率小于0.77 eV时, 非晶态GST-225几乎没有损耗, 其介电常数实部约为16 (折射率约为4); 当频率大于0.77 eV, 非晶态GST-225介电常数虚部(损耗)逐渐增加, 光的吸收也随之增加. 而晶态GST-225的光学带隙约为0.48 eV, 当光频率小于这个值, 晶态GST-225的介电常数虚部反而随着频率的减小而增加, 这是由晶态GST-225内部自由载流子导致的(可通过Drude模型进行描述). 值得注意的是, 若光频率小于1.2 eV, 晶态GST-225的介电常数实部一直大于非晶态. 在中红外波段, 晶态GST-225的介电常数实部高达36 (折射率约为6), 且损耗相对较低(对器件的光学性能的影响较小), 因此可用于减小中红外波段器件的尺寸^[67]. 此外, 在近红外和可见光波段, 晶态GST-225的介电常数实部可以是负数, 因而与金属一样能够支持表面等离激元^[68].
晶态与非晶态GST的二元光学响应可以用来表征二进制信息, 比如常用的光盘存储介质. 实际上, GST的光学响应不仅能提供晶态和非晶态二元离散选择, 还可通过控制晶态与非晶态的不同比例, 获取介于晶态与非晶态之间的光学响应. 如果把非晶态和晶态的GST的介电常数分别表示为${\varepsilon }_{\mathrm{a}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}$

和${\varepsilon }_{\mathrm{c}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}$

, 并假设晶态比例为$ {f}_{\mathrm{c}} $

, 材料的等效介电常数$ {\varepsilon }_{\mathrm{G}\mathrm{S}\mathrm{T}}^{\mathrm{e}\mathrm{f}\mathrm{f}} $

可通过Lorentz-Lorenz公式获得:

$\dfrac{{\varepsilon }_{\mathrm{G}\mathrm{S}\mathrm{T}}^{\mathrm{e}\mathrm{f}\mathrm{f}}-1}{{\varepsilon }_{\mathrm{G}\mathrm{S}\mathrm{T}}^{\mathrm{e}\mathrm{f}\mathrm{f}}+2}={f}_{c}\dfrac{{\varepsilon }_{\mathrm{c}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}-1}{{\varepsilon }_{\mathrm{c}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}+2}+(1-{f}_{\mathrm{c}})\dfrac{{\varepsilon }_{\mathrm{a}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}-1}{{\varepsilon }_{\mathrm{a}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}+2}. $

通过调控晶化比例$ {f}_{\mathrm{c}} $

, 可在$[{\varepsilon }_{\mathrm{a}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}, {\varepsilon }_{\mathrm{c}\text{-}\mathrm{G}\mathrm{S}\mathrm{T}}]$

范围内调节GST的有效介电常数$ {\varepsilon }_{\mathrm{G}\mathrm{S}\mathrm{T}}^{\mathrm{e}\mathrm{f}\mathrm{f}} $

, 实现对器件光学性能的连续调控.
GST的晶化比例可通过控制晶化过程的物理参数获得. 例如, 对非晶态GST进行加热, 晶化比例可通过改变加热温度或加热时间来调控, 以获得不同的折射率, 如图5所示^[23]. 同样地, 还可通过控制激光脉冲的强度^[19,69]或改变施加电压进行调控^[22].

图 5 GST-225薄膜在不同加热温度下的折射率^[23]; GST-225薄膜的厚度为450 nm当温度从140 ℃逐渐增至170 ℃时, 晶态GST的比例不断增加, 材料的射率实部n (实线)与虚部k (虚线)逐渐变大趋近晶态GST的折射率
Figure5. Measured refractive index of a 450-nm thick GST-225 film at different temperatures^[23]. As the heating temperature increases from 140 ℃ to 170 ℃, the degree of GST-225 crystallinity increases, and, accordingly, both the real (solid line) and imaginary parts (dashed lines) of the refractive index increase and approach the values of crystalline GST-225.

2

3.2.VO₂

-->

3.2.VO₂

固态二氧化钒(VO₂)有两个稳定的相态, 且都为晶态. 如图6(a)所示, 当温度低于68 ℃时, VO₂是单斜晶体结构, 为绝缘体. 当温度超过68 ℃后, VO₂相变为四方晶体结构, 转变为金属导体. 当温度低于相变温度, 导体态VO₂又自动还原为绝缘体. 因而, VO₂是一种易失性的相变材料. 另外, VO₂的相变温度只有68 ℃, 与室温相差不大, 相变过程较易操控. VO₂独特的物化特性赋予了它在智能玻璃、节能衣服及储存设备等方面的应用潜力.

图 6 (a)绝缘态与绝缘态与金属态VO₂的相变过程^[70]; (b)不同相态VO₂的介电常数^[71,72]
Figure6. (a) Skectch of phase transitions between insulator and metal phases of VO₂^[70]; (b) dielectric permittivity of VO₂ in different phases^[71,72].

图6(b)给出了绝缘态与金属态VO₂的介电常数曲线. 从中可以看到VO₂两个相态的介电常数差别比较明显^[70-72], 其中金属态的介电常数实部是负数. 此外, 由于金属态具有高浓度的自由载流子, 其介电常数虚部(对应损耗)较大. 与GST类似, 当温度靠近相变温度68 ℃时, VO₂往往处于绝缘态与金属态的中间态, 介电常数由两态比例决定.

5.基于相变材料超表面的动态光学调控

5.1.振幅调控

-->

5.1.振幅调控

对光波(如透射和反射光谱)振幅的调控是超表面最为常见的应用. 为了增强光与物质的作用, 超表面的周期性结构单元大多选择能够支持电磁谐振的微纳结构. 金属是构成谐振结构的常用材料, 这是由于金属微纳结构在其表面支持表面等离激元的缘故. 可以预见, 如果把相变材料放置在金属超表面附近, 激发表面等离激元谐振产生强电场, 可对超表面的光学响应进行有效地动态调控.
Tittl等^[27]将GST-326纳米薄膜集成到表面等离激元超表面中, 实现了工作在中红外波段的可调完美吸收器. 所设计的超表面是金属-电介质-金属(MIM)经典三明治结构: 最上层是周期排列的方形铝纳米天线, 中间是一层100 nm厚的GST-326薄膜, 底层是铝衬底, 如图8(a)所示. MIM三明治结构由于对光的强吸收作用而为人们所熟知, 其工作机理是通过外加光场激发超表面等离激元, 将光场的能量局域在中间层的电介质薄膜中, 进而通过金属或电介质的损耗将光转化为热, 因此该完美吸收器的最佳工作频率由表面等离激元的谐振频率决定, 而后者可以通过相变材料不同相态之间的转化加以调控. 研究者将器件加热至180 ℃并保持30 min, 使GST-326从非晶态(折射率n = 3.5)转变为晶态(n = 6), 从而观察到反射光谱的显著变化, 如图8(a)所示. 由于光不能透过铝衬底(吸收率 = 1 – 反射率), 可知图8(a)中反射光谱的波谷位置对应着吸收谱的波峰, 因此吸收器的最佳工作波长由2.7 μm红移至3.4 μm. 与上述思路类似, Chen等^[29]利用GST-225薄膜对金盘结构超表面的透射光谱实现了动态调控, 如图8(b)所示. 为了使光能够有效地透过超表面, 这里衬底选取了透射率较高的SiO₂.

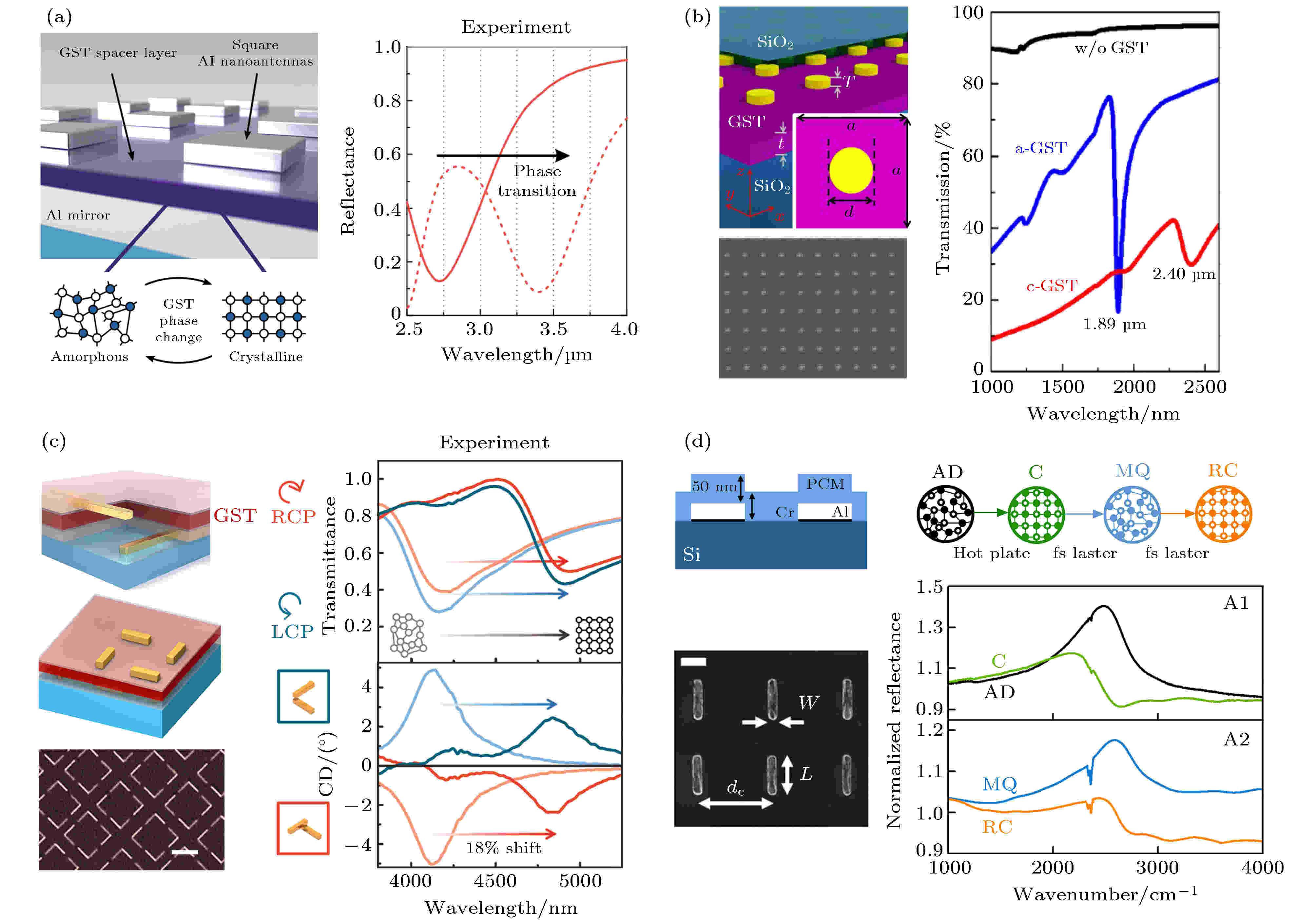图 8 结合GST和表面等离激元超表面的振幅调控　(a)基于表面等离激元超表面的可调完美吸收器^[27]; 左侧: 超表面结构示意图; 右侧: GST-326不同相态下的反射光谱, 谱谷对应最大吸收率; (b)表面等离激元超表面透射光谱的动态调控^[29]; 左侧: 超表面结构示意图和扫描电子显微镜图片; 右侧: GST-225不同相态下的反射光谱; (c)结合GST和表面等离激元的可调手性超表面^[30]; 左侧: 超表面结构示意图和扫描电子显微镜图片; 右侧: GST-326在不同相态和不同圆偏振态下的透射光谱以及圆二色光谱; (d)基于激光脉冲对超表面反射光谱的动态调控^[31]; 左侧: 超表面结构示意图和扫描电子显微镜图片; 右侧: GST-326不同相态下的反射光谱; “AD”表示初始非晶态GST-326; “C”表示经加热后的晶态GST-326; “MQ”表示强功率单激光脉冲照射下由晶态GST-326转化的非晶态GST-326; “RC”表示经弱功率多脉冲激光照射下由非晶态GST-326转化的晶态GST-326
Figure8. Active modulation of light in amplitude by integrating phase-change material GST into plasmonic metasurfaces. (a) Tunable perfect absorber^[27]. Left: sketch of the device; Right: measured reflectance spectra of the metasurface for the GST-326 layer in the amorphous (solid line) and crystalline (dashed line) phases. (b) Plasmonic metasurface with tunable transmittance^[29]. Left: sketch of the device; Right: calculated transmittance spectra of the metasurface for the GST-225 layer in the amorphous (blue line) and crystalline (red line) phases. (c) Tunable chiral metasurfaces^[30]. Left: sketch and SEM image of the device; Right: measured transmittance and CD spectra of the metasurface for the GST-326 layer in the amorphous (lighter curves) and crystalline (darker curves) phases. (d) Optical switching of reflectance spectra using femtosecond laser pulses^[31]. Left: sketch and SEM image of the metasurface; Right: measured reflectance spectra of the metasurface for the GST-326 layer in different phases—as-deposited amorphous phase (AD), thermally crystallized (C) phase, optically reamorphized (MQ) phase, and optically recrystallized (RC) phase

Yin等^[30]将GST-326相变材料应用到手性超表面中, 在中红外波段对透射光的圆二色光谱实现了动态调控. 如图8(c)所示, 手性超表面由上、下两层垂直摆放的金纳米棒阵列构成, 每层超表面的结构单元由四根纳米棒组成, 具有四重旋转对称性. 器件的衬底选取中红外波段透光率较高的CaF₂. 由于结构单元具有手性, 超表面对右旋和左旋圆偏振光的透射率不同, 因此透射光谱具有圆二色性(circular dichroism, CD. $\mathrm{C}\mathrm{D}\equiv 33 \lg({T}_{\mathrm{R}\mathrm{C}\mathrm{P}}/ {T}_{\mathrm{L}\mathrm{C}\mathrm{P}})$

, $ {T}_{\mathrm{R}\mathrm{C}\mathrm{P}} $

和$ {T}_{\mathrm{L}\mathrm{C}\mathrm{P}} $

分别代表右旋和左旋圆偏振光的透射率). 另外, 通过激发上层结构单元的表面等离激元谐振, 手性超表面的CD信号能够大幅度得以提升. 为了实现对CD光谱的动态调控, Yin等^[30] 在两层金纳米棒间夹了一层50 nm厚的GST-326薄膜, 通过加热器件使得GST-326从非晶态转化为晶态, 透射光谱的CD光谱也随之大幅度地改变, 实现了对透射圆二色光谱的动态调控.
除了通过加热, GST的相变还可以借助激光脉冲或外加电压的方式得以完成. 如在文献[31]中, Michel等利用飞秒激光脉冲控制GST-326的相态, 实现了对超表面反射谱的动态调控. 如图8(d)所示, 此超表面由周期性排列的铝纳米天线组成, GST-326覆盖在铝纳米天线上面. 首先器件加工完成后, GST-326的相态是非晶态. 通过加热, 非晶态可以转换为晶态; 相应地, 非晶态(“AD”)反射光谱转变为晶态(“C”)反射光谱. 而要把晶态GST-326转换为非晶态, 则需借助大功率的激光脉冲. 他们通过使用能量密度约为51 mJ/cm², 脉宽约为50 fs的单激光脉冲照射器件, 晶态GST-326升温超过熔点(640 ℃)后液化, 紧接着经快速冷却转化为非晶态. 发生相变后, 晶态(“C”)反射光谱转变为非晶态(“MQ”)反射光谱, 如图8(d)所示. 此外, 使用能量密度约为31 mJ/cm², 脉宽约为50 fs的多激光脉冲照射器件, 非晶态GST-326升温超过其结晶温度(160 ℃)后重新转化为晶态. 非晶态(“MQ”)反射光谱随之转变为晶态(“RC”)反射光谱, 与原先晶态(“C”)反射光谱基本一致. 因此, 通过激光脉冲改变GST的相态可实现对超表面光学性能的有效调控.
与GST类似, VO₂同样能够与表面等离激元超表面结合实现对光振幅的动态调控. 2009年, Dicken等^[71]首次展示了VO₂在该方面的应用. 所设计的超表面结构单元是银与VO₂构成的双层开口环, 如图9(a)所示. 通过加热样品(从20 ℃升至80 ℃), 将VO₂从绝缘态转变为金属态. 由于VO₂相态的改变, 表面等离激元超表面结构的反射光谱因此发生了相应的变化, 如位于3 μm处的谐振峰红移了100 $ \mathrm{n}\mathrm{m} $

. 在此工作的启示下, 基于温度对VO₂相态的控制方法, VO₂逐步应用于表面等离激元超表面在反射光谱、透射光谱、以及偏振态等方面的动态调控^[75-79]. 如在文献[78]中, Jia等将VO₂与各向异性表面等离激元超表面结构相结合, 实现了对反射光偏振的动态调控, 如图9(b)所示. 首先, 将样品的温度保持在20 ℃, 此时VO₂处于绝缘态. 在波长3 μm的线偏光照射下, 超表面的谐振模式被有效地激发, 同时结构单元的各向异性促使反射光的极化角度偏转了30^o. 当样品加热至80 ℃, VO₂变为金属态. 相应地, 超表面谐振模式的频率发生偏移而无法被入射光有效地激发. 因此, 反射光恢复至与入射光相同的偏振方向. VO₂相态的改变还可通过激光脉冲照射实现. 在文献[80]中, Lei等通过紫外激光脉冲控制VO₂的相态实现了超表面的动态调控. 如图9(c)所示, 结构的最上层是周期排列的金纳米圆盘结构, 中间是一层50 nm的VO₂薄膜, 底层是SiO₂衬底. 在实验中, 器件的初始温度设置在68 ℃ (VO₂相变的临界温度)左右. 此时, VO₂薄膜只有少部分区域发生了绝缘态到金属态的相变, 而大部分区域仍保持在绝缘态. 通过紫外激光脉冲照射器件, 绝缘态的VO₂向金属态转变, 并且转变比例与激光脉冲的照射时间成正比. 基于上述原理, 他们通过控制激光照射的时间, 实现了对超表面透射光谱谐振频率的大范围动态调控.

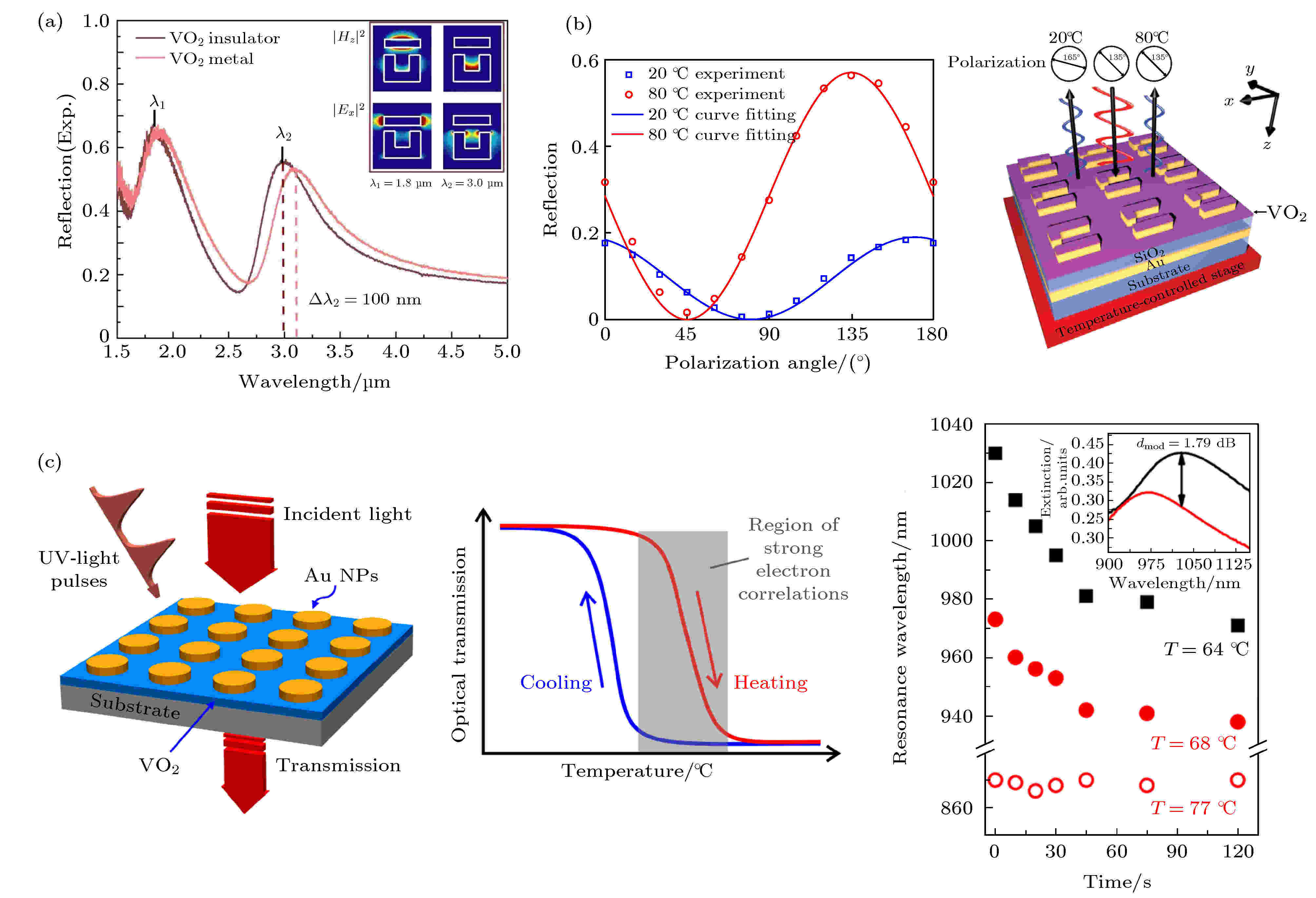图 9 结合VO₂和表面等离激元超表面的振幅调控　(a)表面等离激元超表面反射光谱的动态调控^[71]; 插图: $ {\left|{H}_{z}\right|}^{2} $

与$ {\left|{E}_{x}\right|}^{2} $

在谐振波长处的空间分布图(VO₂处于绝缘态); (b)基于表面等离激元超表面的动态可调偏振片^[78]; 左侧: 反射系数随(放置于超表面结构前)偏振片角度变化的曲线; 右侧: 器件的原理图; (c)紫外激光脉冲照射VO₂实现对超表面的动态调控^[80]; 左侧: 器件的原理图; 中间: 超表面透射率与VO₂温度的关系示意图; 右侧: 表面等离谐振波长随紫外激光脉冲照射时间的变化关系
Figure9. Active modulation of light in amplitude by integrating phase-change material VO₂ into plasmonic metasurfaces. (a) Plasmonic metasurface with tunable relfectance^[71]. Inset: $ {\left|{H}_{z}\right|}^{2} $

and $ {\left|{E}_{x}\right|}^{2} $

distributions at the resonant wavlengthwith VO₂ in the insulator phase. (b) Tunnable plasmonic-metasurface polarizer^[78]. Left: reflectance of the sample as a function of the polarizer angle (put in front of the metasurface) at 3 μm wavelength for VO₂ at 20 ℃ and 80 ℃; Right: sketch of the device. (c) Optical switching of transmittance spectra with UV laser pulses^[80]. Left: sketch of the device; Middle: hysteretic response in the transmttiance during the heating cycle of the phase transition of VO₂; Right: plasmon resonance wavelength of the Au nanodisks of 175-nm diameter on the VO₂ film as a function of the total UV illumination time, while the whole sample was thermally latched at two different temperatures within the phase transition region, 64 ℃ (blacksquares) and 68 ℃ (red circles), and also above (77 ℃, red empty circles).

除了利用相变材料改变金属超表面的介质环境从而定量调控等离激元谐振模式外, 相变材料自身也可支持谐振模式. 比如, GST具有较大的介电常数, 其微结构能够支持米氏谐振模式, 将光场很好地束缚在GST体内. 基于上述思路, Tian等^[28]设计了正方周期排列的GST-225盘状结构超表面, 如图10(a)所示. GST-225微盘的半径是1 μm, 高为220 $ \mathrm{n}\mathrm{m} $

, 排列周期为6 μm. 在145 ℃对加热器件进行加热, 通过控制加热时间实现对GST-225晶化比例的精确控制. 图10(b)和图10(c)分别给出了GST-255在不同晶化比例下消光光谱的实验与理论仿真结果. 可以观察到, 随着晶化比例的增大, 消光光谱最右侧的电偶极子(ED)谐振峰从4 μm红移至约5.25 μm. 图10(d)给出了ED模式下的电场强度分布. 此外, 在ED峰短波长一侧总是存在低位谷A1, 对应了环形电磁场态(anapole state). 当光场处于环形电磁场态时, GST-225微盘结构中的环形偶极子(toroidal dipole)与电偶极子相互抵消, 因此形成了消光光谱中的低谷. 图10(e)和图10(f)分别给出了一阶A1环形电磁场态, 以及二阶A2环形电磁场态的电场分布, 可以看到电场在微盘内具有较大的强度, 而在微盘外由于环形偶极子和电偶极子的相互抵消导致强度较小. 通过改变GST-225的晶化比例, 消光光谱的ED谐振峰和A1环形电磁场态的波谷在同一波长可以互相转换, 以此获得光学调控深度的最大值. 此外, 不同米氏谐振模式(如电偶极子与磁偶极子模式)也可以通过改变GST-225的晶化比例, 实现相互切换, 并大幅度地改变超表面的透射率(变化倍数可达$ \pm 30\;\mathrm{d}\mathrm{B} $

)^[81].

图 10 基于米氏谐振的GST超表面^[28]　(a) GST-225盘状微结构的扫描电子显微镜图像, 图中比例尺代表2 μm; (b), (c)不同晶化比例下GST盘状结构的实验(b)和理论(c)消光光谱, 其中A1和A2代表一阶和二阶环形电磁场态, ED代表电偶极子; (d)?(f) 非晶态GST-255在ED, A1, A2模式的电场强度分布(颜色代表电场强度, 箭头代表电场方向)
Figure10. Tunable metasurface composed of GST nanodisk arrays^[28]. (a) SEM image of GST disks. The scale bar represents 2 μm. (b) Experimental and (c) simulated extinction spectra of disk arrays with a radius of 1 μm and a height of H = 220 nm. A1 and A2 denotes the 1st- and 2nd-order anapole states, respectively. (d)?(f) Simulated near-field distributions of the ED (electric dipole resonance), and A1 and A2 states.

此外, 相变材料还被广泛应用于薄膜与波导结构中. 在文献[22]中, Hosseini等实现了基于GST-255的电致变色薄膜. 器件由三层结构组成: 上、下两层ITO薄膜和中间一层厚度小于20 nm的GST-255薄膜. 当GST-255处于不同的相态时, 薄膜结构由于显著不同的反射与透射光谱显现出不同的颜色. 通过对GST-255薄膜的特定位置进行电加热, 调控颜色的空间分布, 他们实现了电控彩色图像. 在文献[24]中, Ríos等通过GST-255调控波导的输出信号, 实现了光学信息存储. 光学存储器件的关键部分是一段放置在Si₃N₄波导上的GST-255薄膜. 光学信息可以以二进制形式进行存储, 一个比特中的1和0分别由GST-255的晶态与非晶态表示. 信息的存储过程通过中心波长为1.56 μm的大功率纳秒激光脉冲对GST-255的相态进行控制. 在信息的读取过程中, 为保证GST-255的相态不发生变化, 需要换用低功率的脉冲激光或连续激光. 由于晶态GST-255的损耗远大于非晶态, 通过波导后输出光信号的强弱就可以清晰地判断GST-255的相态(非晶态对应强信号, 晶态对应弱信号), 从而实现对存储信息的读取.
2

5.2.相位调控

-->

5.2.相位调控

除了在调控光波振幅上的应用, 基于相变材料(以GST为主)的超表面在相位调制上亦取得丰硕成果, 如成功实现了聚焦成像、光束偏转、电磁隐身等前沿技术的动态调控和重构. Chaudhary等^[36]通过纳秒激光脉冲控制GST的相态, 实现了激光直写超表面透镜用于聚焦声子极化激元模式, 如图11(a)所示. 器件的最上层是厚度为195 nm的hBN (hexagonal boron nitride)薄膜, 用于支持声子极化激元模式的传播; 中间是一层15 nm厚度的ZnS-SiO₂薄膜; 下面是一层沉积在CaF₂衬底上厚度为55 nm的GST-326薄膜. 通过控制激光光斑的空间位置, GST-326薄膜不同位置上的相态得以精确控制. 图12(a)(右侧图)展示了通过激光直写GST-326而制备的平面超表面透镜用于聚焦束缚在hBN薄膜中的声子极化激元模式.

图 11 基于相变材料和表面等离激元超表面的平面透镜和光束偏转器　(a)激光直写GST-326声子极化激元超表面透镜^[36]; 左侧: 激光直写示意图; 右侧: 超表面透镜的光学图像(明暗区域分别对应晶态与非晶态GST), 以及其对hBN支持的声子极化激元的聚焦光场分布; (b)基于GST-326超表面可调光束偏转器^[34]; 左侧: 器件功能示意图; 右上: 器件的扫描电子显微镜图片; 右下: GST-326两种相态下的透射光强的角度分布
Figure11. Tunable metalens and beam switcher based on phase-change materials. (a) Flat polaritonic lenses optically written in a GST-326 film below a hBN film^[36]. Left: optical images of the laser-written metalens; Right: s-SNOM image of the metalens showing focusing of polaritons at 1445 cm^–1. (b) Beam switcher composed of a plasmonic metasurface above a GST-226 layer^[34]. Left: sketch of the device; Top right: SEM image of the device; Bottom right: infrared camera images and intensity plots of the beam transmitted through the device for the GST-226 layer in the amorphous (left) and crystalline (right) phases.

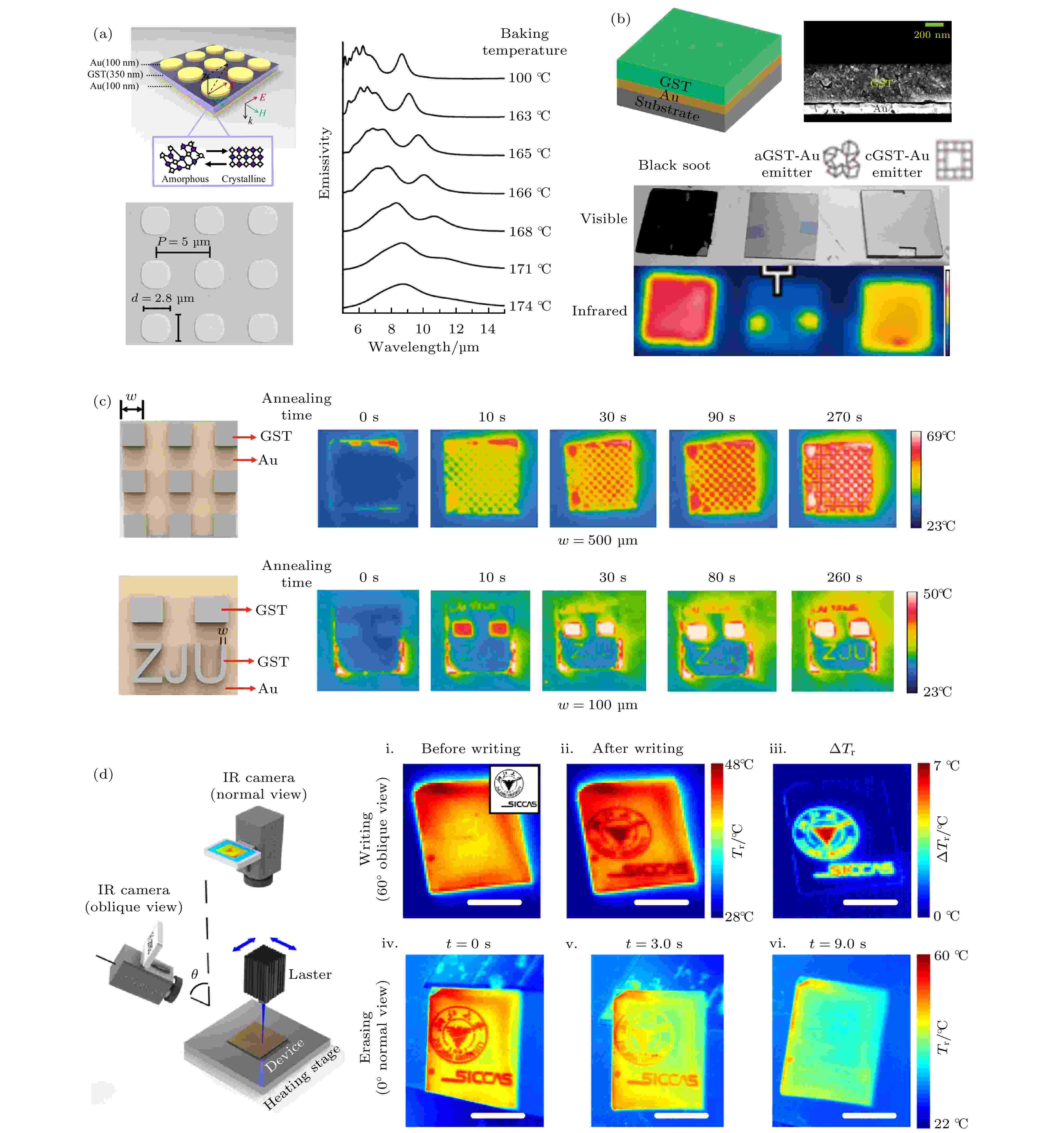图 12 基于相变材料的可调热辐射器　(a)基于GST-225和表面等离激元超表面可调热辐射器^[26]; 左侧: 超表面结构示意图与扫描电子显微镜图片; 右侧: 在不同温度下器件的热辐射光谱; (b)基于GST-225薄膜结构的可调热辐射器^[23]; 上方: 薄膜结构示意图和扫描电子显微镜图片; 下方: 晶态GST薄膜、非晶态GST薄膜和熏黑的不锈钢切片的可见光(上排)与红外(下排)照片; (c) GST-225薄膜热辐射器用于红外“隐身”和图像增强^[82]; 左侧: GST-225薄膜构成的棋盘图案和“ZJU”图案示意图; 右侧: 通过加热控制VO₂导体态比例得到不同的红外热图像; (d)激光直写VO₂重构热图像^[72]; 左侧: 实验装置示意图; 右上侧: 激光直写浙江大学徽标的热图像; 右下侧: 降低VO₂温度, 热图像消失
Figure12. Tunable thermal emitters based on phase-change materials. (a) An ultrathin meta-insulator-metal plasmonic thermal emitter incorporating GST-225^[26]. Left: sketch and SEM image of the device; Right: experimental results of continuously tuning emissivities of the thermal emitter at different baking temperatures. (b) Tunable thermal emitter composed of a GST-225 film on top of a gold film^[23]. Top: sketch and SEM image of the thermal emitter; Bottom: visible and infrared photographs of the black soot (left), the amorphous-GST-Au emitter (middle) and the crystalline-GST-Au emitter (right) at 100 ℃. (c) Thermal camouflage and thermal image sharpening based on GT-225^[82]. Left: optical images of the checkerboard and ZJU patterns of GST-based devices; Right: thermal infrared images recorded after different annealing times. (d) Tunable thermal emitter optically written in a VO₂ film^[72]. Left: sketch of the spatially-resolved thermal-emission control platform; Right: writing (top panels) and erasing (bottom panels) of the bilevel thermal images (Zhejiang University logo).

Yin等^[34]利用GST实现可调光束偏转器和变焦透镜. 以可调光束偏转器为例, 设计的器件由两部分组成: 上层是金纳米天线阵列, 用于控制透射光的相位; 下层是50 nm厚的GST-326薄膜, 用于动态调控器件的光学性能, 如图11(b)所示. 超表面结构单元由长边与短边两种类型金纳米天线组成. 当GST-326处于非晶态时, 长边纳米天线的表面等离子体激元的谐振频率与入射光频率接近, 故可以被有效地激发. 由于纳米天线几何形状的各向异性, 一部分圆偏振的入射光经透射后发生极化反转. 通过长边纳米天线从左往右呈顺时针转动(见图11(b)的电子显微镜图片), 一部分透射光会发生极化反转, 并获得额外的几何相位^[46], 偏离原有的方向. 将非晶态GST-326经加热转化为晶态后, 长边纳米天线的表面等离子体激元的谐振频率发生偏移, 同时短边纳米天线的表面等离子体激元的谐振频率移至入射光频率附近, 从而被有效地激发. 与长边纳米天线不同, 短边纳米天线从左往右呈逆时针转动, 因此极化反转后的透射光获得相反的几何相位, 使其偏离入射光方向且与非晶态时相反. 因此, 通过改变GST-326的相态可实现对透射光偏转角度的调控.
2

5.3.可调热辐射器

-->

5.3.可调热辐射器

目前基于相变材料的超表面光学调控大多聚焦在如何调节光波的反射、透射或空间相位分布上. 在这类研究中, 相变材料对光波能量的吸收大部分转化为无法利用的热能从而导致能量的损失, 这是制约器件性能的主要不利因素. 但如果能把产生的热能充分利用和操控, 用于具有保暖、制冷等多种功能的热辐射器件, 对太阳能资源的开发与利用有着至关重要的意义. 物体的热辐射率等于其在此辐射波段(一般为中红外波段)的吸收率, 因此材料的吸收或损耗是影响热辐射性能的主要因素. 调控器件的热辐射等同于调控它的吸收光谱, 从广义上可以归于振幅调控的范畴, 但从器件对热能利用的角度, 可调热辐射器结合了前沿超表面和传统热辐射的相关理论体系, 在设计中多聚焦在光能和热能之间的相互转化上, 与普通的超表面振幅调控有所不同. 下面将结合国内外最新研究进展对相变材料在可调控热辐射器中的应用做进一步具体介绍.
Qu^[26]等结合GST-255与表面等离子体超表面实现了可调热辐射器, 如图12(a)所示. 超表面热辐射器是金属-电介质-金属的三明治结构: 上层是周期阵性排列的金盘结构阵列; 中间是厚度为350 nm的GST-225薄膜; 底层是厚度为100 nm的金薄膜. 超表面结构支持的表面等离子激元把热辐射电场局域在中间的GST层中. 在靠近表面等离子激元谐振的频率范围, 超表面对光的吸收增强趋于黑体, 因此其热辐射率出现峰值并接近1. 通过加热器件并将温度从100 ℃逐步升高到174 ℃, 他们获得了介于非晶态与晶态间的不同中间态, 并观察到随着晶态GST比例的提高, 热辐射率谱峰发生红移, 且半高全宽逐渐变大.
可调热辐射器还可以通过简单的多层薄膜结构实现. 与微纳结构超表面相比, 薄膜结构的优势在于简单、易于制备, 劣势在于薄膜结构对光场的局域能力相对较弱, 因此在动态调控中调节裕度相对较小. Du等^[23]展示了利用双层薄膜结构的可调热辐射器, 如图12(b)所示. 器件的上层是GST-225薄膜, 下层是金薄膜, 衬底是BK7玻璃. 当GST处于非晶态时, 其在中红外波段的损耗较小, 因此薄膜结构的热辐射率较低. 通过加热器件将非晶态的GST转化为损耗较大的晶态GST, 器件的热辐射率得到显著提高. 他们进一步比较了100 ℃下GST处于晶态与非晶态下的薄膜结构, 以及熏黑的不锈钢切片(近似黑体)的红外热图. 如图12(b)所示, 相比于非晶态GST, 晶态GST的薄膜结构有着较强的热辐射能力, 虽然较之熏黑的不锈钢切片还有待提高. 在此基础之上, Qu等^[82]将上述双层薄膜热辐射器用于热伪装的应用中. 通过对GST-225不同相态的控制, 研究人员可将物体的热辐射调节至与环境近似一致, 从而难以被红外探测器识别, 进而实现“隐身”的功能. 反之, 可以通过设计相应的热辐射器件来放大物体与环境之间的热辐射率差别, 从而达到增强红外热图精度的目的. 如图12(c)所示, 当GST-255处于非晶态时, 双层薄膜所构建的棋盘图案和“ZJU”图案的热辐射信号与背景差别较小, 因此图案对红外相机近似实现了“隐身”. 通过加热该器件至200 ℃, 并逐步增加加热时间, GST的晶化比例逐步增大, 因此图案的热辐射率相应提高, 图案在热图像中的清晰度逐步增强.
除了GST, 研究人员还探索了VO₂等其他相变材料以用于可调热辐射器. Xu等^[72]实现了激光直写VO₂的可调控或重构热辐射器件, 如图12(d)所示. 实验装置由四部分组成: 1)加热台, VO₂样品放置其上, 温度设置为恒温68 ℃, 即VO₂刚开始发生半导体态到金属态相变的温度; 2)热成像仪, 用以测量VO₂辐射温度分布; 3)工作在405 nm的脉冲激光源, 用以微调VO₂的温度, 从而精细控制半导体态与导体态的比例; 4)激光位置移动臂, 用以改变光斑位置. 首先将VO₂加热至68 ℃, 即VO₂开始从半导体态向金属态发生相变的温度. 用405 nm的脉冲激光源照射样品的某特定位置, 该位置处的金属态比例将增大. 由于金属态损耗较大, 其热辐射强度远高于半导体态. 因此可通过控制激光在不同位置的照射时间以达到调控样品热辐射场的空间分布的效果. 如图12(d)所示, 通过激光直写VO₂获得微米级的浙江大学徽标的热图像. 当关闭加热台后, 样品温度冷却至室温, VO₂逐渐恢复为半导体态, 徽标的热图像逐渐消失^[72].

6.总结与展望

本文详细阐述分析了超表面、相变材料以及两者结合实现对光波振幅和相位的定量调控的原理与应用. 在静态调控上, 超表面一般借助激发表面等离激元谐振或相变材料的自身谐振以达到调制光波幅度、相位、极化、偏振和空间分布等多维度参量的目的. 因此, 选择和设计直接影响超表面电磁谐振的材料、形状、尺寸和空间排列等因素是超表面进行定量光学调控的关键. 在动态调控上, 由于相变材料可在不同相态间相互切换, 起到改变超表面介质环境的作用, 因此可以动态地调节自身或辅助调节其他超表面的电磁谐振, 从而进一步调制集体光波前、偏振或振动幅度等, 在实现动态光学信息存储、光学传感、光热显示以及热辐射器等功能器件上有着巨大的科学价值和广阔的市场前景.
作为一个新兴研究方向, 基于相变材料的超表面光调控尽管在近十年间取得了长足的发展, 但仍然存在一些亟待解决的问题. 首先, 在材料选择上, 目前最常用的相变材料主要是GST和VO₂. GST和绝缘态的VO₂在中红外波段的吸收损耗较低, 因此对调控平面透镜、极化转换器、传感器等器件的反射或透射性能的负面影响相对较小. 但当频率增大至近红外或可见光波段后, 电子的带间跃迁极大地增加了相变材料的损耗, 导致器件光学性能的显著衰退. 因此, 研发出包含可见光波段低损耗的相变材料是未来需要解决的重要课题之一.
其次, 相变材料对超表面的光学调控通常借助于谐振模式的改变. 调控的带宽受限于谐振的谱宽, 因此通常较窄. 相比于超表面, 薄膜结构由于谐振谱较宽, 更易于实现宽带调控. 但薄膜结构由于对光的局域能力较弱, 其调控的裕度通常较低. 因此, 如何同时实现大宽带、高裕度的光学调控值得做进一步的深入研究.
此外, 在相变控制上, 现有相变材料多采用加热、激光直写或外加电压的方式促进相变. 在这些手段当中, 激光直写由于能够精确控制相变的空间位置, 以及在纳秒的时间尺度下快速响应, 受到了人们广泛的关注. 因此, 基于激光直写相变材料的可调控或重构微纳光学器件是相变材料发展的重要趋势之一. 为了保证激光能够有效地改变相变材料的相态, 相变材料的尺寸通常需要较小, 例如GST薄膜的厚度一般不超过100 nm. 但另一方面, 高裕度的光学调控要求相变材料的尺寸不能过小. 因此, 如何兼顾激光直写相变材料的效率与光学调控的裕度是值得深入研究的课题. 另外, 着眼于未来的光学存储与光子计算, 无不要求更快、更稳的数据读写功能. 激光直写改变GST相态的动态过程通常在纳秒尺度, 速度较慢. 对于VO₂, 超快飞秒激光脉冲能够在几十飞秒内实现绝缘态到金属态的转变, 而金属态恢复到绝缘态可以在几十皮秒内完成^[83,84]. 因此在追赶甚至超越现有电子计算或存储, 实现皮秒甚至飞秒时间尺度下操控光子信息的目标上VO₂相比GST更具优势.

本站小编 Free考研考试/2021-12-29

English Abstract

Tunable metasurfaces based on phase-change materials

Corresponding author:Qiu Min, qiu_lab@westlake.edu.cn

全文HTML

2.1.超表面光调控原理

2.1.1.振幅调控

2.1.2.相位调控

2.2.超表面光调控应用

2.2.1.振幅调控

2.2.2.相位调控

3.1.GST

3.2.VO₂

5.1.振幅调控

5.2.相位调控

5.3.可调热辐射器

相关话题/材料 结构 光学 激光 光谱

领限时大额优惠券,享本站正版考研考试资料!

含双曲超构材料的复合周期结构的带隙调控及应用

平带光子微结构中的新颖现象:从模式局域到实空间拓扑

光学超构材料芯片上类比引力的研究进展

等离激元能带结构与应用

空域模拟光学计算器件的研究进展

信息超材料研究进展

偏置磁场方向对磁性光子晶体能带结构的影响及其在构建拓扑边界态中的作用

外尔超构材料里频率分离外尔点的数值设计

SeH<sup>+</sup>离子低激发态的电子结构和跃迁性质的理论研究

氟化镁高压萤石结构稳定性及热物性的数值模拟