摘要:不同于延性介质, 脆性介质的失效破坏严重制约着材料的强度. 本文采用一种定量描述脆性介质力学性质的格点-弹簧模型, 研究了金刚石-碳化硅超硬复合材料的冲击强度及其细观损伤机理, 有助于避免灾变破坏、提高冲击强度. 在模型中, 通过构建不同体积分数比的金刚石和碳化硅两相复合材料, 模拟获得了经受冲击波压缩形变后的宏观波剖面, 显示出随着金刚石颗粒含量增加, 冲击强度逐渐增大, 而后减小; 对应于这种变化, 损伤演化分析揭示出存在三种细观损伤模式, 当金刚石颗粒含量在10%—50%范围内增加时, 长距离扩展滑移带占主导; 当金刚石颗粒含量为70%时, 滑移带已由长距离扩展演化为短细滑移带, 损伤主要来自于碳化硅基体, 多数金刚石颗粒未发生损伤; 当金刚石颗粒含量超过70%的临界值后, 短细滑移带也将被强烈限制, 应力集中致使金刚石颗粒被严重损伤, 冲击强度下降. 研究结果为优化设计金刚石-碳化硅超硬复合材料以及制备新型抗冲击材料提供了物理认知.
关键词: 金刚石/
碳化硅/
超硬复合材料/
冲击强度/
细观损伤

English Abstract

全文HTML

--> --> -->

金刚石和碳化硅是典型的硬质脆性陶瓷材料, 两者具有相似的晶体结构, 在一定条件下可以化合成键, 因此金刚石-碳化硅两相复合材料的界面结合良好, 是一种优异的超硬复合材料. 采用化学气相渗透和高温高压合成方法, 可以制备金刚石-碳化硅两相复合材料. 但在化学气相渗透方法中, 难以得到块体材料; 目前较为成熟的金刚石-碳化硅两相复合块体材料大多是基于高温高压方法制备得到, 而且通过调控不同金刚石颗粒含量、不同晶粒尺度可以获得不同性能的金刚石-碳化硅超硬复合材料. 金刚石-碳化硅超硬复合材料的优良物理力学性能已经得到了诸多研究的印证, 例如: 高硬度、高韧性、低密度和低热膨胀系数等^[1—4], 通过高温高压方法制备的纳米结构金刚石-碳化硅超硬复合材料, 断裂韧性高达12 MPa·m^1/2[5]. 这些优良性能为金刚石-碳化硅超硬复合材料的更多应用提供了潜能.
材料强度与微结构之间的关系一直是凝聚态物理和材料科学探究的基础问题. 从传统的颗粒强化、晶须强化, 到近年来的纳米孪晶强化^[6,7]、多级构筑结构强化^[8,9]等, 材料强化的新方法不断地被提出和改进. 然而, 脆性介质的强化, 尤其是在冲击载荷条件下, 如何提高脆性材料的冲击强度仍是颇受关注的课题. 例如, 在冲击防护领域, 通常采用碳化硼(B₄C)、三氧化二铝(Al₂O₃)、二硼化钛(TiB₂)等陶瓷材料用作防护, 但是由于受到材料断裂韧性、塑形变形能力等限制, 普通陶瓷材料的防护性能亟待提高. 不同于金属材料通过塑性变形来吸能, 脆性材料需要借助裂纹萌生、扩展来吸收能量, 以及通过微结构调控来抑制灾难性裂纹失效模式. 值得注意的是, 在天然贝壳类介质中人们发现贝壳在抵御裂纹、吸收能量、增强抗冲击方面具有优异的性能^[10,11]. 贝壳中由有机质和珍珠层构造的交错结构, 有利于滞止裂纹长距离扩展, 促进裂纹频繁偏转, 提高动态断裂性能. 贝壳的这种微结构特征, 为改进陶瓷基复合材料的脆性提供了重要启示.
本文通过建立金刚石-碳化硅超硬复合材料的格点-弹簧模型(lattice-spring model, LSM), 计算模拟了金刚石-碳化硅超硬复合材料在冲击波压缩下的冲击响应特性, 分析了细观损伤机理, 揭示出金刚石-碳化硅超硬复合材料的微结构形变机理类似于贝壳中的交错构造, 在提升抗冲击能力方面具有独特的功能. 这些认识有助于优化设计金刚石-碳化硅超硬复合材料及相关新型防护材料, 拓展抗高速侵彻和防护空间碎片等领域的应用.

在处理材料的动态断裂和裂纹网络扩展问题时, 有限元等基于网格的计算方法会遇到很多挑战^[12]. 而LSM的离散构型使其在处理这类非连续的断裂、破碎问题时具有独特优势; 另外, 该方法还具有物理图像清晰简单的优点. LSM是将连续介质离散为格点和弹簧相互连接成网络来近似表现真实的连续介质材料的力学响应. 格点携带着材料中物质微元的质量、位置、速度等信息, 弹簧则在两格点之间施加相互作用, 并存储应变能和损伤断裂信息. 模型中最近邻格点i和j之间有一对分别沿法向和切向的弹簧. 通过两格点中心的法向弹簧起着抵抗拉伸和压缩的作用, 刚度系数为${k_n}$; 垂直于两格点中心线的切向弹簧起着抵抗剪切和转动的作用, 刚度系数为${k_\tau }$. 法向和切向作用力由(1)式确定:

$\left\{ {\begin{aligned}& {f_{ij}^n = {k_n}\delta _{ij}^n,} \\ & {f_{ij}^\tau = {k_\tau }\delta _{ij}^\tau,} \end{aligned}} \right.$

其中, $\delta _{ij}^n$和$\delta _{ij}^\tau $分别表示格点i和j沿法向和切向的相对位移, $f_{ij}^n$和$f_{ij}^\tau $分别表示作用在法向和切向上的力.
LSM的核心问题是如何严谨且准确地设定模型中的弹簧刚度系数. Gusev^[13]提出了有限元-LSM网格映射方法, 其基本思想是将目标材料参数存储在有限元的总体刚度矩阵中, 再对总体刚度矩阵进行拆分、重组, 获得两个节点之间的刚度子矩阵, 并将其映射到LSM中作为两格点之间弹簧的刚度系数. Gusev^[13]验证了对于模拟不同周期性复合介质LSM的准确性. 另外, Yu等^[14,15]通过回收实验的微观形貌和参数映射后的LSM能定量地表现致密脆性介质的弹性性质以及细观损伤, 验证了LSM的准确性. 本文参考文献[16, 17]设定了金刚石和碳化硅的材料参数, 模型中金刚石和碳化硅的弹性常数分别被设定为杨氏模量E = 1000 GPa, 400 GPa; 密度分别为ρ = 3500 kg/m³, 3200 kg/m³; 泊松比分别为υ = 0.2, 0.16. 采用Gusev的参数映射方法, 将一个由正三角形组成的网络作为二维有限元和LSM共用的模型网格, 并利用这一共用网格实现参数映射.
本文建立的是一种弹性-脆性响应的材料模型, 假设格点之间只在线弹性范围内发生相互作用; 材料本身并不具备塑性变形能力, 因此模型整体的宏观塑性响应只可能是来自不可逆变形与损伤断裂引起的应力松弛和能量耗散引起. 本文采用的弹簧断裂判据是基于Griffith能量平衡原理^[18]的能量阈值. 当一对弹簧中存储的应变能大于等于形成新微裂纹表面所对应的表面能时, 这对弹簧就会发生不可逆的断裂. 此时格点间仍然存在法向的排斥力和沿切向的干摩擦力, 但是不再存在抵抗拉伸和剪切的作用力. 根据典型脆性材料的临界断裂应力条件^[19], 可知剪切应力是压缩状态下导致断裂发生的根本原因. 因此, 我们在模型中假定法向弹簧的压缩(无剪切应力、静水压压缩)不会导致断裂, 从而在计算总弹性势能时没有计入法向弹簧处于压缩状态时的能量. 上述判据由(2)式表示:

$\left\{ {\begin{aligned}& {{U_{ij}} = U_{ij}^n + U_{ij}^\tau ,}\\& {U_{ij}^n = 1/2{k_n}{{(\delta _{ij}^n)}^2}\quad\quad(\delta _{ij}^n > 0),}\\& {U_{ij}^n = 0,}\\& {U_{ij}^\tau = 1/2{k_\tau }{{(\delta _{ij}^\tau )}^2}\quad\quad(\delta _{ij}^n \leqslant 0),}\\& {{U_{ij}} \geqslant 2\gamma {c_0},}\end{aligned}} \right.$

其中${U_{ij}}$表示一对弹簧中储存的总应变能, $U_{ij}^n$和$U_{ij}^\tau $分别表示法向和切向应变能, 但$U_{ij}^n$没有计入压缩变形的贡献; ${c_0}$表示两格点间微裂纹的长度; γ表示断裂表面能. 断裂表面能可以由实验直接测量或根据Bareblatt^[20]的内聚区模型, 通过材料断裂韧性${K_{\rm{c}}}$得出,

$2\gamma \; = \;{{{{({K_{\rm{c}}})}^2}} / {{E'}}},$

在平面应变状态下${E'} = {E / {(1 - {\nu ^2})}}$, 在平面应力状态下${E'} = E$. 模型中金刚石和碳化硅的断裂表面能$\gamma $分别是17.1 J/m², 7.5 J/m^2[21,22]; 在金刚石与碳化硅界面结合良好的前提下, 界面断裂表面能应该大于碳化硅, 小于金刚石, 介于两者之间. 但是, 目前暂没有实验测量结果, 也未见有文献报道, 所以界面处的断裂表面能选择取金刚石与碳化硅断裂表面能的平均值12.3 J/m².
实验中金刚石-碳化硅超硬复合材料显微形貌的金刚石颗粒形状虽然呈多面形^[2,23,24], 但也是比较接近于圆形. 因此, 为了简化构建金刚石颗粒形状, 在建模过程中通过在碳化硅基体中随机撒点获得金刚石颗粒的质点中心, 然后按照既定半径画圆得到金刚石圆形颗粒. 在随机撒点的过程中, 两个质心点之间的距离将大于某个临界长度, 以确保金刚石颗粒不会重叠. 本文构建了金刚石颗粒不同含量(10%, 30%, 50%, 70%, 73%, 76%体积百分比)的金刚石-碳化硅超硬复合材料在冲击波压缩下的演化模型, 如图1所示, 通过改变金刚石颗粒的含量, 来调控两相复合材料的微结构. 由图1可知, 当金刚石颗粒含量少于70%时(图1(a)—(d)), 金刚石和碳化硅两相可以分散; 但超过70%后, 金刚石颗粒出现了团聚, 部分金刚石颗粒相互接触在一起, 如图1(e)和图1(f). 计算模拟中, 金刚石-碳化硅超硬复合材料样品的长度为2 mm, 宽度为0.4 mm, 并且在宽度方向(横向)上施加了周期性边界条件. 金刚石颗粒的直径为20 μm. 每个格点的直径为1 μm; 金刚石格点的质量为1.833 × 10^–12 g, 碳化硅格点的质量为1.676 × 10^–12 g. 在冲击波压缩的模拟计算过程中, 每个格点的位置、速度、应力和每组弹簧的连接状态等信息都在指定的计算步被记录下来.
图 1 金刚石-碳化硅超硬复合材料中金刚石颗粒不同含量(体积百分比)　(a) 10%; (b) 30%; (c) 50%; (d) 70%; (e) 73%; (f) 76%; 红色区域表示金刚石颗粒, 蓝色区域表示碳化硅基体
Figure1. Diamond particle content in diamond-SiC superhard composites (in volume percentage): (a) 10%; (b) 30%; (c) 50%; (d) 70%; (e) 73%; (f) 76%. The red areas represent diamond particles, and the blue areas are the SiC matrix

2

-->

3.1.宏观波剖面和冲击强度

图2为在1300 m/s活塞驱动下, 金刚石-碳化硅超硬复合材料中的宏观冲击波剖面及其演化特征. 对应金刚石颗粒不同含量(10%, 30%, 50%, 70%, 73%, 76%体积百分比), 宏观冲击波剖面的变化主要体现在冲击波速度和冲击强度两方面. 1)冲击波在金刚石颗粒不同含量样品中均出现弹性波(elastic wave)-变形波(deformation wave)的双波结构, 传播速度较快的是弹性波, 传播速度较慢的是变形波, 在变形波后出现的平台是冲击终态(Hugoniot state)^[25]; 弹性波与变形波的拐点, 表示Hugoniot弹性极限(Hugoniot elastic limit, HEL); 图2显示, 随着金刚石颗粒含量的增加, 弹性波速度在逐渐的增加, 同时变形波的传播速度也在加快. 2)图2中的变形波与延性金属的塑性波类似, 但它的塑性变形量小, 且形成机理一般不是位错、孪晶等原子尺度的变形, 而是对应着样品的损伤和微裂纹扩展^[26]. 因此, 弹性波与变形波的拐点(HEL)称为金刚石-碳化硅超硬复合材料的冲击强度(dynamic strength). 随着金刚石颗粒含量的增加, 金刚石-碳化硅超硬复合材料的冲击强度也逐渐增加, 但当金刚石颗粒含量超过70%体积百分比后, 冲击强度出现下降(图3).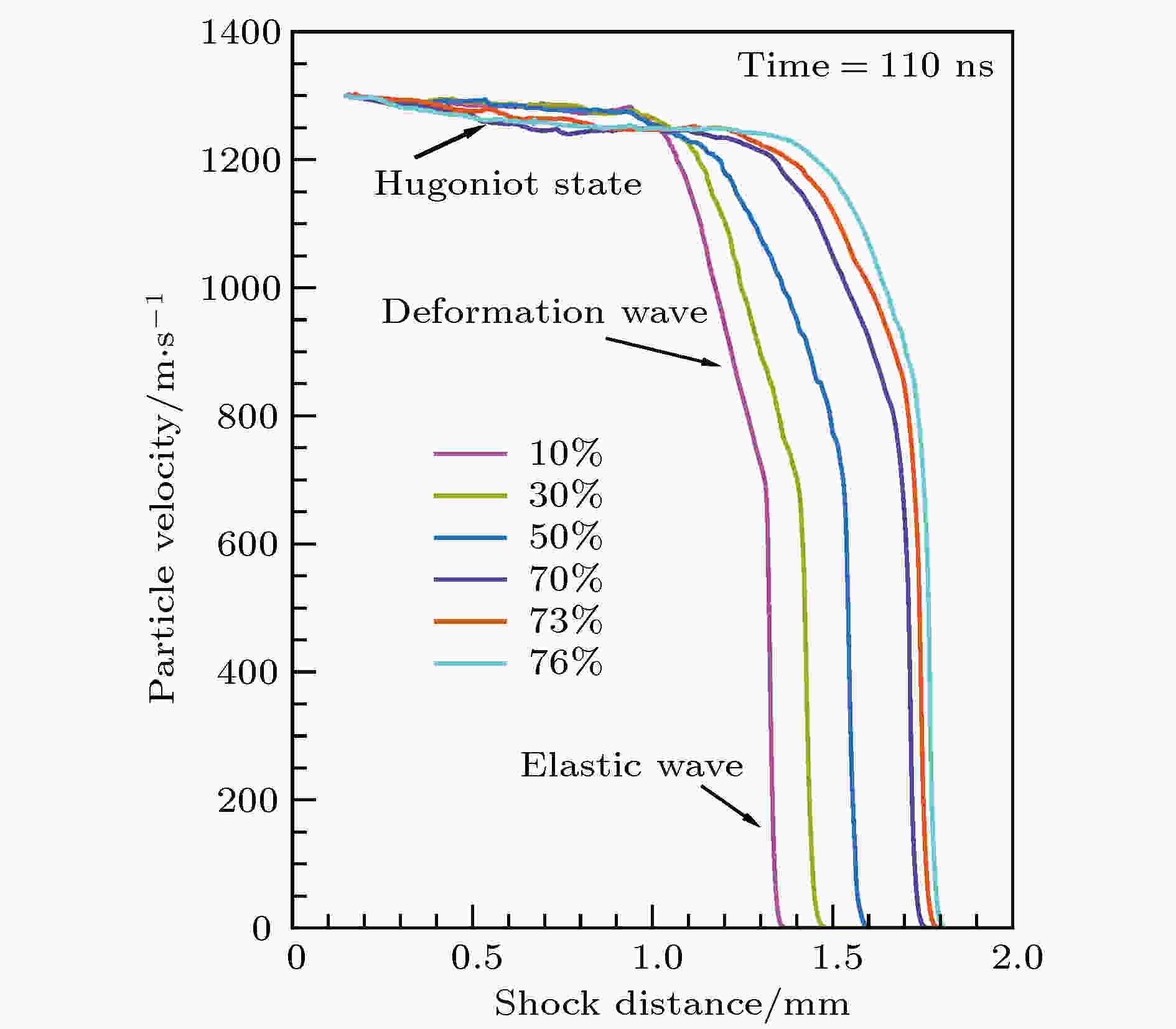
图 2 在1300 m/s活塞驱动下, 金刚石颗粒不同含量(体积百分比)对金刚石-碳化硅超硬复合材料冲击波剖面的影响
Figure2. Influence of diamond content (in volume percentage) on shock wave profiles of diamond-SiC superhard composite under a 1300 m/s piston driven.

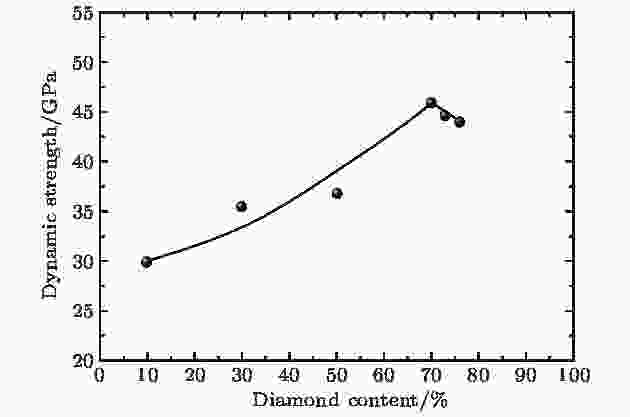图 3 金刚石-碳化硅超硬复合材料的冲击强度随金刚石颗粒含量(体积百分比)的变化
Figure3. Dynamic strength of diamond-SiC superhard composite varies with diamond content (in volume percentage).

然而, 宏观波剖面不能作为材料强度和性能的唯一指标以及更具体的细观损伤演化也无法单纯根据冲击波剖面获得认识. 因此, 下面进一步研究金刚石-碳化硅超硬复合材料的细观损伤特征.
2 -->

3.2.细观损伤特征及其演化

图4展示了金刚石颗粒不同含量(10%, 30%, 50%, 70%, 73%, 76%体积百分比)的金刚石-碳化硅超硬复合材料的细观损伤特征. 在冲击波压缩下, 相对而言碳化硅的强度、硬度明显低于金刚石, 因此在金刚石-碳化硅两相复合材料中, 碳化硅等效于“软性”基体、金刚石为“硬性”颗粒, 继而形成一种“柔性体”包裹金刚石颗粒, 这样的微结构组合非常类似于天然贝壳, 对抵御裂纹、吸收能量、增强抗冲击性能发挥了有效作用. 从图4可以看出, 样品中碳化硅基体都出现损伤破坏(蓝色离散格点), 但当金刚石颗粒含量较少时(图4(a)—(c)), 碳化硅基体中普遍产生长距离扩展的滑移带且滑移带存在滑移带分支, 这与其类似的颗粒增强体复合材料的损伤演化结果相似, 例如Ti₂AlC-TiAl复合材料实验和ZrO₂-Al₂O₃复合材料数值模拟^[27,28]. 这些滑移带遇到金刚石颗粒时, 会被阻碍, 严重时也会切割破坏金刚石颗粒, 使得金刚石、碳化硅均出现严重损伤. 随着金刚石颗粒含量的增加, 碳化硅基体的损伤破坏模式发生了变化, 出现了更多短距离的扩展滑移带, 图4(d)是金刚石颗粒含量为70%的细观损伤分布. 这些短且细的滑移带由于受到金刚石颗粒阻碍, 无法长距离扩展, 损伤被抑制, 金刚石颗粒得到较好的保护. 进一步, 当金刚石颗粒含量增加到73%, 76%时(图4(e)和图4(f)), 尽管短细滑移带仍然占主导, 但是金刚石颗粒反而出现严重的损伤破坏. 分析其原因是由于金刚石颗粒增加到了一定的临界含量, 金刚石颗粒之间出现了接触(团聚), 使得金刚石颗粒间的滑移带不易扩展, 剪应力难以得到松弛而出现严重的剪应力集中, 使金刚石颗粒遭受到严重破坏, 致使金刚石-碳化硅超硬复合材料的冲击强度下降, 如图3.
图 4 在1300 m/s活塞驱动下, 金刚石-碳化硅超硬复合材料中金刚石颗粒不同含量的损伤演化特征, 其中金刚石颗粒含量(体积百分比)分别是(a) 10%; (b) 30%; (c) 50%; (d) 70%; (e) 73%; (f) 76%; 黑色带状区域是扩展滑移带
Figure4. Damage evolution of diamond-SiC superhard composite with different diamond particle content in volume percentage: (a) 10%; (b) 30%; (c) 50%; (d) 70%; (e) 73%; (f) 76%. The piston velocity is 1300 m/s. The thin black lines are slip bands occurred in SiC matrix.

通过上述分析可以发现, 金刚石颗粒含量是影响金刚石-碳化硅超硬复合材料细观损伤特征及其演化的一个重要因素. 随着金刚石颗粒含量的增加, 细观损伤模式出现三种变化: 先是长距离扩展滑移带占主导; 然后演化为短细滑移带; 最后当金刚石颗粒含量超过某一临界值时, 短细滑移带也被严重阻碍, 引起应力集中, 使更多金刚石颗粒遭到损伤破坏. 因此, 在三种细观损伤模式之间探究一定的分布或者平衡, 让金刚石-碳化硅超硬复合材料的总体损伤度最小, 是值得关注的.
2 -->

3.3.损伤度调控

引入损伤度(damage degree, D)的统计方法, 如(4)式所示:

$D = {{{N_{\rm{D}}}} / {{N_{\rm{t}}}}},$

其中, ${N_{\rm{D}}}$表示损伤格点数, ${N_{\rm{t}}}$表示总格点数, 用于统计金刚石-碳化硅超硬复合材料的损伤度. 图5给出了在1300 m/s活塞速度驱动下, 损伤度随金刚石颗粒含量的变化关系. 根据(4)式, 该损伤度统计值是金刚石和碳化硅的损伤量总和. 图5表明, 当金刚石颗粒含量体积百分比在10%—70%范围内增加时, 损伤度呈减小趋势. 该统计值是因为在这个含量范围内, 多数金刚石颗粒未发生损伤, 损伤度主要来自于碳化硅基体的损伤. 但是, 超过70%的含量后, 损伤度明显增大, 说明金刚石也明显损伤, 损伤量也被统计了. 这与3.2节讨论中观察到的现象是一致的, 即含量超过70%这一临界值后, 金刚石颗粒之间出现了接触(团聚), 使得金刚石颗粒间的滑移带不易扩展, 剪应力难以得到松弛, 使金刚石颗粒被严重破坏. 为了验证本文分析是否合理, 我们计算了一个算例, 取金刚石颗粒含量体积百分比为100%, 统计表明这时样品的损伤度高达84%, 见图5的空心统计点. 另外, 本文在模拟中的加载条件是采用恒定活塞速度压缩样品, 对于这种加载条件, 金刚石含量不同, 冲击终态(Hugoniot state)应力略有不同(图2), 这不影响损伤度统计的变化趋势.
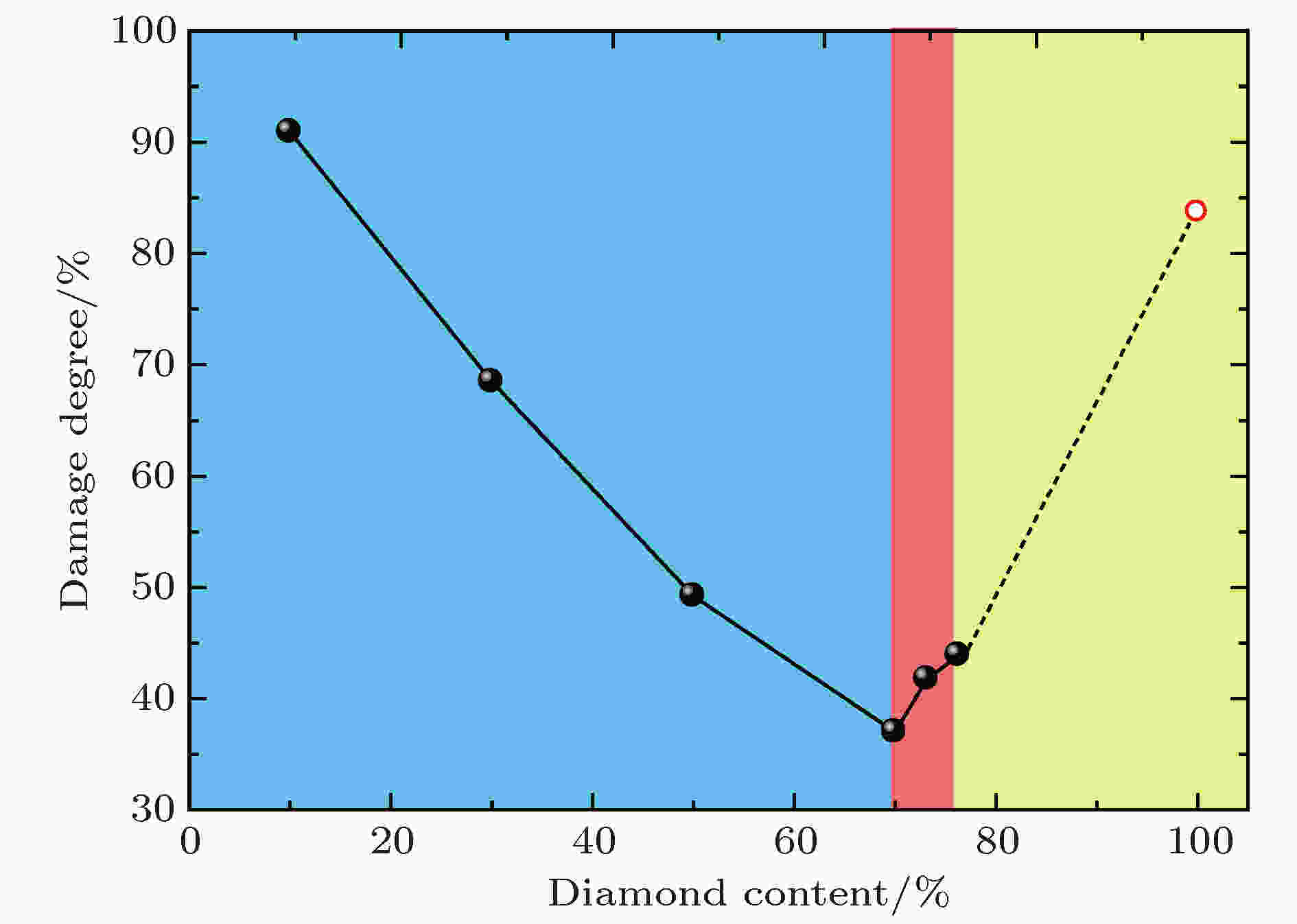图 5 在活塞速度1300 m/s驱动下, 金刚石-碳化硅复合超硬材料的损伤度随金刚石含量(体积百分比)的变化
Figure5. Damage degree of diamond-SiC superhard composite varies with diamond content (in volume percentage) under a 1300 m/s piston.

上述分析表明, 金刚石-碳化硅超硬复合材料的损伤度与金刚石含量有密切关系, 也即改变金刚石颗粒的含量, 可以调控金刚石-碳化硅两相复合材料的损伤度. 根据本文的计算模拟, 当金刚石颗粒含量体积百分比为70%时, 金刚石-碳化硅超硬复合材料的损伤度可以达到最小. 这一现象与文献[5]中报道的纯金刚石的断裂韧性仅有3—5 MPa·m^1/2, 而金刚石-碳化硅复合超硬材料(金刚石与硅的摩尔比为90︰10)的断裂韧性高达12 MPa·m^1/2的结果在定性上是一致的.
损伤度调控对金刚石-碳化硅超硬复合材料的制备和应用具有一定的指导意义. 2015年, Salamone等^[29]对金刚石-碳化硅超硬复合材料开展的抗冲击性能实验表明, 不同金刚石颗粒含量对金刚石-碳化硅超硬复合材料的抗冲击性能有明显影响, 金刚石颗粒含量越高其抗冲击性能越强. 但是, 在Salamone等^[29]的实验中, 金刚石颗粒含量只验证到21%的质量百分比(约为19.5%体积百分比), 通过本文的计算模拟显示出金刚石颗粒含量可以更高, 有利于获得更好的抗冲击性能. 另外, 在陶瓷类装甲防御实验中, 研究认为抗侵彻的一种重要机制是依靠坚硬的陶瓷颗粒对侵彻过程中的弹体进行磨蚀, 来有效地消耗弹体质量和动能^[30]. 最近, Petel等^[31—33]发现超硬颗粒在抗侵彻过程中起着重要作用, Sun等^[34]也表明高硬度以及高强度的材料可以有效地抵抗弹体的侵彻. 因此, 本文提出的损伤度调控思想, 可以有针对性地设计金刚石-碳化硅超硬复合材料, 充分发挥碳化硅基体和金刚石颗粒的各自优势, 主动应对抗高速侵彻、防护空间碎片等领域的应用需求.

本文通过构建不同体积分数比的金刚石和碳化硅两相复合材料, 研究了冲击加载下金刚石-碳化硅超硬材料的宏观冲击特性和细观损伤模式, 指出金刚石-碳化硅两相复合材料的微结构形变机理与天然贝壳中的交错构造相似, 有益于抵抗冲击、提高强度; 而且与天然构造不同, 经由金刚石颗粒含量调节, 可以有效调控金刚石-碳化硅超硬复合材料的损伤度、优化设计冲击强度. 对金刚石-碳化硅超硬复合材料的损伤度进行统计计算表明, 当金刚石颗粒含量体积百分比为70%时, 金刚石-碳化硅超硬复合材料的损伤度达到最低. 本文的研究结果可有助于指导超硬复合材料的制备, 以及为后续工作中对超硬复合材料冲击波压缩破坏的深入研究提供认识.
非常感谢中国工程物理研究院流体物理研究所的邓小良副研究员、操秀霞助理研究员在论文撰写过程中的帮助和讨论.