引 言

激波干扰现象广泛存在于超声速和高超声速流动中^[1-2], 因其容易在飞行器局部壁面产生极高的气动热甚至烧蚀破坏^[3-5], 已成为制约长时间高超声速飞行的关键气动问题之一. 该问题在采用三维内转式进气道^[6-9]的吸气式高超声速飞行器内外流动中, 显得尤为突出和复杂. 特别地, 内转式进气道的唇口型线通常后掠并呈现为V字形^[6-9], 激波在V字形根部位置产生的三维复杂干扰, 不仅给理论分析和预测带来极大困难, 而且严重阻碍了飞行器气动性能的提升.

为了深入认识V字形唇口部位的复杂流动, 肖丰收等^[10-11]率先提炼出由半径比R/r (根部倒圆半径R和前缘钝化半径r)和扩张角β表征的V字形钝前缘简化构型(见图1), 并发现V字形根部主要会产生异侧激波规则反射(regular reflection, RR)、马赫反射(Mach reflection, MR)以及同侧激波规则反射(regular reflection from the same family, sRR) 3种激波干扰类型. 随后, ****们围绕V字形钝前缘深入开展了流场非定常振荡^[12-15]、壁面气动力/热载荷变化规律^[16-18]、下游流场结构^[19-22]以及优化设计^[23-24]等一系列研究^[25], 不仅丰富了对V字形钝前缘激波干扰流动机理的认知, 而且为工程应用提供了许多有价值的参考. 其中, 气动热特性作为V字形钝前缘研究中的重要环节, 因近壁面流动会产生压缩、膨胀、流动分离以及二次激波干扰等现象, 而显得十分复杂和多变. Xiao等^[11]最早在来流马赫数Ma_∞ = 6条件下发现, 改变R/r能够造成V字形钝前缘的热流峰值出现数量级的变化, 而当R/r足够大时, 流场出现sRR反射类型, 可以显著降低热流峰值. 随后, 蒙泽威等^[16-17]在Ma_∞ = 4条件下, 也发现调整R/r可以有效降低V字形钝前缘的热载荷. 实际上, 来流马赫数和几何参数都是通过改变V字形根部的激波反射流场结构, 进而影响壁面热流分布. 在Xiao等^[11]研究的基础上, 张志雨^[15]和Li等^[18]进一步地归纳出V字形钝前缘主要有4种热流峰值产生机制, 分别为超声速气流冲击壁面、激波或膨胀波/边界层干扰、剪切层贴附壁面和异侧超声速射流对撞, 并且建立了热流峰值和压力峰值的关联公式.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
V字形钝前缘示意图



Figure
1.
Schematics of the V-shaped blunt leading edge model



下载:
全尺寸图片
幻灯片


在V字形钝前缘气动热研究方面, 尽管已经取得了长足的进步, 但对气动热随几何参数变化规律的认识, 仍然不够全面和透彻. 以往关于V字形钝前缘气动热的研究, 主要是将R/r或β作为单一变量来分析. 这种基于单一几何参数变化获得的影响规律很难推广, 也限制了对热流峰值的全面把握. 最近, Zhang等^[26]通过改变R/r和β, 对V字形钝前缘根部激波干扰类型进行了系统性的分析, 并在几何参数空间(R/r, β)建立了RR, MR和sRR 3种激波干扰类型的转变准则. Zhang等^[26]的研究表明, R/r和β共同对V字形根部流动结构造成影响. 这种联合作用, 为深入研究气动热的变化规律, 带来了极大的启示. 鉴于R/r和β 对V字形钝前缘气动热影响存在一定的关联, 单一几何参数的改变, 并不能直接构成影响气动热变化的根本因素. 因此, 亟需在几何参数空间(R/r, β)建立对V字形钝前缘气动热规律的认知, 以便在V字形唇口设计中, 综合考虑并权衡不同几何参数的影响.

本文采用数值模拟并辅以激波风洞实验, 以Zhang等^[26]提出的激波干扰转变准则为指导, 有针对性地选取R/r和β的组合, 并综合分析R/r和β的联合作用对V字形钝前缘气动热特性的影响, 以期阐明激波干扰类型与气动热特性之间的联系, 获得气动热在几何参数空间(R/r, β)的变化规律, 为内转式进气道V字形唇口气动热预测与热防护设计提供有价值的参考.

1.
模型与方法

1.1
V字形钝前缘模型

V字形钝前缘模型如图1所示, 由后掠的直前缘和根部倒圆区域组成, 其主要几何特征包括: 半扩张角为β、倒圆区域半径为R、前缘钝化半径为r以及后掠直前缘长度为L. 其中, 坐标轴x方向为流向、y方向为横向、z方向为展向, φ为V字形根部倒圆区域的周向角.

为了系统反映几何参数变化对V字形钝前缘根部不同激波反射类型的流动特征和壁面热流造成的影响, 如表1所示, 本文主要通过数值模拟方法, 并辅以风洞实验验证, 在保持钝化半径r = 2 mm和直前缘长度L = 30r一致的几何条件下, 针对性地选取了不同R/r和β的V字形钝前缘进行分析. 根据Zhang等^[26]提出的激波反射类型随V字形钝前缘几何参数变化的转变准则可知, 表1中列举的几何参数所对应的激波反射类型, 涵盖了RR, MR和sRR 3种主要反射类型. 因此, 能够较为全面地反映出, R/r和β变化后, 近壁面流动特征及气动热的变化趋势.




表
1
几何参数和对应的激波反射类型



Table
1.
Geometric parameters and corresponding shock reflection types



table_type1 ">

R/r	β/ (°)	methods	shock interaction types
1	16	sim.	RR
1	24	exp. + sim.	MR
1	40	sim.	MR
1	56	sim.	MR
3	16	sim.	MR
3	24	exp. + sim.	MR
3	40	sim.	MR
3	56	sim.	MR
3.25	24	exp. + sim.	MR
6	16	sim.	sRR
6	24	exp. + sim	sRR
6	40	sim.	sRR
6	56	sim.	sRR

下载:
导出CSV
|显示表格

1.2
风洞实验方法

实验在中国科学技术大学KDJB330激波风洞^[27]中开展, 风洞来流马赫数Ma_∞ = 6, 静压P_∞ = 800 Pa, 静温T_∞ = 115 K. 如表1所示, 选取了β = 24°的3个不同R/r构型, 拍摄纹影. 高速纹影的拍摄速率为69 kHz, 曝光时间为2 μs. 进一步地, 以几何参数为β = 24°, R/r = 3.25的V字形前缘构型为例, 在倒圆区域壁面中心线上φ = 0°, ± 5°, ± 17°, ± 28°, ± 33°, ± 38°和± 43°处, 安装E型同轴热电偶进行测热实验^[15]. 这些典型工况的实验数据, 将用于考核和验证本文宽几何参数范围的数值模拟.

1.3
数值模拟方法

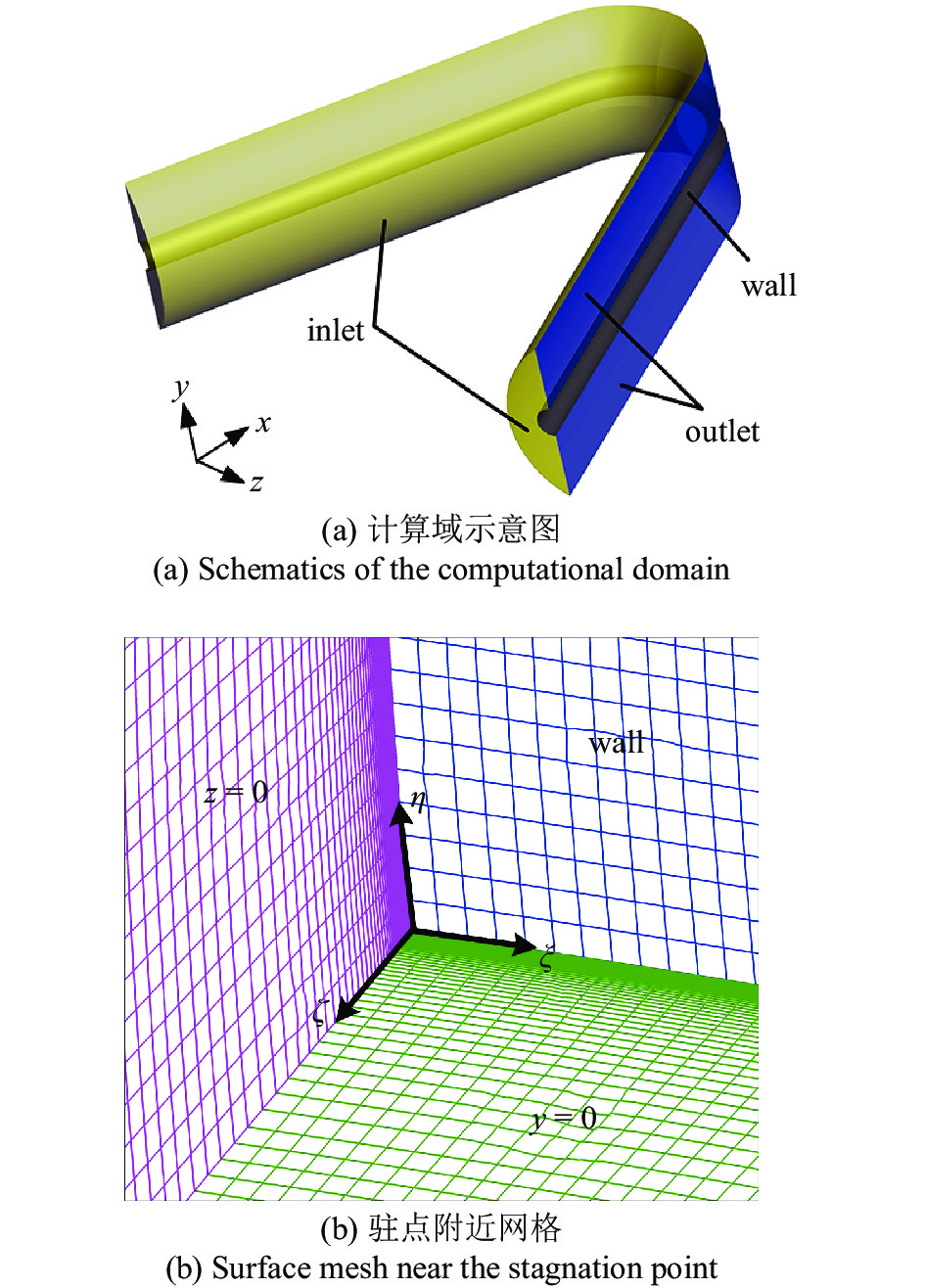
数值模拟方法基于雷诺平均的三维Navier-Stokes控制方程, 无黏通量采用Roe格式进行差分分裂^[28], 对流项采用二阶迎风格式离散, 黏性项采用二阶中心差分格式离散, 使用Spalart-Allmaras湍流模型^[29], 空气采用量热完全气体假设, 分子黏性系数由Sutherland公式^[30]计算. 计算域和边界条件如图2所示, 采用压力远场、压力出口边界和无滑移300 K等温壁面条件, 来流条件与中国科学技术大学KDJB330激波风洞的典型来流条件^[27]一致. 以残差下降4个数量级或者继续迭代残差不再变化, 同时驻点的流场参数保持稳定作为收敛判据. 上述模拟策略, 在课题组前期研究^{[10-11,15,18,23-24]}中已得到广泛地验证.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
计算域、边界条件和网格



Figure
2.
Computational domain with boundary conditions and surface mesh



下载:
全尺寸图片
幻灯片


以R/r = 3.25, β = 24°的V字形前缘构型为例, 采用表2所列的4套不同疏密程度的结构网格, 进行网格无关性验证. 图3对比了不同网格情况下V字形钝前缘壁面中心线上的无量纲热流分布, 并给出了激波风洞实验测得的热流, 其中, q₀为根据Fay-Riddell公式^[31]计算得到的相同来流条件下半径为r的圆柱驻点热流. 从图3可以看出, 采用第3套和第4套网格获得的壁面热流结果几乎重合, 并且都与激波风洞实验结果吻合良好, 表明本文采用的数值模拟方法能够满足热流计算的需求. 为兼顾计算效率, 本文采用第3套网格进行后续计算.




表
2
网格无关性验证中的4套网格



Table
2.
Four sets of grids used in the grid convergence study.



table_type1 ">

case	Nξ × Nη × Nζ	surface cell thickness/m	total mesh number
1	350 × 120 × 100	5 × 10?6	4.2 × 106
2	400 × 150 × 120	1 × 10?6	7.2 × 106
3	500 × 180 × 150	1 × 10?6	1.35 × 107
4	600 × 200 × 200	5 × 10?7	2.4 × 107

下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
壁面中心线热流对比



Figure
3.
Comparison of surface heat flux along the centerline



下载:
全尺寸图片
幻灯片

2.
结果与讨论

后掠直前缘形成的两道脱体激波在V字形根部区域发生激波干扰, 形成了复杂的流场结构. 由于来流和几何条件的对称性, y = 0对称面具有准二维特性, 能够反映V字形钝前缘的主要波系结构, 并且壁面热流最大值位于中心线上^[11,15,18]. 因此, 本文重点分析不同几何参数的y = 0对称面上的流动结构, 并定量比较壁面中心线上的热流分布.

图4给出了V字形钝前缘y = 0对称面上叠加压力等值线的马赫数云图和无量纲壁面热流q/q₀分布云图, 其中, 图4 (b)、图4 (f)和图4 (j)分别以β = 24°为例, 对比了不同R/r构型的实验纹影和马赫数云图. 可以看到, 数值模拟和激波风洞实验得到的激波干扰结构吻合良好, 进一步验证了本文数值模拟方法的可靠性. 如图4所示, 在R/r和β的共同作用下, 激波干扰类型发生了由RR向MR以及由MR向sRR的转变, 这些转变与Zhang等^[26]的理论预测结果相一致. 此外, 在R/r和β的共同作用下, 近壁面流动以及壁面热流分布也发生了变化.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
x-z对称面波系结构和壁面热流



Figure
4.
Flow features in the x-z symmetry plane and the wall heat flux



下载:
全尺寸图片
幻灯片


为了厘清几何参数对流场结构及壁面热流的影响, 下文首先以R/r =1, 3和6为例, 分析β变化对激波干扰流场和壁面热流的影响; 其次, 以β = 16°, 24°, 40°和56°为例, 分析R/r变化对激波干扰流场和壁面热流的影响; 接着, 定量比较不同构型壁面中心线上的热流分布, 阐明波系结构与气动热严酷程度之间的联系; 最后, 梳理本文及文献[11,15,18]中大量的壁面热流数据, 在几何参数空间(R/r, β)揭示V字形钝前缘气动热的变化规律.

2.1
扩张角 β 对流场及气动热的影响

图4 (a) ~ 图4 (d)给出了R/r = 1时, 对称面(y = 0)流场和壁面热流分布随着β增大的变化情况. 当β = 16°时(见图4 (a)), 上下两道脱体激波DS(detached shock)直接相交, 形成异侧激波规则反射RR. 在干扰点IP (intersection point)下游, 透射激波TS(transmitted shock)入射壁面. 穿过多道激波后的气流在驻点附近滞止, 压力急剧升高, 并在壁面造成了极其严酷的热流峰值, 本文称之为第一类中心热流峰值C₁. 在驻点两侧的边界层受到的逆压梯度增大, 出现较大的流动分离, 并产生分离激波SS (separation shock). 当β = 24°时(见图4 (b)), DS的角度随着β增大, 激波反射类型转变为MR. DS与马赫杆MS(Mach stem)干扰产生的透射激波TS以及剪切层, 入射到直前缘与倒圆区域相连接的壁面, 因发生激波/边界层干扰, 产生了局部热流峰值, 本文称之为外侧热流峰值O. 由于TS前后存在较大的逆压梯度, 导致出现小范围的流动分离, 并产生分离激波SS. SS与TS直接相交, 形成规则反射. 包裹在剪切层中的气流由两侧向中心汇聚, 并在驻点附近对撞后导致了局部热流峰值, 本文称之为第二类中心热流峰值C₂. 随着β增大至40°(见图4 (c)), DS的角度进一步增大, 而TS的强度随之减小, 壁面边界层受到的逆压梯度减弱, 使得分离区范围明显减小. 当β = 56°时(见图4 (d)), TS入射壁面的位置进一步向两侧偏离, 边界层受到的逆压梯度大幅减弱, 以至于没有出现明显的分离区. 总体来看, 在R/r = 1时, 随着β增大, 热流峰值的产生机制及其严酷部位发生了明显变化, 主要是由于V字形根部的激波干扰类型由RR转变为MR.

图4 (e) ~ 图4 (h)给出了R/r = 3时的对称面(y = 0)流场和壁面热流分布, 可以看出, 激波反射类型始终呈现为MR, 包裹在剪切层中的射流在驻点附近对撞产生逆流导致MS发生明显的拱起变形, 随着β增大变形程度减小. 此时, 尽管激波反射类型保持为MR, 但是随着β增大, 第二类中心热流峰值C₂和外侧热流峰值O都出现了不同程度的变化, 其原因主要来自于近壁面二次干扰流动的差异. 当β = 16°时(见图4 (e)), MS与DS干扰产生的TS入射到倒圆区域壁面上. 在TS入射位置上游, 由弯曲壁面产生的一系列压缩波CWs (compression waves)叠加形成了弯曲激波CS (compression shock). CS与TS发生二次马赫反射, 并形成马赫杆MS₂和透射激波TS₂. 当β = 24°时(见图4 (f)), 由于β增大, DS的脱体高度减小, 相应的MS₂缩短. 随着β增大至40°(见图4 (g)), TS入射位置上游的弯曲壁面区域进一步减小, 相应的CS强度减弱. TS与CS直接相交后, 形成二次规则反射. 当β = 56°时(见图4 (h)), TS入射在直前缘壁面上, 入射点上游不存在弯曲壁面, 故二次反射结构也随之消失.

R/r = 6时, 随着β增大, 图4 (i) ~ 图4 (l)给出了对称面(y = 0)流场和壁面热流分布的变化情况. 当β = 16°时(见图4 (i)), DS与来自同侧的CS直接相交, 激波反射类型转变为sRR, 原有的MS被内凹的弓形激波BS (bow shock)取代, 从干扰点位置发出膨胀波EWs (expansion waves)入射壁面, 外侧热流峰值明显降低. 当β = 24°时(见图4 (j)), 由于DS的脱体高度减小以及波后参数的变化, DS与CS相交位置以及BS形状有所变化. 随着β增大至40°(见图4 (k)), DS的波后马赫数进一步减小, 削弱了CWs的汇聚效应, 以至于CWs能够直接与来自同侧的DS相交, 使得DS弯曲成激波CDS (curved detached shock). CDS与BS干扰, 产生TS入射到壁面. 当β =56°时(见图4 (l)), CWs直接与DS以及TS相交. 在R/r = 6时, V字形根部的激波干扰类型都已转变为sRR, 相应地中心热流峰值和外侧热流峰值都处于较低的水平.

R/r = 1, 3和6时, V字形钝前缘根部流动特征的变化表明, 随着β增大, DS的激波强度逐渐增大, DS的波后马赫数减小, 同时DS距离直前缘的高度逐渐减小, 共同导致了激波干扰类型的转变以及近壁面流动结构的差异, 进而引起壁面热流峰值的变化.

2.2
半径比 R/r对流场及气动热的影响

图4 (a)、图4 (e)和图4 (i)给出了β =16°时对称面(y = 0)流场和壁面热流分布随着R/r增大的变化情况, 可以看出, 激波干扰类型发生了RR(见图4 (a))到MR(见图4 (e))再到sRR(见图4 (i))的转变. 由2.1节可知, 热流峰值部位及其产生机制也发生了明显改变.

图4 (b)、图4 (f)和图4 (j)给出了β = 24°时的对称面(y = 0)流场和壁面热流分布. 当R/r = 1时(见图4 (b)), 激波反射流场为MR, DS与MS干扰产生的TS入射到直前缘和倒圆区域的连接位置, 出现小范围的流动分离和SS. 当R/r = 3时(见图4 (f)), 激波反射流场仍为MR, 此时TS与CS发生二次马赫反射. 当R/r = 6时(见图4 (j)), 激波反射类型转变为sRR. β = 40°时流场随着R/r增大发生的变化(见图4 (c)、图4 (g)和图4 (k))和β = 24°时基本一致, 激波干扰类型都发生了MR向sRR的转变, 差异主要体现在R/r = 3时TS与CS干扰后不再产生二次马赫反射, 而是形成二次规则反射. β = 24°和β = 40°时壁面热流云图的变化表明, 随着R/r的增大, 第二类中心热流峰值C₂和外侧热流峰值O并非单调变化.

图4 (d)、图4 (h)和图4 (l)给出了β = 56°时对称面(y = 0)流场和壁面热流分布, 可以看出, 此时的β已经很大, 随着R/r增大, 尽管激波反射流场发生了MR向sRR的转变, 但TS的强度已经大幅减弱, 近壁面流动的变化不再明显, 对应的热流峰值也都处于较低的水平.

图4中β = 16° ~ 56°时, V字形钝前缘根部流动特征的变化表明, 随着R/r增大, V字形根部倒圆区域累积气流的缓冲空间也随之增大, 直接影响激波干扰类型, 同时也使TS入射壁面位置由直前缘转变至圆弧区域, 热流峰值的位置和严酷程度也随之改变.

2.3
壁面中心线热流分布

前文的流场分析已经表明, R/r和β共同决定了V字形钝前缘根部的激波干扰类型. 即使在相同的激波干扰类型下, 由于R/r和β的差异, 近壁面流动中TS, SS, CWs以及CS等波系结构复杂多变, 对应的壁面热流也发生了不同程度的变化. 为了进一步阐明波系结构与气动热严酷程度之间的联系, 图5给出了不同几何参数V字形钝前缘根部壁面中心线上的无量纲热流q/q₀分布. 考虑到流场结构的对称性, 仅对壁面中心线φ ≥ 0一侧的热流分布进行分析.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
壁面中心线上热流分布



Figure
5.
Heat flux along the centerline of leading edge



下载:
全尺寸图片
幻灯片


图5 (a)给出了R/r = 1时壁面中心线上q/q₀随着β的变化情况. 结合图4 (a) ~ 图4 (d)可以看出, 在β 较小时, 如β =16°, 激波干扰类型为RR, 由于沿来流方向的超声速气流冲击驻点附近壁面后滞止, 导致极其严酷的第一类中心热流峰值C₁, 对应的q/q₀ = 9.8. 当β = 24°, 40°和56°时, 激波干扰类型已转变为MR, 此时, 异侧射流在驻点附近撞击导致了第二类中心热流峰值C₂, 对应的q/q₀分别为5.7, 4.2和2.9; 另外, 位于两侧的TS入射壁面, 因发生激波/边界层干扰, 产生了外侧热流峰值O, 对应的q/q₀分别为4.6, 2.6和1.3.

图5 (b)给出了R/r = 3时壁面中心线上q/q₀分布随着β的变化情况. 结合图4 (e) ~ 图4 (h)可以看出, 从V字形根部倒圆区域和直前缘的切点位置开始, 由于CWs作用, 热流开始都逐渐上升. 直至TS入射壁面后发生激波/边界层干扰, 导致了外侧热流峰值. 当β =16°, 24°, 40°和56°时, 外侧热流峰值q/q₀分别为5.4, 6.2, 3.8和1.3. 相比R/r = 1构型, 此处的外侧热流峰值分布范围小且更剧烈. 异侧射流在驻点附近相互撞击, 导致产生第二类中心热流峰值, 对应的q/q₀分别达到3.3, 3.7, 3.2和2.7. 在第二类中心峰值和外侧热流峰值之间, 壁面的收缩使得超声速气流沿壁面向下游运动, 由于膨胀和压缩效应在近壁面超声速射流结构中交替出现, 相应的壁面热流出现较弱的内侧热流峰值.

图5 (c)给出了R/r = 6时壁面中心线上q/q₀随着β的变化情况. 结合图4 (i) ~ 图4 (l)可以看出, CS与DS发生sRR, 从干扰点位置发出EWs或较弱TS^[15], 当β =16°, 24°, 40°和56°时, 外侧热流峰值q/q₀分别为1.6, 1.7, 1.6和1.4, 都处于较低水平. 此外, 缓慢收缩的倒圆壁面给气流提供了更大的缓冲空间, 超声速气流往驻点汇聚需要经历更长的路径, 增加了超声速射流中CWs和EWs的反射次数. 因此, 外侧热流峰值到驻点之间出现了更多的内侧热流峰值, 并且幅度依次减弱. 最后, 强度较弱的异侧射流在驻点附近相互撞击, 产生的第二类中心热流峰值, 其q/q₀分别对应为1.7, 1.9, 1.8和1.3, 也都变得明显较小.

关于V字形钝前缘不同位置的热流峰值产生机制, 更详细的讨论可以参考文献[15,18]. 综合比较图5中各类峰值可以看出, 内侧热流峰值一般不会超过中心热流峰值和外侧热流峰值, 下文主要关注中心热流峰值和外侧热流峰值随几何参数的变化.

从不同几何参数的中心热流峰值可以看出, 当R/r和β都相对较小时, 激波反射类型为RR, 超声速气流冲击驻点附近壁面导致了最严酷的第一类中心热流峰值. 当激波反射类型由RR转变至MR或sRR后, 第二类中心热流峰值主要由异侧超声速射流在驻点附近对撞导致, 峰值的大小与射流强度有关. R/r或β越大, 射流在对撞之前沿着壁面经过的路径越长, 强度衰减的越明显, 对应热流峰值降低越明显.

从不同几何参数的外侧热流峰值可以看出, 激波反射类型为MR或sRR时, 才会出现此类峰值. 外侧热流峰值主要来自于激波/边界层干扰或膨胀波/边界层干扰, 热流峰值的大小取决于干扰位置的局部流动. 随着β的增大, DS和MS干扰产生的TS强度减弱, 使得外侧热流峰值随之减小. 随着R/r的增大, TS分别与壁面附近的SS和CS干扰产生不同的二次激波反射类型, 近壁面流动出现复杂的变化, 外侧热流峰值总体呈现先增大后明显减小的趋势.

上述分析表明, 不同位置热流峰值的产生机制并不一致, 而几何参数变化直接影响热流最大值的大小和位置.

2.4
热流随几何参数变化

为了全面揭示V字形钝前缘气动热随几何参数变化规律, 后掠直前缘以及V字形根部壁面中心线上的热流变化均应当考虑. 在本文情况下, 后掠直前缘的热流q_L主要受β影响, 可以根据文献[32]提出的后掠圆柱热流经验公式进行预测, 如式(1)所示

$$ left. begin{array}{l} {q_L} = 1.29 times {10^{ - 4}} times V_infty ^3left( {1 - dfrac{{{h_w}}}{{{h_{aw,{text{c}}}}}}} ight){left( {dfrac{{{ ho _infty }}}{r}} ight)^{0.5}} times qquad sin beta ( {1 - 0.18{{cos }^2}beta } ) {h_{aw,c}} = {h_infty } + 0.5V_infty ^2left( {1 - 0.18{{cos }^2}beta } ight)end{array} ight} $$

(1)

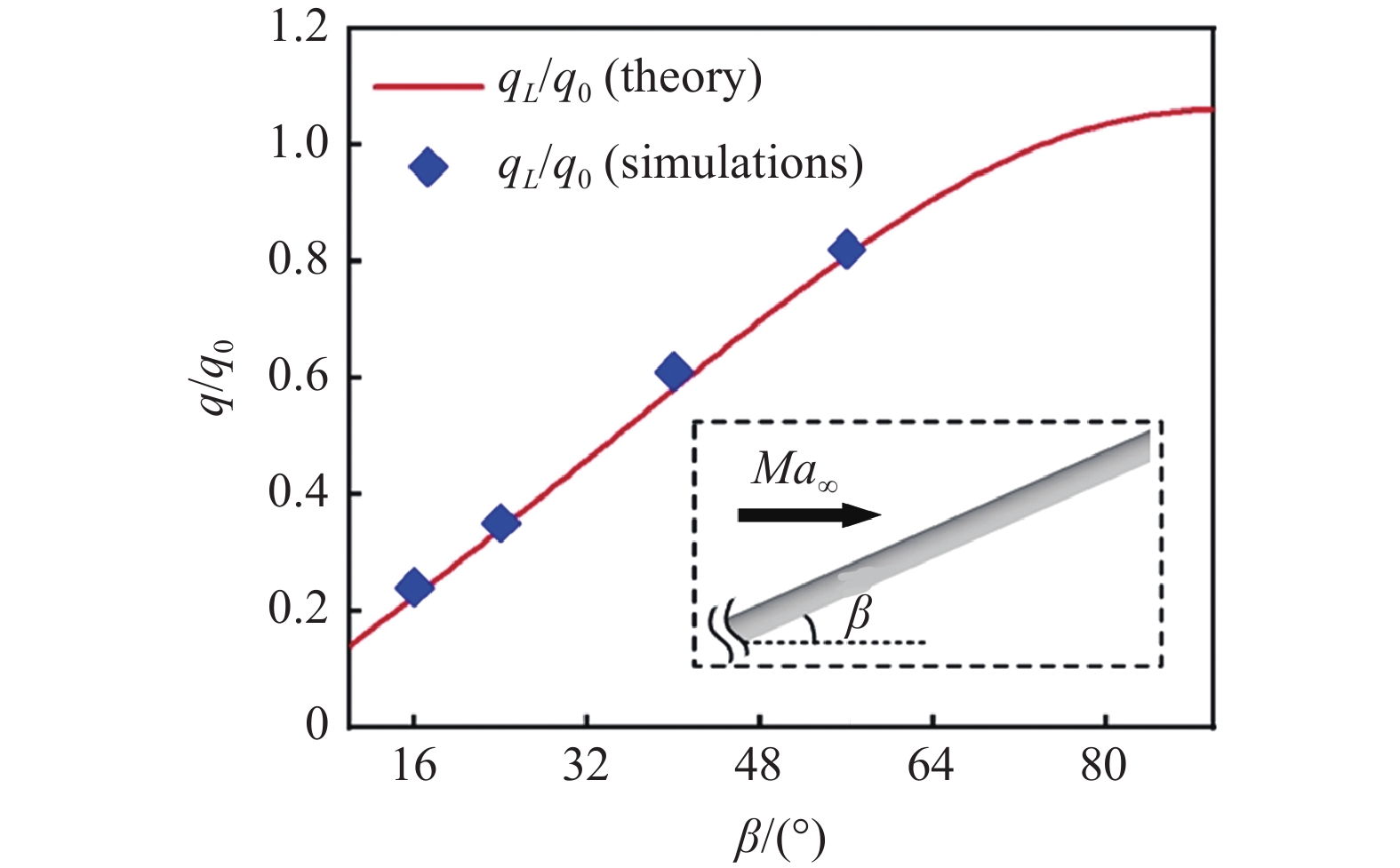
式中, V_∞, ρ_∞, h_∞分别表示来流速度, 来流密度及来流焓值, h_w表示壁面焓值, h_aw,c为中间量. 本文数值模拟得到的后掠直前缘热流与式(1)的对比情况, 如图6所示, 可以看到, 两者吻合良好. 随着β的增大, 后掠直前缘上的热流逐渐增大并最终趋近于q₀. 虽然后掠直前缘上的热流相对较小, 但是由于后掠直前缘暴露在高超声速来流下的面积相对较大, 其气动热防护仍不可忽视.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
后掠直前缘壁面热流



Figure
6.
Heat flux on centerline of the swept leading edge



下载:
全尺寸图片
幻灯片


V字形根部虽然范围相对较小, 但是局部热流极高, 最容易导致烧蚀破坏, 掌握其热流最大值随几何参数的变化规律对于指导热防护设计尤为重要. 图7给出了Ma_∞ = 6 条件下, V字形根部热流最大值q_max/q₀在几何参数空间(R/r, β)分布, 数据点来自于本文以及文献[11,15,18]不同几何参数构型的数值模拟, 符号形状代表热流峰值类型, 颜色代表热流严酷程度. 其中, 图7 (a)采用三维图直观展示了热流最大值随几何参数的变化情况, 图7 (b)给出了图7 (a)在(R/r, β)空间投影后的二维图. 此外, 为便于揭示规律, 图7 (b)还根据Zhang等^[26]提出的V字形钝前缘根部激波干扰类型转变理论, 给出了Ma_∞ = 6时不同R/r和β组合下, RR向MR以及MR向sRR转变的几何边界, 如图7 (b)中的虚线f_RR-MR和点划线f_MR-sRR所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-448-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
Ma_∞ = 6不同几何参数(R/r, β)热流最大值分布



Figure
7.
Domains of the maximum heat flux in the (R/r, β) plane at Ma_∞ = 6



下载:
全尺寸图片
幻灯片


当激波反射类型为RR时, 第一类中心热流峰值为热流最大值, 其中, 几何参数为R/r = 1, β = 20°构型^[15]对应的q_max/q₀能达到12, 远高于其他激波反射类型时的热流最大值. 当激波反射类型为MR时, 随几何参数变化, 热流最大值的变化最明显. 2.3节中的分析已经表明, R/r和β分别对射流强弱及近壁面干扰特征产生不同程度的影响, 导致第二类中心热流峰值和外侧热流峰值呈现不同的变化趋势. 从图7 (b)可以看出, 此时, 热流最大值的位置, 在第二类中心热流峰值和外侧热流峰值之间转变. 当激波反射类型为sRR时, 此时R/r和β都相对较大, 外侧热流峰值和中心热流峰值都已减小至较低水平, 热流最大值位置并不固定.

进一步地, 在几何空间(R/r, β)的MR区域, 根据图7 (b)中热流最大值在第二类中心热流峰值和外侧热流峰值之间的转变位置, 可以大致获得其转变边界如下

$$ R/r = 18beta /{text{π}} - 1.6 $$

(2)

式中, β采用弧度制. 如图7 (b)中的红色虚线所示, 当R/r < (18β/π?1.6)时, 相对较大的β使得TS强度减弱, 导致激波/边界层干扰所带来的外侧热流峰值大幅降低. 此时, 热流最大值为位于驻点附近的第二类中心热流峰值. 当R/r > (18β/π?1.6)时, 相对较大的R/r, 更容易使异侧射流在向驻点汇聚过程中强度减弱, 导致驻点附近由射流相互撞击所带来的热流峰值大幅降低. 此时, 热流最大值为外侧热流峰值.

总体来看, R/r和β之间存在关联, 共同决定了热流最大值的大小和位置. 随着R/r的增大, 热流最大值总体呈现先增大、后减小、最后趋于平稳的趋势, β越大这种趋势的变化幅度越小. 随着β的增大, 热流最大值呈现减小的趋势, R/r越大这种趋势的变化幅度越小. 当R/r ≥ 6或β ≥ 56°时, 热流最大值都几乎减小至q₀水平. 这些结果, 可以为内转式进气道V字形唇口气动热预测和防护设计提供有价值的参考.

3.
结 论

本文采用数值模拟并辅以风洞实验的方法, 在Ma_∞ = 6条件下, 研究了V字形钝前缘在几何参数空间(R/r, β)中的气动热变化规律, 主要得到以下结论.

(1) R/r和β共同决定了V字形钝前缘根部可以出现RR, MR和sRR 3种激波干扰类型, 并使得热流最大值在几何参数空间(R/r, β)中变化显著. 随着R/r的增大, 热流最大值总体呈现先增大、后减小、最后趋于平稳的趋势; 随着β的增大, 热流最大值总体呈现减小趋势. 当R/r ≥ 6或β ≥ 56°时, 热流最大值都几乎减小至q₀水平.

(2)热流峰值的产生机制、严酷部位和严酷程度随激波干扰类型的变化而明显不同. 当发生RR时, 超声速气流冲击驻点附近并导致最高可达12q₀的第一类中心热流峰值. 当发生MR时, 异侧超声速射流对撞和激波/边界层干扰分别导致第二类中心热流峰值和外侧热流峰值, 其严酷程度都仅次于第一类中心热流峰值. 当发生sRR时, 第二类中心热流峰值和外侧热流峰值都明显减小.

(3)在几何空间(R/r, β)中发生MR的区域, 第二类中心热流峰值和外侧热流峰值的强弱关系存在转变边界: 若R/r < (18β/π?1.6), 热流最大值位于驻点附近的第二类中心热流峰值; 若R/r > (18β/π?1.6), 热流最大值为外侧热流峰值.

鉴于V字形钝前缘流动的复杂性, 未来需要将激波干扰类型的转变理论及气动热特性研究拓展到宽马赫数范围.

致 谢

感谢中国科学院力学研究所韩桂来副研究员在气动热测量方面提供的帮助.