删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于子结构解耦的连接特性识别新方法

本站小编 Free考研考试/2022-01-01


引 言


机械结构中广泛存在着各种连接形式, 如螺栓连接、铆接、焊接以及胶接等. 连接结构的动力学特性决定着装配体的动响应预测精度, 因此准确地对其进行辨识显得尤为重要. 而由于连接结构的多样性和复杂性[1-3], 难以建立其一般的解析模型[4], 因此常基于子结构解耦技术并利用模态或频响函数等测试数据对连接特性进行辨识. 该技术从装配体和残余结构的动力学行为中提取连接结构的动态特性[5], 其中基于模态试验数据的方法中振型的测试误差极易导致识别结果不理想[6], 因此更适于有限元环境下应用; 而基于频响函数试验数据的方法则由于测试简单、数据信息充足且精度较高, 得到广泛关注与研究[7-12].

Okubo和Miyazaki[13]最早将基于频响函数的子结构解耦技术应用于连接特性识别, 经过不断地发展与改善, 许多方法被提出, 并在一些实际结构中得到了应用[14-17]. 虽然形式不尽相同, 但几乎所有方法的辨识公式都与Ren和Beards[18]提出的基本公式相似或等价[19], 其思路均为利用实测的装配体频响函数与实测或有限元模型计算的残余结构频响函数来获取连接特性. 连接特性识别所面临的主要难题之一是装配体结构界面自由度频响函数的测量[19]. 对此, ?eli?等[4-5]在Ren等所提基本公式上进行了改进, 详细讨论了忽略部分界面自由度及内部自由度对辨识结果的影响, 并对比了逐频求逆的直接法与对各个频率点进行平均的最小二乘法, 然而其在忽略部分界面自由度时的辨识结果不佳. 此外, 采用旋转自由度的测试技术[16]及未测频响函数估计技术[19-20]是解决该问题的可行方案, 但却增加了测试或计算的成本, 且额外地引入了测试误差或估计误差. 连接特性识别的另一难题是辨识方程对测试噪声的高度敏感性, 即测试数据微小的误差也可能导致结果与真实特性完全无关, 且不同形式的求解方程在辨识精度上有着较大差异[18], 这是由过多的矩阵求逆以及系统方程本身的严重病态造成的. 对含噪数据进行降噪是减小噪声干扰最直接的方法, Peeters等[7]采用模态模型对测试频响函数进行滤波并应用于子结构解耦, 尽管测试噪声得以滤除, 但滤波后的频响函数对真实值的拟合程度仍难以控制. 替代降噪技术的有Zhang等[21-22]提出的一种噪声自校准参数辨识方法, 以谐波基对噪声校准量参数化并与系统参数通过误差函数共同进行估计, 有效提高了参数辨识的准确性. 在优化辨识公式的形式方面, Wang等[23]减少了对噪声有放大作用的矩阵求逆运算, 使得方法对实测数据的适用性增强, 但由于公式中的简化使得在高频时辨识效果不佳. Wang等[19,24]根据基本公式推导了统一形式的辨识方程, 并利用该方程将实测与估算的未测频响函数一起引入辨识过程抑制噪声, 提高了识别结果的准确性, 然而由于采用了逐频求逆的直接法, 在由动刚度矩阵序列估计连接结构物理参数的过程中将产生偏差.

为此, 本文在子结构解耦基本方程基础上, 提取其测试自由度分量并推导了显含连接动刚度矩阵的辨识方程, 该方程直接利用可测的装配体频响函数进行辨识, 而无需针对其界面自由度信息进行未测频响函数的估计或旋转自由度及部分不可测界面自由度的测量. 而后将该方程写为增量格式, 得到了连接特性识别的迭代形式, 其残差相对全量格式显著减小, 因而数值稳定性更好[25], 且通过迭代可使得由连接动刚度与残余结构频响函数重构的装配体频响函数拟合值不断逼近于测量值. 最后, 将动刚度曲线以多项式进行拟合, 得到了拟合系数的估计方程, 并筛选合适的频率点联立方程组求解, 减少了病态矩阵的求逆运算且改善了抗噪性. 弹簧质量系统数值算例和双梁连接结构试验表明该方法辨识效果较好, 能有效地对实际连接特性进行识别.


1.
理论背景



1.1
连接结构动力学特性识别方程


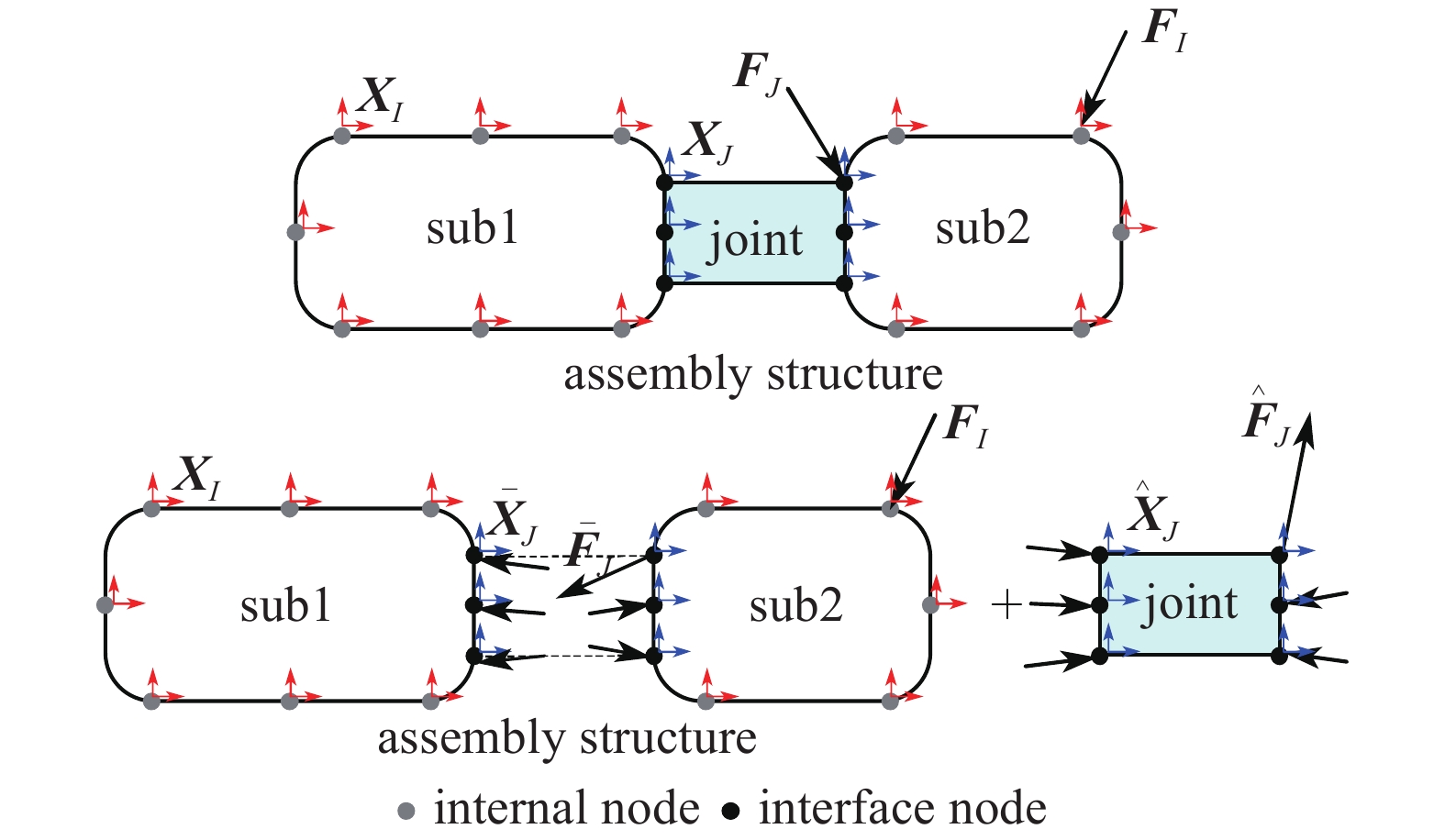
连接结构、残余结构及其组成的装配体结构如图1所示, 令I代表残余结构或装配体结构部分内部节点的自由度, J代表残余结构或连接结构全部界面节点的自由度, A和R分别代表装配体结构和残余结构, 则有输入?输出关系



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
连接结构, 残余结构与装配体结构



Figure
1.
Joint, residual and assembly structure



下载:
全尺寸图片
幻灯片








$$ {boldsymbol{H}}_{
m{A}}^{}{boldsymbol{F}}{text{ = }}{boldsymbol{X}},;;;left[ {begin{array}{*{20}{c}} {{boldsymbol{H}}_{
m{A}}^{{
m{II}}}}&{{boldsymbol{H}}_{
m{A}}^{{
m{IJ}}}} {{boldsymbol{H}}_{
m{A}}^{{
m{JI}}}}&{{boldsymbol{H}}_{
m{A}}^{{
m{JJ}}}} end{array}}
ight]left[ {begin{array}{*{20}{c}} {{boldsymbol{F}}_{
m{I}}^{}} {{boldsymbol{F}}_{
m{J}}^{}} end{array}}
ight] = left[ {begin{array}{*{20}{c}} {{boldsymbol{X}}_{
m{I}}^{}} {{boldsymbol{X}}_{
m{J}}^{}} end{array}}
ight] $$
(1)







$${{bf{H}}_{
m{R}}}{bf{bar F}}{
m{ = }}{bf{bar X}},;;;left[ {begin{array}{*{20}{c}}{{bf{H}}_{
m{R}}^{{
m{II}}}}&{{bf{H}}_{
m{R}}^{{
m{IJ}}}}{{bf{H}}_{
m{R}}^{{
m{JI}}}}&{{bf{H}}_{
m{R}}^{{
m{JJ}}}}end{array}}
ight]left[ {begin{array}{*{20}{c}}{{{bf{F}}_{
m{I}}}}{{{{bf{bar F}}}_{
m{J}}}}end{array}}
ight] = left[ {begin{array}{*{20}{c}}{{{bf{X}}_{
m{I}}}}{{{{bf{bar X}}}_{
m{J}}}}end{array}}
ight]$$
(2)







$$ {boldsymbol{H}}_{
m{J}}^{}{{hat {boldsymbol{F}}}}_{
m{J}}^{}{
m{ = }}{{hat {boldsymbol{X}}}}_{
m{J}}^{}$$
(3)

其中XI, XJ与FI, FJ分别为装配体结构在内部自由度上、界面自由度上的位移矢量与的力矢量, 而X与F为由其组合而成的位移矢量与力矢量, 顶标?与^则分别代表残余子结构与连接结构的相应物理量. HA, HR和HJ分别为装配体结构、残余结构和连接结构的频响函数矩阵.

由界面自由度上位移与力的协调关系有







$$ {boldsymbol{X}}_{
m{J}}{
m{ = }}{{bar {boldsymbol{X}}}}_{
m{J}} {
m{ = }}{hat{boldsymbol X}}_{
m{J}},{boldsymbol{F}}_{
m{J}} {
m{ = }}{{bar {boldsymbol{F}}}}_{
m{J}}{
m{ + }}{hat{boldsymbol F}}_{
m{J}}$$
(4)

可得基于子结构解耦识别连接特性的基本公式[19]







$$ {boldsymbol{H}}_{
m{A}}^{}{text{ = }}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{{
m{R,J}}}^{}{boldsymbol{H}}{_{
m{C}}^{ - 1}}{boldsymbol{P}}_{{
m{R}},{
m{J}}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{} $$
(5)







$$ {boldsymbol{H}}_{
m{C}}^{} = {boldsymbol{H}}_{
m{J}}^{} + {boldsymbol{P}}_{{
m{R,J}}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{{
m{R,J}}}^{} $$
(6)

其中PR,J为筛选HR中界面自由度所在列的布尔矩阵, 即PR,JTHR=[HRJI HRJJ]

连接结构动力学特性识别问题一般忽略连接结构的内部自由度(需满足连接件内部自由度上无外力的假设), 且由XJ所指为完备界面自由度知







$$ {boldsymbol{H}}_{
m{J}}= {boldsymbol{D}}_{
m{J}}^{ - 1} $$
(7)

设实际对装配体结构进行振动测试的自由度上位移矢量为X*, 且X*=P*TX, 其中P*亦为布尔矩阵. 取P*T左乘式(5)得







$$ {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}{text{ = }}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}{boldsymbol{H}}{_{
m{C}}^{ - 1}}{boldsymbol{P}}_{
m {R,J}}^{
m{T}}{boldsymbol{H}}_{
m {R}}^{} $$
(8)

式(8)经移项后左乘广义逆(P*THRPR,J) + 得






$$ {boldsymbol{H}}{_{
m{C}}^{ - 1}}{boldsymbol{P}}_{
m {R,J}}^{
m{T}}{boldsymbol{H}}_{
m {R}}^{}{text{ = (}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}{{text{)}}^ + }{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) $$

注意此处求取广义逆必须满足行大于列的条件, 即要求测试自由度的数目应大于界面自由度数目. 上式两端左乘HC并将式(6)和式(7)代入得






$$ begin{gathered} {boldsymbol{P}}_{
m {R,J}}^{
m{T}}{boldsymbol{H}}_{
m {R}}^{}{text{ = }}({boldsymbol{D}}_{
m{J}}^{ - 1} + {boldsymbol{P}}_{
m {R,J}}^{
m{T}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}){{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}{text{)}}^ + }{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{} - hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) hfill end{gathered} $$

移项并在等式两端左乘DJ得






$$ begin{gathered} {boldsymbol{D}}_{
m{J}}^{}left( {{boldsymbol{P}}_{
m {R,J}}^{
m{T}}{boldsymbol{H}}_{
m {R}}^{} - ({boldsymbol{P}}_{
m {R,J}}^{
m{T}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}){{{text{(}}{boldsymbol{P}}{{_{}^{*{
m{T}}}}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}{text{)}}} }^+{text{(}}{boldsymbol{P}}{{_{}^{*{
m{T}}}}}{boldsymbol{H}}_{
m {R}}^{} - }
ight. hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} left. {{boldsymbol{P}}{{_{}^{*{
m{T}}}}}{boldsymbol{H}}_{
m{A}}^{})}
ight){text{ = (}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{}{boldsymbol{P}}_{
m {R,J}}^{}{{text{)}} ^{+} }{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m {R}}^{} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) hfill end{gathered} $$

而由AX=B的极小二乘解为X=(A)+B知上式等价于







$$ begin{gathered} {text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{text{)}}{boldsymbol{D}}_{
m{J}}^{}left( {{boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{} - ({boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{})} cdot
ight. hfill left.( {{boldsymbol{P}}{{_{}^{
m{*T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{{text{)}}^ + }{text{(}}{boldsymbol{P}}{{_{}^{
m{*T}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{P}}{{_{}^{
m{*T}}}}{boldsymbol{H}}_{
m{A}}^{})}
ight){text{ = }}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{} hfill end{gathered} $$
(9)

将式(9)记为







$$ {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}{text{ = }}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* $$
(10)

式(10)与式(8)形式一致, 其中左、右等效频响为







$$ left.begin{gathered} {boldsymbol{H}}_{{
m{El}}}^{*} = {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} hfill {boldsymbol{H}}_{
m{Er}}^{*} = {boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{} - ({boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}){{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{text{)}}^ + }{text{}} cdot hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} ({boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) end{gathered}
ight} $$
(11)

式(10)即为显含连接动刚度DJ的辨识方程, 是后文推导增量格式以及引入多项式拟合的基础. 其中HR通过校准的残余子结构有限元模型计算得到, 因此对式(10)两端右乘装配体结构振动测试的激励自由度布尔矩阵PI后, 辨识过程所需测试数据仅为装配体在所选测试自由度上的频响函数P*THAPI, 而无需测量或估计其界面自由度的量. 且式(10)由式(5)提取测试自由度上的平衡方程后经矩阵变换得到, 界面协调条件仍成立, 因此仍是精确的. 此外, 所选测试自由度能准确辨识DJ的必要条件为拥有足够多有效信息.


1.2
识别方程增量形式


连接结构界面自由度数目较多时, 由于待求未知量的数目增加而使得辨识精度明显下降, 且噪声对辨识结果的扰动显著增强. 为提高方程数值稳定性并通过迭代逼近最佳辨识值, 将式(10)变换为增量形式. 若给定连接结构动刚度初值DJ0, 欲识别其真实值DJ, 由式(10)分别有







$$ left. begin{gathered} {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}{text{ = }}{boldsymbol{P}}^{{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* hfill {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^0{text{ = }}{boldsymbol{P}}^{{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^0{boldsymbol{H}}{_{{
m{Er}}}^{*}0} hfill end{gathered} ;;;
ight} $$
(12)

其中HA, ${boldsymbol{hat H}}_{
m{A}}^0 $分别为DJ, ${boldsymbol{D}}_{
m{J}}^0 $与HR所重构的装配体结构频响函数真实值与初始拟合值. 两式相减得







$$ {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{text{0}}{text{ = }} - {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* + {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^0{boldsymbol{H}}{_{{
m{Er}}}^{*0}} $$
(13)

设DJ=${boldsymbol{D}}_{
m{J}}^0 $ + ΔDJ, 代入式(13)得







$$ {boldsymbol{P}}{_{}^{
m{*T}}}{boldsymbol{H}}_{
m{A}}^{} - {boldsymbol{P}}{_{}^{
m{*T}}}{boldsymbol{hat H}}_{
m{A}}^{text{0}}{text{ = }}{boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^0({boldsymbol{H}}{_{{
m{Er}}}^{*0}} - {boldsymbol{H}}_{{
m{Er}}}^*) - {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{Delta D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* $$
(14)

又由式(11)知右等效频响函数的差量为






$$ begin{gathered} {boldsymbol{H}}{_{{
m{Er}}}^{*0}} - {boldsymbol{H}}_{{
m{Er}}}^* = ({boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}){{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{text{)}}^ + }{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{text{0}} - hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) hfill end{gathered} $$

将其代入式(14)可得






$$ begin{gathered} {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{Delta D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* = left( {{boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^0({boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}){{{text{(}}{boldsymbol{P}}{{_{}^{*{
m{T}}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{text{)}}}^ + } + }
ight. hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} left. {boldsymbol{I}}
ight){text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{text{0}} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) hfill end{gathered} $$

其中I为单位矩阵, 将上式记为







$$ {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{Delta D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* = {boldsymbol{T}}{_{
m{E}}^{*0}}{text{(}}{boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{text{0}} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}) $$
(15)

其中转换矩阵${boldsymbol{T}}{_{
m{E}}^{*0}} $为







$$ {boldsymbol{T}}{_{
m{E}}^{*0}} = {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^0({boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}){{text{(}}{boldsymbol{P}}{_{}^{{
m{*T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{text{)}}^ + } + {boldsymbol{I}} $$
(16)

式(15)两端左乘(${boldsymbol{T}}{_{
m{E}}^{*0}} $)?1得辨识方程(10)的增量形式







$$ {({boldsymbol{T}}{_{
m{E}}^{*0}})^{ - 1}}{boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{Delta D}}_{
m{J}}^{}{boldsymbol{H}}_{{
m{Er}}}^* = {boldsymbol{P}}{_{}^{{
m{*T}}}}{boldsymbol{hat H}}_{
m{A}}^{text{0}} - {boldsymbol{P}}{_{}^{{
m{*T}}}}{boldsymbol{H}}_{
m{A}}^{} $$
(17)

因此, 由式(5), 式(16)和式(17)可得识别连接特性的迭代方程







$$ {({boldsymbol{T}}{_{
m{E}}^{*(g)}})^{ - 1}}{boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{Delta D}}_{
m{J}}^{(g)}{boldsymbol{H}}_{{
m{Er}}}^* = {boldsymbol{P}}{_{}^{{
m{*T}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)} - {boldsymbol{P}}{_{}^{{
m{*T}}}}{boldsymbol{H}}_{
m{A}}^{} $$
(18)

其中各迭代量为







$$ left. begin{gathered} {boldsymbol{P}}{_{}^{{*{
m{T}}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)} = {boldsymbol{P}}{_{}^{{*{
m{T}}}}}{boldsymbol{H}}_{
m{R}}^{} - {boldsymbol{P}}{_{}^{{*{
m{T}}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}Big( {{{({boldsymbol{D}}_{
m{J}}^{(g)})}^{ - 1}} + } Big. hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {Big. {{kern 1pt} {kern 1pt} {kern 1pt} {boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}} Big)^{ - 1}}{boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{} hfill {boldsymbol{T}}{_{
m{E}}^{*(g)}} = {boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{D}}_{
m{J}}^{(g)}({boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}){{text{(}}{boldsymbol{P}}{_{}^{{*{
m{T}}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}{text{)}}^ + } + {boldsymbol{I}} hfill end{gathered}
ight} $$
(19)

式(18)和式(19)右乘PI后, 给定有限元模型计算数据HR、装配体测试数据P*THAPI与初值${boldsymbol{D}}_{
m{J}}^0$后, 即可由${boldsymbol{D}}_{
m{J}}^{left( {g + 1}
ight)} = {boldsymbol{D}}_{
m{J}}^{left( g
ight)} + Delta {boldsymbol{D}}_{
m{J}}^{left( g
ight)}$迭代更新连接结构动刚度.

全量形式的辨识公式(10)以残余结构与装配体频响函数的残差为极小化目标函数, 增量式(18)则以范数远小于前者的装配体频响函数测试值与初始拟合值的残差为目标函数, 参数识别的数值稳定性得到提高[25], 且减小了噪声对辨识结果的干扰.


1.3
动刚度曲线多项式拟合


若采用直接法[5]逐个频率点依次求解式(18), 对含噪声矩阵HEl*, HEr*(且在界面自由度较多时常因测试自由度信息不足而呈现病态)求逆后将使误差放大. 且连接结构对装配体结构动力学特性的影响在部分频率点几乎可以忽略, 使相应频率点的辨识结果对噪声极为敏感[16]. 为此, 以多项式函数拟合动刚度曲线, 代入式(18)得到关于拟合系数的方程, 并选择合适的频率点联立求解, 则原问题转化为频域内极小化残差函数的参数估计问题.

连接结构动刚度矩阵第m行第n列(m, n=1, 2, ···, NJ, NJ为界面自由度数目)对应元素DJmn(ωk)可用多项式函数表示为(1 + iωkβ)α0mn?ωk2α2mn, 其中β为刚度比例阻尼系数, ωk为第k个频率点, 而拟合系数α0mn, α2mn实际上为连接结构刚度矩阵、质量矩阵的对应分量, 则DJ的增量可写为







$$ {boldsymbol{Delta D}}_{
m{J}}^{}({omega _k}) = (1 + {
m{i}}{omega _k}beta ){boldsymbol{Delta U}}_0^{} - {omega _k}^2{boldsymbol{Delta U}}_2^{} $$
(20)

取ej为振动测试时筛选位移矢量X中第j个激励自由度所在行的位置向量, 在式(18)两端右乘ej得







$$ {({boldsymbol{T}}{_{
m{E}}^*{(g)}})^{ - 1}}{boldsymbol{H}}_{{
m{El}}}^*{boldsymbol{Delta D}}_{
m{J}}^{(g)}{boldsymbol{H}}_{{
m{Er}}}^*{{boldsymbol{e}}_{{j}}} = {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)}{{boldsymbol{e}}_{{j}}} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}{{boldsymbol{e}}_{{j}}} $$
(21)

将式(20)代入(21)得






$$ begin{gathered} {({boldsymbol{T}}{_{
m{E}}^*{(g)}})^{ - 1}}{boldsymbol{H}}_{{
m{El}}}^*left[ {begin{array}{*{20}{c}} {(1 + {
m{i}}{omega _k}beta ){boldsymbol{I}}}&{ - {omega _k}^2{boldsymbol{I}}} end{array}}
ight]left[ {begin{array}{*{20}{c}} {{boldsymbol{Delta U}}_0^{(g)}} {{boldsymbol{Delta U}}_2^{(g)}} end{array}}
ight]{boldsymbol{H}}_{{
m{Er}}}^*{{boldsymbol{e}}_j}{text{ = }} hfill qquad {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)}{{boldsymbol{e}}_j} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}{{boldsymbol{e}}_j} end{gathered} $$

对上式两端进行矩阵的列拉直得







$$ {{boldsymbol{S}}_j}^{(g)}({omega _k}){{boldsymbol{gamma }}^{(g)}} = {{boldsymbol{f}}_j}^{(g)}({omega _k}) $$
(22)

其中






$$ begin{split} &{boldsymbol{S}}_j^{(g)} = ({boldsymbol{e}}_j^{
m{T}}{boldsymbol{H}}_{{
m{Er}}}^{{
m{*T}}}) otimes left({({boldsymbol{T}}_{
m{E}}^{*(g)})^{ - 1}}{boldsymbol{H}}_{{
m{El}}}^*left[ {(1 + {
m{i}}{omega _k}beta ){boldsymbol{I}}};;{ - {omega _k}^2{boldsymbol{I}}}
ight]
ight) &{{boldsymbol{f}}_j}^{(g)} = {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)}{{boldsymbol{e}}_j} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{A}}^{}{{boldsymbol{e}}_j}end{split} $$






$$ {{boldsymbol{gamma }}^{(g)}} = Vleft( {left[ {begin{array}{*{20}{c}} {{boldsymbol{Delta U}}_0^{(g)}}&{{boldsymbol{Delta U}}_2^{(g)}} end{array}}
ight]}
ight) $$

式中$ V( cdot ) $表示矩阵的列拉直, fj(g)即为第g个迭代步的残差向量, 而Sj(g)为残差fj(g)关于拟合系数的灵敏度矩阵, γ (g)则为拟合系数增量.

式(22)对应于频率点ωk以及第j个激励自由度, 对k (k=1, 2,···,Nf, Nf为频率点数目)及j (j=1, 2,···, NI, NI为激励自由度数目)组合可得频域上多输入多输出的参数估计方程组f (g)=S(g)γ(g). 当所联立的频率点及激励自由度包含足够多系统有效信息时, 可有效减小待估计参数较多(即连接结构界面自由度较多)时灵敏度矩阵Sj(g)的病态程度, 且通过联合全频域上所有测点与激励点的信息可提高辨识的准确性.

方法迭代收敛性的证明[21]过程为, 若所选测试自由度集、激励自由度集、频率点集使得形成的S(g)满秩, 记α(g)=$ V $([U0(g) U2(g)]), 且







$$ {boldsymbol{alpha }}^{(g + 1)} = {boldsymbol{alpha }}^{(g)} + {left( {{boldsymbol{S}}{{^{{{(g)}}{
m{T}}}}}{boldsymbol{S}}^{(g)}}
ight)^{ - 1}}{boldsymbol{S}}{^{{(g)}{
m{T}}}}{boldsymbol{f}}^{(g)} $$
(23)

αT为真实拟合系数时, 相应残差f(αT)为0, 即αT是迭代方程(23)的不动点. 而






$$ begin{gathered} left| {{boldsymbol{alpha }}_{}^{(g + 1)} - {boldsymbol{alpha }}_{
m{T}}^{}}
ight| = left| {{boldsymbol{alpha }}_{}^{(g)} + {{left( {{boldsymbol{S}}{{_{}^{{(g)}{
m{T}}}}}{boldsymbol{S}}_{}^{(g)}}
ight)}^{ - 1}}{boldsymbol{S}}{{_{}^{{(g)}{
m{T}}}}}{boldsymbol{f}}_{}^{(g)} - {boldsymbol{alpha }}_{
m{T}}^{}}
ight|= hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} left| {{{left( {{boldsymbol{S}}{{_{}^{{(g)}{
m{T}}}}}{boldsymbol{S}}_{}^{(g)}}
ight)}^{ - 1}}{boldsymbol{S}}{{_{}^{{(g)}{
m{T}}}}}left( {{boldsymbol{f}}_{}^{(g)} + {boldsymbol{S}}_{}^{(g)}left( {{boldsymbol{alpha }}_{}^{(g)} - {boldsymbol{alpha }}_{
m{T}}^{}}
ight)}
ight)}
ight| hfill end{gathered} $$

且由S(g)满秩即S(g)TS(g)可逆及有界性知存在常数M1, M2使得






$$ begin{gathered} left| {{{left( {{boldsymbol{S}}{{_{}^{{(g)}{
m{T}}}}}{boldsymbol{S}}_{}^{(g)}}
ight)}^{ - 1}}}
ight| leqslant {M_1},left| {{boldsymbol{S}}{{_{}^{{(g)}{
m{T}}}}}left[ {{boldsymbol{f}}_{}^{(g)} + {boldsymbol{S}}_{}^{(g)}left( {{boldsymbol{alpha }}_{}^{(g)} - }
ight.}
ight.}
ight. hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} left. {left. {left. {{boldsymbol{alpha }}_{
m{T}}^{}}
ight)}
ight]}
ight| leqslant {M_2}{left| {{boldsymbol{alpha }}_{}^{(g)} - {boldsymbol{alpha }}_{
m{T}}^{}}
ight|^2} hfill end{gathered} $$

故||α(g + 1)?αT||≤M1M2||α(g)?αT||2=d(g)||α(g)?αT||, 当任意α(g)满足||α(g)?αT||<1/M1M2时, 有d(g)<1, 迭代方程(23)为压缩映射, α(g)将收敛至不动点αT. 由此表明给定了合适的连接特性初值后, 方法将收敛于真实值.


1.4
算法实现



1.4.1
方程归一化及频率点的选择

式(22)中系数矩阵Sj的各列之间存在显著的幅值差异, 导致其条件数较大, 因此按式(24)(25)对其各列进行归一化







$$ {{boldsymbol{f}}_j}^{(g)}({omega _k}) = {{boldsymbol{hat S}}_j}^{(g)}({omega _k}){{boldsymbol{hat gamma }}^{(g)}} $$
(24)







$$ left. begin{array}{l}[{{{{hat {boldsymbol{S}}}}}_j}^{(g)}]{;_{_{,r}}} = dfrac{{
m{1}}}{{{sigma _r}}}[{{boldsymbol{S}}_j}{^{(g)}]_{,r}},[{{{bf{hat gamma }}}^{(g)}}]{;_{r,}} = {sigma _r}[{{bf{gamma }}^{(g)}}]{;_{r,}}{sigma _r} = {
m{norm}}({{boldsymbol{S}}_j}^{(g)}{;_{,r}})end{array}
ight}$$
(25)

其中[],r与[]r,分别代表矩阵第r列与第r行, norm(.)代表对列取范数.

实际测试试验中, 共振区受噪声污染小, 且对参数变化灵敏度更高[26], 故信号信噪比较低时可仅选择共振区的频率点参与辨识过程, 当信噪比较高时则可选择给定带宽的共振区邻域. 此外, 由于式(22)以装配体频响函数测量值与拟合值的残差范数为极小化目标, 因此可将其幅值相关性系数[27]作为筛选频率点的准则: 相关性较好的频率点, 其残差较小且可信度较高; 反之, 相关性较低则说明该频率点可能受噪声污染较为严重, 且残差较大不利于准确辨识. 幅值相关性系数αa计算式为







$$ {alpha _{
m{a}}}({omega _k}) = Re left( {frac{{{text{2}}{{left( {{boldsymbol{H}}_{
m{A}}^{}({omega _k}){{boldsymbol{e}}_j}}
ight)}^H}left( {{boldsymbol{hat H}}_{
m{A}}^{}({omega _k}){{boldsymbol{e}}_j}}
ight)}}{{{{left| {{boldsymbol{hat H}}_{
m{A}}^{}({omega _k}){{boldsymbol{e}}_j}}
ight|}^{text{2}}}{text{ + }}{{left| {{boldsymbol{H}}_{
m{A}}^{}({omega _k}){{boldsymbol{e}}_j}}
ight|}^{text{2}}}}}}
ight) geqslant {sigma _{min }} $$
(26)

其中, $ Re $代表取实部, σmin为所允许的相关性最小值, 实践中发现取σmin>0时识别效果较好.


1.4.2
连接结构动力学特性识别流程

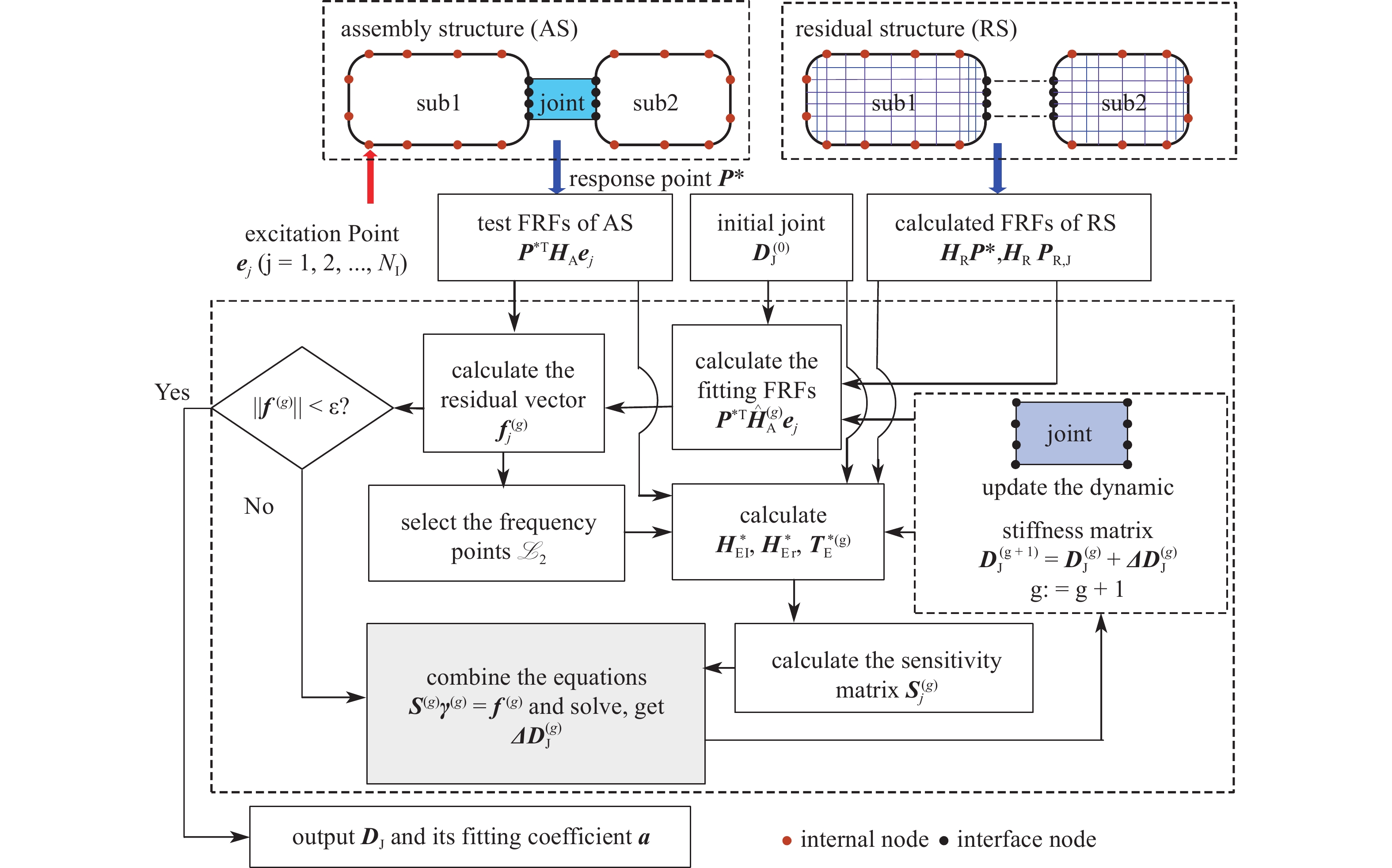
连接特性辨识流程如图2所示, 具体过程如下.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-2.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2" />



图
2
连接结构动力学特性辨识流程



Figure
2.
Workflow of the joint dynamic properties identification



下载:
全尺寸图片
幻灯片


步骤1: 确定完备界面自由度及其对应的布尔矩阵PR,J, 装配体结构的测试自由度及其对应的布尔矩阵P*, 激励自由度及其对应的位置向量ej(j=1, 2, …, NI).

步骤2: 根据激励自由度ej及测试自由度P*对装配体结构进行振动测试, 得到测试频响函数P*THAej. 选择共振区(或其邻域)内的频率点序列${cal L} _1$并利用校准后的残余子结构有限元模型计算相应频响函数HRP*, HRPR,J. 置g=0.

步骤3: 确定初始连接动刚度矩阵DJ(g), 并与HR重构得到装配体频响函数初始拟合值${boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)}{{boldsymbol{e}}_j} $






$$ begin{gathered} {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{hat H}}_{
m{A}}^{(g)}{{boldsymbol{e}}_j} = {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{}{{boldsymbol{e}}_j} - {boldsymbol{P}}{_{}^{*{
m{T}}}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}Big( {{{({boldsymbol{D}}_{
m{J}}^{(g)})}^{ - 1}} + } Big. hfill {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {Big. {{boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{boldsymbol{P}}_{
m{R,J}}^{}} Big)^{ - 1}}{boldsymbol{P}}_{
m{R,J}}^{
m{T}}{boldsymbol{H}}_{
m{R}}^{}{{boldsymbol{e}}_j} hfill end{gathered} $$

根据式(26)在${cal L} _1$中选择参与辨识过程的频率点${cal L} _2$.

步骤4: 由式(11)、式(19)计算所选频率点序列${cal L} _2$对应的左、右等效频响函数HEl*, HEr*ej及转换矩阵TE*(g) .

步骤5: 计算频率点序列${cal L} _2$中ωk处的灵敏度矩阵Sj(g)(ωk)及残差向量fj(g)(ωk)代入式(22), 对k和j组合形成超定方程组f (g)=S(g)γ(g), 并进行归一化. 求解拟合系数增量γ(g)后得到ΔDJ (g), 更新连接动刚度矩阵DJ(g + 1)=DJ(g) + ΔDJ(g), 置g=g + 1.

步骤6: 重复步骤3~5, 直至满足停止准则, 即||f (g)||≤ε, 输出连接结构动刚度矩阵的拟合系数.

当残余结构有限元模型规模较大时, 其频响函数HRP*, HRPR,J的计算量较大且是决定算法效率的关键一环, 因此需在迭代前计算频率点序列${cal L} _1$对应的HR. 且该模型须经过精细的校准, 否则HR将包含较大的误差, 导致错误的识别结果.


2.
算例分析



2.1
仿真算例


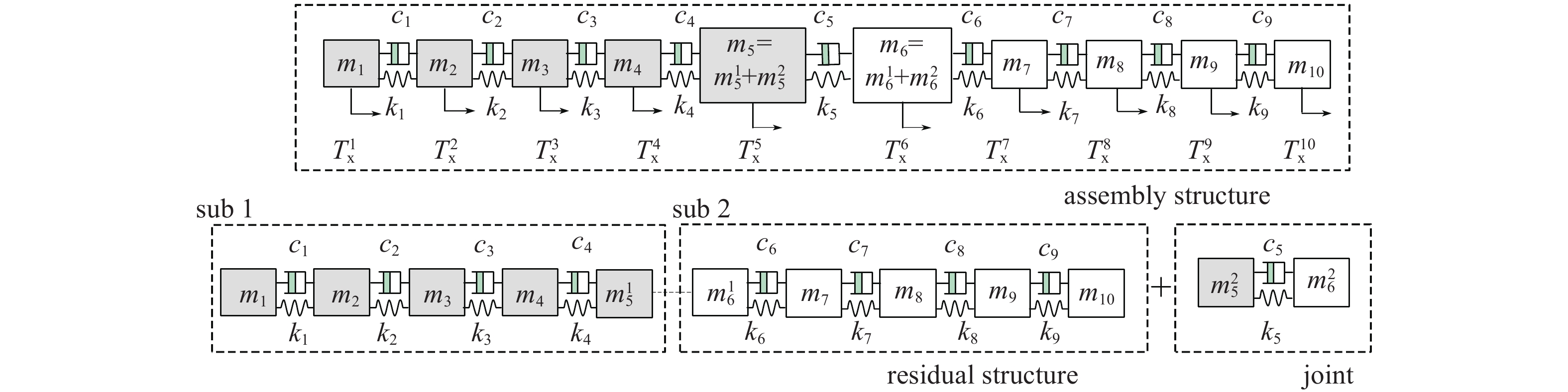
为验证所提方法的正确性及抗噪性, 以具有10个平动自由度($T_{
m{X}}^1 $至$T_{
m{X}}^{10 } $)的简单线性多自由度系统(图3)进行数值仿真. 将其视为由连接结构与两个残余子结构组成的装配体(残余子结构1、2分别在自由度$T_{
m{X}}^5 $、$T_{
m{X}}^6 $处与连接结构耦合), 且该连接结构同时包含质量、刚度及阻尼效应. 系统各参数为m1 =m10=0.078 kg, m2=m3 = ··· = m9=0.156 kg, $m_{{5}}^1 $ = $m_{{6}}^1 $=0.078 kg, $m_{{5}}^2 $ = $m_{{6}}^2 $ = 0.078 kg, k1=k2 = ··· =k9=1.0×107 N/m, 残余结构与连接结构的刚度比例阻尼系数β均取1.0×10?7.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
连接结构与残余结构耦合



Figure
3.
Coupling of joint and residual structure



下载:
全尺寸图片
幻灯片


装配体结构计算的频响函数添加噪声后作为测试值HAej, 残余结构计算的频响函数作为所需HR. 连接动刚度矩阵所取初值DJ0为






$$ left[ {begin{array}{*{20}{c}} { - 0.05{text{0}}{omega ^2} + {{10}^6}(1 + {
m{i}}omega beta )}&{ - {{10}^6}(1 + {
m{i}}omega beta )} { - {{10}^6}(1 + {
m{i}}omega beta )}&{ - 0.04{text{0}}{omega ^2} + {{10}^6}(1 + {
m{i}}omega beta )} end{array}}
ight] $$

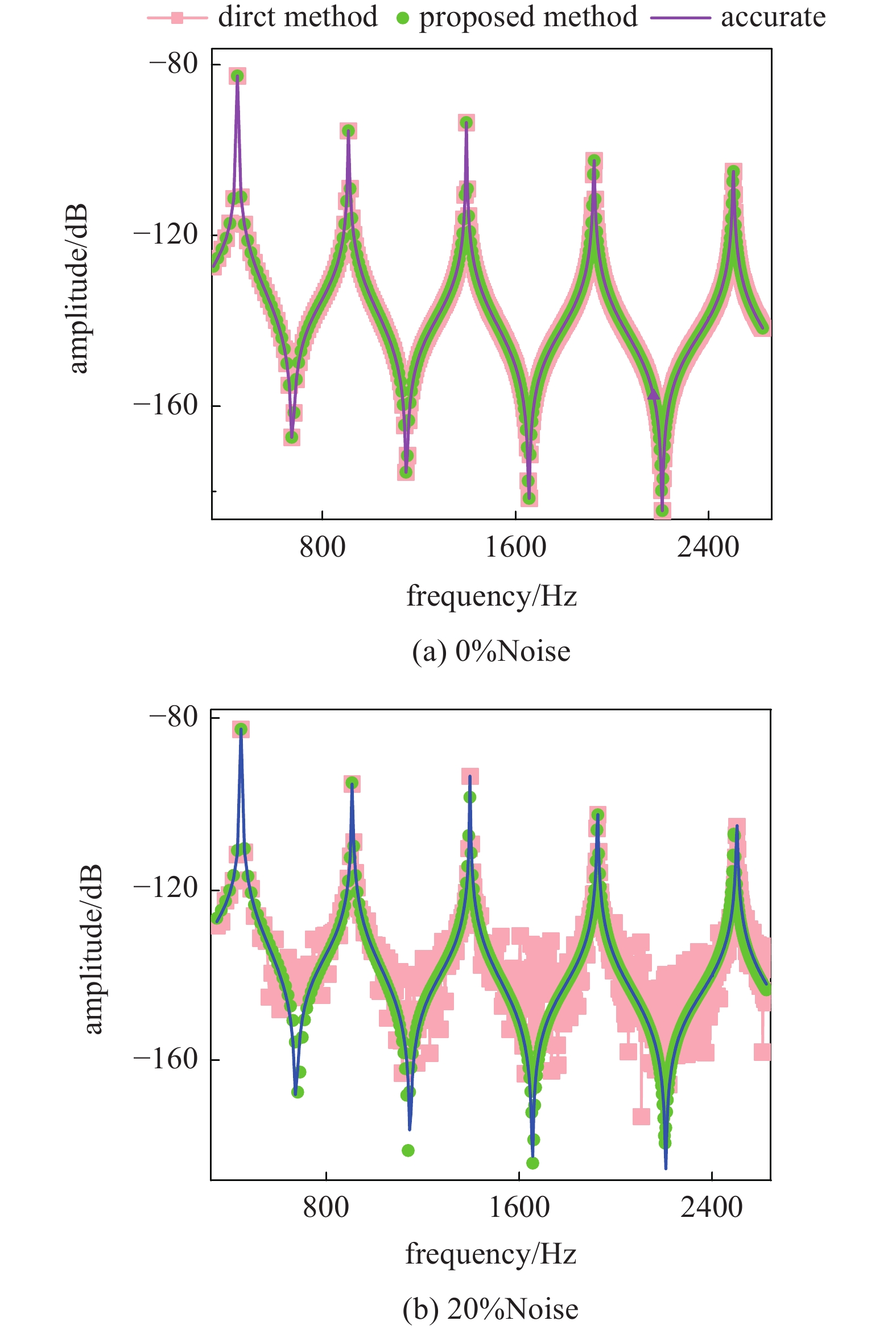
在无噪声情形下, 由本文方法利用测试频响函数P*THAej(P*不包含界面自由度$T_{
m{X}}^5 $、$T_{
m{X}}^6 $)按1.4中所述流程进行辨识, 并与利用完备频响函数HAej由逐频求逆的直接法[5]进行对比. 由图4(a)知两种方法辨识的DJ与HR重构的装配体频响函数均与真实值完全一致, 验证了所提方法仅利用所选测试自由度(无需包含完备的界面自由度)上的装配体频响函数识别连接特性的正确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
装配体结构频响函数重构值与真实值对比



Figure
4.
Comparison of reconstructed and accurate assembly FRF



下载:
全尺寸图片
幻灯片


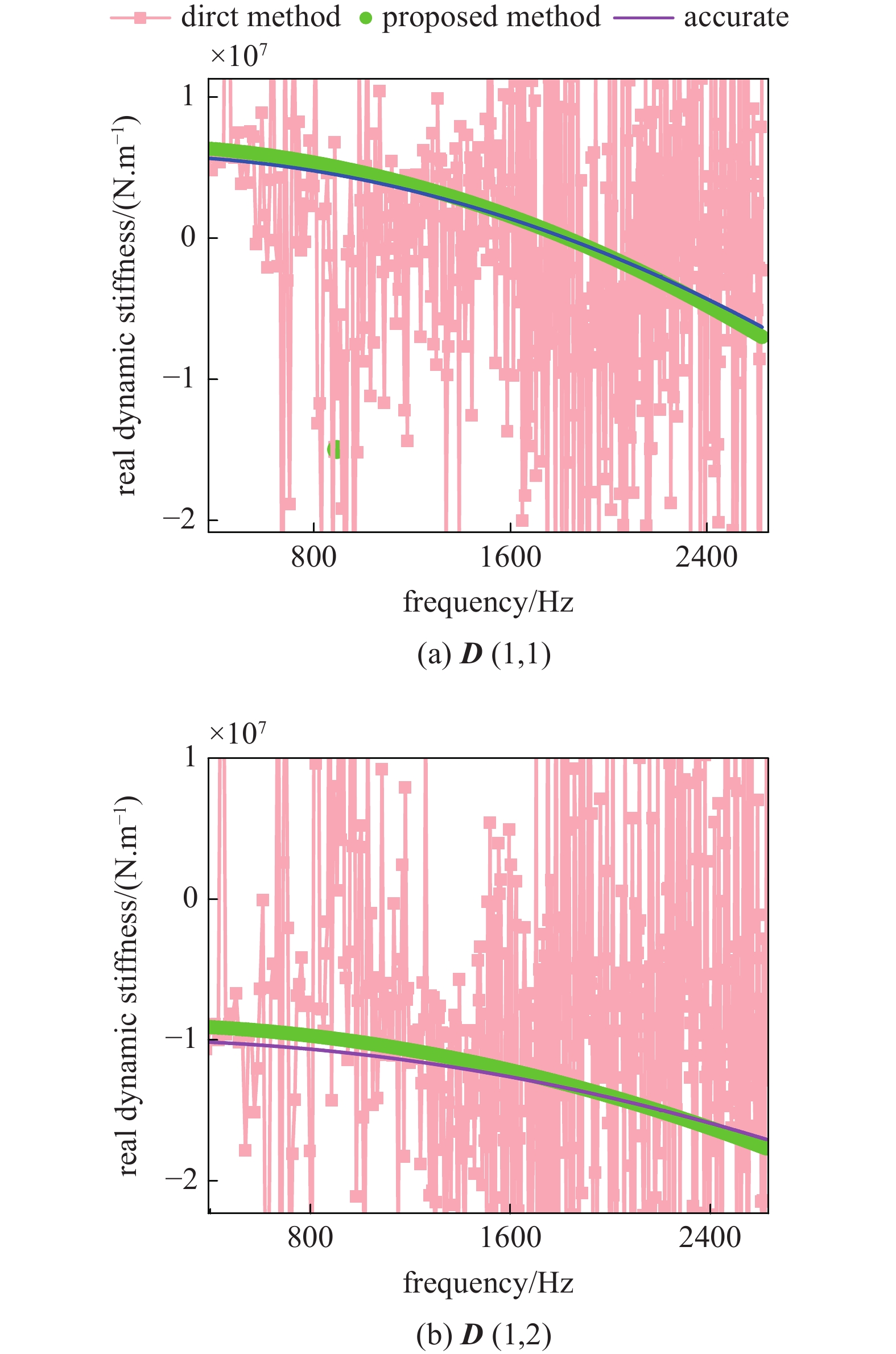
为检验所提方法的抗噪性, 在前述算例的频响函数真实值中加入10%的白色噪声与10%的有色噪声后再次进行识别, 由图4(b)知两种方法在测试噪声较小的共振区识别效果均较好, 而在其余噪声较大的频率点, 所提方法的准确度高于直接方法. 对比两者所识别DJ的对角元素与非对角元素可知(图5), 本文方法辨识结果受噪声的影响远小于直接法.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
所辨识连接结构动刚度实部的对比



Figure
5.
Comparison of real part of the identified joint dynamic stiffness



下载:
全尺寸图片
幻灯片



2.2
实验验证



2.2.1
胶接

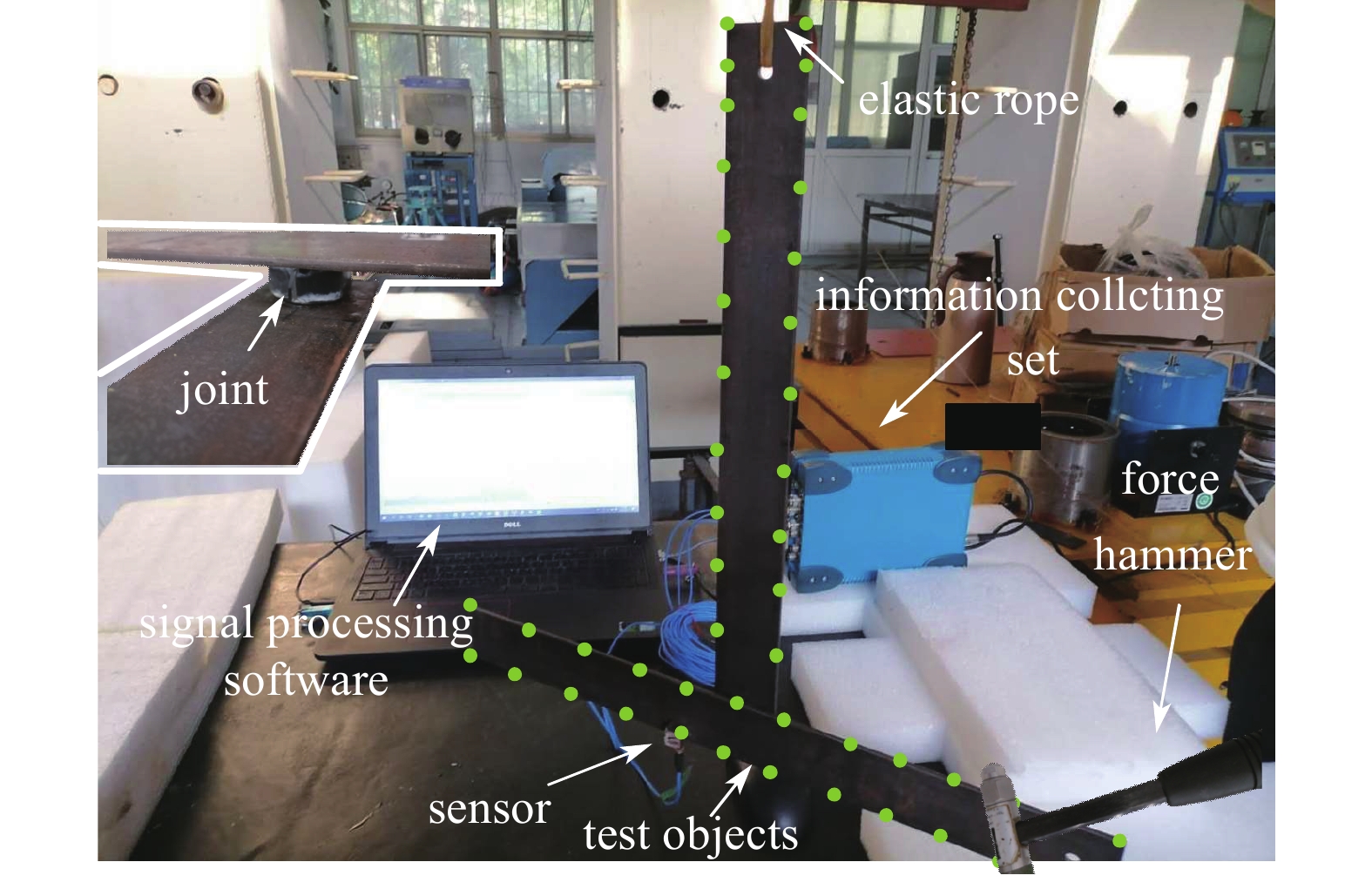
为验证所提方法识别实际连接结构的有效性, 首先对一个T形结构进行了实验. 该装配体结构由两根相同的长为500 mm、宽为50 mm的梁(残余结构)在与一铁块在界面处胶接而成, 且忽略连接界面的非线性行为. 实验中采用了N-Modal模态测试系统, PCB力锤以及PCB三轴传感器. 测试频率范围设置为1000 Hz, 取1600条谱线. 如图6所示, 装配体结构采用弹性绳悬挂的方式模拟自由?自由边界条件, 传感器位于梁I中心位置, 在均匀分布的126个测试点上进行锤击, 获得其频响函数P*THAPI. 辨识公式中(P*THRPR,J) + 要求测试自由度数目大于连接结构自由度数目, 然而为抑制噪声[24]并避免P*THRPR,J出现零列或呈现病态, 应布置更多包含结构有效信息的测试自由度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
含一处连接的耦合结构及其测试装置



Figure
6.
The coupled structure with one joint and its test setup



下载:
全尺寸图片
幻灯片


采用Shell63板单元对残余结构建模, 并按材料参数划分为两个组. 利用自由状态的测试数据对单根梁进行模型修正[27-31]后, 有限元模型计算的频响函数与其测试值匹配程度较高(图7), 由此得到校准的残余结构有限元模型. 其材料参数如表1所示, 其中D与E代表密度与弹性模量, 且残余结构与连接结构的刚度比例阻尼系数均取为1.0$ times $10?7. 由该校准模型计算得残余结构频响HRP*和HRPR,J.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
校准的残余子结构有限元模型计算频响与测试值对比



Figure
7.
Comparison of the residual structure's FRF: calibrated FEM and experimental model



下载:
全尺寸图片
幻灯片





表
1
梁I和II的模型材料参数



Table
1.
The material parameters of Beam I and Beam II



table_type1 ">
ComponentD/(kg·m?3)E/Pa
1118002.619$ times $1011
283401.953$ times $1011





下载:
导出CSV
|显示表格



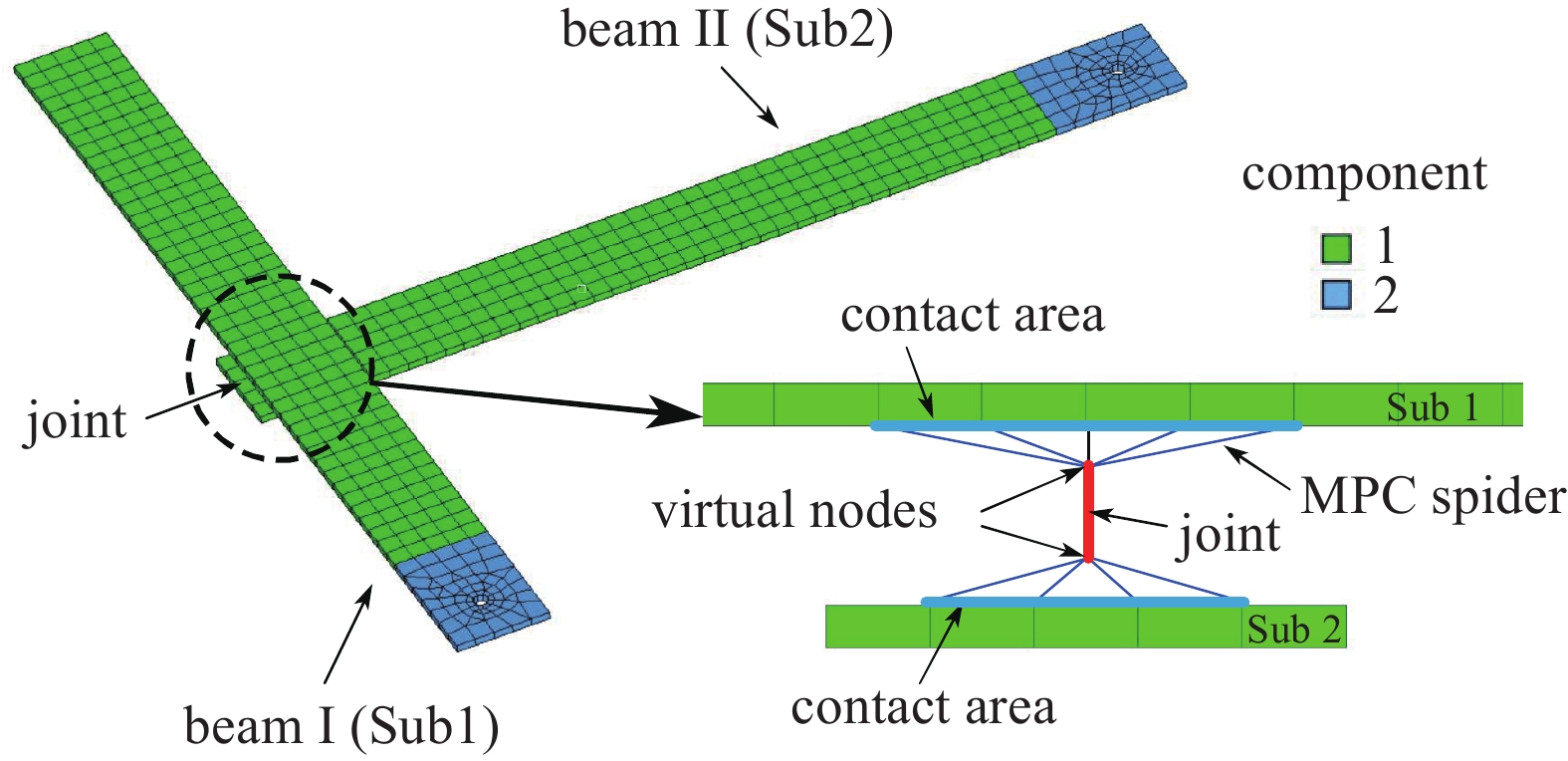
残余结构与连接结构的耦合如图8所示. 连接结构两端的虚拟节点分别通过MPC约束依赖于梁I、梁II被胶接区域内的节点, 使得虚拟节点的平移及转动自由度上的位移代表了胶接区域内节点的位移均值, 且虚拟节点上的力被均匀分配至胶接区域内的节点上[1]. 初值DJ0的取法为: 以密度为90 000 kg/m3、弹性模量为3.0×107 Pa的梁单元连接两虚拟节点, 其形成的动刚度矩阵作为${boldsymbol{ D}}_{
m{J}}^0$. ${boldsymbol{D}}_{
m{J}}^0$与HR所重构的装配体频响函数初始拟合值与测试值对比如图9所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
T形梁的连接结构与残余结构耦合



Figure
8.
Coupling of Joint and residual structure of T-Beam



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
迭代前装配体频响函数重构值与测试值对比



Figure
9.
Comparison of reconstructed and experimental assembly FRF before iteration



下载:
全尺寸图片
幻灯片


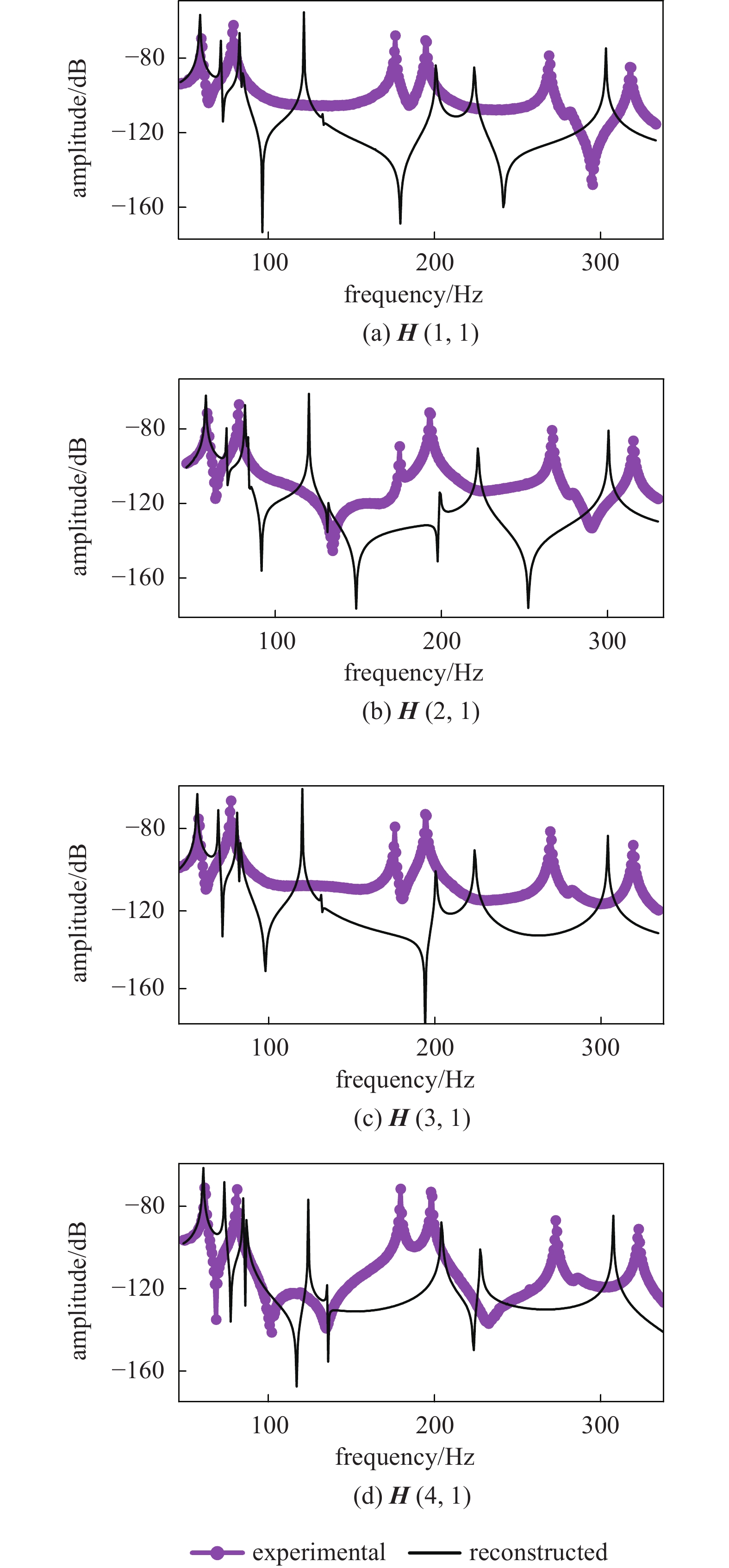
按1.4中所述流程识别得到的DJ拟合系数常数项、二次项作为连接结构的刚度、质量矩阵, 与残余结构有限元模型重组可得到修正的装配体有限元模型, 其频响函数结果与测试值匹配较好(图10), 表明本文方法能有效识别实际连接结构动态特性. 值得注意的是, 由于实际连接结构刚度、质量矩阵的对称性、稀疏性及其他特性将对DJ的拟合系数产生一系列约束, 需在辨识方程中予以考虑. 迭代过程中共振区序列${cal L} _1$中各频率点的装配体重构频响与测试频响的幅值相关性如图11所示, 可见其随着迭代步的增加而不断提高, 即残差范数||f (g)||逐渐减小, 验证了算法的收敛性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
迭代后装配体频响函数重构值与测试值对比



Figure
10.
Comparison of reconstructed and experimental assembly FRF after iteration



下载:
全尺寸图片
幻灯片




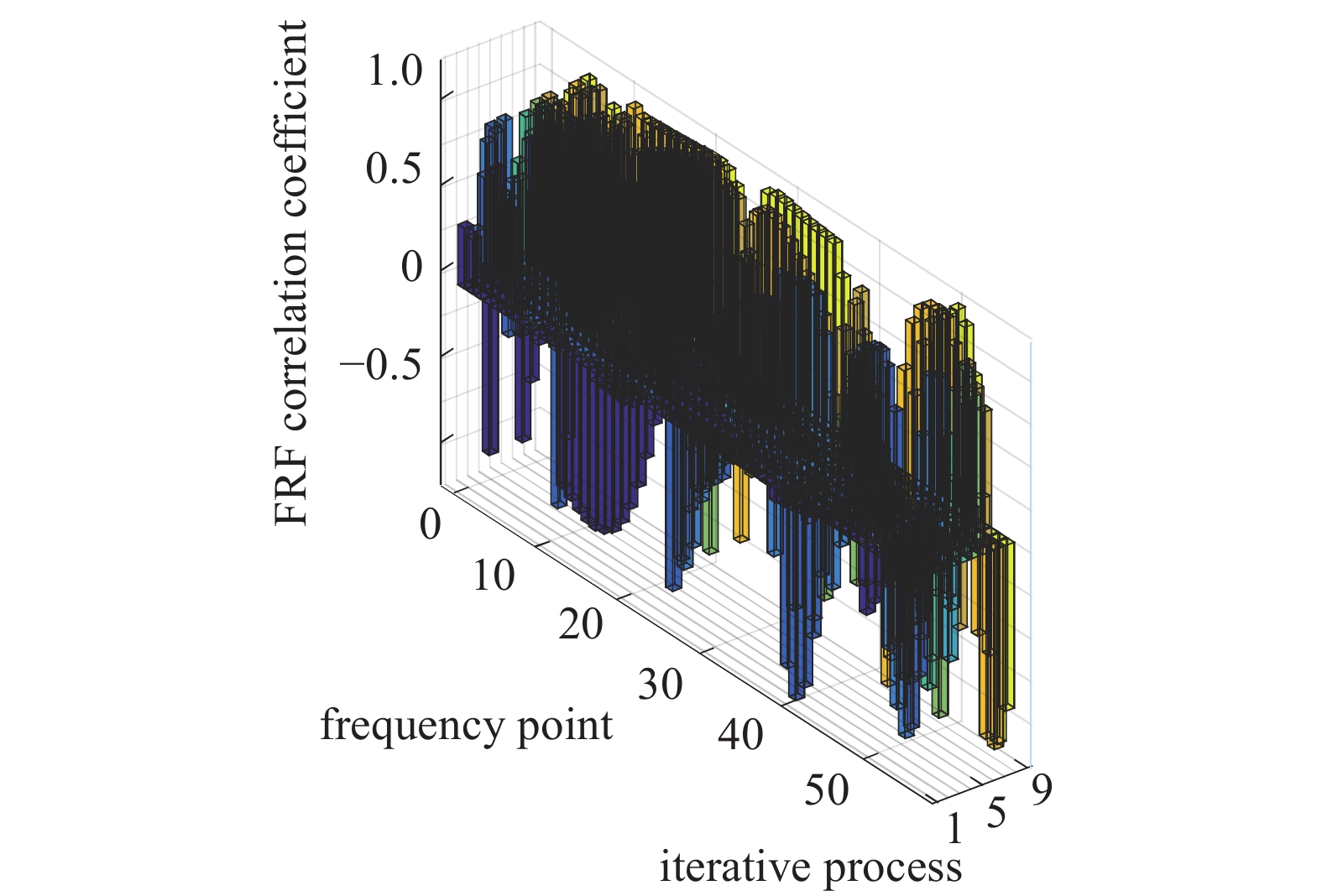onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
频响函数相关性的迭代历程



Figure
11.
Iterative process of FRF correlation



下载:
全尺寸图片
幻灯片



2.2.2
螺栓连接

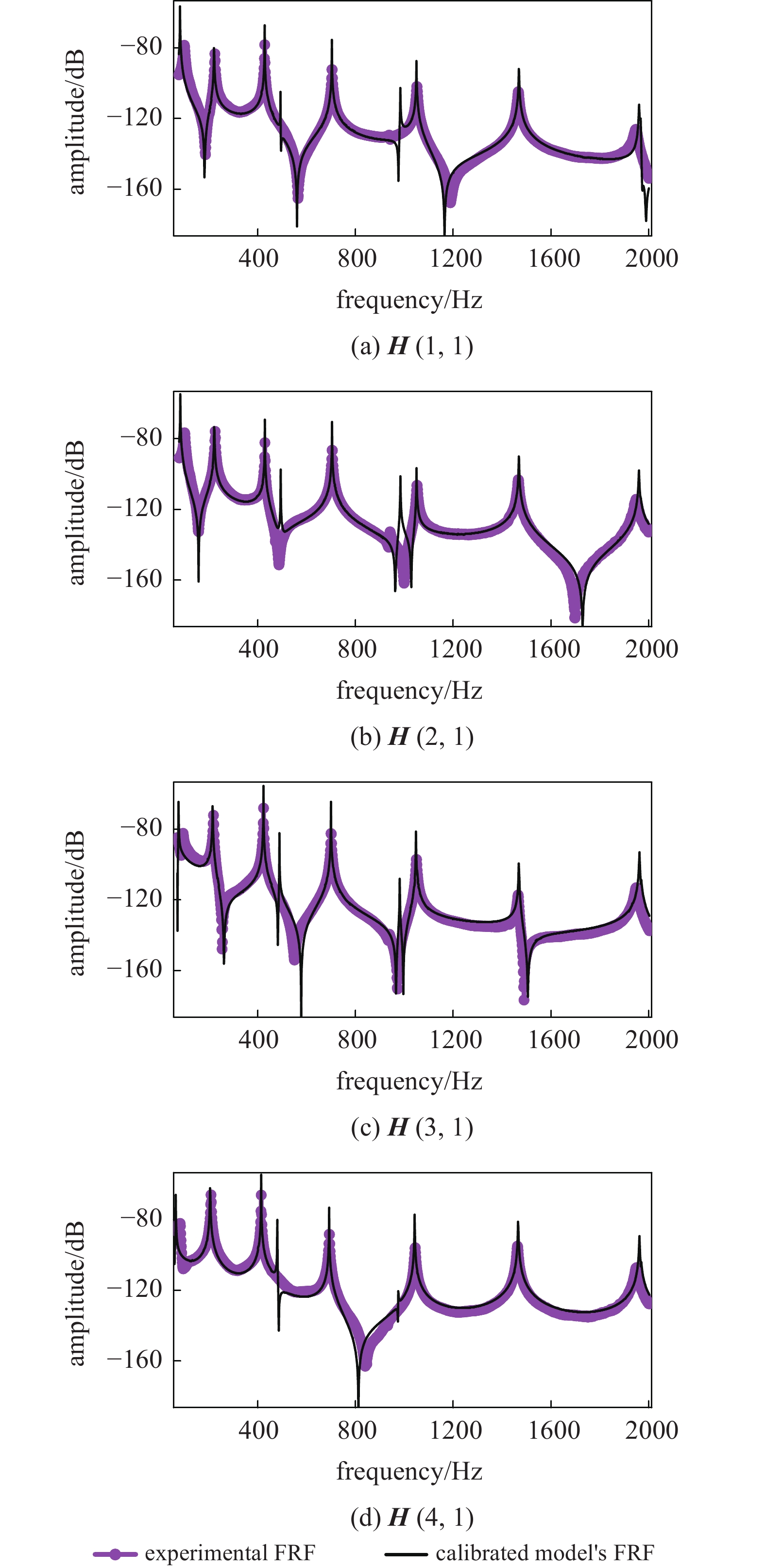
为进一步验证所提方法对较复杂连接动力学特性的识别能力, 对一个包含两处螺栓连接的双梁结构进行了实验. 该装配体结构由两根相同的长度为500mm的L形梁(残余结构)通过螺栓连接而成, 测试中使用的数据采集系统如图12所示. 测试频率范围设置为2 500 Hz, 取1600条谱线. 装配体结构以海绵垫支撑以模拟自由-自由边界条件, 三轴传感器位于螺栓附近, 在均布的138个测试点上进行锤击, 获得其频响函数P*THAPI. 采用Shell63板单元对单根L形梁建模, 并按材料参数划分为3个组. 经模型修正后得到校准的残余结构有限元模型, 其计算的频响函数与测试值吻合较好(图13). 材料参数如表2所示, 且残余结构与连接结构的刚度比例阻尼系数均取为1.0$ times $10?7. 利用该模型可较准确地计算出包含完备界面自由度信息的残余结构频响函数.



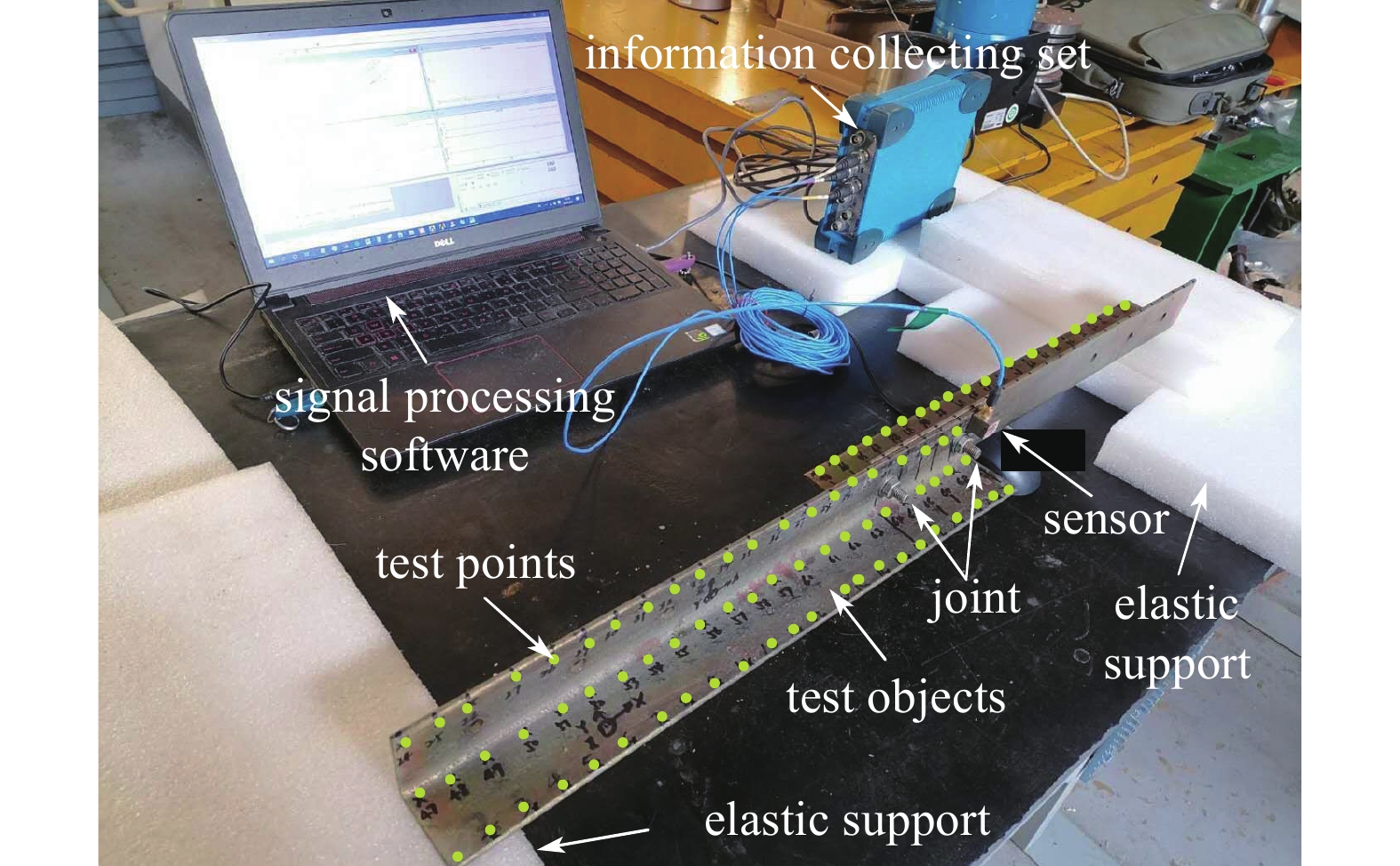onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
含两处连接的耦合结构及其测试装置



Figure
12.
The coupled structure with two joints and its test setup



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
残余结构校准后模型频响与测试值对比



Figure
13.
Comparison of the residual structure's FRF: calibrated FEM and experimental model



下载:
全尺寸图片
幻灯片





表
2
梁I和II的模型材料参数



Table
2.
The material parameters of Beam I and Beam II



table_type1 ">
ComponentD/(kg·m?3)E/Pa
1127004.529×1011
2111205.794×1010
3127004.529×1011





下载:
导出CSV
|显示表格



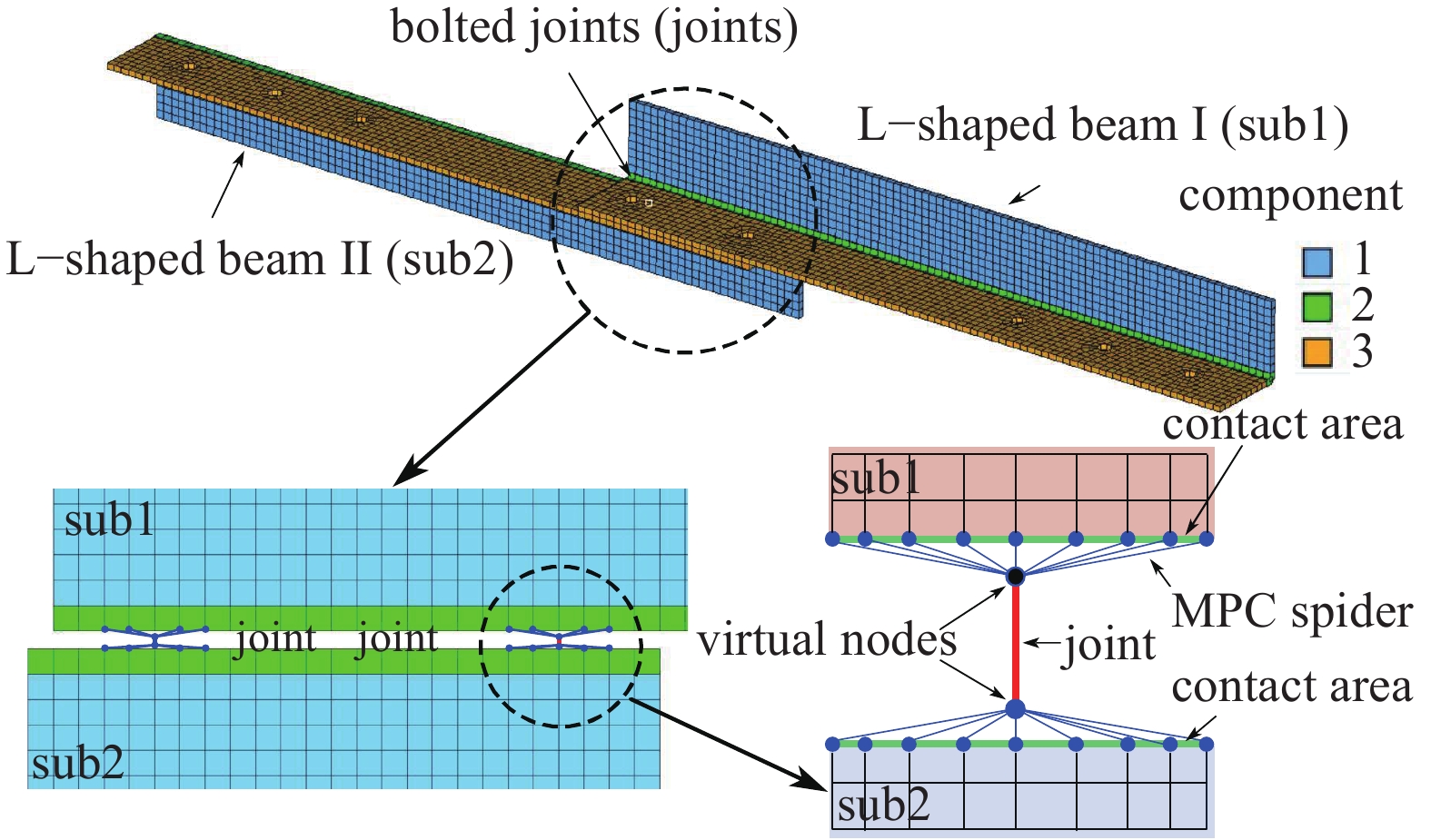
残余结构有限元模型与连接结构的耦合如图14所示, 与实验一类似, 通过MPC约束将梁I、梁II的螺栓压紧区域内的节点与连接结构耦合, 其中压紧区域取螺栓直径的两倍范围. 该结构包含两处相同的连接, 取约束方程使得两者连接参数相同, 即${boldsymbol{D}}_{
m{J}}^{
m{I}} $=${boldsymbol{D}}_{
m{J}}^{
m{II}} $. 由于两处连接无共同自由度, 因此总体连接动刚度矩阵为DJ=diag[${boldsymbol{D}}_{
m{J}}^{
m{I}} $,${boldsymbol{D}}_{
m{J}}^{
m{II}} $]. 初值${boldsymbol{D}}_{
m{J}}^{
m{0}} $的取法为: 以密度为7900 kg/m3、弹性模量为1.8×1011 Pa的梁单元连接虚拟节点, 其动刚度矩阵作为${boldsymbol{D}}_{
m{J}}^0 $. ${boldsymbol{D}}_{
m{J}}^0 $与${boldsymbol{H}}_{
m{R}} $重构的装配体频响函数初始拟合值与测量值对比如图15所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
L形梁的连接结构与残余结构耦合



Figure
14.
Coupling of Joint and residual structure of L-Beam



下载:
全尺寸图片
幻灯片




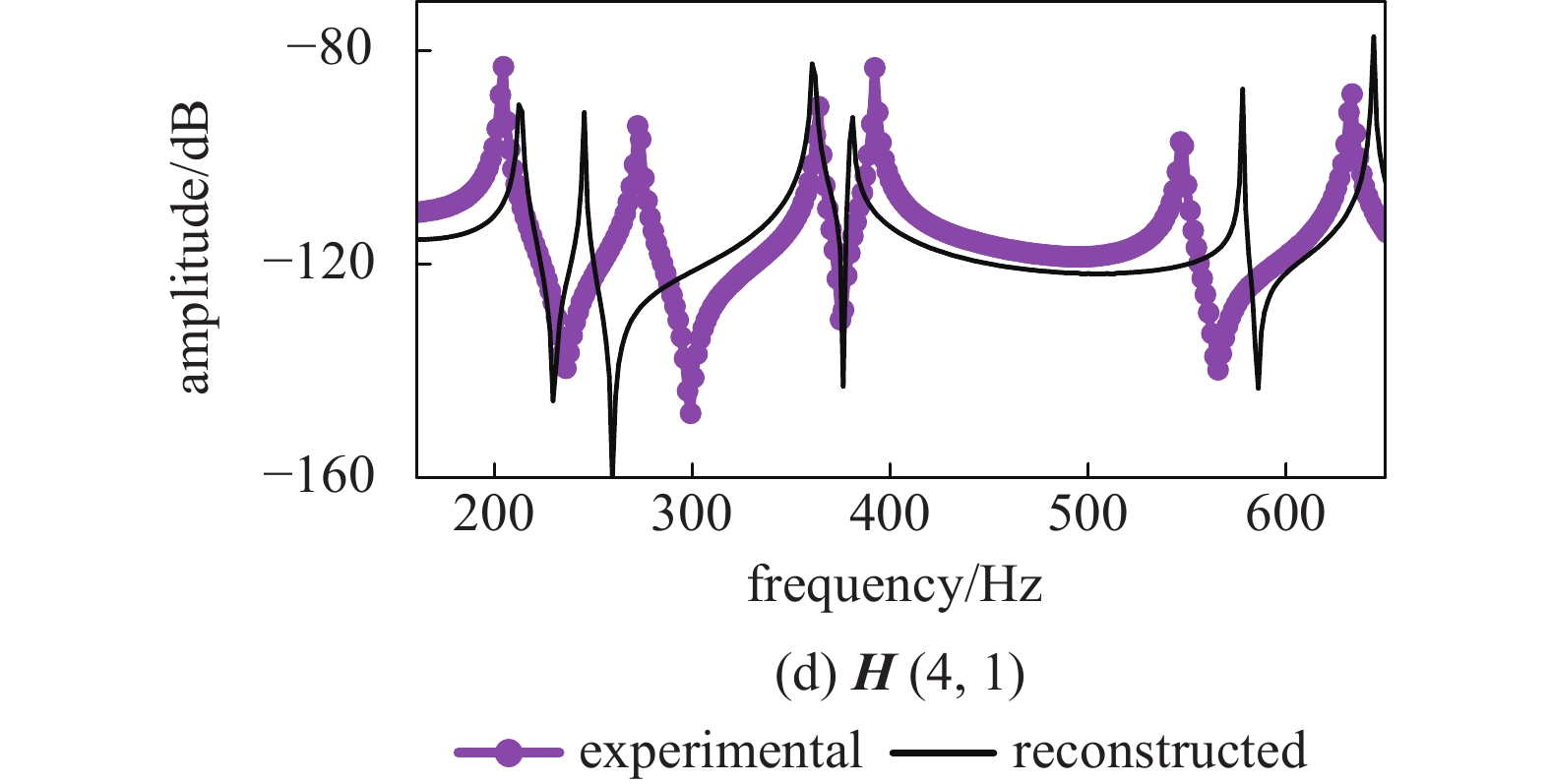onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
迭代前装配体频响函数重构值与测试值对比



Figure
15.
Comparison of reconstructed and experimental assembly FRF before iteration



下载:
全尺寸图片
幻灯片


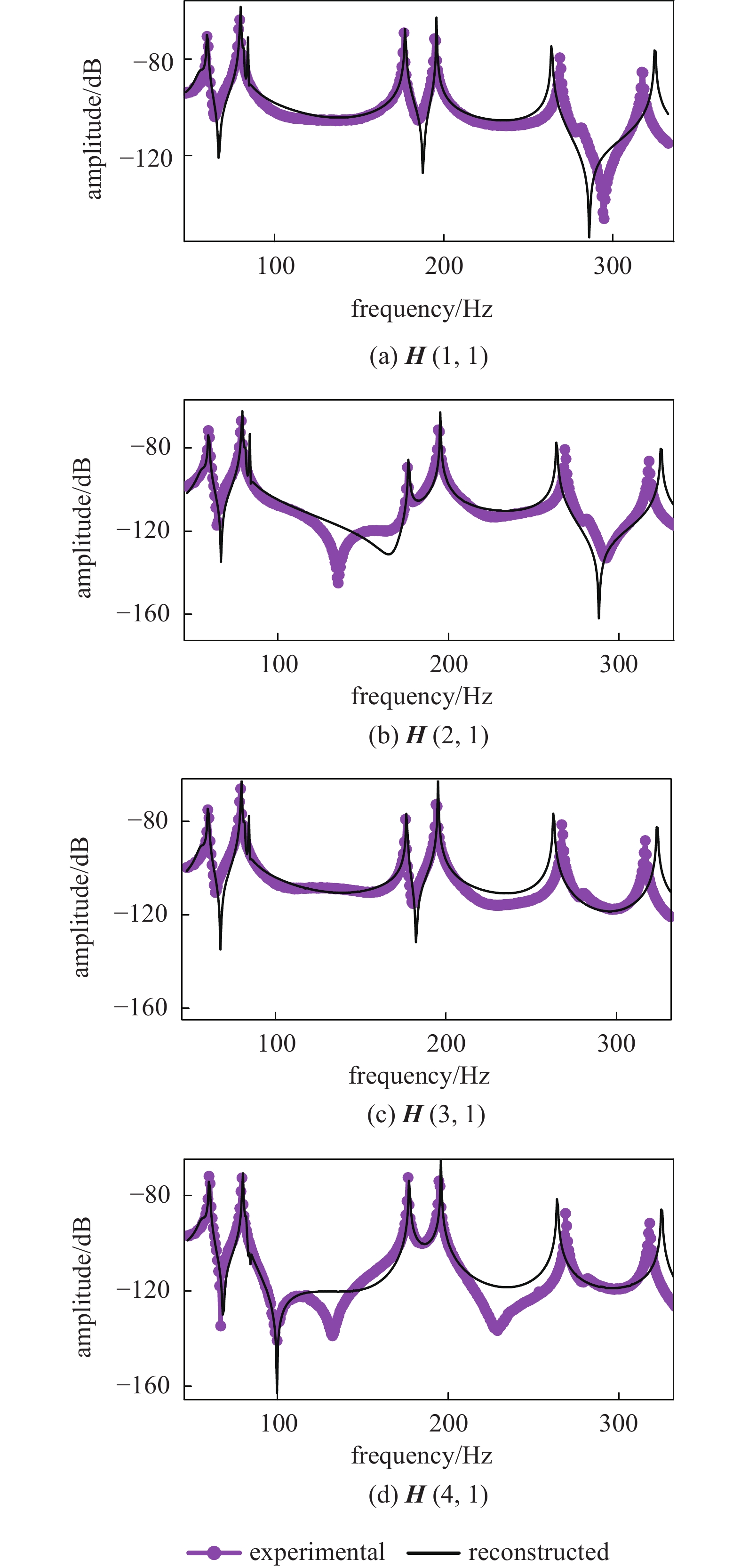
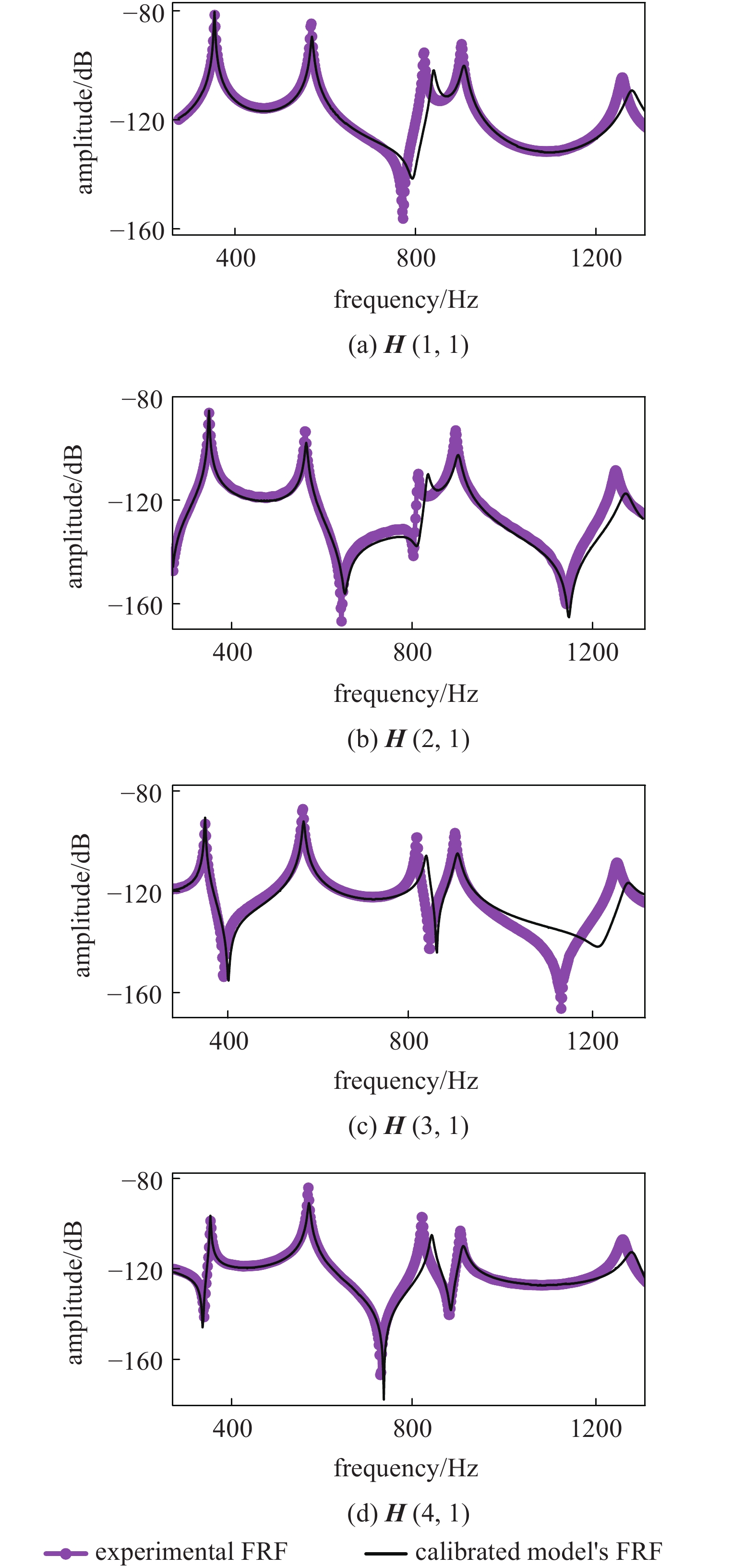
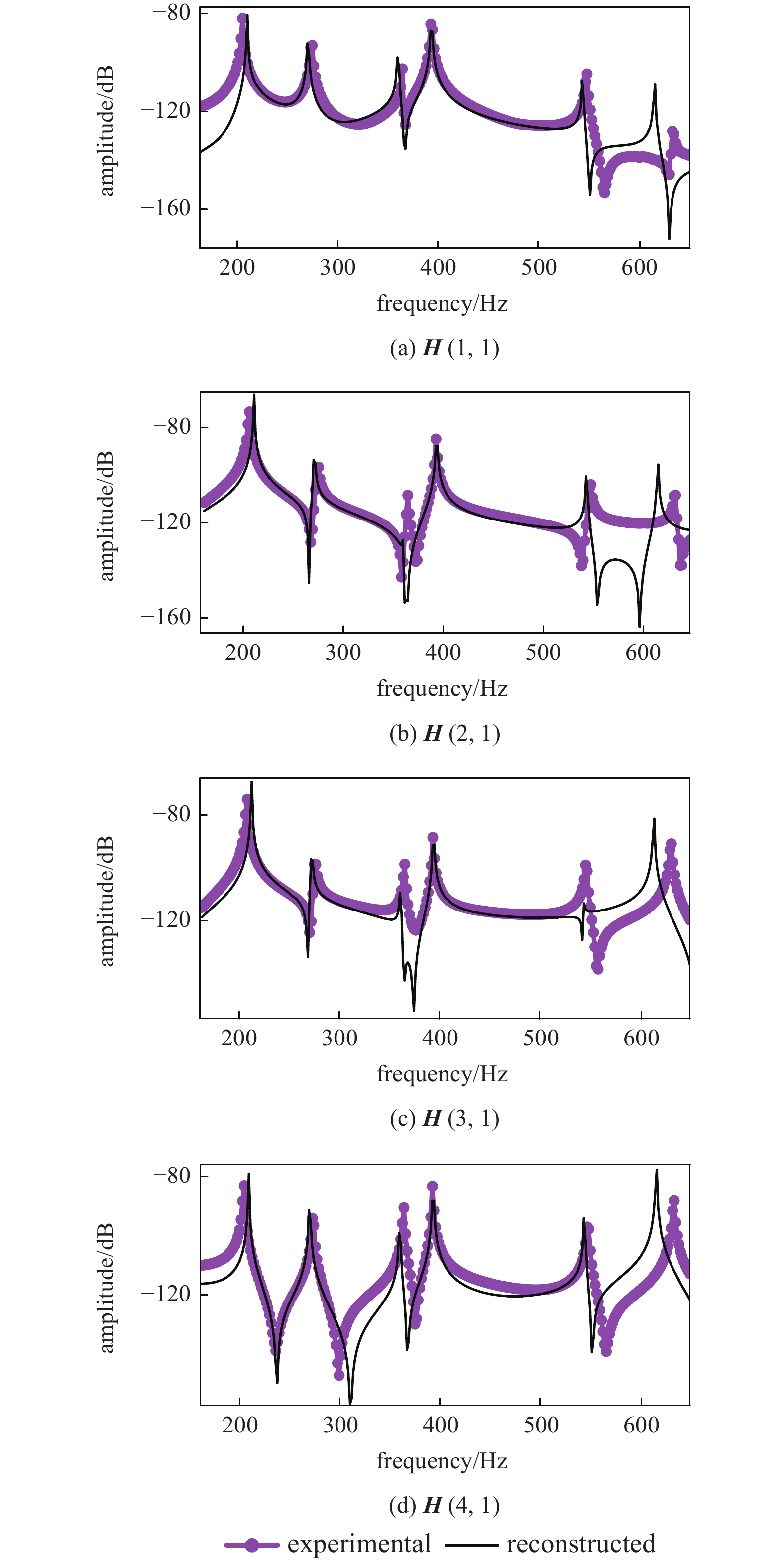
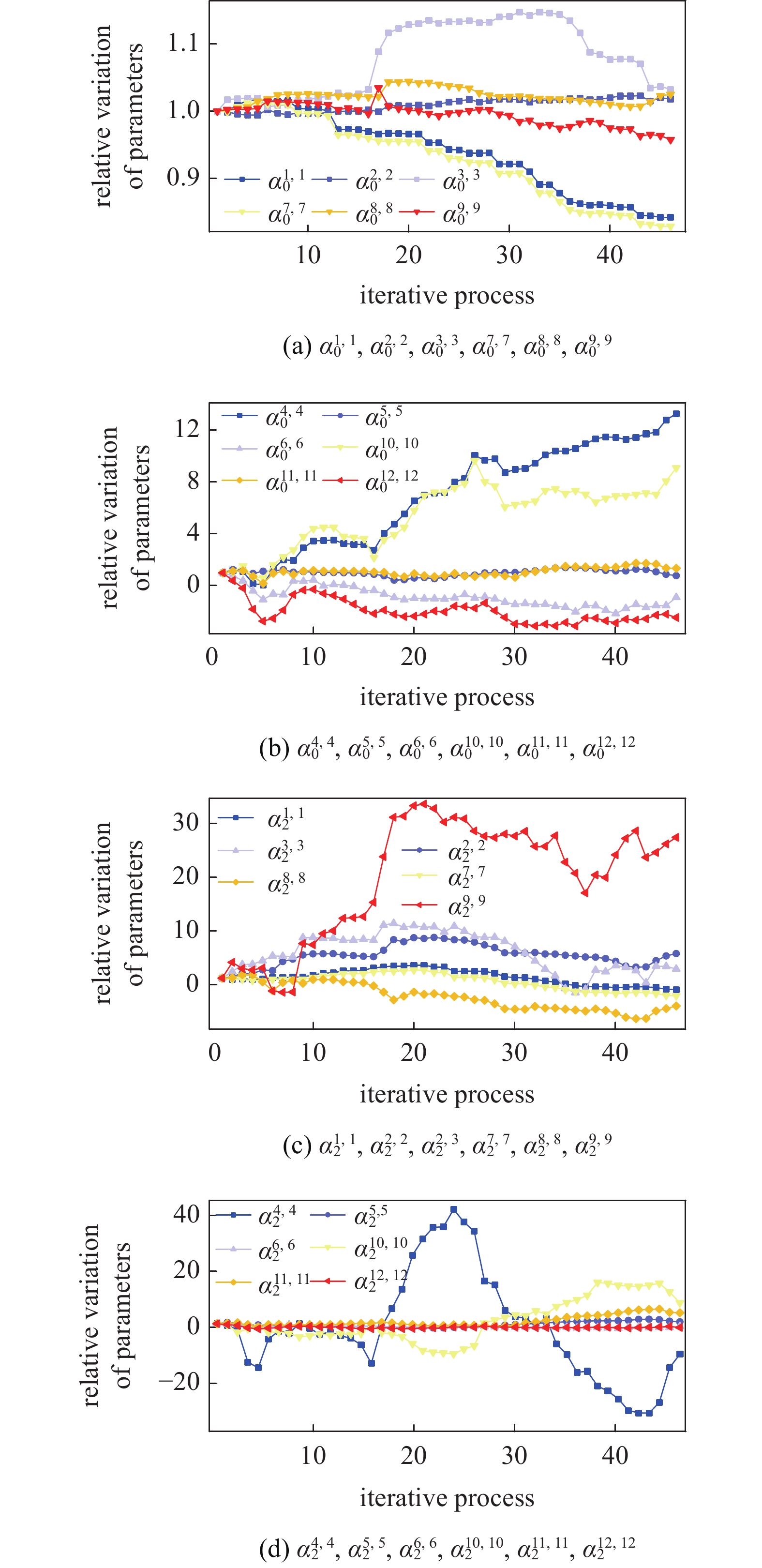
同样地, 所辨识连接结构与残余结构重组得到装配体结构有限元模型, 其频响函数结果与测量值对比如图16所示, 尽管在550 ~ 650 Hz的高频段有所差异, 但150 ~ 550 Hz的频率范围内均匹配较好. 由此证明了所提方法能有效地对较复杂的多处连接特性进行识别. 图17为动刚度曲线相对初值归一化的拟合系数随迭代的变化, 可以发现部分参数振荡较为明显, 装配体结构动响应对这些参数通常有低敏感性的特点因而易受噪声干扰且难以准确辨识, 也正因该特点, 其辨识误差对对连接结构预测装配体动力学特性的准确性影响较小[16].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
迭代后装配体频响函数重构值与测试值对比



Figure
16.
Comparison of reconstructed and experimental assembly FRF after iteration



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-280-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
拟合系数的迭代历程



Figure
17.
Iterative process of fitting coefficient



下载:
全尺寸图片
幻灯片



3.
结 论


本文提出一种新的连接特性识别方法, 直接利用可测的装配体频响函数进行辨识, 避免了旋转自由度及部分不可测界面自由度的测量或估计. 通过具有收敛性质的增量方程增加了界面自由度数目较多时辨识的数值稳定性; 并以多项式拟合动刚度曲线, 在所选频率点上联立方程得到参数估计公式, 减少了对病态矩阵的求逆, 提高了辨识结果的准确性. 通过数值仿真算例了验证所提方法的正确性及抗噪性, 通过含胶接、螺栓连接等结构的试验验证了方法识别较复杂的实际连接结构特性的有效性.

相关话题/结构 测试 图片 计算 系统
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于沿程坐标积分模式颗粒流与结构物阵列相互作用的数值模拟
    引言中国山地面积广袤,超过2/3的面积属于山地和高原,各种大型灾害时有发生[1].其中,以颗粒物质流动主导的大尺度灾害如滑坡、泥石流,对人类的生命安全和各类基础设施有着巨大的威胁[2-3].2010年8月8日,甘肃舟曲县发生特大规模山洪泥石流,造成1467人遇难,298人失踪[4].2017年6月2 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 多稳态俘能系统的准确磁力建模方法
    引言高性能能量俘获技术对状态监测传感器网络的可持续性供能具有重要意义,能够弥补传统电池容量有限且需要及时更换的缺点.这种技术广泛应用于汽车胎压监测[1-2]、机械设备运行故障监测[3-4]、人体健康状态监测[5-6]以及物联网环境信号监测[7]等场合.非线性多稳态技术[8-10]是一种常见的能量俘获 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于压电振动能量俘获的弯曲结构损伤监测研究
    引言近年来,压电材料因其具有能实现电能和机械能互相转换的特性,在工程结构中日益受到重视[1-2],被广泛应用于结构的形状控制、振动和噪声控制、损伤检测等领域[3-4].从机械振动中提取能量的特性极大满足了传感器自给供电的经济需求与生态需求,因此压电材料广泛应用于俘能器中[5-6].到目前为止,最常用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 动力吸振器复合非线性能量阱对线性镗杆系统的振动控制
    引言在机械零件中带孔零件占比为50%~80%[1],因此孔加工在金属切削加工中占有重要地位.孔加工约占金属切削总量的33%[2],而深孔加工是孔加工中的一个重要领域.镗杆在深孔加工中应用广泛,当镗杆的长度与直径比大于5时便容易发生颤振,从而导致零件的加工质量大幅下降[3-5].因此,对镗杆进行减振就 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工神经网络的非结构网格尺度控制方法
    引言网格生成是计算流体力学(computationalfluiddynamics,CFD)数值计算的第一步,也是未来CFD六大重要研究领域之一[1-2].在现代CFD应用过程中,自动生成复杂构型的高质量网格(包括网格自适应)依然是一个重大挑战性问题.自动化程度和网格质量是网格生成过程中最重要的两个问 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 时间尺度上Lagrange系统的Hojman守恒量
    引言力学系统的对称性与守恒律密切相关.通过研究对称性而探索或发现复杂力学系统的守恒律,这是分析力学研究的一个重要方面[1-2].Lie对称性[3-9]、Noether对称性[10-20]和Mei对称性[21-28]是3种概念不同的对称性方法.利用对称性和守恒律,可以简化动力学问题甚至求解力学系统的精 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑胎路多点接触的电动汽车?路面耦合系统振动分析
    引言近年来,轮毂电机驱动电动汽车,因传动效率高、便于实现智能控制等优点,得到了广泛关注[1-3],是未来电动汽车的发展方向.但独立驱动电动汽车的动力学与控制也面临诸多新问题,其一是簧下质量大,导致轮胎动载荷增加,轮胎与路面动力学相互作用更加突出.其二是电机激励进一步加剧车轮振动,影响轮胎的接地安全性 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.