引言

中国山地面积广袤, 超过2/3的面积属于山地和高原, 各种大型灾害时有发生^[1]. 其中, 以颗粒物质流动主导的大尺度灾害如滑坡、泥石流, 对人类的生命安全和各类基础设施有着巨大的威胁^[2-3]. 2010年8月8日, 甘肃舟曲县发生特大规模山洪泥石流, 造成1467人遇难, 298人失踪^[4]. 2017年6月24日, 四川省阿坝州茂县发生特大滑坡灾害, 造成83人死亡, 冲毁民房数十座, 给当地民众带来了巨大损失^[5]. 为了有效应对这类含大量颗粒物质的地质灾害, 通常在重要的聚居区或建筑物前设置一些防护结构, 改变泥石流等灾害的运动路径、消耗能量降低冲击作用, 以达到防治或减轻灾害的效果^[6]. 近年来这类颗粒流动与结构物的相互作用越来越受到关注, 主要集中在建筑物抵抗灾害冲毁作用评估以及设置障碍物系统防灾减灾两方面. 因此, 研究颗粒流与结构物相互作用的动力过程有助于防灾减灾, 具有重要的工程意义.

颗粒材料的本构模型与通常的水体介质有显著不同, 导致颗粒流与结构物相互作用的模式和以水流为主的灾害(如洪水)差别很大^[7-8]. 颗粒流与结构物作用包含冲击、绕流、爬升等行为, 近10年来颗粒流与结构物作用的动力过程吸引了大量****进行研究^[9-10]. Pudasaini等^[11]进行了干颗粒流冲击挡土墙的室内斜槽实验, 挡土墙会导致颗粒流从快速运动的超临界薄层变化到厚度逐渐增加的静止堆积体, 最后的堆积面由颗粒材料的休止角决定. 他们利用粒子图像测速技术(PIV)进行观测, 分析了激波的形成和传播过程、超临界流体深度的演化、冲击速度和动量的变化, 并进行了初步的一维数值模拟. Pudasaini和Kroener^[12]进一步对快速密集颗粒流中的强激波进行了数值研究, 预测得到了大部分Pudasaini等^[11]的实验结果. Teufelsbauer等^[13]发展了一种模拟干颗粒在斜面上流动的离散元模型(DEM), 研究发现考虑旋转约束的DEM更准确地反映干颗粒物质的行为, 同时还模拟了流通、沉积和撞击过程. Zhou等^[14]利用DEM研究了泥石流冲击狭缝坝的爬升高度, 并通过动量定理给出了解析表达式. Bi等^[15]利用DEM模拟研究了不同行间距和列间距的结构物阵列对颗粒流冲击力的影响. 孙新坡等^[16]采用DEM研究了都江堰汶川高速公路龙洞子隧道出口的崩塌体运动过程, 对拦石墙进行了优化设计. Dai等^[17]建立了一个泥石流流过拦沙坝的光滑粒子流体动力学(SPH)模型, 其中泥石流模型使用了黏性流体模型, 拦沙坝被处理为弹性固体, 并研究了文家沟和红椿沟地区的泥石流冲击拦沙坝的冲击力演化过程. Gray等^[18]采用深度积分模型, 计算得到了小尺度颗粒流快速流过四面体结构物形成的激波和真空结构. Cui和Gray^[19]研究了颗粒流流过圆柱体结构物所形成的弓形激波以及真空区等流态结构.

在颗粒流与多个结构物相互作用的研究方面, Juez等^[20]建立了一个类浅水波模型模拟颗粒流通过3个半球结构物的过程, 采用修正重力项表达陡峭地形效应, 模拟得到的障碍物附近的颗粒流流态与实验观测基本吻合, 但在结构物周围附近的深度演化存在较大的偏差. 张睿骁等^[21-23]通过DEM对颗粒流和结构物相互作用的影响因素进行了研究, 分别改变结构物尺寸、拦挡距离主要参数, 得到不同形式的拦挡结构对颗粒流冲击效应的影响. Fei等^[24]在模拟过程中采用了3种不同的方式处理结构物, 并比较了3种方法在研究颗粒流与结构物相互作用问题上的优缺点.

综上所示, 当前对颗粒流与结构物的相互作用的研究主要集中在两个方面: 第一是结构物作用下颗粒流动的流态及演化; 第二是颗粒流对结构物的冲击力作用. 目前看起来, 颗粒流和结构物相互作用的模型主要采用垂向积分模式和DEM模型, 垂向积分模式在处理复杂陡峭地形、障碍物处理以及颗粒流本构方面并没有形成共识, 由此在数值计算方法层面也带来了一定的问题, 而DEM模型的研究对颗粒的尺寸、参数校核等方面提出的要求很多, 造成当前的研究主要集中在实验室尺度的颗粒流和结构物相互作用, 对复杂结构阵列情形下的研究还比较缺乏. 本文建立了基于沿程坐标积分模式的数值模型, 模拟在陡峭地形上颗粒流与结构物的相互作用, 特别是结构物作用下颗粒流的流态演化和堆积特征. 在此基础上深入研究了结构物阵列对颗粒流流态演化和堆积行为的影响, 提出了一个新型的指标偏转效率, 和流通效率一起, 定量评价了四面体结构物阵列对颗粒流阻碍作用和偏转作用.

1.
模型与验证

1.1
控制方程

自然环境中的颗粒流灾害在运动过程中, 相对于流动方向, 垂向的尺度很小, 所以可以对其进行垂向积分, 采取沿程坐标建立曲线坐标系, 如图1所示. 其中红色四面体代表结构物, 紫色曲线代表处在一个陡峭坡面上的颗粒流. 绿色线条代表基础地形, 右侧的水平流通区通过一个圆弧过渡区域与左侧的斜坡区域连接在一起. (x, y, z)为建立的沿程坐标系. 选取沿程坐标的主要目的是为了精确处理陡峭地形效应和颗粒流床面作用力的封闭问题.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
陡峭地形下颗粒流与结构物阵列相互作用模型示意图



Figure
1.
Illustration of granular flow past array of obstacles on steep curved terrain



下载:
全尺寸图片
幻灯片


建立基于沿程坐标系的控制方程^[25-26]

$$ frac{{partial {boldsymbol{U}}}}{{partial t}} + frac{{partial {boldsymbol{F}}}}{{partial x}} + frac{{partial {boldsymbol{G}}}}{{partial y}} = {boldsymbol{s}} $$

(1)

式中

$$ begin{split} &{boldsymbol{U}} = {(h,hu,hv)^{ m{T}}} &{boldsymbol{F}} = {left(hu,h{u^2} + dfrac{1}{2}{k_x}{g_z}{h^2},huv ight)^{ m{T}}}& {boldsymbol{G}} = Biggl({15}hv,huv, h{v^2} + dfrac{1}{2}{k_y}{g_z}{h^2} Bigggr){15}^{ m{T}} & {boldsymbol{s}} = hBigggr[{15}0,{g_x} - dfrac{u}{{sqrt {{u^2} + {v^2}} }} tan delta left({g_z} + dfrac{{{u^2}}}{{{r_x}}} ight) - {g_z}dfrac{{partial {z_b}}}{{partial x}} &quad {g_y} - dfrac{v}{{sqrt {{u^2} + {v^2}} }}tan delta left({g_z} + dfrac{{{v^2}}}{{{r_y}}} ight) - {g_z}dfrac{{partial {z_b}}}{{partial y}}Bigggr]{15}^{ m{T}}end{split}$$

其中, $ t $代表时间, x, $ y $是坐标系的两个方向. $ h $为颗粒物质的深度. $ u $和$ v $分别是颗粒流在$ x $和$ y $方向的深度平均速度. $ {boldsymbol{g}} = {({g_x},{g_y},{g_z})^{
m{T}}} $为重力在坐标系3个方向上的分量, $ {z}_{b} $为相对于曲面地形的局部偏移量, $ {r}_{x} $和$ {r}_{y} $为曲率半径, $ delta $为床面摩擦角.

颗粒流是一种特殊的复杂流体, 既表现出流体的性质, 也有一定的固体特性, 所以需要构建能够准确描述这种特性的本构关系. 从土力学角度出发, 考虑应力的各向异性, $ {k}_{x} $和$ {k}_{y} $是由摩尔?库伦定律确定的沿坡和跨坡方向的土压力系数, 表征运动土体水平和垂向压力的比值, 控制颗粒流沿流向和横向的铺展速率. 对于主要运动方向为沿坡面向下的颗粒流.

$$begin{split} & {k_x} = 2left[ {1 mp sqrt {1 - {{cos }^2}phi left( {1 + {{tan }^2}delta } ight)} } ight]{sec ^2}phi - 1 & {k_y} = dfrac{1}{2}left[ {1 + {k_x} mp sqrt {{{left( {1 - {k_x}} ight)}^2} + 4{{tan }^2}delta } } ight]end{split} $$

方程主要参数是混合流体的内摩擦角$ phi $和床面摩擦角$ delta $. 其中, 内摩擦角主要控制颗粒流体的变形程度, 床面摩擦角主要控制其流动距离^{[25, 27]}.

1.2
地形与结构物的参数化处理

在模拟过程中, 颗粒流流体模型的准确性和结构物的处理方法都是问题的难点. 在本文的研究中, 采用参数化方案生成基础地形和结构物阵列.

首先建立了一个如图1所示的沿程坐标系. 基础地形由3部分组成, 即蓝色虚线代表的坡面区域, 绿色虚线代表的圆弧过渡区域和蓝色实线代表的水平流通区. 其中, 坡面区域与水平面的角度为$ theta $, 圆弧过渡区与坡面区域和水平流通区的边界分别为$ {x_l} $和$ {x_r} $. 通过对这些关键参数, 以及$ x $方向和$ y $方向的范围和网格数等参数进行简单设置, 就可以得到基础地形.

对于结构物(图1中红色凸起区域), 将其处理为一个相对于基础地形的局部偏移量, 用局部床面变化的场函数表示^[10-11]. 同样采用参数化的生成方案来生成结构物, 只需输入不同的结构物种类参数就可以生成长方体、四面体、圆柱体等形式的结构物, 再对结构物的几何参数, 位置以及数量等参数进行设置, 就可以得到不同形式的结构物阵列. 生成初始颗粒堆积体所需要的参数与生成结构物阵列类似. 此时, 结构物被处理为地形, 本文模型可以在统一框架下处理颗粒流在结构物作用下的反射、爬升以及绕射等动力过程.

1.3
数值方法

颗粒流的控制方程是带源项的双曲系统, 这种非线性双曲系统的典型特征是会产生激波. 一阶格式往往会把激波抹平, 所以需要一种能够很好地捕捉激波的高分辨率格式求解控制方程. 除此以外, 还需要正确处理干湿边界条件, 控制启停行为, 以达到在统一的欧拉框架下计算整个颗粒流与结构物相互作用动力过程. 扩展Kurganov和Petrova^[28]在求解浅水方程时提出的激波捕捉格式(Kurganov格式)处理对流项, 采用算子分裂方法计算源项.

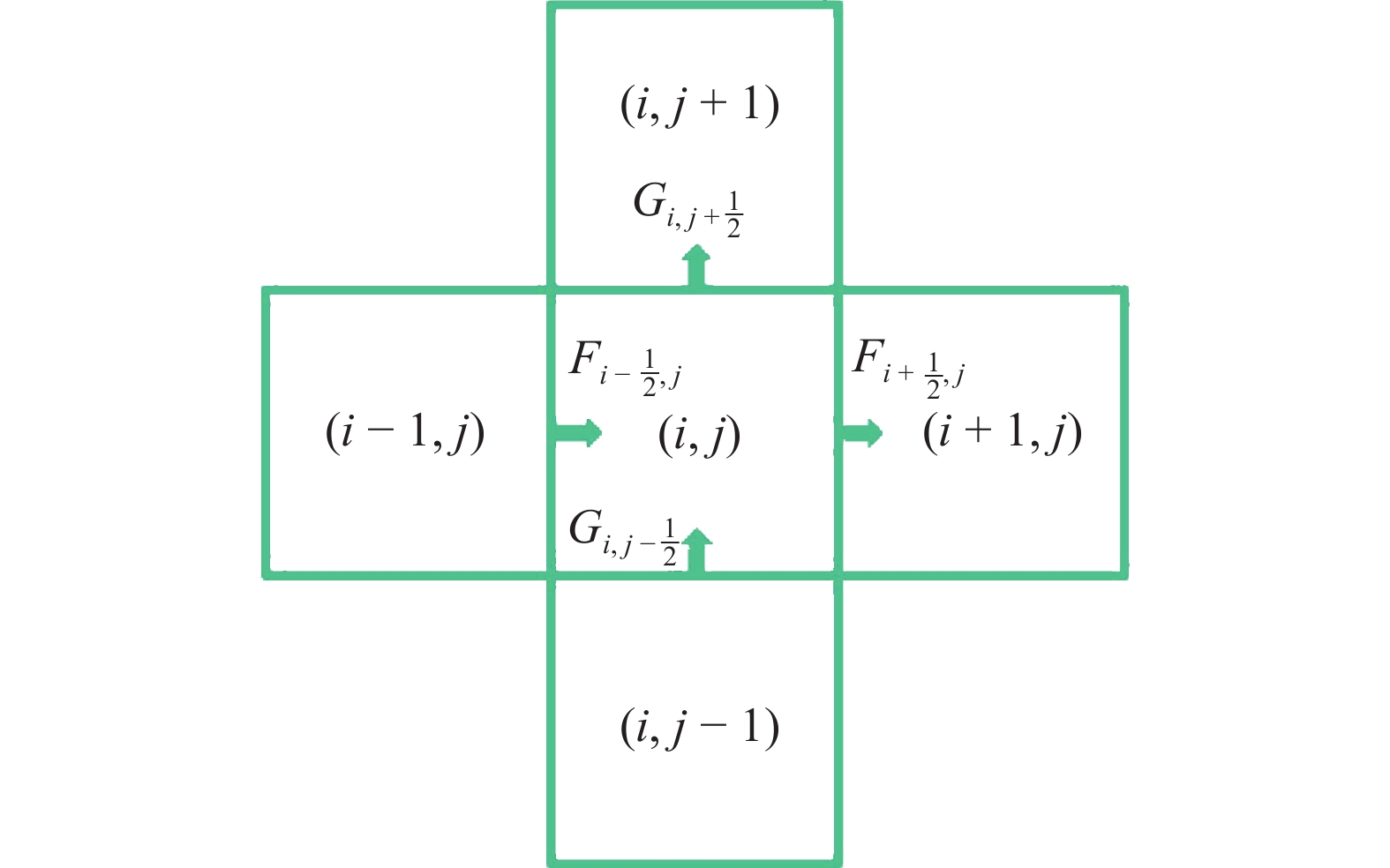
采用基于结构网格的有限体积法的网格划分如图2所示. 对于单元格$ (i,j) $, 定义场变量平均值为$ {{boldsymbol{U}}_{i,j}} = dfrac{1}{{Delta xDelta y}}displaystyleint {{boldsymbol{U}}{
m{d}}x{
m{d}}y} $, 而方程1左侧部分的时间推进格式为

$$ {boldsymbol{U}}_{i,j}^{(k + 1)} = {boldsymbol{U}}_{i,j}^k - frac{{Delta t}}{{Delta x}}left( {{{boldsymbol{F}}_{i + tfrac{1}{2},j}} - {{boldsymbol{F}}_{i - tfrac{1}{2},j}}} ight) - frac{{Delta t}}{{Delta y}}left( {{{boldsymbol{G}}_{i,j + tfrac{1}{2}}} - {{boldsymbol{G}}_{i,j - tfrac{1}{2}}}} ight) $$

(2)

其中$ {{boldsymbol{F}}_{i + tfrac{1}{2},j}} $和$ {{boldsymbol{G}}_{i,j + tfrac{1}{2}}} $是单元格$ (i,j) $右侧和顶部的数值通量, $ Delta t $是时间步长, $ Delta x $和$ Delta y $是单元格的边界尺寸. 采用Kurganov格式^[28]计算数值通量



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
有限体积法网格划分和数值通量示意图



Figure
2.
Index of the mesh and numerical fluxes for finite volume methods



下载:
全尺寸图片
幻灯片

$$ begin{split} &{{boldsymbol{F}}_{i + tfrac{1}{2},j}} = frac{{a_{i + tfrac{1}{2},j}^ + {boldsymbol{F}}left({boldsymbol{U}}_{i + tfrac{1}{2},j}^ - ight) - a_{i + tfrac{1}{2},j}^ - {boldsymbol{F}}left({boldsymbol{U}}_{i + tfrac{1}{2},j}^ + ight)}}{{a_{i + tfrac{1}{2},j}^ + - a_{i + tfrac{1}{2},j}^ - }} + &qquadfrac{{a_{i + tfrac{1}{2},j}^ + a_{i + tfrac{1}{2},j}^ - }}{{a_{i + tfrac{1}{2},j}^ + - a_{i + tfrac{1}{2},j}^ - }}left( {{boldsymbol{U}}_{i + tfrac{1}{2},j}^ + - {boldsymbol{U}}_{i + tfrac{1}{2},j}^ - } ight)end{split} $$

(3)

其中, 采用MUSCL方法插值, 结合Minmod限制器, 构造单元格$ (i,j) $边界上的左右两侧的向量$ {boldsymbol{U}}_{i + tfrac{1}{2},j}^ - $和$ {boldsymbol{U}}_{i + tfrac{1}{2},j}^ + $, 使数值格式的空间精度在光滑区达到二阶^[28], $ a_{i + tfrac{1}{2},j}^ + $和$ a_{i + tfrac{1}{2},j}^ - $分别是单元格$ (i,j) $各边界上最大和最小的波速. 通量$ {{boldsymbol{G}}_{i,j + tfrac{1}{2}}} $的计算方式与$ {{boldsymbol{F}}_{i + tfrac{1}{2},j}} $类似.

为了在统一计算框架下处理颗粒流的移动边界或颗粒流前缘, 仿照浅水波模型的术语, 将颗粒流的前缘也称之为“干湿边界”, 这里应用了一种改进的“干湿边界”处理方法^[29]. 把干单元格定义为单元格内颗粒平均堆积深度小于一个非常小深度$ {h_{min }} $的单元. 当所有相邻单元的平均深度都小于$ {h_{min }} $时, 认为流动停止; 当一些相邻的单元内的平均深度大于$ {h_{min }} $时, 只计算质量守恒方程, 速度从最深的相邻单元外推. 这样可以避免非物理结果, 比如负深度. 先前关于快速颗粒流运动^[29]和浅水波方程的数值求解^[30]都表明, $ {h_{min }} $值取为$ {10^{ - 6}} $时, 界面前缘的捕捉较为理想, 可以避免虚假振荡, 防止薄层水流出现超大速度.

采用Strang分裂方法^[31]对源项进行计算, 由于源项不涉及微分运算, 因此直接采用时间向前积分, 即在对流算子推进的基础上再进行源项直接积分更新动量和速度. 为保障在单个时间步内不出现回流现象, 单个单元的速度如果出现回流, 则直接在本时间步的计算中将其设置为零.

1.4
模型验证

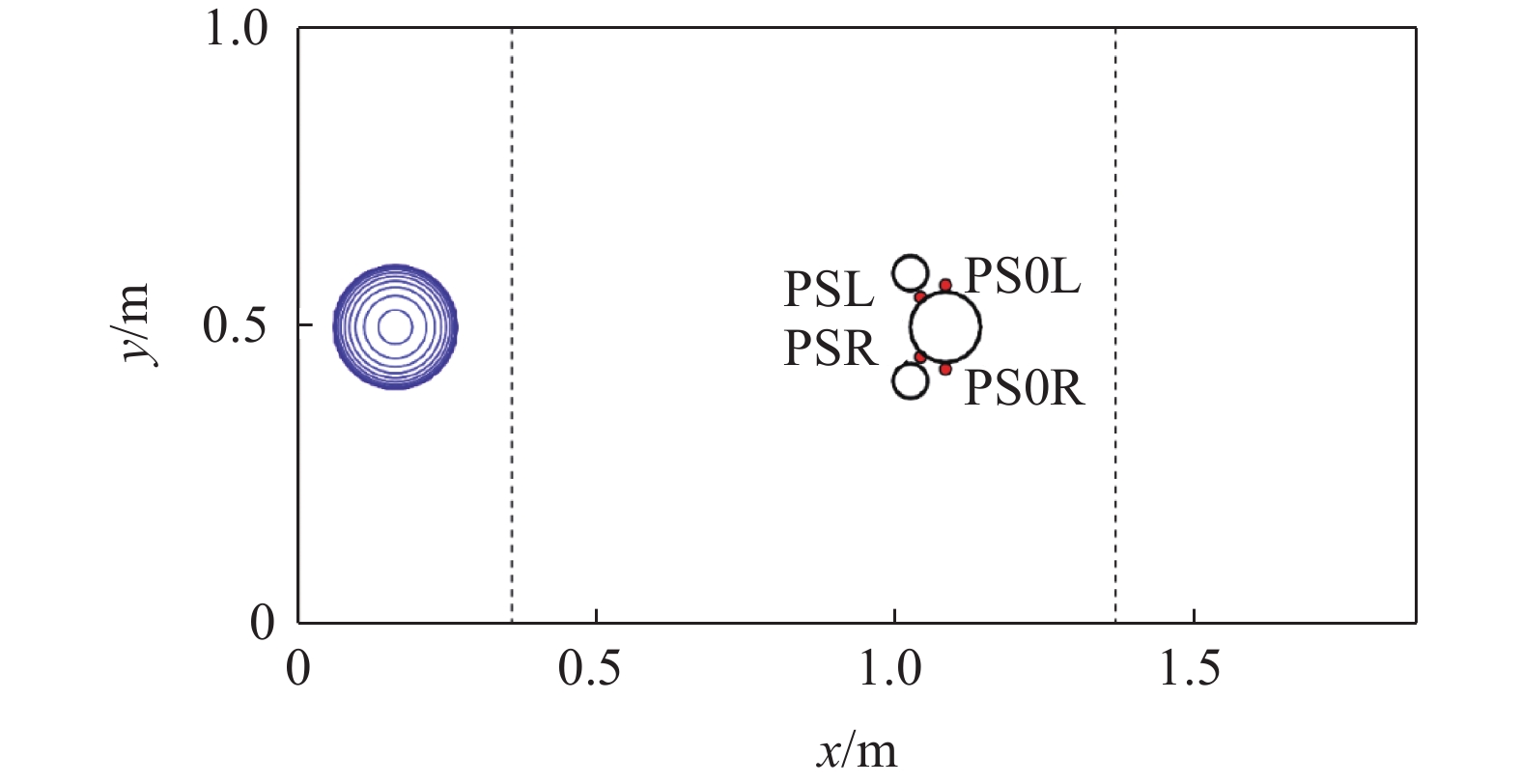
为了验证本文所建立的基于沿程坐标积分模式的数值模型, 模拟Caviedes-Voullième等 ^[32]开展的典型颗粒流与结构物作用实验, 即颗粒流与一大二小共计3个半球相互作用的实验. 首先将文献[32]中的全局坐标转变为本文的沿程坐标, 得到计算区域为[0, 1.88 m] × [0, 1 m]. 初始颗粒堆积体为一个半径为104 mm的半球形堆积体, 位于(162.4 mm, 500 mm)处. 大的半球形结构物的半径为59 mm, 位于(1.083 4 m, 0.5 m)处, 两个小的半球形结构物的半径为29 mm, 分别位于(1.024 8 m, 0.41 m)处和(1.024 8 m, 0.59 m)处, 如图3所示. 主要地形相关参数和物理参数如表1所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
颗粒初始时刻及4个固定测点位置示意图, 虚线之间为过渡区, 虚线左侧为斜坡, 虚线右侧为流通区



Figure
3.
Initial positions of granular flow and four probes, region in between the two dashed lines is transition area, the slope is to the left of the two dashed lines, and the runout zone is to the right of the two dashed lines



下载:
全尺寸图片
幻灯片





表
1
“三半球实验”模拟算例基础地形生成关键参数数值表



Table
1.
Parameters involved in generating steep curved terrain of “three hemi-spheres experiment”



table_type1 ">

$ {x}_{l} $/m	$ {x}_{r} $/m	$ varphi $/(°)	$ delta $/(°)	$ theta $/(°)
0.357 3	1.368 0	34	34	52

下载:
导出CSV
|显示表格



设置了5组不同的网格密度对“颗粒流冲击三半球问题”进行模拟, 对数值模型进行网格无关性测试. 提取了障碍物附近的两个典型测点PSL和PS0L (见图3), 在5次模拟结果中的颗粒流深度并进行对比, 结果如图4所示. 当网格密度设置为50 × 50和100 × 100时, 固体测点的时程曲线变化较大, 并没有收敛; 而网格密度达到200 × 200及以上时, 计算结果达到收敛. 在后续数值算例中, 为保障收敛性, 如无特殊说明, 所有的算例中, 网格数量默认为400 × 400.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同网格数典型测点的颗粒流深度时程曲线



Figure
4.
Depth of granular flow over time at fixed measuring points under different grid densities



下载:
全尺寸图片
幻灯片


文献[32]并没有给出床面摩擦角$ delta $具体数值, 本文对其进行了多次测试, 发现当$ delta = 34^circ $时, 可以更好地描述颗粒堆积与铺展的状态, 与实验结果也更加匹配. 而原实验中, 结构物所在区域的下游地形有一个逐渐弯曲向上的曲率, 但由于那部分区域几乎没有颗粒流经过, 也并不影响颗粒流与结构物相互作用的过程, 所以本文的模型将其处理为水平面, 并不会对最终结果造成显著差异.

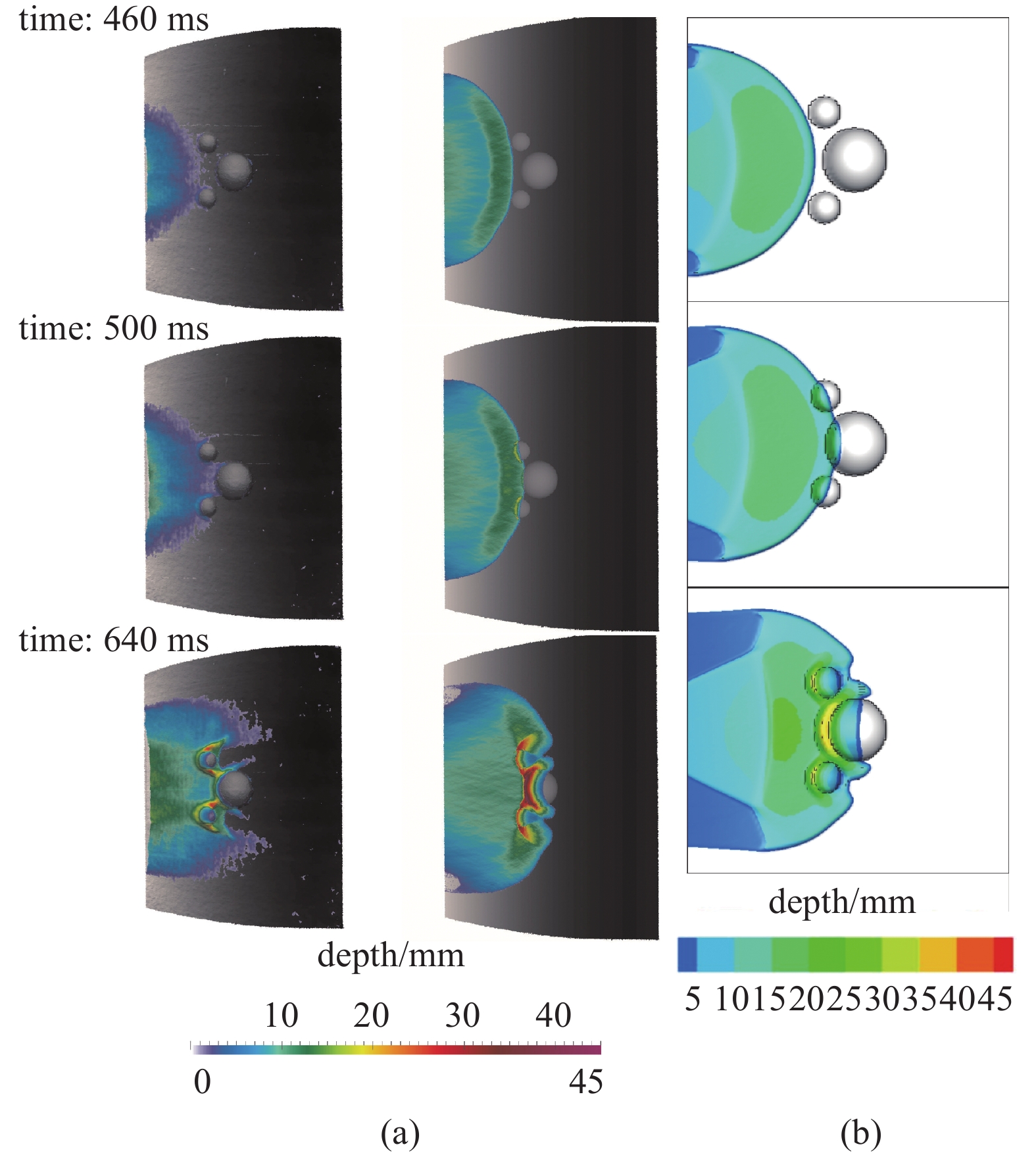
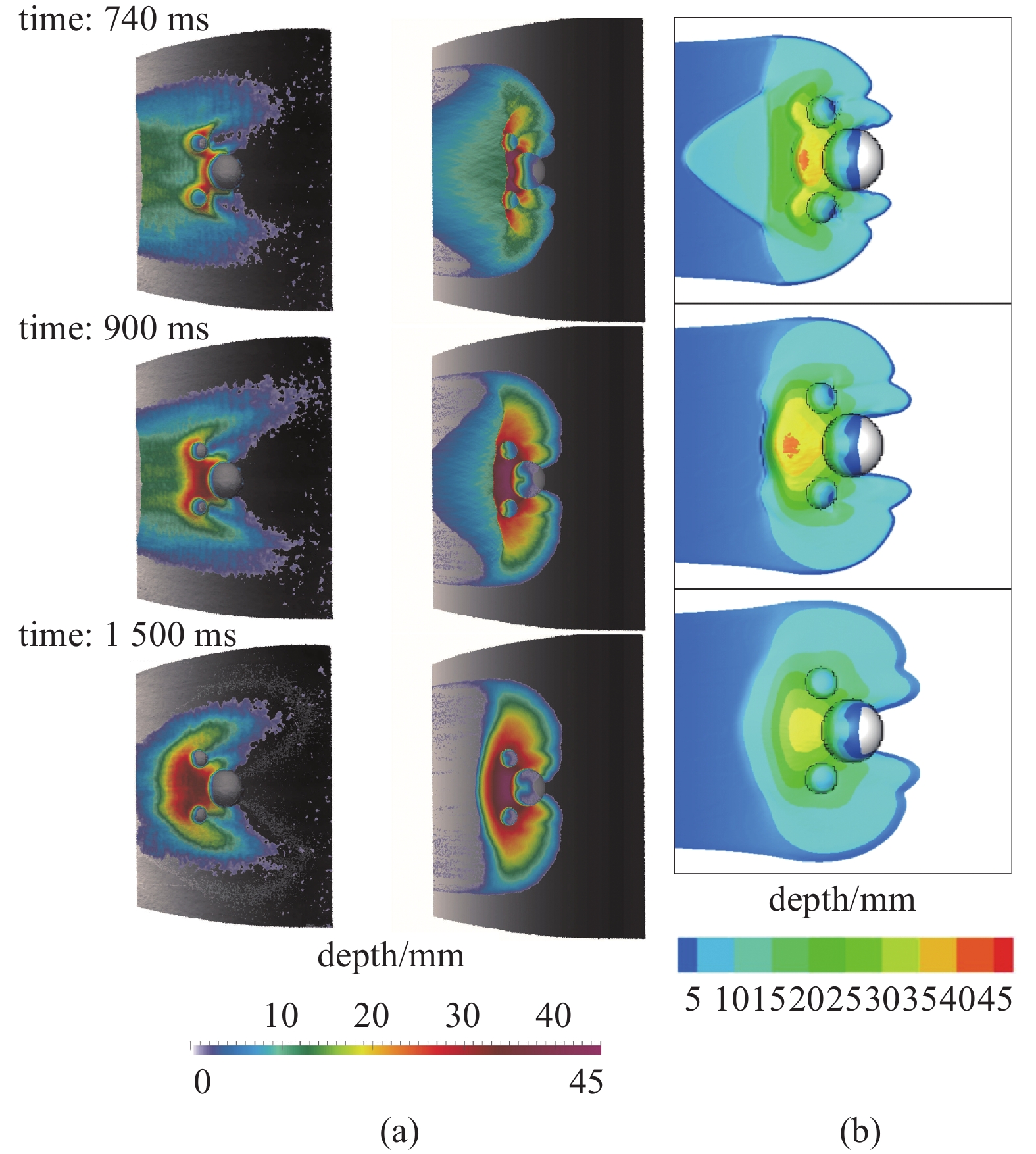
将Caviedes-Voullième等^[32]的实验结果和基于全局坐标积分模式的数值模拟结果与本文的模拟结果进行了比对. 本文对几个典型时刻进行了细致的分析, 如图5和图6所示. 在t = 460 ms时, 颗粒流前缘即将与较小半球发生接触; 在t = 500 ms时, 颗粒流前缘与较大半球开始接触, 仔细观察可以发现, Juez等^[20]的模拟结果在前缘部分有一个狭长的弧形区域集中了大量颗粒物质, 而本文模型模拟结果与实验数据则更为发散. 在t = 640 ms时, 颗粒流与结构物发生冲击, 形成了3个强弱不等的激波. 当t = 740 ms时, 3个激波向上游运动并开始接触; 在t = 900 ms时, 3个激波合并成新的波状激波并向上游运动, 随后慢慢松弛, 形成最终的堆积体. 观察图5结果, 可以发现Juez等^[20]的数值模拟结果和本文的结果均较实验结果略微落后. 本文模型的模拟结果显示, 大量的颗粒物质被截留在结构物所处区域及上游区域, 与实验结果更为吻合, 体现了结构物对颗粒流的截留作用和对下游的保护作用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
几个典型时刻颗粒流深度分布文献结果^{[20, 32]}与本文模拟结果对比. (a) 第1列为实验结果, 第2列为文献中的模拟结果(图片使用得到Elsevier的许可), (b) 本文数值模型模拟结果



Figure
5.
Comparisons between the results from literature^{[20, 32]} and the simulation results of this paper at different times. (a) The first column is the experimental results, and the second column is simulation results from literature (permitted by Elsevier). (b) The numerical simulation results of this paper



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
几个典型时刻颗粒流深度分布文献结果^{[20, 32]}与本文模拟结果对比. (a) 第1列为实验结果, 第2列为文献模拟结果(图片使用得到Elsevier的许可), (b) 本文数值模型模拟结果



Figure
6.
Comparisons between the results from literature ^{[20, 32]} and the simulation results of this paper at different times. (a) The first column is the experimental results, and the second column is simulation results from literature (permitted by Elsevier). (b) The numerical simulation results of this paper



下载:
全尺寸图片
幻灯片


图7给出了4个特定测点的颗粒流深度与实验结果和基于全局坐标垂向模式的模拟结果的比较. 4个测点分别是PSL, PSR, PS0L和PS0R, 它们分别位于大球的肩部和侧面, 如图3所示. 图7中的3条曲线分别是多次实验的平均深度时程演化^[32]、Juez等^[20]的模拟结果和本文的模拟结果. 在大球肩部的两个测点PSL和PSR, 本文模拟的峰值深度小于Juez等^[20]的模拟结果, 更加贴近实验结果, 而最后达到的稳定深度基本和实验结果吻合, 大球肩部两个测点处在形成稳定深度之前出现了一个峰值, 这是由于大球肩部形成了较为显著的激波结构, 如图5(b), 而随着颗粒物质补充的逐渐减少, 激波会逐渐消失, 最后在摩擦阻力的作用下逐渐达到稳定的堆积状态. 在大球两个侧部的两个测点PS0L和PS0R, 已经基本远离激波形成区域, 不存在明显的峰值, 因此大球侧部两个测点的时程表现为逐渐增高直至稳定堆积状态, 本文模拟的稳定深度略高于实验结果, 但是模拟效果略好于Juez等^[20]的模型.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
4个测点的颗粒流深度变化时程曲线



Figure
7.
Depth of granular flow over time at the four probe positions



下载:
全尺寸图片
幻灯片


需要指出的是本文模型基于沿程坐标, 能够较好的表征地形的平均曲率效应, 从而准确反映颗粒动力学过程在陡峭地形情形下受到离心和阻力作用, 但是障碍物作为相对于曲面地形的局部偏差, 在控制方程中以源项体现, 在实际情况下障碍物附近的颗粒流动之三维效应会比较明显, 这是造成激波效应不明显的大球侧部测点计算结果相比实验结果有偏差的主要原因, 而三维效应也导致大球肩部测点处的深度峰值计算结果比实验结果略高. Juez等^[20]的模拟主要基于全局坐标的垂向积分模式, 虽然考虑了薄层颗粒流的约化重力效应, 但是无法准确表征陡峭地形导致的离心和阻力作用^[33], 因此模拟结果不如本文模型.

总体来说, 本文发展的基于沿程坐标的数值模型相比于基于全局坐标的垂向积分模式在表征复杂地形条件颗粒流与结构物相互作用问题上更为准确一些, 数值模型能够很好地模拟颗粒流与结构物作用中的反射、绕射以及爬升等现象, 捕捉相互作用过程中形成的激波结构及其演化等过程.

2.
颗粒流与阵列式结构物的相互作用

2.1
算例设置

为了减轻颗粒流灾害的破坏力, 一种经济有效的减灾措施是在上游地区设置结构物阵列对颗粒流进行调控^[6,10]. 目前, 工程界已经采用了在滑坡泥石流雪崩等灾害性颗粒流的流经路径上布置障碍物的方案防治和减轻灾害^{[10, 27, 34]}, 其设计准则主要依赖于工程经验和室内小尺度实验, 现阶段对该类阵列结构防护效果的数值模拟和定量评估还鲜有报道. 本文主要研究一类典型的四面体结构物阵列^{[10, 34]}对颗粒流的防护效果, 通过设置了不同行数的四面体结构物阵列, 模拟分析颗粒流与结构物阵列之间的相互作用过程, 探究颗粒流动过程和堆积状态的改变. 计算区域设置为[0, 60 m] × [0, 40 m], 网格数量为400 × 400. 选取一个典型斜坡和典型颗粒材料物理参数, 见表2. 在坐标(6 m, 20 m)处设置一个半径为2m的半球形的颗粒堆积物模拟初始滑体.




表
2
“四面体结构物阵列”系列算例基础地形生成关键参数数值表



Table
2.
Parameters involved in generating steep curved terrain of “arrays of tetrahedral obstacles” cases



table_type1 ">

$ {x}_{l} $/m	$ {x}_{r} $/m	$phi$/(°)	$ delta $/(°)	$ theta $/(°)
30	35	25	24	40

下载:
导出CSV
|显示表格



在坡面区域设置不同行数的四面体结构物阵列, 每个四面体的高度为4.5 m, 底面为面积是1 m²的正三角形, 每行结构物由9个完全相同的四面体组成, 每个四面体的间距为4 m, 第一行结构物位于x=13 m, 不同行之间交错排列, 行间距为3 m. 首先模拟了没有结构物情况下初始颗粒堆积体沿斜坡的流动堆积过程, 然后分别模拟1 ~ 5行四面体结构物阵列作用下, 颗粒流的流态演化和堆积过程.

2.2
流动过程的演化

初始颗粒堆积体在释放后, 由于重力和压力梯度的作用, 会开始变形并沿坡面运动, 迅速演变成沿坡面向下的颗粒流. 如果没有结构物作用, 在t = 4 s时, 如图8(a)所示, 大部分颗粒流已经到达平面流通区域. 之后, 由于没有了沿斜坡向下的重力分量作用, 流通到平面区域的颗粒因为摩擦作用会逐渐减速, 而后续颗粒依然会以较高速度持续流入平面区域, 所以在波的前缘会堆积大量颗粒, 集中于一个半月牙型的狭窄区域, 有激波结构存在.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
t = 4 s时颗粒流与不同行数四面体结构物阵列相互作用的流态



Figure
8.
Flow patterns of granular flow facing obstacle array of tetrahedrons of different rows at t = 4.0 s



下载:
全尺寸图片
幻灯片


当存在四面体结构物阵列时, 结构物会与颗粒流发生显著的相互作用而形成新的流动结构与堆积形态. 当设置1行四面体结构物时, 如图8(b)所示, 颗粒在流动过程中正面冲击到四面体后, 由于两个倾斜侧面的存在, 颗粒流会发生偏转, 分成两道继续向下游流动. 四面体结构物的背部没有颗粒物质, 形成一个真空区. 被分流后的颗粒流还会与被前排其他四面体结构物偏转的颗粒流发生汇聚, 相互冲击会消耗大量能量. 在t = 4 s时, 有相当多的颗粒已经到达平面流通区. 当设置2行四面体结构物阵列时, 如图8(c)所示, 相互作用过程更为复杂. 颗粒冲击到第一排四面体结构物后发生上文所述的流动行为, 然后会继续被第2排的四面体结构物重新分流, 再次因为偏转作用被分成两股向下游流动, 被不同四面体分流的颗粒依然可能再次发生汇聚冲击. 由于颗粒流之间发生的多次汇聚冲击以及被偏转后流动路径的变化, 在t = 4 s时, 大部分颗粒依然位于斜坡区域, 仅有少量颗粒物质到达平面区域. 随着四面体结构物行数增加, 如图8(d) ~ 图8(f)所示, 颗粒流之间汇聚冲击的次数也会增加, 流动路径也会变长, 但基本的相互作用模式与2行结构物情况下(图8(c))并无明显区别. 图9给出了5行四面体障碍物作用时, 快速颗粒流形成的典型流态特征, 包括激波特征和偏转特征.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
t = 4 s时颗粒流与5行四面体结构物阵列相互作用的局部流动信息



Figure
9.
Local flow information of granular flow facing obstacle array of tetrahedrons of 5 rows at 4.0 s



下载:
全尺寸图片
幻灯片

2.3
结构物诱导快速颗粒流激波结构特征

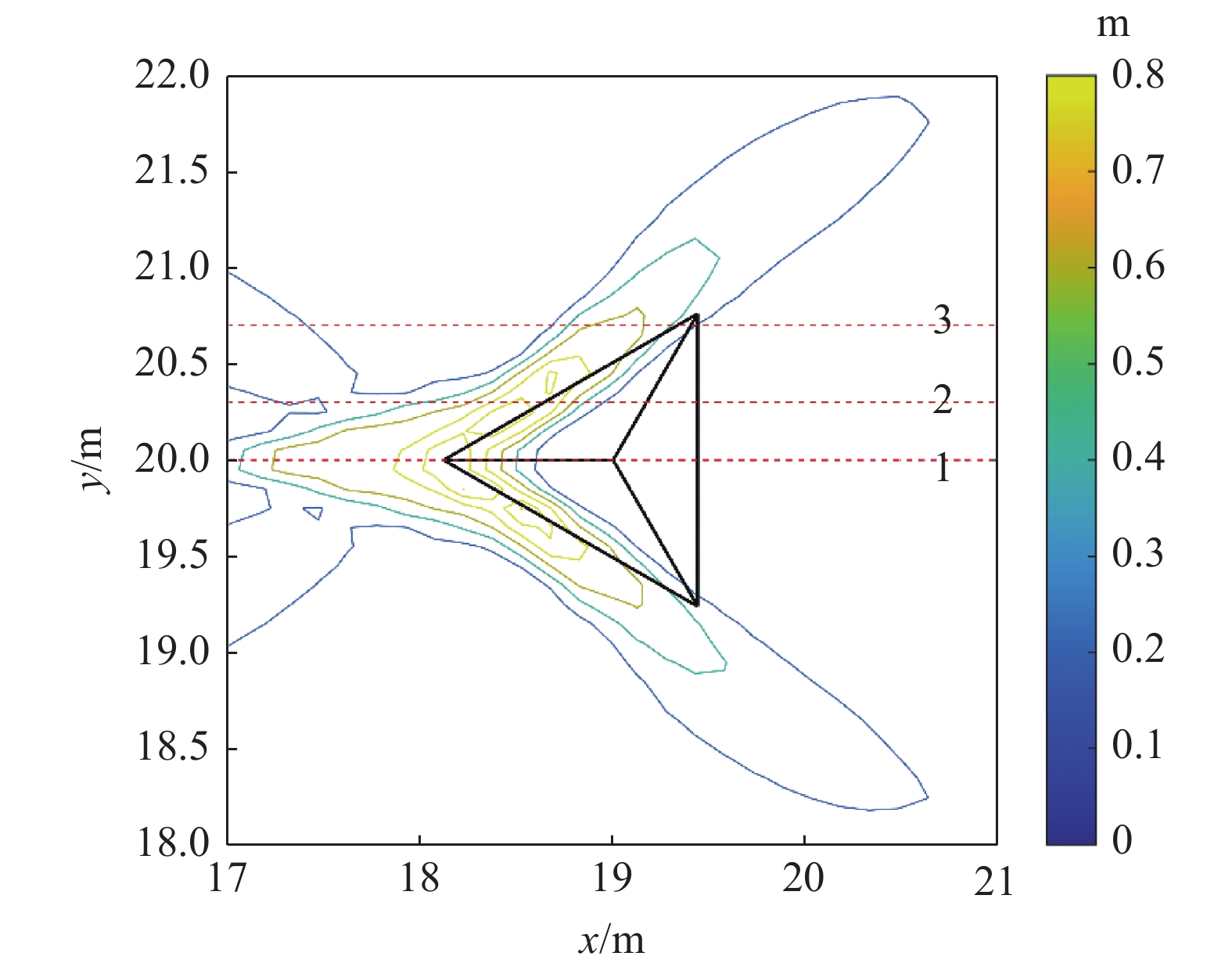
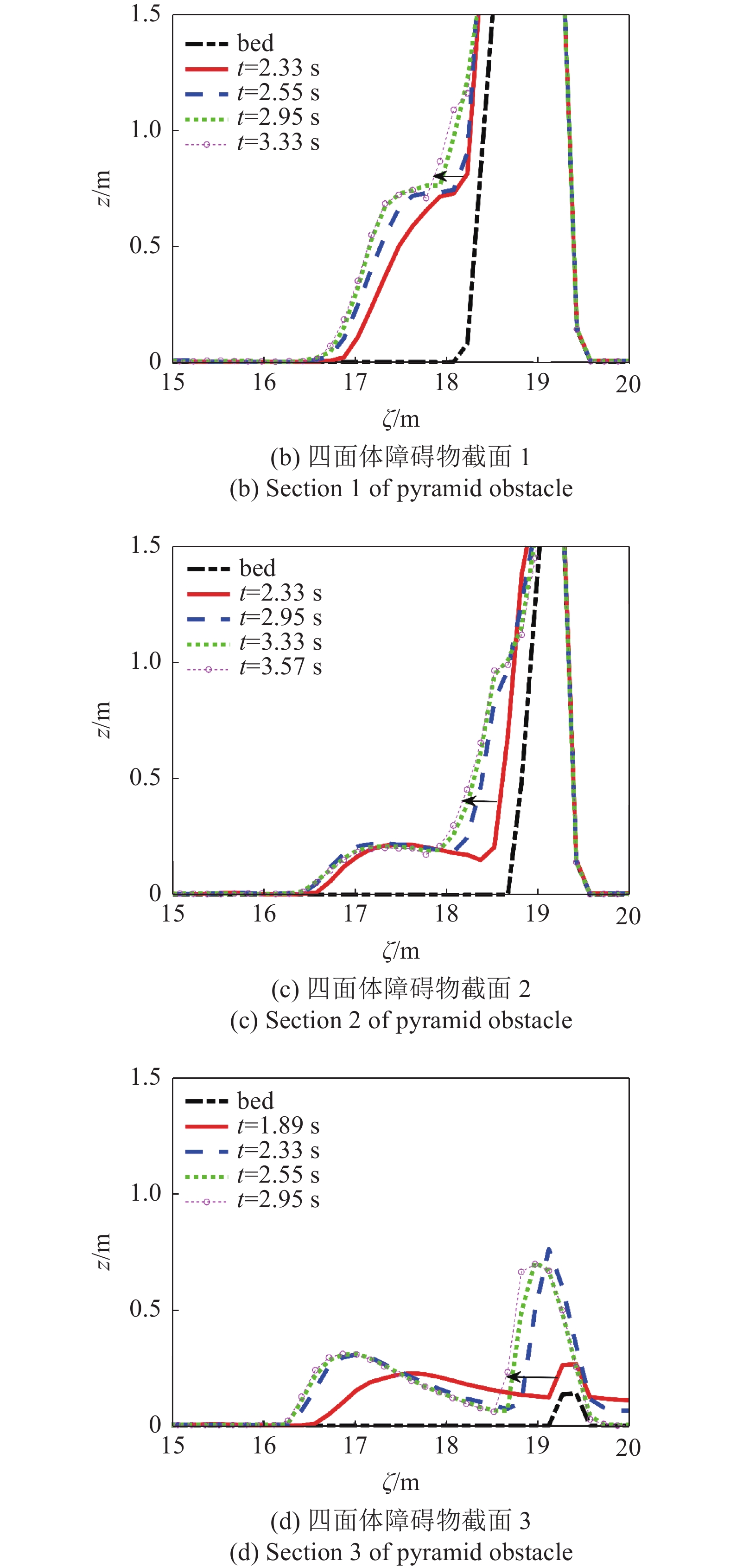
为深入考察颗粒流和结构物作用时激波的形成和特征, 选取了5行障碍物阵列中一个典型的四面体附近的流动为研究对象, 考察3个截面1~3处的颗粒流深度变化特征, 3个截面位置如图10所示, 同时选取3半球算例(图3)在中间截面处(y = 0.5 m)的颗粒流深度变化特征作为比较对象, 结果如图11所示. 图11表明高速颗粒流遇到结构物时会减速甚至堆积形成低速区, 后续的快速颗粒流遇到前方低速的颗粒流动时来不及光滑过渡, 会形成一种类似水跃的间断结构, 在颗粒流领域也被称为激波^{[7, 9, 11-12, 18, 30]}, 这种激波会耗散一部分颗粒流系统的能量, 而障碍物阵列则形成系列的激波结构. 这种激波结构和障碍物的陡峭程度有关, 如图11(a)表明半球附近障碍物接近于垂直墙体, 形成了十分明显的激波向后方运动, 而图11(b)~图11(d)显示, 四面体结构物对颗粒流的降速和阻碍作用相比于接近墙体的半球体要弱, 但依然形成了明显的接近于间断的激波结构向后方传播.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
5排障碍物算例某单个结构物附近颗粒流深度(m)分布, 3条红色虚线1, 2和3为3个考察截面



Figure
10.
Depth distribution (m) of granular flow around a typical obstacle in the case of five rows of obstacles. The three red dashed lines represent three sections for examination



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-11-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11-1" />



11
障碍物附近典型快速颗粒流激波形成与演化



11.
Shock wave formation and evolution for granular flow around an obstacle



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
障碍物附近典型快速颗粒流激波形成与演化(续)



Figure
11.
Shock wave formation and evolution for granular flow around an obstacle (continued)



下载:
全尺寸图片
幻灯片


单一的障碍物可以在障碍物前缘形成弓形激波, 耗散能量; 在遇到障碍物阵列的情况下会形成系列的弓形激波, 耗散更多的能量, 如图8(b)~图8(f)、图9(a)所示. 因此障碍物阵列对颗粒流的作用包括激波的耗散作用和改变流向的偏转作用.

2.4
堆积状态

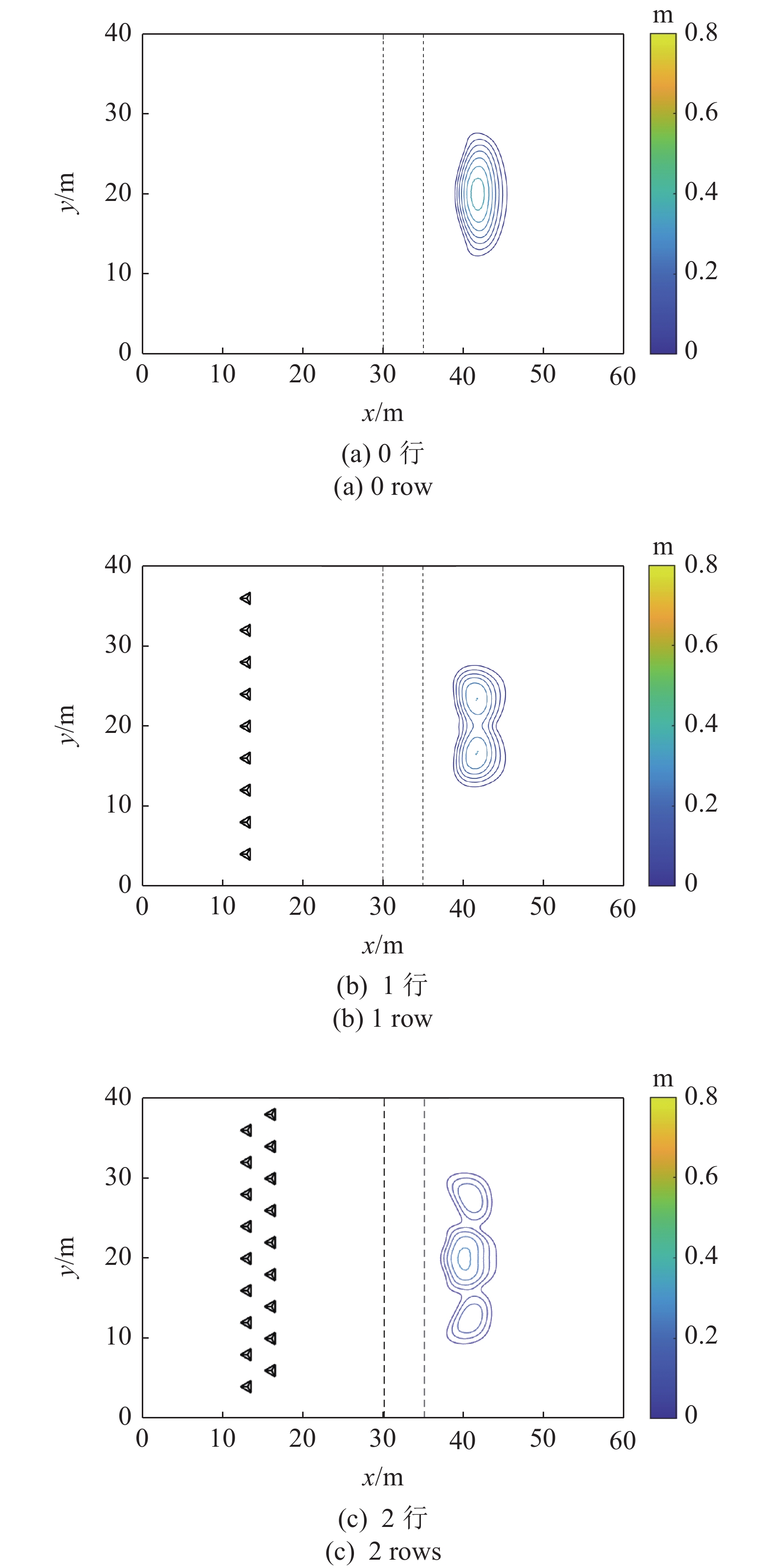
如图12所示, 当各算例模拟到15 s时, 流动行为已经基本全部停止, 颗粒物质以不同的形态堆积在平面流通区. 在没有结构物存在的情况下, 颗粒物质会堆积成一个相对于y方向中心线完全对称的堆积体, 且只有一个堆积峰.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-12-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12-1" />



12
t = 4.0 s时颗粒流冲击不同行数四面体结构物阵列后的堆积厚度分布



12.
Deposits of granular flow facing obstacle array of tetrahedrons of different rows at t = 4.0 s



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
t = 4.0 s时颗粒流冲击不同行数四面体结构物阵列后的堆积厚度分布 (续)



Figure
12.
Deposits of granular flow facing obstacle array of tetrahedrons of different rows at t = 4.0 s (continued)



下载:
全尺寸图片
幻灯片


在有四面体结构物阵列存在的情况下, 最后时刻的堆积状态有了很大的改变. 只有一行四面体结构物时, 颗粒最终会堆积为一个大堆积体, 其中有两个堆积峰. 观察颗粒流动全过程, 可以发现开始堆积时, 这两个堆积峰实际上是分散的两部分堆积体, 但由于偏转次数以及流动距离等的限制, 两部分堆积体比较接近, 随着颗粒增多逐渐合并为一个堆积体.

当存在两行四面体结构物时, 最后颗粒会堆积为3个堆积体, 中间的堆积体略大. 当初始颗粒堆积体向下游流下后被3行四面体结构物阵列调控时, 最终堆积为一大两小3个颗粒堆积体. 其中中部较大的堆积体存在两个堆积峰, 两侧的堆积体比较小. 中部堆积体两个堆积峰的形成原因与一行结构物时的堆积状态形成过程类似, 依然是由于偏转次数较少, 大量颗粒堆积在中部, 使得原本有被分为两个堆积体趋势的颗粒合并为一个.

颗粒流与4行四面体结构物阵列相作用时, 相较于3行阵列多了若干偏转机会, 原来形成中部大堆积体的两股颗粒流还会被偏转一次, 其一部分会相中部集中, 另一部分会被分向两侧, 所以最终会形成五个堆积峰, 颗粒流质量分布情况也会比3行结构物阵列的最终情况更加均匀. 颗粒流与5行四面体结构物阵列相作用时, 有着更多的偏转机会, 同时, 由于分汇次数的增加, 颗粒形成的激波结构耗能增加, 而且流动路径会变得更长, 所以大量颗粒在距离斜坡区域更近的位置停止运动, 在水平流通区的颗粒百分比有所减小.

3.
结果与讨论

3.1
评价堆积状态的两个指标

为了准确描述颗粒流造成的灾害影响范围, 判断防护结构的效果, 需要一些定量指标来直观有效地进行评价. 目前已有的一个评估指标是流通效率(runout efficiency, RE), 它定义为初始颗粒堆积体流出距离与初始高度的比值, 是一个评价滑坡灾害影响范围的重要指标^[28,35]. 各算例在相同的初始颗粒堆积体条件下, RE值越大, 说明流出距离越大, 灾害范围越广; RE值越小, 说明流出距离越小, 结构物防护效果越好.

这个指标显然并不足以精确表述最后的堆积状态. 为了更准确地描述, 从统计学角度出发, 参照流通效率的定义, 提出了一个新的无量纲量, 即偏转效率(deflection efficiency, DE), 来表述颗粒流的偏转效应, 即

$$ left.begin{split} &{sigma }_{y}{}^{2}=frac{{displaystyle int h{(y-{Y}_{C})}^{2}{ m{d}}x{ m{d}}y}}{V}text{ }&{DE=}frac{sqrt{{sigma }_{y}{}^{2}}}{{r}_{0}} end{split} ight}$$

(4)

其中, h为堆积状态各单元格内颗粒堆积深度, $ {Y}_{C} $为堆积体的质心坐标, V为颗粒堆积体的体积, $ {r_0} $为初始颗粒堆积体的底面的半径. DE可以在一定程度上表征防护结构对滑坡灾害的偏转作用, 其值越大, 说明颗粒流被分散的越广. 表3列出了所有计算案例的流通效率和偏转效率.

根据数据可以发现, 由于结构物阵列的作用, RE值减小了, 但减小幅度并不大, 在仅有1行四面体结构物时几乎没有变化. 随着行数增加, 减小幅度约为6%~15%. 以没有障碍物的堆积结果为基准, DE的增大幅度更为显著. 在设置1行结构物后, 就可增大25%; 设置2行结构物, DE增大65%; 在结构物阵列为3行时, 增大77%; 在结构物阵列为4行时, 增大约111%; 当阵列行数为5行时, 增大117%.

综上所述, 无量纲量偏转效率DE指标可以在一定程度上描述阵列结构物对颗粒流的偏转效应. 结合耗散, 结构物阵列对颗粒流有十分有效的综合调控效果. 因为本次模拟的是四面体型结构物, 它的几何形状决定了对颗粒流最大的作用是使其偏转, 主要依靠增加流动路径和不同股颗粒流之间的汇合冲击进行耗能, 因冲击结构物导致的能量损失并不多, 所以RE值的减小幅度并不如DE的增大幅度显著.




表
3
颗粒流与多行四面体结构物阵列作用流通效率和偏转效率



Table
3.
RE and DE of granular flow facing obstacle array of tetrahedrons



table_type1 ">

Row number	0	1	2	3	4	5
RE	1.68	1.67	1.58	1.50	1.46	1.43
DE	1.74	2.18	2.88	3.08	3.68	3.78

下载:
导出CSV
|显示表格

3.2
指定区域的颗粒堆积深度变化

假设在平面流通区有一处需要受到保护的建筑物或人类聚居地, 其坐标为(40 m, 20 m), 临近圆弧过渡区域. 本文提取了整个模拟过程中, 这一点在上游无结构物情况下和上游存在不同行数结构物阵列以作保护的情况下的颗粒堆积深度的数据进行了对比, 如图13所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-200-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
(40 m, 20 m)处颗粒流堆积深度时间历程曲线



Figure
13.
Depth of granular flow over time at (40 m, 20 m)



下载:
全尺寸图片
幻灯片


当上游没有结构物存在时, 颗粒流会在短时内迅速通过这一处, 然后由于能量耗尽后, 颗粒会在松弛堆积时, 再次返回这一点位, 使得图像在7 s左右出现了第二次急速升高的趋势. 当存在一行结构物时, 大量颗粒被分流到两侧, 首先到达的颗粒离开了中轴, 所以这一点位的颗粒通过时间会延后, 堆积峰值也会变小. 当两侧的颗粒成堆时, 会有部分颗粒堆积松散向四周滑落, 两堆颗粒都有滑向中部的颗粒, 所以随着时间推进, 颗粒堆积深度会小幅增大. 当存在两行结构物时, 正如3.1中所述, 第2排结构物对颗粒的偏转反而会使一部分颗粒向中部集中, 所以堆积峰值反而会比无结构物时更大. 当存在3行结构物时, 颗粒流首次通过时的深度峰值明显下降. 从上一节的内容可知, 3行结构物阵列并不能使颗粒流得到充分的偏转分散, 仍然有大部分颗粒流位于中轴附近. 这些通过后的颗粒会慢慢堆积在平面流通区, 同时对后续颗粒流起到阻碍作用, 所以随着时间增加, 深度曲线会缓缓升高. 当存在4行结构物时, 堆积峰值进一步降低, 中轴附近的颗粒在还没到达点位时就已耗尽能量而停止流动. 当存在5行结构物时, 颗粒流得到充分偏转, 大量颗粒被分散到两侧. 流经这一处的颗粒大大减少且通过时间延后, 起到了良好的保护作用. 所以, 当存在一定形式的结构物阵列后, 对于特定地区, 可以起到有效的减灾效果.

4.
结论

针对颗粒流与结构物相互作用问题, 本文使用数值模拟方法, 通过对典型实验^[32]的模拟计算, 验证了模型具有良好的适用性. 在此基础上研究了颗粒流与不同行数四面体结构物阵列的相互作用. 主要结论如下:

(1) 本文建立了基于沿程坐标积分模式建立的数值模型, 可以较为准确的表征陡峭地形条件颗粒流与结构物相互作用的动力过程, 如绕流、反射、爬升. 本数值模型将流动过程、复杂地形、以及障碍物处理融为一体, 基本具备了计算和评估陡峭地形条件颗粒流与复杂障碍物系统相互作用的流态和堆积等动力过程.

(2) 结构物对颗粒流的作用主要包括耗散作用和偏转作用两种模式. 快速颗粒流遇到障碍物并在其前方诱导一个弓形激波, 耗散颗粒的能量. 同时, 障碍物能够改变颗粒流的流动方向, 达到分隔和偏转颗粒流的作用.

(3) 结构物阵列对颗粒流产生综合的耗散和偏转作用, 通过多级作用产生系列的弓形激波耗散能量, 通过偏转作用分隔和偏转颗粒流改变颗粒流的最终堆积形态, 对下游地区产生显著的防护效果.

颗粒流与结构物阵列相互作用的过程十分复杂, 对于如何改变结构物阵列的参数以获得对颗粒流更好的调控效果还有待进一步研究. 此外如何将本数值模型与实际勘测的地质数据相结合也有待解决. 未来希望能够形成具有实际意义的大尺度山地灾害中防护结构调控效果预测模型, 为灾害防治决策提供可靠的科学依据.