基于多层分块算法的激波干扰流场预测

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

引言

激波反射和激波干扰现象是超声速及高超声速流动中最具挑战性的问题之一^[1]. 近年来, 二维/三维激波反射理论及其应用备受关注. 程剑锐等^[2]基于弯曲激波理论与自由干扰理论构建了二维弯曲入射激波/平板边界层干扰的无黏流动模型. Numata等^[3]利用二维激波理论结合三维效应的影响, 分析了特定楔面上激波三维反射结构的形成过程和机理. M?lder^[4]提出了三维弯曲激波理论, 揭示了内收缩约束下曲面激波的汇聚机理. 鉴于三维问题的复杂性, “空间降维”不失为一种有效的方法^[5-6]. 几何激波动力学^[7-9](geometrical shock dynamics, GSD)理论对于解决非均匀激波汇聚和激波面从连续到间断等问题具有独特优势. 关于GSD方法的拓展及三维曲面激波非均匀性的演变特征的工作陆续展开^[10].

对于激波干扰问题, Edney^[11] 以二维平面圆柱诱导的弓形激波和斜激波干扰问题为典型的简化模型, 针对斜激波与弓形激波的相对位置不同, 将激波干扰分为6类. 其中, IV型激波干扰因为其干扰区产生超声速射流直接冲击壁面, 产生极高的热载荷和力荷载而受到特别的关注. Keyes 和Hains^[12] 利用斜激波关系式和Prandtl-Meyer 关系式来求解流场流动参数并预测压力峰值和传热速率. Holden等^[13-14] 和Glass^[15] 较早地针对气动力、气动热影响最显著的第IV类激波干扰开展了风洞试验研究, 总结出壁面压力、热流的分布规律. Sanderson等^[16-17] 研究了第IV类激波干扰产生的热流幅值与来流焓值的变化关系. Kolly^[18]发展了经验公式来描述壁面压力和热流的关系. Holden和Kolly等^[19]发现, 在某些特定的试验条件下, 第IV类激波干扰流动可能存在非定常振荡现象. Zhong^[20] 数值模拟了第IV类激波干扰的非定常流动, 结果表明非定常振荡现象是剪切层、超声速射流和弓形激波共同作用引起的.

第IV类激波干扰流场的几何结构也备受关注, 其中一个重要参数是激波脱体距离. 无干扰情况下关于计算脱体距离的解析、数值和实验方法已经发展成熟^[21-22]. 近年来, 化学非平衡下的激波脱体距离公式的工作也陆续展开^[23-25]. 相比于无干扰情况下, 激波干扰情况下脱体距离尚无理论解, 仅有少数文章指出了III型和IV型激波干扰的流场的几何形状. Peng等^[26]用机器学习的方法给出了IV型激波干扰下激波?激波相互作用点的位置的显式表达式, 为进一步估算出IV型激波干扰流场的几何形状提供了条件, 进而快速地获取最大热载荷的大小和位置.

高温气体效应是高超声速动力学的主要特征之一. 高超声速气体由于激波压缩和黏性阻滞, 其动能迅速转化为内能, 导致飞行器表面附近的温度急剧升高. 高温引起气体分子的振动激发, 解离和电离, 甚至是电子激发等一系列复杂现象, 此时, 气体的量热完全气体假设不再成立, 由此对流场和飞行器性能的影响总称为“高温气体效应^[27] ”或者“真实气体效应”. 张子健等^[28] 通过理论分析和数值模拟研究了振动激发对二维斜劈的气动力/热特性的影响规律. 张翔^[29] 探讨了复杂外形飞行器在不同飞行条件下, 高温气体效应对飞行器的气动力/热特性和规律的影响. 石晓峰^[30]通过理论模型发现了高温气体效应促进马赫杆变形的机制. 张胜涛等^[31]和梁杰等^[32] 分析了真实气体效应对飞行器流场特性和气动热环境的影响. 杨肖峰等^[33]针对火星大气环境, 研究真实气体效应对探测器进入过程的影响.

本文主要考察两种气体模型: 量热完全气体模型(calorically perfect gas, CPG)和仅考虑振动激发的热完全气体模型(thermally perfect gas, TPG). 分别给出两种气体模型下的III型、IV型和IVa型激波干扰的流场结构、流场状态参数等对比结果. 并且利用多层积木块算法, 给出了两种气体模型下的三波点位置、射流结构的预测模型, 并给出激波干扰类型转变准则预测模型及其对比分析, 讨论了高温气体效应对几何结构和转变准则的影响等. 同时, 本文对CPG和TPG模型下的转变准则方程进行了验证.

1.
数值方法和机器学习方法

本文计算程序采用有限体积法, 基于非线性黎曼求解器(Harten-Lax-van Leer contact, HLLC), 使用二阶TVD格式计算通过每个单元面的数值通量. HLLC格式能够准确地捕捉激波, 接触间断和稀疏波, 减少计算量, 降低耗散, 提高分辨率^[34]. 同时, 采用Minmod 限制器能够有效抑制间断面的数值振荡. 时间推进采用隐式双时间步长进行积分计算.

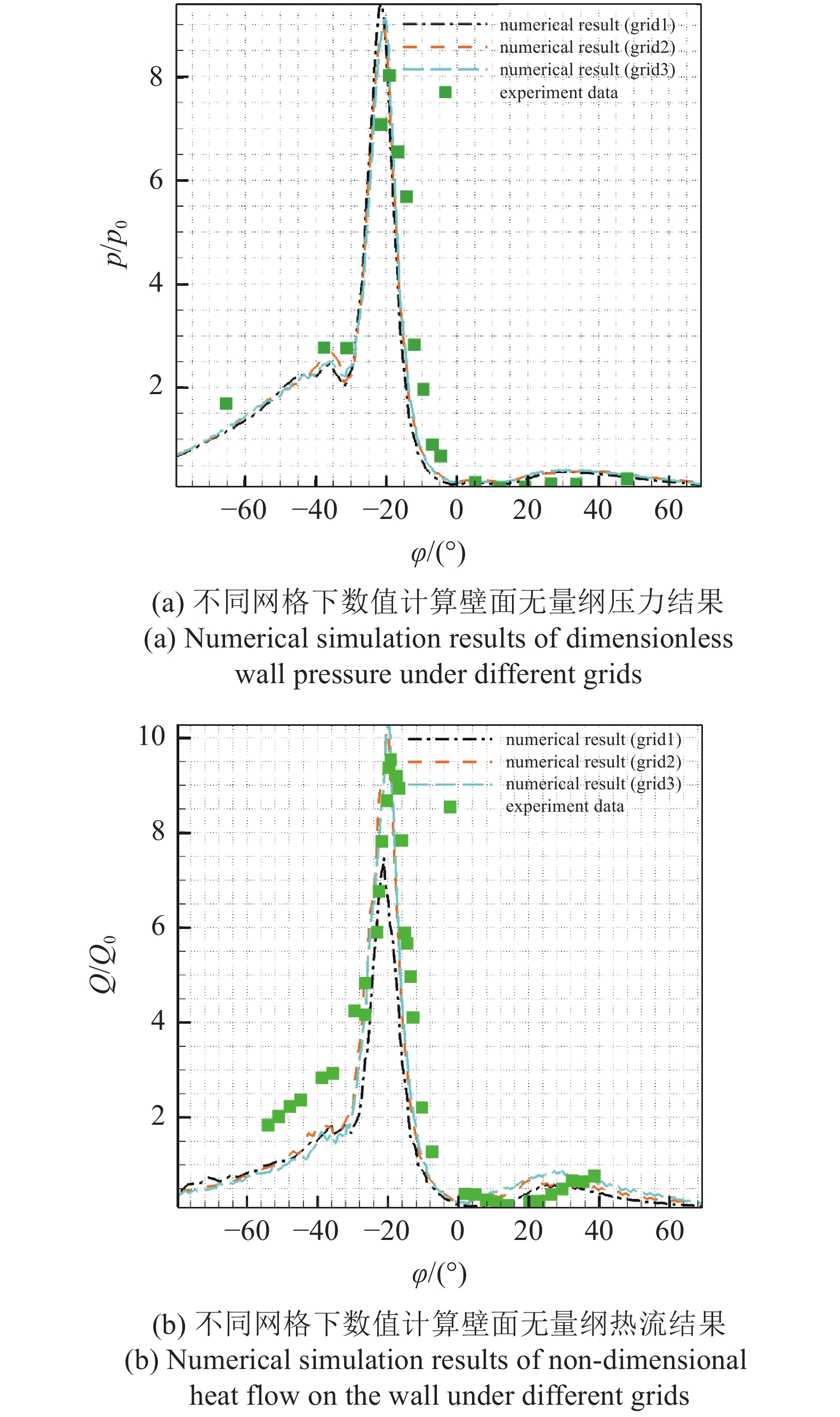
本文开展了网格无关性验证. 图1是网格无关性验证结果, 研究发现grid 2和grid 3的壁面热流和压力的分布几乎一致, 但是grid 1未捕捉到壁面压力和热流峰值, 最终本文所涉及的工况均采用网格grid 2 (500 × 476)进行计算. 具体网格细节如表1所示. 如图1所示, 本文通过相同来流条件下无干扰情况的驻点压力p₀和驻点热流Q₀对壁面压力p和壁面热流Q进行无量纲化.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />

图
1
网格无关性验证

Figure
1.
Grid independence verification

下载:
全尺寸图片
幻灯片

表
1
网格细节

Table
1.
Grid details

table_type1 ">

Grid	N_r × N_φ	Surface cell thickness/m	Grid stretching ratio
grid 1	200 × 336	1 × 10^?5	1.3
grid 2	500 × 476	1 × 10^?6	1.2
grid 3	600 × 696	1 × 10^?6	1.3

下载:
导出CSV
|显示表格

符号回归 ( symbolic regression ) 是一种特殊的回归分析, 它搜索数学表达式空间以找到最适合给定数据集的模型(同时考察准确性和简洁性). 符号回归作为一种监督学习方法, 基于进化算法, 其优点在于可以不用依赖先验的知识或者模型来为非线性系统建立符号模型.

符号回归显然不同于经典的回归方法, 传统的回归方法为预先指定的模型结构, 优化其中的参数, 而符号回归则避免施加先验假设, 从数据中推断出模型. 这意味着与传统的回归方法相比较, 符号回归需要更长的时间才能找到合适的模型和参数. 但是, 符号回归的这一特性也具有如下的优势: 因为进化算法需要多样性才能有效地搜索空间, 所以最终的结果很可能是选择高得分模型 (及其相应的参数集) .

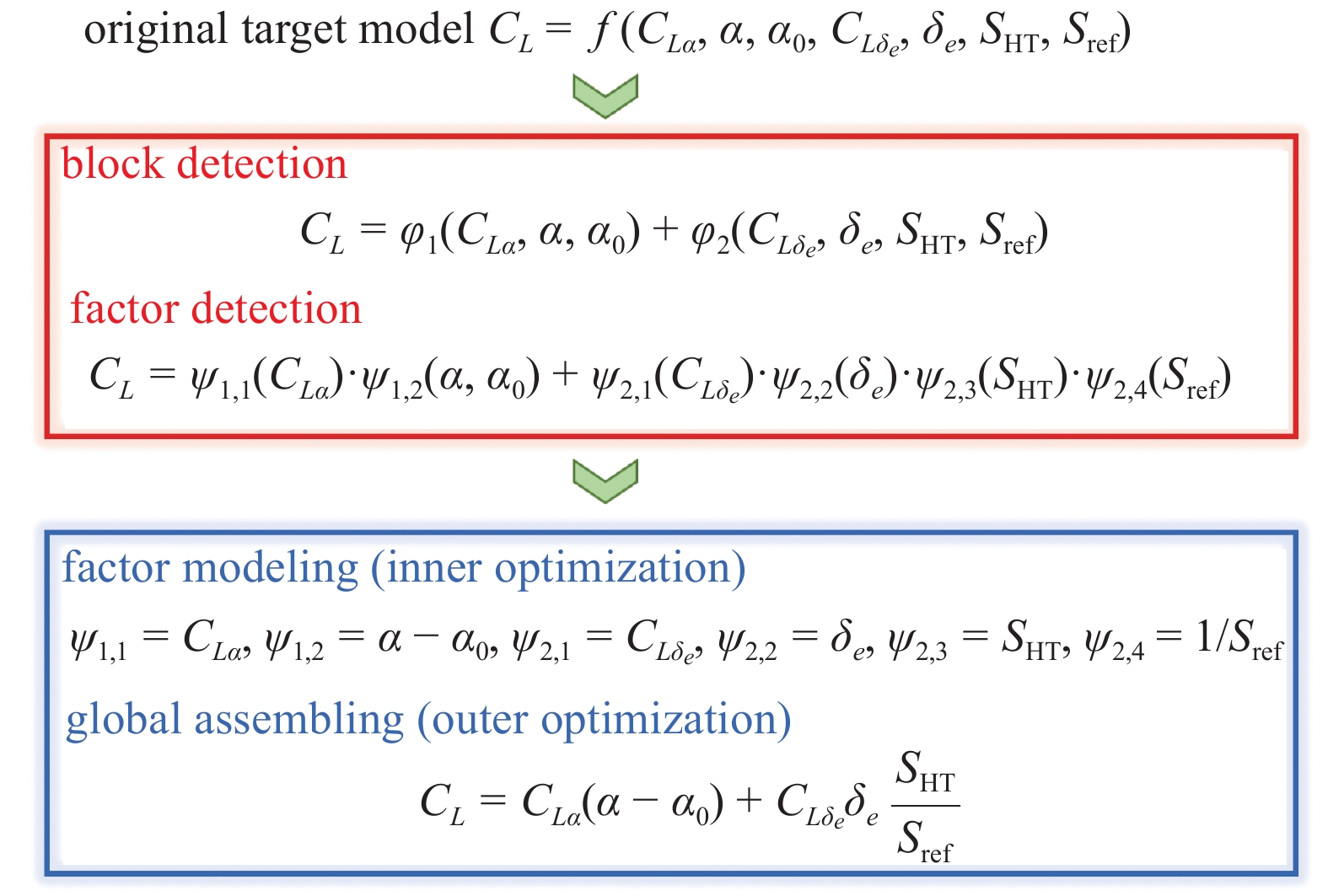
最近, Chen等^[35]提出广义可分模型( generalized separable model, GSM). 与传统的方法相比, 针对大多数可分离的目标模型, 该方法可以大大减少搜索空间, 提高收敛速度. 与最先进的数据驱动拟合工具Eureqa进行比较, 测试结果表明, 该方法在很多算例都表现出良好的性能. 另外, Chen等^[36]在2018年还提出一种新的方法, 即块构建编程(block building programming, BBP). BBP算法将原始目标函数分成几个块, 并进一步分解为多个因子, 然后由优化引擎(例如: 基因编程( genetic programming, GP ))对因子进行建模. 在这种情况下, BBP可以大大减小搜索空间. 一系列的数值结果表明, BBP具有良好的结构和系数优化能力, 计算效率高. BBP 的示意图如图2所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />

图
2
BBP算法根据式(1)的建模过程

Figure
2.
Modeling process of BBP algorithm according to Eq. (1)

下载:
全尺寸图片
幻灯片

$$ {C_L} = {C_{Lalpha }}left( {alpha - {alpha _0}}
ight) + {C_{L{delta _e}}}{delta _e}dfrac{{{S_{{text{HT}}}}}}{{{S_{{text{ref}}}}}} $$

(1)

为了识别具有可能GSM特征的函数的结构, 陈辰^[37]提出了一种多层分块算法(multi-level block building, MBB), MBB是BBP算法的改进版本, 具有更广泛的应用潜力. MBB算法将变量区分为重复变量和非重复变量, 并将目标模型分解为更高层次的块和因子, 直到被确认为最小块和因子. 然后对最小块和因子进行适当的组装, 形成目标函数. MBB算法对于具有一定的可分离特性问题(常见于气动力问题), 该算法大大简化了泛函优化的复杂度, 为流体力学中的数据建模、流体力学实验数据的一致性、相关性提供了快速的算法支持.

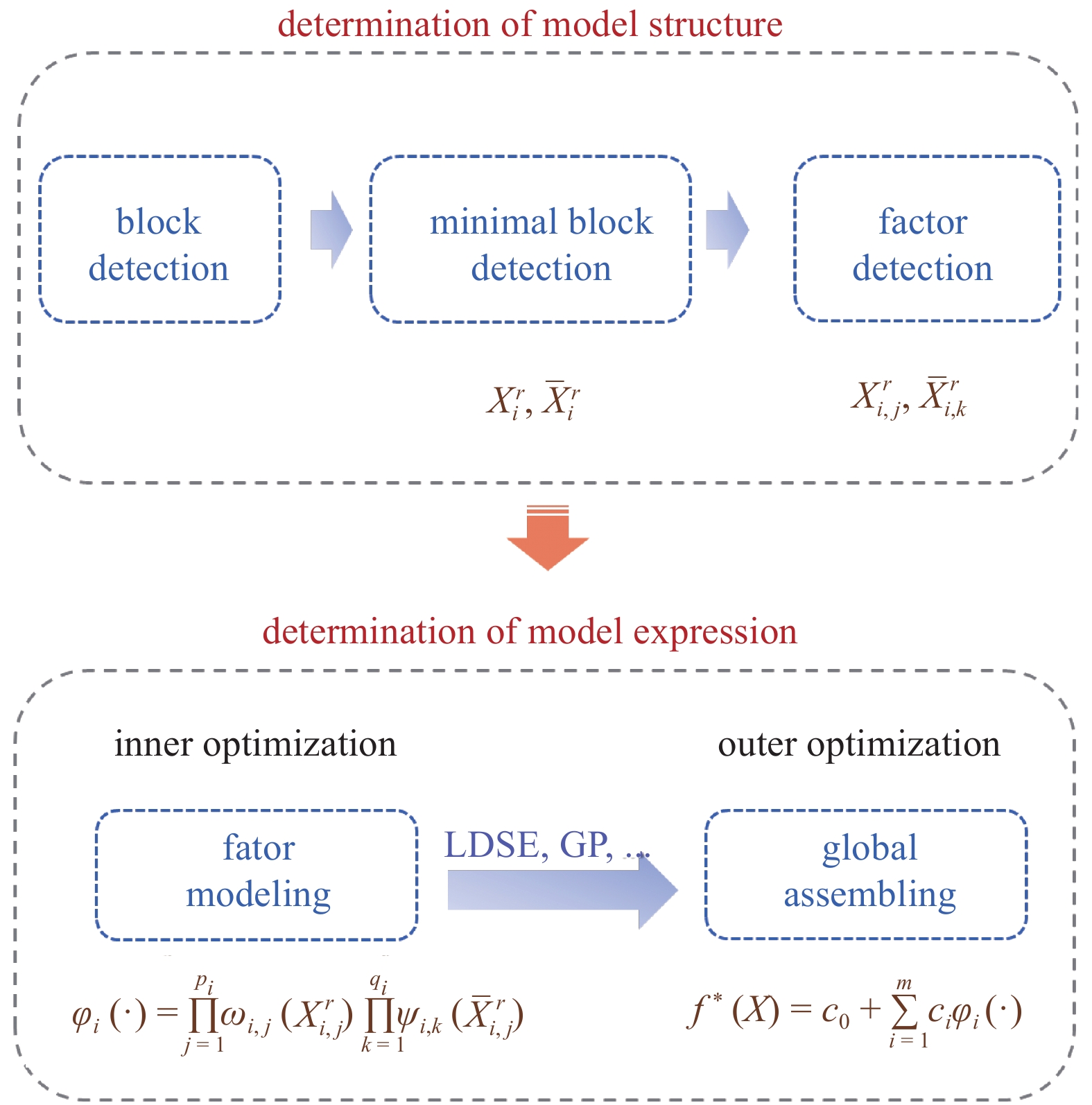
MBB算法具有很强的非线性规律捕捉能力, 能够基于相对少量(非海量)数据, 获得简洁的显式函数表达式, 便于模型解释与应用. 因而, MBB算法适合于激波干扰流场结构预测问题研究. 当然, MBB及其改进算法也可以用来预测更多的物理量, 比如壁面压力、温度、热流等. MBB的示意图如图3所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />

图
3
MBB算法流程

Figure
3.
Work flow of MBB algorithm

下载:
全尺寸图片
幻灯片

2.
高温气体效应对IV型激波干扰流场结构和状态参数的影响

本文采用两种气体模型(CPG, TPG)进行数值计算, 参数设置如表2所示.

表
2
数值模拟的来流参数设置

Table
2.
Free stream parameter settings of numerical simulations

table_type1 ">

Variables	Value
diameter of cylinder $D$/m	0.12
mach number of the free stream $Ma$	6, 7, 8, 9, 10
temperature of the free stream ${T_infty }$/K	200
pressure of the free stream ${p_infty }$/Pa	428
shock angle of the free stream $beta $/(°)	15, 16, 17, … , 22, 23, 24
wall temperature ${T_W}$/K	288
unit Reynolds number of free stream $ {N_{re,}}_infty $/m^?1	2.54 × 10⁷

下载:
导出CSV
|显示表格

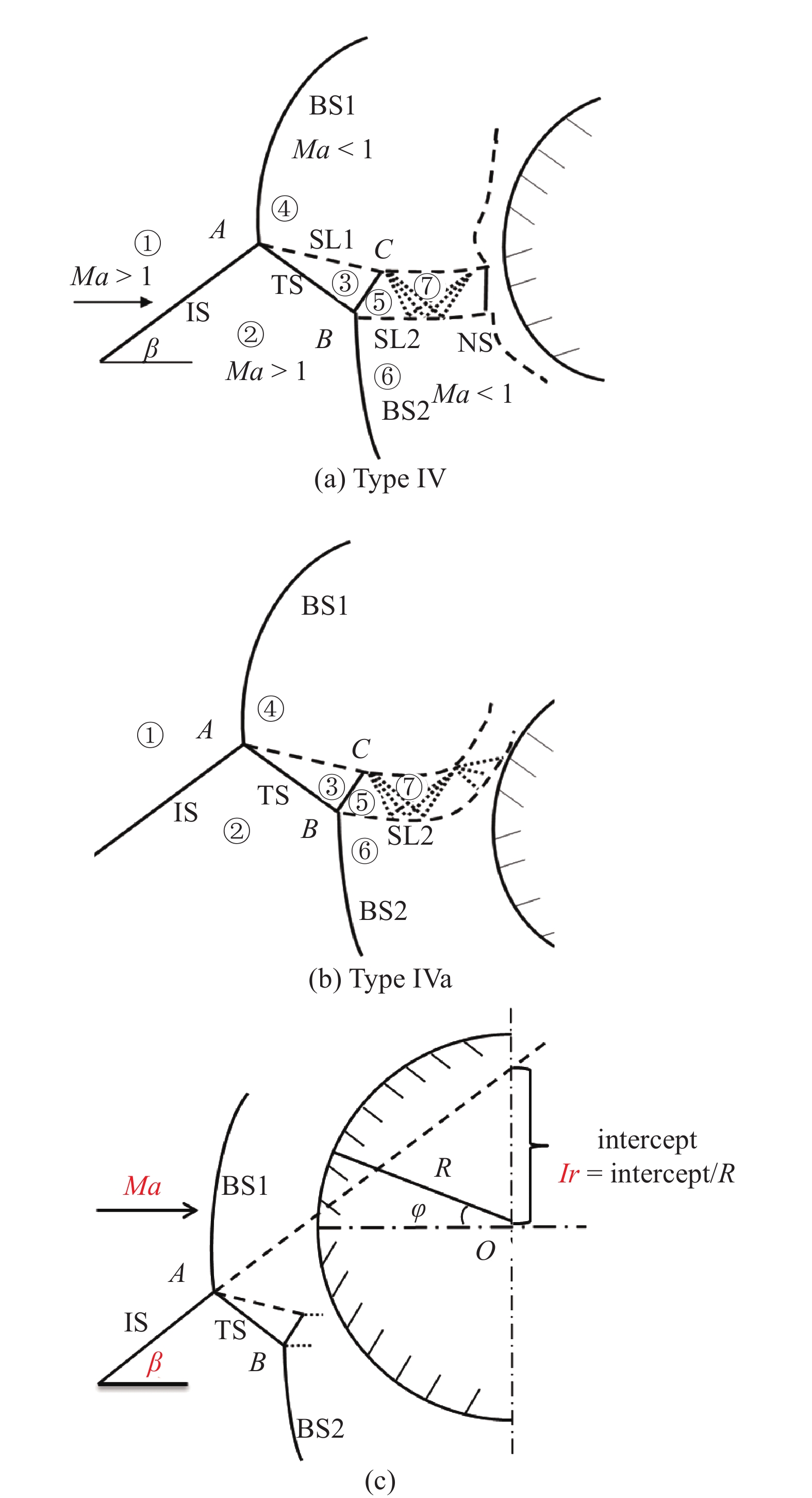
从第IV类激波干扰的流场可以看出, 入射激波和弓形激波相交, 在相互干扰的局部区域内形成超声速射流, 射流内部形成两道剪切层以及其内部不断反射的膨胀波系. 当超声速射流擦拭圆柱壁面并逐渐脱离, 此时发生IVa型激波干扰, 两类激波干扰类型的流场结构如图4 (a)和图4 (b)所示(入射斜激波(incident oblique shock, IS)、透射激波(transmitted shock, TS)、上滑移线(upper slip line 1, SL1)、下滑移线(lower slip line 2, SL2)、上弓形激波(upper bow shock 1, BS1)、下弓形激波(lower bow shock 2, BS2)、正激波(normal shock, NS)). 另外, 将入射激波延长线截距与圆柱半径的比值定义为无量纲参数Ir (图4(c)).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />

图
4
IV和IVa型激波干扰的流场结构示意图和以及无量纲位置参数Ir示意图

Figure
4.
Schematic diagram of the flow field structure of IV and IVa shock interference and schematic diagram of the dimensionless position parameter Ir

下载:
全尺寸图片
幻灯片

首先, 通过数值模拟, 对比了CPG模型和TPG模型下IV型激波干扰流场结构(图5). 图中共给出了3个工况: (a) Ma = 6, β = 17°, Ir = 0.4; (b) Ma = 8, β = 18°, Ir = 0.4; (c) Ma = 10, β = 18°, Ir = 0.5. 结果表明: 在相同来流马赫数Ma、激波角β和位置参数Ir的情况下, 两种模型的流场结构有明显的区别: 较于CPG模型, 考虑高温气体效应的TPG模型其激波脱体距离明显缩短, 整个射流结构发生了一定程度的上移. 这是因为振动激发是一个吸热过程, 气体比热减小, 弓形激波波前波后密度比减小, 进而激波脱体距离减小^[21]. 随着马赫数的升高, 高温气体效应对流场结构的影响越发明显, 主要体现在三波点A的位置的偏移量增大, 激波脱体距离减小速率加快, 同时, 射流冲击点位置偏移量也会增大.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />

图
5
相同来流Ma, β, Ir下CPG和TPG气体模型的激波干扰流场结构对比

Figure
5.
Comparison of shock wave interference flow field structure of different gas models, CPG and TPG, with the same flow conditions, Ma, β, Ir

下载:
全尺寸图片
幻灯片

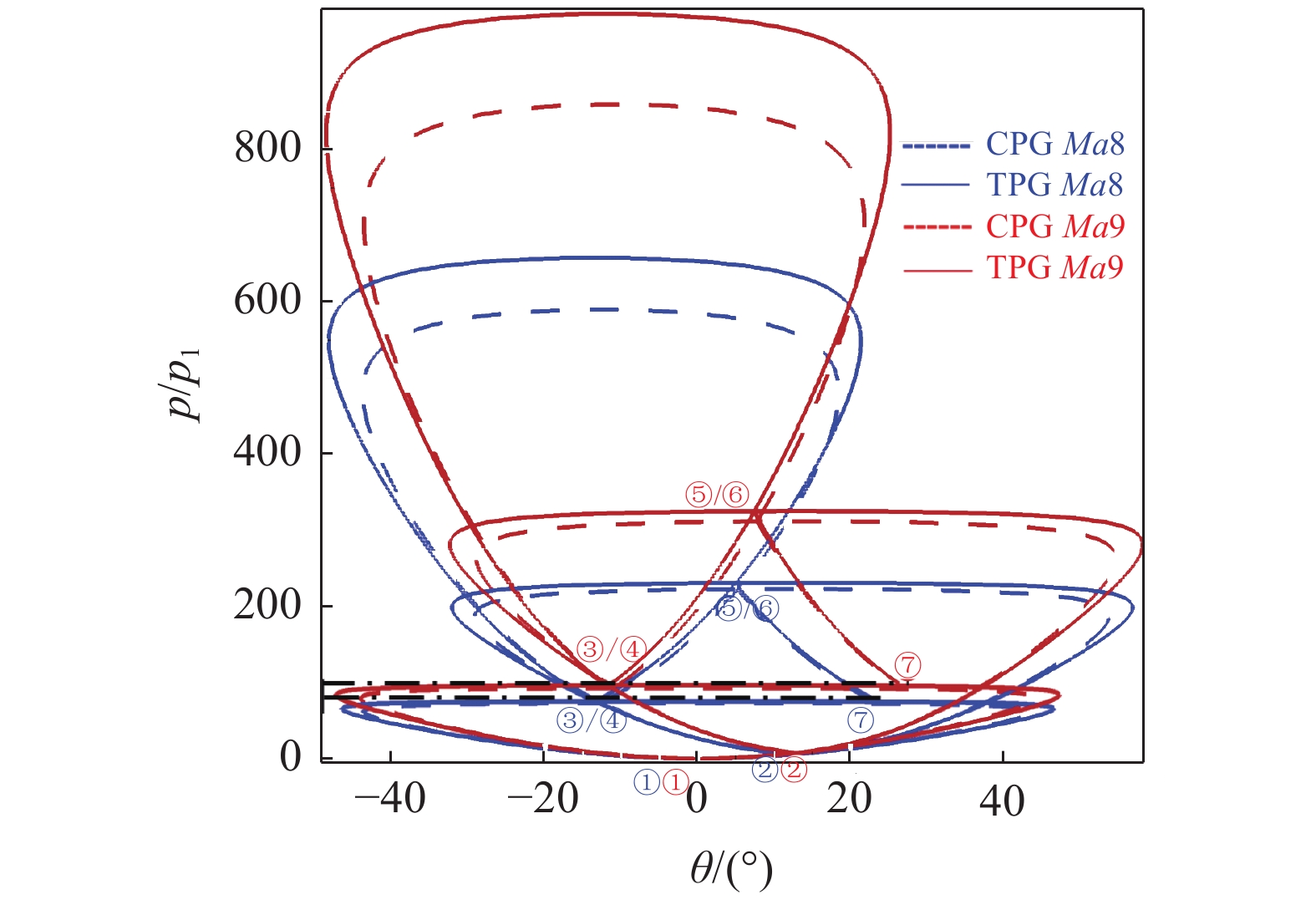
接下来, 根据斜激波关系式、P-M膨胀波关系式和等熵关系以及三波点和滑移线的约束性质, 文章给出CPG模型和TPG模型分别在不同来流马赫数下的压力激波极曲线 (如图6), 给出IV型以及IVa型激波干扰流场各区域的压力的理论值, 其中的各流场编号如图4(a)和图4(b)所示. 如图6所示, 在同一马赫数下, TPG模型的压力极曲线轮廓均要大于CPG模型, 相应的区域的压力值也大于量热完全气体的压力值. 随着马赫数的增加, 高温气体效应愈发明显, 两种模型的激波极曲线轮廓差异逐渐增大, 同时两种模型压力差也随之增大. 另外, 激波极曲线得到的结果和数值计算结果进行对比, 存在一定偏差是IV型激波干扰流场的非定常特性引起的.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />

图
6
自由来流工况为 p_∞ = 428 Pa; T_∞ = 200 K; Ma = 9, 10; β = 18°, CPG模型和TPG模型下IV型激波干扰流场各区域压力极曲线图

Figure
6.
The pressure pole curve diagrams of each area of the IV shock interference flow field under the CPG model and the TPG model in the free flow conditions: p_∞ = 428 Pa; T_∞ = 200 K; Ma = 8, 9; β = 18°

下载:
全尺寸图片
幻灯片

在实际工程中, 近乎垂直冲击壁面的超声速射流会在驻点附近产生极高的压力和热流备受关注. 接下来, 本文给出在不同来流条件下(${p_infty }$

= 428 Pa, ${T_infty }$

= 200 K, Ma₁ = 4 ~ 11, β₁ = 13° ~ 35°), ⑤区和⑦区流场的状态参数值随来流条件的变化图像. 如图7所示, 5区气流通过膨胀波到达⑦区, 故在相同来流条件下, 无论是CPG模型或是TPG模型, 均有${p_5} > {p_7}$

, ${T_5} > {T_7}$

, $ M{a_5} < M{a_7} $

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />

图
7
IV型激波干扰部分区域状态参数随来流条件改变的变化曲线

Figure
7.
Variation curve of state parameters in some areas of type IV shock interference with changes in incoming flow conditions

下载:
全尺寸图片
幻灯片

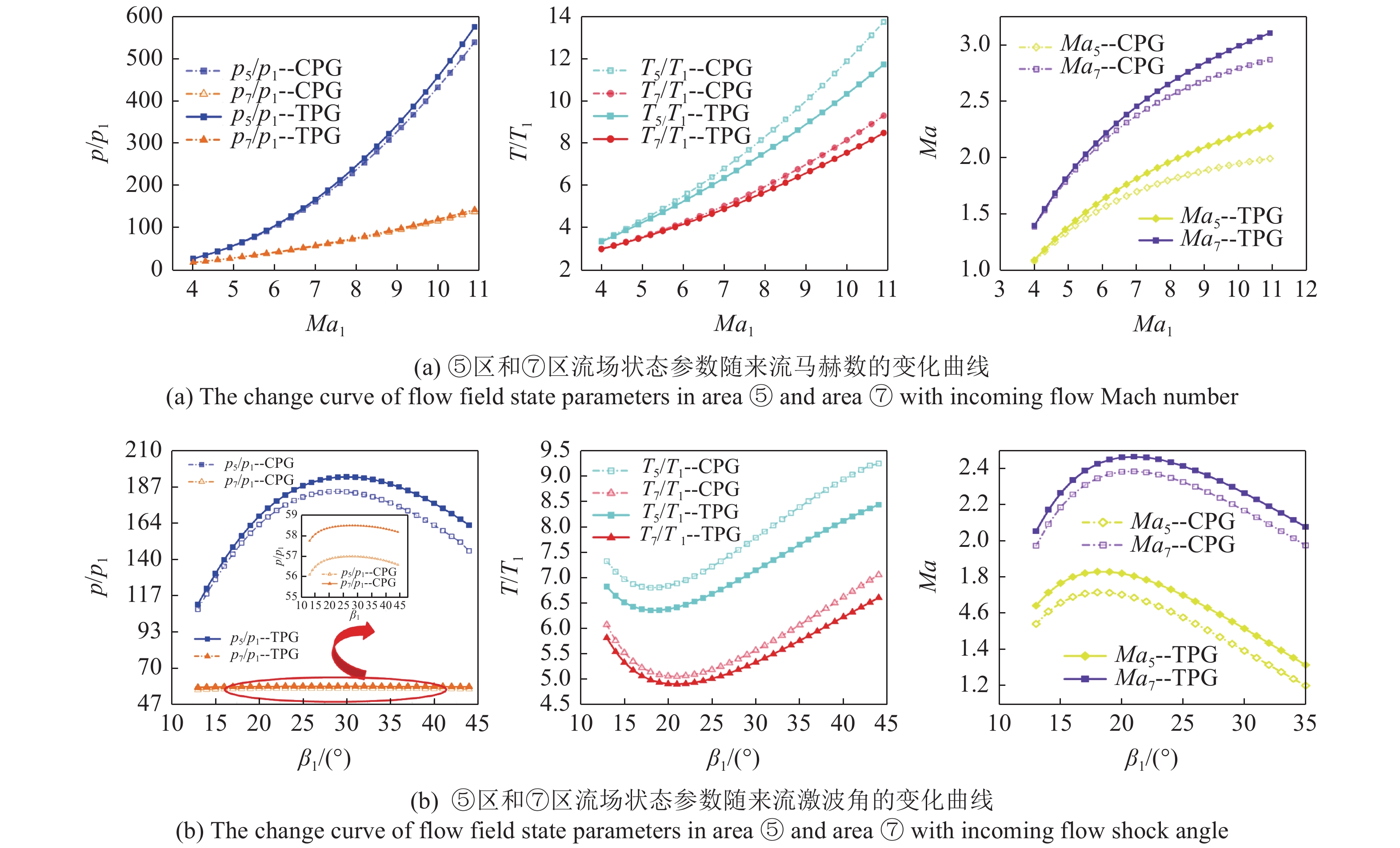
如图7(a)所示, 随着来流马赫数Ma₁的增加, 入射激波强度增强, ⑤区和⑦区的压力, 温度也随之增大, 且增长率也随Ma₁的增加而增大; ⑤区和⑦区的马赫数也随之增大, 但是随着马赫数的增大, 增长愈发缓慢. 对于TPG模型而言, 来流马赫数Ma₁ = 11时⑤区的压力比Ma₁ = 4时增长了约20倍, 温度增长约2.5倍, 马赫数增长约一倍; 来流马赫数Ma₁ = 11时⑦区的压力比Ma₁ = 4时增长了约6.9倍, 温度增长约1.8倍, 马赫数增长约1.2倍.

接下来, 考察来流激波角β₁对于超声速射流流场区域的状态参数的影响. 图7(b)给出⑤区和⑦区的压力、温度和马赫数随着来流激波角的变化曲线. 结果表明, 3幅图中均出现极值点. 这表明, 在其他来流参数不变时, 存在临界激波角$;{beta _p},;{beta _T}$

等, 使得⑤区和⑦区的流动状态参数达到峰值. 当⑤区和⑦区的压力取极大值时, 壁面驻点压力和热流也会升高, 工程中应当予以避免.

3.
多层分块算法(MBB)在激波干扰问题上的应用

MBB 作为一种对具有可分离型特征的工程系统建模的新型算法, 在流体力学建模问题上有其独特的优势. Peng等^[26]曾经用机器学习算法尝试描述了IV型激波干扰流场的几何结构, 包括给出了两个三波点A, B位置坐标的显式表达式, 超声速射流的几何结构以及不同激波干扰类型( type III? type IV和type IV ? type IVa)的转变准则. 在此研究基础上, 本文沿用之前的数值计算的来流参数设置(表3), 计算了如表3所示CPG模型下的250组算例 (Ma = 6 ~ 10, β = 15° ~ 24°, Ir = 0.3 ~ 0.7) , 对比了不同气体模型下的三波点A, B位置公式、超声速射流几何形状和激波干扰类型转变准则等结果.

表
3
量热完全气体计算算例参数组合列表(5 × 10 × 5 = 250)

Table
3.
Parameter combination lists of calorimetric complete gas calculation example (5 × 10 × 5 = 250)

table_type1 ">

Case	Ma	β	Ir
case 1	6	15	0.3
case 2	6	15	0.4
case 3	6	15	0.5
case 4	6	15	0.6
case 5	6	15	0.7
case 6	6	16	0.3
···	···	···	···
case 51	7	15	0.3
···	···	···	···
case 250	10	24	0.7

下载:
导出CSV
|显示表格

3.1
不同气体模型下MBB算法预测三波点位置结果分析

本文统计了上述250组算例的计算结果, 结合第1节介绍的MBB算法, 给出CPG模型和TPG模型下的三波点A的坐标公式

$$begin{split} {x_A} = - 0.479;162 - 0.372;453sqrt beta + 3.567;84Ir - qquad 0.783;48sqrt {Ma} cdot Ir - 2.153;85I{r^2}end{split} $$

(2)

$$ begin{split}{x_A} = 0.692;693 - 5.014;95I{r^2} + 0.819;079I{r^2}sqrt {Ma} + qquad 0.235;192sqrt beta + 0.732;974I{r^2}betaend{split} $$

(3)

观察式(2)和式(3), 当位置参数较小时, ${x_A}$

受马赫数影响较小, 在一定误差内可视作仅为激波角β的函数, 且与$sqrt beta $

基本呈线性关系. 如图8所示, 当Ir = 0.3, 激波角β从15°变化到18°时, 发现不同马赫数(Ma = 9, 10)下三波点A基本重合.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />

图
8
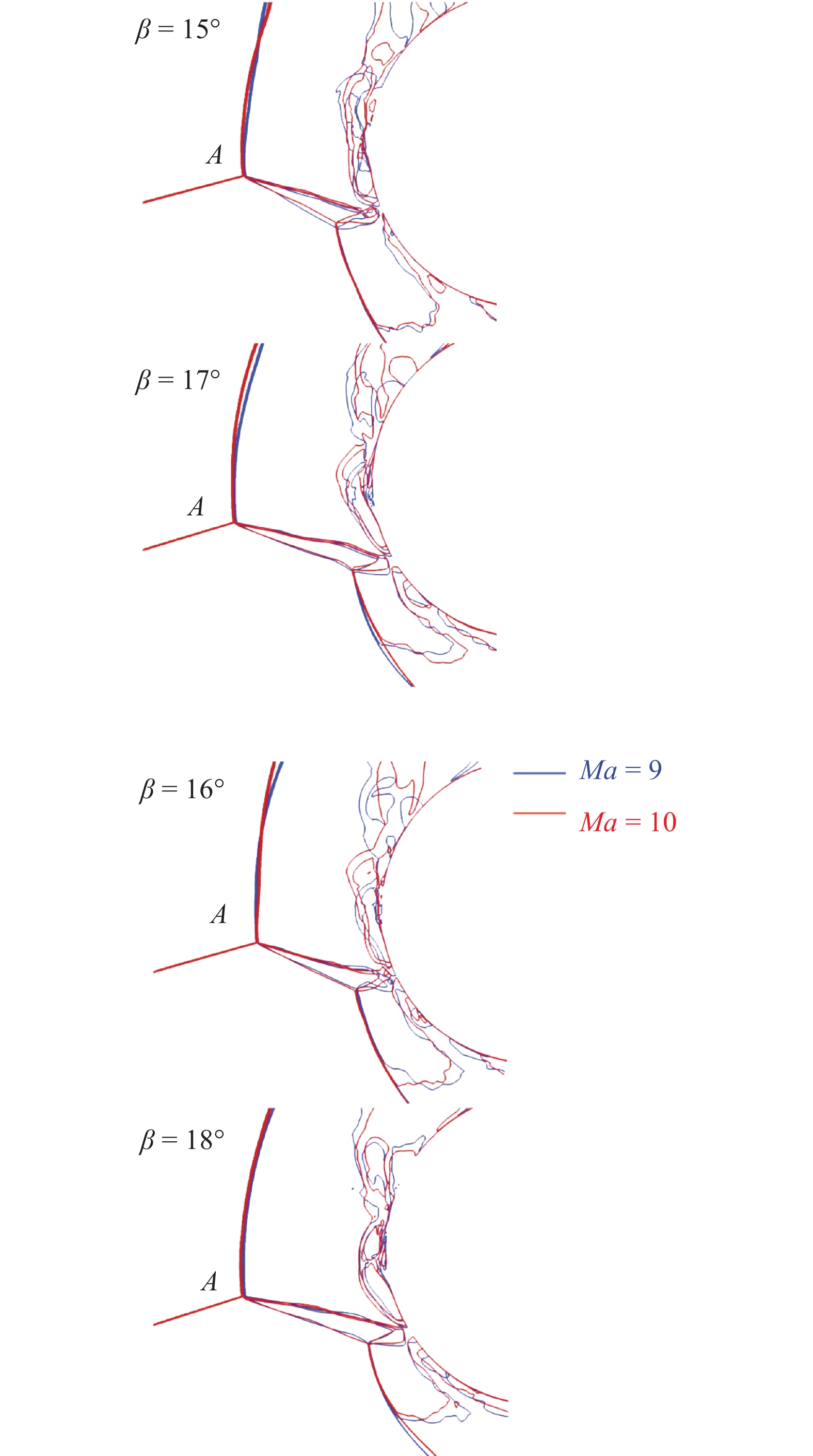
Ma=9, 10; Ir=0.3, 不同激波角β下CPG模型的流场结构

Figure
8.
Flow field structure of the CPG model under different shock angle β, Ma=9, 10; Ir=0.3

下载:
全尺寸图片
幻灯片

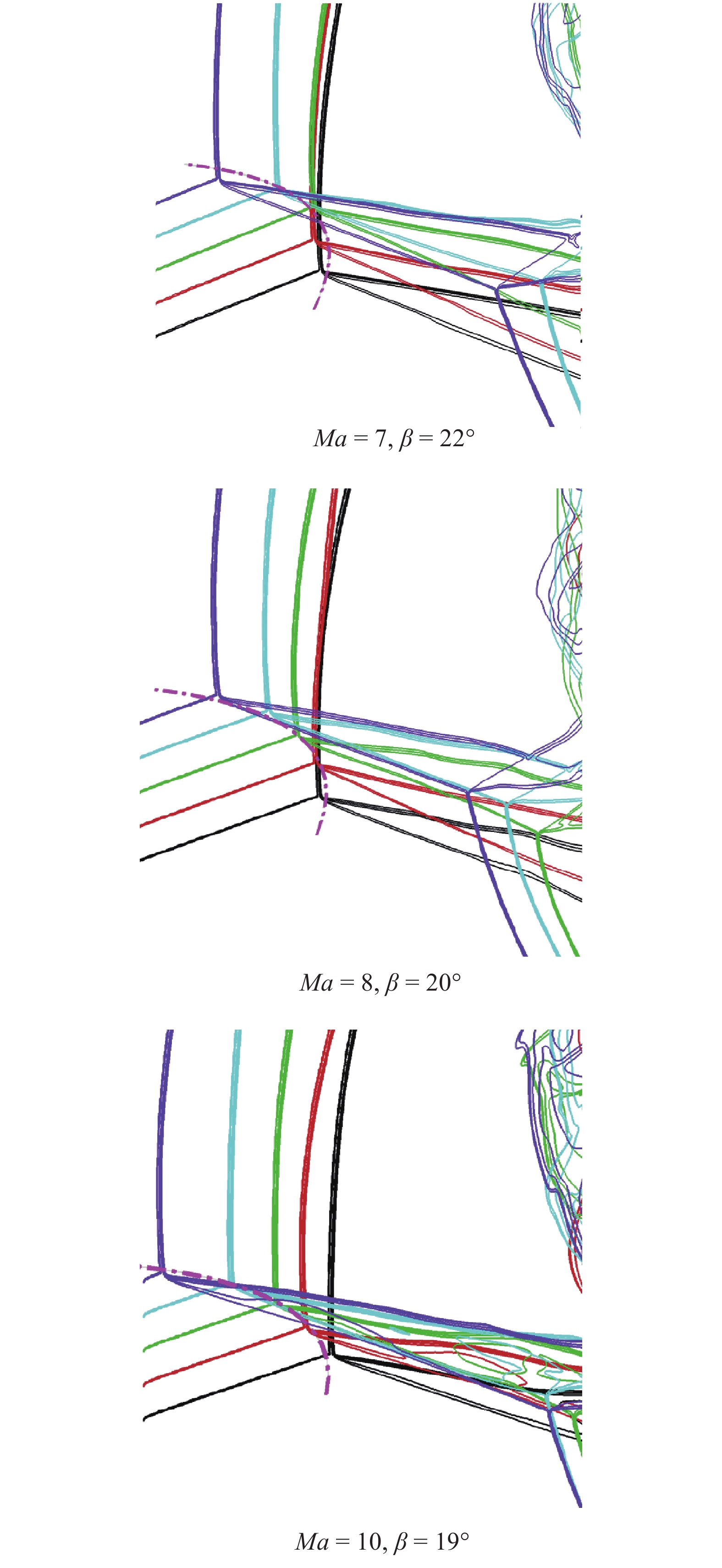
利用数值模拟的结果, 对机器学习获得的式(2)和式(3)进行了验证, 如图9所示. 激波干扰中三波点A附近的流场如图9所示, 图中5种不同颜色的曲线代表着相同马赫数和激波角下, Ir分别等于0.3, 0.4, 0.5, 0.6和0.7工况下的马赫数等值线, 图中的点划弧线是机器学习公式预测的三波点位置. 对比结果可见, 不同工况的三波点较为精确地落在机器学习拟合曲线上, 即机器学习结果利用MBB算法获得的三波点坐标公式和数值计算结果吻合得较好.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />

图
9
机器学习获得的三波点A坐标位置与数值结果对比结果

Figure
9.
Comparison of the triple-wave point A coordinate position obtained by machine learning and the numerical result

下载:
全尺寸图片
幻灯片

同理, CPG模型和TPG模型下的三波点B的坐标公式

$$ begin{split}&{x_B} = - 1.482;69 + 0.001;973{beta ^2} + 0.000;131Ma cdot {beta ^2} + &qquad2.202;54sqrt {Ir} - 0.813;827sqrt beta sqrt {Ir}end{split} $$

(4)

$$ begin{split}&{x_B} = 0.111;626 + 2.376;97sqrt {Ir} - 0.244;051Ma + &qquad 0.262;8Ma cdot cos (Ir) - 0.001;103;49{beta ^2} cdot cos (Ir)end{split} $$

(5)

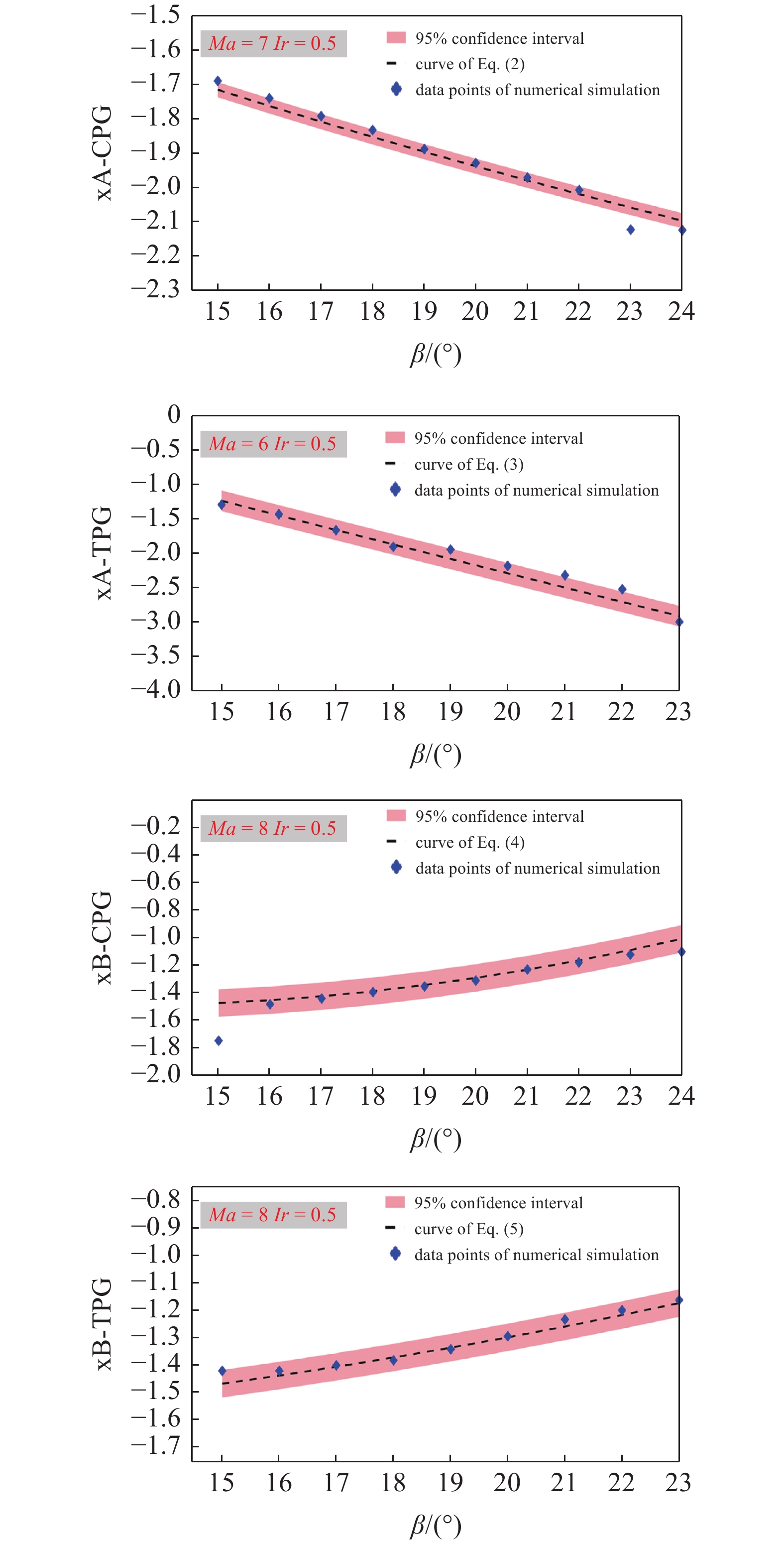
另外, 如图10所示, 文章给出式 (2) ~ 式(5) 关于来流激波角β的曲线图, 并与数值模拟的结果作比较, 并给出四个公式的置信度为95%的置信区间曲线, 可以发现, 数值结果基本落在了置信区间内, 故机器学习得到的三波点坐标公式较为精确.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />

图
10
式(2) ~ 式(5)随来流激波角β变化曲线与数值结果对比, 以及95%置信度下公式预测置信区间曲线

Figure
10.
Comparison between curves obtained by machine learning and numerical results, Eqs. (2)-(5) prediction confidence interval curve with 95% confidence

下载:
全尺寸图片
幻灯片

3.2
不同气体模型下MBB算法预测射流几何结构分析

进一步利用机器学习的预测式(2) ~ 式(5), 可以得到超声速射流的几何形状, 如图11所示, 激波?激波相互作用点以及射流的大致形状 (图中的橙色线段) 都被清楚地描绘出来. 发现理论预测的流场结构与数值模拟获得的流场结构基本吻合.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />

图
11
CPG模型下MBB算法预测超声速射流结构与数值结果对比图

Figure
11.
Comparison of MBB algorithm prediction of supersonic jet structure and numerical results under CPG model

下载:
全尺寸图片
幻灯片

3.3
不同气体模型下MBB算法预测激波干扰转变准则面结果分析

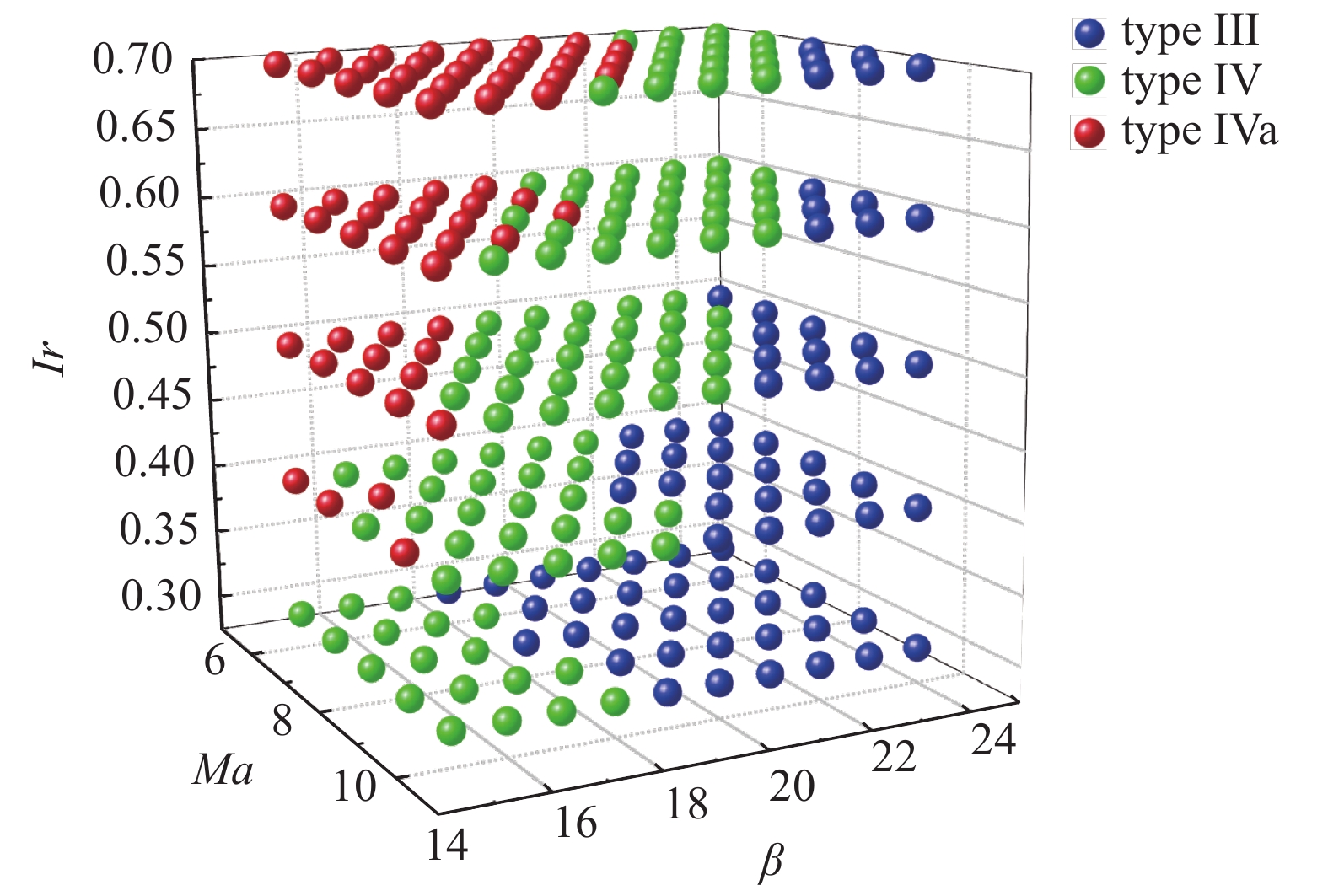
为了清晰地看出不同激波干扰类型的分布, 本文统计了250组算例的激波干扰的类型, 建立出如图12所示的Ma, β, Ir 3个变量的参数空间的三维分布, 比较不同气体模型下的激波干扰转变准则. 其中, 蓝色散点表示在该来流条件下, 会发生III型激波干扰, 同理, 绿色散点代表IV型激波干扰, 红色散点代表IVa型激波干扰.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />

图
12
激波干扰类型在(Ma, β, Ir)空间中的分布

Figure
12.
The distribution of the interaction types in the space of (Ma, β, Ir)

下载:
全尺寸图片
幻灯片

采用前面提到过的MBB算法, 学习得到CPG模型下的激波干扰类型转变准则面的方程, 如式(6)和式(7)所示, 其中拟合优度${R^2} geqslant 92{text{% }}$

(${R^2} = $

$ dfrac{{SSR}}{{SST}} = 1 - dfrac{{SSE}}{{SST}}$

, SSR为回归平方和, SSE为残差平方和, SST为总离差平方和, 且SST=SSR + SSE). 式(8)和式(9)是对TPG模型下的激波干扰类型转变准则面方程^[26]的改进, 得到了拟合优度更高的方程表达式

$$ {
m{type III}} leftrightarrow {
m{ type IV}} ({
m{CPG}}) : sin Big[lg (lg sqrt beta )Big] - Ir = 0 $$

(6)

$$ {
m type IV leftrightarrow type IVa (CPG)} : cos Big(sin sqrt {Ma + beta } ;Big) - Ir = 0 $$

(7)

$$ {
m type IIIleftrightarrow type IV (TPG)} : lg (lg sqrt beta ) - Ir = 0 $$

(8)

$$ {
m {type IVleftrightarrow type IVa (TPG)}} : lg (lg sqrt {Ma + beta } ) - Ir = 0 $$

(9)

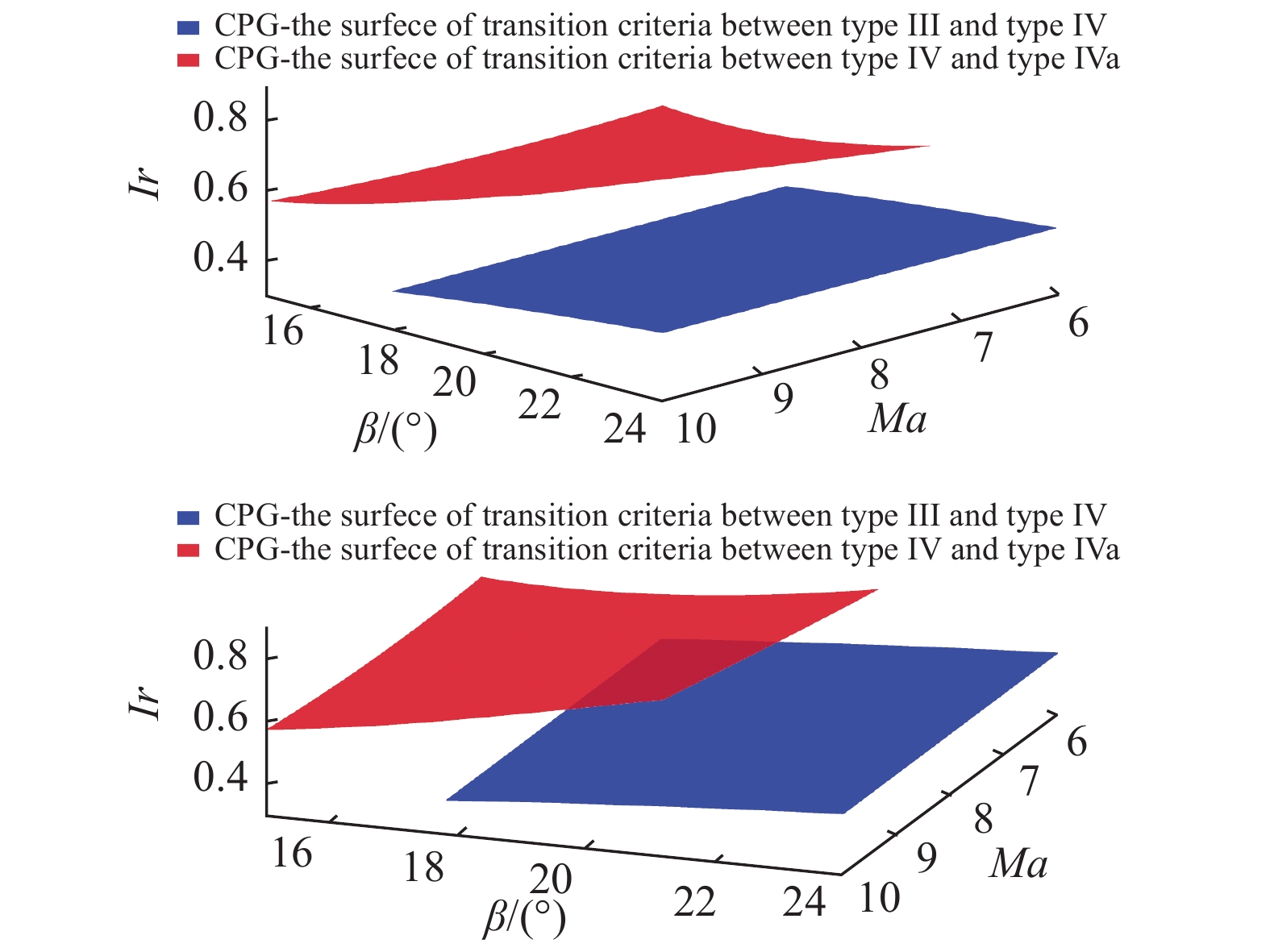
CPG模型下干扰类型转变准则所表示的曲面展现在Ma, β, Ir 3个变量的参数空间中(图13).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />

图
13
CPG气体模型下激波干扰类型准则面

Figure
13.
Criterion surface of shock wave interference type under CPG gas model

下载:
全尺寸图片
幻灯片

结合先前的工作^[26], 对比真实气体模型下转变准则方程, 如图14所示, 可以得到以下结论.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />

图
14
不同气体模型下激波干扰类型转变准则面的比较

Figure
14.
Comparison of the criterion surface of shock interference type transition under different gas models

下载:
全尺寸图片
幻灯片

(1) 4个转变准则面都接近平面, 且其法方向几乎和Ir平行, 说明在3个参数Ma, β, Ir中, 激波干扰的类型对Ir的变化最为敏感, 这也符合研究者们对激波干扰类型的定义的定性认识. 入射激波相对于弓形激波的位置越靠上, 越容易发生从III型到IV型或从IV型到IVa型的转变. 显然, 在参数Ma和β相同的情况下, 发生IV型?IVa型激波干扰比发生III型?IV型激波干扰需要更大的Ir.

(2) 由于真实气体效应, 激波脱体距离减小, 整体射流结构上移, 由图14可知, 发生III型?IV型或IV型?IVa型转变时, 理想气体模型的转变准则面都位于相应真实气体模型转变准则面之上.

(3) 发生III型?IV型激波干扰类型转变时, 观察式(6)和式(8), 发现转变准则面的方程只和激波角β以及位置参数Ir有关, 而与来流马赫数Ma无关, 考虑到拟合方程的精度有限, 定性反映如下规律: 无论量热完全气体模型或是考虑振动激发的真实气体模型, 当发生III型?IV型激波干扰类型转变时, 其转变准则面与激波角β以及位置参数Ir有较大的相关性, 而与Ma的相关性较弱.

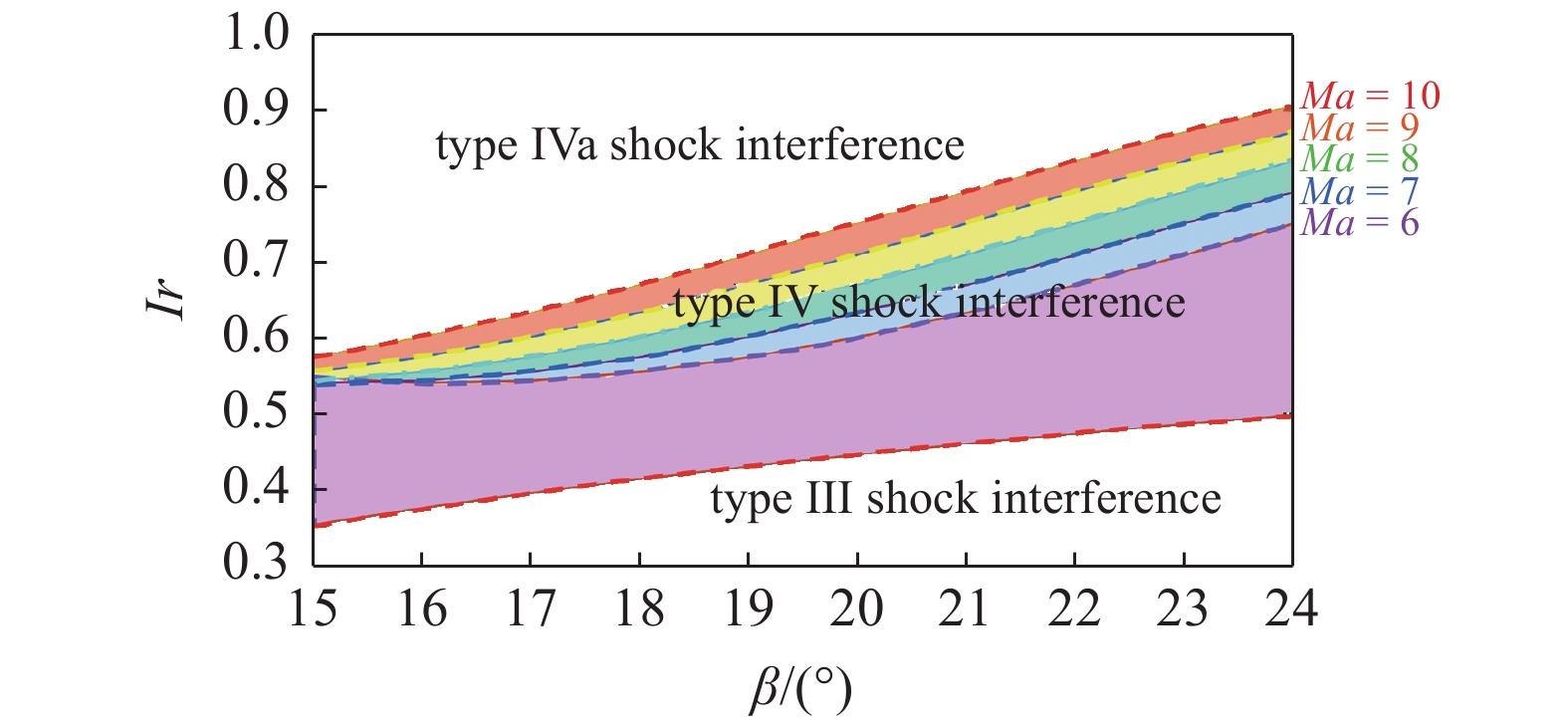
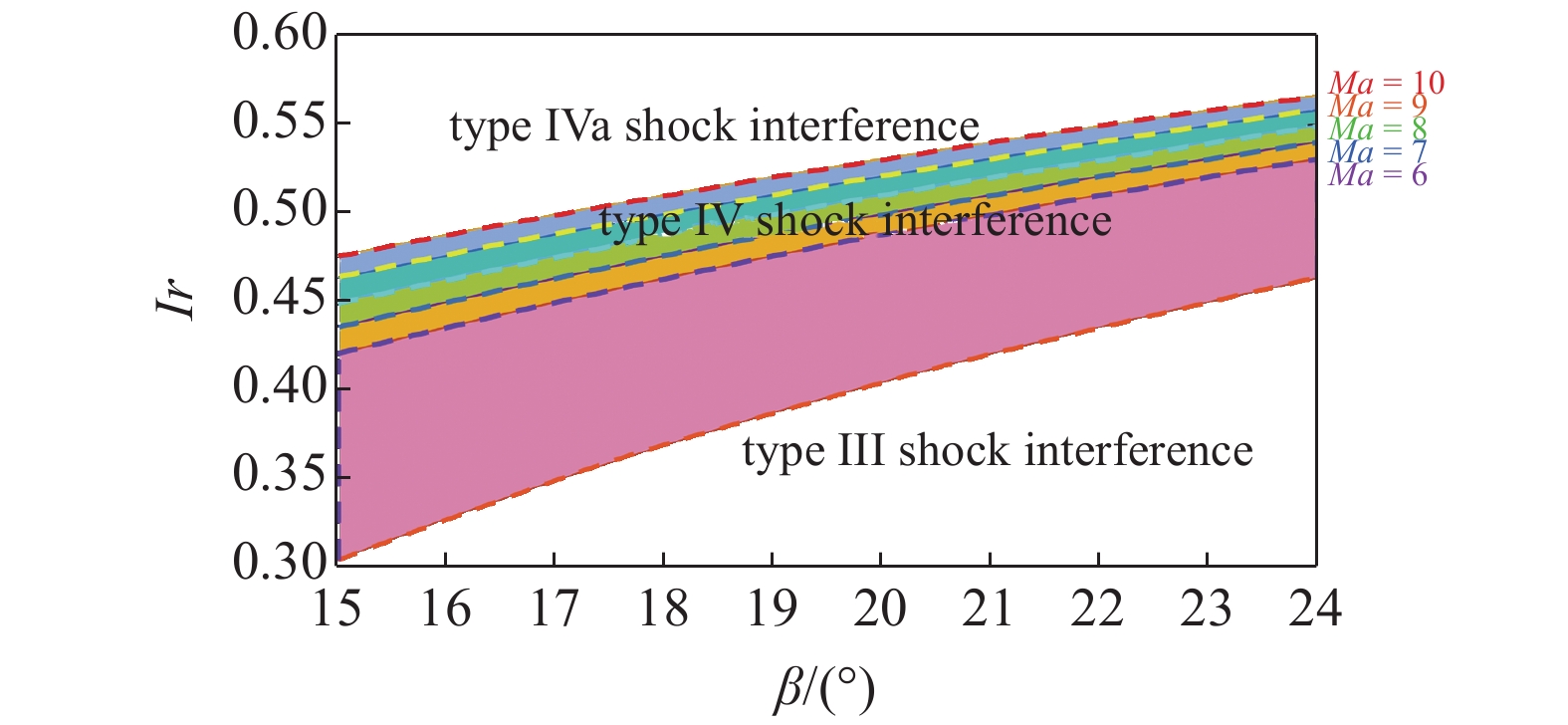
随着马赫数的增加, 高温真实气体效应更加明显. 如图15和图16所示, 随着马赫数的增大, 无论是量热完全气体模型或是真实气体模型, IV型区域占比均增大, 即在相同的激波角范围内, IV型激波干扰所遍历的Ir的范围更广泛. 另外, 计算结果表明, 随着马赫数的增大, 入射激波位置参数相同时, 与量热完全气体模型(CPG)相比, 真实气体模型(TPG)发生III型?IV型或IV型?IVa型激波干扰类型转变所需的激波角更大.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />

图
15
不同马赫数下CPG模型下的激波干扰类型转变分界线示意图

Figure
15.
Schematic diagram of the boundary line of the shock interference type transition under the CPG model under different Mach numbers

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />

图
16
不同马赫数下TPG模型下的激波干扰类型转变分界线示意图

Figure
16.
Schematic diagram of the boundary line of the transition of shock interference types under the TPG model under different Mach numbers

下载:
全尺寸图片
幻灯片

4.
激波干扰类型转变准则适用性验证

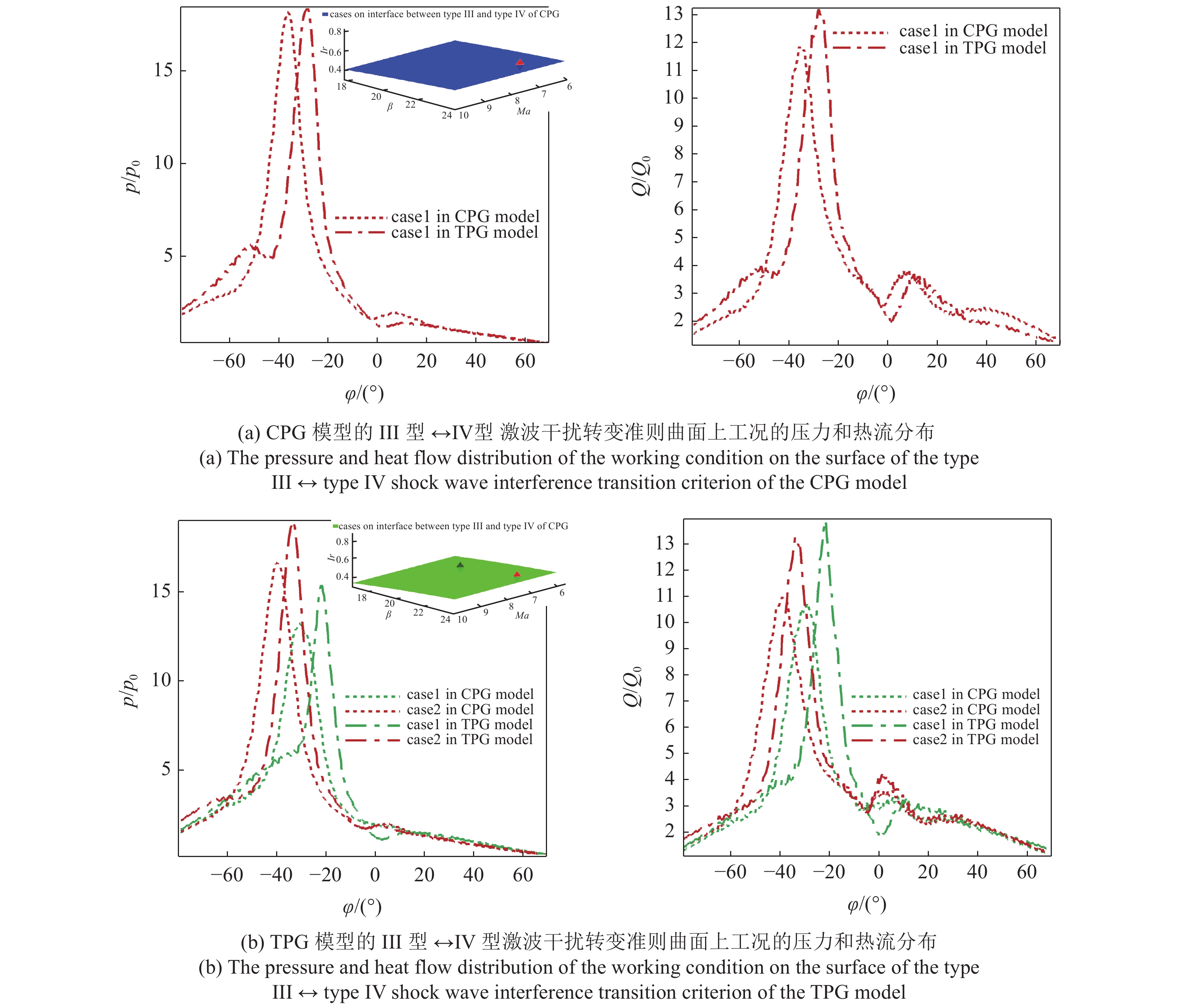
结合3.3节利用机器学习得到的激波干扰类型的转变准则曲面, 在准则面上提取相应的来流参数 (Ma, β, Ir) 进行数值计算, 给出了几组具有代表性的工况结果, 分析其驻点压力和热流分布的变化规律, 验证其适用性, 并探讨高温气体效应对驻点压力和驻点热流的影响. 观察图17, 为了清晰体现工况参数设置, 将每个算例标注在转变曲面上, 并且同一工况的压力热流曲线颜色与实心点颜色相同. 由图17, 可以得到以下规律:

(1) 从图17(a)中可以看出, 当来流参数选取在CPG模型下III型、IV型激波干扰类型转变准则面上(Ma=7, β=23°, Ir=0.4864), 结合图4, 此时对应TPG模型工况已经发生IV型激波干扰, 而TPG模型工况正在发生III型和IV型激波干扰类型的转变过程. 可以发现, 采用TPG模型计算得到的壁面压力和热流峰值均高于采用CPG气体模型计算的结果. 这是因为由于采用不同的气体模型而导致的激波干扰类型发生了变化, 前面提到过, 当来流参数相同时, 干扰类型是影响驻点压力和热流数值的关键因素之一.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-17-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure17-1" />

17
4个准则面上若干算例的压力和热流分布曲线

17.
The pressure and heat flow distribution curves of several examples on four criterion surfaces

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-385-17.jpg'"
class="figure_img
figure_type2 ccc " id="Figure17" />

图
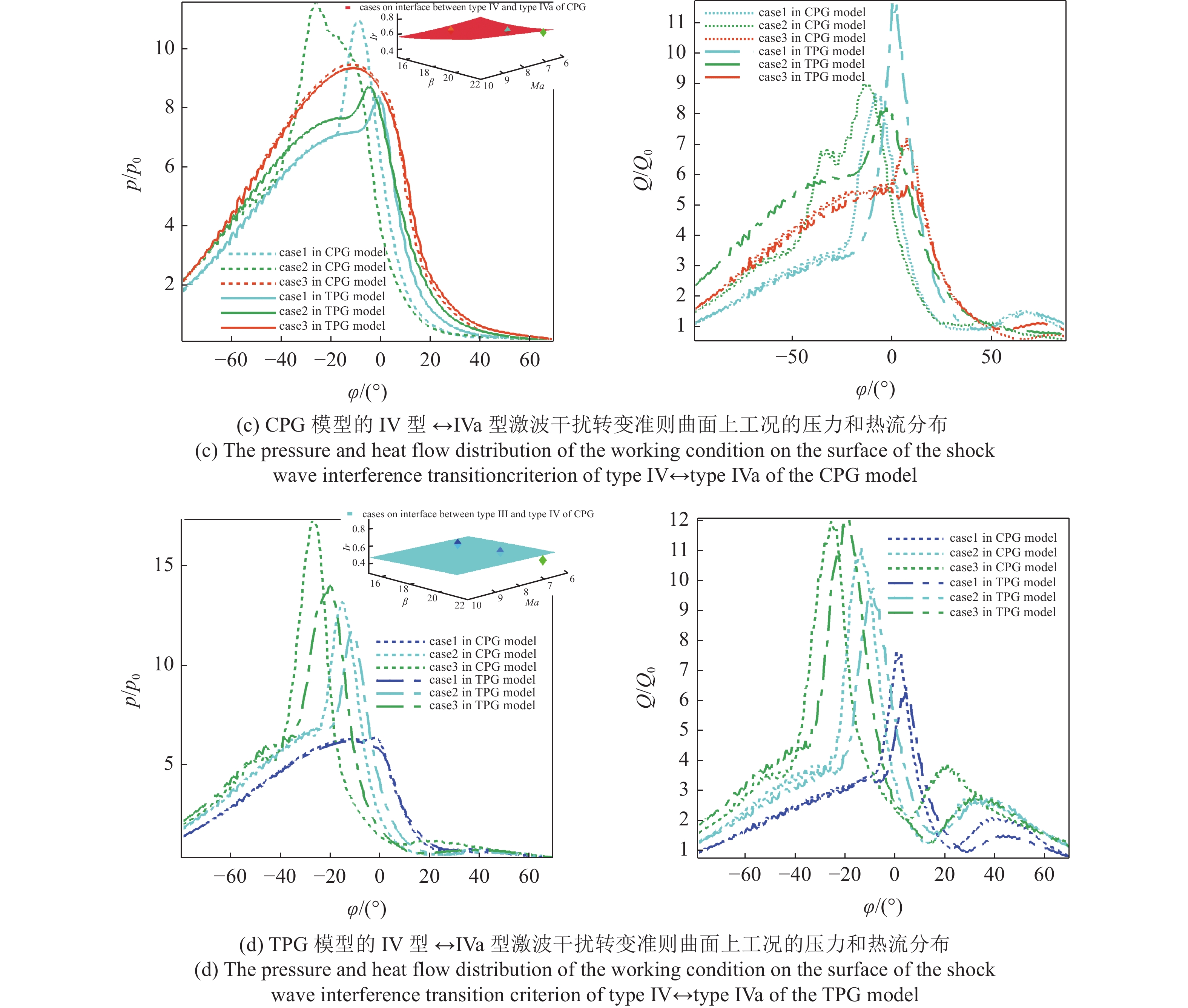
17
4个准则面上若干算例的压力和热流分布曲线 (续)

Figure
17.
The pressure and heat flow distribution curves of several examples on four criterion surfaces (continued)

下载:
全尺寸图片
幻灯片

(2) 观察图17(b), 工况参数位于TPG模型下III型、IV型激波干扰类型转变准则面上(Ma=7, β=19°, Ir=0.3868 ; Ma=7, β=23°, Ir=0.4496). 从流场的几何结构来看, TPG模型工况处于发生III型、IV型转变的情形, 而CPG模型工况仍处于III型激波干扰, 结合III型流场结构, 滑移线SL1冲击壁面, 另有一道斜激波在壁面反射, 波后为超声速, 压力和热流迅速下降.

(3) 如图17(c)所示, 工况参数在CPG模型下IV型、IVa型激波干扰类型转变准则面上(Ma=7, β=19°, Ir=0.6009 ; Ma=7, β=22°, Ir=0.7094; Ma=8, β=16°, Ir=0.5548), 此时采用CPG模型计算的工况发生IV型、IVa型干扰类型转变, 而TPG模型工况均发生IVa型激波干扰. 显而易见, TPG模型下的工况, 压力曲线变得更加平滑, 峰值不再尖锐, 压力峰值也较同一条件下的CPG模型更低.

(4) 如图17(d)所示, 工况参数在TPG模型下IV型、IVa型激波干扰类型转变准则面上(Ma=7, β=16°, Ir=0.4496 ; Ma=7, β=19°, Ir=0.4880; Ma=7, β=22°, Ir=0.5210). 此时, CPG模型工况发生IV型激波干扰, TPG模型工况却即将向IVa型发生转变, 射流顺时针擦拭壁面, 冲击点逐渐上移至脱离壁面, 故3组工况均对应于CPG模型工况压力和热流一致高于TPG模型工况.

由上述几点可见, 本文3.3节所提出的两种模型的激波干扰类型转变准则具有一定的精确性和推广性, 可以用来快速预测工程计算中所发生的激波干扰类型, 以及对采用不同模型计算时所带来的压力和热流分布的差异进行合理假设, 进而对工程计算给出参考.

5.
总结

本文主要讨论了高温气体效应对激波干扰流场结构及状态参数的影响. 同时, 利用MBB算法, 分析了不同物理模型下流场几何结构以及高温气体效应对激波干扰类型转变准则的影响, 并对该准则上的多组临界工况的激波干扰结构及壁面压力和热流分布进行了预测, 主要有以下结论.

(1) 高温气体效应对激波干扰流场的几何结构和流动状态参数的影响主要体现在: 高温气体效应使得激波脱体距离减小, 波后温度大幅度降低; 对于IV型激波干扰, 随着马赫数的增加, CPG和TPG模型下⑤区和⑦区的压力、温度、马赫数等状态参数差值逐渐增大, 体现了高温效应对流场状态影响较大.

(2) 高温气体效应对预测三波点位置、超声速射流形状以及激波干扰类型转变准则的影响主要有: 从三波点位置公式可以看出, 当Ir非常小时, 激波脱体距离与来流马赫数的相干性不强, 这一规律从数值计算的结果中也可以看出; 无论CPG模型或是TPG模型, MBB对三波点A以及射流结构的预测结果与数值结果几乎重合, 体现了该算法在流体力学数据处理上的优越性; 发生激波干扰类型转变时, 两类模型的准则面均近乎于Ir轴垂直, CPG模型的准则面均位于TPG模型的上方; 随着马赫数的增大, 高温气体效应逐渐明显, 两类模型的IV型区域占比均增大, 即在相同的激波角范围内, IV型激波干扰所包含的Ir的范围更广阔.

(3)发生激波干扰时, 壁面压力和热流峰值主要取决于流场的几何结构和干扰类型. 本文提出的激波干扰转变准则可以根据来流条件, 预测激波干扰类型进而判断流场结构以及壁面驻点的大致区域, 为热防护工作做好准备. 同时也讨论了由于采用不同的气体模型导致发生不同的干扰类型, 造成流场结构的差异性, 进而影响壁面周围的热环境, 并以转变准则面上的多组临界工况加以佐证, 揭示了该准则的工程意义.