引 言

随着海洋战略地位日益凸显, 围绕海洋来展开深海环境探索, 资源开发以及武器装备研发变得日趋重要, 未来海洋将会是世界各国科技实力角逐的重要战场. 相比于空气, 水的高黏度流体特性带来的巨大阻力严重制约水下航行体的航速和机动性能, 通气空泡减阻技术能实现高效的水下减阻, 在水下发射、超高速跨介质导弹等领域极具应用前景.

近年来水下动力技术逐渐成为一个新的研究热点问题, 相较于空气, 一方面水中压力会阻碍气体膨胀, 喷管出口处形成很高的背压; 另一方面, 在水气巨大的速度差形成的强剪切影响下, 导致压力振荡, 喷管出口环境很不稳定^[1-2]. 针对水下背压高的问题, 可以通过提高发动机燃烧室的压比, 设计喷管出口为过膨胀状态来解决^[3]. 而喷管出口压力振荡的问题还未有行之有效的办法, 降低出口压力脉动至可控范围内于工程实践具有重要意义.

水下射流流体特性研究进展, 主要包括Shi等^[4-5]在静水塔中开展了超音速气体射流实验, 结果显示压力脉动的频率和喷管内激波振荡相关联. Han等^[6]利用一个实验室尺度的固体火箭发动机在水下开展了推力测试实验, 得出喷管出口处气泡增长和脱落是导致压力脉动的主要原因. 唐云龙等^[7]在VOF模型基础上通过添加相变源项, 建立了考虑相变的可压多相流数值方法, 并模拟了水下固体火箭发动机产生的高温燃气射流. Fronzeo和Kinzel^[8]通过数值仿真研究了不同密度液流环境下气体射流的演化过程. 许昊等^[9]通过水洞实验研究了水流速度对尾喷气体射流的影响, 对比分析有无水流速度两种情况下, 剪切作用差异带来的气体射流形态演化过程与压力脉动特性的变化. Xiang等^[10]考虑了深水环境条件下, 过膨胀气体射流的流动结构和演化过程.

尾喷管出口处的环境, 对发动机参数设计来说如此重要, 是否可以从流动控制的角度去改善出口压力振荡的问题. 张孝石等^[11]在实验中观察到气体射流直接喷在水中和有空泡包裹前提下喷到水中, 两者形态存在很大差异. Zhang等^[12]研究了水下气体射流诱导产生的尾空泡问题, 并分析了不同类型诱导尾空泡转变条件. 王晓辉等^[13]研究了火箭发动机在尾空泡内点火过程, 尾空泡的存在有效降低了燃气射流建立初期形成的极高冲击压力, 但是尾空泡内仍然存在剧烈的压力振荡, 从而引起发动机的推力不稳定.

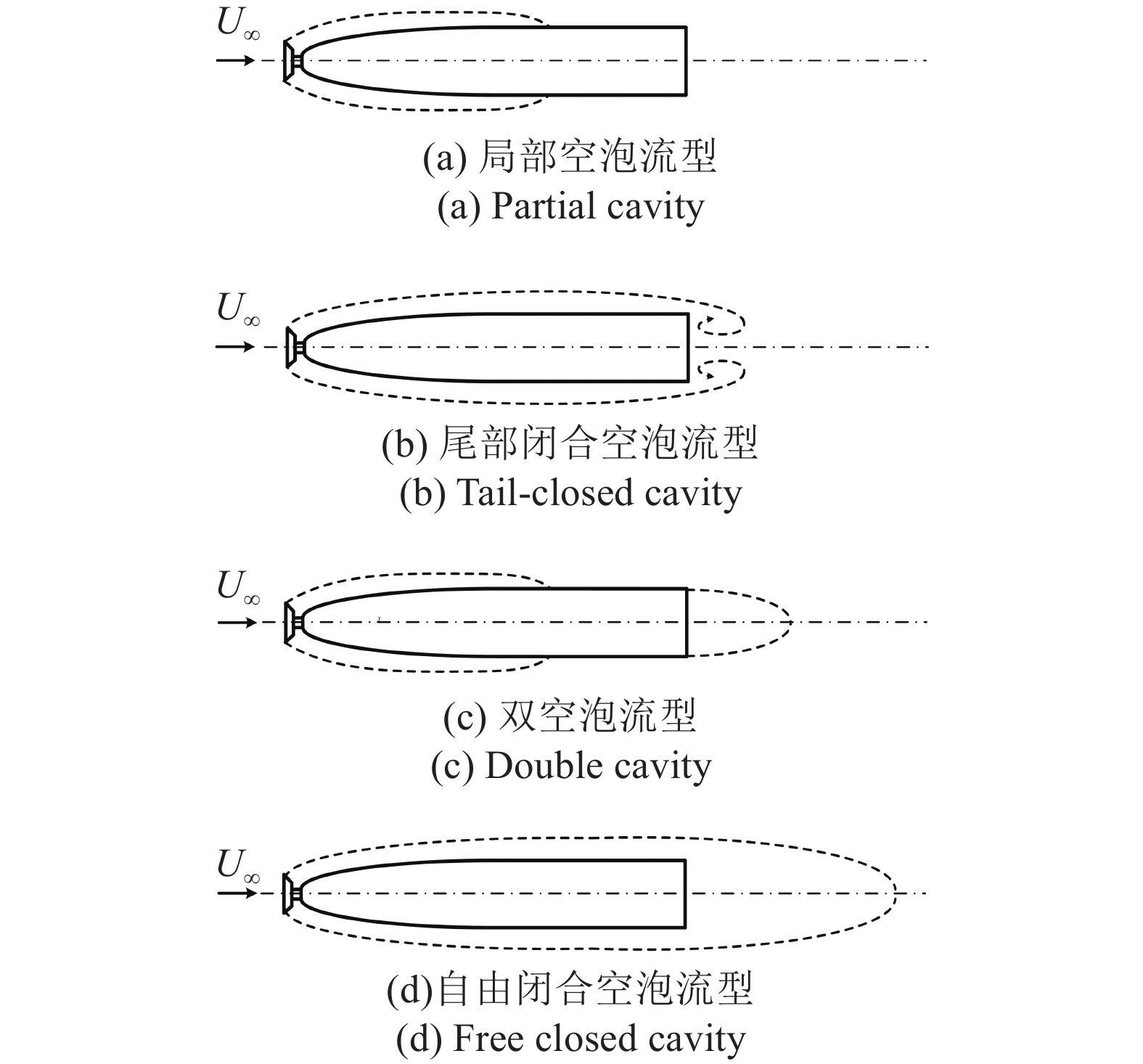
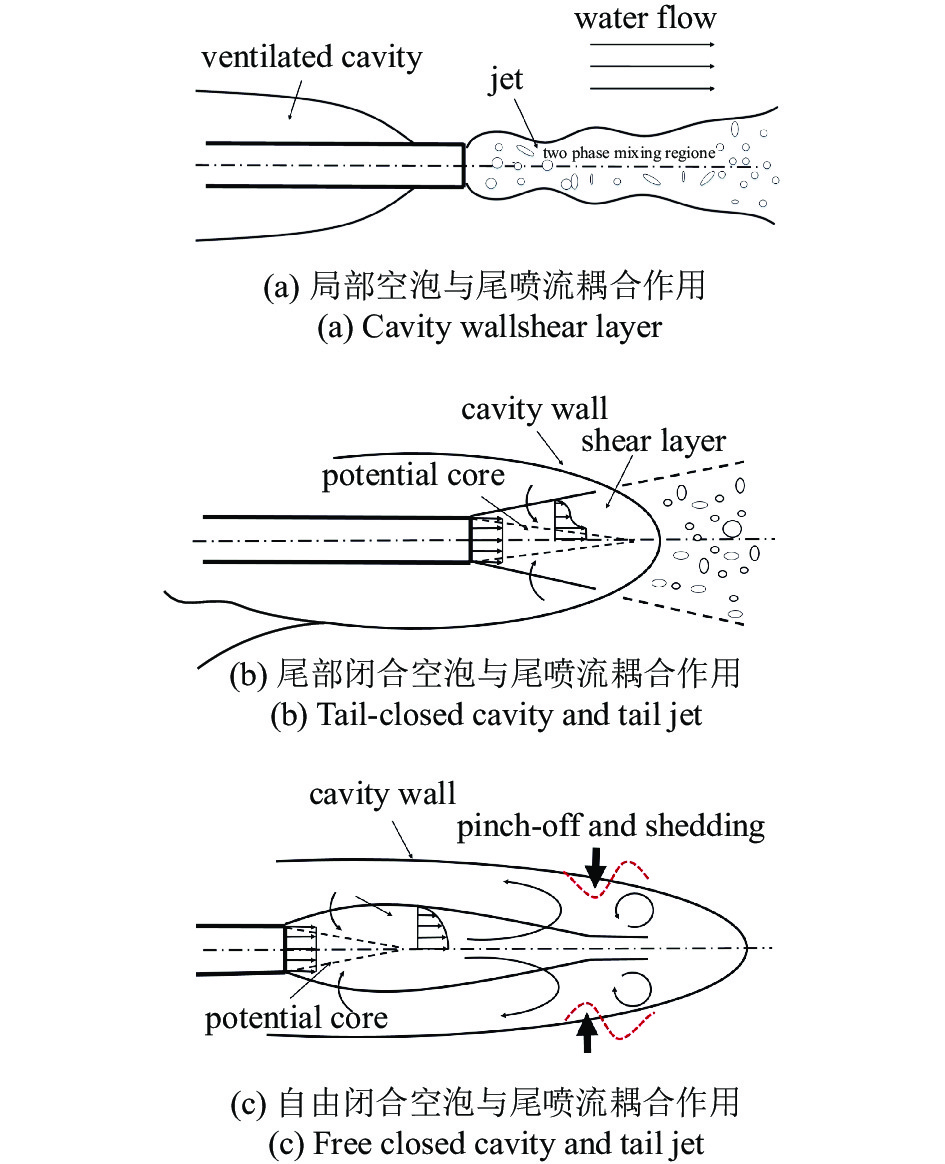
超空泡航行体表面存在4种基本空泡流型, 如图1所示. 局部空泡流型、尾部闭合空泡流型、双空泡流型、自由闭合空泡流型. 不同的空泡流型导致空泡射流耦合流场结构发生变化, 如图2所示. 特别是第3种, 通气空泡包裹整个尾流场的情况, 空泡是否可以为火箭发动机提供稳定的工作环境, 是否可以形成气幕来降低发动机所产生的噪音, 这是非常值得研究的问题. 要达到上述目的, 前提就是要维持空泡形态的稳定性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
航行体空泡的4种基本流型



Figure
1.
Four basic flow patterns of cavitation



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
通气空泡与射流耦合流场结构



Figure
2.
The flow field structure of jet/cavity interaction



下载:
全尺寸图片
幻灯片


水下射流流体特性和空泡演化过程紧密耦合, 相关研究表明高温、高速气流直接作用于空泡内流场和空泡界面, 可引起空泡界面波动甚至断裂. Paryshev^[14]结合空泡截面独立扩张原理和空泡尾部闭合模型, 提出了两个无量纲数($ overline J $和$ overline P $)来判定通气空泡泄气模式和稳定性的理论模型, 两个无量纲数与射流总压和动量相关. Karlikov等^[15]对采用不同喷射方式的通气空泡开展了实验研究. 研究表明: 采用轴向高速喷射气流时, 高速区域压力降低, 导致空泡颈缩断裂. Karlikov等^[15]指出, 喷射速率变化导致空泡表现出不同形态, 其本质在于气流喷射效应引起边界层气体流场结构和尾部泄气方式的改变, 进而改变空泡稳定性. Krane等^[16-19]从理论、实验和计算流体力学3个角度探讨了通气空泡与尾喷射流之间的相互作用规律, 得出: 尾喷射流气体对空泡剪切层内气体流动具有较大影响. 当射流强度较小时, 射流为空泡补气. 当射流强度足够大时, 在射流动量影响下, 空泡泄气模式最终转变为震荡泄气模式, 空泡失稳. 周后村^[20]开展了一系列实验研究, 观测到了尾喷流作用下新型的震荡/双涡管耦合泄气机制. 发现射流强度足够大时将导致连续空泡界面发生颈缩, 而射流诱导的涡结构与空泡界面的相互作用是引起空泡失稳的主要原因.

总的来说, Paryshev理论较好的建立了亚音速射流和空泡耦合作用模型, 但实际工程实践中, 喷流多为超音速工况, 需要考虑气体的可压缩性和总压损失. 除此之外, 射流和空泡相对位置关系的变化等都会影响到不同模式转化临界条件. Paryshev理论模型尚不足以解决上述问题, 且未能对射流作用下空泡形态进行理论描述. 本文利用VOF耦合水平集(level set)界面追踪方法, 考虑气体的可压缩性, 针对自由闭合流型的通气空泡, 改变射流强度和模型长度, 展开了一系列的空泡和超音速尾射流相互作用的数值模拟, 重点分析了通气空泡的稳定性和闭合位置.

1.
可压多相流数值方法

通气空泡和超音速尾喷流相互作用的过程中, 一方面要考虑射流作用下空泡界面的非定常演化特性, 另一方面要考虑气体可压缩性的影响. 空泡内气体可压缩性越明显, 通气空泡越不稳定^[21-22]. 本文基于商业软件Fluent平台, 只考虑气相可压, 并通过CLSVOF方法来模拟空泡界面的演化过程.

1.1
控制方程

多相流中VOF模型的连续方程, 动量方程, 能量方程表达如下

$$ frac{{partial { ho _m}}}{{partial t}} + frac{partial }{{partial {x_i}}}left( {{ ho _m}{u_i}} ight) = 0 $$

(1)

$$ begin{split} &frac{partial }{{partial t}}left( {{ ho _m}{u_i}} ight) + frac{partial }{{partial {x_j}}}left( {{ ho _m}{u_i}{u_j}} ight) = &quad - frac{{partial p}}{{partial {x_i}}} + frac{partial }{{partial {x_j}}}left[ {{mu _m}left( {frac{{partial {u_i}}}{{partial {x_j}}} + frac{{partial {u_j}}}{{partial {x_i}}}} ight)} ight] + { ho _{ m{m}}}{g} + {F_{{ m{CSF}}}}end{split} $$

(2)

$$ begin{split} &frac{partial }{{partial t}}sumlimits_{k = w,g} {left( {{alpha _k}{ ho _k}{E_k}} ight)} + &quadfrac{partial }{{partial {x_j}}}{u_j}sumlimits_{k = w,g} {left[ {{alpha _k}left( {{ ho _k}{E_k} + p} ight)} ight]} = frac{partial }{{partial {x_j}}}left( {{k_{{ m{eff}}}}frac{{partial T}}{{partial {x_j}}}} ight)end{split} $$

(3)

式中$ p $, $ T $, $ u $, $
ho $, $ mu $和$ alpha $分别代表压力、温度、速度、密度、黏性系数和相体积分数. $ {k_{{
m{eff}}}} $代表导热系数. $ {
ho _{
m{m}}}{g} $为体积力, $ {F_{{
m{CSF}}}} $为表面张力. 角标$ m $, $ w $, $ g $分别表示混合相、液相和气相. 混合相的物性参数定义为

$$ { ho _m} = { ho _w}(1 - {alpha _g}) + { ho _g}{alpha _g} $$

(4)

$$ {mu _m} = {mu _w}(1 - {alpha _g}) + {mu _g}{alpha _g} $$

(5)

混合相声速的计算公式如下

$$ ?c={left[ ho left(frac{{alpha }_{g}}{{ ho }_{g}{c}_{{}_{g}}^{2}}+frac{{alpha }_{w}}{{ ho }_{w}{c}_{w}^{2}} ight) ight]}^{-0.5} $$

(6)

1.2
VOF耦合level set 界面捕捉方法

在Bourlioux^[23], Sussman和Puckett^[24]提出的耦合VOF和level-set (CLSVOF)方法中, 通过耦合求解体积分数方程和level-set函数方程来捕获和跟踪界面. 主要思想为: 首先利用VOF方法求解单位网格内的相体积分数, 得到界面位置, 这样可以确保质量守恒. 再利用体积分数初始化level-set距离函数, 通过求解距离函数得到界面分布情况, 采用level-set方法可以得到准确的界面曲率和法向量. VOF方法中体积分数输运方程如下

$$ frac{partial }{{partial t}}({alpha _g}{ ho _g}) + nabla cdot ({alpha _g}{ ho _g}{boldsymbol{u}}) = 0 $$

(7)

level-set方法中符号距离函数$ varphi (x,t) $表达式如下

$$ varphi (x,t) = left{ begin{aligned} & + left| d ight|,;;;;x in {text{the}};{text{primary}};{text{phase}} hfill & 0,;;;;;;;;;x in varGamma hfill & - left| d ight|,;;;;x in {text{the}};{text{second}};{text{phase}} end{aligned} ight. $$

(8)

式中d代表距界面的距离. 对于给定的速度场${boldsymbol{u}}$, 求解level-set函数对流方程确定界面的演化

$$ frac{{partial varphi }}{{partial x}} + nabla cdot left( {{boldsymbol{u}}varphi } ight) = 0 $$

(9)

由于数值计算过程中格式误的差影响, 经式(9)求解得到的距离函数包含误差, 不是真实的界面位置. 因此, 通常需要对距离函数进行重新初始化, 方程如下

$$ left. begin{array}{l}{varphi _tau } =(1 - left| {nabla varphi } ight|) { m{sign}} {{varphi _0}} hfill varphi (x,0) = {varphi _0} end{array} ight} $$

(10)

其中, 角标$ tau $为虚拟时间. ${
m{sign}} {{varphi _0}}$为符号函数, 其定义为

$$ { m{sign}} {{varphi _0}} = 2left[ {Hleft( {{varphi _0}} ight) - {1 mathord{left/ {vphantom {1 2}} ight. } 2}} ight] $$

(11)

$ Hleft( {{varphi _0}}
ight) $为Heaviside函数, 与体积分数相关联, 其定义为

$$ Hleft( varphi ight){text{ = }}left{ begin{aligned} &0, qquadqquadqquad {text{if }}varphi < - varepsilon & {left( {varphi {text{ + }}varepsilon } ight)}/left( {2varepsilon } ight)+ sin ({text{ π }} varphi/varepsilon)/left(2{text{ π }} ight) ,;;;; {text{if }}left| varphi ight| < varepsilon & 1, qquadqquadqquad {text{if }}varphi > varepsilon end{aligned} ight. $$

(12)

其中, 参数$ varepsilon = 1.5Delta x $, $ Delta x $为网格尺度.

Level-set模型中界面单位法向量、曲率计算公式如下

$$ left. begin{aligned}&{boldsymbol{n}} = {left. {frac{{nabla varphi }}{{left| {nabla varphi } ight|}}} ight|_{varphi = 0}}&kappa = nabla cdot {left. {frac{{nabla varphi }}{{left| {nabla varphi } ight|}}} ight|_{varphi = 0}} end{aligned} ight}$$

(13)

计算过程中, 每个迭代时间步都需要重新初始化$ varphi (x,t) $函数使其保持符号距离函数的特征. CLSVOF算法中通过几何方法进行符号距离函数重新初始化. 即由相体积分数确定界面单元中各相分别占单元的几何比例, 即单元格内的切割比例, 而level-set函数的梯度确定界面的方向, 即单元格内的切割方向. 界面重构后, 由几何方法计算符号距离函数.

1.3
湍流模型

k-ω SST湍流模型由k-ε模型和k-ω模型加权平均得到^[25], 兼顾两者的优势, 在边界层分离流动和空化流动中具有广泛的应用. 其湍动能k和湍流比耗散率ω的输运方程可以表达如下

$$ begin{split} &frac{{partial left( {{ ho _m}k} ight)}}{{partial t}} + nabla cdot left( {{ ho _m}k{{boldsymbol{u}}}} ight) = nabla cdot left[ {left( {mu + {sigma _{k1}}{mu _t}} ight)nabla k} ight] +&qquad {tilde P_k} - {beta ^{text{*}}}{ ho _m}omega k end{split}$$

(14)

$$ begin{split} &frac{{partial left( {{ ho _m}omega } ight)}}{{partial t}} + nabla cdot left( {{ ho _m}omega {boldsymbol{u}}} ight) = nabla cdot left[ {left( {mu + {sigma _{omega 1}}{mu _t}} ight)nabla omega } ight] +&qquad gamma { ho _m}{S^2} - {beta _2}{ ho _m}{omega ^2} + left( {1 - {F_1}} ight)C{D_{komega }}end{split} $$

(15)

式中, $ {beta ^{text{*}}} $, $ {beta _2} $, $ {sigma _{k1}} $, $ {sigma _{omega 1}} $, $ gamma $为模型常数, $ {tilde P_k} $为湍动能生成项

$$ left. begin{array}{l} {{{tilde P}_k} = min left( {{p_k},10{beta ^*}{ ho _m}omega k} ight)} {{P_k} = {u_t}{S^2}} end{array} ight} $$

(16)

湍流黏度${mu _t}$定义为

$$ {mu _t} = frac{{{ ho _m}{a_1}k}}{{max left( {{a_1}omega ,S{F_2}} ight)}} $$

(17)

式中, S为应变率, $ {a_1} $为模型常数. 混合函数$ {F_1} $和${F_2}$分别为

$$ {F_1} = tanh ({arg}_1^4), ; {F_2} = tanh ({arg}_2^2) $$

(18)

$$ {ar}{{g}_1}{text{ = }}{ m{min}}left[ {{ m{max}}left( {frac{{sqrt k }}{{{beta ^ * }omega d}},frac{{500v}}{{{d^2}omega }}} ight),frac{{4{ ho _m}{sigma _{omega 2}}k}}{{{C}{{D}_{komega }}{d^2}}}} ight] $$

(19)

$$ C{D_{komega }} = max left( {2{ ho _m}frac{1}{{{sigma _{omega 2}}omega }}nabla knabla omega ,1.0 times {{10}^{ - 10}}} ight) $$

(20)

$$ {arg _2}{text{ = }}{ m{max}}left( {2frac{{sqrt k }}{{{beta ^*}omega d}},frac{{500v}}{{{d^2}omega }}} ight) $$

(21)

各模型参数取值如表1所示.




表
1
k-ω SST湍流模型参数



Table
1.
Model parameters



table_type1 ">

$ {sigma _{k1}} $	$ {sigma _{omega 1}} $	$ {beta _1} $	$ {sigma _{k2}} $	$ {sigma _{omega 2}} $	$ {beta _2} $	$ {beta ^*} $	$ {a_1} $	$ gamma $
0.5	0.5	0.075	1	0.856	0.0828	0.09	0.55	0.44

下载:
导出CSV
|显示表格

1.4
几何模型、网格划分及边界条件

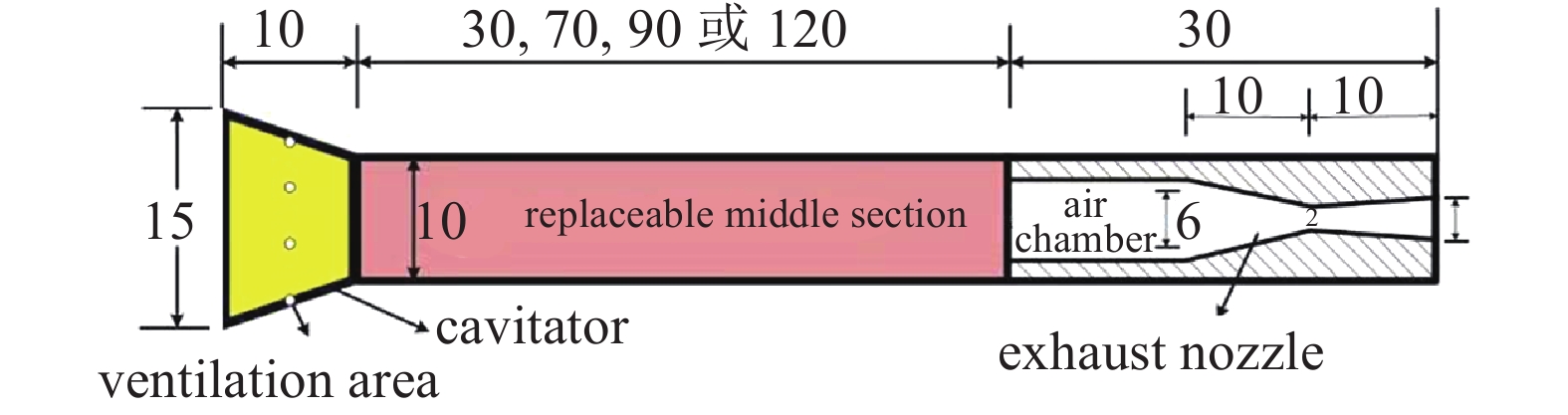
实验模型采用回转体结构, 主要由头部空化器、中间段(共4个长度)和尾喷管构成, 其外形示意图及尺寸如图3所示. 尾喷管结构设计为喉部和出口的扩张比为2.25, 出口设计马赫数 $ M{a_e} $= 2.2. 在不同射流流量条件下, 射流的出口速度范围可以覆盖亚音速到超音速.

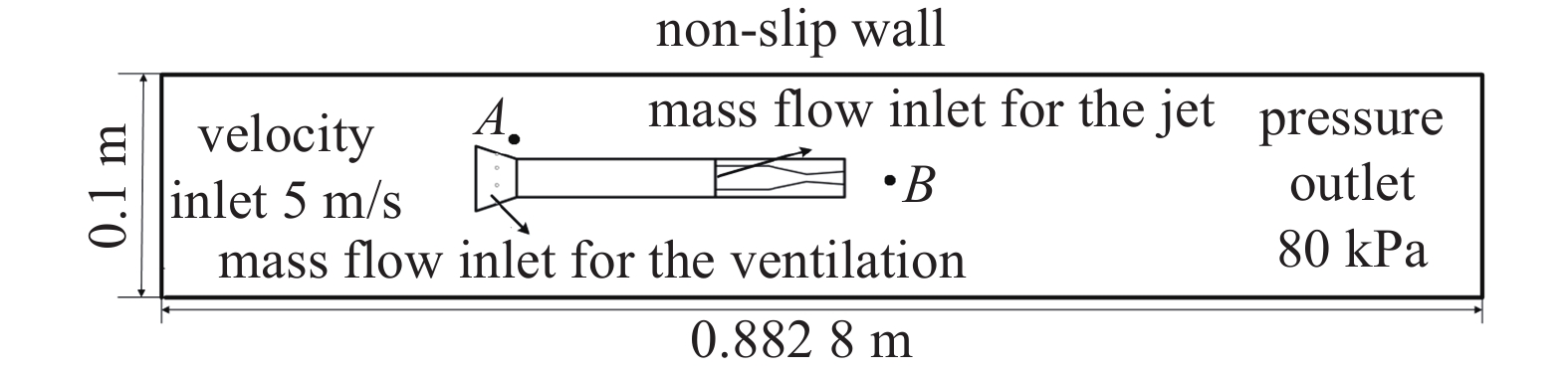
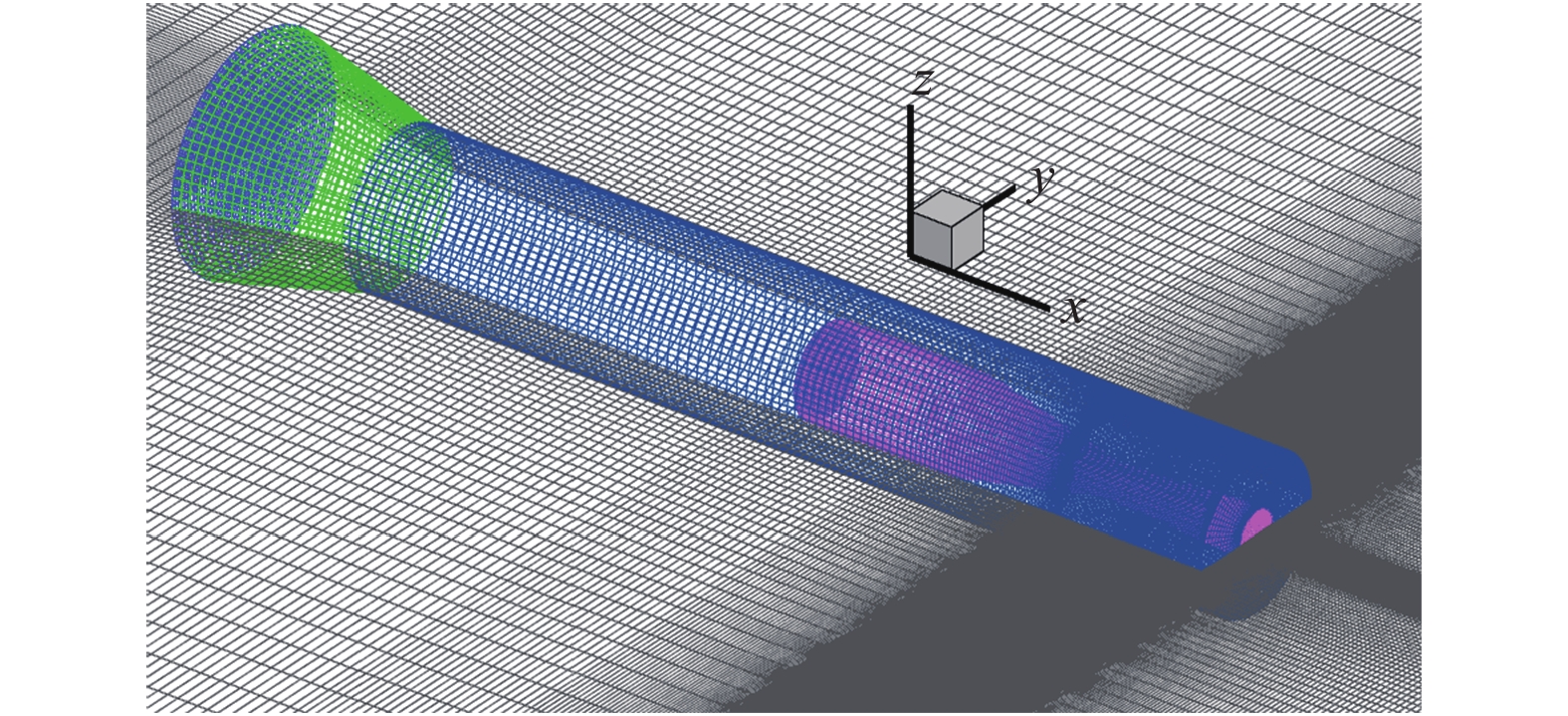
计算域和边界条件设置, 以及喷管出口附近网格如图4和图5所示. 入口速度5 m/s, 出口压力80 kPa, 远场为无滑移壁面边界条件. 通气和射流入口采用质量流量边界条件, 通气质量流量为0.000 1 kg/s. 并在空化器附近和喷管出口附近设置压力监测点A和B. 网格采用结构网格, 网格量为180万, 在空泡界面处和喷管出口处做了网格加密处理.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
几何模型(单位: mm)



Figure
3.
The geometric model (unit: mm)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
计算域和边界条件



Figure
4.
Computation domain and boundary condition



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
模型附近结构网格



Figure
5.
Employed structured mesh near the model



下载:
全尺寸图片
幻灯片

2.
数值仿真结果

2.1
不同射流强度计算结果分析

2.1.1
喷管出口激波结构

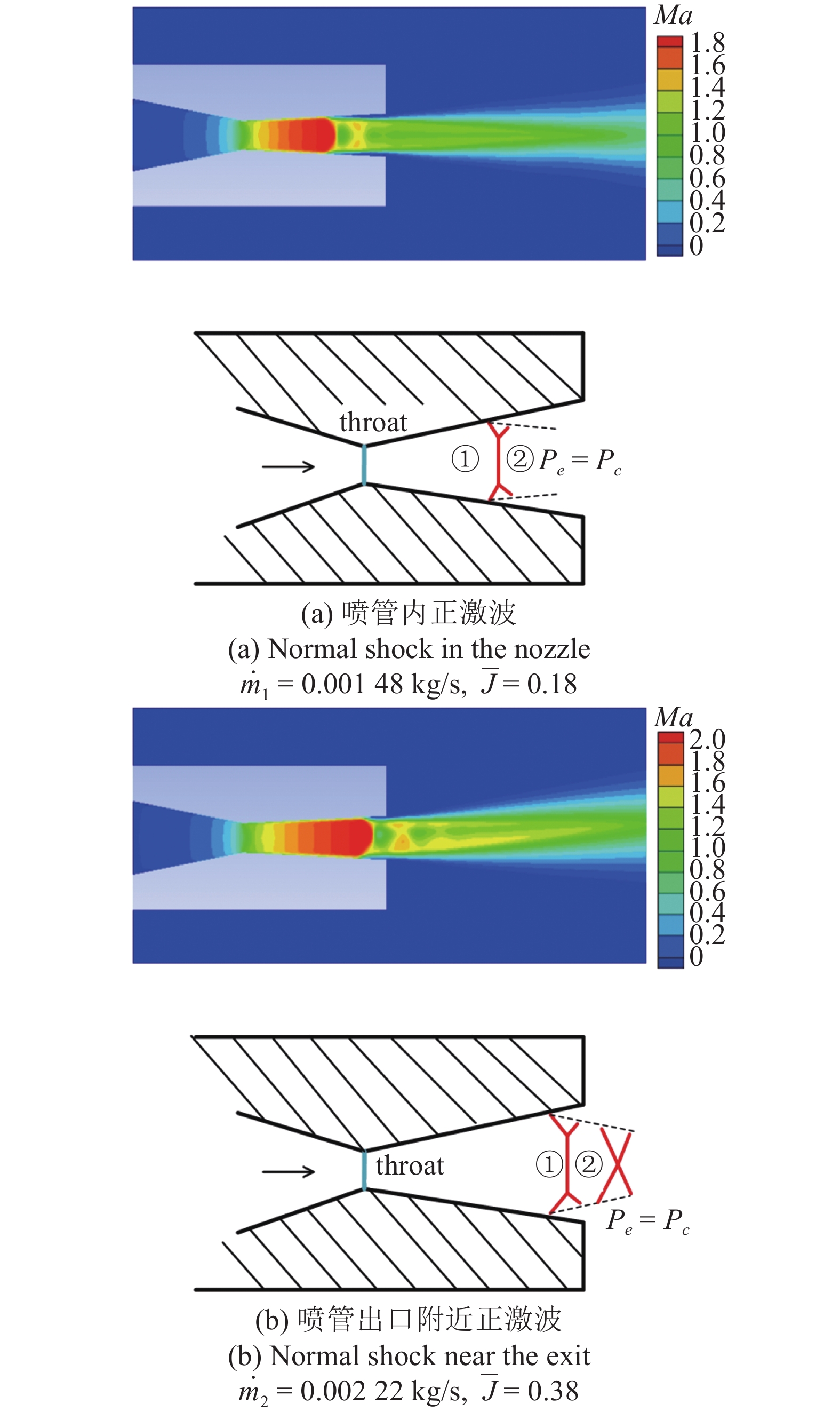
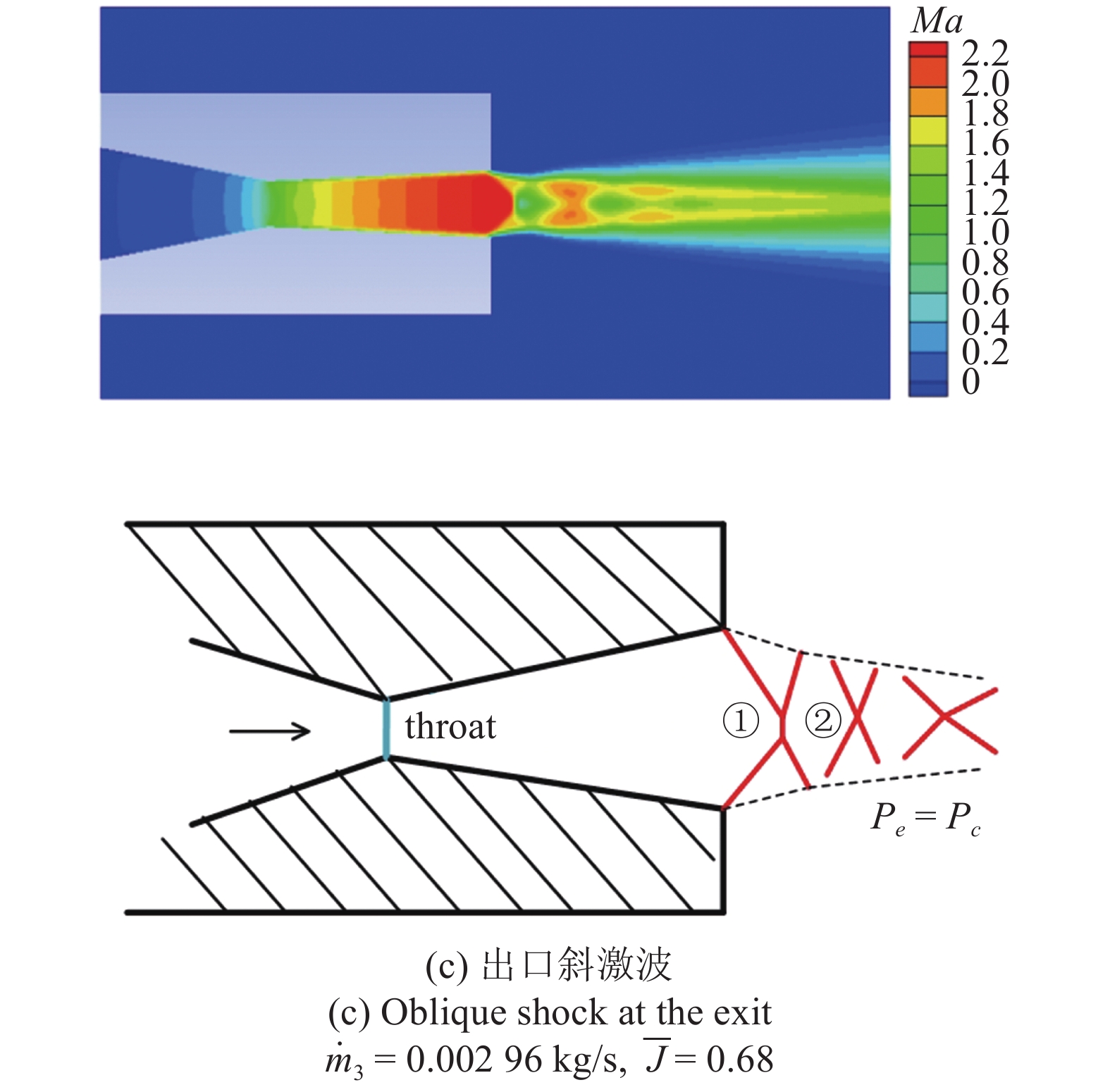
仿真计算过程中对比了4个入口质量流量. 图6展示了t=5 ms时, 不同入口质量流量条件下喷管出口速度云图及激波结构, 其中$ {dot m_1} $代表质量流量, $ overline J $代表射流出口处无量纲动量. 由于此时空泡界面还未变化, 射流直接喷在气的环境中, 未受到水介质的影响. 当$ {dot m_1} = 0.001;48;{{
m{kg}}/ {
m{s}}} $时, 为管内正激波, 出口流动为亚音速流动. 当$ {dot m_2} = 0.002;22;{{
m{kg}}/ {
m{s}}} $时, 管内的正激波靠近喷管出口, 出口流动仍为亚音速流动. 当$ {dot m_3} = 0.002;96;{{
m{kg}}/ {
m{s}}} $时, 管口为相交斜激波, 出口速度达到设计马赫数2.2, 为过膨胀状态.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-6-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6-1" />



6
不同入口质量流量条件下喷管出口速度云图及激波结构



6.
Velocity cloud plot and shock wave structure at the nozzle exit as the inlet mass flow varies



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同入口质量流量条件下喷管出口速度云图及激波结构(续)



Figure
6.
Velocity cloud plot and shock wave structure at the nozzle exit as the inlet mass flow varies (continued)



下载:
全尺寸图片
幻灯片

2.1.2
射流作用下空泡界面的演化过程

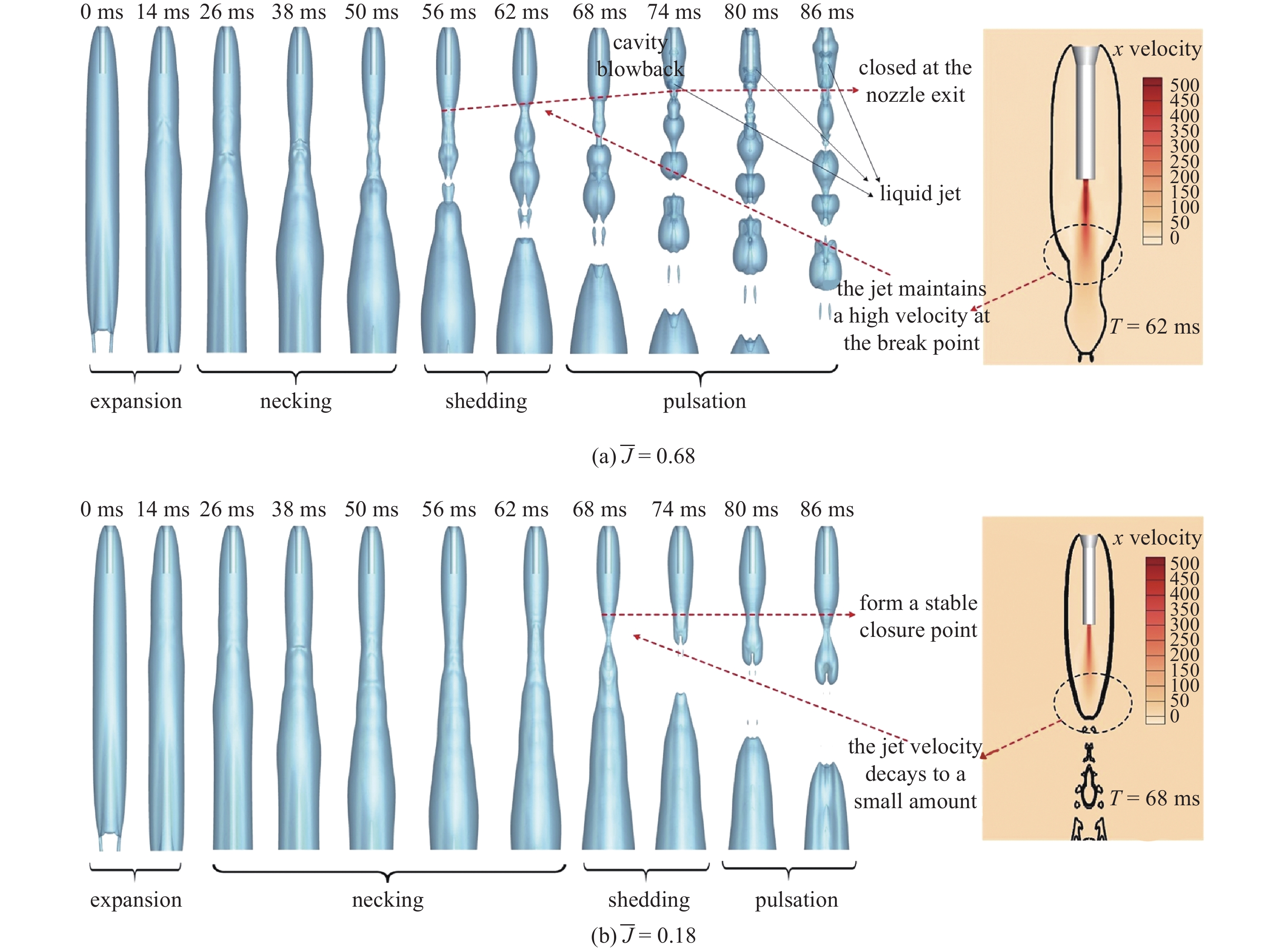
超音速尾流作用下, 射流卷吸周围空泡内气体, 导致空泡内部出现质量流动的不平衡, 空泡界面会经历一个复杂演化过程, 来达到新的平衡状态. 图7展示了空泡界面的非定场演化过程. 射流开启后, 首先大量的气体使得空泡发生膨胀, 膨胀部分向后运动, 接着空泡由于形态拉长而出现中间部分颈缩, 进一步出现断裂, 空泡整体回缩, 长度变短. 之后, 空泡开始进入周期性震荡泄气阶段. 射流强度越强, 空泡出现颈缩断裂的时间越早, 更快的进入到震荡泄气阶段. 当射流的强度超过一定临界值以后, 在空泡尾部会出现液体射流冲击空泡界面的情况, 从而进一步导致空泡失稳.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
空泡界面演化过程



Figure
7.
Cavity inteface evolution process



下载:
全尺寸图片
幻灯片

2.1.3
液体回射流的形成机制及空泡失稳过程

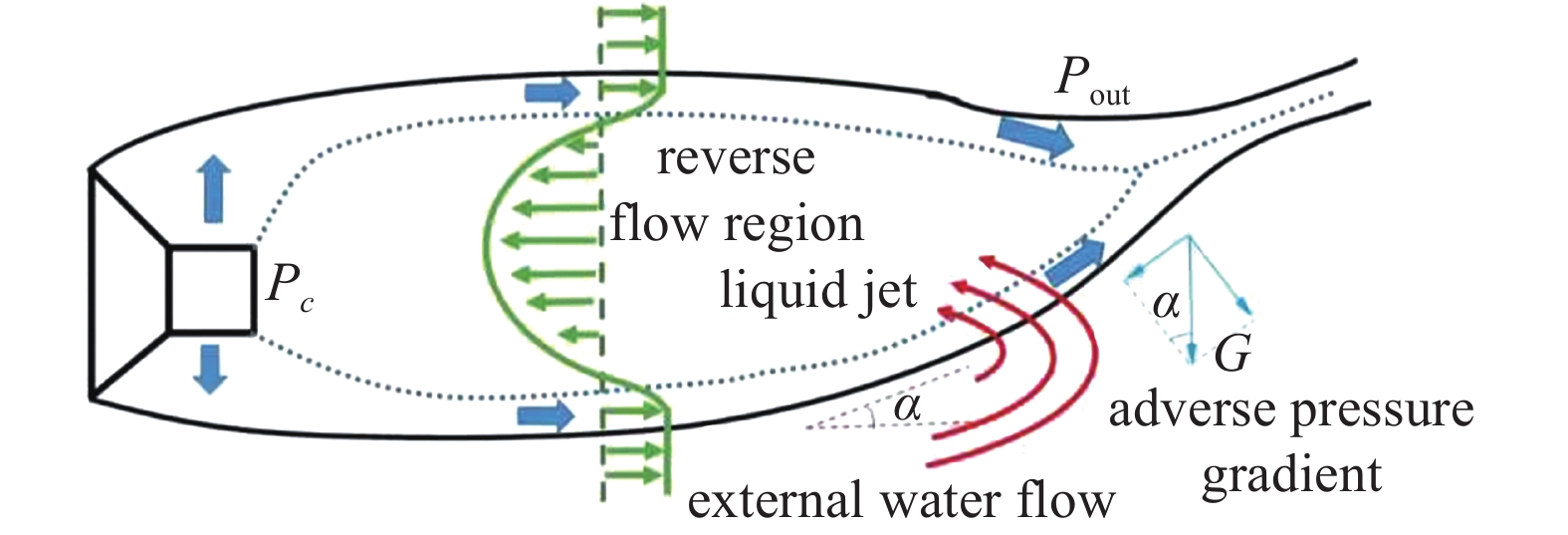
通气空泡尾部一般存在回射流泄气和双涡管泄气两种典型模式^[26]. 其中, 双涡管模式时空泡尾部形成稳定反向螺旋的双涡管流动. 而回射流泄气以空泡尾部非稳定回注射流的出现和螺旋式涡团的脱落为特征, 值得注意的是, 液体回射流只出现在空泡的下表面. 2012年Savchenko和Savchenko^[27]指出Rayleigh-Taylor (RT)不稳定性机制是导致界面不稳定的主要原因. 气体填充界面凹陷过程中导致液流飞溅, 从而出现回射现象. 2019年Wu等^[28]利用流动可视化技术做了更多详细的解释, 由于浮力的影响空泡尾部会上飘形成一定的角度$ alpha $, 如图8所示, 回射现象的发生和这个角度有着紧密的联系. 气液界面外部水流一侧在空泡尾部为扩张流动, 边界层内由于重力分量$ Gsin alpha $形成很强的逆压力梯度, 从而导致液流穿透界面, 空泡内压差会进一步增强液体射流动能, 最终只在空泡尾部下底面出现回射现象.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
通气空泡内液体回射流形成机制



Figure
8.
Formation mechanism of liquid back-jet flow in the ventilated cavity



下载:
全尺寸图片
幻灯片


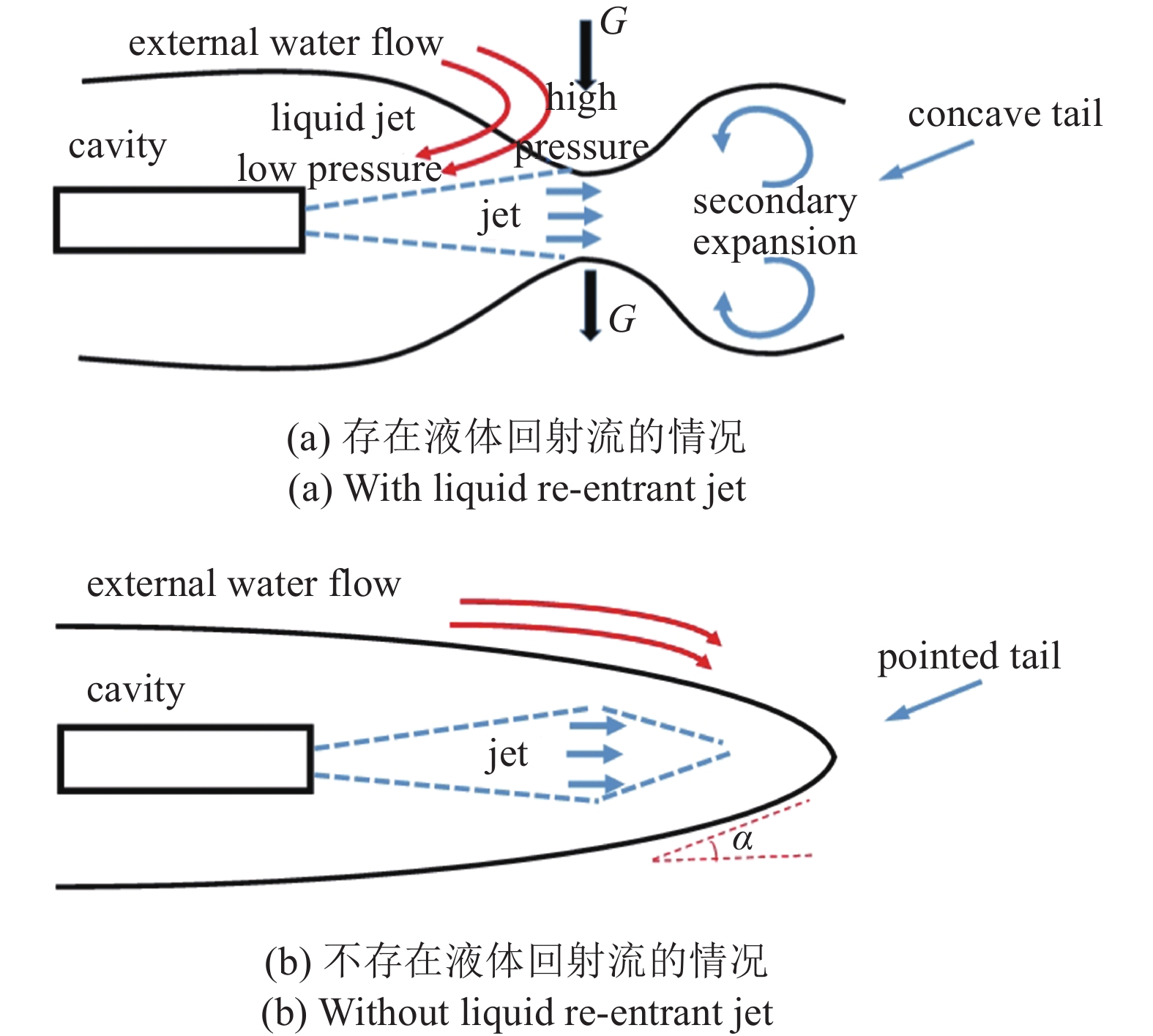
对于尾喷流作用下的通气空泡在夹断过程会出现两种情况, 如图9所示, 第一种射流的强度较弱, 空泡夹断以后空泡尾部为尖尾型, 与图7中$ overline J = 0.{text{1}}8 $工况一致, 此时空泡尾部夹角角度很小, 难以形成回射. 第二种情况射流的强度较强, 射流在空泡断裂点保持着很高的速度, 气体很快形成二次膨胀使得空泡尾部变成凹型尾, 与图7中$ overline J = 0.68 $工况一致. 在凹陷处的上表面, 重力作用使得凹陷的角度更大, 在下表面重力作用趋向于使得界面变平, 结果使得液体射流更容易形成于空泡尾部的上表面, 出现上下不对称的结果. 另外射流的速度越高, 空泡内侧的压力越低, 空泡内外压差导致空泡尾部界面的回击, 同时为液体射流提供足够的能量, 与纯通气空泡相比, 此时向前冲击液体射流拥有更强的动能.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
尾喷流作用下液体回射流形成机制



Figure
9.
Formation mechanism of liquid back-jet flow under the action of a tail jet



下载:
全尺寸图片
幻灯片


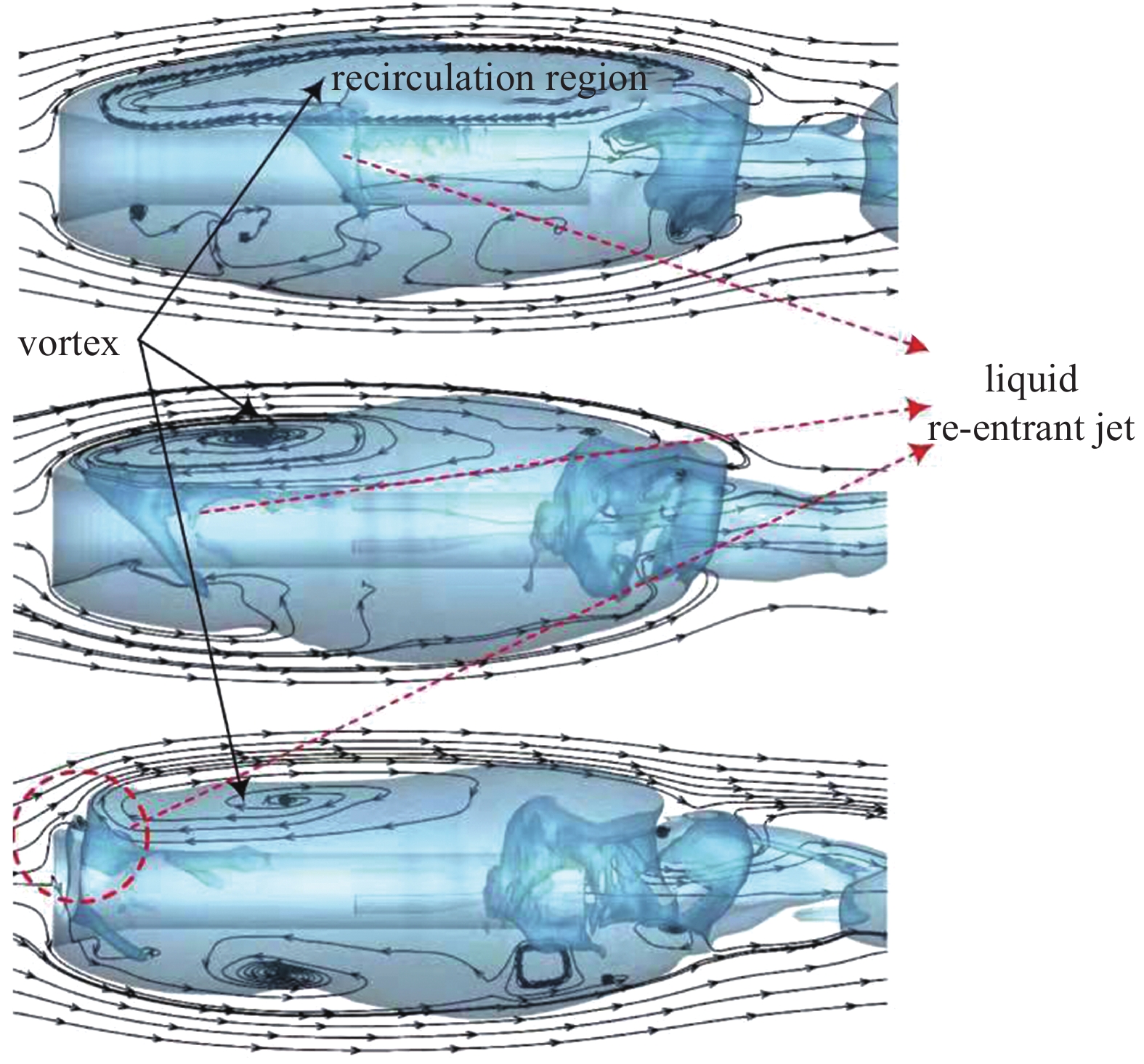
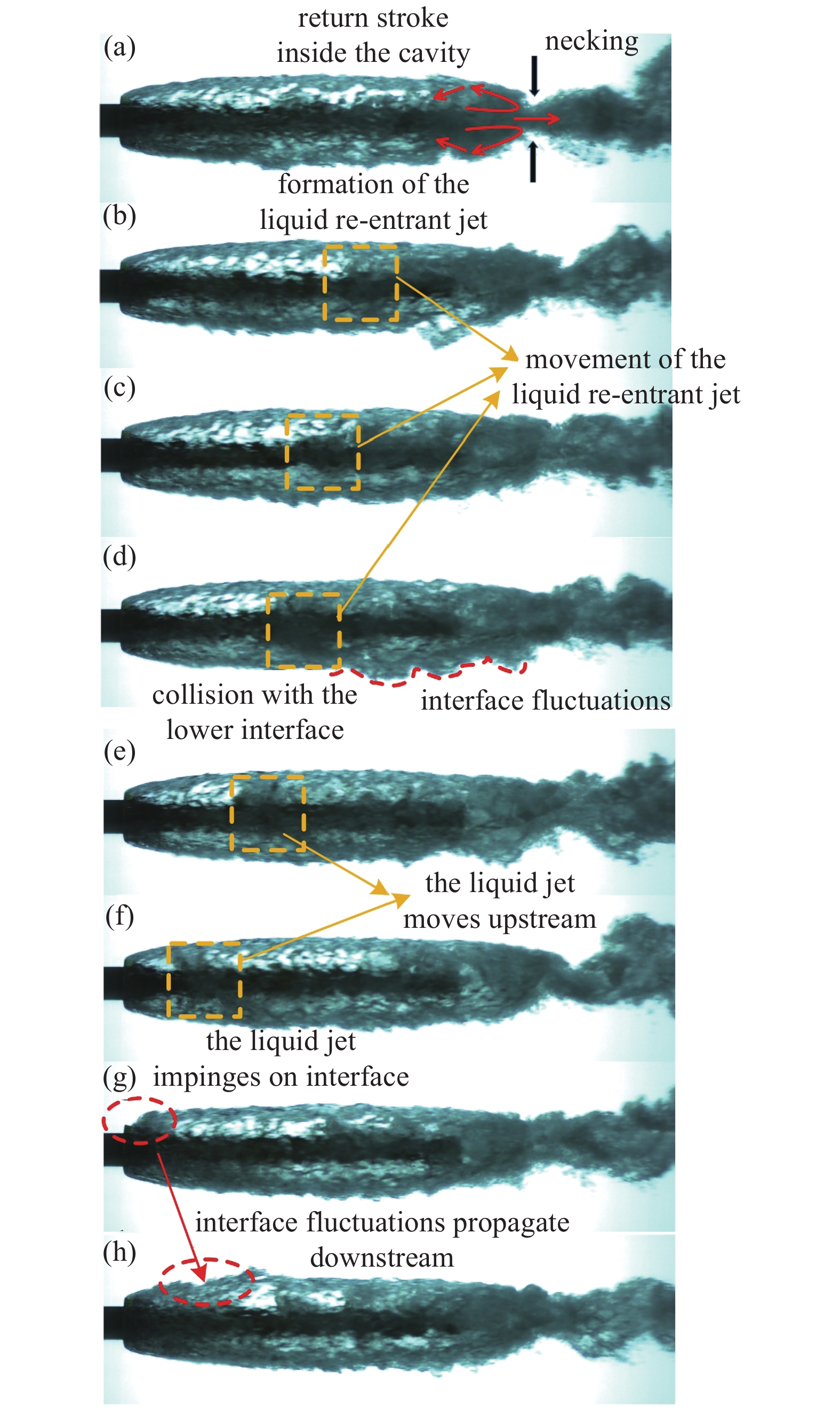
空泡稳定性受到很多流动参数的影响, 为了确定哪些流动参数才是关键所在, 因而对空泡的破坏过程展开了详细研究. 图10展示了液体回射流作用下通气空泡的失稳过程, 液体回射形成之后, 沿着空泡内气体回流的方向向前运动, 直至接触空化器附近的界面, 并与迎面的来流发生碰撞, 对空泡产生巨大破坏, 空泡界面已经严重扭曲变形, 接着空泡界面的振荡会向下游传播, 最终导致整个空泡失稳. 图11为实验中通过高速摄影拍摄到的空泡内部液体回射流和空泡界面发生接触, 从而导致空泡失稳的过程, 实验条件对应仿真工况为$ overline L = 0.{text{6}} $, $ overline J = 0.{text{6}}8 $. 目前的数值仿真结果能很好地预测到这种空泡失稳机制, 同时从可以不同时刻提取的空泡内液体回射流的位置, 辨析出回射流向上游输运的速率, 大小接近于外部水流的一半. 液体回射流使得空泡内部由透明状转变为水气掺混的模糊状态. 并在向上游输运的过程中与空泡界面碰撞, 造成空泡界面波动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
液体回射流作用下空泡失稳过程



Figure
10.
Cavity instablity process under the liquid back-jet flow



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
实验中拍摄液体回射流诱导空泡失稳过程



Figure
11.
Cavity instablity process under the liquid back-jet flow in the experiment



下载:
全尺寸图片
幻灯片

2.1.4
射流强度对空泡稳定性的影响

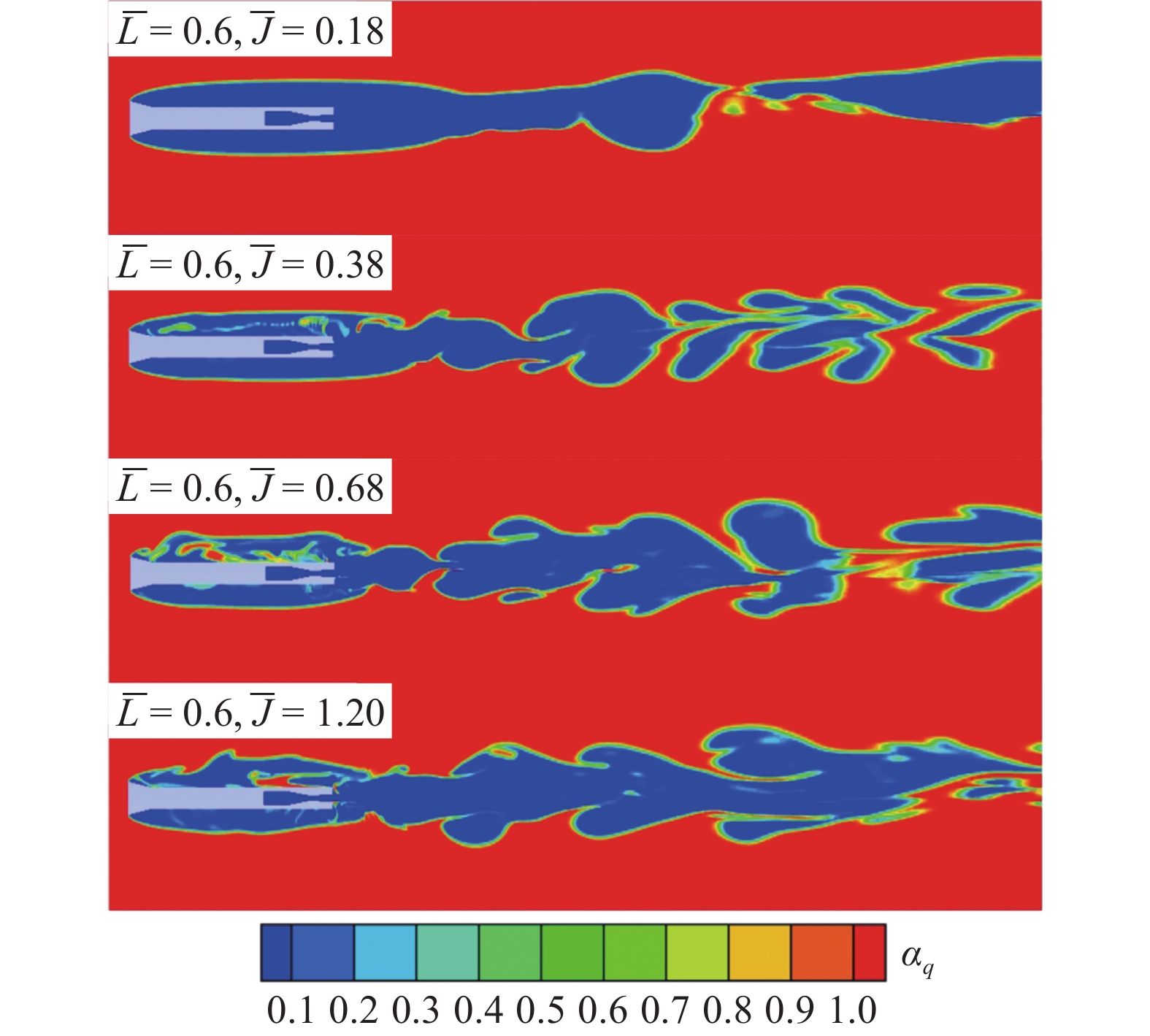
分析在空泡失稳的过程中, 剪切和重力作用是主要因素, 强剪切力使得空泡形态拉长夹断. 而空泡夹断过程中往往伴随着气流的回击现象, 使得泡内压力的突增和突降. 图12展示了随着射流强度的增加, 通气空泡形态的变化. 当$ overline J = 0.{text{1}}8 $时, 射流对空泡的泄气作用, 导致空泡形体相对于初始空泡, 长度减小, 尾部出现气团脱落, 但空泡界面保持稳定. 当射流强度增加至$ overline J = 0.38 $时, 液体冲击界面进入空泡内, 形成液体回射流. 当射流进一步增强至$ overline J = 0.{text{6}}8 $, 空泡颈缩位置逐渐向喷管出口靠近, 通气空泡由自由闭合流型在射流作用下转变为尾部闭合流型. 当射流强度达到$ overline J = {text{1}}{text{.20}} $时, 射流出口位置以前的空泡形态受到扰动发生变形. 此时的空泡具有很强的瞬态特性, 其形状和尺寸较透明空泡随时间变化更为剧烈. 空泡尾部射流区掺混大量离散气团和液滴/气泡云, 形态与纯射流较为接近.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
随着射流强度增加, 通气空泡体积分数云图



Figure
12.
Volume fraction cloud plot for the caity as the jet intensity increases



下载:
全尺寸图片
幻灯片


总的来说, 射流强度越强, 气液两侧的剪切作用越强, 产生的液体回射流的强度越大, 界面越容易破坏, 最终造成液体冲击界面进入空泡内, 形成液体回射流, 进一步空泡界面会破碎, 变成水气掺混的状态.

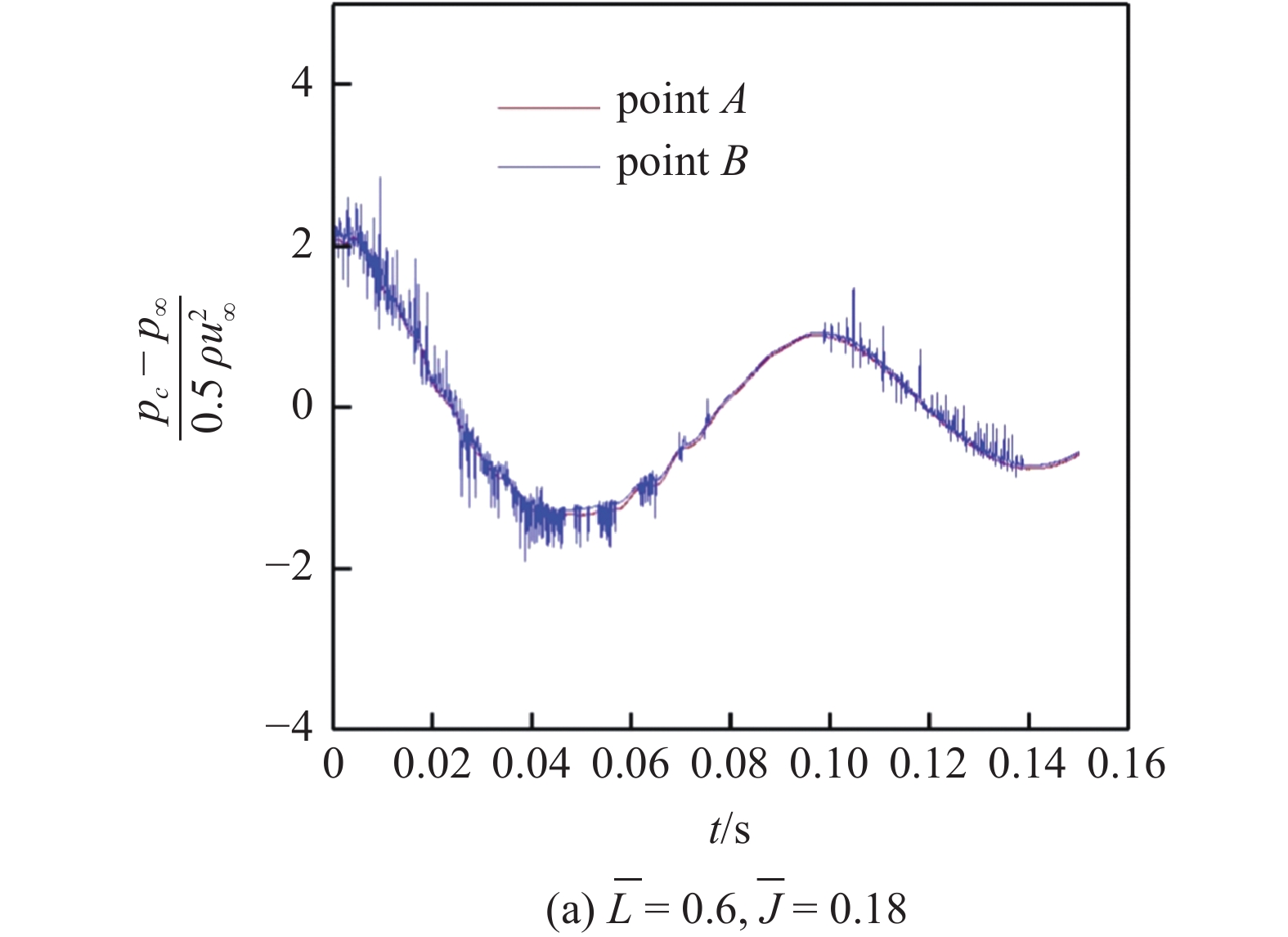
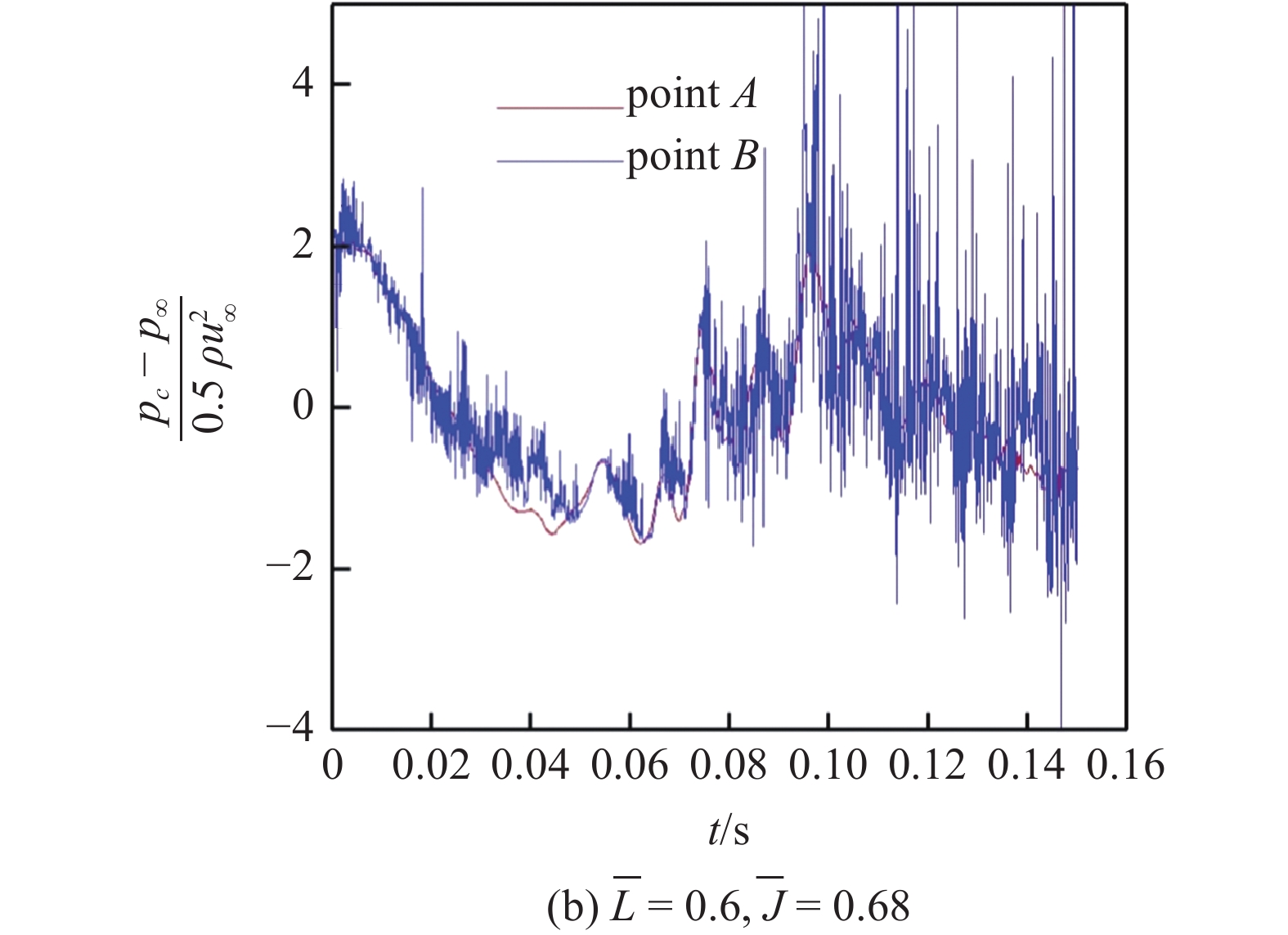
图13对比了射流强度为$ overline J = 0.{text{1}}8 $和$ overline J = 0.{text{6}}8 $两种工况条件下, 空泡内部压力随时间的变化. 前者空泡为稳定状态, 空化器附近压力和喷管出口压力变化基本一致, 频率和变化的幅值较小, 说明通气空泡技术存在为火箭发动机提供稳定工作环境的潜在应用前景. 后者空泡为失稳状态, 空化器附近压力和喷管出口压力变化的趋势一致, 但是喷管出口压力波动的频率和幅值要大很多, 说明空泡尾部的振荡形态逐渐向水下射流形态靠近.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-13-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13-1" />



13
对比不同射流强度条件下空泡内压力随时间的变化



13.
The change of pressure inside the caivty with time is compared under different jet intensity conditions



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
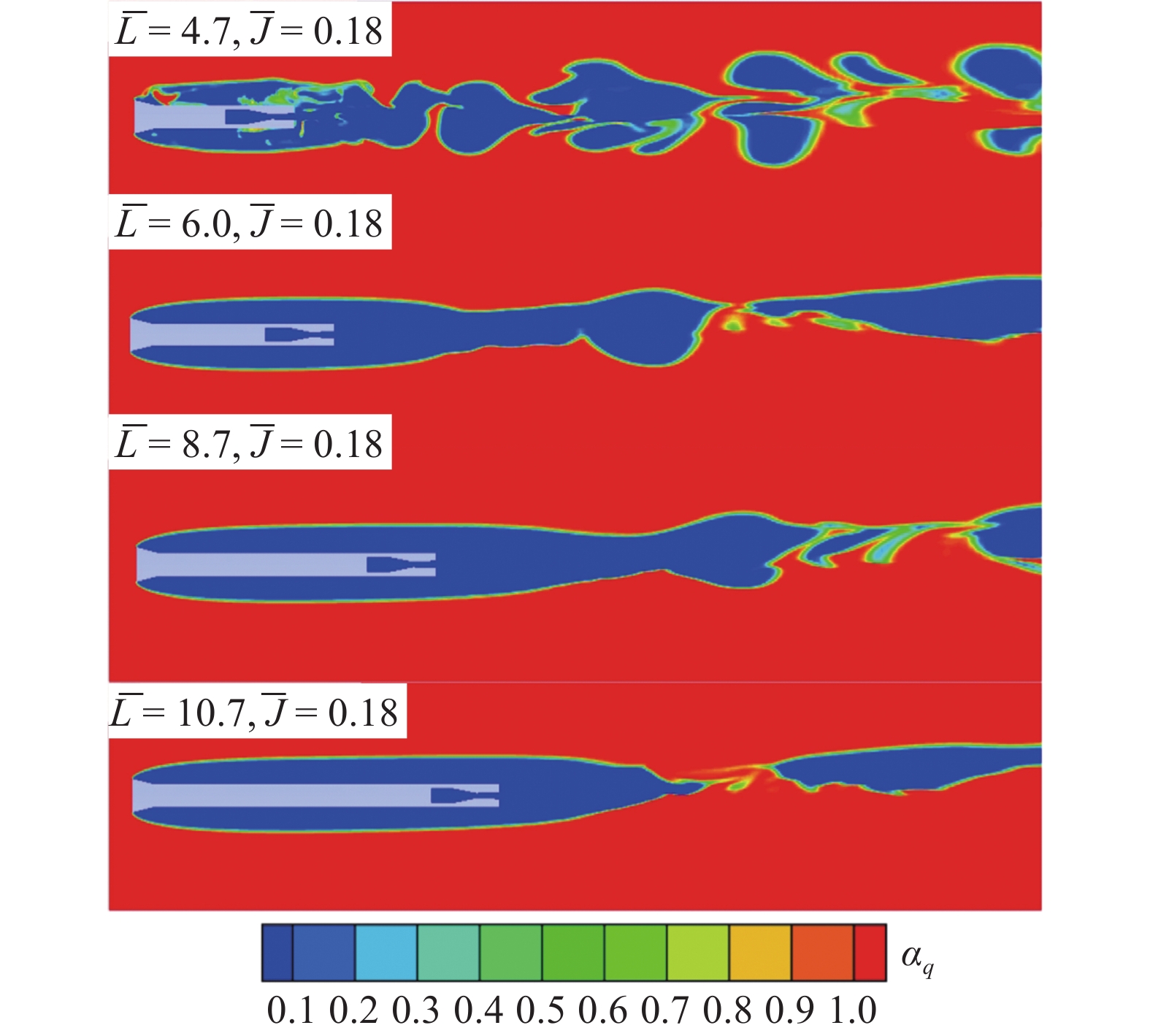
随着模型长度增加, 通气空泡体积分数云图



Figure
14.
Volume fraction cloud plot for the caity as the model length increases



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
对比不同射流强度条件下空泡内压力随时间的变化(续)



Figure
13.
The change of pressure inside the caivty with time is compared under different jet intensity conditions (continued)



下载:
全尺寸图片
幻灯片

2.2
不同模型长度计算结果分析

2.2.1
相对位置对空泡稳定性的影响

仿真计算过程中同时也对比了4个不同的模型长度条件下空泡射流相互作用的结果. 图14展示了随着模型长度的增加, 通气空泡形态的变化. 除了第一个工况$ overline L = 4.7 $, 空泡失稳以外, 其他3个工况, 空泡都保持稳定状态. 原因是射流与空泡头部相对距离越小, 空泡内液体回射流越容易冲击空泡头部界面, 导致空泡越容易失稳.

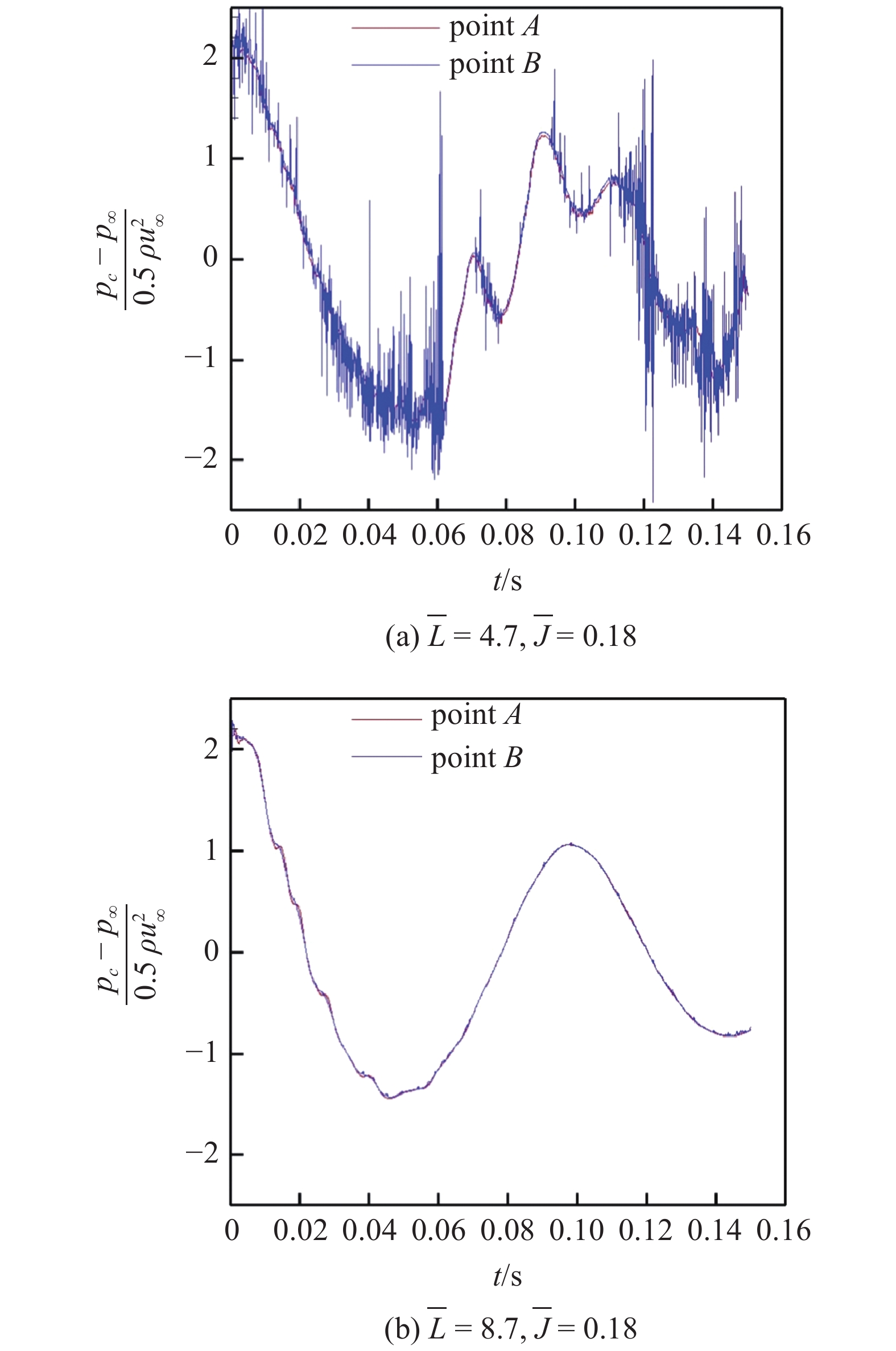
图15对比了射流强度为$ overline L = 4.7 $和$ overline L = 8.7 $两种工况条件下, 空泡内部压力随时间的变化. 前者空泡内存在液体回射流, 空化器附近压力和喷管出口压力变化的趋势一致, 但是喷管出口压力波动的频率和幅值要大很多. 后者空泡为稳定状态, 空化器附近压力和喷管出口压力变化完全一致. 气体的可压缩性是空泡振荡的物理基础, 说明此时空泡的界面完整, 气体的可压缩性不明显, 封闭空间内压力变化具有一致性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
对比不同模型长度条件下空泡内压力随时间的变化



Figure
15.
The change of pressure inside the caivty with time is compared under different model length conditions



下载:
全尺寸图片
幻灯片


特别注意的是当射流强度一定时, 随着模型长度的增加, 液体回射流并没有产生. 分析原因为, 模型长度越长, 在空泡夹断后空泡尾部越容易保持尖尾型. 假定尾喷流作用下空泡横截面仍然保持椭圆曲线, 长半轴为$ 0.5(L + {L_t}) $, 短半轴为$ {R_{max }} $, 如图16所示, 其中$ {R_{max }} $代表空泡最大半径, $ L $为模型长度, $ {L_t} $为喷管出口到空泡夹断处的距离长度. 从图12数值仿真的结果得到, $ {R_{max }} $近似相等. 椭圆曲线在短半轴一致条件下, 长半轴越长, 曲线的曲率变化越小. 即随着模型长度的增加, 空泡尾部的夹角倾向于减小, 抑制液体回射流的形成. 另外液体射流向前运动过程中, 沿着模型壁面, 动能存在一定的损耗, 模型越长, 液体射流到达空化器附近损耗的能量也越大, 对空泡界面的影响也将减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
尾喷流作用下空泡尺寸示意图



Figure
16.
Sketch map of cavity size under the action of a tail jet



下载:
全尺寸图片
幻灯片


总的来说, 模型长度越小, 喷管出口离空化器越近, 空泡内尾流扰动越容易传播至空化器, 界面的初始扰动也越大, 界面越容易破坏.

2.2.2
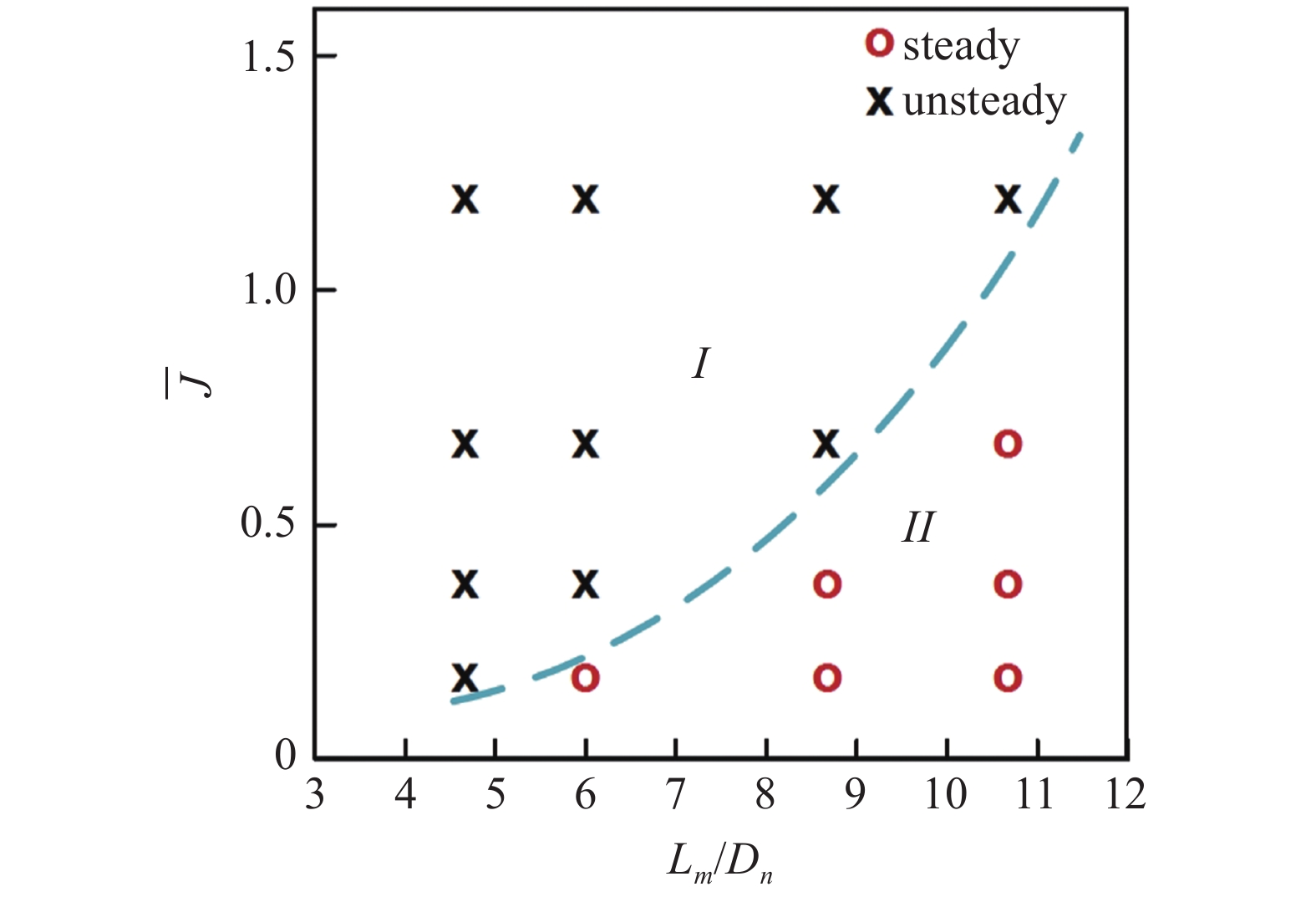
射流作用下空泡稳定和失稳的临界条件

通过上述分析可以得到空泡失稳机制主要取决于两个无量纲参数 $ overline J $和$ overline L $. $ overline J $为无量纲射流动量, 数学形式为射流推力和空化器阻力之比, 代表射流强度. $ overline L $为无量纲模型长度, 数学形式为模型长度和空化器直径之比, 代表射流在通气空泡内的的相对位置. $ overline J $越大, $ overline L $越小, 空泡越容易失稳. 在此基础上, 进一步总结了算例中出现稳定和失稳两种状态的临界曲线, 如图17所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
射流作用下空泡稳定和失稳的临界条件



Figure
17.
Critical conditions for the stable and unstable cavity under tail jet action



下载:
全尺寸图片
幻灯片

3.
尾喷流作用下稳定空泡的闭合位置理论分析

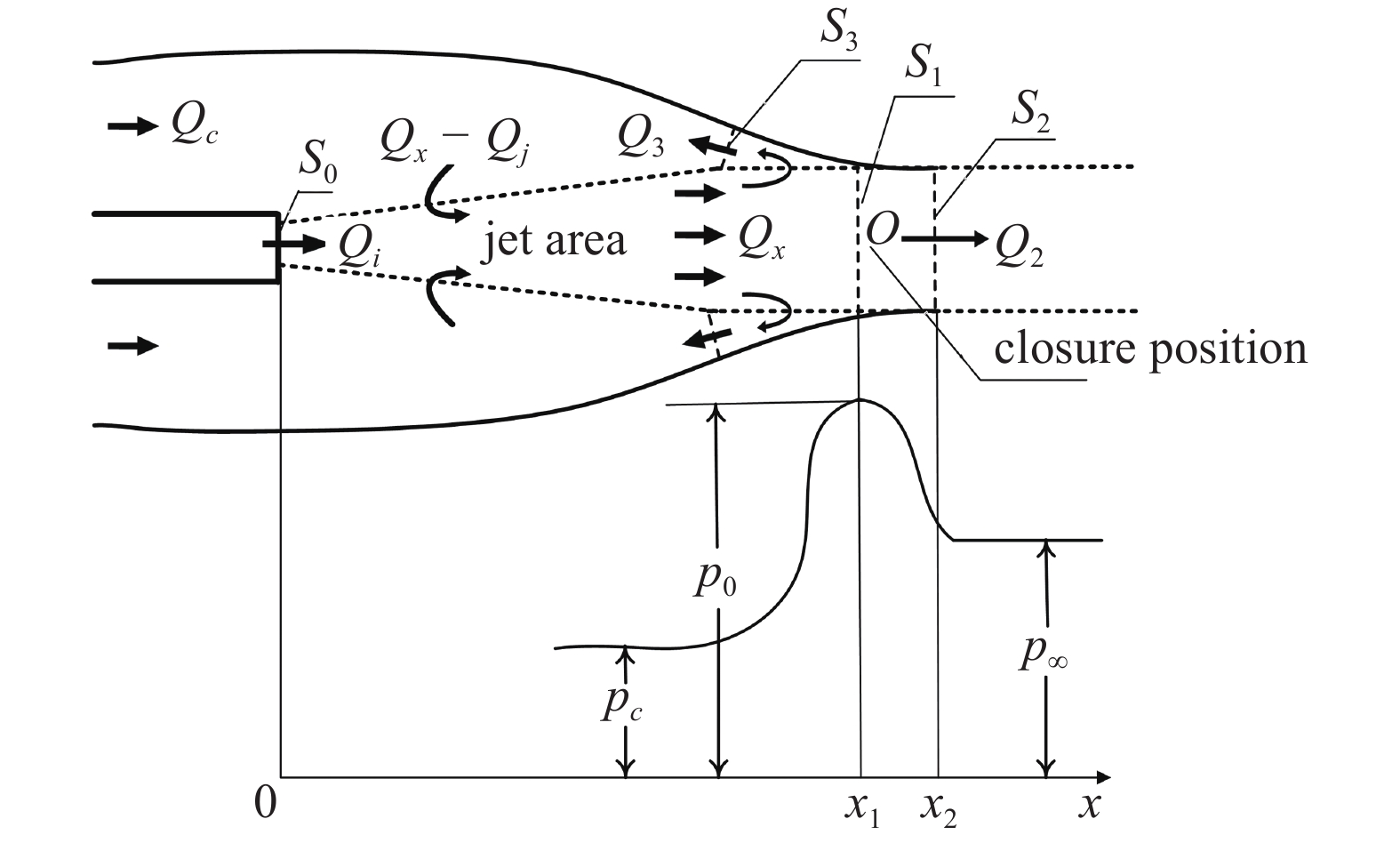
射流在空泡内表现为受限射流, 其卷吸效应的强度一定程度上受到空泡形态变化的影响. 结合经典的射流动力学理论, 对Paryshev理论^[14]推导过程中的连续方程加以合理修正, 并考虑空泡内气体和射流气体之间的湍流扩散和卷吸效应带来的射流速度衰减, 构建空泡射流结构判别模型. 射流作用下空泡内部质量流动和压力分布如图18所示. $ {Q_j} $ 代表喷管出口射流流量, $ {Q_2} $, $ {Q_3} $ .分别代表射流带走和回流的流量. $ {W_c} $ 代表空化器阻力. 空泡截面面积变化可由独立扩张原理^[29]得到

$$ {S_1} - {S_2} = frac{{{W_c}}}{{{p_0} - {p_infty }}} $$

(22)

其中, $ {S_0} $代表喷管出口面积, $ {S_{text{1}}} $和$ {S_{text{2}}} $分别代表空泡闭合处和闭合处下游附近空泡截面面积, $ {S_{text{3}}} $代表射流回流截面面积(如图18所示). $ {U_0} $,$ {U_2} $,$ {U_3} $为对应位置处的速度. 不考虑气体可压缩性, 根据动量方程

$$ { ho _{{ m{jet}}}}({S_2}U_{_2}^2 - {S_3}U_3^2 - {S_0}U_0^2) = {p_c}{S_1} - {p_0}({S_1} - {S_2}) - {p_infty }{S_2} $$

(23)

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-18.jpg'"
class="figure_img
figure_type1 bbb " id="Figure18" />



图
18
射流作用下空泡内部质量流动和压力分布示意图



Figure
18.
Schematic of the cavity internal mass flow and pressure distribution with a gasous jet



下载:
全尺寸图片
幻灯片


空泡稳定闭合以后, 空泡流入和流出的气体质量应该守恒(前提是射流作用下空泡为稳定状态, 因为一旦失稳, 破碎界面带来气体损失不可忽视), 而通气的流量远远小于射流流量, 可以忽略, 得到连续方程, $ {Q_j} = {Q_2} $, 即

$$ {S_0}{U_0} = {S_2}{U_2} $$

(24)

假定射流中心轴线速度衰减和射流卷吸周围气体流量都呈线性关系^[30]

$$ {U_2} = frac{{{k_1}{U_0}}}{{overline x }} $$

(25)

$$ frac{{{Q_x} - {Q_j}}}{{{Q_j}}} = {k_2}overline x + {k_3} $$

(26)

通过上面4个方程式(22) ~ 式(25), 假设射流回流的速度大小近似等于射流在闭合点下游的速度, $ {U_3} approx {U_2} $, 并且空化数

$$ begin{aligned} & sigma = dfrac{{2left( {{p_infty } - {p_c}} ight)}}{{{ ho _infty }U_infty ^2}} < < 1 & overline J = dfrac{{{ ho _0}U_0^2{S_0}}}{{{W_C}}} end{aligned}$$

由此可以得到无量纲的回流流量为

$$ overline {{Q_3}} = frac{{{Q_3}}}{{{Q_j}}} = left( {frac{1}{{overline J {k_1}}} - frac{1}{{{k_1}}}} ight)overline x + 1 $$

(27)

根据空泡内部质量流量平衡, 在空泡闭合处射流卷吸空泡内气体流量应该等于射流的回流流量, 即可得到尾喷射流作用下, 空泡的理论闭合位置离喷管出口距离$ {overline L _t} $可表示为

$$ qquadoverline {{Q_3}} = frac{{{Q_x} - {Q_j}}}{{{Q_j}}} $$

(28)

$$ qquadleft( {frac{1}{{overline J {k_1}}} - frac{1}{{{k_1}}}} ight)overline {{L_t}} + 1 = {k_2}overline {{L_t}} + {k_3} $$

(29)

$$qquad overline {{L_t}} {text{ = }}fleft( {bar J} ight) $$

(30)

对于射流作用下空泡稳定的工况, 空泡尾部闭合位置到喷管出口的无量纲长度$ {overline L _t} $只与$ overline J $有关, 与模型长度无关. 此结论得到数值仿真和实验结果支撑, 如图19所示, 不同模型长度条件下, 空泡闭合位置到喷管出口长度, 实验和仿真结果对比误差均在8%以内. 在水洞中开展的验证实验, 水洞中流速为5 m/s, 模型采用头部支撑方式. 模型内设置两路通道, 一路在头部空化器处通气形成通气空泡, 一路在尾部通气形成射流.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-346-19.jpg'"
class="figure_img
figure_type1 bbb " id="Figure19" />



图
19
不同模型长度条件下空泡尾部闭合位置到喷管出口长度的实验结果



Figure
19.
Experimental and numerical results on the length from the nozzle outlet to the closed position under differert model length



下载:
全尺寸图片
幻灯片

4.
结论

本文利用VOF耦合level set界面追踪方法, 考虑气体的可压缩性, 展开了一系列改变射流强度和模型长度的通气空泡和超音速尾射流相互作用的数值仿真, 重点分析了通气空泡的稳定性和闭合位置. 数值结果表明:

(1)在超音速尾射流作用下, 通气空泡的界面会经历膨胀、颈缩、断裂回缩过程, 然后开始周期性震荡泄气. 通气空泡的形态长度相较于无射流条件下大大减小.

(2)空泡失稳过程中, 空泡尾部产生液体回射流会顺着气体回流路径向前冲击空化器附近界面. 其产生过程与空泡断裂时尾部形态紧密联系, 并表现出上下不对称的特点, 更易形成于空泡尾部上表面.

(3)气液界面两侧强剪切和重力作用诱导了液体射流的形成, 而这种空泡失稳机制主要取决于两个无量纲参数 $ overline J $(射流推力和空化器阻力之比)和$ overline L $ (模型长度和空化器直径之比), $ overline J $越大, $ overline L $越小, 空泡越容易失稳. 在此基础上, 进一步总结了不同工况下出现稳定和失稳两种状态的临界曲线.

(4)空泡越稳定, 喷管出口的压力波动的幅度和频率就越低, 通气空泡能为火箭发动机提供稳定的工作环境.

(5)对于空泡失稳的工况, 空泡闭合在喷管出口; 而空泡稳定的工况, 喷管出口到闭合位置的长度只与$ overline J $有关, 与模型长度无关.